Nonadiabatic Molecular Dynamics on Graphics Processing Units: Performance and Application to Rotary Molecular Motors

Abstract

Nonadiabatic molecular dynamics (NAMD) simulations of molecular systems require the efficient evaluation of excited-state properties, such as energies, gradients, and nonadiabatic coupling vectors. Here, we investigate the use of graphics processing units (GPUs) in addition to central processing units (CPUs) to efficiently calculate these properties at the time-dependent density functional theory (TDDFT) level of theory. Our implementation in the FermiONs++ program package uses the J-engine and a preselective screening procedure for the calculation of Coulomb and exchange kernels, respectively. We observe good speed-ups for small and large molecular systems (comparable to those observed in ground-state calculations) and reduced (down to sublinear) scaling behavior with respect to the system size (depending on the spatial locality of the investigated excitation). As a first illustrative application, we present efficient NAMD simulations of a series of newly designed light-driven rotary molecular motors and compare their S₁ lifetimes. Although all four rotors show different S₁ excitation energies, their ability to rotate upon excitation is conserved, making the series an interesting starting point for rotary molecular motors with tunable excitation energies.

1. Introduction

Nonadiabatic processes such as electronic excitations,¹ radiationless transitions,² and electron transfer³ are of key importance in chemistry and biology. One of the most prominent examples in these fields is the rhodopsin protein, whose chromophore undergoes a photoisomerization when exposed to light.⁴ This energy conversion of light to mechanical motion has inspired chemists to design synthetic light-driven rotary molecular motors,^5,6 for which Bernard Feringa was awarded the Nobel Prize in chemistry in 2016 together with Jean Pierre Sauvage and Sir James Fraser Stoddart.⁷ The description of theses nonadiabatic processes is an ongoing challenge in modern quantum chemistry (e.g., ref (8)). This is mainly due to the fact that (1) excited states have to be taken into account and (2) the dynamics of the nuclei need to be considered.

To tackle the first challenge, several quantum-chemical methods have been developed. Examples include the complete active space self-consistent field (CASSCF) method,⁹ the algebraic-diagrammatic construction (ADC(2)),¹⁰ several coupled cluster methods (e.g., CC2),¹¹ and time-dependent density functional theory (TDDFT).^12,13 The latter serves (despite its well-known limitations using today’s functionals^13,14) as a good compromise between effort and accuracy.^15,16 As a consequence of this, not only excited-state energies but also excited-state gradients¹⁷ and nonadiabatic coupling vectors (NACVs)¹⁸⁻²⁹ have been implemented to provide access to molecular properties at the TDDFT level of theory. Having excited-state energies and properties at hand, trajectory surface hopping (TSH)^30,31 is a straightforward way to conduct nonadiabatic molecular dynamics (NAMD) simulations including several electronic states.

Despite many advances in the field of NAMD³²⁻³⁴ and their broad field of application,³⁵⁻⁴⁴ it remains difficult or even impossible to investigate large molecular systems. The reason for this is that TSH requires, because of its stochastic nature, a large set of independent trajectories including many time steps, which involve expensive (even at the TDDFT level of theory) excited-state energy and property calculations. One way to accelerate NAMD simulations is the use of exciton models.⁴⁵ Another approach is the use of graphics processing units (GPUs) in addition to central processing units (CPUs) for the calculations. It was shown that this leads to significant speed-ups for ground-state energy and forces evaluations⁴⁶⁻⁵³ and was also successfully applied to excited-state energies and properties^45,54−56 as well as ab initio multiple spawning^57,58 and NAMD^59,60 simulations.

In this work, we present efficient NAMD simulations with TDDFT energies, gradients, and NACVs calculated on hybrid CPU/GPU architectures using the FermiONs++ program package.⁵⁰⁻⁵² We start with a brief summary of the theory behind TSH as well as TDDFT energies, gradients, and NACVs in Section 2 and discuss their implementation on GPUs, featuring the hybrid CPU/GPU engine⁵² for the two-electron integrals as well as the preselective screening procedure for the evaluation of exchange kernels.^50,51 Computational details are given in Section 3. In Section 4, we discuss the accuracy and the performance of our GPU-based excited-state routines, investigating the scaling of our integral evaluations and contractions. We show timings for selected molecules containing more than 500 atoms. As a prototypical application, we investigate the photoinduced rotation of four newly designed rotary molecular motors via NAMD in Section 5, followed by a conclusion and an outlook.

2. Theory

All equations in this section use the standard notation for orbitals: i, j, k... denote occupied, a, b, c... denote virtual, and p, q, r... denote arbitrary molecular orbitals, while μ, ν, λ... denote basis functions. I, J, ... denote different electronic states. v_xc and f_xc are the first- and second-order exchange-correlation functional derivatives, respectively. c_x is the amount of exact exchange. F and S are the Kohn–Sham and the overlap matrices, respectively. P is the ground-state density, and h is the one-electron core Hamiltonian matrix. The two-electron integrals are written using Mulliken notation (..|..). Superscript ξ denotes derivatives with respect to the nuclear coordinates, and * and † symbolize complex conjugation and adjungation, respectively. For the sake of simplicity, we use the same symbol for matrices in the atomic orbital (AO) and molecular orbital (MO) bases with different indices (e.g., P_μν vs P_pq).

2.1. Trajectory Surface Hopping

In nonadiabatic molecular dynamics (NAMD), the electronic time-dependent wave function of the system is assumed to be a linear combination of the time-independent electronic wave functions of the individual electronic states weighted by the state amplitudes (c⃗)

1

where x represents nuclear coordinates and {r} is the set of electronic coordinates. Having the state energies (ω_I, see Section 2.2) and nonadiabatic coupling vectors (NACVs, τ_I → J^ξ, see Section 2.4) at hand, it is possible to propagate the state amplitudes along with the nuclei during the molecular dynamics (MD) simulation using a unitary propagator:³⁶

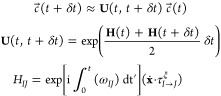2

Here, ω_JI is the energy difference between two states (ω_J – ω_I). The applied δt for the propagation of c⃗ is normally 3 orders of magnitude smaller than the time step of the MD simulation (Δt).³¹ In the fewest-switches surface hopping algorithm,^30,31c⃗ is used to calculate the probability g_I → J^{t → t + Δt} of the system switching from its current state I to another state J at every time step:

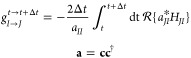3

If a random number between zero and one exceeds g, then the MD simulation is continued on the potential energy surface of state J and the nuclear velocity is rescaled along τ_I → J^ξ. Observables (e.g., lifetimes of states or relaxation pathways) can be drawn from ensembles of trajectories using a different set of random numbers. In the following sections, we will briefly summarize the calculation of the necessary ingredients of TSH (excited-state energies, gradients, and NACVs) at the time-dependent density functional theory (TDDFT) level of theory.

2.2. Excited-State Energies

Excitation energies can be calculated from linear response TDDFT by solving the TDDFT or the random phase approximation (RPA) equation^12,61,62

4

A ± B are the orbital rotation Hessians

5

6

with ϵ_p being the energy of orbital p. X_I and Y_I are the transition densities for excitation and de-excitation, respectively. Neglecting B is known as the Tamm–Dancoff approximation (TDA) of TDDFT,⁶³ simplifying eq 4 to

7

Please note that eqs 4 and 7 are equivalent to the time-dependent Hartree–Fock (TDHF) and configuration interaction singles (CIS) equations, respectively, when c_x is set equal to 1 and all exchange-correlation terms are neglected. TDA is computationally less demanding than TDDFT because fewer two-electron integrals have to be evaluated. It may also be more suitable for NAMD simulations because it is more stable (regarding its convergence) and thus typically delivers better results than TDDFT in the vicinity of conical intersections involving the ground state.^39,64

TDDFT is nowadays widely used for the calculation of excitation energies, being a good compromise between accuracy and computational cost.^15,16 Shortcomings are, however, the inability to calculate double excitations and the poor description of charge-transfer excitations.^13,14 To tackle the latter, range-corrected functionals (e.g., ωB97⁶⁵) have been introduced.

2.3. Excited-State Energy Gradients

To determine the energy gradient of an excited state I, one has to calculate the change in the excitation energy with respect to the nuclear coordinates (ω_I^ξ). The final equation in the AO basis has been derived by Furche et al.¹⁷

8

The calculations of the relaxed difference density matrix (P_I), the energy-weighted difference density matrix (W_I), and the two-particle difference density matrix (Γ_I) are shown in the Appendix. The first two require an iterative solution of a Z-vector equation.¹⁷R_I is X_I + Y_I or X_I in the case of TDDFT or TDA, respectively.

2.4. Nonadiabatic Coupling Vectors

The NACV between two states (I and J) is defined as

9

It thus describes the change of the overlap of the wave functions of I and J with respect to the nuclear coordinates. The first formulation of the NACV involving the ground state (τ_0 → I^ξ) derived by Chernyak and Mukamel¹⁸ was corrected for finite basis set effects by Send et al.²³ in 2010:

10

Equations for the density matrices (P_0I, W_0I, and Γ_0I) are again given in the Appendix. They can be calculated directly from the TDDFT transition densities so that no Z-vector equation needs to be solved. S_μν^[A]ξ denotes an antisymmetric overlap derivative

11

whereas γ_0I is defined as

12

with L_I being X_I – Y_I or X_I in the case of TDDFT or TDA, respectively.

The calculation of NACVs between two excited states has been tackled by many publications showing expressions based on linear and quadratic response at different levels of theory.^{25,26,29,66−71} The main conclusion is that the use of quadratic response theory leads to unphysical poles when the energy difference between excited states matches the excitation energy of another state.⁶⁶⁻⁷⁰ The use of linear response theory or the so-called pseudowave function approach^25−27,29 is therefore recommended. The resulting equation in the AO basis is as follows:

13

Equations for the density matrices (P_IJ, W_IJ, and Γ_IJ) can again be found in the Appendix. γ_IJ is defined as

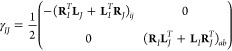14

It was shown by Fatehi et al.²⁵ that the antisymmetric overlap derivatives (eq 11) introduce translational variance into the NACV calculations. Neglecting these terms in eqs 10 and 13 is equivalent to adding electron-translational factors (ETFs). However, trajectory surface hopping (TSH) simulations using NACVs with and without ETFs lead to nearly identical results for larger molecular systems.⁷²

2.5. Graphics Processing Units

Graphics processing units (GPUs) significantly accelerate quantum-chemical calculations because they allow for an efficient evaluation and contraction of two-electron integrals (eq 15) and their derivatives with respect to the nuclear coordinates (eq 16).⁴⁶⁻⁵²

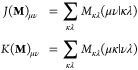15

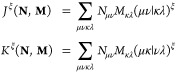16

J and K denote the Coulomb and exchange parts, respectively, and M and N denote general density matrices. For the Coulomb part, large speed-ups can be observed when the J-engine^73,74 is applied to the rearranged shell-pair data.⁴⁷ To see comparable speed-ups for the exchange part, we apply an additional preselective screening (preLinK):^50,51

17

18

It determines the significant shell pairs (those with an expected value above the given thresholds ϑ_pre and ϑ_pre^∇) before their distribution to and calculation on the GPUs. The two-electron integral evaluation can be done even more efficiently when the workload is spread among both GPUs and CPUs.⁵²

In ground-state calculations, M and N are solely the ground-state density (P), whereas for excited states M and N can additionally be P_I, R_I, or L_I. However, the discussed procedure (shell pair rearrangement, J-engine, and preLinK) is still valid and can easily be adapted to excited-state routines when keeping in mind that M is not always equal to N and may be nonsymmetric.

3. Computational Details

3.1. General Remarks

The FermiONs++ program package⁵⁰⁻⁵² was used for all calculations presented in this work. It was compiled using the Intel compiler (2019),⁷⁵ and the Intel Math Kernel Library (MKL). Routines on AMD GPUs were compiled with the AMD APPSDK compiler. In addition, LibXC library v4.0.1^76,77 was used. In all calculations, we used the gm5 grid⁷⁸ (with the modified Becke weighting scheme described in ref (78)) and tight thresholds for the SCF convergence (ϑ_SCF = 10^–7 using the FP-commutator), the integrals (ϑ_INT = 10^–10), and the Z-vector equation convergence (ϑ_Z = 10^–5). Throughout all calculations, we neglected the symmetry of the molecules and solely calculated singlet excitations. Excited-state energies, gradients, and nonadiabatic coupling vectors (with electron transition factors) at the TDDFT level of theory were calculated using eqs 4, 8, 10, and 13, respectively.

3.2. Preparation and Calculation of Systems I, II, III_n, IV_n, V, VI, and VII

To illustrate the performance and/or accuracy of our implementation on GPUs, we use protonated formaldimine (I), the Schiff base of retinal (II), a series of linear polyethynes (III_n) and dialkylethenes (IV_n), a motorized nanocar (without “wheels”, V),⁷⁹ and one (VI) and three (VII) pores of a covalent organic framework⁸⁰ as example molecules. The structures of I, II, and V have been optimized at the PBE0⁸¹⁻⁸⁴/def2-SVP^85,86 level of theory, while III_n and IV_n have not been optimized to maintain their linear structures. VI and VII have been prepared according to ref (80). All structures are available at https://www.cup.uni-muenchen.de/pc/ochsenfeld/download/.

TDDFT energies and properties of I, II, III_n, IV_n, V, VI, and VII were calculated at the PBE0/def2-SVP or PBE/def2-TZVP level of theory. We used tight thresholds for preLinK (ϑ_pre = 10^–4), the preLinK gradient (ϑ_pre^∇ = 10^–10), and the TDDFT convergence (ϑ_TDDFT = 10^–6). For I, II, III_n, IV_n, V, VI, and VII, four, six, five, three, six, seven, and seven states were taken into account, respectively.

When investigating the accuracy, we use a calculation performed on CPUs with tight thresholds (ϑ_TDDFT = 10^–7) as a reference. To allow for a fair comparison, we employed the continuous fast multipole method (CFMM)^87,88 and the LinK scheme^89,90 for Coulomb and exchange kernels (and their derivatives) on CPUs when comparing CPU and GPU performance. Coulomb and exchange kernels on GPUs were calculated with the J-engine^73,74 and the preLinK scheme,^50,51 respectively. Timings of integral evaluations and entire routines were determined as an average over five independent calculations on two Intel Xeon CPU E5 2640 v4 @ 2.20 GHz (20 threads) CPUs and four AMD FirePro 3D W8100 GPUs. The scaling behavior is determined as the slope of the corresponding log–log plots (Supporting Information) using the timings of III_n and IV_n with n = 40, 50, 75, 100. The parallel efficiency is determined as the ratio between the measured and ideal speed-ups.

3.3. Preparation and Calculation of the Rotary Molecular Motors

The structures of the four rotary molecular machines (C, N, S, and O) have been optimized at the ωB97⁶⁵/def2-SVP level of theory. Excited-state properties and timings were calculated at the TDA (ωB97/def2-SVP) level of theory using accurate thresholds (ϑ_pre = 10^–3, ϑ_pre^∇ = 10^–10, and ϑ_TDDFT = 10^–5). NAMD simulations were conducted at the same level of theory. The propagation of the nuclei was calculated using the Velocity Verlet algorithm.^91,92 The extended Lagrangian method⁹³ for the extrapolation of ground-state density was used to accelerate SCF convergence. Transition densities and relaxed difference densities of the previous step were used as guesses for the TDA and Z-vector equation, respectively.

Twenty initial geometries and velocities (available at https://www.cup.uni-muenchen.de/pc/ochsenfeld/download/) were drawn from a 5 ps ground-state NVT simulation (200 fs equilibration, 0.2 fs step size, velocity rescaling thermostat⁹⁴) at the same level of theory. From each initial condition, five independent (different series of random numbers) NAMD simulations were conducted for 1 ps (0.2 fs step size) without equilibration, thermostat, or decoherence correction, starting at the first excited singlet state (S₁). At every step of the simulation, the overall rotation and translation of the molecule was removed. Three excited states were taken into account, whereas only the coupling vector from the ground state to the first excited state was calculated and used for the propagation of the state amplitudes (eq 2) and the calculation of the hopping probability (eq 3).

4. Performance

4.1. Accuracy and Thresholds

We start with an analysis of the errors of excited-state energies and properties introduced by their calculation on GPUs and the use of the preLinK scheme^51,52 for integrals and integral derivatives. Therefore, we compare calculations of the smallest Schiff base (protonated formaldimine, CH₂NH₂⁺, I) and the Schiff base of retinal (C₂₀H₃₀N⁺, II) with GPUs and preLinK to calculations on CPUs without prescreening or the continuous fast multipole method (CFMM). (For computational details, see Section 3.2.) The mean absolute errors for different thresholds are listed in Table 1.

Table 1. Mean Absolute Errors (MAE, in Atomic Units) of Excitation Energies (ω_I), Gradients (ω_I^ξ), and Nonadiabatic Coupling Vectors (τ_I→J) of Protonated Formaldimine (I) and the Schiff Base of Retinal (II) Calculated at the PBE0/def2-SVP Level of Theory on GPUs, Employing the preLinK Scheme and Using Different Thresholds for preLinK (ϑ_pre), the preLinK Gradient (ϑ_pre), and the TDDFT Convergence (ϑ_TDDFT)^a.

screening thresholds and convergence criteria
ϑpre	10–3	10–4	10–4	10–5	10–5	10–5	10–5	10–5
ϑpre∇	10–11	10–11	10–11	10–11	10–11	10–9	10–10	10–11
ϑTDDFT	10–5	10–5	10–6	10–6	10–7	10–7	10–7	10–7

I
MAE(ωI)	2.2 × 10–4	2.2 × 10–4	8.8 × 10–5	8.8 × 10–5	2.3 × 10–6	2.3 × 10–6	2.3 × 10–6	2.3 × 10–6
MAE(ω2ξ)	5.8 × 10–5	5.8 × 10–5	3.7 × 10–5	3.7 × 10–5	6.5 × 10–6	6.7 × 10–6	6.6 × 10–6	6.5 × 10–6
MAE(τ0→1)	5.7 × 10–4	5.7 × 10–4	1.2 × 10–4	1.2 × 10–4	9.2 × 10–5	8.8 × 10–5	9.1 × 10–5	9.2 × 10–5
MAE(τ1→2)	1.0 × 10–3	9.1 × 10–4	4.7 × 10–4	4.7 × 10–4	2.8 × 10–4	9.2 × 10–4	5.5 × 10–4	2.8 × 10–4

II
MAE(ωI)	1.9 × 10–4	1.9 × 10–4	9.6 × 10–5	9.6 × 10–5	1.1 × 10–5	1.1 × 10–5	1.1 × 10–5	1.1 × 10–5
MAE(ω2ξ)	2.8 × 10–5	2.8 × 10–5	1.2 × 10–5	1.2 × 10–5	3.1 × 10–6	3.8 × 10–6	3.2 × 10–6	3.1 × 10–6
MAE(τ0→1)	1.7 × 10–3	1.7 × 10–3	7.5 × 10–4	7.5 × 10–4	2.0 × 10–4	2.0 × 10–4	2.0 × 10–4	2.0 × 10–4
MAE(τ1→2)	8.9 × 10–4	8.9 × 10–4	3.8 × 10–4	3.8 × 10–4	1.1 × 10–4	1.2 × 10–4	1.1 × 10–4	1.1 × 10–4

^aA calculation on CPUs with ϑ_TDDFT = 10^–7 and without CFMM or preLinK is used as a reference. Throughout this work, we will use accurate (ϑ_pre = 10^–3, ϑ_pre^∇ = 10^–10, and ϑ_TDDFT = 10^–5) or tight thresholds (ϑ_pre = 10^–4, ϑ_pre = 10^–10, and ϑ_TDDFT = 10^–6).

The choice of the preLinK threshold (ϑ_pre) for excited-state calculations should always depend on the applied convergence threshold for the TDDFT equation (ϑ_TDDFT). If the chosen threshold is too loose, then the iterative solution of the TDDFT equation does not converge (especially for large molecular systems), while a ϑ_pre that is too tight does not improve the result when ϑ_TDDFT is not adjusted accordingly (Table 1). The latter is also attributed to the small effect of preLinK on these relatively small systems.^50,51 In our calculations with the FermiONs++ program package, the “ideal” ϑ_pre is 2 orders of magnitude larger than ϑ_TDDFT. A tightening of these two parameters (left side of Table 1) systematically leads to smaller errors. However, the errors in the coupling vectors of the large system do not fall below 10^–4 a.u., marking the numerical limit of these second- to third-order properties. The use of the tight thresholds (ϑ_TDDFT = 10^–6, ϑ_pre = 10^–4) should thus, in general, be sufficient because all errors are below 10^–3 a.u. A looser preLinK threshold (ϑ_pre = 10^–3 a.u.), which is expected to give μH accuracy for ground-state properties, is still accurate for excited-state properties and could be used in extensive application calculations such as NAMD simulations, where observables are determined as ensemble averages.

The effect of the preLinK gradient threshold (ϑ_pre^∇) on the error is not straightforward (right side of Table 1). However, we recommend it to be at least as tight as the integral threshold (ϑ_INT = 10^–10). Because the difference between ϑ_pre = 10^–11 and ϑ_pre^∇ = 10^–10 is negligibly small, we apply the latter throughout this work.

4.2. Scaling with the System Size

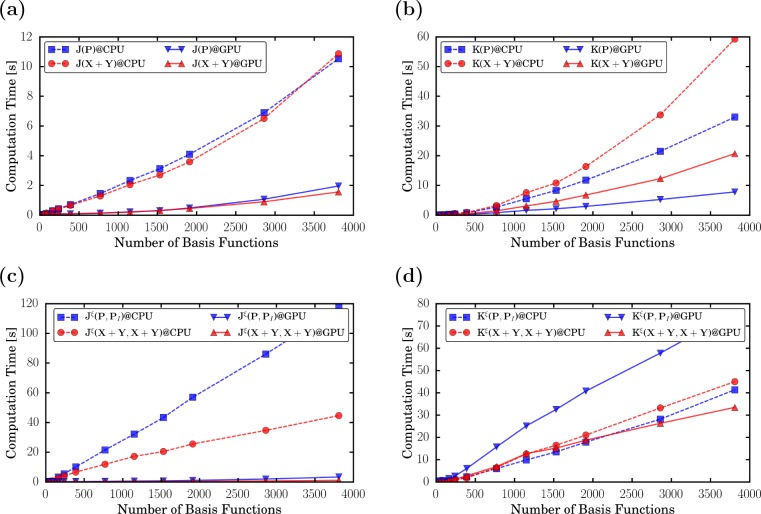
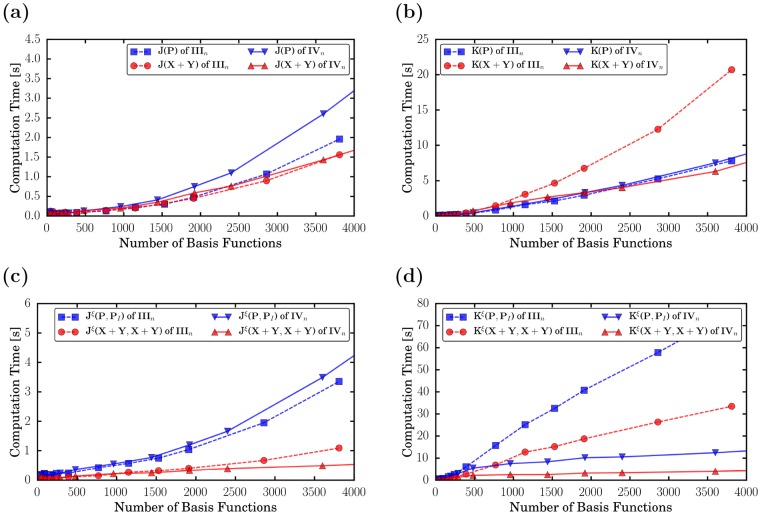
To compare timings on CPUs and GPUs and to investigate the effective scaling behavior of the excited-state integral routines on GPUs, we use integral timings of linear polyethynes (III_n) and dialkylethenes (IV_n) (for structures, see Figure 1). In Figure 2, we compare CPU and GPU timings of Coulomb (Figure 2a,c) and exchange (Figure 2b,d) calculations at the PBE0/def2-SVP level of theory. We show contractions of the ground-state density (J/K(P)), the transition density of the first excited state (J/K(X₁ + Y₁)) (Figure 2a,b), the integral derivatives involving the ground state and the relaxed difference density of the first excited state (J^ξ/K^ξ(P, P₁)), and the transition density of the first excited state (J^ξ/K^ξ(X₁ + Y₁, X₁ + Y₁)) (Figure 2c,d). The same integrals are shown in Figure 3, where we compare the timings of III_n and IV_n on GPUs. The effective scaling behaviors of the integral evaluations are shown in the Supporting Information. Definitions of the integral contractions are given in eqs 15 and 16. Details of the calculations are given in Sections 3.1 and 3.2.

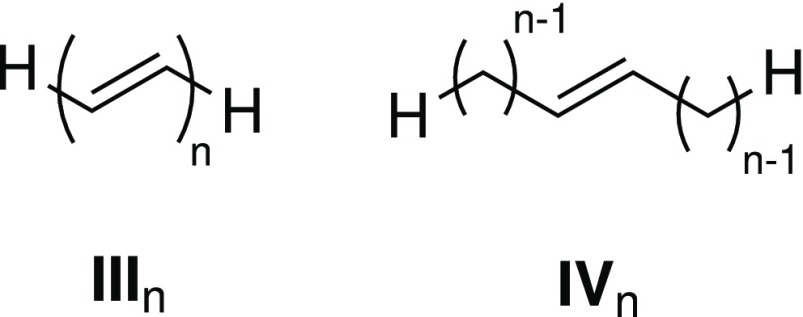
Figure 1.

Structures of the linear polyethynes (III_n) and dialkylethenes (IV_n).

Figure 2.

Timings of (a, c) Coulomb and (b, d) exchange integral evaluations (a, b; eq 15) and their derivatives with respect to the nuclear coordinates (c, d; eq 16) of polyethyne (III_n) with n = 1–100 calculated at the PBE0/def2-SVP level of theory on CPUs (dashed lines) and GPUs (solid lines). For details on the calculations and the computational setup, see Sections 3.1 and 3.2.

Figure 3.

Timings of (a, c) Coulomb and (b, d) exchange integral evaluations (a, b; eq 15) and their derivatives with respect to the nuclear coordinates (c, d; eq 16) of polyethine (III_n, solid line) and dialkylethene (IV_n, dashed line) with n = 1–100 calculated at the PBE0/def2-SVP level of theory on GPUs. For details on the calculations and the computational setup, see Sections 3.1 and 3.2.

For the Coulomb and exchange kernels of the transition densities, we observe similar speed-ups (up to a factor of 5) as for the ground-state kernels (Figure 2a,b). The accelerations of the gradient kernels stem (nearly exclusively) from their Coulomb part, which is extremely efficient on GPUs (Figures 2c). We also see minor speed-ups for K^ξ(X₁ + Y₁, X₁ + Y₁) (Figures 2d). The evaluation of K^ξ(P, P₁) is significantly slower because the GPU routine has to be called twice. This is due to the fact that the analytical exchange evaluation on GPUs⁴⁸⁻⁵¹ does not exploit the full symmetry of the two-electron integral. Please note that this problem can be solved by applying a seminumerical exchange scheme, which is currently developed for GPUs in our group.⁹⁵ For the largest molecule (III₁₀₀), a speed-up of two for the entire determination of an excited-state gradient involving calculations of the ground-state and excited-state energy and gradient is observed. Here, it should be stressed that the linear algebra and the evaluation of the exchange-correlation kernels are performed entirely on CPUs.

When comparing the effective scaling behavior of the Coulomb integrals of III_n (Supporting Information), one can see that the scaling of the GPU integrals is slightly larger than the scaling of the CPU integrals. This is due to the formal quadratic scaling of the J-engine employed on GPUs, in comparison to the (asymptotically linear scaling) CFMM method. This larger scaling behavior is, however, irrelevant as the prefactor of the routines is greatly reduced (Figure 2a,c). The scaling of the exchange integrals is slightly reduced by exploiting the preLinK method on GPUs. We observe ∼1.5 and ∼1.0 scalings for the integrals and the integral derivatives of these system sizes, respectively.

The excitation in III_n is delocalized over the entire molecule, leading to similar scaling behavior for the ground-state and excited-state properties. To show the performance of a system with local excitation, we also investigate IV_n, where only one double bond instead of a conjugated system is excited. This leads to massive speed-ups (Figure 3) of the excited-state exchange integrals and reduces their scaling significantly (Supporting Information). For the exchange integral derivatives, we even observe sublinear scaling behavior as a result of the preLinK screening. The effect on the Coulomb integrals is smaller, mainly because of the fact that these routines take only a few seconds even for the largest investigated molecules.

4.3. Example Calculations

To demonstrate the applicability of our excited-state properties routines in the FermiONs++ program package,⁵⁰⁻⁵² we study four molecules of interest in modern excited-state research and show their timings at the PBE0/def2-SVP and PBE/def2-TZVP levels of theory on GPUs (Table 2). We investigate the Schiff base of retinal (II), a model system of the chromophore in rhodopsin,⁴ a nanocar⁷⁹ (V) using a rotary molecular motor, and one (VI) and three (VII) pores of a covalent organic framework,⁸⁰ which catalyze the formation of hydrogen from water when exposed to light. Details of the calculations and the computational setup are again listed in Sections 3.1 and 3.2.

Table 2. Molecular Structures and Computational Times (t(s)) of the Schiff Base of Retinal (II), a Motorized Nanocar (V), and One (VI) and Three (VII) Pores of a Covalent Organic Framework, Calculating Ground-State Energies (E₀) and Gradients (E₀^ξ), Excited-State Energies (ω_I) and Gradients (ω_I), and Nonadiabatic Coupling Vectors (τ_I→J) at the PBE0/def2-SVP and PBE/def2-TZVP Levels of Theory on GPUs^a.

	II	V	VI	VII
formula	C20H30N+	C51H28S2	C144H102N30	C312H213N69
Natoms	51	81	276	594
PBE0/def2-SVP
t(E0)/step	1.3	4.4	17.8	67.7
t(ω1)/(step and state)	1.6	6.3	34.4	179.5
t(E0ξ)	12.36	54.5	140.9	334.3
t(ω1ξ)	65.4	247.9	668.4	1392.6
t(τ0→1)	24.3	123.4	375.2	914.8
t(τ1→2)	82.7	349.4	959.0	1858.0
PBE/def2-TZVP
t(E0)/step	1.8	1.5	51.5	272.6
t(ω1)/(step and state)	2.1	1.7	30.2	95.3
t(E0ξ)	6.0	5.2	65.3	241.9
t(ω1ξ)	52.5	47.9	576.7	1942.9
t(τ0→1)	12.3	10.1	124.4	377.0
t(τ1→2)	56.1	52.7	523.2	1060.3

^aPlease note that t(E₀) and t(ω₁) are given per step (and state). For details on the calculations and the computational setup, see Sections 3.1 and 3.2.

Table 2 shows that with the presented implementation on GPUs, excited-state properties and dynamics become accessible even for large systems and when applying DFT methods with exact exchange (e.g., PBE0) or triple-ζ basis sets. In our examples, the calculations of excited-state properties at the PBE/def2-TZVP level of theory are even faster than at the PBE0/def2-SVP level of theory mainly due to the fast Coulomb contractions discussed above. The only exception is t(ω₁^ξ) of VII, for which the Z-vector equation converges slowly at the PBE/def2-TZVP level of theory (seven instead of four iterations).

When comparing CPU and GPU timings of the entire calculations, we observe speed-ups of three and eight for VI and VII, respectively. This clearly shows that the use of GPUs becomes more attractive with increasing system size, where the integral evaluations dominate the overall computational time. However, even for relatively small molecule II we already obtain a speed-up of two. These speed-ups exclusively stem from the Coulomb and exchange calculations as the linear algebra and the evaluation of the exchange-correlation kernels are performed entirely on CPUs. The entire calculations of II and VII at the PBE0/def2-SVP level of theory take ∼5 min and ∼5 h, respectively, enabling NAMD simulations of II and the calculation of excited-state properties of VII on a reasonable time scale and yet good accuracy.

4.4. Scaling with the Computational Resources

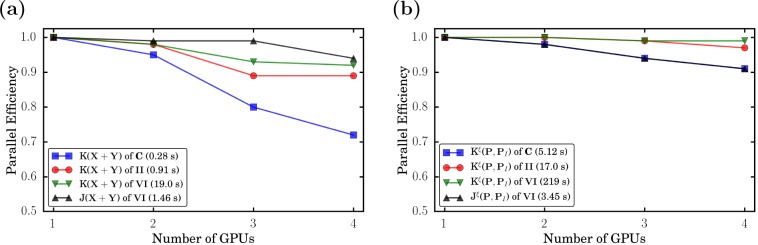
In Figure 4, we show the parallel efficiency of J/K(X_I + Y_I) (Figure 4a) and J^ξ/K^ξ(P, P_I) (Figure 4b) for II, VI, and rotary molecular machine C (C₁₀H₁₃FN), which will be investigated in the next section using up to four GPUs. The Coulomb integrals of II and C are not analyzed because their computational time is too short.

Figure 4.

Parallel efficiency of selected GPU integral routines for the calculations of C, II, and VI. The computational time of the integral evaluation using four GPUs is given in parentheses. For details on the calculations and the computational setup, see Section 3.

Figure 4 again shows the suitability of GPUs for large molecular systems. For the time-consuming integral evaluations of VI, we observe a nearly perfect scaling of >0.9. This also indicates that adding even more GPUs will still lead to decent speed-ups of the calculations. The parallel efficiency observed in the case of the smaller molecules is lower but still remarkable considering that some computational times are <1 s. This strong scaling makes the use of GPUs also attractive for small to medium-sized molecules, as shown in the rotary molecular machine example presented in this work.

5. Illustrative Examples: Rotary Molecular Machines

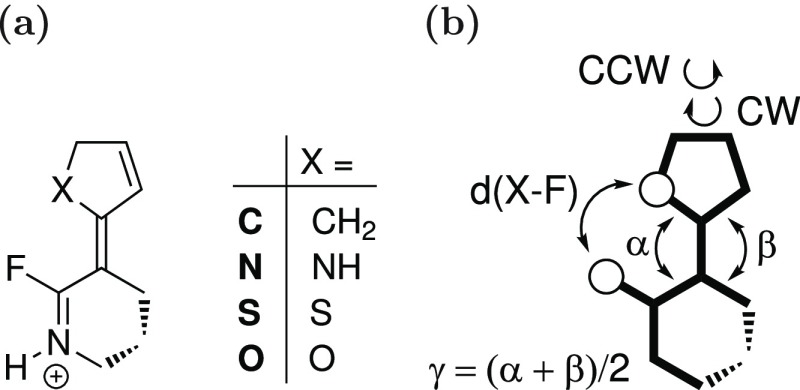
As a prototypical example, we investigate the properties and the dynamics of four newly designed rotary molecular machines. For structures and definitions, see Figure 5. Similar to previous ab initio studies,⁴¹⁻⁴⁴ our machines contain a C=N⁺ motif, which is also present in the chromophore of rhodopsin. Upon excitation, the molecule should rotate around the central C–C double bond. The fluoride substituent should accelerate this rotation because of the steric repulsion, whereas the puckering of the six-membered ring should influence the direction of the rotation.^43,44 Here, we want to investigate the influence of the atom or group X adjacent to the central double bond on the light-driven rotation of the molecule. We use CH₂, NH, S, and O as X denoted as C, N, S, and O, respectively.

Figure 5.

(a) Structures of rotary molecular machines C, N, S, and O and (b) definitions of the X–F distance (d(X–F)), the dihedral angle (γ), and the direction of rotation: clockwise (CW) and counterclockwise (CCW).

When calculating the excited-state properties and dynamics of the rotary molecular machines, we switch to the Tamm–Dancoff approximation (TDA).⁶³ As discussed in Section 2.2, this accelerates the calculation and leads to more stable trajectories close to conical intersections.^39,64 A comparison of the excited-state energies and properties at the TDA and RPA levels of theory is presented in the Supporting Information, where we show mean differences as well as plots of the difference density, the first excited-state gradient, and the NACV between the ground state and the first excited state. We observe an average difference below 10^–2 a.u., with the state ordering and the shape of relaxed difference densities not being affected. The comparison of TDA and CASSCF energies (Supporting Information) also proves the suitability of TDA for the investigated problem. Trends between the systems and the energies close to the conical intersection agree remarkably well. Moreover, we apply the looser accurate thresholds (ϑ_pre = 10^–3, ϑ_pre^∇ = 10^–10, and ϑ_TDDFT = 10^–5) because they introduce only a maximum average error of a few 10^–5 a.u. (Supporting Information). Additional details on the calculations are listed in Section 3.3.

In Figure 6, we show the excitation energies of C, N, S, and O. Changing the substituent has an influence on the bright S₁ state of the rotary molecular motor. While the difference density plots look similar for all molecules, the excitation energies increase (S < C < N < O) and the directions of the gradients and NACVs change slightly. This is due to the different electronegativities of the substituents (C ≈ S < N < O) and the fact that S, N, and O atoms have free electron pairs.

Figure 6.

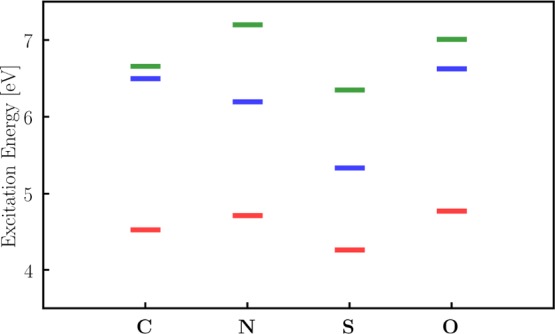
Singlet excitation energies of the four rotary molecular machines (C, N, S, and O) calculated at the TDA (wB97/def2-SVP) level of theory. For details on the calculations, see Section 3.3.

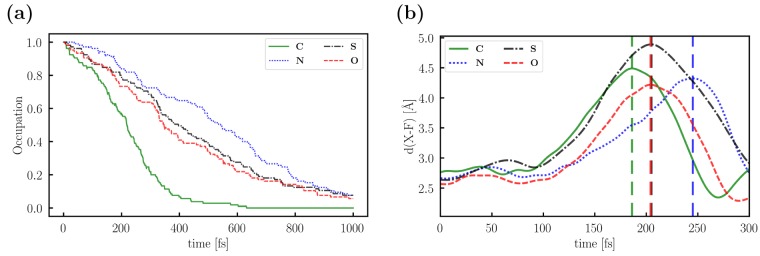
To study their effect on the light-induced rotation, we conducted NAMD simulations (105 trajectories for each rotor). In Table 3, we list the percentage of the trajectories that showed a rotation (η) as well as the ratio of clockwise and counterclockwise rotations (r). The direction of the rotation has been determined using the dihedral γ. (See the Supporting Information for plots.) The time-dependent occupation of the S₁ state (calculated as an average over all trajectories) and d(X–F) for the trajectory with the fastest rotation of C, N, S, and O, respectively, are shown in Figure 7.

Table 3. Efficiency (η, Determined from the Percentage of Rotating Molecules in the NAMD Simulations) of the Four Rotary Molecular Machines (C, N, S, and O) and Ratio [r = n(CW)/n(CCW)] of CW and CCW Rotations.

	C	N	S	O
η	70%	61%	54%	56%
r	0.68	0.78	1.19	1.68

Figure 7.

(a) Time-dependent decay of the occupancy of the S₁ state determined as a mean of all nonadiabatic molecular dynamics simulations. (b) Change in d(X–F) during one selected trajectory of C, N, S, and O, respectively, showing the rotation of the molecule around the central C–C bond. The maxima (180° rotation) are marked by the vertical dashed lines.

For all system, we observed (1) the expected rotation around the central C–C bond, which can be detected using either γ or d(X–F) and (2) the relaxation from S₁ to the ground state (S₀). Movies of the rotations are available at https://www.cup.uni-muenchen.de/pc/ochsenfeld/download/. The decay of the S₁ population (Figure 7a) seems to correlate with the rotational speed of the corresponding rotary molecular machine (Figure 7b). C shows the fastest rotation and the fastest decay, followed by S and O, which behave nearly identically. The rotation of N is the slowest, so is the decay of the S₁ occupancy. The trend in the rotational speeds (N < S < O < C) can easily be explained. O rotates slower than C because the nuclear repulsion between X and F is smaller. In the case of S, the repulsion of the S atom should be similar to that of the CH₂ moiety, but the time for the rotation increases because of its larger mass. The rotation of N is even slower because of the hydrogen bond between the NH moiety and the F atom.

However, this trend cannot be observed when looking at the rotational efficiency (η, see Table 3). Although C shows the largest number of trajectories featuring a rotation (70%), the η of S and O (∼55%) is significantly smaller than the η of N (61%). The reason for this might be the slightly different coupling vectors between the ground state and the first excited state (Supporting Information). In contrast to refs (43) and (44), we do not observe an influence of the puckering of the ring on the rotation. The ratios of CW and CCW rotations (r) are close to 1 for all four rotors, and no general trend is visible in the γ plots (Supporting Information).

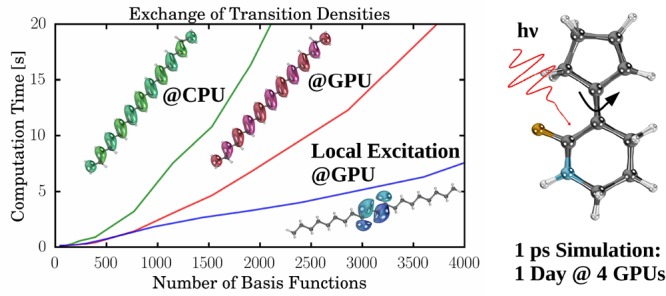
Changing X thus has an interesting effect on the rotary molecular machines. While the excitation energy changes significantly, the ability of the molecule to rotate around the central C–C bond is (nearly) preserved. These systems may thus be a good starting point for the design of a series of molecular rotors with tunable excitation energy. Our GPU-based routines aide these investigations by accelerating NAMD simulations even for these small systems. Because of the strong scaling (shown in Figure 4), we observe speed-ups in Coulomb and exchange integral evaluations (even when their computing time is shorter than 1 s), leading to a total speed-up of two with respect to a calculation entirely on CPUs. One trajectory took ∼1 day on two Intel Xeon CPU E5 2640 v4 @ 2.20 GHz (20 threads) CPUs and four AMD FirePro 3D W8100 GPUs.

6. Conclusions

Throughout this work, we have examined the use of graphics processing units (GPUs) for the evaluation of two-electron integrals in excited-state energies and property (gradients and nonadiabatic coupling vectors) calculations at the time-dependent density functional theory (TDDFT) level of theory. Similar to ground-state calculations, we observe that the use of GPUs along with the J-engine^73,74 and the preLinK scheme^50,51 leads to decent speed-ups of the integral calculations while additionally showing a reduced scaling behavior depending on the locality of the examined excitation. These speed-ups may even become larger with our currently developed seminumerical exchange scheme.⁹⁵ By using GPUs, nonadiabatic molecular dynamics become more efficient for large but also small molecules (as the a result of the strong scaling) without a loss of accuracy or the introduction of further assumptions. As a first example, we investigated a series of newly designed rotary molecular machines showing that one can tune the excitation energy of these systems without losing their ability to rotate by changing the hetereocycle. For future applications, we consider extending the current implementation toward decoherence corrections⁹⁶ and triplet states.⁹⁷

Notation

All equations in this section use the same notation as in Section 2. g_xc are the third order exchange correlation functional derivatives. The linear transformations H⁺ and H^– are defined as follows:

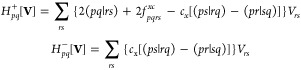19

Excited-State Energy Gradients

The unrelaxed difference density matrix T is calculated as follows:

20

To obtain the Lagrangian multiplier Z_I it is necessary to solve the following Z-vector equation:

21

22

Solving this Z-vector equation thus leads to the calculation of Z_I, which is used to determine the relaxed difference density matrix (P_I):

23

Using the calculated matrices, the energy-weighted difference density matrix (W_I) can be formed:

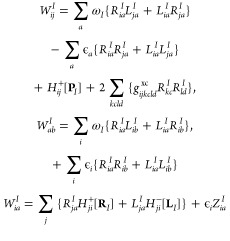24

The calculation of the effective two-particle difference density matrix is

25

Nonadiabatic Coupling Vectors between the Ground and an Excited State

First the Lagrangian multipliers Z_0I and W_0I need to be determined. In order to obtain Z_0I the following Z-vector equation has to be solved:

26

An iterative solution of eq 26 is not necessary. Z_0I is equal to R_I and the relaxed difference density matrix (P_0I) is calculated as follows:

27

The calculation of W_0I is presented in eq 28.

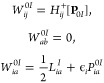28

Γ_0I is defined as

29

Nonadiabatic Coupling Vectors between Two Excited States

The unrelaxed difference density matrix (T_IJ) is calculated as follows:

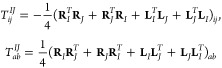30

To obtain the Lagrangian multiplier Z_IJ it is necessary to solve the following Z-vector equation:

31

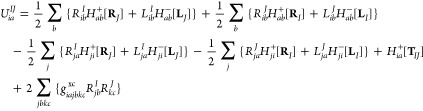32

Z_IJ is used to calculate the relaxed difference density matrix (P_IJ):

33

The calculation of W_IJ is

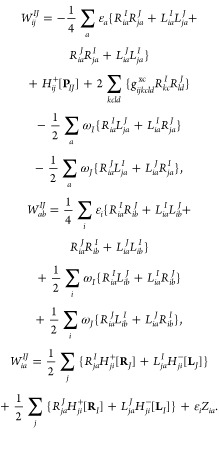34

Γ_IJ is defined as

35

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jctc.9b00859.

• log–log plots of the integral timings for the determination of the scaling behavior; validation of the use of the TDA and accurate thresholds, with excited-state energies, relaxed difference density plots, and plots of excited-state gradients and nonadiabatic coupling vectors at the TDA and RPA levels of theory; behavior of the dihedral γ during all trajectories (PDF)

The authors declare no competing financial interest.