Skip to main content
PMC home page
Brain Connectivity logoLink to Brain Connectivity
. 2018 Jun 1;8(5):255–267. doi: 10.1089/brain.2017.0571

Investigating the Intersession Reliability of Dynamic Brain-State Properties

Derek M Smith 1,✉, Yrian Zhao 2, Shella D Keilholz 2, Eric H Schumacher 1,✉
PMCID: PMC6909700  PMID: 29924644

Abstract

Dynamic functional connectivity metrics have much to offer to the neuroscience of individual differences of cognition. Yet, despite the recent expansion in dynamic connectivity research, limited resources have been devoted to the study of the reliability of these connectivity measures. To address this, resting-state functional magnetic resonance imaging data from 100 Human Connectome Project subjects were compared across 2 scan days. Brain states (i.e., patterns of coactivity across regions) were identified by classifying each time frame using k means clustering. This was done with and without global signal regression (GSR). Multiple gauges of reliability indicated consistency in the brain-state properties across days and GSR attenuated the reliability of the brain states. Changes in the brain-state properties across the course of the scan were investigated as well. The results demonstrate that summary metrics describing the clustering of individual time frames have adequate test/retest reliability, and thus, these patterns of brain activation may hold promise for individual-difference research.

Keywords: : arousal, brain states, dynamic connectivity, reliability

Introduction

The important relationship between dynamic changes in functional brain connectivity and human neurocognitive processing has recently begun to be recognized (Chang and Glover, 2010; Hutchison et al., 2013). For example, temporal features of functional connectivity have been linked to major depression, schizophrenia, and Alzheimer's disease (Hutchison et al., 2013). In addition, in healthy individuals, brain dynamics has been shown to be related to attention and cognitive flexibility (Nomi et al., 2017; Thompson et al., 2013). Unfortunately, limited attention has been paid to the stability and reliability of these dynamic patterns (Abrol et al., 2016; Choe et al., 2017). This is a critical limitation because if the signals are not reliable, then their association with human behavioral traits such as general intelligence and executive functioning is suspect.

It has been demonstrated that static functional connectivity measures are reliable and consistent (Shah et al., 2016; Shehzad et al., 2009; Varikuti et al., 2017), and there are improvements in intersession reliability of static functional connectivity plateau at scan lengths of between 9 and 12 min (Birn et al., 2013). These factors paint a hopeful picture of what the future might hold for the application of functional connectivity metrics in individual-difference research, but the same assessment must be applied to the myriad of new dynamic connectivity methods.

An assessment of reliability will also provide information regarding the functional nature of the signal's spatiotemporal features. Assuming that intraindividual and interindividual differences in spatiotemporal patterns are not the result of spurious factors such as head motion, high reliability may suggest that such patterns are functionally relevant and predictive of behavioral states and/or traits.

Dynamic connectivity methods may allow researchers to capture changes in network configuration and how they affect neurocognitive processes, but these new approaches bring with them new challenges (Chen et al., 2016; Cocchi et al., 2013; Fornito et al., 2012; Liu and Duyn, 2013; Majeed et al., 2011). A large portion of dynamic connectivity methods are grounded on sliding window correlation analysis, but this approach is constrained by the choice of the window size (Hindriks et al., 2016; Shakil et al., 2016). Unfortunately, the few studies that have assessed the reliability of dynamic connectivity metrics have not evaluated the impact of the global signal on reliability (Abrol et al., 2016; Choe et al., 2017). Global signal removal has been shown to attenuate the reliability of static connectivity (Varikuti et al., 2017).

Despite the pitfalls of sliding window-based methods, connectivity states derived from these methods have been shown to be reliable (Abrol et al., 2016; Choe et al., 2017). For example, Abrol and colleagues identified five connectivity states in 28 groups comprising 250 age-matched subjects and showed that the patterns that defined the connectivity states were highly reproducible across groups. The reliability of connectivity state properties (dwell time, number of change points from one brain state to another) based on sliding window and dynamic conditional correlation methods was moderate, but the mean and variance of the dynamic correlations exhibited a high degree of reliability (Choe et al., 2017). Given these findings, it can be said that connectivity states are fairly reliable. However, the reliability of brain states derived from activation patterns has yet to be investigated.

An alternative to the sliding window approach of assessing dynamic brain states is to capture brain dynamics via the classification of individual time frames (single volumes). Some researchers have even suggested that discrete neural events form the basis of the canonical intrinsic connectivity networks (Liu and Duyn, 2013; Petridou et al., 2013; Tagliazucchi et al., 2012). One popular approach is the coactivation pattern (CAP) method developed by Liu and Duyn. They showed that the activation maps produced by averaging over a small number of time frames and seed region spatial correlation maps based on the entire scan time course are nearly identical.

In addition, they showed that the temporal decomposition of resting-state networks into discrete patterns of coactivation was possible by applying k-means clustering to a subset of the data (Liu and Duyn, 2013). Essentially, Liu and Duyn demonstrated that functional connectivity networks can be driven by a brief portion of the total scan time and that these periods can be divided into instances of different CAPs. Methods of classifying individual time frames lack the shortcomings of sliding window approaches and can provide insights into factors that drive connectivity.

Before using CAP-like methods in correlational research, it is imperative to properly assess their reliability. To test the reliability of single-volume brain-state analyses, we used k-means clustering of resting-state time courses from two sessions (collected on separate days) of 100 subjects from the Human Connectome Project (HCP) (Van Essen et al., 2013). The properties of the clusters were compared between sessions. Cluster analysis was performed before and after the application of global signal regression (GSR) to better understand the global signal's role in determining clusters and the reliability of their properties. Given the reliability of static functional connectivity and recent research demonstrating that dynamic connectivity can predict certain behavioral traits, it was expected that brain dynamics would be reliable (Demirtaş et al., 2016; Nomi et al., 2017).

Materials and Methods

Subjects and preprocessing

Subjects were recruited by the HCP (Van Essen et al., 2013). Data were taken from the “500 subject” release. Analysis was restricted to the “100 Unrelated Subjects” set, which consists of 54 females and 46 males. Resting-state scans from 2 days were used each with a scan duration of 14.4 min (repetition time [TR] = 720 msec). Data were preprocessed with the HCP's minimal preprocessing pipeline, and denoising was performed by the ICA-FIX procedure (Glasser et al., 2013; Griffanti et al., 2014; Salimi-Khorshidi et al., 2014).

Three additional preprocessing steps were applied to the data. First, the voxels were smoothed with a 4 mm full-width half-maximum kernel. This step was followed by the application of a 0.01–0.1 Hz bandpass filter. Voxel time courses were then z-scored (each individual voxel demeaned and normalized by its temporal standard deviation). The other procedure was identical to the one just described except for the addition of whole-brain GSR, which was performed before the previously outlined steps. The GSR is intended to shed light on how the global signal may influence the clustering results.

Regions of interest

To reduce computational load, 90 regions of interest (ROIs) that have been shown to produce similar temporal clusters to those obtained from individual voxels were used in the analysis (Chen et al., 2015; Shirer et al., 2012). Shirer et al. (2012) derived these 90 ROIs by thresholding (using a different threshold for each network) 14 independent component networks found in a group-level analysis of 15 subjects. Before the application of k means clustering, each ROI time course was z-scored (each ROI demeaned and normalized by its temporal standard deviation) so that deviations from regional baseline could be viewed in terms of a region's variance.

Clustering

Clustering of the scan time points based on ROI z-scores was carried out at a global level. Each ROI z-score time course was concatenated across all subjects separately for each session. Clustering was performed via the k means algorithm with a squared Euclidean distance metric (Everitt et al., 2011). For each session, k values of 2–9 were used and for each k value, 25 replications were made. The replicate with the smallest within-cluster sums of point to centroid distances was chosen to represent its corresponding k value. The k value that marked the elbow of a cumulative within-cluster sum of squared error scree plot was selected for further analysis. The set of clusters meeting the elbow criterion is referred to as brain states.

Brain-state metrics

Several properties of brain states are commonly assessed and measured here: the temporal fraction, which is the frequency of each brain state's occurrence (Chen et al., 2015; Liu and Duyn, 2013); the average dwell time, which was defined as the average number of consecutive time frames an individual remained in a given brain state (Allen et al., 2014); and the transition fractions (i.e., the number of transitions from one state to another over all transitions to that state).

The Pearson correlation coefficient was used to measure the test/retest reliability of the temporal fraction, the average dwell time, and the transition fraction. This approach measures association between sessions but ignores absolute discrepancies between sessions. Therefore, the mean absolute difference between the two scan sessions, which captures the absolute discrepancy between sessions and is less vulnerable to outliers than measures based on sums of squares (Varikuti et al., 2017), was calculated to ensure that differences between scan sessions were not overlooked. In addition, the intraclass correlation coefficient (ICC) was used to measure test/retest reliability (Kim 2013; McGraw and Wong, 1996; Shrout and Fleiss, 1979). The version of the ICC we used (see Supplementary Data; Supplementary Data are available online at www.liebertpub.com/brain) can be interpreted as a measure of absolute agreement (McGraw and Wong, 1996).

Brain-state occurrence, time, and motion

Brain-state frequency may not be uniform across a scanning session. To investigate this, scans for each subject were divided into quarters and the temporal fraction and average dwell time of each brain state were calculated for each quarter. This approach allowed us to investigate the evolution of the brain-state properties across a session. Motion may also vary across scans and may be related to brain-state frequency (Siegel et al., 2014). Therefore, the mean framewise displacement (FD) was calculated from six motion parameters (Power et al., 2012). This measure of motion was then averaged across each of the quarters of a scanning session.

The main effect of time (four levels) was tested with a one-way repeated-measures analysis of variance (ANOVA). The Greenhouse–Geisser correction for violations of the sphericity assumption was applied in all cases where ANOVA was used throughout the examination of the data set. The relationships between grand average FD and the brain-state properties were examined to help determine the extent of motion's influence on the brain states.

Surrogate data

A supplemental analysis was conducted to compare the observed evolution of the temporal fraction and the mean dwell time with what would be expected in simulated time series with the same static functional connectivity profile (Allen et al., 2014; Hindriks et al., 2016; Prichard and Theiler, 1994). A phase randomization procedure was used to create surrogate data that shared the correlation structure of the HCP data set (Allen et al., 2014; Hindriks et al., 2016; Prichard and Theiler, 1994). This process was conducted by introducing random phase shifts. The Fourier transformations of each series were rotated by the same set of random phases (consistent randomization) and the subsequent application of the inverse fast Fourier transform yielded the surrogate time series. Consistent application of randomization across the time series preserves the correlation structure.

To determine if the evolution of the brain-state properties found in the HCP data would be expected in a null data set of matching static connectivity, 200 surrogate data sets were generated with consistent phase randomization reproducing the static connectivity profile (Prichard and Theiler, 1994). For each surrogate data set, clustering was performed with a k of 4. The temporal fraction and mean dwell were calculated for each quarter. Confidence intervals (with a two-tailed alpha corrected for the number of quarters) were determined for each scan quarter for each brain state.

Results

Brain states without GSR

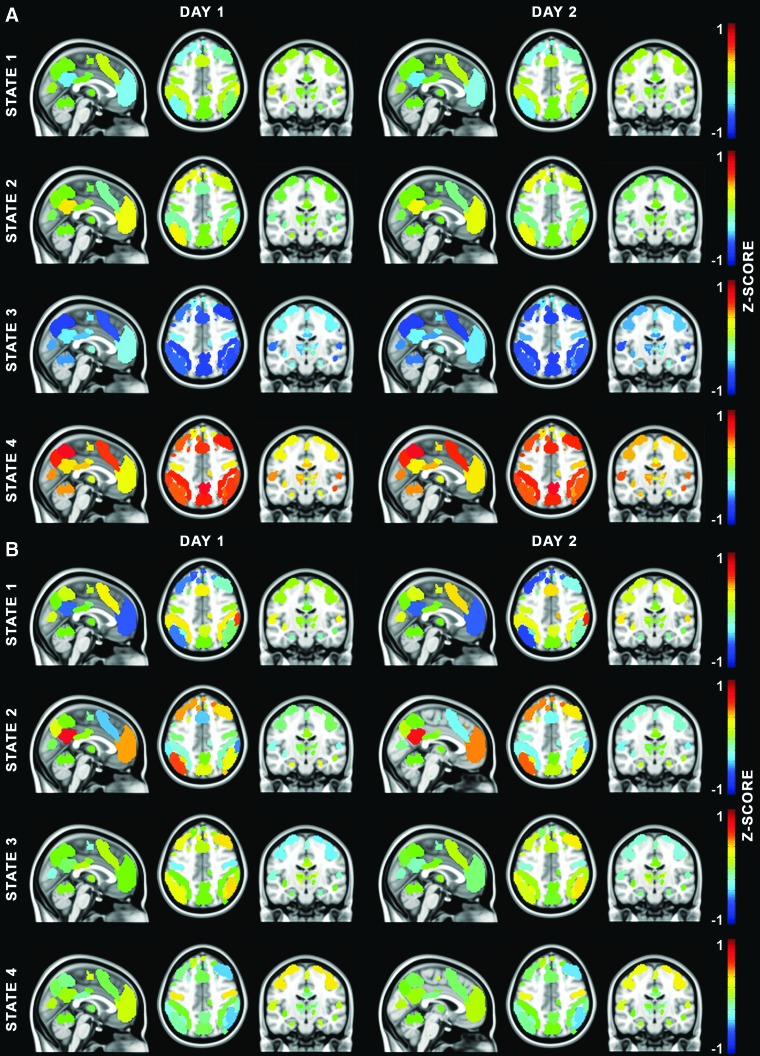
We used the elbow method to determine that a k of 4 was appropriate for both Sessions 1 and 2 (Everitt et al., 2011). Elbow plots are presented in Supplementary Figure S1. The four brain-state centroids for Sessions 1 and 2 are shown in Figure 1A. The first pair is marked by more pronounced deviations from baseline in two nodes of the default mode network (DMN).

FIG. 1.

FIG. 1.

Open in a new tab

The brain-state centroids, Sessions 1 and 2 without GSR (A) and with GSR (B). Brain-state centroids are presented in the sagittal (x = 0), axial (z = 44), and coronal (y = −16) planes. In all figures when referring to the states derived without GSR, brain state 1 = DMN deactivation, brain state 2 = DMN activation, brain state 3 = universal deactivation, and 4 = universal activation. In all figures when referring to the states derived with GSR, brain state 1 = DMN deactivation, 2 = DMN activation, 3 = motor deactivation, and 4 = motor activation. The scale (shown to the right of each row) is identical for all images. DMN, default mode network; GSR, global signal regression.

State 1 shows activity below baseline in regions of the posterior cingulate, inferior precuneus, and medial prefrontal cortices (regions of the DMN) and activity above baseline in the anterior cingulate, superior parietal regions, and the prefrontal cortex (regions of the frontoparietal and salience networks). State 2 showed the inverse pattern of activity to State 1. Activity in the anterior and posterior DMN nodes was above baseline and the nodes of the frontoparietal and salience networks showed below baseline activity. An inversion pattern was present in the other pair of brain-state centroids as well. All nodes in State 3 showed activity below baseline and all nodes in State 4 showed activity above baseline.

The centroids for States 1–4 were very similar for both sessions. Supplementary Table S6 displays the between-session centroid reliability measures. Correlations were greater than or equal to r = 0.95 for all states. This finding is similar to the between-session spatial correlations found by Choe et al. (2017), for connectivity defined brain states. Given the centroid correlations, the brain states are clearly reliable in terms of their spatial configuration across scanning sessions.

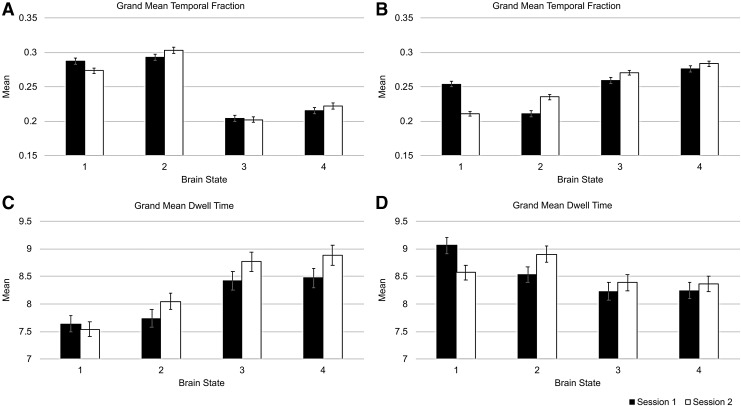
Box plots for the temporal fraction and mean dwell time can be found in Supplementary Figure S3. The mean temporal fraction for each brain state is presented in Figure 2A. Brain States 1 and 2 occurred more often than brain States 3 and 4. The Pearson correlations between Sessions 1 and 2 show test/retest reliability for the temporal fractions of the four brains states. As shown in Table 1, all the correlations were significant after applying a Bonferroni correction for multiple tests. Brain State 1 had the weakest correlation and the lowest ICC, whereas brain State 2 had the strongest correlation and highest ICC. The mean absolute difference did not differ much between states.

FIG. 2.

FIG. 2.

Open in a new tab

The grand mean temporal fractions (A, B) and grand mean dwell times (C, D) for the four brain states during Sessions 1 and 2. (A, C) Show the data without GSR. (B, D) Show the data after GSR. The error bars represent the standard error of the mean.

Table 1.

Reliability Measures of the Temporal Fraction for Brain States Without Global Signal Regression

Brain state Pearson correlation Mean absolute difference Intraclass correlation
State 1 0.40* 0.04 0.36*
State 2 0.56* 0.04 0.54*
State 3 0.49* 0.03 0.49*
State 4 0.53* 0.03 0.53*
Open in a new tab

An asterisk denotes values that survived the Bonferroni-corrected threshold. *p < 0.0125.

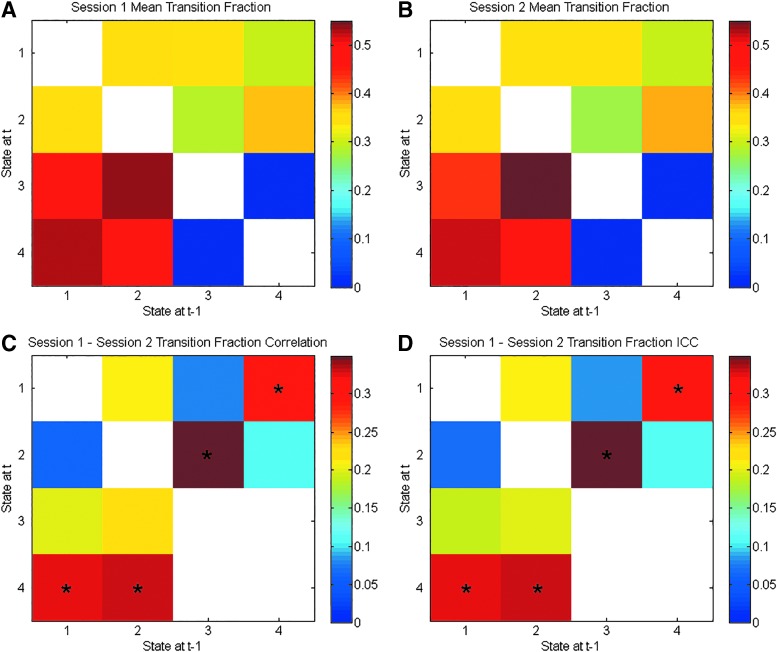
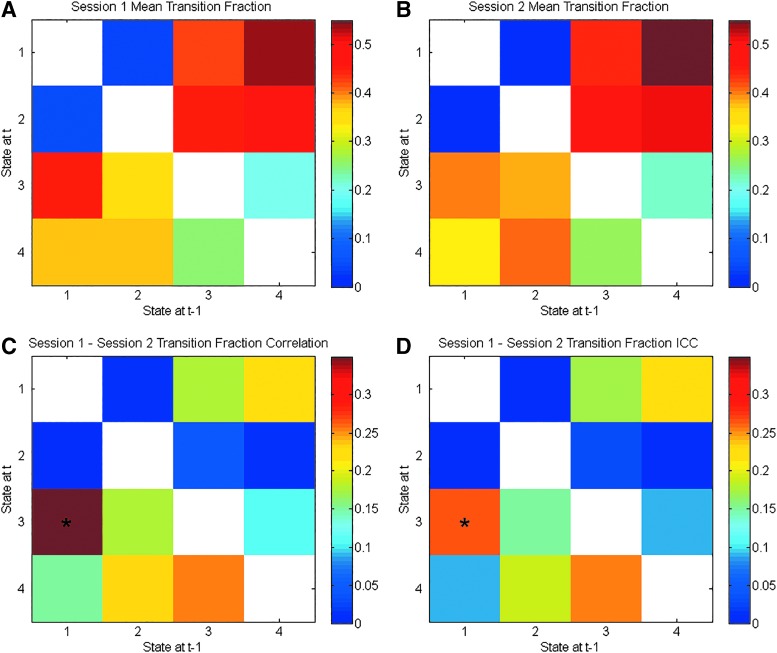
Figure 3A and B displays the mean transition fraction matrices for Session 1 and 2. Like the mean temporal fractions for each session, these values appear similar. However, this apparent similarity is somewhat misleading. Figure 3C and D shows the matrix of transition fraction correlations and ICC values for these fractions. It is clear that there is a fair amount of variability between sessions given the maximum correlation magnitude of r = 0.39. Yet, the between-pair transition fractions for States 1–4, 2–4, 3–2, and 4–1 all survived multiple comparison correction. Thus, there was some consistency between scan sessions. The most striking characteristic of the transition fraction matrices is the lack of particular transitions. On Sessions 1 and 2, State 3 (global deactivation) never directly transitioned to State 4 (global activation) and vice versa.

FIG. 3.

FIG. 3.

Open in a new tab

The transition fractions for the brain states derived without GSR. Each element represents the mean transition fraction, going from a state along the x-axis to a state along the y-axis, for the first (A) and second (B) sessions. Each cell in (C) representing the Pearson correlation between sessions for a given transition fraction and each cell in (D) representing the ICC values that survived the Bonferroni correction are marked with an asterisk. White cells show the diagonal (nontransitions) or transitions that were not observed. ICC, intraclass correlation coefficient.

As shown in Figure 2C and Table 2, the average dwell time was similar for each state and consistent across sessions although less so than the temporal fraction. State 2 had the highest correlation and ICC. State 3 had the lowest correlation values. The mean absolute difference did not differ much between states, but States 3 and 4 exhibited values somewhat higher than States 1 and 2.

Table 2.

Reliability Measures of the Average Dwell Time for Brain States Without Global Signal Regression

Brain state Pearson correlation Mean absolute difference Intraclass correlation
State 1 0.43* 1.16 0.43*
State 2 0.48* 1.27 0.47*
State 3 0.41* 1.47 0.40*
State 4 0.47* 1.44 0.45*
Open in a new tab

An asterisk denotes values that survived the Bonferroni-corrected threshold. *p < 0.0125.

State properties across scan time

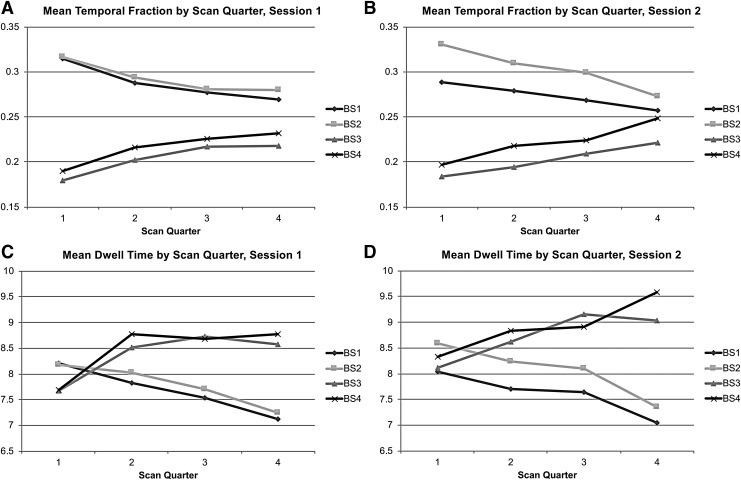
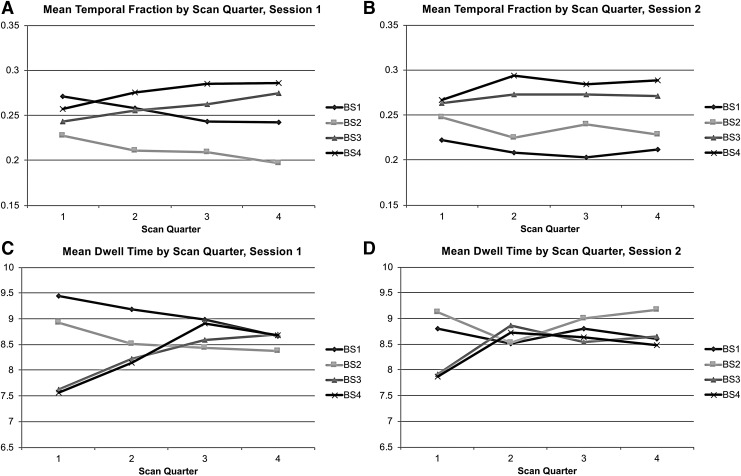
Figure 4A and B presents the mean temporal fraction for each quarter of the scan. For both sessions, States 1 and 2 decrease and States 3 and 4 increase in frequency as the scan progresses. Figure 4C and D displays the mean dwell times for each scan quarter across sessions.

FIG. 4.

FIG. 4.

Open in a new tab

Regularities in the properties of brain states without GSR across the four quarters of each scan. The grand mean temporal fraction is shown for Session 1 (A) and Session 2 (B) for each brain state (shown as separate lines). (C, D) Show the grand mean dwell time data organized the same way.

The dwell times of the DMN states (1 and 2) show a minor downward trend and those of the universal activation/deactivation states (3 and 4) increase with time. As can be seen in Table 3, the temporal fraction significantly differed from the null distribution for the most part during the first two scan quarters. Temporal fractions for States 1 and 2 exceeded the upper bounds and States 3 and 4 fell below the lower bounds of the quarterly confidence intervals. As shown in Table 3, despite being relatively lower than those observed for States 3 and 4, the average dwell time for States 1 and 2 was above the upper bounds of their corresponding confidence intervals for the first three quarters for both sessions. The average dwell times for States 3 and 4 fell below the lower bounds of their corresponding confidence intervals for the first quarter for both sessions, and during the fourth quarter of Session 2, State 4's dwell time exceeded the upper bound.

Table 3.

The Average Quarterly Temporal Fractions and Average Dwell Times from Both Sessions for the Brain States Derived Without Global Signal Regression

Brain state Quarter 1 Quarter 2 Quarter 3 Quarter 4
Session 1: Temporal fraction by scan quarter significance
 State 1 *> *>    
 State 2 *> *>    
 State 3 *< *<    
 State 4 *< *<    
Session 2: Temporal fraction by scan quarter significance
 State 1 *>      
 State 2 *> *> *>  
 State 3 *< *< *<  
 State 4 *< *<    
Session 1: Average dwell time by scan quarter significance
 State 1 *> *> *>  
 State 2 *> *> *>  
 State 3 *<      
 State 4 *<      
Session 2: Average dwell time by scan quarter significance
 State 1 *> *> *>  
 State 2 *> *> *>  
 State 3 *<      
 State 4 *<     *>
Open in a new tab

An asterisk significantly differed from what would be expected given the corresponding surrogate-based null distribution (*p < 0.0125).

<, Signifies less than the confidence interval; >, signifies greater than the confidence interval.

Brain states with GSR

For the sake of comparison with the analysis without GSR, a k of 4 was chosen for the post-GSR clusters. The set of four brain states present after the inclusion of GSR did not include universal activation and deactivation states. State 1 was defined by a centroid with deactivation in the DMN especially in the two nodes showing the most pronounced deviations from baseline in the analysis without GSR and the frontoparietal/salience network regions showed above baseline activation. State 2 showed deactivation in the nodes of the frontoparietal and salience networks and activation in the DMN. The magnitude of the activation/deactivation in these states was greater than in their counterparts in the analysis without GSR.

Deactivation in the motor cortex was the defining feature of State 3. The inferior parietal lobules and the middle frontal gyri showed above baseline activity. State 4 was marked by activation in the motor cortex. Deactivation was present in the inferior partial lobules and the middle frontal gyri for this state. As can be seen in Figure 1B, the centroids were similar between the two sessions.

Figure 2B shows the temporal fraction means for each session. As with the original set of states, the temporal fraction means were similar for the two sessions. The grand means of the dwell times (Fig. 2D) were less similar between sessions than those of the temporal fraction (Fig. 2B). Test/retest reliabilities as measured by the Pearson correlation (Table 4) were moderate, with the default mode activation state (State 2) having the greatest reliability in terms of this metric. All correlations survived correction for multiple comparisons. The ICC values were similar to the Pearson correlations for the motor states, but they were much lower for both DMN states. The default mode deactivation state (State 1) did not have a significant ICC. For the most part, the rankings of the mean absolute differences corresponded to those of the ICC.

Table 4.

Reliability Measures of the Temporal Fraction for Brain States After Global Signal Regression

Brain state Pearson correlation Mean absolute difference Intraclass correlation
State 1 0.43* 0.07 0.04
State 2 0.55* 0.06 0.42*
State 3 0.47* 0.06 0.43*
State 4 0.41* 0.06 0.40*
Open in a new tab

An asterisk denotes values that survived the Bonferroni-corrected threshold. *p < 0.0125.

As in the absence of GSR, the transition fractions averaged to approximately the same values each session (Fig. 5A, B). In contrast to the output of the analysis that did not include GSR, all possible transitions were observed (Fig. 5). Transitions to the default mode deactivation state (State 1) were more likely on average to come from the motor activation state (State 4). Transitions to the default mode activation state (State 2) were more likely on average to come from the motor activation state (State 4) as well. A smaller share of the transitions to the default mode states came from the motor deactivation state (State 3) relative to its opposite. Transitions from the default mode activation state to the default mode deactivation state (States 2 and 1) and vice versa were rare. Transitions between the states marked by motor activation/deactivation (States 4 and 3) were not as infrequent as those between the DMN states.

FIG. 5.

FIG. 5.

Open in a new tab

The transition fractions for the brain states derived after the application of GSR. Each element represents the mean transition fraction, going from a state along the x-axis to a state along the y-axis, for the first (A) and second (B) sessions. Each cell in (C) representing the Pearson correlation between sessions for a given transition fraction and each cell in (D) representing the ICC values that survived the Bonferroni correction are marked with an asterisk. White cells show the diagonal (nontransitions) or transitions that were not observed.

Also, the correlations between the two sessions were generally weaker than those found when GSR was not conducted and only one (transition fraction for going from State 1 to 3) of these correlations survived correction for multiple tests (Fig. 5C). As with the states derived without GSR, the ICC values for the transition fractions (Fig. 5D) were similar to the Pearson correlations.

The average dwell times (Table 5) showed moderate correlations between the two sessions as well. The correlations for the State 1 (DMN deactivation) were very low in magnitude and did not survive correction for multiple tests. This was paralleled by State 2 (default mode activation) displaying the highest Pearson correlation for both measures. For average dwell time, the mean absolute difference followed the same trend as the correlations with the State 1 having the largest absolute difference between sessions and the opposite state having the lowest. For the most part of the average dwell time, the ICC values were similar to the values of the corresponding Pearson correlations. The DMN deactivation state's coefficients did not reach significance.

Table 5.

Reliability Measures of the Average Dwell Time for Brain States After Global Signal Regression

Brain state Pearson correlation Mean absolute difference Intraclass correlation
State 1 0.15 1.45 0.12
State 2 0.48* 1.25 0.46*
State 3 0.39* 1.35 0.38*
State 4 0.38* 1.30 0.38*
Open in a new tab

An asterisk denotes values that survived the Bonferroni-corrected threshold. *p < 0.0125.

When looking at the temporal fraction across the course of the scan, the two sessions were not as consistent post-GSR, but commonalities certainly exist between the two scan sessions. As can be seen in Figure 6A, for Session 1, States 3 and 4 (motor network states) increased in frequency across the scan duration. The opposite was true for the DMN states. Figure 6B clearly shows this was not the case for Session 2, but the mean temporal fractions remained higher for the motor states throughout the course of the scan. On average, the motor states had somewhat higher temporal fractions than the DMN states over most of the scan time for both sessions.

FIG. 6.

FIG. 6.

Open in a new tab

Regularities in the properties of brain states derived after the application of GSR across the course of a scan. The grand mean temporal fraction is shown for Session 1 (A) and Session 2 (B) for each brain state (shown as separate lines). (C, D) Show the grand mean dwell time data organized the same way.

As is shown in Table 6, the temporal fraction for State 1 fell above upper bounds of its confidence intervals for Session 1's first two scan quarters and fell below the lower bound for the third quarter of Session 2. State 2's temporal fraction fell below the confidence interval for Session 1's fourth quarter and above the upper bounds for the first and third quarters of Session 2. State 3's temporal fraction only significantly differed from the null distribution for the first quarter of Session 1 (below lower bound), and State 4's temporal fraction only significantly deviated from the null during Session 2's second quarter (above the upper bound).

Table 6.

The Average Quarterly Temporal Fractions and Average Dwell Times from Both Sessions for the Brain States Derived with Global Signal Regression

Brain state Quarter 1 Quarter 2 Quarter 3 Quarter 4
Session 1: Temporal fraction by scan quarter significance
 State 1 *> *>    
 State 2       *<
 State 3 *<      
 State 4        
Session 2: Temporal fraction by scan quarter significance
 State 1     *<  
 State 2 *>   *>  
 State 3        
 State 4   *>    
Session 1: Average dwell time by scan quarter significance
 State 1 *> *>    
 State 2        
 State 3     *> *>
 State 4     *> *>
Session 2: Average dwell time by scan quarter significance
 State 1        
 State 2 *>      
 State 3   *>   *>
 State 4   *> *>  
Open in a new tab
*

p < 0.0125.

<, Signifies less than the confidence interval; >, signifies greater than the confidence interval.

The grand average dwell times are presented in Figure 6C and D. The motor states showed minor increases in dwell time over the course of the scan. The opposite was true of the DMN states. Table 6 shows that when the post-GSR quarterly dwell time differed from the null distribution, it only fell above the upper bound. State 1's dwell time only reached significance for the first two quarters of Session 1 and State 2's dwell time only reached significance during the first quarter of Session 2. The average dwell time for State 3 was significant for the third and fourth quarters of Session 1 and the second and fourth quarters of Session 2. State 4 was significant for the third and fourth quarters of Session 1 and the second and third of session 2.

Brain states and global signal

As can be seen in the Supplementary Data (see Supplementary Table S1), global signal's variance was reliable and strongly correlated (r = 0.73) from Session 1 to 2. The magnitude of the global signal, however, differed between time frames from brain states without GSR on Session 1, F(1.164, 115.262) = 694.717, p < 0.05, 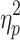Inline graphic = 0.875, and Session 2, F(1.096, 108.533) = 511.595, p < 0.05, 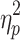Inline graphic = 0.838. Post hoc paired t-tests were carried out for each scan session. The means and standard deviations of the global signal for each brain state can be found in the Supplementary Data (see Supplementary Table S2) in addition to the post hoc comparisons. State 3 had a significantly lower global signal than the other states. State 4, on the contrary, had a higher mean signal than the other states.

The time frames for the brain states obtained after the application of GSR exhibited statistically significant differences in average global signal as well. Essentially the preregression global signal differed between brain states. The effect of brain state on global signal was significant for Session 1, F(1.496, 148.085) = 16.339, p < 0.05, 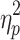Inline graphic = 0.142, and Session 2, F(1.470, 145.570) = 17.835, p < 0.05, 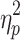Inline graphic = 0.153. The means and standard deviations for the global signal in these data and post hoc comparisons are in the Supplementary Data (see Supplementary Table S3).

Motion and brain states

Motion varied across the course of both sessions in a systematic way (motion increased over the course of the scan as can be seen in Supplementary Figure S2). The influence of quarter on mean FD was assessed via repeated-measures ANOVA for each session. There was a statistically significant effect of scan quarter for both Session 1, F(1.872, 185.281) = 9.868, p < 0.05, 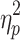Inline graphic = 0.091, and Session 2, F(1.808, 178.980) = 5.565, p < 0.05, 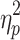Inline graphic = 0.053. No significant correlations were found between the properties of the brain states without GSR and each scan session's grand average FD.

For the brain states obtained with GSR, only the motor activation state's temporal fraction for Session 1 correlated significantly with the grand average FD (r = 0.26, p < 0.01). State 3, the motion deactivation state is correlated with across the scan motion during Session 2 (r = 0.29, p < 0.01). The average dwell time for the motor activation state was positively correlated with the grand average FD for both sessions (Session 1: r = 0.27, p < 0.01; Session 2: r = 0.28, p < 0.01).

Brain states obtained without GSR also differed in average motion. A statistically significant effect of brain state on average motion (grand average FD for a brain state) was present on Session 1, F(2.741, 271.368) = 33.107, p < 0.05, 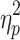Inline graphic = 0.251, and Session 2, F(2.289, 226.595) = 28.730, p < 0.05, 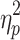Inline graphic = 0.225. Means, standard deviations, and post hoc comparisons can be found in the Supplementary Data (Descriptive statistics for states derived without GSR are found in Supplementary Table S4 and descriptive statistics for states derived with GSR are found in Supplementary Table S5). State 3 showed significantly lower average motion, and State 4 showed significantly higher average motion than the other states.

Because the distribution of average motion showed signs of deviation from normality for all brain states especially on Session 2, a nonparametric alternative to the single-factor, within-subject ANOVA, the Friedman test, was performed and yielded the same pattern of results. In addition, a Wilcoxon signed-ranked test produced the same pattern of significant results as the paired t tests (see Supplementary Data). The brain states detected after the application of GSR did not differ in average motion on Session 1, F(2.707, 267.990) = 2.250, p = 0.089, 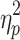Inline graphic = 0.022, and Session 2, F(2.428, 240.358) = 1.813, p = 0.157, 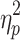Inline graphic = 0.018.

Discussion

Overview of results

Considered together, these findings demonstrate that brain-state properties are reliable across sessions conducted on separate days. The reliability of these measures implies that brain-state metrics have the potential to predict behavioral factors. The properties of brain states were shown to be reliable with and without GSR. The temporal fraction, or the frequency of occurrence of each brain state, exhibits the strongest reliability, and the average dwell time (i.e., duration of each brain state) is the next most reliable measure over time. The transition fraction (i.e., the number of transitions from one state to another over all transitions to that state) was reliable without GSR but not after GSR.

Changes in the temporal fraction across the course of the scan were also consistent across sessions. States 1 and 2 showed decreasing temporal fractions and dwell time within each session. These metrics increased over the same period in States 3 and 4. Given the consistency of this pattern across sessions, numerous observations of significant deviations from the surrogate null distributions, and the lack of this pattern in the surrogate data, these changes over time likely reflect an underlying temporal dependence in the brain-state properties. In addition, significant differences in the effect of global signal were found between brain states. Differences in the centroids of the states derived before and after the application of GSR suggest that global signal is tied to the composition of brain states.

Interpretation of results

We used both the Pearson correlation coefficient and the ICC to show that dynamic connectivity measures are reliable across sessions. Both measures demonstrated reliability, however, they were not identical. State 1 had ICC values much lower than the Pearson correlation for both the temporal fraction and mean dwell time after GSR. These discrepancies likely stem from the fact that the Pearson correlation coefficient is a measure of association and the ICC is a measure of absolute agreement. State 2 after GSR showed large mean temporal fraction differences between sessions and relatively large discrepancies between the correlation and ICC measures.

The Pearson correlation is not sensitive to the differences in the temporal fractions between sessions, as a measure of association it is sensitive to the consistency of the relative standing of individuals between sessions. These observations illustrate why it is important to use both measures of relative agreement and absolute agreement when assessing reliability.

After denoising, GSR leads to a minor attenuation of reliability but major changes in the detected patterns of activation. While motion, as measured by the mean FD across the entire time course, did not correlate consistently with any of the brain states except State 4 (the motor activation state). The State 4's dwell time and temporal fraction were positively related to grand average motion.

Considering that it is related to motion throughout the course of the scan, the motor activation state may reflect the neural impetus of motion, but there was a lack of a significant difference in motion between time frames belonging to the motor activation state and time frames belonging to other states derived after the application of GSR. The sluggish nature of the blood oxygen level–dependent (BOLD) response likely accounts for the lack of motion differences between the time frames of the post-GSR states and the correlation between overall motion and the motor activation state.

There was also an interaction between motion and global signal. Motion before the application of GSR differed between brain states. The universal activation/deactivation states were marked by relatively high and low motion, respectively. The time frames that belonged to these states were also associated with high and low global signal and the average motion of post-GSR brain states did not differ. Global signal did not correlate with motion, the average correlation across subjects between the two standing at r = 0.01 for both scan sessions. This is not surprising considering the incorporation of motion parameters in the denoising procedure (Salimi-Khorshidi et al., 2014). Nevertheless, without GSR, statistically significant differences in motion are found between brain states, but states derived after GSR do not show significant differences in motion and this suggests that motion-related information remains in the post-denoising global signal.

Motion's influence on the brain states cannot be ruled out given the persistent and complex nature of motion's effects (Power et al., 2014). A portion of the effect of motion on brain state may be reflected in the global signal but it is unlikely the primary factor driving state differentiation, given the large difference in the effect size of brain state on motion (Session 1: 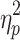Inline graphic = 0.251; Session 2: 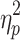Inline graphic = 0.225) and global signal (Session 1: 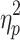Inline graphic = 0.875; Session 2: 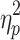Inline graphic = 0.838).

The global signal is widely believed to contain both nuisance components and functionally relevant neural components (Liu et al., 2017; Murphy and Fox, 2017). Considering that a denoising procedure was applied to this data set before the implementation of GSR, it is possible that the global signal captured in this analysis was a manifestation of factors with less weight in the global signal present in most studies (Griffanti et al., 2014; Salimi-Khorshidi et al., 2014). Changes in arousal over the course of scanning sessions might be one such factor.

It is likely that the global signal in the present data is more related to a factor such as arousal than in other studies due to the denoising procedure, which mitigates the influence of numerous factors of minimal to no behavioral relevance. A growing line of research has documented a negative relationship between global signal and measures of vigilance or arousal (Chang et al., 2016; Goldman et al., 2002; Liu et al., 2012; Olbrich et al., 2009; Wong et al., 2013, 2016). For example, in macaque monkeys, the expression of a functional magnetic resonance imaging (fMRI) arousal template closely follows electrophysiological arousal such that periods positively correlated with arousal show widespread cortical deactivation and those negatively correlated with arousal show widespread cortical activation (Chang et al., 2016).

Given the literature on arousal templates, States 3 and 4, which show whole-brain activity changes (Fig. 1), may be a manifestation of a neuromodulatory process that contributes to the global signal and is implicated in arousal. However, despite the similarity between these states and the BOLD signal patterns associated with high and low arousal, the arousal literature typically shows that activation in the thalamus is inversely related to the neocortex (Chang et al., 2016), and this pattern did not appear in the current analysis of the HCP data. Nevertheless, evidence suggests there are a progressive decrease in arousal during monotonic stimulation (Baumann et al., 1968; Richter et al., 2005) and an increase in the probability of sleep as the resting-state scan continues (Tagliazucchi and Laufs, 2014). The temporal fraction and mean dwell time measures in States 3 and 4 (universal deactivation/activation) may relate to these changes in arousal.

Potential limitations

The current analyses were based on a set of 90 ROIs that have been shown to produce similar clustering results as voxel-based analyses in other data (Chen et al., 2015). Nevertheless, one cannot be completely sure the results here are not specific, at least to some extent, to the ROIs used. In addition, k means clustering has its own inherent limitations. It ignores regional differences in the lag of the BOLD signal (Handwerker, et al., 2004). This factor could lead to patterns of BOLD coactivation that do not reflect the underlying pattern of neural coactivation. Another challenge is that brain states may occur at time scales faster than the temporal resolution of fMRI (Khanna et al., 2015). In addition, clustering of individual time frames does not measure extended spatiotemporal patterns. Such patterns may have been missed by the time frame clustering approach (Majeed, et al., 2011; Yousefi et al., 2018).

Despite the limitations of the k-means clustering algorithm, it was used here because k-means is a common approach for measuring brain states and was therefore a good choice to test brain state reliability. However, alternative methods such as hierarchical clustering might reveal embedded clusters that may be missed by k-means clustering (Ward, 1963). For example, during periods of dwelling within an overarching cluster, it might be the case that the start of the period tends to be grouped into one of the cluster's two subclusters and the second half of the dwelling periods is more frequently classified into the other subcluster. This is an area for future research.

Future directions

The lack of universal activation/deactivation states for the GSR analysis was predicable but more needs to be learned about these universal activation/deactivation states (c.f., Yousefi et al., 2018). The upward trend in motion across time corresponds with the progressive increase in the temporal fraction observed for these two states, but the progressive increase in the temporal fraction and mean dwell time could be the result of changes in arousal. Also, information relevant to behavior and mental states might be contained in sequences of brain states. The universal activation/deactivation states might be stages of an overarching pattern of state transitions considering that they never directly transition to each other. The post-GSR states infrequently transitioned directly between opposites further suggesting that the brain states might be stages of some sort of cycle.

Other researchers have produced evidence of state sequences in the HCP resting-state data set (Chen et al., 2016). Chen and colleagues used a Gaussian hidden Markov model to capture a brain-state switching process. The authors reported nine reproducible brain states consisting of combinations of activated and deactivated regions. Many of the states resembled the canonical intrinsic brain networks. Two states that stood out were defined by across the brain activation and deactivation. The most interesting findings concerned the brain-state transitions. States were likely to transition to a baseline state, and there was a tendency to transition from a default mode state to an attention network state (Chen et al., 2016).

Future research should focus on determining brain-state sequences and comparing them to patterns detected by other means (Chen et al., 2016; Majeed et al., 2011). The universal activation/deactivation states we found resemble the states reported by Chen and colleagues (2016), BOLD signal templates indicative of arousal, and stages of quasiperiodic patterns in the BOLD signal (Chang et al., 2016; Chen et al., 2016; Majeed et al., 2011). The regularities associated with the brain states we found, not to mention their parallels to states derived by other researchers using different methods, mandate further investigation into the nature of these states.

Conclusions

Prior research suggests that fluctuations in the correlation structure of BOLD signal might be attributed to head motion and level of arousal (Laumann et al., 2017). The results presented here are generally consistent with these results. Arousal is physiologically meaningful and its relationship to patterns of coactivation and with global signal deserves more investigation. In addition, the reliability metrics, for the temporal fraction and the dwell time, were generally greater than or roughly equal to those reported for the dwell times of brain states derived using sliding windows (Choe et al., 2017). Furthermore, as with static functional connectivity, reliability was attenuated by GSR. However, post-GSR, temporal fractions and dwell times remained reliable (Liao et al., 2013; Varikuti et al., 2017; Zuo et al., 2013).

The brain states identified here are similar in terms of their spatial composition to those measured with other techniques (e.g., Chen et al., 2016; Choe et al., 2017) and are reliable across experimental sessions. The application of GSR is detrimental to the reliability of the brain-state properties but does not catastrophically affect the measures' reliability. Much remains to be learned about the role of global signal in these brain states, but changes in arousal may be a key factor.

Global signal has an effect on brain-state composition, and motion-related information seems to be present in this postdenoising global signal. Nevertheless, the similarity of the universal activation/deactivation states to templates of arousal and the relatively low frequency of occurrence that these states exhibit early in the scanning sessions suggest that arousal fluctuations have a role in defining and driving these states. We believe that these explanations are not mutually exclusive and that neither can be ruled out. Finally, the approach used here has the potential to capture reoccurring patterns of brain activation in resting-state data without making many assumptions regarding the nature of brain-state sequences and thus has the potential to lead to future important discoveries.

Supplementary Material

Supplemental data
Supp_Data.pdf (230.3KB, pdf)

Acknowledgments

The authors thank Behnaz Yousefi, Tiffany Nguyen, Julia Ting, and Bruno Dos Santos for their assistance. Data were provided [in part] by the HCP, WU-Minn Consortium (Principal Investigators: David Van Essen and Kamil Ugurbil; 1U54MH091657) funded by the 16 NIH Institutes and Centers that support the NIH blueprint for neuroscience research; and by the McDonnell Center for Systems Neuroscience at Washington University.

Author Disclosure Statement

No competing financial interests exist.

References

  1. Abrol A, Chaze C, Damaraju E, Calhoun VD. 2016. The chronnectome: evaluating replicability of dynamic connectivity patterns in 7500 resting fMRI datasets. Conf Proc IEEE Eng Med Biol Soc 2016:5571–5574 [DOI] [PubMed] [Google Scholar]
  2. Allen EA, Damaraju E, Plis SM, Erhardt EB, Eichele T, Calhoun VD. 2014. Tracking whole-brain connectivity dynamics in the resting state. Cereb Cortex 24:663–676 [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Baumann H, Baumann R, Gurk C, Wolter F. 1968. Electrophysiological studies of central nervous performance during monotony. Electroencephalogr Clin Neurophysiol 24:259–273 [DOI] [PubMed] [Google Scholar]
  4. Birn RM, Molloy EK, Patriat R, Parker T, Meier TB, Kirk GR, et al. . 2013. The effect of scan length on the reliability of resting-state fMRI connectivity estimates. Neuroimage 83:550–558 [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Chang C, Glover GH. 2010. Time–frequency dynamics of resting-state brain connectivity measured with fMRI. Neuroimage 50:81–98 [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Chang C, Leopold DA, Schölvinck ML, Mandelkow H, Picchioni D, Liu X, et al. . 2016. Tracking brain arousal fluctuations with fMRI. Proc Natl Acad Sci U S A 113:4518–4523 [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Chen JE, Chang C, Greicius MD, Glover GH. 2015. Introducing co-activation pattern metrics to quantify spontaneous brain network dynamics. Neuroimage 111:476–488 [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Chen S, Langley J, Chen X, Hu X. 2016. Spatiotemporal modeling of brain dynamics using resting-state functional magnetic resonance imaging with Gaussian hidden Markov model. Brain Connect 6:326–334 [DOI] [PubMed] [Google Scholar]
  9. Choe AS, Nebel MB, Barber AD, Cohen JR, Xu Y, Pekar JJ, et al. . 2017. Comparing test-retest reliability of dynamic functional connectivity methods. Neuroimage 158:155–175 [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Cocchi L, Zalesky A, Fornito A, Mattingley JB. 2013. Dynamic cooperation and competition between brain systems during cognitive control. Trends Cogn Sci 17: 493–501 [DOI] [PubMed] [Google Scholar]
  11. Demirtaş M, Tornador C, Falcón C, López‐Solà M, Hernández‐Ribas R, Pujol J, et al. . 2016. Dynamic functional connectivity reveals altered variability in functional connectivity among patients with major depressive disorder. Hum Brain Mapp 37:2918–2930 [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Everitt BS, Landau S, Leese M, Stahl D. 2011. An Introduction to Classification and Clustering. Cluster Analysis, 5th ed. Hoboken, NJ: Wiley [Google Scholar]
  13. Fornito A, Harrison BJ, Zalesky A, Simons JS. 2012. Competitive and cooperative dynamics of large-scale brain functional networks supporting recollection. Proc Natl Acad Sci U S A 109:12788–12793 [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Glasser MF, Sotiropoulos SN, Wilson JA, Coalson TS, Fischl B, Andersson JL, et al. . 2013. The minimal preprocessing pipelines for the Human Connectome Project. Neuroimage 80:105–124 [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Goldman RI, Stern JM, Engel J, Jr., Cohen MS. Simultaneous EEG and fMRI of the alpha rhythm. Neuroreport 2002;13:2487–2492 [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Griffanti L, Salimi-Khorshidi G, Beckmann CF, Auerbach EJ, Douaud G, Sexton CE, et al. . ICA-based artefact removal and accelerated fMRI acquisition for improved resting state network imaging. Neuroimage 2014;95:232–247 [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Handwerker DA, Ollinger JM, D'Esposito M. 2004. Variation of BOLD hemodynamic responses across subjects and brain regions and their effects on statistical analyses. Neuroimage 21:1639–1651 [DOI] [PubMed] [Google Scholar]
  18. Hindriks R, Adhikari MH, Murayama Y, Ganzetti M, Mantini D, Logothetis NK, Deco G. 2016. Can sliding-window correlations reveal dynamic functional connectivity in resting-state fMRI? Neuroimage 127:242–256 [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Hutchison RM, Womelsdorf T, Allen EA, Bandettini PA, Calhoun VD, Corbetta M, et al. . 2013. Dynamic functional connectivity: promise, issues, and interpretations. Neuroimage 80:360–378 [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Khanna A, Pascual-Leone A, Michel CM, Farzan F. 2015. Microstates in resting-state EEG: current status and future directions. Neurosci Biobehav Rev 49:105–113 [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Kim HY. 2013. Statistical notes for clinical researchers: evaluation of measurement error 1: using intraclass correlation coefficients. Restor Dent Endod 38:98–102 [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Laumann TO, Snyder AZ, Mitra A, Gordon EM, Gratton C, Adeyemo B, et al. . 2017. On the stability of BOLD fMRI correlations. Cereb Cortex 27:4719–4732 [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Liao XH, Xia MR, Xu T, Dai ZJ, Cao XY, Niu HJ, et al. . 2013. Functional brain hubs and their test–retest reliability: a multiband resting-state functional MRI study. Neuroimage 83:969–982 [DOI] [PubMed] [Google Scholar]
  24. Liu TT, Nalci A, Falahpour M. 2017. The global signal in fMRI: nuisance or information? Neuroimage 150:213–229 [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Liu X, Duyn JH. 2013. Time-varying functional network information extracted from brief instances of spontaneous brain activity. Proc Natl Acad Sci U S A 110:4392–4397 [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Liu Z, de Zwart JA, Yao B, van Gelderen P, Kuo LW, Duyn JH. 2012. Finding thalamic BOLD correlates to posterior alpha EEG. Neuroimage 63:1060–1069 [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Majeed W, Magnuson M, Hasenkamp W, Schwarb H, Schumacher EH, Barsalou L, Keilholz SD. 2011. Spatiotemporal dynamics of low frequency BOLD fluctuations in rats and humans. Neuroimage 54:1140–1150 [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. McGraw KO, Wong SP. 1996. Forming inferences about some intraclass correlation coefficients. Psychol Methods 1:30–46 [Google Scholar]
  29. Murphy K, Fox MD. 2017. Towards a consensus regarding global signal regression for resting state functional connectivity MRI. Neuroimage 154:169–173 [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Nomi JS, Vij SG, Dajani DR, Steimke R, Damaraju E, Rachakonda S, et al. . 2017. Chronnectomic patterns and neural flexibility underlie executive function. Neuroimage 147:861–871 [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Olbrich S, Mulert C, Karch S, Trenner M, Leicht G, Pogarell O, Hegerl U. 2009. EEG-vigilance and BOLD effect during simultaneous EEG/fMRI measurement. Neuroimage 45: 319–332 [DOI] [PubMed] [Google Scholar]
  32. Petridou N, Gaudes CC, Dryden IL, Francis ST, Gowland PA. 2013. Periods of rest in fMRI contain individual spontaneous events which are related to slowly fluctuating spontaneous activity. Hum Brain Mapp 34:1319–1329 [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Power JD, Barnes KA, Snyder AZ, Schlaggar BL, Petersen SE. 2012. Spurious but systematic correlations in functional connectivity MRI networks arise from subject motion. Neuroimage 59:2142–2154 [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Power JD, Mitra A, Laumann TO, Snyder AZ, Schlaggar BL, Petersen SE. 2014. Methods to detect, characterize, and remove motion artifact in resting state fMRI. Neuroimage 84:320–341 [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Prichard D, Theiler J. 1994. Generating surrogate data for time series with several simultaneously measured variables. Phys Rev Lett 73:951–954 [DOI] [PubMed] [Google Scholar]
  36. Richter S, Marsalek K, Glatz C, Gundel A. 2005. Task‐dependent differences in subjective fatigue scores. J Sleep Res 14:393–400 [DOI] [PubMed] [Google Scholar]
  37. Salimi-Khorshidi G, Douaud G, Beckmann CF, Glasser MF, Griffanti L, Smith SM. 2014. Automatic denoising of functional MRI data: combining independent component analysis and hierarchical fusion of classifiers. Neuroimage 90:449–468 [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Shah LM, Cramer JA, Ferguson MA, Birn RM, Anderson JS. 2016. Reliability and reproducibility of individual differences in functional connectivity acquired during task and resting state. Brain Behav 6:e00456. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Shakil S, Lee CH, Keilholz SD. 2016. Evaluation of sliding window correlation performance for characterizing dynamic functional connectivity and brain states. Neuroimage 133:111–128 [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Shehzad Z, Kelly AM, Reiss PT, Gee DG, Gotimer K, Uddin LQ, et al. . 2009. The resting brain: unconstrained yet reliable. Cereb Cortex 19:2209–2229 [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Shirer WR, Ryali S, Rykhlevskaia E, Menon V, Greicius MD. 2012. Decoding subject-driven cognitive states with whole-brain connectivity patterns. Cereb Cortex 22:158–165 [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Shrout PE, Fleiss JL. 1979. Intraclass correlations: uses in assessing rater reliability. Psychol Bull 86:420–428 [DOI] [PubMed] [Google Scholar]
  43. Siegel JS, Power JD, Dubis JW, Vogel AC, Church JA, Schlaggar BL, Petersen SE. 2014. Statistical improvements in functional magnetic resonance imaging analyses produced by censoring high‐motion data points. Hum Brain Mapp 35:1981–1996 [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Tagliazucchi E, Balenzuela P, Fraiman D, Chialvo DR. 2012. Criticality in large-scale brain fMRI dynamics unveiled by a novel point process analysis. Front Physiol 3:15. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Tagliazucchi E, Laufs H. 2014. Decoding wakefulness levels from typical fMRI resting-state data reveals reliable drifts between wakefulness and sleep. Neuron 82:695–708 [DOI] [PubMed] [Google Scholar]
  46. Thompson G, Magnuson M, Merritt M, Schwarb H, Pan W, McKinley A, et al. . 2013. Short time windows of correlation between large scale functional brain networks predict vigilance intra-individually and inter-individually. Hum Brain Mapp 34:3280–3298 [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Van Essen DC, Smith SM, Barch DM, Behrens TE, Yacoub E, Ugurbil K; WU-Minn HCP Consortium. 2013. The WU-Minn Human Connectome Project: an overview. Neuroimage 80:62–79 [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Varikuti DP, Hoffstaedter F, Genon S, Schwender H, Reid AT, Eickhoff SB. 2017. Resting-state test–retest reliability of a priori defined canonical networks over different preprocessing steps. Brain Struct Funct 222:1447–1468 [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Ward JH. 1963. Hierarchical grouping to optimize an objective function. J Am Stat Assoc 58:236–244 [Google Scholar]
  50. Wong CW, DeYoung PN, Liu TT. 2016. Differences in the resting-state fMRI global signal amplitude between the eyes open and eyes closed states are related to changes in EEG vigilance. Neuroimage 124(Pt A):24–31 [DOI] [PubMed] [Google Scholar]
  51. Wong CW, Olafsson V, Tal O, Liu TT. 2013. The amplitude of the resting-state fMRI global signal is related to EEG vigilance measures. Neuroimage 83:983–990 [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Yousefi B, Shin J, Schumacher EH, Keilholz SD. 2018. Quasi-periodic patterns of intrinsic brain activity in individuals and their relationship to global signal. Neuroimage 167:297–308 [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Zuo XN, Xu T, Jiang L, Yang Z, Cao XY, He Y, et al. . 2013. Toward reliable characterization of functional homogeneity in the human brain: preprocessing, scan duration, imaging resolution and computational space. Neuroimage 65:374–386 [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplemental data
Supp_Data.pdf (230.3KB, pdf)

Articles from Brain Connectivity are provided here courtesy of Mary Ann Liebert, Inc.

RESOURCES