Damage Caps and Defensive Medicine: Reexamination with Patient-Level Data

Abstract

Physicians often claim that they practice “defensive medicine,” including ordering extra imaging and laboratory tests, due to fear of malpractice liability. Caps on noneconomic damages are the principal proposed remedy. Do these caps in fact reduce testing, overall health-care spending, or both? We study the effects of “third-wave” damage caps, adopted in the 2000s, on specific areas that are expected to be sensitive to med mal risk: imaging rates, cardiac interventions, and lab and radiology spending, using patient-level data, with extensive fixed effects and patient-level covariates. We find heterogeneous effects. Rates for the principal imaging tests rise, as does Medicare Part B spending on laboratory and radiology tests. In contrast, cardiac intervention rates (left-heart catheterization, stenting, and bypass surgery) do not rise (and likely fall). We find some evidence that overall Medicare Part B rises, but variable results for Part A spending. We find no evidence that caps affect mortality.

I. Introduction

Physicians often claim that they practice “defensive medicine,” notably ordering extra imaging and laboratory tests, due to fear of medical malpractice (“med mal”) liability, which drives up health-care costs. The concept of defensive medicine has no precise definition, but includes conducting tests and procedures with no (or even negative) clinical value, or whose value is too low to justify the associated cost. Imaging and laboratory tests are widely believed to be overused, partly for defensive reasons. An often proposed remedy is caps on noneconomic damages.

We study whether damage caps affect imaging rates, cardiac interventions, and lab and radiology spending, using patient-level data, with extensive fixed effects and patient-level covariates. Relative to prior research on defensive medicine, much of which principally studies overall spending, we innovate in two principal ways. First, we study specific areas that are likely to be sensitive to med mal risk. Second, we use a very large longitudinal dataset (the 5 percent Medicare random sample, covering around 2 M patients), with zip code fixed effects (FE), plus extensive covariates.

We study “third-wave” damage caps, adopted during 2002–2005. We use a difference-in-differences (DiD) research design. We compare nine “New-Cap” states that adopted caps during this period to a narrow control group of 20 “No-Cap” states, with no caps in effect during our sample period, and a broad control group that also includes the 22 “Old-Cap” states, with caps in effect throughout our sample period. We study rates for the principal cardiac stress tests (stress electrocardiogram [stress ECG], stress echocardiography [stress echo], and single-photon emission computed tomography [SPECT]); other computed tomography (CT) scans, and magnetic resonance imaging (MRI). We also study the principal invasive cardiac procedures: left-heart catheterization (LHC, also called coronary angiography); percutaneous intervention (PCI, often called stenting); cardiac artery bypass grafting (CABG); and any revascularization (PCI or CABG). For spending, we study two categories that are generally thought to be sensitive to malpractice risk—outpatient laboratory (“lab”) and radiology spending (including stress tests, MRI, and CT scans) (e.g., Baicker et al. 2007). We also study overall Medicare Part A and Part B spending, for comparison to prior studies.

Our base specification uses No-Cap states as the control group, and includes zip code and calendar year FE, plus extensive patient-level and county-level covariates. Thus, we ask whether caps affect testing rates, cardiac intervention rates, and lab and imaging spending, in the same location, with controls for patient age, comorbidities, and other time-varying factors that could affect clinical decisions. To this base specification, we also add either patient * zip code FE (“patient FE,” which control for unobserved but time- constant patient health characteristics) or physician * zip code FE (“physician FE,” which control for unobserved but time-constant physician FE). There are advantages and costs to either patient or physician FE; we cannot feasibly use both. The choice of whether to prefer the narrower or broader control group is also a close one. We also assess the sensitivity of our results to a number of alternative specifications, including using more or fewer covariates, controlling for tort reforms other than damage caps, and adding linear state trends.

Note that physicians may respond to malpractice risk in two distinct ways. They may order tests and other procedures with little or no health benefit that reduce malpractice risk—sometimes called “assurance behavior.” Physicians may also avoid risky patients or risky procedures—sometimes called “avoidance behavior.” If risk declines, physicians may engage in both less assurance behavior (hence fewer tests and lower spending), and less avoidance behavior (hence higher spending, and perhaps more testing as well). Providers may also order tests and perform procedures with limited clinical value for reasons other than liability risk, including economic incentives, patient preferences, desire to be thorough, and local norms. If physicians have multiple reasons to “do more,” tort reform could have only a modest impact on clinical decisions and spending. Thus, the effect of caps on imaging rates and other clinical decisions is an empirical question. The balance between the effect of caps on assurance versus their effect on avoidance behavior could vary across physicians, patients, and procedures.

We find heterogeneous results, consistent with the balance between assurance and avoidance behavior varying across patients and procedures. Point estimates are directionally consistent with patient and physician FE. Cardiac stress testing rates rise and, in most specifications, MRI and CT rates also rise. Using a distributed lag specification, which allows the effect of caps to phase in during the postcap period, point estimates for percentage increases in testing rates are generally in the mid-single digits with both patient FE and physician FE. These results are not entirely robust, however. The increases in stress testing and MRI are statistically significant or marginally significant across specifications, but could reflect continuation of pretreatment trends. The rise in CT scan rates is significant across most specifications, with flat pretreatment trends, but weakens if we include state-specific linear trends.

The conventional wisdom is that physicians conduct more testing in response to malpractice risk. Our results for stress tests, MRI, and CT scans provide no support for this view. They instead provide evidence of, if anything, modestly higher testing rates following damage cap adoptions.

In contrast, cardiac intervention rates appear to fall. With physician FE, which is our preferred specification for cardiac procedures, all point estimates are negative and statistically significant, and of substantial economic magnitude—9–20 percent depending on the procedure. With patient FE, the percentage point estimates are smaller and statistically insignificant, but still meaningful at around 4–6 percent.

Turning from specific tests and procedures to spending, we find evidence for modest increases in radiology and lab spending. Radiology spending (which includes stress tests, MRIs, and CT scans, among other tests) rises by 6 percent with patient FE and by 10 percent with physician FE, with strong statistical significance and flat pretreatment trends. Lab spending rises insignificantly, but this is relative to declining pretreatment trends. Combined lab and radiology spending rises by a significant 4 percent with patient FE and by 6 percent with physician FE, again with flat pretreatment trends. Here, too, our results are contrary to conventional wisdom.

For broad spending categories, we can use physician FE only for Part B spending; physician identities are not available for Part A (hospital) spending. The point estimates for Part B spending are positive and significant at +3.8 percent with patient FE, and significant but smaller in magnitude at +1.9 percent with physician FE; the estimates are significant or marginally significant in most specifications, but become smaller and lose significance when we include linear state trends. The coefficient for Part A spending with patient FE is similar in magnitude at +3.5 percent, but is insignificant in all specifications, and is near zero (indeed, slightly negative) without patient FE. Combined Part A and Part B spending is positive and marginally significant at +3.6 percent with patient FE, but near zero and insignificant without patient FE.¹ The point estimates with patient FE, which is the stronger specification, are close to those reported by Paik et al. (2017) using county-level data. Thus, here, too, we find no support for claims by damage cap supporters that caps will limit healthcare spending, and modest evidence of higher spending.

We find no evidence that damage caps affect mortality. This is expected given the modest effects of caps on utilization, and the likelihood that any effects are principally for patients at the margin for being tested or treated, versus not.

A core finding is that damage caps do not have a unidirectional effect on clinical decisions; instead, procedure rates and spending appear to rise in some areas and fall in others. Determining how caps affect specific clinical decisions requires close examination of particular practice areas. We begin that effort in a companion paper (Steven Farmer et al. 2018), where we focus on clinical decisions whether to conduct an initial ischemic evaluation for possible coronary artery disease (CAD), how to conduct that evaluation, and whether to engage in follow-up testing or treatment. We find that overall ischemic evaluation rates do not change—the rise in stress test rates that we find here is offset by lower use of LHC as an initial diagnostic test. We also find a sharp drop in progression from an initial stress test to LHC (as a second, more precise test), and in progression from ischemic evaluation to revascularization. These results are consistent with physicians being more willing to tolerate clinical ambiguity and accompanying med mal risk when med mal risk falls. These nuanced results for CAD testing and treatment make sense of the otherwise puzzling finding that stress testing, if anything, rises after cap adoption. Clinically plausible stories can also explain our counterintuitive evidence for higher CT and MRI rates, and greater overall lab and imaging spending, after cap adoption.

The heterogeneous effects from damage caps, and lack of evidence for lower over-all health-care spending, suggest that if the policy goal is to limit health-care spending, damage caps are simply the wrong tool. If the goal is to reduce physician incentives to engage in assurance behavior by ordering tests with little or no clinical value, damage caps are too blunt a tool to achieve that goal.

The rest of the article is organized as follows: Section II provides a literature review. Section III describes the data and estimation strategy. Section IV presents results for procedure rates. Section V presents results for Medicare spending. Section VI provides results for mortality rates. Section VII provides robustness checks. Section VIII discusses our findings and some study limitations, and Section IX concludes.

II. Literature Review

A. Effects of Damage Caps on Malpractice Risk

Many states have adopted a variety of tort reforms that are intended to reduce med mal liability risk. Damage caps, adopted in 31 states as of the end of the third reform wave in the early 2000s, are the most important of the commonly adopted reforms. There is evidence that they significantly reduce both claim rates and payout per claim. In the principal datasets, which cover only closed claims, the effects on claim rates and payouts appear gradually during the postreform period as prereform claims are closed (Paik et al. 2013a, 2013b).²

B. Effects of Damage Caps on Health-Care Spending

A principal policy rationale for cap adoption is the belief that caps will decrease defensive medicine and its associated costs. However, studies of the impact of damage caps on health-care spending find mixed results. We discuss prior DiD studies here; Paik et al. (2017) provide a recent, more complete review.³

The best-known studies are by Kessler and McClellan (1996, 2002). They studied the effect of mid-1980s damage caps on Medicare spending for in-hospital care for heart disease (acute myocardial infarction or ischemic disease) and found that damage caps and other “direct” tort reforms reduced in-hospital spending over the next year by 4–5 percent without adverse health outcomes. The Congressional Budget Office (CBO 2006) found a 5.2 percent drop in Part A (hospital services) spending. However, when the CBO controlled for hospital prices prior to the 1984 implementation of the Medicare prospective payment system for hospitals, the estimated postcap drop in Part A spending fell to 1.6 percent and was statistically insignificant. The CBO also found a statistically insignificant 1.7 percent drop in Part B spending. Sloan and Shadle (2009) studied the effect of second-wave tort reforms on Medicare spending for hospitalized patients, in the year in which hospitalization occurs for heart attack, breast cancer, diabetes, and stroke over 1984–2000, with mixed results across these conditions.

Paik et al. (2017) study third-wave damage caps using county-level spending data. They found that damage caps have no significant impact on Part A spending, but predict 4–5 percent higher Medicare Part B spending. Avraham and Schanzenbach (2015 [A&S]) study in-hospital treatment of patients with acute myocardial infarction (AMI, or heart attack) after third-wave reforms and find a postcap increase in medical management and a corresponding drop in combined PCI and CABG rates, but also substitution away from less-invasive PCI toward more-invasive CABG.

A notable non-DiD study by Baicker et al. (2007) used med mal payments by physicians reported to the National Practitioner Database and med mal insurance premia from Medical Liability Monitor as a proxy for med mal risk. They found an insignificant overall association between med mal premia and total Medicare spending, but found that higher premia predict higher spending on imaging tests, but not for other diagnostic tests.

C. Trends in Diagnostic Imaging Procedures

Rates for various imaging rates increased through 2005–2010, depending on the test, but have since leveled off or even declined (e.g., Lucas et al. 2006; Andrus & Welch 2012; results for our sample in the Appendix in the Supporting Information). Physician fear of malpractice has been cited as a reason for higher utilization of diagnostic testing for emergency department patients presenting with possible acute coronary syndrome (Katz et al. 2005; Kanzaria et al. 2015).

In response to rising imaging rates, several organizations launched initiatives aimed at reducing inappropriate testing. In 2005, the American College of Cardiology Foundation in conjunction with subspecialty societies and organizations developed Appropriate Use Criteria for echocardiography, nuclear cardiology, and interventional cardiology (Hendel et al. 2013). The criteria are periodically revised as new evidence emerges. In 2009, the National Physicians Alliance launched the Choosing Wisely Campaign (Morden et al. 2014). There is some evidence that these campaigns have reduced cardiac imaging rates for low-risk patients (Rosenberg et al. 2015), which could help explain why, in our data, cardiac stress testing rates peak in the mid-2000s, and then begin to decline.

D. Med Mal Risk and Physician Specialty

While all specialties face a reasonable chance of facing a malpractice claim, there is substantial variation in the likelihood of a malpractice lawsuit and the size of payouts by specialty (Jena et al. 2011). Which physicians we study in this project depends on which outcomes one is looking at. Cardiac imaging tests are ordered and performed principally, but not exclusively, by cardiologists. LHC and PCI are performed by interventional cardiologists; CABG is performed by cardiac surgeons. Cardiologists have moderate malpractice risk compared with other specialties, while cardiac surgeons face relatively high risk. Other imaging tests, including CT scans and MRIs, are ordered by a wide range of specialties.

III. Data and Methodology

A. Datasets and Covariates

Our core dataset is the 5 percent Medicare fee-for-service random sample, covering Medicare Part A (hospital services, both inpatient and outpatient) and Part B (physician services), for patients age 65+. Our cap adoption events are from 2002–2005. We report our principal, regression-based results using data for 1999–2011.⁴ In univariate calendar time graphs, presented in the Appendix (see Supporting Information), we extend the sample period through 2013. These are patient-level data on roughly 2 million beneficiaries per year. They include complete “claims” data—all tests, procedures, diagnoses, physician visits, and so forth, and actual Medicare payments for these services, but not clinical data, such as lab test results. Medicare should be the principal source of insurance for most patients, but we do not observe other sources, such as “Medigap” insurance. As beneficiaries leave the sample (principally through death), the sample is “refreshed” with new beneficiaries, about 70 percent of whom are age 65 when they enter our sample.

Our principal outcome variables are 0–1 count variables for whether a beneficiary received a test or procedure in a given year, or Medicare spending in 1999 dollars.⁵ The tests we study are cardiac stress tests (stress ECG, stress echo, and SPECT), CT scans (other than SPECT), and MRIs. The cardiac interventions we study are LHC (an invasive diagnostic test) and revascularization through PCI or CABG. The Medicare spending categories we study are outpatient radiology and lab spending, and overall Part A, Part B, and “total” (Part A plus Part B) spending. The Appendix (see Supporting Information) contains details on the diagnostic codes we use to define our outcome variables.

We include the following patient-level covariates: dummy variables for male, white, black (the omitted race category is “other”), for each of the 17 elements of the Charlson comorbidity index, and for patient age in years.⁶ We include the following time-varying county characteristics: percent male, white, black, Hispanic, aged 65–74, 75–84, and 85+ and above, In(population), active practicing nonfederal physicians per capita, unemployment rate, ln(median household income), percent of Medicare enrollees receiving Social Security disability benefits, and managed-care penetration (fraction of Medicare recipients enrolled in Medicare Advantage plans; linear and quadratic).⁷

Table 1 provides a covariate balance table for 2002, just before the third reform wave. We compare the means for outcome variables and covariates in New-Cap and NoCap states. Treatment intensity is generally higher in the New-Cap states. Stress echo is an exception, but patients in New-Cap states receive more stress ECGs, SPECT tests, and more total stress tests. All differences are statistically significant due to the large sample size. A better measure of whether the differences are large is the “normalized difference” measure defined in Table 1—roughly, how many standard deviations apart the two groups are. At the same time, treatment intensity per physician is similar—physicians in New-Cap states conduct stress tests on a similar proportion of their patients. This should make the physician FE specification less vulnerable to concerns about nonparallel trends, driven by underlying differences in population testing rates.

Table 1:

Summary Statistics and Covariate Balance

				New- v. No-Cap
States	New-Cap	No-Cap	Old-Cap	ND	T Test	Repeat Patients	Repeat Treated Patients
Per-patient rates
Imaging (number per 1,000 patients)
Stress echo	10.81 (0.41)	12.18 (0.42)	16.71 (0.48)	0.11	2.34**	25,256	4,139
SPECT	74.88 (1.07)	61.64 (0.87)	56.05 (0.79)	0.47	9.59***	244,692	55,589
Stress ECG	14.58 (0.30)	12.95 (0.28)	18.60 (0.35)	0.19	3.91***	22,002	3,995
Any Stress Test	95.78 (1.09)	82.76 (0.92)	86.05 (0.89)	0.44	9.10***	310,610	73,123
MRI	87.73 (0.97)	81.07 (0.89)	77.65 (0.76)	0.25	5.06***	337,918	65,275
CT scan	190.23 (1.59)	185.88 (1.51)	169.31 (1.26)	0.10	1.98**	750,306	149,068
Cardiac procedures (number per 1,000 patients)
LHC	32.22 (0.53)	26.42 (0.41)	25.47 (0.35)	0.42	8.68***	72,537	15,858
LHC or stress test	110.02 (1.16)	94.56 (0.99)	97.15 (0.94)	0.49	10.10***	353,827	83,581
PCI	10.26 (0.18)	9.00 (0.18)	8.94 (0.15)	0.24	4.95***	20,329	3,535
CABG	4.99 (0.12)	4.59 (0.11)	4.31 (0.10)	0.12	2.40**	261	64
PCI or CABG	14.82 (0.24)	13.28 (0.21)	12.88 (0.37)	0.23	4.83***	25,973	4,787
Medicare spending per enrollee (in 1999 $s)
Laboratory	219.46 (2.53)	220.97 (2.24)	225.03 (2.60)	0.02	0.44	1,626,609	436,826
Imaging	193.56 (2.38)	187.55 (1.93)	175.31 (1.69)	0.10	1.96**	1,450,322	384,155
Imaging + lab	413.02 (4.74)	408.52 (3.96)	400.35 (4.01)	0.03	0.72	1,907,955	506,600
Part A	2732.96 (27.19)	2863.21 (41.68)	2693.99 (30.17)	0.13	2.62**	685,616	146,396
Part B	2033.04 (19.46)	1976.70 (18.17)	1964.03 (17.05)	0.10	2.11**	1,699,704	458,688
Total	4765.99 (42.63)	4839.91 (56.06)	4658.03 (44.37)	0.05	1.05	1,704,428	459,616
Per-physician rates
Imaging (tests ordered by each physician per 1,000 patients)
Stress echo	1.74 (2.33)	1.79 (4.89)	2.69 (2.69)	0.01	0.26
SPECT	11.41 (5.93)	8.72 (5.70)	8.75 (6.96)	0.46	8.93***
Stress ECG	2.79 (2.37)	2.19 (1.80)	3.47 (2.62)	0.26	5.45***
Any Stress Test	15.31 (6.61)	12.28 (7.50)	14.27 (7.54)	0.43	8.37***
MRI	21.40 (10.25)	18.75 (7.54)	19.70 (10.94)	0.29	5.65***
CT scan	42.86 (14.84)	40.08 (14.27)	39.33 (12.59)	0.19	3.70***
Cardiac procedures (number ordered by each physician per 1,000 patients)
LHC	5.04 (3.49)	3.98 (3.21)	3.96 (2.62)	0.32	6.14***
LHC or stress test	18.11 (7.49)	14.62 (8.23)	16.44 (10.25)	0.44	8.65***
PCI	1.46 (1.31)	1.23 (1.66)	1.32 (1.19)	0.15	2.95***
CABG	1.35 (1.44)	1.32 (1.78)	1.52 (1.51)	0.02	0.44
PCI or CABG	2.79 (2.13)	2.54 (2.55)	2.83 (2.08)	0.10	2.04**
Medicare spending per physician (in 1999 $s)
Laboratory	57.40 (19.06)	54.26 (15.47)	59.04 (23.00)	0.18	3.48***
Imaging	48.49 (15.88)	44.02 (12.64)	44.05 (13.34)	0.31	6.00***
Imaging + lab	105.88 (31.47)	98.28 (25.11)	103.08 (31.93)	0.27	5.15***
Part B	518.84 (105.54)	472.24 (104.65)	506.73 (107.46)	0.44	8.61***
Patient covariates
Mean age	75.65 (0.05)	75.957 (0.04)	75.71 (0.03)	0.256	5.24***
Number of Charlson comorbidities	1.09 (0.01)	1.12 (0.01)	1.06 (0.01)	0.15	3.03***
Covariates (state averages, with population weights)
Percent of population age 65–74	6.53 (0.08)	6.70 (0.05)	5.99 (0.04)	0.09	1.88*
Percent of population age 75–84	4.42 (0.06)	4.73 (0.04)	4.19 (0.03)	0.20	4.13***
Percent of population above age 85	1.45 (0.02)	1.65 (0.01)	1.45 (0.01)	0.35	7.21***
Percent white	80.16 (0.46)	82.41 (0.52)	82.14 (0.37)	0.16	3.23***
Percent black	16.41 (0.45)	13.11 (0.47)	10.15 (0.37)	0.25	5.05***
Percent Hispanic	16.30 (0.65)	8.92 (0.34)	15.31 (0.46)	0.50	10.10***
Percent male	49.11 (0.04)	48.77 (0.04)	49.36 (0.03)	0.279	5.72***
Percent below poverty line	13.24 (0.17)	11.75 (0.17)	11.63 (0.13)	0.30	6.20***
Unemployment rate	5.95 (0.06)	5.82 (0.07)	5.90 (0.06)	0.07	1.40
Managed-care penetration	10.78 (0.42)	13.04 (0.45)	17.66 (0.48)	0.18	3.68***
Physician per capita	2.01 (0.04)	2.51 (0.06)	2.57 (0.05)	0.34	7.08***
Percent of Medicare enrollees who are disabled	14.24 (0.13)	14.73 (0.14)	13.61 (0.11)	0.12	2.53**
Population (millions)	0.11 (0.002)	0.11 (0.003)	0.09 (0.003)	0.01	1.07
Median household income ($ thousands)	41.01 (0.33)	43.78 (0.39)	45.95 (0.34)	0.26	5.42***

Notes: The table presents summary statistics for 2002 (just before third reform wave) for outcome variables and averages for outcome variables and selected covariates for nine treated states versus 20 No-Cap states, normalized difference, and two-sample t test for difference in means. Amounts in 1999 $s. Normalized difference (ND) is defined as $N{\text{D}}_j=\left({\overline{x}}_{jt}{\overline{x}}_{jc}\right)/{\left[\left(s_{jt}^2+s_{jc}^2\right)/2\right]}^{1/2}$ (see Imbens Sc Rubin 2015). Repeat patients are those who have the same test or procedure more than once during the sample period; repeat treated patients live in treated states and have the same test or procedure both before and after cap adoption, t test is for two-sample difference in means.

^{*, **, ***}indicates statistical significance at the 10 percent, 5 percent, and 1 percent level; significant differences at 5 percent level are in boldface.

Spending differences between New-Cap and No-Cap states are smaller; the New-Cap states have somewhat lower Part A spending but higher Part B spending, slightly higher radiology spending, and similar lab spending.

With regard to covariates, Medicare recipients in New-Cap states are slightly younger and healthier (fewer comorbidities) than those in No-Cap states. New-Cap states have a lower share of white population, and higher black and Hispanic shares. New-Cap states are somewhat poorer (higher percent in poverty; lower median household income) and have lower managed-care penetration than No-Cap states.

B. Treatment and Control States

We identify treatment and control states relying on Avraham’s (2014) Database of State Tort Reforms. We use the “exact” year in which a cap is adopted; in contrast, Avra-ham’s spreadsheet accompanying his database time-shifts caps forward by six months (with some errors in coding the time shifting). Our treatment group is patients in nine treatment states that adopted nonecon caps during the third reform wave of 2002–2005: Florida (2003), Georgia (2005), Illinois (2005), Mississippi (2003), Nevada (2002), Ohio (2003), Oklahoma (2003), South Carolina (2005), and Texas (2003). The Georgia and Illinois caps were invalidated by state supreme courts in 2010; we consider these states as treated through 2009, but drop them from the sample for 2010 and after. Table App-1 in the Supporting Information provides additional information on each cap.

Our principal “narrow” control group is patients in 20 states that had no damage caps in place during our sample period. Tennessee and North Carolina adopted caps in late 2011. We treat these states as No-Cap states in 2011. We also compare the New-Cap states to a broader control group that also includes 22 “Old-Cap” states that had damage caps in effect throughout the sample period.

Many states have adopted a number of separate med mal reforms, often in packages. We view the results for damage caps as estimating the average effect of “serious” reform, with a damages cap as the central element, but often not the only element, of a reform package. Some studies of the effects of med mal reform either estimate the separate effects of a number of reforms, including damage caps, by including dummy variables for each reform in a single regression, or group different types of reforms together. We control separately for the principal reforms in sensitivity checks, but prefer our main specification because: (1) other reforms do not significantly affect med mal litigation outcomes (Paik et al. 2013b); (2) given this, we should not expect them to significantly affect our outcomes; and (3) including other reforms in a regression model may provide misleading inferences for the impact of damage caps. We summarize our concerns in a note.⁸

While limiting defensive medicine is an often-cited policy rationale for adopting damage caps, the principal political driver behind the three waves of med mal reforms, of which we study the third, has been rapidly increasing med mal insurance rates. Thus, it seems reasonable to treat these reforms as plausibly exogenous when studying for health-care outcomes. We assess below the extent to which pretreatment trends are parallel; they are reasonably so for total Medicare spending, but sometime nonparallel for other outcomes.

C. Methodology

We study two main sets of outcome variables, using several variants on a difference-in-differences (DiD) research design. First, we study rates for diagnostic imaging tests. We study the three main diagnostic imaging tests: cardiac stress tests (Any Stress Test = any stress ECG, stress Echo, or SPECT), CT scans (other than SPECT), and MRI.⁹ Second, we study rates for the most common interventional cardiac procedures—LHC, PCI, and CABG—and for any revascularization procedure (PCI or CABG). Third, we study Medicare spending. We study the specific Part B subcategories for radiology and lab spending, which are especially likely to be influenced by assurance behavior. We also study Part A, Part B, and total Medicare spending.

DiD methods are a standard way to estimate the causal impact of legal changes, including adoption of damage caps. Atanasov and Black (forthcoming) summarize the core requirements for DiD and other “shock-based” designs as: shock strength; shock exogeneity; “as-if random” assignment of patients to treated versus control states; covariate balance between treated and control states; and the only-through condition—the apparent effect of the shock on the outcome must be due only to the shock, not any other shock at around the same time.

The DiD model makes the “parallel trends” assumption that the treated and control groups would have evolved in parallel, but for the treatment. This assumption is not directly testable, but one can assess whether trends appear parallel during the pretreatment period. Parallel pretreatment trends make it more likely that the parallel trends assumption is met, especially if there is also good covariate balance between treated and control states. Conversely, lack of covariate balance increases the risk that the parallel trends assumption would be violated in the posttreatment period, even if it is met in the pretreatment period. Below, we provide graphs showing the year-by-year evolution treatment effects in event time, using the leads and lags models discussed below. The Supporting Information provides univariate graphs in calendar time of sample means for the three main groups of states: New-Cap, No-Cap, and Old-Cap.

The core innovations in our study include: (1) use of a very large, longitudinal, patient-level dataset that allows us to follow the same patient over time; (2) use of extensive fixed effects and time-varying covariates to control for background factors that can affect outcomes; (3) studying rates for specific procedures that are often believed to be sensitive to med mal risk; and (4) careful assessment of whether any after-minus-before differences can be explained by nonparallel trends between treated and control states.

We use several graphical and regression approaches: (1) calendar-time graphs comparing treated and control groups; (2) leads and lags graphs showing pre- and posttreatment trends; (3) “simple DiD” regressions that assume the cap effect “turns on” in the year after cap adoption; and (4) “distributed lag” regressions, which allow the treatment effect to appear gradually over time. The simple DiD model allows for a one-time postreform change in outcomes and is specified in Equation (1):

$${\text{Y}}_{\text{izct}}=\mathrm{\alpha }+{\mathrm{\delta }}_{\text{z}}+{\mathrm{\gamma }}_{\text{t}}+\mathrm{\lambda }\left({\text{X}}_{\text{it}}\right)+\mathrm{\theta }\left({\text{X}}_{\text{ct}}\right)+{\mathrm{\beta }}_{*}\left({\text{cap}}_{\text{st}}\right)+{\mathrm{\epsilon }}_{\text{izt}}$$ (1)

Here, i indexes patients, z indexes the zip code in which the service was rendered (the δ_z are zip code FE), and t indexes year (the γ_t are year FE). Y_izt is either a 0–1 dummy variable for tests or procedures (did patient i received that test or procedure in zip code z in year t), or spending in one of the spending categories. X_it is a vector of patient characteristics and X_ct is a vector of time-varying county characteristics, with c indexing county. The treatment variable cap_st = 0 in control states for all t. In treated states, cap_st = 0 for years before the adoption year; =1 in years after the adoption year. For treated states, year 0 does not fit cleanly into either the pre- or postreform period. For the cap adoption year, we drop that year for treated states. We use a linear probability model (LPM) rather than a logit or probit model because the extra computational demands of logit or probit estimation are prohibitive for our very large sample. Angrist and Pischke (2009:§ 3.4.2) discuss why LPM, logit, and probit should, and in practice do, provide very similar estimates. Standard errors are clustered on state.¹⁰

We also consider the patient * zip code fixed effects (FE) model in Equation (2a), and a similar physician * zip code FE model (Equation (2b)):

$${\text{Y}}_{\text{ict}}=\nu +{\mathrm{\alpha }}_{\text{i}}+{\mathrm{\gamma }}_{\text{t}}+\mathrm{\lambda }\left({\text{X}}_{\text{it}}\right)+\mathrm{\theta }\left({\text{X}}_{\text{ct}}\right)+{\mathrm{\beta }}_{*}\left({\text{cap}}_{\text{st}}\right)+{\mathrm{\epsilon }}_{\text{izt}}$$ (2a)

$${\text{Y}}_{\text{ipct}}=\nu +{\mathrm{\alpha }}_{\text{p}}+{\mathrm{\gamma }}_{\text{t}}+\mathrm{\lambda }\left({\text{X}}_{\text{it}}\right)+\mathrm{\theta }\left({\text{X}}_{\text{ct}}\right)+{\mathrm{\beta }}_{*}\left({\text{cap}}_{\text{st}}\right)+{\mathrm{\epsilon }}_{\text{izt}}$$ (2b)

Here, α_i and α_p are the patient * zip or physician * zip FE. To investigate whether pretreatment trends differ between treatment and control states, we use a leads and lags model in event time, with the reform year set to zero, following Equation (3), and similar models that include patient * zip or physician * zip FE.

$${\text{Y}}_{\text{izct}}=\nu +{\mathrm{\delta }}_{\text{z}}+{\mathrm{\gamma }}_{\text{t}}+\mathrm{\lambda }\left({\text{X}}_{\text{it}}\right)+\mathrm{\theta }\left({\text{X}}_{\text{ct}}\right)+{\sum }_{k=4}^6\left({\mathrm{\beta }}^{{\text{k}}^{*}}{{\text{D}}_{\text{zt}}}^{\text{k}}\right)+{\mathrm{\epsilon }}_{\text{izt}}$$ (3)

Here, k indexes “event time” relative to the cap adoption year. ${\text{D}}_{\text{zt}}{}^{\text{k}}$ = 0 for control states for all t and k. For treatment states ${\text{D}}_{\text{zt}}{}^{\text{k}}$, = 1 for the k^th year relative to the adoption year, 0 otherwise. For example, ${\text{D}}_{\text{zt}}{}^{\text{-4}}$ takes the value of 1 four years before the nonecon cap adoption year, 0 otherwise; ${\text{D}}_{\text{zt}}{}^{+\text{2}}$ = 1 two years after cap adoption year, 0 otherwise. Therefore, β⁰ provides the estimated effect at the year when caps are enacted. β¹ provides the effect of reform one year after the enactment, and β⁻¹ is the estimated effect one year before the reform’s adoption. We include four leads (as many as our data will permit) and six lags in our specification. We combine years 6 and after into a single “lag 6+” dummy variable. We adjust the coefficients by subtracting β⁻³ from each so that the reported β⁻³ ≡ 0.

We also report results from a “distributed lag” model that allows for a different treatment effect in each post reform year. Without patient or physician FE, this model is:

$${\text{Y}}_{\text{izt}}=\nu +{\mathrm{\delta }}_z+{\mathrm{\gamma }}_{\text{t}}+\mathrm{\lambda }\left({\text{X}}_{\text{it}}\right)+\theta \left({\text{X}}_{\text{ct}}\right)+{\sum }_{k=0}^3\left({\mathrm{\beta }}^{{\text{k}}^{*}}{\text{D}}_{\text{zt}}^{\text{k}-\text{lag}}\right)+{\mathrm{\epsilon }}_{\text{izt}}$$ (4)

Here, the first treatment lag $D_{zt}^{0lag}$ equals 1 for a patient in a treated state in the cap adoption year and all subsequent years; $D_{zt}^{1lag}$ turns on in the year after reform, and stays on, $D_{zt}^{2lag}$ turns on in the second year after reform, and stays on, and so on for additional lags. Thus, the coefficient on $D_{zt}^{0lag}$ estimates the impact of reform in the year of reform; the coefficient on $D_{st}^{1lag}$ estimates the additional impact in the first full year after reform; the coefficient on $D_{zt}^{2lag}$ estimates the additional impact in the second year after reform, and so on. One can sum the lagged effects to obtain an overall treatment effect $\left({\sum }_{k=0}^n{\mathrm{\beta }}^k\right),$ and accompanying t statistic (using the lincom command in Stata). The principal difference between the leads and lags and distributed lag models is that the leads and lags model provides a coefficient and standard error for each year by itself, relative to a base year. In contrast, the distributed lag model provides estimates for annual incremental changes, starting from a prereform average; we then compute a “sum of coefficients” for the postreform period.

D. Benefits and Costs of Using Patient or Physician FE

We can follow patients over time, and thus potentially use patient FE to control for unobserved but time-invariant patient characteristics, when we measure the effect of cap adoption. However, patient fixed effects can be problematic for revascularization because some of the identifying variation comes from patients who receive revascularization more than once, yet the first procedure changes the patient. This is a concern principally for PCI; repeat CABG is rare. Table 1 shows the number of patients who have each procedure more than once.

Alternatively, we can use physician FE (not available for Part A spending) to control for unobserved, time-invariant physician characteristics. This is our preferred specification when available; it allows us to estimate the effect of cap adoption on the behavior of the same physicians However, physician FE have two costs. First, if a patient does not see any physician in a given time period, with patient FE we can treat this as a true zero, but with physician FE, the observation is missing because we do not know which physician to which to assign this patient. Second, caps could affect which physicians choose to move to, or start practicing in, a state, as well as how physicians already there choose to practice. We lose that source of variation if we use physician FE.

We respond to these considerations by reporting results with patient FE, physician FE (where available), and neither, and assess robustness across these three approaches. Using both patient and physician FE, regressions on a large sample is challenging; regressions do not run in a reasonable time period, even on a well-powered server.

IV. Results for Diagnostic Imaging Tests and Cardiac Procedures

A. Imaging Tests

Physicians often cite fear of malpractice liability as an important driver of overuse of diagnostic testing (Katz et al. 2005; Kanzaria et al. 2015). We examine here the effects of damage cap adoption on rates for the three main cardiac stress testing (stress ECG, stress ECHO, and SPECT), and two major noncardiac imaging tests: CT scans, and MRI.

1. Leads and Lags Graphs for Imaging Tests

Figure 1 presents leads and lags graphs of the treatment effects in event time for Any Stress Test, CT scan, and MRI, without patient FE (left-hand graphs), with patient FE (middle graphs), and with physician FE (right-hand graphs). In Figure 1, the y-axis shows coefficients on annual lead and lag dummies; vertical bars show 95 percent confidence intervals (CIs) around each coefficient. We peg the coefficient for Year –3 to zero, so there is no associated CI.

Figure 1: Imaging rates: leads and lags graphs of effect of damage cap adoption.

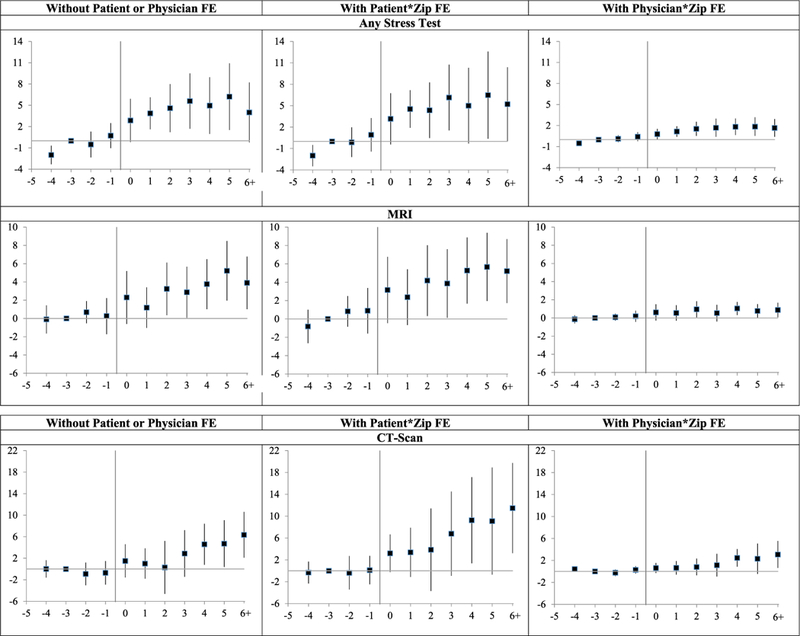
Notes: Leads and lags regressions (linear probability model) of dummy variables for whether a patient had the indicated imaging test in a given year, for nine New-Cap states versus narrow control group of 20 No-Cap states, over 1999–2011. Leads and lags coefficients are multiplied by 1,000, so provide predicted effect of cap on annual rates per 1,000 patients. Sample, covariates, and fixed effects are the same as for corresponding regressions in Table 2 (with patient * zip FE, physician * zip FE, or neither). y-axis shows coefficients on lead and lag dummies; vertical bars show 95 percent confidence intervals (CIs) around coefficients, using standard errors clustered on state. Coefficient for Year −3 is set to zero.

Consider first Any Stress Test. In all three graphs, postcap rates are higher than precap rates. However, there is also a rising pretreatment trend. We cannot tell with confidence whether the postreform rise in rates that we observe is a true increase in response to reform versus continuation of a pretreatment trend. We can say, however, that there is no evidence of a drop in stress testing rates after cap adoption.

Note, too, that coefficient magnitudes are much smaller with physician FE than in the other two specifications. The smaller magnitude coefficients with physician FE persist across outcomes.

For MRI, Figure 1 also shows a postreform increase in rates across specifications. There is some evidence of nonparallel pretreatment trends with patient FE, but no similar trends in the other specifications. For CT scans, we again find higher postreform rates, and the pretreatment trends are reasonably flat in all three specifications.

Taken as a whole, there is no evidence that imaging rates fall after cap adoption. There is some evidence—strongest for CT scans—that imaging rates rise. We return in the discussion section to what might cause these increases, assuming they are real.

2. Regression Results for Imaging Tests

Table 2, Panel A, presents the results of simple DiD regressions, using No-Cap states as the control group, without patient FE (first three regressions), with patient FE (next three regressions), and with physician FE (last three regressions). These regressions assume a one-time change in outcomes due to cap adoption. The coefficients on the damage cap variable can be interpreted as the change in the probability of receiving the indicated test in a given year due to a state adopting a damage cap.

Table 2:

DiD Regression Analyses: Effect of Damage Caps on Imaging Test Rates

	No			Patient * Zip			Physician * Zip
Patient or Physician FE	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)
Dependent Variable	Any Stress Test	MRI	CT	Any Stress Test	MRI	CT	Any Stress Test	MRI	CT
Panel A: Simple DiD
Damage cap dummy	4.04***	1.48	3.92**	5.30***	3.05**	6.38**	0.99***	0.42	1.21*
	(1.44)	(1.21)	(1.45)	(1.32)	(1.35)	(2.72)	(0.34)	(0.32)	(0.63)
Male	0.02***	−0.02***	−0.01***				0.005***	−0.001***	0.0003**
	(0.001)	(0.001)	(0.001)				(0.0002)	(0.0001)	(0.0001)
White	0.01***	0.02***	0.02***				−0.001***	0.0001	−0.0003
	(0.001)	(0.001)	(0.001)				(0.0002)	(0.0001)	(0.0003)
Black	−0.005***	−0.002*	0.01***				−0.001***	−0.001***	−0.001**
	(0.002)	(0.001)	(0.002)				(0.0002)	(0.0002)	(0.0005)
Hispanic	0.01***	0.01***	0.03***				0.0003	0.001***	0.001*
	(0.002)	(0.003)	(0.003)				(0.0002)	(0.0001)	(0.001)
Fraction of population age	−0.14*	−0.19	−0.12	−0.08	−0.28**	−0.30	0.04	0.04	0.06
65–74	(0.08)	(0.11)	(0.11)	(0.08)	(0.13)	(0.25)	(0.03)	(0.04)	(0.05)
Fraction age 75–84	0.19	0.06	−0.04	0.06	0.10	0.43	−0.03	−0.03	−0.005
	(0.11)	(0.14)	(0.23)	(0.17)	(0.18)	(0.33)	(0.04)	(0.04)	(0.07)
Fraction age 85+	−0.16	0.29	0.26	−0.04	0.40*	0.68	−0.02	−0.02	0.09
	(0.34)	(0.19)	(0.37)	(0.43)	(0.21)	(0.60)	(0.09)	(0.06)	(0.16)
Fraction white	−0.08*	0.14***	0.30***	−0.04	0.04	0.54**	−0.03	0.04**	0.05*
	(0.04)	(0.05)	(0.06)	(0.06)	(0.06)	(0.22)	(0.02)	(0.02)	(0.03)
Fraction black	−0.20***	0.16***	0.34***	−0.18*	0.09	0.68***	−0.05*	0.03*	0.08**
	(0.07)	(0.05)	(0.09)	(0.09)	(0.07)	(0.24)	(0.03)	(0.02)	(0.03)
Fraction male	−0.01	−0.30***	−0.48***	−0.002	−0.44***	−0.58***	0.04	0.03	−0.05
	(0.11)	(0.06)	(0.13)	(0.14)	(0.09)	(0.19)	(0.05)	(0.02)	(0.08)
Fraction Hispanic	0.10***	−0.02	−0.03	0.06**	−0.002	−0.01	0.02**	−0.03***	−0.08***
	(0.03)	(0.02)	(0.03)	(0.03)	(0.02)	(0.06)	(0.01)	(0.01)	(0.02)
Fraction below poverty line	0.01	0.002	0.04*	0.01	−0.0003	0.05**	−0.0003	−0.001	0.02
	(0.02)	(0.01)	(0.02)	(0.01)	(0.02)	(0.02)	(0.005)	(0.004)	(0.01)
Unemployment rate	0.04	0.02	0.06	0.03	−0.0005	0.08*	0.01	−0.005	−0.01
	(0.03)	(0.02)	(0.04)	(0.03)	(0.02)	(0.04)	(0.01)	(0.01)	(0.01)
Fraction of population	−0.03	−0.03	0.09*	−0.06	−0.01	0.18*	−0.01	0.01	0.05**
disabled	(0.05)	(0.04)	(0.05)	(0.04)	(0.05)	(0.11)	(0.01)	(0.01)	(0.02)
Ln(population)	0.01*	0.02***	0.04***	0.01	0.02***	0.06***	0.0003	0.003	0.01**
	(0.01)	(0.01)	(0.01)	(0.01)	(0.01)	(0.02)	(0.003)	(0.002)	(0.003)
Physicians/1,000	−0.00**	0.001	0.003	−0.003*	0.001**	0.0005	−0.001**	−0.001**	−.00005
population	(0.001)	(0.001)	(0.002)	(0.002)	(0.001)	(0.003)	(0.0004)	(0.0003)	(0.001)
Ln(household median	0.02***	0.001	0.001	0.02***	−0.01	−0.003	0.003*	−0.0001	−0.002
income)	(0.005)	(0.01)	(0.01)	(0.005)	(0.01)	(0.01)	(0.001)	(0.002)	(0.003)
Medicare penetration	−0.02*	−0.02***	−0.008	−0.02	−0.03***	−0.01	−0.01***	−0.01***	−0.005*
	(0.01)	(0.01)	(0.01)	(0.01)	(0.01)	(0.02)	(0.003)	(0.002)	(0.003)
(Medicare penetration)2	0.01	0.01	−0.04**	0.003	0.02	−0.05	0.02***	0.01	0.01
	(0.02)	(0.01)	(0.02)	(0.03)	(0.02)	(0.04)	(0.005)	(0.005)	(0.01)
Constant	0.06	0.05	−0.04	−0.04	0.20***	−0.07	0.02	−0.03	0.01
	(0.05)	(0.05)	(0.08)	(0.08)	(0.06)	(0.21)	(0.03)	(0.02)	(0.04)
R2	0.05	0.03	0.11	0.36	0.34	0.41	0.11	0.11	0.11
Observations	13,524,405	13,524,405	13,524,405	11,559,309	11,559,309	11,559,309	65,438,019	65,438,019	65,438,019
Panel B: Distributed Lags
Cap adoption year or after	2.80**	1.10	2.55**	3.11**	2.40*	4 43***	0.46*	0.32	0.64*
	(1.10)	(1.16)	(1.23)	(1.14)	(1.36)	(1.49)	(0.23)	(0.29)	(0.34)
Cap Year 1 or after	0.64	−0.71	−0.50	1.34	−0.56	0.81	0.50	0.10	0.57
	(1.11)	(0.85)	(0.92)	(1.38)	(0.91)	(1.55)	(0.30)	(0.28)	(0.43)
Cap Year 2 or after	0.43	1.12	0.15	−0.37	0.90	0.77	0.20	0.18	0.04
	(0.83)	(0.75)	(1.45)	(0.86)	(0.74)	(1.63)	(0.18)	(0.11)	(0.34)
Cap Year 3 or after	0.61	−0.21	2.06	1.39	0.01	2.56	0.09	−0.35**	0.13
	(0.64)	(0.60)	(1.43)	(0.84)	(0.87)	(1.67)	(0.23)	(0.15)	(0.72)
Cap Year 4 or after	0.621	1.65	2.35	0.12	1.48	3.32	0.29	0.43	1.50***
	(1.06)	(1.17)	(1.63)	(0.99)	(1.08)	(2.49)	(0.21)	(0.29)	(0.46)
Sum of coefficients	5.09**	2.94*	6.61***	5.59**	4.22**	11.89***	1.56***	0.69*	2.88***
	(1.86)	(1.49)	(1.95)	(2.10)	(1.90)	(3.89)	(0.52)	(0.39)	(0.94)
R2	0.04	0.03	0.10	0.36	0.34	0.40	0.11	0.11	0.11
Observations	14,057,920	14,057,920	14,057,920	12,020,886	12,020,886	12,020,886	67,952,511	67,952,511	67,952,511
Percentage change	+5.3%	+3.4%	+3.5%	+5.8%	+4.8%	6.3%	+10.2%	+3.2%	+6.7%

Notes: Panel A: Simple DiD. DifFerence-in-difFerences regressions of dummy variables for whether a patient had the indicated test in a given year. Damage cap dummy =1 in New-Cap states, in years with a cap in effect. We drop cap adoption year.

Panel B: Distributed lags. Distributed lag regressions of dummy variables for whether a patient had the indicated test in a given year. Variable for “cap adoption year and after” =1 for treated states in cap adoption year and after; 0 otherwise. Variable for “cap Year n and after” = 1 is similar but turns on in Year n after cap adoption.

Both panels: Regressions use linear probability model. Coefficients on cap-related variables are multiplied by 1,000, to provide predicted effect of cap on annual rates per 1,000 patients. Regressions include indicated covariates, patient age dummies (for each year of age, from 65 on), 17 dummy variables for elements of Charlson comorbidity index, and year dummies. Regressions (l)–(3) include zip code FE. (4)–(6) include patient * zip FE (which absorb gender, race, and ethnicity). Regressions (7)–(9) include physician * zip FE. Sample period is 1999–2011. We drop IL and GA from treatment group for 2010 on due to cap reversals in 2010. Standard errors, clustered on state, in parentheses.

^{*, **, ***}indicates statistical significance at the 10 percent, 5 percent, and 1 percent level. Significant results, at 5 percent level or better, in boldface. Percentage change is relative to base rate in 2002 for new-cap states.

We prefer, and discuss below, the FE specifications; we present results without them principally for comparison, and to assess robustness. With patient FE, the predicted effect for Any Stress Test is 5.3 additional tests per 1,000 patients (t = 4.02). However, as noted above, there is evidence of nonparallel pretreatment trends. The point estimates are also positive and statistically significant for both MRI and CT scans, at 3.1 additional MRIs/1,000 patients (t = 2.26) and 6.4 additional CT scans/1,000 patients (t = 2.35). However, here, too, the positive coefficient for MRI could reflect continuation of nonparallel pretreatment trends.

In Table 2, Panel B, we present distributed lag estimates, which allow the treatment effect to phase in over time. We include the cap adoption year plus three lags; the last lag captures the average effect for Year 3 and later years. We generally prefer the distributed lag approach over simple DiD because it can better capture an effect that appears gradually over time—which, from Figure 1, appears to be the case for all three outcomes. The principal costs of this approach are: (1) larger standard errors for the sum of coefficients estimate than for simple DiD estimates; and (2) greater sensitivity to any continuation of pretreatment trends into the posttreatment period. For all three outcomes, the sum of coefficients estimates are statistically significant and larger than the simple DiD estimates, at 5.6 additional stress tests/1,000 patients (t = 2.66), 4.2 additional MRIs/1,000 patients (t = 2.22), and 11.9 additional CT scans/1,000 patients (a 6 percent increase; t = 3.06). In economic magnitude, the posttreatment rises, compared to base rates in the New-Cap states of about 96 stress tests, 88 MRIs, and 190 CT scans, imply testing rate increases of about 6 percent, 5 percent, and 6 percent, respectively—”economically” meaningful, but not huge.

When we switch to physician FE in regressions (7)-(9), the coefficients decrease substantially. However, regressions with patient versus physician FE measure different things. The coefficients from regressions with patient FE can be interpreted as the change in the number of tests per 1,000 patients, while the coefficients from regressions with physician FE can be interpreted as the change in the number of tests per 1,000 visits to a physician. The percentage changes from these two approaches are presented in Table 2 and later tables, and are similar in magnitude. The distributed lag sums of coefficients remain statistically significant for Any Stress Test and CT scans, and are marginally significant for MRI. The distributed lag sums of coefficients with physician FE imply percentage increases of around 10 percent for stress tests, 3 percent for MRIs, and 7 percent for CT scans.

B. Results for Cardiac Procedures

The results in Section IV.A for imaging tests seem contrary to simple models of assurance and avoidance behavior, which suggest that a drop in malpractice risk should reduce screening tests and other forms of assurance behavior. We consider next the three most common invasive cardiac procedures: LHC, PCI, and CABG. LHC is a minimally invasive diagnostic test that provides a more accurate assessment of coronary artery blockage than a stress test, which is noninvasive. It can be ordered either following an ambiguous stress test, or directly as an initial ischemic evaluation, when other evidence of CAD is strong enough to justify this. LHC is also a necessary precursor to revascularization through PCI or CABG. PCI is also minimally invasive—generally about a one-hour procedure, with no significant recovery period. CABG is open heart surgery—a major operation, with significant operative mortality and a lengthy recovery.

A&S (2015) examine the effect of damage caps on in-hospital treatment of heart attack patients. Their sample is very different than ours: they study heart attack patients of all ages; we study only the elderly, but do not limit to post-heart-attack treatment; many revasculariza-tions are preventive, and precede an actual heart attack. They find a postcap increase in medical management and, for patients who receive revascularization, less PCI (about a 5 percent drop) but more CABG (about a 5 percent increase).¹¹ They interpret this relative change as physicians substituting a more remunerative, but riskier procedure (CABG) for a less remunerative, safer procedure (PCI). However, their assumption that physicians have financial incentives to prefer CABG over PCI is problematic; we summarize our concerns in a note.¹²

As we did for imaging tests, we present leads and lags graphs in event time, and simple DiD and distributed lag regressions.

1. Leads and Lags Graphs for Cardiac Procedures

Figure 2 provides leads and lags graphs for cardiac procedures. Consider first the right-hand graphs, with physician FE. Pretreatment trends are reasonably flat for all three procedures. Rates for all three procedures drop postreform. Thus, with physician FE, there is consistent evidence that damage caps reduce intervention rates.

Figure 2: Cardiac intervention rates: leads and lags graphs of effect of damage cap adoption.

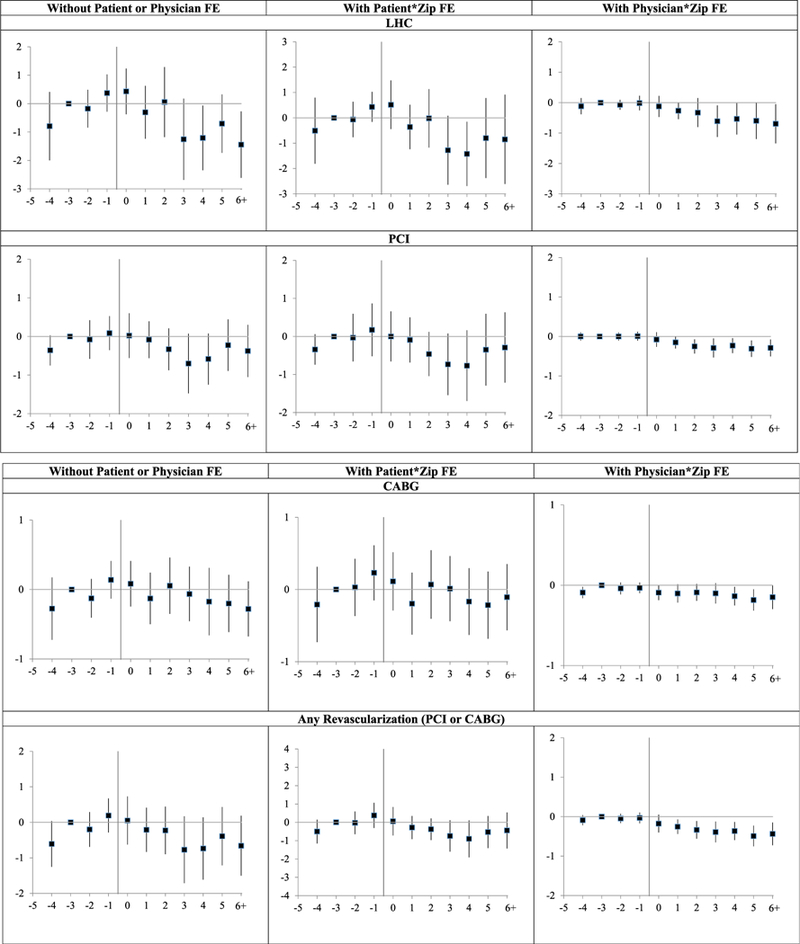
Notes: Leads and lags regressions (linear probability model) of dummy variables for whether a patient had the indicated procedure in a given year, for nine New-Cap states versus narrow control group of 20 No-Cap states, over 1999–2011. Coefficients on leads and lags are multiplied by 1,000, so provide predicted effect of cap on annual rates per 1,000 patients. y-axis shows the coefficients on the lead and lag dummies; vertical bars show 95 percent CIs around coefficients, using standard errors clustered on state. Coefficient for Year −3 is set to zero. Sample, covariates, and fixed effects are the same as for the corresponding graphs in Figure 1.

Graphical results are less clean for the other two specifications, but suggest lower intervention rates. There are rising pretreatment trends for all three outcomes. At a minimum, these rising trends flatten postcap. For LHC they mostly decline. For PCI they decline by Year+3, but rebound in Year +5. For CABG, there is no apparent postreform trend with patient FE, but a declining trend beginning in Uear +3 without either patient or physician FE.

For PCI, a competing explanation for the postcap decline is cardiologist response to the Courage trial, whose results were released early in calendar 2007 (Boden et al. 2007), thus in event years +2 to +5, depending on state. This trial compared PCI to medical management for stable CAD, and found that PCI did not reduce subsequent cardiovascular event rates or mortality. The response to this trial could vary by state, although we know of no reason to expect a larger response in the New-Cap states. Our judgment, from all three specifications, is that the postreform decline in PCI rates, and in overall revascularization rates, is likely to be a response to tort reform, but that one cannot be fully confident in that attribution.

The “any revascularization” results are driven by PCI, which is more common than CABG. These results should be interpreted with caution because they implicitly assume that the clinical choice is to revascularize or not, with PCI and CABG as substitutes. Actual decision making is more complex. For patients without acute symptoms, the principal choice will often be between medical management and PCI; for others, with stronger need for revascularization, but no acute heart attack, the principal choice may be PCI versus CABG; while for patients with acute heart attack, the immediate intervention will be PCI, which may later be followed by CABG.

2. Regression Results for Cardiac Procedures

Table 3, for cardiac procedures, is similar in structure to Table 2, for imaging tests. It presents the results for simple DiD (Panel A) and distributed lag regressions (Panel B) for LHC, PCI, CABG, and any revascularization. Regressions (1)-(4) do not use either beneficiary or physician FE; regressions (5)-(8) add patient FE, regressions (9)-(12) instead use physician FE. All coefficients, in all specifications, are negative. We discuss here the distributed lag results, which allow the cap effect to phase in over time.

Table 3:

DiD Regression Analyses: Effect of Damage Caps on Cardiac Intervention Rates

	No				Patient* Zip				Physician* Zip
Patient or Physician FE	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)	(11)	(12)
Dependent Variable	LHC	PCI	CABG	Any Revasc.	LHC	PCI	CABG	Any Revasc.	LHC	PCI	CABG	Any Revasc.
Panel A: Simple DiD
Damage cap	−0.80**	−0.30	−0.14	−0.41*	−0.29	−0.17	−0.11	−0.26	–0.47***	−0.22***	−0.08*	–0.29***
dummy	(0.39)	(0.19)	(0.11)	(0.23)	(0.44)	(0.22)	(0.14)	(0.25)	(0.16)	(0.06)	(0.04)	(0.08)
R2	0.03	0.01	0.01	0.01	0.30	0.28	0.24	0.28	0.07	0.04	0.13	0.08
Observations	13,524,405	13,524,405	13,524,405	13,524,405	11,559,309	11,559,309	11,559,309	11,559,309	65,438,019	65,438,019	65,438,019	65,438,019
Panel B: Distributed Lags Cap adoption 0.30		0.07	0.07	0.11	0.44	0.07	0.05	0.08	−0.19	−0.09	−0.06**	−0.14**
year or after	(0.30)	(0.21)	(0.08)	(0.25)	(0.42)	(0.25)	(0.11)	(0.31)	(0.13)	(0.06)	(0.03)	(0.07)
Cap Year 1 or after	−1.01**	−0.20	−0.32**	−0.44	−1.10**	−0.22	–0.41***	−0.56*	−0.19*	−0.09*	−0.03	−0.12**
	(0.38)	(0.25)	(0.15)	(0.31)	(0.41)	(0.27)	(0.12)	(0.33)	(0.09)	(0.05)	(0.03)	(0.05)
Cap Year 2 or after	0.59**	−0.15	0.29*	0.17	0.54*	−0.24	0.37**	0.12	0.01	−0.07	0.04	−0.02
	(0.26)	(0.16)	(0.16)	(0.20)	(0.30)	(0.17)	(0.17)	(0.20)	(0.08)	(0.04)	(0.04)	(0.05)
Cap Year 3 or after	−1.29***	−0.40*	−0.19	−0.64**	−1.25***	−0.34	−0.11	−0.48*	−0.29***	−0.05	−0.01	−0.06
	(0.34)	(0.22)	(0.12)	(0.24)	(0.40)	(0.24)	(0.13)	(0.27)	(0.10)	(0.04)	(0.03)	(0.05)
Cap Year 4 or after	0.15	0.26	−0.05	0.23	0.11	0.09	−0.07	0.04	0.02	0.0001	−0.07***	−0.07
	(0.43)	(0.25)	(0.14)	(0.34)	(0.39)	(0.29)	(0.11)	(0.32)	(0.12)	(0.04)	(0.02)	(0.04)
Sum of coefficients	−1.26**	−0.41	−0.20	−0.58	−1.26	−0.64	−0.18	−0.79*	−0.65**	−0.29***	−0.12**	–0.41***
	(0.47)	(0.25)	(0.16)	(0.33)	(0.77)	(0.38)	(0.20)	(0.46)	(0.26)	(0.08)	(0.06)	(0.11)
R2	0.03	0.01	0.01	0.01	0.29	0.28	0.23	0.27	0.07	0.04	0.13	0.08
Observations	14,057,920	14,057,920	14,057,920	14,057,920	12,020,886	12,020,886	12,020,886	12,020,886	67,952,511	67,952,511	67,952,511	67,952,511
Percentage change	−3.9%	−4.0%	−4.0%	−3.9%	−3.9%	−6.3%	−3.6%	−5.4%	−12.9%	−20.1%	−9.2%	−14.7%

Notes: Panel A: Simple DiD. Difference-in-differences regressions of dummy variables for whether a patient had the indicated procedure in a given year.

Panel B: Distributed lags. Distributed lag regressions of dummy variables for whether a patient had the indicated procedure in a given year.

Both panels: Regressions use linear probability model. Coefficients on cap-related variables are multiplied by 1,000, to provide predicted effect of cap on annual rates per 1,000 patients. Sample, main variables, covariates, and fixed effects are same as corresponding specifications in Table 2 (using patient * zip FE, physician * zip FE, or neither); coefficients on covariates are suppressed. Standard errors, clustered on state, in parentheses.

^{*, **, ***}indicates statistical significance at the 10 percent, 5 percent, and 1 percent level, respectively. Significant results, at 5 percent level or better, in boldface. Percentage change is relative to base rate in 2002 for New-Cap states.

Consider first the results with physician FE, which is our preferred approach for cardiac procedures. The distributed lag sums of coefficients are statistically significant in all cases, and the point estimates are economically important, at −9 percent for CABG, - 13 percent for LHC, and −20 percent for PCI. The percentage changes are smaller and statistically insignificant with patient FE, but are still of meaningful magnitude. Note that the regression models ignore the graphical evidence of rising pretreatment trends for procedure rates with patient FE. Taking the leads and lags graphs and the regressions together, we have reasonably convincing evidence—although less than definitive—of a meaningful postcap decline in procedure rates.¹³

V. Results for Medicare Spending

A. Laboratory and Radiology Spending

We turn next from counts of specific tests and procedures to Medicare spending. We first consider the subcategories of Part B spending for laboratory tests, radiology (including SPECT, MRI, and CT scans), and combined lab and radiology spending. Conventional wisdom is that if damage caps reduce assurance behavior, that should reduce spending in these categories. In contrast, we find higher spending, consistent with our assessment above that damage caps, if anything, predict higher imaging rates.¹⁴

Figure 3 provides leads and lags graphs for laboratory spending, radiology spending, and both categories combined. The radiology graphs show reasonably flat pretreatment trends. The laboratory spending graphs suggest, if anything a declining pretreatment trend. The graphs for combined laboratory and radiology spending blend both results; pretreatment trends are reasonably flat, perhaps gently declining. Spending in New-Cap states gradually increases following cap adoption for radiology spending and combined lab and radiology spending; the graphs for laboratory spending suggest a rise in spending with patient FE, but show little for the other two specifications. The individual year point estimates are statistically significant for each year from Year 0 on for radiology spending, and positive but not significant for lab spending.

Figure 3: Medicare spending: leads and lags graphs of effect of damage cap adoption. Panel A: Part B SpendingPanel B: Part A and Total Spending.

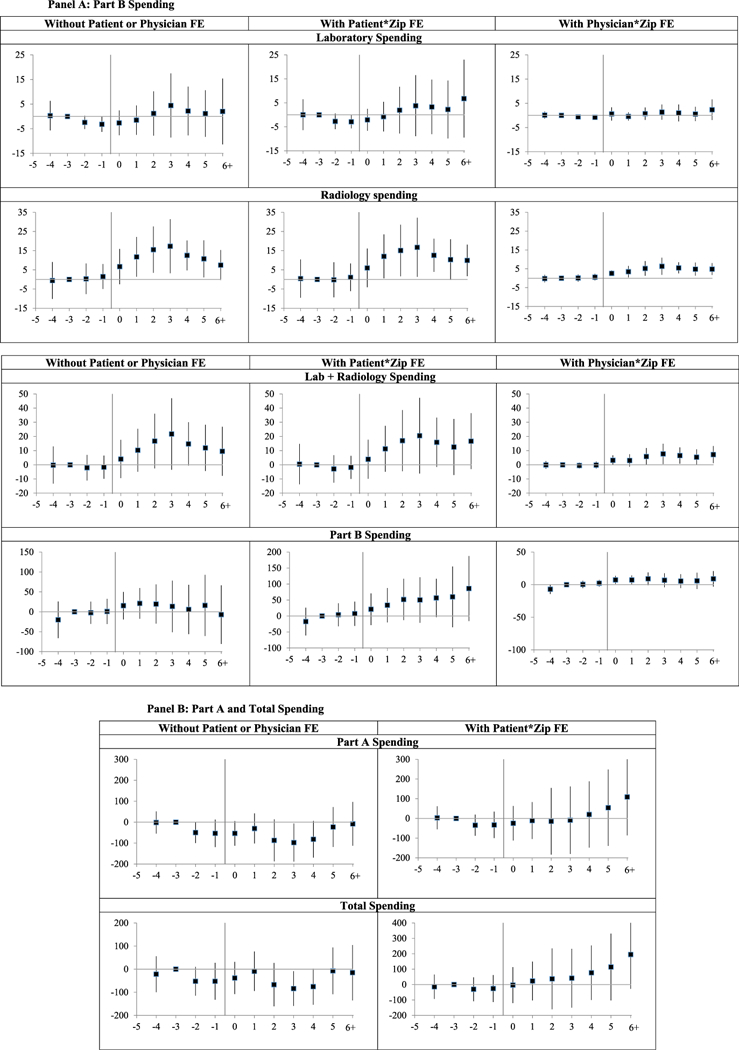
Notes: Leads and lags regressions of outpatient laboratory, radiology spending, and combined (lab and radiology) spending per beneficiary over 2000–2011, and Part A, Part B, and total Medicare spending over 1999–2011, for nine New-Cap states versus narrow control group of20 No-Cap states. y-axis shows coefficients on the lead and lag dummies; vertical bars show 95 percent CIs around coefficients, using standard errors clustered on state. Coefficient for Year −3 is set to zero. Sample, covariates, and fixed effects are the same as for the corresponding graphs in Figure 1. Amounts in 1999 $s.

Table 4 presents simple DiD and distributed lag regressions for lab, radiology, and combined lab + radiology spending. All coefficients, in all specifications, are positive. The coefficients for radiology spending and combined lab + radiology spending are always statistically significant; the coefficients for laboratory spending are not significant. We discuss here the distributed lag sums of coefficients. With patient FE, the point estimates are for $12 in additional radiology spending (around 6 percent) and $18 in combined extra spending (4.4 percent). With physician FE, the estimated percentage changes are larger, at 10.0 percent for radiology spending and 6.0 percent for combined spending. Taking the graphical and regression results together, there is evidence supporting higher combined lab and radiology spending following cap adoption, driven principally by higher radiology spending.

Table 4:

DiD Regression Analyses: Effect of Damage Caps on Outpatient Laboratory and Radiology Spending

	No			Patient * Zip			Physician * Zip
Patient or Physician FE	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)
Variables	Lab	Radiology	Both	Lab	Radiology	Both	Lab	Radiology	Both
Panel A: Simple DiD
Damage cap dummy	3.58	10.63***	14.21**	5.13	12.36***	17.53**	0.43	3.47***	3.90**
	(4.04)	(2.93)	(5.92)	(4.32)	(3.34)	(6.654)	(1.11)	(0.94)	(1.84)
R2	0.20	0.12	0.19	0.61	0.50	0.59	0.21	0.12	0.19
Observations	13,524,405	13,524,405	13,524,405	10,748,076	10,748,076	10,748,076	64,462,133	64,462,133	64,462,133
Panel B: Distributed Lags
Cap year adoption and after	1.43	4.08*	5.506	1.00	4.56*	5.57	−0.44	−2.05***	−2.49
	(2.30)	(2.21)	(3.93)	(2.16)	(2.43)	(4.14)	(1.01)	(0.68)	(1.54)
Cap Year 1 or after	−0.75	6.39**	5.636	0.61	7.05**	7.66*	0.27	5.27***	5.54**
	(1.40)	(3.03)	(3.34)	(1.48)	(3.13)	(3.83)	(1.27)	(1.41)	(2.44)
Cap year 2 or after	2.24	2.53	4.771	2.68	2.87	5.55	0.71	1.35**	2.05*
	(2.27)	(2.43)	(3.95)	(2.28)	(2.93)	(4.65)	(0.56)	(0.64)	(1.00)
Cap Year 3 or after	2.54	2.749**	5.29	1.25	2.63	3.88	0.62	1 24***	1.86**
	(2.42)	(1.25)	(3.44)	(2.62)	(1.63)	(3.86)	(0.55)	(0.41)	(0.90)
Cap Year 4 or after	−1.08	−5.905	−6.98	0.59	−4.88	−4.28	0.23	−0.80	−0.57
	(3.26)	(3.59)	(6.19)	(2.16)	(3.89)	(4.67)	(0.52)	(0.99)	(1.234)
Sum of coefficients	4.37	9.85***	14.22**	6.14	12.23***	18.37**	1.39	5.01***	6.41**
	(5.50)	(3.49)	(6.49)	(6.63)	(3.82)	(7.37)	(1.78)	(1.32)	(2.53)
R2	0.20	0.12	0.19	0.61	0.49	0.59	0.21	0.12	0.19
Observations	13,039,123	13,039,123	13,039,123	11,209,653	11,209,653	11,209,653	64,462,133	64,462,133	64,462,133
Percentage change	+2.0%	+5.1%	+3.4%	+2.8%	+6.3%	+4.4%	+2.4%	+10.3%	+6.0%

Notes: Panel A: Difference-in-differences regressions for indicated outpatient Medicare spending categories per enrollee, per calendar year, on damage cap dummy and covariates. Coefficient on damage cap dummy are multiplied by 4, so coefficients provide estimated effect of cap on annual spending per patient. Coefficients on covariates are suppressed, but presented in the Supporting Information (Table App 3).

Panel B: Distributed lag regressions for indicated Medicare spending categories per enrollee, per year. Distributed lag analysis in a given year. Coefficients on covariates are suppressed.

Both panels: Column (1): laboratory spending; Column (2): radiology spending; Column (3): combined laboratory and radiology spending. Sample, main variables, covariates, and fixed effects are same as corresponding specifications (using patient * zip FE, physician * zip FE, or neither) in Table 2; coefficients on covariates are suppressed. Amounts in 1999 $s. Standard errors, clustered on state, in parentheses.

^{*, **, ***}indicates statistical significance at the 10 percent, 5 percent, and 1 percent level, respectively. Significant results, at 5 percent level or better, in boldface. Percentage change is relative to base rate in 2002 for New-Cap states.

B. Overall Medicare Spending

We turn next, and last, to assessing the effect of damage caps on overall Medicare spending. This topic is studied in several prior papers. We examine separately Part A spending, Part B spending, and total (Part A + Part B) spending. Our principal contribution is to reexamine this issue with a large, patient-level dataset, with ability to use patient FE for all of these spending categories, and to also use physician FE for Part B spending.

1. Leads and Lags Results for Overall Spending

Figure 3 provides leads and lags graphs for these broad spending categories. The Part A graph shows a possible declining trend in relative spending prior to reform—actual spending increases in both New-Cap and No-Cap states, but increases a bit faster in NoCap states. The downward trend flattens out in Year −1 and remains flat through Year +3, before beginning a gradual rise. This delayed rise is modest and could be unrelated to cap adoption. Overall, the Part A graph provides little evidence that cap adoption meaningfully affects Part A spending.

Part B spending increases after damage cap adoption with patient FE, but this could reflect continuation of a rising pretreatment trend. There is little evidence of rising spending in the other two graphs. The total spending graph is a blend of the Part A and Part B graphs: with patient FE, point estimates are flat during the pretreatment period followed by a slight increase in years +1 to +3, well short of statistical significance, and then a strengthening trend toward higher spending beginning in Year +4.

We view the Part A, Part B, and total spending graphs, taken together, as offering mild evidence of higher postcap spending, stronger for Part B than for Part A. It is also troubling that there is evidence of nonparallel trends for both Part A and Part B spending, even though these trends roughly offset each other, leading to reasonably flat pretreatment trends for total spending.

2. Regression Results for Overall Spending

Table 5 presents simple DiD and distributed lag regressions for Part A, Part B, and total Medicare spending. In our preferred patient FE specification, all three point estimates are positive, and are statistically significant for Part B spending. The distributed lag point estimate is a $77 (about a 4 percent) increase in spending. However, the point estimate with physician FE is much smaller, at only $10, and the estimate without patient or physician FE is insignificant.

Table 5:

DiD Regression Analyses: Effect of Damage Caps on Medicare Part A and Part B Spending

	No			Patient * Zip			Physician * Zip
Patient or Physician FE	(1)	(2)	(3)	(4)	(5)	(6)	(7)
Variables	Part A	Part B	Total	Part A	Part B	Total	Part B
Panel A: Simple DiD
Damage cap dummy	−17.52	24.99	7.47	11.97	55.11**	67.08	8.73**
	(36.25)	(20.45)	(35.92)	(59.06)	(22.45)	(68.79)	(3.84)
R2	0.09	0.17	0.13	0.41	0.63	0.48	0.11
Observations	13,524,405	13,524,405	13,524,405	11,559,309	11,559,309	11,559,309	68,874,253
Panel B: Distributed Lags
Cap year adoption and after	−16.67	27.73*	11.06	12.34	25.76	38.10	−0.65
	(23.96)	(13.89)	(31.41)	(33.34)	(17.76)	(44.75)	(6.60)
Cap Year 1 or after	17.90	−8.297	9.606	20.23	12.58	32.82	8.93
	(20.63)	(7.501)	(21.12)	(22.75)	(9.109)	(27.36)	(6.64)
Cap Year 2 or after	−37.03	14.24	−22.79	8.315	26.81	35.12	4.26
	(33.91)	(16.86)	(42.91)	(39.51)	(16.76)	(51.53)	(3.00)
Cap Year 3 or after	−20.20	−5.12	−25.32	−7.32	1.22	−6.10	−1.721
	(20.53)	(11.68)	(28.44)	(27.31)	(13.12)	(37.83)	(1.92)
Cap Year 4 or after	46.07***	−12.31	33.76	61.56**	11.04	72.60*	−0.75
	(14.86)	(13.93)	(22.24)	(27.82)	(17.78)	(37.88)	(3.29)
Sum of coefficients	−9.93	16.25	6.32	95.13	77.41**	172.54*	10.07**
	(45.25)	(30.82)	(45.47)	(87.22)	(33.88)	(95.16)	(4.64)
R2	0.09	0.17	0.13	0.40	0.63	0.48	0.11
Observations	14,057,920	14,057,920	14,057,920	12,020,886	12,020,886	12,020,886	68,874,253
Percentage change	−0.4%	+0.8%	+0.1%	+3.5%	+3.8%	+3.6%	+1.9%

Notes: Panel A: Difference in differences regressions for indicated Medicare spending categories per enrollee, per calendar year, on damage cap dummy and covariates. Coefficient on damage cap dummy are multiplied by 4, so coefficients provide estimated effect of cap on annual spending per patient. Coefficients on covariates are suppressed, but presented in the Supporting Information (Table App 3).

Panel B: Distributed lag regressions for indicated Medicare spending categories per enrollee, per year. Distributed lag analysis in a given year. Coefficients on covariates are suppressed.

Both panels: Column (1): Part A spending; Column (2): Part B spending; Column (3): combined Part A and Part B spending. Sample, main variables, covariates, and fixed effects are same as corresponding specifications (using patient * zip FE, physician * zip FE, or neither) in Table 2; coefficients on covariates are suppressed. Physician FE are not available for Part A or total spending. Amounts in 1999 $s. Standard errors, clustered on state, in parentheses.

^{*, **, ***}indicates statistical significance at the 10 percent, 5 percent, and 1 percent level, respectively. Significant results, at 5 percent level or better, in boldface. Percentage change is relative to base rate in 2002 for New-Cap states.

In the distributed lag regressions with patient FE, the Part A estimate is similar in magnitude to the Part B estimate, at $95 (+3.5 percent), but insignificant, and both the simple DiD and distributed lag point estimates without patient FE are negative. Total spending is a blend of the Part A and Part B results. With patient FE, the distributed lag point estimate is $173 in additional spending (+3.6 percent) and marginally significant. However, the estimate without patient FE is near zero.

We see the graphical and regression results together as providing mild evidence of higher postcap spending, principally for Part B.

3. Comparison to Prior Results on Medicare Spending

Our results for overall Medicare spending can usefully be compared to those of Paik et al. (2017). They have only county-level data (rather than the patient-level data we rely on) but smaller standard errors because they have data for the entire Medicare population; we have only a 5 percent sample. They found higher postcap Part B spending, but no evidence for a change in Part A spending. In Figure 4, we compare their estimates for Part A and Part B to the patient FE estimates in this article by plotting both sets of results together (converting our dollar estimates to percentages).

Figure 4: County-level spending: leads and lags.

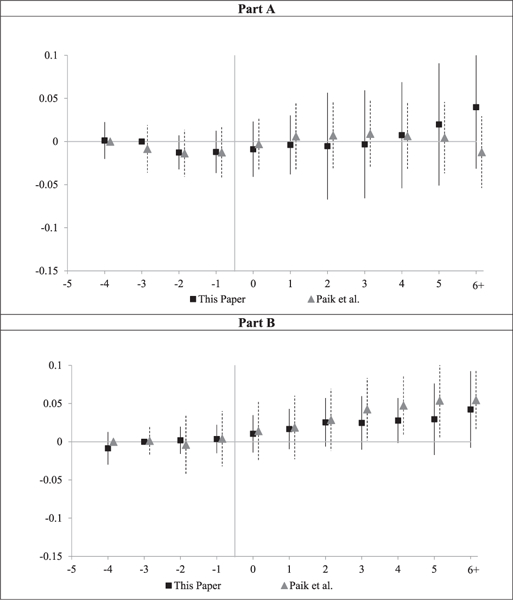
Notes: Figures compare our results for Part A and Part B Medicare spending from Figure 3 (converted from dollars to percent of 2002 spending) to results from Paik et al. (2017), who have county-level data on Part A and Part B spending, and regress In (Medicare spending per enrollee) on leads and lags relative to reform year, county and year fixed effects, covariates, and constant term, with weights based on average number of enrollees in each county over 1998–2011. The figure shows coefficients on leads and lags relative to year (t −4), which is set to zero. Vertical bars show 95 percent CIs around coefficients, using standard errors clustered on state.

For Part B spending, our estimates and the Paik et al. estimates are close to each other for all years. For Part A spending, our estimates are similar to those of Paik et al. through Year +4; the estimates diverge after that, but both sets of estimates are insignificant. The overall consistency of results across both papers, especially for Part B spending, lends additional credibility to both sets of estimates. They also strengthen the evidence that damage caps do not predict lower overall spending.

Yet the lower percentage estimates for Part B spending with physician FE suggest caution in concluding that damage caps cause higher spending. In our view, the more compelling picture, from our results as a whole, is of heterogeneous outcomes, with spending rising in some areas, but neutral or falling in others.

VI. Effects of Damage Caps on Mortality Measures

Several prior papers assess whether damage caps affect mortality, and find no effect. We do the same in Figure 5, with the same null result. There is some year-to-year bouncing, in both the pretreatment and posttreatment periods, but no visual evidence of a postreform change. This null result is expected, given the modest effects of damage caps on treatment decisions. In the Supporting Information, we also find that damage cap adoption has no significant effect on mortality one year after hospitalization.

Figure 5: Mortality: leads and lags graphs of effect of damage cap adoption.

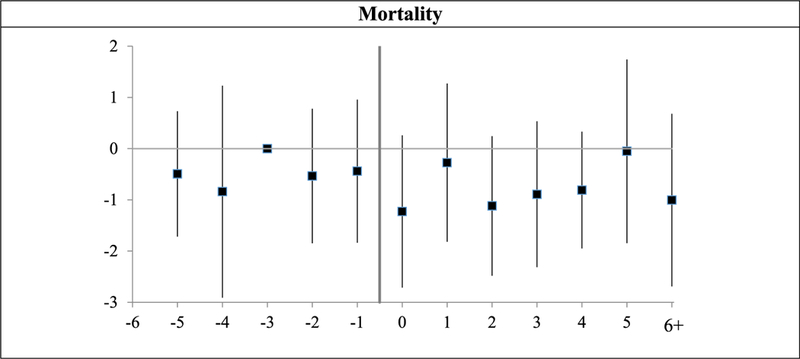
Notes: Leads and lags regressions (linear probability model) of dummy variables for whether a patient had died in a given year, for nine New-Cap states versus narrow control group of 20 No-Cap states, over 1999–2011. Coefficients on leads and lags are multiplied by 1,000, so provide predicted effect of cap on annual rates per 1,000 patients. Sample, covariates, and fixed effects are same as in Figure 1 (without patient * zip or physician * zip FE). y-axis shows coefficients on lead and lag dummies; vertical bars show 95 percent CIs around coefficients, using standard errors clustered on state. Coefficient for Year −3 is set to zero.

VII. Additional Results and Limitations

We have a random 5 percent sample of Medicare fee-for-service beneficiaries, which lets us follow beneficiaries over time. We can also observe the physicians who treated these beneficiaries over time. We exploited these features of our database above to present three main specifications: with patient * zip FE, physician * FE, and with only zip code FE. In this section, we conduct an array of additional robustness and sensitivity tests. In Table 6, Panel A presents results for imaging tests, Panel B for cardiac procedures, Panel C for lab and radiology spending, and Panel D for overall Medicare spending.

Table 6:

Additional Regression Results

Panel A: Imaging Tests
	No			Patient * Zip FE			Physician * Zip FE
Patient or Physician FE	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)
Dep. Variables	Any Stress Test	MRI	CT	Any Stress Test	MRF	CT	Any Stress Test	MRF	CT
Results from Table 2 (No-Cap control group)	4.040***	1.48	3.92**	5.30***	3.05**	6.38**	0.99***	0.42	1.21*
	(1.44)	(1.21)	(1.45)	(1.32)	(1.35)	(2.72)	(0.34)	(0.32)	(0.63)
Remove all time-varying covariates	6.08**	3.82**	8.41***	6.62***	4.52**	8.98**	1.06**	0.49	1.10
	(2.31)	(1.66)	(2.16)	(1.74)	(1.68)	(3.51)	(0.38)	(0.31)	(0.93)
Remove Charlson dummies as covariates	4.48***	1.92	5.61***	5.15***	2.92**	6.39**	0.97***	0.41	1.24*
	(1.55)	(1.21)	(1.60)	(1.32)	(1.33)	(2.71)	(0.34)	(0.32)	(0.64)
Add controls for other reforms	4.51*	2.00	5.56***	6.04***	2.84**	6.98**	1.01**	0.18	0.48
	(2.26)	(1.51)	(1.47)	(2.05)	(1.27)	(3.00)	(0.44)	(0.33)	(0.71)
Broad control group (main specification)	5.28***	2.66**	5.19***	5.60***	3.61***	8.37***	1.02***	0.40	0.85
	(1.21)	(1.17)	(1.16)	(1.030)	(1.17)	(2.19)	(0.30)	(0.27)	(0.62)
No-Cap control group with state trends	3.94***	1.06	−0.19	4.77***	2.11*	−0.46	0.74***	0.22	−0.78*
	(1.10)	(1.02)	(1.45)	(1.41)	(1.21)	(1.83)	(0.22)	(0.35)	(0.42)
Broad control group with state trends	3.99***	1.96*	0.45	4.59***	2.69**	−0.28	0.48**	0.42	−0.68
	(1.12)	(1.14)	(1.44)	(1.35)	(1.23)	(1.71)	(0.22)	(0.35)	(0.41)
Distributed Lags: Sum of Coefficients
Results from Table 2 (No-Cap control group)	5.09**	2.94*	6.61***	5.59**	4.22**	11.89***	1.56***	0.69*	2.88***
	(1.86)	(1.49)	(1.95)	(2.10)	(1.90)	(3.89)	(0.52)	(0.39)	(0.94)
Broad control group (w. main specification)	6.62***	4.09***	7.65***	6.16***	4.72***	14.29***	1.66***	0.49	2.11**
	(1.59)	(1.41)	(1.52)	(1.77)	(1.69)	(3.32)	(0.42)	(0.31)	(0.93)
No-Cap control group with state trends	4.47***	2.58	4.38**	3.59	3.04	5.28*	0.98***	0.33	1.03
	(1.47)	(2.58)	(2.10)	(2.12)	(2.98)	(2.87)	(0.34)	(0.55)	(0.70)
Broad control group with state trends	6.14***	3.34	3.74**	4.36*	3.33	4.41	1.00***	0.37	0.98
	(1.96)	(2.33)	(1.69)	(2.25)	(2.60)	(2.69)	(0.34)	(0.44)	(0.68)

Panel B: Cardiac Interventions
	No				Patient * Zip FE				Physician * Zip FE
Patient or Physician FE	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)	(11)	(12)
Dependent variable	LHC	PCI	CABG	Any Revasc.	LHC	PCI	CABG	Any Revasc.	LHC	PCI	CABG	Any Revasc.
Panel A: Simple DiD
Results from	−0.80**	−0.30	−0.14	−0.41*	−0.29	−0.17	−0.11	−0.26	−0.47***	−0.22***	−0.08*	−0.29***
Table 3 (No-Cap control group)	(0.39)	(0.19)	(0.11)	(0.23)	(0.44)	(0.22)	(0.14)	(0.25)	(0.16)	(0.06)	(0.04)	(0.08)
Remove all	−0.47	−0.28	−0.16	−0.40	−0.33	−0.20	−0.20	−0.35	−0.57***	—0.26***	−0.09*	−0.35***
time-varying	(0.37)	(0.23)	(0.14)	(0.31)	(0.50)	(0.22)	(0.17)	(0.28)	(0.18)	(0.08)	(0.05)	(0.10)
covariates
Remove Charlson	−0.57	−0.22	−0.13	−0.31	−0.36	−0.19	−0.14	−0.30	−0.47***	−0.22***	−0.08*	−0.30***
dummies as	(0.36)	(0.19)	(0.10)	(0.22)	(0.44)	(0.22)	(0.14)	(0.26)	(0.16)	(0.06)	(0.04)	(0.08)
covariates
Add controls for	−0.50	−0.12	−0.18	−0.28	−0.15	0.09	−0.22	−0.09	−0.37**	−0.17***	−0.04	−0.21***
other reforms	(0.43)	(0.17)	(0.13)	(0.25)	(0.43)	(0.17)	(0.18)	(0.26)	(0.14)	(0.05)	(0.04)	(0.07)
Broad control	−0.45	−0.04	−0.24**	−0.26	−0.21	−0.05	−0.25***	−0.27	−0.42***	−0.17***	−0.07*	−0.23***
group (main specification)	(0.34)	(0.13)	(0.09)	(0.18)	(0.42)	(0.16)	(0.11)	(0.20)	(0.15)	(0.05)	(0.04)	(0.07)
Narrow control	0.40	0.01	0.07	0.08	0.58	0.09	−0.05	0.07	−0.06	−0.10*	−0.02	−0.12*
group with state trends	(0.40)	(0.25)	(0.13)	(0.33)	(0.43)	(0.26)	(0.15)	(0.29)	(0.11)	(0.05)	(0.03)	(0.07)
Broad control	0.36	−0.04	0.06	0.03	0.38	0.01	−0.07	−0.03	−0.12	−0.12**	−0.03	−0.14**
group with state trends	(0.43)	(0.26)	(0.13)	(0.34)	(0.46)	(0.26)	(0.14)	(0.30)	(0.12)	(0.05)	(0.03)	(0.07)
Distributed Lags: Sum of Coefficients
Results from	−1.26**	−0.41	−0.20	−0.58	−1.26	−0.64	−0.18	−0.79*	−0.65**	−0.29***	−0.12**	−0.411**
Table 3 (No-Cap control group)	(0.47)	(0.25)	(0.16)	(0.33)	(0.77)	(0.38)	(0.20)	(0.46)	(0.26)	(0.08)	(0.06)	(0.11)
Broad control	−0.74*	−0.02	−0.32	−0.34	−0.92	−0.28	−0.37**	−0.63*	−0.56**	−0.21***	−0.10*	−0.30***
group (main specification)	(0.41)	(0.19)	(0.14)	(0.27)	(0.63)	(0.28)	(0.15)	(0.35)	(0.24)	(0.07)	(0.05)	(0.10)
No-cap control	−0.46	−0.44	−0.03	−0.45	−1.21*	−0.92	−0.26	−1.09**	−0.16	−0.15**	−0.08	−0.23**
group with state trends	(0.59)	(0.39)	(0.25)	(0.53)	(0.61)	(0.43)	(0.31)	(0.53)	(0.23)	(0.07)	(0.05)	(0.10)
Broad control	−0.36	−0.38	0.02	−0.36	−1.07	−0.67	−0.23	−0.83	−0.26	−0.14**	−0.08*	−0.22***
group with state trends	(0.64)	(0.41)	(0.23)	(0.56)	(0.64)	(0.42)	(0.28)	(0.51)	(0.25)	(0.06)	(0.04)	(0.08)

Panel C: Outpatient Laboratory and Radiology Spending
	No			Patient * Zip FE			Physician * Zip FE
Patient or Physician FE	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)
Dep. Variables	Lab	Radiology	Lab + Radiology	Lab	Radiology	Lab + Radiology	Lab	Radiology	Lab + Radiology
Results from Table 4 (No-Cap control group)	3.58	10.63***	14.21**	5.13	12.36***	17.53**	0.43	3.47***	3.90**
	(4.04)	(2.93)	(5.92)	(4.32)	(3.34)	(6.65)	(l.11)	(0.94)	(1.84)
Same but remove all time-varying	7.54	14.04***	21.58**	7.62	14.51***	22.13***	0.84	4.15***	4.99
covariates	(6.72)	(3.00)	(8.22)	(5.86)	(3.11)	(7.44)	(2.26)	(1.13)	(3.08)
Remove Charlson dummies as	6.11	12.30***	18.41**	5.33	12.18***	17.54**	0.77	3.61***	4.38**
covariates	(4.54)	(3.11)	(6.70)	(4.38)	(3.37)	(6.74)	(1.15)	(0.92)	(1.87)
Add controls for other reforms	8.80*	12.17***	20.96***	7.28	11.64***	18.87**	1.18	3.70***	4.89***
	(4.75)	(2.89)	(6.95)	(5.41)	(3.84)	(8.47)	(1.07)	(0.74)	(1.62)
Broad control group (main	9.86**	9.83***	19.70***	9.48**	10.00***	19.52***	1.90	3.14***	5.04**
specification)	(3.93)	(2.42)	(4.80)	(4.24)	(3.35)	(6.17)	(1.21)	(0.96)	(1.96)
No-Cap control group with state trends	4.41	13.92***	18.33**	4.76	13.91**	18.73**	0.06	3.01**	3.07*
	(3.17)	(4.99)	(7.50)	(2.97)	(5.31)	(7.70)	(0.53)	(1.23)	(1.53)
Broad control group with state trends	5.68*	15.69***	21.37***	6.23**	15.06***	21.29***	0.30	3.32**	3.63**
	(2.97)	(4.96)	(7.11)	(2.73)	(5.317)	(7.38)	(0.60)	(1.26)	(1.60)
Distributed Lags: Sum of Coefficients
Results from Table 4 (No-Cap control	4.37	9.85***	14.22**	6.14	12.23***	18.37**	1.39	5.01***	6.41**
group)	(5.50)	(3.48)	(6.49)	(6.63)	(3.82)	(7.37)	(1.78)	(1.32)	(2.53)
Broad control group (main	11.61**	7.57**	19.18***	12.17*	7.60**	19.77***	3.27*	3.77***	7.04***
specification)	(5.39)	(2.83)	(4.97)	(6.49)	(3.75)	(6.15)	(1.75)	(1.05)	(2.24)
No-Cap control group with state trends	9.60**	19.76***	29.36***	4.54	17.63***	27.55***	0.31	4.67***	4.98*
	(4.33)	(4.73)	(8.28)	(5.96)	(5.66)	(8.87)	(1.29)	(1.44)	(2.50)
Broad control group with state trends	13.42**	21.41***	34.83***	9.45*	18.10***	27.55***	1.09	4.47***	5.56***
	(5.24)	(4.43)	(8.58)	(5.59)	(4.67)	(8.87)	(1.14)	(1.17)	(2.04)

Panel D: Medicare Part A and Part B Spending
	No			Patient * Zip FE			Physician * Zip FE
Patient or Physician FE	(1)	(2)	(3)	(4)	(5)	(6)	(7)
Dep. Variables	Part A	Part B	Total	Part A	Part B	Total	Part B
Results from Table 4 (No-Cap control group)	−17.52	24.99	7.47	11.97	55.11**	67.08	8.74**
	(36.25)	(20.45)	(35.92)	(59.06)	(22.45)	(68.79)	(3.84)
Same but remove all time-varying covariates	20.43	86.87**	107.30**	−32.95	85.61*	52.65	12.96**
	(42.19)	(34.92)	49.88)	(77.97)	(42.76)	(91.94)	(6.27)
Remove Charlson dummies as covariates	28.38	57.00**	85.38*	17.80	58.37**	76.17	10.79**
	(40.32)	(24.36)	(44.04)	(59.97)	(23.50)	(71.05)	(4.47)
Add controls for other reforms	−45.87	71.92***	26.05	−81.41	67.71*	−13.70	13.76***
	(49.84)	(20.34)	(40.07)	(55.76)	(36.85)	(76.70)	(4.65)
Broad control group (main specification)	−34.49	47.19**	12.71	17.84	68.00***	85.85	7.16*
	(30.98)	(22.63)	(30.89)	(51.00)	(24.85)	(57.25)	(3.77)
No-Cap control group with state trends	5.103	38.72**	43.83	−49.33*	28.24	−21.09	4.46
	(29.07)	(16.58)	(34.09)	(28.13)	(18.86)	(40.85)	(4.834)
Broad control group with state trends	29.99	44.91**	74.90*	−42.24	29.32	−12.92	5.89
	(30.60)	(17.47)	(40.19)	(26.45)	(18.00)	(40.17)	(5.398)
Distributed Lags: Sum of Coefficients
Results from Table 4 (narrow control group)	−9.93	16.25	6.32	95.13	77.41**	172.54*	10.07**
	(45.25)	(30.82)	(45.47)	(87.22)	(33.88)	(95.16)	(4.64)
Broad control group (main specification)	−45.76	44.89	−0.87	96.21	95.32**	191.53**	6.95
	(39.35)	(30.94)	(32.98)	(77.18)	(38.06)	(78.59)	(4.65)
No-Cap control group with state trends	10.65	57.32**	67.97	23.77	44.06	67.83	4.24
	(50.59)	(21.87)	(63.53)	(50.89)	(29.47)	(73.91)	(6.15)
Broad control group with state trends	16.45	66.42***	82.88	16.94	40.47	57.40	2.97
	(43.13)	(23.30)	(58.72)	(44.56)	(27.16)	(65.70)	(5.91)

Notes: DifFerence-in-difFerences and distributed lag regressions. Specification and sample is same as in Tables 2–5, except as indicated. Broad control group includes 20 No-Cap states and 22 Old-Cap states. Dollar amounts in 1999 $s. Standard errors, clustered on state, in parentheses.

^{*, **, ***}indicates statistical significance at the 10 percent, 5 percent, and 1 percent level. Significant results, at 5 percent level or better, in boldface.

A. Results with Fewer or More Covariates

In addition to our three main specifications, with varying FE, we use extensive patient- and county-level covariates to control for time-varying factors that could affect our outcome variables. However, no set of covariates can completely control for patient health. We therefore sought to assess whether our results were sensitive to the covariates we included by rerunning our regressions with either (1) no covariates at all; (2) all covari-ates except the dummy variables for the 17 elements of the Charlson comorbidity index; and (3) our main covariates plus additional county-level health covariates for percent of the population obese, with diabetes, inactive, rate of death from heart disease, and percent of the population that smokes daily (state level).¹⁵

We discuss here results with either patient or physician FE. The effects of removing covariates are larger in regressions with neither patient * zip nor physician * zip FE, but no one would suggest that a specification with neither FE nor patient-level covariates is a sound one. Across all four panels, if we take the extreme step of removing all time-varying covariates (second row of each panel), while keeping patient or physician FE, coefficients generally increase moderately in magnitude, suggesting that these covariates are important to include.

Our main specification includes dummy variables for each of the 17 elements of the Charlson comorbidity index to account for differences in patient health that may affect treatment. We expect sicker beneficiaries, with more comorbidities, to consume more healthcare. However, causation could also run from local practice norms $\to$ healthcare utilization → more reported comorbidities. If so, controlling for comorbidities could mask the effect of tort reform. The effects of dropping the elements of the Charlson comorbidity index are generally small, with mixed effects on the magnitude of the core DiD coefficient across specifications and outcome measures. This suggests that adding finer controls for patient health likely would not affect our results very strongly. This is the case with patient * zip FE, which would not be surprising if the patient FE and other patient variables (age dummies, gender, race) already do a reasonable job of capturing patient health. More surprisingly, it is also the case with physician * zip FE. Whenever coefficients are statistically significant with full covariates, they remain significant, with similar magnitudes, if we remove the Charlson comorbidities.

Motivated by the differences in estimates between the all- and no-covariates results, we searched for additional potential covariates and found data on several county-level health characteristics (listed above). Results reported in the Supporting Information are similar to our main specification. In unreported results, we also ran specifications with patient * state or physician * state FE, instead of the patient * zip or physician * zip FE report; results were similar.

B. Controlling for Other Tort Reforms

Notwithstanding our doubts, discussed above, about whether this is a sensible approach, we reran our regressions controlling for seven other tort reforms (punitive damages cap, punitive damages evidence reform, collateral source reform, split recovery reform, periodic payment reform, certificate of merit requirements, and removal or weakening of joint and several liability).

In our preferred patient and physician FE specifications, changes in coefficient magnitudes are modest, and coefficients for imaging tests, cardiac procedures, and lab and imaging spending that are statistically significant without these controls remain significant. Coefficient magnitudes increase somewhat for imaging tests, decrease somewhat for invasive cardiac procedures, and are sometimes larger and sometimes smaller for lab and imaging spending. For Part B spending, the coefficient with patient FE increases in magnitude but becomes only marginally significant due to a larger standard error.

C. Results with Broad Control Group

We reran all results using the broad control group, which includes both the 20 No-Cap states and 22 Old-Cap states. We present leads and lags graphs with the broad control group in the Supporting Information and regression results in Table 6. Differences for tests and procedures are again modest. Lab spending with patient FE strengthens and becomes statistically significant, while Part B spending with physician FE weakens and becomes only marginally significant.

D. Adding State-Specific Trends

A common robustness check when nonparallel trends may exist is to add unit (here, state) specific linear time trends. Using linear trends assumes that any nonparallel trends would have continued in the posttreatment period, and that the world is linear; they are problematic for our setting, where overall cardiac testing rates first rise, then fall (see Figures App-1 and App-2 in the Supporting Information). We nonetheless implement this approach in Table 6. The coefficients change substantially for several outcomes. Among imaging tests, the coefficient for CT scans becomes small and statistically insignificant, and indeed reverses sign for both control groups. For cardiac procedures, the coefficients with patient FE switch sign for LHC and PCI, and PCI/CABG switch signs with both control groups, but remain insignificant. With physician FE, results for all outcomes weaken, although the negative coefficient for PCI remains marginally significant with the narrow control group and the negative coefficients for PCI and any revascularization remain statistically significant with the broad control group.

Inference with state-specific trends is similar for lab and radiology spending. However, among the broader spending categories, the coefficients for Part B spending become insignificant, and the Part A coefficients switch sign.

E. Equal State Weights and Leave-One-Out Regressions

We assess whether our results are driven by a particular state by: (1) including analytical weights in our regressions, which give equal weight to each treated state (our main specification gives equal weight to each beneficiary, and hence greater weight to larger states);¹⁶ and (2) conducting “leave-one-out” regressions in which we reran our results after removing one New-Cap state from the sample. We present results with equal state weights in the Supporting Information. Coefficients are very similar.

F. Results with Synthetic Controls

We conducted synthetic control analyses, following Abadie et al. (2010), for all results. The synthetic controls method does not provide analytical standard errors, but does permit qualitative examination of whether the trends we find for the New-Cap states, taken together, are consistent across states. The results are mixed. For Any Stress Test, for example, rates rise in six treated states relative to their synthetic controls, but fall in the other three; for CT scans, rates rise in five treated states, fall in one state, and are similar in the other three states.

G. Overview of Robustness

Which of our results seem strong, and which more fragile, after this array of additional tests? The results for Any Stress Test are robust across specifications. However, these results, even though robust to state-specific trends, could still reflect continuation of pretreatment trends. The increase in radiology spending is robust across specifications, and drives a similar result for combined lab + radiology spending. CT scan results are mostly strong, but disappear with linear state trends. This concern is muted by the flat pretreatment trends for CT scans (see Figure 1). The evidence for a modest decline in cardiac intervention rates is also strong with physician FE, which is our preferred specification for these tests.

Note, too, that we have what might be called a reverse Bon-Ferroni problem. Even if, say, CT scan rates really do rise, if we run enough different specifications, we may find some in which the results are weaker, perhaps statistically insignificant.

The other results are less consistent, as to both magnitude and statistical significance.

VIII. Discussion

A. Plausibility: Why Might Imaging Rates Rise ?

Our results for imaging—both rates for stress tests, MRIs, and CT scans, and overall imaging spending, point toward higher imaging rates and higher spending. They are not entirely robust, but suppose that imaging rates really do rise as a result of damage cap adoption. This is a puzzling result. The usual defensive medicine story posits that physicians overtest to protect against liability, and predicts that testing rates will fall after reform. To be sure, tort reform could lead to both less assurance behavior (hence less testing and associated spending) but also less avoidance behavior (hence more spending), with no prediction for overall spending, but this still does not readily explain why testing rates would rise. A third story, in which physicians test for multiple reasons, and do not react much to a change in malpractice liability, would predict little change in testing rates.

Can a postreform rise in testing rates be explained on theoretical grounds? We believe that it can, based on a close assessment of clinical context. That assessment has not been pursued in the defensive medicine literature. Consider stress testing for patients with CAD symptoms, prior to a cardiac event. Physicians can assess the likelihood of CAD, and the possible need for intervention, by (1) starting with a stress test, and then proceeding to LHC when the stress test is positive or ambiguous for CAD; or (2) starting with LHC. In Steven Farmer et al. (2018), we use a physician FE specification and find that initial screening rates do not materially change following damage cap adoption. Instead, physicians in New-Cap states switch from LHC to stress test as an initial test: Stress testing rates rise, but rates for “initial” LHCs (not preceded by a stress test) fall. Progression from an initial stress test to a follow-up LHC falls, as does progression from an initial ischemic evaluation (either stress test or initial LHC) to revascularization (through PCI or CABG).

These results are consistent with physicians being more willing to tolerate clinical ambiguity when med mal risk falls by: (1) accepting the less precise results from stress testing; and (2) intervening less often and relying instead on medical management. Overall treatment intensity falls, even though stress testing rates rise.

A similar story can be told for other imaging tests. Consider the common case in which a patient comes to the emergency department (ED) with ambiguous symptoms. The emergency physician can either admit the patient for more careful evaluation, or conduct a “rule-out” MRI or CT scan, and release the patient when the test is negative. In a lower-med-mal-risk environment, the physician may be more willing to “test and release” instead of admit. In this story, assurance behavior would indeed fall, but in ways not as simple as “less testing.” Testing rates would rise, but admissions from the ED would fall. Further research is needed to assess whether this story fits the data.¹⁷ In a similar vein, physicians often face a choice between inpatient and outpatient surgery. In a lowerrisk environment, they may be more willing to opt for outpatient surgery, which is lower cost and more convenient for the patient, but conveys small risks of adverse events (e.g., severe allergic reaction to anesthesia) that pose greater risks in an outpatient setting. Such a shift could explain why we find some evidence of differential spending trends for Part A and Part B spending.

B. Heterogeneous Responses to Tort Reform

Damage caps are prominent on the state and national reform agendas because they are seen as a simple policy lever that proponents claim will reduce defensive medicine and thus health-care spending. One core message from the array of results presented here is that clinical response to this crude policy level is nuanced, and depends on clinical context. Rates appear to rise for several common imaging tests, and for overall lab and imaging spending, yet appear to fall for the common cardiac interventions.

At the same time, a core message from our findings is that, writ large, the “adopt damage caps, reduce spending” story lacks empirical support. Instead, measures to reduce overtreatment will need to be carefully targeted to particular areas of concern.¹⁸

C. Limitations

Our study, like most others in this literature, is limited to the Medicare fee-for-service population; that is where the best data are. Our results may not generalize to other populations, such as younger insured patients, whether uninsured or commercially insured. We study only third-wave damage cap adoptions, during 2002–2005. The second-wave reforms of the mid-1980s could have had different effects on health-care spending.¹⁹

As we note above, the New-Cap states are not a random subset of all states. They have higher stress testing and LHC rates than other states. The New-Cap states also have somewhat higher Medicare spending than the narrow control group of No-Cap states. These differences affect the reliability of inference that the postcap changes we observe are caused by the cap adoptions.

It is unfortunate that CMS generally provides researchers who want national Medicare data with only a 5 percent sample, which is around 2 million beneficiaries. Especially with patient, rather than physician FE, we turn out to be underpowered to reliably find statistical significance for changes in imaging and cardiac procedure rates in the range of our point estimates, generally around 4–5 percent.

IX. Conclusion

Damage caps are physicians’ preferred remedy for med mal risk. Physicians have long claimed that fear of med mal risk leads them to practice defensive medicine, including ordering unnecessary tests. Many policymakers have accepted the argument that adopting damage caps will reduce defensive medicine and thus reduce health-care spending. We report evidence, from a careful study with a large, patient-level dataset, of a more complex and nuanced response to caps. Rates for cardiac stress tests and other imaging tests appear to rise, instead of falling, and overall, as does Medicare Part B lab and radiology spending. Yet cardiac interventions do not rise, and likely fall. There is no evidence of a fall in overall Medicare spending and, consistent with a recent prior paper (Paik et al. 2017), some evidence of higher Part B spending.