Abstract
The low energy structures of neutral and cationic pyrene clusters containing up to seven molecules are searched through a global exploration scheme combining Parallel Tempering Monte Carlo algorithm and local quenches. The potential energies are computed at the Density Functional based Tight Binding level for neutrals and Configuration-Interaction Density-Functional based Tight Binding for cations in order to treat properly the charge resonance. New simplified versions of these schemes are also presented and used during the global exploration. Neutral clusters are shown to be made of compact assemblies of sub-blocs containing up to three units whereas cations present a charged dimer or trimer core surrounded by neutral units. The structural features of the clusters are analyzed and correlated for the cation with the charge distribution. The stability of clusters is also discussed in terms of cohesive and evaporation energies. Adiabatic and vertical ionization potentials are also discussed.
Introduction
The investigation of Polycyclic Aromatic Hydrocarbons (PAHs) clusters properties from both experimental or theoretical sides is motivated by the understanding of processes involved in different scientific domains. In astrophysics, PAHs are suspected to be responsible for a family of infrared emission bands1,2 and to contribute to UV-Visible absorption features, known as Diffuse Interstellar Bands.3–6 In order to explain spectral bands broadening observed in different objects,7–9 it has been proposed that these molecules could aggregate in regions where they are protected from stars UV photons. PAH clusters have also been proposed to be at the origin of some of the DIBs and the extended red emission.10,11 They are also suspected to play a role in the growth of astrophysical PAHs themselves thanks to the creation of chemical bonds between the different units following a photoexcitation.12,13 Few studies have investigated the competition between formation and evaporation of such clusters under interstellar conditions.14–16 The latter studies were restricted to neutral systems, whereas singly ionized clusters are expected to be more strongly bonded than their neutral counterparts and easier to form due to long range polarisation interactions between a cationic cluster and a neutral PAH. Many PAH clusters studies are also motivated by the understanding of their role as a precursors to soot formation in flames.17–34 The knowledge of PAH clustering followed by oligomerization is necessary to build flames kinetic models. Let us also mention that PAH clusters are investigated as prototypes to understand organic crystal properties or to design organic solar cells devices. Electronic gaps and transport properties within clusters are investigated in that context.25,35–46
From the experimental side, mostly driven by the identification of astrophysical nanograins, the spectroscopic properties of PAH clusters have been reported in the IR-FIR as well as in the UV range.11,39,47–49 Most of the experiments devoted to the characterization of PAH clusters structural properties reported stacked structures for small clusters, sometime suggesting a Parallel Displaced (PD) pattern.31,50,51 For instance, Wang et al.32 produced nanoclusters of hydrocarbon molecules by annealing coronene films deposited on Pt(111) and observed stacking patterns with scanning tunneling microscopy. Ion mobility spectra suggest a formation as a single stack perturbed by side molecule when the number of units increases.52 Energetic properties were also investigated, for instance measuring ionization energies of PAH clusters.53 The stability of PAH clusters at thermal equilibrium or submitted to low or high energetic collision has also been investigated.54–62 Oligomerization of PAHs within the cluster induced by such a collision,63 photoabsorption13,64,65 or high pressure conditions66,67 has also been reported.
From the theoretical side, due to the size of the systems, most of the reported investigations were performed at the DFT level and were most of time limited to dimers.39,41,48,51,68–72 One should however mention a few studies at the MP251,72,73 or SAPT74 levels for dimers and the investigation at the DFT level of dimers with an hetero-atom.26,75–77 Although benzene dimers present a low energy T-shape conformation, 78,79 it is now widely accepted that dimers of larger PAHs like coronene form stacks eventually with a twisted or parallel displaced configuration,68,69,71,74,80,81 with the exception of the work by Obolenski et al.70 Let us also mention investigations concerned with gaps and electronic transport properties of these dimers.25,39,40,40–44 Addressing larger clusters has been generally carried out using force field schemes21,27,28,31,36,39,71,82–92 or coarse grains models19,35,81,93 which can be combined with extensive PES exploration schemes to derive thermodynamical properties35,89,93 or to find lowest energy structures.71,81,84,86,87,91 Most of these studies agree on the fact that, for coronenes, clusters growth proceed by stacking for small clusters followed by assemblies of stacks for larger systems.28,31,48,71,80,81,88,93 For smaller PAHs like anthracene or pyrene, assemblies of dimers or non stacked configuration compete for being the lowest energy structures. 48,91 One should mention that the previously reported studies deal with neutral systems and that very few is known about structural and energetic properties of singly charged clusters which is the main topic of the present paper, apart from the work by Bouvier et al.94 who investigated, at a semi-empirical level, clusters of anthracene and naphtalene.
The treatment of singly charged clusters requires to use a method able to describe correctly the interplay between the intermolecular interaction with a computational cost allowing for dealing with large systems. This can be conveniently done via charge resonance models as an alternative to delocalized molecular orbitals (MO) schemes. Charge resonance in valence-bond theory concerns singly ionized systems made of equivalent or similar subunits where several charge-localized forms with identical or close energies are in competition. Hence the wavefunctions are correctly described as combinations of those valence bond forms and not a single one.95,96 These models were largely used to describe charge localisation in singly ionsed rare gas clusters.97 In the past decade, we have developed a model combining the Density Functional based Tight Binding with a small Configuration Interaction scheme (CI-DFTB)98–101 which allows to treat properly the charge resonance between the different units. The scope of the present work is to determine the low energy structures of cationic clusters. The global exploration of PAH clusters, even with a rather efficient computational scheme such as CI-DFTB is not easy, due to the quite complex shape of the potential energy surface resulting of multiple degrees of freedom involving stacks or multi-stack structure, parallel displacements, twists along the axis or mutual orientation of stacks or of isolated molecules around stacks. We have developed a hierarchical strategy consisting for each size in (i) achieving global optimization within a frozen molecule framework and using a simplified however computationally very efficient parameterized version of the CI-DFTB scheme and (ii) finally relaxing a sample of the lowest-energy structures thus found at the actual CI-DFTB level. The methodology is introduced in the next section. We then report and discuss the structural, energetic and electronic properties of the most stable isomers found for neutral and cationic pyrene clusters.
Method
Modelling neutral clusters
DFTB
The Density Functional based Tight-Binding (DFTB)102–107 is an approximated DFT scheme with a reduced computational cost particularly well suited to study large systems. In this approach, molecular orbitals {ϕi} are expressed in a minimal basis set of atomic orbitals (AO) {φμ}
| (1) |
The DFT energy is then expanded with respect to the electronic density fluctuation δρ around a reference density ρ0. The expansion up to second order is known as the Self Consistent Charge (SCC-)DFTB. Neglecting three centers integrals allows then to write the SCC-DFTB energy as :
| (2) |
with is a repulsion potential between atoms α and β, ni is the occupation of the orbital i, is the matrix element of the KS operator at the reference density expressed in the AO basis. The second order term depends on atomic Mulliken charges qα and a function of biatomic distances γαβ(Rαβ).
Several modifications have to be considered for a correct treatment of PAH clusters. The dispersion, which is poorly described by traditionally used DFT functionals and consequently in the SCC-DFTB framework can be corrected by adding an empirical correction term69,108,109 and the intermolecular Coulomb potential can be improved by going beyond Mulliken charges definition to compute the second order term, in particular computing atomic charges based on the Charge Model 3 approach.110 In the present work, we use the combination of SCC-DFTB using the mio-set104 parameterization with a dispersion correction term and CM3 charges69 in consistency with our previous work on ionization potentials.53
To accelerate the global exploration scheme, we have first developed a simplified version of DFTB which consists in removing the self consistent process, i.e. performing a single diagonalization step. This scheme is different from zeroth-order DFTB102,103 as we still use the second order term of Eq. 2 but we only consider the first order perturbation with respect to the density (charges) computed at the previous geometry. We call this partial SCC scheme SCC-DFTBp, the idea being to perform several SCC-DFTBp steps between two SCC-DFTB steps involving the full self-consistent process.
Fast Force Field
In addition to SCC-DFTB and SCC-DFTBp, we have developed a Fast Force Field (FFF) scheme, which still uses the DFTB parameterisation. In this model, we initially determine the SCC-DFTB atomic charges of an isolated pyrene monomer. In the following, the molecular units are kept frozen and clusters geometries are governed by the inter-molecular energy which is decomposed as:
| (3) |
Ecoul is the coulomb energy depending on the precomputed atomic charges in the monomer and defined by :
| (4) |
where α and β are respectively atoms on molecules A and B. We use the same dispersion energy expression as in the SCC-DFTB scheme. The exchange-repulsion energy between molecules can be based on the orbital overlap,111 we define as :
| (5) |
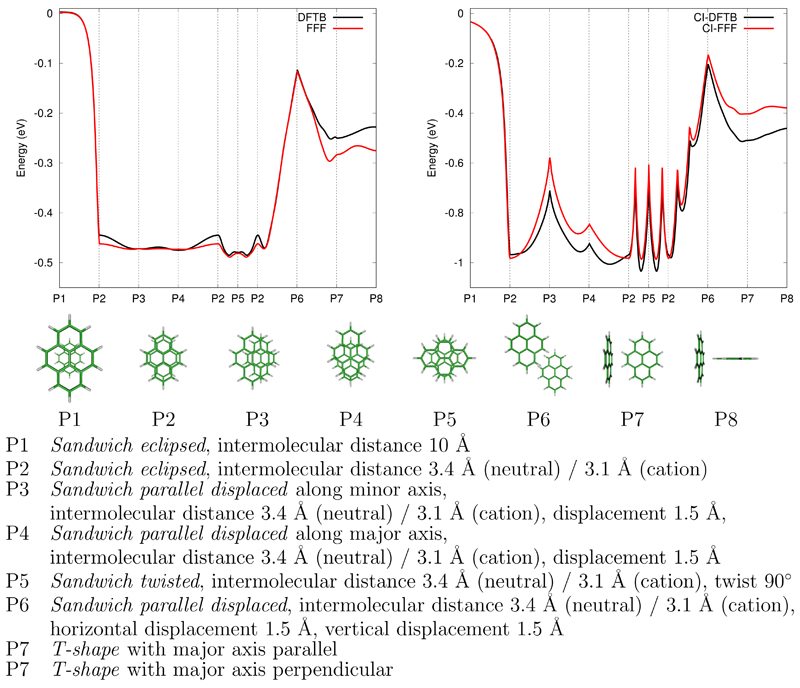
where Sμν is the DFTB atomic orbital overlap matrix. K1 is an empirical parameter (0.85) determined to reproduce the SCC-DFTB results for specific geometries. Figure 1 illustrates that the main trends of SCC-DFTB are well reproduced by the FFF model along a generic path, consisting of geometric linear interpolations between characteristic structures.
Figure 1.
Comparison of FFF and SCC-DFTB (neutral dimer, left panel) and CI-FFF and CI-DFTB (cation dimer, right panel) potential energies along specified pathways.
Modelling cationic clusters
CI-DFTB
In the case of singly ionized molecular clusters, the problem of self-interaction has to be carefully addressed because, in such systems, the wavefunction of the system Ψ is strongly multiconfigurational which is problematic for most of traditionally used DFT functionals112,113 and consequently also at the DFTB level. To address such situations, we have developed the CI-DFTB scheme, which is and adaptation of the CI-DFT method114 to the DFTB framework. In this approach, the global wavefunction of the system Ψ is expressed on a basis {Φi} corresponding to configurations where the charge is fully localized on one specific molecule A.
| (6) |
Each charge localized configurations ΦA is calculated by constrained-DFTB (98,99,115) which is the DFTB version of Constrained-DFT.116 A small Configuration Interaction scheme can then be constructed
| (7) |
where the diagonal elements Ei are the charge-localized configuration energies. The off-diagonal elements F are coupling terms between charge-localized configurations and are computed following the formula of derived by Wu and Van Voorhis.114,117 The overlap between the charge-localized configurations T is computed using the MO coefficients obtained from the charge localized calculation and the DFTB atomic overlap basis. Let us mention that the dispersion and charge corrections mentioned for the neutral DFTB calculations are also used and that the ”SCC-” term is omitted in the name of CI-DFTB, for sake of conciseness, although the SCC process is actually involved. More details are given in the original CI-DFTB paper98 as well as benchmarks showing the ability of this scheme in reproducing ab initio binding energies of benzene and water dimers.
Let us finally mention that, in order to gain in computational efficiency and similarly to SCC-DFTBp scheme, the self-consistent process can be removed from the constrained-DFTB calculation, leading to the CI-DFTBp scheme.
CI-FFF
Finally, we have also developed a force-field version for the CI scheme, still solving the CI Eq. 7 but with a simpler scheme to compute the matrix elements, in the spirit of the approximations of the FFF model (Eq. 3). Configuration ΦA is built using the MOs of an isolated cation for A and those of isolated neutrals for the other units. Consistently, the energies EA of the charge constrained forms are computed taking the frozen monomer charges to compute the coulomb energy from Eq. 4, namely the Coulomb energy of a configuration ΦA is calculated with the charges of an isolated cation molecule for unit A and those of a frozen neutral molecule for the other units.
Moreover, we have parameterized the CI-DFTB matrix elements according to the empirical following expressions
| (8) |
| (9) |
where and K3 have been fitted to reproduce the CI-DFTB matrices elements over a sample of geometries ( and K3 = −0.0572). As can be seen in Figure 1, the CI-FFF model reproduces the main trends of the CI-DFTB energies along typical geometrical paths.
Global exploration
The currently most used global optimization techniques include: basin hopping and derived techniques,118–121 simulated annealing122 and developments concerned with ergodicity (multi-tempering, parallel-tempering in Molecular Dynamics or Monte Carlo schemes123,124), genetic/evolutionary algorithms,125 and particle swarm algorithms.126–129 In this work, we essentially use a parallel temperiing Monte Carlo (PTMC) scheme completed by relaxation. The detailed scheme consists in three steps: We first perform an ’All-Exchange Parallel Tempering Monte-Carlo’130,131 exploration. In this step, the molecules are kept frozen (rigid-body approximation) and the potential energy is computed with the FFF model for neutrals and the CI-FFF model for cations, respectively. We have performed about 107 Monte Carlo steps for each temperature, the distribution of the latter following a geometrical suite between 10 and 500 K. At each step, the probability of attempting the all-exchange procedure is 1 %. From these dynamics, we select up to 2000 lowest energy structures for a given geometrical pattern. The geometrical pattern is defined by the size of sub-stacks and the moment of inertia. In a second step, these selected structures are optimized locally through a conjugated gradient algorithm still using the rigid molecules approximation and making use of the potentials SCC-DFTBp and CI-DFTBp for neutrals and cations, respectively. The last step consists in a local optimization (conjugated gradient), relaxing all degrees of freedom and performed at the highest level of theory used in this work to compute the potential, namely SCC-DFTB and CI-DFTB for neutrals and cations, respectively. Obviously, an advantage of global exploration schemes as used here is the access not only to the most stable structure (presumably) but also to higher energy isomers.
Results
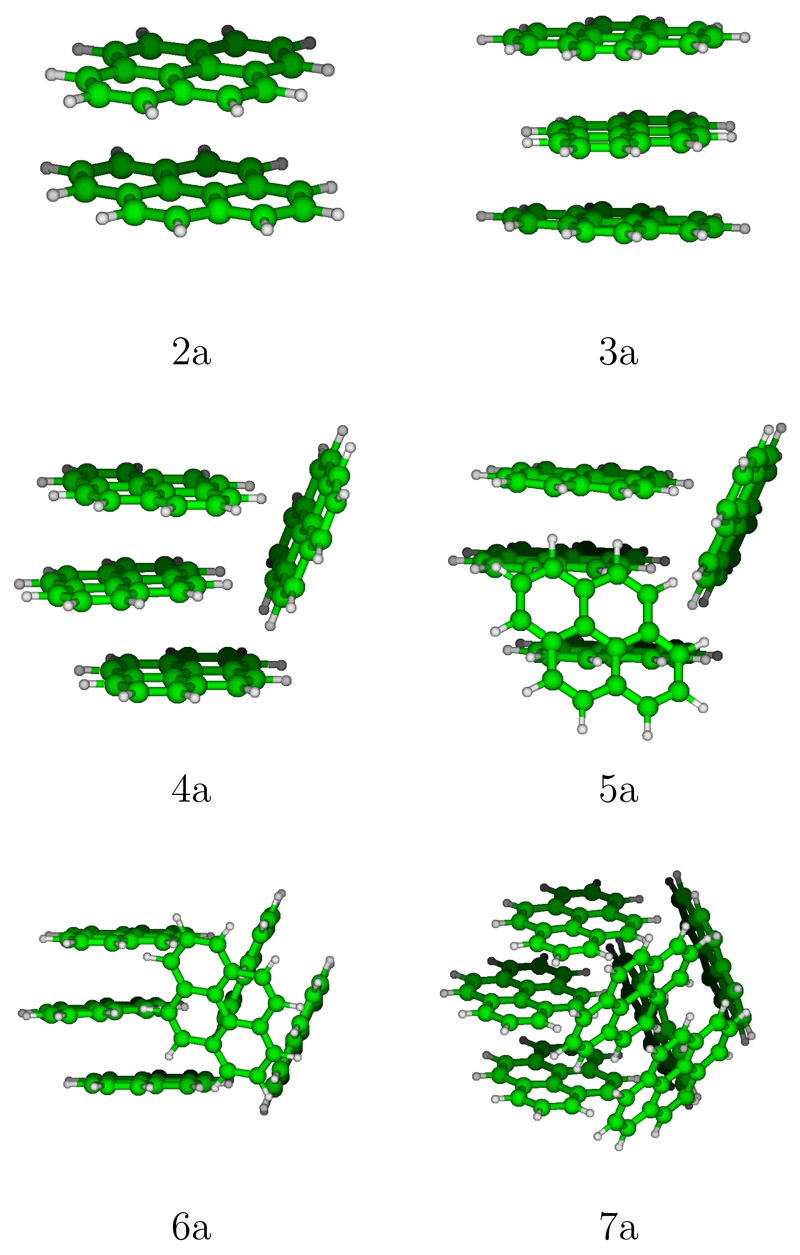
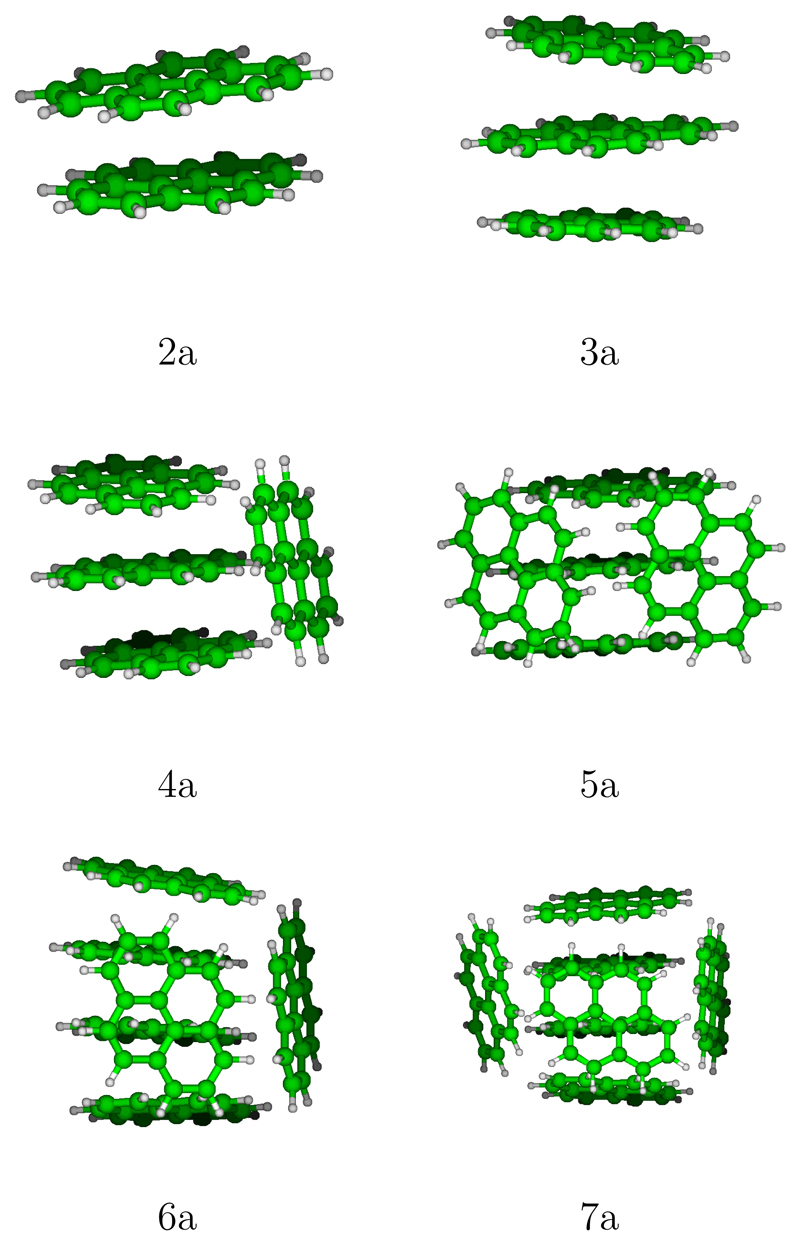
In this section, we present and discuss the most stable structures found for pyrene clusters up to 7 units for cations and neutrals. We define the nomenclature that will be used to characterize these clusters based on the number of units in each stack. For instance, the hexamer of Figure 2 (bottom left) is labelled 3/2/1 as it consists of two stacks of 3 and 2 units respectively plus one isolated monomer and the heptamer (bottom right) is labelled 3/2/2. The energies for evaporating a neutral monomer from a neutral cluster, a neutral monomer from a cation cluster and a cation monomer from a cation cluster are :
| (10) |
| (11) |
| (12) |
where and are respectively the energy of a neutral and cationic cluster of size N. We also define the cohesive energy per molecule for each stable isomer
| (13) |
| (14) |
Figure 2.
Most stable structures for neutral pyrene clusters.
Neutral pyrene clusters
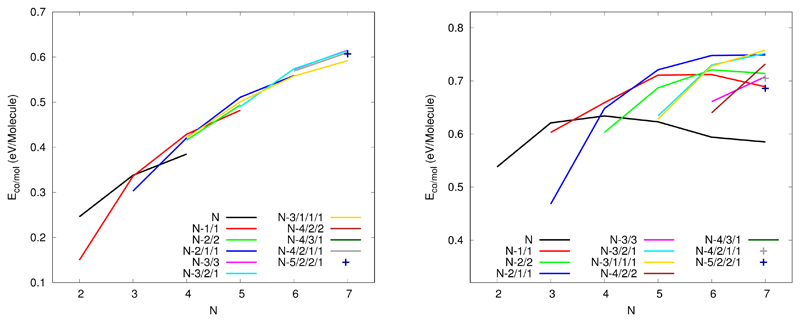
In Figures S1-S6 of the supporting information, we report the global minimum structure, the two or three most stable isomers that belong to the family of the global minimum, the most stable isomer for the following most stable families1 and the most stable stack structure. These isomers are in the following denoted by a number (the number of units) and a letter given following the energetic ordering. The most stable structures found for pyrene clusters (labelled with a ”a”) from 2 to 7 units are represented on Figure 2. It can be seen that the most stable dimers and trimers form stacks whereas larger clusters are made of adjacent stacks containing 1, 2 or 3 units. Clearly, the most stable structures correspond to compact forms, which is an expected trend to maximise the van der Waals interactions. We can also notice that, when possible, hydrogen atoms (slightly positive) lie pointing towards external carbon atoms (slightly negative) of another unit, as expected to maximise the stabilisation through Coulomb interactions. Whereas the best structures for the dimer and the trimer are found to be stacks, the 4-molecule stack (4g) is only the fifth family of the tetramer and lies at 0.187 eV above the lowest energy structure 4a that belongs to the 3/1 family. The structural excitation energies from the most stable structure to the other reported isomers are reported in Table 1. The excitation gap towards another family remains small for all sizes (if one excepts the special case of the dimer), the largest gap is obtained for the pentamer with a value of 56 meV. For each families, lot of stable structures generally exist with a quasi-degeneracy energy (almost 10-15 meV) due to the twisted quasi-degeneracy structures in the dimer/trimer stacks. In order to discuss the geometries in more details, we have calculated the distances between the centers of mass of the constituting molecules, the mutual twist angles around the axis in the case of stack subblocks and the dihedral angle of neighbouring molecules planes within the stacks. If we consider for reference the stack structures, the typical distances (between the centers of mass) are almost the same, namely 3.43 Å in the dimer 2a, 3.42/3.42 Å in the trimer 3a and 3.41/3.40/3.41 Å in the tetramer stack 4g. Also the mutual 1-2 and 2-3 twist angles between two neighboring molecules are around 68 degrees. The main structure difference between 3a and 3b is the clockwise or counter-clockwise twist angle (i.e. in 3a, clockwise/counter-clockwise angles lead to a twist angle close to 0 degree between the two external 1-3 molecules and in 3b, clockwise/clockwise angles result into a 1-3 twist angle close to 44 degrees). This twist isomerization of course also concerns subblocks stacks of larger size clusters producing energetically close-lying isomers. Isomers 5a, 5b and 5c all belong to the 3/1/1 family. Actually in 5a, the trimer stack is symmetric (bond lengths of 3.91/3.91 Å) while in 5b and 5c the trimer stack is non-symmetric (3.49/3.88 Å in 5b and 3.63/3.82 Å in 5c). Furthermore isomers 5b and 5c differ via the orientational order of the molecules around the axis in the trimer stack, namely respective twists of 2/84 degrees in 5c instead of 12/4.75 degrees in 5b. Hexamers 6b and 6c also belong to the same 3/3 family. In 6b, both pairs of trimers stacks are non symmetric (3.98/3.55 Å and 3.71/3.52 Å) while they are symmetric in 6c (3.73/3.73 Å and 3.73/3.73 Å). Heptamers 7a, 7b and 7c also all belong to the 3/2/2 family. They differ either via twist angles in one of the dimer stack or via mutual locations of the stacks. The observation that several families are energetically competing for being the most stable at each size can also be seen from their cohesive energy per unit as reported in Figure 3 as for a given size, several famillies compete for having the largest cohesive energy. In this plot, lines connect clusters which only differ by changing the number of units in the largest central stack, for instance the red N-1/1 (resp. blue N-2/1/1) line connects the most stables structures with a single (resp. two) side molecule, namely the structures 1/1, 2/2, 3/1, 4/1 (resp. 1/1/1, 2/1/1, 3/1/1, 4/1/1/1). It can be seen that the shapes of these curves look similar allways increasing with the number of units, the increase being larger for the smaller number of units. Let us consider the N-1/1-red curve. It’s cohesive energy increases strongly between 2 and 3 units in the stack (clusters of size 3 and 4). This familly is the most stable at for tetramer (largest cohesive energy) and the familly N-2/1/1 is not competitive at all for this size. However, the cohesive energy increase between tetramer and pentamer is stronger for the familly N-2/1/1 as it corresponds to central stack passing from 2 to 3 units than for the N-1/1/1 familly where the number of units in the main stack increases from 3 to 4 units. To generalize, we can say that, although the trends are similar for these families, their relative positions depend of course on the number of units removed from the main stack and how the latter are positioned around the main stack. The crossing between these curves govern the stability switches between the different families as a function of size.
Table 1. Properties of neutral pyrene clusters (C16H10)N: isomerization energy ΔE, cohesive energy per molecule Eco/mol and absolute DFTB energy E in Hartree.
| N | name | family | ΔE (eV) | Eco/mol | E (Ha) |
|---|---|---|---|---|---|
| 1 | a | 1 | - | - | -30.98132298 |
| 2 | a | 2 | - | 0.248 | -61.98086275 |
| 2 | b | 2 | 0.005 | 0.246 | -61.98069401 |
| 2 | c | 1/1 (T-shape) | 0.197 | 0.150 | -61.97363821 |
| 3 | a | 3 | - | 0.339 | -92.98131455 |
| 3 | b | 3 | 0.001 | 0.338 | -92.98126463 |
| 3 | c | 2/1 | 0.009 | 0.336 | -92.98098180 |
| 3 | d | 1/1/1 | 0.108 | 0.303 | -92.97733323 |
| 4 | a | 3/1 | - | 0.431 | -123.98871559 |
| 4 | b | 3/1 | 0.006 | 0.430 | -123.98850709 |
| 4 | c | 3/1 | 0.012 | 0.429 | -123.98828068 |
| 4 | d | 2/1/1 | 0.042 | 0.421 | -123.98718280 |
| 4 | e | 1/1/1/1 | 0.043 | 0.421 | -123.98711967 |
| 4 | f | 2/2 | 0.063 | 0.416 | -123.98639958 |
| 4 | g | 4 | 0.187 | 0.385 | -123.98183460 |
| 5 | a | 3/1/1 | - | 0.513 | -155.00083290 |
| 5 | b | 3/1/1 | 0.002 | 0.512 | -155.00075753 |
| 5 | c | 3/1/1 | 0.010 | 0.115 | -155.00046391 |
| 5 | d | 2/1/1/1 | 0.056 | 0.501 | -154.99876182 |
| 5 | e | 1/1/1/1/1 | 0.073 | 0.498 | -154.99814018 |
| 5 | f | 3/2 | 0.095 | 0.494 | -154.99733475 |
| 5 | g | 2/2/1 | 0.115 | 0.490 | -154.99661840 |
| 5 | h | 4/1 | 0.155 | 0.482 | -154.99513447 |
| 6 | a | 3/2/1 | - | 0.574 | -186.01447459 |
| 6 | b | 3/3 | 0.002 | 0.574 | -186.01441614 |
| 6 | c | 3/3 | 0.008 | 0.573 | -186.01418802 |
| 6 | d | 2/2/1/1 | 0.031 | 0.569 | -186.01333046 |
| 6 | e | 4/1/1 | 0.092 | 0.559 | -186.01110622 |
| 6 | f | 3/1/1/1 | 0.096 | 0.558 | -186.01095231 |
| 6 | g | 2/1/1/1/1 | 0.119 | 0.554 | -186.01010675 |
| 7 | a | 3/2/2 | - | 0.619 | -217.02846307 |
| 7 | b | 3/2/2 | 0.007 | 0.618 | -217.02819446 |
| 7 | c | 3/2/2 | 0.027 | 0.615 | -217.02748774 |
| 7 | d | 4/3 | 0.027 | 0.615 | -217.02748153 |
| 7 | e | 4/2/1 | 0.033 | 0.614 | -217.02723629 |
| 7 | f | 3/2/1/1 | 0.062 | 0.610 | -217.02619265 |
| 7 | g | 2/2/2/1 | 0.080 | 0.607 | -217.02553117 |
| 7 | h | 3/3/1 | 0.102 | 0.604 | -217.02471473 |
| 7 | i | 3/1/1/1/1 | 0.114 | 0.603 | -217.02425950 |
| 7 | j | 2/1/1/1/1/1 | 0.184 | 0.593 | -217.02169512 |
| 7 | k | 2/2/1/1/1 | 0.190 | 0.592 | -217.02147485 |
| 7 | l | 4/1/1/1 | 0.191 | 0.592 | -217.02145512 |
Figure 3.
Cohesive energy per molecule for of the various structural families of neutral (left) and cationic (right) pyrene clusters. The family labelling explained in the text and is the same as used in tables 1 and 3
The intermolecular distance in the neutral dimer 2a is 3.42 Å. One can notice that this distance only slightly varies when the twist angle is changed: in isomer 2b, characterized by a twist angle of 50 degrees, the intermolecular distance is 3.34 Å. The intermolecular distances in the trimer stack 3a are the same as in the dimer, which is consistent with the fact that dispersion-repulsion is the most important contribution to the bonding. In larger clusters, the main stacks are significantly deformed and bent, due to the interactions with the side molecules. Correlatively, the intermolecular distances within the stacks increase, namely 3.91/3.91 Å, 3.49/3.89 Å, 3.99/3.99 Å in the trimer stacks of the tetramer, pentamer and hexamer respectively. The same is observed in the dimer stacks of the hexamer (3.79 Å) and of the heptamer (two dimer stacks at 3.88 Å). The twists become irregular, with a juxtaposition of large and small twists angles for molecules along a same stack. Also and correlatively with the axis bending, the dihedral angles become significant.
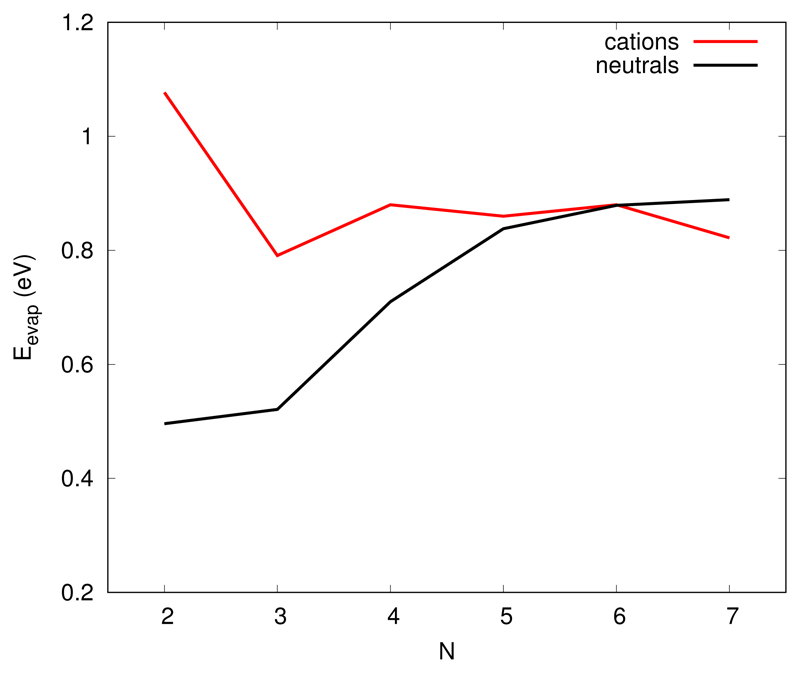
The evaporation of a monomer is always the energetically lowest fragmentation channel. For instance in the lowest energy hexamer 6a which is composed of a trimer stack, a dimer stack and a single molecule, the channel corresponding to the evaporation of a dimer is located 0.34 eV above that corresponding to a monomer evaporation. Likewise, the channel for evaporation of a dimer from the 3/2/2 heptamer 7a is located 0.38 eV above that corresponding to the evaporation of a monomer. As can be seen from Figure 4 and Table 2, the evaporation energy is an increasing value with size, starting at about 0.5 eV for the dimer, which tends to stabilize around 0.9 eV for the largest clusters. Within a pair- additive approximation of the dispersion and Coulomb interactions, the attachment of one unit to the clusters is expected to grow with the number of units inside the cluster. On the other hand, as these interactions decrease with the distance, especially the van der Waals interaction, the evaporation energy in large clusters is expected to reach a limit which would correspond to the evaporation of a monomer from a bulk surface.
Figure 4.
Evaporation energy of a neutral monomer from neutral and cationic clusters.
Table 2. Evaporation energy of a neutral monomer from neutral clusters a neutral monomer from cationic clusters and a cationic monomer from cationic clusters
| N | |||
|---|---|---|---|
| 2 | 0.496 | 1.077 | 1.077 |
| 3 | 0.521 | 0.791 | 1.372 |
| 4 | 0.710 | 0.880 | 1.731 |
| 5 | 0.838 | 0.860 | 1.881 |
| 6 | 0.879 | 0.880 | 1.923 |
| 7 | 0.889 | 0.822 | 1.865 |
Let us notice that in our previous work80 using a force field scheme, the single stack structure was found to be the most stable up to 6 units instead of 3 as in the present work. Interestingly, by comparing some typical structures (single stacks, intertwined, herringbone, …), Ricca et al.48 also concluded from DFT B3LYP+D2 calculations that the single stack is the most stable structure up to three units, suggesting structures made of dimer block assemblies. The cohesive energies per molecule reported by Ricca et al. are systematically larger by 0.10 to 0.14 eV with respect to the values reported in Table 1 for all computed sizes, but the evolution with size is similar. We however notice that our value for the cohesive energy of the dimer is in reasonable agreement (0.248 vs 0.215 eV/mol) with SAPT calculations.132 From a global exploration with a force field scheme, Takeuchi et al.91 reported for pyrene clusters made of subblocks arranged in an amorphous way instead of herringbone patterns. This is in line with the present results except that the subblocks contains two or three units in our case and not more that two in the former work.
Cationic pyrene clusters
Following the same way for labelling and presenting the results as the one used for neutral clusters, the most stable isomers are presented in Figure 5 whereas all the discussed isomers are presented in Figures S7-S12 of Supporting Information. At first glance, the most stable structures found for cationic pyrene clusters (Figure 5) look similar to those obtained for the neutral clusters, at least up to the tetramer whereas differences are observed for larger clusters, in particular the hexamer and the heptamer. The latter clusters (6a and 7a) are made of a central stack consisting of four molecules with isolated side molecules whereas in their neutral counterpart, the main stack is smaller (three units) and the outer molecules tend to form dimer blocks. Beyond this purely geometric aspect, can examines the distribution of the charge over the various molecular units which is reported in Table 3 for each cluster size and the various isomers. It appears that, whatever the number of units, the charge is mostly localized on less than four units of the central stack. In cluster 7a, the charge is mostly carried by two units (a charged dimer core with charges 0.43/0.40) whereas it is delocalized over three units for the trimer (charges 0.27/0.46/0.26) and the tetramer (charged trimer core with charges 0.24/0.49/0.25), the central unit of the core carrying twice more charge than each of the two edge unit. The case of the hexamer and the pentamer occurs as intermediate between a charged dimer and trimer core. All clusters beyond N=3 can therefore be seen as a charged core of two or three units with the other units organizing to form a solvation shell around the charge instead of maximizing the dispersion term that would favor, as in the case of neutral clusters, a more compact structure with external dimer blocks. Let us notice that Bouvier et al.94 already concluded from an empirical valence bond model investigation that the charge in cationic clusters of benzene, naphtalene and anthracene is mostly carried by two to four units. Again, as in the case of the neutral clusters, quasi-degeneracy situations occur between families and within a same family. For instance isomers 5b and 5c geometrically differ via the orientational order within the tetramer stack core. The intermolecular distances are 3.12/3.14/3.94 Å in 5b and 3.25/3.07/3.58 Å in 5c, while the orientational twist angles are 60/61/3 degrees in 5b and 3/59/37 degrees in 5c.
Figure 5.
Most stable structures of cationic pyrene clusters.
Table 3. Properties of pyrene cluster cations : isomerization energy ΔE, cohesive energy per molecule Eco/mol, charge distribution over the constituting monomer units and absolute CI-DFTB energy E in Hartree.
| N | label | family | ΔE (eV) | Eco/mol | charge distribution (%) | E (Ha) |
|---|---|---|---|---|---|---|
| 1 | a | 1 | - | - | 100 | -30.70613754 |
| 2 | a | 2 | - | 0.538 | 50/50 | -61.72702634 |
| 2 | b | 1/1 (T-shape) | 0.513 | 0.282 | 88/12 | -61.70818114 |
| 2 | c | 1/1 (coplanar) | 0.706 | 0.185 | 50/50 | -61.70108551 |
| 3 | a | 3 | - | 0.622 | 46/27/26 | -92.73740273 |
| 3 | b | 3 | 0.004 | 0.621 | 48/26/26 | -92.73727340 |
| 3 | c | 2/1 | 0.058 | 0.603 | 49/48/3 | -92.73528438 |
| 3 | d | 1/1/1 | 0.462 | 0.468 | 56/40/5 | -92.72041806 |
| 4 | a | 3/1 | - | 0.687 | 49/25/24/2 | -123.75107186 |
| 4 | b | 3/1 | 0.110 | 0.659 | 50/44/4/2 | -123.74702819 |
| 4 | c | 2/1/1 | 0.155 | 0.648 | 49/44/4/3 | -123.74538115 |
| 4 | d | 4 | 0.211 | 0.634 | 37/36/15/11 | -123.74331647 |
| 4 | e | 2/2 | 0.337 | 0.603 | 45/43/8/4 | -123.73868538 |
| 5 | a | 3/1/1 | - | 0.721 | 60/21/15/3/2 | -154.76399468 |
| 5 | b | 4/1 | 0.045 | 0.721 | 46/30/20/3/1 | -154.76234587 |
| 5 | c | 4/1 | 0.054 | 0.711 | 47/33/17/3/1 | -154.76199711 |
| 5 | d | 3/2 | 0.174 | 0.687 | 48/42/5/3/1 | -154.75760938 |
| 5 | e | 2/2/1 | 0.436 | 0.634 | 41/38/13/5/2 | -154.74796448 |
| 5 | f | 2/1/1/1 | 0.466 | 0.628 | 60/32/6/2/0 | -154.74686925 |
| 5 | g | 5 | 0.491 | 0.623 | 35/26 /25/7/6 | -154.74596807 |
| 6 | a | 4/1/1 | - | 0.748 | 46/33/12/3/3/2 | -185.77763936 |
| 6 | b | 3/2/1 | 0.109 | 0.730 | 48/37/5/4/4/3 | -185.77362124 |
| 6 | c | 3/1/1/1 | 0.122 | 0.728 | 61/21/13/3/3/-1 | -185.77316871 |
| 6 | d | 4/2 | 0.159 | 0.721 | 45/31/15/4/3/2 | -185.77180727 |
| 6 | e | 5/1 | 0.213 | 0.712 | 48/25/21/3/2/0 | -185.76981713 |
| 6 | f | 3/3 | 0.522 | 0.661 | 54/22/15/7/2/0 | -185.75845231 |
| 6 | g | 2/2/2 | 0.645 | 0.640 | 30/23/20/14/7/6 | -185.75393935 |
| 6 | h | 6 | 0.924 | 0.594 | 33/29/17/14/4/3 | -185.74369280 |
| 7 | a | 4/1/1/1 | - | 0.758 | 43/40/7/4/3/3/0 | -216.78915352 |
| 7 | b | 4/2/1 | 0.042 | 0.752 | 39/38/9/8/4/2/1 | -216.78760053 |
| 7 | c | 5/1/1 | 0.062 | 0.749 | 50/24/20/2/2/1/0 | -216.78687604 |
| 7 | d | 3/2/2 | 0.184 | 0.732 | 52/22/13/5/4/4/0 | -216.78240968 |
| 7 | e | 5/2 | 0.312 | 0.714 | 42/27 /19/5/4/2/1 | -216.77768495 |
| 7 | f | 3/3/1 | 0.347 | 0.709 | 56/20/12/5/4/2/0 | -216.77640031 |
| 7 | g | 4/3 | 0.354 | 0.708 | 51/36/10/2/1/0/-1 | -216.77614668 |
| 7 | h | 3/2/1/1 | 0.374 | 0.705 | 50/40/5/3/1/1/-1 | -216.77540955 |
| 7 | i | 6/1 | 0.488 | 0.689 | 48/26/23/3/1/0/-1 | -216.77122228 |
| 7 | j | 2/2/2/1 | 0.509 | 0.686 | 44/38/10/8/1/0/0 | -216.77043755 |
| 7 | k | 7 | 1.213 | 0.585 | 29/23/23/11/10/2/2 | -216.74456065 |
Despite global structural similarities with neutrals mentioned above, the details of the geometries show significant quantitative differences. We first discuss as reference the intermolecular bond lengths of the single stacks clusters (not the lowest structures for N > 3). In dimer 2a, the intermolecular distance is reduced from 3.43 in the neutrals species to 3.04 Å in the charged species while the twist angle is also reduced from 67 to 55 degrees. This bond shortening can also be evidenced in the stack trimer 3a, where the bond length decreases from 3.42/3.42 Å in the neutral to 3.09/3.09 Å in the charged species. This is clearly associated with a stronger bonding due to charge resonance. For the larger sizes, as discussed previously, single stack clusters are not the lowest structures and the intermolecular bond lengths within the central the stack present noticeable variations along the axis, namely 3.15/3.18/3.15 Å in the tetramer and 3.16/3.25/3.25/3.16 Å in the pentamer.
The intermolecular separation tends to increase for the largest clusters, namely 3.28/3.26/3.22/3.26/3.28 Å in the stack hexamer with a vanishing variation between the edge and the center, and 3.24/3.24/3.24/3.24/3.24/3.24 Å in the stack heptamer. All single stack clusters present systematic twist angles in the range 50-56 degrees. Correlatively in these single stack and rather regular structures, the charge distribution approximately follows a square cosine dependence along the stack with a charge maximum about the center of the stack and decreasing values down to the the edges, as would be obtained in a simple topological Hückel model or even in a one-dimensional square well.99 We now discuss in more details the geometries of the lowest energy structures for N > 3. Obviously the increased longitudinal compactness is also observed in the charged dimer or trimer cores of the larger clusters, namely bond lengths of 3.10/3.10 Å in the trimer core of 4a, 3.31/3.33 Å for 5a. The intermolecular distances in the tetramer core of the cation hexamer 6a are 3.33/3.18/3.25 Å, quite similar to those of the tetramer core in the cation heptamer 7a, namely 3.45/3.11/3.30 Å. One distance at a stack edge is thus somewhat larger and this is consistent with the fact that the charge is dominantly carried by the two central molecules of the stack as already mentioned. Finally, one can examine the closest distances between the side neutral molecules to the closest ones in the core stack. These core-neutral distances range is between 5.63 Å (nearest core-neutral intermolecular distance in isomer 4a for instance) and 6.55 Å depending on the cluster sizes and the isomers. The dihedral angles between the molecules in the central stack are smaller and the stack axes for cations with size N > 4 have less bending than in the neutral equivalent geometries.
Evaporation of a neutral monomer from a cluster cation is always more favorable than evaporation of a cationic one (see Table 2). Neutral monomer evaporation is actually the lowest fragmentation channel of cluster cations, it costs 1.175 eV to evaporate a dimer from the most stable tetramer and only 0.88 eV to evaporate a neutral monomer In the following we discuss the neutral monomer evaporation channel only, dissociation energies for other channels can be easily computed from the absolute energy values given in tables 1 and 3. Contrary to the case of neutrals, the evaporation energy (Figure 4) is not monotonous anymore. For the dimer, it corresponds to a binding energy almost twice larger than for neutral dimer and this is due to the strong stabilisation arising from charge resonance. In the trimer, the less bonded molecules are the two external molecules, each of them being less involved in the charge transfer (they only carry one fourth of the total charge). This explains why removing an external unit is less costing in term of charge resonance stabilisation energy. For the larger systems, the less bonded (external molecules) are even less involved in the charge resonance stabilisation (carrying less that 2 % of the total charge), this should make them easier to remove but, at the same time, dispersion interactions increase with the cluster size. This explains why the evaporation energy remains almost constant for clusters between four to seven units, with values close to those observed for neutrals.
The first structural excitation energy toward another family (see table 3) can vary between 0.04 eV in the case of the pentamer or the heptamer up to 0.15 eV for the tetramer, while it was shown to be smaller than 0.06 eV in all cases for neutrals (except the dimer). The most stable isomers of the different families are spread over a larger energy range than what is observed for neutrals. For instance, in the case of the neutral heptamer, 10 families present isomers with energies lower than 0.2 eV above the most stable structure whereas only four families could be identified within the same energy range for cations. Indeed, an energy range of 0.49 eV is necessary to observe at least 9 different families for the cationic heptamer. The cohesive energies are reported in Figure 3. For the stack family, we can observe the strongest stabilisation when the central stack grows from two to three units due to better charge resonance effect. Adding more units to the stack brings only van der Waals and Coulomb stabilisation energy, resulting in a decrease of the cohesive energy per unit from the tetramer. This increase/decrease behavior is also visible for the N-1/1, N-2/1/1 and N-2/1/1 families allways with a cohesive energy maximumobtained when the central stack contains 4 units. For the other families, only the increase is visible, the deacrease occuring probably for sizes larger that the ones investigated here.
Ionization potentials
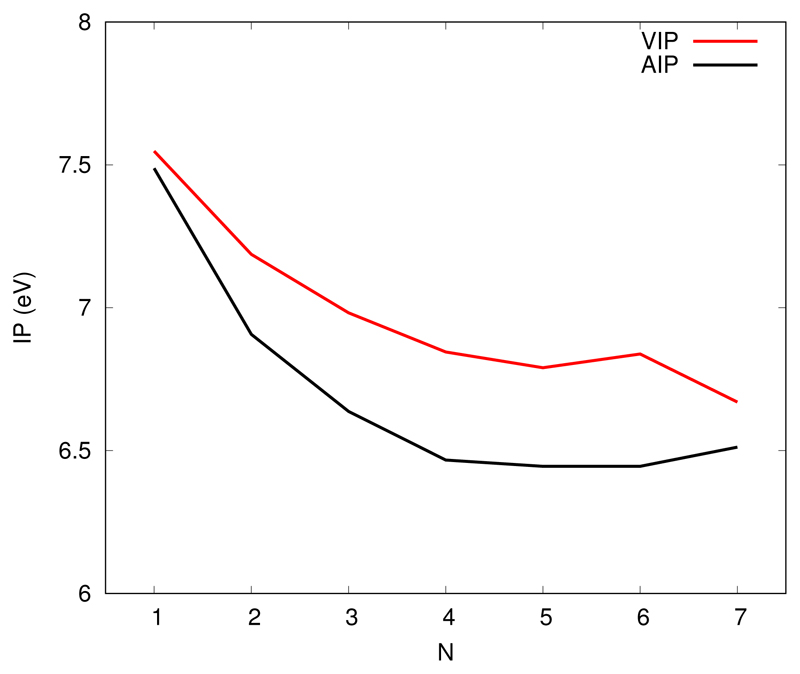
Figure 6 and table 4 presents the adiabatic ionization potentials obtained as differences between the energies of the most stable structures presented in Figures 2 and 5. It presents a decrease up the tetramer which comes from the fact that, in the cation, the charge resonance stabilisation energy increases with size. However, and as already discussed previously, the charge resonance mostly concerns the small dimer/trimer core and, as a consequence, the ionization potential is expected to converged fast. The limit should be the energy required to ionize the central core, which is approached for the largest clusters. Of course, the polarization of the molecules surrounding the core is expected to continue decreasing the ionization potential but it seems to be a smaller contribution here.
Figure 6.
Vertical and adiabatic ionization potential of pyrene clusters
Table 4. Vertical (VIP) and Adiabatic (AIP) Ionization Potentials of pyrene clusters.
| N | VIP (eV) | AIP (eV) |
|---|---|---|
| 1 | 7.55 | 7.49 |
| 2 | 7.19 | 6.91 |
| 3 | 6.98 | 6.64 |
| 4 | 6.85 | 6.47 |
| 5 | 6.79 | 6.44 |
| 6 | 6.84 | 6.44 |
| 7 | 6.67 | 6.51 |
Figure 6 and table 4 also report the vertical ionization potentials (i.e. difference between neutral and cation energies computed both the neutral most stable structure). Although the trend is similar with that of adiabatic IPs, we can clearly see non continuous size effects around the hexamer. Actually, the energetic contribution driving the geometries of the most stable neutrals clusters lead to structures which may or may not be favorable to charge resonance when the cluster is ionized or in other word, how large the relaxation in the ion is vs in the neutral. Interestingly, considering the ions at the geometries of the neutral, although the pentamer, hexamer and heptamer clusters present a main stack of three units, only the pentamer and heptamer present efficient charge delocalization over the three units with some symmetric pattern (charge distribution of 0.67/0.16/0.16 and 0.61/0.16/0.16 respectively) whereas in the case of the hexamer, the charge is carried by only two units with a very unequal distribution (0.68/0.23). The energetic contribution in neutral clusters lead to a geometry not favorable to charge delocalization in the case of the the hexamer. Let us mention that, in agreement with our calculations, this size effect has been shown to be clearly present in experimental measurements of pyrene IP’s.53
Conclusions
The most stable structures for neutral and cationic pyrene clusters containing up to seven units have been searched through a global exploration scheme combining Parallel Tempering Monte Carlo algorithm followed by local Conjugated Gradient quenches on the potential energy surface. In the final stage, the potential energy is computed for neutral clusters using the SCC-DFTB model and for cations using the CI-DFTB model. The latter accounts for charge resonance by performing explicit interaction between charged localized configurations obtained at the constrained SCC-DFTB level. We have also developed faster approaches which are used in the global exploration procedure : the Fast Force Field (FFF) scheme for neutrals, which consists to summing dispersion, coulomb, repulsion terms, computed from the DFTB parameters with some empirical formulae. For cations, we developed the CI-FFF scheme, which is build on the same CI scheme as in the CI-DFTB method but the energies of the charged localized configurations are computed at the FFF level and an empirical formula is derived to compute the coupling terms from the overlap of the unperturbed HOMO of the sub-units. FFF and CI-FFF are shown to behave similarly to DFTB and CI-DFTB on some selected PES pathways.
The most stable structures obtained for pyrene neutral clusters are made of assemblies of small sub-units containing less than four units. These sub-units are arranged to form compacts structures, maximizing the pair-pair Coulomb and dispersion interactions. In cations, the charge remains localized on a dimer or trimer stack core and the other molecules remain essentially neutral and arrange around this core either at the top of the stack or on the sides, initiating a first solvation shell not yet completed at N=7. We have analyzed the correlation between the intermolecular distances and the localization of the charge in the cations. We have shown that in the dimer and the trimer, despite a similar stack arrangements for neutrals and cations, intermolecular distances are reduced respectively to those in the neutrals, associated with the charge resonance stabilization. The same distance contraction affects the core parts of the larger clusters investigated in the present work.
The energetic analysis shows that the cohesive energy per molecule increases regularly from 0.25 eV to 0.61 eV in the neutrals, from 0.54 eV to 0.74 ev for the cations. For all clusters, neutrals and cations, evaporation of a neutral monomer is the lowest channel. The energy required to evaporate a molecule from a neutral cluster increases with the number of units, as it essentially consists in atomic pairwise additive contributions. Although similar energies for neutrals and cations are obtained for the largest clusters investigated, the situation is different for small clusters as removing a molecule from the charged core results in weakening the charge resonance contribution to the stabilization of the cation. As a consequence, the pyrene dimer appears to be the most stable cluster with respect to evaporation. After reaching a minimum, the evaporation energy of cations increases again, due to increased stabilization via polarization of a larger number of molecules by the charged core. Finally, the adiabatic ionization potential appears to decrease smoothly with size whereas the vertical ionization potential may present size effects (irregularity at N=6) resulting from significant differences in the relaxed geometries of neutrals clusters and those of cations.
Obviously, a strong quasi-degeneracy is observed in the competition for the lowest energy structures. The present work has been achieved in the context of DFTB, which is subject to various uncertainties in describing molecular clusters. The present version is an improvement to the basic scheme since dispersion is added and self interaction problems are circumvented in the CI-DFTB scheme. Nevertheless DFTB and CI-DFTB remain parametric methods and we hope that the present work will stimulate further investigations with higher status methods such as double hybrid DFT or even wavefunction methods, which have up to now only have applied to smaller PAH systems, essentially neutral dimers.
Finally, we also hope that the energetic data determined in the present work and in particular will be of interest for various groups working on PAH chemistry in astrochemistry or atmospheric chemistry context and also in laboratory experiments. Chemistry of PAH clusters could be a step in the stabilization of carbonaceous species either via bottom-up formation of larger systems or top-down dissociative processes. Finally clusters might provide an alternative or complementary source to large single PAH molecules with more than several tens carbon atoms in the explanation of some of the unindentified IR bands.
Supplementary Material
The supporting information presents all the structures of neutral and cationic pyrene clusters discussed in this paper.
Acknowledgment
We acknowledge the financial support of the Agence Nationale de la Recherche through the GASPARIM project Gas-phase PAH research for the interstellar medium (ANR-10-BLAN-0501), the computing ressources provided by the CALMIP HPC mesocenter for allocation P0059 and GDR CNRS EMIE. L.D. thanks the ERC for support under grant ERC-2013-Syg-610256-NANOCOSMOS and EUR grant NanoX n 080876 in the framework of the ”Programme des Investissements dAvenir”.
Footnotes
Only one isomer of the most stable family is reported in the case of the hexamer as the other isomers found in this family are less stable than the most stable isomers of other families
References
- (1).Léger A, Puget JL. Identification of the ’unidentified’ IR emission features of interstellar dust? Astron Astrophys. 1984;137:L5–L8. [Google Scholar]
- (2).Allamandola LJ, Tielens AGGM, Barker JR. Polycyclic aromatic hydrocarbons and the unidentified infrared emission bands - Auto exhaust along the Milky Way. Astrophys J Lett. 1985;290:L25–L28. [Google Scholar]
- (3).van der Zwet GP, Allamandola LJ. Polycyclic aromatic hydrocarbons and the diffuse interstellar bands. Astron Astrophys. 1985;146:76–80. doi: 10.1086/307978. [DOI] [PubMed] [Google Scholar]
- (4).Leger A, D’Hendecourt L. Are polycyclic aromatic hydrocarbons the carriers of the diffuse interstellar bands in the visible? Astron Astrophys. 1985;146:81–85. [Google Scholar]
- (5).Crawford MK, Tielens AGGM, Allamandola LJ. Ionized polycyclic aromatic hydrocarbons and the diffuse interstellar bands. Astrophys J Lett. 1985;293:L45–L48. doi: 10.1086/307978. [DOI] [PubMed] [Google Scholar]
- (6).Salama F, Bakes ELO, Allamandola LJ, Tielens AGGM. Assessment of the Polycyclic Aromatic Hydrocarbon–Diffuse Interstellar Band Proposal. Astrophys J. 1996;458:621–+. doi: 10.1086/176844. [DOI] [PubMed] [Google Scholar]
- (7).Rapacioli M, Joblin C, Boissel P. Spectroscopy of polycyclic aromatic hydrocarbons and very small grains in photodissociation regions. Astron Astrophys. 2005;429:193–204. [Google Scholar]
- (8).Berné O, Joblin C, Deville Y, Smith JD, Rapacioli M, Bernard JP, Thomas J, Reach W, Abergel A. Analysis of the emission of very small dust particles from Spitzer spectro-imagery data using blind signal separation methods. Astron Astrophys. 2007;469:575–586. [Google Scholar]
- (9).Berné O, Joblin C, Rapacioli M, Thomas J, Cuillandre J-C, Deville Y. Extended Red Emission and the evolution of carbonaceous nanograins in NGC 7023. Astron Astrophys. 2008;479:L41–L44. [Google Scholar]
- (10).Rhee YM, Lee TJ, Gudipati MS, Allamandola LJ, Head-Gordon M. Charged polycyclic aromatic hydrocarbon clusters and the galactic extended red emission. Proc Natl Acad Unit States Am. 2007;104:5274. doi: 10.1073/pnas.0609396104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (11).Lemmens AK, Gruet S, Steber AL, Antony J, Grimme S, Schnell M, Rijs AM. Far-IR and UV spectral signatures of controlled complexation and microhydration of the polycyclic aromatic hydrocarbon acenaphthene. Phys Chem Chem Phys. 2019;21:3414–3422. doi: 10.1039/c8cp04480e. [DOI] [PubMed] [Google Scholar]
- (12).Chen T. Formation of Covalently Bonded Polycyclic Aromatic Hydrocarbons in the Interstellar Medium. Astrophys J. 2018;866:113. [Google Scholar]
- (13).Zhen J, Chen T, Tielens AGGM. Laboratory Photochemistry of Pyrene Clusters: An Efficient Way to Form Large PAHs. The Astrophysical Journal. 2018;863:128. [Google Scholar]
- (14).Rapacioli M, Calvo F, Joblin C, Parneix P, Toublanc D, Spiegelman F. Formation and destruction of polycyclic aromatic hydrocarbon clusters in the interstellar medium. Astron Astrophys. 2006;460:519–531. [Google Scholar]
- (15).Joblin C, Tielens AGGM, Biennier L, Sabbah H, Klippenstein SJ, Chandrasekaran V, Sims IR, Rowe BR. Insights into the condensation of PAHsin the envelope of IRC +10216, PAHs and the Universe. In: Joblin C, Tielens AGGM, editors. EAS Publications Series. Vol. 46. EDP Sciences; 2011. pp. 191–199. [Google Scholar]
- (16).Montillaud J, Joblin C. Absolute evaporation rates of non-rotating neutral polycyclic aromatic hydrocarbon clusters. Astron Astrophys. 2014;567:A45. [Google Scholar]
- (17).Fiedler SL, Izvekov S, Violi A. The effect of temperature on nanoparticle clustering. Carbon. 2007;45:1786–1794. [Google Scholar]
- (18).Eaves NA, Dworkin SB, Thomson MJ. The importance of reversibility in modeling soot nucleation and condensation processes. Proc Comb Inst. 2015;35:1787–1794. [Google Scholar]
- (19).Violi A, Izvekov S. Soot primary particle formation from multiscale coarse-grained molecular dynamics simulation. Proc Comb Inst. 2007;31:529–537. [Google Scholar]
- (20).D’Anna A, Sirignano M, Kent J. A model of particle nucleation in premixed ethylene flames. Combust Flame. 2010;157:2106–2115. [Google Scholar]
- (21).Totton TS, Misquitta AJ, Kraft M. A quantitative study of the clustering of polycyclic aromatic hydrocarbons at high temperatures. Phys Chem Chem Phys. 2012;14:4081–4094. doi: 10.1039/c2cp23008a. [DOI] [PubMed] [Google Scholar]
- (22).Raj A, Sander M, Janardhanan V, Kraft M. A study on the coagulation of polycyclic aromatic hydrocarbon clusters to determine their collision efficiency. Combust Flame. 2010;157:523–534. [Google Scholar]
- (23).Veshkini A, Eaves NA, Dworkin SB, Thomson MJ. Application of PAH-condensation reversibility in modeling soot growth in laminar premixed and non-premixed flames. Combust Flame. 2016;167:335–352. [Google Scholar]
- (24).Eaves NA, Dworkin SB, Thomson MJ. Assessing relative contributions of PAHs to soot mass by reversible heterogeneous nucleation and condensation. Proc Comb Inst. 2017;36:935–945. [Google Scholar]
- (25).Adkins EM, Giaccai JA, Miller JH. Computed electronic structure of polynuclear aromatic hydrocarbon agglomerates. Proc Comb Inst. 2017;36:957–964. [Google Scholar]
- (26).Giaccai JA, Miller JH. Examination of the electronic structure of oxygen-containing PAH dimers and trimers. Proc Comb Inst. 2018 [Google Scholar]
- (27).Mao Q, van Duin ACT, Luo KH. Formation of incipient soot particles from polycyclic aromatic hydrocarbons: A ReaxFF molecular dynamics study. Carbon. 2017;121:380–388. doi: 10.1039/c9cp00354a. [DOI] [PubMed] [Google Scholar]
- (28).Herdman JD, Miller JH. Intermolecular Potential Calculations for Polynuclear Aromatic Hydrocarbon Clusters. J Phys Chem A. 2008;112:6249–6256. doi: 10.1021/jp800483h. [DOI] [PubMed] [Google Scholar]
- (29).Saggese C, Ferrario S, Camacho J, Cuoci A, Frassoldati A, Ranzi E, Wang H, Faravelli T. Kinetic modeling of particle size distribution of soot in a premixed burner-stabilized stagnation ethylene flame. Combust Flame. 2015;162:3356–3369. [Google Scholar]
- (30).Aubagnac-Karkar D, El Bakali A, Desgroux P. Soot particles inception and PAH condensation modelling applied in a soot model utilizing a sectional method. Combust Flame. 2018;189:190–206. [Google Scholar]
- (31).Totton TS, Chakrabarti D, Misquitta AJ, Sander M, Wales DJ, Kraft M. Modelling the internal structure of nascent soot particles. Combust Flame. 2010;157:909–914. [Google Scholar]
- (32).Wang CS, Bartelt NC, Ragan R, Thürmer K. Revealing the molecular structure of soot precursors. Carbon. 2018;129:537–542. [Google Scholar]
- (33).Mosbach S, Celnik MS, Raj A, Kraft M, Zhang HR, Kubo S, Kim K-O. Towards a detailed soot model for internal combustion engines. Combust Flame. 2009;156:1156–1165. [Google Scholar]
- (34).Sabbah H, Biennier L, Klippenstein SJ, Sims IR, Rowe BR. Exploring the Role of PAHs in the Formation of Soot: Pyrene Dimerization. J Phys Chem Lett. 2010;1:2962–2967. [Google Scholar]
- (35).Heinemann T, Palczynski K, Dzubiella J, Klapp SHL. Coarse-grained electrostatic interactions of coronene: Towards the crystalline phase. J Chem Phys. 2015;143 doi: 10.1063/1.4935063. 174110. [DOI] [PubMed] [Google Scholar]
- (36).Grančič P, Bylsma R, Meekes H, Cuppen HM. Evaluation of All-Atom Force Fields for Anthracene Crystal Growth. Crystal Growth & Design. 2015;15:1625–1633. [Google Scholar]
- (37).Sancho-García JC, Pérez-Jiménez AJ, Olivier Y. Determining the cohesive energy of coronene by dispersion-corrected DFT methods: Periodic boundary conditions vs. molecular pairs. J Chem Phys. 2015;142 doi: 10.1063/1.4907268. 054702. [DOI] [PubMed] [Google Scholar]
- (38).Fedorov I, Zhuravlev Y, Berveno V. Properties of crystalline coronene: Dispersion forces leading to a larger van der Waals radius for carbon. Phys Stat Sol (b) 2012;249:1438–1444. [Google Scholar]
- (39).Fioressi SE, Binning RC, Bacelo DE. Effects of cluster formation on spectra of benzopyrene and benzopyrene. Chem Phys Lett. 2008;454:269–273. doi: 10.1016/j.cplett.2008.02.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (40).Sancho-García JC, Pérez-Jiménez AJ. Theoretical study of stability and charge-transport properties of coronene molecule and some of its halogenated derivatives: A path to ambipolar organic-based materials? The Journal of Chemical Physics. 2014;141 doi: 10.1063/1.4897205. 134708. [DOI] [PubMed] [Google Scholar]
- (41).Sancho-García JC, Pérez-Jiménez AJ. Charge-transport properties of prototype molecular materials for organic electronics based on graphene nanoribbons. Phys Chem Chem Phys. 2009;11:2741–2746. doi: 10.1039/b821748c. [DOI] [PubMed] [Google Scholar]
- (42).Pérez-Jiménez ÁJ, Sancho-García JC. Conductance Enhancement in NanographeneGold Junctions by Molecular -Stacking. J Am Chem Soc. 2009;131:14857–14867. doi: 10.1021/ja904372d. [DOI] [PubMed] [Google Scholar]
- (43).Yoshida Y, Isomura K, Kishida H, Kumagai Y, Mizuno M, Sakata M, Koretsune T, Nakano Y, Yamochi H, Maesato M, et al. Conducting Columns of Highly Symmetric Coronene, The Smallest Fragment of Graphene. Chemistry – A European Journal. 2016;22:6023–6030. doi: 10.1002/chem.201505023. [DOI] [PubMed] [Google Scholar]
- (44).Sanyal S, Manna AK, Pati SK. Effect of Imide Functionalization on the Electronic, Optical, and Charge Transport Properties of Coronene: A Theoretical Study. J Phys Chem C. 2013;117:825–836. [Google Scholar]
- (45).Scholz R, Luschtinetz R, Seifert G, Jägeler-Hoheisel T, Körner C, Leo K, Rapacioli M. Quantifying charge transfer energies at donor–acceptor interfaces in small-molecule solar cells with constrained DFTB and spectroscopic methods. J Phys Condens Matter. 2013;25 doi: 10.1088/0953-8984/25/47/473201. 473201. [DOI] [PubMed] [Google Scholar]
- (46).Darghouth AAMHM, Casida ME, Taouali W, Alimi K, Ljungberg MP, Koval P, Sánchez-Portal D, Foerster D. Assessment of Density-Functional Tight-Binding Ionization Potentials and Electron Affinities of Molecules of Interest for Organic Solar Cells Against First-Principles GW Calculations. Computation. 2015 [Google Scholar]
- (47).Roser JE, Ricca A. Polycyclic aromatic hydrocarbon clusters as sources of interstellar aromatic infrared emission. Astrophys J. 2015;801:108. [Google Scholar]
- (48).Ricca A, Charles W, Bauschlicher J, Allamandola LJ. The Infrared Spectroscopy of Neutral Polycyclic Aromatic Hydrocarbon Clusters. Astrophys J. 2013;776:31. [Google Scholar]
- (49).Friha H, Féraud G, Pino T, Parneix P, Dhaouadi Z, Bréchignac P. Electronic spectra of cationic PAH and PAH clusters. EAS Publications Series. 2012;58:373–378. [Google Scholar]
- (50).Goulart M, Kuhn M, Rasul B, Postler J, Gatchell M, Zettergren H, Scheier P, Echt O. The structure of coronene cluster ions inferred from H2 uptake in the gas phase. Phys Chem Chem Phys. 2017;19:27968–27973. doi: 10.1039/c7cp04999d. [DOI] [PubMed] [Google Scholar]
- (51).Birer Ö, Yurtsever E. Dimer formation of perylene: An ultracold spectroscopic and computational study. J Mol Struct. 2015;1097:29–36. [Google Scholar]
- (52).Beitz T, Laudien R, Löhmannsröben H-G, Kallies B. Ion Mobility Spectrometric Investigation of Aromatic Cations in the Gas Phase. J Phys Chem A. 2006;110:3514–3520. doi: 10.1021/jp055335n. [DOI] [PubMed] [Google Scholar]
- (53).Joblin C, Dontot L, Garcia GA, Spiegelman F, Rapacioli M, Nahon L, Parneix P, Pino T, Bréchignac P. Size Effect in the Ionization Energy of PAH Clusters. J Phys Chem Lett. 2017;8:3697–3702. doi: 10.1021/acs.jpclett.7b01546. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (54).Schmidt M, Masson A, Bréchignac C. Coronene cluster experiments: Stability and thermodynamics. Int J Mass Spectrom. 2006;252:173–179. [Google Scholar]
- (55).Gatchell M, Stockett MH, de Ruette N, Chen T, Giacomozzi L, Nascimento RF, Wolf M, Anderson EK, Delaunay R, Vizcaino V, et al. Failure of hydrogenation in protecting polycyclic aromatic hydrocarbons from fragmentation. Phys Rev A. 2015;92 050702. [Google Scholar]
- (56).Holm AIS, Zettergren H, Gatchell M, Johansson HAB, Seitz F, Schmidt HT, Rousseau P, Ławicki A, Capron M, Domaracka A, et al. Ionization and fragmentation of cold clusters of PAH molecules –collisions with keV ions. J Phys Conf Ser. 2012;388 012051. [Google Scholar]
- (57).Johansson HAB, Zettergren H, Holm AIS, Seitz F, Schmidt HT, Rousseau P, Ławicki A, Capron M, Domaracka A, Lattouf E, et al. Ionization and fragmentation of polycyclic aromatic hydrocarbon clusters in collisions with keV ions. Phys Rev A. 2011;84 043201. [Google Scholar]
- (58).Holm AIS, Zettergren H, Johansson HAB, Seitz F, Rosén S, Schmidt HT, Ławicki A, Rangama J, Rousseau P, Capron M, et al. Ions Colliding with Cold Polycyclic Aromatic Hydrocarbon Clusters. Phys Rev Lett. 2010;105 doi: 10.1103/PhysRevLett.105.213401. 213401. [DOI] [PubMed] [Google Scholar]
- (59).Gatchell M, Rousseau P, Domaracka A, Stockett MH, Chen T, Schmidt HT, Chesnel JY, Méry A, Maclot S, Adoui L, et al. Ions colliding with mixed clusters of C60 and coronene: Fragmentation and bond formation. Phys Rev A. 2014;90 022713. [Google Scholar]
- (60).Gatchell M, Zettergren H. Knockout driven reactions in complex molecules and their clusters. J Phys B. 2016;49 162001. [Google Scholar]
- (61).Rousseau P, Ławicki A, Holm AIS, Capron M, Maisonny R, Maclot S, Lattouf E, Johansson HAB, Seitz F, Méry A, et al. Low-energy ions interacting with anthracene molecules and clusters. Nucl Instrum Methods Phys Res B. 2012;279:140–143. [Google Scholar]
- (62).Seitz F, Holm AIS, Zettergren H, Johansson HAB, Rosén S, Schmidt HT, Ławicki A, Rangama J, Rousseau P, Capron M, et al. Polycyclic aromatic hydrocarbon-isomer fragmentation pathways: Case study for pyrene and fluoranthene molecules and clusters. J Chem Phys. 2011;135 doi: 10.1063/1.3622589. 064302. [DOI] [PubMed] [Google Scholar]
- (63).Delaunay R, Gatchell M, Rousseau P, Domaracka A, Maclot S, Wang Y, Stockett MH, Chen T, Adoui L, Alcamí M, et al. Molecular Growth Inside of Polycyclic Aromatic Hydrocarbon Clusters Induced by Ion Collisions. J Phys Chem Lett. 2015;6:1536–1542. doi: 10.1021/acs.jpclett.5b00405. [DOI] [PubMed] [Google Scholar]
- (64).Gámez F, Hortal AR, Martínez-Haya B, Soltwisch J, Dreisewerd K. Ultraviolet laser desorption/ionization mass spectrometry of single-core and multi-core polyaromatic hydrocarbons under variable conditions of collisional cooling: insights into the generation of molecular ions, fragments and oligomers. J Mass Spectrom. 2014;49:1127–1138. doi: 10.1002/jms.3433. [DOI] [PubMed] [Google Scholar]
- (65).Bréchignac P, Schmidt M, Masson A, Pino T, Parneix P, Bréchignac C. Photoinduced products from cold coronene clusters. Astron Astrophys. 2005;442:239–247. [Google Scholar]
- (66).Chanyshev AD, Litasov KD, Shatskiy AF, Furukawa Y, Yoshino T, Ohtani E. Oligomerization and carbonization of polycyclic aromatic hydrocarbons at high pressure and temperature. Carbon. 2015;84:225–235. [Google Scholar]
- (67).Chanyshev AD, Litasov KD, Furukawa Y, Kokh KA, Shatskiy AF. Temperature-induced oligomerization of polycyclic aromatic hydrocarbons at ambient and high pressures. Scientific Reports. 2017;7 doi: 10.1038/s41598-017-08529-2. 7889. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (68).Zhao Y, Truhlar DG. A Prototype for Graphene Material Simulation; Structures and Interaction Potentials of Coronene Dimers. J Phys Chem C. 2008;112:4061–4067. [Google Scholar]
- (69).Rapacioli M, Spiegelman F, Talbi D, Mineva T, Goursot A, Heine T, Seifert G. Correction for dispersion and Coulombic interactions in molecular clusters with density functional derived methods: Application to polycyclic aromatic hydrocarbon clusters. J Chem Phys. 2009;130:244304–10. doi: 10.1063/1.3152882. [DOI] [PubMed] [Google Scholar]
- (70).Obolensky OI, Semenikhina VV, Solov’yov AV, Greiner W. Interplay of electrostatic and van der Waals forces in coronene dimer. Int J Quant Chem. 2007;107:1335–1343. [Google Scholar]
- (71).Bartolomei M, Pirani F, Marques JMC. Modeling Coronene Nanostructures: Analytical Potential, Stable Configurations and Ab Initio Energies. J Phys Chem C. 2017;121:14330–14338. [Google Scholar]
- (72).Piacenza M, Grimme S. Van der Waals Complexes of Polar Aromatic Molecules: Unexpected Structures for Dimers of Azulene. J Am Chem Soc. 2005;127:14841–14848. doi: 10.1021/ja053613q. [DOI] [PubMed] [Google Scholar]
- (73).Yurtsever E. Stacking of triphenylene: characterization of the potential energy surface. Theo Chem Acc. 2010;127:133–139. [Google Scholar]
- (74).Podeszwa R. Interactions of graphene sheets deduced from properties of polycyclic aromatic hydrocarbons. J Chem Phys. 2010;132:044704–8. doi: 10.1063/1.3300064. [DOI] [PubMed] [Google Scholar]
- (75).Philpott MR, Kawazoe Y. Bonding and magnetism in transition metal sandwich structures with the aromatic hydrocarbon coronene C24H12 outer layers. Chem Phys. 2007;342:223–235. [Google Scholar]
- (76).Philpott MR, Kawazoe Y. Chemical bonding in metal sandwich molecules MnR2 with R=pyrene C16H10 and tetracene C18H12. Chem Phys. 2007;337:55–67. [Google Scholar]
- (77).Philpott MR, Kawazoe Y. Transition metal sandwich molecules with large (Cn, n24) zigzag poly aromatic hydrocarbons. Chem Phys. 2008;348:69–82. [Google Scholar]
- (78).Lee EC, Kim D, Jurecka P, Tarakeshwar P, Hobza P, Kim KS. Understanding of Assembly Phenomena by Aromatic; Aromatic Interactions: Benzene Dimer and the Substituted Systems. J Phys Chem A. 2007;111:3446–3457. doi: 10.1021/jp068635t. [DOI] [PubMed] [Google Scholar]
- (79).Podeszwa R, Bukowski R, Szalewicz K. Potential Energy Surface for the Benzene Dimer and Perturbational Analysis of Pi-Pi Interactions. J Phys Chem A. 2006;110:10345–10354. doi: 10.1021/jp064095o. [DOI] [PubMed] [Google Scholar]
- (80).Rapacioli M, Calvo F, Spiegelman F, Joblin C, Wales D. Stacked Clusters of Polycyclic Aromatic Hydrocarbon Molecules. J Phys Chem A. 2005;109:2487–2497. doi: 10.1021/jp046745z. [DOI] [PubMed] [Google Scholar]
- (81).Hernández-Rojas J, Calvo F, Wales DJ. Coarse-graining the structure of polycyclic aromatic hydrocarbons clusters. Phys Chem Chem Phys. 2016;18:13736–13740. doi: 10.1039/c6cp00592f. [DOI] [PubMed] [Google Scholar]
- (82).Piuzzi F, Dimicoli I, Mons M, Millié P, Brenner V, Zhao Q, Soep B, Tramer A. Spectroscopy, dynamics and structures of jet formed anthracene clusters. Chem Phys. 2002;275:123–147. [Google Scholar]
- (83).Totton TS, Misquitta AJ, Kraft M. A First Principles Development of a General Anisotropic Potential for Polycyclic Aromatic Hydrocarbons. J Chem Theor Comput. 2010;6:683–695. doi: 10.1021/ct9004883. [DOI] [PubMed] [Google Scholar]
- (84).Chakrabarti D, Totton TS, Kraft M, Wales DJ. A survey of the potential energy surface for the (benzene)13 cluster. Phys Chem Chem Phys. 2011;13:21362–21366. doi: 10.1039/c1cp22220a. [DOI] [PubMed] [Google Scholar]
- (85).Totton TS, Misquitta AJ, Kraft M. A transferable electrostatic model for inter-molecular interactions between polycyclic aromatic hydrocarbons. Chem Phys Lett. 2011;510:154–160. [Google Scholar]
- (86).Easter DC, Roof JA, Butts LJ. A Monte Carlo Study of Isomers and Structural Evolution in BenzeneCyclohexane Clusters: (C6H6)(C6H12)n, n = 37, 12. J Phys Chem A. 2007;111:12914–12931. doi: 10.1021/jp075214i. [DOI] [PubMed] [Google Scholar]
- (87).Bowal K, Martin JW, Kraft M. Partitioning of polycyclic aromatic hydrocarbons in heterogeneous clusters. Carbon. 2019;143:247–256. [Google Scholar]
- (88).Pascazio L, Sirignano M, D’Anna A. Simulating the morphology of clusters of polycyclic aromatic hydrocarbons: The influence of the intermolecular potential. Combust Flame. 2017;185:53–62. [Google Scholar]
- (89).Chen D, Totton TS, Akroyd JWJ, Mosbach S, Kraft M. Size-dependent melting of polycyclic aromatic hydrocarbon nano-clusters: A molecular dynamics study. Carbon. 2014;67:79–91. [Google Scholar]
- (90).Nakamura M, Ichimura A. Stability of multiply charged clusters of polycyclic aromatic hydrocarbons. Physica Scripta. 2013;2013 014063. [Google Scholar]
- (91).Takeuchi H. Structures, stability, and growth sequence patterns of small homoclusters of naphthalene, anthracene, phenanthrene, phenalene, naphthacene, and pyrene. Comput Theor Chem. 2013;1021:84–90. [Google Scholar]
- (92).Calvo F, Yurtsever E, Birer Ö. Possible Formation of Metastable PAH Dimers upon Pickup by Helium Droplets. J Phys Chem A. 2016;120:1727–36. doi: 10.1021/acs.jpca.5b12394. [DOI] [PubMed] [Google Scholar]
- (93).Hernández-Rojas J, Calvo F, Niblett S, Wales DJ. Dynamics and thermodynamics of the coronene octamer described by coarse-grained potentials. Phys Chem Chem Phys. 2017;19:1884–1895. doi: 10.1039/c6cp07671h. [DOI] [PubMed] [Google Scholar]
- (94).Bouvier B, Brenner V, Millié P, Soudan J-M. A Model Potential Approach to Charge Resonance Phenomena in Aromatic Cluster Ions. J Phys Chem A. 2002;106:10326–10341. [Google Scholar]
- (95).Shaik SS, Hiberty PC. A Chemist’s Guide to Valence Bond Theory. Wiley-Interscience; New Jersey: 2008. pp. 1–290. [Google Scholar]
- (96).Pauling L. The nature of the Chemical Bond. Cornell University Press; New York; 1939. pp. 183–220. [Google Scholar]
- (97).Milko P, Kalus R, Paidarová I, Hrušák J, Gadéa FX. Ab initio excited states calculations of Kr3+, probing semi-empirical modelling. Theoretical Chemistry Accounts. 2009;124:169–178. [Google Scholar]
- (98).Rapacioli M, Spiegelman F, Scemama A, Mirtschink A. Modeling Charge Resonance in Cationic Molecular Clusters: Combining DFT-Tight Binding with Configuration Interaction. J Chem Theor Comput. 2011;7:44–55. doi: 10.1021/ct100412f. [DOI] [PubMed] [Google Scholar]
- (99).Rapacioli M, Spiegelman F. Modelling singly ionized coronene clusters. Eur Phys J D. 2009;52:55–58. [Google Scholar]
- (100).Dontot L, Suaud N, Rapacioli M, Spiegelman F. An extended DFTB-CI model for charge-transfer excited states in cationic molecular clusters: model studies versus ab initio calculations in small PAH clusters. Phys Chem Chem Phys. 2016;18:3545–3557. doi: 10.1039/c5cp06344b. [DOI] [PubMed] [Google Scholar]
- (101).Rapacioli M, Simon A, Dontot L, Spiegelman F. Extensions of DFTB to investigate molecular complexes and clusters. Phys Stat Sol (b) 2012;249:245–258. [Google Scholar]
- (102).Porezag D, Frauenheim T, Köhler T, Seifert G, Kaschner R. Phys Rev B. 1995;51:12947–12957. doi: 10.1103/physrevb.51.12947. [DOI] [PubMed] [Google Scholar]
- (103).Seifert G, Porezag D, Frauenheim T. Calculations of Molecules, Clusters, and Solids with a Simplified LCAO-DFT-LDA Scheme. Int J Quantum Chem. 1996;58:185–192. [Google Scholar]
- (104).Elstner M, Porezag D, Jungnickel G, Elsner J, Haugk M, Frauenheim T, Suhai S, Seifert G. Phys Rev B. 1998;58:7260–7268. [Google Scholar]
- (105).Frauenheim T, Seifert G, Elsterner M, Hajnal Z, Jungnickel G, Porezag D, Suhai S, Scholz R. A Self-Consistent Charge Density-Functional Based Tight-Binding Method for Predictive Materials Simulations in Physics, Chemistry and Biology. Phys Stat Solidi (b) 2000;217:41–62. [Google Scholar]
- (106).Frauenheim T, Seifert G, Elstner M, Niehaus T, Köhler C, Amkreutz M, Sternberg M, Hajnal Z, Carlo AD, Suhai S. Atomistic simulations of complex materials: ground-state and excited-state properties. J Phys Cond Mat. 2002;14:3015. [Google Scholar]
- (107).Oliveira A, Seifert G, Heine T, duarte H. Density-functional based tight-binding: an approximate DFT method. J Braz Chem Soc. 2009;20:1193–1205. [Google Scholar]
- (108).Elstner M. The SCC-DFTB method and its application to biological systems. Theo Chem Acc. 2006;116:316–325. [Google Scholar]
- (109).Zhechkov L, Heine T, Patchovskii S, Seifert G, Duarte H. An Efficient a Posteriori Treatment for Dispersion Interaction in Density-Functional-Based Tight Binding. J Chem Theor Comput. 2005;1:841–847. doi: 10.1021/ct050065y. [DOI] [PubMed] [Google Scholar]
- (110).Li J, Zhu T, Cramer C, Truhlar D. New Class IV Charge Model for Extracting Accurate Partial Charges from Wave Functions. J Phys ChemA. 1998;102:1820–1831. [Google Scholar]
- (111).Söderhjelm P, Karlström G, Ryde U. Comparison of overlap-based models for approximating the exchange-repulsion energy. J Chem Phys. 2006;124 doi: 10.1063/1.2206182. 244101. [DOI] [PubMed] [Google Scholar]
- (112).Gräfenstein J, Kraka E, Cremer D. The impact of the self-interaction error on the density functional theory description of dissociating radical cations: Ionic and covalent dissociation limits. J Chem Phys. 2004;120:524–539. doi: 10.1063/1.1630017. [DOI] [PubMed] [Google Scholar]
- (113).Gräfenstein J, Kraka E, Cremer D. Effect of the self-interaction error for three-electron bonds: On the development of new exchange-correlation functionals. Phys Chem Chem Phys. 2004;6:1096–1112. [Google Scholar]
- (114).Wu Q, Cheng C-L, Van Voorhis T. Configuration interaction based on constrained density functional theory: A multireference method. J Chem Phys. 2007;127:164119–9. doi: 10.1063/1.2800022. [DOI] [PubMed] [Google Scholar]
- (115).Hourahine B, Aradi B, Frauenheim T. DFTB + and lanthanides. J Phys Conf Ser. 2010;242 012005. [Google Scholar]
- (116).Wu Q, Van Voorhis T. Direct Calculation of Electron Transfer Parameters through Constrained Density Functional Theory. J Phys ChemA. 2006;110:9212–9218. doi: 10.1021/jp061848y. [DOI] [PubMed] [Google Scholar]
- (117).Wu Q, Van Voorhis T. Extracting electron transfer coupling elements from constrained density functional theory. J Chem Phys. 2006;125:164105–9. doi: 10.1063/1.2360263. [DOI] [PubMed] [Google Scholar]
- (118).Li Z, Scheraga HA. Monte Carlo-minimization approach to the multiple-minima problem in protein folding. Proceedings of the National Academy of Sciences. 1987;84:6611–6615. doi: 10.1073/pnas.84.19.6611. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (119).Wales DJ, Doye JPK. Global Optimization by Basin-Hopping and the Lowest Energy Structures of Lennard-Jones Clusters Containing up to 110 Atoms. The Journal of Physical Chemistry A. 1997;101:5111–5116. [Google Scholar]
- (120).Yoo S, Shao N, Koehler C, Fraunhaum T, Zeng XC. Structures and relative stability of medium-sized silicon clusters. V. Low-lying endohedral fullerenelike clusters Si31–Si40 and Si45. The Journal of Chemical Physics. 2006;124 doi: 10.1063/1.2191494. 164311. [DOI] [PubMed] [Google Scholar]
- (121).Pei Y, Gao Y, Zeng XC. Exohedral silicon fullerenes: SiNPtN2 (20N60) The Journal of Chemical Physics. 2007;127 doi: 10.1063/1.2749514. 044704. [DOI] [PubMed] [Google Scholar]
- (122).Kirkpatrick S, Gelatt CD, Vecchi MP. Optimization by Simulated Annealing. Science. 1983;220:671–680. doi: 10.1126/science.220.4598.671. [DOI] [PubMed] [Google Scholar]
- (123).Sugita Y, Okamoto Y. Replica-Exchange Molecular Dynamics Method for Protein Folding. Chem Phys Lett. 1999;314:141–151. [Google Scholar]
- (124).Geyer CJ. In: Keramidas EK, editor. Computing Science and Statistics: Proceedings of the 23rd Symposium on the Interface; Fairfax Station: Interface Foundation; 1991. p. 156. [Google Scholar]
- (125).Goldberg DE. Genetic Algorithms in Search, Optimization and Machine Learning. Addison-Wesley Longman Publishing Co., Inc.; 1989. p. 372. [Google Scholar]
- (126).Kennedy J, Eberhart R. Particle swarm optimization. Proc of IEEE int conf on neural networks; 1995. pp. 1942–1948. [Google Scholar]
- (127).Chen BL, Sun WG, Kuang XY, Lu C, Xia XX, Shi HX, Maroulis G. Structural Stability and Evolution of Medium-Sized Tantalum-Doped Boron Clusters: A Half-Sandwich-Structured TaB12 –Cluster. Inorganic Chemistry. 2018;57:343–350. doi: 10.1021/acs.inorgchem.7b02585. [DOI] [PubMed] [Google Scholar]
- (128).Sun WG, Wang JJ, Lu C, Xia XX, Kuang XY, Hermann A. Evolution of the Structural and Electronic Properties of Medium-Sized Sodium Clusters: A Honeycomb-Like Na20 Cluster. Inorganic Chemistry. 2017;56:1241–1248. doi: 10.1021/acs.inorgchem.6b02340. [DOI] [PubMed] [Google Scholar]
- (129).Sun W, Xia X, Lu C, Kuang X, Hermann A. Probing the structural and electronic properties of zirconium doped boron clusters: Zr distorted B12 ligand framework. Physical Chemistry Chemical Physics. 2018;20:23740–23746. doi: 10.1039/c8cp03384f. [DOI] [PubMed] [Google Scholar]
- (130).Hansmann UHE. Parallel Tempering Algorithm for Conformational Studies of Biological Molecules. Chem Phys Lett. 1997;281:140–150. [Google Scholar]
- (131).Calvo F. All-exchanges parallel tempering. J Chem Phys. 2005;123:124106–7. doi: 10.1063/1.2036969. [DOI] [PubMed] [Google Scholar]
- (132).Podeszwa R, Szalewicz K. Physical origins of interactions in dimers of polycyclic aromatic hydrocarbons. Phys Chem Chem Phys. 2008;10 doi: 10.1039/b719725j. 2735. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.