Optimal Designs for Pairwise Calculation: an Application to Free Energy Perturbation in Minimizing Prediction Variability

Abstract

Pairwise-based methods such as the Free Energy Perturbation (FEP) method have been widely deployed to compute the binding free energy differences between two similar host-guest complexes. The calculated pairwise free energy difference is either directly adopted or transformed to absolute binding free energy for molecule rank-ordering. We investigated, through both analytic derivations and simulations, how the selection of pairs in the experiment could impact the overall prediction precision. Our studies showed that a) the estimated absolute binding free energy $(\stackrel{\wedge }{\mathrm{\Delta }G})$ derived from calculated pairwise differences (∆∆G) through weighted least squares fitting is more precise in prediction than the pairwise difference values when the number of pairs is more than the number of ligands and b) prediction precision is influenced by both the total number of pairs and the specifically selected pairs, the latter being critically important when the number of calculated pairs is limited. Furthermore, we applied optimal experimental design in pair selection and found that the optimally selected pairs can outperform randomly selected pairs in prediction precision. In an illustrative example, we showed that, upon weighing ligand structure similarity into design optimization, the weighted optimal designs are more efficient than the literature reported designs. This work provides a new approach to assess retrospective pairwise-based prediction results, and a method to design new prospective pairwise-based experiments for molecular lead optimization.

Graphical Abstract

Optimally selected pairs can outperform randomly selected pairs in prediction precision. It underlines the importance of designing optimal perturbation graph in pairwise-based calculations.

INTRODUCTION

Predicting the binding free energy of ligand-protein complexes has been a grand challenge in the field of computational chemistry since the early days of molecular modeling.^1,2 Multiple computational methodologies exist to predict ligand binding affinities. Pathway-based Free Energy Perturbation (FEP),^3–6 Thermodynamic Integration (TI),^7,8 as well as Linear Interaction Energy (LIE),^9–11 and Molecular Mechanics-Poisson Boltzmann/Generalized Born Surface Area (MM-PBSA/GBSA)^12–15 have been applied to a variety of biologically relevant problems and achieved different levels of predictive accuracy. Recent advancements in computer hardware and simulation algorithms of molecular dynamics and Monte Carlo sampling, as well as improved general force field parameters, have made FEP a principal approach for calculating the free energy differences, especially when calculating the host-guest binding affinity differences upon chemical modification.^16–20

Since the FEP-calculated binding free energy difference, denoted ∆∆G^FEP, only characterizes the differences in free energy between pairs of ligands or complexes, not the absolute binding free energy value of each individual host-guest system, denoted ∆G, we examine here two rarely asked questions in FEP application:

1. Which values would be more appropriate as the prediction to assess the ligands prospectively: the calculated pairwise free energy difference, ∆∆G^FEP, or the estimated absolute binding energy, $\stackrel{\wedge }{\mathrm{\Delta }G}$, transformed from ∆∆G^FEP?

2. In the situation where only a limited number of ligand pairs can be calculated in FEP, can the perturbation pairs be optimally selected with respect to the reference ligand(s) to maximize the prediction precision?

These two questions underline the viability of an often neglected assumption in pairwise comparisons: that the pairwise value is sufficient to make a quantitative and reliable characterization of an individual ligand’s properties or activities. This implicit assumption would be true if there were no error in each pairwise calculation. Recently, some perturbation pair selection approaches such as multiple pathways²¹ or cycle closure analyses²² provided calculation error estimations, but did not address the related statistics of the two questions above.

In an ideal scenario, the pair selection resulted impact could be minimized by conducting an exhaustive study that obtains all ${\hspace{0.17em}}_N{C}_2=N(N-1)/2$ pairs for a set of N molecules; more pairs to consider if there is directionality $(\mathrm{\Delta }\mathrm{\Delta }{G}_{i,j}\ne -\mathrm{\Delta }\mathrm{\Delta }{G}_{j,i})$. Obviously, that study of all possible pairs is impractical and unnecessary. Thus we desire to have a FEP study to collect sufficient amount of ∆∆G data, such that the data set is 1) feasibly attainable, 2) topologically sufficient, and 3) mathematically synthesizable; in this way, we can mitigate inherent calculation errors and have higher confidence in our conclusions.

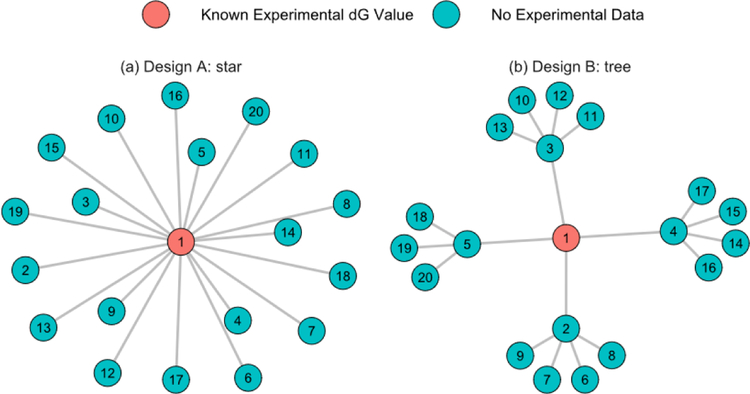
The significance of the above questions can be illustrated by a motivating example with simulated data shown in Figure 1 and Table 1, which considers two different perturbation graph designs for 20 ligands with the same number of FEP perturbation pairs, 19, and the same reference, Ligand 1. These two designs reached different conclusions in rank ordering ligand potencies due to errors inherent in the FEP derived estimates. Based on design A, ligands 5, 7, 14, and 15 would be selected as the best four (20%) picks as their $\stackrel{\wedge }{\mathrm{\Delta }G}$ estimates are the most favorable. Design B would yield ligands 5, 12, 18, and 19 as the best for the same reason. Without knowing the true value, ∆G^True of the other 19 ligands, we lack a prospective metric to assess which perturbation graph design could be more precise although, retrospectively, we know that both design A and B designs had reasonably good agreement with the true values, as measured through correlation and error metrics, listed in Table 1. However, the top picks from neither design were consistent with the true top four ligands, which are ligands 7, 10, 12, and 18. Yet, if all of the ₂₀C₂ =190 pairs could have been calculated as listed in the last column of Table 1, the best four ligands would have been correctly identified. Additionally, the other metrics included in Table 1 were significantly improved when all pairs are included. However, as mentioned above, calculating all possible pairs, or even a significant fraction of all possible pairs, is impractical, especially when the number of molecules is large. Given this restriction, is it possible to objectively determine whether design A or B will give more precise predictions?

Figure 1:

Graphs of two different perturbation designs of 20 ligands. (a) Design A, star-shaped, (b) Design B, tree-shaped. Ligand 1 is the reference. There is a total of 19 perturbations in both designs.

Table 1:

Summary results of design A, design B and all 190 pairs. 20 ∆G^True are generated in the range of −12 to −6. The 190 calculated ∆∆G^FEP are generated based on ∆∆G^True with randomly added error (R function: rnorm(mean = ∆∆G^True, sd = 1.0)). The complete data is available in SI. The top 4 ligands based on the corresponding metric are in bold.

		Design A				Design B
	∆GTrue	$\stackrel{\wedge }{\mathit{\Delta }\mathit{G}}$	PairID	∆∆GTrue	∆∆GFEP	$\stackrel{\wedge }{\mathit{\Delta }\mathit{G}}$	PairID	∆∆GTrue	∆∆GFEP	$\stackrel{\wedge }{\mathit{\Delta }\mathit{G}}$c
1	−8.87
2	−10.38	−9.65	(2,1)	1.51	0.78	−9.65	(2,1)	1.51	0.78	−10.53
3	−7.87	−7.89	(3,1)	−1.00	−0.98	−7.89	(3,1)	−1.00	−0.98	−8.59
4	−6.43	−5.34	(4,1)	−2.44	−3.53	−5.34	(4,1)	−2.44	−3.53	−7.14
5	−9.28	−10.77	(5,1)	0.41	1.90	−10.77	(5,1)	0.41	1.90	−9.54
6	−8.71	−10.14	(6,1)	−0.16	1.26	−7.63	(6,2)	−1.67	−2.03	−9.27
7	−11.52	−12.42	(7,1)	2.65	3.55	−9.31	(7,2)	1.14	−0.34	−11.65
8	−8.09	−6.49	(8,1)	−0.79	−2.38	−7.46	(8,2)	−2.29	−2.20	−8.86
9	−9.25	−7.81	(9,1)	0.38	−1.06	−9.76	(9,2)	−1.13	0.11	−9.63
10	−11.08	−9.57	(10,1)	2.21	0.70	−10.05	(10,3)	3.21	2.16	−11.36
11	−6.43	−5.58	(11,1)	−2.44	−3.29	−6.91	(11,3)	−1.44	−0.99	−6.80
12	−11.30	−9.78	(12,1)	2.43	0.91	−12.06	(12,3)	3.43	4.16	−11.89
13	−8.23	−7.51	(13,1)	−0.64	−1.36	−9.50	(13,3)	0.36	1.61	−8.68
14	−9.94	−11.29	(14,1)	1.07	2.42	−9.28	(14,4)	3.51	3.94	−10.56
15	−10.33	−10.78	(15,1)	1.46	1.91	−8.18	(15,4)	3.90	2.84	−10.96
16	−9.23	−8.51	(16,1)	0.36	−0.37	−8.46	(16,4)	2.80	3.12	−9.52
17	−6.46	−5.19	(17,1)	−2.41	−3.68	−6.81	(17,4)	0.03	1.48	−6.88
18	−11.16	−9.71	(18,1)	2.29	0.84	−11.89	(18,5)	1.88	1.12	−11.71
19	−9.81	−10.02	(19,1)	0.94	1.15	−11.90	(19,5)	0.53	1.12	−9.96
20	−5.62	−3.89	(20,1)	−3.25	−4.98	−6.76	(20,5)	−3.66	−4.02	−6.36
	Spearman ρ	0.79a				0.80a				0.99a
	MSE	1.40b			1.40a	1.37a			0.83b	0.46a

^abetween ∆G^True and $\stackrel{\wedge }{\mathrm{\Delta }G}$. $\stackrel{\wedge }{\mathrm{\Delta }G}$ is derived from 19 ∆∆G^FEP values of design A or B.

^bbetween ∆∆G^True and ∆∆G^FEP of 19 pairs.

^c$\stackrel{\wedge }{\mathrm{\Delta }G}$ is derived from 190 ∆∆G^FEP values.

In this report, we first investigate the performance of the calculated ∆∆G^FEP values compared to the pairwise differences in weighted least squares-derived $\stackrel{\wedge }{\mathrm{\Delta }G}$ estimates, both analytically and through simulations. Based on our findings, we recommend applying weighted least squares to the transformation of ∆∆G^FEP values into $\stackrel{\wedge }{\mathrm{\Delta }G}$ estimates. Second, we investigate the factors that contribute to the precision of the $\stackrel{\wedge }{\mathrm{\Delta }G}$ estimates, such as the total number of computed pairs, the selections of computed pairs, and the uncertainty in the computed ∆∆G^FEP values. The mean squared error, denoted MSE, and Spearman’s rank correlation, denoted ρ,²³ are used as performance metrics.

Furthermore, we demonstrate how structural similarity can be incorporated in design optimization, and its potential impact on prediction precision. In a majority of the reported FEP studies, the ∆∆G^FEP pairs were selected based on chemical structure similarity^21,22 under the assumption that pairs with small chemical difference would have smaller errors in FEP ∆∆G^FEP calculations, on average. To that point, we show that incorporating structural similarity as weighting function in design optimiztion can increase design efficiency, and consequently improve prediction precision if the structural similarity assumption is true.

Using both the constructed mathematical system and literature examples, we demonstrate that some pair-selection schemes (perturbation designs) are better than others. Accordingly, to minimize the prediction uncertainty, it is recommended to select design optimality criterion to suit each practical application.

METHODOLOGY

Mathematical Structure

Some necessary notation used throughout this section is as follows:

Let ${\underset{\_}{\mathrm{\Delta }G}}^{True}$ represent the (N × 1) vector of true but unknown absolute binding affinities for all N ligands of interest:

$${\underset{\_}{\mathrm{\Delta }G}}^{True}={\left[\mathrm{\Delta }{G}_1^{True},\mathrm{\Delta }{G}_2^{True},\hspace{1em}\dots ,\mathrm{\Delta }{G}_N^{True}\right]}^{\text{'}}.$$

Define the collection of m_Exp experimental (reference) and m_FEP calculated data as ${\underset{\_}{\mathrm{\Delta }G}}^{Data}={\left[{\underset{\_}{\mathrm{\Delta }G}}^{Exp}\hspace{1em}{\underset{\_}{\mathrm{\Delta }\mathrm{\Delta }G}}^{FEP}\right]}^{\text{'}}$, and relate the ${\underset{\_}{\mathrm{\Delta }G}}^{Data}$ to true unknown binding affinities ${\underset{\_}{\mathrm{\Delta }G}}^{True}$ as

$${\underset{\_}{\mathrm{\Delta }G}}^{Data}=\mathbf{A}.{\underset{\_}{\mathrm{\Delta }G}}^{True}+\underset{\_}{ϵ}.$$ (1)

The matrix A can be decomposed into two sub-matrices

$$\mathbf{A}={\left[\begin{array}{c}{\mathbf{A}}_{\mathrm{\Delta }G}\\ {\mathbf{A}}_{\mathrm{\Delta }\mathrm{\Delta }G}\end{array}\right]}_{(m_{Exp}+m_{FEP},N)},$$

where the sub-matrix A_∆G maps $\mathrm{\Delta }{G}_i^{Exp}$ to $\mathrm{\Delta }{G}_i^{True}$ by having a 1 in the i^th column and zeros elsewhere, while sub-matrix A_∆∆G maps $\mathrm{\Delta }\mathrm{\Delta }{G}_{i,j}^{FEP}$ to $\mathrm{\Delta }{G}_i^{True}-\mathrm{\Delta }{G}_j^{True}$ by having a 1 in the i^th column, a −1 in the j^th column, and zeros elsewhere. The matrix A defines the design topology of pairwise-based calculation. More details can be found in Supplementary Information.

The vector $\underset{\_}{ϵ}$ in eq. (1) represents errors with variance Wσ², where W is a diagonal matrix of user-defined weights w_i for each element in ${\underset{\_}{\mathrm{\Delta }G}}^{Data}$. This allows us to consider different precisions across the experimental and calculated values, but could also be modified to represent varying levels of molecular similarity or complexity in the calculated values.

To uniquely estimate all N binding affinities in ${\underset{\_}{\mathrm{\Delta }G}}^{True}$, necessary conditions include m_Exp ≥ 1, and m_FEP ≥ N −m_Exp, and Rank(A) ≥ N. From eq. (1), the estimate of ${\underset{\_}{\mathrm{\Delta }G}}^{True}$, denoted $\underset{\_}{\stackrel{\wedge }{\mathrm{\Delta }G}}$, can be solved via weighted least squares²⁴ as follows:

$$\underset{\_}{\stackrel{\wedge }{\mathrm{\Delta }G}}={({\mathbf{A}}^{\prime }{W}^{-1}\mathbf{A})}^{-1}{\mathbf{A}}^{\prime }{W}^{-1}{\underset{\_}{\mathrm{\Delta }G}}^{Data}$$ (2)

The variance-covariance matrix of the estimated $\underset{\_}{\stackrel{\wedge }{\mathrm{\Delta }G}}$ expressed in eq. (2) is well-established as:

$${({\mathbf{A}}^{\prime }{W}^{-1}\mathbf{A})}^{-1}{\sigma }^2.$$ (3)

The inverse of eq. (3) is functionally related to the Information Matrix, I. Using the model in eq. (1), the predicted values where experimental and calculated data are collected, ${\underset{\_}{\stackrel{\wedge }{\mathrm{\Delta }G}}}^{Data}$, are obtained through $H\cdot {\underset{\_}{\mathrm{\Delta }G}}^{Data}$, where H is an (m_Exp + m_FEP ) × (m_Exp + m_FEP ) matrix written as

$$H=\mathbf{A}{({\mathbf{A}}^{\prime }{W}^{-1}\mathbf{A})}^{-1}{\mathbf{A}}^{\prime }{W}^{-1}.$$ (4)

The expression in eq. (4) is well known from linear models as the hat matrix, and that the variance of the i^th predicted values at those conditions where data are observed is written as $Var({\stackrel{\wedge }{\mathrm{\Delta }G}}_i^{Data})=h_{ii}{\sigma }^2$ where h_ii is the i^th diagonal element of H and 0 ≤ h_ii ≤ 1.²⁵ This immediately implies that the predicted ${\stackrel{\wedge }{\mathrm{\Delta }G}}_j-{\stackrel{\wedge }{\mathrm{\Delta }G}}_k$, as a linear function of all the data, will have greater or equal precision than any single FEP-derived $\mathrm{\Delta }\mathrm{\Delta }{G}_{j,k}^{FEP}$ that doesn’t consider the design matrix A. This intuitively makes sense, as back-transformed estimates of binding affinity incorporate more information via the design topology than a single FEP-calculated value.

Computer Generated Optimal Designs

The choice of the design matrix, A, can greatly influence precision of the estimated ${\underset{\_}{\mathrm{\Delta }G}}^{True}$ values used for absolute free energy comparisons, especially when the number of ligands N is large and number of calculated pairs m_FEP is small. A poor choice of matrix A will compromise the prediction quality. For a set of N ligands, the _NC₂ number of pairs will almost assuredly be too many to compute, as well as having a potentially limited return in gaining additional knowledge. However, given a smaller and feasible subset m_FEP < _NC₂, the objective becomes to identify the specific m_FEP pairs that maximize the precision of ${\stackrel{\wedge }{\mathrm{\Delta }G}}_i$, i = 1, …, N.

Experimental designs should be tailored to accommodate any resource or physical constraints, yet preserve desirable properties based on model and prediction precision. Given restrictions, such as computational resource, the optimal design construction can be accomplished by computer. Computer-generated designs and the area of optimal design theory can be attributed to Kiefer^26,27 and Wolfowitz. ²⁸ General algorithm inputs minimally include a hypothesized model (as in eq. (1)), an objective function reflecting a property of interest (typically from eq. (3)), and targeted sample size. Once the inputs are provided, the design that optimizes the objective function is generated.

There are several objective functions that speak to design properties of interest and are referred to as alphabetic optimality criteria. Generally speaking, the most common optimality criterion is D-optimality, which minimizes the joint confidence region on the estimated parameters of interest (here, ${\underset{\_}{\mathrm{\Delta }G}}^{True}$). A-optimality is a related and common criterion that minimizes the average size of a confidence interval on the estimated parameters of interest. Both D- and A-optimality use functions of eq. (3) to obtain the appropriate design. Specifically, the algorithm finds the set of design points that minimizes the determinant (D-optimality) or the trace (A-optimality) of eq. (3). In practice, both optimal design criteria target minimizing variance, which corresponds to maximizing the information. In this work, both D-optimal and A-optimal designs are obtained through the Fedorov-exchange algorithm.^29,30

Simulation Study

To numerically and visually compare design quality and performance, a few statistical measures are computed. Measures that speak to design quality, such as MSE, are analytically derived. However, measures that quantify the accuracy level of a data set, such as Spearman’s rank correlation (or Spearman’s ρ), must be estimated via a simulation study. The procedure is as follows:

1. Create N true ∆G values ${\underset{\_}{\mathrm{\Delta }G}}^{True}$.

2. Randomly generate the set of N experimental ∆G^Exp values centered at the N ∆G^True values with variance ${\sigma }_{Exp}^2$.

3. Generate the full set of _NC₂ FEP-derived ∆∆G^FEP values centered at all possible _NC₂ differences of ∆G^True values with variance ${\sigma }_{FEP}^2$.

4. The study design consists of a subset of selected FEP pairs and experimental data used to estimate ∆G^True. The design topology is either fixed as the A- or D-optimal design, or randomly generated in each iteration. If randomly generated, need to ensure Rank(A) ≥ N.

5. Use weighted least squares to estimate $\underset{\_}{\stackrel{\wedge }{\mathrm{\Delta }G}}$. For example, where the weights are defined as $\frac{1}{{\sigma }_{FEP}^2}$ or $\frac{1}{{\sigma }_{Exp}^2}$ for the study listed in Table 2 and Table 3.

6. Summarize and store MSE, ρ, and determine if the best ligand was identified based on the estimated $\underset{\_}{\stackrel{\wedge }{\mathrm{\Delta }G}}$ values derived from simulated ∆∆G^FEP and ∆G^Exp values.

7. Repeat steps 1–6 M times, keeping the optimal design matrix A constant throughout and storing summary statistics each time.

8. Numerically and visually analyze the distribution of the summary statistics.

Table 2:

Analytically derived and simulated metrics for different designs.

Pairs	Design	$\mathit{M}\mathit{S}{\mathit{E}}_{\stackrel{\wedge }{\mathit{\Delta }\mathit{G}}}$	$\mathit{M}\mathit{S}{\mathit{E}}_{\mathit{\Delta }\stackrel{\wedge }{\mathit{\Delta }\mathit{G}}}$b	$\mathit{M}\mathit{S}{\mathit{E}}_{\mathit{\Delta }\stackrel{\wedge }{\mathit{\Delta }\mathit{G}}}^{\mathit{A}\mathit{l}\mathit{l}}$c	Median ρ d	Accuracye
20	Random*	4.08	0.95	3.79	0.60 (0.38–0.77)	30.5%
	D-optimal	3.83	0.95	3.50	0.60 (0.38–0.77)	31.5%
	A-optimal	1.42	0.95	1.83	0.70 (0.54–0.82)	35.3%
30	Random*	1.66	0.63	1.33	0.77 (0.62–0.87)	40.9%
	D-optimal	1.36	0.63	0.91	0.81 (0.68–0.88)	49.2%
	A-optimal	1.08	0.63	1.10	0.79 (0.67–0.88)	45.3%
50	Random*	0.98	0.38	0.54	0.87 (0.78–0.92)	55.0%
	D-optimal	0.92	0.38	0.44	0.89 (0.80–0.93)	58.3%
	A-optimal	0.79	0.38	0.50	0.88 (0.79–0.93)	57.5%

^*The averages across 5,000 different randomly selected designs.

^a$MS{E}_{\stackrel{\wedge }{\mathrm{\Delta }G}}$ was analytically derived from equation (3).

^b$MS{E}_{\mathrm{\Delta }\stackrel{\wedge }{\mathrm{\Delta }G}}$ was analytically derived from equation (3) and includes only pairwise differences with corresponding FEP values.

^c$MS{E}_{\mathrm{\Delta }\stackrel{\wedge }{\mathrm{\Delta }G}}^{All}$ was analytically derived from equation (3) and includes all _NC₂ = 190 possible pairwise differences.

^dSpearman’s rank correlation (ρ) between the ∆G^True and estimated $\stackrel{\wedge }{\mathrm{\Delta }G}$ values of 20 ligands with the 15th and 85th quantiles in parenthesis.

^eProbability of correctly identifying the ligand with the lowest absolute free energy.

Table 3:

Analytically derived and simulated metrics for different designs with different $MS{E}_{\mathrm{\Delta }\mathrm{\Delta }{G}^{FEP}}$ variability and ∆G^True distributions.

		a∆GTrue from standard normal
		$\mathit{M}\mathit{S}{\mathit{E}}_{\mathit{\Delta }\mathit{\Delta }{\mathit{G}}^{\mathit{F}\mathit{E}\mathit{P}}}=\mathbf{1.0}$			$\mathit{M}\mathit{S}{\mathit{E}}_{\mathit{\Delta }\mathit{\Delta }{\mathit{G}}^{\mathit{F}\mathit{E}\mathit{P}}}=\mathbf{2.25}$
Pairs	Design	$\mathit{M}\mathit{S}{\mathit{E}}_{\stackrel{\wedge }{\mathit{\Delta }\mathit{G}}}$c	Median ρd	Accuracye	$\mathit{M}\mathit{S}{\mathit{E}}_{\stackrel{\wedge }{\mathit{\Delta }\mathit{G}}}$	Median ρ	Accuracy
20	Random	4.02	0.60	30.5%	9.00	0.46	20.4%
	D-optimal	3.83	0.60	31.5%	8.61	0.46	22.8%
	A-optimal	1.42	0.70	35.3%	3.19	0.55	24.6%
30	Random	1.66	0.77	40.9%	3.73	0.63	27.8%
	D-Optimal	1.36	0.81	49.2%	3.12	0.68	34.6%
	A-Optimal	1.08	0.79	45.3%	2.43	0.66	34.3%
50	Random	0.98	0.87	55.0%	2.21	0.77	43.2%
	D-Optimal	0.92	0.89	58.3%	2.09	0.79	47.2%
	A-Optimal	0.79	0.88	57.5%	1.78	0.78	43.9%
		b ∆GTrue from uniform between −12.0 and −6.5
20	Random	4.02	0.77	28.1%	9.00	0.65	22.6%
	D-optimal	3.83	0.78	30.2%	8.61	0.65	23.7%
	A-optimal	1.42	0.85	32.9%	3.19	0.74	24.8%
30	Random	1.66	0.89	38.0%	3.73	0.80	30.2%
	D-Optimal	1.36	0.91	41.7%	3.12	0.84	32.3%
	A-Optimal	1.08	0.91	41.1%	2.43	0.83	30.7%
50	Random	0.98	0.94	49.0%	2.21	0.89	37.8%
	D-Optimal	0.92	0.95	49.4%	2.09	0.91	39.3%
	A-Optimal	0.79	0.94	49.0%	1.78	0.90	39.4%

^a∆G^True values were generated from a normal distribution with µ = 0 and σ = 1

^b∆G^True values were generated from a continuous uniform distribution between −12.0 and −6.5.

^c$MS{E}_{\stackrel{\wedge }{\mathrm{\Delta }G}}$ was analytically derived from equation (3) for optimal designs.

^dSpearman’s rank correlation (ρ) between the ∆G^True and estimated $\stackrel{\wedge }{\mathrm{\Delta }G}$ values of 20 ligands.

^eProbability of correctly identifying the ligand with the lowest absolute free energy.

One of the endpoints under investigation is the difference between the $\mathrm{\Delta }\mathrm{\Delta }{G}_{j,k}^{FEP}$ values and the corresponding estimated pairwise differences from ${\stackrel{\wedge }{\mathrm{\Delta }G}}_j-{\stackrel{\wedge }{\mathrm{\Delta }G}}_k$, denoted $\mathrm{\Delta }\mathrm{\Delta }{\widehat{G}}_{j,k}$. We demonstrate in the results that the latter is more statistically precise.

It is worth noting that there are some generalization in this simulation study:

1. Errors in each FEP calculation and each experimental result are independent of each other. In practical studies, the errors of different pairs can be related because of their shared ligands; thus, the aforementioned weight matrix, W, can be further adjusted accordingly to address the pair-pair relationship. Blocking techniques^31–33 can be helpful if the relationship is well-defined. However, given that there has not been any reported discussion or study on the inter-correlation of perturbation errors, we think that the independence generalization is reasonable for our simulated study.

2. Perturbation is feasible between any pairs and pairs do not have direction (i.e., ∆∆G_j,k = −∆∆G_k,j). In reality, the non-feasible pairs are pairs of compounds with large structural differences, which can lead to large calculation errors. These pairs are typically excluded from perturbation designs to avoid large calculation errors, on average. However, keeping those pairs in our simulation study won’t have any impact on our final results and conclusions since the errors of those pairs are simulated in the same range as the others (e.g., σ = 1.0 kcal/mol). If pairs have direction, $\mathrm{\Delta }\mathrm{\Delta }{G}_{j,k}\ne -\mathrm{\Delta }\mathrm{\Delta }{G}_{k,j}$, it ultimately leads to an increased error in each FEP calculation ${\underset{\_}{\mathrm{\Delta }\mathrm{\Delta }G}}^{FEP}$. Both situations can be represented by increasing simulation variance ${\sigma }_{FEP}^2$ in step 3.

3. The weighing factors in weight matrix, W, are set as constant in simulation, because it is assumed that the pairs have roughly the same degree of precision. If certain pairs of calculation are known to be more accurate and reliable than others, their corresponding weights can be adjusted higher. An example of structure-similarity based weighting is discussed later in the results.

It also should be noted that in our study, the matrix A represents a certain topological design. Each simulation, from step 1 to 6, represents a new independent experiment. Figure S1 in the supplementary information exemplifies the distinction between different designs and experiments. Additionally, an example of generating and analyzing simulated data is described in the supplementary information as well. We believe that this is an appropriate approach to studying the relationship between topological design and prediction accuracy because the simulated scenarios are not limited by specific targets or ligands, so that the conclusions can therefore be applied to a broad scope of such pairwise-based design of experiment.

RESULTS and DISCUSSION

Design Topology

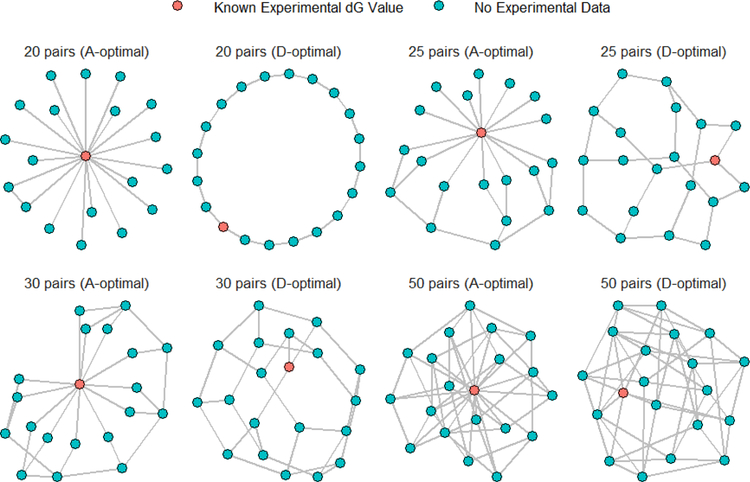
Without loss of generality, we considered the case of N = 20 ligands and designs that contained m_FEP = 20, 25, 30, 50 pairs of ∆∆G^FEP values and m_Exp = 1 experimentally obtained ∆G^Exp value. Given these design parameters, A-optimal and D-optimal designs were generated. These designs are presented in graphical form in Figure 2, where each line or edge in perturbation graph represents calculated ∆∆G^FEP value and the red node indicates the ligand with an experimentally obtained ∆G^Exp value (sometimes referred to as the ”reference ligand”).

Figure 2:

Visualization of designs under different optimality criteria. Each node represents a ligand. Lines represent the presence of ∆∆G^FEP values between pairs of ligands. The ligand colored in red is the reference ligand and has an experimentally obtained ∆G^Exp.

For the designs containing 20 pairs of FEP-calculated ∆∆G^FEP results, the D-optimal design forms a ring while the A-optimal design has the reference ligand paired with all the other ligands in a star-like structure. When the number of pairs is increased to 25, 30, and 50, the D-optimal designs retain the ring structure with more internal pairs. Interestingly, the A-optimal designs do not retain the perfect star-like structure (i.e., not all the 19 other ligands are paired with the reference ligand). A few more examples of A-optimal designs with different number of ligands, references and pairs are shown in Figure S3 and they do not look topologically obvious.

Simulation and Analytically Derived Results

In this section, we present the summary statistics that have been both analytically derived and obtained via simulation. We followed the procedure outlined in the methodology section to simulate experiments. The ∆G^True values were generated from a standard normal distribution (µ = 0, σ = 1.0). Additionally, ${\sigma }_{FEP}^2$ was set at 1.0 and ${\sigma }_{Exp}^2$ at 0.5 so that the relative weight factor w_i is 2, representing that the experimental results are twice as precise as the FEP-calculated results. Given that the reported experimental mean error is around 0.44 pK_i with standard deviation of 0.54 pK_i ¹⁶, we believe that the ${\sigma }_{Exp}^2$ value used in the simulation is a reasonable approximation. The summarized results were based on the average of 5,000 simulated experiments for each design.

Table 2 summarizes the results of these simulations. $MS{E}_{\stackrel{\wedge }{\mathrm{\Delta }G}}$ is the average mean squared error between the estimated $\stackrel{\wedge }{\mathrm{\Delta }G}$ values and the ∆G^True values. $MS{E}_{\mathrm{\Delta }\stackrel{\wedge }{\mathrm{\Delta }G}}$ is the average mean squared error between the pairwise differences of $\stackrel{\wedge }{\mathrm{\Delta }G}$ estimates (i.e., $\mathrm{\Delta }\mathrm{\Delta }{\widehat{G}}_{i,j}={\stackrel{\wedge }{\mathrm{\Delta }G}}_i-{\stackrel{\wedge }{\mathrm{\Delta }G}}_j$) and the pairwise differences between the ∆G^True values for only the pairs that were in the design (i.e., had ∆∆G^FEP values). $MS{E}_{\mathrm{\Delta }\stackrel{\wedge }{\mathrm{\Delta }G}}^{All}$ is similar to the second column but considers all possible _NC₂ pairwise differences. ρ is the median Spearman rank correlation between the estimated $\stackrel{\wedge }{\mathrm{\Delta }G}$ values and the ∆G^True values, with the 15^th and 85^th quantiles in parentheses. Lastly, the accuracy column reports the percentage of simulations where the ligand with the lowest absolute free energy (top 1 ligand) was correctly identified based on $\stackrel{\wedge }{\mathrm{\Delta }G}$ estimates. Note that the first three columns are all derived analytically while the last two are computed from the simulation study.

Starting with $MS{E}_{\mathrm{\Delta }\stackrel{\wedge }{\mathrm{\Delta }G}}$, it’s clear that the pairwise differences of back-transformed $\stackrel{\wedge }{\mathrm{\Delta }G}$ estimates are more accurate than the calculated ∆∆G^FEP values, as all of the values in this table are less than σ_FEP (=1.0 kcal/mol, as defined above), corresponding to the $MS{E}_{\mathrm{\Delta }\mathrm{\Delta }{G}^{FEP}}$. It’s also clear that the precision of the back-transformed pairwise differences increases as more pairs are included in the design. This should not be a surprising result, considering that the back-transformed $\stackrel{\wedge }{\mathrm{\Delta }G}$ estimates combine knowledge from many different sets of pairs with one common reference ligand, whereas any single ∆∆G^FEP value cannot synthesize all of this information. Lastly, note that there is not any difference in average $MS{E}_{\mathrm{\Delta }\stackrel{\wedge }{\mathrm{\Delta }G}}$ with respect to different designs of the same size, though the individual $MS{E}_{\mathrm{\Delta }\stackrel{\wedge }{\mathrm{\Delta }G}}$ value varies across different designs in each simulation. Finally, by back-transforming, we have the ability to compare two ligands which do not have a computed ∆∆G^FEP value between them.

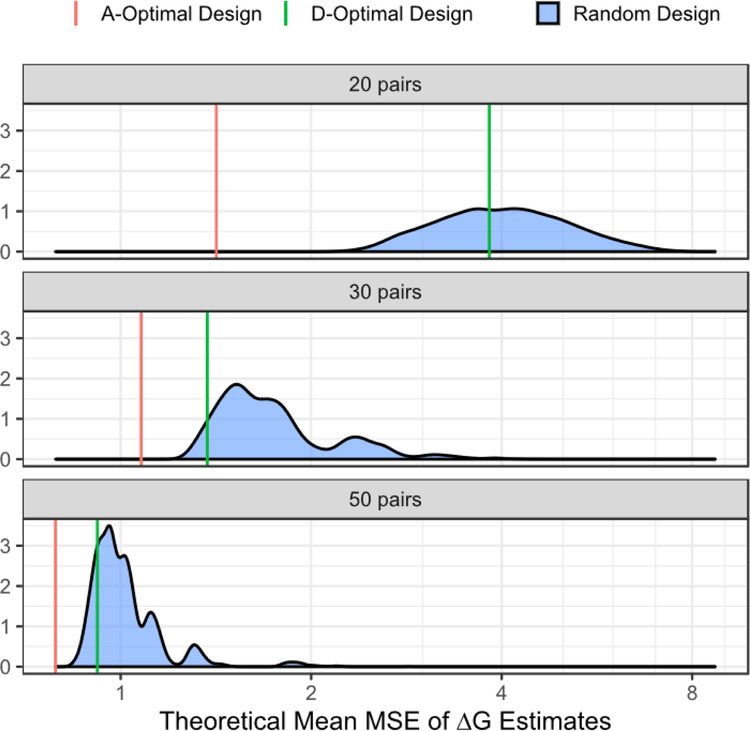
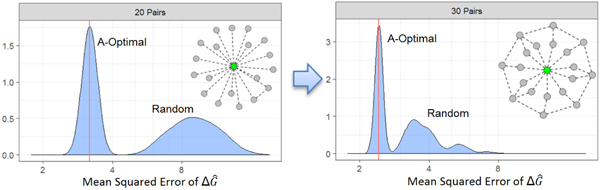
Another prediction assessment metric is the average MSE of the back-transformed $\stackrel{\wedge }{\mathrm{\Delta }G}$ estimates, $MS{E}_{\stackrel{\wedge }{\mathrm{\Delta }G}}$ in the table. The A-optimality design yields the most precise estimates on average; this was expected, as this is the metric that the criterion seeks to minimize. The D-optimal designs, while not quite as precise as the A-optimal designs, still provide a significant improvement over the average of the random designs. This can be seen in Figure 3, where the theoretical average MSE of the A- and D-optimal designs are better than the MSE distribution obtained from randomly generated designs. One can observe that with only 20 pairs included in the design, the A-optimal design gives a significantly better MSE than either a randomly chosen or D-optimal design, and is nearly equivalent to what the D-optimal design gives with 30 pairs. Additionally, the random designs with only 20 pairs display wide $MS{E}_{\stackrel{\wedge }{\mathrm{\Delta }G}}$ range, with most values between 2 to 8, indicating large variability in $\stackrel{\wedge }{\mathrm{\Delta }G}$ estimates and reinforcing the superiority of the computer-generated optimal designs. The graphical comparison of $MS{E}_{\mathrm{\Delta }\mathrm{\Delta }{G}^{FEP}}$, $MS{E}_{\mathrm{\Delta }\stackrel{\wedge }{\mathrm{\Delta }G}}$, and $MS{E}_{\stackrel{\wedge }{\mathrm{\Delta }G}}$ distributions can be found in Figures S4, S5 and S6 in supplementary information.

Figure 3:

Comparison of $MS{E}_{\stackrel{\wedge }{\mathrm{\Delta }G}}$ estimates from different designs. The distribution of $MS{E}_{\stackrel{\wedge }{\mathrm{\Delta }G}}$ are generated from 5,000 random designs and shown in blue. The theoretical average $MS{E}_{\stackrel{\wedge }{\mathrm{\Delta }G}}$ of optimal design is derived from equation (3). They are denoted by red (A-optimal) and green (D-optimal) lines.

While the MSE represents the precision of the $\stackrel{\wedge }{\mathrm{\Delta }G}$ estimates, Spearman’s rank correlation and the probability of successfully identifying the best ligand are statistics that are easier to interpret and are of more practical importance regarding the ligand rank-ordering problem. As demonstrated in Table 2, both the A- and D-optimal designs are either equal to or better than randomly generated designs with respect to Spearman’s rank correlation and have the ability to detect the best ligand. Interestingly, the A-optimal design performs best with respect to these metrics for 20 pair designs, but slightly loses the advantage to the D-optimal designs when more pairs, such as 30 or 50, are included. This is an interesting result, although not completely surprising, as the A-optimal design minimizes $MS{E}_{\stackrel{\wedge }{\mathrm{\Delta }G}}$, it does not take into account the correlation between the $\stackrel{\wedge }{\mathrm{\Delta }G}$ estimates and this correlation structure will impact the ability to rank order ligands. We also see that more pairs lead to more accurate and precise outcomes with respect to both of these statistics, with the Spearman’s rank correlation improving significantly from 20 pair designs (ρ = 0.6 (Random), 0.6 (D-optimal), 0.7 (A-optimal)) to 50 pair designs (ρ = 0.87 (Random), 0.89 (D-optimal), 0.88 (A-optimal)). The ability to identify the best of the 20 ligands also improves as the design size increases, ranging from 30.5% for a random design with 20 pairs to 58.3% for a D-optimal design with 50 pairs. Additionally, the rank correlation values are more variable with smaller designs, as seen in Figure S7.

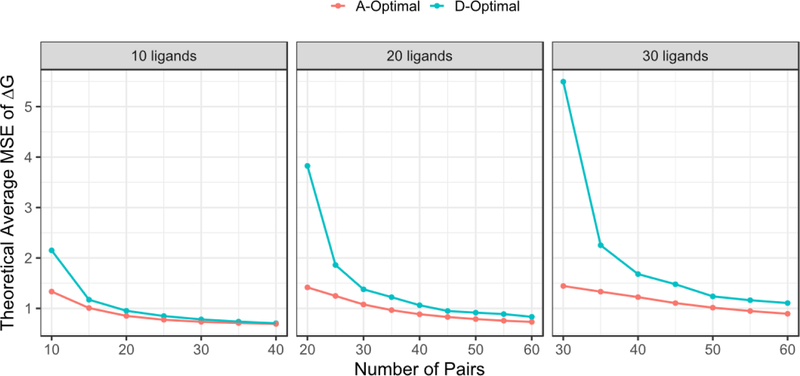
Furthermore, we computed the theoretical accuracy as a function of both design, total number of ligands, and total number of pairs, the sample size. Figure 4 illustrates an example with total 10, 20 and 30 ligands using MSE as an accuracy metric. Again, the theoretical MSE in $\stackrel{\wedge }{\mathrm{\Delta }G}$ improves along with the increasing pair numbers in both the A-optimal and D-optimal designs. The maximum theoretical MSEs from different designs ultimately converge when the number of pairs is large enough, such as 30 pairs for 10 ligands, 50 pairs for 20 ligands and 60 pairs for 30 ligands in this example.

Figure 4:

The theoretical MSEs of $\stackrel{\wedge }{\mathrm{\Delta }G}$ estimates derived from A-optimal (red) and D-optimal (green) designs for 10, 20 and 30 ligands. In this case, σ is set 1.0 kcal/mol in equation (3) for all the calculation.

Impact of Data Distributions and Variability

Unlike the MSE statistics, Spearman’s rank correlation and the ability to correctly identify the best ligand depend not only on variability, but also on the spacing of the underlying ∆G^True values. Considering two $\stackrel{\wedge }{\mathrm{\Delta }G}$ estimates both with standard errors of 1.0 kcal/mol, the ability to correctly rank-order them is better when the estimates are 1.0 and 10.0 kcal/mol rather than 1.0 and 1.2 kcal/mo. For this reason, we examine how the different distributions of ∆G^True values and different levels of variability affect the metrics mentioned in the previous section.

Table 3 summarizes the results of this type of simulation study. Note that $MS{E}_{\mathrm{\Delta }\mathrm{\Delta }{G}^{FEP}}$ is set to 1.0 (kcal/mol)² in the first column and 2.25 (kcal/mol)² in the second column, corresponding to $RMS{E}_{\mathrm{\Delta }\mathrm{\Delta }{G}^{FEP}}=1.15 \text{kcal}/\text{mol}$. The top half set of results were obtained by generating ∆G^True values from a standard normal distribution while the bottom set were obtained by generating ∆G^True values from a uniform distribution between −12.0 kcal/mol and −6.5 kcal/mol.

Across the various design quality metrics, computer-generated optimal designs consistently perform better in these two distribution scenarios. Only when the sample size is quite large do the randomly generated designs become competitive. Naturally, as variability in the ∆∆G^FEP values increases, the variability in the $\stackrel{\wedge }{\mathrm{\Delta }G}$ estimates increases, resulting in lower rank-ordering success. Lastly, the uniform distribution performs better with respect to rank correlation, as the ligands are more evenly spaced than they would be from a normal distribution where the majority of ligands are typically concentrated at the center of a bell curve. Conversely, this also makes it slightly more challenging to accurately select the best ligand, because the uniform distribution will not produce points as extreme as the normal distribution is capable of doing.

Table 4 shows one example where the intrinsic error is not strictly normally distributed among the pairs (edges on the design graph). It was meant to build a scenario in which there are a certain number of outliers from FEP calculations. In this case, the errors associated with the ∆∆G^FEP values were first generated from a normal distribution in all the pairs with σ set to 1.0 kcal/mol as described in Table 2. Then, an extra +3.0 kcal/mol or −3.0 kcal/mol error was added to 10% of the total pairs. Table 4 shows the average MSE of $\stackrel{\wedge }{\mathrm{\Delta }G}$ for each scenario, estimated from the simulations, as the theoretical MSEs are no longer derivable. The results showed that with such outliers, the optimal designs still outperformed the random designs in all cases, although the margin is smaller due to the unpredictable large errors. Obviously, the large errors consequently resulted in lower predictability across all the corresponding designs compared to those in Table 2. In this case, increasing the number of pairs is beneficial in obtaining better prediction precision in both MSE and rank-ordering.

Table 4:

Simulated metrics for different designs with none-norm distributed error on edges.^a

Pairs	Design	$\mathit{M}\mathit{S}{\mathit{E}}_{\stackrel{\wedge }{\mathit{\Delta }\mathit{G}}}$	$\mathit{M}\mathit{S}{\mathit{E}}_{\mathit{\Delta }\stackrel{\wedge }{\mathit{\Delta }\mathit{G}}}$b	$\mathit{M}\mathit{S}{\mathit{E}}_{\mathit{\Delta }\stackrel{\wedge }{\mathit{\Delta }\mathit{G}}}^{\mathit{A}\mathit{l}\mathit{l}}$c	Median ρ d	Accuracye
20	Random	7.49	1.80	7.28	0.50 (0.26–0.69)	22.0%
	D-optimal	6.92	1.81	6.69	0.49 (0.25–0.68)	25.3%
	A-optimal	2.23	1.81	3.49	0.61 (0.43–0.75)	24.7%
30	Random	2.91	1.21	2.59	0.67 (0.49–0.79)	31.3%
	D-optimal	2.16	1.20	1.73	0.71 (0.54–0.82)	38.5%
	A-optimal	1.62	1.21	1.93	0.70 (0.54–0.81)	36.3%
50	Random	1.48	0.72	1.04	0.80 (0.67–0.88)	46.6%
	D-optimal	1.30	0.72	0.83	0.82 (0.70–0.88)	48.8%
	A-optimal	1.06	0.72	0.94	0.80 (0.68–0.88)	47.0%

^aThe averages across 5,000 simulation. The errors in all the pairs were from a normal distribution with σ = 1.0 to represent $MS{E}_{\mathrm{\Delta }\mathrm{\Delta }{G}^{FEP}}$. Then, an extra error of +3.0 or −3.0 kcal/mol was added to 10% of the total pairs to represent outliers.

^b$MS{E}_{\mathrm{\Delta }\stackrel{\wedge }{\mathrm{\Delta }G}}$ includes only pairwise differences with corresponding FEP values.

^c$MS{E}_{\mathrm{\Delta }\stackrel{\wedge }{\mathrm{\Delta }G}}^{All}$ includes all _NC₂ = 190 possible pairwise differences.

^dSpearman’s rank correlation (ρ) between the ∆G^True and estimated $\stackrel{\wedge }{\mathrm{\Delta }G}$ values of 20 ligands with the 15th and 85th quantiles in parenthesis.

^eProbability of correctly identifying the ligand with the lowest absolute free energy.

In summary, computer-generated optimal designs outperform randomly chosen designs with respect to all metrics we considered. A-optimal designs best reduce the uncertainty associated with each individual $\stackrel{\wedge }{\mathrm{\Delta }G}$ estimate and perform better in all metrics for designs with 20 pairs. D-optimal designs perform better with respect to rank correlation and the ability to select the best ligand for larger designs with 30 or 50 pairs. We recommend choosing the optimality criteria based on the prediction accuracy metrics of interest.

Optimal Designs with Structure-Similarity Based Weighting

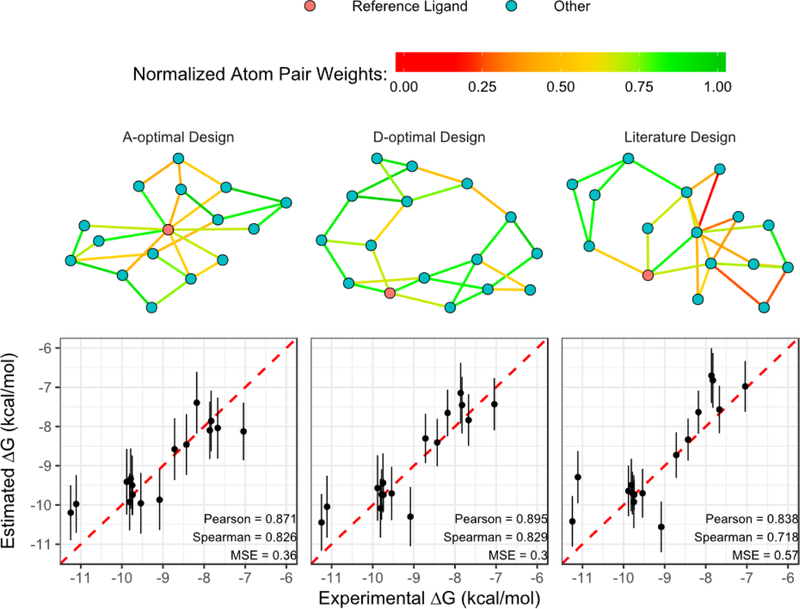
As discussed in methodology section, the calculated ∆∆G^FEP between pairs can have different levels of precision and accuracy and this difference can be considered in the design process through the weight matrix W in eq. (2). Using chemical structural similarity for example, if it is true that small structural differences result in small calculation errors in FEP, different weighting factors w_i,j can be assigned to pairs, based on structural similarity, to account for these differences in precision. In our previous work we had naively assigned weights as w=1 for every FEP-derived ∆∆G^FEP, and w=2 for the reference ligand with known experimental ∆G^Exp. As a practical example, we consider a weighting function based on structural similarity and use these weights when deriving the optimal designs. The structural similarity is considered as a non-naive weighting function in optimization. In such similarity-weighted design, the weighting function assigns each $\mathrm{\Delta }\mathrm{\Delta }{G}_{i,j}^{FEP}$ value weight proportional to the similarity score between the two molecules. For example, a pair with a weighing score of 0.8 is assumed to be 80% as precise as a pair with a weighing score of 1 under this weighting scheme. We applied this weighting strategy to a set of CDK2 ligands. ²² Weighted A- and D-optimal designs were generated using the normalized Tanimoto score of AtomPair fingerprint³⁴ as the weighting factor for the ligand pairs. The ligand with the highest total Tanimoto score (Total Score of ligand $k={\sum }_{j=1}^n{\text{Tanimoto Score}}_{k,j}$) is selected as the reference, which has a fixed weighting of w=2. In this CDK2 example, ligand 1oi9 is considered as the reference for all the designs. The perturbation graphs of the different designs are shown in Figure 5. It is observed that both weighted A- and weighted D-optimal designs include more pairs with high similarity scores while D-optimal design has more ligands (nodes) connected to each other and A-optimal design has more ligands connected to the reference ligand. The literature design contains a number of pairs with low similarity score. We ran FEP calculation for the reported 25 pairs ²² from the noted literature design, and the same number of pairs, 25, from each of the two weighted optimal designs. The detailed weight matrix construction and FEP calcualtion can be found in supplementary information. The results clearly show that the estimated $\stackrel{\wedge }{\mathrm{\Delta }G}$ values from weighted A- and D-optimal designs are better than those from literature design in both precision (MSE) and rank-ordering (Pearson r and Spearman ρ). It is also worth noting that, as summarized in Table 5, the $MS{E}_{\stackrel{\wedge }{\mathrm{\Delta }G}}$ are lower than the $MS{E}_{\mathrm{\Delta }\mathrm{\Delta }{G}^{FEP}}$ in all designs, including optimal and non-optimal (literature) designs. This is consistent with what we demonstrated in both simulation and analytic derivation that $\stackrel{\wedge }{\mathrm{\Delta }G}$ estimates can be more precise than ∆∆G^FEP values in prediction because it uses all the available pairwise information. Consequently, the $MS{E}_{\mathrm{\Delta }\stackrel{\wedge }{\mathrm{\Delta }G}}$ is also lower than $MS{E}_{\mathrm{\Delta }\mathrm{\Delta }{G}^{FEP}}$.

Figure 5:

Designs and FEP calculation results of the CDK2 ligand set from reference 22²². Top row is the visualization of weighted A-optimal, weighted D-optimal and literature designs. Ligand 1oi9 is selected as the reference and colored in red for illustration purpose. Each edge is colored with normalized AtomPair Fingerprint Tanimoto score of the connecting ligands. All the designs have the same reference ligand and the same number of pairs. Bottom row are the plots of ∆G^Exp vs. estimated $\stackrel{\wedge }{\mathrm{\Delta }G}$ from different designs. The error bar indicates one standard error based on least square fitting. The list of pairs in each design and their FEP calculation results are available in the SI table.

Table 5:

FEP calculation results from different designs on CDK2.²²

Design	$\mathit{M}\mathit{S}{\mathit{E}}_{\mathit{\Delta }\mathit{\Delta }{\mathit{G}}^{\mathit{F}\mathit{E}\mathit{P}}}$	$\mathit{M}\mathit{S}{\mathit{E}}_{\stackrel{\wedge }{\mathit{\Delta }\mathit{G}}}$	$\mathit{M}\mathit{S}{\mathit{E}}_{\mathit{\Delta }\stackrel{\wedge }{\mathit{\Delta }\mathit{G}}}$a	rb	ρ	Design Efficiencyc
Literature	0.91	0.57	0.80	0.84	0.72	–
Weighted A-optimal	0.57	0.36	0.48	0.87	0.83	1.38
Weighted D-optimal	0.60	0.30	0.47	0.90	0.83	1.38

^a$MS{E}_{\mathrm{\Delta }\stackrel{\wedge }{\mathrm{\Delta }G}}$ only includes the 25 pairs with corresponding FEP values.

^bPearson correlation (r) and Spearman’s rank correlation (ρ) between the ∆G^Exp and estimated $\stackrel{\wedge }{\mathrm{\Delta }G}$ values of 16 ligands.

^cRelative efficiency of the optimal design is calculated as the ratio of the corresponding criteria of literature design to its A-Optimality or D-Optimality criteria: $tr(I_{literature}^{-1})/tr(I_{A-optimal}^{-1})$ and $det(I_{literature}^{-1})/det(I_{D-optimal}^{-1})$.

We have shown that the optimal designs are obtained by optimizing the Information Matrix I (eq. 3) according to different optimality criteria. Considering the global minimum of det(I⁻¹) (D-optimal) or tr(I⁻¹) (A-optimal) as the maximum design effectiveness that can be achieved with the same amount of information (number of pairs), the ratio of the optimality criteria of different designs reflects how much more efficiently one design can generate precise predictions compared to another. Using the same CDK2 ligand set for example, the efficiency of different optimal designs relative to the literature design²² is listed in the last column of Table 5. As expected, both weighted A- and weighted D-optimal designs have higher efficiency (> 1) than literature design, demonstrating that the topologically optimized designs are capable of generating more precise predictions than structurally derived design using the same amount of pairs and reference(s).

The purpose of adding weights to design matrix is to bias the pathway selection toward to the pairs that are believed to be more important than the others, in our case, pairs that have more accurate FEP calculations. Therefore, if FEP calculations were not limited by structure similarity or they were equally accurate for all the pairs, as discussed in previous simulated study, there would be no need for weight matrix. An example of A- and D-optimal designs on BACE ligands²² with and without structural similarity weighting is shown in supplementary information to illustrate the effect of weighting function on design efficiency. In reality, due to the physics and the current limit of FEP methodology, certain constraints are needed to restrict or bias the selection. Hence, the selection or construction of weight matrix would be largely dependent on the prior knowledge of the FEP techniques used in the calculation. In the CDK2 example, we used the normalized Tanimoto score of atom pair fingerprint as weighting factor, but we think that other types of similarity metric could serve the same purpose as well. However, if it is known that the used FEP calculation has challenges in handling chiral center switching and or ring opening and closing, it would be better to give those pairs low or zero weights to avoid the large calculation errors regardless the Tanimoto similarity score. Since it is unlikely that there exists a universal weighing scheme that fits all FEP calculation scenario, it is important and good practice to construct the weight matrix W carefully based on the FEP technology in use in order to achieve high prediction accuracy and maximum precision for $\stackrel{\wedge }{\mathrm{\Delta }G}$ estimation and subsequent rank-ordering.

CONCLUSIONS

Pairwise comparisons are widely used in experiment design because it is intuitive to interpret the difference in free energy between a pair of molecules. However, the interpretation of pairwise comparison results could potentially be misleading in rank ordering the full set of molecules due to the small sample sizes and errors in each pair calculation. Although including all possible pairs (at least _NC₂) may not be necessary or technically feasible, including more than the minimum number of pairs, N, will result in more accurate predictions.³⁵ Predictions derived from only minimal number of pairs can be questionable.

In this report, we first formulated the mathematical structure to represent the relationship among true ∆G^True values, experimentally derived ∆G^Exp values, and FEP calculated ∆∆G^FEP values. Through both analytic derivations and simulation studies, it was demonstrated that transforming pairwise FEP values (∆∆G^FEP) into $\stackrel{\wedge }{\mathrm{\Delta }G}$ estimates can improve predictive accuracy if more than the minimum number of pairs is included in the calculations. Two different computer-generated optimal designs (A-optimal and D-optimal) were evaluated in our study and it was demonstrated that both optimal designs are better in generating more precise prediction than non-optimal (random) designs, especially when the number of pairs is small with respect to the number of ligands. Furthermore, we applied structural similarity based weighting to the design optimization. In a real FEP calculation example, CDK2, where there are 16 ligands and 25 pairs, we demonstrated that the prediction results from weighted A- and D-optimal design were more precise than the original design or perturbation graph reported in the literature.

Optimal Designs are to minimize the variability due to the selection of different pairs regardless the errors in individual FEP calculations. In the meanwhile, under the assumption that “high structural similarity” might lead to less FEP calculation error, the structural similarity based weighting can indicate the pairs that could be feasibly or more accurately calculated in FEP. We believe strongly that combining optimal design and structural similarity constraint could be the best approach to achieve better prediction by taking account of both variability in pair selection and expected errors in FEP calculation.