Slow and steady? Strategic adjustments in response caution are moderately reliable and correlate across tasks

Abstract

Speed-accuracy trade-offs are often considered a confound in speeded choice tasks, but individual differences in strategy have been linked to personality and brain structure. We ask whether strategic adjustments in response caution are reliable, and whether they correlate across tasks and with impulsivity traits. In Study 1, participants performed Eriksen flanker and Stroop tasks in two sessions four weeks apart. We manipulated response caution by emphasising speed or accuracy. We fit the diffusion model for conflict tasks and correlated the change in boundary (accuracy – speed) across session and task. We observed moderate test-retest reliability, and medium to large correlations across tasks. We replicated this between-task correlation in Study 2 using flanker and perceptual decision tasks. We found no consistent correlations with impulsivity. Though moderate reliability poses a challenge for researchers interested in stable traits, consistent correlation between tasks indicates there are meaningful individual differences in the speed-accuracy trade-off.

1. Introduction

Response control is one of the cornerstones of cognitive psychology, and a topic of interest for both experimental and correlational approaches. Individual differences in tasks such as the Stroop (Stroop, 1935) and Eriksen flanker (Eriksen & Eriksen, 1974), have been linked to executive functioning (Miyake et al., 2000), impulsive behaviour (Sharma, Markon, & Clark, 2014), and a variety of neuropsychological conditions (Chambers, Garavan, & Bellgrove, 2009; Gauggel, Rieger, & Feghoff, 2004; Lansbergen, Kenemans, & van Engeland, 2007; Moeller et al., 2002; Verdejo-Garcia, Perales, & Perez-Garcia, 2007). From an experimental perspective, response control paradigms feature prominently in modelling and neurophysiological studies, where the goal is to characterise the general mechanisms responsible for the control of action (Bompas, Hedge, & Sumner, 2017; Logan, Yamaguchi, Schall, & Palmeri, 2015; Munoz & Everling, 2004). Though the application of these tasks across different disciplines is promising for the development of a coherent understanding of response control, recent work has illustrated that there are challenges to interpreting individual differences because they can arise from different sources, including strategic processes (Boy & Sumner, 2014; Hedge, Powell, Bompas, Vivian-Griffiths, & Sumner, 2018; Miller & Ulrich, 2013). Here, we ask whether strategic processes, often considered to be a confound in cognitive studies, represent a reliable and general component of decision making.

1.1. Multiple processes underlying individual differences in response control

In conflict tasks, such as the Stroop, flanker or Simon tasks, we typically subtract reaction times or errors in a baseline condition (congruent or neutral) from a condition in which the stimulus provides conflicting information (incongruent). When used in an individual differences context, the resultant RT or error costs are treated as an index of the individual’s ability to resolve competition between conflicting response options (e.g. Friedman & Miyake, 2004). However, the processes underlying behaviour are multifaceted, and variability in the magnitude of an RT cost or error cost cannot easily be attributed to a single mechanism (Hedge, Powell, Bompas, et al., 2018; Miller & Ulrich, 2013). For example, it has long been theorised that an individual’s reaction time reflects not only their ability to process a stimulus, but also their strategic choice to favour speed or accuracy (Pachella, 1974; Wickelgren, 1977). Indeed, one of the reasons why we use within-subject designs when examining differences between conditions in average RTs is to account for this so called speed accuracy trade-off (SAT). However, individual differences in strategy still contribute to variability in the RT costs. Individuals who favour accuracy over speed produce larger RT costs, as well as smaller error costs (Hedge, Powell, Bompas, et al., 2018; Hedge, Powell, & Sumner, 2018; Wickelgren, 1977).

In order to dissociate contributions of strategy and ability in a cognitive task, we require a framework that characterises the contributions of both to behaviour. One such framework is that of sequential sampling models (Brown & Heathcote, 2008; McKoon & Ratcliff, 2013; Ratcliff & McKoon, 2008; Ulrich, Schroter, Leuthold, & Birngruber, 2015). These models assume that choice RT behaviour can be captured by a process of accumulating evidence sampled from the environment, until a boundary or threshold is reached. The rate at which evidence is accumulated represents the efficiency of processing, and the height of the boundary reflects the amount of evidence that an individual waits for before deciding on the response (i.e. their level of response caution, or strategy). By dissociating these processes, and for their ability to simultaneously account for both the RT and accuracy of responses, sequential sampling models could provide a useful window into individual differences in response control (see e.g. Hedge, Powell, Bompas, et al., 2018; White, Curl, & Sloane, 2016).

1.2. Response caution as a meaningful component of response control

To many researchers conducting choice RT tasks, strategic processes are considered a confound to the mechanisms of interest. For example, composite measures of RT and accuracy have been proposed with the explicit intention of providing a better control for SATs than traditional subtractions in studies of (e.g.) executive functioning (Draheim, Hicks, & Engle, 2016; Liesefeld & Janczyk, 2018). However, there is evidence that strategic control itself may be a meaningful measure of individual differences, as captured by sequential sampling models. For example, more cautious response strategies are often observed in healthy older adults, relative to younger adults (e.g. Ratcliff, Thapar, & McKoon, 2006; Thapar, Ratcliff, & McKoon, 2003). Studies have also observed changes in response caution in individuals with autistic spectrum disorders, though the studies vary in the direction of the effect (Karalunas et al., 2018; Pirrone, Dickinson, Gomez, Stafford, & Milne, 2017; Powell et al., 2019). Finally, in multiple response control task datasets, we observed a correlation between tasks in model parameters representing response caution, in the absence of correlations in parameters reflecting conflict processing (Hedge, Powell, Bompas, & Sumner, 2019).

Participants in the aforementioned studies are typically instructed to be both fast and accurate, such that the levels of response caution observed are interpreted as the individual’s ‘default’ strategy when given no explicit instruction to favour speed or accuracy. However, individuals are also able to flexibly adjust their strategy if instructed. In SAT paradigms, participants are instructed to prioritise speed in some blocks and accuracy in others, which is (primarily) captured in sequential sampling models by an individual decreasing or increasing their boundary (for a review, see Heitz, 2014). The extent to which individuals are able or willing to adjust their level of caution has also been the subject of individual differences research. Larger decreases in caution under speed emphasis relative to accuracy emphasis in a perceptual decision task were correlated with increased BOLD activation in the striatum and pre-SMA (Forstmann et al., 2008), as well as increased structural connectivity between those regions (Forstmann et al., 2010; though see Boekel et al., 2015 for a non-replication of the connectivity). An association has also been observed between response caution under speed emphasis and self-reported “need for closure” (Evans, Rae, Bushmakin, Rubin, & Brown, 2017). Need for closure is a personality trait theorised to reflect an individual’s preference for certainty over ambiguity (Webster & Kruglanski, 1994), from which Evans et al. predicted that a greater need for closure would lead to more urgent decision making. In line with this prediction, when the data were fit with the linear ballistic accumulator model (Brown & Heathcote, 2008), individuals with a greater need for closure set a lower threshold (Evans et al., 2017).

In sum, the research to date suggests that individual differences in response caution and its strategic adjustments have the potential to inform our understanding of cognitive functioning in both healthy individuals and neuropsychological conditions. However, this promise is tempered by several unknowns. First, the psychometric properties of response caution and its strategic adjustments are not well understood. Test-retest reliability is an important consideration for individual differences research, reflecting the degree to which individuals can be consistently ranked on the dimension of interest (i.e. more or less cautious). Recent work has suggested that traditional measures of response control have sub-optimal reliability, and these concerns may also extend to model-based analyses (Hedge, Powell, & Sumner, 2018; Paap & Sawi, 2016). Though a few studies have examined the test-retest reliability of model parameters representing response caution (Enkavi et al., 2019; Lerche & Voss, 2017; Schubert, Frischkorn, Hagemann, & Voss, 2016), to our knowledge none have examined the reliability of strategic adjustments of caution in a SAT paradigm.

A second consideration is the extent to which individual differences in strategic control adjustments can be generalised from a single task. Several studies have observed correlations in response caution between tasks when neither speed nor accuracy are preferentially reinforced (Hedge et al., 2019; Lerche & Voss, 2017; Ratcliff, Thompson, & McKoon, 2015), though those that have examined the SAT have used a single perceptual decision task (Evans et al., 2017; Forstmann et al., 2008, 2010).

Here, we address this gap in the literature with two experiments. In the first, we apply a model of response control (the diffusion model for conflict tasks; Ulrich et al., 2015) to test-retest data from the flanker and Stroop tasks under different SAT instructions. This allows us to examine whether adjustments in control are reliable over time within the same task, and whether they generalise across tasks within the same cognitive domain. In the second experiment, we examine generalisability more broadly by comparing a response control task (flanker) to a perceptual decision task (random dot motion) commonly used in the decision making literature. To examine potential relationships with related constructs, we also collected data on self-reported impulsivity in both studies, as well as compliance and personality in Study 2.

2. Study 1: Method

2.1. Participants

Participants were 57 (6 male) undergraduate and postgraduate psychology students. Participants took part either for payment or for course credit. All participants gave their informed written consent prior to participation in accordance with the revised Declarations of Helsinki (2013), and the experiments were approved by the local Ethics Committee.

2.2. Design and procedure

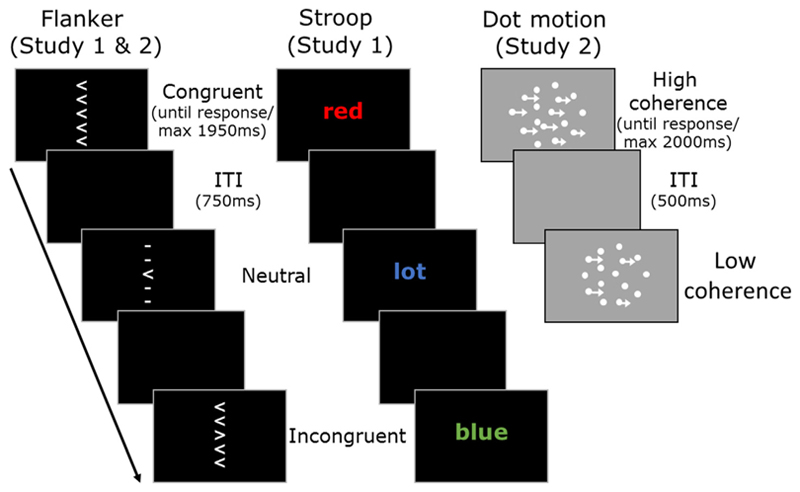
Participants completed both the Stroop and flanker task in two 90 min sessions taking place approximately 4 weeks apart. A schematic of these tasks, as well as the random dot motion task used in study 2, can be seen in Fig. 1. We administered the UPPS-P, a self-report measure with subscales for different types of impulsivity, (Lynam, Whiteside, Smith, & Cyders, 2006; Whiteside & Lynam, 2001), after participants complete the behavioural tasks. Participants completed the tasks in a dimly lit room from a viewing distance of approximately 60 cm. Stimuli were presented on a 36.5 cm by 27.5 cm display (60 hz, 1280 × 1024).

Fig. 1.

Schematic of tasks used in Study 1 (flanker and Stroop) and study 2 (flanker and random dot motion). The stimuli for the flanker and Stroop task are identical to those we have used previously (Hedge, Powell, & Sumner, 2018). See text for details.

2.2.1. Eriksen flanker task

Participants responded to the direction of a centrally presented arrow (left or right) using the z and m keys. On each trial, the centrally presented arrow (1 cm × 1 cm) was flanked above and below by two other symbols separated by 0.75 cm, so that flankers were individually visible. Flanking stimuli were either arrows pointing in the same direction as the central arrow (congruent condition), straight lines (neutral condition), or arrows pointing in the opposite direction to the central arrow (incongruent condition). Trials were separated by an interval of 750 ms.

2.2.2. Stroop task

Participants responded to the colour of a centrally presented word (Arial, font size 70), which could either be red (z key), blue (x key), green (n key) or yellow (m key). The colours were not purposely matched for luminance. The presented word could be the same as the font colour (congruent condition), one of four non-colour words (lot, ship, cross, advice; neutral condition), or a colour word corresponding to one of the other response options (incongruent). Trials were separated by an interval of 750 ms.

For each session and task, participants completed 12 blocks, consisting of 4 each for speed, standard and accuracy instructions. Each block consisted of 144 trials, with 48 each of congruent, neutral and incongruent stimuli (192 trials total per congruency and instruction condition). The order of blocks was randomised, as was the order of trials within blocks. At the beginning of speed-emphasis blocks, participants were instructed “Please try to respond as quickly as possible, without guessing the response”. For accuracy blocks, participants were told “Please ensure that your responses are accurate, without losing too much speed”. For standard instruction blocks, participants were instructed “Please try to be both fast and accurate in your responses”. In speed blocks, if participants responded slower than 500 ms in the flanker or 600 ms in the Stroop, the message “Too slow” appeared on screen for 500 ms. In the accuracy condition, the message “Incorrect” appeared if participants made an error. In all blocks, the message “Too fast” appeared if participants responded faster than 150 ms in the flanker and 200 ms in the Stroop task (typically < 1% of trials). Participants received feedback about both their average RT and accuracy after each block in all instruction conditions.

Stimuli were presented until response. In the Stroop task, stimuli were presented for a maximum duration of 1950 ms. Trials exceeding this were rare (0.3% and 0.2% of trials in session 1 and 2).

2.3. Data processing

Two participants were removed because they did not return for the second session. We excluded participants if there average accuracy across all instruction blocks fell below 60%. This resulted in more participants being retained for the flanker task (N = 47) than the Stroop (N = 43). These participants were retained for the reliability analysis in the flanker task, but were excluded when calculating correlations across tasks. We removed RTs less than 100 ms, and greater than the individual’s median plus three times their median absolute deviation for each condition (Leys, Ley, Klein, Bernard, & Licata, 2013). We did not code trials as incorrect on the basis that they exceeded our deadline for feedback in speed blocks, as changing the relationship between RT and accuracy would confound our modelling. The data are available on the Open ScienceFramework (https://osf.io/zag7c/).

For the reliability analysis, we calculated Intraclass Correlation Coefficients using the psych package in R (ICC2; Revelle, 2018; Team & R Development Core Team, 2016). This value is the ratio of between-subject variance in the measure to the total variance, comprising between-subject variance, between-session variance, and error variance. The form of the ICC corresponds to a two-way random effects model for absolute agreement (Shrout & Fleiss, 1979).

While the ICC is interpreted as a correlation, ranging from zero to one, different criteria are used to interpret the degree of reliability compared to interclass correlation effect sizes (Pearson’s R and Spearman’s rho). ICCs above 0.8 are typically considered excellent, while 0.6 and 0.4 are categorised as good and moderate reliability (Cicchetti & Sparrow, 1981; Fleiss, 1981; Landis & Koch, 1977). In contrast, Pearson’s R values of 0.5, 0.3 and 0.1 are typically interpreted as large, medium and small effect sizes respectively (Cohen, 1988). The higher convention for the ICC primarily reflects the application rather than the calculation, as high levels of reliability are typically a pre-requisite to correlational work. When calculated on the same data, intra and interclass correlations usually produce similar values (see supplementary material A for different calculations).

2.4. The diffusion model for conflict tasks

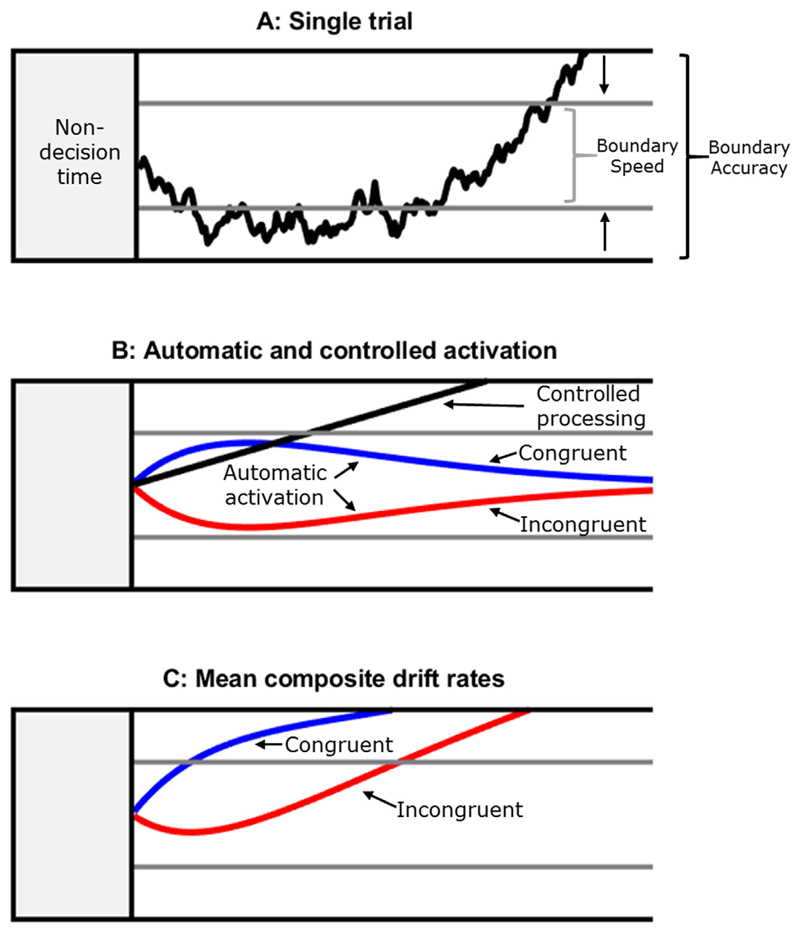
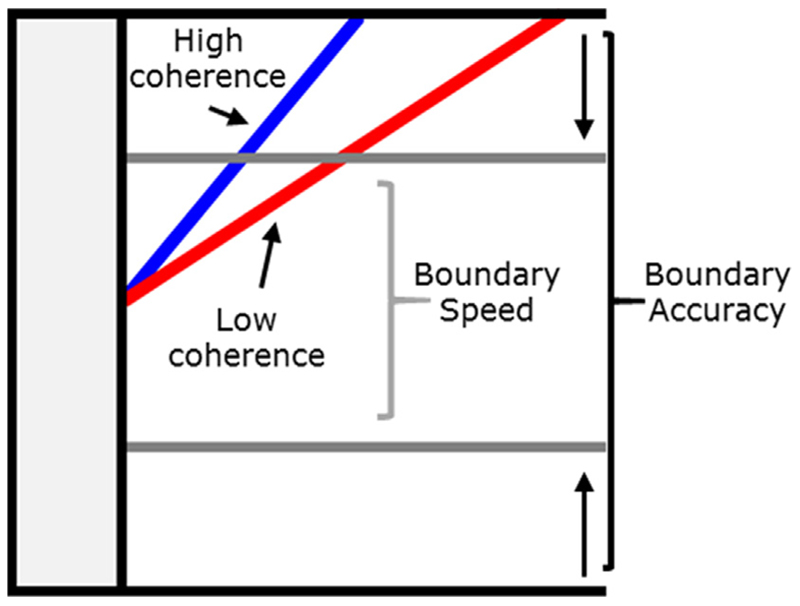
The diffusion model for conflict tasks (DMC; Ulrich et al., 2015) is a mathematical model of two-choice reaction time behaviour in response conflict tasks. It assumes that the response options are represented by an upper and lower boundary, here corresponding to the correct and incorrect response respectively. The decision processes can be described by a process of accumulating evidence from the stimulus until one or the other boundary is reached (see Fig. 2A). The reaction time on a given trial is determined by the time it takes for a boundary to be reached, plus the duration of sensory and motor (non-decision) processes. For mathematical details, see Ulrich et al. (2015).

Fig. 2.

Schematic of the diffusion model for conflict tasks (Ulrich et al., 2015). Panel A shows the noisy accumulation of evidence to a boundary on a single trial. It is assumed that when speed is emphasised, participants set the boundary (grey line) closer to the start of the accumulation processes than under accuracy emphasis (black horizontal line), corresponding to waiting for less evidence before making a response. A small distance between the upper and lower boundary leads to faster RTs, but an increased likelihood of hitting the lower boundary, producing an error. This change in boundary between accuracy and speed emphasis, represented by the arrow, is the strategic adjustment of response caution that is the focus of this study. Panel B shows the average underlying patterns of activation. The black diagonal line corresponds to the speed of controlled processing, represented by a drift rate parameter. The blue and red functions represent automatic activation in congruent and incongruent trials respectively. The function initially receives a strong input until reaching a maximum value (amplitude parameter) at a point defined by the time-to-peak parameter. Panel C shows the composite drift rates for congruent and incongruent trials. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Boundary separation is the critical parameter for our current goal of measuring individual differences in response caution. Individuals who are more averse to making errors and slow their responses to avoid them should have higher boundary separation values. When participants are instructed to emphasise speed, this is primarily captured by lowering their boundary in that block (for reviews, see Heitz, 2014; Ratcliff, Smith, Brown, & McKoon, 2016). Recent evidence has indicated that the changes under speed emphasis are also reflected in non-decision time to a degree in non-conflict tasks, and sometimes also by a change in drift rate (see e.g. Rae, Heathcote, Donkin, Averell, & Brown, 2014). However, the sensitivity of DMC parameters to the SAT manipulations have not been examined. Given the time-consuming nature of the fitting process for our datasets, and the relatively large number of possible variants, we make the simplifying assumption that only boundary separation varies across SAT instruction conditions here.

The DMC assumes that the accumulation process on a trial is a combination of processing from controlled and automatic pathways (De Jong, Liang, & Lauber, 1994; Ridderinkhof, 2002). The controlled route is responsible for processing the task-relevant stimulus feature (e.g. the central arrow in the flanker task), and is represented by drift rate parameter that is constant across conditions. Automatic activation is implemented as a re-scaled gamma function, described by two free parameters (amplitude and time-to-peak) and one fixed parameter (shape). Initially, the automatic activation receives a strong input, reflecting the capture of a prepotent response by (e.g.) the flanking arrows. After it reaches a maximum value (amplitude) at a specified point in time (time-to-peak), the automatic activation decreases, reflecting decay or active suppression (Hommel, 1994; Ulrich et al., 2015). In addition to the aforementioned parameters, which are typically the focus of interest, the model has two parameters describing variability in the starting point of the accumulation processes and variability in the duration of non-decision time respectively.

2.5. Model fitting

For each participant and task, we estimated nine parameters: boundary separation under speed emphasis, boundary separation under standard instructions, boundary separation under accuracy emphasis, the amplitude of automatic activation (A for congruent trials, 0 for neutral trials, -A for incongruent trials), the time to peak automatic activation, mean non-decision time, drift rate of the controlled process, the shape parameter of the starting point distribution, and variability in non-decision time. Variability in starting points and non-decision time are captured by a beta and normal distribution respectively. As with Ulrich et al. (2015), the diffusion constant/within-trial noise (σ) was fixed to 4, and between-trial variability in drift rates was fixed to 0. We fixed the shape parameter of the automatic activation function to 2 for all tasks, following Ulrich et al. (2015).

We accuracy-coded our data, such that the upper and lower response boundaries corresponded to the correct and incorrect response options. This allowed us to collapse across different stimulus configurations (e.g. a congruent flanker stimulus irrespective of whether the arrow was pointing left or right), and also to fit the same model to the four-choice Stroop data (Voss, Nagler, & Lerche, 2013). Though this level of abstraction is not ideal, it relates RT and accuracy to capture the strategic processes that we are interested in, and there is currently no extension of the model for four choice tasks.

After excluding outlier RTs as described above, correct and incorrect RTs from congruent, neutral and incongruent conditions in each instruction block were separately binned into quantiles. We fit the DMC to experimental data using the similar approach to that used by the Diffusion Model Analysis Toolbox (DMAT; Vandekerckhove & Tuerlinckx, 2008). Correct RTs were binned using five quantiles (0.1, 0.3, 0.5, 0.7, 0.9). Incorrect RTs were binned using five quantiles if the total number of errors in that condition > 10, otherwise they were not used. The application of five quantiles produced six bins per RT distribution (corresponding to: 0–10%, 10–30%, 30–50%, 50–70%, 70–90%, 90–100%). Therefore, participants’ fits would be based on either 6 or 12 data points per instruction and congruency condition, resulting in between 54 and 108 data points in total. These quantiles are commonly used when fitting sequential sampling models (c.f. Ratcliff & Tuerlinckx, 2002). We calculated the deviance (-2 log-likelihood) between observed and simulated quantiles, which was minimised with a Nelder-Mead simplex (Nelder & Mead, 1965) implemented in the fminbnd function in Matlab. We constrained the search such that all free parameters were positive, and the shape of the starting point distribution was greater than one.

Initially, we fit each participant’s data using 5000 parameter sets that were randomly generated from a uniform distribution (see supplementary material B for maximum and minimum values). This was done to explore plausible starting points for our fitting algorithm. We then took the 15 best parameter sets resulting from this initial search, and submitted each of those to the simplex algorithm, in which we simulated 10,000 trials per condition at each iteration. The simplex was re-initialised 3 times to avoid local minima. After the process was completed, we took the single best fitting parameter set for each individual. This process took approximately 6 days per dataset, and was performed on Cardiff University Brain Research Imaging Centre’s (CUBRIC) high performance computer cluster.

3. Results and discussion

3.1. Descriptive statistics

3.1.1. Behavioural data

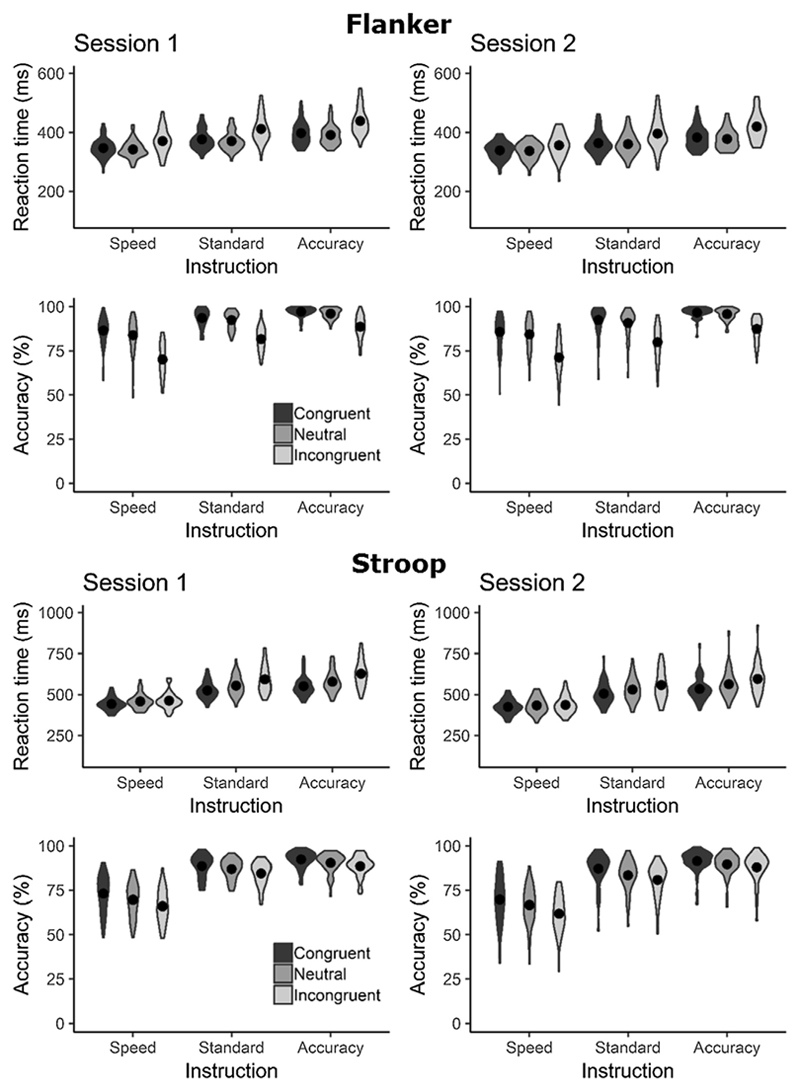
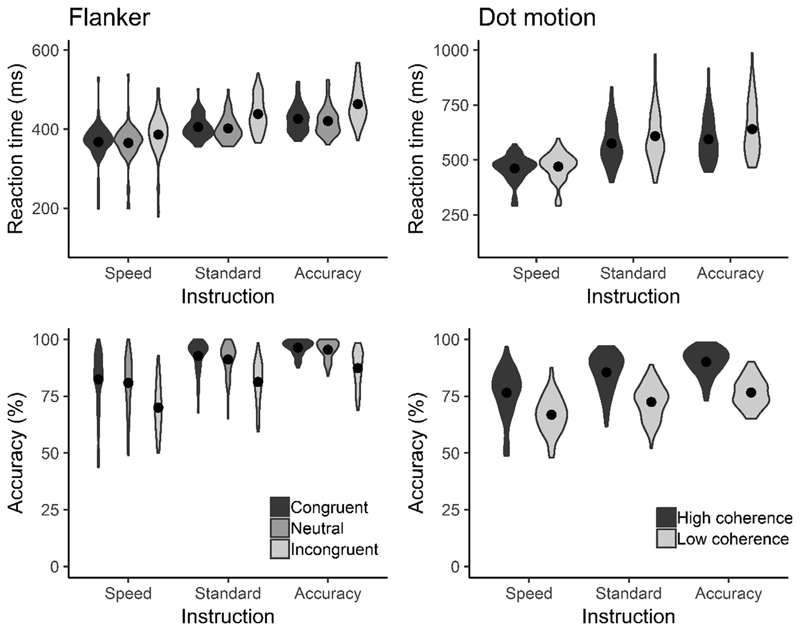
Reaction times and error rates for both tasks are shown in Fig. 3. To verify that the average performance reflected the expected manipulations, we conducted separate 3(instruction) × 3(congruency) repeated-measures ANOVAs on RTs and error rates for each session and task. In all cases we observed significant main effects for both congruency and instruction (all p < .001; see Supplementary Material C for full ANOVA results). Error rates and RTs increased for incongruent relative to congruent stimuli. Further, error rates increased and RTs decreased when participants were instructed to prioritise speed over accuracy.

Fig. 3.

Violin plots showing the distribution of mean reaction times and accuracy for each task and session. Filled circles show the means. All plots show the expected patterns, with accuracy and RT increasing from speed to accuracy emphasis.

3.1.2. Model parameters

Descriptive statistics for the best fitting parameters can be seen in Table 1. Graphical displays of the model fits can be seen in Supplementary Material D.

Table 1.

Mean and standard deviations (in parentheses) of parameters from the diffusion model for conflict tasks (Ulrich et al., 2015).

	Flanker (N = 47)		Stroop (N = 43)
Parameter	Session 1	Session 2	Session 1	Session 2
Response caution
Boundary: Speed	26 (12.4)	25.5 (11.9)	31.4 (13.4)	22.7 (13.9)
Boundary: Standard	46.8 (13.5)	43.5 (15.8)	62.9 (12.8)	56.2 (19.6)
Boundary: Accuracy	64.8 (16.4)	58 (13.7)	71.4 (15)	67.1 (18.1)
Boundary: Accuracy – Speed	38.8 (20.5)	32.5 (18.7)	39.9 (16.4)	44.4 (19.6)
Boundary: Standard – Speed	20.7 (12.1)	18 (16.2)	31.5 (13.4)	33.5 (17.3)
Conflict processing
Amplitude	27.9 (9.8)	26.3 (8.6)	20.8 (8.8)	20.2 (9.3)
Time-to-peak	132 (47)	135 (39)	543 (161)	575 (211)
Non-conflict parameters
Drift rate	0.73 (0.19)	0.73 (0.18)	0.29 (0.07)	0.31 (0.09)
Non-decision time	316 (23)	310 (24)	385 (34)	385 (35)
Start shape	2.2 (0.9)	2.3 (0.9)	8.3 (4)	8.7 (5.4)
Non-decision variability	50 (10)	48 (10)	80 (21)	84 (21)

The values are numerically similar to previous fits we have observed in a non-SAT context (Hedge et al., 2019), with the Stroop showing a relatively slower time-to-peak and a higher value for the shape of the starting distribution (corresponding to less variability in start points). This reflects that the manual Stroop task does not tend to show fast errors (see Supplementary Material D). The model was successful in capturing the relative speed and accuracy of participants, though the data show more fast errors under speed-emphasis than the model. In both tasks and sessions, boundary separation was decreased under speed relative to neutral and accuracy emphasis, indicating that the parameter captured the SAT manipulation in the expected way.

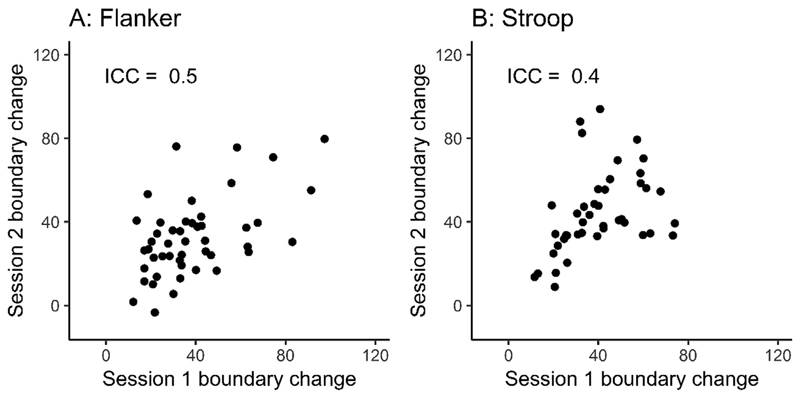
3.2. Within-task reliability of strategic adjustments of response caution

We quantified strategic adjustments in response caution by taking the difference in boundary separation under speed-emphasis relative to accuracy emphasis for each individual. Strategic adjustments showed moderate reliability across both tasks (flanker ICC = 0.5, Stroop ICC = 0.40; see Fig. 4). To put these model parameter correlations in context of the behaviour from which they’re derived, we also examined the reliability of adjustments to RT and accuracy rates in isolation (averaged across congruency conditions). This led to a similar range of values, with ICCs from 0.46 to 0.68 (see Supplementary Material A for a full report). In other words, the reliability of the model parameters were not systematically higher or lower than the behavioural measures. Note that boundary separation is theorised to reflect a balance between RT and accuracy, and so would not have the same interpretation as either behavioural measure in isolation.

Fig. 4.

Test re-test reliability for strategic adjustments of control in the Flanker task (N = 47; panel A) and Stroop task (N = 43; panel B). Strategic adjustments in response caution are defined as the change in boundary separation in the diffusion model for conflict tasks under speed emphasis relative to accuracy emphasis. The measurement units are the absolute differences in the upper boundary parameter values.

See Table 2 for the reliability of all the DMC parameters. We also draw attention to the 95% confidence intervals (CI) given in this table. While a CI cannot be interpreted as an indicator of the precision of an estimate (c.f. Morey, Hoekstra, Rouder, Lee, & Wagenmakers, 2016), under similar assumptions as those used to calculate a p-value, it can be interpreted to contain the values we cannot reject based on our statistical test (Morey, Hoekstra, Rouder, & Wagenmakers, 2016). In other words, just as we reject the null hypothesis (ICC = 0) based on the interval for adjustments in the flanker task (95% CI: 0.26–0.69), we also reject values that correspond to excellent or clinically required levels of reliability (ICC > 0.7).

Table 2.

Test re-test reliability of model parameters in the flanker task (N = 47) and Stroop task (N = 43), and between task correlations (N = 43). 95% confidence intervals are shown in parentheses.

Parameter	Reliability (ICC)		Between task (rho)
	Flanker	Stroop	Session 1	Session 2
Response caution
Boundary: Speed	0.53 (0.29–0.71)	0.41 (0.09–0.65)	0.53 (0.23–0.72)	0.64 (0.36–0.82)
Boundary: Standard	0.71 (0.53–0.83)	0.39 (0.12–0.61)	0.57 (0.31–0.75)	0.63 (0.39–0.79)
Boundary: Accuracy	0.49 (0.22–0.69)	0.5 (0.24–0.69)	0.4 (0.13–0.62)	0.33 (0.01–0.59)
Boundary: Accuracy – Speed	0.5 (0.26–0.69)	0.4 (0.12–0.62)	0.56 (0.31–0.73)	0.4 (0.05–0.67)
Boundary: Neutral – Speed	0.43 (0.17–0.63)	0.44 (0.16–0.65)	0.62 (0.41–0.76)	0.44 (0.14–0.65)
Conflict processing
Amplitude	0.55 (0.32–0.72)	0.47 (0.2–0.67)	0.2 (−0.1–0.46)	0 (−0.29–0.29)
Time-to-peak	−0.04 (−0.33–0.25)	0.19 (−0.12–0.46)	−0.02 (−0.3–0.28)	0.2 (−0.12–0.49)
Non-conflict parameters
Drift rate	0.77 (0.62–0.86)	0.48 (0.22–0.68)	0.38 (0.09–0.6)	0.04 (−0.32–0.36)
Non-decision time	0.73 (0.54–0.84)	0.57 (0.33–0.75)	0.38 (0.09–0.61)	0.5 (0.23–0.69)
Start shape	0.15(−0.14–0.42)	0.04 (−0.27–0.33)	0.19 (−0.14–0.47)	−0.03 (−0.33–0.28)
Non-decision variability	0.61 (0.39–0.76)	0.41 (0.14–0.63)	0.18 (−0.17–0.47)	0.31 (−0.01–0.58)

Note. Confidence intervals for Spearman’s rho were calculated using a bootstrap method (Revelle, 2018).

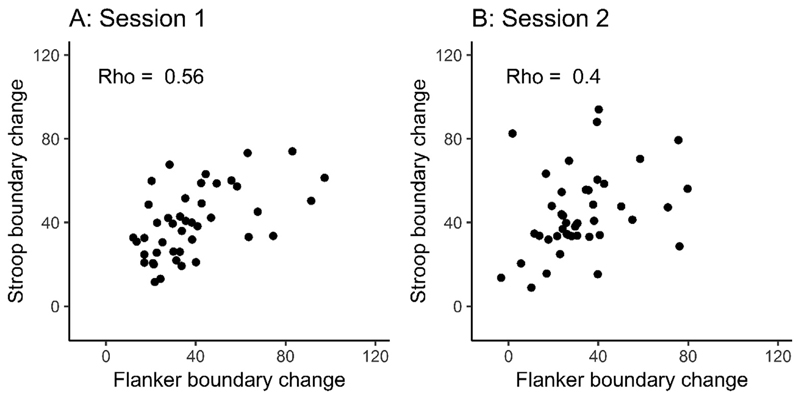
3.3. Between-task correlation of strategic adjustments of response caution

Our second key question is whether strategic adjustments in response caution correlate between tasks, which we assessed using Spearman’s rho. We observed moderate to large correlations between tasks in each session (session 1 rho = 0.56, p < .001; session 2 rho = 0.40, p = .038; Fig. 5). Again, these were similar to the correlations observed in the adjustments of RTs and accuracy in isolation, which ranged from 0.31 to 60 (see Supplementary material A).

Fig. 5.

Correlation (Spearman’s rho) between strategic adjustments in response caution in the Flanker and Stroop task. Session 1 (panel A) and session 2 (panel B) shown separately (both N = 43). Strategic adjustments in response caution are defined as the change in boundary separation in the diffusion model for conflict tasks under speed emphasis relative to accuracy emphasis. The measurement units are the absolute differences in the upper boundary parameter values.

We present the correlations between strategic adjustments of response caution and UPPS-P subscales in supplementary material E. Briefly, we see no consistent correlation across our datasets.

3.4. Reliability of other model parameters

As we are the first to examine the test re-test reliability of the DMC parameters (not just the strategic adjustments to boundary), we present these in Table 2, along with the between task correlations. The reliability of the three main non-conflict parameters (drift rates, boundary separation in each instruction condition and non-decision time) ranges from moderate to good, and are similar to those observed for the standard drift-diffusion model (Lerche & Voss, 2017). For conflict processing parameters, the amplitude of the automatic activation showed moderate reliability in both tasks, whereas the time-to-peak was relatively poor. The between-task correlations are generally similar to that which we observed with these tasks in our other work (that did not include a SAT manipulation; Hedge et al., 2019).

3.5. Interim discussion

We discuss the implications of these values in more detail in the general discussion. First, we follow up on the observation that strategic adjustments in response caution correlate between the flanker and Stroop tasks in both sessions. This result is promising, and suggests that we can generalise our interpretation of individual differences in strategic control beyond a single task. However, it raises the question of whether it generalises outside of response control tasks, or if strategic adjustments may differ depending on the broad cognitive domain. This is particularly relevant as previous papers that have examined individual differences in strategic adjustments have used a perceptual decision task, rather than conflict tasks (Evans et al., 2017; Forstmann et al., 2008, 2010). To assess whether individual differences in response caution also generalise across cognitive domains, we conducted a second study in which participants performed the flanker task along with a random dot motion discrimination task under a SAT manipulation.

4. Study 2: Method

4.1. Participants

Participants were 81 (6 male) undergraduate and postgraduate psychology students. Participants took part either for payment or for course credit. Six participants that participated in Study 1 also participated in Study 2. The studies took place a year apart. All participants gave their informed written consent prior to participation in accordance with the revised Declarations of Helsinki (2013), and the experiments were approved by the local Ethics Committee.

4.2. Design and procedure

Participants completed both the flanker task and a dot motion discrimination task based on (Pote et al., 2016). The participants also completed a number of questionnaires for the purpose of exploratory analyses: the UPPS-P impulsivity scale, the NEO-FFI personality inventory (McCrae & Costa, 2004), the Gudjonsson Compliance Scale (Gudjonsson, 1989), and a Situational Compliance Scale (Gudjonsson, Sigurdsson, Einarsson, & Einarsson, 2008).

The flanker task appeared as described above. Participants performed 12 blocks of 144 trials in total. Twelve participants did not complete all blocks within the allotted time, so data were only available for 11 (11 participants) or 10 (1 participant) blocks.

In the dot motion task, each frame consisted of 50 white dots (5x5 pixels in size) displayed within an oval patch (14.7 cm high × 23.7 cm wide) in the centre of a grey screen (60 hz, 1680 × 1050). On each frame, either 30% (high coherence) or 15% (low coherence) of the dots were chosen as signal dots, which moved in a consistent direction (left or right) by 29 pixels. The lifetime of the dots was 3 frames. Non-signal dots reappeared in a random position on each frame. The stimulus was displayed for a maximum of 2000 ms, with a 500 ms ISI. Participants were asked to determine the direction of the coherent motion. Each block consisted of 120 trials, 60 of each coherence level. Participants performed 12 blocks in total, except for 5 participants who completed 11 blocks, and 1 participant who completed 10.

Feedback relating to speed, accuracy or neutral blocks was given as described in Study 1. For the dot motion task, participants were informed that their responses were too slow in speed blocks if their RT exceeded 700 ms. Participants were informed that they were too fast in all blocks if their responses were shorter than 250 ms.

4.3. Data processing

The same inclusion criteria and RT cut-offs described in study 1 were applied. After exclusions, 73 participants were retained for the analysis of between-task correlations.

4.4. The drift-diffusion model

As the dot-motion task is not a conflict task, and the DMC extends the standard drift-diffusion model with conflict-specific parameters, we opted to fit the dot motion data with the standard drift-diffusion model (DDM; Ratcliff, 1978; Ratcliff & Rouder, 1998). Though the DMC is an extension of the DDM, it is possible that they capture variance associated with response caution in slightly different ways due to different parameterisations. However, we are interested in the conclusions that researchers would draw if they had used the model that was most appropriate for the task they had used. Critically for our purposes, strategic adjustments in response caution are conceptually captured by a change in boundary separation in both models.

The primary difference between the DMC and the DDM is that, whereas accumulation rates in the DMC reflect a composite of controlled and automatic processes, accumulation rates in the DDM are determined by a single drift rate parameter. This means that the underlying accumulation rate in a given trial is constant over time, albeit subject to noise as in the DMC. Conditions with varying difficulty are captured by differences in average drift rates (see Fig. 6).

Fig. 6.

Schematic of the average underlying processing in the drift-diffusion model (DDM; Ratcliff, 1978; Ratcliff & Rouder, 1998). The blue and red lines correspond to evidence accumulation rates to stimuli with more and less information respectively. Strategic changes in response caution are captured by lowering the boundary when speed is emphasised. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

4.5. Model fitting

We fit the DMC to the flanker data using the same process described for study 1. For the DDM, we used the Diffusion Model Analysis Toolbox (DMAT; Vandekerckhove & Tuerlinckx, 2008). Similar to our approach with the DMC, observed RT quantiles from correct and incorrect are compared to data simulated from the model, and the deviance minimised using a Nelder-Mead simplex (Nelder & Mead, 1965). As with the flanker task, for simplicity we assumed that only boundary separation varied across instruction condition. For each participant and task, we estimated eight parameters: boundary separation under speed emphasis, boundary separation under standard instructions, boundary separation under accuracy emphasis, drift rate for high coherence trials, drift rate for low coherence trials, mean non-decision time, starting point variability and non-decision variability. Between-trial variability in drift rates was fixed to 0.1, starting point bias was fixed to boundary separation/2, and within-trial noise was fixed to 0.1. Note that DMAT assumes uniform distributions for starting point and non-decision variability, whereas our implementation of the DMC uses a beta and normal distribution respectively (following Ulrich et al., 2015).

5. Results and discussion

5.1. Descriptive statistics

5.1.1. Behavioural data

Reaction times and error rates for both tasks are shown in Fig. 7. As in Experiment 1, we verified that the average performance reflected the expected manipulations by conducting separate repeated-measures ANOVAs on RTs and error rate in each task. In all cases we observed significant main effects for both congruency/coherence and instruction (all p < .001; see Supplementary Material C for full ANOVA results). Error rates and RTs increased for incongruent (flanker) and low-coherence (dot-motion) stimuli relative to congruent and high-coherence stimuli. Further, error rates increased and RTs decreased when participants were instructed to prioritise speed over accuracy.

Fig. 7.

Mean reaction times (top row) and accuracy (bottom row) for Flanker task (left panels) and dot-motion (right panels; N = 73 for both tasks).

5.1.2. Model parameters

Descriptive statistics and graphical displays of the fits for the best fitting parameters can be seen in Supplementary material F. In both tasks, as expected, boundary separation was decreased under speed relative to neutral and accuracy emphasis. Values for the flanker task are similar to those observed in Study 1. Values for the DDM parameters fit to the dot-motion task were within typically observed ranges (Donkin, Brown, Heathcote, & Wagenmakers, 2011; Matzke & Wagenmakers, 2009).

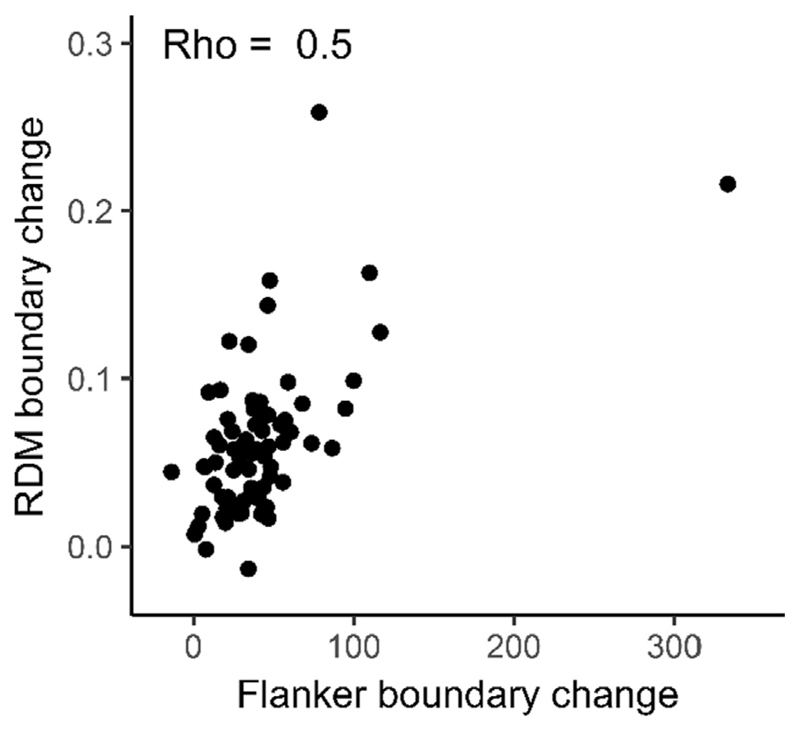
5.2. Between-task correlation of strategic adjustments of response caution

As in study 1, we observed a large correlation in strategic adjustments in response caution (rho = 0.50, p < .001; Fig. 8). Thus, behavioural variability captured by parameters representing response caution do share commonality across tasks from different cognitive domains. As in Study 1, this was numerically similar to the correlation observed in the adjustments in RT and accuracy in isolation (both rho = 0.40).

Fig. 8.

Between task correlation (Spearman’s rho) for strategic adjustments of control (boundary under accuracy emphasis – boundary under speed emphasis) in the flanker task and dot motion task. The measurement units are the absolute differences in the boundary separation parameter values. Note that the data point on the far right came from unusually low and high fitted boundary separation values under speed and accuracy emphasis respectively, leading to an apparently large strategic adjustment. However, excluding this individual from our correlational analysis had little impact on the observed effect.

For correlations between self-report measures and strategic adjustments in response caution, see Supplementary material E. Correlations with self-report were generally small and inconsistent across the tasks.

6. General discussion

The aim of the current work was to examine whether individual differences in strategic adjustments of response caution are a reliable and generalisable dimension of response control. The answer to both questions is yes, though this is caveated by the magnitude of the effects that we observe. In Experiment 1, we observed moderate test-retest reliability in the change in response caution in both the flanker and Stroop tasks, as represented by the change in boundary separation between accuracy-emphasis and speed emphasis instructions. It is not trivial that these strategic adjustments show non-zero reliability, though the magnitude is below the levels typically considered good or excellent for conducting individual differences research (Cicchetti & Sparrow, 1981; Fleiss, 1981; Landis & Koch, 1977). The implication of this is that researchers interested in examining relationships between strategic adjustments in response caution and personality or brain structure will likely require large sample sizes to detect relationships, if they exist.

With regards to generalisability, we show medium to large correlations in response caution adjustments across tasks conducted in the same experimental session. We observed this between conflict tasks (study 1), and between a conflict and a perceptual decision task (study 2). We focus our discussion on the interpretation of strategic control adjustments, and practical recommendations for researchers interested in response caution.

6.1. Meaningful individual differences in default caution and its strategic adjustment

There is increasing evidence that there are meaningful individual differences in response caution (Evans et al., 2017; Forstmann et al., 2010; Hedge et al., 2019; Karalunas et al., 2018; Pirrone et al., 2017; Powell et al., 2019; Ratcliff et al., 2006a). Recently, we applied the DMC to three response control datasets, comprising the flanker and Simon tasks, flanker and Stroop tasks, and two variants of the Simon task. Our aim was to examine whether the model could uncover hidden correlations between mechanisms of conflict processing that are obscured in traditional measures (Hedge, Powell, Bompas, et al., 2018). Though we observed no correlation in the conflict parameters (amplitude and time-to-peak), we consistently observed correlations in boundary (see also Lerche & Voss, 2017; Ratcliff et al., 2015). This finding is mirrored in our results here, with boundary separation consistently showing correlation between tasks. The novel contribution of this work is that we also see correlation in the strategic adjustment in response caution, captured by the change in boundary separation between different SAT instructions.

We manipulated participant’s levels of response caution through verbal instruction, which is the same method used by the previous studies that have examined individual differences in response caution adjustments (Evans et al., 2017; Forstmann et al., 2008, 2010). There are numerous alternative methods for eliciting a SAT (for a review, see Heitz, 2014). These include the use of payoff structures, in which participants receive different rewards and penalisations based on accuracy and/or RT (e.g. Fitts, 1966; Swensson & Edwards, 1971); and the use of response deadlines, where participants are informed that they must respond within certain time limits (e.g. Pachella & Pew, 1968). Heitz notes that verbal instructions are popular because they are easily understood by participants, and produce large effects with relatively few trials. However, just as the interpretation of the common instruction in choice RT tasks to be both fast and accurate is subjective, so too is the instruction to favour speed. Our reliabilities and correlations suggest that participants interpret these instructions somewhat consistently, though we do not know what the basis is for the criteria they set. In part, this is what we seek to understand by examining correlations with personality constructs such as impulsivity. To our knowledge there has not been a systematic examination of the consequences of the choice of SAT manipulation for individual differences relationships (though some have been compared experimentally, e.g. Dambacher & Hübner, 2013). It would benefit future research in this area to elucidate whether the method makes a difference.

6.2. Do strategic control adjustments go beyond boundary separation?

A wealth of literature exists for the speed-accuracy trade-off, spanning both behavioural and neurophysiological approaches (for a review, see Heitz, 2014). In the context of the sequential sampling models, faster RTs and lower accuracy under speed emphasis are primarily attributed to reduced boundary separation: a relative decrease in the amount of evidence required to initiate a response (Ratcliff et al., 2016). However, performance under speed emphasis has also been captured by additional reductions in non-decision time, as well as sometimes lower drift rates (Rae et al., 2014; Starns, Ratcliff, & McKoon, 2012; Zhang & Rowe, 2014). Further, it has been argued that strategic adjustments can be captured by time-varying decision processes, such as urgency signals or collapsing boundaries (Cisek, Puskas, & El-Murr, 2009; Ditterich, 2006a, 2006b; Drugowitsch, Moreno-Bote, Churchland, Shadlen, & Pouget, 2012; though see Hawkins, Forstmann, Wagenmakers, Ratcliff, & Brown, 2015). Here, we fit a relatively simple model that only allowed boundary separation to vary across instruction conditions. Therefore it is possible that our fits absorbed variance in behaviour that might be captured by other parameters in a more complex model. Note that in the introduction, we highlighted the difficulty in translating assumptions from within-subject contexts to the study of individual differences. The SAT paradigm is also an approach that has largely been developed in within-subject experimental contexts, and the average best fitting model may not be appropriate for every individual. For example, we could ask whether every individual shows a decrease in boundary, non-decision time, and/or information processing parameters (c.f. Haaf & Rouder, 2018). Our results here provide a starting point for further examination; that we observe some reliability and cross-task correlation in response caution here suggests that there is reliable variance in the behaviour to be captured.

6.3. Previous literature on the reliability of response caution

To our knowledge, we are the first to examine the reliability of parameters of the diffusion model for conflict tasks. Previous work has examined the test-retest reliability of the standard drift-diffusion model (Lerche & Voss, 2017; Schubert et al., 2016), including applications to conflict tasks (Enkavi et al., 2019), though not in a SAT paradigm. Nevertheless, we can contrast our estimates of the reliability of boundary separation under standard instructions with theirs.

Lerche and Voss (2017) reported one week reliability for a lexical decision task, a recognition memory task, and an associative priming task. They observed correlations of approximately r = 0.8 for boundary separation in all tasks (see maximum likelihood estimates in their Fig. 2). Schubert et al. (2016) report eight month reliabilities for three tasks, including a two- and four-choice variant of a visual choice RT task, a Sternberg memory scanning task, and a Posner letter matching task. Correlations for boundary separation between sessions ranged from r = 0.2 to r = 0.6 (see their Table A2). Recently, Enkavi et al. (2019) applied the hierarchical drift diffusion model (Wiecki, Sofer, & Frank, 2013) to reliability data from 15 choice RT tasks, including a three choice Stroop task. The average time between sessions was approximately 16 weeks. The reliability of boundary separation in the Stroop task was 0.29, which was slightly below the median reliability for all the tasks (0.31; see their HDDM values in Fig. 5). Taking these previous studies together, our results fall within the range of reliabilities previously observed, but the range is broad. It would be premature to suggest that there are systematic differences between tasks in the consistency of response caution that they elicit, though we note that it was relatively low for the Stroop task in both our Study 1 and in Enkavi et al. (2019) data.

6.4. Model choice and model complexity

To examine the reliability of strategic adjustments in response caution, we applied the drift-diffusion model (Ratcliff, 1978), and an extended diffusion model for conflict tasks (Ulrich et al., 2015). Though the drift diffusion model is widely applied in SAT studies (e.g. Mulder et al., 2010; Ratcliff, 1985; Zhang & Rowe, 2014), there are alternative models for both conflict (Hubner, Steinhauser, & Lehle, 2010; White, Ratcliff, & Starns, 2011) and non-conflict tasks (Brown & Heathcote, 2008; Usher & McClelland, 2001). Several empirical and theoretical reviews have considered the relationship between different models, and it has been noted that there is often a high degree of mimicry between them, such that researchers would often reach the same conclusion irrespective of the model chosen (Bogacz, Brown, Moehlis, Holmes, & Cohen, 2006; Donkin et al., 2011; Ratcliff & Smith, 2004; White, Servant, & Logan, 2017). Nevertheless, we briefly consider the potential impact of this choice.

Both Forstmann et al. (2010) and Evans et al. (2017) examined individual differences in response caution adjustments using the Linear Ballistic Accumulator model (Brown & Heathcote, 2008). Whereas in the DDM a single drift process represents the difference in evidence between to alternatives, the LBA consists of separate accumulators for each response alternative and a single threshold. Starting points for the accumulators in the LBA are drawn from a uniform distribution, and response caution is captured by the difference between the edge of the start point distribution and the height of the threshold. Forstmann et al. (2010) noted that applying the drift-diffusion model to their data did not produce the correlation between white matter strength and caution adjustments seen with the LBA (see their Supplementary Online Material). They suggested that this may be because the diffusion model captured the SAT manipulation in both non-decision time and drift rates, in addition to boundary separation. An imperfect mapping between the response caution parameters has also been noted when fitting one model to data generated from the other (Donkin et al., 2011). Given this discrepancy, researchers may wish to check the robustness of conclusions drawn from one model to another.

Though we made the simplistic assumption that the SAT manipulation was specifically captured by changes in boundary separation in our fits, we added complexity by including parameters representing inter-trial variability in non-decision time and the starting point of the accumulation process. Including these variability parameters often produces better fits to empirical data at the sample average level (Ratcliff & Tuerlinckx, 2002), but they may also lead to poorer recovery of individual differences in the main parameters of interest, particularly with fewer trial numbers (Lerche & Voss, 2016; van Ravenzwaaij, Donkin, & Vandekerckhove, 2017). We reran some of our analyses without including the variability parameters, and it produced almost identical estimates for the reliability of strategic adjustments (see Supplementary Material G). This may be in part because we had a large number of trials, and a model that was quite well constrained across multiple conditions. Where researchers have smaller trial numbers, they may wish to implement a simpler model, or check that their conclusions are not specific to a particular parameter choice.

6.5. Strategic adjustments and personality traits

Willingness or reluctance to commit errors while attempting speeded responses has been linked to the concept of impulsivity (Kagan, 1966), and recently correlated with need for closure (Evans et al., 2017) and brain structure (Forstmann et al., 2010). However, we see little evidence for a correlation with any self-report impulsivity dimension in our data (Supplementary Material E; see also Dickman & Meyer, 1988). We also tested correlations with self-report compliance and the big five personality traits (neuroticism, extraversion, openness, agreeableness, conscientiousness; Digman, 1990; McCrae & Costa, 2004; McCrae & John, 1992). There were no consistent relationships.

The absence of a correlation with impulsivity measures is particularly notable here, given the conceptual overlap between impulsivity and a lowered boundary. For example, Metin et al. (2013) examined whether differences in RT and accuracy in children with attention-deficit/hyperactivity disorder relative to healthy controls were best captured by “inefficient” or “impulsive” information processing in the context of the drift diffusion model. These corresponded to drift rate and boundary separation respectively. Despite the common terminology, our findings mirror a trend in the impulsivity literature to observe little to no correlation between behavioural and self-report measures (Sharma et al., 2014). It remains a possibility that there are non-zero correlations that we did not have sufficient power to detect. As we discuss in the next section, given that the reliability of strategic adjustments is suboptimal, we should expect correlations with other variables to be small.

6.6. Practical considerations for future research

The consistent between-task correlation in strategic adjustment indicates that the extent to which an individual adjusts their behaviour is not entirely task or domain specific. A practical consideration for researchers interested in response caution and its strategic adjustments, and are not specifically interested in a particular cognitive domain (e.g. response conflict) is that fitting the DMC to our response conflict tasks was substantially more demanding on time and/or computational resources than fitting the DDM to a perceptual decision making task. Note that this is not specific to the DMC (White et al., 2017), but rather reflects more complex models that do not have analytical solutions that allow faster estimation. Until faster methods can be realised (e.g. Mestdagh, Verdonck, Meers, Loossens, & Tuerlinckx, 2018), it may be more tractable to use non-conflict tasks to which the DDM or linear ballistic accumulator (Brown & Heathcote, 2008) can be applied.

The reliabilities of strategic adjustments of response caution that we observe fall in the range typically interpreted as “moderate” (Cicchetti & Sparrow, 1981; Fleiss, 1981; Landis & Koch, 1977). We have recently discussed how reliabilities in this region are potentially problematic for examining individual differences in cognitive tasks (Hedge, Powell, & Sumner, 2018). The ICC reflects the relative contribution of between-subject variance (individual differences) and measurement error to variance in the variable of interest. In order to examine whether adjustments in response caution are related to trait measures (e.g. personality), we desire variance in our behavioural measure to also reflect individual differences that are stable over time. When measures are noisy, correlations with external variables will be weaker and require larger samples to detect.

To put the ICCs we observe in context, they are similar to or exceed those we observed for several commonly used measures of response control and processing (e.g. flanker RT cost: 0.50, stop-signal reaction time: 0.43, Navon global precedence: 0; Hedge, Powell, & Sumner, 2018). Notably in the case of those traditional measures, we did not observe correlation between tasks in our previous study, despite it being commonly assumed that they share common mechanisms (see also Rey-Mermet, Gade, & Oberauer, 2017). Here, with strategic adjustments of response caution, we do consistently observe a correlation between tasks. Nevertheless, poor reliability corresponds to a reduced ability to detect correlation using those measures that must be compensated for (e.g. by increasing statistical power).

It is possible that future work would benefit from developments in model-based analyses, by integrating individual differences measures of interest in to the parameter estimation (Evans et al., 2017; Turner et al., 2013; Wiecki et al., 2013). Here, we fit the models to each task and individual independently. In contrast, hierarchical models describe both the sample and individual simultaneously, as well as allow for regressors to be used to inform parameter estimation. For example, Evans et al. (2017) compared three different models when examining the relationship between response caution and need for closure. They first fit a hierarchical linear ballistic accumulator model in which parameters were determined by the behavioural data alone. The second model did not allow for individual differences in response caution, assigning everyone the same value, though differing between speed- and accuracy-emphasis. In the third model, rather than estimating response caution from the behavioural data, it was determined by a function that linked the parameter values to participants’ questionnaire values. Unsurprisingly, the first (unconstrained) model provided the best fit to the data. However, the third model outperformed the second, suggesting that there are common individual differences in the personality questionnaire and behavioural responses. In a second experiment by Evans et al. this improvement when comparing models contrasted against non-significant correlations between parameter estimates (and RTs) fit independently and subsequently correlated with the questionnaire values. Such joint modelling techniques may provide more powerful tests where appropriate.

6.7. Conclusions

The extent to which an individual prioritises accuracy or speed in choice RT tasks is commonly discussed but has less often been the focus of interest than individual differences in cognitive abilities. Here, we provide evidence that questions about individual differences in caution and its strategic adjustment are at least somewhat viable. On a given occasion, individuals show consistency in the extent to which they strategically adjust their levels of response caution across different tasks. Across time points, individuals show non-zero, but sub-optimal, levels of reliability in strategic adjustments. Though these levels of reliability raise power concerns for future research, we believe that our results and previous literature are evidence that there is value in pursuing such questions.

Supplementary Material

Supplementary data to this article can be found online at https://doi.org/10.1016/j.concog.2019.102797.