Dynamics of awake hippocampal-prefrontal replay for spatial learning and memory-guided decision making

SUMMARY

Spatial learning requires remembering and choosing paths to goals. Hippocampal place cells replay spatial paths during immobility in reverse and forward order, offering a potential mechanism. However, how replay supports both goal-directed learning and memory-guided decision making is unclear. We therefore continuously tracked awake replay in the same hippocampal-prefrontal ensembles throughout learning of a spatial alternation task. We found that during pauses between behavioral trajectories, reverse and forward hippocampal replay support an internal cognitive search of available past and future possibilities, and exhibit opposing learning gradients for prediction of past and future behavioral paths, respectively. Coordinated hippocampal-prefrontal replay distinguished correct past and future paths from alternative choices, suggesting a role in recall of past paths to guide planning of future decisions for spatial working memory. Our findings reveal a learning shift from hippocampal reverse-replay-based retrospective evaluation to forward-replay-based prospective planning, with prefrontal read-out of memory-guided paths for learning and decision-making.

Graphical Abstract

eTOC Blurb

Shin, Tang and Jadhav use continuous activity tracking to show that awake CA1 reverse and forward replay events predict past and future choices respectively with opposing spatial learning gradients. CA1-PFC replay supports recall and planning for spatial working memory tasks.

INTRODUCTION

The hippocampus is necessary for formation and retrieval of episodic memories to guide daily behavior, including goal-directed spatial learning and navigation (Eichenbaum and Cohen, 2004; Squire, 1992). Hippocampal place cells are active in specific spatial locations during exploration (O’Keefe and Nadel, 1978). While this spatial code provides information about current location, spatial memories require learning links between sequences of locations that encode specific paths, and choices that lead to goals, which is likely to be supported by another phenomenon called “replay”. Hippocampal replay is associated with high frequency sharp-wave ripple (SWR) events prevalent during offline periods in both sleep and non-exploratory waking states (‘awake replay’) (Buzsáki, 2015). During replay, temporally compressed sequences of place cells reactivate spatial trajectories in explored environments in either forward or reverse order (Ambrose et al., 2016; Diba and Buzsáki, 2007). Notably, while sleep replay is associated with offline memory consolidation, awake replay during pauses in exploration is ideally suited to support processes associated with ongoing memory-guided behavior, including retrospection, retrieval, prospection, and planning. (Carr et al., 2011; Foster, 2017; Joo and Frank, 2018).

Converging evidence from rodents (Buzsáki, 2015; Carr et al., 2011; Foster, 2017), primates (Leonard et al., 2015), and humans (Vaz et al., 2019), suggests that awake replay is important for memory-guided behavior and cognition. In rodents, awake reverse and forward replay represent behavioral trajectories in spatial environments (Ambrose et al., 2016; Diba and Buzsáki, 2007; Foster and Wilson, 2006; Gupta et al., 2010; Karlsson and Frank, 2009; Xu et al., 2019), and both loss-of-function (Jadhav et al., 2012) and gain-of-function experiments (Fernandez-Ruiz et al., 2019) have shown a causal role of awake replay in spatial working memory tasks. Several reported features of hippocampal awake replay (area CA1) are suggestive of its functional roles. First, replay is enhanced by reward and novelty (Ambrose et al., 2016; Cheng and Frank, 2008; Foster and Wilson, 2006; Singer and Frank, 2009), specifically for reverse replay on linear tracks (Ambrose et al., 2016), and is coordinated with sub-cortical reward activity (Gomperts et al., 2015; Lansink et al., 2009), pointing to a role in temporal credit assignment and reinforcement learning of paths leading to goals (Foster, 2017; Foster and Knierim, 2012; Haga and Fukai, 2018). Additionally, replay is hypothesized to support memory retrieval for planning upcoming choices (Carr et al., 2011; Singer et al., 2013) – there is evidence that replay is involved in fear memory retrieval (Wu et al., 2017), and specifically forward replay is associated with planning of future trajectories (Pfeiffer and Foster, 2013; Xu et al., 2019). Further, awake replay can represent random (Gupta et al., 2010; Stella et al., 2019), and remote trajectories (Karlsson and Frank, 2009), suggesting a role in free recall. In agreement with rodent studies, recent evidence identifies an analogous role of human and primate awake replay in cognitive processing (Leonard and Hoffman, 2017; Liu et al., 2019; Norman et al., 2019; Vaz et al., 2019).

Despite this mounting evidence, how reverse and forward replay together support the proposed roles in learning, retrieval, and memory-guided decision making remains unclear. Further, whether and how replay content changes over the course of learning to support memory-guided choices is not known. Addressing these questions requires monitoring the evolution of replay content in the same neural populations over the entire duration of learning.

In addition, it is hypothesized that hippocampal replay of behavioral paths may contribute to a cognitive search process based on previous experience, which can impact target regions (Joo and Frank, 2018; Singer et al., 2013; Tang and Jadhav, 2019). Indeed, goal-directed behavior relies on a wider neural network for evaluation and selection of task-relevant memories during retrieval and decision making, and the cognitive processes of learning, deliberation, and spatial navigation are known to require the prefrontal cortex (PFC; Eichenbaum 2017; Epstein et al. 2017; Ito et al. 2015; Pezzulo et al. 2014; Redish 2016; Tang and Jadhav 2019; Yu and Frank 2015). How hippocampal and PFC networks together support learning and planning, especially for replay-dependent working memory tasks, remains an open question. CA1-PFC neural activity is coordinated during SWRs for reactivation of spatial paths (Jadhav et al., 2016; Peyrache et al., 2009; Tang et al., 2017), but whether this coordinated CA1-PFC reactivation can distinguish hippocampal replay content in a behavioral context, and how it plays a role in memory-guided behavior, is not known.

We therefore used continuous and simultaneous tracking of neural ensembles in CA1 and PFC throughout the course of learning of a replay-dependent W-track spatial alternation task to address three key questions: (i) how is awake CA1 replay involved in choice behavior during decision making; particularly how do reverse and forward replay relate to past and future choices; (ii) how replay content changes over learning, and the evolution of reverse and forward replay as learning progresses; (iii) whether coordinated CA1-PFC replay can distinguish hippocampal replay content, and its relationship to ongoing behavioral choices.

RESULTS

Continuous tracking of forward and reverse replay throughout learning

We used continuous and simultaneous electrophysiological monitoring of ensembles of CA1 and PFC neurons in rats learning a novel W-track spatial alternation task within a single day (Figures 1, S1). This task involves continuous alternation between reward wells on the three maze arms (Figure 1A). Animals are rewarded upon completion of a correct inbound or outbound sequence according to the following rules: (i) starting from either side well, animals have to return to the center well (inbound trajectories 2 and 4), and (ii) starting from the center well, animals have to recall the previous inbound trajectory and choose the opposite side well from the previously visited one (outbound trajectories 1 and 3).

Figure 1. Hippocampal place-cell sequences distinctly represent different behavioral trajectories during learning of a W-maze spatial memory task.

(A) W-maze spatial alternation task design, depicting the correct behavioral sequence of outbound (blue) and inbound (teal) trajectories (labelled 1–4) for reward. Right-left indicated according to animal direction.

(B) Past and future trajectories during transitions at reward wells. (i) Two correct behavioral sequences at the center well. (ii) One correct behavioral sequence for each side well (left or right well).

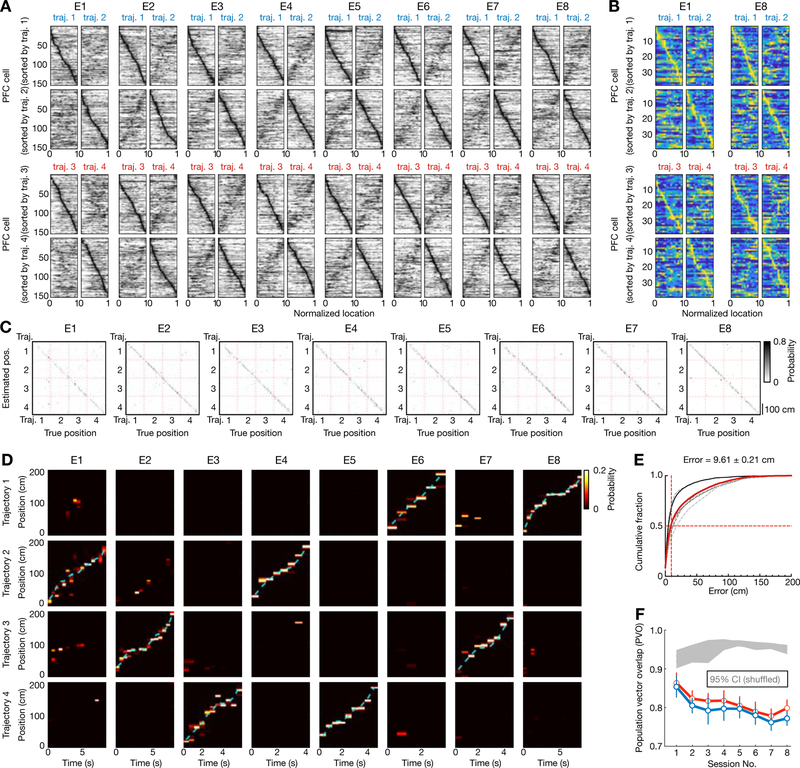
(C) Place fields of all CA1 place cells (n = 216) recorded from 6 rats continuously across 8 learning sessions (or epochs; denoted as E1–8) in single-day learning. The fields for trajectories 1 and 2, sorted according to peak positions on trajectory 1 or 2, are shown on the top two rows. The bottom two rows are for trajectories 3 and 4. Horizontal axes denote normalized position along the start to end of the corresponding trajectory.

(D-F) Position reconstruction based on CA1 ensemble spiking during active running behavior on trajectories (> 5 cm/s). Decoding performance was estimated using a leave-one-out cross-validation. (D) Example confusion matrices depicting true and estimated positions during running on trajectories 1–4. (E) Illustrative estimated position probabilities using data from a single animal for individual sessions. Cyan line: actual animal trajectory. (F) Cumulative position decoding errors across all animals. Dashed lines: individual animals; Red line: all animals; Solid black line: the example animal shown in (D-E). Median error of all sessions (vertical red line) noted on top. Decoding error: 6.30 ± 0.47 cm for Session 1; 3.58 ± 0.35 cm for Session 8 (in median ± SEM).

(G and H) Directional selectivity of place cells. (G) Directionality index (DI) of place cells across learning sessions. Red and blue bars above indicate significant increases from the first session (p < 0.05, Friedman tests with Dunn’s post hoc). Error bars: SEM. (H) Similarity of the place-cell population in two running directions was computed using the population vector overlap (PVO). Grey shadings: 95% CIs of the shuffled distributions from each animal using trial-label shuffles. Blue and red lines with error bars: means with SEMs for right (i.e., trajectories 1 vs. 2) and left (i.e., trajectories 3 vs. 4) trajectories, respectively. Note that distinct templates for each direction are apparent in the first session (p’s < 0.0001 compared to the shuffled data for individual rats, permutation tests).

See also Figure S1, and Table S1.

Awake replay, as well as functional hippocampal-prefrontal interactions, are important for learning the outbound, spatial working memory component of this task (Fernandez-Ruiz et al., 2019; Jadhav et al., 2012; Maharjan et al., 2018). The history-dependent, spatial working-memory behavioral sequence consists of two consecutive trajectories with a center-well transition (Figure 1B_i), where the past path is an inbound trajectory terminating at the center well, and the future path is an outbound trajectory proceeding to the opposite side-arm. In contrast, the inbound component requires implementation of a “return-to-center” rule based only on the current location from each side-well (Figure 1B_ii), and this reference memory rule is history-independent. For side well transitions, the past path is outbound, and the future path is inbound; the past and future paths are thus reversed at the center and side wells (Figure 1B).

Animals (n = 6 rats) were tasked with learning the W-maze rules in eight behavioral sessions (epochs 1–8, or E1–8, 15–20 mins per session) in a single experimental day, interleaved with rest sessions in a sleep box (single-day learning; learning curves in Figure S1; see STAR Methods) (Maharjan et al., 2018). We continuously and simultaneously recorded from the same stable ensembles in dorsal CA1 (n = 216 cells with place fields on the track) and PFC (pre-limbic and anterior cingulate cortical regions; n = 154 cells) for all 8 sessions over the course of learning (5.5–6.5 hours; see STAR Methods; recording locations in Figures S1A–C; isolation and stability parameters for simultaneously recorded neurons in six rats shown in Figures S1D–G). This experimental design thus enabled investigation of CA1-PFC replay dynamics using the same ensembles, starting from initial acquisition through later memory performance.

CA1 place cells exhibited spatial and direction selectivity, with unique sequential representations of different trajectories (Figures 1C–H). Figure 1C shows responses of all recorded CA1 place cells for the 4 trajectories in each behavioral session. Place cell encoding of spatial locations enabled accurate decoding of animal position during trajectory-running (Figures 1D–F) (Ambrose et al., 2016). Comparison of opposing outbound-inbound trajectory pairs (Figure 1C shows linearized place-cell responses in pairs of trajectories with opposite running directions; 1 vs. 2, and 3 vs. 4) confirmed that place cells were directionally selective starting with the first session on the novel track (Foster and Wilson, 2006), and direction selectivity significantly improved over experience (Figures 1G–H) (Frank et al., 2004; Navratilova et al., 2012; Xu et al., 2019). Despite the presence of bidirectional cells (37.7 ± 17.1%, mean ± SD; number of unidirectional cells in Table S1), place-field templates for all trajectories were distinguishable for all sessions (illustrated in the confusion matrices in Figures 1D–F; cross-validated decoding error: 3.81 ± 0.13 cm in median ± SEM). Further, the stability and specificity of place-cell activity increased with familiarity (Frank et al., 2004; Jadhav et al., 2012), although the proportion of place cells remained constant (Figures S2A–C). Thus, there was a change in average decoding error over sessions, but notably, the highest decoding error (Session 1: 6.30 ± 0.47 cm) was comparable to previous reports (Ambrose et al., 2016; Davidson et al., 2009; Farooq and Dragoi, 2019; O’Neill et al., 2017). Therefore, CA1 ensembles exhibited independent population representations of the 4 behavioral trajectories starting from the first novel session, enabling accurate position decoding.

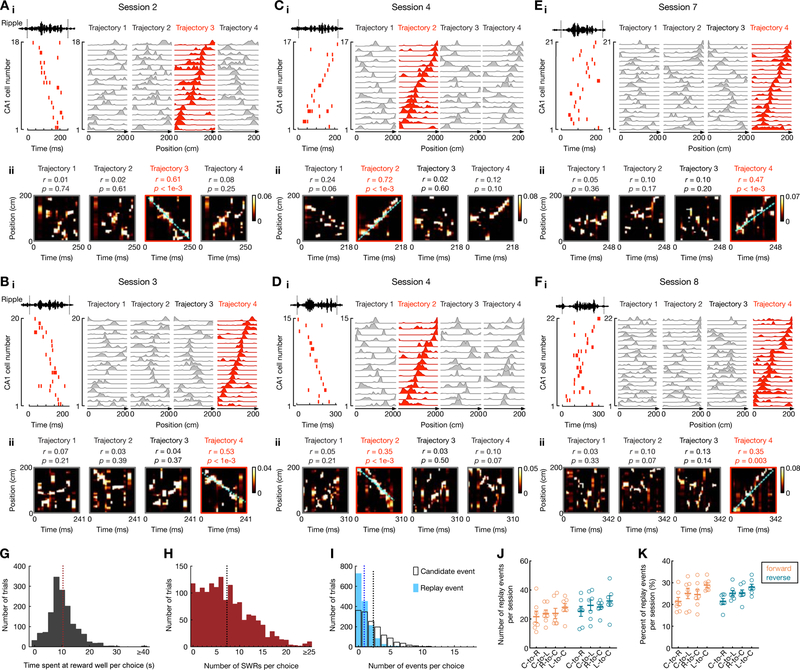
We used these template place-cell sequence representations from stably recorded ensembles to detect and continuously track forward and reverse CA1 replay events throughout learning (Figures 2, S2). To investigate replay content, we used established methods to detect SWRs and candidate events during immobility periods at reward wells, and used Bayesian decoding to identify CA1 replay events, with each event distinctly determined as forward or reverse replay of one of the four trajectories (Ambrose et al. 2016; Davidson et al. 2009; Tang et al. 2017; see STAR Methods). Examples of forward and reverse replay sequences from the same CA1 ensembles in different learning stages of one animal are shown in Figures 2A–F (additional examples in Figure S2). During immobility periods at reward-well transitions (immobility time: 10.3 ± 5.7 sec in mean ± SD; Figure 2G), multiple SWRs and replay candidate events were detected (Figures 2H–I; immobility periods with ≥ 2 events, 85.7% or 1313/1533 trials for SWRs; 53.4% or 818/1533 trials for replay candidate events). Further, there was no overall bias toward reverse or forward replay of any particular trajectory type (Figures 2J–K).

Figure 2. Continuous tracking of forward and reverse replay throughout learning.

(A-F) Six examples of forward and reverse replay of behavioral trajectories in different learning sessions using continuously tracked CA1 ensembles in one animal. (i) Left: Place-cell activity during a SWR, with ripple-filtered LFP (150–250 Hz) from one tetrode shown on top. Right: Corresponding linearized place fields on trajectories 1 to 4 sorted by their peak locations on the replayed trajectory (red). (ii) Bayesian reconstruction of the decoded behavioral trajectories with the replay quality (r) and p-value based on time-shuffled data denoted on top. Cyan lines: the linear fit maximizing the likelihood along the replayed trajectory. Color bars: posterior probability. See also Figure S2 for additional replay examples.

(G-I) Distributions of (G) animals’ immobility times at reward wells, (H) the number of SWRs, and (I) candidate events (open bars) and replay events (solid bars) detected in immobility periods per choice (i.e., per transition). Only correct trials are shown. Vertical dashed lines on the histograms represent the mean values (Immobility time: 10.3 ± 5.7 sec; SWRs: 7.3 ± 5.5 events; Candidate events: 2.3 ± 2.4 events; replay events: 0.9 ± 1.2 events; data are presented in mean ± SD).

(J and K) (J) Number and (K) percentage of forward and reverse replay events of different trajectory types (i.e., center-to-right, C-to-R; center-to-left, C-to-L; right-to-center, R-to-C; left-to-center, L-to-C). Each dot represents a session, summing over all 6 animals (sessions 1 and 2 were combined). Error bars: mean ± SEM. Note that the number of replay events of different trajectories was similar (F(7, 42) = 3.062 and p = 0.053 for J, F(7, 42) = 2.227 and p = 0.12 for K; repeated measures ANOVA).

Reverse replay of possible past paths, forward replay of available future paths

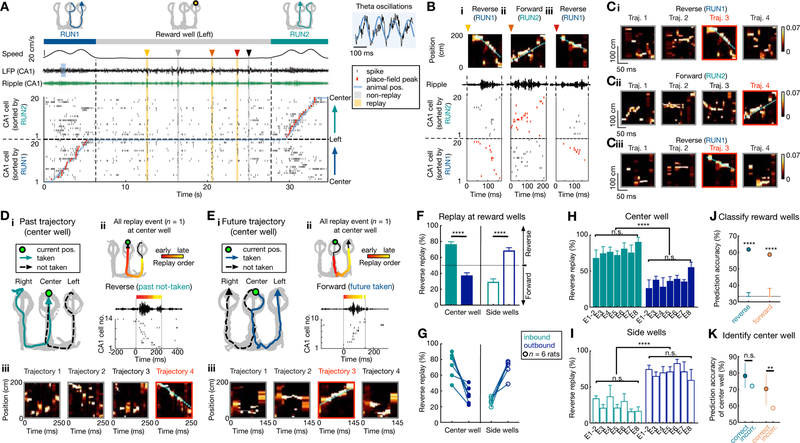
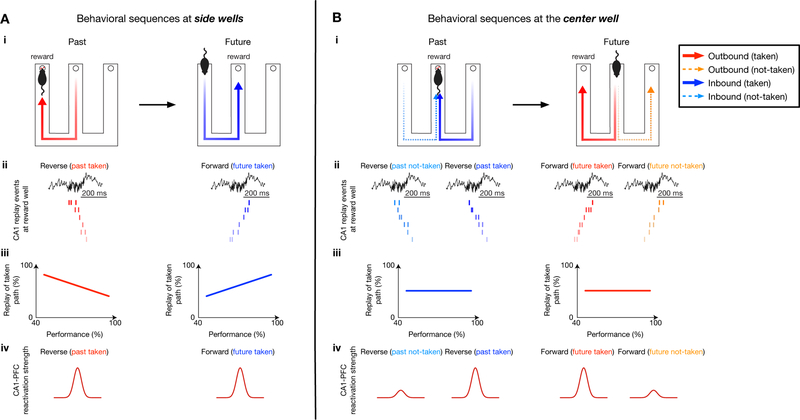
In order to examine the relationship between replay content and behavioral choices, we focused on transition periods between trajectories. A correct behavioral sequence comprising two consecutive trajectories is illustrated for a side-well transition (Figures 3A–C; similar example for a center-well transition in Figures S3A–B). This transition comprises an outbound past trajectory (RUN1, center-to-left), followed by an inbound future trajectory (RUN2, left-to-center), with the place-cell sequences ordered for RUN1 and RUN2 shown in the sorted CA1 activity (Figure 3A). Three replay events during this transition were identified as two reverse replay events of the past (RUN1), and one forward replay event of the future trajectory (RUN2) (Figures 3B–C), in an inter-mixed order of occurrence (reverse-forward-reverse). Replay events at the side well thus reactivated the past outbound trajectory in reverse, and the future inbound trajectory in a forward order.

Figure 3. Reverse replay of possible past paths, forward replay of possible future paths.

(A-E) Illustration of past and future trajectories replayed by reverse and forward place-cell sequences at reward wells.

(A-C) Example of side reward well transition. (A) CA1 neural activity during an outbound-inbound sequence (RUN1 to RUN2), with replay events at the left side well. From top to bottom, the behavioral sequence, animal speed, broadband and ripple-filtered LFPs from one CA1 tetrode, raster plot of 20 place cells ordered by the positions of their place-field peaks (red ticks; linearized animal position in overlaid blue line). CA1 exhibits theta oscillations (8–10 Hz; blue LFP shading) during running, and SWRs during immobility, coincident with synchronous activity of place cells (indicated by arrowheads and shadings). Five synchronous candidate events were seen, with 3 events detected as significant replay sequences (yellow shadings). (B) Expanded view of the 3 replay events from (A), identified as reverse replay of RUN1 (past) and forward replay of RUN2 (future). (B_i-B_iii) Each column shows the Bayesian reconstruction of the animal’s trajectory during replay (top), ripple-filtered LFP (middle), and spike raster of place cells (bottom) sorted as in (A) (raster corresponding to replayed trajectory, red). (C_i-C_iii) Bayesian reconstructions of the decoded behavioral trajectories 1–4 for replay events in B_i-B_iii, (replayed trajectory bordered as red). Color bars: posterior probability. See also Figure S3 for similar center reward well example.

(D and E) Replay events during two example transitions at the center well. (i) Behavioral sequences for the center-well transition. (ii) A single replay event at the center well. Top: Bayesian reconstruction of the replayed trajectory. Colored points overlaid on the replay trajectory (black arrowhead line) indicate the Bayesian-decoded positions (see STAR Methods), with the color denoting relative time within the replay event. Bottom: ripple-filtered LFP and the sequential SWR spiking of place cells. (iii) Bayesian reconstructions of the decoded behavioral trajectories. See also Figure S3 for additional examples for replay of past and future paths.

(F) At the center well, inbound (past paths) and outbound trajectories (future paths) were preferentially replayed in a reverse and forward order, respectively. At the side wells, outbound (past) and inbound trajectories (future) were preferentially replayed in a reverse and forward order, respectively. ****p < 1e-4, session-by-session rank-sum paired test. Error bars: SEM.

(G) The bias in (F) is consistent in each rat (circles; n = 6).

(H and I) The bias in (F) at the center (H) and side (I) wells appeared similarly across all 8 behavioral sessions (E1–8). n.s.: non-significant (Center well: main effect of group, p = 0.52 and 0.44 for inbound and outbound, respectively; Side wells: main effect of group, p = 0.30 and 0.59 for inbound and outbound, respectively; Kruskal-Wallis tests). ****p < 1e-4, session-by-session rank-sum paired test.

(J) Patterns of reverse and forward replay can discriminate goal-locations (n = 3 wells). The cross-validated decoder using SVM is significantly better than chance (error bars) defined by permutation tests (****p < 0.0001; See STAR Methods). Only correct trials were used for (A-J).

(K) Comparison of well-prediction accuracy for correct and incorrect future outbound trials originating at the center well. Error bars indicate 95% confidence intervals based on bootstrapped data (n.s., p = 0.06; **p = 0.01).

See also Figures S3–S4, and Table S2.

A similar pattern of replay was seen at center-well transitions (Figures 3D–E, S3), with preferential reverse replay of past inbound trajectories and forward replay of future outbound trajectories (examples show reverse replay of the alternative, not-taken past path in Figure 3D, and forward replay of the behaviorally actualized, taken future path in Figure 3E). Thus, for both center and side well transitions, reverse and forward replay preferentially reactivated past and future trajectories (both actual and alternative paths), respectively (additional examples in Figure S3).

We quantified this relationship of forward and reverse replay content with ongoing behavioral trajectories, and found a strong and consistent prevalence of reverse replay of the two possible past choices (actual taken and alternative past paths to reward well), and forward replay of the two possible future choices (actual taken and alternative future paths from reward well), at the respective reward well location (Figures 3F–I, S4). At the center well, this manifested as reverse replay of inbound trajectories (possible past paths; reverse/forward events, 324/91, p < 1e-4, z-test for proportions), and forward replay of outbound trajectories (possible future paths; reverse/forward events, 116/202, p < 1e-4, z-test for proportions), which was reversed at the side wells (reverse/forward events for outbound trajectories: 267/115, reverse/forward events for inbound trajectories: 101/272, p’s < 1e-4, z-tests for proportions; session-by-session comparison in Figure 3F; see also Table S2). This effect was consistent across all six animals (Figure 3G), and in different learning stages (Figures 3H–I).

This phenomenon persisted when we included only significantly unidirectional CA1 cells to rule out any unintended bias due to bidirectional cells (Figure S4A). Further, we ruled out the effect of “splitter” cells, which exhibit trajectory-dependent firing on the central arm of the maze (Ainge et al., 2007; Frank et al., 2000; Ito et al., 2015; Wood et al., 2000) (Figures S4B–D). Most replay events had at least two active side-arm cells, which can unambiguously detect left vs. right trajectory replays, and further, the bias in reverse and forward replay persisted with exclusion of center-arm cells (Figures S4C–D).

We next asked if there was a tendency for reverse and forward replay to occur at the end of previous trajectory and prior to the upcoming trajectory, respectively (Diba and Buzsáki, 2007). As previously reported (Ambrose et al., 2016), no such bias was apparent, and reverse replay of past paths and forward replay of future paths continued in an inter-mixed order in immobility periods (Figures S4E–F). We did, however, find that replay rate was significantly higher during ‘disengaged’ compared to ‘engaged’ periods during reward-well transitions (Ólafsdóttir et al., 2017) (Figures S4G–I; engaged periods defined by proximity to arrival and departure times, see STAR Methods). Finally, we also confirmed that the observed effect was not a result of bias in the distribution of place fields or decoded replay positions (Figures S4J–N). In fact, the distribution of decoded positions in replay events again revealed the over-representation of past paths in reverse replay and future paths in forward replay (Figures S4K–L).

The behavioral relevance of this replay pattern was confirmed by using the identity of reverse and forward replay events during a specific reward-well transition to predict the current location of the animal (i.e. left, center, or right reward well; see STAR Methods). For correct trials, we observed prediction accuracies that were significantly higher than chance-level (Figure 3J), indicating the existence of unique replay patterns that discriminate between goal locations. Thus, replay content was dependent on the current goal location and further, was also associated with an initiation bias (Davidson et al., 2009; Foster and Wilson, 2006; Karlsson and Frank, 2009) and over-representation of current position specifically for reverse replay (Figures S4L–N). We compared this effect of reverse past replay and forward future replay for correct and error outbound working-memory trials that originated from the center well, and observed an impairment specifically in forward replay of future paths. For these trials, animals were located at the center well after performing a correct past trajectory (inbound; rewarded), and about to choose the next outbound trajectory either correctly or incorrectly. Thus, both future correct and error trials were preceded by a rewarded inbound trajectory, with no differences in immobility time, SWR number or replay rate between correct vs. error trials (Figures S3I–J). We found, however, that there was a significant decrease in prediction accuracy using forward replay during error trials compared with correct trials (Figure 3K), corresponding to absence of bias in forward replay (for error trials, forward replay of future: 45%, p = 0.53; reverse replay of past: 68.5%, p = 0.008; z-test for proportions). Further, for trials that were unrewarded (which occurred at the side wells upon the completion of an incorrect outbound trajectory), the bias in both forward and reverse replay was absent (Figures S3K–M).

Contrasting evolution of reverse and forward replay with learning

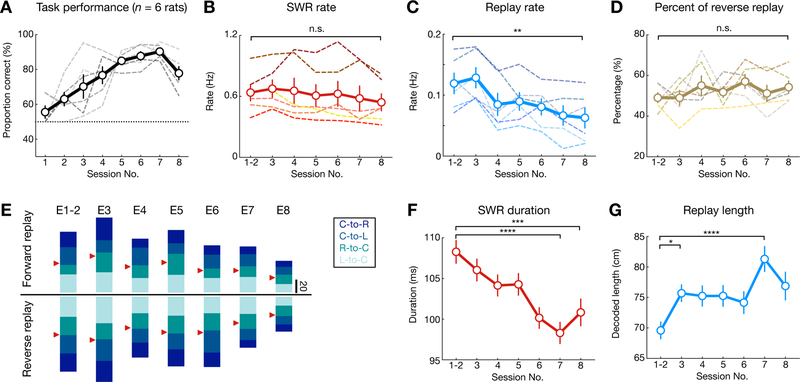
Since reverse and forward replay events consisted of both actual taken and alternative (not-taken) past and future paths, respectively (Figures 3, S3, S4), we next asked if there was any relationship between replay content and memory demands at different learning stages. First, even as performance improved over learning sessions (Figures 4A, S1H), there was no change in the balance of overall reverse and forward replay events (Figures 4B–E). SWR rate, amplitude, and frequency did not change (Figures 4B, S5A), but there was a decrease in replay rate over learning for both reverse and forward replay (Figures 4C, S5G). The decrease in replay rate corresponded to a decrease in place-cell activation during SWRs, which was attributed specifically to a decrease in activation for non-replay events, thus leading to a reduction in candidate events (Figures S5C–F). In addition, as animals became increasingly proficient in the task, there was a decrease in immobility duration at reward wells (Figure S5B), resulting in an overall reduction in the total number of SWRs and replay events at reward wells (Figures S5H–M). However, the fraction of reverse and forward replay events of any trajectory type did not change throughout learning (Figures 4D–E, S5G). Interestingly, we observed a decrease in SWR duration, but an increase in decoded replay length over learning (Figures 4F–G). Enhanced SWR duration in novel environments agrees with previous reports (Fernandez-Ruiz et al., 2019), and the increase in replay length suggests that the speed of replay increases over learning. Together, the shorter SWR duration, sparser place-cell activity, and longer trajectories reactivated during SWRs may reflect enhanced efficiency of replay over learning.

Figure 4. Dynamics of SWR replay properties over the course of learning.

(A) Task performance, showing proportion correct of outbound trajectories per session for all animals (n = 6 rats).

(B) Total SWR rate did not change across sessions (p = 0.28 and F(6, 30) = 1.44, repeated measures ANOVA).

(C) Replay rate decreased over learning (p = 0.0005, F(6, 30) = 14.21, repeated measures ANOVA; **p = 0.003, Tukey’s post hoc tests).

(D) Percentage of reverse replay out of all replay events did not change across sessions (p = 0.12, F(6, 30) = 2.370, repeated measures ANOVA).

(E) Number of forward and reverse replay events of the 4 behavioral trajectory types across 8 learning sessions (E1–8). The trajectory types are color-coded with red arrowheads indicating 50% level for forward and reverse replay.

(F) Duration of SWR events decreased over learning (p < 1e-4, Kruskal-Wallis test; ***p = 0.0003, ****p < 0.0001, Dunn’s post hoc tests).

(G) Decoded length of replay trajectories increased over learning (p = 0.0004, Kruskal-Wallis test; ***p = 0.0001, *p = 0.039, Dunn’s post hoc tests).

Dashed lines in (A-D): individual animals. Solid line and error bars: mean and SEMs.

See also Figure S5.

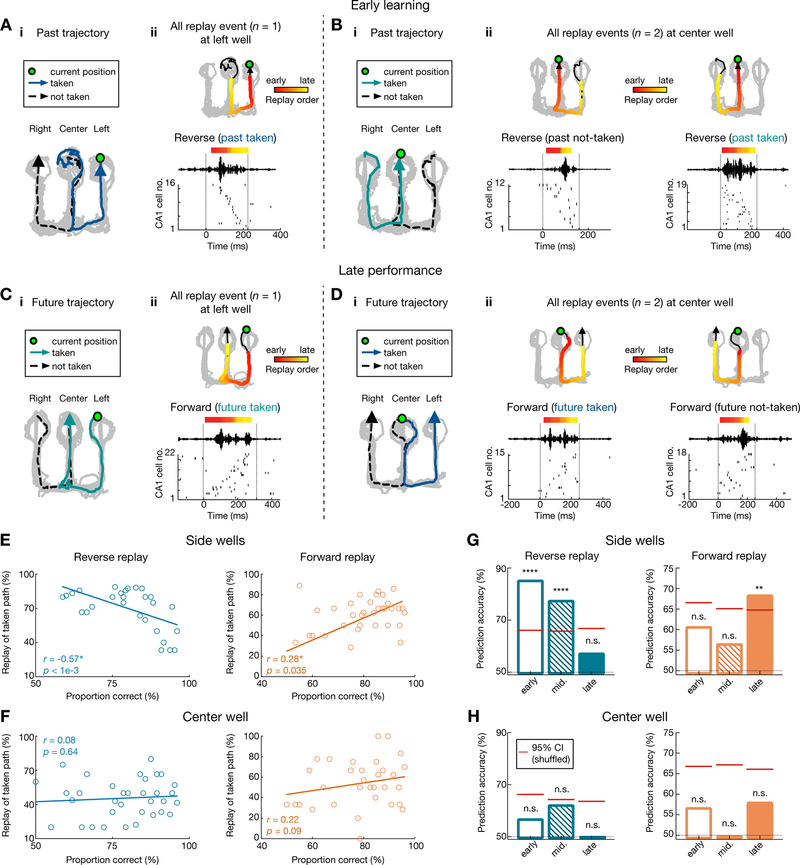
We further examined replay content at different learning stages independently at center-and side-well transitions, since outbound and inbound trajectories originating from these reward wells entail distinct memory demands (spatial working memory and spatial reference memory, respectively) (Jadhav et al., 2012). Examples of replay events during early learning in initial sessions (E1–3), and late performance in final sessions (E6–8), are shown in Figures 5A–D, S3 (behavioral performance on the outbound and inbound component, 59.9 ± 9.1% and 65.5 ± 28.2% for early learning, and 83.8 ± 9.6% and 97.14 ± 0.03% for late performance, respectively, in mean ± SD; see STAR Methods and Figure S1H). At the side wells, reverse replay events preferentially reactivated the actual taken past path during early learning, with this bias lost as performance improved (Figures 5A, E). On the other hand, forward replay events at side wells shifted their content from no initial bias during early learning to preferential replay of the future taken path during late sessions, when animals started performing well above chance levels (Figures 5C, E; overall, forward replay events of future taken vs. not-taken paths: 169/387 vs. 103/387, 43.7% vs. 26.7%, p < 1e-4; reverse replay events of past taken vs. not-taken paths: 200/376 vs. 67/376, 53.2% vs. 17.7%, p < 1e-4, z-test for proportions; See also Table S2).

Figure 5. Contrasting evolution of reverse and forward replay during the course of learning.

(A and B) Example reverse replay events during early learning at (A) the side well and (B) the center well. Data are presented as in Figure 3.

(C and D) Example forward replay events during late performance at (C) the side well and (D) the center well. See also Figure S3 for additional examples.

(E and F) Relationship between task performance and fraction of reverse replay of past taken paths (left), or forward replay of future taken paths (right) at (E) the side wells and (F) the center well. Each dot represents one session from a subject. Note the significant negative correlation for reverse replay (r = −0.57*, p < 0.0001) and positive correlation for forward replay (r = 0.28*, p = 0.035; permutation tests) at the side wells, but not the center well (r = 0.08, p = 0.64 for reverse replay; r = 0.22, p = 0.09 for forward replay).

(G) At side wells, reverse replay events predict taken past paths during early learning sessions (left), while forward replay events predict future taken paths during late performance sessions (right). Cross-validated SVM decoders were trained during early, middle and late sessions (sessions 1–3, 4–5, and 6–8, respectively). Significant prediction power was only observed during early and middle sessions for reverse replay (left; p < 0.0001****, 0.0001****, and = 0.43 for early, middle, and late sessions, respectively), and late sessions for forward replay (right; p = 0.23, 0.35, and 0.003** for early, middle, and late sessions, respectively).

(H) Taken paths cannot be predicted from patterns of replay events at the center well (p = 0.36, 0.08, and 0.68 for reverse replay, p = 0.38, 0.56, and 0.15 for forward replay during early, middle, and late sessions, respectively). Red horizontal lines on columns represent chance levels calculated by permutation tests.

Only correct trials are shown. See also Figure S6.

In contrast, at the center well, reverse and forward replay events continued to reactivate, in an unbiased manner, both the actual taken and the alternative (not-taken) past and future paths, respectively, throughout learning (Figures 5B, D, F; overall, reverse replay events of past taken vs. not-taken paths: 146/439 vs. 177/439, 33.6% vs. 40.3%; forward replay events of future taken vs. not-taken paths: 111/293 vs. 91/293, 37.9% vs. 31.6%; p = 0.55, z-test for proportions). Replay content thus exhibited distinct dynamics over learning at the side and center wells. We also confirmed that changes in splitter cells are not the primary reason for the observed changes in replay (Figures S6A–B).

At the side wells, consistent with the correlation of replay content with behavioral performance (Figure 5E), reverse replay content accurately predicted the actual past path during early learning stages, but not later performance (Figure 5G, Left; see STAR Methods); whereas accurate prediction of actual future path based on forward replay emerged only after learning during later performance sessions (Figure 5G, Right). In contrast, at the center well, reverse replay could not predict the actual taken past path (Figure 5H, Left), and although there was a non-significant correlation trend for increase in forward replay of taken path (Figure 5F, Right), forward replay content was unable to predict the actual taken future path (Figure 5H, Right). A similar lack of prediction ability was seen for incorrect trials at the center well (Figures S6C–D). We therefore hypothesized that behaviorally relevant replayed trajectories are distinguished in networks outside the hippocampus, with PFC a likely candidate (Shin and Jadhav, 2016; Tang and Jadhav, 2019; Yu and Frank, 2015; Zielinski et al., 2017).

Coordinated hippocampal-prefrontal replay distinguishes past-future trajectory sequences

We therefore examined the relationship of coherent CA1-PFC replay of spatial paths (Tang et al., 2017) to ongoing behavioral trajectories. Similar to CA1 (Figure 1), PFC neurons exhibited spatially and directionally selective firing, and PFC ensembles formed unique spatial representations of trajectories for all sessions (Figure 6). PFC neurons have significantly lower spatial specificity and multi-peaked fields as compared with CA1 neurons (Jadhav et al., 2016; Tang et al., 2017; Yu et al., 2018; Zielinski et al., 2019), but PFC ensembles can still represent spatial location with high accuracy (Fujisawa et al., 2008; Mashhoori et al., 2018; Zielinski et al., 2019). Just as in CA1, although spatial stability and specificity of PFC cells increased across sessions (Figures S7A–B), spatial- and directional-selective firing was seen starting with the first novel track session (Figures 6A–F), supporting accurate position decoding of individual trajectories (position reconstruction and confusion matrices in Figures 6C–E; cross-validated decoding error: 9.61 ± 0.21 cm in median ± SEM). Trajectory-dependent firing on the center arm was also observed in PFC cells (Baeg et al., 2003; Fujisawa et al., 2008; Ito et al., 2015), similar to CA1 splitter cells; and the fraction of PFC splitter cells did not significantly change over learning (Figure S7C). PFC ensembles thus uniquely represent different trajectories on the maze for all sessions (Tang et al., 2017; Zielinski et al., 2019).

Figure 6. Spatial coding and distinct representations of behavioral trajectories by prefrontal ensembles.

(A) Spatial maps of all PFC cells (n = 154) recorded from 6 rats continuously across 8 learning sessions (E1–8). Data are presented as Figure 1C. Note that mirror-image patterns between pairs of trajectories on each row reflect path equivalent properties of PFC neurons (Yu et al., 2018).

(B) Spatial maps of all PFC cells (n = 38) recorded from an example animal in the first and last sessions.

(C-D) Position reconstruction based on PFC ensemble spiking from the example animal in (B) during active running. Decoding performance was estimated using a leave-one-out cross-validation. (C) Confusion matrices (estimated vs. true position). (D) Estimated position probabilities. Cyan line: actual animal trajectory. Data are presented as Figures 1D–E.

(E) Cumulative PFC decoding errors across all animals (n = 6 rats). Dashed lines: individual animals; Red line: all animals; Solid black line: the example animal shown in (B-D). Median error of all sessions (vertical red line) noted on top. Decoding error: 14.58 ± 0.63 cm for Session 1, 8.99 ± 0.57 cm for Session 8 (in median ± SEM).

(F) Population vector overlap (PVO) of PFC population activity in two running directions across 8 learning sessions. Data are presented as in Figure 1H. Note that the spatial maps of PFC population in two running directions became less similar across sessions, but distinct templates for each direction were apparent in the first session (p’s < 0.0001 compared to the shuffled data for individual rats, trial-label permutation tests).

See also Figure S7.

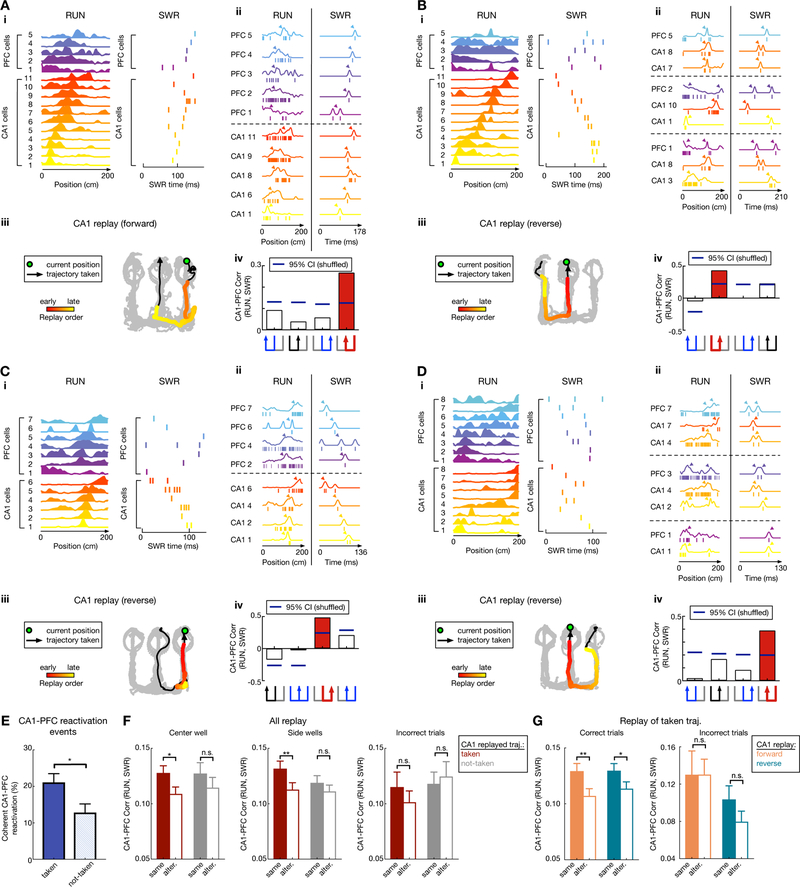
Prefrontal reactivation occurs during hippocampal SWRs (Benchenane et al., 2010; Jadhav et al., 2016; Peyrache et al., 2009), and we have previously reported coordinated CA1-PFC replay of spatial memory during awake SWRs (Tang et al., 2017). We therefore examined the relationship between coherent CA1-PFC replay and ongoing behavioral choices. Here, coherent CA1-PFC reactivation is defined as a CA1 replay event where the same trajectory is also significantly reactivated by CA1-PFC ensembles, detected as ‘reactivation strength’ using a template matching method established in previous reports for hippocampal-cortical and - subcortical networks (Figures 7, S7, S8; see STAR Methods; a comparison of the template matching method with Bayesian decoding and line-fitting methods is detailed in Figure S8) (Girardeau et al., 2017; Lansink et al., 2009; Peyrache et al., 2009; Tang et al., 2017). Using template spatial maps of CA1 and PFC neurons for candidate coherent replay events (≥ 5 PFC and CA1 place cells active; Figures 7A–D), we measured the reactivation strength of CA1-PFC ensembles during each candidate SWR event as the correlation of population activity during the SWR event and during running for each of the four possible trajectories. Illustrative coherent CA1-PFC replay events, with both forward and reverse CA1 replay, are shown in Figures 7A–D.

Figure 7. Coherent hippocampal-prefrontal (CA1-PFC) replay of past and future trajectories.

(A-D) Four examples of coherent CA1-PFC reactivation of future and past taken paths. (i) Linearized CA1-PFC spatial-map template with cell IDs on y-axis (left), and the corresponding raster plot during the SWR (right). (ii) Detailed view of CA1-PFC coordination during RUN and the SWR using example cells. Left (RUN): the spiking pattern from a single running trial (ticks) with linearized spatial maps obtained by averaging over all trials (overlaid lines). Right (SWR): spikes (ticks) during the SWR, and the response curves (overlaid lines) created by smoothing observed spikes with a Gaussian kernel. Arrowheads indicate the peak locations. (iii) CA1 trajectory replay, with data presented as in Figure 5A. Green circle: animal’s current position; Black arrowhead line: trajectory taken; Colored dots: decoded CA1-replay path. (iv) Reactivation strength, measured as the correlation coefficient of CA1-PFC activity during RUN vs. SWR using template matching, for four possible trajectories (trajectory schematic on the bottom; red for CA1-replayed path, black for alternative path, blue for the other paths). Blue horizontal lines on columns represent 95% confidence intervals computed from shuffled data (SWR spike time shuffle). Selected PFC cells with highest contribution to the reactivation strength are shown for ease of presentation, illustrating the synchronized firing pattern for CA1-PFC cells during RUN, which is reactivated during the SWR event.

(E) The proportion of coherent CA1-PFC reactivation events during correct trials is significantly higher during CA1 replay of taken vs. not-taken trajectories (p = 0.02*, session-by-session rank-sum paired test).

(F) Paired comparison of CA1-PFC reactivation strength for CA1-replay of taken vs. alternative path during correct trials at center (Left) and side (Middle) wells, and for incorrect trials (Right). Note that during correct trials, CA1-PFC reactivation strength is significantly higher for the CA1-replayed path compared to its alternative (alter.), only when this replayed path was the behaviorally taken path at both center (p = 0.032*; n = 246 and 110 replay events for taken and not-taken respectively) and side wells (p = 0.0075**; n = 244 and 212 replay events for taken and not-taken respectively), but not when the CA1-replayed path was the “not-taken” path ( p = 0.35 and 0.16 for side and center wells, respectively; event-by-event rank-sum paired tests). This bias of CA1-PFC reactivation during correct trials is absent during incorrect trials (n = 49 and 56 replay events, and p = 0.20 and 0.96 for taken vs. not-taken respectively; event-by-event rank-sum paired tests).

(G) Left: Stronger CA1-PFC reactivation of taken path compared to not-taken path during correct trials for both forward and reverse CA1 replay (p = 0.0058** and n = 215 events for forward replay of taken path; p = 0.039* and n = 275 events for reverse replay of taken path; event-by-event rank-sum paired tests). Right: During incorrect trials, CA1-PFC reactivation did not show significant difference for taken vs. alternative path for either forward or reverse CA1 replay (p = 0.96 and n = 21 events for forward replay of taken path; p = 0.10 and n = 28 events for reverse replay of taken path; event-by-event rank-sum paired tests).

See also Figures S7 and S8.

We found that coherent CA1-PFC reactivation (quantified as the fraction of coherent CA1-PFC replay events) was higher when CA1 replayed taken paths as compared to not-taken paths (Figure 7E). Crucially, measuring reactivation strength enabled us to compare the strength of coherent CA1-PFC replay when CA1 replayed either the behaviorally taken path, or the not-taken path, as a paired comparison with the corresponding alternative path during each event (see STAR Methods; for each replay event, CA1-PFC reactivation strength for either past or future trajectories was compared for the actually replayed CA1 trajectory vs. that for the alternative trajectory). Using this measure for correct trials, we found that coherent CA1-PFC reactivation was significantly stronger when CA1 replayed the actual taken paths as compared with the alternative trajectory, but not when CA1 replayed the not-taken paths (Figure 7F; effect seen at both center and side wells). This stronger coherent CA1-PFC replay for behaviorally actualized trajectories was true for both forward CA1 replay of future taken paths, as well as reverse CA1 replay of past taken paths (Figure 7G).

Coherent CA1-PFC replay can thus distinguish, through stronger reactivation, actual (i.e., behaviorally instantiated) past and future paths during reverse and forward CA1 replay, respectively (Figures 7E–G), suggesting differential PFC coupling based on CA1 replay content. This was not a result of any difference in average activation probabilities or firing rates of PFC neurons for taken vs. not-taken paths (Figure S7E), or difference in CA1 replay quality (Figure S7F). Further, this differential PFC coupling was not detected for incorrect outbound trials originating at the center well (Figures 7F–G, right panels). Finally, we also found a significant positive correlation between higher CA1-PFC reactivation (Figures S7J–L) and the peak working-memory performance levels achieved by each animal; but surprisingly, a negative correlation for CA1-reactivation that can partially be attributed to longer immobility times and disengagement periods (Figures S7M–N). This is suggestive of a relationship between stronger coherent CA1-PFC replay and better memory performance on the task.

DISCUSSION

Our results provide novel insights into the role of replay, and suggest a role of coordinated hippocampal-prefrontal replay in spatial learning and memory-guided decision making. Continuous tracking of replay over the course of spatial choice learning revealed an association of reverse replay with retrospective evaluation of possible past paths leading to goals, and that of forward replay with prospective planning of available future choices toward goals. Further, these findings reveal dynamic changes in functional roles of replay depending on the learning stage, and a mechanism of coherent hippocampal-prefrontal replay for learning and performance of spatial memory tasks.

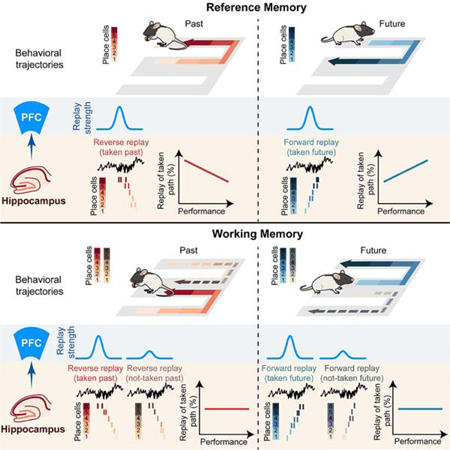
Previous studies have established a causal role of awake replay in W-maze learning (Fernandez-Ruiz et al., 2019; Jadhav et al., 2012), but how replay supports such memory tasks is not clear; neither are the specific roles of reverse and forward replay, which have been primarily reported on linear-trajectory tracks with a single back-and-forth path between reward wells (Ambrose et al., 2016; Diba and Buzsáki, 2007; Foster and Wilson, 2006). Singer et al. (2013) reported that CA1 co-activity during SWRs was enhanced prior to correct trials during initial learning in the W-maze, and this activity did not correspond to specific paths, although this study did not examine replay of place-cell sequences. These findings hint, in agreement with hypotheses from other studies (Gupta et al., 2010; Jadhav et al., 2012; Stella et al., 2019), that hippocampal replay may support an evaluative process, and target regions outside the hippocampus are necessary to link hippocampal replay to ongoing behavioral choices. Our results suggest a model (Figure 8) with differing roles of replay in (i) history-independent spatial reference-memory tasks, where hippocampal replay showed dynamic changes over learning; and (ii) history-dependent spatial working-memory tasks, with a role of coherent hippocampal-prefrontal replay in recall of actual past experiences to guide planning of future choices.

Figure 8. Schematic: hippocampal-prefrontal replay supports retrospection and prospection for learning and planning in spatial memory-guided tasks.

(A) The role of hippocampal-prefrontal replay in learning history-independent, spatial reference-memory rules. (A_i) Past and future paths at side wells. (A_ii-A_iii) Hippocampal replay dynamics over learning. (A_iv) Stronger coherent CA1-PFC replay of taken paths.

(B) The role of hippocampal-prefrontal replay in learning history-dependent, spatial working-memory rules. (B_i) Past and future paths at the center well. (B_ii-B_iii) Persistent trends of hippocampal replay over learning. (B_iv) Discrimination of taken paths by coherent CA1-PFC replay.

At the side wells, replay showed a shift from reverse-replay-based prediction of past path during early learning, to forward-replay-based prediction of future path during late performance (Figure 8A). Reverse and forward hippocampal replay of past and future paths are in agreement with observations for deterministic spatial tasks (i.e., pre-determined correct paths between reward wells) on linear-trajectory tracks (Ambrose et al., 2016; Diba and Buzsáki, 2007; Foster and Wilson, 2006; Wu et al., 2017). Our findings reveal a learning gradient for the role of replay in spatial reference memory, where the correct path to goal depends only on the animal’s current location, and indicate that with repeated experience of the same inbound return-to-center trajectory, forward replay prediction of future path leading to reward (Pfeiffer and Foster, 2013; Xu et al., 2019) emerges over learning, confirming previous hypotheses (Pfeiffer, 2017). Interestingly, disrupting SWR replay does not impair inbound learning (Jadhav et al., 2012), suggesting that other mechanisms can support this learning.

Reverse replay at side wells supported retrospection of the past outbound (center-to-side) paths leading to reward. Notably, recall of this past path is not required for execution of the future inbound reference-memory path; rather, the observed reverse replay occurs at the completion of the outbound spatial working-memory trajectory, and thus aligns with a role in working-memory updates, similar to previous reports in a radial-arm maze (Xu et al., 2019). Intriguingly, we found that the reverse bias toward taken past path to goals is present only during early learning, and can thus play a role in temporal credit assignment during novel learning (Foster and Knierim, 2012; Haga and Fukai, 2018; Mattar and Daw, 2018). The observed loss of bias over learning (Figure 8A) suggests that this reinforcement is no longer required after task acquisition (Foster and Knierim, 2012). Finally, stronger CA1-PFC replay of taken (i.e. behaviorally actualized) paths at the side wells signifies that CA1-PFC replay of the future taken trajectory may support planning of the upcoming reference-memory trajectory, and that replay of the past taken trajectory may support reinforcement of the completed working-memory path.

In contrast, results at the center well indicate that hippocampal replay underlies a cognitive search role, and not a predictive element, for execution of working-memory trajectories (Figure 8B). We found that the hippocampus persistently reverse-replayed both possible past choices and forward-replayed both available future choices throughout learning and performance. Replay of possible choices is indicative of a priming process for retrospective evaluation and prospective planning (Buzsáki, 2015), underlying a cognitive exploration of possible paths (Redish, 2016; Singer et al., 2013; Stella et al., 2019) (Figure 8B). For individual hippocampal replay events, coherent CA1-PFC replay discriminates the behaviorally actualized past and future paths, and can thus support planning of the future choice based on past experience. This PFC read-out interpretation aligns with a bias toward CA1-leading-PFC directionality during replay (Jadhav et al., 2016; Rothschild et al., 2016).

Our results thus suggest a mechanism by which replay supports acquisition and performance of spatial working memory tasks. Multiple paths to and from the center well underlie a non-Markovian structure (Mattar and Daw, 2018), which requires animals to integrate across space and time to learn sequences of past and future choices that lead to reward (i.e. action-outcome associations). In our model, hippocampal reverse and forward replay underlie an evaluative process for retrospection and prospection, respectively, supporting a cognitive exploration of available paths that can be utilized by other networks for reinforcement learning and decision-making. These processes involve prefrontal reactivation, since coherent CA1-PFC replay can distinguish behaviorally taken past and future paths in CA1 replay. It is important to point out that our experimental design enabled a rapid learning time-scale, and it is possible that this replay role is not seen in repeatedly trained tasks, where other habitual systems can contribute to learning and performance (Kim and Frank, 2009; Packard and McGaugh, 1996). In addition, although PFC reactivation is known to occur during hippocampal SWRs (Khodagholy et al., 2017; Tang et al., 2017; Vaz et al., 2019), independent cortical reactivation cannot be ruled out (O’Neill et al., 2017). Further, since there is evidence that theta-mediated and SWR-mediated activity can play complementary roles in deliberation and cognition (Papale et al., 2016; Pezzulo et al., 2019; Redish, 2016), the relationship between theta- and SWR-mediated CA1-PFC interactions in memory-guided behavior (Gordon, 2011; Ito et al., 2015; Shin and Jadhav, 2016; Spellman et al., 2015) is an important avenue for future investigation.

The suggested mechanism of hippocampal cognitive evaluation with differential coupling of prefrontal and other networks based on replay content has implications for neural mechanisms of model-based learning and planning, for spatial as well as non-spatial memories (Doll et al., 2012; Liu et al., 2019; Miller et al., 2017; Vikbladh et al., 2019). The results of this study also connect well to machine learning literature based on hippocampal replay (Caze et al., 2018; Mattar and Daw, 2018), and thus may inspire improved algorithms. We hypothesize that replay in the awake state represents an internal cognitive state that engages a broad, multi-region network, similar to a default network mode (Buckner, 2010; Logothetis et al., 2012), to support ongoing learning, prospection, and abstraction.

STAR★METHODS

LEAD CONTACT AND MATERIALS AVAILABILITY

Further information and requests for resources and reagents should be directed to the Lead Contact, Shantanu P. Jadhav (shantanu@brandeis.edu). This study did not generate new unique reagents.

EXPERIMENTAL MODEL AND SUBJECT DETAILS

All procedures were approved by the Institutional Animal Care and Use Committee at the Brandeis University and conformed to US National Institutes of Health guidelines. Six adult male Long-Evans rats (450–550 g, 4–6 months; RRID: RGD_2308852) were used in this study. Animals were individually housed and kept on a 12-hr regular light/dark cycle.

METHOD DETAILS

The W-maze spatial memory task

Animals learned a novel W-maze continuous spatial alternation task within a single day. During this experimental day, all animals ran eight 15–20 min sessions on a W-maze interleaved with 20–30 min rest sessions in a sleep box (W-maze sessions: 17.9 ± 1.0 mins per session, 8 sessions per rat; rest sessions: 23.0 ± 4.9 mins per session, 9 sessions per rat; total recording duration: 6.04 ± 0.37 hrs per rat; mean ± SD). The W-maze was novel in the first behavioral session (sleep box was opaque, and the animal had no visibility of the W-maze until it was introduced in the first run session), and had dimensions of ~ 80 × 80 cm with ~7-cm-wide track sections. Three reward food wells (i.e., right, center and left wells) were located at the end of three arms of the W-maze (Figure 1). Calibrated evaporated milk reward was automatically delivered in the reward wells triggered by crossing of an infrared beam by the animal’s nose. Rewards were delivered according to the following rules (Figure 1A): returning to the center well after visits to either side well (inbound trajectories), and choosing the opposite side well from the previously visited side well when starting from the center well (outbound trajectories). Incorrect alternations (visiting the same side well in consecutive outbound components – outbound error), or incorrect side-to-side well visits (without visiting the center arm – inbound error) were not rewarded. Repeated visits to the same well were also not rewarded (i.e., turn-around error). Therefore, animals performed four types of trajectories during correct behavioral sequences (Figure 1A): center-to-right (C-to-R), right-to-center (R-to-C), center-to-left (C-to-L) and left-to-center (L-to-C). Among these trajectory types, C-to-R and C-to-L are outbound trajectories, while R-to-C and L-to-C are inbound trajectories. When animals paused at one reward well during correct trials, two of these four trajectory types represented the immediate past and future paths taken, and the other two represented the alternative not-taken paths (Figure 1B). For visualization purposes, the alternative, not-taken trajectories corresponding to a taken behavioral sequence were selected from the adjacent trials (e.g., Figure 3D). Only behaviorally correct trials were included for replay and reactivation analyses, unless otherwise specified. At the end of each W-maze session, animals were transferred to a black opaque box for rest (~ 30 × 30 cm with a 50-cm high wall). The raw performance of the task was calculated as proportion correct (Singer et al., 2013) (Figure 4A), and the learning curves were estimated using a state-space model (Jadhav et al., 2012; Smith et al., 2004) (Figure S1H). Each animal’s maximal performance level (Figures S7M and S7N) was measured as the highest performance reached on the outbound learning curve (Figure S1H). All 6 animals performed > 80% correct in the W-maze task toward the end of learning (maximal proportion correct of outbound for individual animals: 91.2 ± 4.1%; mean ± SD).

Surgical implantation and electrophysiology

Surgical implantation procedures were as previously described (Jadhav et al., 2012; Jadhav et al., 2016; Tang et al., 2017). Animals were implanted with a microdrive array containing 30–32 independently moveable tetrodes targeting right dorsal hippocampal region CA1 (−3.6 mm AP and 2.2 mm ML) and right PFC (+3.0 mm AP and 0.7 mm ML). On the days following surgery, hippocampal tetrodes were gradually advanced to the desired depths using characteristic EEG patterns (sharp wave polarity, theta modulation) and neural firing patterns as previously described (Jadhav et al., 2012; Jadhav et al., 2016). One tetrode in corpus callosum served as hippocampal reference, and another tetrode in overlying cortical regions with no spiking signal served as prefrontal reference. A ground (GND) screw installed in skull overlying cerebellum also served as a reference. All spiking activity and ripple-filtered LFPs (150–250 Hz; see below) were recorded relative to the local reference tetrode. Electrodes were not moved at least 4 hours before and during the recording day.

Data were collected using a SpikeGadgets data acquisition system (SpikeGadgets LLC) (Tang et al., 2017). Spike data were sampled at 30 kHz and bandpass filtered between 600 Hz and 6 kHz. LFPs were sampled at 1.5 kHz and bandpass filtered between 0.5 Hz and 400 Hz. The animal’s position and running speed were recorded with an overhead color CCD camera (30 fps) and tracked by color LEDs affixed to the headstage.

Spiking activity was continuously monitored during the experimental day for ~6–7 hrs. This design enabled us to link replay dynamics to behavioral learning, without the possible confound that different ensembles were monitored in different learning stages. Single units were identified by manual clustering based on peak and trough amplitude, principal components, and spike width using custom software (MatClust, M. P. Karlsson) as previously described (Jadhav et al., 2016; Tang et al., 2017). Only well isolated neurons with stable spiking waveforms and stable clusters across sessions were included – clusters that split or merged across sessions were discarded (Figure S1). Cluster quality was measured using isolation distance (Schmitzer-Torbert et al., 2005) and cluster center-of-mass shift (Mallory et al., 2018), and also assessed using spike-waveform correlation (Li et al., 2017) (Figure S1). Cluster center-of-mass shift between two different sessions was calculated as the Mahalanobis distance between the cluster centroids of the same single unit from these sessions. The spike-waveform correlation was quantified as the correlation coefficient between averaged spike waveforms of the same single unit from two consecutive sessions, and the resulting correlation was Fisher-transformed to make it normally distributed (Li et al., 2017).

Unit inclusion

Units included in analyses fired at least 100 spikes in each session. Putative interneurons were identified and excluded based on spike width and firing rate criterion as previously described (Jadhav et al., 2016; Tang et al., 2017). Peak rate for each unit was defined as the maximum rate across all spatial bins in the linearized spatial map (see Spatial maps). A peak rate ≥ 3 Hz was required for a cell to be considered as a place cell. Only cells recorded continuously across all 8 behavioral sessions with stable spiking waveforms were analyzed (Figure S1). All manually clustered units included satisfied at least one of the cluster-quality criteria described above, and a majority of cells (98.6%, 213/216 for CA1 and 98.1%, 151/154 for PFC) met the thresholds for the primary criteria of isolation distance and center-of-mass shift. 93.1% (201/216) CA1 and 94.8% (146/154) PFC units met all 3 criteria, including spike-waveform correlation (Figures S1F and S1G).

Behavioral state definition

Movement or exploratory states were defined as periods with running speed > 5 cm/s, whereas immobility was defined as periods with speed ≤ 4 cm/s. The animal’s arrival and departure at a reward well was detected by an infrared beam triggered at the well. The well entry was further refined as the first time point when the speed fell below 4 cm/s before the arrival trigger, whereas the well exit was defined as the first time point when the speed rose above 4 cm/s after the departure trigger (Figure 3A). The animal’s time spent at a reward well (i.e., immobility period at well) was defined as the period between the well entry and exit. For trials with an immobility duration at a reward well longer than 6 s, the total time spent at the well was equally divided into 4 parts; the first and last parts were defined as engaged periods, and the rest were considered as disengaged (Figures S4G–S4I) (Ólafsdóttir et al., 2017).

QUANTIFICATION AND STATISTICAL ANALYSIS

Sharp-wave ripple detection

SWRs were detected as described previously during immobility periods (≤ 4 cm/s) (Jadhav et al., 2016; Karlsson and Frank, 2009; Tang et al., 2017). In brief, LFPs from CA1 tetrodes were filtered into the ripple band (150–250 Hz), and the envelope of the ripple-filtered LFPs was determined using a Hilbert transform. SWRs were initially detected as contiguous periods when the envelope stayed above 3 SD of the mean on at least one tetrode, and further refined as times around the initially detected events during which the envelope exceeded the mean. The amplitude of a SWR event was defined in terms of exceeded SDs above the mean as described previously (Figure S5A) (Tang et al., 2017). To determine the frequency of a SWR event, we first estimated the spectrogram of peri-event CA1 LFPs around the SWR onset using multi-taper time-frequency analysis (Chronux toolbox; http://chronux.org/), and the power at each frequency band was individually z-scored across a given session. The frequency of this event was then defined as the frequency with the highest power within the ripple band (100–250 Hz) during the event (Middleton et al., 2018; Ramirez-Villegas et al., 2015; Sullivan et al., 2011). For replay and reactivation analysis (see below, Replay decoding and CA1-PFC reactivation analysis), only SWRs with a duration ≥ 50 ms were included, similar to previous studies (Pfeiffer and Foster, 2013; Wu et al., 2017).

Spatial maps

Spatial maps were calculated only during movement periods (> 5 cm/s; all SWR times excluded) at positions with sufficient occupancy (> 20 ms). Two-dimensional occupancy-normalized spatial rate maps were calculated as previously described (Jadhav et al., 2012; Jadhav et al., 2016; Tang et al., 2017). To construct the spatial-map templates of different trajectory types on a W-maze (Figure 1C), we calculated the linearized activity of each cell as previously described (Jadhav et al., 2012; Jadhav et al., 2016; Karlsson and Frank, 2009; Singer et al., 2013). The rat’s linear position was estimated by projecting its actual 2D position onto pre-defined idealized paths along the track, and was further classified as belonging to one of the four trajectory types. The linearized spatial maps were then calculated using spike counts and occupancies calculated in 2-cm bins of the linearized positions and smoothened with a Gaussian curve (4-cm SD) as previously described (Jadhav et al., 2012; Tang et al., 2017). To cross-validate the linearized positions, an alternative linearization method was also used based on nearest-neighbor Delaunay triangulation (Ferbinteanu et al., 2011). Completed trials detected based on both methods, i.e., linearized trajectories starting from and ending at reward wells, were used for replay and reactivation analyses.

To quantify spatial coverage of place-cell populations, a spatial bin was considered as represented if at least one cell from the population had an occupancy-normalized rate ≥ 3 Hz within the bin (Kay et al., 2016; Zielinski et al., 2019). The spatial coverage of the population was then expressed as the percentage of the spatial bins covered. Across the populations of recorded place cells, we found place fields at all positions along each trajectory type (spatial coverage per subject over sessions, shown as mean ± SD: 99.9 ± 0.1%, 99.4 ± 0.8%, 97.4 ± 2.1%, 99.5 ± 0.8%, 91.5 ± 9.3%, 96.2 ± 1.6%; n = 6 rats; see also Figures 1C and S4J). The stability of spatial maps was defined as the correlation between the linearized maps for all 4 trajectory types for two consecutive behavioral sessions (Figures S2A and S7A) (Jadhav et al., 2012). In addition, we calculated the correlation after shuffling the cell identity among all other simultaneously recorded cells in the latter session, and compared this shuffled measure to the actual correlation. The specificity of spatial maps was measured as (1 – spatial sparsity), where spatial sparsity is calculated as a fraction of linearized place field with a firing rate >25% of its peak rate (Figures S2B and S7B) (Jadhav et al., 2016; Tang et al., 2017).

Place-field directionality

For each place cell, a directionality index (DI) was calculated based on firing rates in the preferred (FR_pref) and non-preferred (FR_npref) running directions of the left or right trajectories (Figure 1G) as (FR_pref - FR_npref) / (FR_pref + FR_npref), similar to previous studies (Navratilova et al., 2012; Ravassard et al., 2013). A directionality index of 0 indicates identical firing in both directions, whereas 1 indicates firing in one direction only. The similarity of the place-field population in two running directions was computed using the population vector overlap (PVO; Figures 1H and 6F) (Ravassard et al., 2013). The population vector (PV) was the activity vector of all place cells in a certain linear position bin. The PVO was defined as the vector dot product between the PVs across all linear positions in two running directions:

$$PVO=\frac{\sum _x\sum _{i}F{R}_{f,i}\left(x\right)F{R}_{b,i}\left(x\right)}{\sqrt{\sum _x\sum _{i}F{R}_{f,i}\left(x\right)F{R}_{f,i}\left(x\right)\sum _x\sum _{i}F{R}_{b,i}\left(x\right)F{R}_{b,i}\left(x\right)}}$$

where FR_f,i(x) is the firing rate of the i-th place cell at the linear position x along the track in a forward running direction, and FR_b,i(x) is for the backward running direction. The PVO ranges from 0 to 1, with 1 representing identical population place-field templates in two running directions. To determine the significance values for the PVO and DI, we created 1,000 shuffle surrogates by randomly shuffling running directions from trial to trial, and computed PVO and DI from the shuffled data. Unidirectional cells were defined as cells with a DI significantly higher than its shuffle surrogates (p < 0.05; See Table S1 for the number of unidirectional cells of each animal, and Figure S4A for replay analysis using the unidirectional cells).

Trajectory-dependent firing

It has been shown that the spatial maps of both CA1 (Ainge et al., 2007; Ferbinteanu and Shapiro, 2003; Frank et al., 2000; Wood et al., 2000) and PFC (Baeg et al., 2003; Fujisawa et al., 2008; Ito et al., 2015) cells on the center stem of spatial mazes can discriminate among different trial types in the same running direction, termed “splitter cells”. For cells with robust fields (> 2 Hz) on the center stem of the W-maze, we further analyzed their trajectory-dependent firing. The firing rate was calculated in 2-cm bins of the linearized positions on the stem and smoothened with a Gaussian curve (3-cm SD) for each trial, and then the firing rate difference between different trajectories was compared (i.e., center-to-left vs. center-to-right outbound trajectories, and left-to-center vs. right-to-center inbound trajectories) as firing rate (FR) index:

$$\text{FR}\hspace{0.17em}\hspace{0.17em}\text{index}\hspace{0.17em}\text{=}\frac{|\sum _i\left(F{R}_L\left(i\right)-F{R}_R\left(i\right)\right)|}{\sum _i\left(F{R}_L\left(i\right)+F{R}_R\left(i\right)\right)}$$

where FR_L(i) is the firing rate in the i-th spatial bin on the stem during left trials (i.e., center-to-left trial for outbound, or left-to-center trial for inbound), and FR_R(i) is for the right trials. To assess significance, the trial labels (left or right) were randomly shuffled 1,000 times, and cells with a FR index significantly higher than its shuffle surrogates (p < 0.05) were defined as splitter or trajectory-dependent cells (Figures S4B and S7C). Note that the method here is less conservative than that used in some previous studies for defining “splitter cells” (e.g., parameters such as running speed could potentially contribute to the differential firing; Ito et al. 2015; Wood et al. 2000), since we only used trajectory-dependent firing of center-stem cells to assess their contribution to templates for different replay sequences. Note that most replay events identified comprised at least two side-arm cells (Figures S4C–S4D, and Figures S6A–S6B), which were defined as the cells that have the firing rate peak past the choice point and outside the center arm (Fernandez-Ruiz et al., 2019; Singer et al., 2013).

Bayesian decoding and replay detection

Bayesian decoding of spatial location and replay was implemented as previously described (Ambrose et al., 2016; Davidson et al., 2009; Karlsson and Frank, 2009; Tang et al., 2017). A memoryless Bayesian decoder was built for each of the four trajectory types to estimate the probability of animals’ position given the observed spikes (Bayesian reconstruction; or posterior probability matrix): P(X, tr| spikes) = P(spikes| X, tr)P(X, tr)/P(spikes), where X is the set of all linear positions on the track for different rajectory types (tr ∈ {center-to-right, right-to-center, center-to-left, left-to-center}), and we assumed a uniform prior probability over X and tr. Assuming that all N place cells active during a candidate event fired independently and followed a Poisson process:

$$P\left(\mathbf{\text{spikes}}|X,tr\right)={\prod }_{i=1}^{N}P\left(spike{s}_i|X,tr\right)={\prod }_{i=1}^N\frac{{\left(\hspace{0.17em}\tau f_i\left(X,tr\right)\right)}^{spike{s}_i}{e}^{-\tau f_i\left(X,tr\right)}}{spike{s}_i!}$$

where T is the duration of the time window (i.e., 10 ms for replay events, and 500 ms for active behavior), f_i(X,tr) is the expected firing rate of the i-th cell as a function of sampled location X and trial type tr, and spikes_i is the number of spikes of the i-th cell in a given time window. Therefore, the posterior probability matrix can be derived as follows:

$$P\left(X,tr|\mathbf{\text{spikes}}\right)=C\left({\prod }_{i=1}^N{f}_i{\left(X,tr\right)}^{spike{s}_i}\right)e^{-\tau {\sum }_{i=1}^N{f}_i\left(X,tr\right)}$$

where C is a normalization constant.

This Bayesian decoding algorithm was used to estimate the animal’s location during active running (speed > 5 cm/s) (Figures 1 and 6), similar to previous studies (Ambrose et al., 2016; Davidson et al., 2009; Farooq and Dragoi, 2019; Ólafsdóttir et al., 2017). To decode spatial location during running, the population activity was binned into 500-ms non-overlapping bins. Decoding performance was estimated using a leave-one-out cross-validation as follows. For the trial that was chosen to be decoded (i.e., test data), the rest of the trials (i.e., training data) were used to estimate the spatial maps f(X,tr). For each time bin of the test trial, the location with maximum decoded probability was compared to the actual position of the animal in that bin, and decoding error in this bin was determined as the linear distance between estimated position and actual position. This procedure was repeated for all trials to be tested.

We identified replay during SWRs based on the Bayesian decoder described above. First, candidate events were defined as the SWR events during which ≥ 5 place cells fired. Each candidate event was then divided into 10-ms non-overlapping bins, and the spatial probability distribution (i.e., posterior probability matrix) was computed based on the Bayes’ rule. The assessment of replay events for significance was implemented as previously described (Karlsson and Frank, 2009). The p-value was calculated based on a Monte Carlo shuffle. First, we drew 10,000 random samples from the posterior probability matrix for each decoded bin and assigned the sampled locations to that bin. Then, we performed a linear regression on the bin number versus the location points. The resulting R-squared was compared with 1,500 regressions, in which the order of the temporal bins was shuffled (i.e., time shuffle) (Foster, 2017; Trimper et al., 2017). A candidate event with p < 0.05 based on the time shuffle was considered as a replay event. Since the shuffling procedure measured how well the decoded positions along SWR time matched a behavioral trajectory, we considered the trajectory with the lowest p-value from the shuffling procedure as the replay trajectory (instead of the one with the highest summed posterior probability) (Tang et al., 2017), and its R-squared (or r) was reported as replay quality. Since there was a bias towards reward locations for place cells and their associated replay events (Figures S4J and S4L), similar to previous reports (Davidson et al., 2009; Dupret et al., 2010; Pfeiffer and Foster, 2013), we excluded the spatial positions within 15 cm of reward wells from the place-field templates to detect replay (all our main results were similar without the 15-cm exclusion) to ensure that this bias did not affect our detection of the replay events representing an animal’s moving path. For plotting purposes only, a moving window (20 ms advanced in steps of 10 ms) was used for displaying replay sequences (Figures 2, 3, S2 and S3) (Farooq and Dragoi, 2019). Only behavioral sessions with more than one replay event per analyzed category were included for calculating the percentage (Figures 3F–3I, Figures 5E and 5F).

Replay prediction

For replay prediction (Figures 3J and 3K, Figures 5G and 5H), trial-by-trial classification analysis was performed using support vector machines (SVMs) through the libsvm library (version 3.12) (Chang and Lin, 2011). During immobility periods at a given reward well (see Behavioral state definition), the number of each replay event type was used as a feature (n = 8 possible features, 4 trajectory types x 2 replay orders, i.e., forward and reverse). Unless otherwise noted, all classifiers were C-SVMs with a radial basis function (Gaussian) kernel and trained on behaviorally correct trials. Hyperparameter (C and γ; regularization weight and radial basis function width, respectively) selection was performed using a random search method with leave-one-out cross-validation to prevent overfitting. The selected hyperparameters were then used to report the leave-one-out cross-validation accuracy. The percentage of correctly inferred trials was computed across all training/test trial combinations to give prediction accuracy. The significance of this prediction was determined by comparing to the distribution of shuffled data. Each “shuffled” dataset was constructed by randomly shuffling the trial labels (see below), and this shuffled dataset was used to train a classifier in the same way as the actual dataset. A prediction accuracy based on the actual dataset that was higher than the shuffled ones with p < 0.05 was considered as significant.

Specifically, to classify well identity (Figures 3J and 3K), two independent SVMs were trained on forward and reverse replay, respectively. For a given replay order (i.e., forward or reverse), the number of each replay event type during immobility at a given well was used as a feature (n = 4 features; 4 trajectory types) and the well ID was used as the trial label (k = 3; center, right and left wells). For this prediction, a trial (or transition) is therefore defined based on the immobility period at the well during a given behavioral sequence. Only transitions where at least one replay event occurred for a given replay order were used. Since incorrect trials mostly occurred during learning of the outbound rule across sessions (Figure S1H) (Jadhav et al., 2012), these incorrect trials were selected to compare the replay predictions of future correct vs. incorrect choices that originated at the center well. During these incorrect trials, the animal was located at the center well after performing a correct past trajectory (inbound; rewarded), but was about to choose the next outbound trajectory incorrectly. Thus, both future correct and incorrect trials were preceded by the presence of reward at the center well. The numbers of the 4 replay event types during immobility at the center well for these incorrect trials were used as input features (n = 4 features) to predict the well IDs (k = 3; center, right and left wells) using the SVMs trained on all correct trials. The percentage of these trials that correctly predicted the center well was reported as prediction accuracy. To calculate statistical significance, correct trials at the center well were randomly subsampled 1,000 times to match the number of incorrect trials for computing prediction accuracy (Figure 3K).

To predict actual taken vs. not-taken paths based on replay (Figures 5G and 5H), independent SVMs were trained for each learning stage (i.e., early, middle and late) and replay order (n = 6 SVMs, 3 learning stages x 2 replay orders) at either center or side wells. Early (sessions 1–3), middle (sessions 4–5), late (sessions 6–8) learning stages were chosen to balance the number of trials per stage (n = 79, 85, and 85 trials for reverse, and n = 87, 95, and 104 trials for forward during early, middle and late stages, respectively). For a given replay order (i.e., forward or reverse), the numbers of events replayed for all 4 possible paths during the immobility period at a given well were used as features (n = 4 features), and the taken behavioral sequence was used as the trial label (k = 2; taken vs. not-taken sequences; see Figure 1B). To investigate the change of replay content during incorrect trials, the replay events during immobility at the center well for the incorrect trials (as described above) were used as input features of the SVMs trained on all correct trials (Figures S6C and S6D). Only trials with at least one replay event in the given replay order were used for prediction.

CA1-PFC population reactivation analysis

In substance, the method to measure CA1-PFC reactivation here is similar to the “template matching” or “reactivation strength” approaches used in several previous studies (Euston et al., 2007; Girardeau et al., 2017; Kudrimoti et al., 1999; Lansink et al., 2009; Peyrache et al., 2009; Tang et al., 2017; Wilber et al., 2017), but operated on a timescale of replay dynamics to examine finer temporal structure of the reactivation activity (i.e., 10 ms instead of 50–100 ms binning in the previous studies). Reactivation candidate events were defined as the SWR events during which ≥ 5 place cells and ≥ 5 PFC cells fired; therefore, they represent a subset of replay candidate events that were defined using only the CA1 place cell criterion. For a candidate event with N CA1 and M PFC cells firing (N ≥ 5, and M ≥ 5), a (N x M) synchronization matrix during RUN (C_RUN) was calculated with each element (C_i,j) representing the Pearson correlation coefficient (C_i,j) of the linearized spatial maps on a certain trajectory type (2-cm bin) of the i-th CA1 cell and the j-th PFC cell. To measure the population synchronization pattern during the SWR, the spike trains during the candidate event were divided into 10-ms bins as in the CA1 replay analysis and z transformed:

$$Q_{i,t}=\frac{S_i\left(t\right)-\overline{S_i\left(t\right)\hspace{0.17em}}}{{\sigma }_{S_i}}$$

where s_i(t) is the spike train of the i-th cell during the candidate event, and $\overline{S_i\left(t\right)\hspace{0.17em}}$ and ${\sigma }_{S_i}$ are the mean and standard deviation of s_i(t), respectively. The (N x M) synchronization matrix during the candidate event (C_SWR) was then calculated with each element (C_i,j) representing the correlation of a CA1-PFC cell pair: $C_{i,j}=Q_i^{CA1}{Q}_j^{PFC}/B$, where i ≤ N, j ≤ M, and B is the total number of time bins during the SWR. The reactivation strength of this event was measured as the correlation coefficient (R) between the population matrices, C_RUN and C_SWR. To evaluate the significance of the reactivation strength, the spike times during the SWR were randomly shuffled 1,500 times, in order to randomize the synchronization between CA1 and PFC cells, but conserve the structure of their spatial maps. A candidate event with p < 0.05 versus its shuffled data was considered as a reactivation event. As in the replay analysis, the reactivated trajectory was determined as the one (among the four possible trajectory types) with the lowest p-value determined by the shuffling procedure. This was used to identify coherent CA1-PFC ensemble reactivation that was aligned with CA1 replay, and a graphical illustration of the method is provided in Figure S8. We used this synchronization measure because a synchronous, rather than sequential, timing relationship of cross-regional reactivation, including CA1-PFC reactivation, was reported in previous studies (Girardeau et al., 2017; Lansink et al., 2009; Tang et al., 2017), and it also allows us to directly compute and examine the combined cross-regional reactivation, rather than detecting reactivation separately in each region and then measuring their correlation.

Model simulations for reactivation analysis

We created a simulated neuronal population as an illustrative example of the reactivation method described above (Figure S8), in comparison to other potential methods. We used model simulations here because while the “true” connectivity of recorded CA1-PFC populations is inaccessible, using the forward-modelling scheme, in which the “ground truth” is known and the neuronal connectivity among the simulated population can be defined, allows for validation of the method for identifying synchronous reactivation. For simplicity, we formulate the model for 5 CA1 and 5 PFC cells. From neurophysiological data, it is known that when an animal moves along a trajectory, CA1 place cells often exhibit narrowly tuned single-peaked place fields, whereas the spatial maps of PFC cells are often broadly tuned and multi-peaked, suggesting a many-to-one mapping between hippocampal and PFC representations (Jadhav et al., 2016; Tang et al., 2017; Yu et al., 2018). Motivated by these response properties, the estimated firing rate (i.e., place field) of each place cell i, r_i (t ), is defined as a Gaussian tuning curve,

$$r_i\left(t\right)=f_i\left(x\left(t\right)\right)=r_{i,\max }\exp \left(-\frac{1}{2}{\left(\frac{x\left(t\right)-x_{i,\max }}{{\sigma }_f}\right)}^2\right)$$

where r_i,max is the maximum firing rate of the i-th cell, x(t ) is the linear position of the animal at time t, x_i,max is the position evoking the maximum average rate r_i,max of the cell, and σ_f determines the width of the tuning curve (σ_f = 5 cm for CA1 cells). The synchronization pattern between CA1 and PFC cells within the population is defined by a many-to-one connectivity matrix. If the activity of the k-th PFC cell is synchronized with that of n CA1 cells (n ≥ 1), the estimated firing rate (i.e., spatial map) of the k-th PFC cell, r_k(t), is determined as,

$$r_k\left(t\right)=\sum _{i=1}^n{w}_{i,k}\exp \left(-\frac{1}{2}{\left(\frac{x_i\left(t\right)-x_{i,\max }}{{\sigma }_f}\right)}^2\right)+c_k$$

where w_i,k is the connectivity weight between the i-th CA1 cell (i = 1, 2, …, n) and the k-th PFC cell, c_k is the baseline firing rate of the k-th PFC cell, and σ_f is 10 cm for PFC cells. Thus, the peak positions of the PFC spatial map were determined by the synchronized CA1 cells as {x_i,max} for i = 1, 2, …, n. We assume that the spiking activity of each neuron follows an inhomogeneous Poisson process. Thus, spike sequences were simulated by using the estimated firing rate r (t ) to drive a Poisson process. The probability of observing N_i,t spikes of the i-th cell in a bin of size τ is given by a Poisson distribution with a rate parameter r_i (t )τ,

$$P\left(N_{i,t}|r_i\left(t\right)\right)=\frac{{\left(r_i\left(t\right)\tau \right)}^{N_{i,t}}}{N_{i,t}!}\exp \left(-r_i\left(t\right)\tau \right).$$

As in the real data, τ is 10 ms for SWR events and 500 ms for active behavior. Note that this Poisson process generates an irregular firing pattern during SWRs that reflects the underlying spatial map. The reactivation method was then applied to the simulated data as described above, and compared to Bayesian decoding (O’Neill et al., 2017) and line-fitting (Ólafsdóttir et al., 2016, 2017) methods.

CA1-PFC activation ratio and pairwise reactivation

For each cell activated during a SWR synchronous event (i.e., candidate event), the average firing rate of the cell during the SWR divided by its average firing rate across the behavioral session was used as its activation ratio. The activation ratio for a SWR synchronous event was then measured as the mean activation ratio across all cells activated during the SWR (Figures S7J–S7N). Pairwise reactivation strength was measured as the correlation coefficient between spatial correlation and SWR cofiring of cell pairs (Figures S7L–S7N), as described previously (Tang et al., 2017). In brief, the spatial correlation of a cell pair was defined as the Pearson’s correlation coefficient between their linearized spatial maps across all 4 trajectory types. SWR cofiring of a cell pair was calculated as the Pearson’s correlation coefficient between their spike trains occurring during SWR events using 50-ms bins.

Statistical analysis

Data analysis was performed using custom routines in Matlab (MathWorks, Natick, MA). We used nonparametric and two-tailed tests for statistical comparisons throughout the paper, unless otherwise noted. We used repeated measures ANOVA for multiple comparisons of paired Gaussian distributions, followed by a Tukey’s test, when appropriate. For non-Gaussian distributions of multiple groups, we used Kruskal-Wallis or Friedman test, with post hoc analysis performed using a Dunn’s test. P < 0.05 was considered the cutoff for statistical significance. Unless otherwise noted, values and errors in the text denote means ± SEM.

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Chemicals
Cresyl Violet	Acros Organics	Cat#: AC229630050
Formaldehyde	Fisher	Cat#: 50-00-0,67561,7732-18-5
Isoflurane	Patterson Veterinary	Cat#: 07-806-3204
Ketamine	Patterson Veterinary	Cat#: 07-803-6637
Xylazine	Patterson Veterinary	Cat#: 07-808-1947
Atropine	Patterson Veterinary	Cat#: 07-869-6061
Bupivacaine	Patterson Veterinary	Cat#: 07-890-4881
Beuthanasia-D	Patterson Veterinary	Cat#: 07-807-3963
Sucrose	Sigma-Aldrich	Cat#: S8501-5KG
Experimental Models: Organisms/Strains
Rat: Long Evans	Charles River	Cat#: Crl:LE 006;RRID:RGD_2308852
Software and Algorithms
MATLAB 2017a	Mathworks, MA	RRID: SCR_001622
Trodes	SpikeGadgets	http://www.spikegadgets.com
Matclust	Mattias P. Karlsson	https://www.mathworks.com/matlabcentral/fileexchange/39663-matclust, V1.7
Libsvm	Chang and Lin 2011	https://www.csie.ntu.edu.tw/~cjlin/libsvm/, V3.12
Chronux	Partha Mitra	http://chronux.org/, V2.12
Prism 8	GraphPad Software	RRID: SCR_002798
Other
128 Channel electrophysiology data acquisition system	SpikeGadgets	http://www.spikegadgets.com
12.7 µm NiCr tetrode wire	Sandvik	Cat#: PX000004

Highlights.

Continuous hippocampal-prefrontal (CA1-PFC) replay tracking during spatial learning

Reverse replay for retrospective evaluation, forward replay for prospective planning

Opposing learning gradients for CA1 reverse and forward replay prediction of paths

CA1-PFC replay supports past recall and future decisions for spatial working memory