Modeling tissue-selective cavitation damage

Abstract

The destructive growth and collapse of cavitation bubbles are used for therapeutic purposes in focused ultrasound procedures and can contribute to tissue damage in traumatic injuries. Histotripsy is a focused ultrasound procedure that relies on controlled cavitation to homogenize soft tissue. Experimental studies of histotripsy cavitation have shown that the extent of ablation in different tissues depends on tissue mechanical properties and waveform parameters. Variable tissue susceptibility to the large stresses, strains, and strain rates developed by cavitation bubbles has been suggested as a basis for localized liver tumor treatments that spare large vessels and bile ducts. However, field quantities developed within microns of cavitation bubbles are too localized and transient to measure in experiments. Previous numerical studies have attempted to circumvent this challenge but made limited use of realistic tissue property data. In this study, numerical simulations are used to calculate stress, strain, and strain rate fields produced by bubble oscillation under histotripsy forcing in a variety of tissues with literature-sourced viscoelastic and acoustic properties. Strain field calculations are then used to predict a theoretical damage radius using tissue ultimate strain data. Simulation results support the hypothesis that differential tissue responses could be used to design tissue-selective treatments. Results agree with studies correlating tissue ultimate fractional strain with resistance to histotripsy ablation and are also consistent with experiments demonstrating smaller lesion size under exposure to higher frequency waveforms. Methods presented in this study provide an approach for modeling tissue-selective cavitation damage in general.

1. Introduction

Cavitation occurs when a sufficient pressure rarefaction causes microscopic nuclei in a fluid or solid to rapidly grow into macroscopic bubbles (Brennen 2014). These bubbles can mechanically damage surrounding material by inducing large stresses, strains, and strain rates in their surroundings as they grow and collapse. Cavitation has been studied extensively for hydrodynamic applications and is known to erode even the hardest steels (Richman et al 1995). Recently, interest has grown in cavitation damage to biological materials including tissue (Mancia et al 2017, Pahk et al 2019) and surgical mesh (Bigelow et al 2019) given its relevance to therapeutic ultrasound and traumatic injuries. Cavitation is a potential source of neuron damage in blast traumatic brain injury (Goeller et al 2012, Estrada et al 2017, Franck 2017), and it has also been proposed as a useful context in which to study tissue damage incurred through high-strain-rate injuries (Estrada et al 2018). Laser surgery (Brujan and Vogel 2006) and therapeutic ultrasound (Brujan 2004) also motivate studies of controlled cavitation damage. In particular, cavitation contributes to kidney stone fractionation in shock wave lithotripsy (Coleman et al 1987), and histotripsy is a noninvasive, nonthermal focused ultrasound procedure that uses targeted groups of microscopic bubbles to homogenize soft tissue into acellular debris. Histotripsy has been investigated as a potential treatment for benign prostate hyperplasia, thrombolysis, and solid tumors (Khokhlova et al 2015).

Cavitation damage mechanisms are challenging to study because stresses and strains developed in surrounding tissue by individual cavitation bubbles are too localized and transient to measure experimentally (Vlaisavljevich et al 2016a, Mancia et al 2017). The opacity of tissues also limits optical access. Computational modeling can circumvent these experimental limitations and quantify stress, strain, and strain rate fields in tissue. Previous studies have modeled deformations produced by single cavitation bubbles in viscoelastic materials under harmonic (Church and Yang 2006) and high intensity focused ultrasound (HIFU) (Pahk et al 2019) forcing. Although HIFU can still involve cavitation as a secondary damage mechanism (Rabkin et al 2005), it is a predominantly thermal therapy. Histotripsy ablation is more dependent on the mechanical effects of inertial cavitation, which occurs when applied tension causes nanoscale nuclei to grow into cavities that subsequently collapse under the inertia of the surrounding medium (Miller et al 1996). Bubble growth subjects tissue to high strain rates and induces large compressive radial stress and strain components in the tissue that are maximized at maximum bubble radius. Bubble collapse is also a high-strain-rate phenomenon and generates large tensile radial stress and strain components in the tissue (Mancia et al 2017). These damage mechanisms are common to cavitation injury in other settings (Estrada et al 2018), making histotripsy a useful model for studying cavitation-induced tissue damage in general. Previous work has considered stresses and strains induced by bubbles under histotripsy forcing (Vlaisavljevich et al 2016a, Mancia et al 2017). These studies calculated the spatiotemporal evolution of stress and strain fields around a single cavitation bubble in a general viscoelastic medium exposed to different forcing conditions. However, consideration of more specific and relevant tissue types is needed to fully explain observations of tissue-selective cavitation damage. Furthermore, recent observations suggest that strain rate plays a unique role in cell injury (Bar-Kochba et al 2016) and thus deserves a more detailed investigation. Prior modeling work has used maximum bubble radius as a cavitation damage metric for histotripsy (Bader and Holland 2016), but correlations between damage extent and physical damage mechanisms have been limited.

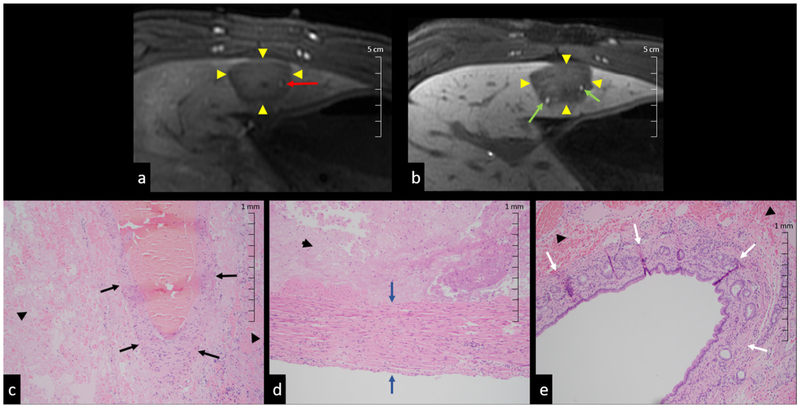
Experimental studies of histotripsy applied to different tissues suggest that differential tissue responses to cavitation can be used to design treatments that are self-limiting and vessel-sparing, preventing damage to critical anatomical structures (Vlaisavljevich et al 2013). Figure 1 shows MRI images and histopathology slides illustrating the preservation of bile ducts and hepatic arteries in treated porcine liver. It was hypothesized that differences in tissue mechanical properties were responsible for these effects, and examination of gross lesions revealed that tissues with higher ultimate stress and ultimate fractional strain were more resistant to histotripsy-generated cavitation. These findings suggest that mechanical stress and strain in particular could play important roles in cavitation damage. There is also evidence that lesion size correlates with waveform amplitude (Lin et al 2014a) and that higher frequency histotripsy waveforms produce smaller lesions (Lin et al 2014b). The objective of this study is therefore to model bubble behavior and proposed damage mechanisms in different tissue types in order to provide an understanding of observed tissue-selective cavitation effects. Tissues in this study are most relevant to a liver tumor ablation application given recent experimental interest (Vlaisavljevich et al 2016b, Smolock et al 2018) and the variety of tissues involved. The methods presented in this study could potentially be applied to estimate cavitation-induced tissue damage for treatment planning and injury diagnostics.

Figure 1.

Histotripsy liver lesions with preserved vessels ((a), (c) and (d)) and bile ducts ((b) and (e)). Results show (a) arterial phase MR image of patent artery (red arrow) in ablation zone (arrow heads), (b) liver-specific contrast MR image with patent bile ducts (green arrows) in ablation zone (arrow heads). H&E slides of (c) portal vein (black arrows), (d) intact artery wall (blue arrows), and (e) bile ducts (white arrows) with adjacent necrosis (arrow heads) in ablation zone.

This study uses a spherical bubble dynamics model with viscoelasticity to quantify mechanical stress, strain, and strain rates produced by single cavitation bubbles exposed to histotripsy forcing at different frequencies in specific tissues whose viscoelastic and acoustic properties are obtained from the literature. First, the theoretical model for bubble dynamics in viscoelastic media which has been applied to experiments in polyacrylamide gels (Estrada et al 2018) is presented. Subsequently, a literature review is provided summarizing data from viscoelastic and acoustic parameter measurements for our tissues of interest. We then discuss the problem setup and numerical methods used to perform the simulations. Equations for mechanical stress, strain, and strain rate fields in tissue are provided. Results are presented showing radial dynamics and field quantities for each tissue at three relevant waveform frequencies (0.5 MHz, 1 MHz, and 3 MHz). Calculated strain fields are then compared to ultimate fractional (tensile) strain measurements to estimate damage radii in tissues of interest.

2. Methods

2.1. Theoretical model

Simulations model a single, spherical, homobaric bubble in a homogenous viscoelastic medium exposed to a histotripsy waveform. Previous computational studies of histotripsy cavitation have used a similar model to study bubble dynamics in water (Vlaisavljevich et al 2016c) and agarose tissue phantoms (Vlaisavljevich et al 2014, 2015a, Vlaisavljevich et al 2016a, Mancia et al 2017, Wilson et al 2019). Table 1 lists viscoelastic and acoustic properties of each model tissue, and table 2 gives the constant initial conditions and thermodynamic properties used in all simulations. Radial bubble dynamics are described by the Keller–Miksis equation (Keller and Miksis 1980):

$$\left(1-\frac{\dot{R}}{c_{\infty }}\right)R\ddot{R}+\frac{3}{2}\left(1-\frac{\dot{R}}{3c_{\infty }}\right){\dot{R}}^2=\frac{1}{{\rho }_{\infty }}\left(1+\frac{\dot{R}}{c_{\infty }}+\frac{R}{c_{\infty }}\frac{d}{dt}\right)\times \left[p_B-\left(p_{\infty }+p_f(t)\right)-\frac{2S}{R}+J\right],$$ (1)

where R is the bubble radius, and c_∞ and ρ_∞ are the constant sound speed and density of each tissue (table 1). The pressure of air inside the bubble is p_B, and pressure in the surrounding tissue is the sum of the ambient pressure, p_∞, and the acoustic forcing pressure, p_f(t). The variables S and J are the tissue surface tension and integral of the deviatoric stresses, respectively. Although the chosen Keller–Miksis model risks under-predicting the minimum bubble radius and maximum wall velocity at bubble collapse (Prosperetti and Lezzi 1986), precise dynamics at bubble collapse are beyond the scope of the present study. Histotripsy bubbles undergo more complex behavior at collapse, including breakup into smaller bubbles (Duryea et al 2015), so this work primarily concerns bubble dynamics until the point of collapse. Due to a lack of surface tension data for various tissues, surface tension is assumed equal to that of water at 25°C for all simulations: S = 0.072 N m⁻¹. This is a reasonable assumption given the high water content of tissues considered in this study and the limited effect surface tension is expected to have on the bubble dynamics.

Table 1.

Tissue viscoelastic and acoustic properties, taken from the literature.

Tissue	Shear modulus (kPa)	Density (kg m−3)	Sound speed (m s−1)	UTS (MPa)	Ultimate true strain
Liver	1.8 ± 0.4	1060	1577 ± 11	0.27	0.38
HCC	23.4	1060	1555 ± 15	—	—
Diseased liver	19.8	1060	1559 ± 4	—	—
Hepatic artery	210 ± 47	1050	1616 ± 25	1.4	0.63
Gallbladder	85 ± 8.2	1060	1584	2.5	0.43 ± 0.3
Bile duct	166 ± 67	1060	1600	—	—
Stomach	0.637	1058	1619.4 ± 21	0.43	0.66

Tissue viscosity is assumed to be 0.01 Pa s, and all viscoelastic properties were measured under quasistatic conditions for all tissues. Additional assumptions discussed in section 2.2. References: general (Duck 2013); liver, HCC, and diseased liver (Bamber and Hill 1981, Palmeri et al 2008, Webb et al 2011, Honjo et al 2014); hepatic artery (Deng et al 1994, Holzapfel et al 2005); gallbladder (Karimi et al 2017); bile duct (Duch et al 2004); stomach (Saijo et al 1991, Lim et al 2009).

Table 2.

Parameters fixed for all simulations.

Parameter	Value
R0	5 nm
pA	30 MPa
n	3.7
δ	5 s
p∞	101.325 kPa
T∞	25°C
κ	1.4
KA	5.28 × 10−5 W mK−2
KB	1.165 × 10−2 W mK−1

Tissue is modeled using a finite deformation Kelvin–Voigt constitutive equation (Gaudron et al 2015), resulting in the following integral of the deviatoric contribution of the stresses in the surrounding medium:

$$J=-\frac{4\mu \dot{R}}{R}-\frac{G}{2}\left[5-4\left(\frac{R_0}{R}\right)-{\left(\frac{R_0}{R}\right)}^4\right],$$ (2)

where R₀, the bubble radius in stress-free surroundings, is equal to the initial bubble radius. As in previous studies (Vlaisavljevich et al 2014, 2015a, 2016a, 2016c, Mancia et al 2017), all simulations are initialized with R₀ = 5 nm. This assumption is in accordance with previous experimental studies that inferred nuclei sizes in the range of nanometers (Maxwell et al 2013); however, it can have significant consequences for subsequent field calculations which are discussed further in section 4.2. All simulations also use a fixed tissue viscosity, μ = 0.01 Pa · s, given the lack of tissue viscosity data at relevant frequencies and the dependence of viscosity measurements on the assumed viscoelastic constitutive equation. This viscosity value for liver has also been used previously in cavitation modeling (Webb et al 2011) and was justified by expected shear-thinning behavior of tissue. Tissue shear modulus, G is selected for each tissue (table 1) according to reference values from the literature. Tissue acoustic parameters are also literature-sourced and are discussed further in section 2.2.

Changes in internal bubble temperature are considered following the approaches described in Prosperetti et al (1988), Kamath et al (1993) and Warnez and Johnsen (2015). Previous authors (Barajas and Johnsen 2017, Estrada et al 2018) have also considered mass transfer effects, but in this study the tissue-bubble boundary is assumed to be impervious to gas, and vapor inside the bubble is neglected. Although these simplifications could underpredict the lifespan of the bubble and distort subsequent rebounds (Bader 2018), such effects are likely negligible in the single collapse case considered here. The mass boundary layer thickness is also expected to be small relative to the bubble radius during expansion, so mass transfer effects can be safely neglected during bubble growth (Barajas and Johnsen 2017, Mancia et al 2017).

The energy equation for air inside the bubble is coupled to the Keller–Miksis equation (equation (1)) by the internal bubble pressure, p_B(t):

$${\dot{p}}_B=\frac{3}{R}\left((\kappa -1)K\frac{\partial T}{\partial r}{|}_R-\kappa p_B\dot{R}\right)$$ (3)

$$\frac{\kappa }{\kappa -1}\frac{p_B}{T}\left[\frac{\partial T}{\partial t}+\frac{1}{\kappa p_B}\left((\kappa -1)K\frac{\partial T}{\partial r}-\frac{r{\dot{p}}_B}{3}\right)\frac{\partial T}{\partial r}\right]={\dot{p}}_B+\frac{1}{r^2}\frac{\partial }{\partial r}\left(r^{2}K\frac{\partial T}{\partial r}\right),$$ (4)

where T(r, t) is the temperature field of air inside the bubble, which has a ratio of specific heats κ, and its thermal conductivity is given by K = K_AT + K_B, where constants K_A and K_B were determined empirically for air (Prosperetti et al 1988). The initial pressure inside the bubble is p_B(0) = p_∞ + 2S/R. A boundary condition is prescribed for the center of the bubble: ∇T = 0 at r = 0. Following (Prosperetti 1991, Estrada et al 2018), the bubble wall boundary condition is simplified to T(R) = T_∞ under the assumption that the surrounding tissue remains at its constant ambient temperature through this single cycle of growth and collapse.

The far-field pressure equals the sum of the ambient pressure in surrounding tissue, p_∞, and the time-varying histotripsy pulse, p_f(t):

$$p_f(t)=\{\begin{array}{ll}{p}_A{\left(\frac{1+\text{cos}[\omega (t-\delta )]}{2}\right)}^n,\hfill & |t-\delta |⩽\frac{\pi }{\omega },\hfill \\ 0,\hfill & |t-\delta |>\frac{\pi }{\omega }.\hfill \end{array}$$ (5)

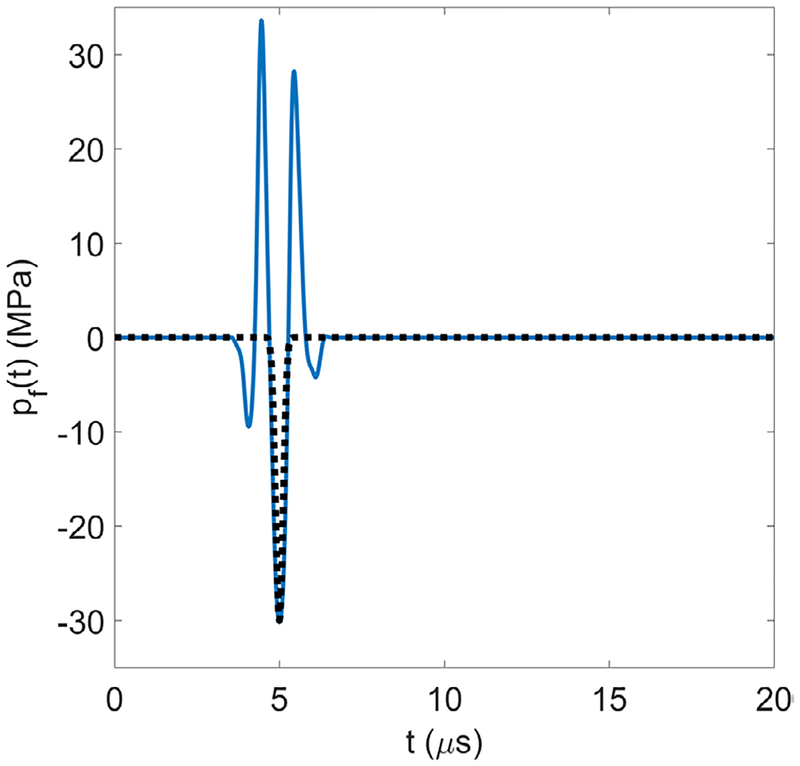
The ‘frequency’, f of this half-cycle pulse (ω = 2πf) is varied between 0.5–3 MHz. In particular, the frequencies 0.5, 1, and 3 MHz have been chosen to encompass the frequency range in use for the widest variety of potential clinical applications (Vlaisavljevich et al 2015a, 2015b, Lin et al 2014b). The peak tensile pressure, p_A = −30 MPa, time delay, δ = 5 μs, and fitting parameter, n = 3.7, are chosen to be representative of an experimental histotripsy pulse (Vlaisavljevich et al 2014, 2015a, 2016a, 2016c, Mancia et al 2017) and are constant for all simulations (table 2). Figure 2 shows the 1 MHz analytic waveform (black dotted trace) over a representative experimental waveform of the same frequency (solid blue trace). Although the analytic waveform is a simplification, its use is supported by previous work showing that bubbles produced via intrinsic threshold histotripsy are generated directly from the negative pressure of the incident waveform and are not dependent on the positive portion of the waveform (Maxwell et al 2013, Lin et al 2014a).

Figure 2.

Analytic waveform (black dotted trace) over a representative experimental waveform (solid blue trace); both have a frequency of 1 MHz.

2.2. Viscoelastic and acoustic parameters

Viscoelastic and acoustic properties representative of healthy liver, hepatocellular carcinoma (HCC), diseased liver, hepatic artery, gallbladder, bile duct and stomach are given in table 1. In the table, ‘HCC’ refers to samples that consist entirely of tumor while ‘diseased liver’ includes only liver tissue adjacent to tumors. Given the lack of tissue viscosity data in the MHz frequency range, viscosity is taken to be 0.01 Pa s for all tissues. This value is near Webb et al’s estimate for liver at 1 MHz (Webb et al 2011) and accounts for expected shear-thinning behavior of soft tissues at this frequency (Madsen et al 1983, Yang and Church 2006). All viscoelastic properties were measured under quasistatic conditions.

The shear modulus of healthy liver is taken to be 1.8 kPa, corresponding to a mean in vivo measurement of a healthy human volunteer based on acoustic radiation force (Palmeri et al 2008). Shear moduli for HCC and diseased liver are taken to be the mean of their respective shear wave elastography measurements made in liver tumor patients with chronic liver disease due to NASH (one sample), alcohol (four samples), and HBV (two samples) (Honjo et al 2014). Hepatic artery shear modulus is the lower bound of the right coronary artery shear modulus measured by Deng et al (1994) given the similar luminal diameters of hepatic and coronary arteries (Holzapfel et al 2005, Silveira et al 2009). Assuming all tissues are incompressible (Poisson’s ratio, ν = 0.5), the shear moduli of gallbladder, bile duct, and stomach are taken to be 1/3 the value of their measured Young’s moduli. A gallbladder shear modulus of 85 ± 8.2 kPa is used, which was measured in the transverse direction (Karimi et al 2017). A bile duct shear modulus of approximately 166 ± 67 kPa is obtained from the average of 10 porcine bile ducts measured under circumferential (cross-sectional) strain (Duch et al 2004). The mean shear modulus of stomach obtained from measurements under different indentation depths is estimated to be 0.637 kPa (Lim et al 2009).

The density of liver and stomach tissues were found in Duck (2013). The density of hepatic artery is taken to be the lower bound of a mixed sample of arteries from the same reference. Tissue density data was not available for gallbladder, bile duct, diseased liver, and HCC, so these were taken to have the same density as liver (1060 kg m⁻³). The sound speed in liver, HCC, and diseased liver are taken to be the mean values given for 15 healthy liver specimens, seven liver tumor samples, and four liver specimens with tumor present (Bamber and Hill 1981). Sound speed in hepatic artery is assumed equal to the mean of whole healthy artery (including intima, media, and adventitia) given in Duck (2013) and used as a reference value in studies of diseased arteries (Hoskins 2007). No sound speed data was available for bile duct, so simulations use a velocity that is intermediate between that of hepatic artery and gallbaldder: 1600 m s⁻¹. Sound speed of stomach was taken to be the value measured for ‘normal mucosa’ (Saijo et al 1991).

Ultimate tensile strength (UTS) is defined as the tensile stress needed to produce rupture of a gross tissue sample. The UTS values for human liver, gallbladder, and stomach are given in Duck (2013). A specific UTS for hepatic artery was not found in the literature, so the mean UTS for a mixed sample of arteries subjected to tension in the transverse (cross-sectional) orientation is used: 1.4 MPa. This value is close to the UTS of coronary artery adventitia given by Holzapfel et al (2005): 1.43 MPa. Ultimate (tensile) strain values for liver, a mixed sample of arteries, gallbladder, and stomach were obtained from Yamada et al (1970). These values were measured with respect to the original length of the specimens and are thus engineering strains. Before inclusion in table 1, these engineering strains, e, are converted to equivalent true strains, ϵ, using the expression: ϵ = ln(1 + e).

2.3. Problem setup

The equations are nondimensionalized (Barajas and Johnsen 2017) using the initial bubble radius, R₀, atmospheric pressure, p_∞, tissue density, ρ_∞, and far-field temperature, T_∞ to define a characteristic velocity, $U_c=\sqrt{p_{\infty }/{\rho }_{\infty }}$ and dimensionless parameters: Reynolds number, Re = ρ_∞U_cR₀/μ, Cauchy number, Ca = p_∞/G, Weber number, We = p_∞R₀/2S, dimensionless sound speed, C = c_∞/U_c, and χ = T_∞K(T_∞)/p_∞R₀U_c. A variable-step, variable-order solver based on numerical differentiation formulas (MATLAB ode15s) is used for numerical time marching (Shampine and Reichelt 1997, Shampine et al 1999). Equations are integrated over a dimensional time span of t = [0, 100] in microseconds. The maximum step size is 1.0 μs. Using numerical methods described by Barajas and Johnsen (2017) and Estrada et al (2018), the PDE is spatially discretized on a mesh of N_s + 1 points in r-space (Prosperetti et al 1988) inside the bubble and solved via second-order central differences. Simulations use N_s = 30 points inside the bubble, for which results are sufficiently converged. Each stress and strain trace contains 10 000 points.

2.4. Stress and strain fields

A Kelvin–Voigt-based Neo–Hookean constitutive model relates the deviatoric stress, τ, and strain, E, tensors in the surrounding tissue whose coordinates span r ∈ [R, L], where R is the time-dependent bubble radius and L ≫ R is the arbitrary size of the domain. The radial and hoop stresses at any field coordinate r in the surroundings are given by,

$${\tau }_{rr}=-4\mu \frac{R^2\dot{R}}{r^3}+\frac{2G}{3}\left[{\left(\frac{r_0}{r}\right)}^4-{\left(\frac{r}{r_0}\right)}^2\right]=-2{\tau }_{\theta \theta },$$ (6)

which is derived from finite deformation theory (Gaudron et al 2015). In equation (6), the original and current radial coordinates are related by:

$$r_0(r,t)=\sqrt[3]{r^3-R^3+R_0^3}.$$ (7)

This model has been used to represent the significant nanometer-to-micron-scale growth that occurs in histotripsy (Mancia et al 2017) and was applied to laser-induced cavitation experiments in polyacrylamide gels (Estrada et al 2018). Applicability of the Neo-Hookean model can be challenged given these extremely large deformations; however, it remains superior to commonly used models assuming infinitesimal deformations. Furthermore, results obtained with a Neo-Hookean constitutive model for single, attached murine myoblasts achieved excellent agreement with measured force-deformation curves (Peeters et al 2005). The cells in that study were also modeled as homogeneous and isotropic incompressible elastic solids.

Strain fields in the surrounding tissue are computed using the Hencky (or true) strain definition used previously in models of histotripsy (Mancia et al 2017) and laser-induced (Estrada et al 2017) cavitation:

$$E_{rr}=-2\text{\hspace{0.17em}ln\hspace{0.17em}}\left(\frac{r}{r_0}\right)=-2E_{\theta \theta }.$$ (8)

It is expected that tissue will behave differently under tension and compression; however, the distinct damage consequences of either mode of deformation require further experimental study. For example, despite observations of tensile stress wave emission at optical breakdown in laser cavitation and the known greater susceptibility of cells to damage under tension versus compression (Brujan and Vogel 2006), experiments to date have been unable to separate the damage effects due to an emitted stress wave from those due to bubble expansion (Cherian and Rau 2008). Given these uncertainties and our present interest in general tissue failure, radial and hoop stresses and strains are converted into their von Mises equivalent invariants as in von Mises (1913) and Estrada (2017):

$$\overline{\tau }=\sqrt{\frac{3}{2}{\tau }_{ij}{\tau }_{ij}}=\sqrt{\frac{3}{2}\left[{\tau }_{rr}^2+2{\left(-\frac{1}{2}{\tau }_{rr}\right)}^2\right]}=\frac{3}{2}\left|{\tau }_{rr}\right|,$$ (9)

$$\overline{E}=\sqrt{\frac{2}{3}{E}_{ij}{E}_{ij}}=\sqrt{\frac{2}{3}\left[E_{rr}^2+2{\left(-\frac{1}{2}{E}_{rr}\right)}^2\right]}=\left|E_{rr}\right|.$$ (10)

3. Results

3.1. Radial dynamics

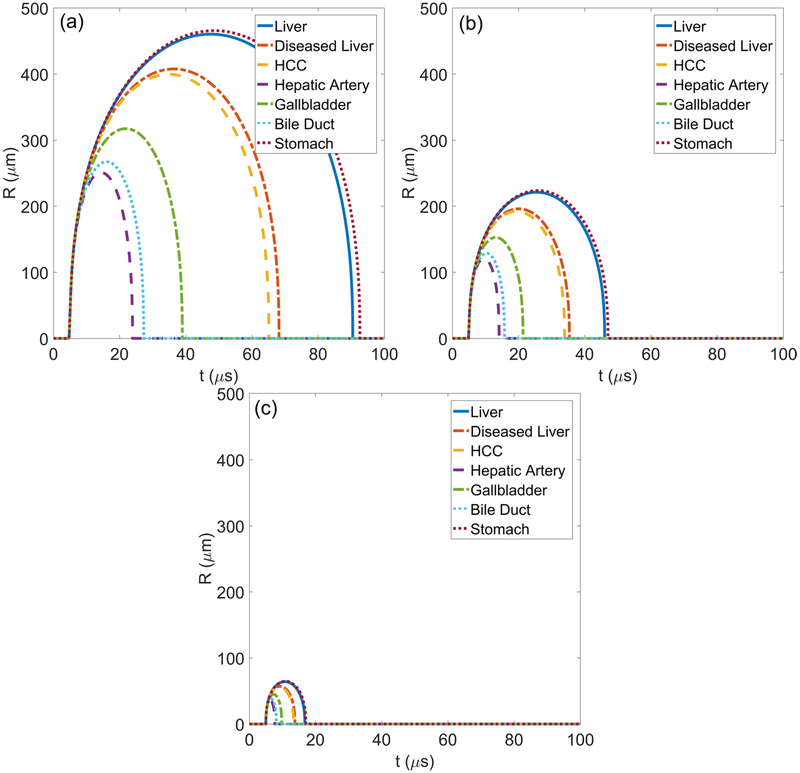
Radial dynamics for each tissue are modeled at waveform frequencies of 0.5 MHz, 1 MHz, and 3 MHz as shown in figure 3. The bubbles grow and collapse with no visible rebounds, as expected from experiments in tissue-mimicking gels (Wilson et al 2019). Bubble growth is restricted in tissues with the highest shear moduli. In particular, the smallest maximum radius is achieved in stiff hepatic artery and the largest maximum radii occur in liver and stomach. There is also notable similarity in the radius versus time behavior for tissues that have similar shear moduli such as diseased liver and HCC tumor. Bubble growth in all tissues is responsive to waveform frequency with smaller bubble growth observed in all tissues exposed to higher frequency waveforms.

Figure 3.

Simulated radius as a function of time traces for (a) 0.5 MHz, (b) 1 MHz, and (c) 3 MHz waveforms in tissues with properties given in table 1.

3.2. Stress fields

Stress fields are calculated using equations (6) and (9) with the constant parameters given in tables 1 and 2. To determine the loads experienced by cells in the vicinity of the bubble, stresses with respect to starting distance from the bubble center are determined by following a (Lagrangian) particle starting at some initial distance from the bubble nucleus in the undeformed tissue. The particle then moves with the tissue as the tissue is deformed by the bubble. Stresses experienced by the particle can be calculated for different starting distances, r₀, from the center of the nucleus, starting at the nucleus wall (r₀ = R₀).

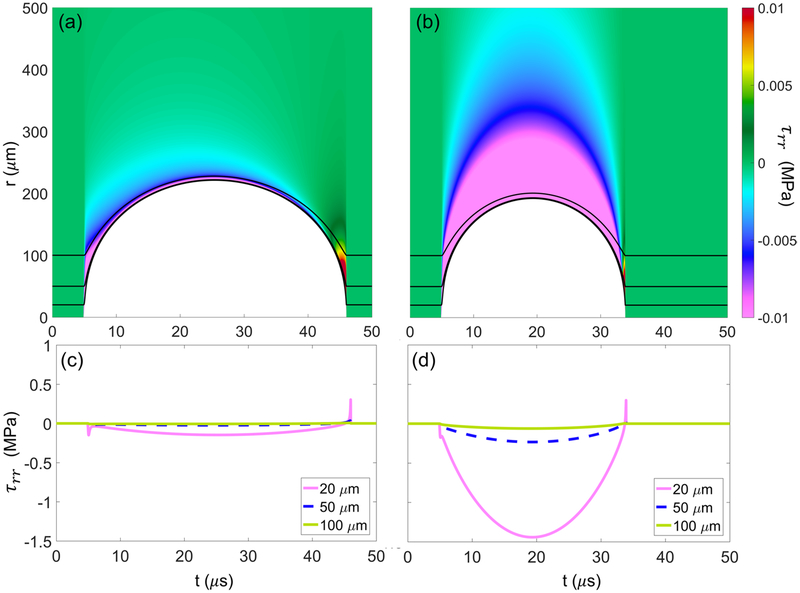
Figure 4 shows the total deviatoric radial stress (equation (6)) developed in (a) liver and (b) HCC tumor exposed to a 1 MHz waveform as each tissue is deformed by a bubble (shown in white). Black lines correspond to Lagrangian paths for particles starting at 20, 50, and 100 μm from the bubble nucleus. Total stress is quantified along each Lagrangian trajectory as a function of time below each respective tissue in (c) and (d), showing larger stress magnitudes in the higher shear modulus tissue (HCC) at all starting distances. Radial stresses are seen to be predominantly compressive (negative) during bubble growth and early collapse with a brief, localized maximum in tensile (positive) stress when the bubble reaches its minimum radius.

Figure 4.

Total deviatoric radial stress fields developed in liver (a) and HCC (b) exposed to 1 MHz waveform. White region corresponds to tissue deformation with respect to distance from the bubble nucleus as a function of time. Black lines correspond to Lagrangian paths taken by particles starting 20, 50, and 100 μm from the bubble nucleus. Plots (c) and (d) show the numerical magnitudes of total stress along the Lagrangian paths shown in (a) and (b), respectively.

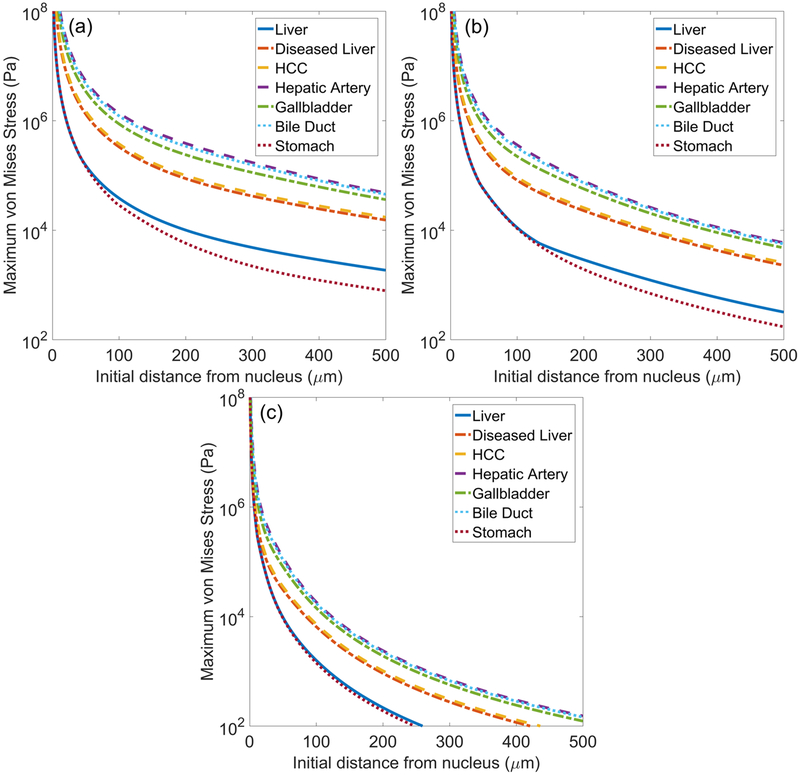
Figure 5 shows traces of maximum von Mises stress (equation (9)) in each tissue as a function of initial distance from the bubble nucleus (r₀) under waveform frequencies of (a) 0.5, (b) 1, and (c) 3 MHz. The ultimate tensile strength (UTS) values of liver, stomach, hepatic artery, and gallbladder are given in table 1. Under all forcing conditions, stresses in these tissues attenuate below the UTS within 100 microns from the bubble wall. Distances before attenuation below UTS are greatest for hepatic artery and gallbladder while attenuation below UTS occurs closest to the bubble wall for liver and stomach.

Figure 5.

Maximum von Mises stress surrounding bubble as a function of initial distance from the bubble nucleus for different tissues exposed to (a) 0.5 MHz, (b) 1 MHz, and (c) 3 MHz waveforms.

Stress is higher at all distances from the bubble in tissues with higher shear moduli such as hepatic artery and bile duct. In tissues with lower shear moduli (e.g. stomach and liver), stresses are consistently smaller. Additionally, stress traces for these low shear moduli cases exhibit an abrupt change in slope or discontinuous second derivative that is most prominent in figure 5(b). These points correspond to the distance at which the viscous stress component in equation (6) first exceeds the elastic component. This ‘elastic-to-viscous’ transition point is dependent on the relative magnitudes of viscosity and shear modulus. It can be predicted for a range of tissue and waveform parameters (Mancia et al 2017). A transition from dynamics dominated by tissue elasticity to more prominent viscous effects farther from the bubble has also been noted to occur in laser cavitation (Estrada et al 2018). Stresses attenuate more rapidly in the high forcing frequency cases, reflecting the significantly smaller bubble growth in these cases.

3.3. Strain fields

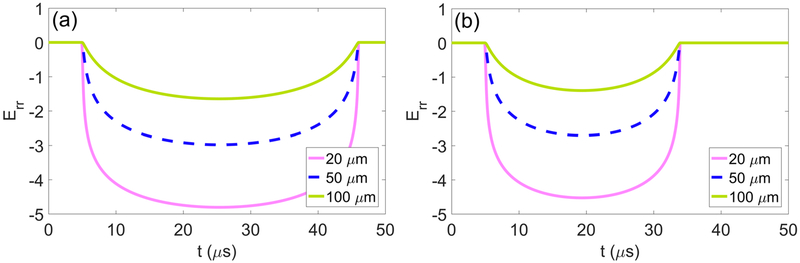
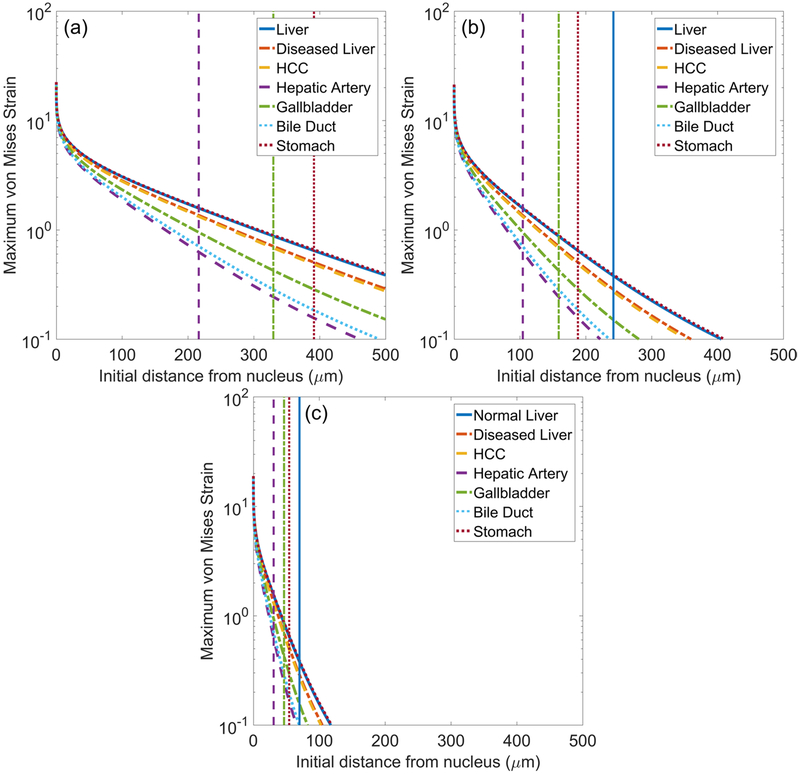
Strain fields are calculated using equations (8) and (10). As with stresses, strains are determined with respect to starting distance from the bubble nucleus in the undeformed tissue using a Lagrangian framework. Figure 6 quantifies total radial strain along Lagrangian trajectories starting 20, 50, and 100 μm from the nucleus as a function of time for (a) liver and (b) HCC. Radial strains are compressive and maximized at maximum bubble radius at all distances. Maximum von Mises strain as a function of initial distance from the bubble nucleus is shown in figure 7 for each tissue under waveform frequencies of (a) 0.5, (b) 1, and (c) 3 MHz. Vertical lines correspond to the distance at which the strain first attenuates below the ultimate fractional (tensile) strain of liver, stomach, hepatic artery, and gallbladder (ultimate strain values are given in table 1). At each forcing frequency, distances for which strain is larger than its ultimate value are greatest for liver and stomach while attenuation below ultimate strain occurs closest to the bubble for hepatic artery and gallbladder. A comparison of the distance to attenuation below ultimate strain and the maximum bubble radius achieved in each case is presented in table 3. Von Mises strain is highest at all starting distances in low shear moduli tissues such as liver and stomach. In contrast, tissues with higher shear moduli such as hepatic artery and bile duct experience smaller deformations. Strains also attenuate more rapidly in all tissues as waveform frequency increases. The extremely high strains observed near the bubble wall are discussed further in section 4.2.

Figure 6.

Total radial strain along the Lagrangian paths starting 20, 50, and 100 μm from the bubble nucleus in (a) liver and (b) HCC exposed to a 1 MHz waveform.

Figure 7.

Maximum von Mises strain surrounding bubble as a function of initial distance from the bubble nucleus for different tissues exposed to (a) 0.5 MHz, (b) 1 MHz, and (c) 3 MHz waveforms. Vertical lines indicate the distance at which strain first attenuates below the ultimate true strain of liver, hepatic artery, gallbladder, and stomach.

Table 3.

Strain-related damage extent, x_D and maximum radii, R_max in microns for different waveform frequencies.

	0.5 MHz		1 MHz		3 MHz
Tissue	xD	Rmax	xD	Rmax	xD	Rmax
Liver	503	460	242	221	70.0	64.0
Stomach	391	466	188	224	54.3	64.7
Gallbladder	330	317	159	153	46.6	44.8
Hepatic artery	216	251	104	121	30.8	35.7

3.4. Strain rate fields

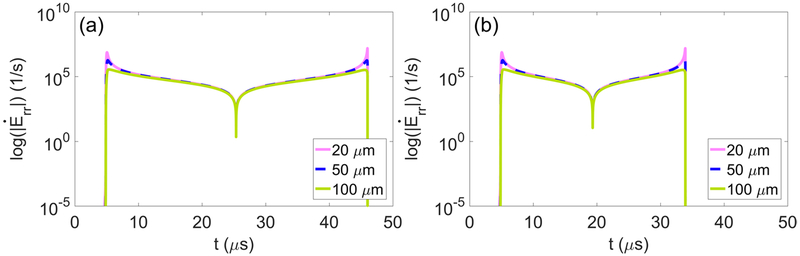
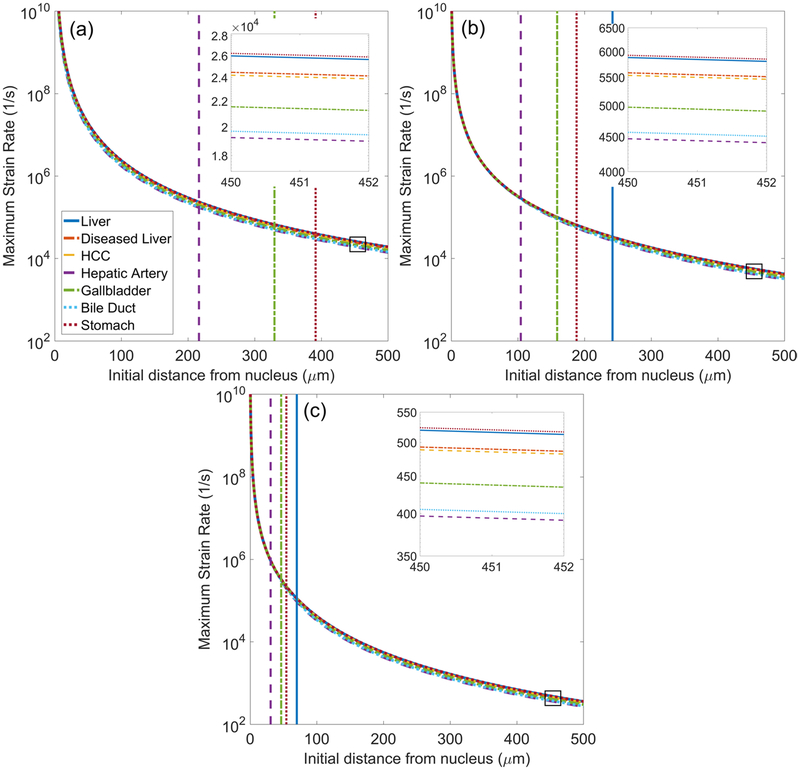
Radial strain rate fields and von Mises strain rate fields are calculated from the time derivatives of equations (8) and (10), respectively. Maximum strain rates are determined with respect to starting distance from the bubble nucleus and are plotted for each tissue. Figure 8 shows radial strain rate histories along Lagrangian trajectories starting 20, 50, and 100 μm from the nucleus as a function of time for (a) liver and (b) HCC. Strain rates are spatially localized to the bubble wall with nearly symmetric local maxima at the onset of bubble growth and at collapse to minimum radius (Mancia et al 2017). The largest strain rates occur at the onset of bubble growth and when the bubble reaches its minimum radius. Figure 9 shows traces of maximum strain rates for waveform frequencies of (a) 0.5, (b) 1, and (c) 3 MHz. Given the similar magnitude of strain rates in different tissues, inset figures showing maximum strain rate magnitude at starting distances of 450–455 μm from the nucleus (boxed region of traces) are included. Vertical lines indicating the point of strain attenuation below ultimate true strain of select tissues are reproduced from figure 7.

Figure 8.

Total radial strain rate along the Lagrangian paths starting 20, 50, and 100 μm from the bubble nucleus in (a) liver and (b) HCC exposed to a 1 MHz waveform.

Figure 9.

Maximum von Mises strain rate surrounding bubble as a function of initial distance from the bubble nucleus for different tissues exposed to (a) 0.5 MHz, (b) 1 MHz, and (c) 3 MHz waveforms. Inset figures show enlargement of strain rate traces in the boxed region. Vertical lines indicate the distance at which strain first attenuates below the ultimate true strain of liver, hepatic artery, gallbladder, and stomach.

Of note, strain rates achieve extremely high values near the bubble wall. This is a consequence of taking the equilibrium bubble radius to be on the order of nanometers. The chosen nucleus size is based on present knowledge of nucleation in water and can be refined with future experiments to obtain more accurate estimates of strain rate within microns from the bubble wall. For an arbitrary nucleus size, strain rates approach a decay proportional to r⁻³. The specific rates of attenuation in each tissue are proportional to the extent of deformation, and the separation between traces in the inset figures parallels variations in maximum radius. As waveform frequency increases, strain-rate magnitude decreases. As shown in the inset figures, strain rates are approximately an order of magnitude lower for each incremental increase in forcing frequency.

4. Discussion

Observed differences in histotripsy ablation of tissues with different mechanical properties (Vlaisavljevich et al 2014, 2015a, 2016a, 2016c) prompted the hypothesis that mechanical stress, strain, and strain rate are predominant mechanisms of cavitation-induced tissue damage. Although histotripsy treatments involve bubble clouds, a thorough understanding of single-bubble damage will ultimately be needed to guide the development of bubble cloud damage models. This study aims to identify how mechanical cavitation damage mechanisms depend on tissue properties in the context of a histotripsy liver ablation application. First, a summary of results for each hypothesized damage mechanism considered in this study is provided. We then use strain data and ultimate strain measurements to predict the spatial extent of mechanical cavitation damage.

4.1. Mechanical damage mechanisms

Given the uncertain consequences of radial versus hoop components of stress and strain, their scalar von Mises equivalents permit comparisons with measured ultimate strain and stress values. Stress is smaller at all distances from the bubble wall in tissues with lower shear moduli and in all tissues exposed to higher frequency waveforms. The rate of stress attenuation is also greater in these cases. The increased rate of stress attenuation at high waveform frequency is likely explained by reduced bubble growth. However, at a given forcing frequency, stress attenuates more rapidly in low-shear-modulus tissues despite larger bubble growth. This is a consequence of differences in shear modulus, which is two orders of magnitude smaller in liver than in hepatic artery. From the UTS data in table 1, it is expected that stresses capable of gross tissue rupture are localized to within 100 microns from the bubble wall at all forcing frequencies. This suggests that stress-induced effects could be localized to a single cell. Studies of laser cavitation in an elastic medium have also noted that stress effects are typically confined to the cellular and subcellular level (Brujan and Vogel 2006).

Maximum strain is largest at maximum bubble radius when the tissue is maximally deformed. Consequently, strain is highest at all starting distances in tissues in which bubbles achieve larger maximum radii. Strain also decreases more rapidly as waveform frequency increases, again as a consequence of the smaller maximum radii reached as frequency is increased. The close relationship of strain to maximum bubble radius makes it an attractive quantity for potential damage extent predictions. For example, observations of single bubbles in the periphery of a bubble cloud have noted that damage appears proportional to maximum bubble diameter (Vlaisavljevich et al 2016a). Furthermore, studies of cavitation damage to neurons found that cell fragmentation correlates with maximum bubble radius (Estrada et al 2017). At present, strain is also a more experimentally accessible quantity than either stress or strain rate. For these reasons, this study compares calculated strain to literature-sourced ultimate strain measurements to estimate the single-bubble damage extent in different tissues.

Studies of neurons under compression found that strain magnitude was related to time to cell death while strain rate affected injury morphology and the extent of cell death across a population (Bar-Kochba et al 2016). Thus, strain rates in addition to strain are considered given the potential for distinct contributions to tissue damage. In contrast to stresses and strains, strain rates attain large magnitudes that remain large (~10³ 1/s) even 500 μm away from the bubble wall. This is consistent with previous theoretical and experimental studies suggesting that the effects of viscosity and strain rate tend to dominate farther from the bubble (Mancia et al 2017, Estrada et al 2018). Strain rate magnitude parallels bubble expansion, a consequence of the nearly symmetric phases of bubble growth and collapse in all tissues and at all forcing frequencies considered in the present study. Asymmetry of growth and collapse phases that could give rise to significant differences in strain rate behavior has been noted in tissues with wider variation in viscosity (Mancia et al 2017). That study also found that strain rate, while typically more significant farther from the bubble, dominated tissue response closer to the bubble wall in tissues with larger viscosity to shear modulus ratios. In the present study, low-shear-modulus tissues (i.e. those with a larger viscosity to shear modulus ratio) exhibit the highest strain rates at all forcing frequencies. Minimal distinction between strain rate traces in different tissues suggests strain rate is not a significant mechanism for tissue-selective effects; however, this could change if needed viscosity measurements are obtained for these tissues.

4.2. Extent of damaged region

Measurements of ultimate true strain are used for comparisons of the approximate extent of the damaged region, x_D, in different tissues. We define the ‘damaged region’ as the spatial region extending from the bubble nucleus to where strains first attenuate below the ultimate true strain of a given tissue. Table 3 shows the damage radius in each tissue for a given forcing condition alongside the associated maximum bubble radius obtained from simulations. As tissue shear modulus increases, there is a decrease in damage radius at all frequencies. This general trend agrees with experimental observations (Cherian and Rau 2008, Vlaisavljevich et al 2013) and suggests mechanical strain plays a key role in tissue-selective effects, particularly given the significant difference in damage radii between liver and hepatic artery (Vlaisavljevich et al 2013). Damage radii shift to proportionally lower values as waveform frequency increases from 0.5 to 3 MHz, a finding consistent with experimental observations of smaller lesion size at higher waveform frequencies (Lin et al 2014b).

Table 3 also includes the maximum bubble radii achieved in each simulation. As expected, high-shear-modulus tissues exhibit stronger resistance to deformation and have reduced maximum bubble radii. Reduced bubble growth is also seen at higher frequencies due to decreased exposure to the driving tensile pulse. The predicted damage radius is smaller than the maximum bubble radius in stomach and hepatic artery under all forcing conditions. This behavior is consistent with trends seen in laser-induced cavitation damage to rat corneas (Cherian and Rau 2008). Liver tissue and, to a smaller degree, gallbladder have damage radii that are slightly larger than maximum radius at all frequencies. This behavior is a consequence of the lower ultimate strains of these tissues. In general, the proportional relationship between predicted damage radius and maximum bubble radius supports the proposed use of maximum bubble radius as a damage metric for histotripsy (Bader and Holland 2016, Mancia et al 2017). Correlations between maximum bubble radius and damage extent have also been observed experimentally in histotripsy (Vlaisavljevich et al 2016a) and laser-induced cavitation in hydrogels (Estrada et al 2017). In general, predictions of damage radii that are comparable to the maximum bubble radius are supported by observations of highly localized cavitation damage and the sharply demarcated boundaries of histotripsy lesions (Parsons et al 2006, Vlaisavljevich et al 2016a).

The proportional relationship between damage radius and maximum bubble radius can be shown to depend on the ultimate true strain of a given tissue. The Keller–Miksis equation (equation (1)) includes only first-order compressibility effects, so tissues in this study are nearly incompressible. It follows that strain fields are entirely determined by R through equations (7) and (8). Given the further assumption that R₀ ≪ R_max, an expression can be derived for the ratio x_D/R_max in terms of the ultimate true strain, ϵ, that is constant for a given tissue under all forcing conditions:

$$\frac{x_D}{R_{max}}={\left[\text{exp\hspace{0.17em}}\left(\frac{3}{2}ϵ\right)-1\right]}^{-1/3}.$$ (11)

For tissues with an ultimate strain larger than a critical value ${ϵ}^{*}=\frac{2\text{\hspace{0.17em}ln\hspace{0.17em}}2}{3}=0.46$, the damage radius will be less than the maximum bubble radius. This is clearly true for stomach (ϵ = 0.66) and hepatic artery (ϵ = 0.63) while gallbladder has an ultimate strain (ϵ = 0.43) only slightly below the critical value. In contrast, liver (ϵ = 0.38) has the smallest ultimate strain and demonstrates x_D > R_max behavior at all waveform frequencies. Previous authors have developed metrics to predict R_max in histotripsy for given forcing conditions and tissue parameters (Bader and Holland 2016), so these methods and equation (11) can be used to predict the single-bubble damage radius. Of note, use of equation (11) permits substitution of an ultimate strain measured at an elevated strain rate.

The proposed strain-based damage metric and maximum bubble radius show good qualitative agreement with experimental observations and thus provide direction for future treatment planning algorithms. However, it should be noted that model assumptions tend towards an upper-bound estimation of the single-bubble damage radius. In particular, the spherical symmetry and first-order compressibility assumed by the Keller–Miksis equation lead to higher pressures, stresses, and strains developed at bubble collapse. Since maximum stresses and strains tend to occur at maximum bubble radius and at collapse, these assumptions could overestimate the predicted damage radius. Additionally, this study bases damage radii predictions on quasistatic measurements of ultimate true strain in each tissue. The vast majority of tissue measurements to date have been performed under quasistatic conditions not applicable to the ultra-high strain rates (>10⁸ 1/s) generated during cavitation bubble growth and collapse. However, the ultimate strength or strain of a gross tissue sample as well as its shear modulus should be measured at more relevant strain rates (Brujan and Vogel 2006). For example, studies of ballistic gelatin, the closest tissue surrogate studied under high strain rates, found that the gel’s compressive strength increased from 3 kPa at a strain rate of ~0.001/s to 6 MPa at a strain rate of ~3200/s (Kwon and Subhash 2010). This again suggests the damage radii predicted here could over-estimate the true damage extent. New approaches for determining tissue properties under high strain rate stand to improve the accuracy of stress, strain, and strain rate calculations in this study (Estrada et al 2018) and of treatment planning applications seeking to avoid collateral damage.

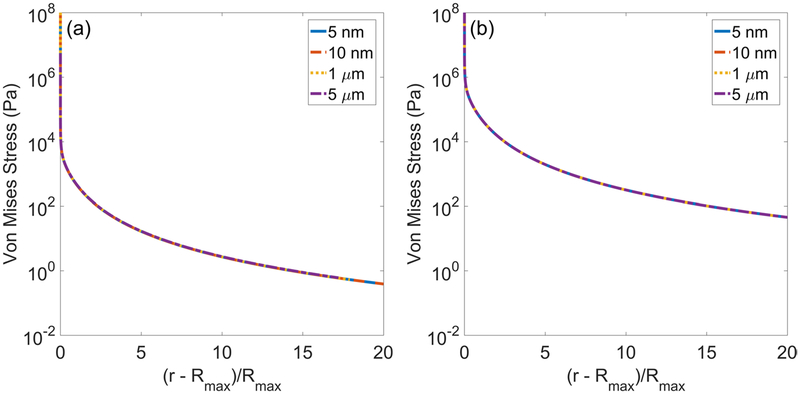
Cavitation-induced damage most likely involves a combination of direct mechanical destruction of cells and changes in cell microenvironment that induce apoptosis. Thus, a more rigorous definition of tissue ‘damage’ is needed. Relating stress, strain, and strain rate calculations to the spatial extent of tissue damage is challenging given the limited measurements that can be made at time and length scales relevant to cavitation. Future work applying the methods of a recent study correlating cellular changes with cavitation damage extent will be valuable for this purpose (Estrada 2017). Furthermore, the mechanics of cavitation in soft matter are likely more complex than current theories can represent. For example, no known material can tolerate the extremely high stresses and strains calculated at the bubble without immediate rupture. The assumption of continuous stretching of tissue from a nanometer-sized nucleus is likely an oversimplification, and this work motivates the need for future experiments clarifying the sequence of events producing cavitation damage. The choice of a 5 nm nucleus in this study was based on experimental predictions of nucleus size in water and other fluids calculated to match experimentally observed cavitation thresholds using intrinsic threshold histotripsy (Maxwell et al 2013). More likely, however, the ultra-high strain rates generated at cavitation inception would immediately rupture tissue. This early tissue rupture could then briefly give rise to a larger ‘stress-free’ or equilibrium radius that acts as an effective initial radius for calculations of stress and strain fields. This process would then repeat until the bubble reaches its maximum size. Alternatively, bubble nuclei present in extracellular fluid might fail to exert significant stress and strain on surrounding cells until they reach a large enough size. The consequences that a larger effective initial radius could have for stress magnitudes are illustrated in figure 10. This figure shows von Mises stress as a function of scaled distance from the maximum bubble radius in (a) liver and (b) hepatic artery for four different initial radii. Relative to the assumed case of bubble growth from a 5 nm nucleus (solid blue trace), the larger initial radii lead to significantly smaller stresses at the bubble wall (r = R_max). However, notably, the rates of stress attenuation in all traces are unaffected, and the stress traces for each R₀ are self-similar. While experiments would ultimately be needed to inform the choice of initial radius, this presently assumed parameter is unlikely to significantly affect the predicted damage radii in this study given the relatively weak dependence of R_max on R₀. For example, in figure 10(a) for liver, the R_max values are 220, 240, 264, and 275 microns. Thus by equation (11), the x_D values are 241, 263, 289, and 301 microns. Similarly, for figure 10(b) for hepatic artery, the R_max values are 120, 130, 140, and 155 microns, and the x_D values are 103, 112, 121, and 133 microns.

Figure 10.

Von Mises stress as a function of scaled distance from maximum bubble radius for different initial radii in (a) liver (R_max/R₀ = 4.4 × 10⁴, 2.4 × 10⁴, 264, 55) and (b) hepatic artery (R_max/R₀ = 2.4 × 10⁴, 1.3 × 10⁴, 140, 31) under 1 MHz forcing.

5. Conclusions

This study models bubble dynamics in a variety of tissues with literature-sourced viscoelastic and acoustic properties to investigate potential mechanisms responsible for experimental observations of tissue-selective cavitation damage. Results are presented showing radial dynamics, stress, strain, and strain rate fields for different tissues at three waveform frequencies (0.5 MHz, 1 MHz, and 3 MHz) relevant to focused ultrasound applications. Calculated von Mises strain fields are then compared to available ultimate true strain data to compare predicted strain-related damage extent in different tissues. The distinct viscoelastic properties of each tissue affect the magnitudes of stress, strain, and strain rate more significantly with increasing distance from the bubble. Findings support the hypothesis that differential tissue mechanical responses could be used to design tissue-selective treatments and are also consistent with experiments demonstrating resistance to ablation in stiffer tissues (Vlaisavljevich et al 2013), smaller lesion size associated with higher frequency waveforms (Lin et al 2014b), and sharp boundaries of the histotripsy ablation zone (Parsons et al 2006).

This work is limited by the available viscoelastic and acoustic property measurements in each tissue. Strain rate trends, in particular, are dependent on tissue viscosity; however, measurements of viscosity in the same tissue vary widely based on testing method and assumed constitutive relationship. The applicability of results in this study could be strengthened by recent advances in measurement techniques for the mechanical properties of inhomogeneous soft tissue (Margueritat et al 2019). Further study of tissue failure under compression and in response to high strain rates could also improve damage predictions.