Significance
Multivalency can enhance molecular affinity and specificity by modulating binding kinetics through proximity-induced effective concentrations. The effective concentrations between multivalent protein ligands and receptors depend on their structures, but a mechanistic framework linking biophysical and biochemical properties has not been well established. Here, we present a mathematical model that, without parameter fitting, can predict observed multivalent binding kinetics by considering the full network of microstate binding configurations, with the dynamics of each microstate dictated by monomer kinetics and protein structure. The model provides molecular-level understanding of macroscopic, noncanonical binding kinetics; identifies rate-determining parameters and microstates; and elucidates mechanisms and design principles that relate the networked ensemble to the strength and duration of interaction, facilitating rational engineering of multivalent binding dynamics.
Keywords: multivalency, protein interaction map, kinetic modeling, surface plasmon resonance
Abstract
Protein multivalency can provide increased affinity and specificity relative to monovalent counterparts, but these emergent biochemical properties and their mechanistic underpinnings are difficult to predict as a function of the biophysical properties of the multivalent binding partners. Here, we present a mathematical model that accurately simulates binding kinetics and equilibria of multivalent protein–protein interactions as a function of the kinetics of monomer–monomer binding, the structure and topology of the multidomain interacting partners, and the valency of each partner. These properties are all experimentally or computationally estimated a priori, including approximating topology with a worm-like chain model applicable to a variety of structurally disparate systems, thus making the model predictive without parameter fitting. We conceptualize multivalent binding as a protein–protein interaction network: ligand and receptor valencies determine the number of interacting species in the network, with monomer kinetics and structural properties dictating the dynamics of each species. As predicted by the model and validated by surface plasmon resonance experiments, multivalent interactions can generate several noncanonical macroscopic binding dynamics, including a transient burst of high-energy configurations during association, biphasic equilibria resulting from interligand competition at high concentrations, and multiexponential dissociation arising from differential lifetimes of distinct network species. The transient burst was only uncovered when extending our analysis to trivalent interactions due to the significantly larger network, and we were able to predictably tune burst magnitude by altering linker rigidity. This study elucidates mechanisms of multivalent binding and establishes a framework for model-guided analysis and engineering of such interactions.
Multivalency is a recurrent structural feature of biomolecules. Be it through domain accretion (1, 2), mRNA splicing (3), posttranslational modification (4, 5), supramolecular assembly (6, 7), or combinations thereof (8), instances of multivalency are evident across all biological systems. Multivalent interactions play central roles in the functional compartmentalization of the cell (9–11), in establishing cooperative and ultrasensitive binding dynamics (12, 13), and as the basis for information coding (14–18), enabling receptors to discriminate among a pool of downstream effectors. Inspired by these biological displays, multivalency additionally serves as an immensely useful and easy-to-implement design feature in engineered systems. Therapeutic antibodies (19, 20) and related biologics (21, 22) have leveraged the multivalency effect to achieve ultrahigh affinity and selectivity and to create novel ligands and scaffolds for cellular differentiation (23, 24), patterning (25), and tissue engineering (26).
However, the structural and combinatorial complexity of multivalent systems poses significant challenges in developing and implementing mechanistic models of interaction dynamics, which limits our understanding of natural systems and often leaves intuition and trial and error as the most accessible approaches when incorporating multivalent features into synthetic designs (27). Despite these challenges, the numerous applications of multivalency have led to many iterations of experimental and theoretical model systems designed to describe, predict, and explore particular aspects of these interactions (28–30). However, because the biophysical features are unique to each interaction pair, multivalent models are often tailored in a system-specific manner (31, 32), having an in-depth focus on a subset of the parameter space (33–35) and using fitted parameters to account for nonideal behaviors and unmeasurable properties (36, 37). For example, many descriptions have focused on the important role of valency in the binding mechanisms of complexes such as dimeric zinc-finger transcription factors and bivalent IgG antibodies (30). Here, the low valencies and relative absence of conformational heterogeneity can enable the effective use of simplified models describing a single bivalent species driven through a single effective concentration. In systems where higher valencies and complex, heterogeneous topologies occur, multivalency can be simplified in 1 of 2 ways (13, 36). In a “disordered” multivalent system, there are no steric effects imposed that favor a subset of states over others (i.e., all possible binding configurations are regarded as being equally probable). Conversely, a “rigid” multivalent system permits only those receptor–ligand interactions that are precisely in register (i.e., the intramolecular distances between adjacent receptor and ligand binding domains are fixed and equal). However, multivalent molecules—especially multidomain proteins and even multichain antibodies—have variable topologies, conformational flexibility, and interaction domains with steric bulk. Thus, multivalent binding phenomena exist on a continuum, ranging from completely disordered to uniformly rigid, that dictates the accessibility of each binding configuration within a network of combinatorial possibilities.
Here, we constructed a general mechanistic model of multivalent binding kinetics based on the dynamic evolution of a network of configurational states. In contrast to prior approaches, we use a structure-guided, odds ratio-based determination of effective concentrations to more accurately model the steric permissibility and interconversion of every possible binding configuration within the multivalent network. While the model is designed to be applicable to a range of multivalent systems, we experimentally tested our model predictions using synthetic proteins containing SH3 domains, which are integral organizers of cell signaling with instances of multivalency playing important roles in such processes as receptor tyrosine kinase and T cell receptor signaling cascades. For example, experimental and model-guided studies have identified central roles for bivalent, trivalent, and higher-order SH3 scaffolds in mediating high effective concentrations of signaling components through scaffolding and receptor clustering (38, 39). Not exclusive to SH3-containing proteins, diverse bivalent, trivalent, and tetravalent architectures are recurrently observed with other protein interaction domains such as those in SH2, WW, zinc finger, BTB, and PDZ domain-containing proteins (40–43).
We hypothesized that, by using an explicit treatment of the structures of multivalent proteins coupled with measured binding rate constants of the single domains, we could predict multivalent interaction dynamics without post hoc fitting. Our model predictions of binding association and dissociation were validated with our synthetic experimental system, in which valency and linker structure were systematically varied, and with disparate examples of multivalency in the literature. Our results not only reveal a number of noncanonical binding features—transient burst during association, biphasic equilibria, and multiexponential dissociation—but our model also identifies specific classes of species that drive these behaviors, which would be difficult to determine experimentally. Notably, our studies on trivalent–trivalent interactions provided unexpected insights into an underlying mechanism of binding, namely the importance of relative binding orientation in modulating early-stage binding dynamics. This mechanistic insight was further tested through model-guided design of a trivalent ligand with increased linker rigidity that exhibited a more pronounced early-stage transient burst during association, as computationally predicted. Our work thus elucidates kinetic mechanisms of binding in multivalent protein–protein interactions and can be used for rational engineering of binding dynamics.
Results
Zero-Fit Model of Multivalent Binding Dynamics.
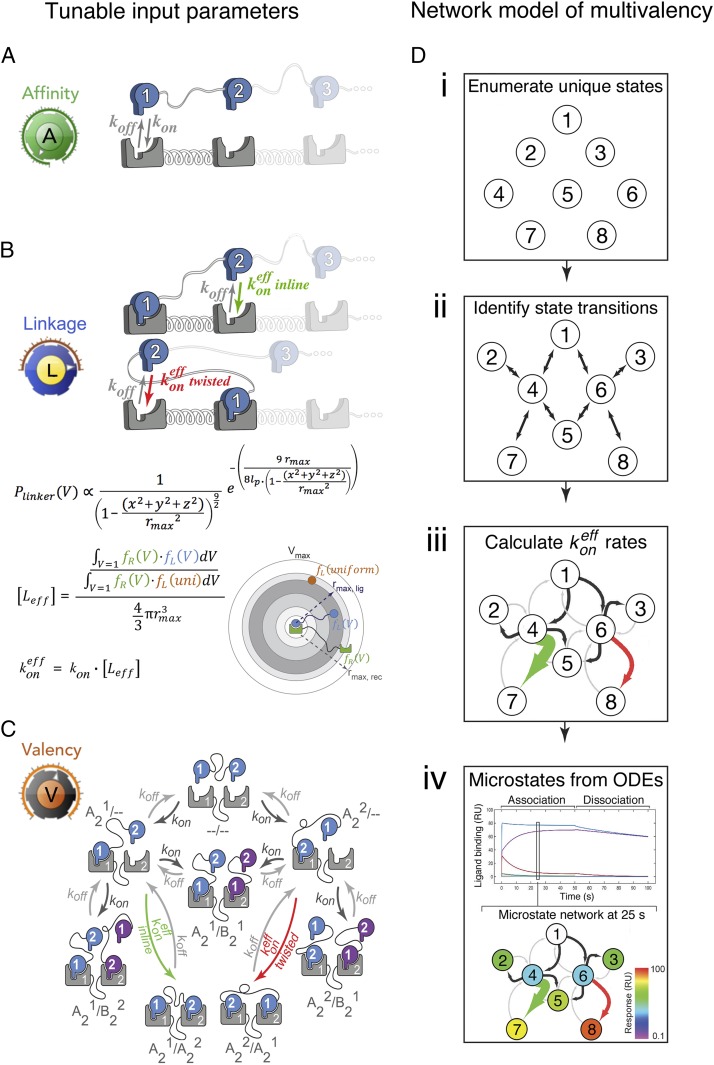
The complexity of binding that occurs among multivalent receptors and ligands can be understood, and subsequently modeled, as the interplay among 3 foundational biochemical and biophysical molecular properties. First, monovalent rate constants of association and dissociation determine the initial encounter between multivalent molecules (Fig. 1A). Second, the domain architecture and topological constraints of the molecules establish the relative proximity and effective concentrations that either drive or impede subsequent “intracomplex” interactions (Fig. 1B). Third, the valencies of the species define the combinatorics of the interaction, and thereby the number of binding configurations and interconversions within the network (Fig. 1C). Together, these 3 properties can generate avidity enhancement by populating the configurational ensemble and anchoring the interacting species within it (36).
Fig. 1.
The modeling framework treats multivalent receptor–ligand interactions as a dynamic network of microstate configurations controlled through 3 tunable molecular parameters. (A) Affinity relates to the monovalent rate constants of association, kon, and dissociation, koff, that dictate the nature of the initial encounter between a multivalent ligand and receptor. (B) Linkage describes the topological constraints that favor or disfavor subsequent intracomplex interactions computed using an odds ratio of probability density functions (SI Appendix). (C) Valency establishes the total number of microstates that a multivalent ligand and receptor can sample within their interaction network (nomenclature for the microstates is described in SI Appendix, Supplemental Methods). (D) The multivalent network model features 4 fundamental computational steps (see SI Appendix for a detailed description): (i) for a set of specified receptor–ligand valencies, all binding configurations are enumerated; (ii) configurational transitions are identified and represented as connections (edges) between pairs of microstates (nodes); (iii) effective ligand concentrations, [Leff], are calculated for each intracomplex association; and (iv) the system of ordinary differential equations (ODEs) is solved to yield the association and dissociation kinetics of the multivalent network.
In contrast to prior efforts to model multivalent interactions, which have typically focused on bivalent interactions and employ a single effective concentration to model “inline” binding configurations (33–35), our network modeling approach explicitly tracks the evolution of all possible binding configurations for both bivalent and trivalent interactions (Fig. 1D and SI Appendix, Fig. S1). To do so, each configuration is enumerated and represented as a node (Fig. 1 D, i and SI Appendix, Fig. S1A). We assume that transitions between configurations occur stepwise through a single association or dissociation event at a time. This yields topological connections among the configurational nodes (Fig. 1 D, ii and SI Appendix, Fig. S1B)—effectively, a multivalency-driven interaction network—that can be represented as a matrix of intracomplex association and dissociation constants (SI Appendix, Figs. S2 and S3). The magnitudes of the intracomplex kinetic constants are represented as edge thickness values in the configurational network and are proportional to an effective concentration (Fig. 1 B and D, iii and SI Appendix, Fig. S1C). In the instance of a bivalent ligand engaging a bivalent receptor, for example, 2 effective concentrations are generated: 1 for the inline configuration (A21/A22 in our nomenclature, described in SI Appendix, Supplemental Methods) and 1 for the twisted state (A22/A21) (Fig. 1C and SI Appendix, Fig. S4). By contrast, 12 effective concentrations are required to fully describe the configurational transitions in a trivalent receptor–trivalent ligand system (SI Appendix, Figs. S5 and S6). Mapping these calculated effective concentration values to the appropriate species in the multivalent network allows the system of ordinary differential equations to be solved, yielding the time-dependent evolution of each configuration during association and dissociation phases (Fig. 1 D, iv and SI Appendix, Fig. S1D).
Modeling the effective concentrations requires the probability density function (PDF) for the binding surfaces of each of the domain-linker-domain motifs (Fig. 1B). To calculate these PDFs, we approximated the receptors and ligands as rods with a distance rprot between the binding surface and the protein–linker interfacial point, and we modeled the end-to-end distance using a worm-like chain model (44) for a given amino acid linker sequence (SI Appendix, Fig. S1C). The PDF for the distance between the complementary active sites is then computed as the joint PDF of the linker PDF and the 2 rods with length rprot joined to each end of the linker. Though an idealized representation, this description of multivalent topology can be readily extended to higher valencies by appending additional linkers and rods to the ligands and receptors. The resulting receptor and ligand PDFs are then used to generate an effective ligand concentration, [Leff], by an odds ratio between such a tethered ligand and a uniformly distributed ligand (SI Appendix, Supplemental Methods). Notably, this treatment enables zero-fit estimates of each effective concentration for each unique intracomplex association using a minimal set of theoretical geometric parameters and constraints: the contour length (rmax) and persistence length (lp) of the interdomain linkers (Fig. 1B), the hinge-like rotation and excluded volume about the binding domain–linker interface, and the end-to-end distances of the receptor/ligand binding domains themselves. Moreover, in cases where the binding domain consists of a peptide (e.g., SH3 domain ligands), the disordered-to-ordered conformational change that occurs upon receptor binding is explicitly treated through configuration-dependent persistence length values. Finally, because our framework treats the PDF calculation of [Leff] as a modular mathematic step (Fig. 1B and SI Appendix, Fig. S1C), our model is compatible with an array of polymer end-to-end density functions (e.g., freely jointed, Gaussian, and spatially inhomogeneous chain models) that may befit the topology of the multivalent system of interest (45, 46).
Parameter Sensitivity of Model Simulations.
At their simplest, short flexible linkers and high monovalent affinities in bivalent and trivalent systems drive an apparently concerted transition to a single multivalent state that is described well by single-exponential kinetics (SI Appendix, Fig. S7). Exploration of the parameter space manifests the linker length-dependent transition from low avidity to high avidity configurations (SI Appendix, Fig. S8). A 300 amino acid flexible linkage tethering the bivalent ligand and receptor yields a system with largely monovalent character (SI Appendix, Fig. S8A). Shortening the flexible linkers increases [Leff], yields a high avidity interaction by driving the formation of the bivalent species, and reduces the bivalent twisted configuration by imposing steric constraints (SI Appendix, Fig. S8 B and C).
Further, the interdomain linkages that create effective concentrations are the basis for multivalent cooperativity via the “chelate effect” (47, 48). Here, rather than having to explicitly treat cooperativity in our model, our simulations show that positive and negative cooperativity are inherent to our linker-driven framework. Specifically, under conditions of competitive dissociation of a bivalent complex by a monovalent inhibitor (SI Appendix, Fig. S9A), positive cooperativity is observed (SI Appendix, Fig. S9B). The multivalent chelate effect approaches perfect cooperativity (i.e., a Hill coefficient of 2 for a bivalent system) as [Leff] is maximized through very short, in-register linkers (SI Appendix, Fig. S9B). Conversely, with receptors and ligands of differing linker lengths the multivalent interactions become increasingly out of register as the 2 linkers are rigidified (SI Appendix, Fig. S9C). This results in [Leff] falling below the spatially uniform ligand concentration, causing linker inhibition whereby multivalent modes of binding become less favorable than the monovalent association of a freely diffuse ligand.
With a higher valency, complex modes of binding become more apparent. The 12 intracomplex effective concentrations underlying a trivalent network (SI Appendix, Fig. S6) yield an ensemble of 78 unique configurations (SI Appendix, Fig. S10). Of these, 23 entail twisted topologies, which constitute nearly a third of the network and suggest the potential for fundamentally different modes of binding as valency is increased, a point that we explore in greater detail below. Simulated association and dissociation kinetics show complex configurational transitions in early association (SI Appendix, Fig. S10A), with the relative distribution of states in the ensemble dependent upon the receptor–ligand input parameters (SI Appendix, Fig. S10B). Importantly, this modeling framework identifies conditions under which multivalent interactions do not possess canonical, single-exponential kinetics and provides a means for more nuanced understanding of the mechanisms of multivalency.
Experimental Testing of Model Predictions with an SH3-Peptide System.
To assess the accuracy of our model, we benchmarked the simulations against an experimental, biomimetic signaling complex comprising variable repeats of the Gads SH3 domain and its cognate peptide as the receptor–ligand pair. This pair was also chosen based on its monovalent binding kinetics (experimentally measured to be kon = 913,000 M−1 s−1, koff = 1.35 s−1; SI Appendix, Fig. S11), which are within a region of parameter space that exhibits noncanonical binding features based on our model simulations (SI Appendix, Fig. S10A). A modular construction congruent with the model enabled facile incorporation of linkers with desired biophysical properties.
Surface plasmon resonance (SPR) quantifies, in real time, the mass of ligand bound to a receptor surface and is thus especially attuned to multiple ligands engaging a single multivalent receptor. Such interactions constitute a significant fraction of the configurational network (SI Appendix, Fig. S10B), so their accurate modeling is essential for a complete description of multivalency. Simulations performed with monovalent ligands yield binding responses with approximately 1-, 2-, and 3-fold mass amplitude increases against receptor valencies of 1, 2, and 3, in agreement with experimental sensorgrams for mono, bi, and trivalent SH3 domain-containing receptors, with no change to the binding kinetics (SI Appendix, Fig. S12A). SPR is additionally sensitive to avidity effects through crosslinking. Here, at sufficiently high receptor density, a multivalent ligand may interact with 2 or more receptors simultaneously. This phenomenon can be observed biologically in areas of high local concentrations, such as within clustered signaling molecules present at the plasma membrane. To account for crosslinking—both artifactual and biologically relevant—the model simulates pairwise distances between individual receptors as a function of their density (SI Appendix, Fig. S12B). The crosslinking-induced multivalency of the system is sensitive to receptor density and linker length and results in biphasic dissociation kinetics (SI Appendix, Fig. S12B).
Bivalency versus Trivalency: Mechanistic Description of Atypical Multivalent Phenomena.
The combinatorial complexity of multivalent interactions makes experimental quantification of these systems challenging. This is notable in SPR-based approaches. While benefitting from label-free, real-time quantification, SPR signals represent the summation of multiple interconverting configurations that can produce seemingly spurious kinetics. Because our model of multivalency explicitly tracks the evolution of each possible configurational state, we sought to use the model to understand the mechanistic underpinnings of these atypical signal features.
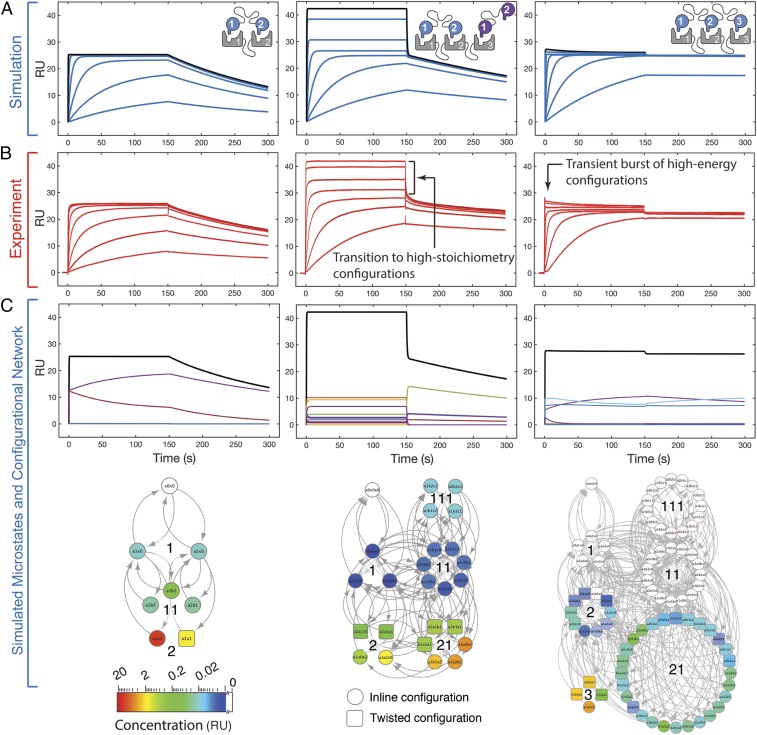
Simulations performed on bivalent receptor–bivalent ligand pairs display largely monoexponential association and dissociation kinetics (Fig. 2 A, Left). This behavior was similarly observed experimentally (Fig. 2 B, Left) and is indicative of a largely concerted transition from the unbound to the inline and twisted bivalent states, with intermediate, monovalent configurations very lowly populated (Fig. 2 C, Left). Performing these simulations and experiments with a trivalent receptor introduces an added, accessible binding domain in the presence of a bivalent ligand. The simulations demonstrate the formation of multiliganded receptors as the ligand concentration approaches the monovalent dissociation constant. This results in a second saturable mode of binding followed by a significant biphasic dissociation phase (Fig. 2 A, Middle), again in agreement with experiment (Fig. 2 B, Middle). Assessing the simulated configurations in this trivalent–bivalent interaction demonstrates that the system is able to exceed its bivalent equilibrium (∼25 resonance units [RU]; Fig. 2 A–C, Middle) as the configurational network populates monovalent states (Fig. 2 C, Middle). Upon dissociation, networks with significant populations of high-stoichiometric configurations display multiexponential macroscopic decay. At the microstate level, class “11” and “111” states undergo rapid dissociation of monovalently bound species, followed by a degree of first-order reassociation to bivalent configurations, which, in turn, contribute to the slower phase of dissociation. As linker length increases (and effective concentration decreases), transitioning from the bivalent configurations to the higher stoichiometric monovalent configurations becomes more permissible (SI Appendix, Fig. S13). Simulations performed on trivalent ligand–trivalent receptor systems (Fig. 2 A, Right) display a significantly reduced proportion of monovalent states, as they are effectively outcompeted for receptor binding by the high-avidity trivalent configurations. The small transient burst at the start of the association phase is quickly followed by signal decay as the system reconfigures to a more thermodynamically favorable state (Fig. 2 A, Right). During the dissociation phase, the system exhibits modest biphasic kinetics due to the loss of monovalent configurations. SPR experiments performed on a trivalent–trivalent interaction (Fig. 2 B, Right) show good agreement with the features observed in the simulation.
Fig. 2.
Simulations provide quantitative and mechanistic descriptions of the characteristics unique to multivalent interactions that can present as spurious binding events in experimental kinetic studies. (A) Simulated kinetics using the network-based model of multivalency. Simulations were performed at 2,000, 1,000, 250, 60, 15, 5, and 1 nM ligand; the 2,000-nM trace is highlighted in black. (B) Experimental sensorgrams performed on bivalent–bivalent (Left), trivalent–bivalent (Center), and trivalent–trivalent (Right) SH3 receptor and peptide ligand interactions. Experiments were performed with the same ligand concentrations as in A. Atypical features are indicated that result from high-stoichiometric and the burst of high-energy configurations. (C) Underlying microstate ensembles are shown for each 2,000-nM trace (black).
To further evaluate model-experiment agreement, we sought to alter parameters affecting the computed set of [Leff] values because this should alter ligand dynamics throughout the configurational network (SI Appendix, Fig. S14). First, removing the steric constraints that the model can impose on twisted configurations results in proportional representation of the inline and twisted configurations resulting in a diminished burst of association that overshoots the equilibrium state (SI Appendix, Fig. S14B). Second, we imposed a more significant restriction on the simulated evolution of the configurational network by only permitting “nearest neighbor” intracomplex associations (SI Appendix, Fig. S14C). Because such a network evolves through only 1 effective rate constant of association (out of a total of 12), a significant amount of the network is inaccessible. This alteration to the model creates an overrepresentation of monovalent “11” and bivalent “21” class configurations, resulting in a jump to a higher stoichiometric equilibria and a prominent biphasic dissociation (SI Appendix, Fig. S14C), in contrast to the experimental data (Fig. 2 B, Right). Third, altering the [Leff] calculations to forbid all twisted configurations yields simulations that significantly overpopulate transient monovalent and bivalent states at the expense of twisted trivalent states, leading to an exaggerated and erroneous initial burst of association (SI Appendix, Fig. S14D). Together, these tests of the model demonstrate the importance of accurate assessments of effective concentration for a meaningful mechanistic description of multivalency.
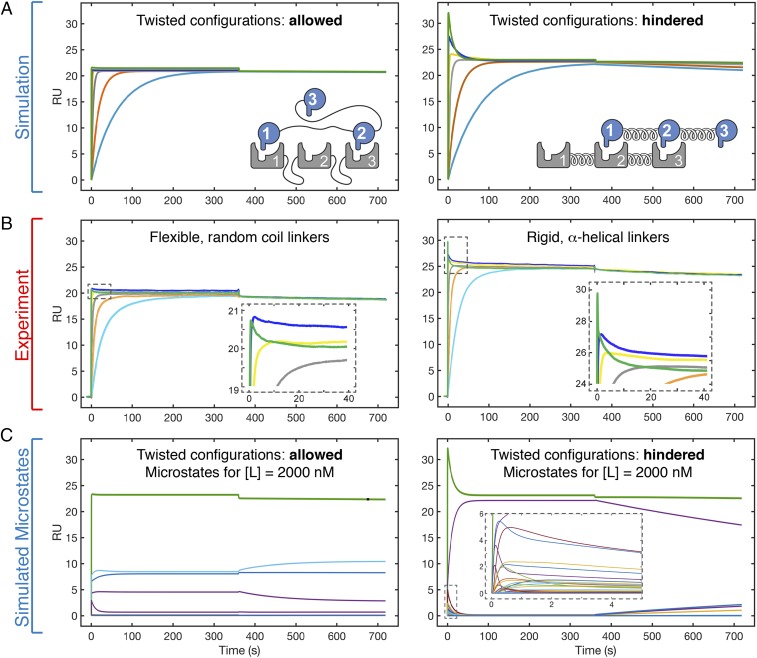
Notably, simulations and experiments with the trivalent system were critical in identifying the phenomenon of a transient burst during association. As with the other atypical manifestations of multivalency, our simulated binding kinetics not only reveal this behavior but also provide a mechanistic explanation for its occurrence (Fig. 2 C, Right). Here, the simulations reveal a rapid initial phase of association populated predominantly by monovalent, bivalent, and twisted trivalent configurations. These configurations undergo conversions to the thermodynamically favored inline, trivalent configuration. The mechanistic insights from the trivalent simulations indicate that the kinetically driven burst phase can be significantly enhanced by favoring the formation of monovalent and inline bivalent configurations and by impeding the formation of twisted bivalent and trivalent configurations (Fig. 3A). We sought to validate this prediction of the model by experimentally restricting the formation of twisted configurations through the incorporation of rigid, alpha-helical linkers into both receptor and ligand. Here, in close agreement with the simulation, rigidly tethered trivalent receptor–ligand interactions display a far more prominent transient burst compared with the flexibly tethered constructs (Fig. 3B). Depicting the transient burst as its composite microstates (Fig. 3C) indicates that a trivalent system that is hindered from accessing twisted configurations is entropically driven to regions of the network (i.e., high-stoichiometric states) not significantly populated in a sterically unhindered system. Populating these configurations additionally enables the hindered system to undergo the intracomplex rearrangements needed to form the single, accessible low-energy configuration (the inline trivalent species), which predominates the network at equilibrium (Movie S1).
Fig. 3.
Atypical binding kinetics manifest prominently in trivalent interactions and can be tuned through controlled sampling of the configurational network. (A) Simulations were performed for a trivalent receptor–ligand interaction as in B. The sensorgrams are represented with colored lines indicating ligand concentrations ranging from 2,000 nM (green trace) to 2 nM (light blue trace). Simulations were performed with either the standard model (i.e., twisted configurations allowed; Left) or an altered model (Right) restricting twisted configurations with low [Leff] values. (B) To experimentally approximate the simulations performed in A, SPR binding kinetics were measured for trivalent receptor–ligand pairs with either flexible, random-coil linkages (i.e., allowing twisted configurations; Left) or rigid, alpha-helical linkages (i.e., hindering twisted configurations; Right). The ligand concentration series is the same as in A. Insets highlight the region of the initial transient burst. (C) Mechanism of atypical binding kinetics is identified by inspection of the underlying binding configurations through simulation. Simulated kinetics for the 2,000-nM ligand concentration (green trace) and composite microstates (subordinate colored traces). Inset highlights the microstates that comprise the transient burst. The kinetic traces for the allowed and hindered simulations are animated in Movie S1.
Taken together, our results indicate that this expanded and idealized treatment of effective concentrations within multivalent networks reflects experimental observations, elucidates mechanisms behind these observations, and demonstrates that our core modeling framework gives qualitatively and quantitatively different results when applied to increasing receptor–ligand valencies.
Application of the Model to Structurally Disparate Multivalent Systems.
The direct correlation between multivalent topology and effective concentrations led us to examine our use of the worm-like chain model with system topologies that differ significantly from our SH3 “beads-on-a-string” constructs. The major limitation of the worm-like chain model is its treatment of multivalent species as “persistent” polymers (i.e., composed of linear, noninteracting, and hinged segments with a uniform stiffness). In reality, multivalent species display widely varying types of connectivity, degrees of nonuniform stiffness, and local and long-range self-interaction. However, we reasoned that if the multivalent system of interest were sufficiently well described structurally, our model could be parameterized with linkers, hinged-rods, and contour and persistence lengths to reasonably approximate the interaction volume and the regions within it that the binding domains sample. To examine the utility of our zero-fit framework in this regard, we assessed the model’s ability to simulate SPR sensorgrams from 2 disparate systems described in the literature.
As a first case study, we examined the multivalent interactions between the trivalent TNF family ligand, BAFF, and bivalent Fc fusions of its receptors, BCMA and BAFFR, as reported by Day et al. (49). Here, notably, the nature of the multivalency arises through multimeric assembly (SI Appendix, Fig. S15 A–C). Moreover, through multimerization, BAFF’s trivalency exists with 3-fold radial symmetry rather than a linear, beads-on-a-string topology. The radial symmetry of BAFF results in an equal pairwise distance between all 3 of the binding domains (∼33 Å, SI Appendix, Fig. S15B). We simulated this unique topology by using a single PDF calculation for each of the 2 inline and 2 twisted effective concentrations. Additionally, the linkage connecting the 2 BCMA/BAFFR domains was modeled as a linker-rod-linker segment, in which the rod represents the rigid 15 Å spanning the 2 C-termini of the Fc dimer (SI Appendix, Fig. S15C). Using this structure-guided parameterization, we observed good agreement between our zero-fit simulations and the experimental dataset, particularly with regard to the calculated effective equilibrium dissociation constants (SI Appendix, Fig. S15D).
As a second case study, we explored the potential applicability of our computational framework beyond protein–protein interactions by modeling the intercalation of bivalent DAPI analogs into double-stranded DNA (dsDNA) with tandem “AATT” motifs, as reported by Liu et al. (50). Notably, the uniform rigidity of the dsDNA makes this system more sensitive to linker inhibition (SI Appendix, Fig. S16A). Making use of structure-based parameters (e.g., the dimensions and lp values for dsDNA and alkyl ether linkers) again resulted in good agreement between our simulations and the experimental data, both in regard to the binding enhancement seen with the increase in valency (SI Appendix, Fig. S16B vs. SI Appendix, Fig. S16C) and the reduction of bivalent avidity, as the shortening linkages place the binding domains increasingly out of register (SI Appendix, Fig. S16 C–E).
Tailoring the Multivalent Effect with Model-Guided Exploration of the High-Dimension Parameter Space.
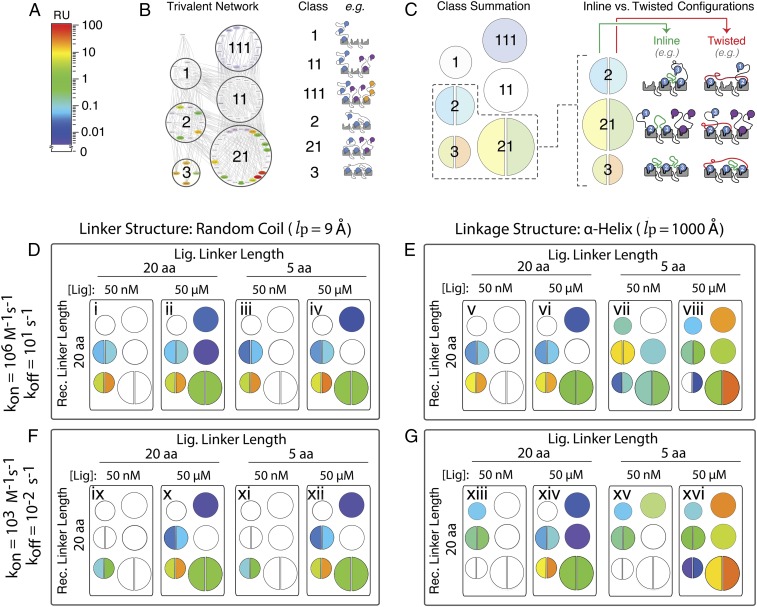
Having established the utility of our mechanistic computational framework, we sought to use the model to more broadly explore the biophysical landscape of multivalency through sensitivity analyses of the parameters underlying the affinities, avidities, and structural topologies of complex biomolecules. Here, we use class summation to provide a simplified representation of the 78 configurations in a trivalent receptor–ligand ensemble (Fig. 4 A–C).
Fig. 4.
Mapping of a cross-section of the multidimensional, trivalent receptor–ligand interaction space details the parameter sensitivities of the multivalent effect. Overview of simplified representation: Microstate concentrations (A) were binned based on “class” of interaction (B) and represented as a summed color intensity with inline and twisted microstate conformations separately indicated for the 3 classes in which they occur (C). Sampling of the parameter space for simulated trivalent–trivalent interactions after a 50-s association with a monovalent KD = 10 mM of either fast on/off (D and E) or slow on/off (F and G). Linkers were either flexible “random coil” (D and F) or rigid “alpha-helical” (E and G), each with lengths of either 20 or 5 amino acids. Ensemble simulations were performed with low (50 nM) or high (50 μM) ligand concentrations.
Our multivalent simulations indicate that when linkages between binding domains of the receptor or ligand are flexible and large relative to the diameter of the binding domains, the ensemble is insensitive to modest changes in their length (Fig. 4 D, i–iv). Similarly, adding rigidity to the receptor–ligand linkages imposes a strong sensitivity to their relative positioning. When helical linkers of equal length are simulated (Fig. 4 E, v and vi), the resulting ensemble is able to fully populate the trivalent configurations. Positioning the receptor–ligand binding domains out of register with rigid linkers of differing lengths (Fig. 4 E, vii and viii) nearly completely forbids the formation of trivalent states, favoring instead misaligned bivalent configurations (SI Appendix, Fig. S17). The model’s use of structure-guided, linker-driven calculations of [Leff] was the basis for describing the out-of-register linkage effects. Simplifying the model by describing these interactions with a uniform model, in which [Leff] is represented by soluble ligand confined to a sphere bounded by the linker contour lengths, failed to properly account for out-of-register steric constraints between receptor and ligand due to inaccurate assignments of effective ligand concentrations to individual microstates (SI Appendix, Fig. S18). Further, the importance of binding site registration for avid interactions is highly sensitive to the length and flexibility of the linkages (SI Appendix, Figs. S9C and S16).
Additionally, because the avidity enhancement caused by multivalency derives from the ability to anchor a receptor–ligand complex within the configurational network, the avidity benefits of a large network can be offset by a koff that operates on a sufficiently fast timescale such that intramolecular reassociations are less likely despite favorable effective ligand concentrations (Fig. 4 F and G). This functions to expedite a ligand’s path from a fully bound state to freely dissociated, thus reducing the half-life of the multivalent assembly. Conversely, while the avidity effect and half-life increase with decreasing koff, the time required for high-valency configurations to achieve maximum occupancy at equilibrium can increase by several orders of magnitude, from seconds to days (SI Appendix, Fig. S17).
Together, these sensitivity analyses demonstrate that topological constraints and the monovalent rate constants impose significant effects on the size, distribution, and stability of the multivalent network.
Discussion
The numerous instances of multivalency in natural biological systems and synthetic designs derive from its abundant utility and ease of implementation. The physical linkage of intermolecular binding events creates a network of effective concentrations that can profoundly alter the overall kinetics and energetics of a molecular interaction—without the need to mutate or otherwise alter specific intermolecular contacts. Further, the introduction of added layers of posttranscriptional and posttranslational modification can create a multivalency coding language that specifies the type, nature, and duration of a biomolecular interaction. While straightforward to implement, predicting the behavior of specific instances of multivalency is hindered by the combinatorial complexity of these systems and by the effects of the structures and topologies of the interacting species.
Here, we found mechanistic utility in explicitly modeling the relationship between domain topology and effective concentration, combined with a complete description of the multivalent network. By limiting assumptions about the steric permissibility of configurational transitions, good agreement between our zero-fit model and experiment was observed across a range of concentrations, valencies, and topologies. We show that small accretions in valency cause large increases in network size. Through simulation and experiment, we further link the ability of a multivalent system to traverse and populate its network to the topological constraints imposed by the receptor and ligand structures. Here, the diameter of the binding domain relative to the length of the linker, the linker rigidity, and degree of registration between receptor and ligand have substantial effects on the rates of intracomplex association and the ability to form high-avidity configurations.
In addition to the insights obtained from these parameter sensitivity analyses, our model enables mechanistic descriptions of kinetic phenomena that would otherwise be poorly described by conventional 1:1 or rigid-bivalent curve fitting procedures. With our network model, these noncanonical features become quantitative markers of multivalency. For example, the magnitude, duration, and decay of the transient burst at the outset of the association phase describe the paths through the network that receptor–ligand complexes take to reach their lowest-energy configurations. Further, the ligand concentration-dependent transitions between configurational classes of differing stoichiometries provide a means to backcalculate interdomain effective concentrations and linker lengths for structurally uncharacterized molecules. Additionally, the multiphasic dissociation kinetics yield mechanistic insights into the composition of the configurational network, and how a receptor may “process” ligands of differing valency.
Finally, the modular construction of our network model enables its integration with specialized treatments of multivalency not explicitly addressed here. For example, distributive binding (51) and statistical rebinding (52, 53) can enhance the multivalency effect in nonintuitive ways. Similar to our treatment of receptor crosslinking, models of these effects can be incorporated into the terminal configurational transitions connecting the network to the unbound receptor state. Additionally, rule-based modeling has powerful applications for combinatorial systems (54, 55). Here, local rules governing topology-driven binding can be determined from our network model and incorporated into a larger rule-based network that is extensible to much higher valencies and longer linker lengths without the computational demand required to calculate full sets of probability density functions and differential rate equations. Such extensions should enable increasingly expansive descriptions of multivalency over large ranges of chemical and biological space, leading to a more detailed understanding of the elegant power of multivalency in natural and engineered systems (56).
Materials and Methods
Computational Model.
The mechanistic model was formulated with mass-action kinetic equations to describe the formation and loss of each species through binding and dissociation. Intracomplex binding utilized a structure-based effective ligand concentration that was calculated via an odds ratio of probability density functions between a tethered ligand and a uniformly distributed ligand. The resulting set of ordinary differential equations was solved using ode15s in MATLAB to simulate association and dissociation kinetics.
Experimental Methods.
Multivalent receptors were constructed using the C-terminal SH3 domain of the human adaptor protein Gads, and multivalent ligands incorporated a peptide sequence from the Gads cognate ligand, SLP-76 (57). Association and dissociation kinetics between ligand and receptor constructs were quantified by surface plasmon resonance measurements on a Biacore S200 instrument.
More detailed descriptions of the computational and experimental methods are provided in SI Appendix. All materials and data are available upon request.
Supplementary Material
Acknowledgments
We thank Robyn Stoller and Fernando Bazan for assistance with SPR experiments and Patrick Holec for design insights into the model framework. This work was supported by funding from the Higher Education Excellence Program of the Ministry of Human Capacities in Biotechnology at the Budapest University of Technology and Economics (to B.B.) and from the National Institutes of Health (R01GM113985 and R21EB022258 to C.A.S.). The Biacore S200 instrument was made available through a shared instrument grant (S10OD021539) from the Office of Research Infrastructure Programs at the National Institutes of Health.
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission. G.G. is a guest editor invited by the Editorial Board.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.1902909116/-/DCSupplemental.
References
- 1.Pawson T., Protein modules and signalling networks. Nature 373, 573–580 (1995). [DOI] [PubMed] [Google Scholar]
- 2.Bashton M., Chothia C., The generation of new protein functions by the combination of domains. Structure 15, 85–99 (2007). [DOI] [PubMed] [Google Scholar]
- 3.Mantovani F., et al. , Pin1 links the activities of c-Abl and p300 in regulating p73 function. Mol. Cell 14, 625–636 (2004). [DOI] [PubMed] [Google Scholar]
- 4.Oh E., Akopian D., Rape M., Principles of ubiquitin-dependent signaling. Annu. Rev. Cell Dev. Biol. 34, 137–162 (2018). [DOI] [PubMed] [Google Scholar]
- 5.Shi Q., et al. , Hedgehog-induced phosphorylation by CK1 sustains the activity of Ci/Gli activator. Proc. Natl. Acad. Sci. U.S.A. 111, E5651–E5660 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Hashimoto K., Panchenko A. R., Mechanisms of protein oligomerization, the critical role of insertions and deletions in maintaining different oligomeric states. Proc. Natl. Acad. Sci. U.S.A. 107, 20352–20357 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Li P., et al. , Phase transitions in the assembly of multivalent signalling proteins. Nature 483, 336–340 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Kang S. A., et al. , mTORC1 phosphorylation sites encode their sensitivity to starvation and rapamycin. Science 341, 1236566 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Kaiser T. E., Intine R. V., Dundr M., De novo formation of a subnuclear body. Science 322, 1713–1717 (2008). [DOI] [PubMed] [Google Scholar]
- 10.Bernardi R., Pandolfi P. P., A dialog on the first 20 years of PML research and the next 20 ahead. Front. Oncol. 4, 23 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Ditlev J. A., Case L. B., Rosen M. K., Who’s in and who’s out–compositional control of biomolecular condensates. J. Mol. Biol. 430, 4666–4684 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Curk T., Dobnikar J., Frenkel D., “Design principles for super selectivity using multivalent interactions in multivalency” in Multivalency: Concepts, Research & Applications, Huskens J., Prins L. J., Haag R., Ravoo B. J., Eds. (Wiley, 2017), pp. 75–101. [Google Scholar]
- 13.Stevers L. M., de Vink P. J., Ottmann C., Huskens J., Brunsveld L., A thermodynamic model for multivalency in 14-3-3 protein–protein interactions. J. Am. Chem. Soc. 140, 14498–14510 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Davey N. E., Morgan D. O., Building a regulatory network with short linear sequence motifs: Lessons from the degrons of the anaphase-promoting complex. Mol. Cell 64, 12–23 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Gabius H. J., Roth J., An introduction to the sugar code. Histochem. Cell Biol. 147, 111–117 (2017). [DOI] [PubMed] [Google Scholar]
- 16.Liu F., Walters K. J., Multitasking with ubiquitin through multivalent interactions. Trends Biochem. Sci. 35, 352–360 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Sims R. J. 3rd, Reinberg D., Is there a code embedded in proteins that is based on post-translational modifications? Nat. Rev. Mol. Cell Biol. 9, 815–820 (2008). [DOI] [PubMed] [Google Scholar]
- 18.Kilic S., Bachmann A. L., Bryan L. C., Fierz B., Multivalency governs HP1α association dynamics with the silent chromatin state. Nat. Commun. 6, 7313 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Cuesta A. M., Sainz-Pastor N., Bonet J., Oliva B., Alvarez-Vallina L., Multivalent antibodies: When design surpasses evolution. Trends Biotechnol. 28, 355–362 (2010). [DOI] [PubMed] [Google Scholar]
- 20.Holliger P., Prospero T., Winter G., “Diabodies”: Small bivalent and bispecific antibody fragments. Proc. Natl. Acad. Sci. U.S.A. 90, 6444–6448 (1993). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Mammen M., Choi S. K., Whitesides G. M., Polyvalent interactions in biological systems: Implications for design and use of multivalent ligands and inhibitors. Angew. Chem. Int. Ed. Engl. 37, 2754–2794 (1998). [DOI] [PubMed] [Google Scholar]
- 22.Lee C. C., MacKay J. A., Fréchet J. M., Szoka F. C., Designing dendrimers for biological applications. Nat. Biotechnol. 23, 1517–1526 (2005). [DOI] [PubMed] [Google Scholar]
- 23.Curk T., Dobnikar J., Frenkel D., Optimal multivalent targeting of membranes with many distinct receptors. Proc. Natl. Acad. Sci. U.S.A. 114, 7210–7215 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Conway A., et al. , Multivalent ligands control stem cell behaviour in vitro and in vivo. Nat. Nanotechnol. 8, 831–838 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Yang K., et al. , Multiscale, hierarchically patterned topography for directing human neural stem cells into functional neurons. ACS Nano 8, 7809–7822 (2014). [DOI] [PubMed] [Google Scholar]
- 26.Petrie T. A., et al. , Multivalent integrin-specific ligands enhance tissue healing and biomaterial integration. Sci. Transl. Med. 2, 45ra60 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Nuñez-Prado N., et al. , The coming of age of engineered multivalent antibodies. Drug Discov. Today 20, 588–594 (2015). [DOI] [PubMed] [Google Scholar]
- 28.Perelson A. S., Receptor clustering on a cell surface. III. Theory of receptor cross-linking by multivalent ligands: Description by ligand states. Math. Biosci. 53, 1–39 (1981). [Google Scholar]
- 29.Macken C. A., Perelson A. S., “Branching processes applied to cell surface aggregation phenomena” in Lecture Notes in Biomathematics, Cowan J. D., et al., Eds. (Springer, 1985), pp. 13–42. [Google Scholar]
- 30.Müller K. M., Arndt K. M., Plückthun A., Model and simulation of multivalent binding to fixed ligands. Anal. Biochem. 261, 149–158 (1998). [DOI] [PubMed] [Google Scholar]
- 31.Potoyan D. A., Bueno C., Zheng W., Komives E. A., Wolynes P. G., Resolving the NFκB heterodimer binding paradox: Strain and frustration guide the binding of dimeric transcription factors. J. Am. Chem. Soc. 139, 18558–18566 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Reader P. P., Shaw A. M., Kinetic analysis of the multivalent ligand binding interaction between protein A/G and IgG: A standard system setting. J. Phys. Chem. B 121, 8919–8925 (2017). [DOI] [PubMed] [Google Scholar]
- 33.Kane R. S., Thermodynamics of multivalent interactions: Influence of the linker. Langmuir 26, 8636–8640 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Ruiz-Herrero T., Estrada J., Guantes R., Miguez D. G., A tunable coarse-grained model for ligand-receptor interaction. PLoS Comput. Biol. 9, e1003274 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Xu H., Shaw D. E., A simple model of multivalent adhesion and its application to influenza infection. Biophys. J. 110, 218–233 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Dubacheva G. V., Curk T., Auzély-Velty R., Frenkel D., Richter R. P., Designing multivalent probes for tunable superselective targeting. Proc. Natl. Acad. Sci. U.S.A. 112, 5579–5584 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Kitov P. I., Bundle D. R., On the nature of the multivalency effect: A thermodynamic model. J. Am. Chem. Soc. 125, 16271–16284 (2003). [DOI] [PubMed] [Google Scholar]
- 38.Good M. C., Zalatan J. G., Lim W. A., Scaffold proteins: Hubs for controlling the flow of cellular information. Science 332, 680–686 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Shin Y., Brangwynne C. P., Liquid phase condensation in cell physiology and disease. Science 357, eaaf4382 (2017). [DOI] [PubMed] [Google Scholar]
- 40.Emerson R. O., Thomas J. H., Adaptive evolution in zinc finger transcription factors. PLoS Genet. 5, e1000325 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Stogios P. J., Downs G. S., Jauhal J. J., Nandra S. K., Privé G. G., Sequence and structural analysis of BTB domain proteins. Genome Biol. 6, R82 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Ingham R. J., Gish G., Pawson T., The Nedd4 family of E3 ubiquitin ligases: Functional diversity within a common modular architecture. Oncogene 23, 1972–1984 (2004). [DOI] [PubMed] [Google Scholar]
- 43.Wagner M. J., Stacey M. M., Liu B. A., Pawson T., Molecular mechanisms of SH2- and PTB-domain-containing proteins in receptor tyrosine kinase signaling. Cold Spring Harb. Perspect. Biol. 5, a008987 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Kratky O., Porod G., Röntgenuntersuchung gelöster fadenmoleküle. Recl. Trav. Chim. Pays Bas 68, 1106–1123 (1949). [Google Scholar]
- 45.Giacomin G., Random Polymer Models (Imperial College Press, 2007). [Google Scholar]
- 46.Bar-Sinai Y., Bouchbinder E., Gaussian fluctuations of spatially inhomogeneous polymers. Soft Matter 13, 995–1005 (2017). [DOI] [PubMed] [Google Scholar]
- 47.Hunter C. A., Anderson H. L., What is cooperativity? Angew. Chem. Int. Ed. Engl. 48, 7488–7499 (2009). [DOI] [PubMed] [Google Scholar]
- 48.Jiang W., et al. , Chelate cooperativity and spacer length effects on the assembly thermodynamics and kinetics of divalent pseudorotaxanes. J. Am. Chem. Soc. 134, 1860–1868 (2012). [DOI] [PubMed] [Google Scholar]
- 49.Day E. S., et al. , Selectivity of BAFF/BLyS and APRIL for binding to the TNF family receptors BAFFR/BR3 and BCMA. Biochemistry 44, 1919–1931 (2005). [DOI] [PubMed] [Google Scholar]
- 50.Liu Y., et al. , Designed compounds for recognition of 10 base pairs of DNA with two at binding sites. J. Am. Chem. Soc. 134, 5290–5299 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Tang X., et al. , Composite low affinity interactions dictate recognition of the cyclin-dependent kinase inhibitor Sic1 by the SCFCdc4 ubiquitin ligase. Proc. Natl. Acad. Sci. U.S.A. 109, 3287–3292 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Vauquelin G., Charlton S. J., Long-lasting target binding and rebinding as mechanisms to prolong in vivo drug action. Br. J. Pharmacol. 161, 488–508 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Weber M., Bujotzek A., Haag R., Quantifying the rebinding effect in multivalent chemical ligand-receptor systems. J. Chem. Phys. 137, 054111 (2012). [DOI] [PubMed] [Google Scholar]
- 54.Chylek L. A., et al. , Rule-based modeling: A computational approach for studying biomolecular site dynamics in cell signaling systems. Wiley Interdiscip. Rev. Syst. Biol. Med. 6, 13–36 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Hogg J. S., Harris L. A., Stover L. J., Nair N. S., Faeder J. R., Exact hybrid particle/population simulation of rule-based models of biochemical systems. PLoS Comput. Biol. 10, e1003544 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Bashor C. J., et al. , Complex signal processing in synthetic gene circuits using cooperative regulatory assemblies. Science 364, 593–597 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Liu Q., et al. , Structural basis for specific binding of the Gads SH3 domain to an RxxK motif-containing SLP-76 peptide: A novel mode of peptide recognition. Mol. Cell 11, 471–481 (2003). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.