Unveiling dimensions of stability in complex ecological networks

Significance

While the need to consider the multidimensionality of stability has been clearly stated in the ecological literature for decades, little is known about how different metrics of stability relate to each other in ecological communities. By simulating multispecies trophic networks, we measure how frequently used stability metrics relate to each other, and we identify the independent components they form based on their correlations. Our results open a way to a simplification and better understanding of the overall stability of ecological systems.

Abstract

Understanding the stability of ecological communities is a matter of increasing importance in the context of global environmental change. Yet it has proved to be a challenging task. Different metrics are used to assess the stability of ecological systems, and the choice of one metric over another may result in conflicting conclusions. Although each of the multitude of metrics is useful for answering a specific question about stability, the relationship among metrics is poorly understood. Such lack of understanding prevents scientists from developing a unified concept of stability. Instead, by investigating these relationships we can unveil how many dimensions of stability there are (i.e., in how many independent components stability metrics can be grouped), which should help build a more comprehensive concept of stability. Here we simultaneously measured 27 stability metrics frequently used in ecological studies. Our approach is based on dynamical simulations of multispecies trophic communities under different perturbation scenarios. Mapping the relationships between the metrics revealed that they can be lumped into 3 main groups of relatively independent stability components: early response to pulse, sensitivities to press, and distance to threshold. Selecting metrics from each of these groups allows a more accurate and comprehensive quantification of the overall stability of ecological communities. These results contribute to improving our understanding and assessment of stability in ecological communities.

Stability has been a core topic of research in complex systems across disciplines. From socioeconomic models of political regimes (1, 2), to financial systems (3–5), social organizations (6, 7), or biological systems of genetic regulatory circuits (8, 9), the study of dynamical stability keeps drawing the attention of the scientific community. This interest has been particularly prominent in ecology, where it has fuelled decades of research (10–15). Yet, progress in understanding what determines the stability of complex systems such as ecological communities has been hampered by unclear and sometimes conflicting results. One of the main reasons has proved to be the broad definition of the concept of stability itself (12), which has led to confusion and a lack of clear guidelines about the practical quantification of stability in empirical studies (14, 16). Probably one of the best examples of this confusion is the long-standing controversy of how stability varies with species diversity (17). While some studies have shown that biodiversity can enhance stability (18–20), others have found the opposite result (21–23), both effects (24), or even nonmonotonous relationships (25). The explanation behind this apparent contradiction is that stability is a multidimensional concept: it has several facets and can be described by different metrics, which do not all vary positively with biodiversity (13, 24, 26). While the multidimensional nature of the stability concept has been well recognized in the literature (10–12), our understanding of it has remained limited (14). The vast majority of studies typically include only 1 metric of stability at a time, and the few studies that have simultaneously measured multiple metrics of stability have considered them as independent when, in fact, it has been acknowledged that they could be interdependent (27). This possible interdependence implies that measuring multiple metrics may more broadly estimate stability to the extent that these metrics quantify relatively independent components of stability. Therefore, to advance toward a thorough and more systematic assessment of ecological stability, we need to understand how stability can be decomposed into different components—also referred to as dimensions in the literature (27)—and if so, how many there are and how they can be best measured.

We tackle this challenge from a theoretical perspective by investigating the interdependence of stability metrics in trophic ecological networks. Combining structural food web models (28) with bioenergetic consumer–resource models (29, 30), we simulate the dynamics of multispecies trophic communities under different perturbation scenarios. Perturbations are changes in the biotic or abiotic environment that alter the structure and dynamics of communities (14, 31). We consider 3 main types of perturbations: pulse (32), i.e., instantaneous disturbances, after which community recovery can be measured (e.g., forest fires or floods); press (32), i.e., lasting disturbances after which postperturbed communities can be compared to preperturbed ones (e.g., climatic changes or extinction of a species); and environmental stochasticity (33–35), where communities are constantly affected by small external changes. We quantify the stability of our simulated communities to these perturbations with 27 metrics frequently used in the ecological literature (see Table 1). We then explore how these metrics correlate with each other. If metrics are found to be uncorrelated, that would mean that they all inform very different aspects of stability of an ecological community and that a more coherent concept of stability currently lacks empirical support. In the opposite case, if all metrics are found to be perfectly correlated with each other, considering only a single metric would be enough to assess the overall stability of an ecological community. Therefore, by studying the correlations between stability metrics, we can evaluate whether the different metrics considered provide similar information about the stability of an ecological community or whether they form distinct groups that reflect partly independent dimensions of community stability.

Table 1.

Stability metric’s names (characteristic time scales), definitons, and, when relevant, reference to the equation in SI Appendix, section 10

Name (time scale)	Acronym [equation in SI Appendix, section 10]	Description
Reactivity (initial)	$R_0$ [6], $M{R}_0$ [11]	Maximum instantaneous rate at which perturbations can be amplified. Measures the velocity of the system when initially going away from the equilibrium after a pulse perturbation. Driven by the most abundant species. Median reactivity over all species ($M{R}_0$) represents the whole community.
Maximum amplification (transient)	$A_{max}$ [9], $M{A}_{max}$ [12]	Factor by which the perturbation that grows the largest is amplified after a pulse perturbation. The factor by which the median displacement over all species deviates ($M{A}_{max}$) represents the whole community.
Time to maximum amplification (transient)	$t_{max}$, $M{t}_{max}$	Time to achieve the maximum amplification and time to achieve the maximum amplification of the median displacement after a pulse perturbation ($M{t}_{max}$).
Resilience (long-term)	$R_{inf}$ [10], $M{R}_{inf}$ [13]	Asymptotic (i.e., long-term) return rate to the reference state after a pulse perturbation. Metric driven by the least abundant species. The median resilience over all species ($M{R}_{inf}$) represents the whole community.
Stochastic invariability (long-term)	$I_s$ [14]	Measures if the environmental noise (assumed to be white noise) is amplified, i.e., if the fluctuations in species’ biomass are larger than the environmental noise.
Sensitivity matrix (long-term)	$<s_{ij}>$ [16], $S$ [15]	Average change in the biomass of species $i$ after a press perturbation is applied to species $j$ (assuming that postperturbed and preperturbed systems are at nearby fixed-point steady state and that perturbations are sufficiently small). The accumulated change over all species ($S$) represents the whole community.
Tolerance (long-term):
To mortality	$T{M}^G$ [17]	Minimum global increase in mortality (press perturbation applied on all species) that leads to at least 1 extinction.
	$<T{M}^L>$, $T{M}_{min}^L$	Minimum local increase in mortality (press perturbation applied on 1 species) that leads to at least 1 extinction. Each species is attacked in turn. The average (over all species) and the minimum increases that caused an extinction are measured.
To extinctions	$<TE>$	Measured as robustness, i.e., the number of actively performed (random) extinctions (press perturbation) required to reduce the number of surviving species to $50\%$ of the original number.
Resistance of total biomass (long-term):
To mortality	$R{M}^G$ [18]	Relative change in total biomass before and after a global increment of $10\%$ mortality (press perturbation applied on all species).
	$<R{M}^L>$, $R{M}_{max}^L$	Relative change in total biomass before and after a local increment of $10\%$ mortality (press perturbation applied to 1 species). Each species is attacked in turn. The average and maximum changes in total biomass are measured.
To extinctions	$<RE>$ [20], $R{E}_{max}$	Relative change in total biomass before and after each of the species goes extinct (and subsequent secondary extinctions have taken place) (press perturbation). The average and maximum changes in total biomass (over all extinction events) are measured.
Cascading extinctions (long-term)	$<CE>$, $C{E}_{max}$	Average number of secondary extinctions following 1 extinction (press perturbation). Each species is removed in turn. The average and maximum number of secondary extinctions over all extinction events are measured.
Sensitivity of species’ biomass (long-term):
To mortality	$S{M}^G$ [19]	Total accumulated change in species’ biomass before and after a global increment of $10\%$ mortality (press perturbation applied to all species).
	$<S{M}^L>$, $S{M}_{max}^L$	Total accumulated change in species’ biomass before and after a local increment of $10\%$ mortality (press perturbation applied to 1 species). Each species is attacked in turn. The average and maximum accumulated changes (over all events) are measured.
To extinctions	$<SE>$ [21], $S{E}_{max}$	Total accumulated change in individual biomass before and after each of the species goes extinct (and subsequent secondary extinctions take place) (press perturbation). Each species is attacked in turn. The average and maximum accumulated changes (over all extinction events) are measured.

See Material and Methods for a guide to the metrics’ acronyms. Stability metrics’ names (characteristic time scales), definitions, type of perturbation they are associated to (in bold letters in the description), and when relevant, reference to the equation in SI Appendix, section 10.

Results and Discussion

Community Size and Stability Metrics’ Correlations.

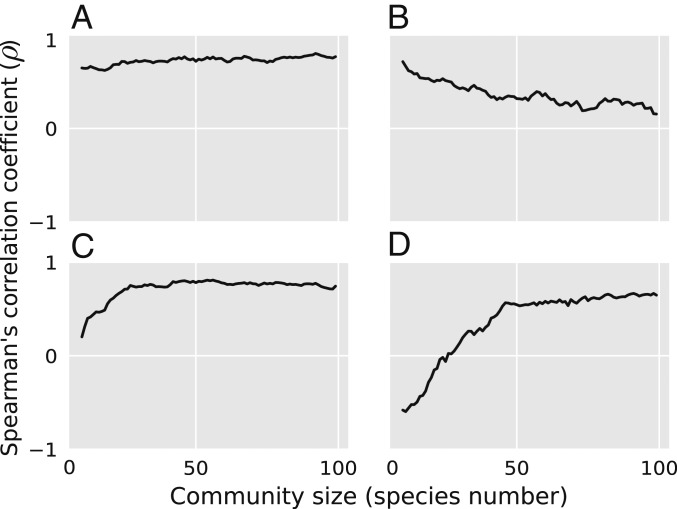
Community size (i.e., the number of species) has been shown to play a fundamental role in the stability of ecological networks, although it is not entirely clear if it promotes their stability, hinders it (13), or both (24, 25). For example, a food web simulation study showed that persistence (i.e., the fraction of surviving species) and population variability were either negatively or positively correlated depending on the species richness of the community (25). We therefore start by investigating if the pairwise correlations between the stability metrics are affected by community size in our simulated trophic communities. Overall, many pairwise correlations (∼44$\%$ out of the 351 correlation pairs) are not highly affected by community size (Fig. 1A). Some pairwise correlations (∼32$\%$) become weaker as community size grows (Fig. 1B), while others (∼20$\%$) become stronger (Fig. 1C). In a few cases (∼3$\%$), the correlation between 2 metrics can switch sign as community size changes (Fig. 1D). The dependence of pairwise correlations on community size is especially present in communities with fewer than 50 species. In contrast, most correlations (∼94$\%$) remain largely constant in species-rich communities ($>$50 species; SI Appendix, Fig. S1). Given the dependence of pairwise correlations on community size, we next study stability metric correlations across 3 levels of species richness: small (5 to 15 species), medium-sized (45 to 55 species), and large communities (85 to 95 species). In what follows, we present the results for medium-sized communities, while the results for small and large communities can be found in SI Appendix.

Fig. 1.

Spearman’s $\rho$ pairwise correlation coefficient between stability metrics as a function of community size (i.e., number of species at steady state). (A) Some pairwise correlations are not affected by community size, e.g., correlation between 2 metrics of tolerance to increased mortality at a global (i.e., community) and local (i.e., species) scale ($T{M}^G$ and $<T{M}^L>$, respectively). (B) Some metrics are only strongly correlated in small communities, e.g., correlation between stochastic invariability ($I_s$) and time to maximum amplification ($t_{max}$). (C) Other metrics are only strongly correlated in large communities, e.g., correlation between resilience ($R_{inf}$) and the average strength of the sensitivity matrix ($<s_{ij}>$). (D) Some pairwise correlations change sign with community size, e.g., correlation between the resistance of total biomass ($R{M}^G$) and the sensitivity of species biomass to a global increase in mortality ($S{M}^G$). See Table 1 and Materials and Methods for metrics’ definitions.

Three Groups of Stability Metrics.

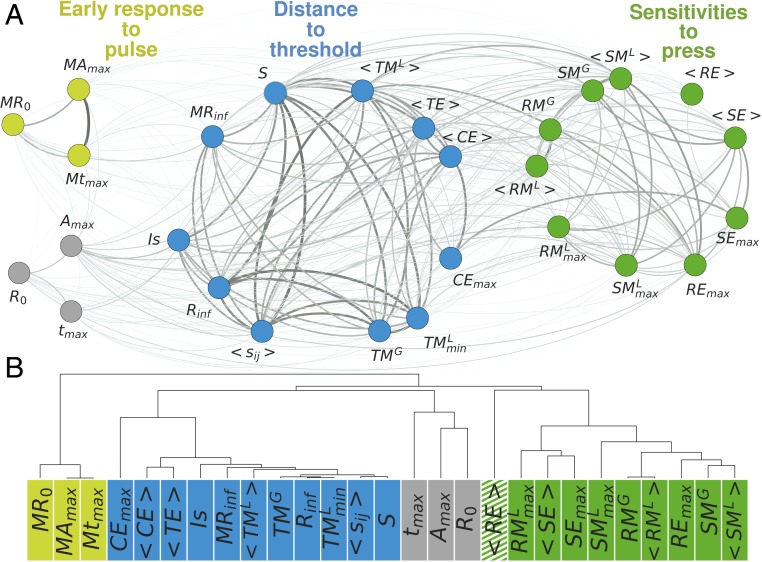
To explore if there is any structure in the way metrics are correlated with each other, we build a network of stability metrics in which nodes represent the metrics and links their weighted (unsigned) pairwise correlations (Materials and Methods). Using a community detection algorithm based on maximizing modularity (Materials and Methods), we find that metrics form 3 distinct groups such that metrics that belong to the same group are more strongly correlated with each other than with metrics outside of their group (Fig. 2A and SI Appendix, Fig. S3).

Fig. 2.

(A) Network of stability metrics for medium-sized communities (45 to 55 species). Nodes represent stability metrics and the thickness of links their unsigned pairwise Spearman’s $\rho$ correlation coefficients. Node colors distinguish the 3 groups identified by the modularity algorithm, with a modularity of $Q$ = 0.177: early response to pulse group in light green, distance to threshold group in blue, and sensitivities to press group in darker green. In gray are metrics that the modularity algorithm was not able to unambiguously place in any group. (B) Hierarchical clustering applied to the network of stability metrics. Correlations are used to compute a distance between all pairs of metrics, which are represented here by a dendrogram. The key to interpreting such a dendrogram is to focus on the first branch at which any 2 metrics are joined together; the farther away 2 metrics are from this common ancestor, the less similar they are. The goodness of fit of distances based on the dendrogram to the distances in the original data (pairwise correlations) is quantified by the cophenetic coefficient ($c=$ 0.85). Metrics are clustered similarly as by the modularity partitioning, except for the resistance to extinction metric ($<RE>$) represented with a striped pattern, which is therefore considered to not clearly belong to one of the groups in upcoming analyses. See Table 1 for metrics’ definitions.

The early response to pulse group (light green in Fig. 2A) contains measures of the initial and short-term deviations of a community from its reference state after a pulse perturbation. The sensitivities to press group (green in Fig. 2A) includes metrics that quantify changes in total and individual species’ biomass between postperturbed and preperturbed communities after a press perturbation. The distance to threshold group (blue in Fig. 2A) consists of metrics that measure how easily a system crosses thresholds to new dynamical states, for example, the amount of external pressure before a community experiences an abrupt change, the closeness of the rarest species to extinction, the population variability, and secondary extinctions caused by random extinctions.

Three metrics (in gray in Fig. 2A) were not clearly assigned to any of the 3 groups (SI Appendix, section 2). These metrics include measures of the initial and transient responses of the most abundant species to pulse perturbations. Because of their idiosyncratic correlations with the rest of the metrics, we kept them apart from the other metrics.

Interestingly, the 3 emergent groups split metrics in terms of both the temporal scale of the response and the type of perturbation. Indeed, the early response to pulse group only contains metrics describing transient behavior, while the sensitivities to press and distance to threshold groups contain metrics describing long-term (asymptotic) dynamics. Furthermore, the early response to pulse and sensitivities to press form 2 contrasting groups containing metrics that refer to pulse and press perturbations, respectively, while metrics in the distance to threshold group refer to both types of perturbations. The weak correlations between the 3 groups of metrics (with an average correlation of ∼0.13; SI Appendix, Fig. S2 and section 3) suggests that the metrics within a group can be considered as relatively independent from metrics in other groups. Therefore, these 3 groups reflect major components that constitute different dimensions of the stability of trophic communities (27) that should be measured in an ecological community to comprehensively assess its overall stability.

Further studying the degree of (dis)similarity between the different stability metrics with a hierarchical clustering analysis (36, 37) (Materials and Methods) confirms the partitioning found by the modularity algorithm, except for 1 outlier metric (striped in Fig. 2B), which was not attributed to the same group by both analyses (SI Appendix, section 4) and is therefore not considered to clearly belong to 1 of the 3 groups for subsequent analyses. The generated dendrogram allows one to visualize a more detailed structure, with subgroups of highly similar metrics within the 3 groups identified by the modularity algorithm (SI Appendix, section 4). Practically, this implies that for these sets of highly similar metrics, only 1 of the metrics could be selected interchangeably. Moreover, some of these close similarities could also be of theoretical interest. For example, in the distance to threshold group, we find 5 strongly connected metrics of very different nature: resilience (a metric of dynamical stability, $R_{inf}$), tolerance metrics (which assess structural stability; $T{M}^G$, $T{M}_{min}^L$), and sensitivity metrics (which are based on the inverse Jacobian; $S$, $<s_{ij}>$). Some of these connections have been previously reported (38, 39), but we still lack a complete theoretical map of most metrics’ relationships.

The Sign of the Correlations Between Stability Metrics.

The sign of the correlations between metrics is important because negative correlations between metrics would suggest trade-offs: promoting stability according to 1 of the metrics would happen at the expense of stability according to another metric. In our simulated trophic communities, however, we only find a few negative correlations (SI Appendix, section 5 and Fig. S4). Most of the negative correlations are identified in small communities (below 20 species) between metrics of resistance (i.e., total change in aggregated community biomass before and after a press perturbation) and sensitivity (total change in species’ populations after a press perturbation; see Table 1). In fact, in communities of more than 20 species, there is only 1 relatively strong negative correlation ($\rho \sim -0.4$) between reactivity ($R_0$) and time to maximum amplification ($t_{max}$). The relationship between these 2 metrics has been previously studied and found to be complex (40). Our results here suggest that communities whose abundant species initially deviate fast from their original state (i.e., high $R_0$) are also those that tend to start recovering early (i.e., low $t_{max}$); conversely, communities with abundant species that are less reactive tend to take longer before they start their recovery.

The vast majority of positive correlations (from ∼$86\%$ of all 351 pairs in small communities to ∼93$\%$ in large communities) found here is in line with recent experimental findings, where multiple positive correlations between stability metrics were found in communities of similar size to our simulated communities (24, 27). For example, we find a positive correlation ($\rho =$ 0.54) between invariability ($I_s$) and resistance to small press perturbations ($S$) in agreement with ref. 24. We also find a positive correlation ($\rho =$ 0.57) between invariability ($I_s$) and the number of secondary extinctions ($<CE>$), in communities of similar sizes to those studied by ref. 27. In light of this, stability trade-offs seem to be a rare exception in complex trophic communities.

Mapping the Stability Metrics.

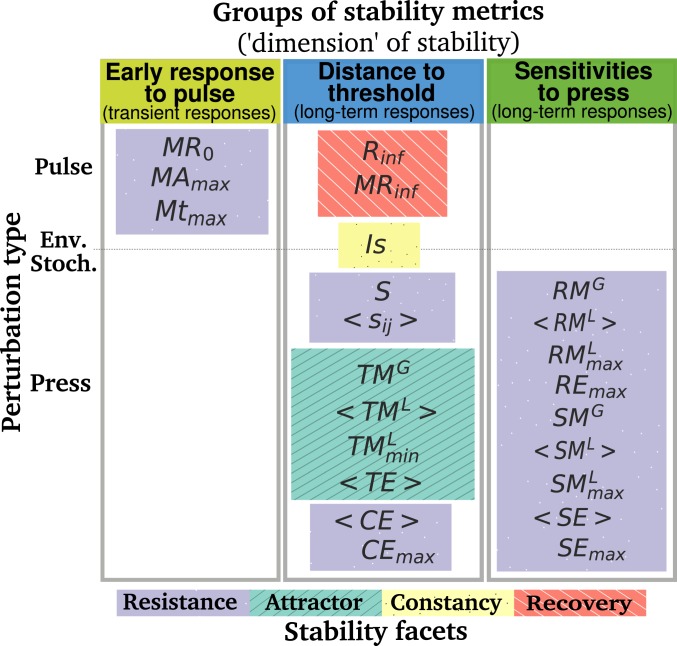
Past reviews of stability in ecology have highlighted the multidimensional nature of stability and have attempted to group metrics in a few stability facets based on the similarity in their definition (10–13). Here, 3 relatively independent groups of metrics emerged from the analysis of the correlations between metrics, and we argue that these groups can be interpreted as different dimensions of stability. In what follows, we map all metrics according to their stability group (or dimension), perturbation type, and stability facet in an attempt to better understand the relationships between these different categories (Fig. 3).

Fig. 3.

Classification of the stability metrics according to 3 axes: the perturbation type (pulse, press, or environmental stochasticity), the stability group (early response to pulse, distance to threshold, and sensitivities to press), and the stability facets typically describing stability properties in the literature. There is currently no consensus on the names of these facets; we here refer to them as resistance in purple (how much the system changes under a press perturbation), attractor in green (the type and number of attractors of the system), constancy in yellow (how variable the system is), and recovery in red (if and how the system recovers from a pulse perturbation) (15). Colors of the groups of stability metrics are the same as in Fig. 2. Metrics not clearly associated to 1 of the 3 groups in Fig. 2 (i.e., the metrics in gray and $<RE>$) were not included here. See Table 1 for metrics’ definitions.

This mapping reveals that the stability facets and the stability groups do not map 1-to-1. For example, resistance metrics can belong to all 3 stability groups, while metrics from the 4 stability facets can be highly correlated with each other and belong to the same stability group (e.g., the distance to threshold group). More strikingly, our mapping shows that it is not possible to simultaneously capture the 3 stability dimensions with an experiment that would involve only 1 type of perturbation. Early response to pulse, i.e., transient responses (Fig. 3, Left), can only be studied in communities that experience a pulse perturbation, while all resistance and sensitivity of biomass metrics are, by definition, the results of a press perturbation. The fact that knowledge about stability to a given type of perturbation does not extend to another type of perturbation confirms that we cannot get away from specifying the stability “of what” and “to what” (14, 16).

Conclusion

Perhaps the most important finding of our analysis is that the multiplicity of stability metrics can essentially be mapped into 3 relatively independent groups that reflect 3 different components, or dimensions, of stability. This suggests that the dimensionality of the stability of trophic ecological communities is much lower than the number of metrics used to quantify it and that stability could therefore be assessed using a small number of metrics.

Each of the many stability metrics allows addressing specific questions by quantifying a given aspect of stability. At the same time, however, the grouping of many metrics in just a few components raises the question of which specific metrics to choose if one wants to assess the overall stability of an ecological system. An intuitive guess is that combining metrics from each of the 3 groups could be a way of decreasing the amount of metrics used, while still accurately estimating the multiple dimensions of the stability of an ecological community. Preliminary analyses suggest that using only 3 metrics—those with the highest explained variance in each of the groups—explains 54$\%$, 52$\%$, and 59$\%$ of the original variance in small, medium, and large communities, respectively (see SI Appendix, section 6, for more details). Moreover, analyses of the volume of the covariance ellipsoid confirm that selecting metrics from the 3 different groups, rather than the same number of metrics from the same group, best describes the different stability dimensions (see SI Appendix, section 7 and Fig. S7). However, due to the high correlations between metrics within a group, it is difficult to propose a single best way of selecting metric(s) in each of the groups. Although the choice of the metrics will always depend on the system studied and on practical constraints, hierarchical analyses (Fig. 2B and SI Appendix, Fig. S3) and explained variance analyses (SI Appendix, section 6) can help making informed choices.

Interestingly, our analysis confirms previously known relationships between metrics, but it also reveals unexpected dependencies, which could be either due to mathematical relationships yet to be investigated or because the metrics actually expose latent dimensions of stability. Although, our approach does not elucidate the causes for the metrics’ correlations, it does point toward future areas of research. In that sense, our results are of interest to both theoreticians—because they hint toward yet unknown mechanisms underlying correlations between stability metrics—and experimentalists, who can use the patterns of correlations to choose which metrics to evaluate in their experiments.

Finally, although our study focuses on the stability of food webs, the relationships found here could be of interest to understand the stability of other types of networks, in ecology as well as in other disciplines. In fact, even if the exact number of identified groups of metrics could be altered in other systems or by the incorporation of additional stability metrics, the framework we propose is flexible enough to accommodate to different conditions and opens a way toward simplifying the study of overall stability in different types of complex dynamical system. After all, directed networks of many kinds describe transport of matter, information, or capital in a similar way to how food webs describe fluxes of biomass from primary producers to apex predators.

Materials and Methods

Stability Metrics.

We review the ecological literature to identify the most frequently used metrics for assessing community stability. Specifically, we consider metrics that quantify stability in communities that yield stable (fixed equilibrium) dynamics. We do not consider measures of community invasibility. For metrics that can be quantified in multiple ways, we only retain a single way of measuring that metric. With these criteria, we obtain 27 metrics that are described in Table 1, specifying their temporal scale (below the name) and the type of perturbation they are associated to (in bold letters in the description). Metrics include analytical responses to small pulse perturbations—i.e., instantaneous disturbances causing a sudden change in species abundances—obtained from the community matrix (or Jacobian) covering initial (reactivity), transient (maximum amplification and time to maximum amplification), and asymptotic (resilience) temporal regimes, both quantified at the individual species level and at the community level (21, 40, 41). Responses to environmental noise are assessed with the stochastic invariability metric (34). Analytical responses to small press perturbations—i.e., lasting disturbances causing the abundance of species to be permanently changed—are measured by means of the sensitivity matrix (inverse of the Jacobian matrix) (32, 38, 42). We also apply 2 different types of more intense press perturbations empirically: an increase in mortality both at the local (i.e., only on 1 individual species at a time) and at the global (i.e., on all species of the community simultaneously) scales and random extinctions of species. Structural stability (43, 44) to these 2 types of press perturbations is assessed with the tolerance metrics (Table 1). Tolerance to mortality is measured as in previous studies (45, 46), and tolerance to extinctions is measured with robustness (47). We also include metrics of community resistance to random extinctions (48) as cascading extinctions. Empirical measures of resistance to both types of press perturbations, named resistance of total biomass and sensitivity of species’ biomass, are also quantified in a similar fashion as in previous studies (49). All of the metrics are defined in such a way that an increase in their value means an increase in community stability. Definitions of metrics can be found in SI Appendix, section 10, and the dataset of stability metrics can be found in Dataset S1.

The acronyms of the metrics that quantify responses to empirical press perturbations are encoded as follows: the first letter represents if they are a measure of tolerance (T), resistance (R), or sensitivity (S), followed by the initial letter of the perturbation, which is either mortality (M) or random extinctions (E). The superscript differentiates, when needed, if the perturbation is global (G) (i.e., applied on all species of the communities as the same time) or local (L) (i.e., applied on 1 species at a time). When nothing is indicated, the perturbation is assumed to be local. In the case of local perturbations, the subscripts $min$ and $max$ indicate whether the metric is the extreme (minimum or maximum, respectively) value observed, while the brackets $<>$ indicate that the metric is the average of all observed values.

Generating Communities and Model Simulations.

We use the niche model (28) to construct food web communities. We then use the produced community structure to simulate the biomass of each species using a bioenergetic consumer–resource model with allometric constraints (30):

$$\frac{d{B}_i}{dt}=r_i{G}_i{B}_i+B_i\sum _{j\in prey}{e}_{0j}{F}_{ij}-\sum _{k\in pred}{B}_k{F}_{ki}-x_i{B}_i-d_i{B}_i,$$ [1]

where the interaction term $F_{ij}$ is defined as

$$F_{ij}=\frac{w_i{a}_{ij}{B}_j^{1+q}}{m_i\left(1+w_i{\sum }_{k\in prey}{a}_{ik}{h}_{ik}{B}_k^{1+q}\right)}.$$ [2]

During the simulations, species biomass adjusts dynamically, and some extinctions may occur before a steady state is achieved. Thus, the species that compose the final dynamical trophic networks are selected by structural constraints and energetic processes among the species. We fix the parameter of the functional response to $q=0.3$ and the predator/prey body mass ratio to $Z=1.5$. Values for all of the other scaling parameters are averages of values presented in ref. 50. We generate networks with an initial species richness ranging from 5 to 115 species and a fixed connectance of $c=0.15$. During the simulations, if species biomass crossed the extinction threshold ($1E^{-6}{m}_i$, where $m_i$ is the mass of species i), we consider that species extinct. If more than $10\%$ of the initial number of species goes extinct, we discard this community. Following this procedure, we simulate more than 10,000 different dynamical trophic communities with species richness ranging from 5 to 105 species. For more details, see SI Appendix, sections 8 and 9.

Pairwise Correlations and Networks of Stability Metrics.

For each community size, ranging from 5 to 100 species (with a step of 1), we sample 100 trophic communities of each size (Dataset S2) and compute the pairwise correlations among all stability metrics using Spearman’s correlation rank, $\rho$. We consider that pairwise correlations remain unchanged throughout a gradient of species richness if the variation in the correlation between the initial and final community sizes ($\mathrm{\Delta }\rho$) is below 0.1. We use the pairwise correlations to build a network of stability metrics. In this network, each node is a metric and the links are the pairwise correlations between the metrics. The links are weighted (i.e., the stronger the correlation, the thicker the link) and unsigned (i.e., we consider absolute correlations and ignore if 2 metrics are negatively or positively correlated). We assemble in this way networks of stability metrics for different classes of community sizes: small (5 to 15 species), medium (45 to 55 species), and large (85 to 95 species) communities by considering the average value of correlations (i.e., average $\rho$) within these size ranges.

Grouping Stability Metrics.

We search for groups of metrics in the stability network such that pairs of metrics are more strongly correlated to other metrics of the same group than to metrics in other groups. Modularity quantifies the quality of a particular partition of a network into such clusters (i.e., groups of nodes) (51). The modularity algorithm detects clusters by searching over many possible partitions of a network and finding the one that maximizes modularity (52). We apply such a community detection algorithm on our pairwise-correlation weighted networks using Gephi (53). We repeat the computations 10 times for each network, and we select the partition in clusters that renders the highest value of modularity (i.e., $Q$ = 0.177).

Stability Metric (Dis)similarity.

We use hierarchical clustering (36) to aggregate stability metrics according to their similarity (based on correlation). Starting with the closest pair of metrics, subsequent metrics are joined together in a hierarchical fashion from the closest (i.e., most similar) to the furthest apart (most different) until all metrics are included. The distance between a pair of metrics is defined as $d=\left(1-\rho \right)$, where $\rho$ is the Spearman’s rank correlation. We constructed the dendrogram with the hierarchical agglomerative clustering (HAC) algorithm in Python (54). We selected the linkage method (average) that rendered distances in the dendrogram closest to the original pairwise correlation (goodness of fit based on the cophenetic correlation coefficient $c$ = 0.85). The closer $c$ is to 1, the better the correspondence.

Data Availability.

Datasets of stability metrics are included as Datasets S1 and S2. Analysis code is available in GitHub (55). Simulation code is available upon request.