Magnetoelastoresistance in WTe₂: Exploring electronic structure and extremely large magnetoresistance under strain

Significance

Strain is a widely employed technique to probe and control the electronic properties of quantum materials. Primary examples are studies of the elastoresistance, which describes the change of resistance due to applied strain, that have elucidated the nature of nematicity in iron-based superconductors. In this work, we introduce the measurement of magnetoelastoresistance (MER) and analyze in detail the combined effect of strain, caused by uniaxial stress, and magnetic field on the semimetal ${\mathrm{W}\mathrm{T}\mathrm{e}}_2$. We show that this material exhibits a large MER that is dominated by changes of the electronic structure caused by the elastic deformation. We further demonstrate that MER provides insight into strain-induced modifications of the band structure and transport quantities that goes beyond the zero-field elastoresistance.

Abstract

Strain describes the deformation of a material as a result of applied stress. It has been widely employed to probe transport properties of materials, ranging from semiconductors to correlated materials. In order to understand, and eventually control, transport behavior under strain, it is important to quantify the effects of strain on the electronic bandstructure, carrier density, and mobility. Here, we demonstrate that much information can be obtained by exploring magnetoelastoresistance (MER), which refers to magnetic field-driven changes of the elastoresistance. We use this powerful approach to study the combined effect of strain and magnetic fields on the semimetallic transition metal dichalcogenide ${\mathrm{W}\mathrm{T}\mathrm{e}}_2$. We discover that WTe₂ shows a large and temperature-nonmonotonic elastoresistance, driven by uniaxial stress, that can be tuned by magnetic field. Using first-principle and analytical low-energy model calculations, we provide a semiquantitative understanding of our experimental observations. We show that in ${\mathrm{W}\mathrm{T}\mathrm{e}}_2$, the strain-induced change of the carrier density dominates the observed elastoresistance. In addition, the change of the mobilities can be directly accessed by using MER. Our analysis also reveals the importance of a heavy-hole band near the Fermi level on the elastoresistance at intermediate temperatures. Systematic understanding of strain effects in single crystals of correlated materials is important for future applications, such as strain tuning of bulk phases and fabrication of devices controlled by strain.

The application of strain is a widely employed technique to probe and control electronic properties of quantum materials (1–6). Important examples are studies of the elastoresistance (ER), which describes the change of resistance due to applied strain, that have given valuable insights about the nature of nematic electronic order in iron-based superconductors (4, 7, 8), heavy fermions (9), and rare-earth intermetallics (10). Other examples are the use of strain to modify transition temperatures and tune through the phase diagram in systems with superconducting (2, 3, 5), magnetic (6), or ferroquadrupolar order (11). One of the main advantages of using strain is that it provides control over the symmetry of the elastic deformation and can therefore selectively probe the elastic response along certain crystallographic directions, induce a desired symmetry change of the electronic and lattice structure, or couple to particular electronic orders and their fluctuations (7, 10, 11). Strain can be varied continuously and, unlike chemical doping, does not inherently introduce additional disorder. As we show here, it can also be combined with other external perturbations such as magnetic fields.

One crucial question that must be addressed in order to understand and control the transport behavior of materials under strain is to quantify its effect on the electronic and lattice structure, carrier densities, and mobilities. This requires insight from various probes such as angle-resolved photoemission spectroscopy (ARPES), X-ray, and neutron scattering and transport measurements, as well as first-principle calculations. Here, we demonstrate that measurements of the magneto-ER (MER), which refers to magnetic field-driven changes of the ER, yield additional, complementary information about strain-induced modifications of transport parameters, such as carrier densities and mobilities. This follows from the observation that strain derivatives of those microscopic parameters contribute differently to ER in the zero and finite magnetic field. Analogous to magneto-resistance (MR), MER shows a rich behavior as a function of temperature and field, which we analyze thoroughly below using Lifshitz–Kosevich (12) and semiclassical approaches (13).

We exemplify the capability of this measurement technique by applying it to single crystals of the transition metal dichalcogenide (TMDC) ${\mathrm{W}\mathrm{T}\mathrm{e}}_2$. This is a promising system to investigate MER due to its low carrier density, high mobility, and large MR (14, 15). Like many other TMDCs, ${\mathrm{W}\mathrm{T}\mathrm{e}}_2$ has a layered structure with weak van-der-Waals bonding between chalcogenide layers (16) and can be easily exfoliated. The electronic bandstructure of ${\mathrm{W}\mathrm{T}\mathrm{e}}_2$ is well characterized by ARPES and first-principle calculations (14, 15, 17–21) and corresponds to that of a semimetal with several small electron and hole pockets. ${\mathrm{W}\mathrm{T}\mathrm{e}}_2$ is known to exhibit extremely large and unsaturating positive MR (XMR) due to a (nearly) perfect compensation of electron and hole carrier densities (14, 15). The XMR signal can be suppressed by the application of high pressure ($>2.5$ GPa), leading to the appearance of a superconducting state (22, 23). Such tunability by hydrostatic pressure is characteristic of various TMDCs (16, 24, 25) and suggests that uniaxial stress may also be a powerful tuning parameter. While previous ab initio calculations have suggested that strain can tune electronic characteristics of two-dimensional TMDCs such as band gap, effective masses, or spin-orbit coupling (SOC) (26), a systematic experimental study for bulk materials is still lacking.

Here, we demonstrate that bulk single crystals of ${\mathrm{W}\mathrm{T}\mathrm{e}}_2$ exhibit a large and temperature-nonmonotonic ER that is highly tunable by an external magnetic field. Using a combination of quantum oscillation data analysis, first-principle density functional theory (DFT), and analytical transport calculations, we elucidate the physical origin of these results. We find that strain tuning of carrier densities is the dominant effect in ${\mathrm{W}\mathrm{T}\mathrm{e}}_2$, as opposed to modifications of effective masses and scattering rates. Our analysis also identifies the important role of a heavy hole pocket in the intermediate temperature transport, which is located just below the Fermi surface (FS) and gets lifted upward by strain. This demonstrates that measurements of MER and quantum oscillations under strain provide valuable information about stress-induced changes of carrier densities, mobilities, and effective masses in ${\mathrm{W}\mathrm{T}\mathrm{e}}_2$. Our work thus provides insights into the interplay of elastic and electronic degrees of freedom in ${\mathrm{W}\mathrm{T}\mathrm{e}}_2$ that will facilitate strain engineering of electronic properties of this, and possibly other, TMDCs.

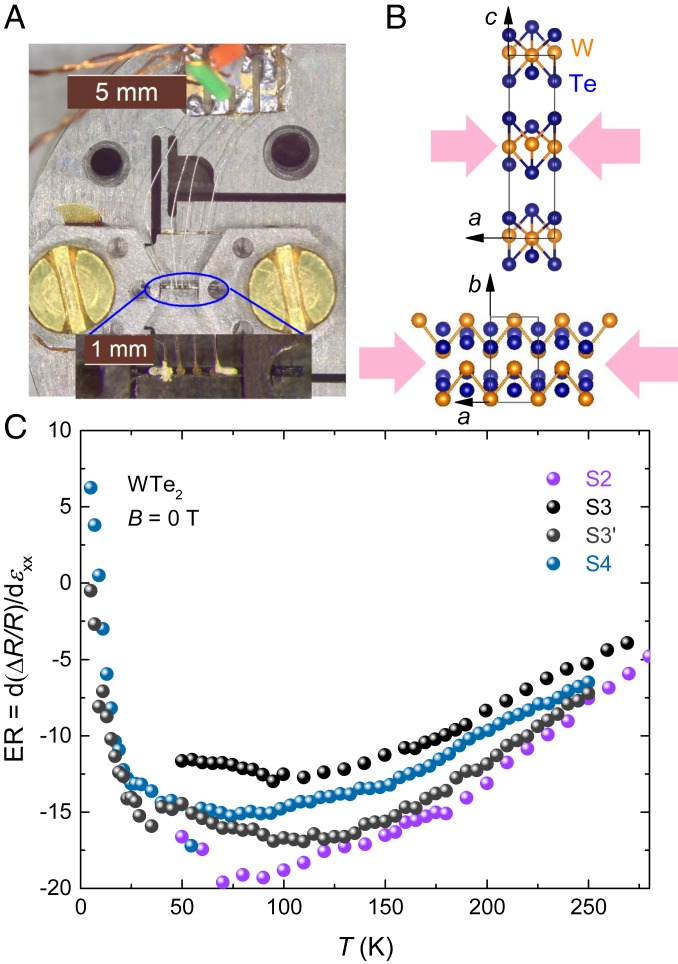
${\mathrm{W}\mathrm{T}\mathrm{e}}_2$ has orthorhombic crystal symmetry (space group $Pnm{2}_1$) and exhibits a pseudo-1D lattice structure (16) with distorted zig-zag chains of W atoms running along the crystallographic $a$ direction. We therefore applied uniaxial stress and electric current along the $a$ direction. The experimental setup and the crystal structure are shown in Fig. 1 A and B. As presented in Fig. 1C, uniaxial stress along $a$ direction resulted in a large $\text{ER}=\frac{d\left(\mathrm{\Delta }R/R\right)}{d{\epsilon }_{xx}}\left(T\right)$, where $\mathrm{\Delta }R=R\left({\epsilon }_{xx}\right)-R\left({\epsilon }_{xx}=0\right)$, that reached values as low as $\text{ER}\approx -20$ around a temperature of $T=100$ K. Neither the sign nor the magnitude of the ER can arise from purely geometric changes, given that the in-plane Poisson ratio is about 0.16 (27) [the isotropic Poisson ratio is 0.23 (28)], suggesting a positive geometric contribution of 1.32 (or 1.46 from the isotropic Poisson ratio). ER is thus clearly governed by the strain-induced changes to the electronic structure. We verify this hypothesis below by directly monitoring the effect of strain on electronic FS properties that we infer from measuring Shubnikov–de Haas (SdH) oscillations. Interestingly, as temperature is lowered, ER exhibits a nonmonotonic behavior. It increases rapidly below 35 K and becomes positive at the lowest temperatures. We show below that this behavior can be understood within a low-energy, three-band model calculation as arising from a strain-induced redistribution of carriers among electron and hole pockets with different effective masses. Whereas at low temperatures the redistribution only occurs among states right at the Fermi energy, at higher $T$, one must consider contributions from bands within a range of $k_{B}T$.

Fig. 1.

Measurement setup and zero-field ER. (A) A single crystal of ${\mathrm{W}\mathrm{T}\mathrm{e}}_2$ is mounted on Razorbill CS100 cryogenic uniaxial stress cell. The electrical current and mechanical stress were applied along the crystallographic $a$ direction, and the magnetic field was applied along the crystallographic $c$ direction. A maximum voltage applied to the piezoelectric material of $V$ = $\pm$5 V. (B) Crystal structure of ${\mathrm{W}\mathrm{T}\mathrm{e}}_2$. (B, Upper) Structure shows the $ac$ plane which demonstrates layered structure along the $c$ axis. (B, Lower) Structure shows the $ab$ plane with distorted zig-zag chains of W atoms in the $a$ direction. (C) ER of ${\mathrm{W}\mathrm{T}\mathrm{e}}_2$ in the temperature range of $5\hspace{0.17em}\mathrm{K}\le T\le 270\hspace{0.17em}\mathrm{K}$ with $B=0$ T for samples S2, S3, S3′, and S4. All samples exhibit a large, negative ER at not-too-low temperatures. S3 and S4 show a pronounced upturn at low temperatures $T\lesssim 25$ K. Quantitative differences between samples can be due to differences in quality and/or strain transmission through the sample.

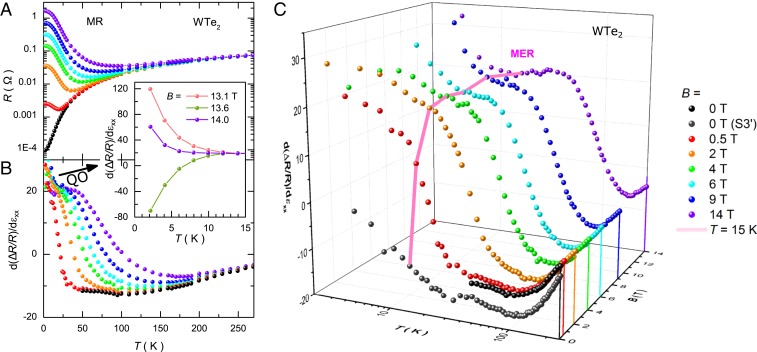
In Fig. 2, we present MR and $\text{MER}=\frac{d\left(\mathrm{\Delta }R/R\right)}{d{\epsilon }_{xx}}\left(B,T\right)$ results of ${\mathrm{W}\mathrm{T}\mathrm{e}}_2$. As seen in Fig. 2A and reported in ref. 14, the resistance exhibited a large increase in an applied magnetic field. This behavior was traced back to a nearly perfect compensation of electron and hole charge carriers (14, 19, 22). Fig. 2B shows that the temperature-dependent ER also has pronounced response to an applied magnetic field. The observed behavior in field is different at low, intermediate, and high temperatures. In the quantum regime, at temperatures $T<12$ K, where MR exhibits SdH oscillations, the ER changed dramatically, with relatively small changes in the magnetic field. This is highlighted in Fig. 2 B, Inset, which shows the low-$T$ ER for three nearby magnetic field values. Over this relatively small field range of 0.9 T, the ER varied from 120 to $-75$ and back to 50. This behavior is an immediate consequence of strain tuning of SdH oscillations due to a variation of carrier densities and effective masses, which we show in detail below. We also observed quantum oscillations in the difference of the resistance at finite- and zero-strain $\mathrm{\Delta }R$ as a function of magnetic field. These oscillations retained the same frequencies as SdH oscillations (see SI Appendix for details). For intermediate temperatures above the quantum regime (e.g., $T\gtrsim 15$ K), the MER increased rapidly as a function of magnetic field and eventually saturated (solid pink line in Fig. 2C). By performing a semiclassical transport analysis based on a two-band model of electron and hole carriers, we explicitly demonstrate below that this saturation value is a direct measure of the change in mobility due to strain: $\frac{d\mu }{d{\epsilon }_{xx}}$. Finally, at high temperatures, the ER only weakly depended on magnetic field. Fig. 2C shows a 3D plot of the $\text{MER}\left(B,T\right)$.

Fig. 2.

MR and MER of ${\mathrm{W}\mathrm{T}\mathrm{e}}_2$. (A) Resistance of sample S3 as a function of temperature for various magnetic fields, $H=\mathrm{0,0.5},\mathrm{2,4,6,9,14}$ (in units of T). The key is shown on the right. The field is applied along the crystallographic $c$ direction. (B) ER of sample S3 as a function of temperature in the same magnetic fields $H$. B, Inset shows ER in the low-temperature regime ($2\hspace{0.17em}\mathrm{K}\le T\le 15\hspace{0.17em}\mathrm{K}$) with an applied magnetic field of 13.1, 13.6, and 14 T. (C) A 3D representation of MER data from B including $H=0$T data of sample S3′. The pink line connects the data at $T=15$ K, highlighting the rapid increase and eventual saturation of MER in the magnetic field.

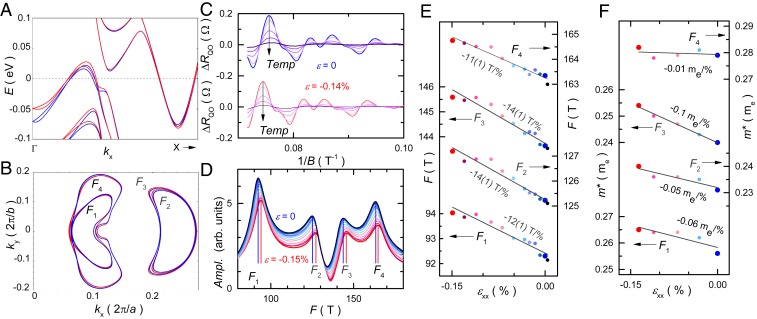
We can directly monitor the effect of strain on the carrier effective masses and the cross-sections of extremal orbits on the FS (perpendicular to the applied magnetic field) by measuring SdH oscillations and comparing with DFT band structure calculations. Fig. 3A shows DFT calculations with and without strain. The band structures have been calculated by using relaxed ionic positions with unit cell volume and shape subjected to strain along the $a$ direction and a Poisson ratio of 0.16 (27). We have carefully checked that our results do not differ much if we vary the out-of-plane Poisson ratio from 0 to 0.16 to 0.23. This insensitivity stems from the weak van-der-Waals interaction and the large $c$-axis spacing between the layers. More importantly, given that the curvature of a band at the Fermi level relates to the effective mass of the charge carrier, one can clearly see in Fig. 3 that the effective masses change as strain is applied. In addition, the FS areas enclosed by extremal orbits (29) in the $k_x$–$k_y$ plane at $k_z=0$ also vary as a function of strain, as shown in Fig. 3B.

Fig. 3.

DFT results and quantum oscillation analysis under strain. (A) Results of DFT band structure calculation along the $\mathrm{\Gamma }$-$X$ direction without strain (${\epsilon }_{xx}=0\%$; blue) and with strain (${\epsilon }_{xx}=-0.2\%$; red) applied along the $a$ axis. (B) Strain-induced modification of extremal orbits at $k_z=0$ from DFT calculation. Blue and red lines refer to the same strain as in A. FSs $F_1$ and $F_4$ correspond to hole bands and $F_2$ and $F_3$ to electron bands. (C) Experimental results for SdH oscillations after subtracting the background at temperatures $T=$2, 3, 5, 7, and 10 K for sample S2. The upper plot is for ${\epsilon }_{xx}=$ 0$\%$, and the lower plot is for ${\epsilon }_{xx}=$ –0.14$\%$. (D) FFT results at various ${\epsilon }_{xx}$. Blue lines indicate the frequencies at 0 ${\epsilon }_{xx}$, and red lines are located at the frequencies at −0.15$\%$ strain. (E) SdH oscillation frequencies of the 4 extremal orbits $F_{\mathrm{1,2,3,4}}$ as a function of strain ${\epsilon }_{xx}$. The numerical values of the slopes are given in the figure. (F) Effective cyclotron masses of the 4 extremal orbits $F_{\mathrm{1,2,3,4}}$ as a function of strain, with slopes given in the figure.

The changes of the extremal FS areas ($S_i$) and the effective (cyclotron) masses can be experimentally inferred from analyzing SdH oscillation frequencies $F_i$ and their amplitudes as a function of temperature. After subtracting a quadratic background, the residual oscillatory parts of resistance, with and without strain, are plotted as a function of $1/B$ in Fig. 3C. In order to quantify the FS changes, we performed a fast Fourier transform (FFT) in Fig. 3D, which revealed that all four frequencies shifted to higher values under compression. Since the frequency is related to the extremal orbit of the FS via the Onsager relation, $F_i=\frac{\hslash c}{2\pi e}{S}_i$ (12) , these positive shifts indicate enlarged FS orbits, in agreement with DFT calculations. Fig. 3E shows a linear dependence of frequency on strain. Fig. 3C also shows that the amplitudes of the SdH oscillations decreased with increasing temperature. This allowed us to extract the effective masses $m_i^{*}$ using Lifshitz–Kosevich theory (12). Fig. 3F demonstrates that all 4 masses increased linearly under compressive strain, yet with different slopes.

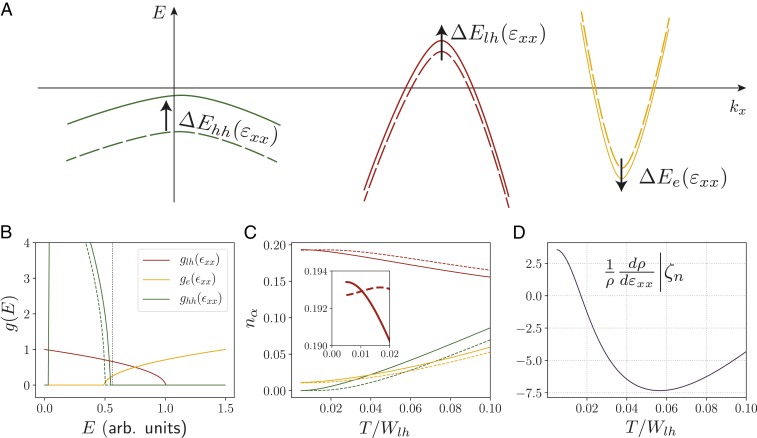
To interpret our ER and MER measurements, we employed an effective low-energy model that can account for the salient experimental features. Using input from DFT calculations as well as ARPES and quantum oscillation measurements (14, 15, 17, 19–21), our minimal low-energy model consists of three parabolic bands, as sketched in Fig. 4A: one electron pocket with effective mass $m_e^{*}$ and two-hole pockets with different effective masses $m_{lh}^{*}\ll m_{hh}^{*}$. The electron pocket and the light-hole $\left(lh\right)$ pocket cross the Fermi energy $E_F$, whereas the heavy-hole ($hh$) pocket sits slightly below $E_F$ (17, 19, 20).

Fig. 4.

Theoretical low-energy model analysis. (A) Schematics of electron and hole pockets in the low-energy three-band model before (dashed) and after (solid) application of compressive strain. Direction of strain-induced band shifts $\mathrm{\Delta }E\left({\epsilon }_{xx}\right)$ were taken from DFT calculations (Fig. 3). (B) Density of states $g\left(E\right)$ of three-band model before (dashed) and after (solid) rigid band shifts $\mathrm{\Delta }{E}_e=-4\times 10^{-3}$ and $\mathrm{\Delta }{E}_{\text{hh}}=4\times 10^{-2}$. All energies are in units of the light-hole bandwidth $W_{lh}$. The shift ratio $\mathrm{\Delta }{E}_{hh}/\mathrm{\Delta }{E}_e=10$ is taken to be 5 times larger than the one found within DFT (see SI Appendix for a detailed discussion). Bandwidths are set to $W_e=W_{lh}=1$ and $W_{hh}=0.5$. Effective masses are assumed to be strain-independent for simplicity, and their ratios were set to $m_e*/m_{lh}*=1$ and $m_{hh}*/m_{lh}*=4.6$, which approximately agrees with SdH oscillation analysis (SI Appendix). The bottoms of the bands are at $E_{lh}^{\text{min}}=E_{hh}^{\text{min}}=0$ and $E_e^{\text{min}}=0.5$. The chemical potential $\mu \left(T=0\right)=0.56\hspace{0.17em}{W}_{lh}$ is indicated by the vertical dotted line (total electronic filling $\mathcal{N}=0.77$). (C) Carrier densities of the different bands $n_{\alpha }$ as a function of temperature $T$ for 0 and finite strain. Colors and line styles are identical to A and B. C, Inset shows that $n_{lh}$ increases at low $T$ [as long as $|E_{hh}\left({\epsilon }_{xx}\right)-\mu |\ll T$], but decreases at higher $T$, eventually causing the sign change of the ER. (D) Elastoresistivity contribution that arises from redistribution of carriers due to rigid band shifts $\mathrm{\Delta }E\left({\epsilon }_{xx}\right)$ is shown in B. We have assumed that these band shifts are caused by strain of size ${\epsilon }_{xx}=-0.2\%$. Comparison with DFT yields that $\mathrm{\Delta }{E}_{hh}=0.04W_{lh}\simeq 16\hspace{0.17em}\text{meV}$ (relative shift to the $lh$ pocket) and, thus, $T=0.06W_{lh}\simeq 300$ K. At $T=0$, $ER>0$ as electrons move from the $lh$ to the $e$ band, increasing the total number of carriers (C, Inset). At $T>0$ (or, more specifically, $T\gtrsim |E_{hh}-\mu |$), the $hh$ band is only partially filled, and moving it closer to the chemical potential shifts hole carriers from $lh$ to the $hh$ pocket, where their contribution to the conductivity is smaller. We note that the total ER also contains a contribution from the strain-induced increase of the effective masses, which leads to an approximately $T$-independent negative shift of ER.

Let us first discuss the elastoresistivity in 0 magnetic field. Within a semiclassical approach, the conductivity is given by $\sigma ={\sum }_{\alpha }{\sigma }_{\alpha }$, with ${\sigma }_{\alpha }=n_{\alpha }{e}^2/\left({\mathrm{\Gamma }}_{\alpha }{m}_{\alpha }^{*}\right)$ being the contributions from individual bands. Here, $n_{\alpha }$ is the carrier density, and ${\mathrm{\Gamma }}_{\alpha }$ is the scattering rate of band $\alpha$. Zero-field elastoresistivity thus reads

$$\frac{1}{\rho \left(0\right)}\frac{d\rho \left(0\right)}{d{\epsilon }_{xx}}=\sum _{\alpha }\frac{{\sigma }_{\alpha }\left(0\right)}{\sigma \left(0\right)}\left[\frac{{\zeta }_m^{\left(\alpha \right)}}{m_{\alpha }^{*}}+\frac{{\zeta }_{\mathrm{\Gamma }}^{\left(\alpha \right)}}{{\mathrm{\Gamma }}_{\alpha }}-\frac{{\zeta }_n^{\left(\alpha \right)}}{n_{\alpha }}\right],$$ [1]

where $\rho \left(0\right)\equiv \rho \left(\mathbf{B}=0\right)$, and we have introduced the strain derivatives ${\zeta }_m^{\left(\alpha \right)}=\frac{d{m}_{\alpha }^{*}}{d{\epsilon }_{xx}}$, ${\zeta }_{\mathrm{\Gamma }}^{\left(\alpha \right)}=\frac{d{\mathrm{\Gamma }}_{\alpha }}{d{\epsilon }_{xx}}$, and ${\zeta }_n^{\left(\alpha \right)}=\frac{d{n}_{\alpha }}{d{\epsilon }_{xx}}$. Increasing $m_{\alpha }^{*}$ and ${\mathrm{\Gamma }}_{\alpha }$ increases $\rho$, whereas increasing the carrier density $n_{\alpha }$ reduces $\rho$. Contributions from different bands were weighted according to their contribution to the total conductivity. One can estimate the strain response of the scattering rates ${\zeta }_{\mathrm{\Gamma }}^{\left(\alpha \right)}$ using expressions for impurity and phonon scattering rates ${\mathrm{\Gamma }}_{\text{imp}}^{\left(\alpha \right)}$ and ${\mathrm{\Gamma }}_{\text{ph}}^{\left(\alpha \right)}$ from Boltzmann theory and using Matthiessen’s rule (13), as shown in detail in SI Appendix. The result is that $\frac{{\zeta }_{\mathrm{\Gamma }}^{\left(\alpha \right)}}{{\mathrm{\Gamma }}_{\alpha }}=\frac{{\zeta }_m^{\left(\alpha \right)}}{m_{\alpha }^{*}}\frac{{\mathrm{\Gamma }}_{\text{imp}}^{\left(\alpha \right.}-{\mathrm{\Gamma }}_{\text{ph}}^{\left(\alpha \right)}}{{\mathrm{\Gamma }}_{\alpha }}+\frac{{\zeta }_n^{\left(\alpha \right)}}{n_{\alpha }}\frac{{\mathrm{\Gamma }}_{\text{imp}}^{\left(\alpha \right)}}{3{\mathrm{\Gamma }}_{\alpha }}-\frac{{\zeta }_{c_s}}{c_s}\frac{4{\mathrm{\Gamma }}_{\text{ph}}^{\left(\alpha \right)}}{{\mathrm{\Gamma }}_{\alpha }}$. Here, ${\zeta }_{c_s}$ denotes the derivative of the sound velocity with respect to strain, which we expect to be negative.

At low temperatures, where impurity scattering dominates, the elastoresistivity then becomes $\frac{1}{\rho \left(0\right)}\frac{d\rho \left(0\right)}{d{\epsilon }_{xx}}=2{\sum }_{\alpha }\frac{{\sigma }_{\alpha }}{\sigma }\left(\frac{{\zeta }_m^{\left(\alpha \right)}}{m_{\alpha }^{*}}-\frac{1}{3}\frac{{\zeta }_n^{\left(\alpha \right)}}{n_{\alpha }}\right)$. From our analysis of quantum oscillations, we conclude that both strain derivatives have the same sign ${\zeta }_m^{\left(\alpha \right)},{\zeta }_n^{\left(\alpha \right)}<0$, such that the two effects compete with each other. Which of the two dominates depends on microscopic details. We performed a DFT transport calculation, which keeps the scattering rates constant, and found a positive elastoresistivity, in agreement with experiment (see SI Appendix for details). As shown in Fig. 4D, a positive elastoresistivity at low temperatures is also readily captured within our effective three-band model, where we use as input from DFT that the two-holes bands move up in energy under compressive strain, while the electron band moves down (Fig. 3A). Interestingly, the heavy-hole band shifts up by an amount about 10 times larger than the other two bands, yet still remains below $E_F$. At low temperatures, it thus remains completely filled and does not contribute to transport. Electrons redistribute solely among the electron and light-hole pockets such that both $n_e$ and $n_{lh}$ increase, causing an increase in the total carrier density $n$ with compressive strain. An increase of $n$ results in a decrease of the resistivity $\rho$. As this occurs for compressive (i.e., negative) strain, this corresponds to a positive elastoresistivity, as this is the slope $d\rho /d{\epsilon }_{xx}$ (Fig. 4D). In the experiment, this effect seems to dominate over the strain-induced enhancement of the effective masses, which tends to reduce the elastoresistivity.

The situation is different at intermediate temperature, where one needs to take into account additional bands that lie within a range of approximately $k_{B}T$ of the Fermi energy $E_F$. The experimentally observed nonmonotonic behavior and associated sign change of the ER as a function of $T$ (Fig. 1) can be understood as a result of a redistribution of carriers between bands within $k_{B}T$ of $E_F$, i.e., including the $hh$ band. A precise modeling of the strain-induced modifications of the band structure at finite $T$ requires further experimental studies, e.g., ARPES under finite strain, or first-principle calculations that take thermal-expansion effects into account. We can, however, qualitatively capture the behavior within our low-energy model. The decrease of the elastoresistivity (as $T$ increases) follows from the fact that as the heavy-hole pocket is shifted upwards by an amount proportional to the strain, holes move from the light-hole to the heavy-hole pocket. At intermediate temperatures $k_{B}T\gtrsim |E_{hh}\left({\epsilon }_{xx}\right)-E_F|$, the number of light holes therefore decreases as strain is applied (Fig. 4 C, Inset). This leads to the observed increase of the resistivity at intermediate temperatures and the eventual sign change. The broad minimum of the elastoresistivity between 50 and 100 K arises within our model from a competition of electrons moving from the heavy-hole pocket to both the light-hole band (decreasing $n_{lh}$ and $\rho$) and the electron band (increasing $n_e$ and $\rho$). Specifically, the slope of the elastoresistivity is determined by the ratio of the density of states $g_{lh}/g_e$ at the chemical potential $\mu \left(T\right)$. The slope is negative for $g_{lh}>g_e$, as electrons from the heavy-hole pocket are then more likely to enter the light-hole one. The precise value of this ratio depends on microscopic details. Finally, there is also an additional negative contribution to elastoresistivity from the increase of the effective masses.

Let us now turn to the ER in the presence of a magnetic field. As a function of field, the MER shows distinct behavior at low temperatures $T\lesssim 15$ K and in the semiclassical regime at higher $T$. As discussed above, the sensitivity of MER to strain and magnetic field in the low-$T$ quantum regime readily follows from strain tuning of the SdH oscillation frequencies. As we show now, the observed MER in the semiclassical regime $T\gtrsim 15\hspace{0.17em}\text{K}$ can be captured by an effective two-band model of electron and hole carriers with densities $n_e,n_h$ and mobilities ${\mu }_e=e/\left(m_e^{*}{\mathrm{\Gamma }}_e\right)$ and ${\mu }_h$. We describe the contribution of the two-hole pockets via an effective hole mobility ${\mu }_h=e/\left({\overline{m}}_h^{*}{\overline{\mathrm{\Gamma }}}_h\right)$, where ${\overline{m}}_h^{*},{\overline{\mathrm{\Gamma }}}_h$ are averages of the two-hole pockets. As shown in detail in SI Appendix, we start from the well-known semiclassical form of the resistivity $\rho \left(B\right)=\rho \left(0\right)\frac{1+{\left(B/B_1\right)}^2}{1+{\left(B/B_{\text{sat}}\right)}^2}$ with characteristic field strengths $B_1={\left[e\rho \left(0\right)\left(n_e{\mu }_h+n_h{\mu }_e\right){\mu }_e{\mu }_h\right]}^{-1/2}$ and $B_{\text{sat}}={\left[e\rho \left(0\right){\mu }_e{\mu }_h|n_e-n_h|\right]}^{-1}$ (12), to arrive at

$$\mathrm{\Delta }\text{MER}=-\frac{2{\left(B/B_1\right)}^2}{1+{\left(B/B_1\right)}^2}\frac{1}{B_1}\frac{d{B}_1}{d{\epsilon }_{xx}}+\frac{2{\left(B/B_{\text{sat}}\right)}^2}{1+{\left(B/B_{\text{sat}}\right)}^2}\frac{1}{B_{\text{sat}}}\frac{d{B}_{\text{sat}}}{d{\epsilon }_{xx}},$$ [2]

where $\mathrm{\Delta }\text{MER}=\frac{1}{\rho \left(B\right)}\frac{d\rho \left(B\right)}{d{\epsilon }_{xx}}-\frac{1}{\rho \left(0\right)}\frac{d\rho \left(0\right)}{d{\epsilon }_{xx}}$. For ${\mathrm{W}\mathrm{T}\mathrm{e}}_2$, the saturation field is much larger than the fields we consider, $B_{\text{sat}}\gg B$, and $\mathrm{\Delta }$MER is determined by the first term. It increases quadratically for small $B\ll B_1$ and reaches saturation for $B\gg B_1$. This agrees well with our experimental observations (SI Appendix, Figs. S2C and S9). Importantly, under the approximation ${\mu }_e\approx {\mu }_h\equiv \mu$, which holds reasonably well for ${\mathrm{W}\mathrm{T}\mathrm{e}}_2$ (30), one finds that $\frac{1}{B_1}\frac{d{B}_1}{d{\epsilon }_{xx}}=-\frac{{\zeta }_{\mu }}{\mu }$ (see SI Appendix for the general case). The saturation value is then a direct measure of the strain-induced change of the mobility. Since we observe a positive saturation value for all temperatures, corresponding to $\frac{{\zeta }_{\mu }}{\mu }=-\frac{{\zeta }_m}{m^{*}}-\frac{{\zeta }_{\mathrm{\Gamma }}}{\mathrm{\Gamma }}>0$, we conclude that the nonmonotonic behavior of the zero-field ER as a function of temperature must be rooted in a nonmonotonicity of the strain derivative of the carrier densities ${\zeta }_n^{\left(\alpha \right)}$ (Eq. 1). Furthermore, the trend of the saturation value to decrease with increasing temperature is consistent with a semiclassical analysis. As shown in SI Appendix, it follows from the contribution of phonon scattering to the mobility that becomes increasingly important at higher temperatures. Investigating MER thus provides insights beyond zero-field ER measurements. Finally, we note that the value of $B_1$ can also be extracted from the coefficient of the nonsaturating, quadratic MR $={\left(B/B_1\right)}^2$ (14). This yields that $B_1$ increases from $B_1\left(30\hspace{0.17em}\text{K}\right)=1.4$ T to $B_1\left(90\hspace{0.17em}\text{K}\right)=12$ T, which is in good agreement with our findings.

To conclude, we report a large and nonmonotonic ER in high-mobility crystals of ${\mathrm{W}\mathrm{T}\mathrm{e}}_2$ that is highly tunable by an external magnetic field. We demonstrate that measuring the MER and quantum oscillations under strain provides information about the effect of strain on transport parameters in a generic setting. This follows from the fact that MER depends on different combinations of strain derivatives of these microscopic parameters than the zero-field ER. Our semiclassical transport analysis reveals that the observed saturation of MER at intermediate temperatures and fields provides immediate access to the change in mobility due to applied strain. Measurements of quantum oscillations under strain directly provide changes of the carrier densities and their effective masses. Combining these measurements of strain-induced changes of the electronic bandstructure with density-functional and analytical low-energy model calculations, we explain the ER behavior as resulting from an increase as well as a redistribution of carriers between bands with different mobilities. We highlight the important role of a heavy-hole band below the Fermi energy in intermediate temperature transport. Our results reveal a strong coupling of elastic and electronic degrees of freedom in ${\mathrm{W}\mathrm{T}\mathrm{e}}_2$, opening a route to control magneto-transport properties via strain. Materials with low carrier densities, large MR, and that are known to exhibit large responses to pressure or stress, i.e., that have small and anisotropic elastic moduli (e.g., due to a layered structure), are natural candidates for future MER investigations, as they may allow for a significant tuning of relative carrier densities $\mathrm{\Delta }{n}_{\alpha }/n_{\alpha }$ by strain. Interesting future research directions are to investigate the impact of thermal expansion and electronic correlations on the bandstructure and its response to strain, as well as the role of the edge states in magnetotransport under finite strain.

Methods

Single crystals of ${\mathrm{W}\mathrm{T}\mathrm{e}}_2$ were grown out of a Te-rich, binary melt, following the procedure described in ref. 15. Resistance measurements under uniaxial stress were carried out by using a Razorbill CS100 cryogenic uniaxial stress cell. As we applied uniaxial stress along the crystallographic $a$ axis, 3 strain tensor components were nonzero in Voigt notation (SI Appendix). However, we measured only one component, ${\epsilon }_{xx}$, due to the experimental setup. In this paper, we define strain as ${\epsilon }_{xx}\left[\%\right]=\left[\left(L-L_0\right)/L_0\right]\times 100$, where $L_0$ is the unstrained length. Thus, a positive sign represents tensile strain, and a negative sign stands for compressive strain. Band structures of ${\mathrm{W}\mathrm{T}\mathrm{e}}_2$ at strains from 0 to −0.2% were calculated in DFT (31, 32) by using local density approximation (33, 34) with SOC effect included. The dimensions of the unit cells were determined from experimental lattice constants (35) ($a$ = 3.477 Å, $b$ = 6.249 Å, and $c$ = 14.018 Å) plus strain and a Poisson ratio (27) of 0.16. The ionic positions in the unit cells were relaxed at different strains, and then band structures were calculated. The band structure with relaxed ionic positions at this strain range is insensitive to the out-of-plane strain because of the weak van-der-Waals interaction and large spacing between the stacking layers along the $c$ axis. Detailed information can be found in SI Appendix.