The impact of rising CO₂ and acclimation on the response of US forests to global warming

Significance

The benefit of climate change for forests is that higher atmospheric CO₂ allows trees to use less water and photosynthesize more. The problem of climate change is that warmer temperatures make trees use more water and photosynthesize less. We predicted the outcome of these opposing influences using a physiologically realistic model which accounted for the potential adjustment in forest leaf area and related traits to future conditions. If forests fail to adjust, only 55% of climate projections predict a CO₂ increase large enough to prevent warming from causing significant drought and mortality. If forests can adjust, the percentage of favorable outcomes rises to 71%. However, uncertainty remains in whether trees can adjust rapidly and in the scatter among climate projections.

Abstract

The response of forests to climate change depends in part on whether the photosynthetic benefit from increased atmospheric CO₂ (∆C_a = future minus historic CO₂) compensates for increased physiological stresses from higher temperature (∆T). We predicted the outcome of these competing responses by using optimization theory and a mechanistic model of tree water transport and photosynthesis. We simulated current and future productivity, stress, and mortality in mature monospecific stands with soil, species, and climate sampled from 20 continental US locations. We modeled stands with and without acclimation to ∆C_a and ∆T, where acclimated forests adjusted leaf area, photosynthetic capacity, and stand density to maximize productivity while avoiding stress. Without acclimation, the ∆C_a-driven boost in net primary productivity (NPP) was compromised by ∆T-driven stress and mortality associated with vascular failure. With acclimation, the ∆C_a-driven boost in NPP and stand biomass (C storage) was accentuated for cooler futures but negated for warmer futures by a ∆T-driven reduction in NPP and biomass. Thus, hotter futures reduced forest biomass through either mortality or acclimation. Forest outcomes depended on whether projected climatic ∆C_a/∆T ratios were above or below physiological thresholds that neutralized the negative impacts of warming. Critically, if forests do not acclimate, the ∆C_a/∆T must be above ca. 89 ppm⋅°C⁻¹ to avoid chronic stress, a threshold met by 55% of climate projections. If forests do acclimate, the ∆C_a/∆T must rise above ca. 67 ppm⋅°C⁻¹ for NPP and biomass to increase, a lower threshold met by 71% of projections.

The future will continue to bring elevated atmospheric CO₂ (C_a) and warmer temperatures (T) to the world's forests (1). These 2 atmospheric shifts (∆C_a = elevated CO₂, ∆T = climatic warming) can have opposite effects on the uptake and storage of CO₂ by trees and influence their potential to mitigate further increases in C_a. A ∆C_a in isolation typically stimulates photosynthesis (2) and can “fertilize” an increase in forest net primary productivity (NPP) (photosynthesis minus autotrophic respiration) as free air CO₂ enrichment (FACE) studies have shown (3, 4). If CO₂ fertilization is accompanied by greater tree and ecosystem carbon storage, trees will continue to slow the rise in C_a from fossil fuel emissions (4, 5). However, climate change also brings ∆T, which can have the opposite effect from ∆C_a. Warmer air will have a greater vapor pressure deficit (D) (6), which can reduce photosynthesis by inducing stomatal closure, both directly in response to greater transpiration (7) and indirectly in response to faster soil drying by root uptake (8). In extremis, ∆T contributes to drought-related mortality (9, 10). The negative influences of ∆T would contribute to a faster rise in C_a. There is already evidence for both positive and negative impacts of climate change on forests globally (5, 11–13), and the response is complicated beyond basic physiology by changing land use, fire regimes, pathogen and pest impact, species turnover, and other factors. Here we focus on the fundamental question of how trees will respond physiologically to the conflicting stimuli of ∆C_a and ∆T and the implications for future forests.

While the competing influences of ∆C_a and ∆T on tree function are well-established empirically, experiments with trees have inherent difficulties distinguishing shorter-term physiological responses from longer-term adjustments (here termed “acclimation”) to a new steady state. Short-term stimulation of growth by ∆C_a does not necessarily mean an increase in the biomass carrying capacity of a mature forest (14). Acclimation, particularly in notably plastic traits of individual tree leaf area (LA) and leaf photosynthetic capacity (carboxylation capacity, V_max25; and electron transport capacity, J_max25 at 25 °C), can alter the leaf-level response to ∆C_a and ∆T over time (2, 15–18). Stand structure, especially the density of trees (basal area per ground area, BAI), forest LA per ground area (LAI), and tree rooting depth, combine to determine the level of resource competition, which also influences a tree’s response to a given ∆C_a or ∆T. Given the roles of growth, stress-avoiding acclimation, and resource availability, it is not surprising that widespread variability in forest responses is often observed across ∆C_a and ∆T experiments (3, 4, 19).

Predictive models are likewise challenged with representing the physiological response to ∆C_a and ∆T at multiple spatial (leaf–tree–stand) and temporal (short- to long-term) scales (20). Uncertainty begins at the leaf-level with stomata. Stomatal pores are the gatekeepers of terrestrial photosynthesis and transpiration, and their aperture actively adjusts to multiple external cues including C_a, D, and root zone soil water status. Most landscape-scale models predict stomatal responses from empirical functions fitted to historic conditions (21–23), but there is no guarantee these physiologically blind functions will predict a changing future with potentially acclimating vegetation (24). Acclimation of tree LA and leaf photosynthetic capacity complicates stomatal regulation, which is known to be coordinated with these internal factors (25–28). Despite these complexities, it is essential to improve the modeling of stomatal gas exchange, because instantaneous rates of photosynthesis and transpiration underlie long-term projections of NPP and stand water stress. Models also must connect soil drought to the plant stress response, and whether the response ultimately leads to mortality or adaptive acclimation.

In this paper, we combine optimality theory and established physiological mechanisms to make robust estimates of the response of trees and stands to future ∆C_a and ∆T. The proposed optimizations apply regardless of climate and C_a, meaning the basis of prediction is as valid for any future climate as it is for historic conditions. As outlined below, these optimizations were used to 1) solve stomatal regulation, 2) justify basic hypotheses for how trees acclimate LA and photosynthetic capacity to environmental conditions, and 3) control for the influence of stand structure and root depth on drought stress and mortality. The optimizations apply at different scales, but all are mechanistically connected by the central process of vascular water transport, the “functional backbone of terrestrial productivity” (29). Water supply and transport is essential to plant functioning, and its failure by stress-induced xylem cavitation limits plant gas exchange and survival (30). Threshold losses of plant hydraulic conductance on the order of 60 to 85% have been reliably linked to the risk of drought mortality (31–37).

Stomatal optimization assumed that stomatal regulation evolved to balance a trade-off between photosynthesis and transpiration-induced water stress (6, 29, 38, 39). Thus, we balance stomatal aperture to maximize the difference between relative photosynthetic gain minus the corresponding relative risk of canopy desiccation caused by transpiration-induced xylem cavitation (40, 41). This “gain–risk” optimum is calculated from commonly measured traits of photosynthetic and hydraulic capacity and the environmental conditions. The balance point solves for stomatal fluxes of water and CO₂ under any combination of environmental cues without the need for ad hoc empirical parameters. Variations in stomatal sensitivity to water stress emerge from variation in photosynthetic and hydraulic properties. Importantly, the gain–risk calculation has been experimentally validated by successfully predicting physiological responses to C_a, D, soil moisture, and rainfall/irrigation as measured in growth chamber and plantation experiments designed to evaluate the approach (15, 36). The gain–risk concept outperformed other optimization approaches in a large-scale analysis of over 30 woody species across the world (42).

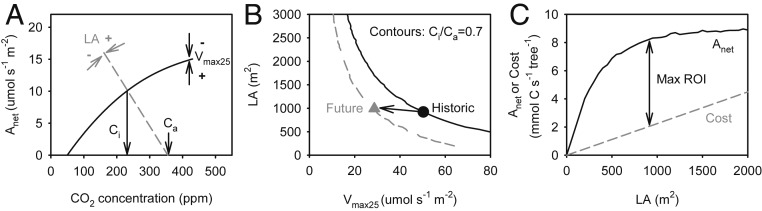
The established concept of an optimal metabolic set point for CO₂ concentration inside the leaf (C_i) leads to a hypothesis for how tree LA should be coordinated with leaf photosynthetic capacity. Under photosynthetically favorable conditions (field capacity soil, low D, and saturating light), plants tend to maintain an approximately constant C_i/C_a ratio (ca. 0.7), regardless of variation across time and space in what constitutes favorable conditions, including different C_a (3, 26, 43–45). An optimal C_i generally represents the balance or colimitation of dark vs. light reactions of photosynthesis (46, 47). Too low of a drawdown in C_i under light-saturating conditions exposes an underutilized photosynthetic capacity to light damage and energy-draining photoprotection and repair (2). The C_i/C_a set point is achieved by an optimal balance between photosynthetic capacity per LA (V_max25 and J_max25) and prevailing stomatal aperture (Fig. 1A). The stomatal aperture depends in turn on the hydraulic conductance of the tree (K_tree, volume flow rate per soil-canopy pressure drop) per LA, a behavior captured by the gain–risk algorithm (40). A constant hydraulic conductance of root and stem system specifies the coordination between LA and photosynthetic capacity that satisfies C_i/C_a homeostasis for prevailing environmental conditions (Fig. 1B, C_i/C_a contours).

Fig. 1.

Basis for modeling tree-level acclimation of LA and photosynthetic capacity (maximum carboxylation capacity, V_max25, coupled to electron transport capacity, J_max25). (A) Trees acclimate LA and V_max25 to achieve a homeostatic ratio between leaf internal (C_i) and atmospheric (C_a) CO₂ concentrations (C_i/C_a = 0.7) under favorable site “reference” conditions. The C_i is determined by the balance between V_max25 (V_max25 arrows) and the stomatal conductance to CO₂ (absolute value of slope of dashed gray line). Stomatal conductance depends on LA through its effect on the tree hydraulic conductance per LA (LA arrows). (B) For each set of environmental reference conditions there are infinite combinations of LA and V_max25 that satisfy C_i/C_a = 0.7 (solid black contour for historic conditions and gray dashed contour for future conditions), but only one LA–V_max25 combination is optimal (historic, black circle; future, gray triangle). (C) The optimal LA–V_max25 maximizes the ROI (Max ROI arrow), calculated as the difference between the net whole canopy assimilation (solid A_net curve) and leaf construction cost amortized over the GS (gray cost line).

In addition to optimizing C_i/C_a, we assumed that trees optimize the return on investment (ROI) in LA (27, 48–50). Many combinations of LA and photosynthetic capacity can satisfy the C_i/C_a criterion (Fig. 1B, C_i/C_a contours), but if leaf investment scales with LA, only one pair will maximize photosynthetic returns relative to the cost of leaf production (Fig. 2C, arrow and Fig. 2B, symbols). The optimization of C_i/C_a and ROI allowed us to predict tree-level acclimation of LA and photosynthetic capacity, traits which are known to be highly responsive to environment within a species (16–18, 27). Alternatively, if trees fail to acclimate to future conditions, we were able to assess the degree of metabolic stress caused by suboptimal C_i/C_a.

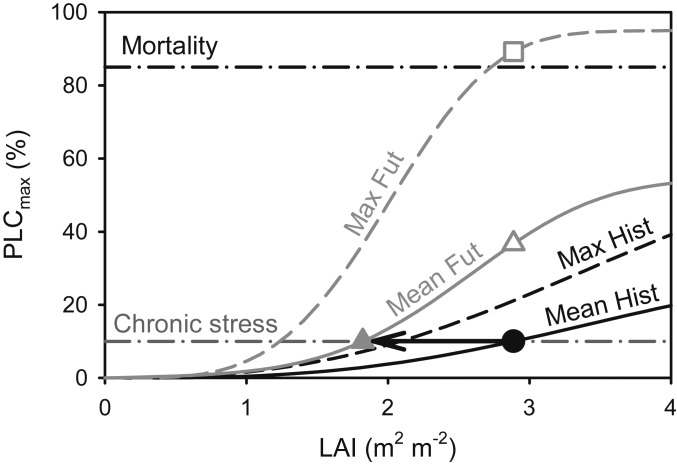
Fig. 2.

Stand-level acclimation to ecohydrologic equilibrium. At equilibrium for historic conditions, the LA index (LAI) is maximized without exceeding a chronic stress threshold, defined by an average maximum percentage loss in tree hydraulic conductance over multiple GSs of variable historic weather (mean PLC_max = 10 in this study, dashed-dotted chronic stress line). The equilibrium LAI is at the intersection between the stress threshold and the “Mean Hist” PLC_max curve (solid black circle). Equilibrium LAI also cannot allow the PLC_max in any given (dry) year (“Max Hist” dashed curve) to exceed a mortality threshold (black dashed-dot mortality line, here set to PLC_max = 85; ref. 36). If the historic LAI is too high for future conditions, it will induce chronic stress (open gray triangle on “Mean Fut” curve) and possibly trigger mortality (open gray square on “Max Fut” curve). Acclimation in this case requires a reduction in LAI (black arrow) to eliminate stress (solid gray triangle). Alternatively, if the historic LAI was too low for the future, it was increased until reaching the chronic stress or mortality thresholds.

Finally, the theory of ecohydrologic equilibrium (51–54) was used to scale from acclimation of single trees to adjustments at the stand scale. Over a multiyear timeframe of variable weather, the theory poses that a mature stand will maintain a demand for water that maximizes productivity but does not significantly stress or kill individual trees. Indeed, mature stands in drier habitats attain a lower BAI and LAI than mature stands in wet habitats (54), at least up to a maximum light-limiting LAI (ca. 8 m²⋅m⁻²). We exploited this definition of sustainable carrying capacity to adjust BAI and LAI of rain-fed (no access to groundwater) mature stands of given tree size and rooting depth to weather conditions (Fig. 2). The equilibrium LAI and tree biomass was defined as the maximum possible without inducing meaningful loss in tree hydraulic conductance from xylem cavitation, as averaged over multiple growing seasons (GSs) (Fig. 2, solid circle at chronic stress threshold on historic mean PLC_max curve).

Ecohydrologic equilibrium allowed us to predict the stand level “acclimation” in LAI and tree biomass to future conditions. Important to the question of tree carbon storage capacity, these biomass adjustments represented sustainable, steady-state carrying capacities of a mature stand rather than potentially transient changes in growth rate. Alternatively, if stands fail to acclimate to a new equilibrium, we could quantify the consequences. If the historic LAI is too high for future conditions, average GS cavitation will become significant (Fig. 2, open triangle on future mean PLC_max curve) and the maximum cavitation in any given year can exceed a mortality threshold in loss of hydraulic conductance (Fig. 2, open square on future maximum PLC_max curve). If historic LAI is too low, the stand is nonstressed but below its maximum productivity and biomass.

This nested series of optimizations allowed us to quantify how future forests will balance the potential benefits of ∆C_a vs. the potential disadvantages of ∆T. “Forests” were modeled as monospecific stands (either a conifer or an angiosperm) of identically sized mature trees, watered only by incident precipitation. Stands were given the soil type, climate, and dominant species of 20 locations sampling the forested regions of the continental United States (2 species per location for a total of 40 stands; Dataset S1). Stands were initially acclimated to historic C_a and weather to minimize metabolic stress (Fig. 1B, symbol on historic C_i/C_a contour at maximum ROI), and to minimize drought exposure at ecohydrologic equilibrium (Fig. 2, circle on historic mean PLC_max curve). We then posed the following questions about future forest responses. 1) If there is no acclimation, future ∆C_a and ∆T will drive stands out of C_i/C_a homeostasis and away from ecohydrologic equilibrium. To what extent will a ∆C_a-driven boost in NPP be compromised by a ∆T-driven rise in stress and mortality? 2) If there is stress-avoiding acclimation to future C_i/C_a homeostasis and hydrologic equilibrium, to what extent will the ∆C_a-driven boost to NPP and tree biomass be offset by a ∆T-driven reduction in NPP and tree biomass? 3) Are the projections of ∆C_a sufficiently high relative to ∆T for acclimated forests to increase NPP and tree carbon storage?

Results

The future climate (2070 to 2099) across the 20 sites projected by 6 coupled climate–Earth system models (ESM; Dataset S2) was significantly warmer, with drier air and a longer GS as compared to historic climate (1976 to 2005; SI Appendix, Fig. S1). Both historic and future weather included interannual fluctuations typical to each site, but the overall mean GS temperature increased by an average ∆T = 2.5 ± 1.0 °C (± SD; RCP4.5; average C_a = 531.9 ppm) and ∆T = 4.5 ± 1.0 °C (RCP8.5; average C_a = 804.0 ppm). The average ∆T varied little across sites (under 17% of variation explained by site, ANOVA), and variation in ∆T was primarily between ESM projections (56 to 63% of variation). The mean GS D increased 27.1 ± 12.8% (RCP4.5) and 55.6 ± 23.3% (RCP8.5) relative to historic climate. The ∆T was strongly correlated with ∆D (RCP4.5, R² = 0.58, P < 0.0001; RCP8.5, R² = 0.53, P < 0.0001). There was no significant change in mean daily GS precipitation or annual precipitation, indicating no overall trend in water supply for the rain-fed stands during the GS (SI Appendix, Fig. S1). As a result of warming, the GS length increased an average of 6.1 and 9.6 d for RCP 4.5 and RCP 8.5, respectively. GS length increased proportionally more for sites with historically shorter GS.

Future Projections without Forest Acclimation.

By definition, no acclimation to future ∆C_a and ∆T resulted in trees failing to maintain C_i/C_a homeostasis and stands falling out of ecohydrological equilibrium. Under these conditions, NPP (tree photosynthesis − tree respiration, mean annual over 30 y) increased by an approximately constant percentage across all sites, species, and climate models and showed only a slight decrease with ∆T projections within each ∆C_a regime (Fig. 3A, gray symbols). Mean NPP increased less for the representative concentration pathway (RCP) 4.5 conditions (30.0 ± 8.4%) than for RCP8.5 (57.5 ± 15.3%). Low variation in the NPP response was consistent with ∆C_a as the major NPP driver, given the variation in ∆T (Fig. 3A) and the diversity of species traits (Dataset S3). Our no-acclimation simulations meant no adjustment in tree LA or stand LAI, and as a result stand biomass and carbon storage capacity did not change. Stand transpiration (E, mean annual over 30 y) decreased slightly for futures with less warming (low ∆T) but increased above historic levels with more warming (higher ∆T; Fig. 3C).

Fig. 3.

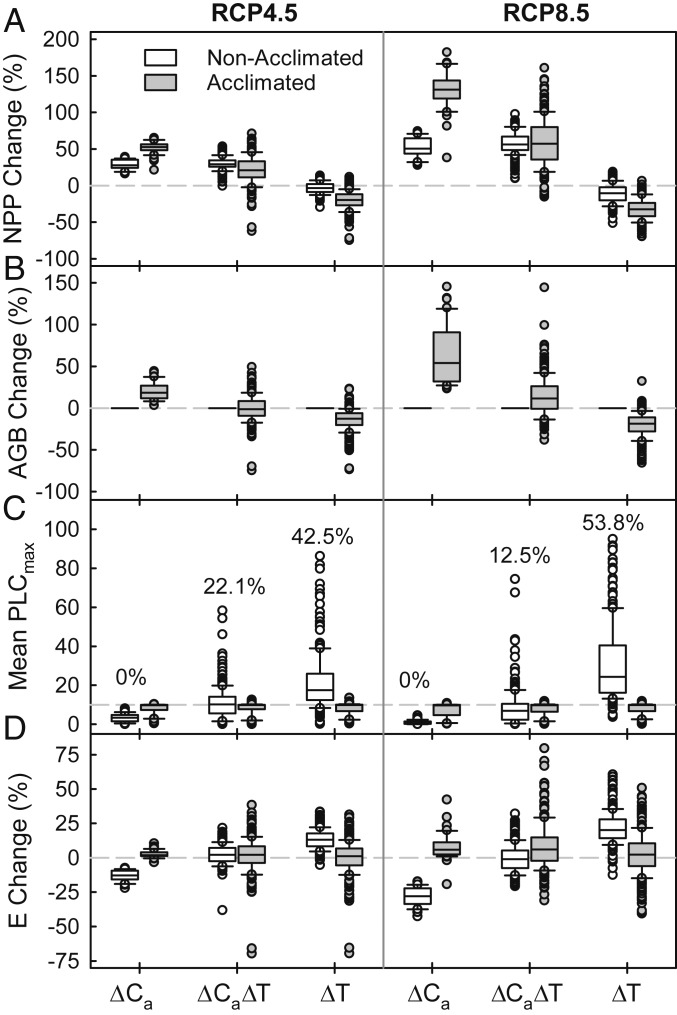
Stand responses to the increase in GS temperature (∆T) at 2 elevated atmospheric CO₂ concentrations, RCP4.5 (∆C_a = 177 ppm, Left) and RCP8.5 (∆C_a = 449 ppm, Right). Nonacclimated stands are in gray and acclimated stands are in black. Symbols indicate regions: Mountain West, +; Pacific Northwest, □; Southeast, ×; Boreal, ○. Regressions (solid lines) were highly significant (n = 240, P < 0.001; 95% confidence intervals, dashed lines). (A) The percentage change (all percentages relative to historic) in mean annual NPP. (B) Percentage change in AGB. (C) Percentage change in mean annual stand transpiration (E). (D) Mean maximum percentage loss in soil-to-canopy tree conductance at the end of the GS (mean PLC_max). Dashed-dotted horizontal line is the 10% chronic stress threshold (Fig. 2). Red symbols are simulations in which maximum PLC_max exceeded the mortality threshold (PLC_max = 85; Fig. 2) in at least one year, with the percentage of total simulations (n = 240 per RCP CO₂ concentration) indicated. Acclimated stands by definition did not exceed either threshold.

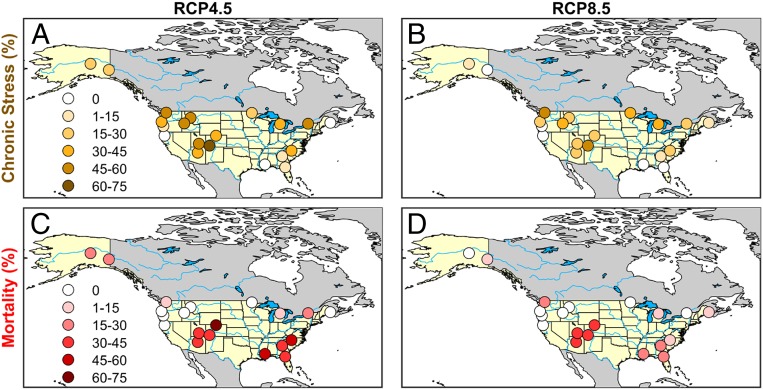
Warmer futures (greater ∆T) induced more chronic water stress within both ∆C_a scenarios (Fig. 3D, mean PLC_max > 10 PLC_max stress threshold). Regionally, the highest incidence of chronic water stress was predicted for the Mountain West region of the United States, followed by Pacific Northwest and Boreal regions with the lowest incidence in the Southeast (Fig. 4 A and B).The risk of drought-induced mortality followed a different pattern, being more weakly related to average warming (Fig. 3D, red symbols exceeded PLC_max = 85 in at least one year of 30), and being highest in the Southeast and Mountain West, lower in the Boreal, and least in the Pacific Northwest (Fig. 4 C and D). The percentage of stands exceeding the mortality threshold was greater in the moderate (RCP4.5, 22.1%) vs. the high (RCP8.5, 12.5%) ∆C_a scenario (Fig. 3D), as was average chronic stress. Greater stress for RCP4.5 was consistent with its having a lower ∆C_a relative to the average ∆T (∆C_a/∆T = 71 ppm⋅°C⁻¹) compared to RCP8.5 (∆C_a/∆T = 100 ppm⋅°C⁻¹).

Fig. 4.

Regional distribution of chronic hydraulic stress and mortality for nonacclimated stands. Chronic hydraulic stress (orange-toned circles) indicated as the percentage of simulations per site (n = 12, 6 climate models and 2 species per location) exceeding the chronic stress threshold in average percentage loss of hydraulic conductance (Fig. 2, mean PLC_max = 10) over a 30-y period. Mortality (red-toned circles) is indicated as percent of simulations per site exceeding the hydraulic mortality threshold in any year (Fig. 2, max PLC_max > 85). Darker symbols represent higher levels of stress as labeled. (A) Chronic stress for RCP4.5 CO₂ concentration. (B) Chronic stress for RCP8.5. (C) Mortality for RCP4.5. (D) Mortality for RCP8.5.

Trees experienced greater “metabolic stress” as indicated by a reduced mean annual C_i/C_a (weighted by the photosynthetic rate) relative to historically acclimated stands (SI Appendix, Fig. S2). The C_i/C_a declined with greater mean annual PLC_max (linear regression, r = −0.46 and P < 0.0001), meaning that the greater warming associated with water stress (Fig. 3D) also contributed to increased metabolic stress. Both metabolic and water stress occurred in warmer futures where historic LAI was too high to maintain ecohydrological equilibrium under future conditions (SI Appendix, Fig. S3).

Future Projections with Acclimation.

Acclimation to future ∆C_a and ∆T required changing tree LA and photosynthetic capacity to maintain C_i/C_a homeostasis and maximize ROI (i.e., no metabolic stress) and adjusting stand biomass to stay in ecohydrologic equilibrium (i.e., no long-term drought stress). Under these conditions, NPP declined strongly with climatic warming within each ∆C_a scenario (Fig. 3A, black symbols). Less warming allowed for greater NPP fertilization compared to nonacclimated stands. In contrast, under strong warming scenarios our model predicted a much weaker NPP increase, and in some instances a decline in NPP, relative to historic levels (Fig. 3A). Biomass carrying capacity mirrored the NPP response (Fig. 3B). The weakest NPP and biomass responses were seen for RCP4.5 with its smaller ∆C_a/∆T ratio as compared to RCP 8.5. The acclimation to ecohydrological equilibrium eliminated the increase in stand E with warming: instead E either declined with warming (RCP4.5; Fig. 3 C, Left) or showed no trend (RCP8.5; Fig. 3 C, Right).

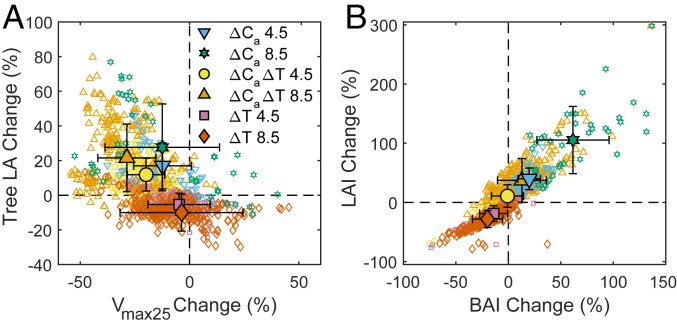
At the tree scale, our acclimation hypothesis predicted an increase in tree LA and a decrease in V_max25; however, the response varied substantially (Fig. 5A) and depended on ∆C_a, ∆T, and factors specific to site and species. The adjustments were greater for the higher ∆C_a scenario (Fig. 5A). For RCP8.5, LA increased by 21.5 ± 19.5% and V_max25 decreased −28.7 ± 13.3%, whereas for RCP4.5, LA increased by 11.8 ± 9.4% and V_max25 decreased −19.9 ± 8.6% (Fig. 5A, ∆C_a∆T). Within ∆C_a scenario, there was a trend for less adjustment of LA and larger decrease in V_max25 with greater ∆T (SI Appendix, Fig. S4 A and B).

Fig. 5.

Acclimation at the tree and stand scale to 6 future scenarios of elevated atmospheric CO₂ (∆C_a) and warming of the GS (∆T). Scenarios by color: ∆C_a 4.5, historic climate with RCP4.5 atmospheric CO₂ concentration (blue downward triangle, n = 40); ∆C_a 8.5, historic climate with RCP8.5 C_a (green star, n = 40); ∆C_a∆T 4.5, future RCP4.5 weather and C_a (yellow circle, n = 240); ∆C_a∆T 8.5, future RCP8.5 weather and C_a (orange upward triangle, n = 240); ∆T 4.5, future RCP4.5 weather and historic C_a (pink square, n = 240); ∆T 8.5, future RCP8.5 weather and historic C_a (vermillion diamond, n = 240). Open symbols are individual simulations, and solid symbols are simulation means (SD bars). (A) Tree-level acclimation by percentage change (all percentages relative to historic) in maximum carboxylation rate (V_max25, coupled to electron transport capacity, J_max25) and percentage change in tree LA. (B) Stand-level adjustment by percentage change in stand basal area (BAI) and percentage change in LA index (LAI) as required to satisfy ecohydrologic equilibrium.

At the stand level, the adjustment to ecohydrologic equilibrium resulted in little change in average LAI and BAI for RCP4.5 and an increase for RCP8.5 (Fig. 5B). However, the individual responses varied substantially depending on ∆T: Less warming resulted in more LAI and BAI relative to historic levels, while greater warming resulted in reductions (SI Appendix, Fig. S4 C and D). This pattern drove the trend for tree NPP and biomass to decrease with ∆T (Fig. 3 A and B). Warmer futures where hydrologic equilibrium required reductions in stand biomass were the same futures inducing stress in nonacclimating stands (Fig. 3D).

The Conflict between ∆C_a and ∆T.

The tension between the advantages of higher C_a vs. the disadvantages of greater warming as seen within future climate projections (∆C_a∆T, Figs. 3–5) were also evident by comparing the mean future response (Fig. 6, ∆C_a∆T) with simulations that uncoupled C_a from climate (Fig. 6, ∆C_a, ∆T). In nonacclimating stands (Fig. 6, open bars), where tree biomass was fixed by definition, raising C_a to future levels without any warming increased average NPP (Fig. 6A, ∆C_a). There was no chronic stress or mortality (Fig. 6C, ∆C_a) as a result of a decrease in stand transpiration (Fig. 6D). Adding warming maintained the potential NPP increase but induced stress and mortality (Fig. 6C, ∆C_a∆T) along with a rise in average stand transpiration (Fig. 6D, ∆C_a∆T). A warm future without elevated C_a resulted in either no increase in average NPP (RCP4.5; Fig. 6A, ∆T) or an NPP decline (RCP8.5; Fig. 6A, ∆T) and triggered a major spike in chronic water stress and mortality (Fig. 6C, ∆T) that was associated with a further increase in stand transpiration (Fig. 6D, ∆T).

Fig. 6.

Response of stands to 6 future scenarios of elevated atmospheric CO₂ (∆C_a) and warming of the GS (∆T). (Left) RCP4.5 ∆C_a. (Right) RCP8.5. The ∆Ca treatment (bottom axis) is future CO₂ enrichment with historic weather (n = 40 simulations); ∆C_a∆T is the future CO₂ and weather (n = 240); ∆T is future weather with historic CO₂ concentration (n = 240). Box and whisker plots characterize the distribution of individual simulations within each scenario (boxes = 25th to 75th percentile with median line; whiskers = 10th and 90th percentiles; symbols = remainder). Nonacclimated stands are open boxes, acclimated stands are gray. (A) Percentage change in NPP (all percentages relative to historic). (B) Percentage change in AGB. (C) Mean GS percent loss in tree hydraulic conductance (Mean PLC_max). Percentages above the open nonacclimated simulations are the percent of simulations that reached the mortality threshold (Fig. 2, PLC_max ≥ 85) at least once in the 30-y simulation period. (D) Percentage change in stand transpiration (E).

Acclimation accentuated the CO₂ fertilization of NPP and increased the carrying capacity of tree biomass in the absence of warming but sacrificed productivity and biomass accrual to eliminate warming-induced stress and mortality (Fig. 6, gray bars). Compared to nonacclimated stands, acclimation resulted in higher NPP for elevated C_a without warming and greater tree biomass (Fig. 6 A and B, ∆C_a) but caused lower NPP and nearly neutral biomass with both warming and increased C_a (Fig. 6 A and B, ∆C_a∆T). Warming without elevated C_a resulted in a major reduction in NPP and tree biomass (Fig. 6 A and B, ∆T) to avoid stress. The absence of stress and mortality in acclimated stands was associated with maintenance of average stand transpiration across all scenarios, consistent with ecohydrologic equilibrium (Fig. 6 C and D).

Trends in the adjustment of LAI and BAI (Fig. 5B) to ecohydrological equilibrium explained trends in the indicators of stress and mortality in nonacclimated stands. When acclimation to equilibrium drove a reduction in LAI and BAI, as in the warming only situation (Fig. 5B, ∆T), nonacclimated stands had LAI in excess of equilibrium and stress resulted (SI Appendix, Fig. S3). When acclimation drove an increase in LAI and BAI (Fig. 5B, ∆C_a, ∆C_a∆T), nonacclimated stands had an excess water supply and experienced no stress (SI Appendix, Fig. S3). At the tree level, acclimation to higher C_a without warming predicted lower V_max25 and greater tree LA, much as reported for higher C_a with warming (Fig. 5A). In contrast, acclimation to warming without elevated C_a required little change in average V_max25 and a reduction in tree LA (Fig. 5A).

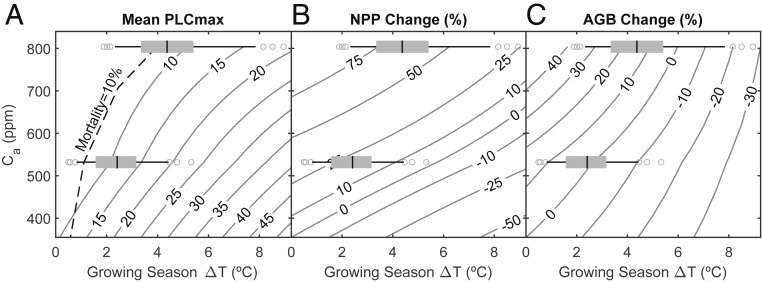
We used the model to predict ∆C_a/∆T thresholds that were necessary to counteract the negative effects of future warming. If forests do not acclimate to climate change, the C_a must rise at least 89 ppm for every 1 °C of warming to avoid chronic water stress (Fig. 7A; gray 10 mean PLC_max contour), and a much steeper 332 ppm⋅°C⁻¹ to prevent mortality (Fig. 7A, dashed 10% mortality contour). Mean ∆C_a/∆T projections for both ∆C_a scenarios did not meet these stress thresholds (Fig. 7A), hence the negative effects of warming as predicted for nonacclimating stands (Figs. 3D and 4). As noted, the ∆C_a/∆T for RCP4.5 (71 ppm⋅°C⁻¹) was further below the thresholds than RCP8.5 (100 ppm⋅°C⁻¹), explaining the greater incidence of stress and mortality in the RCP4.5 projections (Figs. 3D and 4).

Fig. 7.

Competing effects of atmospheric CO₂ enrichment (C_a) and warming of the GS (∆T). Contour lines for each response variable were obtained from linear regressions with ∆T (based on historic, RCP4.5, and RCP8.5 weather) at each of 3 C_a (historic, RCP4.5, and RCP8.5; n = 520 per C_a). Superimposed are ∆T distributions for an RCP4.5 future (lower box and whisker, n = 240) and an RCP8.5 future (upper box and whisker, n = 240; boxes = 25th to 75th percentile with median line; whiskers = 10th and 90th percentiles; symbols = remainder). (A) Stress in nonacclimated stands indicated by contours of mean PLC_max (gray) and the 10% mortality contour (dashed black; 10% of simulations reaching PLC_max ≥ 85). (B) NPP in acclimated stands indicated by contours of percentage change (all percentages relative to historic) of acclimated stands. (C) AGB in acclimated stands indicated by contours of percentage change.

If forests do acclimate to climate change, C_a must rise at least 31 ppm for every 1 °C of warming for C_a fertilization of NPP to occur (Fig. 7B, zero NPP contour), and 67 ppm⋅°C⁻¹ for the carrying capacity of tree biomass to increase (Fig. 7C, zero biomass contour). Average ∆C_a/∆T projections for both RCP4.5 and 8.5 were above the C_a fertilization threshold (Fig. 7B) and at or above the biomass accrual threshold (Fig. 7C). The greater ∆C_a/∆T for RCP8.5 was more hospitable to future forests, resulting in a greater boost in NPP and biomass under RCP8.5 projections (Figs. 3, 6, and 7). The considerable uncertainty in warming and C_a rise translated into NPP uncertainty ranging from over +75% (Fig. 7B, RCP8.5 outliers) to 0% (Fig. 7B, RCP4.5 outliers) and biomass uncertainty from over +35% (Fig. 7C, RCP8.5 outliers) to below −25% (Fig. 7B, RCP8.5 outliers). Overall, the degree of stress or strength of CO₂ fertilization and tree carbon storage was quantifiably sensitive to the climatic ∆C_a/∆T ratio.

Discussion

Our fundamental question was whether ∆C_a and acclimation can compensate for ∆T-induced impacts on US forests. Our sensitivity analysis did indeed identify compensating ∆C_a/∆T thresholds that neutralized climate change impacts on stand stress, mortality, NPP, and biomass. Acclimation did succeed in avoiding ∆T-driven stress and mortality through a reduction in stand LA. However, for this same reason acclimation cannot compensate for ∆T-driven declines in stand NPP and biomass. The answer to our question thus depends on whether future climate produces ∆C_a/∆T ratios in excess of compensating thresholds for acclimating stands. If NPP and biomass are both to increase for future stands, there must be at least a 67 ppm increase in C_a for every °C (zero contour in Fig. 7C). The sampled climate projections spanned this threshold. Over both ∆C_a scenarios, 71% of the projections predicted an increase in biomass and 29% predicted a decrease. If stands fail to acclimate, the bar is raised to a compensating ∆C_a/∆T threshold of 89 ppm⋅°C⁻¹ to avoid water stress (10 PLC contour in Fig. 7A). In this case, only 55% of the ∆C_a/∆T projections were sufficiently high to compensate for ∆T-induced stress.

The negative effects of warming acted in our model primarily through the increase in D (SI Appendix, Fig. S1). Higher D increased stand transpiration relative to incoming precipitation and root zone storage, pushing nonacclimating stands out of ecohydrologic equilibrium and causing water stress and mortality. Although the gain–risk stomatal algorithm typically responds to a rise in D by partial stomatal closure, the closure is usually not sufficient to prevent an increase in transpiration (40), which increases the rate of soil drying (8). If root zone withdrawals exceed precipitation inputs, soil moisture declines and xylem pressures become more negative, causing cavitation to accumulate during the GS. The gain–risk stomatal algorithm ensured that cavitation developed in a controlled manner, allowing the plant to exploit its capacity for water extraction while avoiding complete hydraulic failure (at 100 PLC_max) and instant desiccation. Unless rainfall intervenes, cavitation will eventually rise above the mortality threshold of 85 PLC_max. This stress cycle was more gradual in fine-textured soils where pressure dropped more gradually with drying, but it could develop over a matter of days in coarser soils where pressures plummet abruptly as large soil pores empty. In either case, the nonlinear dynamics of water stress made its onset highly sensitive to the timing of GS rainfall and the D regime, both which varied annually in our 30 y simulations and created considerable interannual variation in water stress.

The tipping-point nature of stand water stress resulted in the development of increasingly skewed distributions in mean PLC_max (e.g., Fig. 6C, outliers) as warming caused more stands to transition to a stressed state. Because mortality can be triggered by a single dry year, it was stochastic and only loosely coupled to chronic stress and ∆T, which tracked 30-y average conditions. This model behavior supports the importance of subtle changes in drought timing, atmospheric D, and stand density as major drivers of future mortality (8, 55–57). The predicted vulnerability of the southeastern United States to future stress (Fig. 4) is consistent with the tree ring record showing sensitivity of these forests to seasonal drought and elevated D (58, 59).

Water stress was associated with low C_i/C_a, or “metabolic” stress caused by chronic reductions in stomatal aperture in response to high D and drier soil. Whereas the consequences of water stress were quantified in terms of reduced photosynthesis, increased cavitation, and loss of hydraulic conductance, additional downsides of operating at overly low C_i are more difficult to calculate. Beyond the reduction of gas exchange caused by stomatal closure and cavitation, for lack of definitive information we did not subtract any additional effects of stress and putative mortality on NPP. In particular we assumed full hydraulic recovery between GSs, erasing the drought legacy between GSs. For this reason, our NPP and biomass estimates for nonacclimated stands under stress-inducing conditions represented potential maxima.

The acclimation scenario, which minimized metabolic and water stress averaged over a 30-y period of variable conditions (Figs. 1 and 2), produced realistic trends in tree LA, V_max25, and stand LAI for a variety of climatic scenarios (Fig. 5). Direct comparison with experiments is complicated because the degree of acclimation as we defined it was not always assessed, and experiments combine changes from growth rate and ontogeny with adjustments in steady-state carrying capacity. FACE studies (3, 4) which raise C_a (to ca. 550 to 580 ppm) without warming generally compare favorably with simulation results for ∆C_a at RCP4.5 (C_a = 532 ppm). The LAI of FACE tree stands increased +21% on average (range +43% to −8%; refs. 3 and 4) within the wide range of our simulations (+13% to +94%, mean 40%; ∆C_a 4.5; Fig. 5B). LA per tree sapwood area also increased with elevated C_a in a number of studies (27, 60), which is consistent with the simulated increase in tree LA (Fig. 5A, ∆C_a 4.5). The trend for greater LAI in elevated C_a experiments is generally accompanied by no apparent change in C_i/C_a and a decline in V_max25 in trees (ca. −6% for FACE trees; refs. 3, 26, 44, and 45). This result was consistent with acclimation to a constant reference-condition C_i/C_a and the simulated decline in V_max25 (−38% to +10%, mean −12%; Fig. 5A, ∆C_a 4.5). Above-ground tree biomass increased 28% on average in FACE studies (3) with considerable variation (4), which was consistent with our average +21% increase (range +3% to +44%; Fig. 6B, ∆C_a 4.5). Variation between experiments is a prominent theme in elevated CO₂ studies (3, 4) and is consistent with the highly variable results of the simulations (Fig. 6). Clearly, the acclimation response to a specific C_a change depends on many other factors, climate and species traits being among them.

Fewer experiments have addressed acclimation to warming in the absence of elevated C_a and in the presence of rising D and a constrained soil water supply (SI Appendix, Fig. S1). Warming treatments either increase or decrease V_max25 (19, 61), which was consistent with the highly variable V_max25 acclimation predicted by our model (Fig. 5A, ∆T). Area of individual leaves generally decreases in plants grown under higher D (62, 63), and LA per sapwood area tends to decrease (27, 64–67, but see ref. 68), and both observations are consistent with our prediction of reduced tree LA under warmer and drier air (Fig. 5A). Tests of the ecohydrological equilibrium concept generally support the simulated trend toward reduced LAI, BAI, and above-ground biomass in regions with warmer and drier air (Fig. 5B and ref. 54). Overall, the acclimation of traits required by the model is within the observed range of responses, indicating that at least some degree of acclimation to climate change will continue to happen.

The degree of C_a fertilization, as predicted by increases in acclimated stand NPP (Figs. 3, 6, and 7), was generally consistent with trends from experiments. The relatively constant percentage boost of NPP from C_a fertilization, regardless of species or site, was also reported across a range of FACE sites (3, 4). Some studies report a nutrient-limited saturation of C_a fertilization after several years or altered nutrient cycles (69–72). Although we did not model nutrient limitation, the V_max25 per ground area either remained approximately constant or even declined in our simulations (SI Appendix, Fig. S5, ∆C_a∆T), suggesting that this proxy of nitrogen demand was not likely to limit NPP as long as historic N availability is sustained. Importantly, we modeled NPP as annual production of fixed carbon (canopy photosynthesis minus plant respiration), whereas measured NPP is based on tracking the fate of this carbon in harvestable biomass, which is challenging below ground and excludes losses to herbivory, volatiles, exudates, and mycorrhizal uptake. The 2 NPP estimates often do not track each other owing to the difficulty of closing the plant's carbon budget (3, 4, 14, 73).

Our model simulations were structured to focus on the response of a given species to changing C_a and climate, with acclimation limited to LA, V_max25, and LAI–BAI. Although species differed considerably in their photosynthetic and hydraulic traits (Dataset S3), they all responded in a similar manner to a particular shift in climate and C_a. At a given site, the response was more sensitive to variation between the 6 ESM weather projections rather than the 2 species tested (e.g., for NPP % change “site” explained 21% and 40% of variance for RCP4.5 and RCP8.5, respectively, “species” explained 5% in both RCP scenarios, and “ESM” 70% and 50% of variance for RCP4.5 and RCP8.5, respectively; P < 0.001, ANOVA). The differences between species would become much more important if climate change was accompanied by a change in species composition at a site, rather than just the response of a given species. We also did not attempt to model acclimation in other traits besides LA, V_max25, and LAI–BAI, chiefly because there was less known about their plasticity and spatial-temporal variation (52, 74, 75). Acclimation of other traits can be incorporated as their plasticity and adaptive significance becomes established. Species turnover and a wider sphere for acclimation could have a major impact on predictions of future forest function.

Uncoupling C_a fertilization from warming quantified the critical balance between these often opposing influences on stand function. As long as there is sufficient rise in C_a, it appears to offset mortality and loss of productivity associated with the rise in T (and associated rise in D) in our model simulations. Our results support previous modeling which indicated a pronounced reduction in warming-induced mortality risk caused by rising C_a (76, 77). In our case, elevated C_a dropped mortality (simulations reaching PLC_max ≥ 85) from 43 to 22% for RCP4.5 and from 54 to 13% for RCP8.5 (Fig. 6C). Mortality was predicted to be especially sensitive to warming at lower C_a, requiring very steep increases in C_a to compensate (Fig. 7A, dashed mortality contour). This resulted in greater projected mortality for the moderate RCP4.5 ∆C_a scenario (22%) vs. the high ∆C_a one (13% for RCP8.5). High sensitivity at low C_a is also consistent with recent incidence of forest mortality worldwide (9, 78). The extent of C_a fertilization for acclimated and nonstressed forests was more uniformly sensitive to warming, requiring ca. 31 ppm⋅°C⁻¹ to just offset warming-induced productivity loss. The greater the ∆C_a/∆T ratio, the greater the C_a fertilization, as exemplified by the NPP comparison of RCP8.5 (100 ppm⋅°C⁻¹, +58.4% NPP at mean ∆T) vs. RCP4.5 (71 ppm⋅°C⁻¹, +21.6% NPP). The same trend was seen for the C_a-stimulated increase in stand biomass, although a higher threshold of 67 ppm⋅°C⁻¹ was required (Fig. 7C). Staying above these ∆C_a/∆T ratios would insure C_a fertilization and increased tree carbon storage to potentially mitigate the C_a rise from emissions.

Critically, the benefits of CO₂ fertilization, even for acclimating forests, are not guaranteed in a much hotter world. Uncertainty in ∆T and C_a meant that NPP could go up or stay unchanged, and tree biomass could go up or down depending on ∆T and C_a projections (Fig. 7 B and C). The ∆C_a/∆T thresholds of Fig. 7 are specific to rain-fed and water-limited forests of the United States with LAI mostly below 3.5 (SI Appendix, Fig. S5), and facing an essentially precipitation neutral future (SI Appendix, Fig. S1). However, the consequences of even small shifts in the balance between rising C_a and rising T can apply globally. The ∆C_a/∆T ratio may decrease with latitude, given that C_a rises fairly uniformly (79) while ∆T increases more at higher latitudes (80). A lower boreal ∆C_a/∆T (although not seen in our US-limited sample; SI Appendix, Fig. S1) would result in lower CO₂ fertilization and biomass increase, a speculation that is consistent with boreal forests showing a limited growth response to warming (11, 81). By the same logic, tropical forests exposed to the highest ∆C_a/∆T should absorb and store more carbon, at least up to a light-limiting threshold. This agrees with at least some modeling that shows significant tropical CO₂ fertilization (82) and strong resilience to potentially negative effects of warming (77), although this may be modified by declines in precipitation observed in some climate models (83–85).

The main advance in our modeling approach was to constrain a mechanistic plant hydraulic–gas exchange model with optimality principles operating at a hierarchy of scales from leaf to forest. In some form, the concept could be scaled up to replace the empirical approach generally utilized in land surface models and ESMs, particularly with the increasing prevalence of demographic vegetation models (20, 28, 86). These models face the enormous challenge of integrating basic plant ecophysiology with potentially critical impacts of fire regime, land use, soil biogeochemistry, pathogen and pest activity, and the like. Our results provide an important step forward in projecting the future of Earth’s forests in the 21st century.

Methods

Sites, Species, and Stands.

We compared historic vs. future climate scenarios at 20 locations in 4 forested regions across the United States: Pacific Northwest, Mountain West, Boreal, and Southeast (Dataset S1 and SI Appendix, Fig. S6). Two monospecific stands were simulated per location, the species being a regionally abundant conifer or diffuse porous angiosperm (Table 1). Trees were uniformly spaced and of mature size with equal diameter at breast height (DBH) and height to standardize for demography and biomass at ecohydrologic equilibrium. Four to 6 locations were selected per forested region that 1) were within the focal species range (Table 1 and ref. 87), 2) had a nearby weather station with at least 13 y of hourly data for the variables of interest accessible through MesoWest (https://mesowest.utah.edu; Dataset S1 and ref. 88), and 3) covered a wide spatial and environmental range within the region (Dataset S1 and SI Appendix, Fig. S6). Soil texture for each location was obtained from the US Department of Agriculture Soil Survey Database (89).

Table 1.

Selected focal tree species

Region	Species	Family	Common name	Type	Leaf habit
Boreal	Betula papyrifera Marsh.	Betulaceae	Paper birch	Angiosperm	Deciduous
	Picea glauca (Moench) Voss	Pinaceae	White spruce	Conifer	Evergreen
Mountain West	Populus tremuloides Michx.	Salicaceae	Trembling aspen	Angiosperm	Deciduous
	Pinus ponderosa Douglas ex C.Lawson	Pinaceae	Ponderosa pine	Conifer	Evergreen
Pacific West	Populus trichocarpa Torr. & A.Gray ex. Hook	Salicaceae	Black cottonwood	Angiosperm	Deciduous
	Pseudotsuga menziesii (Mirb.) Franco	Pinaceae	Douglas fir	Conifer	Evergreen
Southeast	Liriodendron tulipifera L.	Magnoliaceae	Yellow poplar	Angiosperm	Deciduous
	Pinus taeda L.	Pinaceae	Loblolly pine	Conifer	Evergreen

ESM Weather Projections Selection.

We used climate from 6 coupled climate–ESMs from a sample of 30 in the Coupled Model Intercomparison Project Phase 5 (CMIP5) (90) to force our forest model and estimate changes in temperature and precipitation between historic (1976 to 2005) and future (2070 to 2099) periods. The 30 ESM sample (Dataset S2) met the following model output criteria: 1) available through the Centre for Environmental Data Analysis (Natural Environment Research Council, https://www.ceda.ac.uk/); 2) included historic, RCP4.5 (91, 92), and RCP8.5 (93) simulations; and 3) included daily air surface temperature and precipitation for the historic and future 30-y periods. We used data from the first model realization (r1i1p1). For each ESM+RCP+location combination we calculated the delta change in mean annual temperature (∆MAT) and percent change in mean annual precipitation (MAP%) and graphed them against each other. The changes were studentized (subtracting the mean and dividing by the SD per RCP scenario) to give each location and scenario equal weight in model comparison. We selected the 2 mean ESMs that were graphically closest on average to the overall mean ∆MAT and mean MAP%, and 4 extreme ESMs closest on average to the following extremes: hot–dry (maximum ∆MAT, minimum MAP%), cool–dry (minimum ∆MAT, minimum MAP%), hot–wet (maximum ∆MAT, maximum MAP%), and cool–wet (minimum ∆MAT, maximum MAP%). As a result, the 6 ESMs selected (Dataset S2) covered a wide range of ∆MAT and MAP%, both across all sites (SI Appendix, Fig. S7) and within regions (SI Appendix, Fig. S8). Selected ESMs were from different research groups and used different oceanic, atmospheric, and vegetation submodels (Dataset S2).

Weather Generation.

The hourly weather data required by our forest model (precipitation, air temperature, wind speed, solar radiation, and atmospheric D) was simulated with AWEGEN (Advanced Weather Generator; refs. 94 and 95). To obtain the parameters for weather generation, AWEGEN was “trained” on hourly weather records for each location (minimum of 13 y) and on annual precipitation records from 1976 to 2005 (National Weather Service, https://www.ncdc.noaa.gov, or 4- × 4-km gridded PRISM data, http://prism.oregonstate.edu). Once trained, AWEGEN was used to generate 35-y historic time courses (including a 5-y burn-in period) with the interannual (AR1) precipitation regime model activated (94). The 35 simulated years incorporated the interannual variation representative of each site. Future weather was generated by modifying AWEGEN parameters according to the climate change shifts from the 6 ESMs (the factor change in precipitation and delta change in temperature; refs. 94 and 96). The AWEGEN program simulated 35 y of future hourly weather, with interannual variation, for each of the 6 ESMs and 2 ∆C_a scenarios per site. Simulations assumed constant atmospheric CO₂ concentrations (C_a) over the 30-y periods. Historic C_a was set to 354.8 ppm, which is the mean annual concentration for 1976 to 2005 (Earth System Research Laboratory, National Oceanic and Atmospheric Administration, https://www.esrl.noaa.gov/). Future C_a was set to the mean of the 3 decadal values (2070 to 2100) from the RCP4.5 (531.9 ppm) and RCP8.5 (804.0 ppm) scenarios (RCP Database 2009, https://www.iiasa.ac.at/web-apps/tnt/RcpDb/dsd?Action=htmlpage&page=welcome).

GS length was estimated from annual plots of cumulative thermal degree days above 5 °C (97) from February 1. We determined the start and end day of the GS from the intersections of a 3-line best fit to the annual time course of cumulative degree days (SI Appendix, Methods S1 and Fig. S9).

Model Simulations.

The model (36, 40) was parameterized with species traits from the literature (Dataset S3). Species-specific (nonplastic) inputs included leaf hydraulic conductance per LA, leaf width, rooting depth, and xylem vulnerability to cavitation curves for root, stem, and leaves (leaf and root curves were not available for white spruce or the leaf curve for aspen; these were replaced with the stem curves; Dataset S3). Cavitation was assumed irreversible during the GS (36) and quantified by the accumulated loss of soil-canopy hydraulic conductance by season’s end (PLC_max). Tree hydraulic conductance was fully restored between GSs. If model parameters were obtained from more than one study per species we used the mean value (or fit a vulnerability curve to pooled data). Tree height was calculated from mature DBH using the Greenhill equation with a safety factor of 4.66 (98). The rhizosphere soil resistance, averaged from field capacity to the water extraction limit, was set to 50% of soil–canopy hydraulic resistance (15, 36, 99).

Literature values for the plastic traits, tree LA and photosynthetic capacity (V_max25 and corresponding J_max25 = V_max25 ⋅ 1.67; ref. 100), were used to estimate species-specific values for the hydraulic conductance of the mature tree’s root and stem network (K_wood, root:stem components in 1:2 ratio) and the cost of leaf production amortized over the GS (moles CO₂⋅s⁻¹⋅m⁻² LA). Species-specific estimates of K_wood and leaf cost assumed species-specific historic “reference” environmental conditions (i.e., where C_i/C_a = 0.7; Fig. 1) which were obtained by averaging the location-specific reference conditions for the species. Location-specific reference conditions were defined by field capacity soil, elevation, and mean atmospheric parameters (solar radiation, air temperature, D, and wind speed) for clear sky (cloudiness ≤10%) hours 0900 to 1159 of the first quarter of every GS for the 30 y of simulation (Dataset S4). The K_wood was set to achieve C_i/C_a homeostasis for species’ LA and V_max25 (Fig. 1B, historic curve and symbol). The cost of leaf production (Fig. 1C, dashed line) was set to maximize ROI at the species’ LA based on the modeled rise in tree net photosynthesis (integrated over sun and shade layers; ref. 36) as LA was increased along the C_i/C_a = 0.7 contour (Fig. 1C, solid A_net curve). Species K_wood and leaf cost were then used to determine location-specific LA and V_max25 (and corresponding J_max25) for site-specific reference conditions. Acclimation to future conditions adjusted the LA+V_max25 setting to satisfy C_i/C_a homeostasis and ROI maximization for the future reference conditions assuming no change K_wood or leaf cost (Fig. 1B, future curve and symbol). Species traits other than LA and photosynthetic capacities were not altered (i.e., not acclimated) other than by standard temperature responses of hydraulic conductance (via water viscosity), photosynthesis (100–102), and respiration (103).

Tree LA and stand BAI were used to determine stand-level LA per ground area (LAI). This allometric LAI was converted to an optical canopy LAI as typically measured with hemispheric canopy photographs (104). The optical LAI was used to partition sun and shade layers of the canopy (36, 105).

Beneath a 2-cm rootless surface layer, the root zone was divided into 5 soil layers of equal root biomass (36). The fraction of total root biomass above depth d (in centimeters) was given by 1 − B^d, where the extinction coefficient B (0 < B < 1) determined the maximum root system depth (Rd = d yielding 99.5% root system biomass). After each hourly timestep, soil water budget was updated based on net flux for each layer from root exchange, soil evaporation, and vertical fluxes between layers including infiltration of precipitation. All incident precipitation infiltrated instantly to field capacity from the top down, with any excess draining from the bottom of the root zone. Outside of the GS transpiration and soil evaporation were assumed zero. Off-season activity of evergreen conifers was not modeled. With no interception or runoff and no water loss in the off season besides vertical drainage, the simulations represent maximum possible usage of GS precipitation and maximum recharge from off-season precipitation.

Stand LAI was adjusted by altering BAI to satisfy ecohydrologic equilibrium for historic conditions (Fig. 2). To ascertain equilibrium, 35 y were simulated starting from a soil profile at field capacity. After a 5-y burn-in period to allow the soil moisture profile to adjust, the annual PLC_max was averaged over the remaining 30 y. The greater the BAI and LAI, the faster the stand consumed water, and the greater the 30-y mean PLC_max. A mean PLC_max of 10 represented the chronic stress threshold (Fig. 2). Mortality was indicated if PLC_max in any single year exceeded 85 (Fig. 2, upper mortality line) based on the results of Venturas et al. (36). Ecohydrologic equilibrium was attained when LAI was maximized without pushing the stand across either threshold. Stand acclimation to future conditions followed the same process.

The mean equilibrium BAI is influenced by rooting depth (Rd), an important parameter with considerable uncertainty. To better constrain Rd, we first used one of the deeper depths in the literature (Dataset S3). If the resulting mean equilibrium BAI was equal or lower than the reported mean BAI of Forest Inventory of America (FIA) plots where the species was dominant (Dataset S3) we kept that Rd for the species. If the equilibrium BAI was greater than the FIA mean, the Rd was reduced to make the equilibrium BAI mean 5% or less below the FIA mean. As for other species-specific (nonplastic) inputs, the Rd was equal across species sites and between historic and future simulations.

Biomass and Respiration.

Leaf biomass (kilograms per hectare) was calculated for all scenarios dividing the allometric LAI (square meters per hectare) by specific LA (square meters per kilogram; Dataset S3). We used species-specific allometric equations for calculating total above-ground biomass (AGB, kilograms per hectare) and stem biomass (kilograms per hectare) based on DBH and leaf biomass (Dataset S3). We used the same relationship for estimating root biomass from AGB for all species (106).

Leaf respiration during the GS is accounted for in the gain–risk algorithm which calculates net canopy assimilation on an annual basis per ground area (A_net, kilograms of carbon per hectare per year). Conifer leaf respiration in winter was neglected (107), and modeled angiosperms were deciduous; therefore, we did not calculate A_net out of the GS. Annual woody (stem and root) respiration (Resp_wood; kilograms of carbon per hectare per year) was summed over hourly increments (103):

$${\text{Resp}}_{\text{wood}}={\displaystyle \sum \left(\text{Biomass}\cdot \left(\frac{{\text{r}}_{15}}{8,760}\right)\cdot {\text{q}}_{10}^{\frac{\text{T}-15}{10}}\right)},$$

where Biomass is the stem plus root biomass (kilograms of carbon), q₁₀ a dimensionless temperature coefficient, r₁₅ the maintenance respiration parameter (kilograms of carbon per kilogram of sapwood carbon per year), and T the air temperature (degrees Celsius) of each hour. We used q₁₀ = 1.4 and r₁₅ = 0.01 for angiosperms and q₁₀ = 1.7 and r₁₅ = 0.025 for gymnosperms (103). We used a 0.5 conversion factor for transforming biomass from kilograms per hectare to kilograms of carbon per hectare (108). NPP per ground area was calculated on an annual basis as NPP = A_net − Resp_wood.

Data Analysis.

The model output for NPP, stand E, mean PLC_max, and assimilation-weighted C_i/C_a were mean annual values over the 30 simulation years. Percent changes are with respect to historic weather and C_a. Temperature increases (∆T) were future minus historic average GS temperature. Mortality percentage was based on the number of location+species+ESM simulations (for a given C_a) that exceeded PLC_max = 85 in any of the 30 simulation years. “Future” simulations (∆C_a∆T) were for RCP-defined ∆C_a and the corresponding ESM defined weather and ∆T. “Enrichment” simulations (∆C_a) were for RCP-defined ∆C_a and historic weather (∆T = 0). “Warming-only” simulations (∆T) were for the same ESM-defined weather and ∆T used for future simulations, but with historic C_a (∆C_a = 0). For generating the contours in Fig. 7, 2 additional simulations were run that 1) combined RCP4.5 ∆C_a with RCP8.5 weather (∆T) and 2) RCP8.5 ∆C_a with RCP4.5 weather (∆T). Contours in Fig. 7 were based on linear regressions between all ∆T's (for both RCP4.5 and 8.5 weathers) and mean PLC_max (Fig. 7A), NPP (Fig. 7B), and AGB (Fig. 7C) at each of 3 ∆C_a: 0, 177 ppm (RCP4.5), and 449 ppm (RCP 8.5). ANOVAs were used to partition variation in model output between site, ESM, and species [Y ∼ ESM(site) + species(site)].

Data and Code Availability.

The gain–risk model code (written in C++), the acclimation codes (Visual Basic Macros), the simulated hourly weather data used for running simulations, and the main model output data are publicly available at Figshare (DOI: 10.6084/m9.figshare.8805110) (109).