Bubble pinch-off in turbulence

Significance

As a bubble breaks apart, the final pinching culminates in a singularity. We investigate the pinch-off of a bubble in turbulence and demonstrate that the turbulent flow field freezes during the pinching process, opening the route for a self-similar collapse close to the one predicted for unperturbed configuration. The role of the turbulent flow field is, therefore, to set the complex initial conditions, which can lead to oscillations of the neck shape during the collapse and the eventual escape from self-similarity with the appearance of a kink-like interfacial structure. This work can be seen as a prototype for understanding the route to finite-time singularities in realistic multiscale systems where random perturbations are present, with both fundamental and practical implications.

Abstract

Although bubble pinch-off is an archetype of a dynamical system evolving toward a singularity, it has always been described in idealized theoretical and experimental conditions. Here, we consider bubble pinch-off in a turbulent flow representative of natural conditions in the presence of strong and random perturbations, combining laboratory experiments, numerical simulations, and theoretical modeling. We show that the turbulence sets the initial conditions for pinch-off, namely the initial bubble shape and flow field, but after the pinch-off starts, the turbulent time at the neck scale becomes much slower than the pinching dynamics: The turbulence freezes. We show that the average neck size, $\overline{d}$, can be described by $\overline{d}\sim {\left(t-t_0\right)}^{\alpha }$, where $t_0$ is the pinch-off or singularity time and $\alpha \approx 0.5$, in close agreement with the axisymmetric theory with no initial flow. While frozen, the turbulence can influence the pinch-off through the initial conditions. Neck shape oscillations described by a quasi–2-dimensional (quasi-2D) linear perturbation model are observed as are persistent eccentricities of the neck, which are related to the complex flow field induced by the deformed bubble shape. When turbulent stresses are less able to be counteracted by surface tension, a 3-dimensional (3D) kink-like structure develops in the neck, causing $\overline{d}$ to escape its self-similar decrease. We identify the geometric controlling parameter that governs the appearance of these kink-like interfacial structures, which drive the collapse out of the self-similar route, governing both the likelihood of escaping the self-similar process and the time and length scale at which it occurs.

The breakup dynamics of bubbles and droplets are central to many natural and engineering processes, playing a role in heat, mass, and momentum transfer at the ocean–atmosphere surface (1, 2), rain drops falling on solids and liquids (3), and industrial liquid atomization and fragmentation (4). In such configurations, the gas–liquid interface is often surrounded by a violent turbulent flow characterized by perturbations of various strengths at various scales. As a result, the external forcing can strongly deform the bubble or droplet interface, leading to a complex geometrical shape and various breaking scenarios (5, 6). During the final instant of the collapse, the pinching dynamics approach a finite-time singularity, which has been studied extensively in idealized configurations in an attempt to identify such singularities and their regularization by viscous forces (7, 8). For these practical and fundamental reasons, the final pinching of a gas bubble or liquid droplet continues to draw extensive research interest.

In a quiescent fluid, starting from a purely axisymmetric fluid neck, the dynamic eventually becomes independent of the initial condition as it approaches the finite-time singularity corresponding to the time of pinch-off. Experiments and theories for the breakup of air bubbles or liquid droplets (8–14) have described the interface neck diameter, $d$, thinning toward pinch-off by a self-similar dynamic $d\propto {\left(t_0-t\right)}^{\alpha }$, where $t$ is the time, $t_0$ is the pinch-off or singularity time, and $\alpha$ is the similarity exponent, which depends on the driving forces. For a water droplet detaching in air, an inertiocapillary collapse is observed with $\alpha =2/3$, while in the viscocapillary and inertioviscocapillary limits, $\alpha =1$ (8). In the case of an air bubble in water, a purely inertial collapse leads to a slowly evolving exponent close to $\alpha =1/2$ (14), with the reported experimental values between 0.54 and 0.57 (11, 12). Varying the density ratio allows the behavior to transition from the droplet to the bubble limit (15), while recently, oscillations between viscous asymptotic pinch-off regimes have been reported when perturbing the initial and boundary conditions (16, 17).

A central assumption of the above description is the circular shape of the neck at the start of pinch-off and the axisymmetry of the surrounding flow field. Memory effects in bubble pinch-off, evidenced by initial perturbations to the neck shape yielding shape oscillations throughout the collapse, have been identified and described (18–20) as have misalignments of the neck with respect to gravity and the rapid injection of gas, which alter the singularity (19, 21). These studies have extended our understanding of pinch-off to controlled asymmetric situations, but they are limited to idealized configurations in which background perturbations are of a high degree of symmetry. Here, we investigate the final pinch-off dynamics of a bubble in a fully developed turbulent flow. This study can be seen as a prototype for understanding the route to singularities in realistic multiscale systems where perturbations at multiple scales are inherently present.

Frozen Turbulence during Pinch-Off

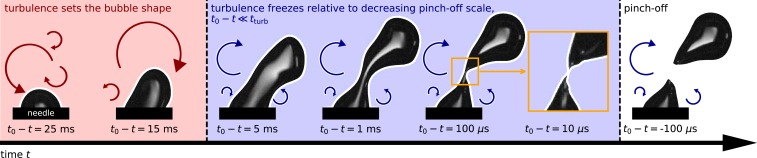
Fig. 1 shows a schematic of the bubble deformation and pinch-off scenario in a turbulent flow. We blow air through needles with inside diameter $d_{\mathrm{n}}$ between 1.4 and 4.8 mm placed in the middle of a 3-dimensional (3D) homogeneous and isotropic water turbulent flow of variable intensity characterized by an integral length scale $L\approx 13\hspace{0.17em}\mathrm{m}\mathrm{m}$, a Taylor microscale $\lambda$ between 1.2 and 1.7 mm, and a Kolmogorov scale $l_{\mu }$ between 34 and 58 $\mathrm{\mu }$m so that the bubble size is within the inertial range (Materials and Methods). The turbulence dissipation rate $ϵ$ is between 600 and 5,400 cm²/s³. The growth of the air bubble lasts from $\sim 5$ to $\sim 100$ ms, during which the turbulent background deforms the bubble shape continuously. When the bubble reaches a large-enough size, the combined effect of buoyancy forces, surface tension, and turbulent fluctuations triggers the formation of a neck, which begins to collapse.

Fig. 1.

Sketch of the bubble pinch-off scenario in a turbulent flow. The initial bubble shape is set by turbulent fluctuations, with the flow field evolving as the bubble deforms. When a neck of millimetric size starts to form, its dynamics speed up, and the neck quickly collapses, leading to the singularity time, $t_0$, at which breakup occurs. The duration of the final pinching process, $t_0-t\lesssim 10$ ms, is shorter than the turbulence fluctuation correlation time at the scale of the neck, $t_{\text{turb}}\sim {ϵ}^{-1/3}{d}_{\tau }^{2/3}\sim$ 15 to 70 ms. As a consequence, the turbulent fluctuations freeze and stay frozen during the subsequent pinch-off process.

During the collapse in a quiescent fluid, the flow space and timescales shrink to 0 with accelerating dynamics up to the pinch-off singularity time $t_0$. Notably, in the presence of a turbulent background flow, the velocity fluctuations $v_{\mathrm{t}\mathrm{u}\mathrm{r}\mathrm{b}}$ induced by the turbulence are relatively small compared with the neck collapse speed $v_{\mathrm{c}\mathrm{o}\mathrm{l}\mathrm{l}}$. The characteristic velocity fluctuations over a distance $\mathrm{\Delta }r$ scale as $v_{\mathrm{t}\mathrm{u}\mathrm{r}\mathrm{b}}\sim {\left(ϵ\mathrm{\Delta }r\right)}^{1/3}$ (6, 22). For a power law collapse described by $d=d_{\tau }{\left[\left(t_0-t\right)/\tau \right]}^{\alpha }$, with the initial neck diameter $d_{\tau }$ at time $t_0-t=\tau$, the speed of the collapse is $v_{\mathrm{c}\mathrm{o}\mathrm{l}\mathrm{l}}=\alpha d_{\tau }{\left(1/\tau \right)}^{\alpha }{\left(t_0-t\right)}^{\alpha -1}$. Comparing the turbulence and collapse velocities, with $\mathrm{\Delta }r=d$, we have $v_{\mathrm{c}\mathrm{o}\mathrm{l}\mathrm{l}}/v_{\mathrm{t}\mathrm{u}\mathrm{r}\mathrm{b}}=\alpha d_{\tau }^{1/\alpha }{\tau }^{-1}{ϵ}^{-1/3}{d}^{2/3-1/\alpha }$, which $\to \infty$ as $d\to 0$ for $\alpha <3/2$. Therefore, all self-similar collapse of droplets and bubbles in turbulent flows will experience freezing of the turbulence, and in practice, this occurs well before the Kolmogorov dissipative scale is reached. The frozen nature of the turbulence in the later stage of pinching can also be seen from a comparison between 2 timescales. The pinch-off dynamics occur in $t_0-t\lesssim 10$ ms, which in our experiment, is a duration shorter than the turbulent timescale $t_{\mathrm{t}\mathrm{u}\mathrm{r}\mathrm{b}}\sim {ϵ}^{-1/3}{d}_{\tau }^{2/3}\sim$ 15 to 70 ms at the needle scale. This fundamental result implies that the turbulence only sets the initial conditions for the pinching and remains frozen through the process, opening the route toward a self-similar collapse.

Experimental Collapse with a Turbulent Background

Despite the divergence of the turbulence and pinching scales, individual observations of pinch-off in a turbulent background reveal rich dynamics absent with quiescent backgrounds. Among the $\sim 300$ experiments conducted in turbulence, we observe a complex thinning process that suggests that the effects of the turbulence persist beyond the turbulent scales: a large variability in the pinch-off behavior is observed between experiments, especially when considering the neck from a single vantage point. While in the limit of minimal shape perturbations, the neck maintains its circular shape, and the collapse resembles that observed in quiescent backgrounds; when the frozen turbulent field has deformed the bubble, the entirety of the collapse is affected. Perturbations to the neck shape yield persistent asymmetries or shape oscillations, which grow relative to the collapsing neck and come to dominate the collapse dynamics.

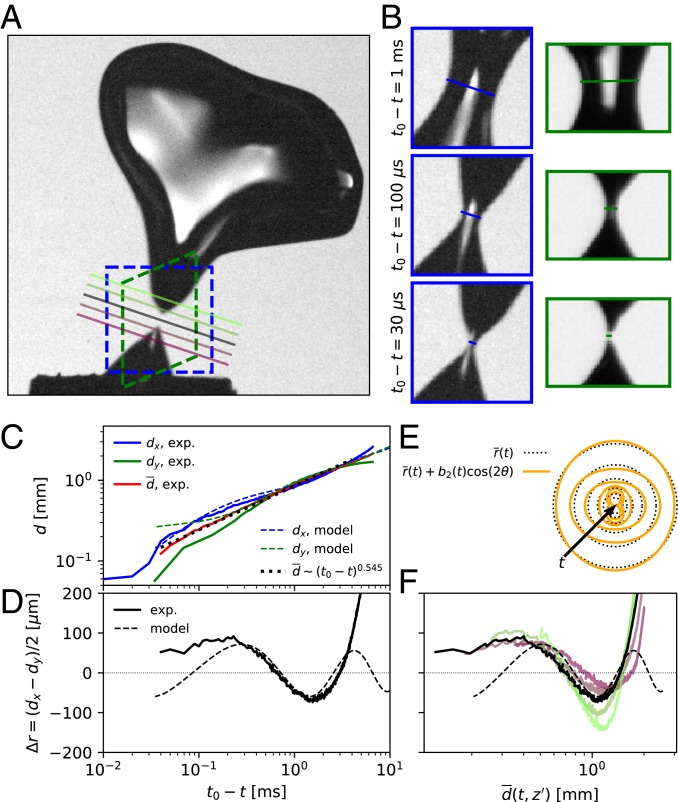
Evidence of these memory effects in turbulent pinch-off is given for an experimental observation in Fig. 2. We record the bubble pinching off from a needle with 2 orthogonal high-speed cameras, yielding the views of the neck region in the laboratory $x-z$ and $y-z$ planes outlined in blue and green in Fig. 2 A and B. An image processing algorithm is used to infer the orientation of the neck axis $z\prime$ and map the points imaged on the neck to 3D space (Materials and Methods and Fig. 2 B and C). The blue and green curves in Fig. 2C show the neck sizes $d_x$ and $d_y$, the widths of the neck measured in the 2 imaged planes, each taken to pass through the pinch-off point and be perpendicular to $z\prime$. During the collapse, $d_x$ and $d_y$ oscillate about the average neck size $\overline{d}=\left(d_x+d_y\right)/2$, shown in red in Fig. 2C, indicating that the neck shape is an oscillating ellipse with average size that follows closely the unperturbed results described in the literature, $\overline{d}\propto {\left(t-t_0\right)}^{\alpha }$, with $\alpha \approx 0.55$. The oscillatory behavior is captured in the $\mathrm{\Delta }r=\left(d_x-d_y\right)/2$ signal shown in Fig. 2D. This oscillation is characteristic of the Bell–Plesset collapse, which describes an interface undergoing a prescribed acceleration. This phenomenon was treated analytically by Bell (23) and Plesset (24); more recently, the temporal evolution of this collapse was derived independently (18, 25) in the context of a collapsing bubble neck subject to small-amplitude azimuthal shape perturbations. A neck with a mode $n$ perturbation has a cross-section described by $r\left(\theta ,t\right)=\overline{r}\left(t\right)+b_n\left(t\right)\cos \left(n\theta \right)$. When some initial perturbation $b_n\left(0\right)$ is prescribed to a collapse with mean dynamics that are described by $\overline{r}=\overline{d}/2\sim {\left(t_0-t\right)}^{\alpha }$, the perturbation scale $b_n\left(t\right)$ “chirps” as the singularity is approached, oscillating with increasing frequency but nearly fixed amplitude. This is described by an ordinary differential equation for $b_n\left(t\right)$ (18),

$${\ddot{b}}_n+\left(\frac{2\dot{\overline{r}}}{\overline{r}}\right){\dot{b}}_n+\left(\left(1-n\right)\frac{\ddot{\overline{r}}}{\overline{r}}+n\left(n^2-1\right)\left(\frac{\sigma }{\rho {\overline{r}}^3}\right)\right)b_n=0,$$ [1]

where inertia and surface tension $\sigma$ set the oscillatory behavior (18). Our data show that turbulence in the water can be the source of this shape perturbation leading to the oscillation and that, in many cases, the fundamental mode accurately describes the logarithmic period of the perturbation’s oscillation as predicted by the model (18). Fig. 2 C and D shows, as dashed lines, results from the azimuthal perturbation model, where an $n=2$ (elliptical shape) perturbation has been fit to the experimental data. The model captures reasonably well the period of oscillation, which is not a fitting parameter but is instead set by the mean collapse dynamics $\overline{r}\left(t\right)$, showing that the collapse is inertial and independent of the frozen turbulence in the background. The resolved amplitude of oscillation is ∼100 $\mathrm{\mu }$m, and the model no longer follows the experimental data when the average size of the neck is $\overline{d}\approx 400\hspace{0.17em}\mathrm{\mu }\mathrm{m}$, at which point the small-amplitude assumption used in Eq. 1 no longer holds. Moreover, Fig. 2F shows that the oscillation phase is set by the local neck size over a vertical range near the neck minimum. This suggests that the perturbation from the cylindrical shape does not vary significantly along the neck axis. Other examples of similar oscillatory dynamics are shown in SI Appendix. In many cases, oscillations occur about $\left(d_x-d_y\right)/2\ne 0$, suggesting that the mean shape of the neck is elliptical. Similar offsets have been attributed to asymmetric external flows (19), which we relate to deformed bubble shapes below. Further evidence for initial turbulent perturbations inducing bubble shape oscillations is obtained by performing direct numerical simulations using the open source package Basilisk (26, 27) (Materials and Methods). We initialize a bubble in a quiescent background with a neck cross-section that is initially slightly elliptic (mode $n=2$ perturbation) and recover the oscillatory behavior of the pinch-off described above (shown in SI Appendix).

Fig. 2.

Reconstruction of the bubble pinch-off in a turbulent flow from 2 views, with $d_{\text{n}}=2.7\hspace{0.17em}\text{mm}$ and $ϵ=\mathrm{1,500}\hspace{0.17em}{\text{cm}}^2/{\text{s}}^3$. (A) Large-scale view of the bubble in the first frame after pinch-off, where the green and blue dashed regions indicate the 2 fields of view (separated by a ${90}^{○}$ angle) in the $x-z$ and $y-z$ planes. Colored lines indicate various vertical planes used for the vertical analysis of the neck. (B) Close-up views at various times showing that the thinnest neck position does not move vertically and that both views exhibit necks of different sizes. Movie S1 shows the collapse. (C) Neck diameters $d_x$ and $d_y$ in the 2 views during the pinch-off. The 2 do not superpose, hence breaking the circular invariance. While the individual time evolution of $d_x$ and $d_y$ does not exhibit self-similar pinch-off, the mean diameter (red) follows a self-similar scaling, $\overline{d}\propto {\left(t_0-t\right)}^{\alpha }$, with $\alpha =0.55$ fitted to the data (black dotted line), which are very close to the values observed for bubble pinch-off in still water and predicted theoretically. (D) Difference $\mathrm{\Delta }r=\left(d_x-d_y\right)/2$ as a function of time $t_0-t$. The oscillating behavior can be described up to $t_0-t\approx 0.1$ ms by the dynamics of an elliptical perturbation indicated in dashed lines [reconstructed using Eq. 1, with $b_2\left(t=t_0-10\text{ms}\right)=-24\hspace{0.17em}\mathrm{\mu }\text{m}$ and ${\dot{b}}_2\left(t=t_0-10\text{ms}\right)=-3.2$ mm/s]; this is also shown in colored dashed lines in C. (E) Snapshots of the neck shape reconstructed with Eq. 1 (orange; solid lines) and the mean circular shape (black; dotted lines) during the collapse. (F) Difference $\mathrm{\Delta }r=\left(d_x-d_y\right)/2$ as a function of the mean neck diameter $\overline{d}\left(t,z\prime \right)$ for the different vertical neck planes $z\prime$, with the colors corresponding to the slices shown with the similarly colored line in A. When plotted against the local average neck size, different slices of the neck evolve in phase with each other and exhibit similar oscillatory behavior, showing that no vertical dynamics take place.

Escape from Self-Similarity Close to Singularity

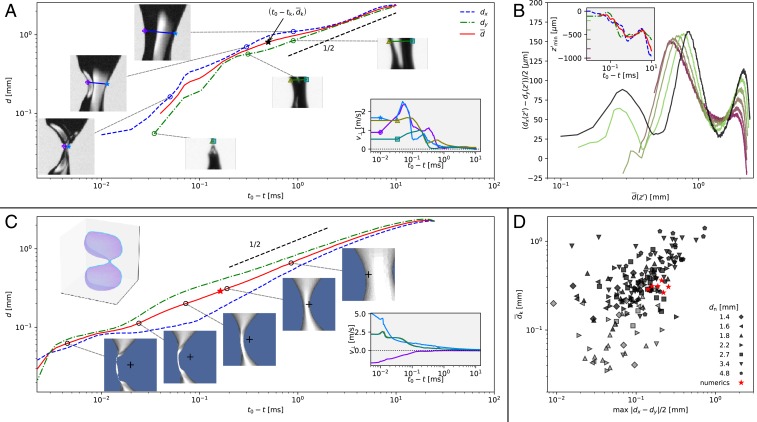
Next, we address the cases where the initial dynamics of the average neck size are still described by the self-similar route to finite-time singularity, but the neck thinning eventually escapes self-similarity at some point before pinch-off. We observe that such events arise more often for larger initial neck sizes and stronger turbulence and that the escape from self-similarity can be preceded by shape oscillations, such as those in Fig. 2, or displacement of the thinnest portion of the neck in either the vertical or horizontal direction, which indicates more complex 3D dynamics. A combination of the 2 perturbations has also been observed. The final escape from self-similarity is accompanied by a kink structure appearing in the interface near the neck minimum. We record the size of the neck, ${\overline{d}}_{\mathrm{k}}$, when the first indication of the ensuing abrupt change in curvature is visually identified.

Fig. 3A shows an example of the appearance of a kink associated with a vertical displacement of the thinnest neck position. In this case, the kink structure first appears on the left side of the $x-z$ plane view (colored purple in Fig. 3A) and corresponds to the first inflection point in $d_x$ at $t_0-t\approx 500\hspace{0.17em}\mathrm{\mu }\mathrm{s}$ and the increase in the collapse velocity of this side of the neck (shown in Fig. 3A, Inset). The kink next appears in the 2 sides of the neck viewed in the $y-z$ plane, coinciding with the change in slope in $d_y$ and increase in the corresponding collapse velocities at $t_0-t\approx 300\hspace{0.17em}\mathrm{\mu }\mathrm{s}$, and finally, it is seen in the right side of the $x-z$ plane view at $t_0-t\approx 90\hspace{0.17em}\mathrm{\mu }\mathrm{s}$. Fig. 3B shows that the axial position of the thinnest point of the neck changes as the kink develops so that the final pinch-off point is clearly distinct from the initial neck. As evidence for the complex 3D structure of the perturbation, the axial locations of the minimum $d_x$ and $d_y$ values are also shown in blue and green, respectively, in Fig. 3B: these oscillate about the average. Plotting the oscillation signal $\left(d_x-d_y\right)/2$ for various slices through the neck in Fig. 3B as a function of the local neck thickness, we see that various slices of the neck no longer share the same oscillation characteristics as had been the case in Fig. 2. In other cases, shape oscillations are not observed, but there is a persistent horizontal displacement of the thinnest part of the neck related to a large asymmetry, leading to different sides of the neck collapsing at consistently different rates. Such configurations, together with additional cases similar to Fig. 3 A and B, are shown in SI Appendix, all of which display a kink that forms and causes the collapse to escape self-similarity in its final stages.

Fig. 3.

Bubble pinch-off in a turbulent flow, with the dynamics escaping the self-similar behavior close to the finite-time singularity, associated with a kink-like structure. (A) Experimental snapshots and neck-thinning curves from a bubble collapse with $d_{\text{n}}=2.7\hspace{0.17em}\text{mm}$ and $ϵ=600\hspace{0.17em}{\text{cm}}^2/{\text{s}}^3$, showing that the thinnest neck position moves vertically and that the neck is systematically bigger in the $x$ direction than in the $y$ direction. The mean diameter (red) steepens after the kink-like structure appears (star). This coincides with rapid variation in the neck collapse velocity, shown in Inset, in which the 4 colors and markers correspond to the 4 sides of the neck marked in the snapshots. (B) Oscillation of the neck shape for various vertical planes below the pinch-off plane (mapped to $z\prime$ in Inset). Contrary to the case presented in Fig. 2, a phase shift is observed between the different planes, showing that the perturbation structure has a vertical dependence. The vertical displacement of the thinnest neck position is shown in Inset; it moves upward as the kink grows. (C) A 3D simulation of an asymmetric bubble pinching off in a quiescent fluid, with the initial shape in Upper Left Inset. Snapshots of the neck region and kink structure are provided, showing the leftward motion of the neck induced by the asymmetric shape. The collapse velocity of 4 points in the pinch-off plane is in Lower Right Inset, showing the asymmetric manner in which the bubble pinches off. (Sides of the neck are colored as they are in A; the green and yellow curves overlap due to the symmetry about the $x-z$ plane.) (D) Size of the neck when the kink appears, ${\overline{d}}_{\text{k}}$, against the maximum asymmetry observed in the neck prior to the kink (and after $\overline{d}$ reaches $d_{\text{n}}/3$ for the experiments), where black and gray markers are the $\sim 200$ experiments in which a kink is observed and red markers are numerical simulations with shapes similar to those shown in C. For the gray experimental markers, ${\overline{d}}_{\text{k}}$ is taken as $d_x$ at the kink formation, since the formation time $t_0-t_{\text{k}}$ is below the temporal resolution of the slower camera measuring $d_y$. The Pearson correlation for all of the experimental points is 0.748; this calculation is explained in SI Appendix. Movies S2 and S3 show examples of such collapses.

To show that this 3D behavior responsible for escaping self-similarity can be induced only by the initial bubble shape itself, we perform direct numerical simulations of an asymmetric bubble collapsing due to surface tension. We initialize an asymmetric bubble shape resembling a dumbbell with an off-center circular axis, shown in Fig. 3C, and a quiescent initial condition. The result is an elliptical neck shape with asymmetry that persists through the pinch-off without oscillation, evidenced by the plots of $d_x$ and $d_y$ shown as dashed and dotted lines in Fig. 3C. The asymmetry is further understood by considering the motion of 4 separate points on the neck interface, the collapse velocities of which are shown in Fig. 3C, Insets: one side of the neck consistently moves away from the neck center during the collapse, as the side opposite to it collapses much more quickly. Eventually, a kinked structure appears in the neck region. Given the initially quiescent state of the simulation, the complex pinching dynamics can be attributed to the bubble’s initial asymmetric shape. Fig. 3D shows, for the experimental and numerical cases in which a kink is observed, the size of the neck at kink formation ${\overline{d}}_{\mathrm{k}}$ as a function of the maximum asymmetries in the neck region prior to kinking $max\left(|d_x-d_y|/2\right)$. The positive correlation suggests that larger asymmetries in the neck shape promote earlier kink development, when the average neck size is larger. Correlation metrics are given in SI Appendix.

As shown in Figs. 2 and 3, the averaged neck thinning in turbulence initially follows the unperturbed results described in the literature, $\overline{d}\propto {\left(t-t_0\right)}^{\alpha }$, with $\alpha \approx 0.5$. This behavior is highly reproducible over the various observed cases, even those for which Eq. 1 does not capture the neck evolution. In some cases, these dynamics are followed until the end of the observable time window (Fig. 2), while in other cases, the collapse escapes self-similarity (Fig. 3). Fig. 4A shows the normalized ensemble-averaged mean neck diameter, $⟨\overline{d}/d_{\mathrm{n}}⟩$, which follows $⟨\overline{d}⟩\propto {\left[\left(t_0-t\right)/t_{\mathrm{t}\mathrm{u}\mathrm{r}\mathrm{b}}\right]}^{\overline{\alpha }}$ with $\overline{\alpha }\approx 0.5$, the ensemble-averaged data being in good agreement with the theoretical axisymmetric self-similar pinch-off of an underwater bubble. The distribution of power law slopes measured in turbulence, shown in Fig. 4A, Inset, is also centered around $\alpha \approx 0.5$.

Fig. 4.

Role of the turbulence in kink formation. (A) Ensemble average of the normalized average neck diameter $⟨\overline{d}/d_{\text{n}}⟩$ over all experiments for various needles and levels of turbulence, with the time until pinch-off normalized by the turbulent timescale at the needle length scale, $t_{\text{turb}}={\left(d_{\text{n}}^2/ϵ\right)}^{1/3}$. The shaded area indicates the standard deviation, and the black line indicates the $\alpha =1/2$ inertial power law scaling. Inset shows the distribution of the exponent $\alpha$ obtained by fitting $\overline{d}\propto {\left(t_0-t\right)}^{\alpha }$ for each experiment (Materials and Methods). The distribution is centered around 0.5. (B) The portion of cases with a resolved kink at each experimental condition as a function of $d_{\text{n}}/d_{\text{H}}$, with kinks rarely appearing at low $d_{\text{n}}/d_{\text{H}}$ but almost always being resolved as the ratio approaches 1. (C) The neck size when the kink appears, $d_k$, as a function of $d_{\text{n}}/d_{\text{H}}$, which exhibits a power law relation $\left({\overline{d}}_{\text{k}}/d_{\text{H}}\right)\sim {\left(d_{\text{n}}/d_{\text{H}}\right)}^{\beta }$, with $\beta =2.1$ obtained by a fit (which is shown in green). (D) Snapshots of the bubble at $t_0-t=1\hspace{0.17em}\text{ms}$ (Upper) and 2/3 of the way between kink formation and pinch-off (Lower) for cases at 3 different $d_{\text{n}}/d_{\text{H}}$, with the background shading mapped to the color bar in B. When $d_{\text{n}}/d_{\text{H}}$ increases, larger initial deformations lead to earlier and larger kink formation. (Scale bar: 1 mm.)

Control of Kink Formation by the Turbulence

In Fig. 3, we showed that the escape from self-similarity by kinking is controlled by the asymmetry in the neck shape induced by the pinching dynamics. Here, we relate this asymmetry to the turbulent initial conditions by considering the competition between turbulent stresses and surface tension, which sets the initial bubble shape. This is parameterized by the ratio of the needle size, $d_{\mathrm{n}}$, to the Hinze scale, $d_{\mathrm{H}}={\left(\sigma /\rho \right)}^{3/5}{ϵ}^{-2/5}/2$, the scale at which the 2 factors are in equilibrium (6). The Hinze scale is relevant to any process in which turbulence acts against surface tension to break apart bubbles or droplets (28), setting, for example, the size distribution of bubbles produced by breaking waves (1, 29). We find that $d_{\mathrm{n}}/d_{\mathrm{H}}$ determines the pinching behavior: at larger $d_{\mathrm{n}}/d_{\mathrm{H}}$, turbulence induces more pronounced deformations to the bubble shape, leading to a higher degree of neck asymmetry during the collapse and an earlier kink. Fig. 4B shows the likelihood of a kink being resolved (up until the experimental limit of $t_0-t=10\hspace{0.17em}\mathrm{\mu }\mathrm{s}$) at each experimental condition. The likelihood of kink formation increases with $d_{\mathrm{n}}/d_{\mathrm{H}}$, going from 0 for $d_{\mathrm{n}}/d_{\mathrm{H}}\to 0$ (the no turbulence condition) up to almost 100% for $d_{\mathrm{n}}/d_{\mathrm{H}}>1$. Furthermore, as shown in Fig. 4C, $d_{\mathrm{n}}/d_{\mathrm{H}}$ controls the point of kink formation, the kink forming earlier (and becoming larger) when $d_{\mathrm{n}}/d_{\mathrm{H}}$ increases, with the data being described by ${\overline{d}}_{\mathrm{k}}/d_{\mathrm{H}}\propto {\left(d_{\mathrm{n}}/d_{\mathrm{H}}\right)}^{\beta }$ with $\beta \approx 2.1$ fitted to the data. The role of $d_{\mathrm{n}}/d_{\mathrm{H}}$ is shown qualitatively in 3 representative cases shown in Fig. 4D. At small $d_{\mathrm{n}}/d_{\mathrm{H}}$, the bubble largely retains its unperturbed shape, despite potentially being stretched away from the needle by a passing eddy of size $\gg d_{\mathrm{n}}$. This leads to small neck deformations and a small, late kink structure. As $d_{\mathrm{n}}/d_{\mathrm{H}}$ is increased, the initial bubble shape becomes more and more deformed, leading to earlier and larger kink structures. We note experimentally that the kink lifetime resembles closely the capillary timescale $\left(t_0-t_{\mathrm{k}}\right)\sim {\left(\rho /\sigma \right)}^{1/2}{\overline{d}}_{\mathrm{k}}^{3/2}$ (SI Appendix), suggesting that capillarity governs the kink development.

The kink dynamics presented are very unlikely to be caused by turbulence intermittency given the high velocity of the kink’s development (which is faster than velocities measured in the tails of velocity fluctuation distribution as shown in SI Appendix). Previous literature suggests that similar kinked structures are indicative of an $n=3$ azimuthal shape perturbation (19), but we were unable to find a satisfactory fit of Eq. 1 with $n=3$. A formalized description of the kink formation would likely entail both axial and azimuthal perturbations to the neck shape in a fully 3D analysis similar to that in ref. 23 as well as the effects of rotational motion near the neck, which can modify the collapse process (25). Such a description is still incomplete.

Conclusion

We present experiments on bubble pinch-off in turbulence and demonstrate that the effect of the turbulent background flow can be reduced to its role in setting the initial conditions. We show that the turbulent fluctuations freeze after the pinch-off process starts (i.e., the turbulent timescale at the scale of the neck is much slower than the pinching dynamic). The frozen turbulence sets the stage for complex behavior, such as neck shape oscillations, during the collapse. We identify a controlling nondimensional parameter, $d_{\mathrm{n}}/d_{\mathrm{H}}$, which compares the initial neck size with a length scale characterizing the ability of the turbulence to deform it. When $d_{\mathrm{n}}/d_{\mathrm{H}}$ increases, we observe an escape from self-similarity at the final instant of pinching involving a kink-like interfacial structure, which grows faster than the power law collapse. The size of the structure and the time of its appearance before pinch-off increase with $d_{\mathrm{n}}/d_{\mathrm{H}}$. At high turbulence Reynolds numbers, we suggest that self-similarity will always break down during a bubble collapse, as a kink naturally forms on the route to the singularity. This study paves the way for a deeper understanding of systems approaching finite-time singularities in natural situations where strong perturbations are present.

Materials and Methods

Experimental Setup and Analysis.

Turbulence in the water is created by 8 submerged pumps with outlets that are attached via flexible tubing to nozzles arranged at the vertices of a 28-cm cube and pointed toward the cube’s center. A sketch of the experimental setup is provided in SI Appendix. Inspired by refs. 30 and 31, this setup induces a largely homogeneous, isotropic flow in the cube center. A needle in the range $1.4\hspace{0.17em}\text{mm}\le d_{\text{n}}\le 4.8\hspace{0.17em}\text{mm}$ is suspended in the center of the cube. Pinch-off is recorded over 4 values of turbulent dissipation rate $ϵ$ between 0 and 5,400 cm²/s³ ($ϵ=0$ being the quiescent state, corresponding to $d_{\text{H}}\to \infty$), with each $ϵ$ characterized with planar 2D particle image velocimetry (PIV) (32) in the absence of bubbles. PIV data and processing details are shown in SI Appendix. For the 3 increasing values of non-0 $ϵ$, the Kolmogorov microscale is 58, 47, and 34 $\mathrm{\mu }$m, respectively, and the Taylor microscale is 1.7, 1.7, and 1.2 mm, respectively. This is comparable with the initial size of the neck as pinch-off begins so that the bubble is initially within the turbulence inertial subrange. The integral length scale is estimated to be $\approx 1.3$ cm from an integral of the spatial autocorrelation function.

The imaging of the pinch-off is done with a 2-camera setup similar to that in refs. 18 and 21, which provides a measure of the neck’s asymmetry with views from 2 orthogonal angles. One camera (Phantom v2012) films at $1/\mathrm{\Delta }t=\mathrm{1,00,000}\hspace{0.17em}\text{fps}$ and a pixel size $\mathrm{\Delta }x=22\hspace{0.17em}\mathrm{\mu }\text{m}$, while the other (Phantom VEO 440-L) films at $1/\mathrm{\Delta }t=$ 24,000 to 29,000 fps and $\mathrm{\Delta }x=29\hspace{0.17em}\mathrm{\mu }\text{m}$. The pinch-off time $t_0$ is identified independently from each recording as the first frame in which the neck is no longer connected. An image-processing algorithm written in Python is used to infer the 3D orientation of the bubble in time and map pixel locations to 3D space. The size of the neck in each view is calculated by intersecting the pinch-off plane with the image plane, with the pinch-off plane fixed through the pinch-off point but potentially rotating at a constant rate in accordance with the frozen turbulent flow. These processing methods are explained in detail in SI Appendix.

Approximately 300 cases of turbulent bubble pinch-off were imaged with the 2-camera setup, and a further $\sim 40$ were measured without turbulence. The comparison with the model in Fig. 2 is done by first fitting $\overline{d}\left(t\right)$ with a power law fit, calculating $\overline{r}$ and its derivatives for use in Eq. 1, and finding the initial conditions $b_2$ and ${\dot{b}}_2$ that yield the best fit to the experimental data when $d_x$ and $d_y$ are extracted synthetically from the model. To do this, we calculate the $\left(x,y\right)$ location of many points on the neck slice and define $d_x=max\left(x\right)-min\left(x\right)$ and $d_y=max\left(y\right)-min\left(y\right)$. Fig. 4A shows the ensemble average of $\overline{d}/d_{\text{n}}$ obtained by averaging all of the turbulent cases together. The probability density function of the exponent $\alpha$ in Fig. 4B is obtained by choosing the time range over which the power law fit is performed independently for each case to maximize the fit coefficient of determination. Here, we enforce that the chosen range of $\left(t_0-t\right)$ spans at least 1 order of magnitude in time before the kink occurs. The portion of cases exhibiting a resolved kink (which appears before $t_0-t=10\hspace{0.17em}\mathrm{\mu }\text{s}$) shown in Fig. 4B is computed for each combination of needle size and turbulence dissipation rate, which defines the ratio $d_{\text{n}}/d_{\text{H}}$. The ensemble-averaged size of the neck at the kink formation for each condition is found by averaging the value of ${\overline{d}}_{\text{k}}$ over each experimental condition after setting ${\overline{d}}_{\text{k}}=0$ for cases that do not have resolved kinks, with the notion that they kink at subresolution scales. When using smaller needles than those presented in this study, unsteady air injection compounded by the fluctuating pressure imposed by the turbulence at the needle outlet creates high-speed airflow through the neck, inducing a Bernoulli suction effect that dominates the pinching (13).

Direct Numerical Simulations.

We perform direct numerical simulations with the open source package Basilisk (26, 27), solving the 3D 2-phase Navier–Stokes equations with surface tension using an air-water density ratio of 850 and a viscosity ratio of 5.12 on an adaptive octree mesh. This solver has been extensively validated for complex multiphase flow processes with interface topological changes and reconnection (1, 33–35). To validate our configuration, we perform a 3D simulation of axisymmetric bubble pinch-off and recover the pinching dynamics expected from the theoretical and experimental results, the neck size following $d\propto {\left(t_0-t\right)}^{\alpha }$, with $\alpha \approx 0.5$. Grid convergence is verified at high resolution, and we adaptively maintain ∼6 to 10 points per neck diameter throughout the pinch-off process, allowing the neck diameter to shrink to 250 to 450 times smaller than its initial thickness. To further confirm the frozen turbulence hypothesis, we reproduce the dynamical behavior observed in Fig. 2 by initializing a small-amplitude elliptical perturbation (mode $n=2$), and we recover an oscillatory behavior as predicted theoretically and observed experimentally. The role of the initial asymmetry on the kink formation is examined numerically by a set of simulations performed with various initial asymmetries (Fig. 3). Details of these simulations are provided in SI Appendix.

Data Availability.

Data and code to reproduce plots are available at http://arks.princeton.edu/ark:/88435/dsp014f16c5691 (36).