Abstract
We present experimental evidence that DNA can be concentrated due to an electrohydrodynamic coupling between a pressure-driven flow and a parallel electric field. The effects of buffer properties on the process were measured in a microfluidic channel. The concentration rates and the efficiency of trapping DNA were quantified as functions of the ion and polymer concentrations of the buffer solution. Buffers with large ion concentrations hindered the ability to trap DNA, reducing the short-time efficiency of the concentration process from nearly 100% to zero. Importantly, DNA was trapped in the microfluidic channel even when the buffer solution lacked any measurable viscoelastic response. These observations indicate that electrohydrodynamic migration drives the concentration of DNA. We found no evidence of viscoelastic migration in these experiments.
I. INTRODUCTION
Solutions of long polyelectrolyte molecules driven through a capillary by a pressure gradient can be focused at the centerline or walls by applying a counter or coaxial electric field, respectively.1–3 This transverse migration can be exploited to concentrate, and even selectively trap, DNA by applying suitable combinations of field strengths within a microfluidic geometry similar to the one shown in Fig. 1(a).4,5
FIG. 1.
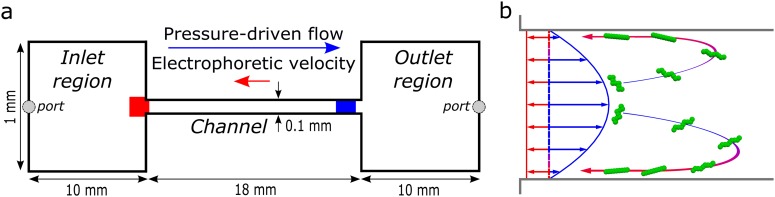
(a) The microfluidic chip consisted of an 18 mm long channel of cross section connecting the inlet and outlet regions of length 10 mm and cross section . Images were collected at the inlet (red area) by focusing on the nearest wall where the DNA concentrates when the pressure-driven flow (blue arrow) and opposing electrophoretic velocity (red arrow) are set appropriately. Images were also collected near the outlet (blue area), with the microscope focused approximately midway between the top and bottom bounding walls. (b) Two-dimensional illustration of DNA molecules (green) entering the microfluidic channel due to the large convective flow (blue). The electric field applied along the channel axis induces an opposing electrophoretic velocity (red) that is one tenth or less of the mean convective velocity. DNA molecules migrate toward the bounding walls of the channel in response to the simultaneous application of the two fields, as confirmed by experimental observations. The DNA molecules return toward the inlet (blue-red arrows) once sufficiently near the wall where the electrophoretic velocity exceeds the fluid velocity. Upon reaching the inlet region, the DNA molecules accumulate in a thin layer near the bounding walls.
This microfluidic process has potential utility as a unit operation in the preprocessing of DNA samples in micrototal analysis systems. Microfluidic processing of biological samples for the purpose of extracting and purifying DNA would have many advantages over traditional methods.6 Full automation of sample preparation within microfluidic devices would enable the collection of smaller samples, reduce the required amount of labor, and increase both the speed and reliability of the processing. Integrating DNA preparation on a chip would be particularly useful for emerging analysis methods that rely on small quantities, or even single molecules, where high DNA integrity is required.7
Many methods of processing DNA on microfluidic platforms have utilized immobilization or capture.8–10 General methods for concentrating analytes that utilize gradients in the buffers or fields11,12 have been used to preconcentrate DNA, including temperature gradient focusing,13 rheotaxis,14 and isotachophoresis.15 Electrokinetic trapping of DNA using membranes16–19 and dielectrophoretic trapping of DNA in a microfluidic channel equipped with an array of electrodes have also been demonstrated.20
However, the microfluidic process shown in Fig. 1(a) relies on different physics from those cited above. As illustrated in Fig. 1(b), DNA enters the microchannel due to the convective flow and then migrates toward the channel walls. Once near a wall, the convective velocity vanishes and electrophoresis transports the DNA molecules back to the inlet. The DNA then accumulates at the inlet to the channel in a thin layer near the walls. The trapping critically depends upon the migration of the DNA to the side walls after entering the channel, as the mean convective velocity is more than ten times larger than the opposing electrophoretic velocity. Spheres of similar size and electrophoretic mobility as the DNA do not migrate and, therefore, are not trapped.4
The transverse migration of long DNA strands has been previously attributed to an electrohydrodynamic interaction.21–25 Calculations of the electrophoretic motion of DNA, and other polyelectrolytes, typically ignore the velocity disturbance caused by the electric field acting on the charged polymer backbone and its surrounding counterion cloud. However, calculations that incorporate these hydrodynamic disturbances predict a deterministic motion perpendicular to the electric field. For polymers elongated and rotated by the shear flow in the channel, the theoretically predicted direction of migration is consistent with observations.
Few mechanisms other than electrohydrodynamic migration can predict the qualitative motion of DNA under the combined fields. Experimental observations1–3 indicate that DNA should migrate to the bounding wall when the electric field causes the DNA to lag the pressure-driven flow and to the center of the channel when the DNA leads the flow. Inertial forces26,27 can cause particle migration toward the center or toward the wall, depending on the direction of the axial electric field with respect to the convective flow. However, the direction of the migration is incorrect: particles that lag the flow migrate toward the center,27 rather than the wall.
Particles,28 and DNA specifically,29 suspended in a viscoelastic fluid can migrate transverse to pressure-driven flows in response to axially directed forces. The direction of migration can be toward the centerline or toward the bounding walls, and, in this case, the directions of the applied fields and resulting motion of DNA match the electrohydrodynamic migration.1–3 Andriamanampisoa et al.30 attributed the concentration of DNA within a microfluidic device to viscoelastic migration.31 Their process used axial flow and electric fields within a geometry similar in shape to that used by Arca et al.4
Here, we distinguish migration due to an electrohydrodynamic disturbance flow from viscoelastic migration by measuring the effects of the buffer solution on the ability to trap DNA. Both the ion concentration and the concentration of neutral polymer in the buffer were varied, and the effects on the trapping of DNA were measured as described in Sec. II. Since the trapping depends on DNA molecules migrating from the channel cross section to the bounding walls, quantifications of concentration rates are proxies for evaluating the mechanisms that control transverse migration. The results demonstrate that increasing the ionic strength reduces the migration, and hence, trapping efficiency (Sec. III A), consistent with the proposal that migration is caused by electrohydrodynamic interactions. Likewise, experiments (Sec. III B) indicate that trapping occurs even when the buffer solution contains no neutral polymer and no measureable viscoelastic response.
II. EXPERIMENTAL METHODS AND MATERIALS
A. DNA solutions
Experiments were performed with DNA suspended in the 21 different solutions listed in Table I. Tris-EDTA (TE) buffer was used in most of the experiments. A solution of concentrated () TE buffer (Sigma) was diluted 100 times with nanopure water to a standard solution containing 10 mM Tris-HCl and 1 mM EDTA. Solutions of TE at concentrations as low as 0.025 were also used in the experiments. All TE solutions were filtered (0.22 m), and the salinity of some of the solutions was increased by adding sodium chloride (NaCl). To study the effect of polymer concentration on the DNA migration and concentration, polyvinylpyrrolidone (PVP) with a molecular weight of 40 kDa was added at the indicated concentrations. This neutral polymer was included in the buffer solution by Arca et al.4 to stabilize the channel coating that eliminates electro-osmosis.
TABLE I.
The composition of the 21 solutions used in the experiments. The ionic strength () and the estimated Debye length () were calculated for the TE buffers; calculations for and were not made for the TBE buffer solutions.
| No. | TE (X) | TBE (X) | NaCl (mM) | PVP (wt. %) | (mM) | (nm) |
|---|---|---|---|---|---|---|
| 1 | 0.025 | 0 | 0.5 | 0.275 | 18.33 | |
| 2 | 0.1 | 0 | 0.5 | 1.1 | 9.17 | |
| 3 | 0.1 | 2.5 | 0.5 | 3.6 | 5.07 | |
| 4 | 0.1 | 5 | 0.5 | 6.1 | 3.89 | |
| 5 | 0.1 | 20 | 0.5 | 21.1 | 2.09 | |
| 6 | 0.1 | 50 | 0.5 | 51.1 | 1.34 | |
| 7 | 0.25 | 0 | 0 | 2.75 | 5.80 | |
| 8 | 0.25 | 0 | 0.5 | 2.75 | 5.80 | |
| 9 | 0.25 | 0 | 2 | 2.75 | 5.80 | |
| 10 | 0.25 | 2.5 | 0.5 | 5.25 | 4.20 | |
| 11 | 0.25 | 20 | 0.5 | 22.75 | 2.02 | |
| 12 | 0.25 | 50 | 0.5 | 52.75 | 1.32 | |
| 13 | 0.5 | 0 | 0 | 5.5 | 4.10 | |
| 14 | 0.5 | 0 | 0.5 | 5.5 | 4.10 | |
| 15 | 0.5 | 0 | 1 | 5.5 | 4.10 | |
| 16 | 0.5 | 0 | 2 | 5.5 | 4.10 | |
| 17 | 1 | 0 | 0.5 | 11 | 2.90 | |
| 18 | 1 | 5 | 0.5 | 16 | 2.40 | |
| 19 | 1 | 20 | 0.5 | 31 | 1.73 | |
| 20 | 2 | 0 | 0 | |||
| 21 | 2 | 0 | 2 |
The Debye screening length of the TE buffer solutions, , was calculated from the molar ionic strength of the solution, (Table I). EDTA at a pH of 8 exists mainly as the anion with an ionic strength for the 1 buffer of 45 mM, as calculated by PHREEQC.32,33 The concentration of the conjugate Tris acid () can be found from the [OH] concentration of , and the concentration of added Tris (); it adds an additional 12.6 mM to the ionic strength of the 1 buffer. Since the solutions are close to ideal, it suffices to determine the ionic strength of the 1 buffer solution and then scale it by the dilution factor of the other buffers. In addition, we must then add the ionic strength of the salt (assuming complete dissociation) to determine the total ionic strength for the solution. The Debye length in nanometers can be found from the formula , with in mmol/l.
Buffer solutions of Tris-borate-EDTA were also used (solutions 20 and 21 in Table I). A concentrated 10 solution (Corning) was diluted with nanopure water to a concentration of 2 (89 mM Tris, 89 mM borate, and 2 mM EDTA) and then filtered (0.22 m). No NaCl was added to the Tris-borate-EDTA (TBE) solutions, but 2 wt. % of PVP (40 kDA) was added to one of the solutions.
All experiments utilized -DNA molecules (New England Biolabs Inc., 48.5 kbp) that were added at a concentration of , no matter the buffer composition. To enable imaging, the DNA was labeled with fluorescent dye (YOYO-1, Molecular Probes) at a ratio of four base pairs to one dye molecule.
B. Microfluidic chip and fields
The constriction-expansion microchannels illustrated in Fig. 1(a) were manufactured (Translume, Inc.) by laser etching silica to a constant depth of . A square channel with a cross section of and the length of 18 mm connects two regions (inlet and outlet, as defined by the direction of fluid flow), which are ten times wider than the channel. Luer connectors, to which the tubing was attached, were affixed to the chip above the access ports indicated in Fig. 1(a). Each time a different buffer solution was used in an experiment, the channels were cleaned by flushing, in sequence, a solution of 1M HCl, nanopure water, a solution of 0.5M NaOH, and then more nanopure water through the device.
As a final step, the channel was coated with PVP by circulating an aqueous solution with a concentration of 1 wt. % PVP (40 kDa) through the channel for at least 14 h. Coatings of PVP can prevent electro-osmosis,34 and previous studies4 confirmed that the coating suppresses electro-osmosis for solutions similar to those used here. We note that electro-osmosis does not affect the migration. However, electro-osmosis opposes the electrophoretic velocity and can reduce, or even eliminate, the rate of concentration if it is not suppressed sufficiently.
Two reservoirs were attached with tubing to the ports via Luer connectors. The reservoir attached to the inlet region contained the DNA and buffer solution, while the reservoir attached to the outlet region contained only the buffer solution. The rate of the pressure-driven flow was governed by adjusting the relative height, , of the reservoirs using a translation stage attached to a stepper motor. Electrodes placed in each of the reservoirs were connected to a DC voltage source that generated a potential difference of up to 400 V. The potential drop occurs almost entirely across the 18 mm length of the channel, due to its small cross section relative to the other portions of the microchip and the tubing.4,5
For each setting of , the rate of concentration was maximized at a potential field of as listed in Table II for the 0.25 TE solution with 0.5 wt. % PVP (solution 8). The measurements agree with previous experiments that utilized the same buffer solution.4,5 Table II also lists the velocity at the centerline, , due to the pressure-driven flow and the electrophoretic velocity, , for each set of conditions. These velocities were calculated from measurements of the DNA motion within the channel in response to independently applied fields.
TABLE II.
The electric potential, , that maximized the rate of concentration at each setting of the height differential, , when using the 0.25 TE solution with 0.5 wt. % PVP and no added NaCl (solution 8 in Table I). The corresponding convective flow and electrophoretic velocities, and , are given for each condition.
| (in.) | () | (V) | () |
|---|---|---|---|
| 0.1 | 800 | 50 | 41.7 |
| 0.15 | 1200 | 60 | 50 |
| 0.2 | 1600 | 70 | 58.3 |
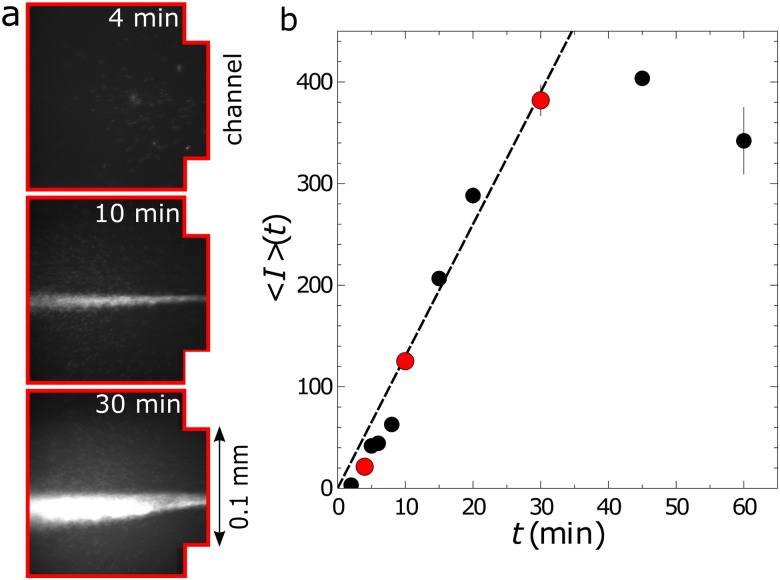
Most of the measurements reported here utilized the height and electric potentials listed in Table II. The pattern of the concentration buildup at the inlet [region in Fig. 1(a)] is shown in Fig. 2(a) for one set of conditions. For some buffer solutions, combinations of height and electric potentials different from those in Table II were used to maximize the rate of concentration. In those cases, the pattern of the concentration was qualitatively similar to the pattern shown in Fig. 2(a).
FIG. 2.
(a) Microscopy images showing the buildup of DNA at the inlet to the channel at three different times for in. ( and ) and solution 8. The images were collected at the inlet of the channel [red area in Fig. 1(a)]. (b) Mean intensity as a function of time at the inlet for the same conditions as the images. The red circles correspond to the mean intensities from the images in (a).
C. Imaging and measurement protocols
The microfluidic chip was mounted on the stage of an inverted epifluorescent microscope (Nikon Diaphot 200) to image the fluorescent DNA. A Leitz Wetzlar EF 63/0.85 objective was used, and the images were recorded with a QImaging Retiga SRV CCD camera with an exposure time of 200 ms for each image. The experimental setup was fully automated, enabling control over the flow, voltage, sample illumination, and image collection. Images were collected at predetermined time intervals at the two locations indicated in Fig. 1(a) to measure the rate of concentration and the efficiency of the trapping, respectively.
Rates of concentration were measured at the inlet [red region in Fig. 1(a)] of the channel, with the microscope objective focused near the bottom bounding wall of the microfluidic chip. Prior to beginning each new experiment, the channel was flushed using a convective flow to remove any excess DNA trapped in previous experiments. After initiating the concentration process by applying a voltage drop, four sets of images were collected at uniform intervals over a total time period of 8–240 min. The computer controlled shutter limited illumination of the sample to a total of 4 s over the course of any one experiment, reducing the effect of photobleaching on the measured intensities to less than 10%.5 Example images showing the increase in DNA concentration with time are shown in Fig. 2(a). Multiple experiments were performed for each set of conditions.
The mean value of the fluorescence intensity as a function of time ,
| (1) |
was calculated from each image by summing over the intensity of each pixel of pixels in the inlet region. Figure 2(b) shows an example of the mean intensity as a function of time. The concentration was determined from the mean intensities,
| (2) |
where was the fluorescence intensity measured in the absence of DNA trapping (no electric field). The calibration parameter was determined by relating known concentrations and intensities, and the calibration was repeated each time the imaging conditions changed. The rates of concentration are reported at short times,
| (3) |
over which the concentration increase is linear. Note that the rate of concentration declines at sufficiently long times,5 as represented in Fig. 2(b) by the deviation of the mean intensity from the linear increase in time at approximately 30 min.
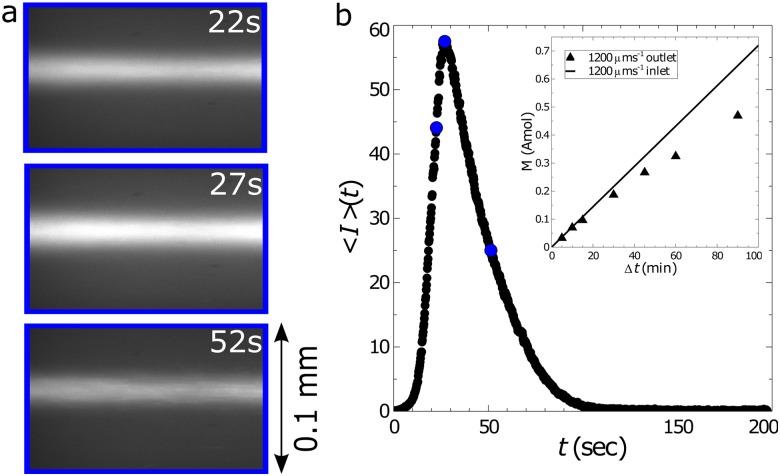
Assessment of the trapping efficiency relied on images collected near the outlet of the channel [blue region of Fig. 1(a)] with the microscope focused approximately midway between the bounding walls. First, DNA was trapped at the inlet for elapsed times () between 5 and 30 min. Then, the trapped DNA was released by turning the electric field off, allowing the pressure-driven flow to convect the DNA through the channel toward the outlet region. Images were collected continuously at the outlet to record the fluorescent intensity of the passing DNA molecules. Example images after the release of the DNA are shown in Fig. 3. The mean fluorescence intensity [Eq. (1)] grew rapidly as DNA passed by the viewing window, then declined until returning to the background level that corresponds to the DNA concentration in the inlet reservoir.
FIG. 3.
(a) Example images showing fluorescent DNA passing through the outlet [blue region in Fig. 1(a)] of the channel after having been trapped for a total time of . The DNA was suspended in buffer solution 8 and was trapped using in. and ( and ). (b) The mean intensity calculated from each image following the release of the trap at . The blue circles correspond to the mean intensities from the images in (a). The subplot compares the total moles of DNA trapped (symbols) with the theoretical maximum (line) as a function of the elapsed time of trapping, .
The mean intensity from each image was converted to a concentration using Eq. (2), but with the calibration factor and the background intensity determined from independent measurements made at the same region where the images were collected. We note that all of the DNA passing through the channel during an image was recorded, as the light emitted by the stimulated YOYO dye molecules is collected automatically from the entire depth of the channel.4 The total amount of DNA trapped in a time within the microfluidic device is given by
| (4) |
where is the volumetric flow rate of the DNA solution through the microchannel. The limits imply that the integral is evaluated over the whole pulse of DNA; in Fig. 3(b), this would be from 0 to approximately 120 s. The efficiency of the trapping mechanism is the ratio of to , the amount of DNA that entered the microfluidic device. Figure 3(b) (inset) compares the actual and maximum amount of DNA trapped as a function of for one set of conditions.
III. RESULTS AND DISCUSSION
The concentration rate and the trapping efficiency were measured for the buffer solutions listed in Table I. The combinations of flow () and electric potential () given in Table II were used, unless otherwise noted. Section III A describes the effects of altering the ionic strength of the solutions while holding the PVP concentration constant at 0.5 wt. %. The effects of varying the PVP concentration are described in Sec. III B.
A. Effect of ionic strength
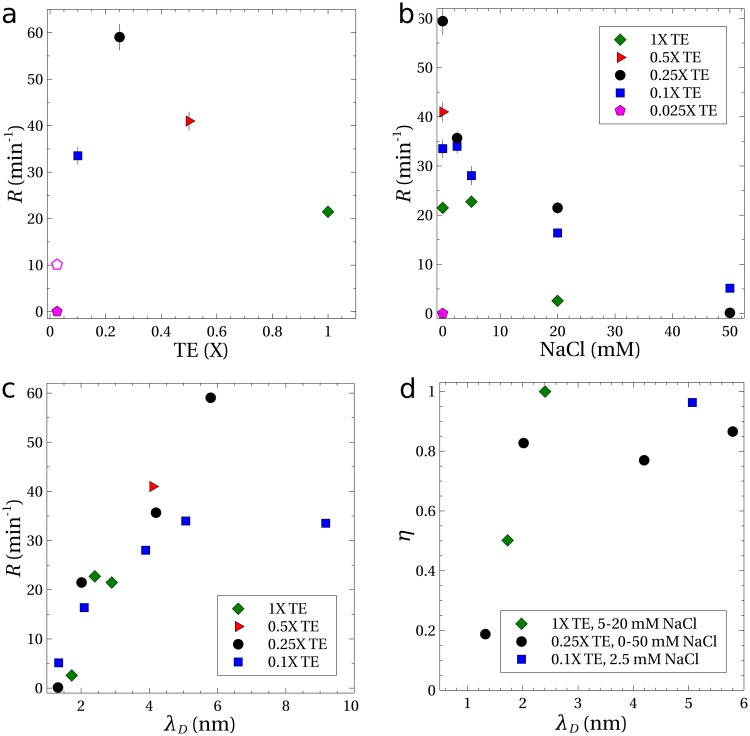
Figure 4(a) shows the rates of concentration () for DNA suspended in TE buffers with no added NaCl and a PVP concentration of 0.5 wt. %. The rate of nearly measured for DNA in the 0.25 TE buffer (solution 8 in Table I) is similar to the rate measured previously ().4 The rate of was the largest observed for the different TE concentrations. For lower strength buffers, the concentration rate declined until no measureable amount of DNA was trapped within the microfluidic device (0.025 TE). The concentration rate declined at buffer strengths higher than 0.25, but was still measureable at 1.
FIG. 4.
Experiments with in. () and electrical potentials of (solid symbols) and (open symbol). All solutions contained 0.5 wt. % PVP, and the error bars indicate the standard error. (a) Concentration rates as a function of TE buffer strength, with no added NaCl. (b) Concentration rates as a function of added NaCl and (c) as a function of the Debye length, . (d) Measurements showing the trapping efficiency as a function of Debye length for an elapsed time of .
The height difference and potential were held constant for the data represented by solid symbols in Fig. 4. The centerline velocity () was independent of the ionic concentration at the same height difference. Also, the velocity of DNA in response to the electric field alone was found to be approximately constant at for TE buffers of 0.25 and higher, implying a constant electrophoretic mobility of .
At the lowest buffer strength of 0.025, the velocity of the DNA in response to the electric field was lower (). Increasing the potential drop from to increased the velocity to a value comparable to experiments with buffer strengths of 0.25 and higher. With this larger electric potential, the concentration rate was measurable [open symbol, Fig. 4(a)], but was only one-sixth of the maximum rate of . The result in the 0.025 buffer is anomalous in that a lower ionic strength in general leads to stronger electrohydrodynamic migration. We speculate that the increased acidity of the solution (pH 6.8) causes some protons to condense onto the DNA backbone, thereby reducing its total charge. This could explain both the reduced electrophoretic mobility and the severely weakened electrohydrodynamic concentration rate. The change in the buffer pH may also have reduced the effectiveness of the coating that suppresses the electro-osmotic flow,34 which would also reduce the concentration rate.
The optimum buffer strength to maximize the rate of concentration of DNA was around 0.25. Adding NaCl to this buffer reduced the rate of DNA concentration, as shown in Fig. 4(b). The electrophoretic mobility was not noticeably altered by added NaCl, but the ability to concentrate DNA vanished with the addition of sufficient NaCl. No measurable concentration rate was observed even with higher flow rates and voltages. Similarly, Fig. 4(b) shows that adding NaCl to the other buffer solutions decreased the rate of concentration.
The higher TE buffer strengths and addition of NaCl increases the ionic strength of the buffer solution and compresses the thickness of the layer of counterions that surround the DNA backbone, as quantified by the Debye length () given in Table I. Experimental results [Fig. 4(c)] show a strong correlation between the concentration rate and the Debye length , with the rate disappearing as the double layer thickness goes to zero. These lower rates of DNA concentration are consistent with the theory that transverse migration of DNA is caused by velocity disturbances induced by the electric field acting on the distorted DNA.21–25 For sufficiently small Debye lengths, the velocity disturbances caused by the electric field are screened and electrohydrodynamic migration disappears. For example, calculations3,22 of DNA dynamics that include this electrohydrodynamic interaction predict that the transverse velocity scales as in the limit of weak shearing flows and electric fields. As a result of eliminating the electrohydrodynamic migration, the microfluidic process fails to trap and concentrate DNA.
The efficiency of DNA trapping in the microfluidic device was measured for some of the TE buffer solutions from Table I. The results, shown in Fig. 4(d), are plotted as a function of Debye length. Note that corresponds to complete trapping of DNA within the device, with no loss of DNA from the exit. For a Debye length greater than 2 nm, regardless of the buffer components, the migration velocity was sufficient to drive most of the DNA to migrate toward the walls and to obtain a device efficiency exceeding 80%. For smaller Debye lengths (more salt), the efficiency dropped rapidly, indicating that the migration was suppressed, in agreement with our hypothesis that migration is driven by an electrohydrodynamic velocity disturbance. A residual trapping of DNA () was observed even at the highest ionic concentration ().
B. Effect of PVP concentration
Buffer solutions tested in Sec. III A and in previous studies4,5 contained PVP at a concentration of 0.5 wt. %. The PVP was added to the solutions to increase the stability of the PVP coating that was applied to the channel walls to eliminate electro-osmosis, which disrupts the ability to trap the DNA. The presence of the PVP in the solutions potentially provides an alternate explanation for the migration and concentration, since viscoelasticity of the buffer solutions can induce a transverse motion of DNA.31,35 However, the inability to trap DNA in the high salt solutions (Fig. 4) indicates that electrohydrodynamic interactions cause DNA migration to the walls of the microchannel. If viscoelasticity were responsible, migration and concentration would likely still occur regardless of the ionic concentration.
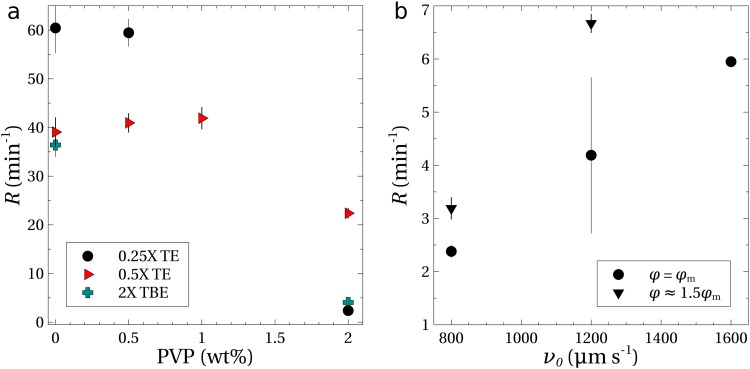
To provide additional evidence that viscoelasticity is not responsible for the migration and concentration of DNA, experiments were performed in which the PVP concentration was altered independently of the ionic concentration of the buffer. Figure 5(a) shows the concentration rates as a function of added PVP in buffer solutions with no NaCl. The concentration rate was independent of the amount of PVP up to at least 0.5 wt. % in the 0.25 buffer and up to 1 wt. % in the 0.5 TE buffer. Even in the absence of PVP (0 wt. %), DNA was trapped and concentrated at the inlet of the channel.
FIG. 5.
(a) Rates of concentration as a function of the PVP concentration for TE and TBE buffers with no added NaCl. Experiments were performed using in. and a potential of for the TE buffers; larger potentials of and 400 V were utilized for the TBE buffers containing 0 and 2 wt. % PVP, respectively. (b) Concentration experiments using the 0.25 TE buffer (no added NaCl, 2 wt. % PVP) as a function of the centerline velocity; experiments were performed with potentials of and (see Table II).
The concentration rate declined once the PVP concentration exceeded 1 wt. % as shown in Fig. 5(a). This was due in part to the increased viscosity of the solution at 2 wt. % PVP (see the Appendix), which reduced the centerline velocity by approximately one-third. To compensate for the reduced flow rate, experiments were performed with 2 wt. % PVP and increased pressure heads (). The rate of concentration increased linearly [Fig. 5(b)], but remained an order of magnitude lower than the rates for the 0.5 wt. % PVP solutions. Since the electrophoretic mobility scales inversely with the viscosity, the potential was increased by 50% in some of the experiments. Figure 5(b) shows that the concentration rate improved again, but still remained nearly one order of magnitude lower than those measured at smaller PVP concentrations.
Measurements of trapping efficiency as a function of trapping time are shown in Fig. 6 for different concentrations of PVP. Efficiencies of 80% and higher were measured for the 0 and 0.5 wt. % PVP solutions. For 2 wt. % PVP, the efficiency was significantly reduced. The values of indicate that the majority of the DNA was not trapped, suggesting that most of the DNA molecules failed to reach the bounding walls before exiting the device.
FIG. 6.
Measurements of the trapping efficiency as a function of (elapsed time) and PVP concentration for 0.25 TE buffer solution with no added NaCl. All measurements were at the same centerline velocity of ; a potential of was used for the 0.0 wt. % and 0.5 wt. % PVP solutions, and a potential of 105 V was used for the 2.0 wt. % PVP solution.
Andriamanampisoa et al.30 concentrated shorter DNA strands [5 kbp, see their Fig. 1(B)] at the junction between circular capillaries of diameter 100 and using parallel flow and electric fields. The concentration was attributed to a migration of the DNA to walls of the smaller capillary, as in Arca et al.,4 Montes et al.,5 and here. However, the migration was claimed to be due to viscoelasticity,31 which cannot explain the observations presented in this paper.
Their experiments used a TBE buffer solution, and measurements of the concentration rates were also done with TBE solutions (see solutions 20 and 21, Table I) as an additional test; the results are shown in Fig. 5(a). In the absence of PVP, the value of was similar to that of the 0.5 TE buffer solution. With 2 wt. % added PVP, the rate declined to less than , similar to the TE buffers. We note that the potential required to maximize the rates in the experiments with TBE was much higher than that required in the TE solutions. For example, the 0 wt. % PVP solution required a potential of 150 V to provide the maximum concentration rate at the inlet.
The key finding that PVP is not required for the migration is evidence that an additional mechanism besides viscoelastic stresses can cause migration. Viscoelastic migration depends upon the presence of non-Newtonian normal stresses, which are found in viscoelastic polymer solutions. Rheological measurements (see the Appendix) indicate that the solutions used here (PVP concentrations ) are Newtonian, with no measurable elasticity over the range of frequencies tested. Hence, no migration due to viscoelasticity would be expected in the current experiments. In contrast, the buffers used by Andriamanampisoa et al.30 were clearly viscoelastic, as they contained PVP of a higher molecular weight (360 kDa vs 40 kDa) and concentration (5 wt. % vs up to 2 wt. %). Tests of their microfluidic device, in the absence of PVP or with a higher ionic concentration, would help to clarify the relative roles of viscoelastic and electrohydrodynamic migration in the concentration of DNA.
IV. CONCLUSIONS
Experimental evidence presented in this paper supports the hypothesis that electrohydrodynamic interaction drives migration and subsequent concentration of DNA within the microfluidic device shown in Fig. 1(a). Increasing the ionic strength of the buffer solution was shown to significantly degrade the rate of concentration and the efficiency of trapping of DNA. Increasing ionic strength reduced the transverse velocity by reducing the Debye length, which theories for electrohydrodynamic migration21–25 indicate should be larger than the diameter of the DNA backbone (). Trapping efficiency [Fig. 4(d)] was found to decline for Debye lengths smaller than 2 nm.
Fluid viscoelasticity has been shown to be unnecessary for trapping DNA. Experiments with PVP-free buffer solutions gave similar rates and efficiencies of trapping as the solutions with 0.5 wt. % PVP as seen in Figs. 5 and 6. This does not contradict the idea that viscoelastic stresses can also cause a similar transverse migration and concentration, although at higher concentrations of PVP and higher shear rates than employed here.
Electrohydrodynamic migration has potential applications for the preprocessing of DNA samples in lab-on-a-chip systems. In addition to preconcentration of DNA, the process described here could be useful for separating DNA from a cell lysate. An advantage of electrohydrodynamic migration and trapping is that it is sensitive to the length and flexibility of the molecule. Shorter DNA strands migrate less than longer ones, and rigid charged particles migrate weakly, or not at all if spherical.4 On the other hand, even rigid charged spheres will migrate in a viscoelastic fluid. Thus, the electrohydrodynamic mechanism has greater potential for separating DNA from proteins and other debris in the lysate.
ACKNOWLEDGMENTS
This work was supported by the National Science Foundation (NSF, Grant No. 1804302). We thank Mr. Benjamin Valley for assistance in making some of the figures.
APPENDIX: RHEOLOGY
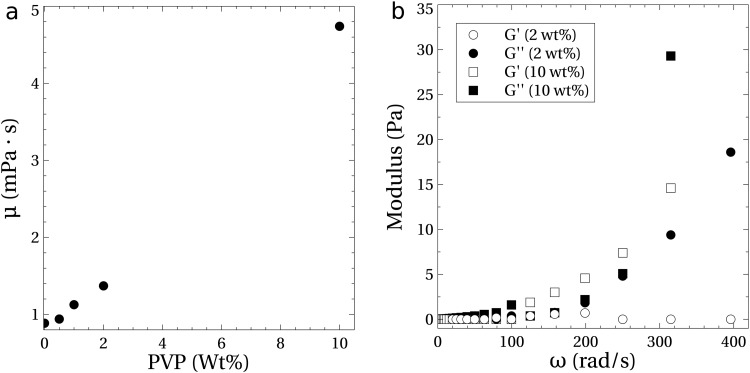
Measurements of the rheology of the 0.25 TE buffer with added PVP are shown in Fig. 7. Measurements of the steady shear viscosity and the small amplitude oscillatory shear (SAOS) were made using an Anton Paar MCR 302 rheometer. A cone and plate geometry with a diameter of 60 mm and a cone angle of was used for the measurements, all performed at a controlled temperature of .
FIG. 7.
Rheological measurements of the 0.25 TE buffer solution with PVP and no added NaCl. (a) Viscosity () as a function of PVP concentration up to 10 wt. %. (b) Loss (filled symbols) and storage (open symbols) modulus for the 2 and 10 wt. % PVP solutions as a function of frequency (); data were generated using a strain amplitude of 0.05 for the 2 wt. % solution and 0.03 for the 10 wt. % solution.
The viscosity reported in Fig. 7(a) shows a linear scaling with PVP concentration and is independent of the shear rate through at least . The intrinsic viscosity, , was calculated to be approximately 0.19 dl/g, where is the viscosity of the suspending fluid and is the PVP concentration. This result is consistent with data available for solutions of PVP with similar molecular weights. For example, the intrinsic viscosity for Kollidon 30 (PVP MW of 44 kDa–54 kDa) is reported to range from 0.19 to 0.25 dl/g in water and that of Kollidon 25 (PVP MW of 28 kDa–34 kDa) from 0.15 to 0.19 dl/g.36 A linear dependence of viscosity on concentration is a characteristic of dilute polymer solutions, and the critical concentration at which the PVP molecules overlap can be estimated37,38 as , or 5.3 wt. %. So, our experiments ( PVP) are clearly in the dilute regime.
Figure 7(b) shows the loss () and storage () moduli measured for the 2 and 10 wt. % PVP solution. Elastic components () were not measureable at the largest frequency tested (400 rad/s). At 400 rad/s, the peak shear rate was in the rheological testing, whereas the maximum rate of shear in the experiments ranged from at up to at . To check the sensitivity of the rheological measurements, we also used a 10 wt. % PVP solution. In this case, a strong elastic response was measured [Fig. 7(b)].
REFERENCES
- 1.Zheng J. and Yeung E. S., “Anomalous radial migration of single DNA molecules in capillary electrophoresis,” Anal. Chem. 74, 4536–4547 (2002). 10.1021/ac0257344 [DOI] [PubMed] [Google Scholar]
- 2.Zheng J. and Yeung E. S., “Mechanism for the separation of large molecules based on radial migration in capillary electrophoresis,” Anal. Chem. 75, 3675–3680 (2003). 10.1021/ac034430u [DOI] [PubMed] [Google Scholar]
- 3.Arca M., Butler J. E., and Ladd A. J. C., “Transverse migration of polyelectrolytes in microfluidic channels induced by combined shear and electric fields,” Soft Matter 11, 375–4382 (2015). 10.1039/C5SM00572H [DOI] [PubMed] [Google Scholar]
- 4.Arca M., Ladd A. J. C., and Butler J. E., “Electro-hydrodynamic concentration of genomic length DNA,” Soft Matter 12, 6975–6984 (2016). 10.1039/C6SM01022A [DOI] [PubMed] [Google Scholar]
- 5.Montes R. J., Butler J. E., and Ladd A. J. C., “Trapping DNA with a high throughput microfluidic device,” Electrophoresis 40, 437–446 (2019). 10.1002/elps.201800287 [DOI] [PubMed] [Google Scholar]
- 6.Cui F., Rhee M., Singh A., and Tripathi A., “Microfluidic sample preparation for medical diagnostics,” Annu. Rev. Biomed. Eng. 17, 267–286 (2015). 10.1146/annurev-bioeng-071114-040538 [DOI] [PubMed] [Google Scholar]
- 7.Friedrich S. M., Zec H. C., and Wang T.-H., “Analysis of single nucleic acid molecules in micro-and nano-fluidics,” Lab Chip 16, 790–811 (2016). 10.1039/C5LC01294E [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Wen J., Legendre L. A., Bienvenue J. M., and Landers J. P., “Purification of nucleic acids in microfluidic devices,” Anal. Chem. 80, 6472–6479 (2008). 10.1021/ac8014998 [DOI] [PubMed] [Google Scholar]
- 9.Parton J., Birch C., Kemp C., Haswell S. J., Pamme N., and Shaw K. J., “Integrated DNA extraction and amplification using electrokinetic pumping in a microfluidic device,” Anal. Methods 4, 96–100 (2012). 10.1039/C1AY05552F [DOI] [Google Scholar]
- 10.Benítez J. J., Topolancik J., Tian H. C., Wallin C. B., Latulippe D. R., Szeto K., Murphy P. J., Cipriany B. R., Levy S. L., Soloway P. D. et al., “Microfluidic extraction, stretching and analysis of human chromosomal DNA from single cells,” Lab Chip 12, 4848–4854 (2012). 10.1039/c2lc40955k [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Zhao C., Ge Z., and Yang C., “Microfluidic techniques for analytes concentration,” Micromachines 8, 28 (2017). 10.3390/mi8010028 [DOI] [Google Scholar]
- 12.Zhu F. and Hayes M. A., “Exploring gradients in electrophoretic separation and preconcentration on miniaturized devices,” Separations 3, 12 (2016). 10.3390/separations3020012 [DOI] [Google Scholar]
- 13.Ge Z., Wang W., and Yang C., “Rapid concentration of deoxyribonucleic acid via Joule heating induced temperature gradient focusing in poly-dimethylsiloxane microfluidic channel,” Anal. Chim. Acta 858, 91–97 (2015). 10.1016/j.aca.2014.12.016 [DOI] [PubMed] [Google Scholar]
- 14.Friedrich S. M., Burke J. M., Liu K. J., Ivory C. F., and Wang T.-H., “Molecular rheotaxis directs DNA migration and concentration against a pressure-driven flow,” Nat. Commun. 8, 1213 (2017). 10.1038/s41467-017-01214-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Rogacs A., Marshall L. A., and Santiago J. G., “Purification of nucleic acids using isotachophoresis,” J. Chromatogr. A 1335, 105–120 (2014). 10.1016/j.chroma.2013.12.027 [DOI] [PubMed] [Google Scholar]
- 16.Dai J., Ito T., Sun L., and Crooks R. M., “Electrokinetic trapping and concentration enrichment of DNA in a microfluidic channel,” J. Am. Chem. Soc. 125, 13026–13027 (2003). 10.1021/ja0374776 [DOI] [PubMed] [Google Scholar]
- 17.Hahn T., O’Sullivan C. K., and Drese K. S., “Microsystem for field-amplified electrokinetic trapping preconcentration of DNA at poly (ethylene terephthalate) membranes,” Anal. Chem. 81, 2904–2911 (2009). 10.1021/ac801923d [DOI] [PubMed] [Google Scholar]
- 18.Cheow L. F. and Han J., “Continuous signal enhancement for sensitive aptamer affinity probe electrophoresis assay using electrokinetic concentration,” Anal. Chem. 83, 7086–7093 (2011). 10.1021/ac201307d [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Ouyang W., Li Z., and Han J., “Pressure-modulated selective electrokinetic trapping for direct enrichment, purification, and detection of nucleic acids in human serum,” Anal. Chem. 90, 11366–11375 (2018). 10.1021/acs.analchem.8b02330 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Asbury C. L. and Van Den Engh G., “Trapping of DNA in nonuniform oscillating electric fields,” Biophys. J. 74, 1024–1030 (1998). 10.1016/S0006-3495(98)74027-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Usta O. B., Butler J. E., and Ladd A. J. C., “Transverse migration of a confined polymer driven by an external force,” Phys. Rev. Lett. 98, 098301 (2007). 10.1103/PhysRevLett.98.098301 [DOI] [PubMed] [Google Scholar]
- 22.Butler J. E., Usta O. B., Kekre R., and Ladd A. J. C., “Kinetic theory of a confined polymer driven by an external force and pressure-driven flow,” Phys. Fluids 19, 113101 (2007). 10.1063/1.2801409 [DOI] [PubMed] [Google Scholar]
- 23.Kekre R., Butler J. E., and Ladd A. J. C., “Role of hydrodynamic interactions in the migration of polyelectrolytes driven by a pressure gradient and an electric field,” Phys. Rev. E 82, 050803 (2010). 10.1103/PhysRevE.82.050803 [DOI] [PubMed] [Google Scholar]
- 24.Pandey H. and Underhill P. T., “Coarse-grained model of conformation-dependent electrophoretic mobility and its influence on DNA dynamics,” Phys. Rev. E 92, 052301 (2015). 10.1103/PhysRevE.92.052301 [DOI] [PubMed] [Google Scholar]
- 25.Ladd A. J. C., “Electrophoresis of sheared polyelectrolytes,” Mol. Phys. 116, 1–13 (2018). 10.1080/00268976.2017.1359347 [DOI] [Google Scholar]
- 26.Saffman P., “Lift on a small sphere in a slow shear flow,” J. Fluid Mech. 22, 385–400 (1965). 10.1017/S0022112065000824 [DOI] [Google Scholar]
- 27.Kim Y. W. and Yoo J. Y., “Axisymmetric flow focusing of particles in a single microchannel,” Lab Chip 9, 1043–1045 (2009). 10.1039/b815286a [DOI] [PubMed] [Google Scholar]
- 28.D’Avino G., Greco F., and Maffettone P. L., “Particle migration due to viscoelasticity of the suspending liquid and its relevance in microfluidic devices,” Annu. Rev. Fluid Mech. 49, 341–360 (2017). 10.1146/annurev-fluid-010816-060150 [DOI] [Google Scholar]
- 29.Kim J. Y., Ahn S. W., Lee S. S., and Kim J. M., “Lateral migration and focusing of colloidal particles and DNA molecules under viscoelastic flow,” Lab Chip 12, 2807–2814 (2012). 10.1039/c2lc40147a [DOI] [PubMed] [Google Scholar]
- 30.Andriamanampisoa C.-L., Bancaud A., Boutonnet-Rodat A., Didelot A., Fabre J., Fina F., Garlan F., Garrigou S., Gaudy C., Ginot F., Henaff D., Laurent-Puig P., Morin A., Picot V., Saias L., Taly V., Tomasini P., and Zaanan A., “BIABooster: Online DNA concentration and size profiling with a limit of detection of and application to high-sensitivity characterization of circulating cell-free DNA,” Anal. Chem. 90, 3766–3774 (2018). 10.1021/acs.analchem.7b04034 [DOI] [PubMed] [Google Scholar]
- 31.Ranchon H., Malbec R., Picot V., Boutonnet A., Terrapanich P., Joseph P., Leïchlé T., and Bancaud A., “DNA separation and enrichment using electro-hydrodynamic bidirectional flows in viscoelastic liquids,” Lab Chip 16, 1243–1253 (2016). 10.1039/C5LC01465D [DOI] [PubMed] [Google Scholar]
- 32.Parkhurst D. L. and Appelo C. A. J., Description of Input and Examples for PHREEQC Version 3—A Computer Program for Speciation, Batch-Reaction, One-Dimensional Transport, and Inverse Geochemical Calculations, Techniques and Methods Vol. 6 (U.S. Geological Survey, 2013), Chap. A43, p. 497.
- 33.Charlton S. R. and Parkhurst D. L., “Modules based on the geochemical model PHREEQC for use in scripting and programming languages,” Comput. Geosci. 37, 1653–1663 (2011). 10.1016/j.cageo.2011.02.005 [DOI] [Google Scholar]
- 34.Milanova D., Chambers R. D., Bahga S. S., and Santiago J. G., “Effect of PVP on the electroosmotic mobility of wet-etched glass microchannels,” Electrophoresis 33, 3259–3262 (2012). 10.1002/elps.201200336 [DOI] [PubMed] [Google Scholar]
- 35.Leshansky A., Bransky A., Korin N., and Dinnar U., “Tunable nonlinear viscoelastic focusing in a microfluidic device,” Phys. Rev. Lett. 98, 4 (2007). 10.1103/PhysRevLett.98.234501 [DOI] [PubMed] [Google Scholar]
- 36.Bühler V., Polyvinylpyrrolidone for the Pharmaceutical Industry (Springer, Berlin, 2005). [Google Scholar]
- 37.Rubinstein M. and Colby R. H., Polymer Physics (Oxford University Press, New York, 2003), Vol. 23. [Google Scholar]
- 38.Larson R. G., The Structure and Rheology of Complex Fluids (Oxford University Press, New York, 1999). [Google Scholar]