DALI and the persistence of protein shape

Abstract

DALI is a popular resource for comparing protein structures. The software is based on distance‐matrix alignment. The associated web server provides tools to navigate, integrate and organize some data pushed out by genomics and structural genomics. The server has been running continuously for the past 25 years. Structural biologists routinely use DALI to compare a new structure against previously known protein structures. If significant similarities are discovered, it may indicate a distant homology, that is, that the structures are of shared origin. This may be significant in determining the molecular mechanisms, as these may remain very similar from a distant predecessor to the present day, for example, from the last common ancestor of humans and bacteria. Meta‐analysis of independent reference‐based evaluations of alignment accuracy and fold discrimination shows DALI at top rank in six out of 12 studies. The web server and standalone software are available from http://ekhidna2.biocenter.helsinki.fi/dali.

ABBREVIATIONS

BLAST

basic local alignment search tool

CATH

a hierarchical structural classification at class, architecture, topology, homology levels

CDD

conserved domain database

CPU

central processing unit; DALI, Distance‐matrix ALIgnment

DDD

Dali Domain Dictionary

ECOD

Evolutionary Classification of Domains

F_max

maximum value of the F₁ score (harmonic mean of precision and recall) over all binary classification thresholds

FSSP

Families of Structurally Similar Proteins

M

million

PDB

Protein Data Bank

PDBnn

a representative subset of amino acid sequences of PDB structures at nn% sequence identity

RMSD

root‐mean‐square deviation

SCOP (SCOPe)

Structural Classification of Proteins (extended)

1. INTRODUCTION

The human eye is very good at detecting patterns, and the human mind likes to classify things in taxonomic name spaces. The concepts for structural classification1, 2, 3 were developed based on visual analysis. Indeed, visual analysis was necessary before journals started to force deposition of the coordinates in the Protein Data Bank (PDB). Protein folds display a natural clustering due to physical convergence and evolutionary descent from common ancestors. Regular backbone H‐bonding patterns and hydrophobic collapse driven by side chains lead to layered architectures and general similarity of topological arrangements between analogous folds. On top of this, sheets and helices twist, curl, bulge, bend, kink, rotate and slide relative to each other, creating a rich set of structural features. Homologous proteins generally share more structural features than analogous folds. Consequently, clusters of homologs are typically nested inside analogs in the morphospace of protein structures.

Computer vision entered the stage in the 1990s. Automated structure comparison programs such as DALI produced a string of discoveries, which were unexpected from the analysis of only sequences. For example, glycogen phosphorylase and beta‐glucosyltransferase were found to share a common core despite extreme size differences.4 The existence of missing links in an emerging superfamily was predicted though sequence analysis did not succeed in pinpointing candidates. Many members of this superfamily, now known as glycosyltransferase clan B,5 have since been structurally characterized. In another example, adenosine deaminase, phosphotriesterase and urease formed the nucleus of a large superfamily of metal‐dependent amidohydrolases. Several more member families were predicted based on conserved sequence motifs,6 and later confirmed by structure determination. The wider use of automated structure comparison programs was propelled by their availability as network services.7, 8

The automated methods allowed all‐against‐all structure comparison and clustering of all known structures, that is, the mapping of fold space.9 There are densely and sparsely populated regions of fold space. The dense regions share simple topological motifs at their core, but the overall structure can be a medley of many patterns that morph smoothly one into the other.10 Consequently, folds do not appear as the quantized entities they were once thought to be (e.g., 11, 12). Rather, the current view emphasizes a continuity of fold space (e.g.,13, 14). Nevertheless, clustering is useful to demarcate different shapes, although there can be partial overlap between folds (Figure 1). The concept of distinct folds lives on in hierarchical structure classifications.3, 17, 18, 19

Figure 1.

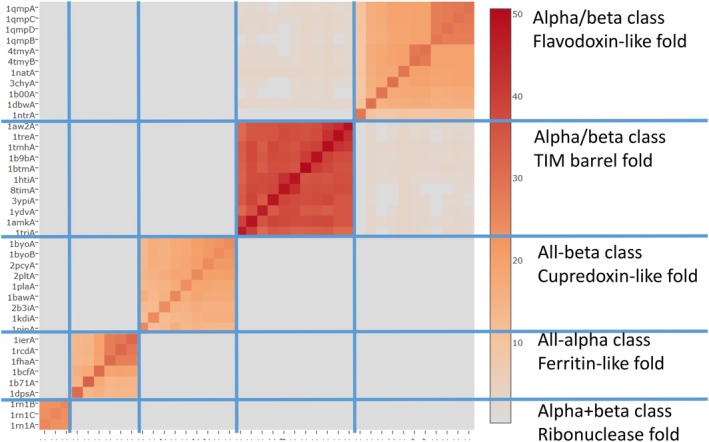
Hierarchically clustered similarity matrix (DALI Z‐scores) for Skolnick test set as described in Reference 15. Fivefold types are indicated by blue lines. Fold types are clearly separated, although shared motifs create connections between some folds of the alpha/beta class. The diagonal corresponds to self‐comparison and it shows that larger structures get higher Z‐scores (darker colors in colorbar)

The current PDB contains over 150,000 structure entries and over 50,000 distinct structures (chains) with less than 90% sequence identity, making automated search and comparison tools necessary. DALI is the collective name for the distance matrix alignment method20 and scoring function (Appendix I), the Open Source DaliLite standalone software,21, 22, 23 and the Dali web server.24 This paper is organized as follows: The first section discusses DALI's formulation of the structural alignment problem. The second section describes the DALI resources and illustrates their use by an example. The third section discusses the limitations of the current implementation. The fourth section reviews how DALI has fared in evaluations against comparable methods. The paper concludes with a discussion of challenges ahead.

2. DISTANCE MATRIX ALIGNMENT

Generally, there are two different problem formulations of structural alignment as either three‐dimensional (3D) or two‐dimensional (2D) comparison.9 In 3D comparison, one explicitly rotates and translates one molecule relative to the other and measures the intermolecular distances between equivalent points in the two chains. The objective is to accommodate the largest possible number of equivalent points within small deviations in position, typically less than 2 to 3 A. In 2D comparison, 3D shape is described by a matrix of all intramolecular distances between the C‐alpha atoms. Such a distance matrix is independent of coordinate frame but contains more than enough information to reconstruct the 3D coordinates, except for overall chirality, by distance geometry methods. The objective is to locate submatrices that have similar intramolecular distances between equivalent points (Figure 2).

Figure 2.

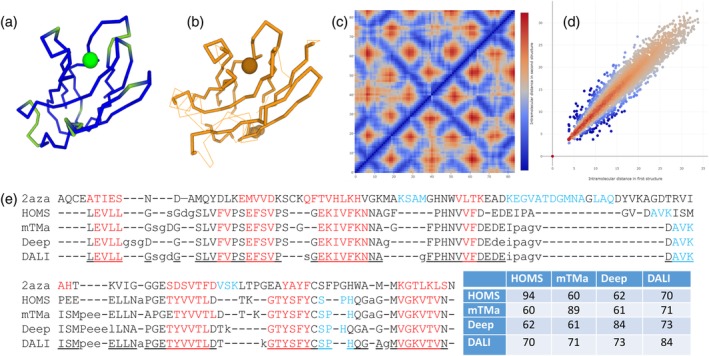
Three‐ (3D), two‐ 2D and one‐dimensional (1D) representations of structural alignment. CA‐traces of plastocyanin (a) and azurin (b) in the same orientation. Blue/green and thick/thin lines show the core/unaligned segments. The copper atom bound to the active site is shown by a sphere. (c) Distance matrices D of the common core, azurin in the upper‐left triangle and plastocyanin in the lower‐right triangle. Blue anti‐diagonal troughs are antiparallel beta strands. (d) Correlation of intramolecular distances between structurally equivalent CA atoms. Each dot corresponds to an element D _ij/D _ji of the distance matrix (c)). The color dimension shows the DALI‐score, red for positive and blue for negative values. Lighter hues are near zero. Note sharp drop for deviations at short distances and damping of contributions from distances longer than 20 A. (e) Detailed comparison of 2azaA/9pcyA structural alignments by HOMSTRAD (HOMS), mTMalign (mTMa), DeepAlign (Deep) and DALI. Lowercase letters indicate unaligned positions. Secondary structure assignments by DSSP25 are red for strands and blue for helix. Underlined positions agree between 3 of 4 alignments. DALI deviates from this consensus in one position, DeepAlign in eight positions and both mTMalign and HOMSTRAD in 12 positions. The table shows how many equivalent residue pairs are in common between two alignments

DALI uses distance matrix alignment for pairwise structure comparison. The scoring function that DALI maximizes (Appendix I) is a weighted sum of similarities of intramolecular distances between equivalent pairs of atoms. The range of the summation is limited to the radius of a typical domain by downweighting distant atoms. Equivalent residue pairs can get both positive and negative scores. The maximum of the total score delineates a common core where every atom included in the alignment makes a net positive contribution. The score is elastic, meaning that the zero line of similarity is defined in terms of relative, rather than absolute, distance deviations. For example, the distance of adjacent strands in a sheet may vary in the range 5 ± 1 A but tertiary contacts between helices may shift in the range 10 ± 2 A and still contribute positively to the score. Occasional larger deviations introduced by loop mobility, helix torsions, curling and twisting of beta‐sheets, and even hinge motion, can be accommodated if they are compensated by a good fit elsewhere. It is important to note that the scoring function of DALI is not designed to optimize rigid‐body superimposition,26 although the program outputs a root‐mean‐square deviation (RMSD) and superimposed coordinates, because this is customary and, in many cases, gives an informative visualization of superimposed chain traces.

The DALI‐score is an open scale of structural similarity. Large structures can get a higher score than a smaller structure compared to itself. The self‐comparison obviously has zero deviations and a maximal score. For this reason, a length‐dependent rescaling of the DALI‐score is used, which has the form of a Z‐score (Appendix I). If the query structure contains multiple domains, small and large, ranking the result list by DALI Z‐score moves up interesting matches to small domains compared to partial matches to large domains.

DALI uses various heuristics to generate seed alignments for final score optimization by a Monte Carlo algorithm.20 The heuristics reduce protein structure to ungapped secondary structure elements to simplify the combinatorial search. The optimization of a sum‐of‐pairs score like that of DALI belongs to the NP‐complete class of computational problems. DALI is not guaranteed to find the global optimum, but it usually gets quite close to it.27

Figure 2E compares structural alignments by DALI, two other programs28, 29 and a human expert.30 The example is plastocyanin/azurin. The methods generally agree on the alignment of secondary structure elements, with most differences in loops next to insertions/deletions. The alignment by DALI is closest to the consensus of all four methods. It is an interesting observation. We can postulate that a consensus (or average) over independent agents is the best approximation of truth. When assigning structural equivalences based on explicit 3D superimposition, the score depends on the radial distance from one focal point. In 2D alignment, a new pair of equivalent points is tethered to all other points of the common core, pinpointing the location of the optimum much more precisely. This gives 2D alignment extra robustness compared to 3D alignment

3. WHAT DOES DALI DO?

Current DALI resources consist of the Dali web server and DaliLite standalone software (Table 1). DALI supports pairwise structural alignment and database search. Database searches use shortcuts to eliminate dissimilar structures from comparison. The idea is that one usually finds a few highly similar structures using quick heuristics. Restricting the search space to neighbors of these previously found matches allows the exclusion of large parts of the database without explicit alignment. The shortcuts make database searches faster than systematic search with little loss in performance.23 The web server goes through a weekly update cycle of importing new PDB structures.31 Users of the stand‐alone program must download their own copy of the PDB. The insertion of new structures to the knowledge base takes a couple of hundred CPU‐hours per week, so a centralized solution is practical. The knowledge‐based search by the stand‐alone program accesses the knowledge base over the Internet to retrieve a sample of “second neighbors” of the query structure. When using the stand‐alone program, confidentiality is preserved, because only public data is transferred over the Internet, while all comparisons involving user data are done locally.

Table 1.

Current DALI resources

URL	DALI is available as a stand‐alone software and a web server. They are accessed from http://ekhidna2.biocenter.helsinki.fi.
Inputs	DALI generates pairwise structural alignments. The structures can be given as PDB entry+chain identifiers, or PDB formatted coordinate files
Methods	Pairwise structural alignment (web server, stand‐alone) one‐to‐one, one‐to‐many, many‐to‐many or all‐against‐all. Systematic comparisons against predefined PDB25 list on the web server. Database search by knowledge‐based (web server, stand‐alone) or hierarchical strategy (stand‐alone). Database search uses heuristics to prune the set of candidates for detailed pairwise alignment.
Data export	The stand‐alone program and web server produce outputs in the same format. All methods produce pairwise structural alignment data for each query structure: Summary statistics of matched structures (Z‐score, RMSD, alignment length, chain length, description from COMPND record). List of structurally equivalent segments (sequential and PDB residue numbers). Translation‐rotation matrices. Stand‐alone has utility script to apply coordinate transformation to superimpose matched structure onto query structure. Pretty pairwise alignments readable by humans (but not computers) All‐against‐all comparison additionally produces: Similarity matrix (Z‐scores) in Phylip format. Newick formatted dendrogram from hierarchical clustering of the similarity matrix.
Visualization	The web server provides embedded views of Selected structures in 3D superimposition, coloring by conservation. Stacked alignment of selected structures. Stacked sequence profiles of selected structures. Hierarchical clustering. Similarity matrix from all‐against‐all comparison.
Outward links	The web server forwards the amino acid sequences of selected structures to sequence analysis servers: Pannzer2 functional annotation (predicted description and GO terms). SANSparallel homology search.
Background resources	Our weekly PDB update consists of: Mirroring PDB and importing new structures. Updating the knowledge base. The update is incremental and takes a few hundred CPU‐hours. The stand‐alone accesses the knowledge base remotely over the Internet. Updating the PDB sequence database of the SANSparallel server. Incrementally updating the database of all against all Blast search of PDB‐sequences. Deriving representative PDB‐sequence subsets (PDB25, PDB50, PDB90, PDB).

The stand‐alone program and web server produce outputs in the same format. A summary of matching structures with alignment statistics is listed in decreasing order of similarity. The cutoff for similarity is Z = 2. An empty result means dissimilar folds (Figure 1). The web server embeds visualization tools for closer inspection of selected matched structures. The web server supports visualization of structural superimposition, mapping of sequence and structure conservation in 3D, and the comparison of evolutionary sequence profiles (sequence logos) of the structurally aligned proteins (Figure 3). Sequence logos34 are generated on the fly. This is enabled by a fast sequence database search server,35 which also powers function predictions by Pannzer2.36 It is often useful to subject a set of top‐scoring matches to all‐against‐all comparison. The resulting structural dendrogram shows which groups of proteins share distinctive structural similarity. Often, these groups coincide with functionally conserved subfamilies (Figure 3).

Figure 3.

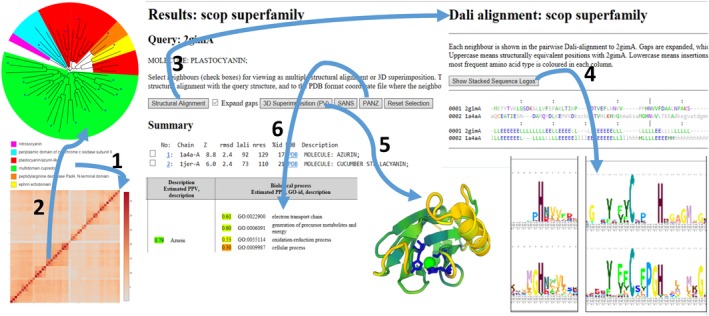
Integrated structure and sequence analytics on the Dali web server. The blue copper domain superfamily of SCOP was subjected to all‐against‐all structure comparison (arrow 1). A neighbor‐joining tree32 was generated from the distance matrix (arrow 2) and displayed in iTOL.33 Domains have the same order in the matrix (bottom‐left to top‐right) and dendrogram (counter‐clockwise). Asterisks denote domains not yet assigned to a specific family in SCOP. SCOP families cluster together except the plastocyanin/azurin family which is divided into plastocyanin, azurin and plantacyanin branches. Structural alignments of selected structures (arrow 3) show conservation of secondary structure. Stacked evolutionary profiles of the protein families (arrow 4) highlight conserved sites. Sequence and structure conservation can be mapped onto the query structure (arrow 5), as well as looking at the superimposed CA traces. Uncharacterized proteins sometimes find functional annotations with PANNZER234 (arrow 6)

3.1. An example of structural analysis with DALI

Structural dendrograms were added to the Dali server in 2016.24 The first use of these dendrograms was in a study on the multiple origins of viral capsid proteins from cellular ancestors.37 Here, I selected the major capsid protein gp5 family as an example of using DALI for explorative analysis. The major capsid protein has an unusual fold, which is conserved despite sequence divergence. The fold occurs in both cellular organisms and viruses.37 A search of the PDB using http://bioinformatics.org/firstglance/fgij//fg.htm?mol=1ohgA as query returns full‐length matches to major capsid proteins including cellular homologs as described before. Interspersed among major capsid proteins are matches to smaller proteins, which match two separate domains. The domains have folds that occur in single‐domain proteins attesting to their being independent folding units (Figure 4). The domain structure is evident as anti‐correlated blocks in the match correlation matrix. The match correlation matrix38 is a still experimental feature. The unusual fold of the major capsid protein is composed of a dodecin‐like fold with an inserted PF0899‐like domain, and a long N‐terminal extension with a dangling beta‐hairpin which makes inter‐subunit contacts. The PF0899 protein has unknown function. The PF0899‐like domain is located around the sixfold symmetry axis of the capsid. Dodecins form oligomers, but the dodecin‐like domain of the capsid protein does not make similar interactions.

Figure 4.

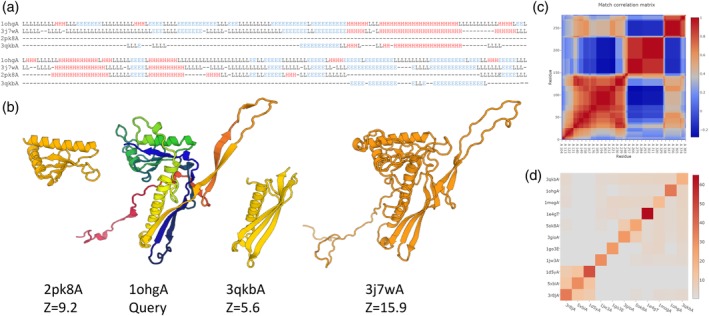
An example of recurrent domain folds. (a) Stacked pairwise structural alignments of single‐domain protein matches to two virus capsid proteins (1ohgA, 3j7wA), PF0899 (2pk8A) and an SHS2‐like domain (3qkbA). The alignment rolls over sequentially from the upper to the lower block. Secondary structures are denoted as H (helix), E (strand) and L (loop). Insertions relative to 1ohgA are not shown. (b) Ribbon diagrams showing the structures superimposed and translated apart horizontally. 1ohgA is rainbow colored (red N‐terminus, blue C‐terminus). The virus capsid proteins have a conserved unusual structure, which can be decomposed into a PF0899‐like domain, an SHS2‐like domain and a long N‐terminal extension. (c) Anti‐correlated blocks in the match correlation matrix of 1ohgA indicate the presence of subdomains. (d) Similarity matrix (Dali Z‐scores) of viral capsid protein and representative structures from each family belonging to the SHS2 clan (CL0319) of Pfam. The viral capsid protein (1ohgA, second from top) is closest to the YjbQ family (3qbkA) and dodecin (1mogA), which occupy a central position in the fold cluster. The three structures at the bottom left have a duplicated SHS2‐fold, which increases their mutual Z‐scores

Database searches using representatives of each of the domains (3qkbA, 2pk8A) as queries were performed to collect similar structures for generating structural dendrograms. The PF0899 protein (3qkbA) was placed firmly within the clade of major capsid proteins. 2pk8A grouped with the YjbQ family and other structures of the dodecin‐like fold. The dodecin‐like fold is a member of the SHS2 clan (Pfam39 clan CL0319). The SHS2 module is found singly and duplicated in a diverse set of protein families.40 The SHS2 module consists of a helix and an antiparallel beta‐sheet with 1–3‐2 topology. The DALI dendrogram placed the major capsid protein clade next to the dodecin‐like clade before other instances of SHS2‐like folds. The structural similarity of 2pk8A is stronger to capsid proteins than to V‐type ATP synthase subunit E mentioned in Pfam.

The connection between major capsid proteins and the SHS2‐like fold was not mentioned in structural and sequence classification databases. SCOPe,19 ECOD18 and Pfam39 treat the major capsid protein as a single domain, whereas CATH14 divides it into two domains. CATH, ECOD and Pfam unify the PF0899 protein and the major capsid protein at homology or clan level; SCOPe notes relatedness as possible but classifies the PF0899 protein as the sole member of its fold. Although CATH recognizes the second domain in the major capsid protein, it and dodecin‐like domains are assigned to different topologies (3.30.110.70 vs. 3.30.2400.30, where C.A.T.H stand for Class, Architecture, Topology and Homology).

In conclusion, the structural analysis by DALI suggests that the major capsid protein gp5 is composed of two domains with recurrent folds, and that one of the newly recognized domains is another instance of the SHS2‐like fold. Based on Dali Z‐scores and dendrograms, a common evolutionary origin for the PF0899 protein and the PF0899‐like domain of the gp5 family is plausible. The SHS2‐like domain of the capsid protein clearly has the topology of the SHS2‐fold, but I see no compelling evidence for homology.

4. WHAT DOES DALI NOT DO?

DALI's niche is pairwise structural alignment and database search. It is designed to work with globular structures with a compact core consisting of alpha‐helices and/or beta‐sheets. Peptides shorter than 30 amino acids are rejected. Complete backbone coordinates must be present for the definition of secondary structure,25 although only the C‐alpha atoms are used in structural alignment. Each chain in a multi‐subunit structure is compared separately. Alignments are constrained to be sequential. Consequently, alignments by DALI will not include circular permutations or strand reversals. DALI does not report similarities that involve more than one chain or interfaces between subunits. Similarities between structures that are non‐globular or have low secondary structure content can be missed (e.g., chlorophyll‐binding protein). Multiple structural alignment seeks a consensus over all pairwise alignments in a set of structures simultaneously, but this has not been implemented in DALI. Specialized softwares exist for most of these tasks that DALI does not do.

In the beginning of DALI, the non‐redundant PDB contained a few hundred protein structures and it was possible to compare them all against all and store the results in a database called FSSP (Families of Structurally Similar Proteins41, 42, 43, 44, 45, 46). Users were able to browse FSSP interactively on the web. Since domains are the natural unit of fold classification, a Dali Domain Dictionary (DDD) was derived. Its aim was a concise description of all structures in terms of a small set of recurrent domains.47 Domain decomposition was achieved by selecting a set of compact protein unfolding units that maximized the sum of Z‐scores over all pairs of selected domains. Both the FSSP and DDD resources were discontinued around the turn of the century, because maintaining the quadratically growing data was no longer cost‐effective after structural genomics really took off. Currently, there are 21,125 chains in a non‐redundant subset of the PDB (PDB25), which corresponds to over 400 M pairwise comparisons. But relatively few pairwise comparisons will be actually looked at by people over the course of a year, and the current DALI generates them only on demand.

The sum‐of‐pairs scoring function that DALI uses for structure–structure alignment has a similar form as pair potentials used in sequence‐structure threading, but the current implementation is too specialized to be applicable to the threading problem. The formulation of the DALI‐score in terms of relative distance differences makes it sensitive to deviations in local geometry. In addition to the sequential constraint, the high penalties for short‐range distance deviations prevent the application of DALI to sketchy backbones. Sketchy backbones could be generated from early interpretations of electron density maps or from averaged templates in homology modeling.

Finally, when DALI is applied to database search, users frequently ask whether a match at a particular Z‐score implies homology or analogy. The answer is that it depends on a wider context. Homologous proteins tend to be structurally more conserved and rank higher in the result list than analogous structures. Thresholds vary between protein families, and one should look at a combination of structural, sequence and functional conservation to infer an evolutionary relationship.48 DALI provides some tools for integrated structural and sequence analysis, but it cannot do automated homolog/analog classification.

5. HOW WELL DOES DALI DO WHAT IT DOES?

This section is based on literature review. DALI has been in uninterrupted service for nearly 30 years, and it has appeared in a number of published method evaluations. Literature was sampled by a keyword search of Medline abstracts. At first glance, different reports give contradictory rankings to different structural alignment programs. This is because of the different evaluation methodologies. Although each benchmark views the data from a different angle, DALI does remarkably well on aggregate (Table 2 and 3). It is worth noting that the studies have used various incarnations of the DaliLite software and Dali web server, and some cases reported as failures in earlier studies give good results with the current version (v.5) of DaliLite.

Table 2.

Evaluations of structural alignment quality (f _car) against manually curated reference alignments

Test set	Test cases	1st	2nd	3rd	4th	Reference
HOMSTRAD	11	FATCAT	DALI	FAST	—	54
CDD	4,017	DALI	Matras	Sheba	FatCat	16
SISYPHUS	69	DALI	Matras	FatCat	CE	53
RIPC	40	FatCat	CA	CE	DALI, Matras, Sheba	53
CDD, MALIDUP, MALISUM	3,591, 241, 130	DeepAlign	DALI	MATT, Formatt, TMalign		28
CDD core regions	3,591	UniAlign	DALI	DeepAlign	TMalign	55
HOMSTRAD	9,536	UniAlign	DeepAlign	TMalign	DALI	55
BaliBASE	1944	UniAlign	DeepAlign	DALI	TMalign	55
HOMSTRAD, RIPC	64, 23	DALI‐score	TM‐score	SO‐score	SP‐score	56

Table 3.

Evaluations of database search against structural classifications

Test set	Test cases	Type	Criterion	1st	2nd	3rd	4th	Reference
CATH	86 x 2,771	Query‐wise	ROC curves	DALI	Matras	Structal	CE	65
SCOP (40% id)	402,077 same‐fold pairs +300,000 random different‐fold pairs	Pooled	ROC curves	FAST	DALI	K2	CE	54
CATH (40% id) topologs	2,930 x 2,930	Pooled	ROC area (native score)	DALI, Structal		CE	SSAP	49
			%TP at 1%FP (native score)	DALI	Structal	CE	SSAP	49
SABmark‐sup	425 groups x all of benchmark	Pooled	ROC area	DeepAlign	TMalign	DALI	Formatt	28
SABmark‐twi	209 groups x all of benchmark	Pooled	ROC area	DeepAlign	DALI	TMalign	Formatt	28
SCOPe same‐fold pairs	500 x all SCOPe domains	Query‐wise	Selectivity of the first 200 results	mTMalign	DALI	SSM	—	29
SCOPe same fold, diff. Sf	51 x 15,211/176022	Query‐wise	F max	DALI	DeepAlign	mTMalign	TMalign	23
SCOPe same sf, diff. Family	119 x 15,211/176022	Query‐wise	F max	DALI, DeepAlign		mTMalign	TMalign	23
SCOPe same family	140 x 15,211/176022	Query‐wise	F max	DeepAlign, DALI, mTMalign			TMalign	23

5.1. Why reference‐based evaluation?

The first task in evaluation is to establish a ground truth. Tables 2 and 3 collate evaluation studies, which used manually curated reference alignments and fold classifications. The motivation for this is that human experts can assess the “biological significance” of structural similarities in a way, which is difficult to quantify exactly, as different features may be given more or less weight in different situations. There is another school of thought, which repurposes any structural alignment program as a means of producing a rigid‐body 3D superimposition by a least‐squares fit of the aligned atoms. This superimposition is then evaluated using RMSD‐related geometrical scores. Because each program optimizes its alignments with respect to the program's native scoring function, this type of evaluation49, 50, 51, 52 informs on the similarity of the program's native score to the evaluator's canonical score. For example, Kolodny et al.49 show that Dali's native score performs very well in receiver operator characteristic (ROC) and error‐coverage plots, although the paper's main thrust is how this performance degrades on moving the goalposts.

5.2. Evaluation of alignment quality against manually curated reference alignments

Several sets of manually curated structural alignments have been created for evaluation purposes (see references in Table 2). The data sets differ in hardness. For example, RIPC is a collection of pathological cases for structural aligners, involving repetitions, large indels, circular permutations and extensive conformational variability.53 The primary evaluation criterion is f _car, the fraction of correctly aligned residues relative to the reference alignment (Appendix II). If the dataset specifies core regions (e.g., the CDD dataset), then only core positions are evaluated. Some data sets, for example, HOMSTRAD, were developed for testing sequence alignment programs, and they align the whole sequences also over structurally variable segments. For example, an N‐terminal helix/coil in the pair 1ed9A/1ew2A is misaligned by DALI with respect to HOMSTRAD.54 Table 2 shows DALI at top rank in at least one test set in three of six evaluation studies. DeepAlign28 and UniAlign55 include sequence similarity as a component of their scoring function and show improvement over DALI, which only uses the C‐alpha coordinates. Recently, the DALI score and three RMSD‐related geometrical scoring functions were compared using a generic global optimization program.56 The ranking in Table 2 is based on recall with block size 4 from table 9 of Reference 56. The conclusion was that the Dali‐score and human experts like the same set of correspondences, which are not optimal with respect to criteria based on rigid‐body superimposition.

5.3. Evaluation of database searches against reference fold classifications

Table 3 collates studies, which include DALI and use various subsets of SCOP or CATH as ground truth. The main parameters used to evaluate binary classifiers are precision and recall, also called selectivity and sensitivity (Appendix III). There are at least four considerations to take into account when choosing an evaluation methodology, discussed below.

5.3.1. Possible misclassification

Manual classifications show discrepancies when compared to each other57 and inconsistencies when compared to the results of automated comparisons.13 To account for possible misclassification, it is common to define correct pairs as having the same fold and incorrect pairs as having different folds. The fold level describes general structural similarity and has clearer distinction than subdivisions within a fold to analogs and remote or close homologs.

5.3.2. Stratification by difficulty

Close homologs have more pronounced structural similarity than remote homologs and analogous folds. Some test pairs are therefore “easier” and others more “difficult” for structural aligners. For example, Holm23 reports evaluation results at different levels of difficulty: fold level, superfamily level and family level. If a database structure is in the same SCOP fold as the query but in a different superfamily, it is counted as correct in fold level evaluation and ignored for superfamily or family level statistics. If a database structure is in the same SCOP superfamily as the query but in a different family, it is counted as correct in superfamily level evaluation and ignored for fold and family level statistics. If a database structure is in the same SCOP family as the query, it is counted as correct in family level evaluation and ignored for fold and superfamily level statistics. This scheme has roots in the benchmarking of sequence alignment software.58

5.3.3. Sample selection

Proteins with clear sequence similarity have trivially similar structures. All studies in Table 3 except the mTMalign paper29 draw their test pairs from a non‐redundant subset of the PDB. When the threshold for sequence identity is 40% or lower, most same‐family pairs are removed. The benchmark for mTMalign29 consists of 500 randomly selected query domains, which are compared against all domains in the full SCOPe database. The lack of stratification is likely to bias test pairs towards easy cases. In very populous fold classes, this happens because the evaluation is restricted to the first 200 results (Appendix IV). In other cases, the fold class may consist of a single family, which also limits the structural diversity of the test cases. The evaluation of FAST54 generated an impressive number of test cases from all non‐redundant SCOP domains. This means that most same‐fold pairs will come from a small number of hugely populous fold classes. Specifically, in a representative subset of SCOPe 2.07,19 fourfolds generate half of all same‐fold pairs, 44 folds contain half of all domains, and 36% of the folds are singletons, that is, have a single member (Figure A1 in Appendix V).

5.3.4. Pooled or querywise evaluation

The F _max criterion is an evaluation metric that balances recall and precision. Calculating F _max involves scanning an ordered list of hits for the optimal threshold that maximizes the harmonic mean of precision and recall. The querywise variant tests whether same‐fold test cases are higher up in each result list than different‐fold test cases. The pooled variant requires that the scale of similarity is comparable across all queries, such as a probability of same‐fold membership. Holm23 showed large differences between average querywise F _max and pooled F _max evaluation for DALI and DeepAlign (Figure 5). mTMalign had excellent precision at the cost of lower recall. Pooling result lists had little effect on mTMalign, because of the scarcity of false‐positives. In contrast, DALI's and DeepAlign's performance collapses in pooled F _max evaluation compared to query‐wise evaluation. This means that they recognize structural similarities in agreement with SCOP, but class boundaries occur at different Z‐scores (DaliLite) or bitscores (DeepAlign) for different queries. DALI outperformed the other programs at fold level and tied with DeepAlign at superfamily level (Figure 5).

Figure 5.

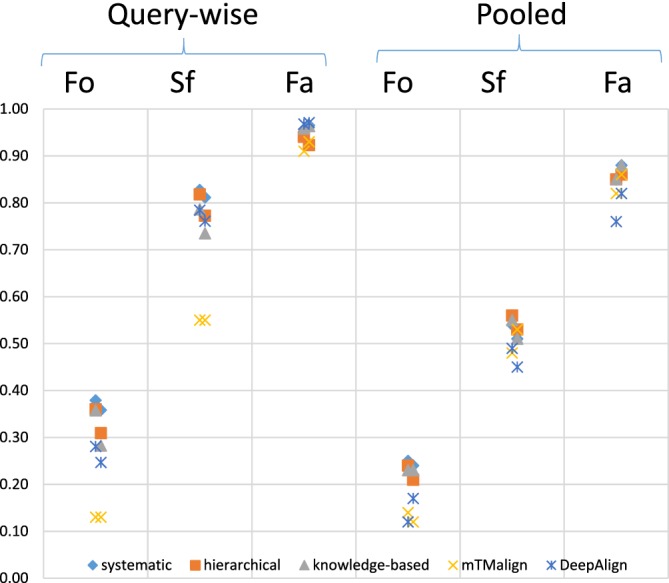
F _max evaluation (adapted from Reference 23). Systematic, hierarchical and knowledge‐based are database search strategies of DALI. Fo = fold level, Sf = superfamily level, Fa = family level. The two data points per method and category correspond to evaluation in PDB70 and PDB

6. CHALLENGES AHEAD

Structural similarities to other proteins can help to elucidate the function of an uncharacterized protein and shed light on molecular evolution. DALI was the first web‐based system to compare protein structures, and to be more effective than the human eye and an expert's memory combined. DALI's problem formulation is sound, in my opinion, because it gives biologically interesting results. The DALI‐score implicitly captures phenotypic plasticity and is sensitive enough to detect topological similarity. Despite statistically more sophisticated proposals (e.g., 28, 52, 59, 60, 61), the problem of modeling structural evolution is difficult and remains open.

The current implementation of DALI should be refactored (not changing functionality) to get rid of restrictive data formats and deprecated design solutions (like Fortran EQUIVALENCE blocks), to restore non‐sequential alignment, and to scale to sizes of structures unimaginable 30 years ago. Other improvements change the way algorithms work. In particular, the Monte Carlo algorithm of the final optimization step would benefit from adding collective shifts of secondary structure elements to the move set. The domain decomposition algorithm62 looks for compact substructures and it is sometimes fooled by tight inter‐domain interfaces. Using recurrence for domain decomposition is an attractive alternative.38

BLAST63 and DALI63 are among the longest‐serving database search programs for protein sequences and structures, respectively. In the age of genomics and structural genomics, protein databases have grown exponentially, which demands new solutions from their software. A new generation of super‐fast sequence comparison algorithms are able to retrieve homologs of a query sequence in the blink of an eye (e.g., 35). It would be nice to restore the ability to move a lens across fold space in real time to DALI. In FSSP and DDD this ability was based on pre‐computed all‐against‐all structural similarities, which is not manageable with current data volumes. What is needed is a fast topological filter, which is both sensitive enough to detect fold‐level similarities, and selective enough to minimize the number of wasteful, uninteresting alignments.

Appendix 1.

 

Appendix I: Scores used in DALI 1.

Distance matrix alignment seeks to optimize a set of one‐to‐one correspondences between two substructures A and B that maximizes the DALI score 19:

$${\text{DALI}}_{\mathit{AB}}=\sum _{i=1}^{\text{LALI}}\sum _{j=1}^{\text{LALI}}\left\{\begin{array}{c}\left(\theta -\frac{2\mid d_{\mathit{ij}}^A-d_{\mathit{ij}}^B\mid }{d_{\mathit{ij}}^A+d_{\mathit{ij}}^B}\right)e^{-{\left(\frac{d_{\mathit{ij}}^A+d_{\mathit{ij}}^B}{2D}\right)}^2},\text{if}i\ne j\\ \theta ,\text{if}i=j\end{array}\right.$$ (A1)

where LALI is the number of aligned residue pairs, θ = 0.2, D = 20 A and the distance matrix element $d_{\mathit{ij}}^X$ contains the intramolecular Cα–Cα distance of substructure X between two residues i ^X and j ^X.

The DALI Z‐score46 is defined as:

$$Z_{\mathit{QT}}=\frac{{\text{DALI}}_{\mathit{QT}}-m\left(L\right)}{\sigma \left(L\right)}$$ (A2)

where L is the geometric mean length $L=\sqrt{L_Q{L}_T}$ of structures Q and T. The relation between the mean score m, standard deviation σ and L was derived empirically from a large set of random pairs of structures. Fitting a polynomial gave the approximation:

$$m\left(L\right)=\left\{\begin{array}{c}7.95+0.71L-0.000259L^2-0.00000192L^3,\mathit{\text{if}}L\le 400\\ m\left(400\right)+L-400,\text{if}L>400\end{array}\right.$$ (A3)

For standard deviation, the empirical estimate was σ(L) = 0.5 * m(L). The Z‐score is computed for every possible pair of domains, and the highest value is reported as the Z‐score of the protein pair. Possible domains are determined by the Puu algorithm (Parser for protein Unfolding Units), which recursively cuts a structure into smaller compact substructures at the weakest interface.61

Structural dendrograms are generated from distance matrices, where the pseudo‐distance of two structures Q and T is defined as:

$$D_{\mathit{QT}}=Z_{\mathit{QQ}}+Z_{\mathit{TT}}-2Z_{\mathit{QT}}$$ (A4)

Appendix II: Evaluation of alignment accuracy 1.

Let R (reference alignment) and T (test alignment) be m × n binary matrix representations of the mapping of equivalent residue pairs from a first structure with m residues to a second structure with n residues. The matrix notation for the fraction of correctly aligned reference alignment positions f _car is

$$f_{\mathrm{car}}=\frac{\mathit{tr}\left(R^{T}T\right)}{\mathit{tr}\left(R^{T}R\right)}$$ (A5)

Reference 53 reported the fraction of correctly aligned pairs relative to the test alignment rather than relative to the reference alignment. The information for 11 examples in their Table IV was converted to f _car to obtain the rankings of Table 2 in this study.

Appendix III: Evaluation of database search 1.

The diagnostic ability of a binary classifier system is characterized by precision and recall. Precision p and recall r are defined as

$$p\left(n\right)=\frac{\mathit{TP}\left(n\right)}{n}$$ (A6)

and

$$r\left(n\right)=\frac{\mathit{TP}\left(n\right)}{T}$$ (A7)

where n is the rank of a (query, match) pair in the ordered list of results, TP(n) is the number of true positives (correct pairs) among the first n pairs in the ordered list of results, and T is the number of structures in the fold class.

The F‐score is the harmonic mean of precision and recall. It gives equal importance to false positives and false negatives. F _max scans the ordered list of results for a cutoff point n which maximizes the F‐score:

$$F_{\max }=\underset{n}{\max }\hspace{0.17em}F\left(n\right)\underset{n}{=\max }\frac{2p\left(n\right)r\left(n\right)}{p\left(n\right)+r\left(n\right)}=\underset{n}{\max }\frac{2\mathit{TP}\left(n\right)}{n+T}$$ (A8)

The ROC curve is a graphical plot of coverage (recall) against the false positive rate (errors). The area under the curve can be used to select optimal models.

Appendix IV: Other evaluation criteria 1.

mTMalign authors present plots of precision and recall for the first n = 1,…,200 results.28 Precision and recall are undefined if n is larger than the size of the result list H. Missing data are filled by imputed precision p’(n) and imputed recall r’(n), defined in28 as

$$p^{\prime }\left(n\right)=\frac{\mathit{TP}\prime \left(n\right)}{n}=\left\{\begin{array}{c}p\left(n\right),\text{if}n\le H\\ p\left(H\right),\text{if}n>H\end{array}\right.$$ (A9)

and

$$r^{\prime }\left(n\right)=\frac{\mathit{TP}’\left(n\right)}{T}=\left\{\begin{array}{c}r\left(n\right),\text{if}n\le H\\ r\left(H\right),\text{if}n>H\end{array}\right.$$ (A10)

We note that recall at the last result position H must be r(H) ≤ H/n in order for the imputed number of true positives to stay within realistic bounds TP’(n) ≤ T.

The evaluation metrics usually used to assess fold discrimination ignore correct prediction of different‐fold cases, because the vast majority of all test cases are negative in our binary classification scheme. A baseline classifier, which predicts every case as negative, would get unduly high accuracy:

$$\text{Accuracy}=\frac{\mathit{TP}+\mathit{TN}}{\mathit{TP}+\mathit{TN}+\mathit{FP}+\mathit{FN}}$$ (A11)

where TP is true positives, TN is true negatives, FP is false positives and FN is false negatives.

Appendix V: Distribution of fold class sizes 1.

Figure A1.

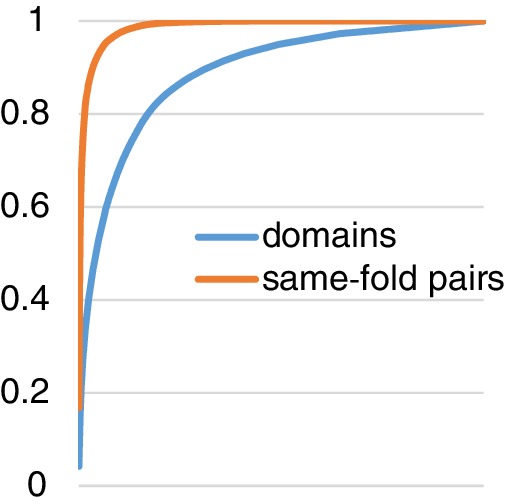
Cumulative frequency of ASTRAL‐40 domains and same‐fold domain pairs. 1,003 folds in SCOPe 2.07 18 classes a‐d are ordered by size (the number of member domains) on the horizontal axis. Four folds generate half of all same‐fold pairs, and 44 folds contain half of all domains. 36% of the folds are singletons, that is, have a single member

Holm L. DALI and the persistence of protein shape. Protein Science. 2020;29:128–140. 10.1002/pro.3749