Temperature dependence of NMR chemical shifts: Tracking and statistical analysis

Abstract

Isotropic chemical shifts measured by solution nuclear magnetic resonance (NMR) spectroscopy offer extensive insights into protein structure and dynamics. Temperature dependences add a valuable dimension; notably, the temperature dependences of amide proton chemical shifts are valuable probes of hydrogen bonding, temperature‐dependent loss of structure, and exchange between distinct protein conformations. Accordingly, their uses include structural analysis of both folded and disordered proteins, and determination of the effects of mutations, binding, or solution conditions on protein energetics. Fundamentally, these temperature dependences result from changes in the local magnetic environments of nuclei, but correlations with global thermodynamic parameters measured via calorimetric methods have been observed. Although the temperature dependences of amide proton and nitrogen chemical shifts are often well approximated by a linear model, deviations from linearity are also observed and may be interpreted as evidence of fast exchange between distinct conformational states. Here, we describe computational methods, accessible via the Shift‐T web server, including an automated tracking algorithm that propagates initial (single temperature) ¹H—¹⁵N cross peak assignments to spectra collected over a range of temperatures. Amide proton and nitrogen temperature coefficients (slopes determined by fitting chemical shift vs. temperature data to a linear model) are subsequently calculated. Also included are methods for the detection of systematic, statistically significant deviation from linearity (curvature) in the temperature dependences of amide proton chemical shifts. The use and utility of these methods are illustrated by example, and the Shift‐T web server is freely available at http://meieringlab.uwaterloo.ca/shiftt.

Abbreviations

DSS

4,4‐dimethyl‐4‐silapentane‐1‐sulfonic acid

fALS

familial amyotrophic lateral sclerosis

HSQC

heteronuclear single quantum coherence spectroscopy

NMR

nuclear magnetic resonance

SOD1

superoxide dismutase 1

TCEP

tris(2‐carboxyethyl)phosphine

1. INTRODUCTION

Nuclear magnetic resonance (NMR) chemical shifts are sensitive probes of protein structure and dynamics. Logically, the determinants of chemical shifts must also be responsible for temperature dependences thereof; however, these determinants may not all vary with temperature to the same extent. Variable‐temperature NMR (VT‐NMR) therefore offers unique insights into the phenomena underlying chemical shift dispersion in general. VT‐NMR may also facilitate the resolution of peaks that are significantly overlapped, that is, they may separate due to differing temperature dependences. Here, we focus on the temperature dependences of amide proton and nitrogen chemical shifts, which may be easily and inexpensively measured via a series of ¹H—¹⁵N heteronuclear single quantum coherence (HSQC) spectra collected at different temperatures.

Empirically, the temperature dependences of both amide proton and amide nitrogen chemical shifts are frequently linear.1 The linear temperature coefficients (i.e., slopes determined by fitting chemical shift vs. temperature data to a linear model) of amide protons have been used to probe the hydrogen bond status of individual amides,2, 3, 4 interpreted as a measure of temperature‐dependent loss of structure,1, 5, 6, 7, 8 and grouped sequentially to distinguish between ordered and disordered protein regions.7, 9, 10, 11 To our knowledge, no similarly straightforward interpretations of amide nitrogen temperature coefficients have been proposed,1, 12 although the determinants of amide nitrogen chemical shifts have been studied in some detail.13, 14, 15, 16 Systematic deviations from linearity (curvature) are also of great interest, as they may be interpreted in terms of fast exchange between distinct conformations,8, 17, 18, 19, 20, 21 but such curvature is often subtle and may be difficult to detect and validate.

In the following, we describe algorithms, accessible via the Shift‐T web server (Figure 1), for automated tracking of ¹H—¹⁵N cross peaks (e.g., from ¹H—¹⁵N HSQC spectra) over temperature, decomposition of this motion in the ¹H—¹⁵N plane into amide proton and nitrogen chemical shift temperature dependences, and subsequent analysis in terms of linear temperature coefficients and curvature. Although not demonstrated here, it may also be feasible to use these methods to analyze other types of 2D NMR spectra, for example, ¹H—¹³C HSQC or ¹H—¹H TOCSY. We illustrate the utility of these algorithms by applying them to disulfide‐reduced, unmetallated superoxide dismutase 1 (apoSOD1^2SH) VT‐NMR data. ApoSOD1^2SH is an immature form of human Cu, Zn SOD1, various mutants, and maturation states of which have been implicated in a progressive neurodegenerative disease called familial amyotrophic lateral sclerosis (fALS).22 Our analysis of this VT‐NMR data reveals conformational heterogeneity in the native ensemble and rationalizes differences in the biophysical characteristics of closely related variants.

Figure 1.

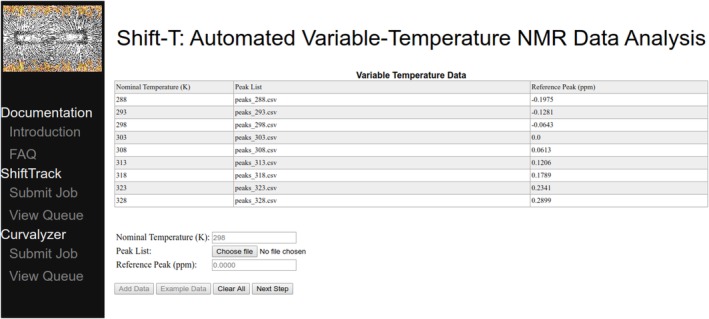
ShiftTrack job submission via the Shift‐T web server: peak lists (one per temperature) and temperature‐invariant reference peaks (e.g., DSS). The Shift‐T server can be found at http://meieringlab.uwaterloo.ca/shiftt

2. RESULTS AND DISCUSSION

2.1. Cross peak tracking and temperature coefficients

In order to combat slow drift in the strength of the field generated by the electromagnet, modern NMR spectrometers use a feedback control system (commonly referred to as the “lock”) that dynamically adjusts the strength of the magnetic field to maintain the resonant frequency of a particular nucleus at a fixed offset to the base frequency. In aqueous solutions such as those suitable for protein NMR, the resonance of deuterium nuclei from D₂O/HDO is monitored for this purpose. The chemical shift of water (including H₂O, D₂O, and HDO) is intrinsically temperature dependent,23, 24 but the feedback control system compensates. Thus, the chemical shift of water appears to be temperature invariant, while all other peaks shift (because of change in the strength of the magnetic field) from their “true” positions by an amount equal to the temperature dependence of water. To recover ¹H and ¹⁵N temperature‐dependent chemical shifts unbiased by this “deuterium lock artefact,” spectra must be referenced to a standard with negligible temperature dependence, for example, 4,4‐dimethyl‐4‐silapentane‐1‐sulfonic acid (DSS)24, 25 (Figure 2c). In spectra that have not been referenced to such a standard, the temperature dependence of water is often the largest contributor to the observed changes in chemical shifts (Figure 2a). Because the set point of the spectrometer temperature controller is not a sufficiently accurate measure of the actual temperature, the chemical shift of DSS (or apparent movement thereof induced by the deuterium lock artefact) may also be used in temperature calculations (see the Methods section).

Figure 2.

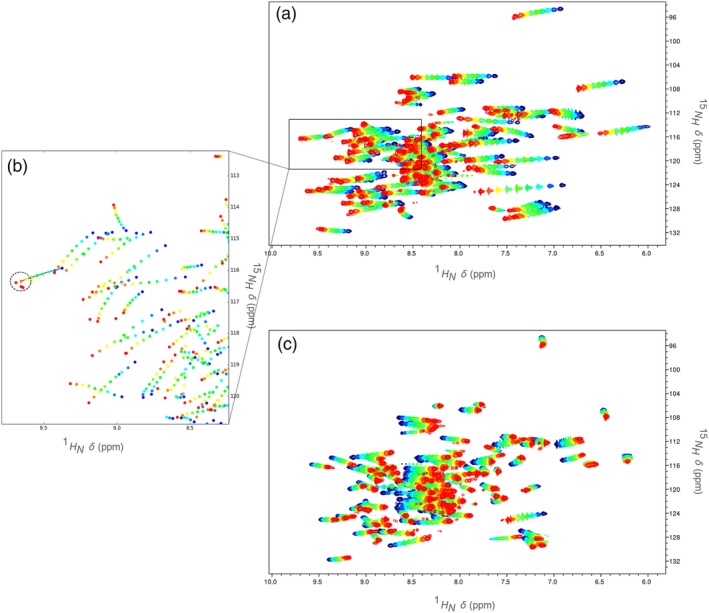
An example of overlaid ¹H—¹⁵N data from HSQC spectra collected over a range of temperatures (blue: low; red: high). (a) unreferenced HSQC spectra; the deuterium lock artefact is evident. (b) peaks picked from the indicated region of the ¹H—¹⁵N plane—line segments join peaks in a ShiftTrack candidate line, and the search radius for the final point is indicated by the dashed circle (peaks are tracked in unreferenced spectra in order to take advantage of deuterium lock artefact‐induced regularity). (c) HSQC spectra referenced to DSS, showing the true temperature dependences of amide chemical shifts

Empirically, movement of cross peaks in the ¹H—¹⁵N plane is often approximately linear with respect to temperature, even after referencing all chemical shifts to DSS. However, prior to such referencing a much greater degree of regularity is apparent (Figure 2a); as temperature increases, cross peaks tend to move downfield in both dimensions in a highly linear fashion. From ¹H—¹⁵N cross peak coordinates for a given amide, specified at a single temperature, our ShiftTrack algorithm finds the set of cross peaks (one per temperature, selected from peaks picked automatically from unassigned spectra, for example, by TopSpin; see the Methods section) with the smallest deviation from linearity, that is, the set for which a simple linear regression gives the lowest residual sum of squares, subject to a weak constraint on the spacings between points. We prefer to apply this algorithm before referencing the spectra to DSS, turning artefact‐induced regularity to our advantage.

ShiftTrack maintains a list of candidate “lines” (sets of points). As the unassigned peak list from each temperature is processed, new candidate lines are constructed through extension of existing candidates by a single point (Figure 2b). In order to avoid a combinatorial explosion, new candidates are constructed using only points found within a user‐defined radius of the cross peak from the previous temperature and filtered to remove candidates with pronounced nonlinearity from consideration. After peak lists from all temperatures have been processed, the list of candidate lines may contain entries with varying numbers of peaks, for example, if no suitable points with which to extend a given candidate were found at one or more temperatures. Preference is shown for full‐length (i.e., one peak per temperature) solutions. If no full‐length solutions below the residual sum of squares linearity threshold are found, shorter solutions are considered. If these are also rejected on the basis of the residual sum of squares linearity criterion, no solution will be reported for the assignment in question. The output of ShiftTrack includes plots of chemical shifts versus temperature, a line determined by simple linear regression, and regression residuals; these plots, particularly the residuals, facilitate verification of ShiftTrack solutions (Figure 3). At the discretion of the user, residuals more than two SDs from the mean (which is typically zero) may be flagged for manual review.

Figure 3.

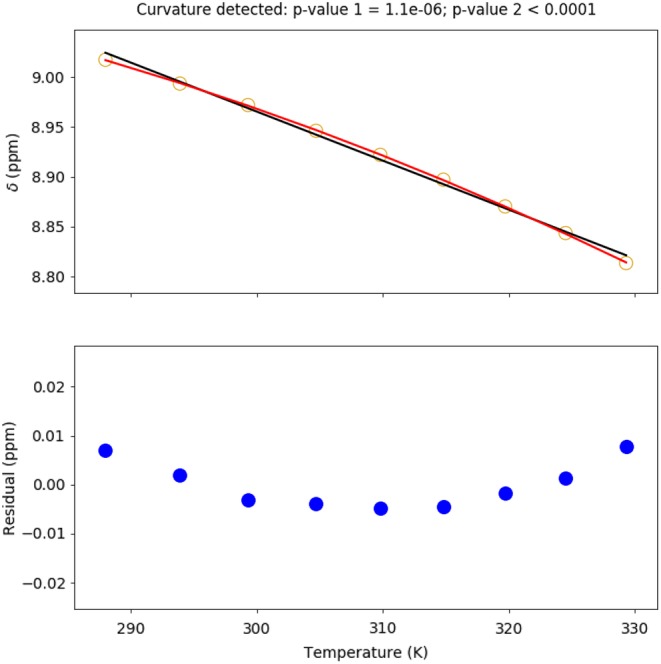
Chemical shifts (referenced to DSS; open circles, top) and residuals (filled circles, bottom) illustrating both temperature coefficient calculation (slope of black line) and curvature detection (red quadratic). The probability that the linear model is correct (from the extra sum of squares F test) is reported as p value 1. The probability that the curvature observed is the result of random errors (from numerical simulation of residual errors) is reported as p value 2

Amide proton temperature coefficients determined by the ShiftTrack algorithm for pseudo wild‐type (pWT) and H46R apoSOD1^2SH are illustrated in Figure 4. Both maturation state and mutations (such as H46R) of SOD1 have been associated with the onset and progression of ALS.22 Fully mature pWT SOD1 (holoSOD1) is an exceptionally thermostable (T _m = 92.0°C)29 homodimeric metalloenzyme, each 153 amino acid subunit of which binds one Cu²⁺ and one Zn²⁺ with very high affinities. Also, the interface between the immunoglobulin‐like β‐barrel subunits is stabilized by a disulfide bond, and the “electrostatic loop” (Loop VII; Figure 4b) contributes to metal binding and function.30 In contrast, pWT apoSOD1^2SH adopts a dynamic, predominantly monomeric structure with much lower thermostability (T _m = 47.6°C).31, 32

Figure 4.

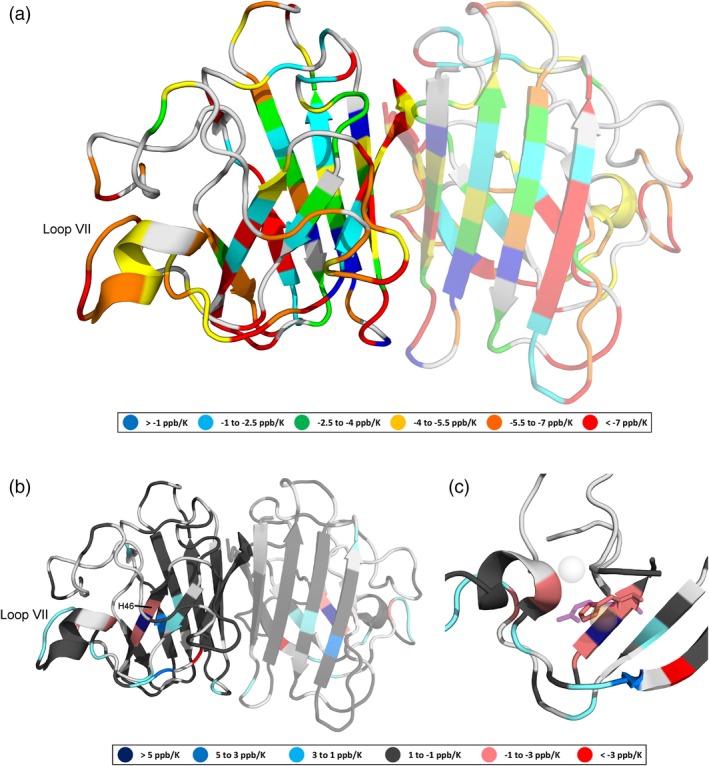
(a) Amide proton temperature coefficients (determined using chemical shifts referenced to DSS) for pWT apoSOD1^2SH, (b) temperature coefficient differences (relative to pWT) resulting from the H46R mutation, and (c) the metal‐binding region of apoSOD1^2SH showing overlaid H46 (pink) and R46 (purple, semitransparent) side chains. Light gray indicates that data are not available. The monomeric, rather than dimeric form of apoSOD1^2SH predominates, but in (a) and (b), we project the data onto a dimeric SOD1 structure (PDB ID: 2AF2)26 with a semitransparent second subunit in order to illustrate the residues that form the dimer interface and present two views (one rotated ∼ 180° relative to the other). In holoSOD1 (PDB ID: 1HL5),27 the H46 residue coordinates the Cu²⁺ ion (orange, semitransparent), while in H46R (PDB ID: 1OZT) the positively charged guanidinium group of the R46 side chain sits between the vacant Cu²⁺ and Zn²⁺ (light gray, semitransparent) binding sites. Figure prepared using PyMOL28

Consistent with this dynamism, we find that the magnitudes of pWT apoSOD1^2SH temperature coefficients (Figure 4a) are frequently greater than those of corresponding pWT holoSOD1 residues,8 indicating that the magnetic environments of the amide protons change more with temperature. Relative to pWT apoSOD1^2SH, some H46R apoSOD1^2SH temperature coefficients increase, while others decrease, with the greatest differences concentrated near the site of mutation and in the electrostatic loop (Loop VII; Figure 4b). Notably, H46R is an fALS‐associated mutation,22 and despite being more stable than pWT apoSOD1^2SH, H46R apoSOD1^2SH exhibits increased propensity to misfold and aggregate.31, 33 There is also evidence that the H46R apoSOD1^2SH electrostatic loop can participate in aberrant, non‐native intermolecular interactions33; interestingly, we show that the magnetic environments of amide protons in the H46R apoSOD1^2SH electrostatic loop actually change less with temperature than the corresponding pWT apoSOD1^2SH protons (Figure 4b), which may further clarify this possible mechanism of H46R‐induced disease.

We previously found that the average of the temperature coefficients can report on protein global stability changes.8 Here we compare the temperature coefficient averages of 103 amides for pWT and H46R apoSOD1^2SH, which are −5.30 ppb/K and − 5.10 ppb/K, respectively. Consistent with our previous results, the magnitude of the average temperature coefficient of pWT apoSOD1^2SH (T _m = 47.6°C) is greater than that of the more stable H46R apoSOD1^2SH (T _m = 52.6°C).31 Insight into the molecular basis for global stabilization of H46R apoSOD1^2SH relative to pWT apoSOD1^2SH is obtained from examination of individual temperature coefficients; the positively charged guanidinium group of R46 is situated between the vacant Zn²⁺ and Cu²⁺ binding sites in H46R apoSOD1^2SH 33 where it may electrostatically stabilize the protein.

2.2. Detection and statistical validation of curvature

Although the temperature dependences of amide proton chemical shifts are predominantly linear, curvature is not uncommon, and may be attributed to temperature‐dependent shifts in the population of distinct conformational states.8, 17, 18, 19, 20, 21 Here, we focus first on strategies for the detection of curvature, which may be subtle, then on statistical validation that the curvature detected is likely to result from changes in the population of conformational states rather than a confluence of random errors. Collectively, these tests (which we refer to as Curvalyzer) are designed to be quite stringent, as detailed later. Temperature‐dependent conformational changes that do not result in curvature are possible; absence of curvature is not particularly informative, therefore false negatives are unlikely to lead to incorrect conclusions. In contrast, false positives (inference of curvature where there is none) may result in serious errors.

Curvalyzer treats curvature detection as a “model selection” problem. Two nested models are considered for each set of chemical shift versus temperature data: linear and quadratic. There is no theoretical reason to believe that experimentally observed curvature should fit a quadratic model. However, as expected given our hypothesis that temperature‐dependent shifts in the relative population of conformational states are causative, curvature generally manifests as a gentle curve with a single minimum or maximum (Figure 3); thus, the quality of fit to a quadratic model is an adequate test of nonlinearity. Unless the temperature dependence is exactly linear, the quadratic model will have a lower sum of squared errors; however, if the improvement (relative to the linear model) is small, it may not be statistically significant. Curvalyzer uses an extra‐sum‐of‐squares F test to quantify the statistical significance of the improvement.34 The p value resulting from this F test is reported (using a significance threshold of 0.01), where the null hypothesis is that the linear model is correct. To increase the stringency of this test, we ensure that nonlinearity introduced by a single outlier (and therefore unlikely to be attributable to the sampling of distinct conformational states) does not introduce false positives by requiring that for each set of points generated by leave‐one‐out resampling without replacement (i.e., from a set of amide proton chemical shifts measured at N different temperatures, N subsets of N−1 points are possible), the quadratic fit must be significantly better (p value less than .01, per the extra sum of squares F test) than that of the linear fit in order for the temperature dependence to be considered curved.

Once the existence of curvature has been established, we must consider its source. The F test referenced above implicitly considers the possibility that deviations from linearity are caused by errors in the data, but each set (one per amide proton) of chemical shifts is evaluated separately. For the set of all chemical shifts (at all temperatures) of amide protons for which curvature was not detected, we can calculate residuals and use them to better estimate the distribution of errors. We find that distributions of residuals are bell shaped with means near zero, but may have heavy tails that indicate deviation from normality. We therefore fit residuals to a “t distribution,” which includes the normal distribution as a special case, but allows for the possibility of heavier tails (Figure S1).34 Plausible sets of residuals can be simulated by drawing random values from this fitted distribution; by doing so many (100000) times, we calculate the probability of observing curvature (due to random errors) of a given magnitude. In our analysis of experimentally observed curvature, these probabilities are equivalent to p values (using a significance threshold of .01) where the null hypothesis is that the curvature is due to measurement errors rather than shifts in the population of distinct conformational states. This statistical test complements the first by screening out cases where, although curvature was detected, there is a significant chance that it is a product of experimental or peak picking error (e.g., as a result of overlapping peaks).

Curvature detected in the temperature dependences of pWT apoSOD1^2SH amide proton chemical shifts is illustrated in Figure 5. Consistent with the aforementioned dynamism of apoSOD1^2SH, curvature is apparent throughout the protein, including within loops and regions of secondary structure. Because the VT‐NMR data were collected at temperatures at temperatures >10^° C below the start of the global unfolding endotherm (measured by differential scanning calorimetry),31 we hypothesize that the distinct conformations contributing to curvature may be substates within the apoSOD1^2SH native ensemble; interestingly, curvature is observed in regions such as the dimer interface and electrostatic loop that were previously found to have high mobility by chemical exchange saturation transfer and Carr–Purcell–Meiboom–Gill relaxation dispersion experiments.32

Figure 5.

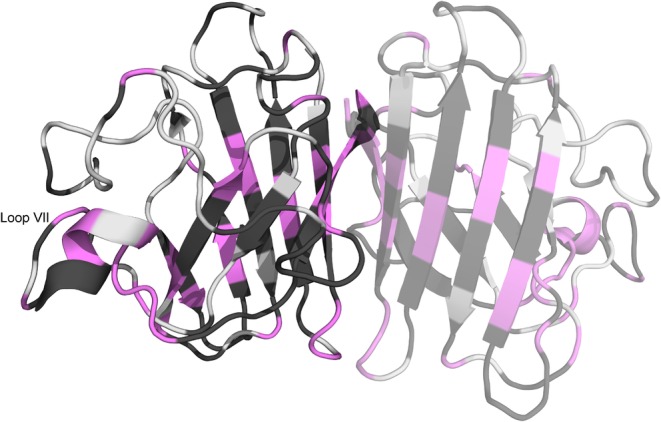
pWT apoSOD1^2SH curvature, as determined by Curvalyzer (using chemical shifts referenced to DSS). Curvature may be interpreted as evidence of exchange between distinct conformations, but the absence of curvature does not rule exchange out. The monomeric, rather than dimeric form of apoSOD1^2SH predominates, but here we project the data onto a dimeric SOD1 structure (PDB ID: 2AF2)26 with a semitransparent second subunit in order to illustrate which residues form the dimer interface and present two views (one rotated ∼ 180° relative to the other). Figure prepared using PyMOL28

3. CONCLUSIONS

Manually tracking ¹H—¹⁵N cross peak movement with temperature is a relatively straightforward, yet labor‐intensive task. Here, we implement an algorithm that automates the bulk of this task, freeing the user to focus on ambiguous cases. We also automate the detection and statistical validation of curvature, which requires stringent tests in order to prevent false (curvature) positives. Overall, these methods form the foundation upon which our analyses of protein VT‐NMR data are built. In general, temperature coefficients and curvature may report on major loss of structure (e.g., unfolding), but here we analyze data collected at temperatures well below the onset of global unfolding. The results of analyses such as these may be widely useful for the characterization of hydrogen bonding in structured2, 3, 4, 32 or disordered7, 9, 10, 11 proteins, and identification of local changes in energetics associated with protein mutation, maturation, or function.1, 8

4. METHODS

4.1. Expression and purification

BL21 Escherichia coli cells were transformed with pHSOD1ASlacIq plasmids35 into which genes encoding pWT SOD1 (wild‐type protein with cysteines 6 and 111 replaced by alanine and serine, respectively22, 31, 35) or its H46R variant had been cloned. ¹⁵N‐labeled protein was prepared by growing these cells in M9 minimal media with ¹⁵NH₄Cl as the sole nitrogen source. Cu,Zn‐SOD1 was purified using a modification of the procedure described by Getzoff et al.35 in which a POROS HP2 hydrophobic interaction column replaced the diethylaminoethyl column. Subsequently, disulfide‐reduced apo (metal free) SOD1 was prepared as previously described.31, 36

4.2. NMR sample preparation

Purified ¹⁵N‐labeled reduced apo SOD1 in buffer‐containing 20 mM HEPES pH 7.4, 1 mM tris(2‐carboxyethyl)phosphine (TCEP), 1 mM DSS, and 90% H₂O/10% D₂O was concentrated using an Amicon Ultra‐4 centrifugal filter (EMD Millipore) to ∼ 15 mg/ml.

4.3. Variable‐temperature NMR

Backbone resonance assignments were determined as previously described.32 Variable‐temperature ¹H—¹⁵N HSQC (Bruker pulse program “hsqcetfpf3gpsi”37, 38, 39, 40) spectra were acquired using a Bruker AVANCE 600 MHz spectrometer equipped with a 5‐mm triple resonance TXI probe. Amide proton chemical shifts used for temperature coefficient calculations and curvature analysis were directly referenced to DSS (i.e., shifted by the same correction required to move the DSS peak in a 1D ¹H spectrum, acquired with appropriate solvent suppression, to 0 ppm), while amide nitrogen chemical shifts are indirectly referenced to DSS41 using a ¹⁵N/¹H Ξ ratio of 0.101329118. Nominal temperatures (T_nom) ranging from 279 K to 305 K (for pWT apoSOD1^2SH) or 283 K to 311 K (for H46R apoSOD1^2SH) in 2 K increments were programmed into the temperature controller via the Bruker TopSpin 1.3 spectrometer control software. Actual temperatures can be determined from the separation between “thermometer” resonances, for example, between H₂O and DSS proton chemical shifts (the method used here) or the chemical shifts of methyl and hydroxyl deuterons in methanol‐d4,24, 42 and provided to the Shift‐T server. Alternatively, if spectra are collected over multiple temperatures without varying the center frequency, the Shift‐T server can be instructed to calculate temperature differentials from movement of the DSS peak (due to the deuterium lock artefact described above) and the known temperature dependence of water (−11.9 ppb/K)23 (Equation (1), where T _ref is the reference temperature):

$$\mathrm{\Delta }T=\frac{\left({\delta }_{\mathrm{DSS}}\left[T_{\mathit{nom}}\right]-{\delta }_{\mathrm{DSS}}\left[T_{\mathrm{ref}}\right]\right)}{11.9\mathrm{ppb}/K}.$$ (1)

Data processing, including automatic peak picking (with parabolic interpolation) from unassigned ¹H—¹⁵N spectra, was performed using the Bruker TopSpin 4.0.6 software. Peak lists were written to comma‐separated variable (CSV) text files. These data were analyzed by the ShiftTrack and Curvalyzer algorithms via the “Shift‐T: Automated Variable‐Temperature Data Analysis” web server (http://meieringlab.uwaterloo.ca/shiftt).

The ShiftTrack and Curvalyzer algorithms are implemented in Python, and the source files are freely available (https://github.com/meiering-lab/Shift-T). The primary output file format is comma‐separated variable (CSV), which can be edited using a spreadsheet program such as Microsoft Excel (an example output file is included in Appendix S1). The first five lines consist of a header specifying the project name, temperature data, and reference shifts (e.g., DSS). The remainder of the file is in a columnar format, with user‐provided residue names and peak coordinates, amide proton, and nitrogen temperature coefficients calculated by linear regression (along with the residual sum of square errors for each), and both raw (subject to the deuterium lock artefact) and re‐referenced (e.g., to DSS) chemical shifts at each temperature.

4.4. Practical Aspects

Here, we include general recommendations for acquiring data that are likely to yield easily analyzed results. Two important considerations are the number of temperatures at which data are acquired and the temperature range. In principle, temperature coefficients (linear slopes) can be calculated using data from as few as two temperatures. However, the ShiftTrack algorithm will work more reliably with data collected at five or more evenly spaced temperatures, and more points will yield better linear approximations in the presence of noise. The server will not currently accept submissions with data from fewer than four different temperatures.

Curvature detection may be substantially improved by increasing both the number of temperatures (we recommend a minimum of eight) and the temperature range. We advocate collecting data over the widest temperature range possible, given limitations imposed by your equipment (such as probe, temperature controller, spinner material) and the biophysical characteristics of your protein. Unless you wish to probe thermally unfolded states, it is advisable to select a temperature range that avoids heat‐ or cold‐induced global unfolding transitions; such temperature limits can be established using differential scanning calorimetry.

DSS or an equivalently temperature‐invariant standard for chemical shift referencing can often be added directly to the sample; however, DSS has been observed to participate in hydrophobic interactions with proteins.43 If your protein unfolds (fully or partially) during the course of your experiments or has exposed hydrophobic patches, you may wish to use a coaxial insert containing DSS instead.

Supporting information

Figure S1 A histogram (blue) showing the distribution of amide proton chemical shift residuals in the example data (from all residues for which curvature is not detected, at all temperatures). A t distribution (black line) fit to these residuals is superimposed.

Appendix S1: Supporting information

Trainor K, Palumbo JA, MacKenzie DWS, Meiering EM. Temperature dependence of NMR chemical shifts: Tracking and statistical analysis. Protein Science. 2020;29:306–314. 10.1002/pro.3785