Automatic segmentation of all lower limb muscles from high-resolution magnetic resonance imaging using a cascaded three-dimensional deep convolutional neural network

Abstract.

High-resolution magnetic resonance imaging with fat suppression can obtain accurate anatomical information of all 35 lower limb muscles and individual segmentation can facilitate quantitative analysis. However, due to limited contrast and edge information, automatic segmentation of the muscles is very challenging, especially for athletes whose muscles are all well developed and more compact than the average population. Deep convolutional neural network (DCNN)-based segmentation methods showed great promise in many clinical applications, however, a direct adoption of DCNN to lower limb muscle segmentation is challenged by the large three-dimensional (3-D) image size and lack of the direct usage of muscle location information. We developed a cascaded 3-D DCNN model with the first step to localize each muscle using low-resolution images and the second step to segment it using cropped high-resolution images with individually trained networks. The workflow was optimized to account for different characteristics of each muscle for improved accuracy and reduced training and testing time. A testing augmentation technique was proposed to smooth the segmentation contours. The segmentation performance of 14 muscles was within interobserver variability and 21 were slightly worse than humans.

1. Introduction

Lower limb skeletal muscles, as the producers of force and movement, play an essential role in athletic performance as well as in injury reduction as muscle strength and imbalance are important risk factors.¹ Quantification of these muscles is of high interest to better understand these relationships by measuring muscle volumes. A positive correlation was reported between sprint velocity, squat jump power, absolute force–velocity leg power, and total leg muscle volume.^2,3 Differences in muscle distributions for athletes were also evaluated and showed that quantitative mapping of all 35 lower limb muscles has the potential to improve power and agility in athletes by targeted training.^4,5

Magnetic resonance imaging (MRI) with fat suppression has been used to accurately measure muscle volumes in the lower limb,⁶ from which individual muscle can be distinguished from the surroundings with segmentation.⁷ However, due to the similarity in intensity values,⁸ reduced edge information, and the variability in muscle shapes, segmenting individual muscles from MRI is challenging so that it is often performed manually by trained experts. As the image volume is large, the segmentation process is extremely time-consuming and also suffers from interobserver variability. Segmentation for muscles of athletes is even more difficult since almost all muscles are well developed and closely packed so that intermuscular boundary information is limited.

Several techniques have been developed for automatic muscle segmentation such as atlas-based and shape-based methods. A deformable registration method to match the edges from the template meshes of muscles and other thigh anatomy to the boundaries of the target image was developed with regularization terms.^9,10 However, this may fail when the edge information is very limited. A technique for incorporating prior shape models built from the training dataset into a random work segmentation framework,¹¹ and a generalized log-ratio segmentation representation on training statistical shape models, which benefited from encoding meaningful localized uncertainty information,¹² were recently proposed. However, the particular shape model may not capture all the shape variability and complicated preprocessing is often required. Furthermore, most methods only focused on major thigh muscles, which have relatively large volumes and distinct features and often ignored smaller thigh and calf muscles. Recently, deep convolutional neural network (DCNN) has been successfully applied in many medical image segmentation tasks from MRI or computed tomography images.^13,14 For muscles, segmentation of human thigh using fully convolutional network was developed to separate quadriceps, bone, and marrow from the backgrounds.¹⁵ A DCNN method was also proposed to get the response vector from each slice and use the principal component analysis to reconstruct two two-dimensional (2-D) parametric images to represent the three-dimensional (3-D) inputs.¹⁶ However, both methods used 2-D slices as the training input, which may lose structural and edge information of the 3-D images since muscle boundaries may not present at every slice. In addition, for individual muscle segmentation, global information of the whole leg is important since muscles are localized with respect to the leg, which gives more information beyond the 2-D slices. However, the graphics processing unit (GPU) memory and computation speed limit a direct adoption of DCNN with large 3-D dataset since high-resolution raw data cannot fit into the GPU without image compression, which leads to significant loss of spatial resolution and boundary information.

In this study, to overcome these issues, we developed a cascaded 3-D DCNN segmentation framework for fully automatic segmentation of all 35 lower limb muscles (70 on both left and right legs). The first stage of the framework extracts bounding boxes for each muscle as the location information using low-resolution images and the second stage obtains accurate contours for each one using cropped high-resolution images. The workflow was also optimized to encode feature variability for all individual muscles and reduce training and testing time. Testing augmentation was proposed to further improve segmentation accuracy and contour smoothness.

2. Methods

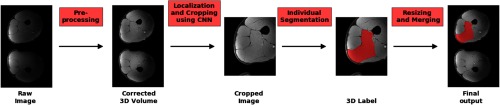
Our proposed segmentation workflow is summarized in Fig. 1. Preprocessing was used to correct the image inhomogeneity. As discussed before, it is impractical and inefficient to feed the raw high-resolution 3-D images into a neural network for simultaneous segmentation of all 70 regions-of-interest (RoIs). Therefore, a two-stage process was designed to capture location and detailed features, respectively, and trained on the 3-D images with different resolutions. The final results for each RoI were combined and merged for evaluation. Details are provided as follows.

Fig. 1.

Workflow of the automated segmentation framework for one target muscle. All the inputs and outputs are 3-D MR images and label map, respectively. After localization, the bounding box is slightly enlarged for actual cropping and individual segmentation.

2.1. Dataset and Preprocessing

The dataset in this study consists of 64 whole leg muscle images from collegiate athletes of different sports, including basketball, baseball, track, football, and soccer. Proton density weighted images with fat suppression were acquired from thoracic vertebrae T12 to ankle on a Siemens 3T scanner for each subject. Two protocols were used in this study: a customized 2-D multislice spiral protocol and an optimized 2-D Cartesian protocol with parallel imaging. For both protocols, the in-plane spatial resolution was $1\mathrm{mm}\times 1\mathrm{mm}$ and slice thickness was 5 mm with 200 to 240 continuous axial slices in total. In-plane matrix size was $512\times 512$ for the spiral protocol and $476\times 380$ for the Cartesian protocol. The total scan time was 25 to 30 min. This study was approved by the Institutional Review Board for Health Sciences Research of the University of Virginia and informed consent was obtained from each subject.

Manual segmentation of all muscles was performed and vetted by trained engineers as the ground truth. Image inhomogeneity due to radiofrequency field (B1) variations was corrected using improved nonparametric nonuniform intensity normalization (N3) bias correction¹⁷ during preprocessing, followed by cropping to unify the in-plane matrix size from both protocols. 51 cases were randomly selected for training and 13 for testing.

2.2. Cascaded DCNN Framework

2.2.1. Muscle localization

The main goal of the first stage is to obtain a bounding box that encloses the target muscle from the entire 3-D lower limb volumes, which can then be used to crop the original images to only keep relevant regions. As the first step, the whole leg images were split into three parts: abdomen, upper leg, and lower leg based on the superior–inferior coordinates and the estimated ratios of the lengths of the three parts. To allow for variations in the ratios, the split was performed with significant overlap, e.g., the upper leg images would contain many slices of abdomen and lower leg images. Therefore, for muscles that belong to the upper leg, only the upper leg images need to be considered. However, even after split, the images at the acquired resolution cannot fit into a typical GPU memory (12 Gb) so that the resolution of the input images needs to be reduced using linear interpolation and kept as high as possible without exceeding the GPU memory.

To generate the bounding box of the RoI from the low-resolution images, detection-based networks such as faster RCNN¹⁸ are usually used, however, in this study, due to the limited number of training images and bounding box labels, it is difficult and time-consuming to train a detection network with good accuracy. In addition, we empirically found that for most muscles, small errors in muscle localization would not hurt the segmentation accuracy in the second stage, as long as all voxels of the target muscle are included in the cropped images. Therefore, a modified 3-D U-Net was built to segment the low-resolution images and generate the bounding boxes based on the pixelwise prediction maps. The network follows the structure of 3-D U-Net, which consisted of an encoder and a decoder, each with four resolution levels. Each level in the encoder contains two blocks of a $3\times 3\times 3$ convolution layer, a batch normalization (BN) layer, and a rectified linear unit (ReLU) activation layer, followed by a $2\times 2\times 2$ maxpooling except for the bottom-most level. In the decoder, each level consists of a $2\times 2\times 2$ deconvolution layer, followed by two blocks of a $3\times 3\times 3$ convolution layer, a BN layer, and a ReLU layer. In addition, feature maps from the encoder were concatenated to those of the same resolution in the decoder as the skip connection. The final block of the network contains a $1\times 1\times 1$ convolution layer to reduce the dimension of the features to match the number of label maps, followed by a pixelwise softmax classifier.

Due to the relatively small training size and a large number of muscles, instead of using single models to segment all muscles in the abdomen, upper leg, and lower leg regions at the same time, using dedicated separate models for each individual muscle or muscle groups can greatly improve the accuracy. However, it is time-consuming to train the models individually since there are 70 RoIs on both left and right legs. To reduce the total training time, the workflow is optimized by training the grouped muscles together in this stage. The total 70 RoIs were divided into 10 groups, each containing about four adjacent muscles on both legs. The division was largely based on the anatomical location along the superior–inferior direction. For each group, the input was the correspondingly split images and the output was the label map for the RoIs within the group with distinguished left and right muscles. It is worth noting that the muscles with extremely small size, such as external rotators, may disappear during the shrinkage of the original images in the first stage so that there are no predicted output labels for them. In this case, these muscles were localized based on the output of neighboring large muscles and then cropped from the estimated regions from the original images.

2.2.2. Individual muscle segmentation

In the second stage, individual networks were trained for each target muscle to obtain more accurate contours from images cropped based on the output of the first stage, whose resolution is close to the originally acquired images. During training, instead of cropping the images from the tight bounding box that just encompasses the target muscle, the images were cropped at a box enlarged with a ratio randomly chosen from a range (e.g., 1.0 to 1.8) along each dimension. As the two edges of the bounding boxes along each dimension were sampled separately, the center of the bounding boxes may also change. However, the target muscle was guaranteed to be within the bounding box. For simplicity, the uniform distribution was used in sampling the ratio. The enlarged bounding box with varied enlargement ratio can enrich the background information at different levels and can serve as training augmentation to improve the segmentation accuracy and robustness. During deployment, an augmentation method was also used to improve the segmentation accuracy and contour smoothness. Specifically, a series of images were cropped at varied bounding boxes based on the first stage output and fed into the network. The range and distribution for the enlargement ratio were the same as during training. The outputs from each input were then averaged after putting back to the uncropped original images as the final label map. The number of bounding boxes was chosen to be six as a balance between deployment time and number of augmentations. To reduce the number of models to be trained and increase the data size, left and right muscles were combined together to share the same model due to their symmetry and similarity. The total number of models to be trained was then 35. For implementation, simplification without accuracy drops, networks for each muscle share the same network structure, except for the input size, which was optimized based on the average muscle sizes to maintain the aspect ratio as much as possible.

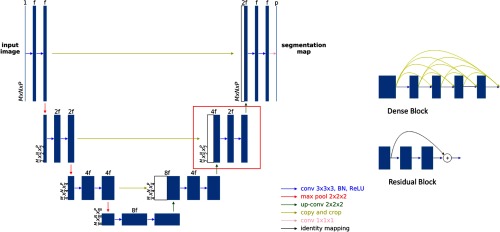
As the goal is to maximize the accuracy, in this stage, different network structures, including the plain U-Net, U-Net with residual and with dense blocks, and different hyperparameters, including number of layers and filters were compared to evaluate their performances. The plain U-Net having the same structure with the network in the first stage was considered as the baseline. Residual blocks contain short connections from previous convolutional layers so that the neural networks can be substantially deeper without gradient vanishing and the training becomes easier.¹⁹ The dense blocks extend the short connections by introducing connections between all layers,²⁰ and its adoption in segmentation showed improved performance.²¹ In this study, we replaced the blocks of convolution, BN and ReLU layers, in the plain U-Net with the residual blocks and the dense blocks, respectively. The detailed structure is illustrated in Fig. 2. For a fair comparison, the number of filters and the depth of the convolutional layers were kept the same. Furthermore, the U-Net structure is compared with two other structures, a fully convolutional network with fusion predictions (FCN-8s)²² and SegNet,²³ which use deeper networks (five resolution levels) for both encoder and decoder. All the comparison studies were conducted to segment the target muscle adductor brevis, which has a relatively small volume and thus is difficult to segment.

Fig. 2.

Multiple network structures for comparison. The plain U-Net structure (left) is used in stage one and two as the baseline. Top right shows an example of residual block, which adds the previous filter to the latter by elementwise addition. Bottom right shows an example of a four-layer dense block, which concatenates each layer to every other layer. Either the residual or the dense block replaces the conventional convolutional block in each resolution level (as shown in red box) to build the corresponding networks.

2.2.3. Implementations

The method was implemented based on the TensorFlow framework and training and testing were performed on two NVidia 1080Ti GPUs with 11 Gb memory each. During training, the weights were initialized randomly from Gaussian distribution and updated using the adaptive moment estimation (Adam) optimizer²⁴ for gradient descent with an initial learning rate of 0.01 and the pixelwise cross-entropy as the loss function. Due to memory limitations, the batch size was set to be 1. Extensive data augmentation including shearing, rotation, and left–right flipping was applied in the training process of both stages. For stage 2, augmentation was performed after cropping. The training time for a muscle group in stage 1 was about 2 h with 2000 iterations and for a muscle in stage 2 was about 6 h with 5000 iterations. Testing time was 25 to 40 s per group in stage 1 and 5 to 8 s per muscle in stage 2, which roughly corresponds from 4 to 6 s per 2-D slice and 18 to 24 min per case for all the muscles on average with a single GPU.

2.3. Postprocessing and Evaluation

Postprocessing workflow includes false-positive reduction through connection analysis and binary closing to guarantee that only one connected, dense and closed 3-D volume is kept for each RoI. When combining all RoIs, since each network makes a voxel-by-voxel prediction of whether it belongs to the target RoI, it is possible that different networks predict the same voxel to be different RoIs in the second stage. To resolve conflict, the output probabilities from all these networks were compared and the label with maximum probability was retained. In the end, a modified Ramer–Douglas–Peucker algorithm²⁵ was used to simplify the original contour boundary points to get a much smaller number of control points, which can be used for convenient contour editing, if necessary.

To evaluate the segmentation performance, different metrics were calculated including the Dice similarity coefficient (Dice), mean surface distance (MSD), and muscle volumes (V), given as follows:

$$\text{Dice}=\frac{S\cap G}{S\cup G},$$ (1)

in which $S$ and $G$ are the automatically segmented RoI label and the ground truth label, respectively. The larger Dice score indicates a larger overlap and more accurate segmentation. The mean distance calculates the average distance between the contour of each segmentation and its corresponding ground truth contour. The distance of a single voxel on one contour to another contour is given as follows:

$$\mathrm{d}(p,C{)=\min }_{p^{\prime }\in C}{\Vert p-p^{\prime }\Vert }_2,$$ (2)

where $p$ is a voxel and $C$ is the contour. We then calculate the mean of the distances of all voxels on our segmented contour to the ground truth contour. In addition, since, in many studies, the volume of each muscle was used for subsequent analysis together with the performance and injury data, and the accuracy in muscle volume quantification is another important criterion for the segmentation quality, which was calculated by taking the summation of the sizes of all voxels belongs to a muscle $m$, given as follows:

$$V_m={\text{sum}}_{i\in m}(v_i).$$ (3)

In comparison, the percentage differences with the ground truth volumes were used to eliminate the effect of volume variations among muscles.

3. Results

3.1. Bias Correction

Figures 3(a)–3(c) show the effect of the improved N3 bias correction method in the data preprocessing step. The bias field in the original image due to B1 inhomogeneity indicated by the red arrow (top row) was corrected with this method [Figs. 3(d)–3(f)]. This normalized the range of pixel values and improved the homogeneity of the images, which can make the training and testing of the model less biased.

Fig. 3.

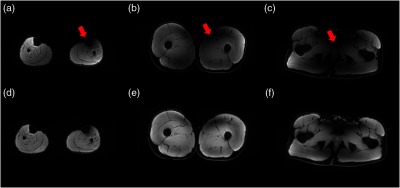
Comparison of the muscle images (a)–(c) without and (d)–(f) with improved N3 bias correction. The bias field due to B1 inhomogeneity indicated by the red arrows is largely corrected with the proposed method.

3.2. Segmentation from Both Stages

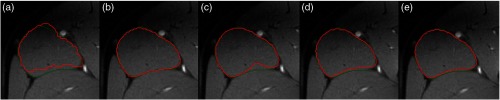
Figure 4 shows one slice of the segmentation contours of the right adductor longus from both stages (red) and the ground truth labels (green). Figure 4(a) shows the output from stage 1. Due to the loss of resolution, the contours were jagged. However, from this contour, the location of the RoI can be accurately identified and the images can be cropped for a more accurate segmentation in stage 2. To show the effectiveness of testing augmentation in stage 2, Fig. 4(b) shows a hypothetical situation in which the images were cropped with the ground truth labels. In practice, the cropping can only be based on the stage 1 output and thus may contain some errors. However, with multiple cropped images at slightly varied boundaries and the averaged output, Fig. 4(e) shows good segmentation quality that is comparable with or even superior than Fig. 4(b) while Figs. 4(c) and 4(d) show the results using only one cropped image based on stage 1 output with different enlargement ratios. The differences between Figs. 4(c) and 4(d) also show that different bounding boxes can affect the model output, especially at hard-to-tell boundaries.

Fig. 4.

Automatically segmented contours (red) for the target muscle adductor longus in different stages and with different input strategies for stage two and the ground truth (green). (a) Output from stage one, (b) output from stage two using the ground-truth contour as the cropping basis, (c) and (d) outputs from stage two using the stage one output with two different enlargement ratios, and (e) output from stage two by averaging multiple enlargement ratios.

3.3. Network Structure Comparison

Comparison among different network structures and hyperparameters were made on adductor brevis on stage 2. Figure 5 shows the averaged Dice scores for all testing cases as a function of the training iterations. Figure 5(a) shows the effect of the number of encoding and decoding blocks, which also reflects the number of spatial-resolution levels. Larger number of resolution levels tend to have better results; however, the difference is very small between three and four. In Fig. 5(b), the results from different number of filters at the root level for the plain U-Net are compared. More filters can lead to higher Dice scores. In Fig. 5(c), the plain U-Net is compared with the U-Net with residual blocks and dense blocks under the same resolution level and similar numbers of filters. Dice score from the model with residual blocks is slightly higher than the other two models, in the end, however, the difference with plain U-Net is small. The U-Net with dense blocks performs the worst among the three network structures. In Fig. 5(d), the U-Net structure is compared with FCN-8s and SegNet. Dice scores from U-Net and SegNet are comparable and slightly better than FCN, especially at early epochs.

Fig. 5.

(a) Mean Dice scores on the validation dataset as functions of training iterations using U-Net with different resolution levels, (b) U-Net with different filter numbers, (c) different convolutional block structures in U-Net, and (d) different network structures.

3.4. Overall Results

Table 1 summarizes the Dice scores of our framework for all 35 muscles as well as the results from an interobserver variability study conducted on three randomly selected subjects. Two independent engineers segmented the same subject and the Dice scores between the two segmentations were calculated. The accuracy of our automated segmentation methods is the same as or even superior than interobserver variability for most muscles, especially for muscles with large volumes.

Table 1.

Dice scores of all lower limb skeletal muscles in an interobserver study and using the proposed automatic segmentation method.

Muscle name	Inter observer	Proposed method
Adductor brevis	0.88	$0.83\pm 0.024$
Adductor longus	0.94	$0.94\pm 0.011$
Adductor magnus	0.92	$0.94\pm 0.015$
Biceps femoris: long head	0.95	$0.94\pm 0.034$
Biceps femoris: short head	0.95	$0.93\pm 0.013$
External rotators	0.84	$0.70\pm 0.101$
Fibulari	0.93	$0.93\pm 0.036$
Flexor digitorum longus	0.94	$0.85\pm 0.032$
Flexor hallucis longus	0.83	$0.87\pm 0.038$
Gastrocnemius: lateral head	0.92	$0.92\pm 0.016$
Gastrocnemius: medial head	0.94	$0.95\pm 0.012$
Gluteus maximus	0.97	$0.97\pm 0.006$
Gluteus medius	0.94	$0.93\pm 0.013$
Gluteus minimus	0.90	$0.88\pm 0.015$
Gracilis	0.96	$0.94\pm 0.010$
Iliacus	0.91	$0.91\pm 0.033$
Obturator externus	0.66	$0.78\pm 0.058$
Obturator internus	0.78	$0.78\pm 0.043$
Pectineus	0.92	$0.84\pm 0.036$
Piriformis	0.86	$0.80\pm 0.050$
Phalangeal extensors	0.89	$0.90\pm 0.030$
Popliteus	0.90	$0.88\pm 0.029$
Psoas major	0.92	$0.78\pm 0.067$
Quadratus femoris	0.89	$0.81\pm 0.057$
Rectus femoris	0.97	$0.96\pm 0.026$
Sartorius	0.95	$0.93\pm 0.020$
Semimembranosus	0.90	$0.93\pm 0.030$
Semitendinosus	0.95	$0.93\pm 0.011$
Soleus	0.93	$0.94\pm 0.019$
Tensor fasciae latae	0.96	$0.94\pm 0.016$
Tibialis anterior	0.88	$0.92\pm 0.015$
Tibialis posterior	0.94	$0.90\pm 0.034$
Vastus intermedius	0.87	$0.88\pm 0.026$
Vastus lateralis	0.95	$0.94\pm 0.018$
Vastus medialis	0.96	$0.95\pm 0.009$

Figures 6(a) and 6(b) show the histograms for percentage volume error and MSD, respectively, when compared with the ground truth values. Most muscles have less than 5% volume errors and less than 4 mm surface distances. The mean volume error between our segmentation results and ground truth is 6.5%, where seven muscles have errors larger than 10%: adductor brevis, flexor digitorum longus, obturator externus, obturator internus, pectineus, piriformis, and quadratus femoris. Variability is generally higher in muscles with small volumes and irregular boundaries, such as quadratus femoris, and in muscles with a medial-lateral orientation, such as the deep hip rotators. The overall mean distance is 2.9 mm, where seven muscles have mean distance values larger than 4 mm. The result is consistent with the Dice scores and shows a strong positive correlation.

Fig. 6.

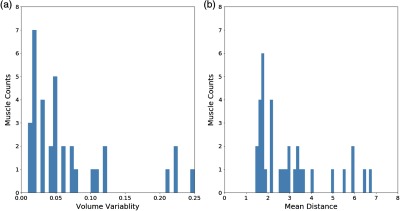
(a) Histograms showing volume errors and (b) MSDs for all muscles.

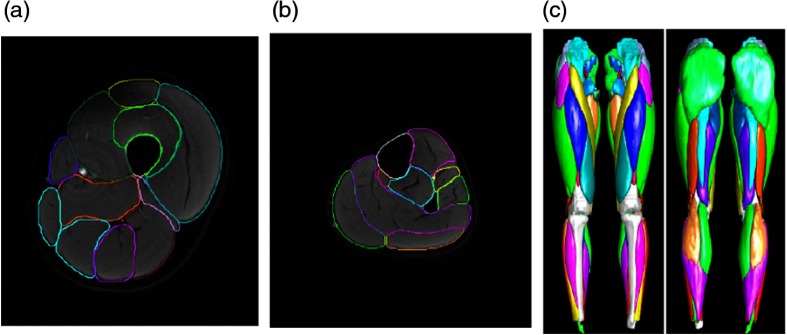
An example of the cross-sectional segmentation results for both the upper and lower legs is shown in Fig. 7, as well as the 3-D rendered muscle maps directly reconstructed from the automatic segmentation. Almost all muscles have good contour quality and 3-D shape.

Fig. 7.

Segmentation results obtained with 3-D cascaded DCNN showing (a) one slice of the upper leg, (b) one slice of the lower leg, and (c) the 3-D rendered muscle maps.

4. Discussions

We have presented the segmentation results of all 35 individual lower limb muscles from high-resolution MRI using a cascaded 3-D DCNN. As shown in Fig. 4, the resolution of the input images is essential to obtain good segmentation quality. Although the major part of the target muscles can be extracted through a network with low-resolution images as the input, the muscle boundaries are inaccurate due to the significant loss of fine details. Therefore, we trained a second network based on the output of stage 1, which keeps the resolution of the input but with cropped field-of-view to make it fit into the GPU memory. Furthermore, to overcome the issue that the error from stage 1 output may negatively affect the accuracy of the stage 2 and further increase the model performance, we used a testing augmentation method by varying the stage 2 input multiple times and averaging the results. The robustness against the stage 1 error is improved and the contours are smoothed due to multiple averages. The final segmentation results achieved similar or even superior performances than humans in 14 muscles while only slightly worse in 21 muscles.

In this study, we also compared the hyperparameters and network structures for segmentation to optimize the results from stage 2. In general, a deeper and wider network can yield better performance, however, it comes at the cost of increased memory requirement and computation time. We observed that the benefit with a deeper network is marginal when the resolution level is larger than 3 while the width of the network has a more significant influence. One explanation is that for muscle segmentation, very high-level information captured with deep layers of the network may not contribute as much to the results as the low-level image structures, such as edges and contrast. Comparing different convolutional block structures, adding short-cut connections to the network only has minimal impact as the differences in Dice scores for the three networks are within 0.01, which is likely due to the fact that the network is relatively shallow so that the effect of short-cut connections to avoid “gradient vanishing”¹⁹ is not significant in this application. With different network structures, Dice scores are also similar. Overall, considering the minimal differences and the fact that the network with residual block needs more parameters and computations, the plain U-Net with three resolution level, two convolutional layers per level, and 96 filters on the first convolutional layer were used to train all the target muscles in stage 2.

Although the promising overall results suggest that the cascaded DCNN method can achieve high segmentation accuracy and robustness for almost all lower limb skeletal muscles, the performances on muscles with small volumes, such as external rotators, are still suboptimal. In stage 1, the localization network performed poorly and even completely failed to generate any labels for these muscles due to class imbalances. Therefore, we cannot directly get any location information from the output labels but have to estimate it from neighboring muscles, which may affect the accuracy. Continued work will focus on these muscles such as using a single output label for the grouped muscles, including the small ones to extract the boundary information. This method cannot use the individually optimized bounding boxes but can greatly reduce the likelihood of failing to predict a bounding box.

Another main limitation is the size and population distribution of the data in this study. Due to the high cost of obtaining MRIs and manual segmentation, the dataset is small and from a single institution. Therefore, the trained model may have worse performances on images using different imaging protocols and/or scanners. Furthermore, although the muscles from athletes are more difficult to segment as there are fewer intermuscular fat, which can be used to distinguish muscles, compared with healthy populations, it may not be the case for patients with metabolic syndrome or disease, whose MR images may contain more abnormal structures. As the application of this study is to examine whether targeted training strategies on different muscles can yield enhanced performances and/or reduced injury risk, the study population is on athletes and the automatic segmentation method developed in this study can greatly facilitate the data analysis process. Furthermore, although the trained model is limited by the population distribution, the training and testing method is generic. Based on our experiences, having 40 to 60 training cases from the desired population can yield good segmentation performances, which can be even reduced if starting from an already-trained model, such as the one optimized for athletes.

In conclusion, we developed a cascaded 3-D DCNN segmentation framework to obtain accurate segmentation for individual skeletal muscles. Our workflow is optimized to segment all 35 lower limb muscles with high quality, validated by various metrics. Compared with previous studies, the deep learning-based method allows more variability in the images and leads to a robust overall result. This can greatly facilitate quantitative study on muscle profiles using high-resolution MRI.

Biographies

Renkun Ni is a research scientist at Springbok, Inc. His research is focused on developing deep learning methods for medical image processing.

Craig H. Meyer is a professor at the Department of Biomedical Engineering from the University of Virginia. His research is in developing magnetic resonance imaging techniques for rapid acquisition and processing of image data in the setting of cardiovascular disease, neural diseases, and pediatrics using tools in physics, signal processing, image reconstruction, and machine learning.

Silvia S. Blemker is a professor at the Department of Biomedical Engineering from the University of Virginia. She is broadly interested in muscle mechanics and physiology, multiscale modeling, mentoring students, and teaching.

Joseph M. Hart is an associate professor at the Department of Kinesiology from the University of Virginia. His research focus is in the area of neuromuscular consequences of joint injury, in particular, neuromuscular factors that contribute to the progression of osteoarthritis following ACL reconstruction and factors that contribute to the low back pain recurrence.

Xue Feng is an assistant professor at the Department of Biomedical Engineering from the University of Virginia. His research is in developing various medical image processing algorithms for detection and segmentation.

Disclosures

R.N. and X.F. are employees of Springbok, Inc. C.H.M., S.S.B., and J.M.H. have stock ownership in Springbok, Inc.