Bayesian Approaches for Missing Not at Random Outcome Data: The Role of Identifying Restrictions

Abstract

Missing data is almost always present in real datasets, and introduces several statistical issues. One fundamental issue is that, in the absence of strong uncheckable assumptions, effects of interest are typically not nonparametrically identified. In this article, we review the generic approach of the use of identifying restrictions from a likelihood-based perspective, and provide points of contact for several recently proposed methods. An emphasis of this review is on restrictions for nonmonotone missingness, a subject that has been treated sparingly in the literature. We also present a general, fully-Bayesian, approach which is widely applicable and capable of handling a variety of identifying restrictions in a uniform manner.

1. Introduction

Missing data is highly prevalent in real datasets. Within a likelihood-based framework, missing data can best be categorized as either ignorable or nonignorable (Rubin, 1976); the former does not require a model for the missingness process, while the latter does. Nonignorable missingness introduces fundamental identifiability issues because, by virtue of the fact that we did not observe the missing data, we have no data with which to estimate its distribution.

The literature is filled with approaches which resolve identifiability issues by making parametric modeling assumptions (see Section 2 for a review). Following Cox and Donnelly (2011, page 96), however, we believe that if an issue cannot be resolved nonparametrically given an infinite sample then it is “usually dangerous to resolve it parametrically.” While parametric approaches are useful, we argue that they should not indirectly resolve identifiability issues. An alternative approach is to incorporate non-identifiability into the analysis. The full-data distribution can be factored into two components: (1) the observed-data distribution, which is identified by the observed data; and (2) the conditional distribution of the missing data given the observed data, sometimes called the extrapolation distribution, which is not identified (Daniels and Hogan 2008, Section 8.2; Little 1995). Different assumptions about the missing data can be expressed in terms of identifying restrictions which allow the analyst to recover the full-data distribution from the observed data distribution. The most well-known identifying restriction is the missing at random (MAR) assumption (Rubin, 1976), but many alternatives exist.

The National Research Council (2010) recommends the routine use of sensitivity analysis to assess the impact of assumptions about the missing data on inference. Two approaches to sensitivity analysis are to first consider many different identifying restrictions (Thijs et al., 2002) and second (in the spirit of Rotnitzky et al. 1998 and Daniels and Hogan 2008, Chapter 9) to introduce an unidentified sensitivity parameter ξ which represents an interpretable deviation from a benchmark identifying restriction. The sensitivity parameter ξ should be such that (1) there is no information in the data to inform ξ and (2) upon specification of ξ, the effects of interest are identified.

Concerns about parametric assumptions have motivated frequentist semiparametric approaches (Robins et al., 1995; Scharfstein et al., 1999) which make minimal assumptions about the full-data distribution. These approaches posit a parametric model for the missing data mechanism and a semiparametric model for the outcome distribution, and produce estimates by solving inverse-probability-weighted (IPW) estimating equations. These procedures are frequently doubly-robust, requiring the analyst to specify one of the two models correctly to attain consistent estimation (Scharfstein et al., 1999; Rotnitzky et al., 1998; Tsiatis, 2007). Recently, there have been various likelihood-based approaches proposed which have the flexibility of semiparametric approaches and allow a flexible sensitivity analysis (Wang et al., 2010; Linero and Daniels, 2015; Linero, 2017). An advantage of the Bayesian approach is that it allows for uncertainty about the unidentified components of the model to be encoded in an informative prior, allowing the analyst to incorporate subject-matter expertise formally into the analysis.

This article has three goals. First, we provide a review of model-based approaches to nonignorable missingness, including parametric approaches which identify the full-data distribution (see National Research Council, 2010; Ibrahim and Molenberghs, 2009, for additional reviews of MNAR modeling strategies). Our second goal is to summarize and review existing identifying restrictions in the literature. A special emphasis is given to recent proposals for nonmonotone missingness, as this subject has received a sparser treatment in the literature. We highlight several recently proposed identifying restrictions and characterize them as generalizations of monotone restrictions.

Our third goal is to propose a flexible, fully-Bayesian, framework for incomplete outcome data. First, a flexible Bayesian nonparametric model is chosen for the observed data distribution. Second, we use an identifying restriction to identify the extrapolation distribution. The framework allows for many different restrictions to be used without needing to change the model used for the observed data, can accommodate both monotone and nonmonotone missingness, and allows for the introduction of sensitivity parameters. The proposed approach might be perceived as a competitor to the IPW approaches which are prevalent in the literature. However, it has several features which IPW approaches do not. First, the Bayesian framework allows for expert knowledge to be formally incorporated into the analysis by eliciting informative priors on sensitivity parameters. Second, the approach allows for simultaneous inference about functionals of the full-data distribution, rather than just a specifically chosen functional such as the mean; for example it is possible to make inferences about means and quantiles simultaneously. Third, we are not required to fit different models depending on the choice of identifying restriction, allowing for a more principled comparison of different restrictions.

To illustrate the necessity of conducting a principled sensitivity analysis, we analyze data from the Breast Cancer Prevention Trial (BCPT). A concern in this study was that the treatment tamoxifen might cause depression. We show that the evidence for this hypothesis is strongly influenced by the assumptions made about the missingness, and that seemingly similar assumptions can yield dramatically different results. This underscores the need for statisticians and subject-matter experts to work together in determining which assumptions about the missing data are most appropriate for a particular problem.

1.1. Notation

Let $Y_j^{(i)}$ denote the measurement of variable j intended to be collected on subject i for i = 1, . . . ,N, and let $Y^{(i)}=(Y_1^{(i)},\dots ,Y_J^{(i)})$. Let $R^{(i)}=(R_1^{(i)},\dots ,R_J^{(i)})$ be a vector of missingness indicators such that $R_j^{(i)}=1$ or 0 according to whether $Y_j^{(i)}$ is observed or not. For a given binary vector r ∈ {0,1}^J, let y_r = (y_j : r_j = 1) and y_−r = (y_j : r_j = 0). The observed data on subject i is then given by $Y_{R^{(i)}}^{(i)}$, and the missing data is given by $Y_{-R^{(i)}}^{(i)}$.

We assume the pairs (Y⁽ⁱ⁾,R⁽ⁱ⁾) are iid with density p(y, r) with respect to some measure; implicitly, p(y, r) may depend on a parameter vector θ. We refer to p(y, r) as the full-data distribution. To lighten notation, we will often work with an iid copy (Y,R) of (Y⁽¹⁾,R⁽¹⁾). For simplicity we omit covariates; in principle all distributions we discuss can be defined conditional on fully-observed covariates X = x.

We will abuse notation, for example writing p(y) for the marginal density of Y or p(r | y) for the probability of R = r given Y = y; it will always be clear from context what density is being referred. When specific arguments are required, we will write for example p(R_j = 1 | Y = y) for the probability of R_j = 1 given Y = y.

For a fixed r, let p(y, r) = p(y_r, r)p(y_−r | y_r, r) denote the extrapolation factorization (Daniels and Hogan, 2008, Section 8.2) of p(y, r). This factors p(y, r) into the product of a term which is identified and a term which is unidentified. Note that p(y_r, r) is the density of the observed data (Y_R,R) while p(y_−r | y_r, r) is the conditional density of the missing data Y_−R. We refer to p(y_r, r) as the observed-data distribution and to p(y_−r | y_r, r) as the extrapolation distribution.

Missingness is said to be monotone if R_j = 0 implies R_j+1 = 0. This commonly occurs in longitudinal trials when missingness is due to dropout. Missingness can then be summarized by the last time at which a subect is measured $S^{(i)}=\max \{j:R_j^{(i)}=1\}$, which we refer to as the (index of the) dropout time. For longitudinal studies it is also useful to let ${\overline{Y}}_j^{(i)}=(Y_1^{(i)},\dots ,Y_j^{(i)})$ denote the history of the response up-to time j, and let ${\tilde{Y}}_j^{(i)}=(Y_{j+1}^{(i)},\dots ,Y_J^{(i)})$ denote the future of the response strictly after time j. Thus, $Y^{(i)}=({\overline{Y}}_j^{(i)},{\tilde{Y}}_j^{(i)})$. We similarly define ${\overline{R}}_j^{(i)}$ and ${\tilde{R}}_j^{(i)}$.

1.2. Running example: the Breast Cancer Prevention Trial

To make the concepts presented concrete, we will focus on applications to the Breast Cancer Prevention Trial (BCPT), a clinical trial which assigned women at high-risk of developing breast cancer to either a preventative drug, tamoxifen, or to a placebo. One aim of this study was to determine if tamoxifen causes depression. The response $Y_j^{(i)}$ is 1 or 0 according to whether subject i is depressed or not at time j. Roughly N = 5000 subjects were assigned to each of tamoxifen (Z = 1) and control (Z = 0). Measurements were scheduled to be taken at baseline and 3, 6, 12, 18, 24, 30, and 36 months from baseline, for J = 8 intended measurements. There was a substantial amount of missingness at all time points, and missingness was highly nonmonotone. A concern is that depression at time j might be associated with missingness at time j, even after conditioning on other observables, resulting in MNAR missingness. Our primary interest is in the intention-to-treat effect ψ = E(Y_J | Z = 1) − E(Y_J | Z = 0).

To help illustrate concepts, we will also consider a simplified setting in which J = 2. We refer to this setting as the reduced Breast Cancer Prevention Trial (RBCPT). We assume that (Y₁, Y₂) represent continuous, rather than binary, measures of depression level (the actual binary responses were created from dichotomizing a quantitative score) to create more generality in the development.

2. Basic MNAR modeling strategies

We divide strategies for modeling p(y, r) into three categories: (1) selection models; (2) pattern mixture models; and (3) shared parameter models. In Section 2.4, we describe how any of these three approaches can be used to obtain a model for the observed data, without modeling the missing data.

2.1. Selection models

The selection modeling approach (Heckman, 1979) is based on the factorization p(y, r) = p(y)·p(r | y). The term p(r | y) is referred to as the missing data mechanism.

Example 1. Consider the RBCPT. With monotone missingness and Y₁ always observed, following Diggle and Kenward (1994), we set

$$\begin{gathered} Y~\mathrm{Normal}(\mu ,\mathrm{\Sigma }), \\ p\left(R_2=1|y_1,y_2,R_1=1\right)=\mathrm{expit}\left({\varphi }_0+{\varphi }_1{y}_1+{\varphi }_2{y}_2\right). \end{gathered}$$ (1)

Selection models are attractive for their conceptual simplicity. In the context of the BCPT, the selection factorization suggests a causal mechanism in which depression causes missingness to occur. As p(y) is directly available, inference is usually straight-forward.

One drawback of parametric selection models is that they may “identify away” the missing data problem. Observe that ϕ₂ = 0 corresponds to an MAR missing data mechanism in (1). One may be tempted to test for MNAR missingness by testing ϕ₂ = 0. As we have stressed, testing for MAR cannot be done without recourse to parametric assumptions. As illustrated by Kenward (1998), inferences about MAR in this setup are extremely sensitive to parametric assumptions. When p(y) is a Gaussian density, (ϕ₁, ϕ₂) function as skewness parameters for p(y₂ | y₁, r) and can be estimated from the observed data. Hence, there are no sensitivity parameters which can be used as a basis of a sensitivity analysis. In practice, the likelihood of ϕ₂ may be flat enough that it can be used as an approximate sensitivity parameter (Carpenter et al., 2002). This problem is mitigated to some extent when semiparametric or nonparametric models for Y are used, although this becomes more difficult as the dimension of the response increases. Note also that p(y_−r | y_r, r) is not available in closed form; consequently, it is difficult to describe on a conceptual level how missing values are imputed relative to the other approaches we describe.

2.2. Pattern mixture models

The pattern mixture approach (Little, 1994, 1993; Hogan and Laird, 1997) is based on the factorization p(y, r) = p(y | r)p(r). This characterizes p(y) as a mixture over missingness patterns ${\sum }_{r}p(y|r)p(r)$. The pattern mixture factorization is closely related to the extrapolation factorization, with p(y_r, r) = p(y_r | r) · p(r). This makes the pattern mixture approach conducive to sensitivity analysis.

Example 2. Consider the RBCPT and assume monotone missingness with Y₁ always observed. We set ϕ = p(R₂ = 1), $(Y_1|R_2=r)~\mathrm{Normal}({\mu }^{(r)},{\sigma }_1^{(r)})$, and $(Y_2|Y_1=y_1,R_2=r)~\mathrm{Normal}({\alpha }^{(r)}+{\beta }^{(r)}{y}_1,{\sigma }_2^{(r)})$. The parameters $({\alpha }^{(0)},{\beta }^{(0)},{\sigma }_2^{(0)})$ are unidentified. One approach to identifying these parameters is to link them to the R₂ = 1 pattern, setting for example $({\beta }^{(0)},{\sigma }_2^{(0)})=({\beta }^{(1)},{\sigma }_2^{(1)})$ and α⁽⁰⁾ = α⁽¹⁾ + ξ. This implies that the influence of Y₁ on Y₂ and the conditional spread of Y₂ do not depend on R₂, while the conditional mean of Y₂ does and is shifted by a fixed amount ξ. The parameter ξ is a sensitivity parameter, and can be varied as part of a sensitivity analysis.

Characteristic of pattern mixture models, the above model allows an interpretable sensitivity analysis and is transparent in how the it imputes missing values on a conceptual level. There are several shortcomings of the pattern mixture approach. Conceptually, it is typically not easy to interpret how the response Y influences the probability of missingness at time j. In the BCPT, a pattern mixture model suggests that those with missing values come from a distinct sub-population; an arguably more natural way to capture this intuition is through the use of latent class models (Roy, 2003) (though as constructed there, they do not allow sensitivity parameters). Pattern mixture models often possess a large number of unidentified parameters that the analyst must specify, with the situation becoming unwieldy in higher dimensions. Additionally, sparsity in the observed missing data patterns R⁽ⁱ⁾ may necessitate further modeling of p(y | r) to share information across times.

2.3. Shared parameter approaches

The shared parameter approach captures dependence between Y⁽ⁱ⁾ and R⁽ⁱ⁾ through shared random effects (Wu and Carroll, 1988; Henderson et al., 2000), setting $p(y,r)=\int p(y|b)p(r|b)G(db)$. The random effect distribution G(·) can be specified parametrically, usually as a multivariate Gaussian distribution, or nonparametrically.

Example 3. Consider the BCPT. We set (b₁, b₂) ~ Normal(μ_b,Σ_b) and assume that, conditional on b, all components of (Y,R) are mutually independent with $\mathrm{logit}p(Y_j=1|b)=Z_j^{\top }{b}_1$ and $\mathrm{logit}p(R_j=1|b)=W_j^{\top }{b}_2$. For example, to get a random quadratic trend over time, we might set $Z_j^{\top }=W_j^{\top }=(1,t_j,t_j^2)$ where t_j is the time of measurement j. This type of shared parameter model is referred to as a correlated random effects model (Lin et al., 2010).

The shared parameter approach provides a highly flexible framework for analyzing nonignorable missingness, and is particularly effective for modeling complex data structures (Dunson and Perreault, 2001). Shared parameter models appeal strongly to intuition, suggesting that Y and R have a shared, unobserved, common cause. A drawback of the shared parameter approach is that it is difficult to separate p(y_r, r) from p(y_−r | y_r, r), making it difficult to anchor a sensitivity analysis to an interpretable identifying restriction (see Section 3). Generally, it is not easy to see what assumptions about the missing data mechanism are encoded in a shared parameter model.

Methods for implementing a sensitivity analysis for shared parameter models have been developed by Creemers et al. (2010, 2011). In our example, one might set $\mathrm{logit}(p(Y_j=1|b,R=r))=Z_j^{\top }(b_1^{(i)}+r_j\delta )$ which gives an adjustment to the random effect b₁ at the times for which r_j = 0. One may then set, for example, δ ~ Normal(μ_δ,Σ_δ), with ξ = (μ_δ,Σ_δ) a sensitivity parameter. We feel that this is somewhat against the spirit of the shared parameter model, as Y and R are no longer conditionally independent and the causally suggestive motivation is stretched.

2.4. Observed data modeling

The models in Sections 2.1–2.3 have been presented as models for the joint density p(y, r). An alternative strategy is to model the observed data distribution p(y_r, r) and leave the extrapolation distribution distribution p(y_−r | y_r, r) unspecified. One can then fit a model for p(y_r, r) to the data and complete the model using one of the identifying restrictions described in Section 3.

Directly modeling p(y_r, r) can be challenging to do in practice, as it requires a model for Y_r for every pattern r. When missingness is monotone, one approach is to specify models for $p(y_j|S\ge j,{\overline{y}}_{j-1})$ and $p(S=j|S\ge j,{\overline{y}}_j)$. For examples of this approach, see Scharfstein et al. (2014) and Wang et al. (2010). Other approaches to directly modeling p(y_r, r) often use the pattern mixture approach, specifying models for p(y_r | r) while leaving p(y_−r | y_r, r) unspecified. See, for example, Little (1994) and Thijs et al. (2002).

A generic approach to modeling the observed data is to specify a working model (Linero, 2017; Linero and Daniels, 2015; Daniels and Linero, 2015). One then implicitly obtains a model for the observed data $p(y_r,r)=\int p^{\star }(y,r)d{y}_{-r}$. In principle, p^⋆(y, r) may be a selection model, pattern mixture model, or shared parameter model. In Section 5 we will apply this approach using a nonparametrically modeled shared parameter to obtain a highly flexible model of the observed data.

A benefit of the working model approach is that it allows models which share information across missingness patterns and time, without identifying the extrapolation distribution. This allows one to avoid a common pitfall of pattern-mixture models; we can estimate p(y_r, r) even when we do not observe some patterns or the amount of data in some patterns is sparse. Because the model p^⋆(y, r) is used only to obtain a model for p(y_r, r), and is not used as a basis for inference, we are allowed complete freedom in how to identify the extrapolation distribution. Conveniently, p^⋆(y, r) can also be used as a basis for Markov chain Monte Carlo algorithms.

In practice, the working model framework has the drawback of being somewhat difficult to implement, in that one must be able to derive the conditional distributions p^⋆(y_r | R = r′). This places restrictions on which models can be tractably used; in particular, selection models and parametric shared parameter models are difficult to use. Fortunately, there are very flexible models that are tractable. An additional concern is that, when p(y_r, r) is modeled parametrically, p(y, r) will usually fall outside of this parametric family. For example, when using identifying restrictions, if p(y_r | r) is modeled with a Gaussian distribution, it will not typically be the case that p(y | r) is Gaussian (Wang and Daniels, 2011). Consequently, the joint model p(y, r) may not be easily interpretable, although causal effects may still be computed using MC integration (see Section 4).

3. Identifying restrictions

Identifying restrictions provide a useful starting point for identifying the extrapolation distribution and conducting a sensitivity analysis. Informally, an identifying restriction is an assumption about p(y, r) which links the observed data distribution p(y_r,r) to the extrapolation distribution p(y_−r | y_r, r).

We remark that identifying assumptions differ subtlely throughout the literature; for example, Seaman et al. (2013) give several non-equivalent definitions of MAR. All restrictions we consider will be phrased in the form of conditional independencies, with (for example) MAR corresponding to the conditional independence statement $(Y_{-r}|Y_r,R=r)\stackrel{d}{=}(Y_{-r}|Y_r)$ for all patterns r.

The goal of specifying an identifying restriction is to nonparametrically identify the parameters of interest.

Definition 3.1. Let $\mathcal{Q}$ denote the set of observed data distributions q(y_r, r), and let $\mathcal{P}$ be some family of full-data distributions p(y, r). The family $\mathcal{P}$ is said to nonparametrically identify a parameter ψ(p) if,

1. For every $q\in \mathcal{Q}$, there exists a $p\in \mathcal{P}$ such that q is the associated observed data density of p.

2. For every $q\in \mathcal{Q}$, if p, $p^{\prime }\in \mathcal{P}$ both marginalize to q, then ψ(p) = ψ(p′).

The family $\mathcal{P}$ is said to be nonparametrically saturated (Robins, 1997; Vansteelandt et al., 2006) if, for each $q\in \mathcal{Q}$, there exists a unique $p\in \mathcal{P}$ which marginalizes to q.

In the absence of strong subject-matter knowledge, it is unwise to assume that a particular identifying restriction holds. Nevertheless, in practice it can be useful to specify a single identifying restriction as a benchmark assumption, and consider interpretable deviations from that benchmark. For example, one might “anchor” an analysis to MAR and consider smooth deviations from MAR. Considering several anchors, and deviations from these anchors, provides insight into how inferences are driven by our assumptions.

We differentiate three different types of identifying restrictions. Joint restrictions completely identify p(y, r); that is, they lead to nonparametrically saturated models. Marginal restrictions do not identify p(y, r), but identify the marginals p(y_j); an example is the sequential explainability assumption (Vansteelandt et al., 2007) discussed later. Marginal restrictions do not lead to nonparametrically saturated models, but are sufficient to nonparametrically identify all marginal effects. Marginal restrictions can be useful because (i) they may be more readily interpretable than joint restrictions, and (ii) they may encode weaker assumptions. Marginal restrictions are special cases of partial restrictions, which are any restrictions which do not identify p(y, r).

3.1. Identifying restrictions under monotone missingness

The missing data problem becomes much simpler when missingness is monotone. In this case, the missing data pattern can be summarized by the dropout time S = max{j : R_j = 1}. Monotonicity occurs naturally when missingness is due to dropout in a longitudinal study. Techniques for monotone missingness can also be applied if there is a method of ordering the components of Y which makes missingness monotone.

Example 4 (NCMV). Consider the BCPT, and assume that missingness is monotone. We conjecture that the, if a subject drops out at time k < j, then their missing response at time j can reasonably be approximated using an equivalent individual who instead drops out at time j; so, we set $(Y_j|{\overline{Y}}_{j-1},S=k)\stackrel{d}{=}(Y_j|{\overline{Y}}_{j-1},S=j)$. Thijs et al. (2002) refer to this as the neighboring case missing value (NCMV) restriction.

Example 5 (ACMV). Consider again the BCPT with monotone missingness. We conjecture that, if a subject drops out at time k < j, then their response at time j can reasonably be approximated by using an equivalent subject who dropped out after time j; so, we set $(Y_j|{\overline{Y}}_{j-1},S=k)\stackrel{d}{=}(Y_j|{\overline{Y}}_{j-1},S\ge j)$. Little (1993) refers to this as the available case missing value (ACMV) restriction.

Example 6 (CCMV). In the BCPT, we decide to use the observations of those who complete the study to estimate the conditional distribution of the missing observations; so, we set $(Y_j|{\overline{Y}}_{j-1},S=k)\stackrel{d}{=}(Y_j|{\overline{Y}}_{j-1},S=J)$; Little (1993) refers to that as the complete case missing value (CCMV) restriction.

The goal of using these restrictions is to provide a starting point for a sensitivity analysis. In practice, when missingness is MNAR, none of the conditional independencies asserted above is realistic; in fact, ACMV is itself equivalent to MAR (Molenberghs et al., 1998)! In the BCPT, if the depression status of an individual at time j is a strong predictor of R_j = 0 then one may expect the conditional distribution of Y_j to be stochastically larger than what is implied by ACMV, NCMV, or CCMV.

Under monotone missingness, ACMV is equivalent to MAR. This suggests that missingness at time j + 1 is causally linked only to the past values of ${\overline{Y}}_j$. The NFD restriction (Kenward et al., 2003) generalizes this idea.

Example 7 (NFD). We posit that missingness at time j+1 is causally due to the past and present values of Y, so that $p(S=j|Y)=p(S=j|{\overline{Y}}_{j+1})$, or equivalently $(Y_{j+1}|S=k,{\overline{Y}}_j)\stackrel{d}{=}(Y_{j+1}|S\ge j,{\overline{Y}}_j)$. This is referred to as the non-future dependence (NFD) assumption.

Despite its causal motivation, we note that NFD is not a causal law; for example if (Y,R) share an unobserved common cause, NFD will usually be violated. Given that MAR implies NFD, but not vice-versa, NFD leads to an under-identified model (and thus is a partial restriction); in particular, the distribution $(Y_j|S=j-1,{\overline{Y}}_{j-1})$ is unidentified for j > 2. This is convenient, as it allows the analyst to consider families of restrictions, all of which satisfy the NFD restriction. For example, Linero and Daniels (2015) centers a sensitivity analysis on the MAR assumption by setting $(Y_j|{\overline{Y}}_{j-1},S=j-1)\stackrel{d}{=}(Y_j+\xi |{\overline{Y}}_{j-1},S\ge j)$, with ξ = 0 corresponding to MAR.

The ACMV, NCMV, and CCMV restrictions are all joint restrictions. Birmingham et al. (2003) consider several partial restrictions, including the following marginal restriction which is implied by CCMV.

Example 8 (Last-occasion-pattern-mixture). We posit that the conditional distribution of Y_J at the end of study, given ${\overline{Y}}_j$ and S = j, can reasonably approximated by the distribution of those who complete the study; hence, we set $(Y_J|{\overline{Y}}_j,S=j)\stackrel{d}{=}(Y_J|{\overline{Y}}_j,S=J)$.

A general tool for extending the restrictions above to the nonmonotone settings is to assume that missingness is partially ignorable given S (Harel and Schafer, 2009). This sets p(R = r | Y = y, S = s) = p(R = r | Y_r = y_r, S = s), and assumes the parameters of p(r | y, s) are independent of the parameters of p(y, s). Analogously to ignorability, partial ignorability ensures that likelihood-based inferences for p(y, s) do not depend on how p(r | y, s) is modeled. See Wang et al. (2010) for an application of this assumption to the BCPT data.

3.2. Identifying restrictions for nonmonotone missingness

The topic of identifying restrictions under nonmonotone missingness was initiated by Robins (1997), who proposed the class of permutation missingness (PM) models. Let ${\overline{O}}_j$ denote the observed data (including the R_j’s) up-to-and-including time j, and ${\tilde{O}}_j$ the data observed strictly after time j. The PM restriction assumes

$$(R_j|Y,{\tilde{R}}_j)\stackrel{d}{=}(R_j|{\overline{Y}}_{j-1},{\tilde{O}}_j)$$ (2)

possibly after applying an a-priori known permutation to Y. In words, (2) states that missingness at time j can depend on the “past” and the “observed future,” but not on the present, where the notion of time is determined by the given permutation. For longitudinal data, one can use (2) without a permutation, or use the reverse permutation to get $(R_j|Y,{\overline{R}}_{j-1})\stackrel{d}{=}(R_j|{\overline{O}}_{j-1},{\tilde{Y}}_j)$ which states that missingness depends on the “future” and the “observed past.”

Our opinion is that PM models are difficult to explain to practitioners. We review several alternative assumptions which have been introduced relatively recently.

Example 9 (Sequential explainability). For the BCPT, we believe that the observed depression levels prior to time j are sufficient to predict whether or not a subject will be measured at time j, while the outcome at time j is not predictive. We therefore impose the sequential explainability restriction (Vansteelandt et al., 2007) $(Y_j|{\overline{O}}_{j-1},R_j=0)\stackrel{d}{=}(Y_j|{\overline{O}}_{j-1},R_j=1)$.

Example 10 (NIP). For the BCPT, we believe that, all other observed quantities being equal, missingness at time j is not predictive of depression at time j. We therefore posit the nearest identified pattern (NIP) (Linero, 2017) restriction, $(Y_j|R=r,Y_r)\stackrel{d}{=}(Y_j|R=r_j^{\star },Y_r)$, where $r_j^{\star }$ is equal to r, but with jth component fixed at 1.

Both NIP and sequential explainability are marginal restrictions. NIP appears similar to NCMV. A more direct analog is the itemwise conditional independence (ICIN) assumption, introduced independently by Sadinle and Reiter (2017a) and Shpitser (2016).

Example 11 (ICIN). For the BCPT, we believe that all other quantities (both observed and unobserved) being equal, missingness at time j is not predictive of depression at time j. We therefore posit the ICIN restriction $(Y_j|R_j=0,R_{-j},Y_{-j})\stackrel{d}{=}(Y_j|R_j=1,R_{-j},Y_{-j})$ where R_−j = (R_k : k ≠ j) and Y_−j = (Y_k : k ≠ j) denote R and Y with the jth component removed.

ICIN and NIP differ in that (i) NIP conditions only on the observed components of Y and (ii) ICIN is a joint restriction. To the extent that conditioning on additional variables makes conditional independence more tenable, ICIN is very attractive. To our knowledge, practical algorithms for conducting inference under ICIN are lacking when J is moderately large. Results of Sadinle and Reiter (2017a) imply that ICIN is equivalent to NCMV when missingness is monotone. A proof of the following proposition is deferred to the supplementary material.

Proposition 3.2. ICIN is an extension of NCMV to nonmonotone missingness.

Tchetgen Tchetgen et al. (2016) introduced the pairwise missing at random assumption. The name is motivated by the observation that it corresponds to MAR when, for fixed r, we assume $R\in \{r,\mathbb{1}\}$, where $\mathbb{1}=(1,\dots ,1)$.

Example 12 (PMAR). For the BCPT, we believe that the distribution of the missing values of a subject can reasonably be approximated using an equivalent subject who was observed at all measurement times. We therefore posit the pairwise missing at random (PMAR) restriction, $(Y_{-r}|R=r,Y_r)\stackrel{d}{=}(Y_{-r}|R=1,Y_r)$.

Just as ICIN is a joint restriction which generalizes NCMV, PMAR is a joint restriction which generalizes CCMV; the following proposition is immediate from the definition.

Proposition 3.3. PMAR is an extension of CCMV to nonmonotone missingness.

3.3. Sensitivity parameters for identifying restrictions

The identifying restrictions in Section 3.1 and Section 3.2 are phrased in terms of conditional independence relationships which, as we have noted, are not themselves particularly plausible when Y_j is thought to directly influence R_j. We consider these assumptions not because we believe the conditional independencies they suggest, but rather to use as benchmark assumptions. These assumptions can be embedded in a family of restrictions indexed by a sensitivity parameter ξ ∈ Ξ such that (1) there is no information in the data to identify ξ and (2) upon specifying ξ, the effects of interest are identified. It is essential that the sensitivity parameter ξ be interpretable; our convention will be to associate the benchmark assumption with ξ = 0. The index ξ can then be thought of as a smooth deviation from our benchmark assumption.

Example 13. For the BCPT, we believe the NIP restriction is unreasonable because depression at time J should increase the risk of missingness, even after accounting for the observed data. We instead assume

$$p(y_J|y_r,R=r)=\frac{p(y_J|y_r,R=r_j^{\star })e^{\gamma y_J}}{E(e^{\gamma Y_J}|Y_r=y_r,R=r_j^{\star })}.$$

Let $A=\{r,r_j^{\star }\}$; using Bayes theorem it can be shown that

$$\log \frac{\mathrm{Odds}(R_J=0|Y_r,Y_J=1,R\in A)}{\mathrm{Odds}(R_J=0,|Y_r,Y_J=0^{\prime },R\in A)}=\gamma ,$$

so that γ denotes the effect, on the log-odds scale, of Y_J = 1 on missingness.

The exponential tilting strategy is very widely applicable, and we now outline it in a general form. Examples of works using this strategy include Birmingham et al. (2003); Wang et al. (2010); Scharfstein et al. (2014, 1999); Tchetgen Tchetgen et al. (2016); Vansteelandt et al. (2007). Consider a restriction of the form

$$(U|V=v,W=w)\stackrel{d}{=}(U|V=v^{\prime },W=w),$$ (3)

where U is a subset of the missing data, W is a subset of the complete data distinct from U, and V is a subset of the missing data indicators. The values v and v′ are such that U is missing when V = v, while U is observed when V = v′. For example, under sequential explainability, one has $\left\{U=Y_j,W={\overline{O}}_{j-1},V=R_j,v=0,v^{\prime }=1\right\}$ while under PMAR one has $\{U=Y_{-r},W=Y_r,V=R,v=r,v^{\prime }=\mathbb{1}\}$. Let f_v(u | w) and $f_{v^{\prime }}(u|w)$ denote the densities of the distributions in (3). The exponential tilting approach sets

$$f_v(u|w)=\frac{f_{v^{\prime }}(u|w)\exp \{t(u,w)\}}{E[\exp \{t(U,w)\}|V=v^{\prime },W=w]}.$$ (4)

The function t(u,w) is a function-valued sensitivity parameter. By Bayes theorem,

$$\log \frac{\text{Odds}(V=v|U=u,W=w,V\in \left\{v,v^{\prime }\right\})}{\text{Odds}(V=v|U=u^{\prime },W=w,V\in \left\{v,v^{\prime }\right\})}=t(u,w)-t(u^{\prime },w).$$

Hence, t(·,w) determines the effect of a change in U on the log-odds of V = v versus V = v′.

Another option is to consider a transformation-based approach similar to Daniels and Hogan (2000). This is particularly useful when the underlying response is continuous.

Example 14. Consider the BCPT, but with Y instead representing a continuous measure of depression level. We believe the NIP restriction is unreasonable because we expect depression levels to be higher among those missing at time j, even after conditioning on the observed data. We instead assume $(Y_j|Y_r=R=r)\stackrel{d}{=}(Y_j+{\xi }_j|Y_r,R=r_j^{\star })$, where ξ_j > 0 represents the expected increase in depression level when a subject is missing rather than observed.

More generally, starting from (3), one can specify a generic transformation

$$(U|V=v,W=w)\stackrel{d}{=}(\mathcal{T}(U,w)|V=v^{\prime },W=w).$$ (5)

In practice we must specify $\mathcal{T}(u,w)$ to be interpretable by subject-matter experts. Location or location-scale transformations, such as ${\mathcal{T}}_j(Y_j)={\xi }_{0j}+{\xi }_{1j}{Y}_j$, are popular (Daniels and Hogan, 2000; Wang and Daniels, 2011; Gaskins et al., 2016) and can be computationally advantageous. Non-affine choices for $\mathcal{T}(\cdot )$ can be used to rescale the data before applying an affine transformation.

A meaningful sensitivity analysis requires serious engagement with subject-matter experts, and as such requires for Ξ to be low dimensional. A common approach that does not formally account for the effect of uncertainty in ξ is a “tipping point” approach. This identifies values, or regions of values, of ξ which result in substantively different conclusions for the effects of interest. If plausible values of ξ do not include any tipping points, then we can have confidence in our substantive conclusions; we note, however, that tipping point analyses do not incorporate uncertainty in ξ when quantifying uncertainty in treatment effects. For illustrations of tipping point analyses, see Scharfstein et al. (2014) and Liublinska and Rubin (2014). An option which formally incorporates uncertainty in ξ is to place an informative prior on ξ. As there is no information in the data about ξ, this prior for ξ will also be the posterior. An advantage of this approach is that it combines all restrictions under consideration to achieve a single, final, inference. For examples of this approach, see Daniels and Hogan (2008, Chapter 9, Case Study 2), Wang et al. (2010), and Gaskins et al. (2016).

3.4. A pattern mixture modeling example

We now show how one might combine the identifying restrictions described above with a model for the observed data for the RBCPT (using the original depression score). We specify a pattern mixture model

$$\begin{gathered} p(R_1=i,R_2=j)={\varphi }_{ij},\left[Y_1,Y_2|R=(1,1)\right]~\mathrm{Normal}({\mu }^{(1,1)},{\mathrm{\Sigma }}^{(1,1)}), \\ \left[Y_1|R=(1,0)\right]~\mathrm{Normal}({\mu }_1^{(1,0)},{\sigma }_1^{(1,0)}),\left[Y_2|R=(0,1)\right]~\mathrm{Normal}({\mu }_2^{(0,1)},{\sigma }_2^{(0,1)}). \end{gathered}$$

All parameters above can be estimated from the observed data using standard techniques; for example, we have ${\widehat{\mu }}^{(1,1)}=\frac{1}{N^{(1,1)}}{\sum }_{i:R_1^{(i)}=R_2^{(i)}=1}{(Y_1^{(i)},Y_2^{(i)})}^{\top }$. For convenience, we write

$$(Y_1|Y_2,R_1=1,R_2=1)~\mathrm{Normal}(\alpha +\beta Y_2,{\tau }^2),$$

where (α, β, τ) is a function of (μ^(1,1),Σ^(1,1)). Suppose that interest is in the parameter ζ = E(Y₁). We demonstrate how ζ is identified under the PMAR, sequential explainability, and NIP assumptions. First, by iterated expectation,

$$\zeta =\sum _{i=0}^1\sum _{j=0}^1{\varphi }_{ij}E(Y_1|R_1=i,R_2=j).$$

Observe that $E(Y_1|R_1=1,R_2=1)={\mu }_1^{(1,1)}$ and $E(Y_1|R_1=1,R_2=0)={\mu }_1^{(1,0)}$. This leaves E(Y₁ | R₁ = 0, R₂ = 0) and E(Y₁ | R₁ = 0, R₂ = 1) to be identified.

Consider first the PMAR assumption. This implies $E(Y_1|R_1=0,R_2=0)=E(Y_1|R_1=1,R_2=1)={\mu }_1^{(1,1)}$. Using iterated expectation, PMAR also implies

$$\begin{gathered} E(Y_1|R_1=0,R_2=1)=E\left\{E(Y_1|Y_2,R_1=0,R_2=1)|R_1=0,R_2=1\right\} \\ =E\left\{E(Y_1|Y_2,R_1=1,R_2=1)|R_1=0,R_2=1\right\} \\ =E(\alpha +\beta Y_2|R_1=0,R_2=1)=\alpha +\beta {\mu }_2^{(0,1)}. \end{gathered}$$

This gives

$${\zeta }_{\text{PMAR}}={\varphi }_{00}{\mu }_1^{(1,1)}+{\varphi }_{10}{\mu }_1^{(1,0)}+{\varphi }_{01}(\alpha +\beta {\mu }_2^{(0,1)})+{\varphi }_{11}{\mu }_1^{(1,1)}.$$

Next, we consider NIP. The derivations under NIP are exactly the same as those under PMAR, with the exception that $E(Y_1|R_1=0,R_2=0)=E(Y_1|R_1=1,R_2=0)={\mu }_1^{(1,0)}$. Therefore, under NIP we have

$${\zeta }_{\text{NIP}}={\zeta }_{\text{PMAR}}+{\varphi }_{00}({\mu }_1^{(1,0)}-{\mu }_1^{(1,1)}).$$

Hence, ζ_NIP will be larger than ζ_PMAR when ${\mu }_1^{(1,0)}-{\mu }_1^{(1,1)}$, and vice versa. Lastly, we consider sequential explainability. At time j = 1 there is no observed history, so sequential explainability implies the marginal independence Y₁ ⊥ R₁. Consequently,

$${\zeta }_{\text{SE}}=E(Y_1|R_1=1)=\frac{{\varphi }_{10}}{{\varphi }_{10}+{\varphi }_{11}}{\mu }_1^{(1,0)}+\frac{{\varphi }_{11}}{{\varphi }_{10}+{\varphi }_{11}}{\mu }_1^{(1,1)}.$$

Sequential explainability differs fundamentally from NIP and PMAR as, due to its sequential nature, it does not use the distribution of (Y₂, R₂) to identify ζ.

We now incorporate sensitivity parameters under sequential explainability. Note that if $(Y_1|R_1=0)\stackrel{d}{=}(Y_1+\xi |R_1=1)$, then ξ = 0 is consistent with sequential explainability. Under this assumption we have

$$\begin{gathered} \zeta (\xi )=p(R_1=1)E(Y_1|R_1=1)+p(R_1=0)E(Y_1|R_1=0) \\ =p(R_1=1){\zeta }_{\text{SE}}+p(R_1=0)({\zeta }_{\text{SE}}+\xi ) \\ ={\zeta }_{\text{SE}}+({\varphi }_{00}+{\varphi }_{01})\xi . \end{gathered}$$

Sensitivity analysis may now proceed either by eliciting an informative prior on ξ, or by identifying values of ξ which lead to substantively different inferences.

4. Inference and computation

We discuss two approaches to computation. First, we describe a fully-Bayesian approach, which can be computationally demanding. Second, we describe multiple imputation, which is a computationally simpler approximation. Let θ denote the parameters of the model of p(y, r), π(θ) a prior for θ, and $\mathcal{O}=(Y_{R^{(1)}}^{(1)},R^{(1)},\dots ,Y_{R^{(N)}}^{(N)},R^{(N)})$ the observed data. We first obtain samples of θ from its posterior distribution $\pi (\theta |\mathcal{O})\propto {\prod }_{i=1}^{N}p(Y_{R^{(i)}}^{(i)},R^{(i)})\pi (\theta )$, usually by Markov chain Monte Carlo. When the working model framework described in Section 2.4 is used, samples of θ can be obtained by fitting the working model by data augmentation, taking advantage of the fact that $p_{\theta }(y_r,r)=\int p_{\theta }^{\star }(y,r)d{y}_{-r}$. A benefit of this approach is that sampling θ can often be accomplished using general-purpose software for fitting Bayesian models. Software packages, such as JAGS and WinBUGS, allow for fast fitting of custom models, and accommodate missing values.

Fully-Bayesian inference then proceeds by computing effects of interest directly from the sampled θ’s and the chosen identifying restriction. Multiple imputation, by contrast, uses the sampled θ’s to impute completed datasets some number of times using the identifying restriction. Practically, these approaches are operationally quite similar. We begin by describing fully-Bayesian inference, and describe the changes required to perform multiple imputation.

4.1. Fully-Bayesian inference

Given sampled values $\theta ~\pi (\theta |\mathcal{O})$, fully-Bayesian inference requires computing the desired effects. These will typically not be available in closed form, but can be computed by Monte Carlo integration. For illustrative purposes, we present the algorithm for sequential explainability in Algorithm 1. In the supplementary material we provide Monte Carlo integration algorithms for PMAR and NIP as well. While we do not pursue this here, Monte Carlo integration can also be implemented using IPW methods (see Robins, 1997; Birmingham et al., 2003; Shpitser, 2016, for such schemes). The number of Monte Carlo samples should be large relative to the sample size; in Section 5, we use 100 times the sample size. This appeal to Monte Carlo to estimate causal effects was initially proposed by Robins (1986) to implement G-computation. While computationally intensive, post-processing of the MCMC output is parallelizable and our experience is that the Monte Carlo integration is not a computational bottleneck. We can avoid repeating these computations for each ξ by using an informative prior, providing another advantage to the fully-Bayesian approach.

Algorithm 1.

Monte Carlo integration for sequential explainability

1: procedure GComp(θ T, j)	▷ Approximates μj by simulating T samples from pθ(y)
2:  for t = 1,..., T do
3:   Sample $(Y_{R^{(t)}}^{(t)},R^{(s)})~p_{\theta }(y_r,r).$
4:   if $R_j^{(t)}=0$ then
5:    Sample $Y_j^{(t)}~p_{\theta }(y_j|{\overline{o}}_{j-1},R_j^{(t)}=1)$
6:   end if
7:  end for
8:  Set ${\mu }_j=T^{-1}{\sum }_{s=1}^T{Y}_j^{(t)}$.
9:  return μj
10: end procedure

4.2. Multiple imputation

Multiple imputation (MI) proceeds by specifying two, potentially different, models. First, we use the sampled values $\theta ~\pi (\theta |\mathcal{O})$ to impute the missing data from p_θ(y_−r | y_r, r) some number M > 1 times. The model p_θ(y, r) is referred to as the imputation model. Next, an analysis model is specified to compute a point estimate ${\widehat{\psi }}^{(m)}$ and standard error ${\widehat{\sigma }}_{\psi }^{(m)}$ from each of the m = 1, . . . ,M completed datasets ${\mathcal{C}}^{(m)}$. Rubin’s rules (see Harel and Zhou, 2007, for a review) are then used to produce a point estimate $\widehat{\psi }$ and standard error ${\widehat{\sigma }}_{\psi }$. The imputation is referred to as congenial (Meng, 1994) when ${\widehat{\psi }}^{(m)}\approx E(\psi |{\mathcal{C}}^{(m)})$ and ${\widehat{\sigma }}_{\psi }^{(m)2}=\mathrm{Var}(\psi |{\mathcal{C}}^{(m)})$, in which case MI-based inference approximates fully-Bayesian inference. MI inference may be valid in the absence of congeniality, particularly when the analysis model is a sub-model of the imputation model. For further discussion of this issue, see Rubin (1996). For textbook level treatments of multiple imputation, see Rubin (1987) or Carpenter and Kenward (2012). For an exploration of impact of uncongeniality, see Daniels and Luo (2017).

Algorithm 2.

Multiple imputation algorithm for sequential explainability

1: procedure $\text{MI}(M,\mathcal{O},j)$	▷ Inference for μj using multiple imputation
2:  for m = 1,..., M do
3:   Sample $\theta ~\pi (\theta |\mathcal{O})$
4:   for i = 1,..., N do
5:    if $R_j^{(i)}=0$ then
6:     Sample $Y_j^{(i)}~p_{\theta }(y_j|{\overline{O}}_{j-1}^{(i)},R_j^{(i)}=1)$
7:    end if
8:   end for
9:   Compute ${\widehat{\mu }}_j^{(m)}=\frac{1}{N}{\sum }_{i=1}^N{Y}_j^{(i)}$.
10:  end for
11:  Compute ${\widehat{\mu }}_j$ and ${\widehat{\sigma }}_{\mu ,j}^2$ using the rules for combining inferences under MI.
12: end procedure

The imputation step for MI is operationally similar to the Monte Carlo integration used in Section 4.1, as it requires simulating from the same conditional distributions. Unlike Monte Carlo integration, MI only requires imputation of the missing data. Additionally, imputations can be used with different analysis models. MI is much more practical for large datasets than fully-Bayesian inference, at the cost of using an approximation. An MI-based algorithm for estimating μ_j = E(Y_j) under sequential ignorability is given in Algorithm 2

Extreme caution is required in using MI with partial restrictions in terms of what analysis models can be used. A minimal condition for MI to be valid is that the analysis model is a submodel of the imputation model. Hence, when a partial restriction is used, the analysis model should not identify any part of the joint distribution which is unidentified by the imputation model. For example, if a marginal restriction identifies the marginals p(y_j) but not the joints p(y_j, y_k), then the analysis model may also identify p(y_j) but must not identify p(y_j, y_k).

We remark that there are other approaches to sensitivity analysis which are applied with multiple imputation. One approach is the so-called “δ-adjustment” (Leacy et al., 2017; Van Buuren, 2012, Section 3.9.1) in which imputations are adjusted, say, by a location shift δ. This approach is ad-hoc and somewhat lacking in transparency regarding what assumptions it encodes about the missing data, but is highly appealing due to its simplicity. Graphical methods for conducting a tipping-point analysis are given by Liublinska and Rubin (2014).

5. Application to the Breast Cancer Prevention Trial data

We apply the working model approach described in Section 2.4, using an infinite product-multinomial mixture (Dunson and Xing, 2009) which is implicitly stratified by treatment,

$$p^{\star }(y,r)=\sum _{k=1}^{\infty }{\pi }_k\left\{\prod _{j=1}^J{\gamma }_{kj}^{r_j}{(1-{\gamma }_{kj})}^{1-r_j}\right\}\left\{\prod _{j=1}^J{\beta }_{kj}^{y_j}{(1-{\beta }_{kj})}^{1-y_j}\right\}.$$ (6)

In the context of missing data, Si and Reiter (2013) applied this model to conduct multiple imputation in large-scale survey data under MAR. For longitudinal responses, various improvements are possible. One shortcoming of this model is that it does not incorporate temporal structure; additionally, a model with dependence within the mixture components would likely perform better (Murray and Reiter, 2016).

We give ${\left\{{\pi }_k\right\}}_{k=1}^{\infty }$ the stick-breaking prior associated with the Dirichlet process (Sethuraman, 1994) ${\pi }_k=V_k{\prod }_{j=1}^{k-1}(1-V_j)$, $V_k\stackrel{\text{iid}}{\sim }\mathrm{Beta}(1,\alpha )$. We approximate this by setting V_K = 1 so that π_k = 0 for k > K. For the BCPT data, we set K = 50 and α = 1. We view this truncation as a computational concession, leading to an approximation of inference under K = ∞; as pointed out by a referee, one may instead view the truncated model as a model in its own right, which is parametric rather than nonparametric. We model ${\gamma }_{kj}\stackrel{\text{indep}}{\sim }\mathrm{Beta}\left\{{\rho }_{\gamma j}{a}_{\gamma j},(1-{\rho }_{\gamma j})a_{\gamma j}\right\}$ and ${\beta }_{kj}\stackrel{\text{indep}}{\sim }\mathrm{Beta}\left\{{\rho }_{\beta j}{a}_{\beta j},(1-{\rho }_{\beta j})a_{\beta j}\right\}$. For ρ_γj and β_γj we specify independent Uniform(0,1) priors. Finally, for a_γj and a_βj we use a uniform shrinkage prior, with density f_σ(a) = σ/(σ + a)² with scale σ = 15. Larger values of σ encourage heavier shrinkage of the β_kj’s and γ_kj’s towards their means. See Daniels (1999) and Wang et al. (2010) for motivation and details for the choice of this uniform shrinkage prior.

We use MCMC to draw samples of θ = (π, γ, β) from the posterior; details are provided in the supplementary material. We will focus our inference on the effect ψ = p(Y_J = 1 | Z = 1) − p(Y_J = 1 | Z = 0), where recall that Z = 1 corresponds tamoxifen and Z = 0 corresponds to the control. We consider four assumptions which identify ψ; the conditional distributions and algorithms needed are given in the supplementary material. First, we consider MAR by fitting the Y -marginal of (6) under ignorability. We also consider PMAR, sequential explainability, and the assumption

$$\begin{gathered} p(Y_J=1|R=r,Y_r=y_r) \\ =\frac{p(Y_J=1|R=\mathbb{1},Y_r=y_r)e^{\xi }}{p(Y_J=1|R=\mathbb{1},Y_r=y_r)e^{\xi }+p(Y_J=0|R=\mathbb{1},Y_r=y_r)}. \end{gathered}$$ (7)

Assumption (7) is a nonmonotone, exponentially-tilted, variant of the last-occasion restriction of Birmingham et al. (2003). We refer to it as the tilted-last-occasion restriction. In addition to the interpretation of the exponential tilting strategy in Section 3.3, the parameter ξ can be interpreted as a location-shift on the logit-scale,

$$p(Y_J=1|R=r,Y_r=y_r)=\mathrm{expit}\left[\xi +\mathrm{logit}\left\{p(Y_J=1|R=\mathbb{1},Y_r=y_r)\right\}\right],$$

where ξ represents the log-odds ratio of [Y_J = 1] relative to equivalent individuals with [R = r] and $[R=\mathbb{1}]$. We posit independent priors for ξ for each treatment; this has the effect of making the posterior variance of ψ large relative to dependent priors. Alternatively, one might take ξ constant across treatments to encode the belief that the effect of depression on missingness does not interact with treatment. To account for the fact that depression is expected to be positively correlated with missingness, we set ξ ~ Uniform(0,B). We set B = 0.8, corresponding to the belief that it is unlikely that the odds ratio of depression exceeds e^0.8 ≈ 2.2. The above specification is made for illustrative purposes and is highly stylized. For a more realistic specification which seriously engages with subject-matter expertise, see Wang et al. (2010), who elicited informative priors from four subject-matter experts about analogous sensitivity parameters ξ; none posited values of ξ larger than 0.8.

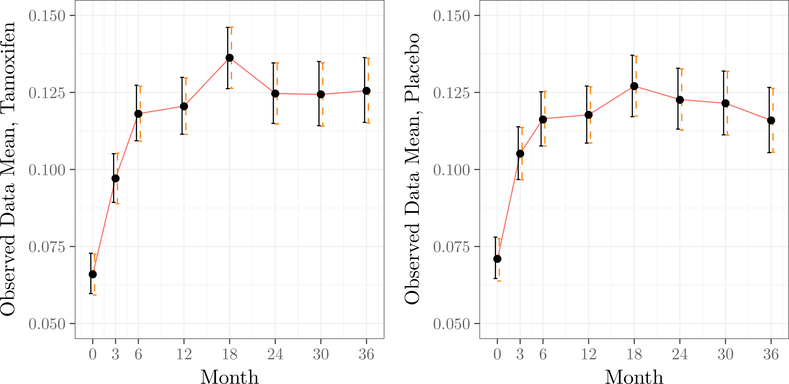
As a sanity check on the model, it is useful to verify that the posterior gives inferences which are consistent with the empirical distribution of the observed data. Let μ_obs,j = E(Y_j | R_j = 1). In Figure 1, we compare the inferences based on the posterior distribution of the μ_obs,j’s to the inferences that would be obtained from the standard model-free estimates ${\widehat{\mu }}_{\text{obs},j}={\sum }_{i=1}^N{Y}_j^{(i)}{R}_j^{(i)}/{\sum }_{i=1}^N{R}_j^{(i)}$. We see that the posterior means are essentially identical to the the ${\widehat{\mu }}_{\text{obs},j}$’s, and the posterior credible intervals agree with the model-free intervals.

Figure 1:

Observed data means over time for the tamoxifen and placebo arms of the study. Dots correspond to the posterior mean using the prior outlined in this section. The line corresponds to the empirical mean of the observed data for each time point. Solid error bars give the 95% credible interval for the observed data mean; dashed error bars given the usual 95% confidence interval based on asymptotic normality of the observed-data means.

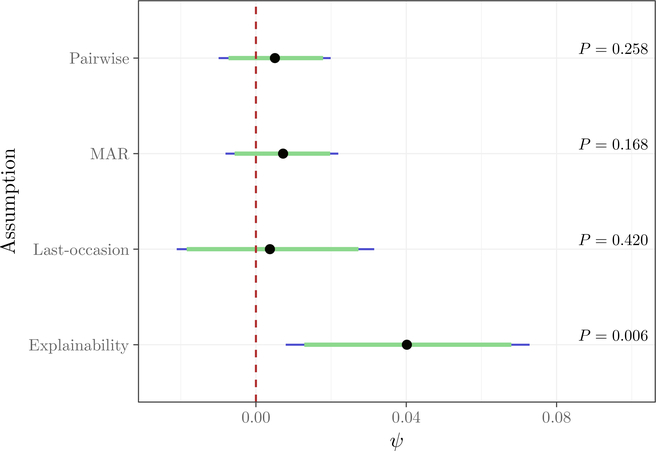
We report inferences for ψ obtained using the fully–Bayesian approach in Figure 2; results using multiple imputation with a nonparametric analysis model for p(y_J) are similar, and are given in the supplementary material, along with exact numerical results. The most striking feature is that inferences obtained under sequential explainability are very different from inferences obtained under either PMAR or MAR. First, the magnitude of the effect of tamoxifen on depression is much larger under sequential explainability; second, the posterior uncertainty is large. This is surprising, as one would expect the additional uncertainty in ξ to cause the tilted-last-occasion model to have the most posterior uncertainty.

Figure 2:

Posterior credible intervals for ψ under different assumptions. Dots give the posterior mean, green bars give two-sided 90% credible intervals, blue bars give two-sided 95% credible intervals. On the right, the posterior probability P = Pr(ψ < 0) is given for each assumption.

The additional posterior uncertainty can be explained from the fact that most of the missingness in the data was monotone. As a result, there is little information about $p(y_J|{\overline{o}}_{J-1},R_J=1)$ for most missingness patterns. On the other hand, there are many fully observed individuals, so there is ample data to estimate $p(Y_J|Y_r,R=\mathbb{1})$ for all patterns.

The fact that sequential explainability produces a larger effect size and leads to substantively different conclusions is concerning, and nessecitates an explanation. Further investigation revealed that, among those who were observed at the end of study, but who missed at least one visit (roughly 650 individuals per treatment), the difference in depression levels was a massive 6%. Moreover, this difference was highly significant, with Fisher’s exact test giving a P-value of 0.002. Under sequential explainability, those who were not observed at the end of the study are associated to this group, whereas under PMAR and the tilted-last-occasion model these individuals are associated to fully observed individuals. As there was no evidence of a difference in depression levels for fully observed subjects (P-value > 0.5 using Fisher’s exact test) the estimate of ψ is much smaller.

Whether PMAR or sequential explainability is more appropriate depends on subject matter considerations, as well as the causes of missingness. Regardless, the sensitivity analysis led us to find a treatment effect in a sub-population (those who were observed at the end of the study, but missed at least one prior visit) which is perhaps itself of interest. Hence, in addition to determining the robustness of our inferences, a sensitivity analysis can give substantive insight into the relationship between the missingness and the response.

6. Discussion and Open problems

In this paper we reviewed identifying restrictions with a focus on recent proposals for nonmonotone missingness. We also combined a flexible modeling approach for the observed data with a variety of identifying restrictions to analyze data from the BCPT.

Several interesting avenues of research exist. Auxiliary covariates are often used to impute missing outcomes under an assumption that MAR holds only conditional on these additional covariates. This is sometimes called A-MAR missingness. The inclusion of such covariates can create parameter interpretation problems (Daniels et al., 2014) for categorical outcomes. A proposal similar to that introduced here for continuous outcomes and auxiliary covariates can be found in Zhou et al. (working paper).

This paper has focused on missing outcome data. Handling missing covariate data is also of general importance (see, e.g., Ibrahim et al., 1999; Xu et al., 2016; Murray and Reiter, 2016). One approach to addressing this would be to specify joint Bayesian nonparametric models, along with identifying restrictions for the combined vector of outcomes and covariates. An interesting problem here is how to specify a parsimonious set of sensitivity parameters which will correspond to conditional distributions of both missing outcomes and missing covariates. Multiple identifying restrictions could be used for such analyses, similar to what was used in Linero and Daniels (2015) for different types of dropouts (see also Sadinle and Reiter, 2017b). Nonignorable missingness for more complex data-structures, such as longitudinal images or networks, remains an underdeveloped area. Much of what has been proposed here could also be used for causal inference. Kim et al. (2017) and Roy et al. (2016) propose Bayesian nonparametric approaches similar to ours in the context of causal mediation and marginal structural models respectively. We are also intrigued by the ICIN restriction as an anchoring assumption, and believe practical methods for performing inference under ICIN would be valuable.

There are few software implementations for conducting sensitivity analysis using identifying restrictions, especially when missingness is nonmonotone. The primary challenge lies in imputing the missing data from the appropriate conditional distributions, as this requires model-specific software. Our R implementation of the multinomial mixture model is available at www.github.com/arlinero/NiNBayes. Beyond this, we mention several tools available for sensitivity analysis. Bunouf et al. (2015) provide SAS and R code for implementing pattern-mixture models under monotone missingness and a Gaussian assumption. Scharfstein et al. (2017) provide the R/SAS package SAMON for implementing semiparametric models under monotone missingness. Outside of our proposed framework, proc MI in SAS now supports δ-adjustments using the MNAR option, and the SOLAS software package implements the tipping-point strategy of Liublinska and Rubin (2014).