Molecular determinants of epistasis in HIV-1 protease: Elucidating the interdependence of L89V and L90M mutations in resistance

Abstract

Protease inhibitors have the highest potency among antiviral therapies against HIV-1 infections, yet the virus can evolve resistance. Darunavir (DRV), currently the most potent FDA approved protease inhibitor, retains potency against single site mutations. However, complex combinations of mutations can confer resistance to DRV. While the interdependence between mutations within HIV-1 protease is key for inhibitor potency, the molecular mechanisms that underlie this control remain largely unknown. In this study, we investigated the interdependence between the L89V and L90M mutations and their effects on DRV binding. These two mutations have been reported to be positively correlated with one another in HIV-1 patient-derived protease isolates, with the presence of one mutation making the probability of the occurrence of the second mutation more likely. The focus of our investigation is a patient-derived isolate, with 24 mutations which we call “KY”, this variant includes both the L89V and L90M mutations. Three additional KY variants with back-mutations, KY(V89L), KY(M90L), and the KY(V89L/M90L) double mutation were used to experimentally assess the individual and combined effects of these mutations on DRV inhibition and substrate processing. The enzymatic assays revealed that the KY(V89L) variant, with methionine at residue 90, is highly resistant, but compromised in catalytic function. When a leucine to valine mutation at residue 89 is present simultaneously with L90M, a rescue in catalytic efficiency is observed. Molecular dynamics simulations of these DRV-bound protease variants reveal how the L90M mutation induces structural changes throughout the enzyme that undermine the binding interactions.

Introduction

Human immunodeficiency virus type-1 (HIV-1) infects nearly 40,000 new patients annually in the United States¹, where it is estimated that 1.1 million patients are living with HIV, while there are approximately 37 million infected patients globally². The current standard of treatment, highly active antiretroviral therapy (HAART), is comprised of several small molecule inhibitors to target enzymes that are critical to the life cycle of the virus^3–4. These viral enzyme targets include the reverse transcriptase, integrase, and protease. Due to the large viral load of untreated HIV-1 infections, relatively high viral replication rate, and the error-prone nature of the reverse transcriptase, drug resistant mutations may develop^5–7.

The HIV-1 aspartyl protease enzyme is a 99-amino homodimer (Figure 1B) that plays an essential role in viral maturation, making it a key drug target. The protease cleaves 12 nonhomologous sites on the HIV-1 gag and gag-pol polyproteins to release structural, enzymatic, and regulatory proteins that are required for viral maturation^8–10. At present, darunavir¹¹ (DRV) (Figure 1C) is the most potent of the FDA-approved protease inhibitors. While there are no known single amino acid substitutions in the protease that cause DRV to lose significant potency, high levels of resistance have been observed when multiple protease mutations are present¹². Primary drug resistant mutations, such as I50V and I84V, occur proximal to the active site and impact inhibitor binding by altering the direct interactions between the protease and inhibitor^13–15. In contrast, so-called secondary mutations, occurring distal to the active site, are thought to be compensatory¹⁶. One such example is the A71V mutation, a secondary mutation that, when observed in conjunction with I50V/L, acts to restore a balance between catalytic efficiency and inhibitor binding^17–18.

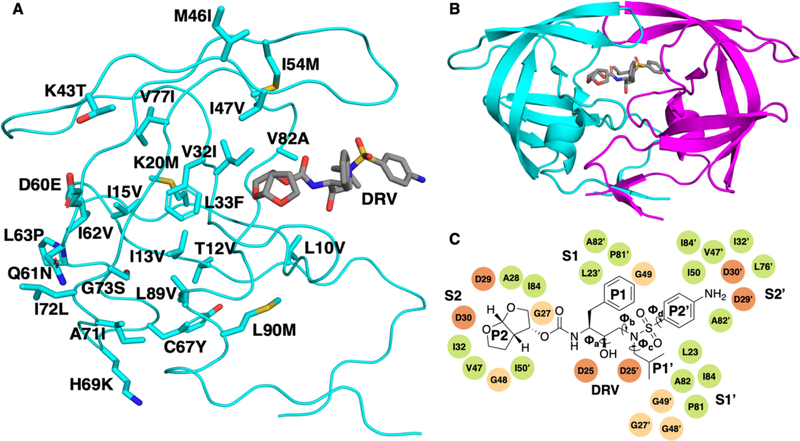
Figure 1.

(A) The 24 mutations of the KY variant (GenBank accession number: AY797430) mapped onto the structure of the HIV-1 protease monomer. (B) HIV-1 protease homodimer bound to DRV (represented in grey). Chain A is shown in cyan and chain B is shown in magenta. (C) 2D chemical structure of DRV with key dihedral angles labeled. These are the four dihedral angles that exhibited the greatest change between molecular dynamics simulations of the different KY variants. The residues corresponding to subsites S2 to S2′, where the different DRV moieties bind are labeled.

The HIV-1 protease has the astonishing ability to tolerate a large number of mutations while retaining sufficient substrate processivity of its cleavage targets. In the 99 residues sequence, 45 are previously reported of tolerating mutations¹⁹. When the effects of these protease mutations on viral fitness are additive, the relative fitness of a double mutant, for example, is equal to the sum of the relative fitness for each of the two individual constituent mutations. Of course, additivity may be generalized to include more than two mutations. In any case, epistasis is present whenever this additivity is violated. In such cases, the fitness effect of one mutation depends upon the presence or absence of one or more additional mutations and these effects can be described as “interdependent”. In the case of HIV-1 proteins, including the protease, the importance of epistasis has been confirmed on the basis of sequence prevalence^20–26 and large-scale fitness measurements²⁷. The fitness effects of mutations in the HIV-1 protease sequence may be decomposed into contributions due to free energy changes in monomeric folding, dimerization, binding of each substrate target²⁸ and inhibitor, along with changes in catalytic efficiency for each of the enzyme’s cleavage targets. While epistasis is known to be important for understanding evolution and the development of resistance in HIV-1 protease, however, insights related to any of these underlying details for specific epistatic interactions are rare.

In this study, we focus on a pair of amino acid substitutions within the protease, L89V and L90M, where non-additivity has been previously reported in HIV-1 subtypes B¹² and G^29–30 without being extensively characterized. The non-additivity of the L89V and L90M mutations in subtype B has been noted on the basis of a significant positive correlation between the two mutations in a large sample of HIV-1 protease sequences derived from subjects treated with a variety of protease inhibitors¹², suggesting an enhanced beneficial effect of the double mutant on the fitness of the virus under treatment by these drugs. This effect, however, could be due to changes in monomeric folding, dimerization, substrate binding affinity and specificity, catalytic efficiency, inhibitor binding or a combination of these properties. For the binding of darunavir specifically, analysis of large-scale binding assays also indicates that the non-additivity between mutations at residues 89 and 90 makes a significant contribution (Figure S1).

The L89V mutation in HIV-1 protease is a so-called accessory mutation that is present in patient-derived isolates and is associated with resistance to DRV inhibition^31–34. Likewise, the L90M mutation is associated with resistance to a variety of protease inhibitors, including atazanavir, indinavir, lopinavir, saquinavir, nelfinavir and darunavir^35–37. As with most other primary resistance-associated mutations in HIV-1 protease, L90M alone is not known to confer resistance against DRV^37–38. However, the L90M mutation has previously been reported to alter the geometry of the main chain of the D25 residue, causing a slight dislocation of the catalytic residue, thereby altering the protein-ligand interactions and dimer stability^39–40. The L90M mutation also has been shown to confer resistance to nelfinavir by perturbing the catalytic residues and the sidechain of residue 84, leading to a loss of affinity with the inhibitor⁴¹.

To study the interdependence of the L89V and L90M mutations, the consensus HIV-1 protease variant from a patient-derived isolate that exhibits little susceptibility to DRV inhibition provided a useful reference. As DRV binds wild-type (WT) sequences of HIV-1 protease with high affinity (<5pM)⁴², binding assays are generally not adequately sensitive to detect the relative impact of the L89V and L90M single amino acid substitutions. This patient derived resistant protease variant (GenBank accession number: AY797430) has 24 mutations⁴³ relative to the HIV1 protease subtype B consensus sequence (Figure S2)⁴⁴. For nomenclature convenience, this highly mutated resistant strain is referred to here as “KY”. Both the L89V and L90M mutations are present in the KY variant protease sequence, so constructs containing back-mutations at each of these residues were purified. These constructs are referred to as KY(V89L) and KY(M90L), respectively, along with a construct that had both mutations reversed, KY(V89L/M90L) that is henceforth referred to as “KY(DM)” for the sake of nomenclature compactness (Figure 1A). Based upon these protease constructs, we report an experimentally determined non-zero change in the relative free energy of inhibitor binding for the double mutant compared to that of the two single mutations: $J_{V89L,M90L}=\mathrm{\Delta }\mathrm{\Delta }{G}_{V89L,M90L}-\mathrm{\Delta }\mathrm{\Delta }{G}_{V89L}-\mathrm{\Delta }\mathrm{\Delta }{G}_{M90L}\ne 0,$ where $\mathrm{\Delta }\mathrm{\Delta }{G}_X=\mathrm{\Delta }{G}_{\text{reference}}-\mathrm{\Delta }{G}_X$ is the inhibitor binding free energy of protease with mutatio X relative to that of a reference strain $\mathrm{\Delta }{G}_{\text{reference}}=-RT\ln K_i^{\text{reference}}\text{and}{K}_i$ is the inhibition constant⁴⁵. From molecular dynamics (MD) simulations, the effects of these mutations on the structure and dynamics of the ligand-protease complex are characterized, along with an experimental assessment of substrate binding, catalytic efficiency, and DRV inhibition.

Materials and Methods

Protease gene construction.

Protease gene construction was carried out as previously described^46–48. In short, the protease variant genes were constructed using QuikChange site-directed mutagenesis (Genewiz) onto NL4–3 WT and KY protease on a pET11a plasmid with codon optimization for protein expression in Escherichia coli. A Q7K mutation was included to prevent autoproteolysis⁴⁹.

Protein expression and purification.

The expression, isolation, and purification of NL4–3, NL43(L89V), NL4–3(L90M), NL4–3(DM), and KY variants used for all assays were carried out as previously described^46–47. Briefly, the gene encoding the desired HIV protease was subcloned into the heat-inducible pXC35 expression vector (ATCC) and transformed into E. coli TAP-106 cells. Cells grown in 6L of Terrific Broth (TB) were lysed with a cell disruptor twice and the protein was purified from inclusion bodies⁵⁰. The inclusion body centrifugation pellet was dissolved in 50% acetic acid followed by another round of centrifugation at 19K for 30 minutes to remove impurities. Size exclusion chromatography was carried out on a 2.1-L Sephadex G-75 superfine (Sigma Chemical) column equilibrated with 50% acetic acid to separate high molecular weight proteins from the desired protease. The cleanest fractions of HIV protease were refolded into a 10fold dilution of refolding buffer [0.05 M sodium acetate at pH 5.5, 5% ethylene glycol, 10% glycerol, and 5 mM dithiothreitol (DTT)]. Folded protein was concentrated down to 0.5–3mg/mL and stored. The stored protease was used in kinetics and binding assays.

Kinetics assays.

Assays to measure K_M were carried out as previously described^13,51–52. Briefly, these assays were done in non-binding surface 96-well black half-area plates. All assays were conducted in 6% DMSO for wells 1–11 and 8% DMSO for well 12 with a total reaction volume of 60 μL. A natural 10-amino acid MA/CA substrate containing an EDANS/DABCYL FRET was 2/3^rd serially diluted from 0–40 μM in 2X assay buffer [100 mM sodium acetate at pH 5.5 and 200mM sodium chloride] and the appropriate DMSO concentration. The reaction was immediately initiated by the addition of 5 μL of 120 nM of HIV-1 protease (NL4–3, NL4–3(L89V), NL43(L90M), NL4–3(DM), and the KY variants) using a PerkinElmer EnVision plate reader. Fluorescence was monitored (excitation at 340 nm, emission at 492 nm) for 200 reads. An inner filter effect correction was applied as previously described⁵³. Substrate concentration points were globally fitted to the Michaelis-Menten equation (Figure S3) to obtain the K_M value for each respective protease variant.

Binding assays.

Assays to measure K_i were carried out as previously described^{13, 51–52}. Briefly, these assays were done in non-binding surface 96-well black half-area plates. All assays were conducted in 4% DMSO with a total reaction volume of 60μL. DRV was 3/5^th serially diluted starting from 2000 nM to 12nM, including a 0 nM inhibitor control. DRV was incubated for 1 hour with 0.35 nM HIV-1 protease for NL4–3 WT and NL4–3(L89V), 1 nM for NL4–3(L90M) and NL4–3(DM), and 5 nM for the KY variants prepared in 2X assay buffer [100 mM sodium acetate at pH 5.5 and 200 mM sodium chloride]. A 10-amino acid optimized substrate⁵² (Bachem) containing an EDANS/DABCYL FRET pair was dissolved in 4% DMSO to a final concentration of 120 mM. After the incubation period, the reaction was initiated by the addition of 5 μL of the 120 mM substrate to each well for a final concentration of 10 μM. Fluorescence was monitored for 200 reads using a PerkinElmer EnVision plate reader (excitation at 340 nm, emission at 492 nm). The concentration points were globally fitted to an equation for tight binding inhibitors using the “Morrison K_i” non-linear regression in the Prism 7 software (GraphPad Software, La Jolla, California U.S.A.).

p55 polyprotein cleavage assay.

The p55 cleavage assay was carried out as previously described¹³. Protein expression and purification was done as described by Bewley et al.⁵⁴. After expression, DNA was removed and p55^Gag-TEV-His was precipitated using ammonium sulfate. On the day of the assay, ammonium sulfate pellets were dissolved in resuspension buffer [10 mM HEPES at pH 7.5, 500 mM NaCl, 0.1 mM TCEP and 0.1 mM EDTA] and diluted 1:5 in resuspension buffer without NaCl. The solution was centrifuged for 20 minutes at 20,000 x g. For each protease variant (i.e. WT, KY or KY V89L), 2 μM of protease were added to 48.2 μM of p55 Gag polyprotein. Cleavage of p55 polyprotein by the HIV-1 protease of interest (NL4–3, KY, or KY(V89L)) was monitored by SDS-PAGE of cleavage products. Coomassie staining was used to visualize cleavage. Samples were taken in 10 μL volumes from the reaction mixture at designated time points. The reaction was quenched by adding 10 μL of gel running buffer containing SDS and boiling for 2 minutes. A molecular weight ladder was used. Samples of p55 alone (labeled “p55” on gel, see Figure S4) and protease alone (labeled “Enz” on gel, see Figure S4) were included for reference. Amprenavir, a potent HIV-1 protease inhibitor, was used as a negative control for the NL4–3 experiment. Darunavir was used as a negative control for the KY and KY(V89L) experiments. Gag cleavage by the protease of interest was monitored at 2, 5, 10, 15, 20, 30, 45, and 60 minutes for NL4–3 and 2, 5, 10, 15, 20, 30, 45, 60, 90, 120, and 180 minutes for KY and KY(V89L). Gel bands quantified by Amersham Imager 600 and analyzed by the software provided by the manufacturer. Only the upper band in the p55 lane was used for total p55 quantification. Minor bands are due to impurities and were not used in p55 qualification.

Molecular dynamics simulations.

As there were no crystal structures available for the KY protease sequence and related variants, homology models were used to generate initial coordinates for the molecular dynamics simulations. A homology model of KY that has previously been reported⁴⁸ was used to construct models for KY(V89L), KY(M90L), and KY(DM). For the simulations of the wild-type protease and its close relatives, high resolution crystal structures of NL4–3, NL4–3(L89V), NL4–3(L90M) and NL4–3(DM) co-crystallized with DRV were used (PDB: 6DGX, 6OOU, 6OOS, 6OOT) with crystallographic water molecules included. All starting structures were prepared using the Protein Preparation Wizard from Schrodinger⁵⁵. Missing atoms were added using Prime^56–57, and PROPKA was used to determine the protonation state of side chains at pH 7.0. The resulting structure was minimized under restraint to a convergence criterion of 0.3 Å using Impref.

All MD simulations were carried out in Desmond⁵⁸ with the OPLS3 force field⁵⁹ used for the inhibitor and protein. Simulated systems were prepared by placing the inhibitor-bound protein within a cubic TIP3P⁶⁰ water box measuring 12Å on each side. Chloride ions were used to neutralize the system and additional sodium and chloride atoms were added to reach a physiological 0.15 M salt concentration. Prior to production, each solvated system was relaxed using a series of restrained minimization stages⁴⁸. These stages consisted of successive minimizations with restraints on i) the heavy protein atoms, ii-iii) the protein backbone atoms and finally iv) no restraints. The restraining force constants were 1000, 1000 and 5 kcal mol⁻¹ Å⁻² for stages i), ii) and iii), respectively and the minimization was done using steepest descent followed with the limited-memory BFGS method to a tolerance of 0.5 kcal mol⁻¹ Å⁻¹. During unrestrained minimization, this tolerance was further reduced to 0.05 kcal mol⁻¹ Å⁻¹.

Unrestrained MD simulations were carried out in the isothermal-isobaric ensemble using a Langevin thermostat⁶¹ and barostat⁶² implemented within the “multigrator” framework⁶³ for integration of the extended dynamical system. The equations of motion were integrated using multiple time steps⁶⁴ for the short-range (2 fs) and long-range (6 fs) interactions with a 10 Å cutoff applied for non-bonded interactions. The smooth particle mesh approximation⁶⁵ to the Ewald sum was used to evaluate Coulombic interactions. Molecular dynamics for each system was carried out in triplicate, with each of the three 100 ns simulations starting with different randomized velocities. The root-mean-square deviation (RMSD) from the starting structures indicates that the simulations reached equilibrium after 20 ns (Figures S5 and S7). Configurations from the equilibrated part of the trajectories only were used for subsequent analysis.

Joint radial-angular distribution function.

The radial distribution function plays a central role in the study of simple fluids⁶⁶. For complex fluids where molecular directionality is important to understand their behavior, joint radial or radial-angular distribution functions can capture valuable information^67–68. In order to characterize the interdependence of inhibitor conformational sampling with that of the protease, a joint radial-angular distribution function $g_2(r,\varphi ),$ was calculated, where r was taken as the distance between selected atoms in the enzyme and ϕ was a selected dihedral angle for the inhibitor. The standard radial distribution function can be recovered by integrating the dihedral angle

$$g(r)=\frac{1}{2\pi }{\int }_0^{2\pi }{g}_2(r,\varphi )d\varphi ,$$

while the angular probability distribution function is

$$P(\varphi )=\frac{g(\varphi )}{2\pi }=2\rho {\int }_0^{\infty }{g}_2(r,\varphi )r^{2}dr,$$

and ρ is the number density for the selected enzyme atoms. Note that if one assumes that the system includes only a single enzyme molecule (no periodic replicas), then ${\lim }_{r\to \infty }{g}_2(r,\varphi )=0,$ as with atomic or molecular clusters⁶⁹. Here, specific pairs of C_α atoms were selected from the inhibitor (e.g. the C_α atoms from residues I50 and I84′). In this case, the integral of the radial distribution function is just $4\pi \rho {\int }_0^{\infty }g(r)r^{2}dr=1$: in the limit of long distances, there is a single tagged C_α atom apart from the one at the origin. Finally, a partial (or conditional) distribution for dihedral angles can be defined

$$P\left(\varphi ;r_l,rh\right)=2\rho {\int }_{r_l}^{r_h}{g}_2(r,\varphi )r^{2}dr,$$

representing the probability distribution for a specific inhibitor dihedral angle, given that the selected enzyme C_α atoms are separated by a distance that is bounded from below by $r_l$ and above by $r_h$

Jensen-Shannon divergence analysis of dihedral angles.

From the MD simulations, all protein dihedral angles, with the exception of the ⍵ angle, were measured over a range of −180° to 180°. The resulting dihedral measurements were used as input for the MutInf software package⁷⁰. The MutInf package can compute the Jensen-Shannon divergence⁷¹ (JSD), which measures the difference between two probability distributions. In applying the JSD to distributions of dihedral angles, it has proven useful to account for finite sample sizes by including a significance test and correction based upon an empirical null distribution⁷². This null distribution is defined via bootstrapping on blocks of samples from the simulation and controls for differences between the distributions that are within the noise associated with finite sampling. Here, the simulations were divided into six blocks and pairs of distributions were filtered out if they were not significant at the ɑ < 0.05 threshold: the JSD was set to zero in such cases and corrected otherwise. For visualization purposes, if a residue had multiple dihedral angles with a non-zero JSD, the greatest value was selected.

Protein crystallography.

The conditions consistently producing co-crystals of DRV bound to wildtype protease and single mutant variants were discovered and optimized as previously described¹³ Briefly, co-crystals for all variants were grown at room temperature by hanging drop vapor diffusion method in a 24-well VDX hanging-drop tray (Hampton Research) with a protease concentration between 1.2–1.6 mg/mL with 3-fold molar excess of DRV. Crystallization drops contained 1 μL protein-inhibitor solution and 2 μL reservoir solution consisting of 23–24% (w/v) ammonium sulfate with 0.1 M bis-Tris-methane buffer at pH 5.5. Drops were micro-seeded with a cat whisker. Diffraction quality crystals were obtained within 1 week. As data were collected at 100 K, cryogenic conditions contained the precipitant solution supplemented with 25% glycerol.

Data collection and structure solution.

Diffraction data were collected and solved as previously described¹³. Diffraction quality crystals of NL4–3, NL4–3(L89V), and NL4–3(L90M) were flash frozen under a cryostream when mounting the crystal to a Saturn 944 x-ray detector (Rigaku, USA). Diffraction data for the much smaller crystals of NL4–3(DM) were collected on the x-ray Operations and Research beamline 23-ID-D (with a mini-beam) at the Advanced Photon Source, Argonne National Laboratory. The co-crystal diffraction intensities were indexed, integrated, and scaled using HKL3000⁷³. Structures were solved using molecular replacement with PHASER⁷⁴. Model building and refinement were performed using Coot⁷⁵ and Phenix⁷⁶. Inhibitor was designed in Maestro and the output sdf file was used in the Phenix program eLBOW⁷⁷ to generate the cif file containing atomic positions and constraints necessary for ligand refinement. Iterative rounds of crystallographic refinement were carried out until convergence was achieved. To limit bias throughout the refinement process, five percent of the data were reserved for the free R-value calculation⁷⁸. MolProbity⁷⁹ was applied to evaluate the final structures before deposition in the Protein Data Bank (PDB). X-ray data collection and crystallographic refinement statistics are presented in the Supporting Information (Table S1).

Results and Discussion

While epistasis between the L89V and L90M mutations in HIV-1 protease has been previously reported¹², the changes in enzymatic structure, dynamics, and function that underlie this specific non-additivity are not understood. In order to study how the interdependence of the L89V and L90M mutations helps HIV-1 protease evade DRV inhibition, the patient-derived KY strain was expressed. Relative to the NL4–3 wild-type strain, KY has 24 amino acid substitutions, including the L89V and L90M resistance mutations (Figure S2). Three additional variants of KY were also expressed and purified, reverting the two sites of interest individually and together: KY(V89L), containing the L90M mutation but not L89V, KY(M90L), containing the L89V mutation but not L90M, and KY(DM) where both residues 89 and 90 were reverted to the NL4–3 sequence 89L and 90L.

Enzymatic activity, using both a fluorogenic peptide and Gag processing, and inhibition assays against DRV were carried out on these protease variants. Molecular dynamics simulations were performed to complement these assays with detailed information regarding the structure and dynamics of the DRV-bound complexes. As the KY variants proved difficult to crystalize, the simulations relied on homology models for starting coordinates⁴⁸. Inspection of the RMSD during these simulations indicates that the solution structures of these DRV-bound HIV-1 protease variants reached thermodynamic equilibrium (Figure S5).

The interdependency of L89V and L90M for binding and cleavage

For the KY protease sequence and each of its variants, along with the NL4–3 wild-type protease, the Michaelis-Menten constant (K_M), turnover number (k_cat) and the catalytic efficiency (k_cat/K_M) (Table 1) were measured using the MA/CA substrate sequence (see Materials and Methods). For all of the HIV-1 protease variants, with the exception of KY(V89L), the Michaelis-Menten constant, K_M, was unchanged, indicating that the affinity for the substrate is similar among the highly mutated KY variants and the NL4–3 enzyme.

Table 1.

Binding, kinetics and energetics of HIV-1 protease variants in complex with DRV. For each variant, the inhibition constant, K_i, Michaelis-Menten constant, K_M, turnover number, k_cat and mean protein-DRV van der Waals energy (from MD simulations), ΔE_vdW, is reported. The enzyme catalytic efficiency, k_cat/K_M, is also reported.

	NL4–3	KY	KY(V89L)	KY(M90L)	KY(DM)
KM (μM)	71.4 ± 6.8	74.4 ± 13.4	ND*	70.5 ± 30.0	77.0 ± 17.0
kcat (s−1)	1282.7 ± 0.06	220.6 ± 0.2	ND	47.7 ± 0.1	77.0 ± 0.01
kcat / KM (μM−1s−1)	17.1 ± 0.1	3.0 ± 0.2	ND	0.7 ± 0.4	1.0 ± 0.2
Ki (nM)	< 0.005	7.0 ± 0.1	24.1 ± 1.0	2.4 ± 0.1	2.4 ± 0.1
∆EvdW (kcal/mol)	-58.5 ± 0.4	-53.0 ± 0.5	-52.3 ± 0.6	-53.6 ± 0.6	-53.9 ± 0.6

^*ND = Could not be determined

In contrast to substrate affinity, the catalytic efficiency varied dramatically among the protease variants that were studied. For example, the turnover number, k_cat, and therefore k_cat/K_M decreases 6-fold for the KY variant relative to the NL4–3 wild-type (Table 1). This observation is consistent with the general trend that resistant protease variants tend to trade inhibitor evasion for some compromise of catalytic efficiency, at least for wild-type cleavage targets⁸⁰. For the KY(V89L) variant, kinetic measurements were beyond the sensitivity of our fluorescence assay, indicating a significant decrease in catalytic efficiency. Since the activity of the KY(V89L) variant could not be determined through traditional kinetics assays, which use a single cleavage site (MACA), a time-course gel assay that monitors the cleavage of full-length Gag polyprotein (p55) over time was used. This gel assay indicates that compared to the KY protease, full-length p55 cleavage by the KY(V89L) protease is approximately 3-times slower compared to KY (Figure S4), representing a fitness penalty for the virus. The cleavage of p55 in KY and KV(V89L) proceeds in the same order as it does in WT protease. The KY(M90L) variant, like KY and KY(V89L), exhibits a diminished turnover number, in this case k_cat is observed to decrease by 27-fold relative to NL4–3. The KY(DM) revertant variant, containing wild-type leucine amino acids at residues 89 and 90, also exhibits diminished catalytic efficiency compared with the NL4–3 wild-type protease, yet is more active than either of the KY(V89L) or KY(M90L) variants (Table 1). Taken together, these results suggest that the L89V mutation acts to “rescue” the enzymatic function of the protease in the presence of the severe catalytic penalty imposed by the L90M resistance mutation.

The L89V and L90M mutations were introduced in the NL4–3 wild-type background to study their enzymatic effects independent of the remaining 22 mutations that are present in the KY variant. Three variants were expressed and purified, NL4–3(L89V), NL4–3(L90M) and NL43(DM) containing both L89V and L90M. As was the case with the wild-type protease, our binding assay was not sensitive enough to accurately measure K_i for DRV binding when the L89V and L90M mutations were introduced, whether individually or together. Due to this limitation, we report that K_i < 0.005nM for this set of protease variants (Table S2). However, alterations in K_M and k_cat were measurable. The catalytic efficiency of the NL4–3(L89V) variant was reduced 57fold, relative to WT, with K_M increasing 1.5-fold and k_cat decreasing by 96-fold. This is a notable departure from the insensitivity of the substrate binding to this mutation in the sequence background of the KY variant. For the NL4–3(L90M) variant, the catalytic efficiency is dramatically reduced by 428-fold relative to wild-type (Table S2) as a result of 2- and 214-fold reductions in K_M and k_cat, respectively. When both L89V and L90M mutations are introduced to the wild-type sequence, however, the penalty in catalytic efficiency is attenuated compared with either mutation on its own: the double mutant exhibits a reduction of 2.5- and 12-fold, respectively in K_M and k_cat. The reduction in k_cat/K_M of the selected variants is driven by a reduction is catalytic turnover. In both the NL4–3 WT background and that of the highly mutated KY resistant variant, the L90M mutation reduces catalytic efficiency while the co-occurrence of L89V acts as a buffer on this effect and restores catalytic efficiency.

To further elucidate the non-additive nature of the L89V and L90M mutations and understand their co-occurrence, the inhibition constant, K_i, of DRV against several HIV-1 protease variants was determined using an optimized substrate (Table 1). As noted previously and elsewhere, DRV is extremely potent against WT protease (K_i < 0.005 nM). The inhibition constants for the KY variants, however, were measurable. While all of the KY variants were resistant to DRV inhibition, exhibiting an approximately 500-fold or greater increase in K_i compared with the NL4–3 WT protease, these effects were not additive. Indeed, the KY variant protease binds DRV about 3.5 times more tightly than would be expected under the assumption of additivity for binding free energies: using the definition from above for excess change in the relative free energy of inhibitor binding, $J_{V89L,M90L}=-{0.73}_{\text{kcal}/\text{mol},}\text{so}{e}^{-J_{V89L,M90L}/RT}=3.44$ The inhibition assays suggest that the L90M mutation provides virtually all of the resistance while both the catalytic assays and the time-course p55 cleavage assay suggest a compensatory role for the L89V mutation, specifically selected for by the KY variant to restore catalytic efficiency.

Alterations in enzyme and inhibitor fluctuations with resistant variants

While the kinetic assays provide insight into the end result of the mutations at residues 89 and 90, they beg the question: what are the molecular mechanisms that underlie the observed differences in catalytic efficiency and resistance? To expand on the insights gained from the kinetic assays, MD simulations were utilized to analyze the structure and dynamics of the studied DRV-bound protease variants. One way that MD simulations can be used to probe the binding of DRV in the protease active site is by interrogating the structural features of the enzyme and inhibitor, respectively.

Before comparing the per-residue root-mean-square fluctuations (RMSF) of C_α atoms among different protease variants, the suitability of the homology modeling for highly mutated variants was first validated by simulating a variant with 8 mutations relative to the NL4–3 wildtype. A series of three independent 100 ns simulations were carried out for this variant starting from either a homology model or an available x-ray crystal structure. Comparing the per-residue RMSF profiles from simulations initiated from the homology model or crystal structure revealed no significant differences (Figure S6), suggesting that any differences observed in these profiles for the KY variants and the NL4–3 wild-type are unlikely to be artifacts of homology modeling.

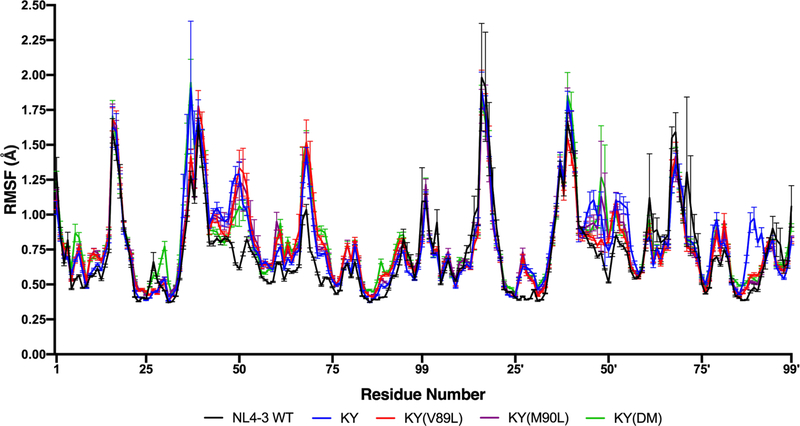
Examining the per-residue RMSF profiles of protease C_α atoms in the simulated DRV-bound systems listed in Table 1, reveals a modest but consistent overall increase among the KY variants versus the NL4–3 wild-type enzyme (Figure 2). More insight is gained, however, when the protein subdomains with the greatest increases in RMSF are identified. The most striking increases in RMSF among the KY variants as compared to the NL4–3 wild-type occur at the flaps, which control access to the active site of the enzyme. Specifically, residues 47–53 of the chain A flap and residues 43′−56′ of the chain B flap, which closely interact with DRV (Figure 1C), show increased RMSF in the resistant KY variants. The per-residue changes in protease C_α RMSF are not symmetric between the two monomers among the KY variants, with fluctuations increased in chain B relative to chain A at residues 16′−19′ (sometimes called the “fulcrum”), at residues 76′−84′ and at residues 25′−31′. Once again, these residues with increased fluctuations are proximal with the P2′ sulfonamide moiety of the protease-bound DRV molecule. In both monomers, fluctuations increased at the dimeric interface (residues 96–98/96′−98′) and the adjacent α-helix (residues 87–93/87′−93′), which includes residues 89 and 90.

Figure 2.

Root-mean-square fluctuation (RMSF) of C_α atoms for NL4–3 and the KY variants. Residues 48–52 in chain A flap exhibit the greatest fluctuations in the KY(V89L) variant and the least fluctuations in the NL4–3 wild-type protease.

To determine if the effects of the L89V and L90M mutations on flap dynamics are independent of the remaining 22 mutations in KY, MD simulations were carried out for DRV bound to NL4–3(L89V), NL4–3(L90M), and NL4–3(DM). After solving high-resolution (1.82–2.13Å) x-ray crystal structures for each of these variants (Table S1), the coordinates were used as starting points for the simulations (Figure S7). Wild-type protease and NL4–3(L89V) were solved in the same P2₁2₁2₁ space group with one protease homodimer in the asymmetric unit. NL4–3(L90M) was solved in the P2₁ space group with two protease homodimers in the asymmetric unit. NL4–3(DM) was solved in the P6₁ space group with one protease homodimer in the asymmetric unit. All co-crystal structures were solved with only one orientation of the bound inhibitor in the protease active site, which was crucial for direct comparison and analysis.

Consistent with the per-residue C_α RMSF profiles of the KY variants, NL4–3(L89V), NL43(L90M), and NL4–3(DM) all show a significant increase in flap fluctuations compared to the NL4–3 wild-type. Unique to the NL4–3(L90M) mutant is a drastic increase in fluctuation at residues 48–49 of the chain A flap and residue 52′ of the chain B flap (Figure S8). As with the KY background, the per-residue changes in C_α RMSF are not symmetric between the two protease monomers. Introducing the L90M mutation to the NL4–3 wild-type protease causes a significant enhancement in the fluctuations at flap residues 48–49 and 52′. This enhancement is not observed for the NL4–3(L89V) or NL4–3(DM) variants. Although these solution phase trends are not observed in the protein crystal due to packing effects, the correlations between RMSF from MD simulations of aqueous systems with x-ray crystallographic B-factors is high (Pearson’s r between 0.68–0.77) (Figure S9).

Contrary to previous reports^39–40, and consistent with our previous observations³⁸, no changes in the position of D25/D25′ were observed due to the presence of the L90M mutation alone. As noted above, however, the presence of the L90M mutation in the NL4–3 background is clearly associated with modulating the dynamics of the flaps. The effect of the L90M mutation on flap dynamics offers a more plausible explanation for the enzymatic penalties discussed above compared with previous reports, indicating that the longer methionine side chain perturbs the catalytic aspartate residues. Given that flap dynamics are essential for access to the active site and therefore substrate processing, and assuming that the increased fluctuations observed for the DRV-bound protease translate to the substrate-bound enzyme, our observation of increased flap fluctuations is consistent with our kinetics measurements.

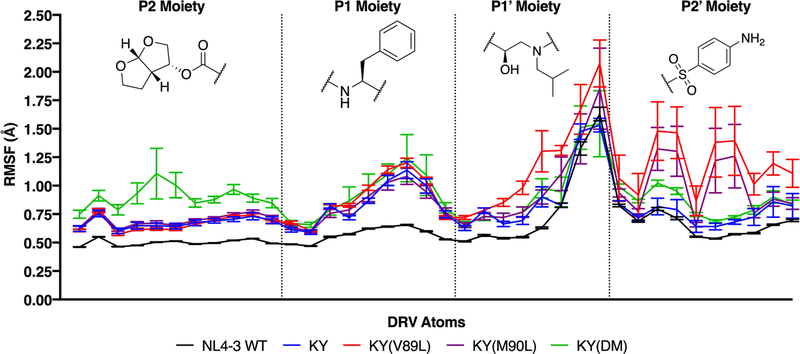
As with the enzyme, the fluctuations of DRV can provide insight into the changes in binding affinity that were observed among these HIV-1 protease variants. Compared with the NL4–3 wild-type protease, DRV exhibits greater fluctuations in all of the resistant variants, with the KY(V89L) variant showing the largest RMSF among those studied here (Figure 3). Note that the increase in RMSF for KY(V89L) is most pronounced within the P2′ sulfonamide moiety, whereas for KY(DM) a greater increase is observed within the P2 bis-tetrahydrofuran moiety (Figure 3).

Figure 3.

Increased inhibitor fluctuations correlate with decreased susceptibility. For DRV, the chemical structures of individual moieties shown along with the root-mean-square fluctuations (RMSF) for each of its heavy atoms. Each profile above corresponds to DRV in complex with a different HIV-1 protease variant. Averaging across each of these RMSF profiles gives: 0.63 ± 0.01 Å (NL4–3), 0.79 ± 0.03 Å (KY), 0.97 ± 0.09 Å (KY(V89L)), 0.88 ± 0.09 Å (KY(M90L)), and 0.91 ± 0.07 Å KY(DM).

Cross-correlation reveals alterations in flap/inhibitor motion in KY variants

Correlated motions within the inhibitor-bound complex can shed light on how mutations modulate the binding interaction, in addition to comparing the RMSF profiles. The examination of cross-correlation matrices for atomic fluctuations sampled during MD simulations is a well-established approach to identify collective motions in biomolecules^81–84. While analysis of cross-correlation directed toward identifying collective motions in proteins rests upon the correlations between all pairs of residues, for studying ligand-protein binding a restricted list of fluctuating atomic pairs may be more appropriate. In particular, examining the cross-correlations between the ligand heavy atoms and each of the protein C_ɑ atoms can make intuitive distinctions between strong and weak binding, with greater correlation between the ligand and proximal residues expected in the former case⁸⁵.

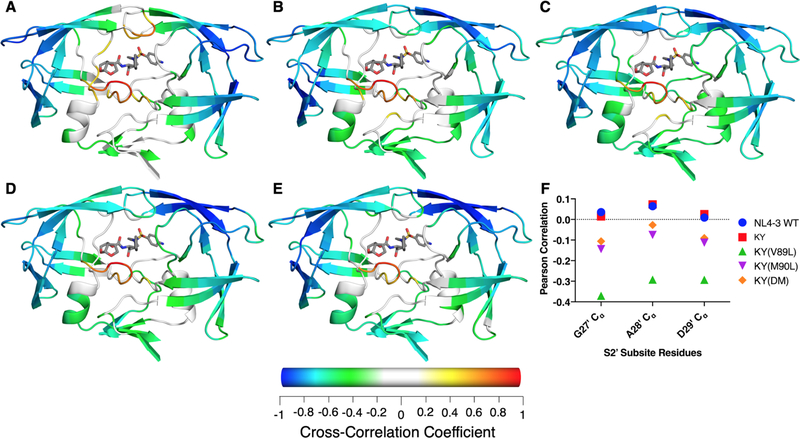
In the NL4–3 protease, DRV fluctuations are highly correlated with those of the active site, the S2 subsite, and flap tips, as previously observed⁸⁵ (Figures 4A and S10). In all KY variants, DRV fluctuations are anticorrelated with the chain A flap tip and exhibit little correlation with flap tip of chain B (Figure 4B–E). The cross-correlation for fluctuations of DRV and those of C_ɑ atoms in the S2 subsite (residues G27, A28 and D29) differs little among the KY variants and the NL43 wild-type. While the darunavir-protease cross-correlations observed for residues in the S2′ subsite (residues G27′, A28′ and D29′) are weakly negative for KY(M90L) and KY(DM) and weakly positive for NL4–3 and KY, those of KY(V89L) exhibit a moderate anticorrelation (Figure 4F).

Figure 4.

Average cross-correlation between fluctuations of C_α atoms and all DRV heavy atoms during the MD simulations. (A) NL4–3, (B) KY, (C) KY(V89L), (D) KY(M90L), and (E) KY(DM). C_α atoms with a Pearson correlation coefficient between −0.2 and 0.2 are colored white. (F) Unique to the KY(V89L) variant is an increased negative correlation with residues 27′ to 29′ in the S2′ subsite.

The presence of the L89V mutation in the NL4–3 wild-type background leads to a loss in correlation between DRV and both flap tips, while maintaining high correlation with the S2 subsite where the bis-THF moiety binds (Figure S11). The introduction of the L90M mutation in NL43(L90M) shows a moderate anticorrelation between the inhibitor and both ɑ-helices while maintaining moderate correlation with the chain A flap tip. In NL4–3(DM), bearing both L89V and L90M, DRV exhibits little correlation with the floor of the active site (residues 25–30/25′−30′) while maintaining moderate correlation with the chain B flap tip.

Residues 89 and 90 within the KY variant modulate the size of the active site.

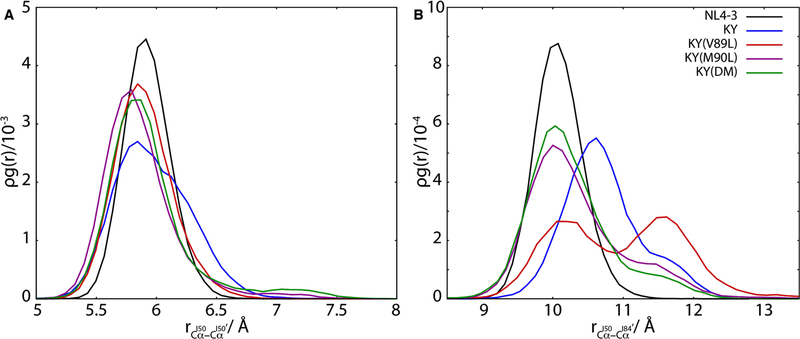
The opening and closing of HIV-1 protease flaps is essential for the mechanism of substrate processing and inhibitor binding. From crystallographic and computational studies, intermediate “semi-open” and “curled” states have been identified along the reaction coordinate that connects the open and closed states of the protease⁸⁶. Inter-residue distances measured between the C_α atoms of flap residues and non-flap residues within the catalytic pocket have been useful features for characterizing the pathway along the opening/closing reaction coordinate⁸⁶. In particular, the distance between the flap tips can be measured by the inter-C_α distance between residues I50 and I50′, while that between flaps and the pocket interior can be measured by the inter-C_α distance between residues I50 and I84′ (or I50′ and I84)⁸⁶.

Comparing the radial distribution functions for these atom pairs (Figure 5) reveals relatively subtle changes in inter-tip distances among the wild-type and KY variants (Figure 5A) and more striking changes in the distribution of distances between the chain A flap tip and chain B intra-pocket I84 residue (Figure 5B). The distributions for the KY variants centered at slightly closer inter-tip distances between the flaps, relative to that of the NL4–3 wild-type. The flap tips of KY exhibit a small shoulder in the radial distribution function at approximately 6.2 Å (Figure 5A), corresponding to a slightly opened conformation.

Figure 5.

Inter-residue distances near the catalytic site of HIV-1 protease are a gauge for inhibitor binding. The radial distribution function for the C_α atoms of residues I50 and I50′, shown in (A), exhibits an average shift to closer separations for the resistant variants relative to the wild-type NL4–3 protease. By contrast, the radial distribution function for the C_α atoms of residues I50 and I84′ (B) varies with resistance to DRV inhibition in these HIV-1 protease variants, with weaker binding variants visiting more open configurations.

The radial distribution function for the C_α atoms of residues I50 and I84′ is bimodal for the KY(V89L) variant, with one maximum at 10.25Å and another at 11.75Å. While the DRV-bound wild-type protease does not sample this expanded state around 11.75Å, all of the KY variants do so to differing degrees, with KY(V89L) showing the greatest density by far. The resistance-associated expansion of the catalytic site in these variants is therefore, best captured by the distance between residues I50 and I84′.

Jensen-Shannon divergence reveals alterations in hydrophobic sliding within the enzyme core

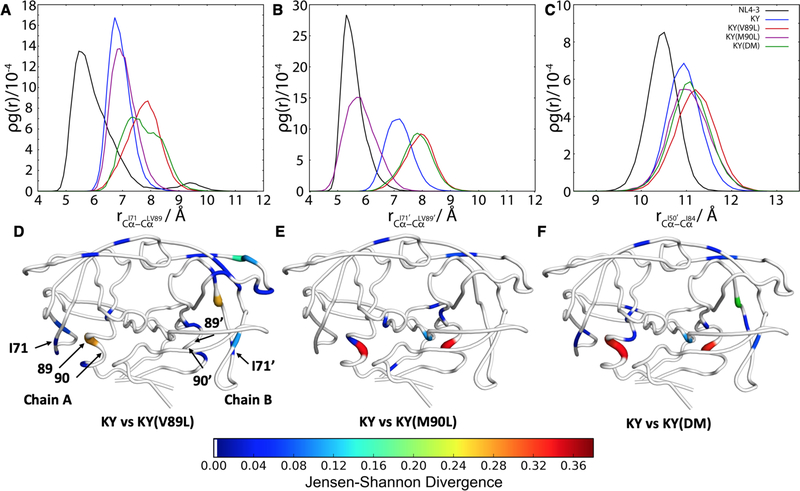
To characterize how the L89V and L90M mutations affect structural changes in the KY protease variants, the Jensen-Shannon divergence (JSD) was utilized to compare the equilibrium conformational ensemble of KY against that of KY(V89L), KY(M90L), and KY(DM) (see Materials and Methods). The JSD is a symmetric generalization of the Kullback-Leibler divergence with the property that it is bounded from above by ln(2) when (as here) it is defined using the natural logarithm⁷². By mapping how the equilibrium distributions differ between sequence variants for each dihedral angle throughout the protease, the strength of structural perturbations at residues distal to the mutations can be assessed. The JSD is sensitive to differences between two probability distributions, so can be significantly different from zero when the distributions differ in any number of ways, for example by a shifted mean value (i.e. a change in mean dihedral angle), width (i.e. a change in fluctuations), a more complicated difference in shape (e.g. a unimodal versus bimodal distribution) or some combination of these effects.

From examining the computed JSD between KY and KY(V89L) for the all dihedral angles, the effects of the L89V mutation are clearly visible throughout the protease, including the α-helix, 70’s loop and flap elbows (Figure 6D). The L89V mutation, located in the α-helix, induces structural changes at residue I71 (Figure 6D). By contrast, the JSD between KY and KY(M90L) (Figure 6E) or between KY and KY(DM) (Figure 6F) is greater within the α-helix and more muted elsewhere in the protease, like the 70’s loop and flap elbows. In using the JSD of dihedral angle distributions to compare KY and KY(M90L) particularly, alterations are detected at residues L24/L24′ in the active site, which may account for the observed 3-fold difference in K_i between these two variants. The situation is similar when the dihedral JSD is used to compare KY with the KY(DM) variant, where both residues 89 and 90 are different: there are mostly proximal changes. Importantly, residue L24′ in the active site samples a different conformation, which may account for the 3-fold difference in K_i between KY and KY(DM). The 70’s β-sheet is also affected when comparing these two variants, yet KY(DM) does not have increased fluctuations at the flaps compared with KY. This observation suggests that the L90M mutation is responsible for altering fluctuations at the flaps, while residue 89 negates those effects by acting on the 70’s β-sheet.

Figure 6.

Hydrophobic repulsion between I71 and L89 in KY(V89L) contribute to large fluctuations at chain A flap tip. Radial distribution functions are shown for selected C_ɑ atom pairs, including those of (A) residues I71 and 89, (B) residues I71′ and 89′, and (C) residues I50′ and I84. In (C), a slight flap opening is evident in all KY variants relative to the NL4–3 wild-type. (D) Jensen-Shannon divergence between KY and KY(V89L). For ease of visualization, only dihedral angles with a JSD above 0.01 are plotted. (E) Jensen-Shannon divergence between KY and KY(M90L). (F) Jensen-Shannon divergence between KY and KY(DM). PyMOL⁸⁹ was used for visualization. Tube thickness and warmer colors indicate larger perturbation of dihedral angles. Residues in white had no significant difference between the two variants.

These findings are directly relevant to the increased flap tip fluctuations and expansion of the catalytic site that are present in the KY(V89L) variant, mutations at residue 89, located in the hydrophobic core of the protein, have previously been reported to perturb hydrophobic sliding, thereby altering the flap motion^87–88. In addition, the side chain of residue 89 makes a van der Waals contact with residue 71, which modulates flap dynamics¹⁴. To further probe alterations in this key contact between the α-helix and 70’s loop, the distributions of distances between C_α atoms of residues 71–89 and 71′−89′ were measured in the MD simulations. The KY variants show an increased 71–89 distance compared to the wild-type, indicating a shift of the 70’s β-sheet and the α-helix away from one another. The KY(V89L) and KY(DM) variants, both of which have the wild-type leucine at residue 89, show the greatest displacement among the KY variants (Figure 6A). The steric interactions between the bulky side chains of residues I71 and L89 may be responsible for the differences observed in the dihedral angle distributions in KY(V89L) and KY(DM). On the B chain, the KY(V89L) and KY(DM) variants again show the greatest displacement compared with the remaining KY variants and the wild-type (Figure 6B). KY samples an intermediate distance between KY(V89L) and the wild-type. KY(M90L) samples the smallest 71′−89′ distance compared to the KY variants, while the NL4–3 wild-type samples the smallest 71′−89′ distance overall. Although KY(V89L) and KY(DM) sample an identical 71–89 distance distribution, only the chain A flap of KY(V89L) open up slightly as indicated by the increased I50-I84′ distance (Figure 5B). Despite 71′−89′ sampling a greater distance in the KY variants, the B chain flap does not open up as indicated by RMSF and all KY variants sampling a very similar I50′-I84 distance (Figure 6C).

Examining the differences in mean intra-protein C_ɑ-C_ɑ distances between KY and KY(V89L) emphasizes that the displacement observed in Figures 6A and 6B broadly involve secondary structure elements of the protease, with the 70’s β-sheet and the α-helix moving away from one another in the KY(V89L) variant (Figure S12). A similar alteration in the mean geometry of the 70’s β-sheet is observed when comparing the KY and KY(DM) variants (Figure S12). Also visible in the maps of differences in C_ɑ-C_ɑ distances between KY and KY(V89L) is the dramatic displacement of the chain B flap elbow (residues 38–39 and 42–43). This observation is consistent with the alterations in the dihedral angles of the flap elbow that were detected using the JSD (Figure 6D; Figure S13).

Coupled with the JSD analysis of the dihedral angle distributions, the increased 71–89/71′−89′ distances suggest that residue 71 plays an important role in modulating flap dynamics in the KY variants. Comparing the same variants, there are a number of changes at the chain B flap elbow, the opposite side from where we observe flap fluctuations. The changes at the flap elbows may ultimately serve to stabilize the B chain flap, preventing fluctuations of chain B flap tips.

Alterations in the protease due to mutations alter the interactions with DRV

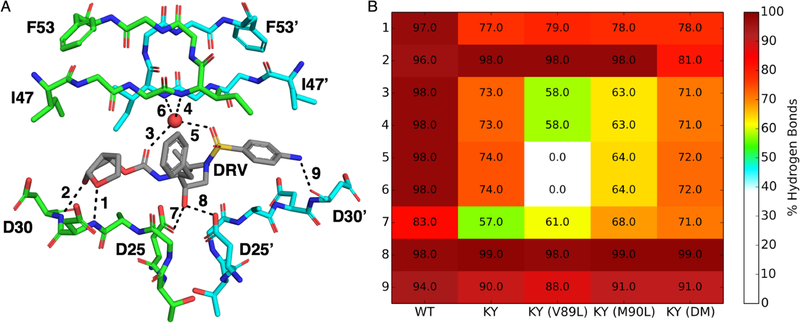
The binding of DRV is highly reliant on its ability to maintain key hydrogen bonds with the protease such that disturbing the hydrogen bonding network inside the active site can lead to reduced potency^90–91. The P2 bis-THF moiety is very important for potency and as such, NL4–3 shows a nearly perfect maintenance of the two hydrogen bonds that the bis-THF group is capable of forming (Figure 7). In contrast, the P2 bis-THF of all KY variants, with the exception of KY(DM), experiences a decrease in the hydrogen bond frequency with the backbone nitrogen of D29, while maintaining WT-like frequency with the nitrogen of D30. The decrease in the hydrogen bond frequency with D29 corresponds to increased sampling of the ϕ₁ DRV angle in KY(DM) as compared to NL4–3 and other KY variants (Figures S14 and S15A). As previously mentioned, all KY variants experience a decrease in hydrogen bonding with the catalytic residues, which is related to ϕ_a sampling a different conformation compared to NL4–3. The P2′ aniline maintains WT-like hydrogen bonding with the backbone oxygen atom of D30′ in the KY variants, despite ϕ₁₅ sampling a different conformation in the KY variants compared to NL4–3 (Figure S15O). KY and KY(DM) maintain nearly identical hydrogen bonding frequencies with the conserved flap water, 74% and 72%, respectively (Figure 7). In complex with KY(M90L), the water-mediated hydrogen bond with the sulfonamide moiety of DRV is reduced to 64%. In KY(V89L), the most resistant of the variants, the water-mediated hydrogen bond between the P2′ sulfonamide oxygen and backbone amide group of I50′ is not formed, while the water-mediated bond between the P2 bis-THF and the backbone amide group of I50 is maintained at 58% (Figure 7). In addition to disrupting the hydrogen bonding network with the flap water molecule, all KY variants have reduced van der Waals contacts with I50 and I47′, in the S2′ pocket, and the P2′ moiety of DRV (Figure S16).

Figure 7.

DRV-Protein hydrogen bonding network. (A) Monitored hydrogen bonds, shown on the NL4–3 structure (PDB: 6DGX), are indicated by a black line and numbered. (B) Heatmap of the frequency from molecular dynamics simulation for each numbered hydrogen bond in WT and all KY variants.

As anticipated from the measured inhibition constants, the mean DRV-protease van der Waals (vdW) interaction energy from the MD simulations is less favorable for each of the KY variants compared to the NL4–3 WT protease (Table 1). The changes in binding free energy and mean DRV-protease vdW energy are highly correlated with one another (Figure S17), with KY(V89L) having the least favorable mean vdW interactions among the studied variants (Table 1).

Mutations at 89 and 90 remotely modulate the conformational sampling of the inhibitor DRV

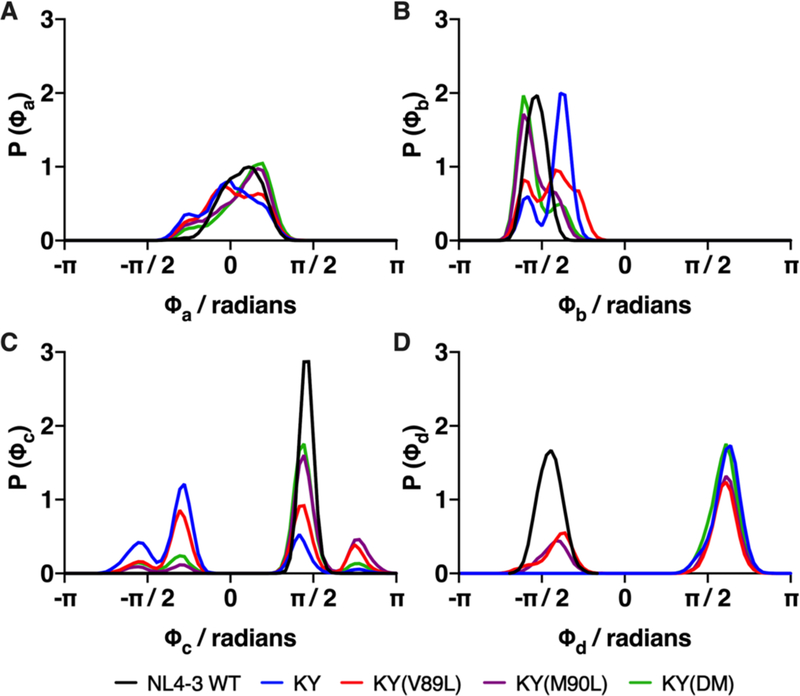
The binding mode of DRV in complex with the wild-type protease and the KY variants was characterized by monitoring the DRV dihedral angles during the MD simulations. All 15 rotatable dihedral angles in DRV were monitored, four of which exhibit striking changes among the variants. These four dihedral angles include those for the uncleavable hydroxyl group (ϕ_a), the C-N bond that defines the orientation of the P1′ and P2′ moieties together (ϕ_b), the P1′ moiety (ϕ_c), and the P2′ aniline group (ϕ_d) (Figures 1C, S14 and 15). The distribution about ϕ_a was similar in the KY and KY(V89L) variants (Figure 8), corresponding to similar hydrogen bonding frequencies between the DRV hydroxyl group and the catalytic D25 residue (Figure 7). By contrast, the distribution about ϕ_a in the KY(DM) and KY(M90L) variants was shifted to a slightly higher mean angle, corresponding to more frequent observation of a hydrogen bond between DRV and D25. This DRV-protease hydrogen bond is most often present in the NL4–3 wild-type (Figure 7), where the distribution of rotameric states about ϕ_a is further biased toward higher angles.

Figure 8.

Sampling of DRV dihedral angles of is sensitive to mutations at residues 89 and 90. Distribution of (A) the ϕ_a dihedral angle for the uncleavable hydroxyl group (see Figure 1C for definitions of DRV dihedral angles), (B) the ϕ_b dihedral angle, about which the P1′ and P2′ moieties together rotate, (C) the ϕ_c angle, about which the P2′ sulfonamide moiety rotates independently of the P1′ group and (D) the ϕ_d angle, about which the P2′ aniline group rotates.

The ϕ_b dihedral angle is important for defining the DRV binding pose, as it affects the orientation of both the P1′ and P2′ moieties (Figures 1C and S14). In the wild-type protease, the distribution about the ϕ_b angle is unimodal and peaked at −90°, corresponding to the optimal DRV binding pose. This ideal ϕ_b = −90° geometry is rarely sampled in any of the resistant KY variants, consistent with the weaker range of binding measurements reported here. Indeed, the distributions of ϕ_b sampled by the KY(M90L) and KY(DM) variants are similar, consistent with the observation that they have the same K_i (Table 1). The widest range of ϕ_b rotameric states and the largest angles are sampled by the highly resistant KY(V89L) variant. For KY(V89L), the most profound consequence due to the changes in ϕ_b is that DRV loses van der Waals contacts with G27′ and A28′, residing in the S1′ and S2′ subsites, respectively (Figure S16). This loss of favorable van der Waals contacts contributes to the anticorrelation noted above between the motions of DRV and those of the G27′ and A28′ residues in the KY(V89L) variant (Figure 4). Although the KY variant also samples larger values of ϕ_b, its distribution is altered from that of KY(V89L) and does not correspond to a loss of van der Waals contacts at G27′ or A28′. The very broad distribution of the ϕ_c angle indicates that the P1′ moiety in KY and its variants is more mobile than it is in the wildtype, an observation that is also apparent from examining the RMSF profile of the P1′ moiety (Figure 3). These fluctuations of the P1′ moiety, however, do not disrupt the van der Waals contacts at the S1′ subsite for any of the KY variants (Figure S16).

The ϕ_d dihedral angle is specific to the P2′ aniline group. The ϕ_d dihedral angle has a C₂ symmetry such that any of its rotameric states that differ by π radians (180°) are indistinguishable from one another, thus at thermal equilibrium, these two equivalent states should be equally populated. The simulations for the NL4–3 wild-type protease and began with ϕ_d at the bound-state energy minimum close to −82°, while those for the KY variants all began at the minimum in the “flipped” state. The P2′ aniline group was observed to interconvert between these two states in the KY(V89L) and KY(M90L) variants, indicating a lowered free energy barrier for these systems compared with KY, KY(DM) and the NL4–3 wild-type. Even in the relatively high entropy ϕ_d states for KY(V89L) and KY(M90L), the sampling between rotamers is not symmetric (the per-dihedral entropy, $S_j=-k_B{\sum }_i{P}_i\left({\varphi }_j\right)\ln P_i\left({\varphi }_j\right),$ is reported in Table S3), with the rotameric state near −82° both less populated and relatively lopsided compared to its counterpart at larger angles. This evident asymmetry is due to a coupling between different dihedral rotations in the inhibitor (Figure S18) and finite sampling.

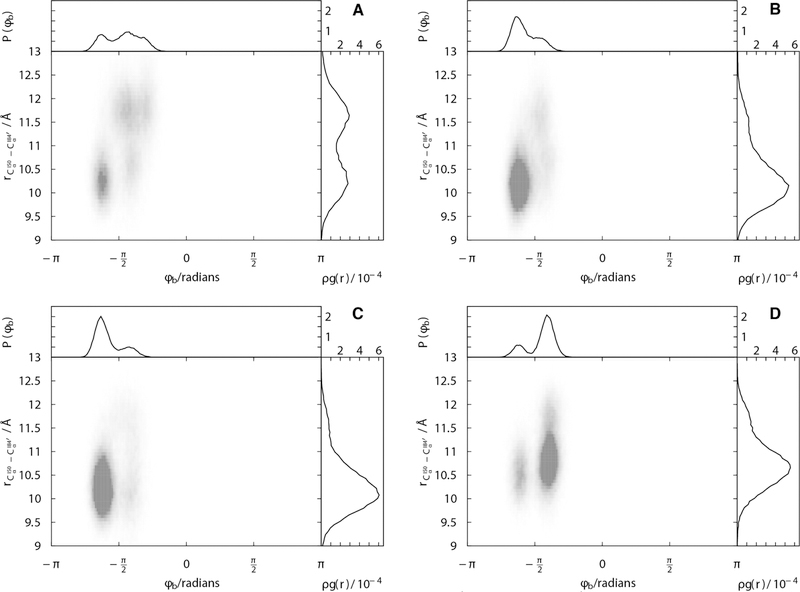
Insight into how resistance-associated changes in the geometry of the catalytic site relate to changes in the conformational sampling of the inhibitor can be derived from examining joint radial-angular distribution functions. Because the ϕ_b dihedral angle of DRV simultaneously measures changes in the positioning of the P1′ and P2′ moieties within the active site, it is informative to see how the distribution of ϕ_b reflects changes active site geometry, indexed the distance between residues I50 and I84′. The expanded catalytic site in the KY(V89L) variant, with the inter-C_α distance between residues I50 and I84′ centered around 11.75Å, is associated with a shifted and broadened distribution of the ϕ_b dihedral angle compared with the other variants (Figures 9A and S19). This broadness in the angular distribution of ϕ_b is associated with the weakened DRV binding measured for KY(V89L). In all KY variants there is a feature in the joint radial-angular distribution, $g_2\left(r_{C_{\alpha }^{I50}-C_{\alpha }^{I{84}^{\prime }}},{\varphi }_2\right),$ at shorter distance and ϕ_b near −5π/8 radians, evidently corresponding to a more tightly bound state (Figure 9B–D). Only in the KY(V89L) variant, is there substantial density in $g_2(r_{C_{\alpha }^{I50}-C_{\alpha }^{I{84}^{\prime }}},{\varphi }_2)$ at larger separations and ϕ_b near -π/4 radians.

Figure 9.

Joint radial-dihedral angle distributions, $g_2\left(r_{C_{\alpha }^{I50}-C_{\alpha }^{I{84}^{\prime }}},{\varphi }_b\right),$ capture the relationship between catalytic site opening and DRV conformational sampling. Joint distributions are shown for (A) KY(V89L), (B) KY(M90L), (C) KY(DM), and (D) KY.

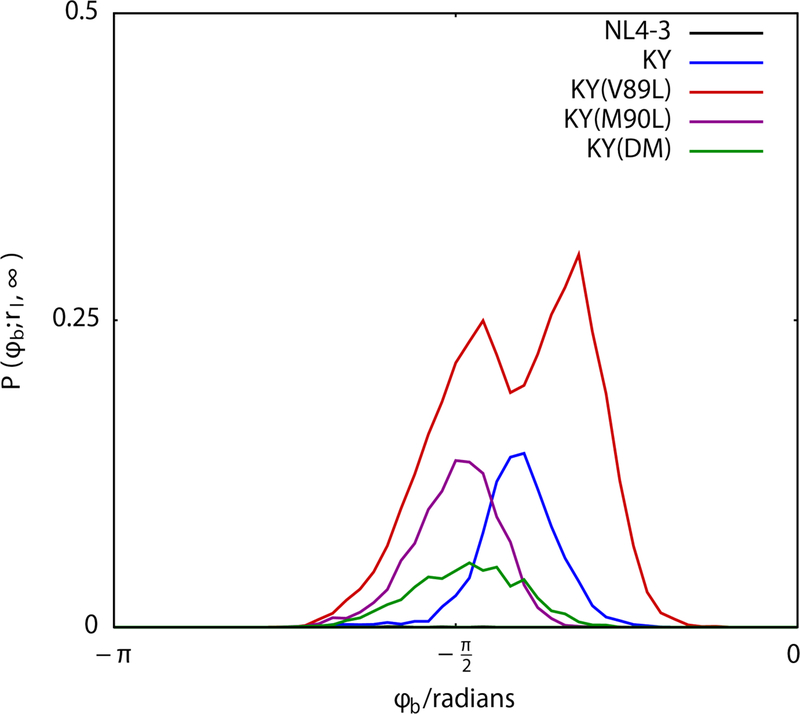
These differences among the KY variants become very clear when a partial distribution for the ϕ_b dihedral angle of DRV is examined, considering the conformational sampling for the inhibitor only when the catalytic site is expanded (Figure 10). Under expanded conditions (with the inter-C_α distance between residues I50 and I84′ greater than 12Å), KY(M90L) and KY(DM) both sample a single peak centered near dihedral angles of -π/2 radians, while KY(V89L) samples two peaks: one at -π/2 radians and another at -π/4 radians. In the KY variant, this partial distribution for the DRV ϕ_b dihedral angle has a single peak that is intermediate to those of KY(V89L), centered near −3π/8 radians.

Figure 10.

In KY(L89V), DRV samples rotameric states that are distinct from those sampled in other variants. The more “open” states of the HIV-1 protease catalytic pocket, characterized by $r_{{\text{C}}_{\alpha }^{\text{I}50}-{\text{C}}_{\alpha }^{\text{I}{84}^{\prime }}}\ge r_l=12\AA$ allow DRV access to a distinct state near -π/4 radians about the ϕ_b dihedral angle.

These observations can help explain the molecular mechanism by which the KY(V89L) variant loses the water-mediated hydrogen bond between the P2′ sulfonamide moiety and residue I50′. As the tip of the chain A flap fluctuates, expanded conformations of the catalytic site are accessed with the sulfonamide moiety rotated so that it is no longer able to form a hydrogen bond with the conserved crystallographic water molecule.

Conclusions

We have presented a detailed analysis of the interdependence between the L89V and L90M drug resistance mutations in HIV-1 protease. Based upon sequence prevalence in patient-derived isolates, the co-occurrence of these two mutations, both located in the alpha helix of the protease, has been previously reported as being more frequent than would be expected under the assumption of independent probabilities. Using as a test-bed an HIV-1 protease variant that is highly resistant to DRV inhibition (here called “KY”), measurements of K_i, K_M and k_cat were carried out on variants that had either L89V or L90M present, along with both or neither of these mutations. These measurements indicate that the L90M mutation provides resistance to inhibition by DRV, but at the expense of a dramatic loss in enzymatic efficiency. When combined with the L89V mutation, however, enzymatic efficiency is partly restored while maintaining much of the resistance to inhibition imparted by the L90M mutation. As K_M was similar among these variants, the observed effects on enzymatic efficiency are primarily driven by k_cat. This “rescue” effect of the L89V mutation for L90M were recapitulated in the widely-studied NL4–3 wild-type protease. Due to its susceptibility to DRV inhibition, however, measurements of K_i in the wild-type background were beyond the sensitivity of our assay.

Further insight into the molecular mechanism and interdependence of these two resistance mutations was derived from molecular dynamics simulations of DRV-bound protease variants. In the sequence backgrounds of both the highly resistant variant and the wild-type protease, the L90M mutation led to increased fluctuations of the flaps, an observation that suggests a loss of affinity for DRV, while the addition of the L89V mutation attenuated this increase in fluctuations.

Along with changes in the per-residue fluctuations of the protease, increases in fluctuations of the inhibitor provide a gauge of resistance. In the KY background, the L90M mutation led to a less tightly bound DRV that exhibited increased fluctuations, particularly at the P2′ moiety. These changes in fluctuations are due to an increased sampling of DRV dihedral angles, with the presence of L90M being associated with the broadest sampling of angles at the P2′ moiety. Examination of the joint radial-angular distribution function, $g_2\left(r_{C_{\alpha }^{I50}}-C_{\alpha }^{I{84}^{\prime }},{\varphi }_2\right),$ for an intra-protease distance that measures the size of the protease’s catalytic site and a key DRV dihedral angle, indicates that the inhibitor accesses distinctive rotameric states only when the catalytic site is expanded. This expansion of the catalytic site and concomitant conformational sampling of the inhibitor lead to a loss of water-mediated hydrogen bonding between residue I50 and the sulfonamide oxygen of DRV when L90M is present without L89V in the KY sequence background.

Finally, examination of the alterations in dihedral angles within the protease using the Jensen-Shannon divergence suggests that alterations in hydrophobic sliding due to the L89V and L90M mutations may modulate the fluctuations at the flap tips. In particular, in the absence of L89V, the L90M mutation causes changes throughout the structure of the DRV-resistant KY variant that encompass secondary structure elements both near and distal to the site of mutation, including an expansion of the catalytic site. In all other combinations, that is when only L89V is present, neither or both mutations are present, the changes to the structure of the protease are more localized and do not include a stable expanded state of the catalytic site.