Modeling cell–cell communication for immune systems across space and time

Abstract

Communicating is crucial for cells to coordinate their behaviors. Immunological processes, involving diverse cytokines and cell types, are ideal for developing frameworks for modeling coordinated behaviors of cells. Here, we review recent studies that combine modeling and experiments to reveal how immune systems use autocrine, paracrine, and juxtacrine signals to achieve behaviors such as controlling population densities and hair regenerations. We explain that models are useful because one can computationally vary numerous parameters, in experimentally infeasible ways, to evaluate alternate immunological responses. For each model, we focus on the length-scales and time-scales involved and explain why integrating multiple length-scales and time-scales in a model remain challenging. We suggest promising modeling strategies for meeting this challenge and their practical consequences.

Cells often communicate with each other to coordinate their behaviors, as seen in bacterial biofilms [1] and groups of immune cells. Despite the wide number of cell types and signaling molecules in nature, one can group quantitative models that describe cell–cell communication into a few classes, thereby raising the hope that synthesizing a generalized modeling framework that is applicable to any organism is a feasible goal. Immune cells, given their diversity of cytokines and distinct cell types, are ideal test beds for developing models of cell–cell communication [2, 3, 4∗∗]. In this article, we describe several classes of models that have so far been applied to immune systems, the lessons to be learned from them, and some major challenges that remain for modeling cell–cell communications.

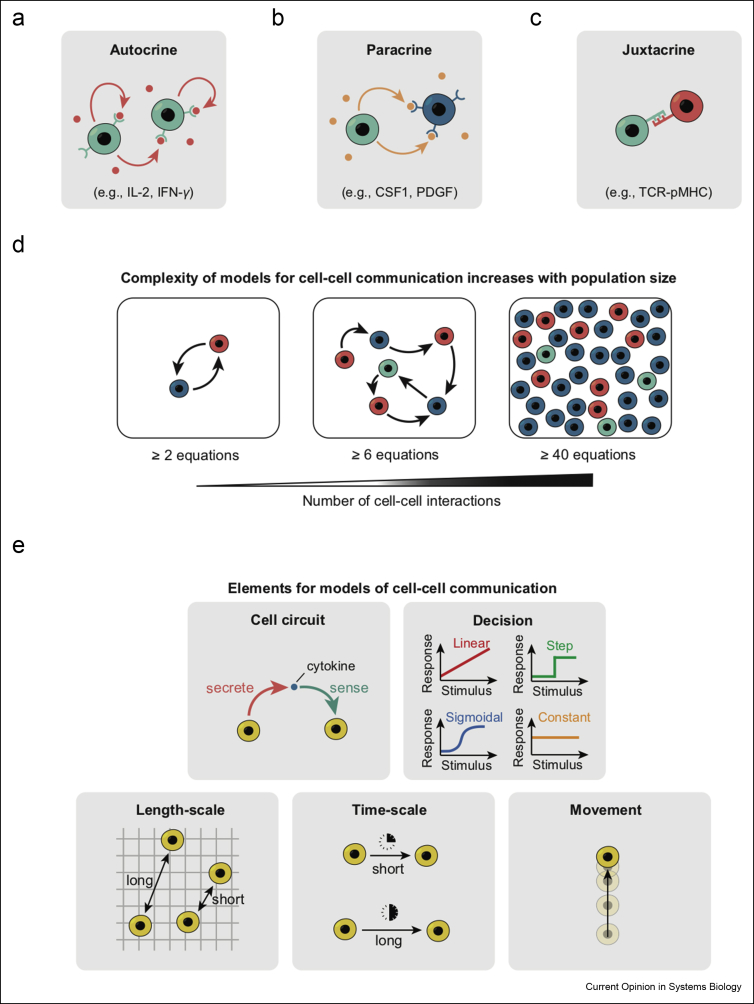
There are broadly three types of cell–cell communications—autocrine, paracrine, and juxtacrine signaling (Figure 1a–c). In autocrine signaling (Figure 1a) [5,6], a cell secretes a cytokine—such as Interleukin-2 (IL-2) [7,8] and Interferon-γ (IFN-γ) [9]—and also has the cognate receptor, thereby allowing the cell to communicate with itself and other cells of the same type [10,11]. Paracrine signaling involves at least two types of cells (Figure 1b)—one cell type, without the cognate receptor, secretes a cytokine such as the Colony-Stimulating Factor-1 (CSF-1) [12] and Platelet-Derived Growth Factor (PDGF) [13], whereas another cell type has the cognate receptor but does not secrete the cytokine. Juxtacrine signaling involves two cells in which one cell has a membrane-bound ligand (e.g., peptide-bound Major Histocompatibility Complex (pMHC)) and another cell has a cognate receptor (e.g., T-Cell Receptor (TCR) for pMHC) [14] (Figure 1c). Modeling an immunological process can be challenging because the process may involve any of the three types of communications, contain multiple cell types, and use multiple cytokines (Figure 1d). Even when an immunological process involves just a single cell type, if the spatial location of each cell matters, then the model would contain a total number of equations that scales up with the total number of cells involved (Figure 1d), thus leading to an unmanageably large number of equations even for a modest population size (e.g., 100 cells). Another complication is that cell–cell communication often spans vast length-scales, depending on the diffusion length-scale of each cytokine and the cells' motility (Figure 1e). Moreover, the time-scale at which cells respond to cytokines can vary and there can be a variety of responses to each cytokine (Figure 1e). A challenge then is to sift through the numerous equations and variables in a model to extract the core principles that guide the immunological process of interest. To put simply, a challenge is to reduce the complexity—the large number of parameters and the vast range of spatial and temporal scales—by going beyond exhaustive computer simulations of every cytokine and cell, to find what makes the immune system “work.”

Figure 1.

Ingredients for modeling cell–cell communication.(a) Autocrine signaling involves one cell type and cytokines such as IL-2 and IFN-γ. (b) Paracrine signaling involves at least two cell types, one that secretes a cytokine (e.g., CSF-1 and PDGF) without a cognate receptor and another cell type has the cognate receptor but does not secrete the cytokine. (c) Juxtacrine signaling involves at least two cell types communicating by a physical contact through a membrane-bound ligand (such as pMHC) and a receptor (such as TCR). (d) Models that describe communications among cells typically have as many equations as the number of cells involved. (e) Elements that enter a model for cell–cell communication. (Top left) Cell circuit that describes which cell secretes and which cell senses a cytokine; (Top right) Distinct responses to cytokines; (Bottom left) Distinct length-scales involved in cytokine-mediated communication; (Bottom middle) Distinct time-scales involved in cytokine-mediated communication; (Bottom right) cell motility.

Examples of modeling cell–cell communication in immune systems

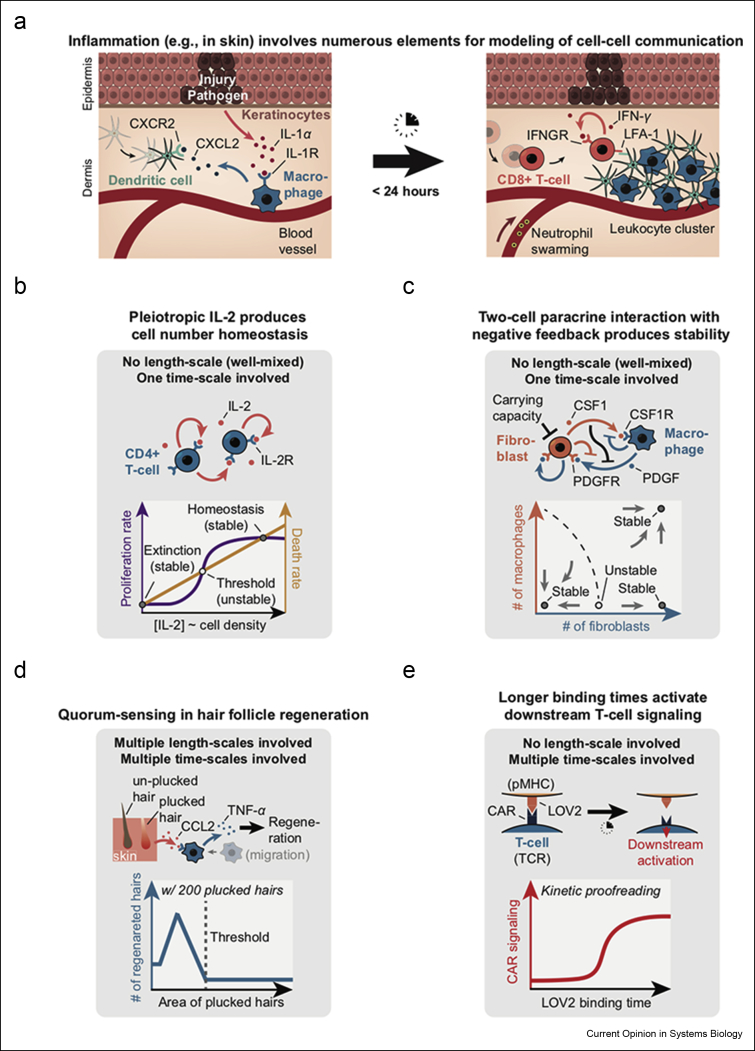
An immune system's primary task is to distinguish the antigens that belong to the body from those of foreign cells, to eliminate the invading pathogens. Eliminating pathogens typically involves several types of immune cells that coordinate their actions by communicating across wide spatial and temporal scales with myriad cytokines [15,16]. As an example, consider a skin inflammation that occurs because of the skin being injured or invaded by pathogens (Figure 2a) [17]. Here, keratinocytes that reside in the epidermis sense the invasion and then respond by secreting cytokines such as IL-1α. Upon sensing IL-1α, macrophages, which are strategically positioned close to the blood vessels underneath the skin, recruit other cells such as the dendritic cells, CD8+ T-cells, and neutrophils to the infected site. In this way, a short-range communication initially clusters nearby immune cells to halt the spread of pathogens, and a long-range communication results in initially distant immune cells being recruited to the site of injury to eliminate the trapped pathogens. A mathematical model that integrates all these processes, which does not yet exist, would likely enable one to determine whether there is any advantage to why certain parameters such as the secretion rate of IL-1α is set the way they are and how tuning such parameters may optimize the immune systems' response to skin infections.

Figure 2.

Case studies for modeling cell–cell communication in immunological processes.(a) Schematic showing skin injury by invading pathogens. Left panel shows the immunological processes that occur soon after the skin injury, and the right panel shows how the skin injury is repaired [17]. (b) Population density of murine CD4+ T-cells controlled by their secreted IL-2 that they sense with the receptor (IL-2R). IL-2 simultaneously controls the proliferation rate (purple curve) and the death rate (orange curve) as shown in the graph. The graph shows two population densities that can be stably maintained (nearly zero and a value below a carrying capacity) and one that can be unstably maintained (“threshold” value) [18,19]. (c) Stable and robust maintenance of a ratio between two population densities (densities of fibroblasts and of macrophages). Fibroblasts secrete the autocrine and paracrine growth factor CSF1 and express the receptor, PDGFR, to sense the PDGF and the receptor, CSF1R, to sense the CSF1. Macrophages secrete the paracrine growth factor, PDGF, and express the receptor, CSF1R, to sense the CSF1. The graph shows three ratios of population densities that can be stably maintained and one that is an unstable, steady-state ratio [20,21]. (d) Regeneration of hair follicles on mouse skin by quorum-sensing. Plucked, distressed hair follicles secrete CCL2 which is sensed by M1 macrophages that are in turn recruited to the distressed follicles. Then, macrophages secrete TNF-α which then activates regeneration of the distressed hair follicles. Graph shows the number of regenerated hairs (blue curve) as a function of the skin area from which 200 hairs are plucked—only high density (small area) leads to appreciable regenerations [30]. (e) Kinetic proofreading as a mechanism to explain how a T-cell can distinguish between self and foreign peptides. Top cartoon shows a schematic of a recent experiment in which the binding time of the CAR (TCR) to LOV2 (pMHC) was optogenetically controlled. Graph shows the downstream activation in T-cell (CAR signaling) occurring only when the pMHC-TCR complex lives longer than a certain threshold duration [43].

Several recent studies serve as insightful case studies for revealing design principles of immune responses by coupling mathematical models of cell–cell communication with experiments. In one study, researchers showed that an autocrine-signaling cytokine, IL-2, controls the population density of CD4+ T-cells (Figure 2b) [18]. IL-2 simultaneously promotes the T-cells' proliferation and death, which seems wasteful and, as the study's authors put it, paradoxical. But a mathematical model revealed why this dual action by IL-2 is beneficial. The researchers devised a minimal mathematical model that treats IL-2 as uniformly mixed (i.e., well-mixed) throughout the cell–culture medium, thus negating the need to treat any spatial arrangements of T-cells on the cell culture plate. The authors also focused on steady-state concentrations of IL-2 because they assumed that IL-2 diffuses much faster than response time of the cells. On the basis of their experiments, the model posits that increasing the IL-2 concentration nonlinearly increases the T-cells' proliferation rate (i.e., as a sigmoidal function of IL-2 concentration), whereas linearly increasing their death rate (Figure 2b, see graph). Because the cells' death rate is higher than their proliferation rate at low IL-2 concentrations, the T-cell populations go extinct when IL-2 is scarce. But the IL-2 nonlinearly increasing the proliferation rate entails that when the IL-2 concentration is above a certain threshold value (Figure 2b, see “threshold”), then the proliferation rate becomes higher than the death rate, which causes net proliferation of T-cells until their population density reaches and stabilize at a value—where the proliferation and death rates match—that is below the carrying capacity (Figure 2b, see “homeostasis”). Because IL-2 is secreted and sensed by the T-cells as an autocrine signal, the authors' model shows that when the T-cell population size is above a certain threshold value, then the population avoids extinction and its density is stably maintained at a level that is below the carrying capacity, which the authors then experimentally confirmed [18,19]. The mathematical model was useful because the authors could then arbitrarily tune the various parameters in their model—such as the death rate's dependence on IL-2—over a range that is too wide to be experimentally feasible. Through such a computational tuning of parameters, the authors could determine why the IL-2's paradoxical control is more beneficial for T-cells than having two separate cytokines—one to control the proliferation and another to control the death. Namely, having IL-2 control both processes is less error-prone for controlling a population density than having two separate cytokines [18].

As seen in the previous example, we can simplify models if the cytokines are uniformly mixed in the environment because one can then ignore any spatial arrangements of cells. In this case, the number of cells becomes just a single variable and thus the number of variables would not scale with the number of cells (Figure 2b). Taking this simplified approach, another recent study combined a mathematical model with experiments to show how two cell-types—fibroblasts and macrophages–that exchange two growth factors, CSF1 and PDGF, stably and robustly maintain a fixed ratio of their cell densities (Figure 2c) [20]. Here, PDGF and EGF are autocrine signals for the fibroblast, whereas CSF1 is a paracrine signal that macrophages sense. PDGF is a paracrine signal that the fibroblasts sense (Figure 2c—see cell circuit). Sensing these cytokines promotes the cells' proliferation. An important feature of this two-cell circuit is a negative feedback that constrains the fibroblasts’ growth. In addition, the receptors for CSF1 and PDGF are endocytosed after binding their ligands, with CSF1 inhibiting the PDGF production. As evident here, the numerous competing interactions (Figure 2c) challenge our intuition and thus necessitate a mathematical model to understand how the abundances of macrophages and of fibroblasts, which evidently depend on each other, would change over time. The authors' model, which assumes well-mixed concentrations of CSF1 and PDGF, revealed three possible ratios of macrophage-population density to fibroblast-population density that can remain stable over time (Figure 2c—see graph). For one such ratio, the fibroblasts and the macrophages are both abundant (Figure 2c—indicated by dashed line). In another, the fibroblasts are abundant, whereas the macrophages are nearly extinct. The final option is that both cell types go extinct [21]. Crucially, the model revealed that these ratios can be stable over time because of the negative regulations—the endocytosis of the ligand-bound receptors and the CSF1 and PDGF cross-inhibit each other. With a model that assimilates all parameters, the authors computationally screened all 144 possible circuit topologies that one can have with two cell types by assigning various values to each parameter. They then found that only 48 of the topologies allow a mixture of two cell types to stably maintain a ratio of the two population sizes for a wide range of parameter values, one of which is the circuit used by the fibroblasts and macrophages (Figure 2c). Such computational evaluations of myriad circuit topologies can help one determine whether a particular circuit topology that nature has chosen for an immune or other cellular system is optimal [22].

As the previous two examples suggest, stably maintaining population densities through cell–cell communication and, conversely, population size influencing T-cell signaling are important topics in immunology for which quantitative models can provide insights [23]. The effects of secreted cytokines can propagate across vast distances, in part because of the body's endocrine systems [23, 24, 25∗∗]. T-cells rely on signals from both their immediate surroundings (e.g., contact-dependent TCR) and more distant surroundings (e.g., diffusing IL-2) to distinguish multiple antigens [26]. Thus, discriminating body's own antigens from foreign ones often involves multiple cells. At times, an immune cell needs to sense multiple cytokines from cells far away (e.g., via the body's endocrine system) as in the case of cytokines controlling the proliferation of T-effector cells [27] or the survival of resting T-cells [28]. At other times, immune cells locally interact, by creating a local niche of diffusing IL-2 around themselves, as in the case of CD4+ memory T-cells controlling their proliferation and differentiation by interacting with their immediate neighbors [29]. Such local cytokine niches have a size that depends on the diffusivity of cytokines and the cytokine consumption rate of surrounding cells—together enabling sizes of 30–150 microns that surround a cytokine-secreting cell [25,32]. The involvement of niches and interaction among the different niches that may be far apart from each other necessitates models that explicitly treat the spatial arrangements of each cell.

Treating spatial arrangements of each cell often necessitates treating multiple length and time-scales because of the cytokines' diffusion and cellular response often taking different length-scales and time-scales. An example of such a model comes from a recent study that revealed how hair follicles on the mouse skin regenerate plucked hairs by using a complex form of quorum-sensing that involves cytokines and chemo-taxing cells on a scale of 1 mm [30] (Figure 2d). Here, the researchers discovered that a hair follicle regenerates its plucked hair if and only if enough of its neighboring follicles have lost their hairs. Namely, if the density of plucked hairs on a skin is above a certain value (Figure 2d—see “threshold”), then all the hair follicles in that region regenerate, whereas they do not regenerate otherwise (Figure 2d). The authors found that when one plucks a sufficient density of hairs on patch of skin, the damaged hair follicles secrete the chemoattractant, CCL2, which in turn recruits M1 macrophages to the damaged follicles and their nearby follicles. The macrophages then secrete TNF-α which then triggers the regeneration of plucked and unplucked hairs in a near millimeter-diameter field that encloses the damaged follicles. Deducing that the quorum-sensing acts over a millimeter-scale rather than on a microscopic scale required a mathematical model. The model treated hair follicles as points on a hexagonal grid and analyzed the steady-state concentrations of both the diffusible factors (CCL2 and TNF-α) and the diffusively moving macrophages. By eliminating the pointlike hair follicles at various locations hexagonal grid and then experimentally testing the resulting predictions, the authors established that the quorum-sensing occurs over a millimeter-diameter skin patch. As in the previous examples, the model was indispensable in revealing a design principle—quorum-sensing enables worthwhile hair regenerations to occur (i.e., only in major hair losses) while ignoring one or a few lost hairs.

Ignoring the spatial distribution of cells does not necessarily mean that the model is simple. A model for a single cell can be highly complex if it includes multiple signals as variables. For example, T-cells perform computations to combine multiple signals into a coordinated response [31, 32, 33, 34, 35], as recently modeled for CD8+ T-cells controlling their proliferation by linearly summing TCR-mediated juxtacrine signals and ligands bound to other receptors (e.g., CD27, CD28) [36]. Different types of cells may also compete for multiple signals in their shared environment as in the case of T-helper and T-regulatory cells that compete for the extracellular IL-2 and other cytokines [32,37].

A model with spatially distributed cells is complex because it typically has multiple equations to incorporate the short length-scale set by diffusing cytokines with larger length-scales set by the spatial arrangements of cells. Similarly, a model of signal transduction within a single cell that involves multiple time-scales can highlight the challenges in treating multiple scales [38]. An example is the modeling of kinetic proofreading—a mechanism by which T-cells are thought to distinguish a small difference in the amount of time that peptides (pMHC) on the body's own cells spend being bound to T-cell's receptor (TCR) from the amount of time that pMHC on foreign cells spend being bound to TCR [39,40] (Figure 2e). Originally, John Hopfield and Jacques Ninio proposed kinetic proofreading as a mechanism for accurately synthesizing desired biochemicals by avoiding thermodynamically allowed, undesired reaction pathways that are in the way [41,42]. Immunologists now believe that T-cells achieve kinetic proofreading by amplifying the small differences in the pMHC-TCR lifetimes through a cascade of biochemical reactions that are triggered by the pMHC-TCR complex. Each step of the cascade involves two competing processes of differing time-scales: (1) a relatively slow progression to the next reaction with a rate that increases with the half-life of the pMHC-TCR complex and (2) a relatively faster return to the starting point of the cascade. In short, this leads to longer lasting pMHC-TCR complex activating the T-cell's response rather than a higher number of pMHC-TCR leading to the activation (Figure 2e). A recent experiment that optogenetically controlled the half-life of the LOV2-CAR complex partly supports the idea that kinetic proofreading occurs in T-cells [43]. A separate study that selectively controlled the ligand-binding to TCR with light supports the idea as well [44]. These and other experimental results together with the model for kinetic proofreading can explain why a T-cell that encounters the myriad pMHCs that belong to the body remains inactive, whereas encountering a few rare foreign pMHCs would become active [45].

Outlook

Here we used examples from immune cells to highlight models of cell–cell communication that vary in complexity. Models with simplifying assumptions such as treating cytokines as well-mixed, which allows one to ignore spatial arrangements of cells, can yield valuable insights. But such simplifications cannot describe immune and nonimmune systems that involve mesoscopic numbers (tens to hundreds) of interacting cells for which spatial and temporal dynamics are important. There are currently few models that can describe such settings. Developing models that incorporate multiple length-scales and time-scales is an important future endeavor as such situations are ubiquitous in, for example, host–pathogen interactions and activations of immune responses.

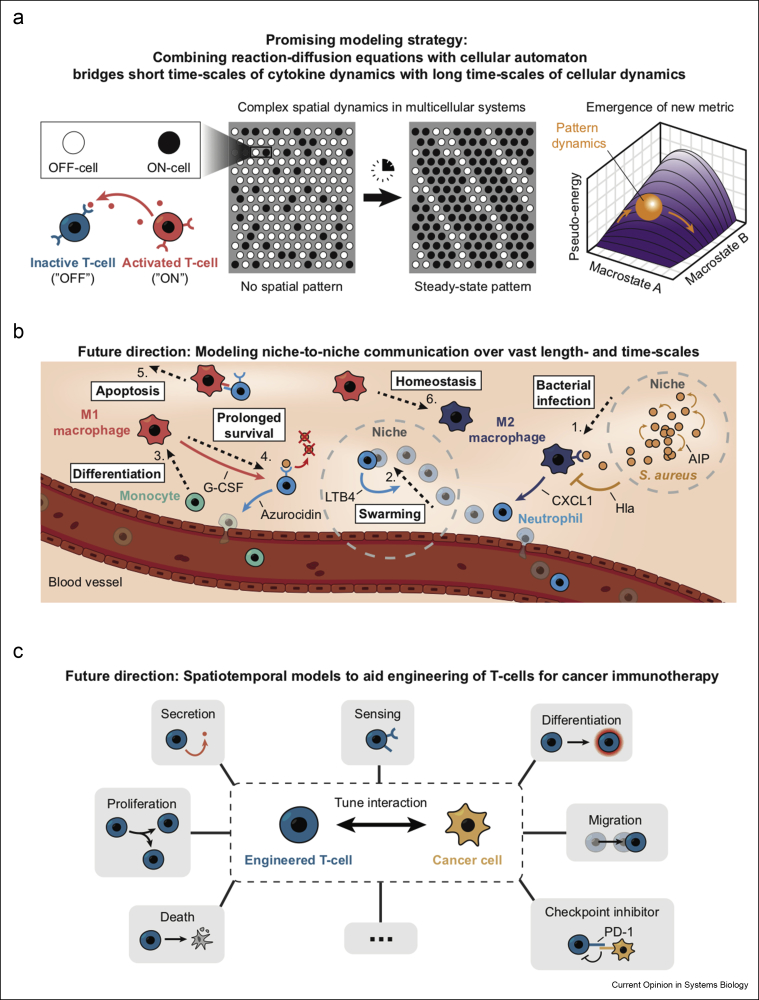
A promising strategy for bridging various scales of cytokine and cellular dynamics is combining reaction–diffusion equations—which describe short time-scales and length-scales—with cellular automata—which describe longer time-scales and length-scales (Figure 3a) [46,47]. Recently, researchers used such a hybrid model to show how mesoscopic numbers of cells use autocrine and paracrine signals to regulate each other's gene expression to form spatial patterns (Figure 3a) [46,47]. Here, the authors allowed the concentrations of secreted cytokines to momentarily reach steady-state values, which then caused each cell to respond to these cytokines by either secreting more or less cytokines, leading to new steady-state concentrations of the cytokines around each cell. The model then iterated this back-and-forth process until every cell and the cytokine concentrations reach their steady states (Figure 3a). Such hybrid models that combine cellular automata with reaction–diffusion equations can lead to new metrics for immune systems that reduce the number of parameters and thus the complexity of the system to just a few “macrostate” parameters, akin to the situation in statistical physics in which myriad microstates are reduced to a few macrostates. Such reductions can yield an emergent, predictive picture such as a ball (representing a field of communicating cells) rolling down a pseudo-energy landscape (a Waddington-like landscape for spatial patterns) until it sticks at a given location, which represents the final spatial pattern that the cells maintain.

Figure 3.

Prospects for modeling cell–cell communication in immune systems.(a) A promising modeling strategy for reducing complexity—combining reaction–diffusion equations and cellular automata. Schematics here summarize two recent studies [46,47]. Two cell types (OFF-cell and ON-cell) communicate via an autocrine-signaling cytokine (bottom left shows a paracrine signal that one of the studies [47] also treats). Two fields of cells are shown. On the left is a disordered field of cells that, after some time, becomes more spatially organized (right field) because of cells coordinating their gene expressions through cytokine-mediated communications. (Rightmost picture): This self-organization dynamics can be quantitatively mapped to intuitive dynamics in which a ball (representing a field of cells) rolls down a Waddington-like landscape whose shape is determined by the various parameters in the model (e.g., secretion rate of the cytokines) [47]. (b) Schematic showing an example of a multistep process—niche-to-niche communication—of the type for which no suitable models exist yet because multiple length-scales and time-scales are involved. Picture shows a step-by-step process (following the numbers in order) that occurs after Staphylococcus aureus infects the skin [49,52]. (c) Various ingredients, shown in each box, that go into engineering T-cells (e.g., CAR-T) for cancer immunotherapy. Quantitative models will likely provide blueprints for better engineering CAR-T cells [53, 54, 55].

Another challenge for the future is modeling immune systems in which cells move and interact across vast distances and involve multiple time-scales. Such phenomena include quorum-sensing bacteria invading a host [48,49], swarming neutrophils fighting the invading pathogens [50,51], and the series of cellular interactions that follow after bacteria (e.g., Staphylococcus aureus) infecting the skin (Figure 3b) [52]. In the case of S. aureus infecting the skin, various forms of cellular communication—including short- and long-range signaling (autocrine, paracrine, endocrine)—occur as well as multiple events that are spatially separate (indicated by dashed arrows in Figure 3b) [49]. A single model that incorporates all these processes and signaling events is currently lacking and thus, unlike in the examples mentioned in Figure 2, a design principle for this multistep phenomenon remains elusive.

A practical use of quantitative models for immune systems, which can yield design principles that tell us why certain topologies of signaling circuits are more beneficial than others, would be as a blueprint for engineering T-cells for cancer immunotherapy [53, 54, 55]. An important question now is how one can tune features such as secreting and sensing of cytokines, cell proliferation, apoptosis, differentiations, cell movements, and checkpoint inhibitors (Figure 3c). Finding optimal ways to coordinate these processes would benefit from a model that incorporates all these processes under one roof and may lead to more effective means to target cancer cells in CAR-T therapies.

Conflict of interest statement

Nothing declared.

This reviews comes from a themed issue on Systems immunology & host-pathogen interaction

Edited by Thomas Höfer and Grégoire Altan-Bonnet