Principles Governing Establishment versus Collapse of HIV-1 Cellular Spread

SUMMARY

A population at low census might go extinct, or instead transition into exponential growth to become firmly established. Whether this pivotal event occurs for a within-host pathogen can be the difference between health and illness. Here we define the principles governing whether HIV-1 spread among cells fails or becomes established, by coupling stochastic modeling with laboratory experiments. Following ex vivo activation of latently-infected CD4 T cells without de novo infection, stochastic cell division and death contributes to high variability in the magnitude of initial virus release. Transition to exponential HIV-1 spread often fails due to release of an insufficient amount of replication-competent virus. Establishment of exponential growth occurs when virus produced from multiple infected cells exceeds a critical population size. We quantitatively define the crucial transition to exponential viral spread. Thwarting this process would prevent HIV transmission or rebound from the latent reservoir.

Graphical Abstract

eTOC

Transition to exponential growth is a canonical mode of population establishment. For HIV spread among cells following latency disruption, Hataye et al. discover that this crucial transition occurs if the initial virus release exceeds a critical growth threshold, which can trigger HIV rebound.

INTRODUCTION

HIV persists in a latent state in long-lived CD4 T cells (Chun et al., 1997; Finzi et al., 1997; Wong et al., 1997). Despite in vivo suppression of de novo infection with combination antiretroviral therapy (ART) for many years, ongoing natural reactivation of latently-infected cells can still result in virus release in lymphoid tissue (Rothenberger et al., 2015), with a low viremia on the order of 2 HIV RNA copies per ml of plasma (Maldarelli et al., 2007; Palmer et al., 2008). When a treated HIV-infected individual stops ART, exponential HIV growth rebounds, usually within a few weeks (Davey et al., 1999).

During exponential growth, the rate of infection spread is directly proportional to the amount of virus present. Such kinetics have been modeled using ordinary differential equations (ODEs), leading to vital understanding of within-host HIV dynamics, including during the exponential phases of acute HIV infection (Ribeiro et al., 2010), viral decay following initiation of ART (Perelson et al., 1996, 1997; Wei et al., 1995), and rebound following ART interruption (Davey et al., 1999; Ruiz et al., 2000). In each study, the overall dynamic trajectory could be well defined using deterministic ODEs because the population of infected cells was large.

In contrast, starting from one infected cell, transition to exponential viral growth is not deterministic (Pearson et al., 2011). If a single infected cell produces virus, this virus might infect a nearby cell, which might eventually result in a sustained chain reaction of infection spread. Alternatively, viral extinction may occur at any early step. The process is highly stochastic, posing challenges for experimental capture and analysis.

To detect one latently-infected cell, resting CD4 T cells from HIV-infected donors on ART are activated and serially diluted into replicate cultures such that exponential viral growth occurs in just a small fraction of replicates. A stochastic model of the cell dilution series (Hu and Smyth, 2009; Rosenbloom et al., 2015) can be used to estimate the frequency of latently-infected cells that were originally placed in the replicate cultures and from which viral outgrowth ensued. Based on this, the latent reservoir has been estimated at ~ 0.1 to 10 cells per one million CD4 T cells in treated HIV-infected individuals with many years of viral suppression (Crooks et al., 2015; Siliciano et al., 2003). However, these rare cells from which outgrowth ensues are just a small fraction (~2%) of the total cells housing an intact HIV proviral genome (Ho et al., 2013). In fact, many such cells that initially do not result in viral outgrowth will do so if given more chances (Hosmane et al., 2017). The ex vivo latency reversal assay can also be executed as viral inhibition cultures by including ART, to quantify just the initial HIV release (Bui et al., 2016; Cillo et al., 2014). The events relating an infected cell, the virus arising from it, and transition to exponential viral growth are fundamental to latent reservoir quantification and the in vivo dynamics by which both acute HIV infection and rebound ensue.

The crucial process by which exponential HIV growth initially forms can be explicitly defined from ex vivo experiments coupled with stochastic computation. For stochastic sampling of probability distributions, Markov chain Monte Carlo algorithms (MCMC) were developed (Metropolis and Ulam, 1949) (Metropolis et al., 1953). An efficient MCMC featuring machine-automated tuning (Hoffman and Gelman, 2014) has been implemented in the statistical programming language Stan for Bayesian inference (Carpenter et al., 2017), and applied to HIV reservoir quantitation (Lorenzi et al., 2016). MCMC was applied in the 1970s to simulate chemical reactions (Gillespie, 1977). More recently Gillespie simulation has been applied to initial HIV replication (Pearson et al., 2011) and transmission (Rouzine et al., 2015), the persistence of the latent reservoir on ART (Conway and Coombs, 2011), and viral rebound following ART interruption (Hill et al., 2014). These theoretical studies have shaped our understanding of how a medical intervention might prevent HIV rebound or initial transmission, however they have mostly been based on extrapolation from the deterministic regime, sharply limiting their applicability to highly stochastic processes. The problem is not specific to understanding viral pathogenesis and remains a basic challenge for population biology across scale and context (Levin et al., 1997). Detailed data sets that feature variability among individuals are essential to discover the underlying processes that lead to successful population establishment from a single or just a few individuals.

Here we acquire time-series data of HIV release from infected cells to quantitatively define the transition to exponential viral growth. We document and model high variability in the timing and magnitude of the initial HIV release following disruption of HIV latency in viral inhibition cultures. Next, given an initial infecting population in the absence of ART, we document the probability of establishing exponential viral growth. We discover, by applying Bayesian inference to condition models on these experimental results, a synergistic de novo infection process that can be interpreted as a critical viral growth threshold.

RESULTS

Detection of Released HIV Following Latency Reactivation

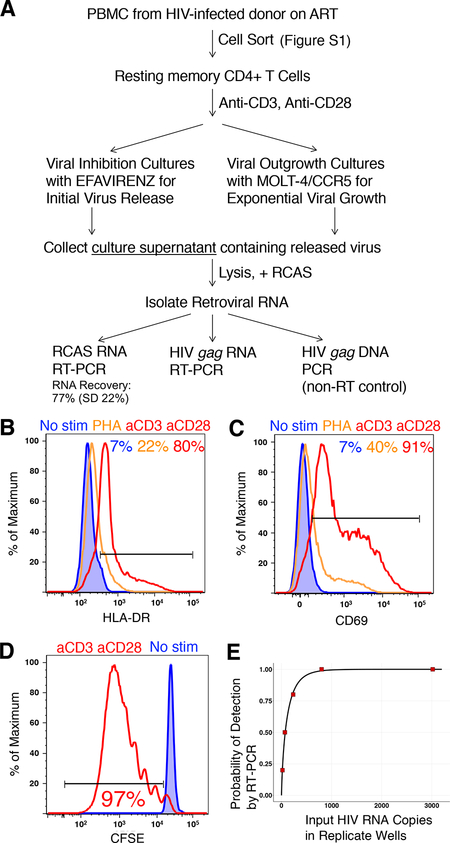
We sought to quantify HIV release arising from one infected cell (Figure 1A). Peripheral blood mononuclear cells (PBMC) from 7 HIV-infected volunteers on suppressive ART (Table S1) were sorted to obtain resting memory (RM) CD4 T cells (Figures 1A and S1). We compared stimulation methods for optimal HIV latency reversal. Consistent with prior studies (Beliakova-Bethell et al., 2017), we found stimulation through CD3 and CD28 was superior to PHA with regard to surface expression of the activation markers HLA-DR (Figure 1B) and CD69 (Figure 1C), and resulted in 97% cell proliferation after 8 days of culture (Figure 1D).

Figure 1. Detection of Released HIV Following CD4 T Cell Latency Reactivation.

(A) Experimental workflow.

(B and C) Resting memory (RM) CD4 T cells were cultured for 3 days with no stimulation, PHA, or stimulation through CD3 and CD28, and assayed for expression of HLA-DR (B) and CD69 (C).

(D) RM CD4 T cells were stained with CFSE and placed into culture for 8 days with or without stimulation through CD3 and CD28.

(E) Detection of ex vivo released HIV following serial dilution into new viral inhibition cultures with stimulated CD4 T cells from an HIV-uninfected donor.

To detect the initial HIV release without de novo infection, replicate cultures included efavirenz to inhibit reverse transcriptase. To instead allow for exponential viral outgrowth, cultures without efavirenz included MOLT-4/CCR5 cells (Baba et al., 2000) that are fully susceptible to HIV infection and rapidly proliferate. This provided an excess of standard target cells across replicate cultures with latent reservoir quantitation equivalent to that using ex vivo CD4 T cells as targets (Laird et al., 2013). We collected the culture supernatants for RNA isolation, and detected genomic HIV RNA by RT-PCR using primers specific for gag (Douek et al., 2002). Accounting for dilution factors during processing and retroviral RNA recovery experimentally determined for each replicate (mean 77%, standard deviation 22%) (Palmer et al., 2003), we estimated the total HIV RNA copies in the entire culture supernatant (Figure 1A). The assay limit of detection was empirically determined such that 70 HIV RNA copies in the entire culture supernatant could be detected 50% of the time (Figure 1E).

From released HIV, we performed single genome amplification of full-length env (Figure S2). The number of unique env clones sequenced from a replicate was consistent with input latently-infected CD4 T cell (LIC) number expectations given the frequency of HIV RNA positive replicates (Figure S2), as determined below. As expected, the env sequences segregated into distinct donor-specific phylogenetic families with considerable within-donor diversity.

The Timing and Magnitude of Initial HIV Releases, Each Arising from Reactivation of ~1 Latently-Infected CD4 T Cell, Are Highly Variable

We documented the timing and magnitude of the initial HIV release arising from 1 or more LICs in viral inhibition culture wells following reactivation. Daily supernatant sampling was followed immediately by a cell wash step, facilitating detection of subsequent releases of low magnitude. Consider a low frequency of reactivating cells that release detectable HIV RNA, 1/π, among C CD4 T cells placed into the culture on day 0. Then Λ = C/π is the expected number of LICs per replicate culture that give rise to detectable HIV RNA. We assumed that the exact number of LICs releasing HIV in a replicate, x, is Poisson distributed around Λ, and that the per infected cell probability of detecting released HIV RNA is independent of x. The probability P_det of detecting released HIV RNA in a replicate well is given by

$$P_{\mathit{\text{det}}}\left(\Lambda \right)=1-e^{-\Lambda }$$ [1]

Given P_det as the frequency of HIV RNA positive wells, Λ with 95% confidence intervals (CI) was estimated using Extreme Limiting Dilution Analysis (ELDA) (Hu and Smyth, 2009), an implementation of Equation [1].

We estimated Λ for each separate CD4 T cell dilution set across 5 human donors (Table S2). Ten of these sets consisted of a total of 225 viral inhibition culture replicates deemed at limiting dilution, with 42 replicates positive for HIV RNA (Figure 2A). Each of the 42 positive wells had a probability ranging between 77% and 96% (mean 87%) of having been seeded with exactly one LIC that gave rise to virus. This was calculated using the derived Λ given that each well was positive as (Poisson probability of exactly 1) / P_det. We estimated an expected total of 48 original LICs that gave rise to detectable virus by summing the product of Λ and the number of replicates for each of the 10 dilution sets. We observed an average detection of 2570 total HIV RNA copies per positive limiting dilution well. The total HIV RNA detected, time to first detection, and detection duration each varied considerably, with up to 7 days of sustained detection.

Figure 2. Kinetics of HIV RNA Release, and CD4 T Cell Proliferation and Survival, in Limiting Dilution Viral Inhibition Cultures.

(A) Detection of HIV release into supernatant (total in red bold), arising from latency reactivation in culture with efavirenz. Of 225 replicate cultures, just the 42 with detectable HIV (5 donors, with Λ ≤ 0.51, Table S2) shown with replicate index.

(B) HIV RNA signal decay in viral inhibition CD4 T cell culture.

(C) Following stimulation of CD4 T cells isolated from HIV-infected donors 3 and 9, the number of live cells is stable in culture.

(D) Day 5 proliferation profile following stimulation of CFSE labeled resting CD4+ T cells.

(E) ODE least-squares fit of cell division and death, assuming these rates are equal (Figure 2C), to the CFSE data in Figure 2D (ρ = μ = 0.48/d).

Detection of released HIV RNA (Figure 2A) reflects the balance of its production and decay. We quantified the HIV RNA signal decay in culture by transferring a primary ex vivo culture supernatant containing released HIV into new viral inhibition cultures with stimulated CD4 T cells from an HIV-uninfected donor. The HIV RNA signal decayed exponentially with a half-life (t_1/2) of 3 days (Figure 2B). With such a persistent HIV RNA signal, less than 20% of HIV RNA released during the 24-hour interval between samplings would have decayed by the time of the next daily sampling. Hence, the HIV RNA detected daily for a limiting dilution well only slightly underestimates the total virus production eventually arising from one LIC placed there on day 0. We conclude the timing and magnitude of the initial HIV production following reactivation of a LIC was highly variable.

Highly Variable Initial HIV Release Rendered by Stochastic Population Dynamics

We hypothesized that the high variability in initial HIV release (Figure 2A) arises from stochastic population dynamics. Consider a set of infected cells I, continuously producing HIV RNA V at rate p per cell before death at rate δ per cell. The average total release per cell is p/δ, and with a series of outcomes of one release event or cell death, the total release is geometrically distributed. The dispersion metric variance/mean (Fano factor, FF), for total HIV RNA detected (Figure 2A), was twice as high (5200, 95%CI [3200, 6700]) as that expected (2600) from a geometric distribution generated from the same mean. To build in dispersion consistent with the data, we considered additional model complexity (Figure 3).

Figure 3. Population Dynamic Models of Initial HIV Release Following Latency Disruption.

Circles represent cell compartments and arrows represent transitions. L is an initial latently-infected CD4 T cell (LIC) that can transition to one of two eclipse phases E, which can transition to a productive-infected cell state I that releases virus V at rate p, and dies at rate δ. V decays at rate c, and under viral inhibition, there are no new infections. Eclipse phase cells E divide at rate ρ and die at rate μ, and transition to the next compartment in series at rate a or b.

Model 1: Single-Compartment Latently-Infected Eclipse Phase

We introduced a compartment of stimulated LICs in a so-called “eclipse phase” E. These cells undergo cell division (Bruner et al., 2019; Hosmane et al., 2017) with rate constant ρ, die with rate constant μ, or activate with rate constant a to the productive virus releasing state I. The HIV RNA signal from released virus V decays with rate constant c = ln 2/t_1/2 (Figure 2B). These processes together comprise Model 1 (Conway and Coombs, 2011) (Figure 3A).

We derived estimates for ρ and μ from 2 experiments, under the assumption that the homeostatic characteristics of LICs are the same as their non-infected counterparts. We stimulated RM CD4 T cells isolated from 2 HIV-infected donors in viral inhibition cultures, and observed 12 days of overall population stability (Figure 2C). Hence, to a first approximation, on average ρ = μ. Next, we labeled RM CD4 T cells with CFSE. These cells were placed in viral inhibition culture for 5 days with stimulation, and then CFSE fluorescence intensity was assayed for the frequency of the population at each cell division generation (Figure 2D). To these data, we fit a birth-death ODE model (De Boer et al., 2006), and derived average rates for cell division and death, ρ = μ = 0.5 /day (Figure 2E).

We implemented our models (Figure 3) deterministically with ODEs and stochastically by direct simulation (Gillespie, 1977). Modeling accounted for daily virus dilution from sampling and washing (Figure 2A), the assay limit of detection (Figure 1E), lineage extinction without virus release, and a Poisson distributed initial number of LICs. Regardless of the initial number of LICs in Model 1, least-squares fitting of the ODE system with unknowns a, p and δ, did not recapitulate the experimental average HIV detection that included a sudden release of most virus around days 3–5 (Figures 4A and 4B).

Figure 4. Stochastic Population Dynamic Model 3 Recapitulates the Highly Variable Initial HIV Release.

Column 1 Indicates the Data Type for a given Row (A–E). Columns 2–5 show HIV RNA on each day (averaged over 225 wells), and histograms scaled to a maximum of 1 for Total HIV RNA Detected, Delay to First HIV Detection, and Detection Duration. Experimental HIV RNA detection data from Figure 2A (Red dots and histograms), ODE model fit (Blue curves), and stochastic model predictions (Orange histograms) are shown. D and p show Kolmogarov-Smirnov statistic comparing experiment and model with p-value.

(A) HIV RNA Detection from 225 viral inhibition wells at limiting dilution, from Figure 2A.

(B) Model 1 Fits. ρ = μ = 0.48/d, a = 0.40/d, δ = 0.40/d, p = 628/d, c = 0.22/d. f_HIV = 0.55 (For a single cell starting in compartment E, f_HIV is the probability of virus detection.).

(C) Model 2 Fits. ρ = μ = 0.48/d, a = 1.50/d, δ = 1.48 /d, p = 1423/d, c = 0.22 /d for n = 5 eclipse phase compartments. f_HIV = 0.40.

(D) Model 3 Fits. ρ = δ = 0.48/d, a = 1.54/d, δ = 1.38/d, p^A = 2166/d, c = 0.22/d, b = 0.75/d, p^B = 112/d, f_a = 10/d, f_b = 5.5/d, for n = 5. f_HIV = 0.41. This parameter set (Table S4) used for Figures 5–7.

(E) Model 3 Fits with ρ = μ = 0. a = 1.52/d, δ = 1.44/d, p^A = 5600/d, c = 0.22/d, b = 1.05/d, p^B = 112/d, f_a = 10/d, f_b = 15/d, for n = 5. f_HIV = 0.64.

(F) Model 3 simulations (with parameters in 4D) of 225 limiting dilution viral inhibition wells (Figure 2A), only the 42 on average that resulted in detectable HIV are shown. Each panel indicates L, the total high producer I^A, total low producer I^B, and simulated total HIV detected.

Model 2: Multi-Compartment Latently-Infected Cell Eclipse Phase

The experimental time delay to first HIV RNA detection, most frequently 3 days (Figure 4A), was not concordant with Model 1 in which the delay time 1/a is exponentially distributed with a maximum frequency at day 1 (Figure 4B). To reconcile this discrepancy, we extended the number of eclipse phase compartments from n = 1 for Model 1, to up to n = 10, with transition to the next compartment in series at rate a, to generate Model 2 (Kakizoe et al., 2015). We performed iterations of replicate stochastic simulations and ODE fitting of Model 2 (Figures 3B, 4C, and S3, Table S3). While n = 5 provided an excellent ODE fit to the average daily HIV RNA detection, the simulated distributions for total HIV RNA detected, delay to first HIV detection, and detection duration (Figures 4C and S3) were still not similarly dispersed as in the experiment (Figure 4A).

Models 1 & 2: Dispersion in Total HIV Released Modulated by Toggling

Consider the simplified case in which ρ = μ = δ = 0 with n = 1 eclipse compartment (Model 1). This is directly analogous to a model of constitutive transcription of RNA V from a promotor in which I designates the ON state, and E the OFF state. With δ = 0, the total V produced is Poisson distributed with FF = 1. A reverse transition at rate a_r from I to E allows toggling between the ON and OFF states (Raj and van Oudenaarden, 2008). Such E ↔ I toggling models “bursty” transcription from the HIV LTR promotor, and leads to a super-Poisson dispersion for total V released with FF ≫1 (Dar et al., 2012; Hansen et al., 2018).

For a productively infected cell I, we do not assume an infinite virus release lifetime with δ = 0. Rather, δ has been estimated on the order of 1 /day (Markowitz et al., 2003), and without toggling the total V distribution is geometric with super-Poisson dispersion. Introduction of toggling to this model led in Gillespie simulation to a decrease in the FF with sub-geometric dispersion. A likewise decrease in dispersion occurred when introducing toggling at E₀ ↔ E₁ or E₄ ↔ I in Model 2 with n = 5 eclipse compartments. Introduction of LIC division and death, ρ = μ = 0.5 /day, to such toggling models led to a small increase in the FF that was insufficient to explain the high dispersion in total HIV detected. To generate high dispersion in a toggle model while fitting the ODE implementation, we had to assume unrealistic rates with ρ₄ > μ₄, such as ρ₄ = 3 /day and μ₄ = 0.5 /day, or ρ₄ = 2.6 /day and μ₄ = 0.1 /day. These parameter sets represent extreme contrasts to that derived from experiment (i.e. ρ₄ ≫ 0.5/day, Figures 2C–2E). Adhering to realistic rates for CD4 T cell division and death, we conclude that toggling cannot fully account for the high variability in total HIV detected.

Model 3: Distinct Dual Latently-Infected Cell Eclipse Phases

With or without toggling, Model 2 yielded a unimodal distribution for total HIV RNA detection (Figure 4C) whereas the experimental distribution was bimodal (Figure 4A). Detailed comparison indicated that Model 2 simulations lacked detections that were simultaneously less than 250 HIV RNA copies, of duration less than 1 day, and with a greater than 4-day delay to first detection; i.e. replicates 210.11, 210.12, 210.13, 211.23, 224.06, 236.48, 236.75 (Figure 2A). To account for the missing population, we introduced an eclipse phase B (Figure 3C), with parameters fixed to yield delayed releases of low magnitude and short duration. We obtained a parameter set that resulted in accurate simultaneous recapitulation of the data from the deterministic ODE system and the stochastic simulation (Figures 4D and 4F, and Table S4). With this parameter set and starting from exactly one LIC (L = 1), f_HIV, the fraction of simulations with a detectable HIV release, was 0.41, with a fraction 0.59 going extinct during the latent eclipse phase, or with virus release below the detection limit. Based on this, we inferred that the initial number of LICs in the 225 limiting dilution wells (Figure 2A) was ~ the 48 that gave rise to detectable virus divided by 0.41 = 117. The simulated distributions for total HIV RNA detected (mean = 2560, and FF = 5380), delay to first HIV detection, and detection duration (Figures 4D and 4F) were consistent with experiment (Figures 4A and 2A). Simulated distributions predicted trends for the non-limiting dilution cultures not used for fitting, providing robust model validation (Figure S4). Given that the releases modeled by eclipse phase B accounted for just 1% of total HIV detection and that the Model 3 parameters are not fully identifiable given the data, we assumed for simplicity n = 5 compartments and ρ = μ = 0 for these cells. However, if we assumed ρ = μ = 0 for eclipse phase A, then we could not recapitulate lengthy sustained detections (Figure 4E).

Consider the sequence of HIV detection, no detection, and a new HIV detection (Figure 2A). This may occur in Model 3 by transition to the productive I state by two or more E cells at different times, either due to initial Poisson distributed seeding of more than 1 LIC in a replicate, and/or from initial seeding of one LIC that underwent proliferation. This pattern may also be explained by the presence of HIV RNA on 3 or more consecutive days, but at the assay detection limit. In Model 3 we have not incorporated transcriptional toggling, but this could be a fourth potential source of the ON-off-ON detection pattern.

The high variability in initial HIV release can be predicted by applying population dynamic principles while assuming 2 LIC populations with distinct virus release potentials. We conclude that the initial HIV release kinetics are consistent with a model in which: 1) many fully stimulated LIC lineages result in no virus release due to cell death, 2) most productive single cell virus releases end within a day of initiation, 3) the total initial HIV release can be sustained for several consecutive days from sequential transitions to the short-lived productive state (E₄ → I) by multiple descendants of a single LIC.

Release of Replication-Competent HIV Does Not Guarantee Viral Establishment

A high initial HIV release should be much more likely to establish exponential viral growth than a low release. To gain quantitative definition of this process, resting CD4 T cells from 7 donors on ART were stimulated and cultured in a series of 4 four-fold cell dilutions, each with 10 replicates, under viral inhibition or outgrowth conditions (Figures 5A, 5B, 5C, and S5). Under outgrowth conditions, a viral establishment definition below 1 × 10⁵ HIV RNA copies was not considered because de novo infection could not be distinguished from an initial HIV release, based on inference from the HIV RNA detection distribution in the corresponding viral inhibition replicates (Figure 5C and S5). Given the highest viral inhibition replicate produced 59,000 HIV RNA copies (Λ = 3.6), we defined viral establishment as attaining at least 2 × 10⁵ HIV RNA copies (Figure 5C). This definition required outgrowth to at least 10-fold, relative to the mean initial releases in the corresponding viral inhibition replicates, with 87% below 20,000 HIV RNA copies (Figure S5).

Figure 5. Initial Release of Replication-Competent HIV Is Often Not Sufficient for Viral Establishment.

The dotted red lines depict viral establishment definitions at 1 × 10⁵, 2 × 10⁵, or 1 × 10⁶ HIV RNA copies. The dashed green line at 5100 HIV RNA copies indicates the critical threshold, predicted from analysis in Figures 6A & 6D and the fit Model 3 (Figure 4D and Table S4). Each panel in A, B, and D represents 10 replicate cultures, many of which had no detectable HIV RNA. Solid red lines (5B) and filled red dots (5C) designate primary outgrowth condition supernatants that were HIV RNA positive on day 8 and that resulted in de novo virus production following transfer to secondary culture, confirming replication-competent (rc) virus.

(A) Primary viral inhibition with efavirenz for Donor 19.

(B) Primary viral outgrowth cultures for Donor 19 with excess target cells.

(C) Each dot indicates the maximum HIV RNA copies detected from 3 samplings (typically days 4, 8 and 12) of one replicate culture, in viral inhibition or outgrowth conditions, pooled from experiments with 7 donors on ART. Figure S5 features faceting by donor and CD4 T cell dilution.

(D) Tertiary cultures in which virus passaged from a Donor 19 primary well was serially diluted (right column) on day 0 with cell wash on day 1. Orange-brown designates establishment to > 2 × 10⁵ HIV RNA copies, purple wells did not establish despite de novo virus production following day 1, indicating the infecting virus was rc.

(E) Count of the 51 replicates, binned by Log10 maximum HIV RNA copies, that were positive beyond day 0 from 5D.

Many but not all outgrowth condition wells with detectable HIV RNA established to at least 2 × 10⁵ HIV RNA copies (Figure 5C). Outgrowth to more than 10⁷ HIV RNA copies was probably or certainly due to seeding multiple LICs, with Λ > 2, or detection of more than one unique HIV env clone in a specific replicate (Figure S2). At the highest CD4 T cell number for donor 19, 9 (of 10) outgrowth condition cultures established (Figure 5B) with 8 viral inhibition replicates producing an initial release above 5100 HIV RNA copies. However, at just a 4-fold cell dilution lower, 0 outgrowth cultures established with just 1 viral inhibition replicate slightly above 5100 HIV RNA copies. This sharp difference from a mere 4-fold cell dilution suggested viral establishment required the initial release to exceed a critical threshold (Figures 5A–C). It was also likely that much of the HIV RNA detected from culture represented replication-defective virus.

However, lack of replication-competent (rc) virus was not the sole reason for non-establishment. We directly tested the replication-competency of supernatants containing HIV RNA by transferring them to new secondary cultures with stimulated CD4 cells isolated from an HIV-uninfected donor. Following a 24-hour infection period starting on day 0, a quadruple cell wash was performed with media replacement, followed by immediate day 1 collection to quantify residual HIV RNA. This procedure allowed distinction of the residual infecting virus signal from new virus production on day 2 or later due to de novo infection. Remarkably, of the 49 primary outgrowth condition wells that had detectable HIV RNA on day 8 below the establishment definition of 2 × 10⁵ copies, 24 (49%) contained rcHIV that resulted in de novo virus production following viral transfer (Figures 5B, 5C, S5), with the expected initial number of LICs per well, Λ, ranging from 0.1 to 5.8 with a median of 0.8. There were 19 primary outgrowth condition wells, inclusive of all 7 HIV-infected donors, that had declining HIV RNA, sometimes to extinction, that nevertheless contained rc virus, proven by de novo virus production after transfer (Figures 5B, 5C, and S5).

Following serial dilution of virus from a single established culture into new replicate cultures, de novo virus production with or without establishment occurred, again distinguishing replication-competency from establishment (Figures 5D and 5E). In this case single genome env sequencing indicated the infecting virus was monoclonal (Figure S2, Series 273), demonstrating that a rc clone released from an infected cell, although capable of establishing, more often does not. We conclude an initial release of rcHIV, even with some de novo infection, is often not sufficient to ensure viral establishment.

Viral Establishment Depends on an Initial HIV Release Amount Exceeding a Critical Threshold

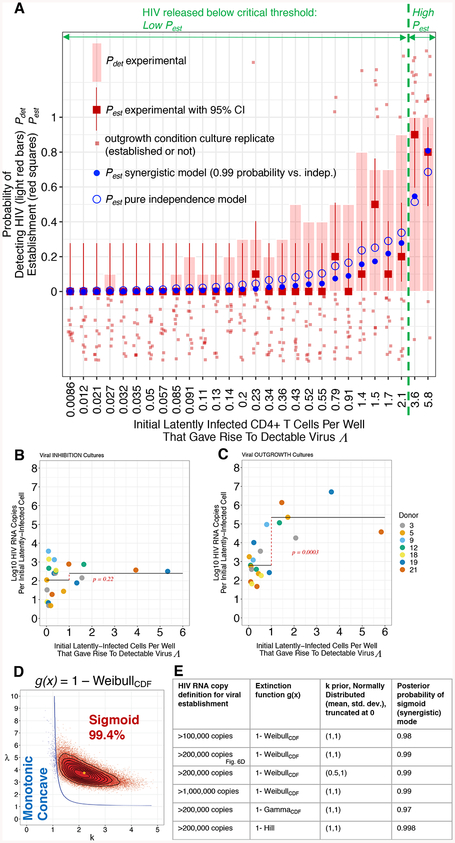
We next considered how the magnitude of Λ, the expected number of LICs per well that each gave rise to detectable virus (derived from Equation [1] given P_det), relates to viral establishment. As Λ increased, so did the probability of viral establishment to at least 2 × 10⁵ HIV RNA copies, P_est (Figure 6A). Consider a model in which each LIC shares an establishment probability θ less than one that is independent of the exact number of these cells initially present. Such independence has been a tacit but untested assumption in HIV reservoir quantitation for which exponential viral outgrowth is the outcome (Rosenbloom et al., 2015). With assay sensitivity sufficient to detect the initial release of rcHIV without outgrowth, we were able to test the independence assumption. In contrast to the cultures in which de novo infection was inhibited (Figure 6B), for the corresponding outgrowth condition replicates the average log₁₀ HIV RNA copies per LIC increased for Λ > 1 (Figure 6C). This indicated the presence of synergy for viral establishment following the initial HIV release.

Figure 6. Viral Establishment Depends on an Initial Release Exceeding a Critical Threshold.

(A) Probabilities of outcomes (y-axis) versus Λ (x-axis). Light red bar: Probability of HIV RNA detection, P_det. Red filled squares: Probability of viral establishment P_est to > 2 × 10⁵ HIV RNA copies for experimental, with 95% confidence interval. Fit to non-summarized outgrowth well data (light red squares): wells that established (top) and did not establish (bottom): P_est synergistic model (Equations [1] and [6] in STAR Methods; Blue filled circle, Figures 6D and S6, and Table S6), and P_est independence model (Equations [1] and [4] in STAR methods; Blue open circle, Figure S6 and Table S7). Critical threshold predicted in 6D shown in green.

(B-C) Expected initial LICs that gave rise to detectable HIV RNA Λ per well (x-axis) versus average log₁₀ maximum HIV RNA copies per cell (y-axis) for viral INHIBITION (B) or OUTGROWTH (C) cultures. Horizontal black lines represent mean log₁₀ HIV RNA copies per Λ, for Λ ≤ 1 and Λ > 1. Cell dilutions with no HIV RNA positive wells were excluded. Welch t-test for comparing these 2 groups, t = −1.26, df = 17.3, p = 0.22 shown in red for viral inhibition (B) and for (C) outgrowth, t = −5.75, df = 8.78, p = 0.0003.

(D) Posterior distribution for k and λ parameters for Weibull-based statistical model to test for an Allee effect (See STAR Methods; Equations [1] and [6]). P_est(Λ) is monotonic concave (blue) up to and including line; inside this line P_est(Λ) is sigmoid (red) with the percentage of posterior k and λ estimates producing sigmoid form (Figure S6) indicated. (E) Bayesian inference results in a sigmoid (synergistic) mode using 3 distinct dual-mode (monotonic concave versus sigmoid) extinction functions g(x), 3 viral establishment definitions, and a prior for k with a maximum frequency at 1 or 0.5, outside the sigmoid regime (6D).

Synergy among individuals leading to population establishment is called an Allee effect in ecology, and this dynamic has been studied across the biologic taxa (Kramer et al., 2009). Detection of an Allee effect signal at low population size can be challenging due to noise from concurrent independent processes that result in stochastic extinction. For a system with only independent processes, as the initial population size (Λ) increases, the establishment probability (P_est) increases in a specific monotonic concave shape (Leung et al., 2004). If a strong synergistic process is concurrent, the Λ versus P_est relationship is expected to be sigmoid shaped, with the inflection point representing a critical population size (Dennis, 2002). Above this threshold, on average, there are a sufficient number of individuals for synergistic growth to establishment, whereas below this threshold the low census population goes extinct. An Allee effect has been previously detected in establishment data by fitting to a Weibull cumulative distribution function (CDF) which can assume either a monotonic concave or sigmoid shape (Kaul et al., 2016).

To test for an Allee effect, we extended such a Weibull_CDF-based model to our viral establishment data, using Bayesian inference in Stan (See STAR Methods for details). This approach is practical to apply here because it begins with a prior probability belief about the system, which is then updated using Bayes’ theorem to a posterior probability upon model conditioning on the data. Through a prior parameter distribution with a maximum within the monotonic concave regime (k parameter, Figures 6D–E), we incorporated a substantial belief that the independence assumption held. Despite use of such a prior, Bayesian analysis indicated a greater than 97% posterior probability of the sigmoid form, supporting a synergistic Allee effect (Figures 6A, 6D–E, S6, and Tables S6). The inflection point, designating the critical population size, occurred at Λ = 2.3 which on average (applying fit Model 3, Table S4) results in an initial release detection of 5100 HIV RNA copies (Figures 5A–B) with 95% probability interval (PI) from 2700 to 6500.

We performed extensive sensitivity analysis. The sigmoid shape was favored over the monotonic concave with greater than 97% posterior probability regardless of whether establishment was defined at 1 × 10⁵, 2 × 10⁵, or 1 × 10⁶ HIV RNA copies, or if a Gamma_CDF (Dennis, 2002) or Hill function (Stefan and Le Novère, 2013) rather than Weibull_CDF was applied to determine the P_est versus Λ curve shape. (Figures 6E and S6). Each Bayesian analysis explicitly incorporated the independence assumption as a prior belief, but the data pulled the model away from this into the synergistic regime.

Furthermore, the critical threshold prediction at 5100 HIV RNA copies is borne out in data not used for model conditioning (Figure 5D). Following low copy HIV infections with a single rc env clone, de novo produced HIV frequently smoldered around the predicted critical value rather than immediately declining to extinction or undergoing rapid exponential growth (Figure 5D), as theoretically expected (Scheffer et al., 2009) and previously observed in the vicinity of an Allee threshold (Dai et al., 2012). The large gap between 10⁴ and 10⁸ copies in the distribution for maximum HIV RNA detected (Figure 5E) provides further support for an Allee effect (Drake and Lodge, 2006).

In summary, the evidence for synergistic establishment was supported by multiple Bayesian analyses (Figure 6E) that each predicted a critical threshold observed in data not used for fitting (Figure 5D). We conclude that HIV was subject to an Allee effect such that viral collapse typically occurred for initial releases below a critical population size of 5100 detected HIV RNA copies.

Stochastic Population Dynamics and an Allee Effect Favor Viral Collapse

Model 3 does not account for cells with a proviral integration site that is transcriptionally silent, or LICs that cannot be stimulated. By this model, just 41% of stimulated single LICs give rise to detectable virus (Figures 4D and 4F, Table S4). Hence to achieve parity with the limiting dilution frequency of HIV RNA detection (Figure 2A), many of the individual stochastic simulations were initiated with more than 1 LIC (Figure 4F). Of the single simulated LICs that gave rise to detectable virus, the total detected initial release was predicted to vary bimodally across 4 orders of magnitude (Figure 7A) with an average 2230 HIV RNA copies. As the exact initial number of LICs in simulation increases from 1, the distribution of initial HIV release shifts toward increasing magnitude (Figure 7A–E).

Figure 7. A Cascade of Stochastic Processes and an Allee Effect Result in Rare Viral Establishment.

Exact number of initial LICs, x (from Model 3 simulation, Figure 4D). Establishment probability to 2 × 10⁵ HIV RNA copies, P_est, for exactly x cells (Equation [5] in STAR Methods), and mapped to the initial HIV release (red shading in A-E) using Model 3 (parameters: Table S4). Dashed green lines depict critical threshold at 5100 HIV RNA copies.

(A-E) Simulated probability density of total initial HIV release detected (lower x-axis) arising from 1–5 exact initial LICs, with percentage resulting in detectable HIV (second column) and P_est (third column).

(F-G) Outcomes of 100 lineages, each from a single initial LIC receiving stimulation. (H) P_est as a function of x. P_est (x = 1) = 0.02.

Using Model 3 (Figures 4D and 4F) with the synergistic establishment model, (Figure 6A and 6D, Table S6), we mapped the relationship between initial virus release and P_est (Figure 7A–E). For exactly one stimulated LIC, stochastic proliferation in the latent eclipse phase results in an initial release sufficiently high to establish just 2% of the time (Figures 7A, 7F, and 7G). For the other 98%: HIV smolders with de novo infection but not exponential growth, HIV is released but results in no de novo infection, or lineage extinction occurs in the latent state without HIV release (Figures 7F and 7G). As the exact number of initial LICs increases from 1, it becomes increasingly probable in a non-independent fashion, that the initial HIV release will exceed the critical growth threshold, and establish a sustained chain reaction of infection spread (Figure 7H).

DISCUSSION

The stochastic transition to exponential growth is the crucial but covert process underlying succession to the readily observable deterministic trajectory. At the scale of cells, this transition can be the pivotal event upon which either health or illness hinges when an individual human faces threat from a pathogen at low abundance. This includes infection from viruses and other microbes, but also other classes of invasive agents such as cancer cells. Across context and scale, consistent challenges include accounting for variability at low population size, and understanding how this impacts population viability. Here we addressed these challenges by integrating experimental and computational approaches to define the origin of exponential HIV spread. This is the keystone event an effective vaccine would prevent.

The previous finding that ex vivo HIV outgrowth occurs for ~2% of stimulated CD4 T cells with intact provirus (Ho et al., 2013) is understood here by stochastic transition out of latency involving cell division and cell death, resulting in a highly variable initial HIV release that is then subjected to an Allee effect. These principles are consistent with many other previous observations including: proliferation of cells with intact provirus following activation (Bruner et al., 2019), that more than one round of culture is often required to result in outgrowth (Hosmane et al., 2017), and highly variable HIV transcription arising from a monoclonal proviral integration (Weinberger et al., 2005).

Cells from donor 5 released one HIV env clone in multiple culture wells, suggesting a population derived from an original cell precursor that underwent in vivo clonal expansion (Cohn et al., 2018; Maldarelli et al., 2014; Wagner et al., 2014). For this single env clone, we observed a highly variable daily virus release among 9 limiting dilution replicates (Figure 2A and S2). If this virus arose from a single T cell clonal population, the high variability in initial virus release (Figure 2A) does not derive from an attribute specific to a particular T cell clone.

The proliferative capacity of a LIC has at least 3 implications for in vivo reservoir dynamics. First, following activation, cell proliferation in the latent state can amplify an initial HIV release while avoiding recognition from the immune system. Second, proliferation is a mechanism for proviral genome expansion and the long-term persistence of the latent reservoir (De Scheerder et al., 2019; Kim and Perelson, 2006; Lorenzi et al., 2016; Wang et al., 2018). And finally, simultaneous reactivation of many LICs that comprise a single clonally expanded population (Cohn et al., 2018; Hosmane et al., 2017; Maldarelli et al., 2014; Wagner et al., 2014; Wang et al., 2018), may occur through the sudden appearance of a shared cognate antigen. This would greatly increase the establishment probability with a massive critical threshold breakthrough.

The anatomic distribution and differentiation state of CD4 T cells are relevant to initiation of a rebound event. Viral establishment may have the highest chance in lymphoid tissue where target cell density is high, and where central memory CD4 T cells (CM) that have high proliferative potential reside (Sallusto et al., 1999), a few of which will be latently-infected (Chomont et al., 2009). In particular, germinal centers have highly activated T follicular helper cells that may serve as susceptible lentiviral targets and sources for initial virus (Banga et al., 2016; Perreau et al., 2013; Petrovas et al., 2012). Compared to CM, effector memory cells (EM) have lower proliferative and survival potential (Wu et al., 2002) and transit to non-lymphoid tissues with fewer susceptible target cells. Thus, latently-infected EM may be less likely to lead to rebound. A testable hypothesis arising from our results is that the two distinct eclipse phases in Model 3 correspond to CM and EM populations.

Multiple mechanisms of viral spread by collective mode have been identified (Sanjuán, 2018). If the basis of synergy for de novo HIV infection could be definitively defined, a medical intervention might be devised to greatly increase the critical growth threshold. A threshold amount of virus might be necessary to achieve biochemical cooperativity such as for cell entry or integration, to overcome the effects of a viral restriction factor, or for genetic recombination.

Our analyses have limitations. We assume some model parameters are shared among human donors or different HIV clonal populations from the same donor. Although additional data could increase the precision of the critical population size estimate, the accumulated evidence for a synergistic mode is considerable. Our conclusion of viral establishment by synergistic mode depends on use of empiric statistical functions rather than a population dynamic model of de novo infection. Toward this challenge, Model 3 can be extended for enhanced definition of infection spread dynamics and prediction of in vivo HIV rebound. The high variability inherent in this complex system has vital implications for whether and when rebound occurs (Rouzine et al., 2014).

A realizable objective is to ensure the naturally rare transition to exponential viral spread does not occur at all. Looking forward, HIV pathogenesis discovery will depend on not only advancing the molecular and cell biology that yielded current ART, but also investigation beyond that paradigm. We anticipate further developments in defining how stochastic and nonlinear transitions occur. Ultimately such understanding could be leveraged toward the concept, development, and clinical testing of new interventions for prevention and treatment, devised to tip the dynamic system into a state of permanent pathogen collapse.

STAR METHODS

LEAD CONTACT AND MATERIALS AVAILABILITY

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Jason M. Hataye (jason.hataye@nih.gov). This study did not generate new unique reagents. The experimental data and computer code for this study can be accessed publicly as detailed in the Data and Code Availability section.

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Experimental Model Design

The experimental model design was to culture ex vivo activated CD4 T cells from human HIV-infected donors on ART, and detect HIV released into the culture supernatant. The initial HIV release arising from latency disruption without de novo infection was determined from viral inhibition cultures with the reverse-transcriptase inhibitor efavirenz. In contrast, exponential viral growth was possible in outgrowth condition cultures with additional target cells susceptible to HIV infection. Please see below for further details.

Research Donor Characteristics

24 adult research donors infected with HIV-1 on ART were recruited between February 2008 and July 2008 from the Whitman Walker Clinic of Washington, District of Columbia, or through the Vaccine Research Center, National Institute of Allergy and Infectious Diseases (NIAID), in Bethesda, Maryland. Several additional adult HIV-negative donors were also recruited. Written informed consent was obtained in accordance with the Declaration of Helsinki and approved by the Institutional Review Board at NIAID. 23 of the 24 HIV-infected donors had clinical viral suppression to below 50 copies of HIV RNA/ml at the time of apheresis. For the 21 of 24 donors for whom the year starting therapy was documented, mean duration of therapy was 6 years (SD 4 years). PBMC were obtained by apheresis. Of the 24 donor PBMC, we used for this study 7 that each had a high frequency of HIV RNA releasing CD4 T cells (Table S1 and Table S5), as determined below.

METHOD DETAILS

Isolation of resting memory CD4 T cells

We processed the apheresis product using Ficoll-Paque buffy coat preparation and stored the donated PBMC in liquid nitrogen freezers. PBMC were thawed, washed with RPMI 1640 supplemented with 100 U/ml penicillin G, 100 U/ml streptomycin, 1.7 mM sodium glutamine, and 10% heat-inactivated fetal calf serum (“R10” media), and stained with a panel of fluorescently labeled antibodies against surface antigens. Resting memory CD4 T cell isolation was performed on the basis of these markers using a custom FACS Aria III (BD Biosciences) capable of sorting on the basis of up to 20 parameters, using Biosafety Level 3 practices and procedures, including a specialized aerosol management and a respiratory system for operator safety (Perfetto et al., 2004). The panel included titered amounts of antibodies for: CD56 Cy7-APC (HCD56, Biolegend 318332), CD4 Cy5.5-PE (S3.5, ThermoFisher Scientific MHCD0418), CD14 Pacific Blue (TuK4, ThermoFisher Scientific MHCD1428), CD19 Pacific Blue (SJ25-C1, ThermoFisher Scientific MHCD1928), violet live/dead cell marker (“vivid” ThermoFisher Scientific L34964), CD69 PE (L78, Becton Dickinson 341652), CD8 Brilliant Violet 785 (RPA-T8, Biolegend 301046), HLA-DR FITC (L243, Becton Dickinson 347363), CD27 PC5 (1A4CD27, Beckman Coulter 6607107), CD45RO ECD (UCHL1, Beckman Coulter IM2712U), and CD25 APC (M-A251, Becton Dickinson 555434). Live lymphocytes not expressing CD14 or CD19 were separated into CD4+CD8- gates. The CD4+CD8- subset was further isolated by excluding cells positive for the activation markers CD25, HLA-DR, and CD69, as well as CD56, a marker for natural killer cells. The non-naive resting memory CD4 cells were gated on the basis of CD45RO and CD27 (Figure S1). Analytical FACS of the sorted resting memory CD4 cells confirmed that greater than 99% expressed CD3 (not included in sort panel) and greater than 97% did not express HLA-DR, CD25, and CD69. All FACS analysis was performed with FlowJo 9.

Viral Inhibition and Outgrowth Ex Vivo Cultures

Stimulation of CD4 T cells with anti-CD3 and anti-CD28 has been reported as superior to that provided by phytohemaglutinin for the purpose of inducing HIV latency disruption (Beliakova-Bethell et al., 2017). We used a T cell Activation Kit (Miltenyi Biotec T cell activation kit 130-091-441) with biotinylated antibodies against CD2, CD3, and CD28 bound to anti-biotin particles per manufacturer guidelines (“Stimulation Particles”). For testing purposes only, we used phytohemaglutinin-M (Sigma-Aldrich L2646) at 5 mg/ml for resting memory CD4+ T cell stimulation followed by flow cytometry assay at day 3 of culture. FACS purified resting memory CD4 T cells were placed in R10 media with stimulation particles containing anti-CD3, anti-CD28, and anti-CD2, and then placed in limiting dilution cultures in a 96-well plate. Typically, these cultures were 10 replicates from 10,000 to 200,000 cells per well at a single cell concentration, or four 4-fold dilutions of 10 replicates each for a total of 40 wells for direct comparison between outgrowth and inhibition. In viral inhibition cultures, 40 nM efavirenz (Sigma-Aldrich SML0536) was used (EC_95% at 20 nM), whereas in viral outgrowth cultures, IL-2 was used at a final concentration of 50 units per ml (PeproTech 200–02). In viral outgrowth wells, 100,000 proliferating MOLT-4/CCR5 cells (kindly provided by Dr. Yasuko Tsunetsugu-Yokota National Institute of Infectious Diseases, Tokyo, Japan) were added on day 1 of culture. Expression of both CXCR4 and CCR5 on MOLT-4/CCR5 cells was confirmed by flow cytometry. This cell line originates from a 19 year old male with acute lymphoblastic leukemia (Minowada et al., 1972). The total culture volume was kept intentionally low at 200 μl and 100 μl, respectively, for viral outgrowth and inhibition cultures to maximize the chance of detecting low copy HIV RNA. We removed 150 μl or 75 μl of culture supernatant from viral outgrowth and inhibition cultures, respectively, with replacement of media containing IL-2 or efavirenz, every 3–4 days. Prior to centrifugation for supernatant collection, the cells were thoroughly mixed by individual well pipetting. For 5 donors, daily supernatant collection in viral inhibition cultures as in Figure 2A was followed by a quantitative cell wash step equivalent to a 1:36 virus dilution.

Secondary Culture of Released HIV

CD4 cells were isolated by positive magnetic bead selection (Miltenyi Biotech CD4 MicroBeads 130-045-101 with LS columns 130-042-401) from PBMC isolated from an HIV-uninfected donor and were placed into culture with stimulation particles and 50 U/ml IL-2 at 160,000 cells per well for 80 wells. 4 days later, 78 of 80 wells were infected with HIV from a primary outgrowth culture well. If the total HIV RNA copies in the source well was greater than 50,000 copies, 1 μl of source well supernatant was used for infection on day 0, whereas if less than 50,000 copies were present, 10 μl was used for infection. Infection with HIV was allowed for 24 hours before a triple cell wash to remove residual virus. Culture supernatants were harvested for assay followed by media replacement on days 2, 6, 10, and 14. This experiment was repeated using CD4 cells isolated from a different HIV-uninfected donor. Virus was deemed replication-competent if de novo virus was produced as determined by an increase in HIV RNA detection on day 2 or later, compared to day 1.

A similar tertiary culture experiment was done on virus obtained from a single well of a secondary outgrowth culture, originally from ex vivo primary outgrowth well 132.01 (Figure 5B at 71000 cells/well), to obtain a single dilution series for virus from one well. In this case, resting memory CD4 T cells were isolated from the PBMC of an HIV-uninfected donor by FACS using the same sorting panel and method as for HIV-infected donors above, and placed into 80 wells at 166,000 cells per well in the presence of stimulation beads and 50U/ml IL-2. 5 days later, on day 0, each tertiary culture well was infected with virus. The top 10 wells were infected with approximately 10⁸ HIV RNA copies, and then each row of 10 wells beneath received a 10-fold dilution of HIV until the bottom row received ~ 10 HIV RNA copies. 24 hours after infection, supernatant was harvested, to be assayed later for the initial infecting quantity (Figure 5D, right column), followed by 4 cell washes to remove residual virus, and a final collection for a post wash assay on day 1. Culture supernatant was collected and replaced every 2–3 days thereafter.

Cell Division Analysis

The fluorescent cell dye CFSE (ThermoFisher Scientific C34544) was used to determine the frequency of cell division generations in a population (Figures 1D (8 days) and 2D (5 days) were from the same experiment). Sort isolated resting memory CD4 T cells from the PBMC of an HIV-uninfected donor were washed with phosphate-buffered saline (PBS) and placed at 1 million cells per ml in phosphate buffered saline at a final working concentration of 0.25 μM CFSE for 7 minutes at 37°C. (Note that this is much lower a CFSE concentration than the manufacturer protocol which is reported to be optimized on PBMC, not isolated CD4 T cells.) Immediately following this, the cells were washed twice with cold filtered heat-inactivated fetal calf serum, followed by wash and re-suspension in R10 media. Following this, the CFSE labeled CD4 T cells were cultured as above using stimulation particles. 5 days after stimulation, the cells were stained with the live/dead marker vivid and analyzed by flow cytometry.

HIV RNA Isolation and Quantification

We isolated RNA from 50 μl of culture supernatant per well with the RNAdvance Tissue Kit (Beckman-Coulter A32646), which uses a solid phase paramagnetic nanoparticle based method (Hawkins et al., 1994). To determine retroviral RNA recovery for each individual isolation, we added an internal RNA standard to the culture supernatant lysis solution. The ideal internal RNA standard would follow HIV through the processing and yet be readily distinguished and quantified by RT-PCR. Toward that ideal, we employed the Rous Sarcoma Virus derived RCAS BP(A) (RCAS) retroviral RNA system (Palmer et al., 2003). RCAS BP(A) virus was obtained from the laboratory of Stephen Hughes. Following elution of nucleic acids from the magnetic particles, DNAse (ThermoFisher Scientific AM2222) was added for a total volume of 50 μl of isolated RNA. The plates were incubated on a heat block at 37°C for 30 minut es for DNAse treatment, followed by 10 minutes at 70°C to heat-i nactivate the DNAse.

Quantitative real-time HIV gag RNA RT-PCR was performed using HIV gag RNA standards. 10 of the 50 μl of isolated RNA was used in an RT-PCR reaction totaling 25 μl volume with primers and probe at 0.625 μM and 0.2 μM final concentration, respectively, using the RNA Ultrasense one step RT-PCR kit (ThermoFisher Scientific Invitrogen 11732927). Isolated RNA from each of the 80 wells from a single time point was used for real time quantitative RCAS RNA RT-PCR, HIV gag RNA RT-PCR, and HIV gag DNA PCR (non-RT control). For HIV gag and RCAS RT-PCR, Stage 1 included 45°C incubation for 30 minutes for cDNA sy nthesis, and then an increase to 95°C for 2 minutes. Stage 2 included 45 cycles of 95°C for 15 seconds, followed by 60°C incubation for 1 minute. Using the fraction sampled at each processing step, the fraction of RNA recovered, and the number of copies of HIV gag RNA detected in each RT-PCR well, an estimate for the total HIV gag RNA copies in each original culture well supernatant was calculated. Each HIV RNA detection data time point is based on one gag RNA RT-PCR reaction. The detection limit of the HIV gag RNA RT-PCR reaction is such that 10 copies of HIV gag RNA standard can be detected 64% of the time. The limit of detection of the entire assay depends on the detection limit of the HIV gag RT-PCR reaction, RNA recovery, dilution factors accumulated during sequential processing steps. This limit of detection was empirically determined by serial dilution of virus, and is such that 70 copies of HIV RNA can be detected in all 100 μl of a viral inhibition culture supernatant 50% of the time (Figure 1E).

Quantitative real-time RCAS RNA RT-PCR was performed using primers and probes and RCAS RNA standards as previously described (Palmer et al., 2003) for each RNA isolation, and used to estimate RNA recovery following robot automated RNA isolation, DNAse treatment, and DNAse heat inactivation, and a single freeze/thaw cycle.

Every well that was positive by HIV gag RNA RT-PCR (and many more that were negative) was tested for HIV gag DNA by PCR (non-RT control) using the same primer and probe set. All DNA PCR reactions were performed with Platinum Taq Polymerase (ThermoFisher Scientific Invitrogen 10966018). A single set of PCR reactions was run for each corresponding culture well. All RT-PCR and PCR runs were performed on Applied Biosystems 7900 HT real-time PCR machines using the AB software. Primers and Probes were synthesized by Biosearch Technologies and prepared for use in water. Primer and probe sequences HIV gag and RCAS RT-PCR were as previously published (Douek et al., 2002; Palmer et al., 2003) (Table S8).

A positive HIV RNA data point was excluded from analysis if the HIV DNA quantified for the well exceeded 1% of the HIV RNA RT-PCR value for that well or in the rare case when the RCAS RNA recovery was less than 10%. Given that the RT-PCR and PCR reactions were different in many ways, including using different polymerase enzymes and primer concentrations, an experiment was performed to produce a comparative correction. The HIV DNA standards were placed into both the RT-PCR reaction and the PCR reaction where we found that the HIV DNA copies amplified in the RT-PCR reaction were equal to 0.22 times the value in the PCR reaction. This linear relationship was used to correct the DNA PCR values in terms of their equivalent in the RT-PCR reactions for direct comparison between the two types of reactions. Out of a total of 1487 HIV RNA positive wells, only 47 (3%) had detectable HIV DNA and 5 (0.4%) were excluded from consideration because HIV DNA exceeded 1% of the HIV RNA. Of 7080 total RNA isolations, 5 were excluded because RCAS RNA recovery was less than 10%, typically due to a pipetting failure on the robot during the RNA isolation procedure. Thus of 7080 total RNA isolations, 10 were excluded from consideration due to RNA recovery failure or HIV gag DNA breakthrough of DNAse treatment. There were a total of 7080 gag RT-PCR reactions, 7080 RCAS RT-PCR reactions, and 5256 gag DNA PCR reactions, for a total of 19416 individual PCR or RT-PCR reactions performed on samples.

For Illumina-based, 3’-half, and env single HIV genome sequencing, we extracted total RNA from viral culture supernatants using RNAzol RT (Molecular Research Center RN190), according to the manufacturer’s protocol.

Illumina-based HIV Sequencing

A small number of RNAzol RT extractions were further purified using Dynabeads Oligo(dT)25 magnetic beads (ThermoFisher Scientific 61005) to obtain polyadenylated RNA. This product was then subsequently fragmented, reverse transcribed and Illumina-ready libraries were generated. The libraries were sequenced on the MiSeq platform from Illumina. Paired-end sequences were adaptor and quality trimmed with Trimmomatic (Bolger et al., 2014). Contigs were then assembled with Trinity 2.0.4 (Grabherr et al., 2011) and HIV transcripts were identified by aligning the contigs against HXB2 using standalone BLAST+ version 2.2.30 (Altschul et al., 1990).

3’-half and env single HIV genome sequencing

RNA extracted using RNAzol RT was subjected to cDNA synthesis using SuperScript III reverse transcriptase according to manufacturer’s recommendations (Invitrogen). In brief, a cDNA reaction of 1× RT buffer, 0.5 mM of each deoxynucleoside triphosphate, 5 mM dithiothreitol, 2 U/ml RNaseOUT (RNase inhibitor), 10 U/ml of SuperScript III reverse transcriptase, and 0.25 mM antisense primer HIV.BK3.R1:5’-ACT ACT TGA AGC ACT CAA GGC AAG CTT TAT TG was incubated at 50°C for 60 min, 55°C for 60 min and then heat-inactivated at 7 0°C for 15 min followed by treatment with 1 U of RNase H at 37°C for 20 min. Env gene or 3’-half genomes were then amplified via limiting dilution PCR where only one amplifiable molecule was present in each reaction. PCR amplification was performed with 1× PCR buffer, 2 mM MgCl₂, 0.2 mM of each deoxynucleoside triphosphate, 0.2 μM of each primer, and 0.025 U/μl Platinum Taq polymerase (Invitrogen) in a 20-μl reaction. First round PCR was performed with sense primer HIV.BK3.F1: 5’– ACA GCA GTA CAA ATG GCA GTA TT and antisense primer HIV.BK3.R1 under the following conditions: 1 cycle of 94°C for 2 min, 35 cycles at 94°C for 15 sec, 55°C for 30 sec, and 72°C for 4 min, followed by a final ext ension of 72°C for 10 min. Next, 1 μl from the first-round PCR product was added to a second-round PCR reaction that included the sense primer HIV.BK3.F2: 5’– TGG AAA GGT GAA GGG GCA GTA GTA ATA C and antisense primer HIV.BK3.R2: 5’– TGA AGC ACT CAA GGC AAG CTT TAT TGA GGC performed under the same conditions used for first-round PCR, but with a total of 45 cycles. In some low RNA samples, Env only PCR was performed identically as described but with unique primers: envB5out: 5’– TAG AGC CCT GGA AGC ATC CAG GAA G; envB3out: 5’– TTG CTA CTT GTG ATT GCT CCA TGT; envB5in: 5’– TTA GGC ATC TCC TAT GGC AGG AAG AAG; envB3in: 5’– GTC TCG AGA TAC TGC TCC CAC CC. Correct sized amplicons were identified by agarose gel electrophoresis and directly sequenced with second round PCR primers and HIV specific primers using BigDye Terminator technology. To confirm PCR amplification from a single template, chromatograms were manually examined for multiple peaks, indicative of the presence of amplicons resulting from PCR-generated recombination events, Taq polymerase errors or multiple variant templates. Sequences, including those obtained on the Illumina platform, were aligned using Geneious 9.1.7. All trees were constructed using the neighbor-joining method.

A complete list of oligonucleotides with sequences can be found in Table S8.

QUANTIFICATION AND STATISTICAL ANALYSIS

R (R Core Team, 2014) was used as the platform for quantification and statistical analysis, as described below. Data graphics were generated with ggplot2 (Wickham, 2009).

Statistical Modeling of Viral Establishment

Introduction: Assumptions and Definitions

The expected number of latently-infected CD4 T cells giving rise to detectible HIV RNA per well, Λ, was estimated from the number of CD4 T cells placed per well C (from an HIV-infected donor on ART) and the frequency of gag RNA RT-PCR positive well supernatants P_det, using Extreme Limiting Dilution Analysis (ELDA) (Hu and Smyth, 2009) from Yifang Hu and Gordon Smyth, implemented in the R statmod library or as a webtool. Another webtool, IUPMstats (Rosenbloom et al., 2015) from Daniel Rosenbloom and the laboratory of Robert Siliciano provides similar analysis. When using such methods, an assumption is that detection of latently-infected cells in wells is Poisson distributed, as in Equation [1].

As such, we assumed that detection of any HIV release arising due to reactivation of a latently-infected cell occurred independently of the number of such cells present in the well. In support of this, we performed a preliminary likelihood ratio test of the independent “single-hit” model in ELDA for each donor, in both the viral inhibition and outgrowth cultures and found that in each case the p-value exceeded 0.10, indicating little evidence for a “multi-hit” model (synergy) for any HIV release.

Consistent with an independence assumption, in the viral inhibition cultures, there was little evidence for a difference in the log₁₀ maximum HIV RNA copies per latently-infected cell for wells with, on average, less than or equal to 1 expected seeded latently-infected cell compared to those with more than 1 (Figure 6B, p = 0.22, Welch t-test). In contrast, for viral outgrowth condition wells there was a profound increase in the log₁₀ maximum HIV RNA copies per seeded latently-infected cell for wells with greater than expected 1 seeded latent cell compared to those with 1 or fewer (Figure 6C, p = 0.0003 Welch t-test). These results together indicate synergy for de novo infection, but not for the initial HIV release during latency disruption.

Consider a non-synergistic model in which each latently-infected cell shares an establishment probability θ less than 1 that is independent of the exact number x of these cells initially present. Such independence has been a tacit but untested assumption in HIV reservoir quantitation for which exponential viral outgrowth is the outcome (Rosenbloom et al., 2015). The probability of viral extinction following reactivation of a single latently-infected cell is 1 − θ, and for exactly x such cells we have extinction probability g(x) = (1 − θ)^x. P_est is then (Leung et al., 2004):

$$P_{\mathit{\text{est}}}\left(x;\theta \right)=1-{\left(1-\theta \right)}^x$$ [2]

However, x is not experimentally known. Assuming x is Poisson distributed around Λ and the probability of extinction in a well with x reactivated latently-infected cells is g(x), then:

$$P_{\mathit{\text{est}}}\left(\Lambda \right)=1-{\sum }_{x=0}^{\infty }g\left(x\right)\frac{{\Lambda }^x}{x!}{e}^{-\Lambda }$$ [3]

with Λ = C/π. Using g(x) = (1 − θ)^x, Equation [3] reduces to:

$$P_{\mathit{\text{est}}}\left(\Lambda ;\theta \right)=1-e^{-\theta \Lambda }$$ [4]

Equations [3] and [4] are formally derived in the next section. For Equation [4], as Λ increases, P_est increases toward 1 in a monotonic concave fashion. Rearranging Equations [2] and [4] to yield 1 – P_est gives the probability of extinction. These then model stochastic extinction due to relevant mechanisms with an independent basis, including virus removal for sampling, and the case in which a fraction of the total released HIV is replication-defective, an interpretation of outgrowth failure in early studies (Tsai et al., 1996).

In addition to extinction processes with an independent basis, a synergistic dynamic may be concurrent by which the per latently-infected cell probability of establishment increases in the presence of 2 or more such cells. In ecology, synergy among individuals leading to population establishment is called an Allee effect (Kramer et al., 2009), named for the zoologist Warder Clyde Allee who studied it. The mechanism generating an Allee effect varies. Zoologic examples of the Allee effect include behaviors such as schooling in fish or cooperative feeding in a pack of wild dogs, but analogous synergistic population dynamics have recently been studied in microorganisms including the yeast Saccaromyces cerevisiae (Dai et al., 2012), bacteria of genera Vibrio (Kaul et al., 2016) and Streptococcus (Smith and Smith, 2016), and Vesicular stomatitis virus (Andreu-Moreno and Sanjuán, 2018).

For a synergistic Allee effect, the initial population size, x, versus P_est curve is expected to be sigmoid shaped rather than monotonic concave (Dennis, 2002), with the inflection point representing a critical population size below which, on average, growth collapses, and above which growth to establishment occurs. Due to stochasticity, extinction may occur above the critical threshold, and establishment from below.

To detect an Allee effect in the presence of stochastic extinction, a Weibull_CDF has been previously applied for x exact individuals (Kaul et al., 2016):

$$P_{\mathit{\text{est}}}\left(x;k;\lambda \right)=1-e^{{\left(-\frac{x}{\lambda }\right)}^k}$$ [5]

The Weibull_CDF [5] is sigmoid shaped for k > 1, indicating synergy, and monotonic concave for k ≤ 1. Incorporating g(x) = exp(− x/λ)^k from Equation [5] into Equation [3] provides an expression for P_est that allows deviation from the pure independence mode given Λ expected latently-infected cells:

$$P_{\mathit{\text{est}}}\left(\Lambda ;k;\lambda \right)=1-{\sum }_{x=0}^{\infty }{e}^{{\left(-\frac{x}{\lambda }\right)}^k}\frac{{\Lambda }^x}{x!}{e}^{-\Lambda }$$ [6]

Like Equation [5] from which it was partly derived, Equation [6] can also assume a monotonic concave versus sigmoid shape, enabling empiric detection of an Allee effect. In this case, the monotonic concave mode is demarcated from the sigmoid as k and λ each approach 1 asymptotically (Figure 6D). We implemented our model incorporating Equations [1] and [6] in the statistical programming language Stan, given the outgrowth data: P_est, P_d, and C; the unknown parameter 1/π_d was estimated for each of 7 donors, and k and λ were estimated assuming their values were the same for all donors.

Statistical Model Details

We define the random variables:

χ, number of resting memory CD4+ T cells placed into a culture well on day 0

X, number of latently infected CD4+ T cells placed into a culture well on day 0

D, indicator (0 or 1) that culture well supernatant has HIV gag RNA detectable by RT-PCR at any point during culture

E, indicator (0 or 1) that a well established viral infection. This is defined as attaining HIV RNA copies greater than 200,000 on any day, as discussed in main text. Alternatively, in some special cases (noted in main text and here) we utilized establishment declaration at 100,000 or 1,000,000.

We define the parameters:

1/π, frequency of latently infected CD4+ T cells among resting memory CD4+ T cells for volunteer donor d. (i.e. 1/10,000 = 1 in 10,000 = 0.0001),

C expected number of CD4 T cells placed in a well,

such that C/π = Λ gives the expected number of latently infected CD4+ T cells (that give rise to detectable virus) in a well.

We aim to describe the joint distributions of D and E. Denoting Pr[E=1] = P_est and Pr[D=1] = P_det,

Pr[D=0, E=1] = 0

Pr[D=0, E=0] = 1 − P_det

Pr[D=1, E=0] = P_det − P_est

Pr[D=1, E=1] = P_est

We make the following distributional assumptions for a well:

χ ~ Poisson(C)

X | χ ~ Binomial(χ, 1/π)

D | X = I[X > 0]

where I is an Indicator function such that D = 0 when X = 0 and D = 1 when X > 0.

This definition of D means that we are defining X as the number of latently-infected cells seeded in a well that give rise to (either directly or through lineage transition or proliferation) detectible virus. This is different than the true number of initial latently-infected cells, since some may die before producing any virus, may not be stimulated to produce virus, or may produce virus that is not detected. We describe the probability of failure to establish given x seeded latently infected cells with a function g(x) such that

$$\text{Pr}\left[\text{E}|X\right]=1-g\left(x\right)$$

g(x) may be chosen to represent independence or synergy among cells.

Marginal distribution of X

The marginal distribution of X (number of initial latently infected cells) is Poisson with parameter Λ = C/π from the following:

$$\begin{gathered} \text{Pr}\left[X=\text{k}\right]={\sum }_{n=k}^{\infty }\text{Pr}\left[X=k|\chi =n\right]\text{Pr}\left[\chi =n\right] \\ ={\sum }_{n=k}^{\infty }\left(\begin{array}{l}n\hfill \\ k\hfill \end{array}\right){\left(\frac{1}{\pi }\right)}^k{\left(1-\frac{1}{\pi }\right)}^{n-k}\frac{C^n}{n!}{e}^{-C} \\ ={\sum }_{n=k}^{\infty }\frac{n!}{k!\left(n-k\right)!}{\left(\frac{1}{\pi }\right)}^k{\left(1-\frac{1}{\pi }\right)}^{n-k}\frac{C^n}{n!}{e}^{-C} \\ =\frac{{\left(\frac{1}{\pi }\right)}^k{e}^{-C}{C}^k}{k!}{\sum }_{n=k}^{\infty }\frac{{\left(1-\frac{1}{\pi }\right)}^{\left(n-k\right)}{C}^{\left(n-k\right)}}{\left(n-k\right)!} \\ =\frac{{\left(\frac{1}{\pi }\right)}^k{e}^{-C}{C}^k}{k!}{\sum }_{n=k}^{\infty }\frac{{\left(\left(1-\frac{1}{\pi }\right)C\right)}^{(n-k)}}{(n-k)!} \\ =\frac{{\left(\frac{1}{\pi }\right)}^k{e}^{-C}{C}^k}{k!}{e}^{\left(\left(1-\frac{1}{\pi }\right)C\right)} \\ =e^{\left(\left(1-\frac{1}{\pi }\right)C-C\right)}\frac{{\left(\frac{C}{\pi }\right)}^k}{k!} \\ =e^{\left(-\frac{C}{\pi }\right)}\frac{{\left(\frac{C}{\pi }\right)}^k}{k!} \end{gathered}$$

which gives X ~ Poisson(C/π).

Marginal Distribution of D

Assuming D = I[X > 0] (I is an Indicator function such that D = 0 when X = 0 and D = 1 when X > 0), the marginal distribution of D (indicator function of any HIV RNA detection) is given by:

$$\begin{gathered} \text{Pr}[\text{D}=1]={\sum }_{x=0}^{\infty }\text{Pr}[D=1|X=x]\text{\hspace{0.17em}Pr}[X=x] \\ =0\times \text{Pr}[X=0]+{\sum }_{x=1}^{\infty }\text{Pr}[X=x] \\ ={\sum }_{x=1}^{\infty }{e}^{\left(-\frac{C}{\pi }\right)}\frac{{\left(\frac{C}{\pi }\right)}^x}{x!} \\ =1-e^{\left(-\frac{C}{\pi }\right)[1]} \end{gathered}$$

This is the Poisson_CDF for seeding one or more latently-infected cells that give rise to detectable virus in a well, Equation [1].

Marginal Distribution of E

The marginal distribution of E (indicator function of establishment) is given by:

$$\begin{gathered} \text{Pr}[E=1]=1-\text{Pr}[E=0] \\ =1-{\sum }_{x=0}^{\infty }\text{Pr}[E=0|X=x]\text{\hspace{0.17em}Pr}[X=x] \\ =1-{\sum }_{x=0}^{\infty }\text{g}\left(\text{x}\right)\frac{{\left(\frac{C}{\pi }\right)}^x}{x!}{e}^{\left(-\frac{C}{\pi }\right)}[3] \end{gathered}$$

This is Equation [3] with generic extinction function g(x). Assuming independence, g(x) = (1 − θ)^x. Alternatively, g(x) may be chosen to allow deviation from the independent mode, as described in more detail below.

Joint Distribution of D, E

As above the joint distribution of D, E is given by

Pr[D=0, E=1] = 0

Pr[D=0, E=0] = 1 − P_det

Pr[D=1, E=0] = P_det − P_est

Pr[D=1, E=1] = P_est

with:

$$P_{\mathit{\text{det}}}=1-e^{\left(-\frac{C}{\pi }\right)}[1]$$

$$P_{\mathit{\text{est}}}=1-{\sum }_{x=0}^{\infty }\text{g}(\text{x})\frac{{\left(\frac{C}{\pi }\right)}^x}{x!}{e}^{\left(-\frac{C}{\pi }\right)}[3]$$

Independent Establishment

If we assume the probability of establishment from one latently infected cell is θ and that this establishment probability is independent of the exact number x of latently-infected cells in a well, we have

$$g\left(x\right)={\left(1-\theta \right)}^X$$

Using g(x) = (1 − θ)^x in the equation for the marginal distribution for E:

$$P_{\mathit{\text{est}}}=1-{\sum }_{x=0}^{\infty }\text{g}\left(\text{X}\right)\frac{{\left(\frac{C}{\pi }\right)}^x}{x!}{e}^{\left(-\frac{C}{\pi }\right)}[3]$$

$$P_{\mathit{\text{est}}}=1-{\sum }_{x=0}^{\infty }{(1-\theta )}^x\frac{{\left(\frac{C}{\pi }\right)}^x}{x!}{e}^{\left(-\frac{C}{\pi }\right)}$$

$$P_{\mathit{\text{est}}}=1-{\sum }_{x=0}^{\infty }\frac{{\left((1-\theta )\frac{C}{\pi }\right)}^x}{x!}{e}^{\left(-\frac{C}{\pi }\right)}$$

$$P_{\mathit{\text{est}}}=1-e^{\left(-\frac{C}{\pi }\right)}{\sum }_{x=0}^{\infty }\frac{{\left((1-\theta )\frac{C}{\pi }\right)}^x}{x!}$$

$$=1-e^{\left(-\frac{C}{\pi }\right)}{e}^{\left((1-\theta )\frac{C}{\pi }\right)}$$

$$=1-e^{\left(-\frac{\theta C}{\pi }\right)}[4]$$

Equation [4] provides the probability of independent establishment, with random variable X Poisson distributed around Λ (= C/π), X ~ Poisson (Λ). Equation [4] can be used with Equation [1] to simultaneously estimate θ and 1/π, given P_det, P_est, and C. For Equation [4] as Λ (= C/π) increases, P_est increases in a monotonic concave fashion.

Synergistic Establishment with X ~ Poisson(Λ)

There are a number of functions that could be used to describe synergistic establishment including but not limited to the Weibull_CDF, Gamma_CDF, and Hill function. We use one of the following for g(x) in [6]:

g(x) = exp(− (x/λ)k)	a, from WeibullCDF,
g(x) = 1 − GammaCDF(x,k,1/λ)	b, from GammaCDF
g(x) = 1 − (xk /(xk + λk))	c, from Hill function

in:

$$P_{\mathit{\text{est}}}=1-{\sum }_{x=0}^{\infty }\text{g}\left(\text{x}\right)\frac{{\left(\frac{C}{\pi }\right)}^x}{x!}{e}^{\left(-\frac{C}{\pi }\right)}$$ [6a][6b][6c]

Equation [6a], [6b], or [6c] provides the probability of establishment, assuming X is Poisson distributed around Λ, using g(x) based on the Weibull_CDF, Gamma_CDF, or Hill respectively. Equation [6a], [6b], or [6c] can be used with [1] to jointly estimate k, λ, and 1/π, given P_det, P_est, and C to test for an independent versus synergistic mode of viral establishment. For [6a] and [6c] based on the Weibull_CDF (Figure 6D and S6A–B) and Hill (Figure S6A and S6D) respectively, k and λ each approach 1 asymptotically in the monotonic concave mode, but beyond this lies the sigmoid regime, with similar behavior for the Gamma_CDF (Figures S6A and S6C).

Model Fitting in Stan

We estimated the parameters of models from the observed HIV RNA detection and establishment data using the probabilistic programming language Stan (Carpenter et al., 2017) via the Rstan interface for Bayesian inference of the unknowns. All model fits were implemented using Stan Hamiltonian Markov chain Monte Carlo (MCMC) with no U-turn sampling, which provides machine-automated tuning (Hoffman and Gelman, 2014). For each fit, we performed 16 Markov chains each with 8000 iterations, the first 4000 of which were warm-up. Log likelihoods were determined through use of an explicit vector in the generated quantities block of the Stan code. In all analyses below fitting proceeded as expected: the split R_hat = 1.00 (< 1.1), the effective sample size was sufficiently high relative to the number of iterations for each parameter, treedepth remained well below the default maximum of 10, and there were no divergent transitions. Posterior distributions do not include warm-up. Leave-one-out cross validation (LOO) (Vehtari et al., 2017) was used to estimate model prediction accuracy with all Pareto k diagnostic parameter estimates less than 0.7.

We first compared ELDA and our implementation in Stan using Equation [1] for estimating the frequency of initial latently-infected CD4+ T cells for each of 7 donors (40 culture replicates per donor for a total of 280 culture replicates for viral inhibition, and a separate set of corresponding 280 culture replicates for viral outgrowth), with HIV RNA detection in the culture supernatant on any day interpreted as a binomial outcome (Figures 5A–C, S5). We performed separate analyses for viral outgrowth and viral inhibition conditions, and, for the Stan implementation, used uniform priors for each parameter 10⁴/π_d (subscript d denotes specific volunteer human donor) with wide bounds (0,100). For optimal scaling during fitting, we scaled the number of cells down by 10⁴, searched for 10⁴/π_d such that the parameter was on the order of 1, and then converted the fit result back to 1/π_d. As expected for wide flat priors, the Stan implementation produced results that were very similar to results obtained with ELDA (Table S5).

Prior and model assumptions and implications

In our analyses incorporating both HIV RNA detection and establishment, we assumed that the values of the parameters of the extinction function g(x) were shared across the volunteer donors. For the independence establishment model, we set the prior for θ as uniform bounded from 0 to 1, θ ~ Uniform (0,1).

Establishment models incorporating Equations [6] each have a synergistic mode versus monotonic concave mode indicated by the k and λ parameters. For Equations [6a] and [6c] derived from the Weibull and Hill respectively, sigmoid form is inside the curve bounding the limits of the monotonic concave form such that k and λ each approach 1 asymptotically (blue line in Figure 6D for Weibull, in Figure S6D for Hill). For Equation [6b] derived from the Gamma, k and λ each approach asymptotes as well (Figure S6C). A defining feature of Bayesian inference is formal incorporation of prior assumptions into the analysis. Because the standard assumption in the field for reservoir quantification based on viral outgrowth is independence (Rosenbloom et al., 2015), Bayesian inference with a prior within the monotonic concave regime is particularly appropriate. We therefore set the prior for k with a maximum frequency at 1 and normally distributed with a standard deviation of 1, k ~ Normal (1,1), truncated at zero. By having a weakly informed prior around 1 we avoid unreasonably high values of k in the posterior distribution (more explanation below), focusing the analysis on the key question of curve shape--monotonic concave versus sigmoid--given the data. Compared to a wide-bounded uniform prior for k with bias toward high k, the k ~ Normal(1,1) prior provides a more stringent test for synergy by providing sufficient density in the non-synergistic, monotonic concave, regime. Using this prior for k, for each of the three models incorporating Equation [1] and [6a,b,or c], allowing for Poisson variability around Λ (X ~ Poisson(Λ)), given the data, we observed a greater than 97% posterior probability of the sigmoid shape (Figures 6D–E, S6, Table S6. The three choices for g(x) in Equation [6] (1-Weibull_CDF, 1-Gamma_CDF, and 1-Hill function) each resulted in equivalent log likelihood and expected log pointwise predictive density (ELPD LOO), indicating that the sigmoid curve posterior is robust across these statistical models (Table S6).

For each Bayesian analysis, we truncated the prior for k at zero because negative k has P_est decreasing as Λ increases, which is blatantly contrary to our prior beliefs of the system. Despite this, to provide a k prior with a normal distribution truly centered at 1, we also performed an analysis using Equations [1] and [6a] in which we allowed for k ~ Normal(1,1) to have wide bounds from −9 to 11. As might be expected, this yielded results equivalent to that utilizing truncation bounds at zero and 10, as in Table S6.

Use of more diffuse normally distributed priors around 1, truncated at zero, such as k ~ Normal(1,4) or Normal(1,8) merely resulted in a k posterior further from 1 (Table S6). For an extreme case, we utilized a uniform prior with wide bounds, k ~ Uniform(0,100) but this resulted in k likelihoods becoming unidentifiable at high values. (Use of a uniform prior with wide bounds can bias toward extreme values, contrary to basic prior assumptions. See case study from Michael Betancourt at http://mcstan.org/users/documentation/case-studies/weakly_informative_shapes.html). Use of a uniform prior with wide bounds for k resulted in extremely high and unreasonable posterior distributions, but also divergent transitions. Hence a weakly informative prior for k, such as k ~ Normal(1,1) was necessary to obtain a valid posterior distribution using Hamiltonian Monte Carlo sampling.

And finally, the synergistic model from [1] and [6a] was favored over the pure independence model from [1] and [4] in both leave-one-out and chi-square comparisons (p < 0.01) (Tables S6–S7).

Population Dynamics of Initial HIV Release

This section provides further rationale and method details for proposing and fitting Models 1–3 (Figures 3 and 4) for the initial HIV release following latency reactivation, in the absence of de novo infection. Here, we define the initial HIV release as the total HIV RNA produced from latency disruption, but in the absence of de novo infection resulting in successful new proviral integration events. As we are specifically interested in the total HIV release potential arising from one latently-infected cell following reactivation, we calculate statistics on the total HIV RNA summed from all days, rather than on a single day.

The statistical properties of the basic model of latency reactivation (Figure 3A with ρ = μ = 0) (Conway and Coombs, 2011; Rong and Perelson, 2009), in isolation, were insufficient to fully account for the observed HIV release kinetics (Figure 2A and 4A). First, productively infected cells were previously estimated to have an average lifetime of 1 day (Markowitz et al., 2003), which is not consistent with the many multi-day sustained detections, up to 7 days, we observed (Figure 2A). Second, we also have to account for disparate delays before initial HIV detection that vary between one day and 9 days, as well as detections that start and stop as in the lower right panel of Figure 2A. And finally, the variability in the observed total HIV detected at limiting dilution was much too high for this model to account for.

To understand this last point in detail, consider just the productively infected cell I that releases virus V at a rate p per cell and dies at rate δ per cell. This 2-compartment model has binary outcomes for an I cell: either an HIV release event with probability p/(p + δ), or I cell death with probability δ/(p + δ). I cell outcomes can be modeled as a series of Bernoulli trials (a fair coin flip is a Bernoulli trial with a probability of success P = 0.5) in which the total HIV release is the number of single HIV RNA release events, or “failures,” before a single “success” of I cell death. The number of Bernoulli trial failures before the first success is by definition distributed geometrically. The probability mass function is (1-P)^kP where k is the number of failures (1 HIV RNA release event is a failure; k is the total HIV release) before the first success (cell death) with probability P = δ/(p + δ). In this formulation of the geometric distribution, the expected value E (mean) = (1 − P)/P and variance = (1 − P)/P², and variance/E = 1/P. This last statistic, variance/E is also known as the Fano factor (FF) (Rouzine et al., 2014) and is a measure of dispersion. Since P = 1/(E + 1), FF = E + 1 for the geometric distribution. The mean from the distribution for total HIV detected from the 42 HIV RNA positive limiting dilution wells (Figure 2A) was E = 2600 HIV RNA copies with an experimental FF of 5200, Bootstrap 95%CI 3200 to 6700. However, with a mean E = 2600, for a geometric distribution we expect FF = 2601 (the same as E considering experimental error and significant figures). Thus, the experimental FF was twice as high as that expected for a geometric distribution generated from the same mean. The observation of such a high experimental FF factor is not likely due to insufficient sampling, as indicated by the lower limit of 3200 for the bootstrapped 95% confidence interval. (Although this initial analysis does not account for the HIV RNA assay detection limit, we formally take this into account later.) We conclude that this basic geometric-based model provides insufficient dispersion relative to the observed high variability in total initial HIV detected.

We allowed for higher variability in the initial HIV release beyond this basic model by introducing additional complexity in three steps corresponding to Models 1–3 (Figure 3) : 1) eclipse phase cell division and death (Figures 3A and 4B), 2) multi-compartment single eclipse phase to better model detection delay (Figures 3B and 4C), and 3) two eclipse phases to model heterogeneity in latent cell potential for producing HIV (Figure 3C and 4D).

We introduced eclipse phase cell division and death during latency reactivation, before transition to the productive state. Not only is proliferation the observed outcome following stimulation of CD4 T cells (Figures 1D and 2D), but incorporation of cell division and death in the model increases the variability in total initial HIV release. As indicated in the main text, we derived estimates for ρ and μ used in Models 1 to 3 from 2 experiments (Figures 2C and 2D). Given the frequency of the population at each cell division generation G (Figure 2D) on day 5, we then used a model with G_i representing the frequency of cells having undergone i divisions for i = 0 to 9.

$$\begin{array}{lll}{G}_i\stackrel{\rho }{\to }2G_{i+1}\hfill & G_i\stackrel{\mu }{\to }\otimes \hfill & \text{for\hspace{0.17em}}i=0\text{\hspace{0.17em}to\hspace{0.17em}}8\hfill \\ G_9\stackrel{\rho }{\to }2G_9\hfill & G_9\stackrel{\mu }{\to }\otimes \hfill & \hfill \end{array}$$

The last stage i = 9 feeds into itself given that CFSE dilution beyond 8 divisions cannot be resolved on our flow cytometer. This well studied model (De Boer et al., 2006) was implemented with a system of ordinary differential equations (ODE) in which ρ = μ (Figure 2E)

$$\frac{d{G}_0}{dt}=-\rho G_0-\mu G_0=-2\rho G_0$$

$$\frac{d{G}_i}{dt}=2\rho G_{i-1}-\mu G_i-\rho G_i=2\rho G_{i-1}-2\rho G_i$$

$$\frac{d{G}_9}{dt}=2\rho G_8+\rho G_9-\mu G_9=2\rho G_8$$

This system of ODEs was solved numerically with the Runge-Kutta-Fehlberg based method ode23 (Bogacki and Shampine, 1989) in the R package deSolve. This system of ODEs has only one unknown, ρ, to be estimated from the CFSE dilution frequency data at day 5 for generations G₀ through G₉ (Figure 2D). We performed nonlinear least-squares fitting of the model with the data using the Levenberg-Marquardt algorithm within the Minpack (More et al., 1980) R package minpack.lm. to derive, ρ = 0.48 per day (Figure 2E). [RSS=0.006, CFSE_fit-nls.R]

To appreciate how variability in HIV release arises from stochastic cell division and death, imagine a set of replicate Gillespie simulations of Model 1 (Figure 3A) in which ρ = μ = 0 and that each start with 1 latently-infected cell in the first eclipse phase compartment E. With no cell division and no cell death in the E compartment, 1 productively infected cell I will be realized in every simulation, and the total HIV release will remain geometrically distributed. Now consider what happens as ρ (= μ) increases from zero. The fraction of simulations resulting in transition to the productive I state begins to decrease from 1 due to cell lineage extinction in some realizations. Given ρ = μ, for every 1 latently-infected cell that enters the eclipse phase, on average 1 productively infected I cell will be realized. Some simulations will realize 2 latently-infected cells from cell division, and these will be averaged out by other simulations in which the only latently-infected cell present dies. In this way, the level of dispersion in total HIV RNA released increases above that expected from a geometric distribution.

Also, each eclipse phase cell (including the original single and any progeny) will transition to the productive I state at different times, providing variability in HIV release timing. These statistical properties made incorporation of cell division and death in the eclipse phase a compelling choice. This choice makes sense if we just consider averages derived from the experimentally observed dynamics. With the average lifetime of a CD4 T cell in culture of 1/μ = 2 days and an average time to first HIV RNA detection of 4 days (Figure 4A), many of the latently-infected CD4 T cell lineages initially present in culture should go extinct before they produce virus.

The experimental time delay to first HIV RNA detection, most frequently 3 days (Figure 4A), was not concordant with a single transition rate a (Model 1) in which the delay time is exponentially distributed with a maximum frequency at day 1 (Figure 4B). To reconcile this discrepancy, we extended the number n of eclipse phase compartments from n = 1 for Model 1, to up to n = 10 (Figure 3B shows n = 5, where n is an integer from 1 to 10), with transition to the next compartment in series at rate a, Model 2. This construct results, for ρ = μ = 0, in an Erlang distributed delay time with mean n/a (Mittler et al., 1998), which has been used for modeling in vitro lentiviral production delay (Kakizoe et al., 2015). For non-zero ρ and μ, as we used here, the distribution for the delay time was determined by direct Gillespie simulation (Figure S3 for n = 5).

We performed nonlinear least-squares fitting for ODE implementations of Models 1, 2, and 3 (Figure 4, Column 2). Model 1 is a special case of Model 2 with n = 1. The following is the system of ODEs for n = 5 latently-infected cell eclipse phase compartments, with no de novo infections. Note that the eclipse phase transition constant here is a times n (n = 5 in example below and in Figures 3B and 4C; transition constant a times n was abbreviated as a in these figures since n was constant). In addition, since ρ = μ, these terms cancel out of the ODE implementation with i = 1 to 4:

$$\frac{d{E}_0}{dt}=-an{E}_0$$

$$\frac{d{E}_i}{dt}=an\left(E_{i-1}-E_i\right)$$

$$\frac{dI}{dt}=an{E}_4-dI$$

$$\frac{dV}{dt}=pI-cV$$

This system of ordinary differential equations was solved numerically with the Runge-Kutta-Fehlberg based method ode23 in the R package deSolve. We performed nonlinear least-squares fitting of the model to the HIV RNA copies detected, averaged over the 225 limiting dilution wells (Figure 4B–4E), using the Levenberg-Marquardt algorithm within the Minpack R package minpack.lm.

We also implemented our models stochastically using Gillespie simulation. Of particular relevance for the stochastic implementation, unlike the ODE model, given ρ = μ these terms must be retained. The branching process model can be represented as a series of “chemical” reactions and a transition matrix.

In this model each reaction rate corresponds to a transition probability with an exponentially distributed delay time, represented in the figure diagrams (Figure 3B for this example) as arrows:

Stochastic Implementation Model 2 Transitions:

$E_i\stackrel{\mu }{\to }\otimes$		Eclipse phase cell death
$E_i\stackrel{\rho }{\to }2E_i$		Eclipse phase cell division
$E_i\stackrel{an}{\to }{E}_{i+1}$	i = 0 to 3	Transition to next eclipse compartment
$E_4\stackrel{an}{\to }I$		Transition to productive/compartment
$I\stackrel{\delta }{\to }\otimes$		Productive/cell death
$I\stackrel{p}{\to }V$		Virus release
$V\stackrel{c}{\to }\otimes$		Viral signal decay

Stochastic Model transition matrix for n = 5 eclipse phase compartments corresponding to Model 2

Reaction Rates (columns) vs. Model Compartment (rows)

μE0	μE1	μE2	μE3	μE4	ρE0	ρE1	ρE2	ρE3	ρE4	anE0	anE1	anE2	anE3	anE4	qI	δI	pI	cV
−1	0	0	0	0	1	0	0	0	0	−1	0	0	0	0	0	0	0	0	E0
0	−1	0	0	0	0	1	0	0	0	1	−1	0	0	0	0	0	0	0	E1
0	0	−1	0	0	0	0	1	0	0	0	1	−1	0	0	0	0	0	0	E2
0	0	0	−1	0	0	0	0	1	0	0	0	1	−1	0	0	0	0	0	E3
0	0	0	0	−1	0	0	0	0	1	0	0	0	1	−1	0	0	0	0	E4
0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	1	−1	0	0	I
0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	−1	V

This branching process model was implemented by direct method Gillespie simulation (Gillespie, 1977) using the GillespieSSA R library (Pineda-Krch, 2008).

A Weibull cumulative distribution function (CDF) was fit to the experimental limit of detection data (Figure 1E). To determine whether to report HIV RNA copies realized from Gillespie simulation as “detected,” we used the probability corresponding to those HIV RNA copies, given by the fit Weibull, in a Bernoulli trial with a binary result of “not detected” or “detected.” Consider an instance in which the Gillespie simulation realizes 70 HIV RNA copies at the day 2 collection. Based on the Weibull fit to the LOD data (Figure 1E) 70 HIV RNA copies has a 50% chance of detection. The reported HIV RNA copies “detected” from simulation will have a 50% chance of being zero, and a 50% chance of being 70.

We note that while the number of initial latently-infected CD4 T cells per replicate that gave rise to detectable HIV, Λ, could be estimated from the frequency of HIV RNA positive replicate wells at a given cell dilution using ELDA, some initial latently-infected CD4 T cell lineages beginning in compartment E₀ would become extinct before transitioning to a virus productive state I, and therefore go undetected. Thus, final model fitting would require an estimate of the initial number of latently-infected CD4 T cells, only some of which would give rise to detectable virus. Stochastic model sensitivity analysis indicated that for simulations, each starting from exactly 1 latently-infected cell at the beginning of the eclipse phase E₀, for a given n, the fraction of simulations resulting in detectable HIV, f_HIV, depended on ρ, μ, and a, but not p and δ, within a range of reasonable values given p ≫ δ.

Each replicate simulation was initiated with an integer number of latently-infected cells in the first compartment, including the integer 0. This integer was drawn randomly from a Poisson distribution with parameter Λ/f_HIV; Λ was derived from the original experiment (Table S2) using ELDA, and f_HIV, the fraction of initial single latently-infected cells that result in detectable HIV, derived as explained in the following paragraphs. Note that f_HIV < 1 for two reasons: 1) the lineage may go extinct before producing any virus, and 2) virus might be realized in Gillespie simulation, but it is below the assay detection limit. In addition, it was possible to draw 0 initial latently-infected cells from the Poisson distribution, and thus such a simulation could not realize an HIV release.

For each number of eclipse phase compartments n, we estimated the fraction of simulations, each starting from exactly 1 initial latently-infected cell giving rise to detectable HIV, f_HIV. We first needed to derive an estimate for a from the daily HIV RNA copies detected in the 225 limiting dilution virial inhibition wells, only 42 of which were positive (Figure 2A). Using a preliminary guess for the initial number of latently infected cells = 126 among 225 wells, we performed least-squares fitting on the deterministic ODE model, simultaneously obtaining a, δ, and p (Columns 2, 3, 4 respectively in Table S3) for each n, 1 through 10 (Column 1, Table S3). Of note, for this fitting, p, but not a and δ, was sensitive to the initial number of seeded latently infected cells in E₀.

As an example, for n = 5, we obtained a reasonable deterministic model fit resulting in a = 0.30/day, δ = 1.48/day and p = 1367/day (Similar to that in Figure 4C). These parameters, along with previously derived ρ = μ = 0.48/day and c = 0.22/day, were then used in stochastic simulations, each starting from 1 latently infected cell seeded in E₀. The fraction of n = 5 simulations resulting in detectable HIV (Column 5, Table S3) was f_HIV = 0.398 (again, this number was sensitive to ρ, μ, and a, but not δ and p). In the original 225 limiting dilution experimental wells, 42 were positive with an ELDA estimated 48 seeded latently infected CD4 T cells that each gave rise to detectable virus. Thus, the initial number of latently-infected cells in the original 225 wells (Column 6, Table S3), under the n = 5 model, was estimated as 48/0.398 = 121. Using this result, the deterministic model was then re-fit for n = 5, with an initial E₀ population = 121/225 (number of seeded latently infected cells per well averaged over 225 wells), resulting in a = 0.30/day, δ = 1.48/day, and p = 1423/day with the residual sum squared (RSS) = 875 [eclipse_phase-fit.R] (Figure 2C). The mean total release for one productively-infected cell over its entire release lifetime was p/δ = 965 HIV RNA copies.

We next compared simulations using the optimized parameter sets for each n to the experimental results from the 225 limiting dilution wells (Figure 2C & Figure S3). We performed 2000 simulations for each of the 225 experimental wells, for a total of 450,000 simulations for n = 1 to 10. Although the residual sum squared (RSS) for the deterministic fit was marginally lowest for n = 7, we found that n = 5 gave better overall agreement of the stochastic model with respect to the experimental total HIV RNA detected, time to first detection, and detection duration (Figures 2C and S3, Table S3). Also, the productively-infected cell lifetime for the n = 7 fit of 1.4 days (1/δ) approached the lifetime of a typical (non-infected) CD4 T cell of 2 days (1/μ). Thus, we favored the n = 5 model with a shorter productively infected cell lifetime of 0.7 days.

Nevertheless, even the n = 5 stochastic Model 2 underestimated the variability in total HIV RNA detected at both extremes, below 100 copies, and above 10,000 copies. Moreover, the stochastic model missed a population of latently-infected cells that yielded releases that were of short duration of less than 1 day, low magnitude less than 250 HIV RNA copies or less, and delayed 4 or more days.

Dual eclipse phase Model 3

We noted that the single eclipse phase yielded a unimodal distribution for total HIV RNA copies detected (Figure 4C), whereas the experimental was bimodal with highest frequencies around 100 and 2000 HIV RNA copies (Figure 4A). We reasoned that the missing population could be modeled by introducing an eclipse phase B, to result in Model 3, with new parameters initial transition into eclipse phase A, f_a, initial transition into eclipse phase B, f_b, transition from eclipse phase B compartments, b, and release rate from productively infected cell B, p^B. Parameters b and p^B were fixed to yield a long delay before a low magnitude release of short duration. f_a and f_b could in principle be fractions rather than rates, but we regard them as rates to facilitate use of them as a rate of latent cell reactivation in other applications. In this case, we simply made f_a and f_b much higher than the other transition rates a and b. A proportion f_a/(f_a + f_b) of the L_i compartment transitions to eclipse phase A, and f_b/(f_a + f_b) transitions to eclipse phase B. Fixing the 4 parameters f_a, f_b, b, and p^B we then performed nonlinear least-squares fitting of the ODE implementation to obtain unknowns a, p^A and δ. Through many cycles of fixing the 4 new parameters (f_a = 10.5/day, f_b = 5 /day, p^B = 112 /day, and b = 0.75 /day), and ODE fitting for a, p^A and δ, and simulation, we arrived at the parameter set in Table S4, and Figures 4D and 4G. For this parameter set in simulation, exactly 1 latently-infected cell in L_i, resulted in detectable HIV 41% of the time. Starting from an initial condition of 48/0.41 = 117, we obtained new estimates for the deterministic ODE fit of a = 1.5 /day (Bootstrap 95% CI 1.1 to 2.3), δ = 1.3 /day (Bootstrap 95% CI 0.4 to 1.9), and p^A = 2030/day (Bootstrap 95% CI 370 to 3600). Given that the stochastic simulations but not the ODE model account for the experimental HIV RNA limit of detection, we increased p^A = 2166/day (determined by cycles of simulation with small incremental increases to p^A) to further improve the stochastic model agreement with the data. We obtained improved fits for total HIV RNA detected, time to first positive, and HIV detection duration (Figure 3D). For all three outcomes, application of the Kolmogorov-Smirnov test indicated little evidence for a significant difference in the distributions from simulation versus experiment.

Notably, for the Model 3 best parameter set (Table S4), the eclipse phase B population represented just 1% of total HIV RNA detected. The Model 3 parameter set is not fully identifiable from the available data such that other combinations of f_a, f_b, and b may be found that would also result in concordance with both the ODE system and stochastic simulation. As discussed in the main text, eclipse phase A and B may correspond to central memory and effector memory populations respectively. Further research such as sorting these two populations and documenting the initial release from each subset in isolation would allow more specific parameter identification of Model 3. Moreover, because the relative proportions of CD4 T cell subsets will differ from donor to donor, ultimate identification of the Model 3 parameters would likely be donor specific.

To better understand our rationale for incorporating cell division and death into eclipse phase A, consider the opposing hypothesis that ρ = μ = 0. For ρ = μ = 0, we can fit the distribution for total HIV RNA copies detected by boosting the per productively infected cell HIV release rate (increase p^A), but this forces a shorter average detection duration and a lower frequency of multi-day sustained detections than that observed experimentally (Figure 4E). This is based on the assumption that the productively infected cell lifetime, 1/δ, does not itself have high variability. A way to fit all of the data assuming no cell division and death, might be to instead assume high variability in 1/δ. This would require many single productively infected cells to release virus for several days to be consistent with the observed sustained detections. We disfavor this hypothesis because such an extended release by a single cell would make it an easy “sitting duck” target for the immune system, which is difficult to reconcile with the fact that HIV has evolved to successfully evade most human immune systems. We instead favor Model 3 (Figure 4D) incorporating latent cell division and death because this leads to potentially covert amplification of the initial release which is consistent with evolutionary pressure to evade the immune system. Incorporation of cell division and death is also consistent with the natural proliferative outcome for CD4 T cells following vigorous stimulation (Figure 2D), the previous in vivo estimate of an average 1 day survival for a productively infected cell (Markowitz et al., 2003) and recent direct evidence of intact proviral amplification due to cell division (Bruner et al., 2019).

Simulating Model 3 with parameters in Table S4, on average, a single latently-infected cell resulted in 934 detected HIV RNA copies, although on an individual basis, just 41% gave rise to detectable virus. In particular, simulations of the limiting dilution experiments from Figure 2A predicted that 50% of initial HIV releases yielding greater than 10,000 HIV RNA copies resulted from stochastic proliferation originating from 1 latently-infected cell (e.g. Figure 4F simulation with 15400 HIV RNA copies), and 50% arising from 2 or more (e.g. Figure 4F simulation with 11200 HIV RNA copies). On the other hand, because of stochastic cell death and/or HIV release below the detection limit, many replicates that were negative for HIV were nevertheless seeded by 1 or more latently-infected cells (not shown in Figure 4F). When considering Figure 4F, recall limiting dilution pertains to the low frequency of HIV RNA positive replicates, statistically equivalent to the culture experiments (42 of 225, Figure 2A). The simulated initial latently-infected cells (Figures 4D and 4F) are not themselves at limiting dilution, because experimental determination of limiting dilution depends on the initial latently-infected cells that give rise to detectable virus. Hence, there are many “limiting dilution” simulations with relatively high numbers of initial latently-infected cells, e.g., 4 to 6 in Figure 4F.

Model 3 Predicts Trends in Data Not Used For Fitting

We next explored the predictive performance of the fit Model 3 on the non-limiting dilution experimental data not used for fitting. We performed stochastic simulations, using the parameters optimized on the limiting dilution data (Table S4), and using the initial number of seeded latently infected cells for 4 groups of experimental results that were not at limiting dilution corresponding to an expected 2.2, 3.9, 4.6, and 5.6 seeded latent cells per well (Figure S4 bottom 4 rows). These initial population sizes are corrected (The four highest Λ from Table S2 divided by 0.41) to account for latently-infected cells that did not give rise to detectable virus due to stochastic death or release below the detection limit.

For total HIV RNA detected per positive well (Figure S4, left), as the number of seeded latent cells increases, the model predicts that the frequency of high copy detections above 10000 should increase. Likewise, the frequency of very low detections below 100 should decrease. This indeed is the overall trend in the experimental data (Figure S4, left). However, there is additional variability in the experimental data that the model does not account for, perhaps variability among different donors or due to a low number of non-limiting dilution replicates.

For time to first positive (Figure S4, center), we have an outlier at 2 latently-infected cells, but otherwise the model predicts the experimental trend, which is the higher the number of initial latent cells, the earlier the first detection.

And finally, the higher the initial latent cells, the longer the detection duration should be on average (Figure S4, right). Again, the model correctly predicted the experimental trend. As the initial latently-infected cells increased, the distribution for detection duration shifted toward longer durations.

Toggling and Dispersion for Total V produced

For an alternative modeled source of dispersion for the initial HIV release, consider the simplified case of the basic 2-compartment model in which virus V is produced at rate p from the I compartment, which has a zero decay rate, δ = 0. Here, the total V produced is Poisson distributed (FF = 1), and this distribution does not change with introduction of an eclipse phase E of latently-infected cells that each can only activate at rate a_f to the I state (Model 1; Figure 3A with ρ = μ = 0 and δ = 0). This construct produces Poisson stochasticity in V, and is directly analogous to that used previously to model constitutive RNA transcription.

As opposed to a constitutive process, RNA transcription from the HIV long terminal repeat (LTR) promotor is episodic, occurring in short bursts interspersed with periods of low or zero transcription resulting in an ON-off-ON-off dynamic (Dar et al., 2012). This can be modeled by introducing a reverse transition from I to E, at rate a_r, with parameterization of a_f / a_r ~ 0.1 (Hansen et al., 2018), such that transcription toggles from ON in state I to off in state E, and vice versa (E ↔ I, also known as random telegraph model) and the distribution for total V produced goes from Poisson for a_r = 0 (constitutive, no toggling) to super-Poisson for a_r > 0 (bursty, with toggling), with FF > 1. For a specific example, consider the parameterization a_f = a_r = 0, δ = 0, and p = 1000. 10000 Gillespie simulations each with an initial condition I = 1, E = 0, V = 0 to time = 12 results in a mean total V production of 12001, with FF = 1.0, as expected for a Poisson process. Introduction of toggling with a_f = 0.3, a_r = 3, δ = 0, and p = 1000 results in a mean total V production of 1370 with FF = 445. Under the assumption δ = 0, introduction of E ↔ I toggling increases dispersion for total V produced above that of Poisson.

However, the assumption of δ = 0 for I, i.e. an infinite lifetime for an HIV producing cell, is not realistic. If this were the case, then there would not be a rapid viral load decline upon initiation of ART. Modeling of in vivo viral load decay after initiation of ART has resulted in an estimate on the order of δ = 1 /day (Markowitz et al., 2003). As discussed earlier in this section, for δ > 0, such as δ = 1 /day, the dispersion without toggling is Geometric, i.e. already super-Poisson with FF = Mean + 1. Without toggling, Gillespie simulation with a_f = a_r = 0, δ = 1, and p = 1000 yields for total V produced, mean = 997 and FF = 993, consistent with a geometric distribution. Introduction of toggling with a_f = 0.3, a_r = 3, δ = 1, and p = 1000 yields a mean total V produced of 665 and FF = 445; the dispersion decreases, becoming sub-geometric. Adjusting p to result in the same mean total V produced in simulation, with a_f = 0.3, a_r = 3 δ = 1, and p = 1490 yields for V, a mean = 1002 and FF = 667. A FF less than the mean for total V produced also occurs when reversing the toggle with a_f = 3, a_r = 0.3, δ = 1, and p = 1490. In summary, for the case in which we assume I cell death (δ > 0), the introduction of toggling results in a decrease in dispersion for total V produced, as measured by FF.

This finding is further confirmed in Gillespie-based direct simulation that additionally accounts for the Poisson distributed latently-infected cells among wells, daily culture virus dilution, and the experimental limit of detection in which the parameters are adjusted so that the simulation results closely match the means for total HIV detected (2600 HIV RNA copies), time to first HIV detected (4.1 days), and detection duration (2.5 days), across the 42 HIV RNA positive limiting dilution wells. Consider Model 1 in which we introduce E ↔ I toggling such that ρ = μ = 0, a_f = 0.22, a_r = 2.2, δ = 1.3, and p = 4850 (each parameter with unit/day); this results for total HIV detected a mean 2661, and FF just 2128, again with FF < mean. For ρ = μ = 0.5, a_f = 0.048, a_r = 0.8, δ = 1.5, and p = 3000 (each/day) results in a total HIV detected mean 2547 and FF 2619. Although the FF marginally increased in the case allowing for division and death in the E compartment, it is still far below the experimental FF and that generated from the fit Model 3 of about 5200. In addition, just as with the non-toggling case (Figure 4B) we could find no parameterizations for a Model 1 E ↔ I toggle for which we could fit the ODE model to the average HIV RNA detected.

To the 5 eclipse phase compartment model (Figure 3B), we next incorporated E₄ ↔ I toggling and explored parameterizations that were limited to a_f4 / a_r4 = 1, 2, 4, 5, 0.01, 0.1, or 0.5. For a_f4 / a_r4 ≤ 4, we were able to obtain good ODE fits (similar to Figures 4C–4E) to the average HIV RNA detected and obtained parameters for a, δ, p, and a_f4. a_f4 / a_r4 = 5 and above resulted in a poor ODE fit. We found that to obtain in simulation a FF for total HIV detected in the 5000–6000 range as in experiment, ρ4 = 3 and μ4 = 0.5, or ρ4 = 2.6 and μ4 = 0.1 would work for the toggled eclipse compartment, with ρ = μ = 0.5 for the eclipse phase compartments 0 to 3. Hence, to match the experimental FF for total HIV detected, we had to assume rates for CD4 T cell division and/or death that were not realistic, conflicting with those derived from experiment. This was also the case for a two toggle E₃ ↔ E₄ ↔ I model. Although the dispersion as measured by FF could be made equivalent using unrealistic rates of cell division, the simulated distributions were still unimodal with a very low frequency of release detections less than 100 HIV RNA copies, unlike that observed experimentally and with the fit Model 3.

Toggling could potentially be used to model the variability in timing of HIV production, particularly for culture replicates in which HIV detection occurs, followed by a period of no detection, and then a second detection. For Model 3 (Figure 3C, without toggling), this ON-off-ON-off dynamic arises due to more than 1 latently infected cell seeded in a well on day 0 giving rise to virus at different times, through stochastic proliferation from an original single latent cell with transition to the productive state at different times, or consecutive presence of HIV at the detection limit. Toggling could be an additional mechanism by which the ON-off-ON-off dynamic arises. Due to the overall complexity and inability to distinguish among specific mechanisms, we have opted to leave toggling out of our core Model 3, but it could be further explored in future experimental and modeling work, particularly for a less heterogenous CD4 T cell population.

Summary

The stochastic Model 3 provides useful framework to understand and predict the process of initial HIV release arising directly from the reservoir following latency disruption. In particular the model features the role of cell division in amplifying the magnitude and temporally extending the total HIV release, and initial latently-infected cell lineages that go extinct without giving rise to detectable virus. It accounts for heterogeneity in CD4 T cell subsets through the use of two eclipse phases. Interestingly, the 2 eclipse phase model (Figure 4D) leading to high and low producers I^A and I^B respectively, fit much better than a single eclipse phase model (Figure 4C), formalizing a hypothesis that virus arises from two cell compartments, such as central memory and effector memory, each with distinct potentials for virus release, as mentioned in the Discussion section. Model 3 with the proposed parameterization (Table S4), defined solely with simple exponential transition rates, quantitatively accounts for the variability in the timing and magnitude of HIV RNA release in the viral inhibition cultures.

Additional Quantitative Analyses

Statistical methods were not used to predetermine sample size, and the investigators were not blinded for experimental allocation or analysis. There was no randomization of experiments.

Kolmogarov-Smirnov tests to compare distributions were performed using ks.test within the stats R library (Figures 4, S3, and S4). Two sample Welch t-tests (t.test in R stats library) were performed to compare the per latently infected cell HIV detection for wells with less than or equal to 1 expected latently-infected cell with wells with greater than 1 expected latently-infected cell (Figure 6B and 6C).

The 95% confidence intervals for outgrowth establishment probability (Figures 6A and S6, red vertical lines) were calculated using previously published R code (Kaul et al., 2016).

The 95% confidence intervals for parameters during deterministic fitting were constructed using a percentile bootstrap procedure ((Efron and Tibshirani, 1993); Section 13.3) from 1000 bootstrap data sets. Each bootstrap data set was generated in a way that preserved the design of the study. Specifically, among the 225 limiting dilution wells, those with the same donor ID and number of cells/well were grouped together, resulting in ten distinct groups. To generate a single bootstrap dataset, wells were sampled with replacement within each of the ten groups. Thus, each bootstrap dataset also had ten groups; further, the number of wells in a group within each bootstrap dataset also matched the number of wells in each group in the original dataset. Parameter estimates for each bootstrap dataset were then obtained by fitting the same deterministic system of ordinary differential equations that was used for the original dataset.

The 95% confidence intervals for viral inhibition simulations (Figure 4) were obtained by a simplified bootstrap sampling method to estimate the range of the mean value given the number of experimental replicates. As an example, for the experimental 225 limiting dilution wells, 42 were HIV RNA positive. Each of the individual wells within these 225 limiting dilution wells was simulated 2000 times, for a total of 450,000 simulations. Thus, from these 450,000 simulations, a random sample of 225 simulations was drawn with replacement, and the means were calculated for total HIV RNA copies detected, time to first positive, and detection duration. This was done 2000 times, to obtain a list of 2000 means, for each. Each of the 3 mean lists were sorted from lowest to highest, and the values at the 2.5% and 97.5%iles were taken as the limits of the 95% confidence interval.

To calculate the establishment probability P_est for an exact number of latently infected cells x (Figure 7), we used the binomial distribution to determine the probability of each possible number of initial cells giving rise to detectable virus and multiplying that with P_est(x), as in (Kaul et al., 2016), given by the Weibull_CDF [5] (k = 2.2 and λ = 3.7 obtained from fitting Equations [1] and [6a] (Figure 6A and 6D)). The sum of these products was reported as the establishment probability.

DATA AND CODE AVAILABILITY

Guide for Accessing Data and Code

The viral sequencing data has been deposited at Genbank (https://www.ncbi.nlm.nih.gov/genbank/) with accession numbers MN515491-MN516420, corresponding to 930 HIV env sequences. Each HIV env sequence has a header indicating the Donor ID, experimental culture set, culture well, and clone in the format: “>DonorID#.experimental-set#.culture-well#.clone#”.

The HIV RNA copy data for each experimental set (in table format and plotted in a single PDF file) and R code for mathematical modeling and analysis are available in a zipped file, “code-data-HatayeJ.zip” and can be accessed on the Dryad Digital Repository (https://datadryad.org) and using “doi:10.5061/dryad.wdbrv15j3” as the Digital Object Identifier, which can be placed into a web browser address bar.

Computer code in this study was written in R or Stan within an R script, implemented using rstan 2.17 and 2.18 interfaces. Scripts were tested and run on R 3.4.2 using RStudio 1.0.153. Several other versions of R have also worked. We tried but could not run rstan using Microsoft R Open. Each script has been successfully run on Mac OS 10.12.6. Both the stochastic simulations and Stan analyses have been run on Ubuntu 16.04 workstations and on the NIAID Locus High Performance Computing cluster running Red Hat Enterprise Linux Server 7.2.

We recommend using a workstation with 4 or more CPU cores with optional use of cluster; the stochastic simulations and Stan code scripts are written to be run in parallel. Here are the steps needed to run the code, which should take about 2 hours:

• 1Install R. https://www.r-project.org
• 2Install Rstudio. https://www.rstudio.com
• 3
  Install R libraries.

  • R libraries needed:
  • deSolve, doMC, dplyr, foreach, ggplot2, GillespieSSA, Hmisc, iterators, loo, MASS, minpack.lm, plyr, RColorBrewer, rstan, scales, statmod. In RStudio, use the “Install” button under the “Packages” tab and enter the name of the package.

• 4Install Stan. https://github.com/stan-dev/rstan/wiki/RStan-Getting-Started
• 5Uncompress the file “code-data-HatayeJ.zip”. This can be done on Mac OS X or Ubuntu by placing this file on the Desktop, and then double clicking on it. If you put the zip file on the Desktop, this will hopefully correspond to the path set in the code.
• 6Place experimental and simulation data files in path, if needed. Many of the scripts require the experimental data tables HIVrna1.txt and HIVrna2.txt, or simulation data tables. To run the script, these files must be placed in a directory and referred to in the script using setwd(“put the path here”). In each script, the setwd is set to setwd(“~/Desktop/code-data-HatayeJ/….”) such that if you unzip the “code-data-HatayeJ.zip” file in “~/Desktop” the code as written should work.

To verify the integrity (verify intact download) of the “code-data-HatayeJ.zip” file, one can check the SHA-256 hash of this file. On Mac OS X, this can be done by opening a terminal, typing “cd Desktop” to change to the Desktop directory (if you put the file there), and typing “shasum -a 256 code-data-HatayeJ.zip”. On a Linux system the command is “sha256sum code-data-HatayeJ.zip”. The SHA-256 hash of “code-data-HatayeJ.zip” is:

92fff454a014518690deb0c2f29592b17993cdc1566db6ef5cf019d3552c99e9

Note that this hash on the “code-data-HatayeJ.zip” file will be different than the hash done on the zip package “doi_10.5061/dryad.wdbrv15j3_v2.zip” which is a zipped version made by Dryad. To check the SHA-256 hash of “code-data-HatayeJ.zip” one needs to first unzip that file downloaded from Dryad. We’ve gathered the most important files here. Additional files are available upon request.

Contents of code-data-Hataye.zip

Experimental Data Tables & Plots

/expData

HIVrna1.txt

HIV RNA detection data from primary ex vivo culture experiments, comprising sets 126, 132, 135, 145, 159, 163, 166, 210, 211, 223, 224, 229, 230, 236, 237.

HIVrna2.txt

HIV RNA detection data from secondary (Sets 169 and 180) and tertiary (Set 273) culture experiments.

exp-set-plots.pdf

PDF document containing plots of HIV RNA copies in culture supernatant for each experimental set.

Simulation Data Tables

/simData/2eclipse

ws-vinh225.txt, dfmini-vinh225.txt, and ss-vinh225.txt

Summary results of running stochastic-2eclipse-225LDwells.R, for a total of 225 × 2000 simulations of Model 3 (parameters Table S4). These results comprise Figure 4 (orange). Running these took several days using 8 cores. However, a smaller run can be done to roughly reproduce the results. For example, one could do 225 × 1 simulations (less than 1 hour to complete), to see the range of HIV RNA positive simulations that result.

/simData/2eclipse

ws-210w.txt and ss-210w.txt

ws-211w.txt and ss-211w.txt

ws-223w.txt and ss-223w.txt

ws-236w.txt and ss-236w.txt

Summary results of running stochastic viral inhibition simulations of Model 3 (parameters Table S4), corresponding to experimental sets 210, 211, 223, and 236. Together with ws-vinh225.txt and ss-vinh225.txt, these results comprise Figure S4.

/simData/1eclipse

n is an integer from 1 to 10

wsLn-42well-8MC-test.txt

ssLn-42well-8MC-test.txt

Summary results running stochastic simulations for Model 2, n = 1 to 10 eclipse phase compartments (Figure 4B shows n = 1 and Figure 4C shows n = 5), for Figure S3.

/simData/2eclipse0rho0mu

dfglobal42.txt

dfmini42.txt

ss-42w.txt

ws-42w.txt

Summary results running stochastic simulations for Model 3, for Figure 4E in which ρ = μ = 0/d.

Plotting and analysis

/figuresCode

To make a plot, open the script in RStudio, press “Source” and then copy/paste the plot code (near the end of the script) into the RStudio console.

assay-LOD.R

Fits HIV RNA RT-PCR limit of detection data to Weibull CDF, for Figure 1E; This fit Weibull was used (for stochastic simulation) to determine whether to report as detected HIV RNA realized from Gillespie simulation.

v_inhibition_plots.R

This takes as input HIV RNA detection data (HIVrna1.txt) and makes plots for Figure 2A and individual plots for each set.

v_inhibition_distributions.R

This takes as input HIV RNA detection data (HIVrna1.txt) and stochastic simulation data (ws-vinh225.txt and ss-vinh225.txt, ws-210w.txt and ss-210w.txt, ws-211w.txt and ss-211w.txt, ws-223w.txt and ss-223w.txt, ws-236w.txt and ss-236w.txt) and makes histograms of total HIV RNA detected, time to first HIV detection, and detection duration. It performs Kolmogorov-Smirnov comparison of experimental vs. simulation distributions. It generates the distribution histograms in Figure 4 and the density plots in Figures 7A–E.

4culture_plot.R

This takes as input HIV RNA detection data from primary cultures (HIVrna1.txt) and secondary cultures (HIVrna2.txt) and makes individual plots for each set.

stacked_outgrowth.R and stacked_inhibition.R

These take as input HIV RNA detection data from primary cultures (HIVrna1.txt) and secondary cultures (HIVrna2.txt) and makes plots respectively for Figures 5B and 5A.

stacked_vmax.R

This takes as input HIV RNA detection data from primary cultures (HIVrna1.txt) and secondary cultures (HIVrna2.txt) and makes plots respectively for Figures 5C and S5.

tertiary_plot.R

This takes as input HIV RNA detection data from tertiary culture Set 273 (HIVrna2.txt) and makes plots.

tertiary_stacked.R

This takes as input HIV RNA detection data from tertiary culture Set 273 (HIVrna2.txt) and makes plot for Figure 5D.

plot-sim42LDwells.R

This takes as input simulation data from ws-vinh225.txt, ss-vinh225.txt, dfmini-vinh225.txt and makes the plot in Figure 4F.

binomial-weibull-Pest.R

This calculates establishment probability for Figure 7 for exact numbers of initial latently-infected cells using the binomial distribution with f_HIV=0.41 (from fitting Model 3 to Figure 2A data, Figures 4D and 4F) with the Weibull CDF (parameters from fitting [1] and [6a] to data) and produces Figure 7H.

Statistical Analysis using Stan

/stanCode

Each of these scripts may be run parallel; set the number of CPU cores on the line that calls stan(….cores=8…..…).

elda_v_stan_vinh.R

This takes as input HIV RNA detection data from primary cultures (HIVrna1.txt) and obtains estimates for the frequency of HIV RNA releasing CD4 T cells for each of 7 donors using ELDA, and an equivalent Stan-based implementation for viral inhibition wells (Table S5).

elda_v_stan_outg.R

This takes as input HIV RNA detection data from primary cultures (HIVrna1.txt) and obtains estimates for the frequency of HIV RNA releasing CD4 T cells for each of 7 donors using ELDA, and an equivalent Stan-based implementation for viral outgrowth condition wells (Table S5).

2Fish.R

This takes as input HIV RNA detection data from primary cultures (HIVrna1.txt) and performs a Stan-based implementation to fit the model incorporating [1] and [6] against the viral outgrowth condition well data. g(x) can be based on a Weibull, Gamma, or Hill function (Chosen in the code by commenting out the other 2 in both the model block and generated quantities block) with X ~ Poisson(Λ). This script will determine estimates for parameters k, λ, and 1/π_d for the respective g(x) in [6]. Results refer to Figures 6A, 6D–6E, S6, Table S6.

indep2Fish.R

This takes as input HIV RNA detection data from primary cultures (HIVrna1.txt) and obtains estimates for the frequency of HIV RNA releasing CD4 T cells for each of 7 donors using ELDA, and a Stan-based implementation for fitting the model incorporating [1] and [4], with X = Poisson(Λ), Figures 6A and S6 and Table S7. g(x) = (1 − θ)^x in [3] for pure independence model incorporating [1] and [4].

Nonlinear least squares fitting of deterministic ODE models

/ODEfitCode

CFSE_fit-nls.R

This script contains CFSE dilution flow cytometry data acquired 5 days after CFSE staining and culturing isolated resting memory CD4 T cells from an HIV-uninfected donor in the presence of stimulation particles (Figure 2D). To these data, it fits an ODE model of cell division and death (Figure 2E).

eclipse_phase_fit.R

This script contains HIV RNA detection data from Figure 2A, the total HIV RNA copies detected on each day, averaged over the 225 limiting dilution wells. It then fits eclipse phase ODE models with n = 1 to n = 10 eclipse phase latently-infected cell compartments to this data. Figures 3A and 3B show model diagrams, and Figures 4B and 4C show ODE fits.

2eclipse_phase_fit.R

This script contains HIV RNA detection data from Figure 2A, the total HIV RNA copies detected on each day, averaged over the 225 limiting dilution wells. It then fits the 2 eclipse phase ODE model in Figure 3C, and produces the ODE fits for Figures 4D and 4E.

Stochastic Simulations of Compartmental Models

/simCode

Each of these scripts utilizes the GillespieSSA (Pineda-Krch, 2008) library to perform direct Gillespie simulation (Gillespie, 1977) and the doMC library to perform these in parallel; set the number of CPU cores by editing nthreads=4.

exp-growth-Gillespie.R

This is a demonstration script that performs Gillespie simulation for a simple model of exponential growth with one compartment, with a birth rate of 2 and a death rate of 1, and starting from an initial number of cells ranging from 1 to 10. The corresponding deterministic model is y = y₀exp(x).

stochastic-1eclipse-225LDwells.R

This script performs simulations of Models 1 and 2 (Figure 3A and 3B) and includes the expected lambdas calculated using ELDA from each of the limiting dilution experiments in Fig. 2A. This script performs stochastic simulations using n = 1 to 10 single eclipse phase latently-infected cell compartments (Figure 4B and 4C, Figure S3). Choices include but are not limited to the initial number of latently infected cells to start with, the number of simulations to run, the number of CPU threads for parallel computation, and the model parameters. Depending on model parameters and the number of simulations, etc., this script can take a very long time to run. The script is set to run 225 × 1 simulations (about 1 minute to run) for n = 5 latent cell compartments, but reported results utilized 225 × 2000 simulations to produce the output in /simData/1eclipse (Figure 4B–4C and S3).

stochastic-2eclipse-225LDwells.R

This script performs simulations of Model 3 (Figure 3C) and includes the expected lambdas calculated using ELDA from each of the limiting dilution experiments in Figure 2A. These results are used to seed individual simulations with an initial number of latently infected cells. The script is set to run 225 × 1 simulations (about 1 minute to run), but reported results utilized 225 × 2000 simulations to produce the output in /simData/2eclipse, specifically ws-vinh225.txt, dfmini-vinh225.txt, and ss-vinh225.txt. (Figure 4D and 4F). After running 225 × 1 simulations, copy the print code at the bottom into the Rstudio console to view the simulations that resulted in HIV RNA release to produce unique plot like Figure 4F.

EIV-toggle-Gillespie.R

This script does Gillespie simulation with toggling between E <-> I compartments for Model 1 (Figure 3A) and was used to generate toggling results in STAR Methods.

KEY RESOURCES TABLE

Please see separate document.

Main Figures Code Index

Figure 1E figuresCode/assay-LOD.R

Figure 2A figuresCode/vinhibition_plots.R

Figure 4B–C simCode/stochastic-1eclipse-225LDwells.R ODEfitCode/eclipse_phase_fit.R figuresCode/v_inhibition_distributions.R

Figure 4D–F simCode/stochastic-2eclipse-225LDwells.R ODEfitCode/2eclipse_phase_fit.R figuresCode/v_inhibition_distributions.R figuresCode/plot-sim42LDwells.R

Figure 5A figuresCode/stacked_inhibition.R

Figure 5B figuresCode/stacked_outgrowth.R

Figure 5C figuresCode/stacked_vmax.R

Figure 5D–E figuresCode/tertiary_stacked.R

Figure 6A, 6D–E stanCode/2Fish.R

Figure 6B figuresCode/synergy-for-virus-release.R

Figure 6C figuresCode/synergy-for-outgrowth.R

Figures 7A–E figuresCode/v_inhibition_distributions.R figuresCode/binomial-weibull-Pest.R

Figure 7H figuresCode/binomial-weibull-Pest.R

Highlights.

• Transition from latency to exponential HIV growth is covert, rare, and stochastic

• After latency disruption, the initial HIV release amount is highly variable

• If the initial virus release exceeds a critical threshold, exponential spread ensues

• Coupling experimental and computational approaches can define the origin of HIV rebound