A large-scale standardized physiological survey reveals functional organization of the mouse visual cortex

Summary

To understand how the brain processes sensory information to guide behavior, we must know how stimulus representations are transformed throughout the visual cortex. Here we report an open, large-scale physiological survey of activity in the awake mouse visual cortex: the Allen Brain Observatory Visual Coding dataset. This publicly available dataset includes cortical activity from nearly 60,000 neurons from 6 visual areas, 4 layers, and 12 transgenic mouse lines from 243 adult mice, in response to a systematic set of visual stimuli. We classify neurons based on joint reliabilities to multiple stimuli and validate this functional classification with models of visual responses. While most classes are characterized by responses to specific subsets of the stimuli, the largest class is not reliably responsive to any of the stimuli and becomes progressively larger in higher visual areas. These classes reveal a functional organization wherein putative dorsal areas show specialization for visual motion signals.

Introduction

Traditional understanding, based on decades of research, is that visual cortical activity can be largely characterized by responses to a specific set of local features (modeled with linear filters followed by nonlinearities) and that these features become more selective and specialized in higher cortical areas^1–4. However, it remains unclear to what extent this understanding can account for the whole of V1^5–7, let alone the rest of visual cortex. A key challenge results from the fact that this understanding is based on many small studies, recording responses from different stages in the circuit, using different stimuli and analyses⁵. The inherent experimental selection biases and lack of standardization of this approach introduce additional obstacles to creating a cohesive understanding of cortical function. On the basis of these issues, influential reviews have questioned the validity of this standard model^5–7, and have argued that “What would be most helpful is to accumulate a database of single unit or multi-unit data that would allow modelers to test their best theory under ecological conditions.”⁵ To address these issues, we conducted a survey of visual responses across multiple layers and areas in the awake mouse visual cortex, using a diverse set of visual stimuli. This survey was executed in pipeline fashion, with standardized equipment and protocols and with strict quality control measures not dependent upon stimulus-driven activity (Methods).

Previous work in mouse has revealed functional differences among cortical areas in layer 2/3 in terms of the spatial and temporal frequency tuning of neurons in each area^8,9. However, it is not clear how these differences extend across layers and across diverse neuron populations. Here we expand such functional studies to include 12 transgenically defined neuron populations, including Cre driver lines for excitatory populations across 4 cortical layers (from layer 2/3 to layer 6), and for two inhibitory populations (Vip and Sst). Further, it is known that stimulus statistics affect visual responses, such that responses to natural scenes cannot be well predicted by responses to noise or grating stimuli^10–15. To examine the extent of this discrepancy and its variation across areas and layers, we designed a stimulus set that included both artificial (gratings and noise) and natural (scenes and movies) stimuli. While artificial stimuli can be easily parameterized and interpreted, natural stimuli are closer to what is ethologically relevant. Finally, as recording modalities have enabled recordings from larger populations of neurons, it has become clear that populations might code visual and behavioral activity in a way that is not apparent by considering single neurons alone¹⁶. Here we imaged populations of neurons (mean 173 ± 115, st. dev, excitatory populations, 19 ± 11, inhibitory populations) to explore both single neuron and population coding properties.

We find that 77% of neurons in the mouse visual cortex respond to at least one of these visual stimuli, many showing classical tuning properties, such as orientation and direction selective responses to gratings. These tuning properties exhibit differences across cortical areas and Cre lines. While subtle differences do exist between the excitatory Cre lines, these populations are largely similar; the more marked differences are among the inhibitory interneurons. The responses to all stimuli are highly sparse and variable. We find that the variability of responses is not strongly correlated across stimuli, in general, but it does reveal evidence of functional response classes. We validate these functional response classes with a model of neural activity that contains most of the basic features found in visual neurophysiological modeling (e.g. “simple” and “complex” components) as well as the running speed of the mouse. For one class of neurons, these models perform quite well, predicting responses to both artificial and natural stimuli equally well. However, for many neurons, the models provide a poor description, particularly those in our largest single class of neurons, those that respond reliably to none of our visual stimuli. The representation of these response classes across areas reveals a separation of motion processing from spatial computations. These results demonstrate the importance of a large, unbiased survey for understanding neural computation.

Results

Using adult C57BL/6 mice (mean age 108 ± 16 days st. dev) that expressed a genetically encoded calcium sensor (GCaMP6f) under the control of specific Cre-drivers lines (10 excitatory lines, 2 inhibitory lines), we imaged the activity of neurons in response to a battery of diverse visual stimuli. Data was collected from 6 different cortical visual areas (V1, LM, AL, PM, AM, and RL) and 4 different cortical layers. Visual responses of neurons at the retinotopic center of gaze were recorded in response to drifting gratings, flashed static gratings, locally sparse noise, natural scenes, and natural movies (Figure 1f), while the mouse was awake and free to run on a rotating disc. In total, 59,610 neurons were imaged from 432 experiments (Table 1). Each experiment consisted of three one-hour imaging sessions, with 33.6% of neurons matched across all three sessions; the rest were present in either one or two sessions (Methods).

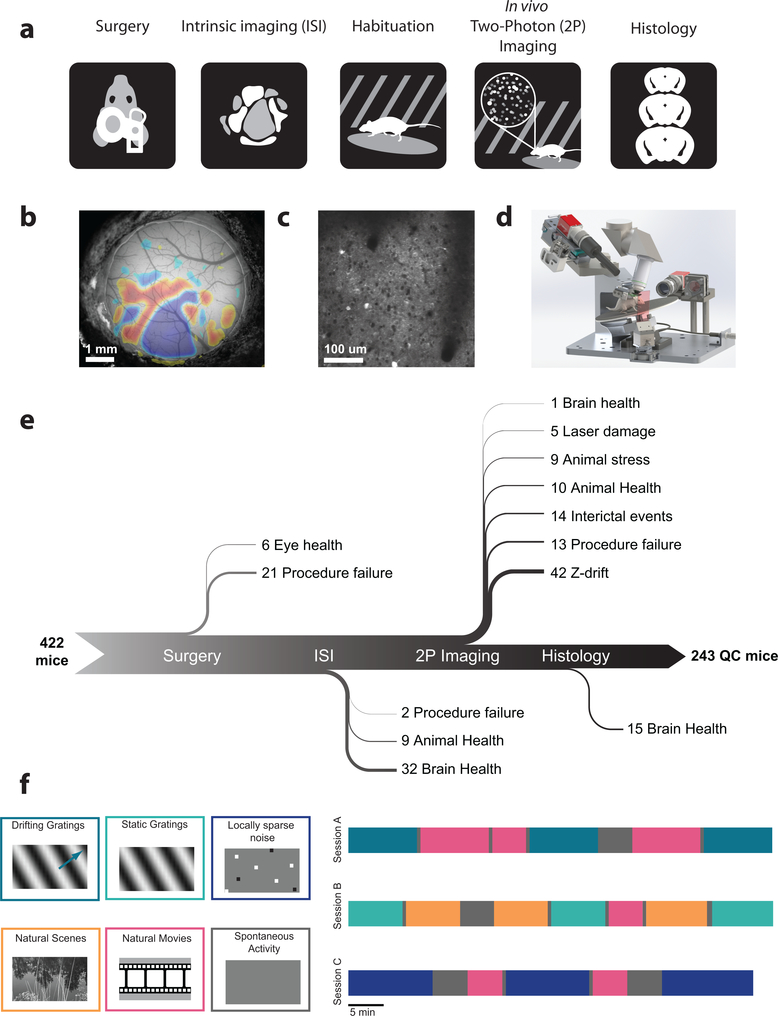
Figure 1: A standardized systems neuroscience data pipeline to map visual responses.

(a) Schematic describing the workflow followed by each mouse going through our large scale data pipeline. (b) Example intrinsic imaging map labelling individual visual brain areas. (c) Example averaged two photon imaging field of view (400 μm x 400 μm) showcasing neurons labeled with GCaMP6f. (d) Custom design apparatus to standardize the handling of mice in two photon imaging. We engineered all steps of the pipeline to co-register data and tools, enabling reproducible data collection (Supplementary Figures 13–16). (e) Number of mice passing Quality Control (QC) criteria established by Standardized Operating Procedures (SOPs) at each step of the data collection pipeline with their recorded failure reason. The data collection pipeline is closely monitored to maintain consistently high data quality. (f) Standardized experimental design of sensory visual stimuli to map responses properties of neurons across the visual cortex. 6 blocks of different stimuli were presented to mice (left) and were distributed into 3 separate imaging session called session A, session B and session C across different days (right).

Table 1: Visual coding dataset.

The number of cells (and experiments) imaged for each Cre line in each cortical visual area. In total, 59,610 cells imaged in 432 experiments in 243 mice are included in this dataset.

Cre line	Layers	E/I	n (M/F)	Age range (days)	V1	LM	AL	PM	AM	RL
Emx1-IRES-Cre; Camk2a-tTA; Ai93	2/3,4,5	E	18 (13/5)	73–156	3073 (10)	2098 (8)	1787 (7)	835 (4)	457 (3)	2152 (9)
Slc17a7-IRES2-Cre; Camk2a-tTA; Ai93	2/3,4,5	E	31 (20/11)	80–149	4840 (17)	3230 (16)	374 (2)	1970 (15)	235 (2)	137 (2)
Cux2-CreERT2; Camk2-tTA; Ai93	2/3, 4	E	38 (26/12)	79–155	5081 (16)	2792 (11)	3103 (13)	2361 (13)	1616 (11)	1578 (12)
Rorb-IRES2-Cre; Camk2a-tTA; Ai93	4	E	24 (14/10)	77–141	2218 (8)	1191 (6)	1242 (6)	764 (7)	735 (8)	1126 (5)
Scnn1a-Tg3-Cre; Camk2a-tTA; Ai93	4	E	7 (3/4)	75–133	1873 (9)
Nr5a1-Cre; Camk2a-tTA; Ai93	4	E	23 (15/8)	78–168	578 (8)	421 (6)	220 (6)	331 (7)	171 (6)	1354 (6)
Rbp4-Cre_KL100; Camk2a-tTA; Ai93	5	E	23 (11/12)	68–144	458 (7)	485 (7)	441 (6)	509 (6)	355 (8)	93 (4)
Fezf2-CreER;Ai148 (corticofugal)	5	E	8 (4/4)	88–134	407 (4)	981 (5)
Tlx3-Cre_PL56;Ai148 (cortico-cortical)	5	E	7 (5/2)	74–136	1181 (6)	946 (3)
Ntsr1-Cre_GN220;Ai148	6	E	10 (5/5)	79–134	573 (6)	719 (7)		581 (5)
Sst-IRES-Cre;Ai148	4, 5	I	30 (20/10)	67–154	266 (17)	301 (15)	24 (1)	247 (14)		46 (2)
Vip-IRES-Cre;Ai148	2/3, 4	I	24 (7/17)	81–148	352 (17)	315 (17)		387 (16)

In order to systematically collect physiological data on this scale, we built data collection and processing pipelines (Figure 1). The data collection workflow progressed from surgical headpost implantation and craniotomy to retinotopic mapping of cortical areas using intrinsic signal imaging, in vivo two-photon calcium imaging of neuronal activity, brain fixation, and histology using serial two-photon tomography (Figure 1a,b,c). To maximize data standardization across experiments, we developed multiple hardware and software tools (Figure 1d). One of the key components was the development of a registered coordinate system that allowed an animal to move from one data collection step to the next, on different experimental platforms, and maintain the same experimental and brain coordinate geometry (Methods). In addition to such hardware instrumentation, formalized standard operating procedures and quality control metrics were crucial for the collection of these data over several years (Figure 1e).

Following data collection, fluorescence movies were processed using automated algorithms to identify somatic regions of interest (ROIs) (Methods). Segmented ROIs were matched across imaging sessions. For each ROI, events were detected from ΔF/F using an L0-regularized algorithm¹⁷ (Methods). The median average event magnitude during spontaneous activity was 0.0004 (a.u., event magnitude shares the same units as ΔF/F), and showed some dependence on depth and on transgenic Cre lines (Extended Data 1).

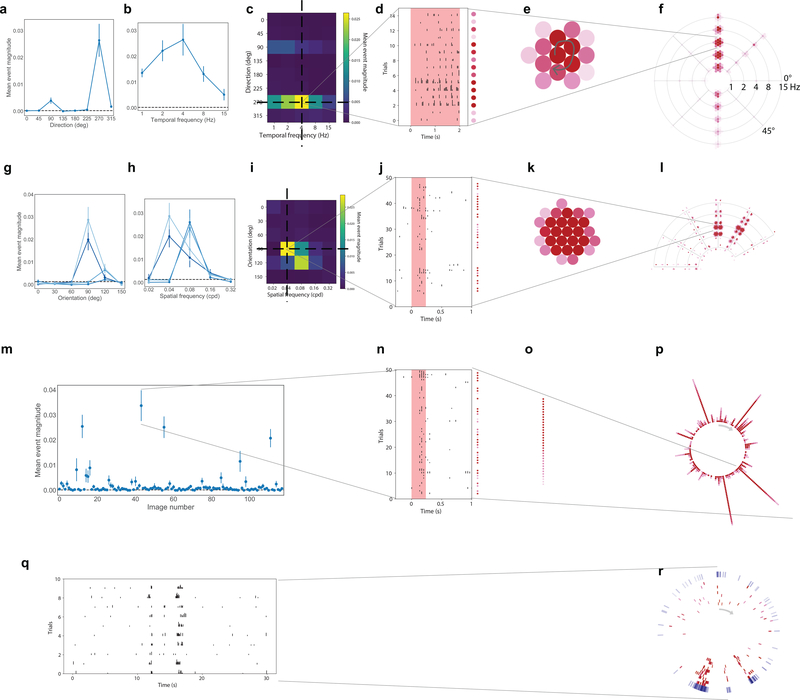
For each neuron, we computed the mean response to each stimulus condition using the detected events, and parameterized its tuning properties. Many neurons showed robust responses, exhibiting orientation-selective responses to gratings, localized spatial receptive fields, and reliable responses to natural scenes and movies (Figure 2a–f, Extended Data 2). For each neuron and each categorical stimulus (i.e. drifting gratings, static gratings, and natural scenes), the preferred stimulus condition was identified as the one which evoked the largest mean response for that stimulus (e.g. the orientation and temporal frequency with the largest mean response for drifting gratings). For each trial, the activity of the neuron was compared to a distribution of activity for that neuron taken during the epoch of spontaneous activity, and a p-value was computed. If at least 25% of the trials of the neuron’s preferred condition had a significant difference from the distribution of spontaneous activities (p<0.05), the neuron was labelled responsive to that stimulus (Methods has responsiveness criteria for locally sparse noise and natural movies). Neurons meeting this criterion showed a change in activity with some degree of reproducibility across trials. The maximum evoked responses were an order magnitude larger than the spontaneous activity (Extended Data 1, median 0.006 (a.u.) for neurons responsive to drifting gratings).

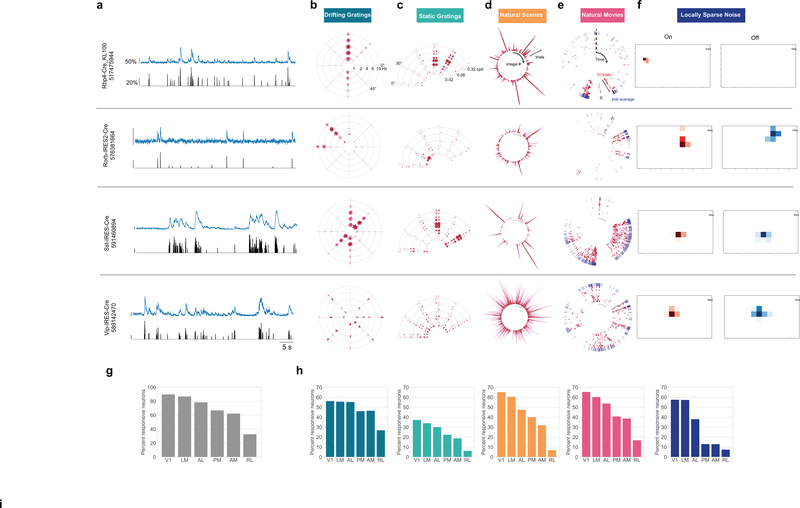
Figure 2: Neurons exhibit diverse responses to visual stimuli.

(a) Activity for four example neurons, two excitatory neurons (Rorb, layer 4, Rbp4, layer 5) and two inhibitory neurons (Sst layer 4, and Vip layer 2/3). ΔF/F (top, blue) and extracted events (bottom, black) for each cell. (b) “Star” plot summarizing orientation and temporal frequency tuning for responses to the drifting gratings stimulus. The arms of the star represent the different grating directions, the rings represent the different temporal frequencies. At each intersection, the color of the circles represent the strength of the response during a single trial of that direction and temporal frequency. (For details on response visualizations see Extended Data 2). (c) “Fan” plot summarizing orientation and spatial frequency tuning for responses to static gratings. The arms of the fan represent the different orientations and the arcs the spatial frequencies. At each condition, four phases of gratings were presented. (d) “Corona” plot summarizing responses to natural scenes. Each arm represents the response to an image, with individual trials being represented by circles whose color represents the strength of the response on that trial. (e) “Track” plot summarizing responses to natural movies. The response is represented as a raster plot moving clockwise around the circle. Ten trials are represented in red, along with the mean PSTH in the outer ring, in blue. (f) Receptive field subfields mapped using locally sparse noise. (g) Percent of neurons that responded to at least one stimulus across cortical areas. (h) Percent of neurons that responded to each stimulus across cortical areas. Colors correspond to the labels at the top of the figure. See Extended Data Figure 3–7 for sample sizes.

In total, 77% of neurons were responsive to at least one of the visual stimuli presented (Figure 2g). The percent of responsive neurons depended on area and stimulus, such that V1 and LM showed the highest number of visually responsive neurons. This dropped in other higher visual areas and was lowest in RL where only 33% of neurons responded to any of the stimuli. Natural movies elicited responses from the most neurons, while static gratings elicited responses from the fewest (Figure 2h). In addition to varying by area, the percent of responsive neurons also varied by Cre lines and layers, suggesting functional differences across these dimensions (Extended Data 3–7).

For responsive neurons, visual responses were parameterized by computing several metrics, including preferred spatial frequency, preferred temporal frequency, direction selectivity, receptive field size, and lifetime sparseness (Methods). We mapped these properties across cortical areas, layers, and Cre lines to examine the functional differences across these dimensions (Figure 3, Supplementary Figure 1, 2).

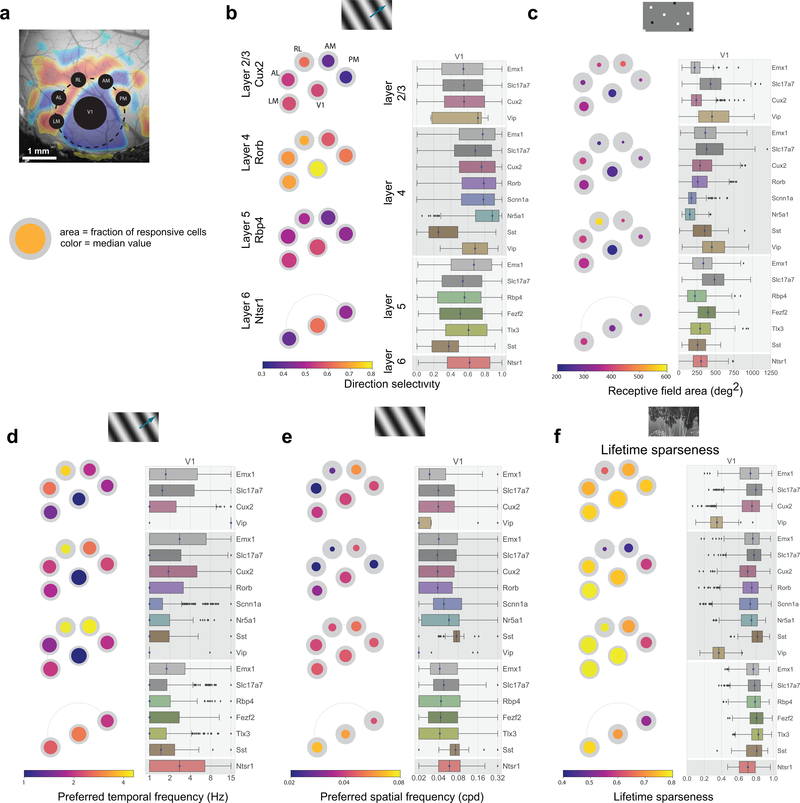
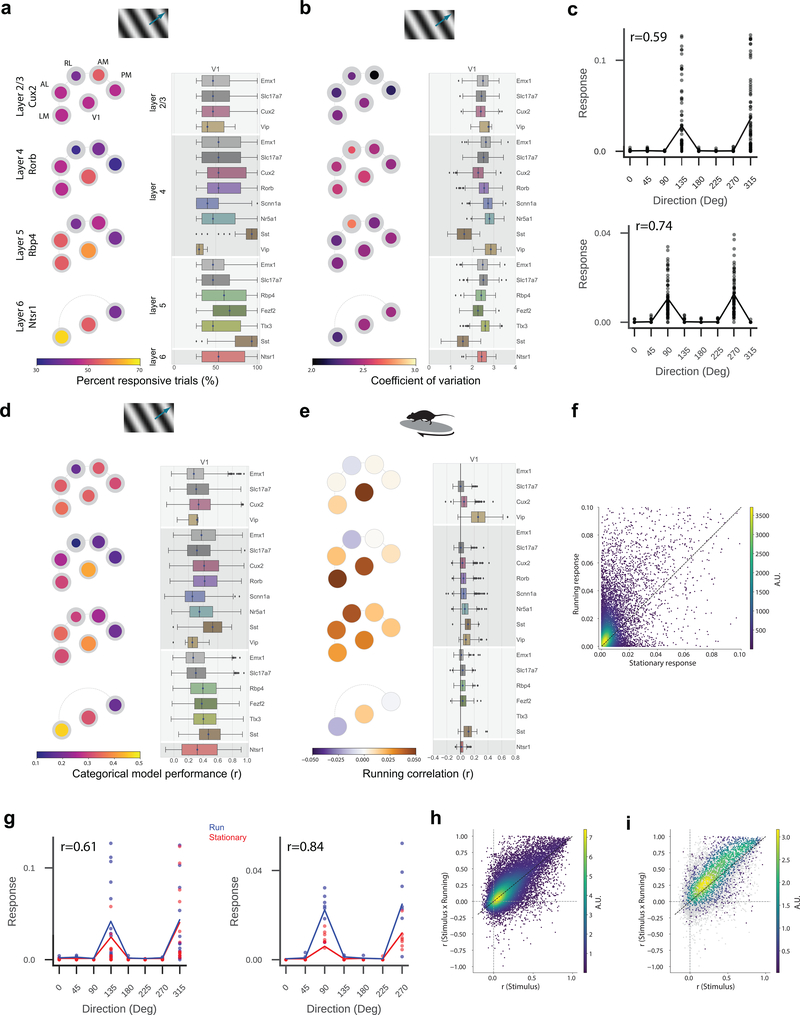
Figure 3: Tuning properties reveal functional differences across areas and Cre lines.

(a) “Pawplot” visualization summarizes median value of a tuning metric across visual areas. Top, each visual area is represented as a circle, with V1 in the center and the higher visual areas surrounding it according to their location on the surface of the cortex. Bottom, each paw-pad (visual area) has two concentric circles. The area of the inner, colored, circle relative to the outer circle represents the proportion of responsive cells for that layer and area. The color of the inner circle reflects the median value of the metric for the responsive cells, indicated by the colorscale at the bottom of the plot. For a metric’s summary plot, four pawplots are shown, one for each layer. Only data from one Cre line is shown for each layer. For each panel, a pawplot is paired with a box plot or a strip plot (for single cell and population metrics respectively) showing the full distribution for each Cre line and layer in V1. Data is assigned to cortical layers based on both the Cre line and the imaging depth. Data collected above 250um from the surface is considered to be in layer 2/3. Data collected between 250μm and 365μm is considered to be in layer 4. Data collected between 375μm and 500μm is considered to be in layer 5. Data collected at 550μm in considered to be in layer 6. The box shows the quartiles of the data, and the whiskers extend to 1.5 times the interquartile range. Points outside this range are shown as outliers. For other cortical areas, see Supplementary Figure 1. (b) Pawplot and box plot summarizing direction selectivity. See Extended Data Figure 3 for sample sizes. (c) Pawplot and box plot summarizing receptive field area. See Extended Data Figure 5 for sample sizes. (d) Pawplot and box plot summarizing preferred temporal frequencies. See Extended Data Figure 3 for sample sizes. (e) Pawplot and box plot summarizing preferred spatial frequencies. See Extended Data Figure 4 for sample sizes. (f) Pawplot and box plot summarizing lifetime sparseness of responses to natural scenes. See Extended Data Figure 6 for sample sizes.

Comparisons across areas and layers revealed that direction selectivity is highest in layer 4 of V1 (Figure 3b). While previous literature has found higher direction selectivity in layer 4 within V1¹⁸, we find here that this result is significant across all layer-4 specific Cre lines, and extends to the higher visual areas as well. Comparisons across the higher visual areas reveals that in superficial layers, the lateral higher visual areas (LM and AL) show significantly higher direction selectivity than the medial ones (PM and AM), but this difference is not significant in the deeper layers. This erosion of the differences between higher visual areas in deeper layers is found for all metrics reported here, wherein the population differences are less pronounced, and often not significant, in layers 5 and 6 (Figure 3c,d,e, Supplementary Figure 2).

Across all areas, layers, and stimuli, visual responses in mouse cortex were highly sparse (Figure 3f). Considering the responses to natural scenes, we found that most neurons responded to very few scenes (examples in Figure 2d). The sparseness of individual neurons was measured using lifetime sparseness, which captures the selectivity of a neuron’s mean response to different stimulus conditions^19,20 (Methods). A neuron that responds strongly to only a few scenes will have a lifetime sparseness close to 1 (Supplementary Figure 3), whereas a neuron that responds broadly to many scenes will have a lower lifetime sparseness. Excitatory neurons had a median lifetime sparseness of 0.77 in response to natural scenes. While Sst neurons were comparable to excitatory neurons (median 0.77), Vip neurons exhibited low lifetime sparseness (median 0.36). Outside of layer 2/3, there was lower lifetime sparseness in areas RL, AM, and PM than in area V1, LM, and AL. Lifetime sparseness did not increase outside of V1; Responses did not become more selective in the higher visual areas. (Figure 3f, Supplementary Figures 3).

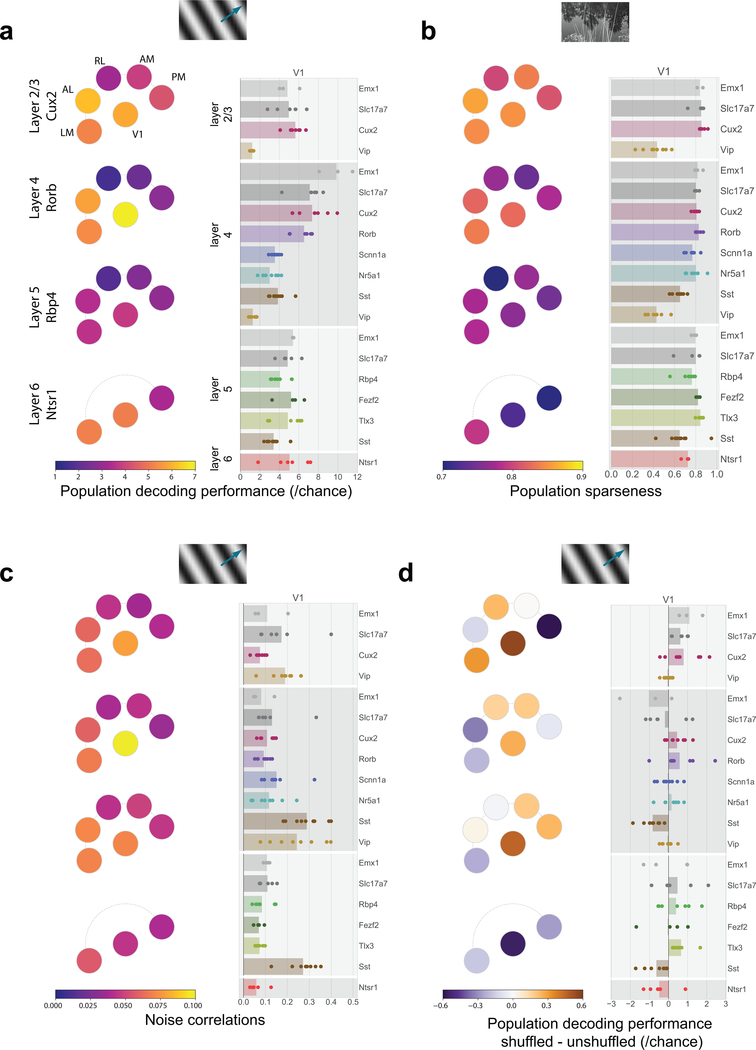
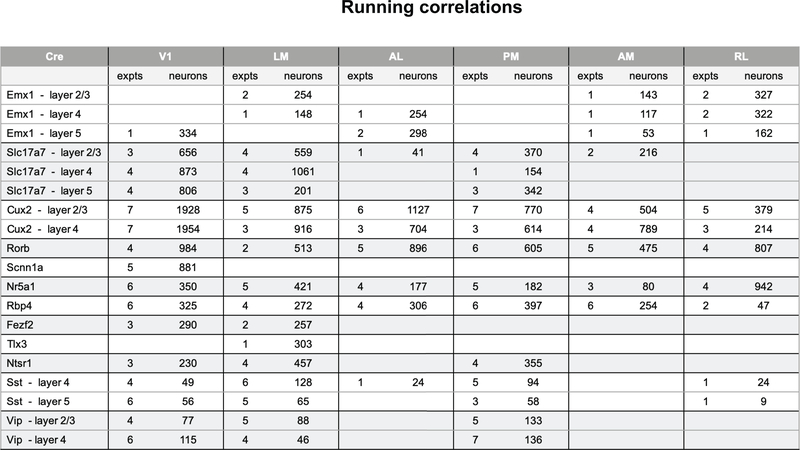
The pattern in single neuron direction selectivity was reflected in our ability to decode the visual stimulus from single-trial population vector responses, using all neurons, responsive and unresponsive (Figure 4a, Supplementary Figure 4). We used a K-nearest-neighbors classifier to predict the grating direction. Matching the tuning properties, areas V1, AL, and LM showed higher decoding performance than areas AM, PM, and RL, and these differences were more pronounced in superficial layers than in deeper layers. Similarly, the population sparseness (Supplementary Figure 3), a measure of the selectivity of each scene (i.e. how many neurons respond on a given trial), largely mirrors the high average lifetime sparseness of the underlying populations (Figure 4b). Such high sparseness suggests that neurons are active at different times and thus their activities are weakly correlated. The noise correlations of the populations reflect this results on population sparsity where excitatory populations show weak correlations (median 0.02) while the inhibitory populations show somewhat higher correlations (Sst median 0.06, Vip median 0.15) (Figure 4c). The structure of the correlations in each population may serve to either help or hinder information processing^16,21. To test this, we measured the decoding performance when stimulus trials were shuffled to break trial-wise correlations. This had variable effects on decoding performance with little pattern across areas or Cre lines (Figure 4d). While the decoding performances for excitatory populations in V1 were aided by removing correlations, consistent with previous literature²², this effect was not consistent across other areas. The decoding performances for Sst populations, on the other hand, were more consistently hurt by removing correlations, suggesting that the high correlations among Sst neurons were informative about the drifting grating stimulus.

Figure 4: Population correlations have heterogenous impact on decoding performance.

(a) Pawplot and strip plot summarizing decoding performance for drifting grating direction using K-nearest neighbors. Each dot represents the mean five-fold cross-validated decoding performance of a single experiment, with the median performance for a Cre-line/layer represented by bar. See Extended Data Figure 3 for sample sizes (column ‘expts’). For other cortical areas, see Supplementary Figure 4. (b) Pawplot and strip plot summarizing the population sparseness of responses to natural scenes. See Extended Data Figure 6 for sample sizes (column ‘expts’). For other cortical areas, see Supplementary Figure 3. (c) Pawplot and strip plot summarizing noise correlations in the responses to drifting gratings. See Extended Data Figure 3 for sample sizes (column ‘expts’). (d) Pawplot and strip plot summarizing the impact of shuffling on decoding performance for drifting grating direction. See Extended Data Figure 3 for sample sizes (column ‘expts’). Note the diverging colorscale representing both negative and positive values.

For all stimuli, the visually-evoked responses throughout cortex showed large trial-to-trial variability. Even when removing the neurons deemed unresponsive, the percent of responsive trials for most responsive neurons at their preferred conditions was low - the median is less than 50% (Figure 5a, Supplementary Figure 5). This means that the majority of neurons in the mouse visual cortex do not usually respond to individual trials, even when presented with the stimulus condition that elicits their largest average response. This is true throughout the visual cortex, though V1 showed slightly more reliable responses than higher visual areas and Sst interneurons, in particular, showed very reliable responses. The variability of responses is reflected in the high coefficient of variation, with median values for excitatory neurons above 2, indicating that these neurons are super-Poisson (Figure 5b). We sought to capture this variability with a simple categorical model for drifting grating responses that attempts to predict the trial response (the integrated event magnitude during each trial) from the stimulus condition (the direction and temporal frequency of the grating, or whether the trial was a blank sweep). This regression quantifies how well the average tuning curve predicts the response for each trial. Comparing the trial responses to the mean tuning curve shows a degree of variability even when the model is fairly successful (Figure 5c). Consistent with this variability in visual responses, this model does a poor job of predicting responses to drifting gratings for most neurons (Figure 5d). Few neurons are well predicted by their average tuning curve alone (21% of responsive neurons have r>0.5, this becomes 11% when considering all neurons, where r is the cross-validated correlation between model prediction and actual response). As expected, the ability to predict the responses is correlated with the measured variability (r=0.8, Pearson correlation).

Figure 5: Neural activity is extremely variable and is not accounted for by running behavior.

(a) Pawplot and box plot summarizing the percent of responsive trials that have a significant response for each neuron’s preferred drifting gratings condition. The responsiveness criterion is that a neuron responded to 25% of the trials, hence the values in the box plots are bounded at 25%. The box shows the quartiles of the data, and the whiskers extend to 1.5 times the interquartile range. Points outside this range are shown as outliers. For box plots for other cortical areas see Supplementary Figure 5. See Extended Data Figure 3 for sample sizes. (b) Pawplot and box plot summarizing the coefficient of variation for each neuron’s response to its preferred drifting grating condition. See Extended Data Figure 3 for sample sizes. (c) Two example neurons showing individual trial responses along with mean tuning curve where r is the Pearson’s correlation coefficient between the measured and predicted values. n=45 trials per stimulus condition. (d) Pawplot and box plot summarizing the categorical regression, where r is the cross-validated Pearson’s correlation between model prediction and actual response. Only neurons that are responsive to drifting gratings using our criterion are included. See Extended Data Figure 3 for sample sizes. (e) Pawplot and box plot summarizing the Pearson’s correlation of neural activity with running speed. Only neurons in imaging sessions where the running fraction is between 20 and 80% are included (Supplementary Figure 6). See Extended Data Figure 8 for sample sizes. For neurons present in multiple session that met the running criterion, mean of their running correlation across those sessions is used here. Note the diverging colorscale representing both negative and positive values. (f) Density plot of the evoked response to a neuron’s preferred drifting grating condition when the mouse is running (running speed > 1 cm/s) compared to when it is stationary (running speed <1 cm/s). Only neurons that are responsive to drifting gratings, and have sufficient number of running and stationary trials for their preferred condition are included, n=10,440. (g) Categorical model for two example neurons (same as in c) in which the running (blue) and stationary (red) trials have been segregated where r is the Pearson’s correlation coefficient between the measured and predicted values. n=14 (left) or 7 (right) trials per condition. (h) Density plot of r for the categorical regression for drifting gratings using only the stimulus condition (horizontal axis) and stimulus condition × running state (vertical axis). Only neurons that are responsive to drifting gratings and have sufficient number of running and stationary trials across stimulus conditions, are included. n=11,799. (i) Same as h. Only neurons that are significantly modulated by running are shown in the density (n=2,791), the other neurons are in gray.

One possible source of trial-to-trial variability is the locomotor activity of the mouse. Previous studies have shown that not only is some neural activity in the mouse visual cortex associated with running, but that visual responses are also modulated by running^22–26. The mice in our experiments were free to run on a disc and animals showed a range of running behaviors (Supplementary Figure 6). Ignoring the stimulus, we found that some neurons’ activities were correlated with the running speed (Figure 5e). While layer 5 showed strong correlations in all visual areas, in the other layers V1 had stronger correlations than the higher visual areas, with some visual areas showing median negative correlations. Within V1, the inhibitory interneurons showed the strongest correlation with running, most notably Vip neurons in layer 2/3 (median 0.25), while the excitatory neurons showed weaker correlations (median 0.03).

For experiments with sufficient stimulus trials for a neuron’s preferred condition when the mouse was both stationary and running (>10% for each), we compared the responses in these two states. Consistent with other reports, many neurons show modulated responses, but the effect was modest (Figure 5f). The majority of neurons showed enhanced responses. Considering the entire population, there was a 1.9 fold increase in the median evoked response. The effect on individual neurons, however, was varied such that only 13% of neurons showed significant modulation in these conditions (p<0.05, KS test).

To test whether running accounted for the variability in trial-wise responses to visual stimuli, we included a binary running state as a condition dependent gain into the categorical regression (i.e. computing separate tuning curves for the running and stationary conditions, Figure 5g). This did not consistently and significantly improve the response prediction. Comparing the model performance when the running state is included to the stimulus-only model, we found that the distribution is largely centered along the diagonal, with a slight asymmetry in favor of the running dependent model for the better performing models (Figure 5h, 28% of responsive neurons have r>0.5 for stimulus x running state; 21% when considering all neurons). This was further corroborated by a simpler model that predicts neural response based on the running speed (rather than a binary condition, and without stimulus information) (Supplementary Figure 7). However, considering only the 13% of neurons that showed significant modulation of evoked responses (Figure 5f), the inclusion of running in the categorical model provides a clear predictive advantage (Figure 5i, mean r for stimulus only is 0.35, for stimulus x running is 0.44 whereas for non-modulated neurons mean r for stimulus only is 0.21, for stimulus x running is 0.20).

One of the unique aspects of this dataset is the broad range of stimuli, allowing for a comparison of response characteristics and model predictions across stimuli. Surprisingly, knowing whether a neuron responded to one stimulus type (e.g. natural scenes, drifting gratings, etc.) was largely uninformative of whether it responded to another stimulus type. Unlike the examples shown in Figure 2, which were chosen to highlight responses to all stimuli, most neurons were responsive to only a subset of the stimuli (Figure 6a). To explore the relationships between neural responses to different types of stimuli, we computed the correlation between the percent of responsive trials for each stimulus. This comparison removes the threshold of “responsiveness” and examines underlying patterns of activity. We found that most stimulus combinations were weakly correlated (Figure 6b), demonstrating that knowing that a neuron responds reliability to drifting gratings, for example, carries little to no information about how reliably that neuron responds to one of the natural movies. There is a higher correlation between the reliability of the responses to the natural movie that is repeated across all three sessions (natural movies 1A, 1B, 1C), providing an estimate of the variability introduced by imaging across days and thus a ceiling for the overall correlations across stimuli. Very few of the cross-stimulus correlations approach this ceiling, with the exception of the correlation between static gratings and natural scenes.

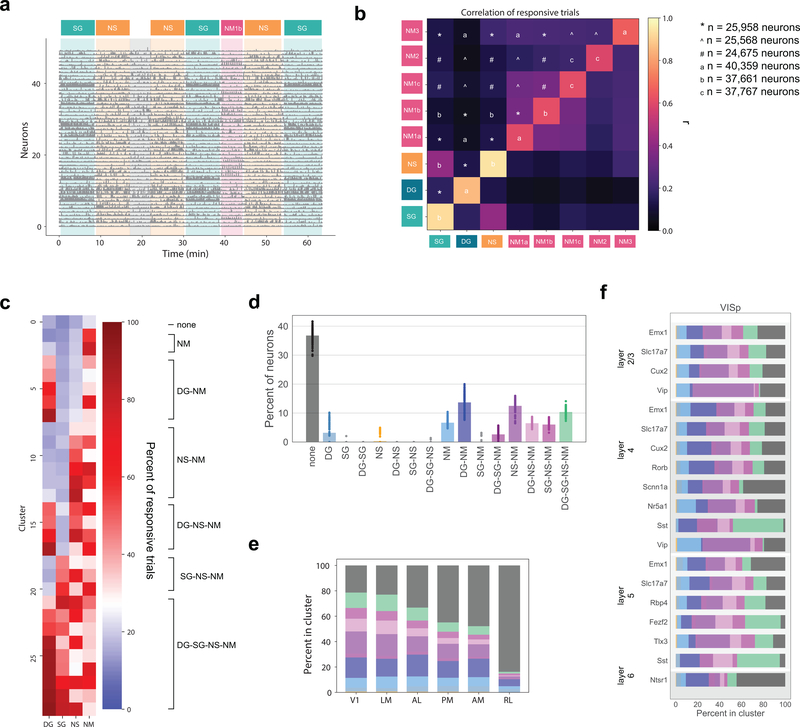
Figure 6: Correlated response variability reveals functional classes of neurons.

(a) Responses of 50 neurons during one imaging session (Cux2, layer 2/3 in V1) with stimulus epochs shaded using stimulus colors from Figure 1f. (b) Heatmap of the Pearson’s correlation of the percent of responsive trials for neurons’ responses to each pair of stimuli. The diagonal is the mean correlation between bootstrapped samples of the percent responsive trials for the given stimulus. (c) Mean percent responsive trials for each cluster per stimulus for one example clustering from the Gaussian mixture model (n=25,958). On the right, classes are identified according to the response profile of each cluster. (d) Strip plot representing the percent of neurons belonging to each class predicted by the model over 100 repeats. The mean across all repeats is indicated by the bar. Clustering was performed on 25,958 neurons imaged in sessions A and B. (e) The percent of neurons belonging to each class per cortical area. Colors correspond to panel d. (f) The percent of neurons belong to each class for each transgenic Cre line within V1. Colors correspond to panel d. For other cortical areas see Supplementary Figure 8.

We characterize the variability by clustering the reliability, defined by the percentage of significant responses to repeated stimuli. We used a Gaussian mixture model to cluster the 25,958 neurons that were imaged in both Sessions A and B (Figure 1f) and excluded the Locally Sparse Noise stimulus due to the lack of a comparable definition of reliability. Using neurons imaged in all three sessions did not qualitatively change the results (see Supplementary Figure 8). The clusters are described by the mean percent responsive trials for each stimulus for each cluster (Figure 6c). Note that there is only a weak relationship between the percent responsive trials to one stimulus and any other. We grouped the clusters into “classes” by first defining a threshold for responsiveness by identifying the cluster with the lowest mean percent responsive trials across stimuli, then setting the threshold equal to the maximum value across stimuli plus one standard deviation for that cluster. This allowed us to identify each cluster as responsive (or not) to each of the stimuli. Clusters with the same profile (e.g. responsive to drifting gratings and natural movies, but not static gratings or natural scenes), were grouped into one of sixteen possible classes.

The clustering was performed 100 times with different initial conditions to evaluate robustness. The optimal number of clusters, evaluated with model comparison, as well as the class definition threshold were consistent across runs (Supplementary Figure 8). By far the largest single class revealed by this analysis is that of neurons that are largely unresponsive to all stimuli, termed “none,” which contains 34±2% of the neurons (Figure 6d). Other large classes include neurons that respond to drifting gratings and natural movies (“DG-NM”, 14±3%), to natural scenes and natural movies (“NS-NM”, 14±2%), and to all stimuli (“DG-SG-NS-NM”, 10±1%).

Importantly, we do not observe all 16 possible stimulus response combinations. For instance, very few neurons are classified as responding to one stimulus alone, the most prominent exception being neurons that respond uniquely to natural movies. Thus, while the pairwise correlations between most stimuli are relatively weak, there is meaningful structure in the patterns of responses. Nevertheless, within each class there remains a great deal of heterogeneity. For example, within the class that responds to all stimuli, there is a cluster in which the neurons respond with roughly equal reliability to all four stimuli (cluster 27 in Figure 6c) as well as clusters in which the neurons respond reliably to drifting and static gratings and only weakly to natural scenes and natural movies (clusters 25 and 28). This heterogeneity underlies the inability to predict whether a neuron responds to one stimulus given that it responds to another.

Classes are not equally represented in all visual areas (Figure 6e). The “unresponsive” class is larger in the higher visual areas than in V1, and is largest in RL (see also Figure 2g). Classes related to moving stimuli, including “NM”, “DG-NM”, and “DG”, have relatively flat distributions across the visual areas, excluding RL. The natural classes, including “NS-NM”, “DG-NS-NM”, “SG-NS-NM”, and “DG-SG-NS-NM”, are most numerous in V1 and LM, with lower representation in the other visual areas. This divergence in representation of the motion classes from the natural classes in areas AL, PM, and AM is consistent with the putative dorsal and ventral stream segregation in the visual cortex³².

In addition to differential representation across cortical areas, the response classes are also differentially represented among the Cre lines (Figure 6f). Notably, Sst interneurons in V1 have the fewest “none” neurons and the most “DG-SG-NS-NM” neurons. Meanwhile, the plurality of Vip interneurons are in the classes responsive to natural stimuli, specifically natural movies.

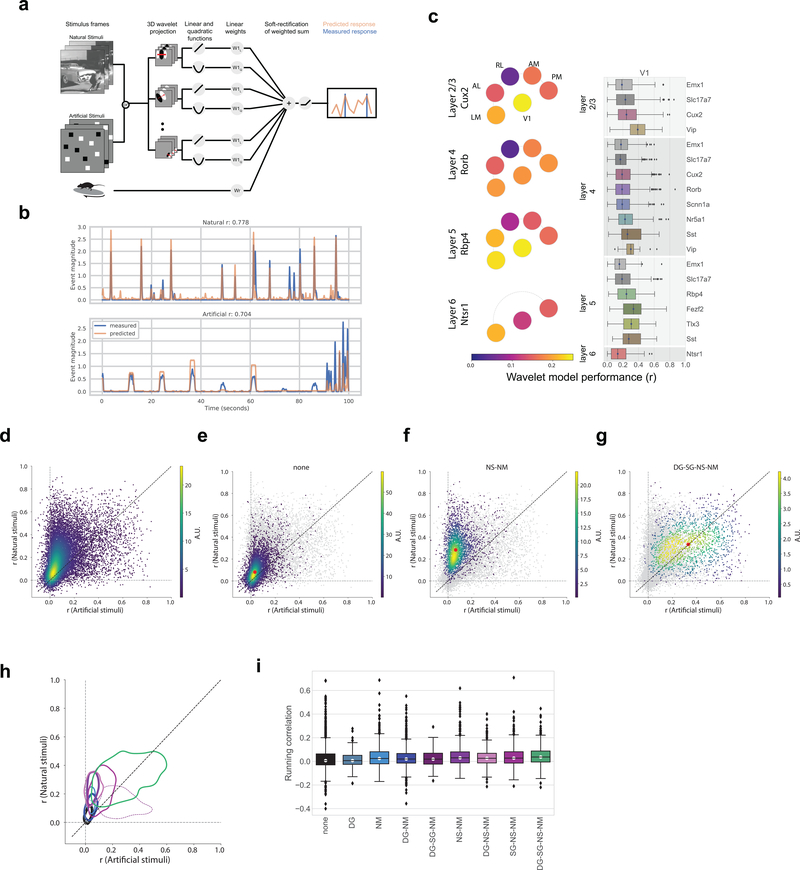
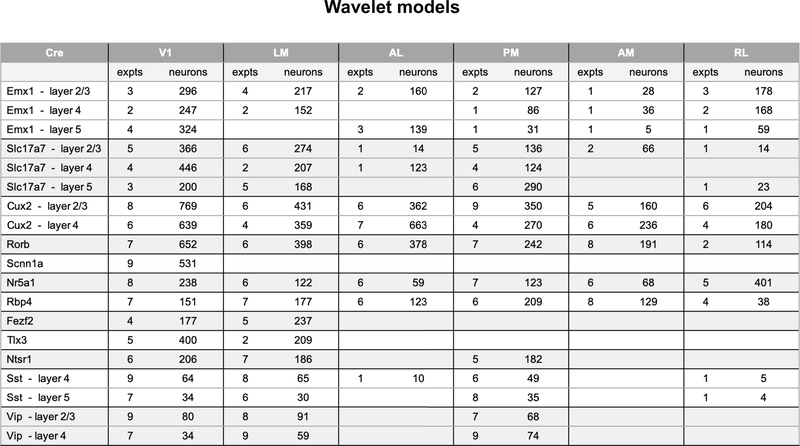
Having characterized neurons by their joint reliability to multiple stimuli, we next ask to what extent we can predict neural responses, not on a trial-by-trial basis but including the temporal response dynamics, given the stimulus and knowledge of the animal’s running condition. We use a model class that remains in widespread use for predicting visual physiological responses and that captures both “simple” and “complex” cell behaviors. The model structure uses a dense wavelet basis (sufficiently dense to capture spatial and temporal features at the level of the mouse visual acuity and temporal response) and computes from this both linear and quadratic features, each of which are summed, along with the binary running trace convolved with a learned temporal filter, and sent through a soft rectification (Figure 7a). We train these models on either the collective natural stimuli or the artificial stimuli to predict the extracted event trace. Whereas we find example neurons for which this model works extremely well (Figure 7b, Supplementary Figure 9, 10, 11), across the population only 2% of neurons are well fit by this model (r>0.5; 2% natural stimuli; 1% artificial stimuli, Figure 7c), with the median r values being ~0.2 (natural stimuli). Model performance was slightly higher in V1 than in the higher visual areas and showed little difference across Cre lines. It is also worth noting that there is a great deal of visually responsive activity that is not being captured by these models (Supplementary Figure 5). Comparing the models’ performances across stimulus categories, we found that the overall distribution of performance for models trained and tested with natural stimuli was higher than the corresponding models for artificial stimuli (Figure 7d), consistent with previous reports^10–15. The running speed of the mouse did not add significant predictive power to the model, as most regression weights were near zero, with the exception of Vip neurons in V1 (Supplementary Figure 10). Similarly, incorporating pupil area and position had little effect as did, at the population level, removing the quadratic weights (Supplementary Figure 10). Well fit models tended to have sparser weights (Supplementary Figure 11).

Figure 7: Class labels are validated by model performance.

(a) Schematic for the wavelet models. (b) Example model performance for one neuron for both natural (top) and artificial (bottom) stimuli where r is the Pearson’s correlation coefficient between the measured and predicted values. (c) Pawplot and box plot of model performance, r, for wavelet models trained on natural stimuli. The box shows the quartiles of the data, and the whiskers extend to 1.5 times the interquartile range. Points outside this range are shown as outliers. Only neurons imaged in all three sessions are included (n=15,921, See Extended Data 9 for sample sizes). For other cortical areas, see Supplementary Figure 10. (d) Density plot comparing the r values for model trained and tested on natural stimuli to the r values for model trained and tested on artificial stimuli, n=15,921. R is the Pearson’s correlation coefficient between the measured and predicted values. (e) Same as d. Only neurons in the “none” class are shown in the density (n=5,566), all other neurons are in gray. The red dot marks the median model performance for neurons in this class. (f) Same as e for the “NS-NM” class (n=2,412). (g) Same as e for the “DG-SG-NS-NM” class (n=1,451). (h) Contours for the density of model performance, as in e-g, for all classes (n=15,921). The contours mark the boundaries of each class within which 66% of datapoints lie. Linewidths reflect the number of neurons in each class as provided in Figure 6d. R is the Pearson’s correlation coefficient between the measured and predicted values. (i) Box plot of running correlation for each class.

When comparing the model performance for the neurons in each of the classes defined through the clustering analysis, we found that these classes occupy spaces of model performance consistent with their definitions (Figures 7e–h). The “none” neurons formed a relatively tight cluster and constituted the bulk of the density close to the origin (Figure 7e). By definition, these neurons had the least response reliability for all stimuli (Figure 6c) and were likewise the least predictable. Neurons in the “NS-NM” class showed high model performance for natural stimuli and low performance for artificial stimuli (Figure 7f). And finally, neurons that reliably respond to all stimuli (“DG-SG-NS-NM”), showed a broad distribution of model performance, with the highest median performance, equally predicted by both artificial and natural stimuli (Figure 7g). As running has been shown to influence neural activity in these data independent of visual stimuli (Figure 5e), one might expect that the “none” class is composed largely of neurons that are strongly driven by running activity rather than visual stimuli. Instead, we found that the “none” class has one of the smallest median correlations, overall, with the running speed of the mouse, while the “DG-SG-NS-NM” class had the largest (Figure 7i).

Discussion

Historically, visual physiology has been dominated by single-neuron electrophysiological recordings in which neurons were identified by responding to a test stimulus. The stimulus was then hand-tuned to elicit the strongest reliable response from that neuron, and the experiment proceeded using manipulations around this condition. Such studies discovered many characteristic response properties, namely that visual responses can be characterized by combinations of linear filters with nonlinearities such as half-wave rectification, squaring, and response normalization⁷, or that neurons (in V1 at least) largely cluster into “simple” and “complex” cells. But these studies may have failed to capture the variability of responses, the breadth of features that will elicit a neural response, and the breadth of features that do not elicit a response. This results in systematic bias in the measurement of neurons and a confirmation bias regarding model assumptions. Recently, calcium imaging and denser electrophysiological recordings²⁷ have enabled large populations of neurons to be recorded simultaneously. Here we scaled calcium imaging, combining standard operating procedures with integrated engineering tools to address some of the challenges of this difficult technique, to create an unprecedented survey of 59,610 neurons in mouse visual cortex, across 243 mice, using a standard and well-studied but diverse set of visual stimuli. This pipeline reduced critical experimental biases by separating quality control of data collection from response characterization. Such a survey is crucial for assessing the successes and shortcomings of contemporary models of visual cortex.

Using standard noise and grating stimuli we find many of the standard visual response features, including orientation selectivity, direction selectivity, and spatial receptive fields with opponent on and off subfields (Figures 2, 3). Based on responses to these stimuli, we observed functional differences in visual responses across cortical areas, layers, and transgenic Cre lines. In a novel analysis of overall reliabilities to both artificial and naturalistic stimuli, we found classes of neurons responsive to different constellations of stimuli (Figure 6). The different classes are largely intermingled, and found in all of the cortical areas recorded here, suggesting a largely parallel organization²⁸. At the same time, the overrepresentation of classes responsive to natural movies and motion stimuli in areas AL, PM, and AM relative to the other classes (which are more responsive to spatial stimuli) is consistent with the assignment of these areas to the putative “dorsal” or “motion” stream²⁹. The lack of an inverse relationship, wherein spatial information is overrepresented relative to motion in a putative “ventral” stream, likely reflects the fact that we were unable to image the putative ventral areas LI, POR, or P within our cranial window. Area LM has previous been loosely associated with the ventral stream, but with evidence that it is more similar to V1 than other higher order ventral areas^9,29, and our results appear consistent with the latter. Area RL has the largest proportion of neurons in the “none” class, over 85%, consistent with the very low percent of responsive neurons (Figure 2). It is possible that neurons in this area are specialized for visual features not probed here, or that they show a greater degree of multi-modality than in the other visual areas, integrating somatosensory and visual features^30.

One of the unique features of this dataset is that it includes a large number of different transgenic Cre lines for characterization that label specific populations of excitatory and inhibitory neurons. On a coarse scale, excitatory populations behave similarly; however, closer examination reveals distinct functional properties across Cre lines. For instance, Rorb, Scnn1a-Tg3, and Nr5a1, which label distinct layer 4 populations in V1, exhibit distinct spatial and temporal tuning properties (Figure 3, Supplementary Figure 1, 2), different degrees of running correlation (Figure 5), and subtle differences in their class distribution (Figure 6). These differences suggest that there are separate channels of feedforward information. Similar differences between Fezf2 and Ntsr1 in V1, which label two distinct populations of corticofugal neurons found in layers 5 and 6 respectively, indicate distinct feedback channels from V1.

The Brain Observatory data also provide the first broad survey of visually evoked responses of both Vip and Sst inhibitory Cre lines. Sst neurons are strongly driven by all visual stimuli used here, with the plurality belonging to the “DG-SG-NS-NM” class (Figure 5f). Their responses to drifting gratings are particularly robust in that 94% of Sst neurons in V1 are responsive to drifting gratings, and respond quite reliably across trials, far more than the other Cre lines (Extended Data 3, Supplementary Figure 5). Vip neurons, on the other hand, are largely unresponsive, even suppressed, by drifting gratings, with only 9% of Vip neurons in V1 labelled responsive. This extreme difference between these two populations is consistent with previous literature examining the size tuning of these interneurons, and supports the disinhibitory circuit between them^23,31,32. Vip neurons, however, are very responsive to both natural scenes and natural movies, the majority falling in the “NS-NM” class (Figure 6f, Extended Data 6, 7, Supplementary Figure 8), but show little selectivity to these stimuli, as their median lifetime sparseness is lower than both the Sst and the excitatory neurons (Figure 3f). Interestingly, receptive field mapping using locally sparse noise revealed that Vip neurons in V1 have remarkably large receptive field areas, larger than both Sst and excitatory neurons (Figure 3f), in contrast to the smaller summation area for Vip neurons, previously measured using windowed drifting gratings^23,33. This suggests that Vip neurons respond to small features over a large region of space. Further, both populations show strong running modulation: they both correlate stronger with the mouse’s running speed than the excitatory populations (Figure 5e), and a model based solely on the mouse’s running speed does a better job at predicting their activity than for the excitatory populations (Supplementary Figure 7).

The true test of a model is its ability to predict arbitrary novel responses, in addition to responses from stimuli used for characterization. Even with the inclusion of running, our models predict responses in a minority of neurons (Figure 7).

Neurons in the “DG-SG-NS-NM” class were well predicted, with values comparable to those found in primates^7,11,34,35, for both natural and artificial stimuli (Figure 7g). Based on the way we chose our stimulus parameters, we expect that neurons with a strong “classical receptive field” would be most likely to appear in this class. However, this class constitutes only 10% of the mouse visual cortex (Figure 6d). Neurons in the “NS-NM” class show equally high prediction for natural stimuli, but poor prediction for artificial stimuli (Figure 7f). It is possible these neurons could be “classical” neurons as well but are tuned for spatial or temporal frequencies that were not included in our stimulus set. As our stimulus parameters were chosen to match previous measurements of mouse acuity, this could suggest that the acuity of mouse has been underestimated³⁶.

Remarkably, the largest class of neurons was the “none” class, constituting those neurons that did not respond reliably to any of the stimuli (34% of neurons). These neurons are the least likely to be described by “classical receptive fields,” as evidenced by their poor model performance for all stimuli (Figure 7f). What, then, do these neurons do? It is possible these neurons are visually driven, but are responsive to highly sparse and specific natural features that may arise through hierarchical processing³⁷. Indeed, the field has a growing body of evidence that the rodent visual system exhibits sophisticated computations. For instance, neurons as early as V1 show visual responses to complex stimulus patterns³⁸. Alternatively, these neurons could be involved in non-visual computation, including behavioral responses such as reward timing and sequence learning³⁹, as well as modulation by multimodal sensory stimuli^39,40 and motor signals^{24,26,41–43}. While we found little evidence that these neurons were correlated with the mouse’s running recent work has found running to be among the least predictive such motor signals⁴³.

We believe that the openly available Allen Brain Observatory provides an important foundational resource for the community. In addition to providing an experimental benchmark, these data serve as a testbed for theories and models. Already, these data have been used by other researchers to develop image processing methods^44,45, to examine stimulus encoding and decoding^46–49, and to test models of cortical computations⁵⁰. Ultimately, we expect these data will seed as many questions as they answer, fueling others to pursue both new analyses and further experiments to unravel how cortical circuits represent and transform sensory information

Online Methods

Transgenic mice

All animal procedures were approved by the Institutional Animal Care and Use Committee (IACUC) at the Allen Institute for Brain Science in compliance with NIH guidelines. Transgenic mouse lines were generated using conventional and BAC transgenic, or knock-in strategies as previously described^51,52. External sources included Cre lines generated as part of the NIH Neuroscience Blueprint Cre Driver Network (http://www.credrivermice.org) and the GENSAT project (http://gensat.org/), as well as individual labs. In transgenic lines with regulatable versions of Cre young adult tamoxifen-inducible mice (CreERT2) were treated with ~200 μl of tamoxifen solution (0.2 mg/g body weight) via oral gavage once per day for 5 consecutive days to activate Cre recombinase.

We used the transgenic mouse line Ai93, in which GCaMP6f expression is dependent on the activity of both Cre recombinase and the tetracycline controlled transactivator protein (tTA)⁵¹. Ai93 mice were first crossed with Camk2a-tTA mice, and the double transgenic mice were then crossed with a Cre driver line. For some Cre divers we alternatively leveraged the TIGRE2.0 transgenic platform that combines the expression of tTA and Gcamp6f in a single reporter line (Ai148(TIT2L-GC6f-ICL-tTA2)⁵³.

Cux2-CreERT2;Camk2a-tTA;Ai93(TITL-GCaMP6f) expression is regulated by the tamoxifen-inducible Cux2 promoter, induction of which results in Cre-mediated expression of GCaMP6f predominantly in superficial cortical layers 2, 3 and 4⁵⁴ (see Supplementary Figure 12, Supplementary Table 1). Both Emx1-IRES-Cre;Camk2a-tTA;Ai93 and Slc17a7-IRES2-Cre;Camk2a-tTA;Ai93 are pan-excitatory lines and show expression throughout all cortical layers^55,56. Sst-IRES-Cre;Ai148 exhibit GCaMP6f in somatostatin-expressing neurons⁵⁷. Vip-IRES-Cre; Ai148 exhibit GCaMP6f in Vip-expressing cells by the endogenous promoter/enhancer elements of the vasoactive intestinal polypeptide locus⁵⁷. Rorb-IRES2-Cre;Cam2a-tTA;Ai93 exhibit GCaMP6f in excitatory neurons in cortical layer 4 (dense patches) and layers 5,6 (sparse)⁵⁵. Scnn1a-Tg3-Cre;Camk2a-tTA;Ai93 exhibit GCaMP6f in excitatory neurons in cortical layer 4 and in restricted areas within the cortex, in particular primary sensory cortices. Nr5a1-Cre;Camk2a-tTA;Ai93 exhibit GCaMP6f in excitatory neurons in cortical layer 4⁵⁸. Rbp4-Cre;Camk2a-tTA;Ai93 exhibit GCaMP6f in excitatory neurons in cortical layer 5⁵⁹. Fezf2-CreER;Ai148 exhibits GCaMP6f in subcerebral projection neurons in the layer 5 and 6⁶⁰. Tlx3-Cre_PL56;Ai148 exhibits GCaMP6f primarily restricted to IT corticostriatal in the layer 5⁵⁹. Ntsr1-Cre_GN220;Ai148 exhibit GCaMP6f in excitatory corticothalamic neurons in cortical layer 6⁶¹.

We maintained all mice on a reverse 12-hour light cycle following surgery and throughout the duration of the experiment and performed all experiments during the dark cycle.

Cross platform registration

In order to register data acquired between instruments and repeatedly target and record neurons in brain areas identified with intrinsic imaging, we developed a system for cross platform registration (Supplementary Figure 13).

Surgery

Transgenic mice expressing GCaMP6f were weaned and genotyped at ~p21, and surgery was performed between p37 and p63. Surgical eligibility criteria included: 1) weight ≥19.5g (males) or ≥16.7g (females); 2) normal behavior and activity; and 3) healthy appearance and posture. A pre-operative injection of dexamethasone (3.2 mg/kg, S.C.) was administered 3h before surgery. Mice were initially anesthetized with 5% isoflurane (1–3 min) and placed in a stereotaxic frame (Model# 1900, Kopf, Tujunga, CA), and isoflurane levels were maintained at 1.5–2.5% for the duration of the surgery. An injection of carprofen (5–10 mg/kg, S.C.) was administered and an incision was made to remove skin, and the exposed skull was levelled with respect to pitch (bregma-lamda level), roll and yaw. (Supplementary Figure 14).

Intrinsic Imaging

A retinotopic map was created using intrinsic signal imaging (ISI) in order to define visual area boundaries and target in vivo two-photon calcium imaging experiments to consistent retinotopic locations⁶². Mice were lightly anesthetized with 1–1.4% isoflurane administered with a somnosuite (model #715; Kent Scientific, CON). Vital signs were monitored with a Physiosuite (model # PS-MSTAT-RT; Kent Scientific). Eye drops (Lacri-Lube Lubricant Eye Ointment; Refresh) were applied to maintain hydration and clarity of eye during anesthesia. Mice were headfixed for imaging normal to the cranial window

The brain surface was illuminated with two independent LED lights: green (peak λ=527nm; FWHM=50nm; Cree Inc., C503B-GCN-CY0C0791) and red (peak λ=635nm and FWHM of 20nm; Avago Technologies, HLMP-EG08-Y2000) mounted on the optical lens. A pair of Nikon lenses (Nikon Nikkor 105mm f/2.8, Nikon Nikkor 35mm f/1.4), provided 3.0x magnification (M=105/35) onto an Andor Zyla 5.5 10tap sCMOS camera. A bandpass filter (Semrock; FF01–630/92nm) was used to only record reflected red light onto the brain.

A 24” monitor was positioned 10 cm from the right eye. The monitor was rotated 30° relative to the animal’s dorsoventral axis and tilted 70° off the horizon to ensure that the stimulus was perpendicular to the optic axis of the eye. The visual stimulus displayed was comprised of a 20° × 155° drifting bar containing a checkerboard pattern, with individual square sizes measuring 25º, that alternated black and white as it moved across a mean-luminance gray background. The bar moved in each of the four cardinal directions 10 times. The stimulus was warped spatially so that a spherical representation could be displayed on a flat monitor⁹.

After defocusing from the surface vasculature (between 500 μm and 1500 μm along the optical axis), up to 10 independent ISI timeseries were acquired and used to measure the hemodynamic response to the visual stimulus. Averaged sign maps were produced from a minimum of 3 timeseries images for a combined minimum average of 30 stimulus sweeps in each direction⁶³.

The resulting ISI maps were automatically segmented by comparing the sign, location, size, and spatial relationships of the segmented areas against those compiled in an ISI-derived atlas of visual areas. Manual correction and editing of the segmentation were applied to correct errors. Finally, target maps were created to guide in vivo two-photon imaging location using the retinotopic map for each visual area, restricted to within 10° of the center of gaze. (Supplementary Figure 15).

Habituation

Following successful ISI mapping, mice spent two weeks being habituated to head fixation and visual stimulation. During the first week mice were handled and head fixed for progressively longer durations, ranging from 5 to 10 minutes. During the second week, mice were head fixed and presented with visual stimuli, starting for 10 minutes and progressing to 50 minutes of visual stimuli by the end of the week, including all of the stimuli used during data collection. Mice received a single 60 min habituation session on the two-photon microscope with visual stimuli.

Two photon in vivo calcium imaging

Calcium imaging was performed using a two-photon-imaging instrument (either a Scientifica Vivoscope or a Nikon A1R MP+; the Nikon system was adapted to provide space to accommodate the running disk). Laser excitation was provided by a Ti:Sapphire laser (Chameleon Vision – Coherent) at 910 nm. Pre-compensation was set at ~10,000 fs2. Movies were recorded at 30Hz using resonant scanners over a 400 μm field of view (FOV). Temporal synchronization of all data-streams (calcium imaging, visual stimulation, body and eye tracking cameras) was achieved by recording all experimental clocks on a single NI PCI-6612 digital IO board at 100 kHz.

Mice were head-fixed on top of a rotating disk and free to walk at will. The disk was covered with a layer of removable foam (Super-Resilient Foam, 86375K242, McMaster).. Data was initially obtained with the mouse eye centered both laterally and vertically on the stimulation screen and positioned 15 cm from the screen, with the screen parallel to the mouse’s body. Later, the screen was moved to better fill the visual field. The normal distance of the screen from the eye remained at 15 cm, but the screen center moved to a position 118.6 mm lateral, 86.2 mm anterior and 31.6 mm dorsal to the right eye.

An experiment container consisted of three 1-hour imaging sessions at a given FOV during which mice passively observed three different stimuli. One imaging session was performed per mouse per day, for a maximum of 16 sessions per mouse.

On the first day of imaging at a new field of view, the ISI targeting map was used to select spatial coordinates. A comparison of superficial vessel patterns was used to verify the appropriate location by imaging over a FOV of ~800 μm using epi-fluorescence and blue light illumination. Once a region was selected, the objective was shielded from stray light coming from the stimulation screen using opaque black tape. In two-photon imaging mode, the desired depth of imaging was set to record from a specific cortical depth. On subsequent imaging days, we returned to the same location by matching (1) the pattern of vessels in epi-fluorescence with (2) the pattern of vessels in two photon imaging and (3) the pattern of cellular labelling in two photon imaging at the previously recorded location.

Once a depth location was stabilized, a combination of PMT gain and laser power was selected to maximize laser power (based on a look-up table against depth) and dynamic range while avoiding pixel saturation. The stimulation screen was clamped in position, and the experiment began. Two-photon movies (512×512 pixels, 30Hz), eye tracking (30Hz), and a side-view full body camera (30Hz) were recorded. Recording sessions were interrupted and/or failed if any of the following was observed: 1) mouse stress as shown by excessive secretion around the eye, nose bulge, and/or abnormal posture; 2) excessive pixel saturation (>1000 pixels) as reported in a continuously updated histogram; 3) loss of baseline intensity in excess of 20% caused by bleaching and/or loss of immersion water; 4) hardware failures causing a loss of data integrity. Immersion water was occasionally supplemented while imaging using a micropipette taped to the objective (Microfil MF28G67–5 WPI) and connected to a 5 ml syringe via extension tubing. At the end of each session, a z-stack of images (+/− 30 μm around imaging site, 0.1 μm step) was collected to evaluate cortical anatomy and evaluate z-drift during the course of experiment. Experiments with z-drift above 10μm over the course of the entire session were excluded. In addition, for each FOV, a full-depth cortical z stack (~700 μm total depth, 5 μm step) was collected to document the imaging site location. (Supplementary Figure 16, 17)

Detection of epileptic mice for exclusion

Prior to two-photon imaging, each mouse was screened for the presence of interictal events in two ways. First, on the habituation day on the two photon rig, we collected a 5 min long video on the surface of S1 using the epifluorescence light path of the two photon rig. For each of these videos, we detected all calcium events present across the entire FOV and counted the number of events with a prominence superior to 10% ΔF/F and a width between 100 and 300 ms⁶⁴. Second, a similar analysis was performed for all two photon calcium videos collected. Except for inhibitory lines, any mouse that showed the presence of these large and fast events was reviewed and excluded from the pipeline. Inhibitory lines were excluded from this analysis as the neuronal labelling was too sparse to reliably assess these events from normal spontaneous activity.

Visual Stimulation

Visual stimuli were generated using custom scripts written in PsychoPy^65,66 (Peirce, 2007, 2008) and were displayed using an ASUS PA248Q LCD monitor, with 1920 × 1200 pixels. Stimuli were presented monocularly, and the monitor was positioned 15 cm from the eye, and spanned 120° × 95° of visual space. Each monitor was gamma corrected and had a mean luminance of 50 cd/m². To account for the close viewing angle, a spherical warping was applied to all stimuli to ensure that the apparent size, speed, and spatial frequency were constant across the monitor as seen from the mouse’s perspective.

Visual stimuli included drifting gratings, static gratings, locally sparse noise, natural scenes and natural movies. These stimuli were distributed across three ~60 minute imaging sessions (Figure 1f). Session A included drifting gratings, natural movies one and three. Session B included static gratings, natural scenes, and natural movie one. Session C included locally sparse noise, natural movies one and two. The different stimuli were presented in segments of 5–13 minutes and interleaved. At least 5 minutes of spontaneous activity were recorded in each session.

The drifting gratings stimulus consisted of a full field drifting sinusoidal grating at a single spatial frequency (0.04 cycles/degree) and contrast (80%). The grating was presented at 8 different directions (separated by 45°) and at 5 temporal frequencies (1, 2, 4, 8, 15 Hz). Each grating was presented for 2 seconds, followed by 1 second of mean luminance gray. Each grating condition was presented 15 times. Trials were randomized, with blank sweeps (i.e. mean luminance gray instead of grating) presented approximately once every 20 trials.

The static gratings stimulus consisted of a full field static sinusoidal grating at a single contrast (80%). The grating was presented at 6 different orientations (separated by 30°), 5 spatial frequencies (0.02, 0.04, 0.08, 0.16, 0.32 cycles/degree), and 4 phases (0, 0.25, 0.5, 0.75). The grating was presented for 0.25 seconds, with no inter-grating gray period. Each grating condition was presented ~50 times. Trials were randomized, with blank sweeps presented approximately once every 25 trials.

The natural scenes stimulus consisted of 118 natural images. Images were taken from the Berkeley Segmentation Dataset⁶⁷, the van Hateren Natural Image Dataset⁶⁸, and the McGill Calibrated Colour Image Database⁶⁹. The images were presented in grayscale and were contrast normalized and resized to 1174 × 918 pixels. The images were presented for 0.25 seconds each, with no inter-image gray period. Each image was presented ~50 times. Trials were randomized, with blank sweeps approximately once every 100 images.

Three natural movie clips were used from the opening scene of the movie Touch of Evil (dir. O. Welles, Universal – International, 1958). Natural Movie One and Natural Movie Two were both 30 second clips while Natural Movie Three was a 120 second clip. All clips had been contrast normalized and were presented in grayscale at 30 fps. Each movie was presented 10 times with no inter-trial gray period. Natural Movie One was presented in each imaging session.

The locally sparse noise stimulus consisted of white and dark spots on a mean luminance gray background. Each spot was square, 4.65° on a side. Each frame had ~11 spots on the monitor, with no two spots within 23° of each other, and was presented for 0.25 seconds. Each of the 16 × 28 spot locations was occupied by white and black spots a variable number of times (mean=115). For most of the collected data, this stimulus was adapted such that half of it used 4.65° spots while the other half used 9.3° spots, with an exclusion zone of 46.5°.

Serial Two-Photon Tomography

Serial two-photon tomography was used to obtain a 3D image volume of coronal brain images for each specimen. This 3D volume enables spatial registration of each specimen’s associated ISI and optical physiology data to the Allen Mouse Common Coordinate Framework (CCF). Methods for this procedure have been described in detail in whitepapers associated with the Allen Mouse Brain Connectivity Atlas and in Oh et al.⁷⁰.

Post-mortem assessment of brain structure

Morphological and structural analysis of each brain was performed following collection of the 2P serial imaging (TissueCyte) dataset (Supplementary Figure 18).

The following characteristics warranted an automatic failure of all associated data: (1) Abnormal GCaMP6 expression pattern; (2) Necrotic brain tissue; (3) Compression of the contralateral cortex that resulted in disruption to the cortical laminar structure; (4) Compression of the ipsilateral cortex or adjacent to the cranial window.

The following characteristics were further reviewed and may have resulted in failure of the associated data: (1) Compression of the contralateral cortex due to a skull growth; (2) Excessive compression of the cortex underneath the cranial window; (3) Abnormal or enlarged ventricles.

Image processing

For each two-photon imaging session, the image processing pipeline performed:1) spatial or temporal calibration specific to a particular microscope, 2) motion correction, 3) image normalization to minimize confounding random variations between sessions, 4) segmentation of connected shapes, and 5) classification of soma-like shapes from remaining clutter (Supplementary Figure 19, 20).

The motion correction algorithm relied on phase correlation and only corrected for rigid translational errors. It performed the following steps. Each movie was partitioned into 400 consecutive frame blocks, representing 13.3 seconds of video. Each block was registered iteratively to its own average 3 times (Supplementary Figure 20a–b). A second stage of registration integrated the periodic average frames themselves into a single global average frame through 6 additional iterations (Supplementary Figure 20c). The global average frame served as the reference image for the final resampling of every raw frame in the video (Supplementary Figure 20d).

Each 13.3 second block was used to generate normalized periodic averages using the following steps. First, we subtracted the mean from the maximum projection to retain pixels from active cells (Supplementary Figure 20e–f–g). To select objects of the right size during segmentation, we convolved all periodic normalized averages with a 3×3 median filter and a 47×47 high-pass mean filter. We then normalized the histogram of all resulting frames (Supplementary Figure 20g–h).

All normalized periodic averages were then segmented using an adaptive threshold filter to create an initial estimate of binarized ROI masks of unconnected components (Supplementary Figure 20i). Given GCaMP6 lower expression in cell nuclei, good detections from somata tended to show bright outlines and dark interiors. We then performed a succession of morphological operations to fill closed holes and concave shapes (Supplementary Figure 20j,k).

These initial ROI masks included shapes from multiple periods that were actually from a single cell. To further reduce the number of masks to putative individual cell somas, we computed a feature vector from each masks that included morphological attributes such as location, area, perimeter, and compactness, among others (Supplementary Figure 20l). A battery of heuristic decisions applied on these attributes allowed to combine, eliminate or maintain ROI (Supplementary Figure 20l,m). A final discrimination step, using a binary relevance classifier fed by experimental metadata (e.g. Cre line, imaging depth) along with the previous morphological features, further filtered the global masks into the final ROIs used for trace extraction.

Targeting refinement for putative RL neurons

In all experiments, the center of the two-photon (2P) FOV was aimed close to the retinotopic center of the targeted visual region, as mapped by ISI. Retinotopic mapping of RL commonly yielded retinotopic centers close to the boundary between RL and somatosensory cortex. Consequently, for some RL experiments the FOV spanned across the boundary between visual and somatosensory cortex. All RL experiments were reviewed using a semi-automated process (Supplementary Figure 21), and ROIs that were deemed to lie outside putative visual cortex boundaries (approx. 25%) were excluded from further analysis.

Neuropil Subtraction

To correct for contamination of the ROI calcium traces by surrounding neuropil, we modeled the measured fluorescence trace of each cell as F_M = F_C + rF_N, where F_M is the measured fluorescence trace, F_C is the unknown true ROI fluorescence trace, F_N is the fluorescence of the surrounding neuropil, and r is the contamination ratio. To estimate the contamination ratio for each ROI, we selected the value of r that minimized the cross-validated error, $E={\sum }_t{\left|{F_C-F}_M+r{F}_N\right|}^2$, over four folds. We computed the error over each fold with a fixed value of r, for a range of r values. For each fold, F_C was computed by minimizing $C={\sum }_t{\left|{F_C-F}_M+r{F}_N\right|}^2+\lambda {\left|L{F}_C\right|}^2$, where L is the discrete first derivative (to enforce smoothness of F_C) and λ is a parameter set to 0.05. After determining r, we computed the true trace as F_C = F_M − rF_N, which is used in all subsequent analysis. (Supplementary Figure 22)

Demixing traces from overlapping ROIs

We demixed the activity of all recorded ROIs, using a model where every ROI had a trace distributed in some spatially heterogeneous, time-dependent fashion:

$$F_{it}=\sum _k{W}_{kit}{T}_{kt}$$

where W is a tensor containing time-dependent weighted masks: W_kit measures how much of neuron k’s fluorescence is contained in pixel i at time t. T_kt is the fluorescence trace of neuron k at time t - this is what we want to estimate. F_it is the recorded fluorescence in pixel i at time t.

This model applied to all ROIs before filtering for somas. We filtered out duplicates (defined as two ROIs with >70% overlap) and ROIs that were the union of others (any ROI where the union of any other two ROIs accounted for 70% of its area) before demixing and applied the remaining filtering criteria afterwards. Projecting the movie F onto the binary masks, A, reduced the dimensionality of the problem from 512×512 pixels to the number of ROIs:

$$\sum _i{A}_{ki}{F}_{it}=\sum _{k,i}{A}_{ki}{W}_{kit}{T}_{kt}$$

where A_ki is one if pixel i is in ROI k and zero otherwise–these are the masks from segmentation, after filtering. At time point t, this yields the linear regression:

$$AF(t)=({AW}^T(t))T(t)$$

where we estimated the weighted masks W by the projection of the recorded fluorescence F onto the binary masks A. On every frame t, we computed the linear least squares solution $\widehat{T}$ to extract each ROI’s trace value.

It was possible for ROIs to have negative or zero demixed traces $\widehat{T}$. This occurred if there were unions (one ROI composed of two neurons) or duplicates (two ROIs in the same location with approximately the same shape) that our initial detection missed. If this occurred, those ROIs and any that overlapped with them were removed from the experiment. This led to the loss of ~1% of ROIs. (Supplementary Figure 22).

ROI Matching

The FOV for each session, and the segmented ROI masks, were registered to each other using an affine transformation. To map cells, a bipartite graph matching algorithm was used to find correspondence of cells between sessions A and B, A and C, and B and C. The algorithm took cells in the pair-wise experiments as nodes, and the degree of spatial overlapping and closeness between cells as edge weight. Maximizing the summed weights of edges, the bipartite matching algorithm found the best matching between cells. Finally, a label combination process was applied to the matching results of A and B, A and C, and B and C, producing a unified label for all three experiments.

ΔF/F

To calculate the ΔF/F for each fluorescence trace, we first calculate baseline fluorescence using a median filter of width 5401 samples (180 seconds). We then calculate the change in fluorescence relative to baseline fluorescence (ΔF), divided by baseline fluorescence (F). To prevent very small or negative baseline fluorescence, we set the baseline as the maximum of the median filter estimated baseline and the standard deviation of the estimated noise of the fluorescence trace.

L0 penalized event detection

We used the L0-penalized method of Jewell, et al for event detection^17,71. We refer to this as “event” detection because low firing rate activity is difficult to detect. For each ΔF/F trace we remove slow timescale shifts in the fluorescence using a median filter of width 101 samples (3.3 seconds). We then apply the L0-penalized algorithm to the corrected ΔF/F trace. The L0 algorithm has two hyperparameters: gamma and lambda. Gamma corresponds to the decay constant of the calcium indicator. We set gamma to be the decay constant obtained from jointly recorded optical and electrophysiology with the same genetic background and calcium indicator. Time constants can be found at https://github.com/AllenInstitute/visual_coding_2p_analysis/blob/master/visual_coding_2p_analysis/l0_analysis.py. Supplementary Figure 23 shows the extracted linear kernels for Emx1-Ai93 and Cux2-Ai93 from which gamma has been extracted by fitting the fluorescence decay with a single exponential. The rise time, amplitude, and shape of the extracted linear kernels are mainly a function of the genetically encoded calcium indicator (GCaMP6f) and appear to be largely independent of the specific promoter driving expression.

To estimate lambda, which controls the strength of the L0 penalty, we estimate the standard deviation of the trace. We set lambda using bisection to minimize the number of events smaller than two standard deviations of the noise, while retaining at least one recovered event. We chose two standard deviations by maximizing the hit-miss rate on eight hand-annotated traces during 8 degree locally sparse noise stimulation. Those traces were uniformly sampled from distribution of signal-to-noise ratio for ΔF/F traces. The noise level was computed as the robust standard deviation (1.4826 times the median absolute deviation) and the signal level was the median ΔF/F after thresholding at the robust standard deviation.

To assess how the events detected using the above procedure relate to actual spikes, we performed event detection on the fluorescence of cells that were imaged simultaneously with loose patch recordings. Since the true spike train is known for these data, we computed the expected probability of detecting an event, as well as the expected event magnitude, as a function of the number of spikes observed in a set of detection windows relevant to the pipeline data analyses (e.g. static gratings, natural scenes, and locally sparse noise templates are presented for 0.25 s each) (Supplementary Figure 23).

Analysis

All analysis was performed using custom Python scripts using NumPy⁷², SciPy⁷³, Pandas⁷⁴ and Matplotlib⁷⁵.

Direction selectivity was computed from mean responses to drifting gratings, at the cell’s preferred temporal frequency, as

$$DSI=\frac{R_{pref}-R_{null}}{R_{pref}+R_{null}}$$

where R_pref is a cell’s mean response in its preferred direction and R_null is its mean response to the opposite direction.

The temporal frequency tuning, at the preferred direction, was fit using either an exponential curve (for highest and lowest peak temporal frequency) or a Gaussian curve (other values). The reported preferred temporal frequency was taken from these fits. The same was done for spatial frequency tuning, fit at the cell’s preferred orientation and phase in response to the static gratings. In both cases, if a fit could not converge, a preferred frequency was not reported.

Spatial receptive fields were computed from locally sparse noise, in two stages. First, we determine whether a cell has a receptive field by a statistical test, described Statistics. Second, we compute the receptive field itself. A second statistical test was used to determine inclusion of each spot in the receptive field, also described in Statistics. Determining statistical significance is a less common but important step necessary because of the size of the dataset.

If a neuron was found to have a receptive field, the spots that were identified for receptive field membership were fit with a two-dimensional Gaussian distribution, with orientation, azimuth/elevation, and x/y standard deviation serving as degrees of freedom for the optimization. On and Off subregions (eg. white and black spots) were fit separately. Subregion area was defined as the 1.5 standard deviation ellipse under this fit gaussian, measured in units of squared visual degrees. Up to two On and Off subregions were fit. The total areas of the receptive field was computed as the sum of all subregion areas, correcting for overlap.

Lifetime sparseness was computed using the definition in Vinje and Gallant²⁰.

$$S_L=\frac{1-\frac{1}{N}\frac{{\left({\sum }_i{r}_i\right)}^2}{{\sum }_i{r}_i^2}}{1-\frac{1}{N}}$$

where N is the number of stimulus conditions and r_i is the response of the neuron to stimulus condition i averaged across trials. Population sparseness was computed with the same metric, but where N is the number of neurons and r_i is average response vector of neuron i to all stimulus conditions.

For each stimulus we computed CC_max, the expected correlation between the sample trial averaged response and the true (unmeasured) mean response. It provides an upper bound on the expected performance of any model that predicts the response from the given stimulus trial structure. We follow the computation from Schoppe, et al.⁷⁶:

$$\frac{1}{{CC}_{max}}=\sqrt{1-\frac{1}{N}\left(\frac{\left(1-\frac{1}{N}\right)\times {\sum }_{n=1}^{N}Var\left(R_n\right)}{Var\left({\sum }_{n=1}^N{R}_n\right)-{\sum }_{n=1}^{N}Var\left(R_n\right)}\right)}$$

where N is the number of trials and R_n is the time series of the response on the nth trial. For R_n we use the trace of extracted event magnitudes at 30Hz, smoothed with a Gaussian window of width 0.25s.

We computed “noise” and “signal” correlations in the population responses. Signal correlations were computed as the Pearson correlation between the trial-averaged stimulus responses of pairs of neurons. To prevent trial-by-trial fluctuations from contaminating our signal correlation estimates, we separated each stimulus’ trials into two subsets and calculated the correlation between the trial-averaged responses with each subset of trials. We averaged the signal correlations over 100 random splits of the trials. Noise correlations were computed as the Pearson correlation of the single-trial stimulus responses for a pair of neurons and a given stimulus, and then averaged over stimuli. For natural movies, we computed the noise and signal correlations of the binned event counts in non-overlapping 10 frame windows. We computed “spontaneous correlations” as the Pearson correlation of the detected event trains during the periods of spontaneous activity recording.

Decoding

We used K Nearest-Neighbors classifiers to decode the visual stimulus identity (e.g. the natural scene number, within the natural scene responses) from the population vector of single-trial responses, using the correlation distance between response vectors. We report the performance on the held-out data from five-fold cross-validation. On each cross-validation fold, we performed an inner-round of 2-fold cross-validation to choose the number of neighbors from eight logarithmically spaced options (1, 2, 4, 7, 14 and 27).

Categorical Regression Model for Trial Responses to Drifting Gratings

We fit linear ridge regression models for the trial-averaged responses (events summed during each stimulus presentation). The response for trial t, R_t is governed by the following equation:

$$R_t=\sum _s{w}_s{I}_s^t$$

where $I_s^t$ is the characteristic function for stimulus condition s during trial t. $I_s^t$ is equal to 1 when the stimulus condition is equal to s during trial t and 0 otherwise, and w_s is the weight for stimulus condition s (it gives the response of the neuron to stimulus s).

We fit two separate models, one for which the stimulus conditions enumerate the different values of the drifting grating (i.e. orientations and temporal frequencies, including the blank sweep, 41 total conditions) and another for which each stimulus condition occurred in pairs, one during running and one when the animal was stationary. On each stimulus trial we classified the locomotion as running or stationary using a gaussian mixture model with a Dirichlet process prior for the number of components. Stationary trials were identified by the component with the smallest variance among those with mean speed < 1 cm/s (if any existed). We used stimulus conditions with at least 5 repetitions in each behavioral state, and used the same number of trials for each stimulus condition in each behavioral state.

We regressed the summed trial against the combination of stimulus condition and behavioral state (e.g., 180 degrees, 4 Hz and running). The regularization weight was chosen by leave-one-out cross-validation on the training data. We also regressed against just the locomotion state, binning the activity and running speed into pseudo-trials of the same length as the drifting grating trials. We measured model performance by the correlation of the predictions and data on held-out trials (5-fold cross-validation).

Regression models for mouse running speed

We performed a polynomial regression of each neuron’s activity against running speed. To do this we rank-sorted the running speed and binned it into 900-point bins. All speeds between −1 cm/s and 1 cm/s were labelled stationary. We summed each neuron’s events in the same speed bins to compute the speed tuning. We then fit a polynomial regression for the speed tuning with 5-fold cross-validation. On each training fold we performed an inner 2-fold cross-validation to select the polynomial degree between 1 and 4. We used ridge regression with leave-one-out cross-validation to choose the regularization parameter between .5 and 100.

3D Gabor Wavelet Model for Temporal Responses

Each neuron is modeled as a sparse linear combination of linear and quadratic basis functions, similar to other approaches^77–79. We use a pyramid of 3D Gabor wavelet filters that tile the stimulus at multiple scales, directions, and temporal frequencies (Figure 6a). The filters are defined by:

$$f(x,y,t:\lambda ,\theta ,\psi ,\sigma ,\gamma )=exp\left(-\frac{{x\prime }^2+{y\prime }^2+\gamma t^2}{2{\sigma }^2}\right)\exp \left(i\left(2\pi \frac{x\prime }{\lambda }+\psi t\right)\right)$$

Where:

$$x^{\prime }=xcos\theta +ysin\theta$$

$$y^{\prime }=-xsin\theta +ycos\theta$$

λ controls spatial frequency, θ orientation, ψ temporal frequency, σ the Gaussian envelope, and γ the Gaussian envelope in time. This linear basis forms a reasonably tight frame. The parameters that generate the set of filters were adapted and scaled to the tuning properties of mouse visual cortex. We estimate weights for 10 time-lags for each basis function to enable fitting of the temporal kernel. The weighted sum of the basis functions is passed to a parameterized soft-plus nonlinearity. The filters are temporally convolved with the stimulus. The output of each filter is Z-scored before fitting with threshold gradient descent.

$$H_i(t)=\sum _{x,y}\sum _{\tau }{f}_i(x,y,\tau )S(x,y,t-\tau )$$

The model is a technically a generalized linear model (where the linear model is built by considering linear combinations of the features H_i(τ) and $H_i^2\left(\tau \right)$, along with a temporal filter for the running signal of the animal, r(t)) with a parameterized soft-plus output. The weights w_i are fit to the data using threshold gradient descent and the Poisson negative log-likelihood cost function, using the rate

$$\widehat{R}(t)=log\left(1+exp\left(k\sum _i\sum _{\tau }{H}_i\left(t-\tau \right)w_i^l\left(\tau \right)+H_i^2\left(t-\tau \right)w_i^q\left(\tau \right)+r\left(t-\tau \right)w^r\left(\tau \right)\right)\right)/k$$

This model, with a quadratic dependence on the stimulus $H_i^2\left(\tau \right)$, is akin to a regularized STA/STC analysis, adapted to fit the full spatio-temporal receptive field using stimuli from the data set.

We estimated a sparse combination of basis functions for each neuron using a variant of threshold gradient descent⁸⁰. In threshold gradient descent, only basis functions whose gradients have magnitudes larger than some threshold, t, of the largest gradient magnitude have their weights updated. All weights start at 0 and the descent is terminated using early stopping. The threshold parameter, which can range from 0 to 1, controls the sparsity of the solution. We used a threshold value of 0.8.

We modified the threshold gradient descent algorithm in three ways. First, we updated the weights at all time lags for any basis function over threshold, allowing the temporal kernel to be smooth. Second, at each iteration, any basis function whose gradient exceeded the threshold had its weight added to the “active set”, which was maintained over the optimization, and then all weights in the active set were updated, preventing oscillations. Third, we used an adaptive step size. The step size increased by a factor of 1.2 at each iteration if generalization to the stopping set improved, and decreased by a factor of 0.5 if generalization worsened⁸¹.

We used a nested six-fold cross-validation framework. We split the data into six sets each containing many 50 sample long continuous blocks from throughout the dataset. A model was trained by starting with five separate models, each trained on a different combination of four of the five training sets, with the remaining set functioning as the stopping set. The five models were averaged together for making predictions on the test set. Reported model performance is the average on the test set across the six folds. Separate models were fit for the natural stimuli and artificial stimuli. The weights for these models were sparse and for all models fewer than 20% of the basis functions had non-zero weight values (see Supplementary Figure 11). The number of parameters for the model is 517451.

Pupil position and area were measured (Supplementary Figure 24), and for some of the models these were incorporated into the models. These corrections had little effect on model performance (Supplementary Figure 10).

We show examples of this model on four neurons in Supplementary Figure 9.

Clustering of reliabilities

We performed a clustering analysis using the reliabilities by stimulus for each cell (defined as the percent of responsive trials to the cell’s preferred stimulus condition). We did not include Locally Sparse Noise in this analysis. We combined the reliabilities for Natural Movies by taking the maximum reliability over the different Natural Movie stimuli. We performed this analysis with two different inclusion criteria. For criteria 1 we included all cells that appeared in both Sessions A and B. For criteria 2 we included all cells that appeared in all three Sessions, A, B, & C. This resulted in a set of four reliabilities for each cell (for the drifting gratings, static gratings, natural movies, and natural scenes). We performed a Gaussian Mixture Model clustering on these reliabilities for cluster numbers from 1 to 50, using the average Bayesian Information Criterion on held out data with 4 fold cross validation to select the optimal number of clusters. Once the optimal model was selected, we defined a threshold for responsiveness by selecting the cluster with the lowest mean reliability over all stimuli. We set the threshold to be the maximum reliability plus one standard deviation over the reliabilities for this cluster. Using this threshold, we identified each cluster according to its profile of responsiveness (i.e. whether it responded to drifting gratings, etc.), defining these profiles as “classes”. For each cell, we predicted the cluster membership using the optimal model, and then the class membership using the threshold. We repeated this process 100 times to estimate the robustness of the clustering and derive uncertainties for the number of cells belonging to each class.

Statistics

No statistical methods were used to pre-determine sample sizes per location but our sample sizes are similar to those reported in previous publications.^8,9 Data collection and analyses were not performed blind to the conditions of the experiments as there was a single experimental condition for all acquired data. Within each transgenic Cre line, mice were randomly assigned to data collection in order to sample different areas and imaging depths. Stimulus conditions for gratings and natural scenes were presented in a randomized order within each epoch, as described. No other randomization was used as there were fixed experimental condition for all other aspects of the data set. Additional research design information can be found in the Nature Research Reporting Summary accompanying this study.

Test for significance of a receptive field map

We performed a chi-square test to assess whether there was a significant response at each location to the locally sparse noise stimulus. For each location, we considered a 7×7 grid of locally sparse noise pixels centered on that location. The null model for this test was defined by assuming that a neuron lacking a receptive field has equal probability of producing a response regardless of the location and luminance (i.e. black or white) of the spots displayed on the screen on any given trial. A neuron has a receptive field if there is a deviation beyond chance based on the null distribution. Chi-square tests for independence were performed for each neuron and for each location using the number of responses to quantify the dependence of responsive trials on the stimulus.

An assumption of the chi-square test is that the response of the neuron on a given trial can only be attributed to a single spot; i.e., only a single stimulus spot is presented on each trial. Although multiple non-gray spots appeared on the screen during each trial, the exclusion region of the locally sparse noise stimulus prevented two non-gray pixels within a 23° radius (for the 4.65° spot size) or 46° radius (for the 9.3° spot size) of one another from being presented on the same trial. Leveraging this structure in the stimulus, chi-square tests were performed on patches in visual space small enough to ensure that two or more non-gray pixels were rarely presented on the same trial, but large enough to ensure that the patch completely contains the receptive field in order for the test to detect the dependence of neuron responses on spot locations. We chose 32.2°x32.2° patches for 4.65° spots and 64.4°x64.4°patches for the 9.3° spot LSN (i.e. 7×7 grid of spot locations in each case). For each neuron, multiple chi-square tests were performed on such patches to tile the entire stimulus monitor and the p-values from these tests were then corrected using the Šidák method to account for multiple comparisons. If the p-value for any patch on the stimulus monitor was significant (p<0.05) after multiple comparison correction, the neuron was considered to have a receptive field.

Test for inclusion of locally sparse noise spots in a receptive field

The receptive field was computed using an event triggered average. Because more than one stimulus spot was present during a given trial, it is not possible to infer the stimulus-response relationship between spot locations and responses on a per-trial basis. Therefore, a statistically significant co-occurrence of spot presentation and responses across trials defined the inclusion criteria for membership of a stimulus spot in the receptive field. To begin, the stimulus was convolved with a spatial Gaussian (4.65° per sigma), to allow pooling of contributions to responses from nearby spots. A p-value was computed for each spot (black and white separately) by constructing a null distribution for the number of trials that a spot was present during responsive trials. This per-spot null distribution was estimated by shuffling the identity of the responsive trials (n=10,000 shuffles). Statistical outliers were identified by computing a p-value for each spot relative to its null distribution. These p-values were corrected for false discoveries using the Šidák multiple comparisons correction, and thresholded at p=0.05 to identify receptive field membership.

Comparison of single cell response metric distributions

To compare the distributions of single cell response metrics across areas, layers, and Cre lines we used a Kolmogorov-Smirnov (KS) test with a Bonferroni correction for the number of comparisons, defined as the number of other distributions to which we were comparing, e.g. for area-wise comparison of the Cux2 line, there are six areas in total and thus five comparisons for each area (first row of Supplementary Figure 2). The KS test was chosen as it does not assume a normal distribution nor equal variance.

Data Product

The Allen Brain Observatory Visual Coding dataset is publicly available, accessible via a dedicated web portal (http://observatory.brain-map.org/visualcoding/), with a custom Python-based Application Programming Interface, the AllenSDK (https://github.com/AllenInstitute/AllenSDK). Data from each imaging session is contained within a NWB (Neurodata Without Borders)⁸².

Extended Data

Extended Data Fig. 1. Spontaneous and evoked event magnitude.

(a) Pawplot and box plots summarizing the mean event magnitude for neurons during the 5 minute spontaneous activity (mean luminance gray) stimulus. For a description of the visualization see Figure 3. The box shows the quartiles of the data, and the whiskers extend to 1.5 times the interquartile range. Points outside this range are shown as outliers. See Extended Data Figure 3 for sample sizes. (b) Pawplot and box plots summarizing the maximum evoked event magnitude for neurons’ responses to drifting gratings. See Extended Data Figure 3 for sample sizes.

Extended Data Fig. 2. Response visualizations.

Conventional tuning curves for drifting grating responses for one neuron. (a) Direction tuning plotted at the preferred temporal frequency (4 Hz) (mean ± sem across 15 trials). Dotted line represents the mean response to the blank sweep. (b) Temporal frequency tuning plotted at the preferred grating direction (270°) (mean ± sem). (c) Heatmap of the direction and temporal frequency responses for cell, showing any possible interaction of direction and temporal frequency. (d) All 15 trials at the preferred direction and temporal frequency, 2 second grating presentation is indicated by pink shading. The mean event magnitude is represented by intensity of the dot to the right of the trial. (e) All trials are clustered, with the strongest response in the center and weaker responses on the outside. (f) Clusters are plotted on a “Star plot”. Arms indicated the direction of grating motion, arcs indicate the temporal frequency of the grating, with the lowest in the center and the highest at the outside. Clusters of red dots are located at the intersection and arms and arcs, representing the trial responses at that condition.

Tuning curves for static gratings for one neuron. (g) Orientation tuning plotted at the preferred spatial frequency (0.04 cpd) for each of the four phases. (mean ± sem across 50 trials) Dotted line represents the mean response to the blank sweep. (h) Spatial frequency tuning plotted at the preferred orientation (90°) for each of the four phases (mean ± sem). (i) Heatmap of the orientation and spatial frequency at the preferred phase (j) All trials at the preferred orientation, spatial frequency and phase, the 250 ms grating presentation is indicated by pink shading. The mean event magnitude is represented by the intensity of the dot to the right of the trial. (k) All trials are clustered, with the strongest response in the center and weaker responses on the outside. (l) Clusters are placed on a “Fan plot”. Arms represent the orientation and arcs represent the spatial frequency of the grating. At each intersection, there are four lobes of clustered dots, one for each phase at that grating condition.

Responses to natural scenes for one neuron. (m) Responses to each image presented (mean ± sem across 50 trials). Dotted line represents the mean response to the blank sweep. (n) All trials of the image which elicited the largest mean response, the 250ms image presentation is indicated by pink shading. The mean event magnitude is represented by the intensity of the dot to the right of the trial. Trials are sorted (o) and are plotted on a “Corona plot” (p). Each ray represents the response to one image, with the strongest response on the inside and weaker responses at the outside.

Responses to natural movies for one neuron. (q) Responses of one neuron’s response to each of 10 trials of the natural movie. (r) Responses are plotted on a “Track plot”. Each red ring represents the activity of the cell to one trial, proceed clockwise from the top of the track. The outer blue track represents the mean response across all ten trials.

Extended Data Fig. 3. Responsiveness to drifting gratings.

(a) Table summarizing the numbers of experiments (expts) and neurons imaged for each Cre line, layer, area combination in response to drifting grating stimulus and the number, and percent, of neurons that were responsive to the drifting grating stimulus. (b) Strip plots of the percent of neurons responsive to the drifting grating stimulus for each experiment.

Extended Data Fig. 4. Responsiveness to static gratings.

(a) Table summarizing the numbers of experiments and neurons imaged for each Cre line, layer, area combination in response to static grating stimulus and the number, and percent, of neurons that were responsive to the static grating stimulus. (b) Strip plots of the percent of neurons responsive to the static grating stimulus for each experiment.

Extended Data Fig. 5. Responsiveness to locally sparse noise.

(a) Table summarizing the numbers of experiments (expts) and neurons imaged for each Cre line, layer, area combination in response to locally sparse noise stimulus and the number, and percent, of neurons that were responsive to the locally sparse noise stimulus. (b) Strip plots of the percent of neurons responsive to the locally sparse noise stimulus for each experiment.

Extended Data Fig. 6. Responsiveness to natural scenes.

(a) Table summarizing the numbers of experiments (expt) and neurons imaged for each Cre line, layer, area combination in response to the natural scenes stimulus and the number, and percent, of neurons that were responsive to the natural scenes stimulus. (b) Strip plots of the percent of neurons responsive to the natural scenes stimulus for each experiment.

Extended Data Fig. 7. Responsiveness to natural movies.

(a) Table summarizing the numbers of experiments (expts) and neurons imaged for each Cre line, layer, area combination in response to any of the natural movie stimuli and the number, and percent, of neurons that were responsive to the natural movie stimuli. (b) Strip plots of the percent of neurons responsive to the natural movie stimuli for each experiment.

Extended Data Fig. 8. Populations for running correlation analysis.

Table summarizing the number of experiments and neurons, for each Cre line, layer, area combination, included in the running correlation analysis. These are from sessions in which the mouse was running between 20–80% of the time.

Extended Data Fig. 9. Populations for wavelet model analysis.

Table summarizing the number of experiments and neurons for each Cre line, layer, area combination for which wavelet models were fit. The neurons had to be present in all three imaging sessions to be included.