Light-induced anomalous Hall effect in graphene

Abstract

Many non-equilibrium phenomena have been discovered or predicted in optically-driven quantum solids¹. Examples include light-induced superconductivity^2,3 and Floquet-engineered topological phases^4–8. These are short lived effects that should lead to measurable changes in electrical transport, which can be characterized using an ultrafast device architecture based on photoconductive switches⁹. Here, we report the observation of a light-induced anomalous Hall effect in monolayer graphene driven by a femtosecond pulse of circularly polarized light. The dependence of the effect on a gate potential used to tune the Fermi level reveals multiple features that reflect a Floquet-engineered topological band structure^4,5, similar to the band structure originally proposed by Haldane¹⁰. This includes an approximately 60 meV wide conductance plateau centered at the Dirac point, where a gap of equal magnitude is predicted to open. We find that when the Fermi level lies within this plateau, the estimated anomalous Hall conductance saturates around 1.8±0.4 e²/h.

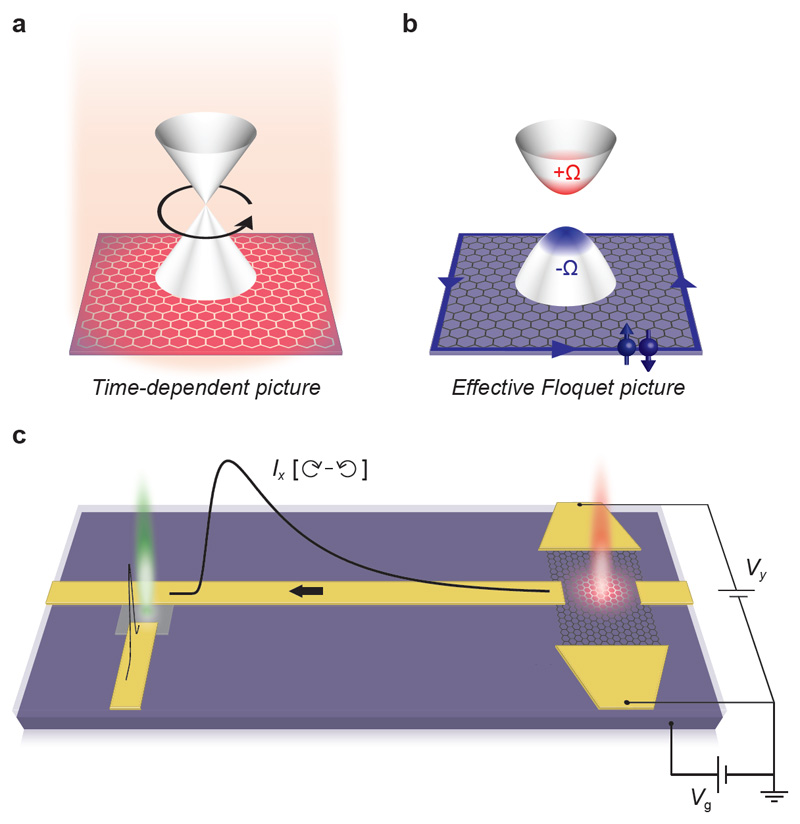
Optical driving has been proposed as a means to engineer topological properties in topologically trivial systems^4–8. One proposal for such a ‘Floquet topological insulator’ is based on breaking time-reversal symmetry in graphene through a coherent interaction with circularly polarized light⁴. In this theory, the light field drives electrons in circular trajectories through the band structure (Fig. 1a). Close to the Dirac point, these states are predicted to acquire a non-adiabatic Berry phase with each optical cycle, and this contribution is equal and opposite for the upper and lower band. This time-averaged extra phase accumulation amounts to an energy shift that lifts the degeneracy of the Dirac point and opens a topological gap in the effective Floquet band structure (Fig. 1b).

Fig. 1. Light-induced topological Floquet bands in graphene and device architecture used to detect ultrafast anomalous Hall currents.

a, A coherent interaction between graphene and circularly polarized light was predicted to open a topological band gap in the effective Floquet band dispersion⁴. b, The gap is characterized by the presence of Berry curvature (Ω), which is identical in both valleys. The experimental signature of the induced nontrivial topology is the emergence of anomalous Hall currents. c, Exfoliated graphene monolayer with four electrical contacts (right) and a photoconductive switch for current detection (left), connected by a microstrip transmission line. The graphene was optically driven using an ultrafast mid-infrared circularly polarized laser pulse (red beam). The generated helicity-dependent anomalous Hall currents I_x [⟳ - ⟲] were probed after a variable time delay at the photoconductive switch, which was activated by a second laser pulse (green beam). Anomalous Hall currents were measured as a function of source-drain voltage bias V_y and backgate voltage V_g, the latter of which controlled the graphene Fermi level (E_F).

The non-trivial topology of the Floquet bands forming this gap arises from their nonzero Berry curvature distribution^4,5, which integrated over the Brillouin zone defines a topological invariant, called the Chern number^11–14. Topologically protected transport is predicted to develop if the Fermi level (E_F) lies inside the gap, exhibiting an anomalous Hall effect carried by edge states in the absence of an applied magnetic field^5,10–15. This corresponds to the formation of a light-induced Chern insulator, equivalent to the phase originally proposed by Haldane¹⁰ and distinct from topological phases induced by spin-orbit interaction^{12–14,16,17}. While quantum simulation experiments have validated aspects of this proposal in synthetic physical settings^18,19, and Floquet-Bloch states have been detected in a topological insulator²⁰, anomalous Hall currents originating from such a photon-dressed topological band structure have not been observed in a real material.

This proposal is unique because the anomalous Hall effect arises from Berry curvature that is coherently induced by light in a material where none is present in equilibrium. This is in contrast to previous observations of photo-induced anomalous Hall effects in semiconductor quantum wells²¹, monolayer transition metal dichalcogenides²² or Weyl semimetals²³, which originate from Berry curvature intrinsic to the equilibrium band structure due to broken inversion symmetry.

Inducing and detecting anomalous Hall currents in graphene presents multiple experimental challenges. The laser electric field strength required to open an observable topological gap is estimated to be of the order of 10⁷-10⁸ V/m, even at mid-infrared wavelengths where the effect is enhanced^4,5,15. Hence, to avoid material damage while still providing sufficient field strength, ultrafast laser pulses must be used. Consequently, the resulting Hall conductance changes are too short-lived to be probed with conventional transport techniques.

In this work, ultrafast anomalous Hall currents were detected on-chip by using a laser-triggered photoconductive switch⁹. A schematic of our device architecture is shown in Fig. 1c. An exfoliated monolayer graphene flake was transferred onto a doped silicon wafer with an oxide layer and contacted in a four-probe Hall geometry using standard lithography procedures^24,25. The metallic leads formed microstrip transmission lines in conjunction with the oxide layer and silicon wafer. These directed ultrafast anomalous Hall currents generated in the graphene to a photoconductive switch for detection. The switch consisted of a resistive amorphous silicon patch that bridged the main transmission line and a probing line. When excited with a visible ultrafast laser pulse, the switch became highly conductive and detected currents flowing in the main transmission line with a time resolution set by the silicon carrier lifetime (less than 1 ps). By adjusting the time delay between the graphene laser drive pulse (pump) and the switch trigger pulse (probe), the temporal profile of ultrafast anomalous Hall currents could be characterized. The amplitude of the detected currents were determined by calibrating the photovoltaic response of the switch using a DC bias field, which is possible in our microstrip geometry because only the fundamental quasi-TEM mode propagates up to THz frequencies.

Graphene was driven using an approximately 500 fs laser pulse at a frequency of 46 THz (so that the photon energy ℏω ≈ 191 meV, wavelength ≈ 6.5 μm). Unless otherwise noted, a peak laser pulse fluence of 0.23 mJ/cm² was used, corresponding to a peak intensity of 4.3 × 10¹² W/m² and peak electric field strength of 4.0 × 10⁷ V/m (in free space, for circular polarization). The pulses were focused to a spot size of roughly 80 μm (FWHM), ensuring homogeneous illumination of the graphene flake and the contacts. A second ultrafast laser pulse centered at 520 nm was used to operate the photoconductive switch. The device was mounted in a microscopy cryostat designed for high-frequency transport measurements and cooled to a base temperature of 80 K. A global backgate formed by the silicon wafer and the oxide layer controlled the Fermi level (E_F) in the graphene flake. The graphene field-effect mobility was measured to be μ ≈ 10,000 cm²/Vs in the vicinity of the Dirac point. The results presented here are from a single device, and consistent results have been obtained using five different devices.

Anomalous Hall currents induced by circularly polarized light are expected to exhibit the following traits: (1) They should be generated in the transverse direction (I_x) with respect to an applied DC voltage bias (V_y). (2) They should reverse polarity upon reversing the light helicity. (3) They should reverse polarity upon reversing V_y, with a linear functional dependence. To probe (1) and (2), we directly detected the difference between currents I_x generated with right- (clockwise from the perspective of the light source) versus left-circular polarization (henceforth referred to as I_x [⟳ - ⟲]), utilizing an optical polarization chopping technique.

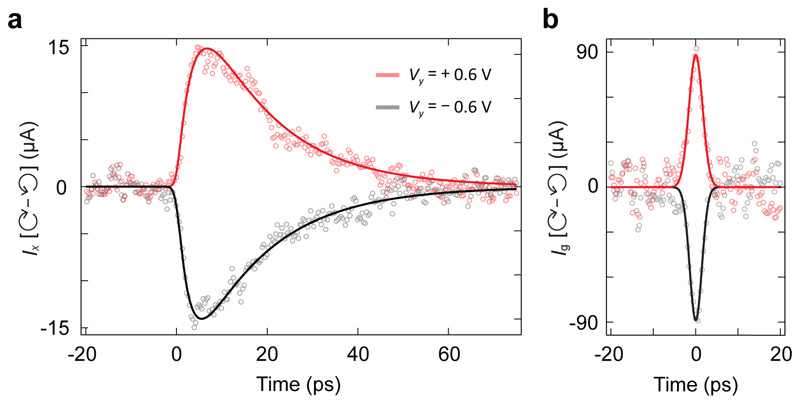
Figure 2a displays the measured I_x [⟳ - ⟲] signal as a function of pump-probe time delay for a positive and negative V_y, with the Fermi level gated to the graphene Dirac point (E_F = 0). The time-resolved signal exhibits a fast rise time followed by an exponential decay, and reverses polarity upon reversing V_y. From the polarity of the signals, we determine that for right circularly polarized light propagating along +z (in a right-handed coordinate system), a DC field applied to the graphene in the -y direction induces a Hall current in the +x direction.

Fig. 2. Ultrafast anomalous Hall currents in graphene driven by circularly polarized light.

a, Time-resolved helicity-dependent anomalous Hall currents I_x [⟳ - ⟲] measured at the photoconductive switch for a positive (red) and negative (black) transverse source-drain voltage V_y. The graphene Fermi level was gated to the Dirac point (E_F = 0). Solid lines are based on the signal propagation model in supplementary S3. A small background observed at V_y = 0 was subtracted from the data sets (see supplementary S4). b, Deconvolved anomalous Hall current signals I_g accounting for the response function of the on-chip circuitry. The current amplitude has a ±22% systematic error from the calibration of the photoconductive switch. Solids lines are Gaussian fits.

The measured data in Fig. 2a contains a convolution between the intrinsic dynamics of anomalous Hall currents in the graphene and the response function of the circuit, which includes the contact resistance, graphene capacitance, microstrip impedance and dispersion in the transmission line. As detailed in supplementary S3, we directly calibrated these system parameters to determine the deconvolved current profiles, shown in Fig. 2b. The signals have a duration of approximately 3 ps, which exceeds that of the driving laser pulse (500 fs). We believe that this difference in timescales is mainly caused by the finite size of the graphene, which leads to arrival-time differences of currents generated in different parts of the flake, as well as the sublinear dependence of the Hall current on the drive laser intensity (Fig. 4a).

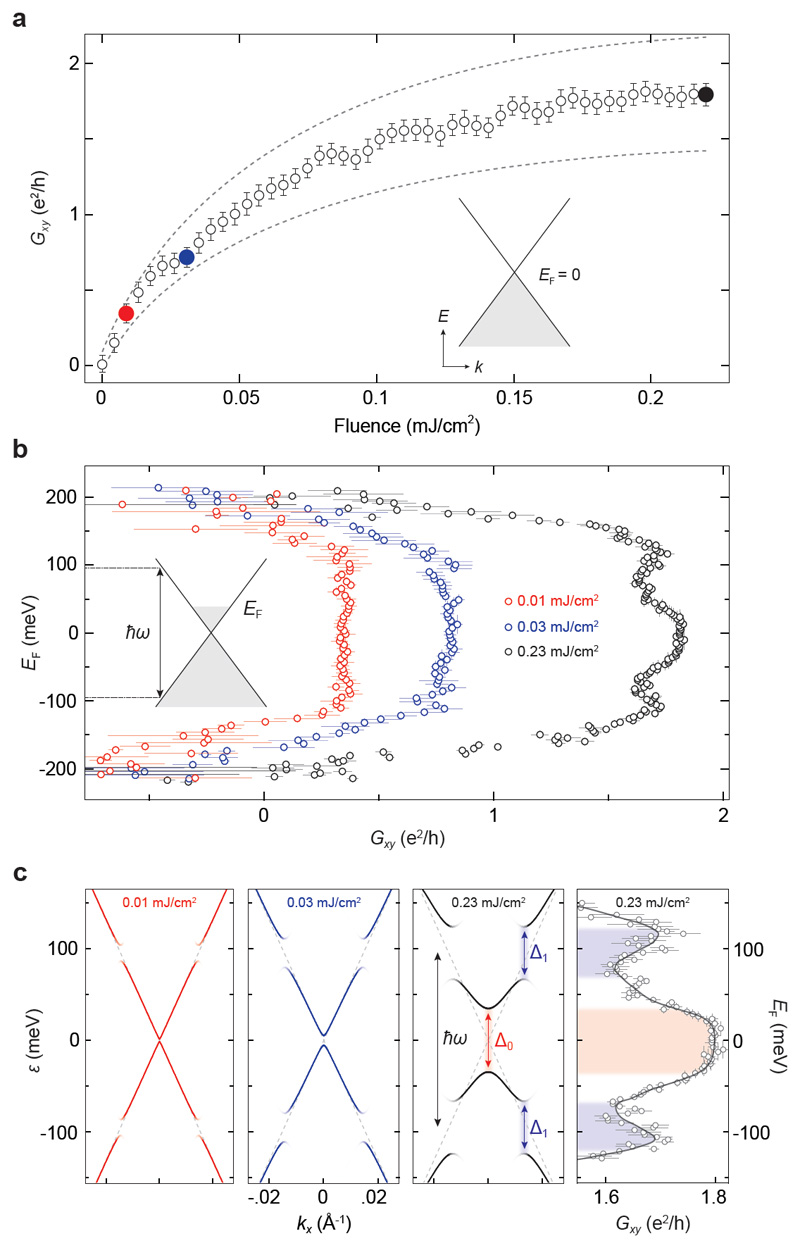
Fig. 4. Evidence for topological Floquet bands.

a, Non-equilibrium anomalous Hall conductance G_xy as a function of the peak laser drive pulse fluence. The equilibrium Fermi level was gated to the Dirac point (E_F = 0). Error bars are the standard statistical error, and the dashed lines denote the systematic error from the calibration of the photoconductive switch. Colored data points correspond to the fluences measured in b. b, G_xy as a function of the equilibrium E_F measured at three fluences. Horizontal error bars are the standard error and vertical error bars denote the uncertainty related to determining the precise value of the Dirac point. The systematic error on G_xy is the same as in (a). c, Left three panels: Effective band structures for the fluences reported in (b) simulated using Floquet theory. At the highest fluence, we calculated Δ₀ ≈ 69 meV and Δ₁ ≈ 56 meV. Right panel: Blow up of the high-fluence data in (b) for comparison. Solid line is the smoothed data. Shaded regions highlight the features corresponding to light-induced band gaps in the Floquet band structure.

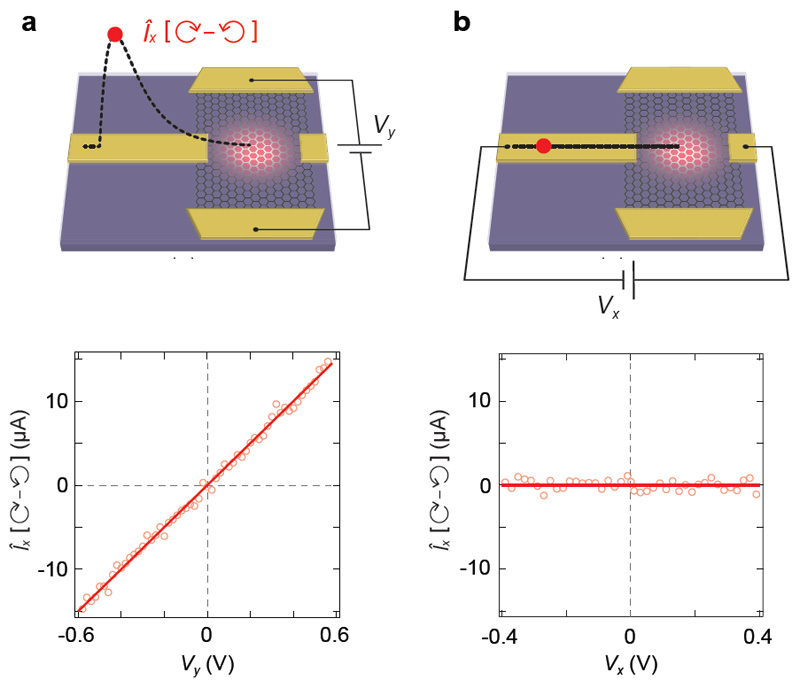
Having established the presence of ultrafast anomalous Hall currents in graphene, we investigated the functional dependence of I_x [⟳ - ⟲] on V_y at E_F = 0. We did so by fixing the pump-probe time delay at the maximum of the I_x [⟳ - ⟲] signal in Fig. 2a, which we refer to as Î_x [⟳ - ⟲], and measured the signal amplitude as a function of V_y (Fig. 3a). The data exhibit the expected linear dependence. We also investigated helicity-dependent currents generated in response to a longitudinal voltage bias V_x (Fig. 3b), which are not expected because graphene has D_6h point group symmetry²⁶. The data in Fig. 3b confirm that no helicity-dependent longitudinal currents were generated.

Fig. 3. Helicity-dependent current behavior under different source-drain voltage geometries.

The peak of the helicity-dependent current Î_x [⟳ - ⟲] measured as a function of a, transverse source-drain voltage V_y and b, longitudinal source-drain voltage V_x. The graphene Fermi level was gated to the Dirac point (E_F = 0). Solids lines are linear fits.

We define the peak anomalous Hall conductance of the non-equilibrium state as G_xy = Î_g [⟳ - ⟲] / 2V_y, where Î_g is the peak of the deconvolved signal in Fig. 2b. Figure 4a displays G_xy as a function of the laser drive pulse fluence, measured for E_F = 0. The data show a sublinear dependence that saturates at high fluence. At the highest achievable fluence, we estimate G_xy = (1.8 ± 0.4) e²/h, consistent with recent numerical simulations of optically-driven graphene for our laser pulse parameters²⁷.

To characterize the predicted topological Floquet bands, we varied E_F (defined as the chemical potential without light excitation) using the backgate²⁸ and compared the variation in G_xy (Fig. 4b) with calculations of the expected effective band structures based on Floquet theory for our laser pulse parameters (Fig. 4c) (see supplementary S7).

We observed that for low drive fluence (red circles), G_xy was independent of the backgate potential for |E_F| ≲ 100 meV ≈ ℏω/2. In this low excitation regime, the Floquet-gap at the Dirac point (Δ₀) is too small to be observable. However, significant gaps Δ₁ appear precisely at ±ℏω/2 as a consequence of resonant Rabi splitting. Because these resonant gaps Δ₁ are opened non-adiabatically, a non-equilibrium electron distribution can be expected in a ring of momenta surrounding the Dirac point where the photon resonance occurs, for |E_F| ≲ ℏω/2. We believe that the observed plateau at low fluence thus results from the resonant excitation of electrons in conjunction with the predicted Berry curvature at the Δ₁ band edges^4,15,29–33. For |E_F| ≳ ℏω/2, where first order resonant excitations are forbidden, G_xy decreased to zero and eventually changed sign when approaching the dielectric breakdown threshold of the device.

At higher fluences (blue and black circles), we resolved additional features near ±ℏω/2 in the G_xy vs. E_F spectrum. They are closely aligned with the band edges of the calculated gaps Δ₁, which are larger in size.

An additional feature appeared at the highest fluence (black circles): close to the Dirac point and away from the photon resonance, a conductance plateau with a width of approximately 60 meV was observed, where G_xy = (1.8 ± 0.4) e²/h (Fig. 4c right). Remarkably, the width of this plateau is very close to the calculated width of the light-induced topological gap at the Dirac point Δ₀ (69 meV, red shading). This suggests that at high fluence there is a second source of anomalous Hall currents carried by a distribution of electrons occupying the lower dressed band beneath Δ₀. For these momenta, the driving frequency is large compared to the splitting of the bands and a quasi-adiabatic transfer between the static and dressed bands is therefore possible. The effective Fermi level-dependent transverse transport then behaves similarly to what one would expect for gapped bands with non-zero total Berry curvature, given a Fermi-Dirac distribution, in that G_xy shows a plateau when E_F lies inside the band gap^11–14. The sharpness of the decrease in G_xy as E_F is moved outside of Δ₀ may depend on multiple factors, including the Berry curvature and non-equilibrium electron distributions in the Floquet bands, which is influenced by the frequency, amplitude and pulse-shape of the laser, as well as disorder, interactions and dissipation^4,15,29–33.

Methods

All methods can be found in the supplementary information.