Microtubules Regulate Localization and Availability of Insulin Granules in Pancreatic Beta Cells

Abstract

Two key prerequisites for glucose-stimulated insulin secretion (GSIS) in β cells are the proximity of insulin granules to the plasma membrane and their anchoring or docking to the plasma membrane (PM). Although recent evidence has indicated that both of these factors are altered in the context of diabetes, it is unclear what regulates localization of insulin granules and their interactions with the PM within single cells. Here, we demonstrate that microtubule (MT)-motor-mediated transport dynamics have a critical role in regulating both factors. Super-resolution imaging shows that whereas the MT cytoskeleton resembles a random meshwork in the cells’ interior, MTs near the cell surface are preferentially aligned with the PM. Computational modeling suggests two consequences of this alignment. First, this structured MT network preferentially withdraws granules from the PM. Second, the binding and transport of insulin granules by MT motors prevents their stable anchoring to the PM. These findings suggest the MT cytoskeleton may negatively regulate GSIS by both limiting the amount of insulin proximal to the PM and preventing or breaking interactions between the PM and the remaining nearby insulin granules. These results predict that altering MT network structure in β cells can be used to tune GSIS. Thus, our study points to the potential of an alternative therapeutic strategy for diabetes by targeting specific MT regulators.

Significance

Insulin is a critical metabolic hormone whose dysregulation results in diabetes, a disease that afflicts ∼9% of the US population. Although numerous factors regulate its dynamics, it has long been thought that the cell’s cytoskeleton has a critical role. What that critical role is, however, has remained elusive. Here, we use imaging and computational modeling to demonstrate two previously unknown mechanisms by which the microtubule cytoskeleton negatively regulates insulin secretion: it 1) limits the amount of insulin near the plasma membrane and 2) inhibits exocytosis of insulin granules by preventing their anchoring to the plasma membrane. These results shed new, to our knowledge, light on how insulin is regulated at the cellular level and may point to new therapeutic targets to better control insulin regulation.

Introduction

Deregulated glucose-stimulated insulin secretion (GSIS) results in diabetes, a disease that afflicts ∼9% of the population in the USA (1, 2, 3, 4). Thus, elucidating how GSIS is regulated is of fundamental importance in understanding glucose homeostasis at both the cellular and systemic level. Pancreatic islet β cells are the insulin factories in the body. Here, insulin is produced and sorted through the endoplasmic reticulum and the Golgi (5), secretory insulin vesicles are generated at the trans-Golgi network, and those vesicles mature into hard-core granules that are distributed through the cell’s cytoplasm for regulated secretion.

The major stimulant for insulin secretion is high glucose, whose entry into and subsequent metabolism in β cells increases the ATP/ADP ratio, triggering insulin secretion (6). The amount of secreted insulin is of critical importance for metabolism and health because over- or undersecretion leads to hypo- or hyperglycemia in patients, respectively. A main determinant of insulin secretion dosage at given stimuli is the number of readily releasable insulin vesicles. These vesicles are biochemically capable of anchoring at the secretion sites and are close enough to the plasma membrane to do so (7). Here, we investigate how cells use the cytoskeleton to regulate this readily releasable pool by controlling the number of granules near the plasma membrane as well as their availability for anchoring.

Although numerous intracellular factors regulate the localization and availability of insulin granules, it has long been thought that the cytoskeleton has a critical role (8, 9, 10). Microtubules (MTs) and MT-dependent molecular motors are the major transport system in mammalian cells (11,12). In many cell types, MTs extend toward the cell periphery in radial (mesenchymal cells) or parallel (neurons, columnar epithelia) arrays, allowing them to serve as long-distance transport highways, for example, for delivery of secretory vesicles, among other functions (13, 14, 15, 16). In pancreatic β cells, MTs also serve intracellular transport roles (17, 18, 19), but MT function in secretion is complex and incompletely understood. A number of observations indicate that prolonged insulin secretion is attenuated in the absence of MTs (20,21) In the long term, MT depletion inhibits new insulin granule formation by interfering with insulin transport through the endoplasmic reticulum and the Golgi ((22) and our unpublished data). Reduced secretion could, however, be explained by lack of new granule production or delivery (23). Without MTs, the net movement of existing secretory insulin granule movement is significantly slowed (24), potentially influencing delivery. Interestingly, in our recent finding, short-term depletion of MTs resulted in immediate facilitation of exocytosis and, as a result, increased GSIS, which is consistent with earlier findings (25,26). Commensurately, MT enrichment in β cells both in taxol-treated islets and in diabetic mice (24) was associated with decreased secretion. Thus, although all studies agree that MT-dependent transport is needed for new insulin granule production, it is not readily apparent how or why MTs regulate secretion of the readily releasable pool or how transport of existing granules is linked to GSIS. Here, we test the hypothesis that this link between MT-based transport and insulin secretion is a consequence of the cytoplasmic architecture of β cells.

One important feature of β cell cytoplasm is the abundance of premade insulin granules in a resting cell. Estimates indicate individual β cells contain on the order of 10,000 insulin granules (27) of 100–300 nm in diameter (28), which are tightly packed in the cytoplasm. At any stimulation, only a small portion of these vesicles was secreted (∼1% within an hour of high glucose stimulation (28)). This raises the question of why these abundant vesicles should be transported for GSIS. Additionally, granule motions analyzed in β cell culture models (29) and in intact pancreatic islets (24) were found to be random and undirected. This is not surprising, given that super-resolution imaging of the MT cytoskeleton in intact islets has indicated that β cell MTs form a spaghetti-like random meshwork (24), which is very different from directed MT arrays in cells that use MTs for directional long-distance transport. Thus, even if transport were important for GSIS, what random transport on an unstructured MT meshwork would accomplish and how it would influence GSIS is unclear.

Our prior data provide a clue to how MTs influence GSIS. In the absence of MTs, high glucose stimulation leads to accumulation of granules at the cell periphery (24), possibly due to the stimulation of glucose-dependent priming or docking (30). Interestingly, the presence of MTs prevents this excess accumulation, suggesting MT-based transport may regulate granule localization even when effective motions (the motion resulting from multiple motors potentially interacting with multiple MTs) are random and undirected. Total internal reflection fluorescence (TIRF) microscopy data point to two possible mechanisms for this regulation. First, quantification of delivery and withdrawal of granules from the cell periphery demonstrates that MT-dependent transport is required to maintain the proper balance between delivery and removal (24). Second, the motions of granules near the membrane (in the TIRF field, within ∼200 nm of the plasma membrane) are predominantly parallel to it (17), indicating there may be organization to the MT network near the membrane and that insulin granule motions may not be random there. To clarify how MTs influence insulin localization and availability, we utilize super-resolution microscopy to image the structure of the MT meshwork near the plasma membrane and computational modeling to assess how the interactions between granules, the meshwork, and the plasma membrane influence GSIS.

There are generally two populations of MTs in cells: dynamic MTs that are undergoing “dynamic instability” (31,32) and stable MTs, characterized by the presence of detyrosinated tubulin (Glu-tubulin) among other modifications (33, 34, 35). Glucose alters the MT network in potentially important ways. Glucose stimulation destabilizes and depolymerizes stable MTs and increases MT nucleation and growth rates. This makes the MT network significantly more dynamic, whereas MT density is only modestly altered. Glucose is also well known to activate docking molecules, which are necessary for GSIS. This body of work thus suggests that glucose stimulation influences granule transport, which in turn alters GSIS.

We hypothesize that MTs have a dual role in negatively regulating GSIS: MTs 1) enhance withdrawal of granules from the periphery to the interior and 2) prevent anchoring and subsequent secretion of those at the periphery (e.g., by preventing the formation of or breaking bonds between granules and the anchoring machinery). This is a compelling hypothesis, but our understanding of MT control on cytoplasmic distribution of insulin granules remains fragmented and insufficient. In particular, the abundance of insulin, the apparently random nature of the MT network, and the seemingly random but complex nature of granule motions (29) make it difficult to deduce how MTs influence GSIS. To test this hypothesis, we will develop a computational model of intracellular insulin granule dynamics to investigate how MT dynamics influence insulin granule localization and availability. The basic elements of this model (e.g., transport rates and MT-binding rates) will be calibrated to data. It will then be tested against independent results, including TIRF observations of peripheral granule densities, along with quantification of GSIS under different conditions, to determine the conditions in which the model matches observations. In this way, the model and experimental observations will be jointly used to infer how interactions between MT dynamics, granule dynamics, and membrane anchoring influence GSIS.

In this study, we will investigate two specific questions, both of which are important to understanding GSIS: how MT-based transport influences the density of insulin granules near the plasma membrane and how the binding of granules to the MT cytoskeleton influences their membrane anchoring, both of which are a prerequisite to exocytosis. Given our focus on the dynamics of granules near the plasma membrane, we will quantify the structural characteristics of the MT network near the membrane (directionality in particular) in pancreatic β cells. These data are used in conjunction with prior three-dimensional tracking of granule motions (24) to develop and simulate a discrete, two-dimensional (2D) computational model of insulin granule dynamics within a single cell. Results of this modeling support the aforementioned hypothesis that MT-based transport negatively regulates GSIS in two important ways: by 1) increasing the rate of transport of granules away from the plasma membrane and 2) reducing the ability of those that are near the membrane to stably anchor to it.

Materials and Methods

Discrete model description

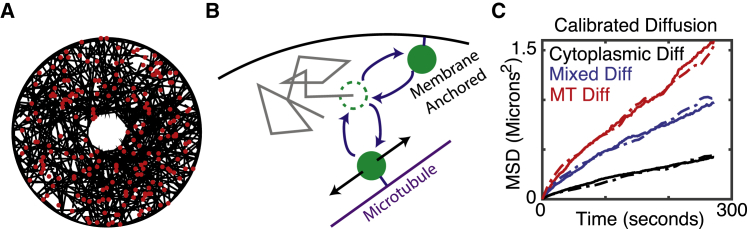
This discrete model accounts for four essential features that impact the transport of granules: 1) transport along MTs, 2) transport independent of MTs, 3) binding and unbinding of granules to MTs, and 4) tethering of granules (that are sufficiently close) to the cell membrane, which renders them immobile (illustrated in Fig. 1 B). We briefly discuss how each of these features is encoded into the model and how aspects of it are calibrated to data.

Figure 1.

Description of model. (A) A snapshot of a simulation with 500 microtubules and 200 insulin granules is shown. (B) A schematic of the basic model elements—including free diffusion, binding of granules to MTs, diffusion along MTs, and membrane anchoring—is given. The dashed green circle indicates the present state of a granule. The gray line indicates a possible diffusive path. The filled green circles depict potential MT-binding and membrane-binding events. (C) An illustration of calibrated diffusion is given. Dashed curves are data, and solid curves are simulated. Cytoplasmic and MT-bound diffusion coefficients were calibrated based on the red and black curves, and the relative fraction of time a granule spends in these two modes of motion was calibrated based on the blue curve. To see this figure in color, go online.

Modeling MT independent transport

We approximately model the cell as a 5 μm radius circle with a 1 μm hole cut out (representing the nucleus). A regular 2D grid is constructed on this cellular domain, and the motion of granules on this lattice is modeled as a subdiffusive (anomalous diffusion with a mean-square displacement (MSD) scaling exponent <1) random walk. Granule motion is assumed to obey the equation of motion for overdamped fractional Langevin equation (FLE) representing viscoelastic subdiffusion:

$$\gamma \underset{-\infty }{\overset{t}{\int }}K\left(t-s\right)\overrightarrow{v}\left(s\right)ds=F_{st},$$ (1)

where v is the velocity of the granule, γ is the drag coefficient for the granule, K is a memory kernel encoding history dependent viscoelastic effects, and F_st is the stochastic forcing obeying the appropriate fluctuation dissipation theorem (36). Here, the drag coefficient satisfies γ = 2k_BT/(Γ(1 + α)D), where k_BT is the standard thermal noise constant and D, α are estimated from data (see (37) for further details of the FLE). The kinetic lattice Monte Carlo method for simulating the overdamped FLE from (38) is used to simulate motion.

Constructing the MT network and modeling MT-mediated transport

To simulate MT-mediated motion, we must first populate the in silico cell with an MT network. We do so by essentially growing a network of 500 discrete, independent, and noninteracting MTs. Of these, 250 are short (mean length 2 μm) and 250 long (mean 5 μm). Short MTs are included to account for possible dynamically unstable MTs, whereas long ones are thought of as stable (similar results are found if all MTs are the same length, though). We specify a start point and initial growth direction for each MT. The MT is then elongated in a straight line until it interacts with the cell periphery (if it does so at all). If the growing MT interacts with the cell border, it either terminates with probability p or bends and grows parallel to the cell periphery with probability 1 − p. Note that those MTs that terminate do not depolymerize. Thus, all probabilities (p) lead to the same interior MT densities. It is only the peripheral MT densities that will differ as a function of p. We also note that other potential mechanisms could lead to the formation of peripheral MT arrays aligned with the plasma membrane. For example, membrane-associated MT-binding proteins could potentially bring them into proximity. Our purpose here is to not investigate the formation of this structure, but rather, its consequences. We thus use this method of constructing the MT network only as a means to generate MT meshes with different properties near the boundary.

For most simulations, a value of p = 0 is chosen, corresponding to a peripherally aligned population of MTs forming. However, in Fig. 3, the effect of this MT structure parameter is considered. For simplicity, we assume the MTs are fixed in place once grown and thus do not model the detailed dynamics of remodeling of the MT cytoskeleton by motors themselves (39,40). The model does incorporate dynamic instability (41) of MTs through removal and replacement of MTs with a specified rate. We fix the average MT lifetime at 1000 s, though we also consider the effects of short MT lifetimes (10 s, Fig. S2). As removal and replacement of MTs has much the same effect on granule motility as MT binding and unbinding, which are considered in somewhat more detail, we do not exhaustively explore the effect of MT catastrophe dynamics.

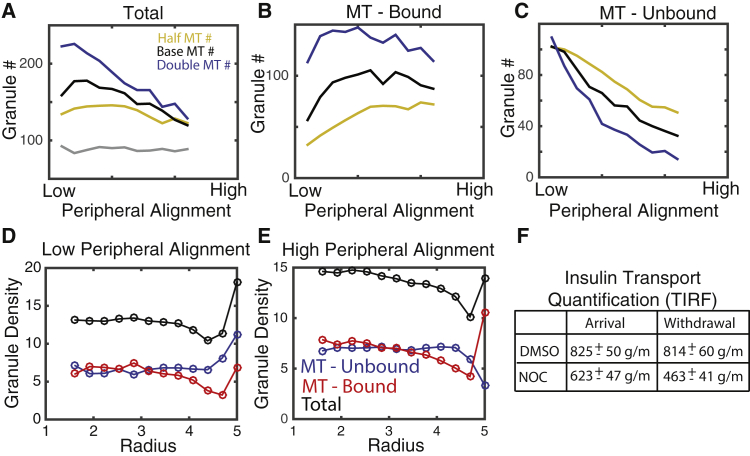
Figure 3.

Effect of MTs on peripheral localization of insulin granules. (A) The total number of granules located within 250 nm of the cell membrane as a function of the peripheral density of MTs as well as the total density of MTs is shown. “Base MT#” refers to simulations with 500 total MTs, and “Half” and “Double” refer to 250 and 1000 MTs, respectively. The gray line depicts the number of peripheral granules when the MT network is removed and the density distribution achieves steady state. (B) The number of MT-bound granules is shown. (C) The number of unbound granules is shown. (D and E) The radial distribution of bound, unbound, and total granules in low and high peripheral density cases is shown. (F) A table depicting change in granule arrival delivery to the cell periphery in cells from experiments in our previous publication is given (data reproduced from (24)). “Arrival” and “Withdrawal” indicate the rate of appearance and disappearance of granules in the TIRF field in control and NOC conditions. To see this figure in color, go online.

Motion of granules is strongly subdiffusive even in the absence of actin, suggesting that individual MT motors are not moving granules along MTs in a directed fashion (this would be superdiffusion). To be clear, we are not suggesting that MT motions are motor independent, only that they are not “ballistic” or directed, as is commonly the case with motor-driven motions. How might motor-driven motions, which typically generate near-ballistic motion, give rise to random motion? It is possible that each granule has a number of motors bound to it at any given time that are constantly competing to be the driver of motility. In this scenario, motions could be directed on very short timescales while appearing random on observed timescales because of the action of multiple motors. This is, however, beyond the scope of this article, and we only model the motions on observed timescales (as subdiffusive) rather than model the actions of large numbers of motors, for which we do not have constraining data. We thus do not model the dynamics of individual motors. Rather, MT-mediated granule motion is modeled as a one-dimensional subdiffusive random walk on the MT to which the granule is bound. The same FLE equation of motion (Eq. 1 above) describes this motion, and the same method of simulation is used.

Granule binding, unbinding, and tethering

It is highly likely that granules bind and unbind from the MT lattice, and thus, their aggregate motion is in some sense an interpolation of motion in those two forms. We assume that an unbound granule can bind to any MT within 250 nm of its center (assuming a 150 nm granule radius along with an additional ∼100 nm reach of the motor head) with a per MT rate of binding k_on. Similarly, granules are assumed to unbind from MTs with a rate of k_off. These two rate constants are not individually accessible because we do not know what specific motors are involved or how granules interact with the dense network of MTs. As discussed, however, we can calibrate their ratio based on data to ensure that the relative fraction of time each granule spends undergoing (un)bound motility is appropriate. We thus fix the rate k_off = 1:30 to represent a roughly 30 s bound lifetime, which is in the same range found for the kinesin Kip2 (42), and calibrate k_on accordingly. Doubling or halving this bound lifetime leads to similar results. Switching of granules from one MT to another is not directly modeled. However, when a granule unbinds from an MT, it can rebind to any other nearby MT. All simulations were carried out with k_off = 1:15, 1:60, yielding similar results.

Anchoring of granules to the cell membrane is modeled similarly, with granules within 250 nm of the cell border binding with a rate constant k_T and unbinding with a rate k_U. We do not have estimates for these rate constants or any way to constrain them directly. However, in this study, we vary the affinity by fixing the unbinding rate and modulating the magnitude of k_T to determine how the relative strength of anchoring (i.e., the relative fraction of time an unbound granule spends tethered to the membrane) influences insulin granule dynamics (see Fig. 4). We further consider two possibilities for which granules can or cannot tether: 1) that all granules can tether or 2) that only unbound granules can tether.

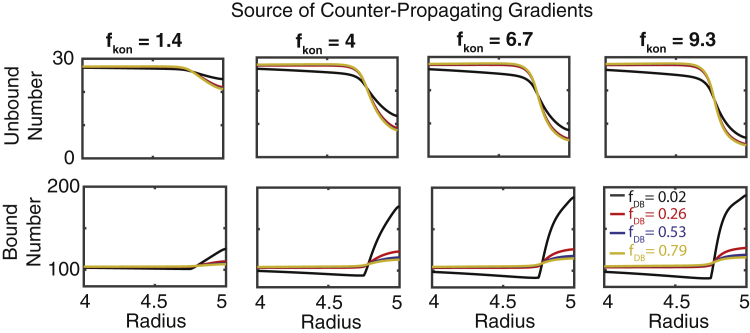
Figure 4.

Effect of MT-binding propensity and reduction in radial diffusivity on granule densities. Simulations of the radially symmetric continuum model in which the rate of MT binding is increased by a factor (f_kon) and rate of radial diffusivity is decreased by a factor of (f_DB) within 250 nm of the cell membrane are shown. Top (bottom) panels show the steady-state insulin densities as a function of radius in different conditions. The notation f_DB = 0.02 and so forth indicates the base value of the relevant parameter is multiplied by the given value in the peripheral region (DB → 0.02 × DB, in this case). To see this figure in color, go online.

Calibrating motility and binding and unbinding parameters

Many of the parameters in this model are directly estimable from data. In particular, using granule motility data, we can extract the values of the subdiffusive exponent (α), the diffusion coefficients for bound and unbound granule motion (D for each), and the relative fraction of time the granule spends in the bound and unbound states.

The data we use for this are derived from (24), in which the MSD of granule motion was measured in control cells, cells with the MT cytoskeleton removed, and cells with the actin cytoskeleton removed. First, from (29), it was determined that α = 0.75. To calibrate the diffusion constants, we will rely on MSD data. For simplicity, we will assume that in the absence of actin, all motion is MT mediated, and in the absence of MTs, all motion is actin mediated. We can thus use the data in which actin is removed to calibrate the diffusion constant for MT motion and the data in which MTs are removed to calibrate the diffusion constant for non-MT motion. See Fig. 1 C (black and red curves) for calibration results.

We can additionally use the control MSD data to calibrate the relative time each granule spends in bound and unbound states; the more time a granule spends in the MT-bound state, the higher its MSD will be and vice versa. We fix the value of k_off and vary the value of k_on until the MSD data of the amalgamated diffusion match that of control data (blue curve in Fig. 1 C). For a list of all parameters for the discrete model, see Table 1.

Table 1.

Synopsis of the Discrete Model Parameters

Parameter Name	Value	Units
Number of MTs	500	Number
Number of granules	1000	Number
Cell radius	5	μm
Nucleus radius	1	μm
Granule radius	0.3	μm
Subdiffusion exponent (α)	0.75	None
MT-bound diffusion constant (D1)	0.015	μm2/s
2D grid diffusion constant (D2)	0.005	μm2/s
MT mean length (short, long)	2, 5	μm
MT length standard deviation	2	μm
MT catastrophe rate	1/1000	1/sec
Granule/MT-binding rate (kon)	1/8	1/(s ⋅ MT)
Granule/MT unbinding rate (koff)	1/30	1/s
Granule/MT-binding radius	0.25	μm
Granule tethering rate (kT)	0	1/s
Granule untethering rate	1/30	1/s
Granule tethering radius	0.25	μm

Simulation protocol

All simulations begin with each of the 1000 granules randomly placed in the cell for a pseudouniform distribution. The time step for simulations granule motions is chosen to be ΔT = 10 ms, with simulations running nominally for 300 s to achieve a steady state. The kinetic lattice Monte Carlo method requires that the spatial grid size be chosen appropriately so that Δx = (2DΔT^α)^0.5. Because the diffusion constant for the MT- and non-MT-mediated motions are different, this yields spatial step sizes of 18 nm for the 2D lattice motions and 30 nm for the one-dimensional motions on MTs. In select simulations, decreasing the time step to ΔT = 5 ms did not alter results. In all results presented, averages of 50 independent simulations are presented unless otherwise stated.

Mice

Mouse usage and handling followed the protocol approved by the Vanderbilt Institutional Animal Care and Usage Committee for Dr. Gu. Wild type CD-1 (ICR) mice were purchased from Charles River (Wilmington, MA). All mice were bred and handled following protocols approved by the Vanderbilt Institutional Animal Care and Use Committee. All mice used were males 8–10 weeks of age.

Islet isolation

Islets isolation followed the previously described procedure (43). Briefly, mouse pancreata were distended by injecting 3 mL 0.8 mg/mL collagenase P (Sigma-Aldrich, St. Louis, MO) through the bile duct and digested at 37°C for 20 min. Islets were hand-picked and cultured to recover in Gibco RPMI 1640 Medium (Thermo Fisher Scientific, Waltham, MA) containing 11 mM glucose, 10% heat-inactivated fetal bovine serum (Atlanta Biologicals, Flowery Branch, GA), 100 IU/mL penicillin, and 100 μg/mL streptomycin.

Immunofluorescence

Isolated mouse islets were treated with 2.8 mM (low) or 20 mM (high) glucose in RPMI media for 2 h and fixed with 4% paraformaldehyde in phosphate-buffered saline with 0.1% saponin (Sigma-Aldrich). Immunofluorescence followed the described procedure (24). Briefly, fixed islets were stained with primary antibodies at 4°C overnight, followed by another staining with fluorophore-conjugated secondary antibodies. After each antibody incubation, islets were washed three times using phosphate-buffered saline with 0.1% saponin. After staining, islets were mounted with Vectashield mounting media (Vector Labs, Burlingame, CA) for microscopy. Primary antibodies used are rabbit anti-β-tubulin (Abcam, Cambridge, MA), guinea pig anti-insulin (DAKO, Houston, TX), rabbit anti-detyrosinated tubulin (Millipore, Burlington, MA), and mouse anti-E-cadherin (BD Biosciences, San Jose, CA). Secondary antibodies used are goat anti-rabbit IgG-Alexa Fluor 488 (Abcam), goat anti-mouse IgG-Alexa Fluor 488 (Invitrogen, Grand Island, NY), and goat anti-guinea pig IgG-Alexa Fluor 650 (Thermo Fisher Scientific).

Microscopy and image processing

All images were captured using a Nikon Eclipse A1R laser scanning confocal microscope equipped with a CFI Apochromat TIRF 100×/1.45 oil objective (Nikon, Tokyo, Japan). The microscope is driven by Nikon Elements software. For directionality analysis, oversampled image stacks (50 nm³ voxels) were acquired and thereafter deconvolved by NIS Elements Software using the Richardson and Lucy algorithm (15 iterations). All images presented in figures were single-slice confocal images, for which the brightness and contrast were adjusted consistently across every image to better present small structural features. MTs were thresholded using the variation Isodata Algorithm default in ImageJ. All values between 55 and 280 were considered positive and used for this analysis.

Image analysis

An image-analysis algorithm was developed to determine the alignment of each point on an MT with the nearest region of the cell border based on tubulin images. β cells within an islet were selected based on their ability to express insulin. Single slices from a deconvoluted confocal stack were used for analysis. Taking into consideration that MT width is below the resolution limit of light microscopy techniques, neighborhood block size was approximated to the pixel size of the oversampled confocal image (50 nm²). Analysis was applied within a mask based on thresholded tubulin images. The local orientation at each pixel of the tubulin image was derived using the method described in (44). The cell outline curve, manually constructed based on the E-cadherin staining, was smoothed and used to estimate orientation of the cell border. Each pixel in the tubulin image was associated with the nearest pixel of the boundary curve. After applying cell border and tubulin threshold masks, the angle difference between local orientation and boundary orientation at the nearest pixel was calculated per pixel of microtubule area (with zero indicating perfect parallel alignment). Results were weighed according to variance of local orientation to avoid data from lumps of tubulin bands of excessive density and MT crossings with ambiguous configuration in the results. All pixels were manually sorted according to their distance from the cell border into 0.5 μm bins.

Results

Peripheral MTs in islet β cells are coaligned with the cell border

Prior imaging of intact islets (24) indicates that the MT network in β cells appears to lack previously assumed radial directionality characteristic commonly seen in mesenchymal cells in culture and instead resembles an undirected random mesh. However, the directionality of MTs in β cells has not been quantitatively characterized, and the functional consequences of variable directionality have not been computationally assessed. Here, we analyze the directionality of MTs in β cells using a custom image-analysis algorithm. In subsequent sections, we use computational modeling to assess the consequences of the type of MT organization near the plasma membrane.

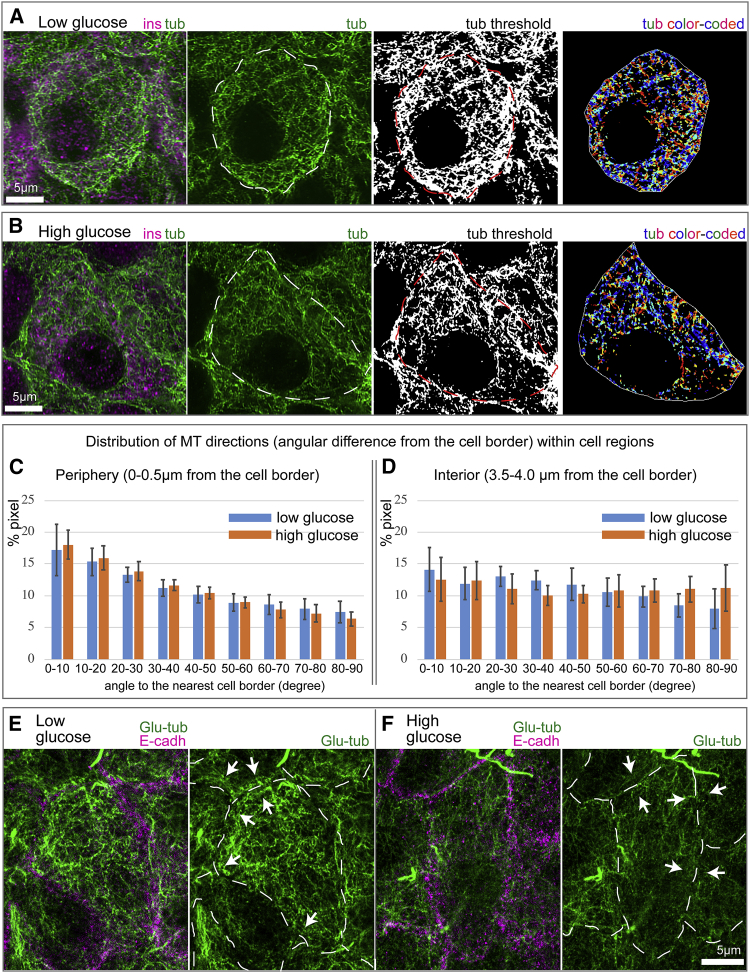
Intact mouse pancreatic islets were isolated and equilibrated according to a standard protocol. After a pretreatment in low and high glucose conditions, islets were fixed and immunostained for insulin to distinguish β cells, E-cadherin for cell border identification, and tubulin for MT network identification. Confocal stacks of whole-mount islets were deconvolved for increased resolution (Fig. 2, A and B). Single 2D slices of MT images were subjected to thresholding (Fig. 2, A and B, second from the right), and the directionality of MTs was determined in respect to the cell border (Fig. 2, A and B, right). Every pixel of the image was analyzed, with inconclusive pixels disregarded. Subsequently, MT directionality was quantified as a function of the distance from the cell border (Fig. 2, C and D).

Figure 2.

MTs parallel to the cell edge in β cells are destabilized in high glucose. (A and B) Examples of MT directionality quantification in low (A) and high (B) glucose are shown. Tubulin, green. Insulin (β cell marker), magenta. Cell outline, as detected by E-cadherin staining, is shown as a dotted line on tubulin and thresholded images. The image on the right shows color-coded MT directions: parallel to the cell edge, blue; perpendicular to the cell edge, red. (C and D) Histograms of MT directionality within two cell regions are shown: periphery (C) and interior (D). Percentage of tubulin-positive pixels in the analyzed cell population is shown. MTs at the periphery tend to be parallel to the edge. Low and high glucose do not differ. Bars indicate averages over N = 12 and 11 cells for low and high glucose, respectively, and error bars indicate standard deviations. Pixel numbers in the analysis: 71,759 (low, periphery); 9622 (low, interior); 43,747 (high, periphery); 5833 (high, interior). Note that a lower number of pixels were identified in high glucose, consistent with the fact that MTs are destabilized under this condition. (E and F) Stable MT marker detyrosinated (Glu-)tubulin (green) in low (E) and high (F) glucose is shown. Cell-cell adhesions are stained for E-cadherin (magenta) in left-hand panels and outlined (dashed line) in right-hand panels. Note multiple Glu-tubulin-positive MTs parallel to the cell border (arrows) in low glucose (E). Glu-tubulin content is decreased in high glucose (F), indicating MT destabilization both across the cell and at the cell border (arrows). To see this figure in color, go online.

Our results indicate that in low glucose conditions, the distribution of MT angles in the cell interior and cell periphery are significantly different (p < 0.05 Kolmogorov-Smirnov (K-S) test, D = 0.09 > D_crit = 0.01). In the cell interior, the MT network lacks directionality and resembles a random interlocked mesh (Fig. 2, C and D, right). However, MTs within a narrow peripheral region exhibit a significant coalignment with the cell border (Fig. 2, C and D, left). Similar structural differences were seen in high glucose conditions (p < 0.05 K-S test, D = 0.057 > D_crit = 0.017). The fraction of MTs that were border aligned were similar in low and high glucose, although the number of detectable pixels was lower in high glucose, consistent with our previous finding of partial MT destabilization under high glucose conditions (24). When the interior angular distributions of low glucose and high glucose are compared, the K-S test indicates the internal and peripheral distributions are not statistically different between the two glucose conditions. Interestingly, visualization of long-lived (stable) MTs by detyrosinated (Glu-)tubulin staining detected many Glu-MTs coaligned with the cell periphery in low (Fig. 2 E), but not in high (Fig. 2 F), glucose. Because MTs parallel to the cell border are still observed in high glucose (Fig. 2 C), we conclude that stability of this peripheral array is significantly diminished by glucose-triggered MT destabilization.

MTs generate counterpropagating density gradients that differentially deliver and remove granules from the cell periphery

In the remainder of this study, we develop and utilize computational modeling to assess how the MT organization features described above, along with MT- and non-MT-dependent transport processes, influence insulin granule localization. For specific model and implementation details, as well as a discussion of how parameters for the model were calibrated to data or chosen, see the Materials and Methods. Briefly, the model used here is composed of a discrete, 2D network of noninteracting MTs, along with a population of granules that undergo MT-dependent and independent motion. These granules are assumed to both bind and unbind to the MT network and to anchor to the plasma membrane when glucose is present.

Based on the above analysis, we consider a range of assumptions for how MTs interact with the plasma membrane. Computationally, we generate the MT network by growing individual MTs from a random seed location. We do not incorporate cyclical growing and shrinking phases of individual MTs (dynamic instability). However, we do allow for the random destruction and replacement of individual MTs (see Materials and Methods for further detail). We consider two assumptions for how MTs interact when they reach the border: they either terminate or bend and grow parallel to the periphery. By varying the likelihood of each in silico MT doing one or the other, we can vary the net orientation of the resulting peripheral network from being highly aligned to having no alignment. Because we do not know a priori the significance of this orientation on insulin granule dynamics, we explore the influence of this and the other model factors (e.g., docking rates) on peripheral granule density.

Granules are assumed to move randomly while on a given MT. Although granules can unbind from a given MT and subsequently bind to a new one, direct transitioning from one MT to another and competitive binding of a single granule to multiple MTs are not considered for simplicity. Granules that are anchored to the membrane are considered immobile. Finally, those granules that are neither anchored nor MT bound are assumed to move randomly within the 2D cell. For further details and model calibration, see Materials and Methods.

We quantified (Fig. 3, A–C) the simulated steady-state number of granules (total, MT bound, and unbound) near the cell border as a function of both the total number of cellular MTs and the peripheral alignment of MTs. Results indicate both influence granule densities. Here, “peripheral alignment” of MTs refers to the fraction of MTs that interact with the boundary and bend and grow parallel to it.

The presence of MTs always leads to an enrichment of granules near the cell periphery relative to densities when the MT network is completely removed (Fig. 3 A). This is true for all MT densities and peripheral MT alignment conditions tested. In this study, we assumed that motors carrying granules stall at the tip of MTs. To ensure this is not the source of these results, we carried out identical simulations in which motors are assumed to disassociate at the tip (Fig. S1) and find similar results. Similar simulations were also performed in which granule motions are purely diffusive rather than subdiffusive, again with similar results (Fig. S1). This suggests that the MT network serves as a sponge that enriches granule densities near the cell border, which is likely the result of the increased density of MT tips near the cell periphery.

Interestingly, this enrichment effect appears to be weakened when the MT network is more aligned at the cell periphery. Specifically, when the MT network at the periphery is more aligned, fewer granules localize to the boundary. Further, when the network is highly aligned, peripheral granule density becomes essentially independent of total MT density. Further inspection of the peripheral densities of bound and unbound granules as a function of peripheral alignment (Fig. 2, B and C) provides a clue to the cause of this observation. Increasing peripheral alignment has little influence on the number of bound peripheral granules but leads to a substantial reduction in the density of unbound peripheral granules. On net, this yields the observed inverse relationship between total peripheral granule density and peripheral MT alignment.

This suggest that an enrichment of peripherally oriented MTs would serve to 1) increase the total binding of peripheral granules to the MT network (thus reducing unbound granule numbers) and 2) transport those excess granules toward the cell interior (thus leaving the fraction of bound granules relatively unchanged). Critically, this transport of bound granules away from the periphery in the model is not due to directional motions of kinesin or dynein motors because all granule motions are random and undirected. This raises an important question. If, at steady state, peripherally aligned MTs serve to soak up and transport granules away from the periphery, what counterbalances that net transport? To answer this, we quantified the density of bound and unbound granules as a function of radial distance from the cell center in simulations at steady state (Fig. 3, D and E) for the two extreme cases of low and high alignment of peripheral MTs. In the highly aligned case (Fig. 3 E), bound and unbound granule densities exhibit opposing density gradients, with unbound granules exhibiting a peripheral deficit and bound granules a peripheral enrichment. When peripheral MTs exhibit low alignment (Fig. 3 D), these opposing gradients are not present. Thus, when there is a substantial number of peripherally aligned MTs, bound and unbound granules form counterpropagating gradients, with unbound granules flowing from the interior to the periphery and bound granules flowing from the periphery to the interior.

This counterpropagating gradient theory is consistent with our prior observations. We found, using TIRF microscopy, that the application of nocodazole (NOC) and glucose led to a ∼25% reduction in granule delivery but a ∼43% reduction in granule withdrawal (24). Thus, removal of granules was more substantially impacted by removal of MTs than delivery, consistent with the counterpropagating gradient hypothesis in which MTs generate a net flow of granules from the periphery to the cell interior. In combination, these results suggest that the peripherally aligned network of MTs maintains a balance between delivery and withdrawal of granules and prevents excess accumulation near the plasma membrane.

Changes in radial diffusion due to MT alignment are the source of counterpropagating gradients

We investigate two potential effects of peripheral MT alignment on insulin localization. Enrichment of these peripherally aligned MTs could serve to either 1) increase binding of granules to MTs or 2) restrict the radial motility of bound granules. In the discrete model, it is impossible to separate these effects; increased peripherally aligned density will necessarily influence both. To assess the relative importance of these effects in potentially generating counterpropagating gradients, we construct a simplified continuum model of granule dynamics where the two can be separately modulated.

For this continuum model, we consider concentrations of granules rather than individual granules and use partial differential equations to describe the time evolution of the spatial concentrations. Because the presence of the counterpropagating gradients in the prior study was not the result of subdiffusion (Fig. S1), we consider the motions of both bound and unbound granules to be purely diffusive. This greatly simplifies the model, allowing it to be described by standard reaction diffusion partial differential equations. For simplicity, the cell is considered to be a radially symmetric circle, and we model only the dynamics in the radial direction because steady-state distributions in the discrete model depend on radius, but not angular position in the cell. This reduces the model to a one-dimensional, radially symmetric system that further simplifies calculations while allowing us to assess the influence of these factors on radial density.

This model encodes three essential components of the discrete model: 1) the ability of granules to bind and unbind from MT-bound to unbound states, 2) diffusion of unbound granules, and 3) diffusion of bound granules. It does not, however, explicitly include discrete MTs. Rather, bound and unbound forms are assumed to move with different rates of diffusion (faster for bound). We assess how increases in the rate of MT binding and decreases in the rate of radial diffusion at the cell periphery (due to MT enrichment) influence distributions of bound and unbound granules. To quantify this, we define a 250 nm zone near the cell border where MT-binding rates (k_on) and the speed of bound granule radial diffusion (D_r) are selectively modulated. The benefit of this continuum approach is that we can separately and selectively change these two parameters near the cell border to assess their influence in isolation.

The model was simulated for a range of different fold increases in the binding rate and fold decreases in the rate of bound granule radial diffusion near or at the periphery. Changes in binding and radial diffusion rates have different roles in setting up these counterpropagating gradients (Fig. 4). An increase in the binding rate is sufficient to induce a depletion of unbound peripheral granules, but not sufficient to induce a significant gradient in bound granules. A reduction in the rate of radial diffusion (in combination with the increase in binding rate) leads to a substantial enrichment of bound granules at the periphery. Thus, a moderate increase in the MT-binding rate in combination with a substantial decrease in the rate of bound granule radial diffusion is required to explain the counterpropagating gradients seen in the discrete model. Both would be expected to occur if MTs are enriched at the cell periphery.

The anomalous nature of granule motion alters localization of granules near the cell membrane in an MT-dependent fashion

It is well established that insulin granule motion (like the motion of many entities within the cell) is subdiffusive (24). It is characterized by MSD curves obeying MSD = Dt^α, where “D” is the generalized diffusion coefficient and “α” is the diffusive exponent: α = 1 corresponds to regular diffusion, whereas α < 1 indicates subdiffusion. For insulin granules, it has previously been found that α ∼0.75 (29), indicating significant anomalousness of diffusion. It has been further found that insulin granule motions exhibit characteristics of fractional Brownian motion (29), which is often associated with viscoelastic drag effects arising from the complex and crowded nature of the cell cytoplasm. Although numerous studies have investigated the anomalous nature of random particle motion in cellular environments (see (45) for a comprehensive review), to our knowledge, the effect of viscoelastic subdiffusion on the spatial distribution of particles (granules) at steady state has not been investigated. Here, we assess how this feature of motion and its changes due to alterations in the MT cytoskeleton affect steady-state spatial densities of granules within the cell.

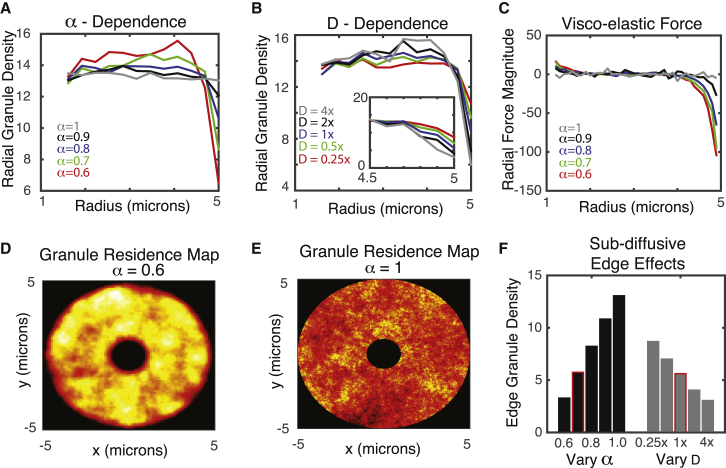
It is well established that when particles obey standard random or Brownian motion, spatial distributions of particles tend to homogenize within a spatial domain. To determine whether this is the case when motions are more complex and governed by viscoelastic subdiffusion, we simulated the spatial distribution of 1000 noninteracting granules over time for different values of the D and α parameters (Fig. 5). To independently assess the influence of anomalous motions, we initially consider only the 2D motions of granules independent of MTs. There is a significant depletion of granules at both the cellular and nuclear borders when granule motions are subdiffusive (Fig. 5 D). Furthermore, as motions become more subdiffusive (smaller α) or faster (larger D), this depletion near the cell border becomes more substantial (Fig. 5, A, D, and F).

Figure 5.

Influence of viscoelastic subdiffusive effects on peripheral granule density. (A) Granule density as a function or radius for different values of the subdiffusion exponent α is shown. The rate of diffusion D is set to its base value here. (B) Radial granule density as a function of diffusion speed (D) for α = 0.7 is shown. (C) Net radial viscoelastic force as a function of radius for different values of α, with D fixed at its base value, is shown. Negative values near the periphery indicate a net inward force. (D and E) A granule residency map showing the distribution of granules over time for two values of α (note the depletion zones near the inner and outer radii) is given. Yellow indicates high density and red low density. (F) Effect of subdiffusive exponent (α) and diffusive strength (D) on the peripheral density of MTs is shown. In the “Vary α” case, the D-value corresponds to 1× (e.g., the base value). Similarly, for the “Vary D” case, α = 0.7. The highlighted bars most closely correspond to the calibrated D- and α-values used to model MT-based diffusion for all other simulations to follow. To see this figure in color, go online.

The explanation for this is subtle but follows readily from the basic assumptions of generalized Langevin dynamics. The physical mechanism often associated with viscoelastic subdiffusion is that as a particle moves in a given direction, resistive forces on that particle build up because of interactions with the crowded, filamentous cellular environment; the more a particle moves in a given direction, the larger the resistive force becomes. If a particle is observed near a cell border, it is more likely that the particle was transported from more interior regions of the cell rather than more exterior regions. This would lead to an expected resistive force that would tend to move the particle back to the interior of the cell, introducing a bias not present in standard diffusion.

To confirm this explanation, we quantified the average radial component of the viscoelastic force as a function of radius within the simulated cell at steady state to generate a force (Fig. 5 C). This force map quantifies the average, expected resistive force that a granule would be subject to as a function of radial location within the cell. When diffusion is close to normal (α = 0.99), that force is effectively zero everywhere. However, as diffusion becomes more anomalous, we begin to see a negative expected radial force near the cell border, suggesting a particle near the boundary would be expected to move inward rather than closer to the periphery. This is the source of the peripheral depletion of granules when motions are governed by viscoelastic subdiffusion.

Although this would be a general phenomenon in any system in which viscoelastic subdiffusion is present (46), it is specifically relevant here because of the dependence of this depletion effect on the speed of motion. The gray bars in Fig. 5 F show that when the speed of motion is reduced by a factor of 1/4, peripheral densities increase by roughly 50%. Interestingly, when MTs are completely removed from β cells via application of glucose + NOC, a roughly 1/4–1/3 reduction in D is observed (Fig. 2 C, with data reproduced from (24)), along with a roughly 50% increase in peripheral granule density.

Other mechanisms may influence insulin granule accumulation near the periphery. Glucose stimulation of β cells influences cells in many ways, including activating docking proteins that bind granules to the membrane. Additionally, the dynamics of MTs significantly influence peripheral granule densities in other ways, independent of augmenting transport speed. Nonetheless, it is expected based on this analysis that the net slowdown in motion would contribute to the peripheral enrichment observed experimentally when glucose and NOC are jointly applied to cells.

Competition between membrane anchoring and MT binding regulates availability of peripheral granules

Here, we consider how the dynamics of MT-mediated motions influence granule localization and availability for membrane anchoring. A set of prior observations will allow us to assess what factors are important in understanding granule localization and constrain aspects of the computational model. In (24), the authors quantified how granule density at the cell periphery changes when glucose, NOC, and glucose + NOC are applied to β cells. Briefly, they found that the application of either factor alone had relatively little influence on granule densities. However, when they were jointly applied, peripheral densities increased by 50%.

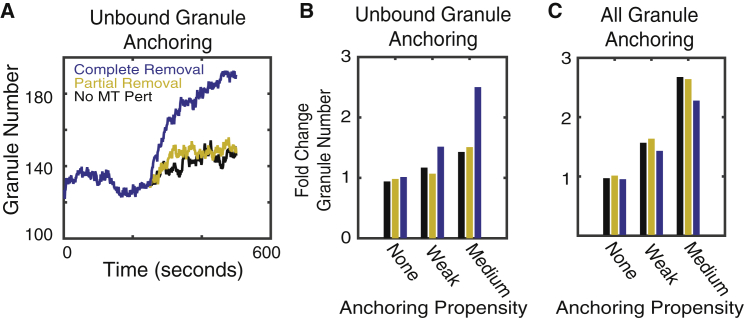
When initially studying peripheral granule accumulation without considering membrane anchoring, we found the model unable to account for these observations. We thus consider the joint effects of membrane anchoring and MT-mediated transport, both of which are altered by glucose stimulation. To study how MT motion might influence membrane anchoring, we consider two possibilities for how granules anchor: 1) that any granule close enough to the periphery can anchor or 2) that only granules not bound to MTs can anchor. The latter possibility is motivated by the hypothesis that motions and forces subjected to granules by MT-associated motors either prevent anchoring or substantially reduce anchoring affinity. Because we do not have anchoring protein affinity data, we consider the effects of low, medium, and high affinity (high not shown in data), as well as the absence of anchoring (relevant for NOC-only treatment), on granule dynamics.

To understand the effect of MTs on the localization and availability of granules, we simulated the full model to steady state, performed both partial and complete removal of MTs in different anchoring scenarios, and quantified changes in peripheral granule density. In the absence of anchoring, neither partial nor complete removal of MTs alone has a significant effect on granule density, and thus, removal of MTs alone is not sufficient to explain granule enrichment when glucose + NOC is applied (Fig. 6, B and C). The inclusion of anchoring can lead to the enrichment of peripheral densities; however, those enrichment dynamics are only consistent with observations when MT-unbound granules anchor to the membrane with low affinity. In this scenario, peripheral granules are increased by 40–50% (Fig. 6 A), consistent with prior experimental observations (24). When all granules can anchor independently of MT binding, enrichment occurs in the absence of any MT perturbation, contrary to observations. Alternatively, when affinity is too high, enrichment becomes extreme and once again independent of MT dynamics. In short, when anchoring is high affinity or all granules (MT bound and unbound) can anchor, MT properties have little effect on peripheral densities.

Figure 6.

Influence of MT perturbations on peripheral granule density. (A) The number of granules within 250 nm of the cell border as a function of time is shown in simulations in which only unbound granules are able to anchor to the membrane. This simulation shows the case for “weak” anchoring. The black curve indicates no MT perturbation is applied, red corresponds to removal of 1/3 of longer MTs, and blue indicates complete removal of all MTs (corresponding to glucose + NOC treatment). (B and C) Quantification of the fold change in peripheral granule density after MTs are perturbed is shown. The vertical axis shows the fold change in peripheral granule density after the relevant perturbation. The horizontal axis corresponds to different anchoring rates (none = 0, weak = 1:32, medium = 1:8). Slow MT dynamics are assumed so that the average lifetime is 1000 s. Alternative simulations were performed with short MT lifetimes (10 s; see Fig. S2). In (B), only MT-unbound granules are allowed to anchor to the membrane. In (C), all granules are assumed to be capable of anchoring. To see this figure in color, go online.

We thus conclude anchoring is necessary to account for enrichment of peripheral granules upon glucose + NOC stimulation but that only unbound granules should anchor and with low affinity. These results suggest MTs may have a role in negatively regulating the availability of peripheral granules by binding them and making them unavailable for anchoring.

Discussion

Glucose homeostasis is tightly regulated at the systemic level in both the amount of insulin in circulation and the response of peripheral tissues to insulin (including liver, skeletal muscles, and fat). This study combines experimental tests and modeling to investigate how β cells regulate the amount of insulin to secrete in response to a given stimuli. We focus on how MTs in β cells regulate the localization and anchoring of insulin granules to the plasma membrane, a prerequisite for insulin secretion. Results here suggest that cytoskeletal factors contribute to the tight regulation of insulin at the level of individual β cells.

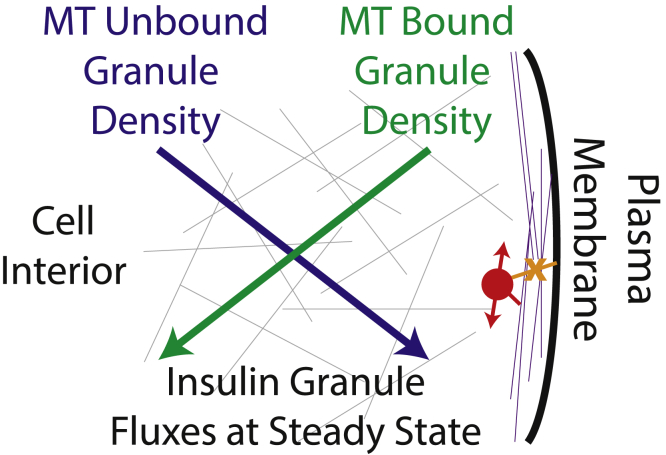
Although individual β cells can contain on the order of 10,000 individual insulin granules, only a few are secreted in response to glucose stimulation (28). Thus, at the cellular level, significant negative regulation of GSIS must be present. A well-established key negative factor is the actin cytoskeleton, which ensures that only a small portion of vesicles are available to break the cell cortex and secreted (47). Here, we have identified two potential alternative mechanisms by which MT dynamics contribute to this negative regulation (see Fig. 7 for a schematic). First, MTs near the cell periphery actively transport insulin granules away from the cell membrane. Second, traction forces generated by MT-associated molecular motors prevent stable granule anchoring to the membrane, which is a precursor to exocytosis.

Figure 7.

Cartoon schematic of the MT-network-induced counterpropagating insulin granule gradients. The blue and green lines depict gradients of insulin that are unbound and bound, respectively, to the MT network. Slopes indicate the direction in which those gradients point (blue toward the plasma membrane and green away from it), and arrow heads depict the direction of flux of each of these insulin populations at steady state. At steady state, the flux of unbound granules toward the plasma membrane is balanced by the flux of bound granules away from it. Gray and purple lines in the background depict the randomly oriented and organized MT networks in the interior and peripheral regions of the cell. The red circle indicates an MT-bound granule that is prevented from docking to the membrane by motor-driven motions. To see this figure in color, go online.

Both mechanisms are supported by prior observations. First, prior imaging (24) demonstrated that depolymerization of the MT cytoskeleton substantially inhibited the removal of insulin granules from the membrane, supporting the conclusion here that MTs predominantly serve to remove granules from the cells surface. Secondly, recent work (30) demonstrated that membrane docking of granules is substantially inhibited in human type 2 diabetes. This along with the observation that MT density is increased in diabetic mouse models (24) supports the conclusion that MT-mediated transport prevents or inhibits anchoring of granules to the membrane.

Interestingly, both phenotypes are consequences of an alteration in the MT structure near the cell membrane. Prior imaging has found that the MT network in β cells is unusually unstructured and randomly oriented (17,24). However, results here demonstrate that in peripheral regions within ∼250 nm of the cell membrane, MTs are predominantly oriented parallel to the membrane. The two previously mentioned negative regulatory mechanisms are a direct consequence of this alteration in organization. As a result, the MT network acts like a sponge near the membrane that soaks up granules and transports them away from the periphery while preventing their membrane anchoring and stimulated release.

Coalignment of MTs at the cell periphery can arise as a result of MT capture at the cortex or cell-cell junctions, which prevents MT catastrophe (48, 49, 50, 51, 52, 53) and thus can promote their turning by the actin retrograde flow (54,55) and polymerization along the cortex. Alternatively, subcellular signals localized at the plasma membrane such as glycogen synthase kinase 3 β (GSK3β) inactivation can locally increase MT coating by microtubule-associated proteins (MAPs), which, in turn, can promote excessive MT growth along the cell periphery (56, 57, 58). Such mechanisms that promote MT turning must also increase their lifetimes and stability, which is consistent with the unusually high levels of stabilization that we observe in the peripheral MT arrays in β cells. Thus, there are a number of potential regulatory mechanisms under the control of cell differentiation and metabolic signals that could produce this aligned peripheral mesh and, as a result, tune insulin availability for GSIS.

Interestingly, MT-mediated withdrawal of peripheral granules does not require directed (i.e., ballistic) motor-driven transport. That is, it does not appear to be the case that granules are being ballistically transported away from the periphery by a plus- or minus-end-directed motor. This would be inconsistent with observations that both the MT network and granule motions on it are random. Instead, it is the topology of the MT network that influences cargo localization, not the specific motor dynamics (similar to (59,60)). Rather, the random but motor-driven granule motions observed in cells, coupled with the structured nature of the network near the membrane, are sufficient to generate directed motion of MT-bound granules away from the membrane. It is interesting that whereas most studies concentrate on kinesin-1 as the main MT-dependent motor that transports insulin granules (17,18), the transport is likely driven by multiple motor transport involving both kinesin and dynein (61). Furthermore, peripherally aligned MT arrays likely lack net polarity: there is no reason to anticipate that MTs growing along the cell periphery will be bundled or oriented in the same tangential directions. Furthermore, MT buckling at the periphery can produce MTs with “reversed” polarity, with their plus ends directed toward the cell periphery (56). In such a complex network, even solely plus-end-directed molecular motors would promote nondirectional transport.

The effects of MT configuration on granule distribution are predicted to persist under glucose stimulation conditions as well. MTs coaligned with the cell membrane and, accordingly, their functional consequences on granule dynamics are observed in both steady state (low glucose levels) and stimulated conditions (high glucose levels). Glucose stimulation does have two important consequences, however. First, it leads to the activation of docking and exocytic machinery (30), which facilitates the secretion of those granules not interacting with the MT cytoskeleton. Secondly, it leads to depletion of stable long-lived MTs (Fig. 2; (24)) and replacement by new, dynamic MTs that are nucleated at the Golgi membrane (24,62) and are characterized by rapid polymerization rates (63). Although this does not lead to a gross reduction in MT density or readily detectable restructuring, it does reduce their lifetime. As our results suggest, this leads to increased interaction between granules and the membrane and, subsequently, to increased secretion. Another way to interpret the result of increased MT dynamics is that it creates a pool of transiently “unbound” granules, which we show here to be prone to accumulation at the cell periphery.

Here, we used imaging and modeling to assess the consequences of MT dynamics specifically on secretion. However, much work is still needed to investigate how the biophysical properties of motors themselves as well as docking proteins influence secretion. One central hypothesis stemming from this work is that the motions and/or traction forces generated by the action of molecular motors on MTs parallel to the membrane inhibit stable membrane anchoring. Does this occur through the prevention of bond formation or the force-dependent breaking of those bonds? Furthermore, how does the nature of the multiple motor transport that these granules are likely subject to influence interactions with the membrane? Addressing these questions will require further experimental investigation of the biophysical interactions between the cytoskeleton, molecular motors, membrane docking proteins, and insulin granules.

These results do, however, suggest that there is a potential therapeutic merit in targeting the cytoskeleton to modulate β cell function. Recent imaging demonstrated that increased MT density was found to correlate with decreased secretion in mouse models (24). Although those results were correlative, our findings here indicate that in silico, a dense peripheral MT network interferes with the proper positioning of insulin granules for secretion. This result predicts that in fact, the link observed in mouse models may be causal, and interference with MT stability in β cells might be used as an approach to increase insulin secretion efficiency. This idea is tempting because numerous MT-targeting small molecule compounds have already been considered or even used for cancer therapies. This potential must be approached very carefully, given the high toxicity of MT drugs on all cells and the likely negative effects of prolonged MT destabilization on insulin biogenesis in β cells specifically. Nevertheless, one can envision that in the future, MT destabilizers could be applied to facilitate insulin secretion and overcome hyperinsulinemia in patients when locally delivered and released in a time-restricted manner. If proposing such an intervention is too bold, it is more realistic that future studies will identify specific MT-stabilizing MAPs, which are responsible for high MT density in diabetes models. Then, potential therapies could specifically target these MT-binding proteins.

Author Contributions

K.M.B. performed imaging and experimental data analysis. K.-H.H. provided samples and performed imaging. D.Y. designed the image-analysis algorithm and program. G.G. supervised mouse work and edited the manuscript. I.K. supervised the experimental part of the study, provided conceptual insight, and edited the manuscript. W.R.H. designed computational simulations, supervised the computational part of the study, provided conceptual insight, and wrote the manuscript.

Editor: Dimitrios Vavylonis.