Role of Membrane Potential on Entry of Cell-Penetrating Peptide Transportan 10 into Single Vesicles

Abstract

Cell-penetrating peptides (CPPs) can translocate across plasma membranes to enter the cytosol of eukaryotic cells without decreasing cell viability. We revealed the mechanism underlying this translocation by examining the effect of membrane potential, φ_m, on the entry of a CPP, transportan 10 (TP10), into the lumen of single giant unilamellar vesicles (GUVs). For this purpose, we used the single GUV method to detect the entry of carboxyfluorescein (CF)-labeled TP10 (CF-TP10) into the lumen of single GUVs. First, we used various K⁺ concentration differences to apply different negative membrane potentials on single GUVs containing gramicidin A in their membrane and confirmed these potentials using the φ_m-sensitive fluorescent probe 3,3′-dihexyloxacarbocyanine iodine. The fluorescence intensity of the GUV membranes (i.e., the rim intensity) due to 3,3′-dihexyloxacarbocyanine iodine increased with |φ_m| up to 118 mV, and its dependence on |φ_m| less than 28 mV agreed with a theoretical estimation (i.e., the dye concentration in the inner leaflet of a GUV is larger than that in the outer leaflet according to the Boltzmann distribution). We then examined the effect of φ_m on the entry of CF-TP10 into GUVs using single GUVs containing small GUVs or large unilamellar vesicles inside the mother GUV lumen. We found that CF-TP10 entered the GUV lumen without pore formation and the rate of entry of CF-TP10 into the GUV lumen, V_entry, increased with an increase in |φ_m|. The rim intensity due to CF-TP10 increased with an increase in |φ_m|, indicating that the CF-TP10 concentration in the inner leaflet of the GUV increased with |φ_m|. These results indicate that the φ_m-induced elevation in V_entry can be explained by the increase in CF-TP10 concentration in the inner leaflet with |φ_m|. We discuss the mechanism underlying this effect of membrane potential based on the pre-pore model of the translocation of CF-TP10 across a GUV membrane.

Significance

Cell-penetrating peptides (CPPs) can translocate across plasma membranes to enter the cytosol without decreasing cell viability. We examined the effect of membrane potential, φ_m, on the entry of a CPP, carboxyfluorescein (CF)-labeled transportan 10 (CF-TP10), into the vesicle lumen using the single giant unilamellar vesicle (GUV) method. We found that CF-TP10 entered the GUV lumen without pore formation and its rate, V_entry, increased with |φ_m|. The CF-TP10 concentration in the GUV membrane increased with |φ_m|, indicating an increase in CF-TP10 concentration in the inner leaflet, which is the main cause of the φ_m-induced increase in V_entry. These results provide the first direct evidence, to our knowledge, for the effect of φ_m on the V_entry of CPPs and its underlying elementary processes.

Introduction

Cell-penetrating peptides (CPPs) are positively charged short peptides that can enter the cytosol of live eukaryotic cells without killing the cells and thus can be used to deliver various biological cargos such as drugs, oligonucleotide, and proteins (1, 2, 3, 4, 5, 6). The various types of CPPs are classified into two categories: amphipathic CPPs and nonamphipathic CPPs. Transportan 10 (TP10) is an extensively studied amphipathic CPP (7, 8, 9, 10, 11). TAT peptide and its model peptide oligoarginine (R_n) are nonamphipathic CPPs (12, 13, 14, 15). The intracellular pathway by which CPPs enter the cytosol has been investigated using endocytosis inhibitors and markers, and the results suggest several pathways: macropinocytosis, receptor-mediated endocytosis, and direct permeation through the plasma membrane (1, 2, 3, 4, 5, 6,16,17). Irrespective of the pathway, CPPs must permeate biomembranes such as the plasma membrane to enter the cytosol, but the mechanism by which this crucial event occurs is poorly understood.

All eukaryotic cells have a negative (resting) membrane potential across their plasma membrane (−55 to −90 mV, depending on the type of cell), and this membrane potential plays various important roles (18, 19, 20, 21, 22), such as distribution of lipids and proteins in the plasma membrane and division of cells. Several studies also suggested that the membrane potential plays a significant role in the entry of CPPs such as TAT and oligoarginine into cells (23, 24, 25). The interactions of CPPs with vesicles have been examined using suspensions of large unilamellar vesicles (LUVs) (26,27). For example, Terrone et al. examined the effect of membrane potential on the uptake of two NBD-labeled CPPs (NBD-penetratin and NBD-R₆) into LUVs and found that the uptake of these peptides into LUVs with various compositions was more efficient in the presence of a membrane potential (27). However, the negative potentials were not quantitatively measured, and the extent of NBD-labeled peptide internalization into the LUVs was determined by measuring the reduction of the NBD label with dithionite. As described previously, this method using LUV suspensions cannot always accurately assess the extent of internalization of NBD-labeled peptides (6). Moreover, the experiments using the LUV suspension method provide only ensemble average of physical quantities of all LUVs, and thus, the elementary processes of the entry of CF-TP10 cannot be elucidated (6,28).

The interactions of CPPs with lipid bilayers and the entry of CPPs into lipid vesicles have been investigated using various methods in efforts to reveal the mechanism by which CPPs permeate the plasma membrane (6). For example, the single giant unilamellar vesicle (GUV) method using confocal laser scanning microscopy (CLSM) is suitable for elucidating the elementary processes involving the entering of CPPs into lipid vesicles (6,29, 30, 31, 32, 33, 34). The single GUV method has provided various data regarding the entrance of fluorescent-probe-labeled CPPs (e.g., carboxyfluorescein (CF)-labeled TP10 (CF-TP10)) into the lumen of single GUVs without (or before) pore formation in their membranes. Using this method, we can obtain the rate of entry of these CPPs, the relationship between entry and pore formation, and the time course of the increase in CPP concentration in the GUV membrane and lumen (29, 30, 31, 32, 33, 34).

Various models of mechanisms for the entry of CPPs into the vesicle lumen have been proposed to date (4, 5, 6). For example, one model is the permeation of CPPs through pores in a lipid bilayer, in which a pore is defined as a water channel through which water-soluble fluorescent probes can pass (35,36). In this model, at first CPPs induce pores in the lipid bilayer, and then CPPs pass through water channels of the pores to enter the vesicle lumen. Another model is the permeation of CPPs via inverted micelle formation (37, 38, 39), in which positively charged CPPs form a neutral complex with negatively charged lipids with a defined stoichiometry of CPPs and the charged lipids to form inverted micelles, which can translocate across the bilayer. One more model is adaptive translocation (23,24,40). The guanidinium of Arg can bind to the phosphate group of phospholipids because of hydrogen bonding, which masks the charges and the polar groups of CPPs, and thus, the complex composed of CPPs with the phospholipids enters the hydrophobic core and diffuses across the membrane. Recently, we have proposed a new mechanism involving the translocation of CPPs through transient hydrophilic pre-pores in lipid bilayers (6,30,31) based on the results obtained using the single GUV method (the detailed description of the pre-pore model is described in the Discussion later). To verify these proposed mechanisms, more experimental data are required.

To this end, here we examined the effects of membrane potential on the entrance of CF-TP10 into the lipid vesicle lumen using the single GUV method. As noted above, the LUV suspension method cannot provide information on the effect of membrane potential on the time course of CPP entrance into the lumen of single vesicles, on the CPP concentration in the membrane, or on the relationship between pore formation and the entry of CPPs. In contrast, the single GUV method can provide these data. First, we applied various negative potentials on single GUVs and confirmed these potentials using a membrane-potential-sensitive fluorescent probe, 3,3′-dihexyloxacarbocyanine iodine (DiOC₆ (3)). Then, we investigated the effect of membrane potential on the entry of CF-TP10 into GUVs comprising dioleoylphosphatidylglycerol (DOPG) and dioleoylphosphatidylcholine (DOPC) (2:8 molar ratio). The entry of CF-TP10 into the GUV lumen was detected using single GUVs containing small GUVs or LUVs in the mother GUV lumens. Based on the obtained results, we discuss the effect of membrane potential on the entry of CF-TP10 into the GUV lumen.

Materials and Methods

Chemicals

DOPC and DOPG were purchased from Avanti Polar Lipids (Alabaster, AL). Bovine serum albumin (BSA) was purchased from Fuji Film Wako Pure Chemical (Osaka, Japan). Biotin-labeled BSA, streptavidin, and gramicidin A from Bacillus brevis were purchased from Sigma-Aldrich (St. Louis, MO). Alexa Fluor 647 hydrazide (AF647), 5-(and 6)-CF succinimidylester, N-((6-(biotinoyl) amino)-hexanoyl)-1,2-dihexadecanoyl-sn-glycero-3-phosphoethanolamine, triethyl ammonium salt (biotin-X-DHPE, referred to as biotin-lipid), and DiOC₆ (3) were purchased from Thermo Fisher Scientific (Waltham, MA). Tetraethylammonium chloride (TEAC) was purchased from Tokyo Chemical Industry (Tokyo, Japan). TP10 was synthesized by the FastMoc method using a 433A peptide synthesizer (PE Applied Biosystems, Foster City, CA) (30). CF-TP10, which has the fluorophore CF at its N-terminus, was prepared using a standard labeling method by the reaction of 5-(and 6)-CF succinimidylester with TP10-peptide resin (29). The methods for peptide cleavage, purification, and identification of the peptide products were described previously (29).

GUV preparation

GUVs comprising DOPG/DOPC/biotin-lipid/gramicidin A (molar ratio: 20:79:1:0.01) (hereafter abbreviated PG/PC (2:8)-GUVs) were prepared by the natural swelling method (29). Briefly, the above lipid mixture in chloroform was dried completely, then the resulting dry lipid films were incubated in buffer K (10 mM HEPES (pH 7.5), 150 mM KCl, and 1 mM EGTA) containing 0.1 M sucrose and containing or not containing 6.0 μM AF647 at 37°C for 2−3 h. GUVs containing small GUVs in their lumen were prepared according to the method (29) as follows. First, a DOPG/DOPC (2:8)-GUV suspension was prepared in buffer K containing 0.1 M sucrose but no fluorescent probe, then the GUV suspension was centrifuged to remove lipid aggregates. This partially purified GUV suspension was mixed with AF647 solution in buffer K containing 0.1 M sucrose, and the resulting suspension was incubated with another dry lipid film of DOPG/DOPC/biotin-lipid/gramicidin A (20:79:1:0.01) at 37°C for 2−3 h, producing PG/PC (2:8)-GUVs containing small GUVs in their lumen. Finally, these GUVs were purified using the membrane filtering method (41).

GUVs containing LUVs in their lumen were prepared according to the method (33) as follows. First, DOPG/DOPC (2:8)-LUVs were prepared in buffer K containing 0.10 M sucrose by the standard extrusion method using a 100-nm-pore-size Nuclepore membrane (42). Next, the LUV suspension was mixed with AF647 solution (at a final concentration of 6.0 μM) in buffer K containing 0.10 M sucrose, and the resulting suspension was incubated with dry lipid films of DOPG/DOPC/biotin-lipid/gramicidin A (20:79:1:0.01) at 37°C for 2−3 h using the natural swelling method. The resulting PG/PC (2:8)-GUVs containing LUVs in their lumen were purified using the membrane filtering method (41). The Bartlett method was used to determine the lipid concentrations of the LUV suspensions (43).

Measurement of membrane potential in the PG/PC-GUVs

We induced a membrane potential in PG/PC (2:8)-GUVs containing gramicidin A by generating a K⁺ concentration gradient across the GUV membranes by diluting the above purified GUV suspension (in buffer K) with various amounts of buffer T (10 mM HEPES (pH 7.5), 150 mM TEAC, and 1 mM EGTA) containing 0.10 M glucose (44). The summation of KCl and TEAC concentrations in the buffer outside the GUVs was 150 mM, producing the same osmolarity as that of the buffer inside the GUVs. 10 min after diluting the GUV suspension (i.e., the application of membrane potential to the GUVs because of the K⁺ concentration gradient), the diluted suspension was mixed with a solution of the membrane-potential-sensitive fluorescent probe DiOC₆ (3) in the same buffer as the outside of the GUV (44). For the φ_m = −118 mV sample, we concentrated the dilute GUV suspension using the membrane filtering method (41), then mixed the concentrated GUV suspension with the DiOC₆ (3) solution. The final concentration of DiOC₆ (3) was 1 or 2 nM, depending on the experiment. Then, the GUV suspension was transferred into a handmade microchamber coated with BSA (28). DiOC₆ (3) was allowed to interact with the GUVs for more than 10 min, then the GUVs were observed through a 60× objective with a numerical aperture of 1.35 (UPLSAPO060X0; Olympus, Tokyo, Japan) using a confocal laser scanning microscope (FV-1000; Olympus) temperature-controlled at 25 ± 1°C by a stage thermocontrol system (Thermoplate; Tokai Hit, Shizuoka, Japan) (30,45). Fluorescence images of GUVs with DiOC₆ (3) and differential interference contrast images were obtained. The values of fluorescence intensity (FI) of the images obtained by CLSM were measured using CLSM software (Fluoview, v. 4.1; Olympus). The FI of the GUV membrane (i.e., rim intensity) due to the binding of DiOC₆ (3) dye was measured using the poly-line mode in the CLSM software as described previously (46).

The membrane potential inside a GUV, φ_in, was calculated based on the Nernst equation:

$${\phi }_{\text{m}}=\frac{RT}{F}\ln \frac{{\left[{\text{K}}^{+}\right]}_{out}}{{\left[K^{+}\right]}_{in}}=25.7\ln \frac{{\left[{\text{K}}^{+}\right]}_{out}}{{\left[{\text{K}}^{+}\right]}_{in}}\left[mV\right],$$ (1)

where F is the Faraday constant, R is the gas constant, T is the absolute temperature, and [K⁺]_out and [K⁺]_in are the K⁺ concentration outside and inside the GUV, respectively. The numerical value of RT/F is 25.7 in Eq. 1 for 25°C. For example, when we diluted the GUV suspension with buffer T in the ratio 1:9, φ_m = −59 mV.

Effect of membrane potential on the entry of CF-TP10 into single PG/PC (2:8)-GUVs

We used the single GUV method with GUVs containing small GUVs (29) or LUVs (33) to detect the entry of CF-TP10 into the lumen of single GUVs. These GUVs contained AF647 in their lumen to detect the CF-TP10-induced pore formation in the GUV membrane. We induced a membrane potential in the GUVs using the same method described in the previous section. For this purpose, we prepared PG/PC (2:8)-GUVs containing gramicidin A in buffer K, then purified them using the membrane filtering method and diluted the purified GUV suspension with buffer T. We investigated the interaction of CF-TP10 with these single GUVs using a confocal laser scanning microscope (FV-1000; Olympus) temperature-controlled at 25 ± 1°C by a stage thermocontrol system (29). The experiments were conducted in the same microchamber described above, but the GUVs were fixed on a coverslip in the chamber using the strong association between biotin and streptavidin (29). At more than 10 min after a purified GUV suspension was diluted into buffer T (i.e., after application of membrane potential to the GUVs), we started the interaction of CF-TP10 with single GUVs. CF-TP10 solution prepared in the same buffer as used outside the GUV was continuously provided to the neighborhood of the GUV through a 20-μm-diameter glass micropipette. During the interaction of peptide solution with single GUVs, the distance from the GUV to the tip of the micropipette was 50−60 μm, and the micropipette had a positive pressure of 30 Pa. The detailed experimental conditions were described previously (45). The FIs of the images obtained by CLSM were measured using CLSM software. The time courses of the FI of the rim and the inside of the GUV during the interaction with CF-TP10 were measured as described previously (29).

Results

Measurement of various negative membrane potential using the DiOC₆ (3) probe

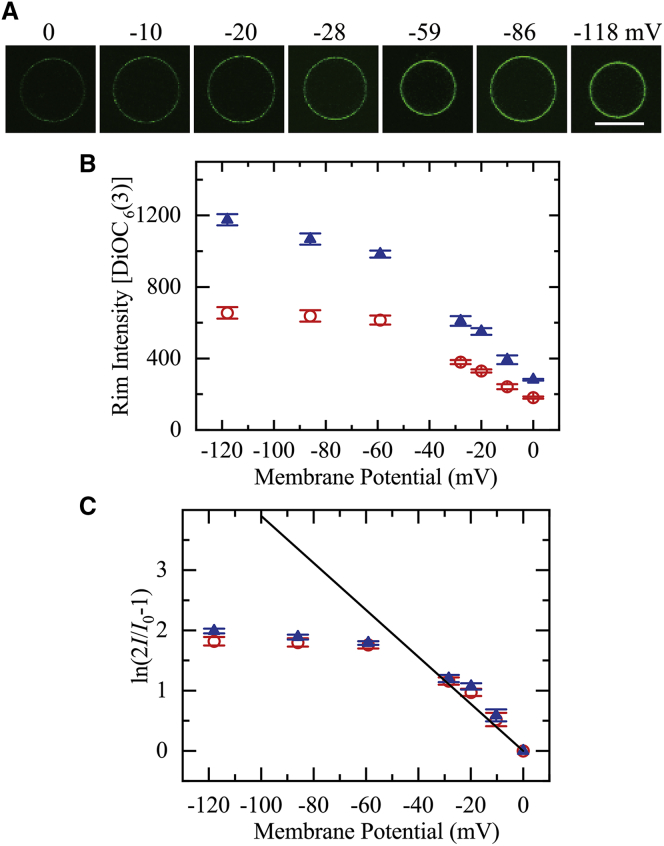
We applied a membrane potential across the GUV membrane, φ_m, using the method (gramicidin A/K⁺ concentration difference) described in our previous report (44). The membrane potential is determined by only the ratio of [K⁺]_out to [K⁺]_in according to Eq. 1. We applied various negative membrane potentials to PG/PC (2:8)-GUVs using various K⁺ gradients across the GUV membrane and observed the interaction of 2 nM DiOC₆ (3) (a membrane-potential-sensitive fluorescent probe) (47, 48, 49) with these GUVs using CLSM. Fig. 1 A shows representative CLSM images of one PG/PC (2:8)-GUV under various negative membrane potentials (i.e., φ_m = 0 to −118 mV). As the absolute value of the membrane potential (|φ_m|) increases, the FI of the GUV membrane (i.e., rim intensity), I (φ_m), increased. It is well-demonstrated that I (φ_m) is proportional to the concentration of DiOC₆ (3) in the membrane at low concentrations at which no fluorescence self-quenching occurs (31). The rim intensity due to DiOC₆ (3) in the GUV membrane remained constant from 10 to 45 min, indicating that equilibrium binding of DiOC₆ (3) from the aqueous phase to the membrane continued throughout this time (Fig. S1). This experiment was conducted independently two times (i.e., N = 2) (except for 0 mV, where N = 6), each time using 9−24 GUVs (i.e., the total number of examined GUVs for each membrane potential, n_t, was 20−41) (except for 0 mV, at which n_t = 87), and the mean values and standard errors (SEs) for the rim intensity at various membrane potentials were obtained. Fig. 1 B shows that the rim intensity of PG/PC (2:8)-GUVs interacting with 2 nM DiOC₆ (3) increased as |φ_m| increased up to 118 mV. We also performed the same experiments using a lower concentration of DiOC₆ (3) (1 nM) and obtained a similar result (Fig. 1 B). We previously reported a similar membrane potential dependence of the rim intensity of GUVs comprising polar lipid extract of Escherichia coli interacting with 1 nM DiOC₆ (3) (44).

Figure 1.

Membrane potential dependence of the rim intensity due to DiOC₆ (3) in single PG/PC (2:8)-GUVs not containing small vesicles. (A) CLSM images of the GUVs that interacted with 2 nM DiOC₆ (3) under various membrane potentials are shown. The number above each image shows the membrane potential on the GUV membrane from 0 to −118 mV. The bar represents 20 μm. (B) Dependence of the rim intensity due to DiOC₆ (3) on membrane potential is shown. Red ○ 1 nM and blue ▲ 2 nM DiOC₆ (3). The mean values of rim intensity and their SEs are shown. (C) Quantitative analysis of the membrane potential dependence of rim intensity. I indicates the rim intensity at φ_m, I(φ_m). Red ○ 1 nM, and blue ▲ 2 nM DiOC₆ (3). A solid line corresponds to Eq. 5. The mean values of ln (2I/I₀−1) and their errors are shown. To see this figure in color, go online.

We next analyzed these results quantitatively. DiOC₆ (3) is believed to translocate rapidly across the lipid bilayer because it has a short hydrocarbon chain and only one positive charge (47,48). As the negative membrane potential increases, the DiOC₆ (3) concentration in the lumen of a GUV, C_in, becomes larger than that outside of the GUV, C_out, because at equilibrium, the Boltzmann distribution of DiOC₆ (3) between the lumen and the outside of the GUV holds as follows (48):

$$\frac{C_{\text{in}}}{C_{\text{out}}}=\exp \left(-e{\phi }_{\text{m}}/kT\right),$$ (2)

where e is elementary charge and k is the Boltzmann constant. We can reasonably infer that the binding equilibrium of DiOC₆ (3) between the GUV lumen and the inner leaflet (the inner monolayer) of the GUV and the binding equilibrium of DiOC₆ (3) between the outside of the GUV and the outer leaflet of the GUV both hold. If the DiOC₆ (3) concentration in the inner leaflet of the GUV, C_IM, and that in the outer leaflet, C_OM, are small, we can use the approximation equations C_IM/C_in = K_B and C_OM/C_out = K_B, where K_B is the binding constant of DiOC₆ (3) from the aqueous solution to the lipid leaflet. Here, we assume that the value of K_B does not depend on the membrane potential. This assumption is correct when the positive charge of DiOC₆ (3) locates at the surface of the lipid leaflet because the electric potential of its surface is the same as that in the contacting aqueous solution. Because the DiOC₆ (3) concentration in the GUV membrane, C_M, is the average of C_OM and C_IM, C_M can be expressed as

$$\begin{array}{l}{C}_{\text{M}}=\frac{C_{\text{OM}}+C_{\text{IM}}}{2}=\frac{K_{\text{B}}\left(C_{\text{out}}+C_{\text{in}}\right)}{2}\\ =\frac{K_{\text{B}}}{2}\left\{1+\exp \left(-e{\phi }_{\text{m}}/kT\right)\right\}{C}_{\text{out}}.\end{array}$$ (3)

If C_M is so low that there is no self-quenching of DiOC₆ (3) fluorescence, the rim intensity of the GUV, I, is proportional to C_M, and hence the ratio of I(φ_m)/I₀ (= I (0 mV)) for the same DiOC₆ (3) concentration outside the GUV, C_out, can be expressed as:

$$\frac{I\left({\phi }_m\right)}{I_0}=\frac{1+\exp \left(-e{\phi }_m/kT\right)}{2}.$$ (4)

Rearrangement of Eq. 4 produces the following equation:

$$\ln \left(\frac{2I\left({\phi }_{\text{m}}\right)}{I_0}-1\right)=-\frac{e}{kT}{\phi }_{\text{m}}.$$ (5)

We replotted Fig. 1 B to show the membrane potential dependence of ln (2I(φ_m)/I₀−1) (Fig. 1 C). Using kT/e = 25.7 mV at 25°C, we plotted the theoretical curve corresponding to Eq. 5 (the solid line in Fig. 1 C). At and below −28 mV, the experimental data almost fit to Eq. 5, indicating that the above-described theory is correct. A small deviation (i.e., the experimental data are a little greater than the theoretical curve) may be due to a slight increase in the value of K_B with membrane potential. At higher membrane potential, the experimental values were smaller than the theoretical values obtained by Eq. 5. We can reasonably explain this deviation as follows. At higher membrane potential, the DiOC₆ (3) concentration in the GUV leaflets (especially in the inner leaflet) approached saturation, and thus, we cannot use the approximation equations C_IM/C_in = K_B and C_OM/C_out = K_B, resulting in the observed deviation.

The results shown in Fig. 1, B and C therefore indicate qualitatively that the negative membrane potential of the GUVs increased as the membrane potential calculated by the Nernst equation increased, i.e., with an increase in the K⁺ concentration gradient. We can thus use these GUVs to investigate the effect of membrane potential on the entry of CF-TP10 into the GUV lumen.

Effects of negative membrane potential on the entry of CF-TP10 into single PG/PC (2:8)-GUVs containing small GUVs

The effect of negative membrane potential, φ_m, on the entry of CF-TP10 into single GUVs was examined here. First, we detected the entry of CF-TP10 into the GUV lumen using the single GUV method with PG/PC (2:8)-GUVs (i.e., mother GUVs) containing small GUVs 1−10 μm in diameter (6,29) in their lumen. Using this method, the detection of fluorescent small GUVs in the mother GUV lumen indicates the entry of CF-TP10 into the lumen. Negative membrane potentials were applied only to the mother GUV membranes using various K⁺ gradients across the GUV membranes. We examined the entry of low concentrations of CF-TP10 (0.50 μM or lower); at such concentrations, CF-TP10 cannot enter PG/PC (2:8)-GUVs without a membrane potential for up to 6 min (29).

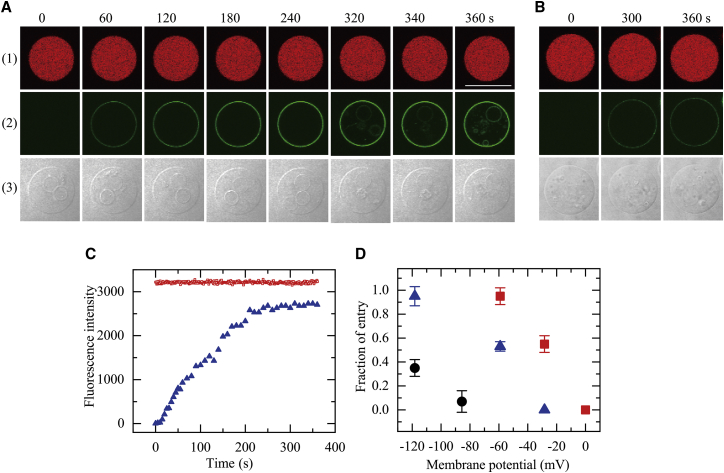
First, we investigated the effect of φ_m = −59 mV on the entry of 0.50 μM CF-TP10 into single GUVs. After maintaining a membrane potential of −59 mV in PG/PC (2:8)-GUVs for more than 10 min, a 0.50 μM CF-TP10 solution was continuously added from a micropipette to the vicinity of a single GUV. At steady state, the CF-TP10 concentration in the vicinity of the GUV was slightly less than in the micropipette (45). Fig. 2 A(1) shows that the FI in the GUV lumen due to AF647 remained essentially constant over 6 min during the interaction of CF-TP10 with the GUV (Fig. 2, A(1) and C). This result shows that AF 647 did not leak during the interaction, indicating that no pores formed in the mother GUV membrane. This is the same result as that obtained in the absence of a membrane potential (29). Fig. 2, A(2) and C show that the rim intensity due to CF-TP10 gradually increased and reached a steady value at 240 s. In contrast, initially no fluorescence was observed in the mother GUV lumen, but at 320 s, the small GUVs in the mother GUV lumen started to emit fluorescence without pore formation (Fig. 2 A(2)). These results indicate the entry of CF-TP10 into the GUV lumen and their binding to the small GUVs without pore formation (29). At present, one cannot determine quantitatively the rate of entry of CF-TP10 into the GUV lumen, V_entry, because of the nonlinear, stochastic characteristics of the time course of the entry of CF-TP10. However, this rate can be estimated by using the fraction of GUVs into which CPPs entered before a specific time t without pore formation with respect to the total number of examined GUVs (hereafter, fraction of entry), P_entry (t) (29). We repeated the experiment shown in Fig. 2 A using 13 single GUVs (n = 13) and obtained P_entry (6 min) = 1.0. This experiment was performed independently two times (N = 2), each time using 10−13 GUVs, and the mean value and its standard deviation (SD) of P_entry (P_entry (6 min) = 0.95 ± 0.07) were determined based on the results. In contrast, for φ_m = 0 mV, no fluorescence was observed from small GUVs in the mother GUV lumen up to 6 min (N = 2), indicating no entry of CF-TP10 into the mother GUV lumen (i.e., P_entry (6 min) = 0) (Fig. 2 B). For φ_m = − 28 mV, P_entry (6 min) = 0.55 ± 0.07 (N = 2). These results indicate that P_entry (6 min) increased as |φ_m| increased (Fig. 2 D).

Figure 2.

Interaction of CF-TP10 with single PG/PC-GUVs containing small GUVs. (A and B) CLSM images of (1) AF647, (2) CF-TP10, and (3) differential interference contrast of a PG/PC (2:8)-GUV interacting with 0.50 μM CF-TP10 under φ_m = −59 mV (A) and 0 mV (B) are shown. The numbers above each image indicate the interaction time of CF-TP10 with the GUV. The bar represents 30 μm. (C) Change in the FI of the GUV shown in (A) over time is given. Red squares and blue triangles correspond to the FI of the GUV lumen due to AF647 and that of the GUV rim due to CF-TP10, respectively. (D) Effect of membrane potential on P_entry (6 min) is shown. Red ▪, 0.50 μM; blue ▲, 0.40 μM; black ●, 0.30 μM CF-TP10. For each condition, the mean values and SDs of P_entry (6 min) of two independent experiments using 7−13 GUVs each were obtained. To see this figure in color, go online.

We also examined the effect of membrane potential on the entry of lower concentrations of CF-TP10 and obtained a similar result (see Supporting Materials and Methods, Section 1 and Fig. S2). Fig. 2 D shows that irrespective of CF-TP10 concentration, the fraction of entry of CF-TP10 increased as |φ_m| increased, indicating that the rate of entry of CF-TP10 was elevated as |φ_m| increased.

Effects of negative membrane potential on the entry of CF-TP10 into single PG/PC (2:8)-GUVs containing LUVs

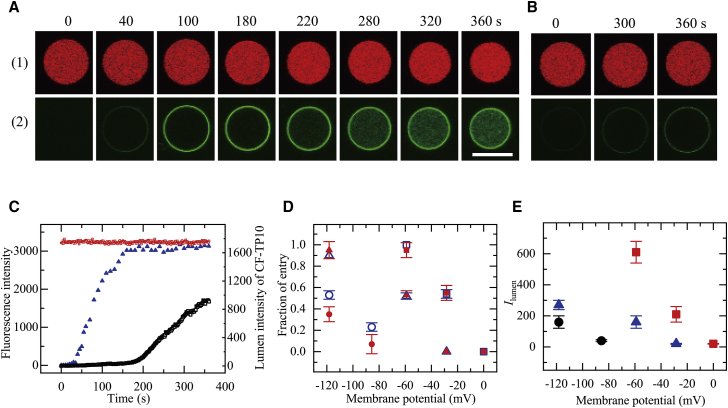
Next, we detected the entry of CF-TP10 into the GUV lumen using a recently reported method employing single PG/PC (2:8)-GUVs containing 1.2 mM LUVs with 100 nm diameter in the GUV lumen (33). In this method, an increase in the FI of the GUV lumen due to CF-TP10-bound LUVs indicates the entry of CF-TP10 into the GUV lumen (33). First, we investigated the effect of φ_m = −59 mV on the entry of 0.50 μM CF-TP10 into PG/PC (2:8)-GUVs. After applying a membrane potential of −59 mV to PG/PC (2:8)-GUVs for more than 10 min, a 0.50 μM CF-TP10 solution was continuously added from a micropipette to the vicinity of a single GUV. During the interaction of CF-TP10 with the GUV, the FI in the GUV lumen due to AF647 remained essentially constant for 6 min (Fig. 3, A(1) and C), indicating that CF-TP10 did not induce pore formation in the GUV membrane. Fig. 3, A(2) and C show that the rim intensity due to CF-TP10 increased gradually to reach a steady value at 160 s. In contrast, initially the FI of the GUV lumen due to CF-TP10, I_lumen, was zero, but after 200 s, I_lumen gradually increased with time to 910 at 6 min (Fig. 3, A(2) and C). These results show that the concentration of CF-TP10 bound to the LUV membranes in the GUV lumen increases, indicating the entry of CF-TP10 into the GUV without pore formation (33).

Figure 3.

Interaction of CF-TP10 with single PG/PC-GUVs containing LUVs. (A and B) CLSM images of (1) AF647 and (2) CF-TP10 of a PG/PC (2:8)-GUV interacting with 0.50 μM CF-TP10 under φ_m = −59 mV (A) and 0 mV (B) are shown. The numbers above each image indicate the interaction time of CF-TP10 with the GUV. The bar represents 20 μm. (C) Change in the FI of the GUV shown in (A) over time is given. Red squares correspond to the FI of the GUV lumen due to AF647. Blue triangles and black squares correspond to the FI of the GUV rim and the GUV lumen due to CF-TP10, respectively. (D) Effect of membrane potential on P_entry (6 min) is shown. Blue □, 0.50 μM; blue △, 0.40 μM; blue ○, 0.30 μM CF-TP10. For each condition, the mean values and SDs of P_entry (6 min) of two to three independent experiments using 5−14 GUVs each were obtained. For comparison, the results of the effect of membrane potential on P_entry (6 min), determined using the GUVs containing small GUVs (the same data as Fig. 2D), are indicated with red ▪ 0.50 μM, red ▲ 0.40 μM, and red ● 0.30 μM CF-TP10. (E) Effect of membrane potential on I_lumen (6 min) without pore formation is shown. Red ▪, 0.50 μM; blue ▲, 0.40 μM; black ●, 0.30 μM CF-TP10. For each condition, the mean values and SEs of I_lumen (6 min) of 13−37 GUVs obtained by two to three independent experiments using 5−14 GUVs were obtained. To see this figure in color, go online.

This method uses the FI in a GUV lumen due to CF-TP10, I_lumen, as a criterion for the entry of CF-TP10 into the GUV lumen: if the I_lumen at a specific time is larger than the threshold intensity of I_lumen (33), then CF-TP10 enters the GUV lumen. The I_lumen of PG/PC (2/8)-GUVs in buffer for 6 min in the absence of CF-TP10 was less than 50 (I_lumen = 20 ± 4, n = 20, N = 2), and thus, we defined the threshold intensity of I_lumen for the entry of CF-TP10 into the GUV lumen to be 50. In other words, I_lumen ≥ 50 indicates that CF-TP10 enters the GUV lumen. Using this condition, we can determine the value of P_entry (6 min) (33). Under this condition (φ_m = −59 mV and 0.50 μM CF-TP10), I_lumen (6 min) > 50 for all the examined GUVs, and hence, P_entry (6 min) = 1.0 (N = 2). We performed the same experiments using various membrane potentials. For φ_m = 0 mV, I_lumen did not increase significantly and I_lumen (6 min) < 50 for all the examined GUVs (Fig. 3 B) (N = 2), indicating no entry of CF-TP10 into the GUV lumen (i.e., P_entry (6 min) = 0). For φ_m = −28 mV, P_entry (6 min) = 0.54 ± 0.04 (N = 2). These results indicate that for 0.50 μM CF-TP10, the fraction of entry of CF-TP10, which is a measure of V_entry, increased as |φ_m| increased (Fig. 3 D). Another measure of V_entry is I_lumen (6 min) because I_lumen (6 min) is proportional to the amount of CF-TP10 entered a GUV lumen at a specific time (here 6 min), although I_lumen does not increase with time linearly. Hence, we can reasonably infer that the mean value of I_lumen (6 min) of all examined GUVs is a measure of the mean value of V_entry. We obtained the mean values and SEs of I_lumen (6 min): for −59 mV, I_lumen (6 min) = 610 ± 70 (n = 20), whereas for −28 mV, I_lumen (6 min) = 210 ± 50 (n = 37). Fig. 3 E shows that the mean value of I_lumen (6 min) increased with increasing |φ_m| for 0.50 μM CF-TP10 concentration.

Next, we investigated the effect of membrane potential on the entry of lower concentrations of CF-TP10 into PG/PC (2/8)-GUVs containing LUVs and obtained a similar result (see Supporting Materials and Methods, Section 2 and Fig. S3). Fig. 3 D indicates that, irrespective of CF-TP10 concentration, the fraction of entry of CF-TP10 increased with increasing |φ_m|. The values for the fraction of entry at 6 min, P_entry (6 min), determined using GUVs containing small GUVs, are almost the same as those determined using GUVs containing LUVs (Fig. 3 D). As we previously demonstrated (33), the two methods provide almost the same values of P_entry (6 min). The results shown in Fig. 3 D indicate that this principle holds for GUVs under a membrane potential and also that the results of the membrane potential dependence of P_entry (6 min) are reproducible. The consistent results obtained using two different methods indicate that the rate of entry of CF-TP10 into the GUV lumen increases as |φ_m| increases.

Fig. 3 E shows the membrane potential dependence of the mean value of I_lumen (6 min) of all examined GUVs, including the GUVs which CF-TP10 did not enter (i.e., I_lumen (6 min) <50). For comparison, Fig. S4 shows the membrane potential dependence of the mean value of I_lumen (6 min) of only the GUVs that CF-TP10 entered. As expected, the mean values of I_lumen (6 min) in Fig. S4 are greater than those in Fig. 3 E, and there are no data of the mean values of I_lumen (6 min) for the conditions of P_entry (6 min) = 0 in Fig. S4. Fig. 3 E indicates that, irrespective of CF-TP10 concentration, the mean value of I_lumen (6 min) increased with increasing |φ_m|. This result also indicates that the rate of entry of CF-TP10 into the GUV lumen increases as |φ_m| increases.

Effects of negative membrane potential on the rim intensity of PG/PC (2:8)-GUVs due to CF-TP10

To obtain further insights into the above results, we examined the effect of negative membrane potential on the rim intensity due to CF-TP10, which is proportional to the CF-TP10 concentration in the GUV membrane. For this purpose, single PG/PC (2:8)-GUVs not containing small vesicles were used because small GUVs and LUVs in the mother GUV lumen affected the intensity of the mother GUV membrane (29,33).

During the interaction of 0.50 μM CF-TP10 with a single GUV containing AF647 at −59 mV, the rim intensity increased gradually with time to reach a steady value at 290 s (Fig. 4, A(2) and C). In contrast, without a membrane potential (i.e., 0 mV), the time-course increase in rim intensity was similar, but the steady value of rim intensity was much smaller than that at −59 mV (Fig. 4, B(2) and C). Fig. 4 D indicates that the rim intensity increased with increasing |φ_m| for 0.50 μM CF-TP10. We conducted similar experiments using different CF-TP10 concentrations and found that for 0.30 μM and 0.40 μM CF-TP10, the steady value of rim intensity increased as |φ_m| increased (Fig. 4 D). These results indicate that the CF-TP10 concentration in the GUV membrane was elevated with increasing |φ_m|. Fig. 4 E shows the relationship between the normalized rim intensity (referenced to the rim intensity at 0 mV) and |φ_m|, indicating that the membrane potential dependence of the normalized rim intensity became larger as the CF-TP10 concentration increased.

Figure 4.

Dependence of rim intensity due to CF-TP10 in membranes on negative membrane potential. (A and B) CLSM images of (1) AF647 and (2) CF-TP10 of a PG/PC (2:8)-GUV (not containing vesicles) interacting with 0.50 μM CF-TP10 under φ_m = −59 mV (A) and 0 mV (B) are shown. The numbers above each image indicate the interaction time of CF-TP10 with the GUV. The bar represents 30 μm. (C) Change in rim intensity due to CF-TP10 shown in (A) (red □) and (B) (blue △) over time is given. (D) Dependence of rim intensity due to CF-TP10 in membranes on negative membrane potential is shown. Red ▪, 0.50 μM; green ▲, 0.40 μM; black ●, 0.30 μM CF-TP10. For each condition, the mean values and SEs of rim intensity of 10−20 GUVs obtained by two independent experiments using 5−10 GUVs were obtained. (E) Dependence of normalized rim intensity due to CF-TP10 in membranes on negative membrane potential, which was obtained the data shown in (D), is shown. The symbols denote the same conditions as (D). The error bars indicate the relative errors estimated using the mean values and SEs shown in (D). To see this figure in color, go online.

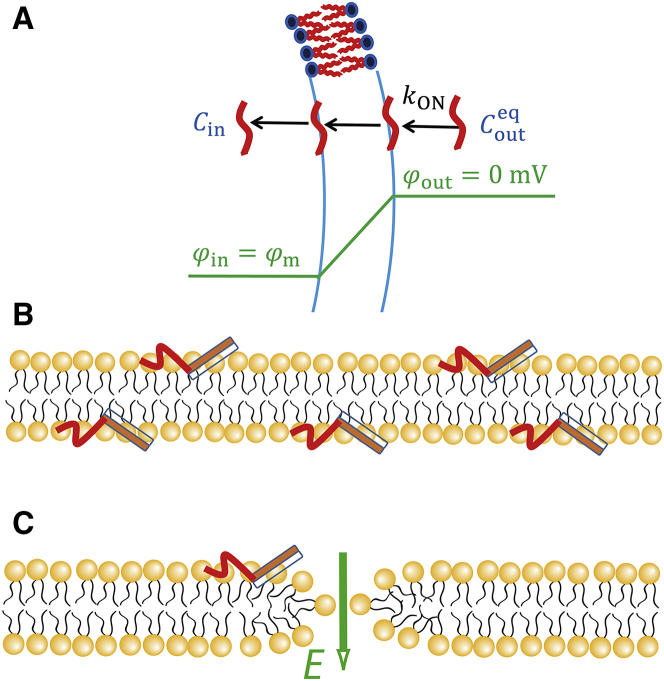
Here, we present a plausible cause for the increase in CF-TP10 concentration in the GUV membrane with increasing |φ_m|. NMR spectroscopy revealed the structure and location of TP-10 in dimyristoyl-PG/dimyristoyl-PC (1:3) bilayers: a major part of the TP10 molecule is located in the membrane interface, with its C-terminal region forming an α-helix (56% helicity) that is inserted into the outer leaflet with a tilt angle of 55° and its N-terminal region forming a flexible structure that is intrinsically unstructured (50). As described in our previous works (29,33), during the interaction of high concentrations of CF-TP10 with single PG/PC (2:8)-GUVs in the absence of membrane potential, the rim intensity due to CF-TP10 increased with time to reach a steady, maximum value before pore formation, and this intensity did not change after pore formation at higher CF-TP10 concentrations. These results can be explained as follows. During the interaction, first CF-TP10 molecules in aqueous solution bind to the membrane interface of the outer leaflet of a GUV with a rate constant k_ON, then they translocate to the membrane interface of the inner leaflet until CF-TP10 concentration in the inner leaflet (C_IM) equals that in the outer leaflet (C_OM) (i.e., C_IM = C_OM) without pore formation in the membrane (Fig. 5 A). In the presence of membrane potential, we can infer that CF-TP10 molecules translocate from the outer leaflet to the inner leaflet of single GUVs without pore formation until C_IM becomes greater than C_OM (i.e., C_IM > C_OM) (Fig. 5 B), given that the energy of positively charged CF-TP10 in the inner leaflet is lower than that in the outer leaflet because of the negative membrane potential. This asymmetric distribution (i.e., C_IM > C_OM) reasonably explains the above experimental results that the CF-TP10 concentration in the GUV membrane increased with increasing |φ_m|. The other factor is the increase in the binding constant of CF-TP10 from aqueous solution to the outer leaflet with increasing |φ_m|. If we assume that this binding constant does not depend on φ_m, C_OM does not depend on φ_m for the same CF-TP10 concentration in aqueous solution outside the GUV (adjacent to the GUV membrane),$C_{\text{out}}^{\text{eq}}$. Thus, the increase in CF-TP10 concentration in the GUV membrane with increasing |φ_m| is due to the increase in only C_IM (in this case, C_IM (φ_m) becomes the maximum among all its estimated values). For example, when we analyze the result that the normalized rim intensity at −59 mV was 2 for 0.50 μM CF-TP10 (Fig. 4 E) under the above condition of no dependence of C_OM on φ_m, we can obtain that C_IM (−59 mV) = 3C_IM (0 mV) because the rim intensity is proportional to the average value of C_IM and C_OM, and thus, (C_IM (−59 mV) + C_OM (−59 mV))/2 = 2 {(C_IM (0 mV) + C_OM (0 mV))/2} and C_OM (−59 mV) = C_OM (0 mV) = C_IM (0 mV) (it is noted that C_IM = C_OM at 0 mV). On the other hand, if we assume that this binding constant increases with |φ_m| and CF-TP10 concentrations in both leaflets are the same (i.e., C_IM = C_OM), the increase in CF-TP10 concentration in the GUV membrane with |φ_m| is due to the increase in both C_IM and C_OM (in this case, C_IM (φ_m) becomes the minimum among all its estimated values). For example, when we analyze the same result that the normalized rim intensity at −59 mV was 2 for 0.50 μM CF-TP10 under the condition of dependence of C_OM on φ_m and C_IM = C_OM, we can obtain that C_IM (−59 mV) = 2C_IM (0 mV) because (C_IM (−59 mV) + C_OM (−59 mV))/2 = 2 {(C_IM (0 mV) + C_OM (0 mV))/2} and C_OM (−59 mV) = C_IM (−59 mV), C_OM (0 mV) = C_IM (0 mV). Under this assumption, the ratio of the rim intensity at membrane potentials to that at 0 mV (i.e., the normalized rim intensity) does not depend on CF-TP10 concentration (i.e., depends on only φ_m) because the binding constant depends only on φ_m. This inference contradicts with the result of Fig. 4 E, which suggests that C_IM increases with CF-TP10 concentration in aqueous solution $C_{\text{out}}^{\text{eq}}$ and C_IM > C_OM. If we consider two factors (i.e., C_IM > C_OM and the φ_m dependence of the binding constant) as described above, we can estimate that 2C_IM (0 mV) < C_IM (−59 mV) ≤ 3C_IM (0 mV) for 0.50 μM CF-TP10. In conclusion, irrespective of the cause for the increase in the CF-TP10 concentration in the GUV membrane with |φ_m|, it is clear that C_IM increases with increasing |φ_m|. This is important when considering the mechanism of the increase in rate of entry of CF-TP10 into GUV lumen with |φ_m| (see the Discussion).

Figure 5.

Model of entry of CF-TP10 into GUV lumen. (A) A scheme of the elementary processes of the entry of CF-TP10 into a GUV under the membrane potential, φ_m, is shown. C_in and $C_{\text{out}}^{\text{eq}}$ are CF-TP10 concentration in the GUV lumen and in aqueous solution outside the GUV adjacent to the membrane. k_ON is the rate constant of the binding of CF-TP10 to the leaflet of a GUV from aqueous solution. (B) A scheme of the structure of TP10 bound to a lipid bilayer based on the NMR data (50) is shown. The rectangle indicates the α-helix, and the red curved line indicates the unstructured part of TP10. (C) A scheme of translocation of TP10 through a transient pre-pore in a lipid bilayer is shown. The electric field, E, due to the negative membrane potential accelerates the translocation of TP10. To see this figure in color, go online.

It is noted that the φ_m dependence of the rim intensity due to CF-TP10 was much smaller than that due to DiOC₆ (3) (Figs. 1 B versus 4 E) (e.g., the normalized rim intensities at −59 mV for CF-TP10 were smaller than those for DiOC₆ (3)). We can explain this result as follows. One can reasonably consider that the rate of translocation of CF-TP10 across the lipid bilayer is much slower than that of DiOC₆ (3) because CF-TP10 is a larger molecule with more positive charges compared with DiOC₆ (3). Consequently, here we observed a transient phenomenon, far from the equilibrium state of the distribution of CF-TP10 (i.e., CF-TP10 continues to transfer from the inner leaflet to the aqueous solution in the GUV lumen).

In our previous work (29), we analyzed the time-course increase in rim intensity due to CF-TP10 (shown in Fig. 4 C) quantitatively by fitting the theoretical equation for the CF-TP10 concentration in the GUV membrane, C_M, and succeeded in obtaining the rate constant of binding of CF-TP10 from aqueous solution to the GUV leaflet and that of the unbinding of CF-TP10 from the GUV leaflet into aqueous solution. To obtain this theoretical equation for C_M in the absence of a membrane potential, we used the assumption that C_IM = C_OM. However, in the presence of a membrane potential, this assumption is not correct, as described above. Hence, we did not analyze the time-course change in the rim intensity.

Discussion

In this study, we applied various negative membrane potentials to PG/PC (2:8)-GUVs using several K⁺ gradients across the GUV membrane and examined these potentials by observing the interaction of DiOC₆ (3) with the GUVs. The increase in rim intensity due to DiOC₆ (3) in the presence of low negative membrane potentials (0 ≥ φ_m ≥ −28 mV) (Fig. 1 C) agreed with the theoretical estimate for the increase in rim intensity based on the Boltzmann distribution of DiOC₆ (3) between the lumen and the outside of the GUV, and hence, the Boltzmann distribution of DiOC₆ (3) between the inner and outer leaflets of the GUV membrane. This result indicates that DiOC₆ (3) achieved an equilibrium distribution within a short interaction time because of its rapid translocation across the GUV membrane.

Next, using this membrane system, we examined the effect of φ_m on the entry of CF-TP10 into single GUVs. It is known that the interaction of higher concentrations of CF-TP10 (≥0.6 μM) with GUVs induced its entry into the GUVs without or before pore formation within 6 min (29,33), and also, the interaction of 1 μM fluorescein-TP10 with giant plasma membrane vesicles induced its entry within 30 min (51). Here, we found that in the presence of φ_m, the interaction of lower concentrations of CF-TP10 (0.3−0.5 μM) with GUVs induced its entry into the GUV lumen without pore formation within 6 min, indicating that φ_m increased the rate of entry of CF-TP10. We also found the stochastic behavior of entry of CF-TP10 into single GUVs (Fig. 3 D; see the detailed discussion later) and thus described the entry using the fraction of GUVs that CF-TP10 entered among all examined GUVs, P_entry (6 min), which increased with an increase in |φ_m|. On the other hand, time courses of I_lumen, because of CF-TP10 in the GUV lumen (e.g., Fig. 3 C), exhibited a complicated behavior (i.e., initially I_lumen was zero for a long time and then suddenly started to increase with time nonlinearly). However, I_lumen (6 min) is proportional to the amount of CF-TP10 entering a GUV lumen at a specific time (here 6 min), and hence, we can regard I_lumen (6 min) as a measure of rate of entry. Because of the stochastic entry of CF-TP10, there are various values of I_lumen (6 min) in all GUVs. However, we can infer that the mean value of I_lumen (6 min) of all examined GUVs is a measure of the mean value of V_entry. We found that the mean value of I_lumen (6 min) increased with an increase in |φ_m| (Fig. 3 E). These results on P_entry (6 min) and I_lumen (6 min) indicate that the rate of entry of CF-TP10 into the GUV lumen increased as |φ_m| increased. This phenomenon can be explained as follows using our model describing the elementary processes underlying the entry of CF-TP10 into a GUV lumen (29,33). First, CF-TP10 in aqueous solution binds with the outer leaflet of a GUV membrane with a rate constant k_ON, then it translocates from the outer leaflet to the inner leaflet stochastically, and finally it transfers from the inner leaflet to the aqueous solution near the GUV membrane. We can reasonably consider that the rate of entry of CF-TP10 into the GUV lumen, V_entry, increases with an increase in C_IM (29,31). Our analysis of the results shown in Fig. 4 indicates that C_IM increases with increasing |φ_m| for the same CF-TP10 concentration in aqueous solution. Therefore, the membrane-potential-induced increase in V_entry can be explained by the increase in C_IM with increasing |φ_m|. To the best of our knowledge, this is the first report to show directly that CPPs entered the GUV lumen without pore formation under membrane potentials and the rate of entry of CPPs into the GUV lumen increased with an increase in |φ_m| and to reveal its mechanism based on the elementary processes underlying the entry of CPPs into a GUV lumen. These findings are owing to the advantages of the single GUV method (6,34).

In this study, to detect the entry of CF-TP10 into GUV lumen, we applied the single GUV method using GUVs (i.e., mother GUVs) containing LUVs or small GUVs in the mother GUV lumen, which is a highly sensitive method to detect the entry of CF-TP10 and thus enables us to measure the CF-TP10 concentration in the mother GUV membrane and lumen simultaneously and continuously. We can reasonably infer that the binding of CF-TP10 to the membranes of the LUVs and small GUVs would decrease the CF-TP10 concentrations in aqueous solution in the mother GUV lumen, inducing further transfer of CF-TP10 from the inner leaflet of the mother GUV to its lumen. This shift of binding equilibrium results in an increase in CF-TP10 concentration in the total lumen (i.e., vesicle membranes and aqueous solution), and as a result, the rate of entry of CF-TP10 increases (33). This inference indicates that the presence of LUVs and small GUVs in mother GUV lumen may induce a perturbation of measurement. However, this method does not change the elementary processes of entry of CF-TP10 and its mechanism. Moreover, in eukaryote cells, there are many membrane structures in their cytoplasm, and hence, GUVs containing LUVs or small GUVs are more suitable as a model of cells (33).

The results of Figs. 2 and 3 indicate that there are two populations of GUVs interacting with CF-TP10, i.e., the GUVs that CF-TP10 entered before a specific time t (e.g., 6 min) and the GUVs that CF-TP10 did not enter, indicating the stochastic behavior of entry of CF-TP10 into single GUVs. Here, we consider the origin of this stochastic behavior of entry of CF-TP10. Entry of CF-TP10 into a GUV lumen consists of several elementary processes: binding of CF-TP10 to the outer leaflet from aqueous solution outside the GUV, translocation of CF-TP10 from the outer leaflet to the inner leaflet, and unbinding of CF-TP10 from the inner leaflet to GUV lumen (Fig. 5 A). We infer that among all the processes involved in the entry of CF-TP10 into single GUVs, the translocation of single CF-TP10 molecules across GUV membrane occurs stochastically because this process occurs because of the thermal fluctuation of the GUV membrane (see the details later). In this case, there are only two populations of single CF-TP10: one is CF-TP10 located at the outer leaflet, and the other is CF-TP10 located at the inner leaflet after the translocation across the lipid bilayer. This is similar to the stochastic transition between two states (i.e., the open state and the closed state) of single ion channels (52). We infer that this stochastic translocation of single CF-TP10 across the lipid bilayer is the main cause of the stochastic behavior of entry of CF-TP10 into a single GUVs. On the other hand, other processes such as the binding of CF-TP10 to the outer leaflet from aqueous solution can be expressed by reaction rate equations. Hence, the lumen intensity due to CF-TP10 at 6 min, I_lumen (6 min), reflects the total elementary processes of entry of CF-TP10. Fig. S5 shows the histogram of I_lumen (6 min) for the data of entry of 0.50 μM CF-TP10 into PG/PC (2:8)-GUVs at −28 mV (P_entry (6 min) = 0.54, the mean value of I_lumen (6 min) = 210). In this histogram, one population for I_lumen (6 min) < 50 (corresponding to the state of GUVs that CF-TP10 did not enter) exhibits a single sharp peak, where the threshold intensity of the entry of CF-TP10 (i.e., I_lumen (6 min) = 50) was determined by the experimental value of I_lumen (6 min) of PG/PC (2/8)-GUVs in the absence of CF-TP10. However, the other population for I_lumen (6 min) ≥ 50 (corresponding to the state of GUVs that CF-TP10 entered) exhibits a broad distribution, although both populations are not clearly separated. Based on the above discussions, we can conclude that P_entry (6 min) is not the fraction of one state in a stochastic two-state transition but a measure of the rate of the entry of CF-TP10 into GUV lumen, which consists of several elementary processes, including stochastic translocation of single CF-TP10 molecules across lipid bilayer. This can explain the broad distribution of the population of the GUVs that CF-TP10 entered.

We previously proposed the pre-pore model to explain the mechanism of translocation of CF-TP10 across a lipid bilayer, in which CPPs translocate through transient hydrophilic pre-pores in the membrane (6,30,31,34). Originally, the existence of pre-pores in lipid bilayers has been proposed in the theory of tension-induced pore formation (53, 54, 55, 56, 57). It is well known that lipid bilayers in the liquid-disordered phase exhibit large thermal fluctuations, and these fluctuations produce an area of decreased density (i.e., rarefaction). Hence, a hydrophilic pre-pore with a toroidal structure is transiently formed where hydrophilic segments of lipid molecules contact with water at the pre-pore wall (Fig. 5 C) (53, 54, 55, 56, 57, 58). This pre-pore is unstable because the edge of the pre-pore has a large line tension and thus rapidly closes. In this way, thermal energy induces a fluctuation of the radius of the pre-pore; if the radius reaches a critical one, the pre-pore transforms into a pore. It is defined that water-soluble fluorescent probes such as AF647 can pass through pores but cannot permeate through pre-pores because the radius of pre-pores is smaller than the pores and the lifetimes of pre-pores are extremely shorter (6,30). When the hydrophilic pre-pore opens transiently, CF-TP10 can translocate across a bilayer by diffusing laterally in a continuous, combined lipid monolayer (composed of outer and inner leaflets and the monolayer at the pre-pore wall) from the outer leaflet to the pre-pore wall and then to the inner leaflet (6). In the presence of a negative membrane potential, we can reasonably assume that the resulting large electric field increases the rate of diffusion of positively charged CF-TP10 in the combined monolayer at the pre-pore wall, from the outer leaflet to the inner leaflet (Fig. 5 C). This increases the rate of translocation of CF-TP10 from the outer leaflet to the inner leaflet, which increases with an increase in |φ_m|. This scenario can reasonably explain why the rate of increase in rim intensity (i.e., the rate of increase in the CF-TP10 concentration in the GUV membrane) increases with an increase in |φ_m|.

The results shown in Fig. 3, D and E indicate that the rate of entry of CF-TP10 into GUV lumen increased greatly with an increase in CF-TP10 concentration under membrane potentials. The same phenomena were observed in the absence of membrane potential (29,33). With an increase in CF-TP10 concentration in aqueous solution outside the GUVs, the CF-TP10 concentration in the GUV membrane increases, which increases the membrane tension and decreases the line tension of pre-pores in the membrane. These changes enhance the frequency of pre-pore formation and enlarge the size of pre-pores, which could increase the rate of translocation of CF-TP10 from the outer leaflet to the inner leaflet (6,30,31). The results shown in Fig. 3, D and E may suggest that the rate of entry of CF-TP10 into GUV lumen increased nonlinearly with CF-TP10 concentration, although the rate of entry of CF-TP10 judged from these results cannot be measured directly, as described above. Currently, we cannot explain the cause of this nonlinearity.

Membrane potential greatly affects the structure and function of plasma membranes; e.g., the function of membrane proteins such as ion channels (22,23), the organization of lipids such as phosphatidylserine, the binding of proteins such as K-Ras (24), and the internalization of dopamine transporter from the plasma membrane (59). Therefore, the reported results of the effects of a change in membrane potential on the entry of CPPs into the cytosol in eukaryotic cells (25, 26, 27) can be interpreted in various ways. However, the results obtained in this study using the single GUV method clearly show that membrane potential greatly elevates the rate of translocation of CF-TP10 across the lipid bilayer (resulting in increase in its concentration in the membrane) and the rate of entry of CF-TP10 into a GUV lumen without pore formation. Based on this result, we can expect that membrane potential has the same effects on the interaction of other cationic CPPs such as TAT peptide and oligoarginine with GUVs. Therefore, we can reasonably infer that membrane potential greatly increases the translocation of CPPs across the lipid bilayer region of a plasma membrane, and hence, membrane potential plays a vital role in the entry of CPPs into the cytosol of cells. Moreover, this study provided experimental evidence to help elucidate the mechanism underlying the membrane-potential-induced elevation of the rate of entry of CF-TP10 into the GUV lumen: namely, the increase in CF-TP 10 concentration in the GUV membrane with an increase in membrane potential. Based on this result, we propose that the CF-TP10 concentration increases in the inner leaflet of the GUV and that this increase clearly relates with the increased rate of entry of CF-TP10 into the GUV lumen. Using the new, to our knowledge, experimental system described in this report, one can investigate the effects of membrane potential on the entry of other CPPs into the vesicle lumen and elucidate their mechanisms in the near future.

Conclusions

The membrane potentials in single GUVs produced by various K⁺ concentration differences were monitored by observing the rim intensity due to DiOC₆ (3). Our results show that the membrane potential dependence of the rim intensity at and below −28 mV agreed with the theory describing the equilibrium distribution of this dye between the inner and outer leaflets of a GUV. The rate of entry of CF-TP10 into the GUV lumen, V_entry, increased as the negative membrane potential increased without pore formation. Moreover, the CF-TP10 concentration in the GUV membrane was elevated with an increase in negative membrane potential, likely due to the increase in CF-TP10 concentration in the inner leaflet of the GUV. Based on the elementary processes underlying the entry of CF-TP10 into a GUV lumen, we can conclude that the increase in CF-TP10 concentration in the inner leaflet with increasing membrane potential is one of main causes of the membrane-potential-induced increase in V_entry.

Author Contributions

M.M.R.M. and M.Y. designed the research. M.M.R.M. and M.Z.I. performed the experiments. M.M.R.M., F.H., S.K.S., and M.Y. analyzed data. M.M.R.M. and M.Y. wrote the article.

Editor: Charles Deber.