Recruiting RyRs to Open in a Ca²⁺ Release Unit: Single-RyR Gating Properties Make RyR Group Dynamics

Abstract

In cardiac myocytes, clusters of type-2 ryanodine receptors (RyR2s) release Ca²⁺ from the sarcoplasmic reticulum (SR) via a positive feedback mechanism in which fluxed Ca²⁺ activates nearby RyRs. Although the general principles of this are understood, less is known about how single-RyR gating properties define the RyR group dynamics in an array of many channels. Here, we examine this using simulations with three models of RyR gating that have identical open probabilities: the commonly used two-state Markov gating model, one that utilizes multiple exponentials to fit single-channel open time (OT) and closed time (CT) distributions, and an extension of this multiexponential model that also includes experimentally measured correlations between single-channel OTs and CTs. The simulations of RyR clusters that utilize the multiexponential gating model produce infrequent Ca²⁺ release events with relatively few open RyRs. Ca²⁺ release events become even smaller when OT/CT correlations are included. This occurs because the correlations produce a small but consistent bias against recruiting more RyRs to open during the middle of a Ca²⁺ release event, between the initiation and termination phases (which are unaltered compared to the uncorrelated simulations). In comparison, the two-state model produces frequent, large, and long Ca²⁺ release events because it had a recruitment bias in favor of opening more RyRs. This difference stems from the two-state model’s single-RyR OT and CT distributions being qualitatively different from the experimental ones. Thus, the details of single-RyR gating can profoundly affect SR Ca²⁺ release even if open probability and mean OTs and CTs are identical. We also show that Ca²⁺ release events can terminate spontaneously without any reduction in SR [Ca²⁺], luminal regulation, Ca²⁺-dependent inactivation, or physical coupling between RyRs when Ca²⁺ flux is below a threshold value. This supports and extends the pernicious attrition/induction decay hypothesis that SR Ca²⁺ release events terminate below a threshold Ca²⁺ flux.

Significance

This work provides insights into ryanodine receptor (RyR)2-mediated Ca²⁺ release by a cluster of RyRs interacting only via their fluxed Ca²⁺. It is shown that 1) common proxies like the single-RyR open probability versus cytosolic [Ca²⁺] curve and mean open or closed times are poor predictors of sarcoplasmic reticulum Ca²⁺ release dynamics, 2) Ca²⁺ release events can self-terminate below a flux threshold without any other regulatory mechanisms, 3) commonly used two-state Markov gating models can produce qualitatively different Ca²⁺ release events (larger and longer) compared to simulations in which complete single-channel open and closed time distributions are used, and 4) correlations between an RyR’s open times and previous closed duration (and vice versa) significantly limit Ca²⁺ release by tamping down the number of open RyRs.

Introduction

Over the last two decades, modeling of Ca²⁺ release from the cardiac sarcoplasmic reticulum (SR) through Ca²⁺ release units (CRUs) has revealed the underlying nature of Ca²⁺ sparks, calcium-induced calcium release (CICR), and intracellular Ca²⁺ movement and cycling during a heart muscle contraction (1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14). At the core of these macroscopic processes is a fundamental nanoscale process, the release of Ca²⁺ through ryanodine receptors (RyRs) in the membrane of the SR. RyRs are both Ca²⁺-conducting and Ca²⁺-activated channels that release Ca²⁺ from the SR via a positive feedback system: an initial Ca²⁺ flux (either through dihydropyridine receptors or a random RyR opening) activates one or more RyRs (CICR) whose fluxed Ca²⁺ activates more and more RyRs (inter-RyR CICR) within the cluster of RyRs that defines a CRU. Although much is known about the downstream effects of this Ca²⁺ release (e.g., the making of a spark), relatively few details are known about the mechanism of inter-RyR CICR.

Because there are no experiments that can directly measure what occurs in a CRU, simulations are the only avenue to explore the nanoscale dynamics of RyRs opening and closing because of fluxed Ca²⁺. There are two main computational difficulties. First, it is difficult to make Markov gating models from single-RyR data that elucidate all the open and closed states (15,16), especially under physiological ionic conditions in which open probability (P_o) is low and currents small. Second, modeling Ca²⁺ flux and its buffering by various chelators in the very narrow subsarcolemmal space (∼10–15 nm tall and ∼400 nm wide) is computationally extremely challenging. To sidestep these challenges, it is common to use simplified gating models like two-state gating models with one open (conducting) and one closed (nonconducting) state (C ↔ O) (2, 3, 4, 5, 6, 7, 8, 9,17) defined by single-RyR mean open times (MOTs) and mean closed times (MCTs) (18). Also, the Ca²⁺ movement in the subsarcolemmal space is often simplified, for example, by assuming the [Ca²⁺] to be homogeneous throughout the subspace and other compartments (6, 7, 8, 9, 10, 11).

These approximations have been vital because they make calculations of Ca²⁺ sparks and intracellular Ca²⁺ movement possible and therefore are directly responsible for our basic understanding of these processes. With this foundational knowledge in hand, we must now develop a more nuanced understanding of RyR group dynamics within a CRU RyR cluster. Only then will we be able to define the pathological effects on RyR-mediated Ca²⁺ release of proarrhythmic mutations (19, 20, 21, 22) and diseases such as heart failure and atrial fibrillation (23,24), as well as the therapeutic effects of RyR-targeted drugs and drug candidates (25, 26, 27). These mutations, diseases, and drugs, as well as regulatory proteins, alter RyR gating and Ca²⁺ sensitivity. Therefore, we must first understand how single-RyR gating properties affect the group dynamics of a multi-RyR cluster. This is our goal here.

There are several open questions in particular that we want to probe in this study:

• 1)Are composite quantities that describe RyR gating like P_o sufficient to give at least a qualitative prediction of SR Ca²⁺ release? If not, are MOT and MCT, the constitutive parts of P_o, sufficient? These quantities are commonly used to assess the “Ca²⁺ sensitivity” of the RyR, but here we find that none of these are enough to give even a qualitative assessment of Ca²⁺ release; the entire distributions of open times (OTs) and closed times (CTs) are required, not just their mean values. This has ramifications for modeling of SR Ca²⁺ release because most simulations currently rely on gating models derived solely from MOTs and MCTs.
• 2)What is the impact of correlations between RyR OTs and CTs, and what might their physiological role be, if any? We recently showed that RyR OTs are highly correlated to the length of previous closure and vice versa (28). These can be seen in Fig. S3. Moreover, we showed that RyR only responds to cytosolic Ca²⁺ when it is closed. These observations have not been included in previous simulations, and here we probe the importance of the OT/CT correlations. We find that the correlations have a moderating effect on SR Ca²⁺ release, making release events with fewer open RyRs. (The lack of Ca²⁺ response in the open state prevents RyR from activating itself with its own fluxed Ca²⁺. Because this is not seen in experiments, we do not explore it further.)
• 3)Can RyRs in a cluster that interact only via their fluxed Ca²⁺ initiate and terminate release? We examine what such clusters can and cannot do in the absence of things like physical coupling between RyRs, calmodulin, calsequestrin, low luminal [Ca²⁺], or Ca²⁺-dependent inactivation. These are gating modulators or have been proposed as Ca²⁺ release termination mechanisms. By stripping away these factors, one can start to define their roles and assess whether they are necessary for termination or act as modulators. Previous work by us and others has given rise to the idea that termination occurs automatically and inevitably in clusters of RyRs that interact only via fluxed Ca²⁺. Specifically, there is a threshold Ca²⁺ flux below which RyR interactions are not strong enough to sustain release (a mechanism named pernicious attrition by us (13) and induction decay by others (4,5)). Because this mechanism is similar to a phase change seen in statistical mechanics (29,30), it should be unavoidable. Here, we find further support for this idea, whereas future work will focus on the specific effects of calsequestrin and luminal [Ca²⁺] on regulating this termination mechanism.

We probe these questions by using a very simple model of inter-RyR CICR. The idea is that with a stripped-down nonphysiological system, we can elucidate physiologically relevant information about RyR clusters in general. This approach is akin to single-RyR recordings in a bilayer; the system is far from that in vivo, but historically they have revealed physiologically relevant properties like RyR’s Ca²⁺ responsiveness and what factors modulate gating, selectivity, and conduction.

In our reduced model, we do not model the geometry of the subsarcolemmal space, cytosolic Ca²⁺ buffers, or depletion of Ca²⁺ from the SR. Rather, each RyR is a point source of Ca²⁺ whose flux is constant when it is open (but the channel may open and close repeatedly), with Ca²⁺ diffusing radially outward into an infinitely large reservoir. It is as if we placed an array of RyRs into the bilayer of a single-channel experiment and recorded the resulting openings and closings. Because the RyRs still interact via Ca²⁺, we will be able to see what factors significantly alter the RyRs’ response and group dynamics. In this way, our results will provide physiological insights because our underlying single-RyR data were taken under physiologically relevant conditions and because the RyR group dynamics seen in this reduced system are likely present in more complex systems.

To address the questions listed above with this system, we consider three subtly different models of RyR gating and compare the results. The three models of single-RyR gating are all derived from the same experimental data, and at every measured cytosolic [Ca²⁺], the three models have identical MOT, MCT, and P_o. They differ in how their OT and CT distributions are summarized for each cytosolic [Ca²⁺]: one model is the equivalent of a two-state Markov gating model and fits a single-exponential distribution to the OTs and CTs; another model fits them with up to five exponentials; the third model also uses multiple exponentials but, as described later, takes into account the measured correlations between OTs and CTs. As a shorthand, we refer to these as the two-state, uncorrelated multi-τ, and correlated multi-τ gating schemes, respectively. (Multi-τ refers to the multiple time constants τ, as opposed to the single time constant for the two-state model.)

Collectively, our simple model reveals several new, to our knowledge, insights into RyR2 group dynamics in a CRU and SR Ca²⁺ release in general:

• 1)The single-RyR P_o versus cytosolic [Ca²⁺] curve is a poor predictor of SR Ca²⁺ release properties. By design, all three of our gating models have identical P_o curves, but all three have very different release properties, especially for the largest release events. Moreover, SR Ca²⁺ release was qualitatively different just by switching from the two-state gating scheme to the uncorrelated multi-τ scheme. The only difference between the two is how many exponentials are used to describe the OT and CT distributions. Thus, we conclude that RyR group dynamics depend strongly on the details of the single-RyRs gating properties and how well the gating model recapitulates the single-RyR OT and CT distributions.
• 2)The correlations between RyR OTs and CTs significantly decrease the number of RyRs open during a Ca²⁺ release event (which we define throughout as first channel open to last channel closed). Interestingly, they do not alter release event initiation or termination but instead only limit the recruitment of more channels to open. This core phase of Ca²⁺ release occurs between initiation (the initial recruitment of a few channels) and termination (the closing of the last few channels) and determines the number of RyRs open during the main part of the release event. To our knowledge, this phase of Ca²⁺ release has not been considered in detail before.
• 3)In the model, the RyRs interact only via their fluxed Ca²⁺, and if the flux is sufficiently small, the Ca²⁺ release events terminate spontaneously even though there is no SR Ca²⁺ depletion; a decrease in SR [Ca²⁺] is not necessary to stop release. This lends support to the pernicious attrition idea that there is a threshold Ca²⁺ flux below which release events cease (4,5,13). Those works assume that a decreasing SR [Ca²⁺] is vital for termination. Our results, with a constant SR [Ca²⁺], extend the pernicious attrition hypothesis by showing SR depletion is not strictly necessary for Ca²⁺ release self-termination; there is a threshold of constant Ca²⁺ flux below which Ca²⁺ release events always terminate. Overall, this work supports the idea that termination is a built-in property of RyRs in clusters and that molecular modulators of gating potentially regulate that process but may not drive it (but more on this needs to be done).
• 4)The two-state gating scheme, which has been used in many earlier studies (2, 3, 4, 5, 6, 7, 8, 9,17), behaves qualitative differently during all three phases of Ca²⁺ release from our other gating schemes (the two multi-τ schemes). If initiation of a release event is defined as the opening the first few channels (e.g., (3)), then initiation is the rate at which one- and two-channel events do not end before they become three-channel events. The two-state scheme is significantly more successful at converting one- and two-channel events into release events with two and three channels opens, respectively; it is far more efficient at initiating a Ca²⁺ release event than the multi-τ schemes. During the core phase of the Ca²⁺ release, the two-state scheme is similarly more successful at opening other RyRs than either multi-τ scheme, leading to more open RyRs per event. Lastly, the time required to close the last few RyRs is much shorter for the two-state scheme. This suggests that two-state models are likely not the best choice to replicate how RyRs work in clusters. We propose that this is because the two-state model is a poor representation of the single-RyR OT and CT distributions. With its single exponential for these distributions, it severely underrepresents both short and long events in the single-channel distributions and therefore in the simulations.

Lastly, we note one aspect of our simulation method that may be of wider interest to the modeling community. Specifically, we use an algorithm to stochastically flip channel states that may be an effective alternative to traditional Markov gating models. It is fast and easy to implement because it directly translates the OT and CT distributions into closing and opening probabilities after fitting the data to a sum of exponentials (see Supporting Materials and Methods). As such, it does not provide physical insights into the gating process like a Markov model might; increasing the number of exponentials has no physical interpretation in our algorithm. However, our algorithm is much easier to set up because the sole purpose of our fitting is to accurately reproduce the data, for which increasing the number of exponentials can be helpful.

Materials and Methods

We briefly describe the experiments, the simulations, and the three gating schemes, with complete details given in the Supporting Materials and Methods.

Experiments

The single-RyR data we use have been previously published (31) and analyzed (28). Specifically, rat RyR2s were recorded in artificial bilayers with 1000 μM luminal (intra-SR) Ca²⁺ and with 0.1, 1, 10, 50, 200, and 1000 μM cytosolic Ca²⁺ with cell-like cytosolic Mg²⁺ and ATP levels, which are potent modulators of RyR2 gating (32,33). This ensures gating and divalent ion concentrations are as close to physiological as possible while a large Cs⁺ gradient was used to make large, easily measured currents. Further details are in the Supporting Materials and Methods and Tables S1 and S2.

As described in (28), our native (nonpurified) RyRs exhibit different modes of gating. RyRs in cells are subject to post-translational modifications like phosphorylation and oxidation and are also known to be associated with various protein partners like calmodulin, calsequestrin, FKBP, kinases, junctin, and triadin. The single-RyR recordings used here were made by fusing native SR microsomes into planar lipid bilayers. Consequently, the post-translational modification status and/or protein complement of the RyRs fused into our planar bilayers likely varies from channel to channel, not unlike the situation within living cells.

In our simulations here, we use an averaged version of the different modes, lumping all the data together to produce OT and CT distributions. This does not affect our results because our aim is not complete physiological accuracy, but rather, to understand how changes in the descriptions of single-RyR gating (e.g., using one exponential or multiple exponentials for the OT and CT distributions) affect Ca²⁺ release through multiple RyRs in an array.

Simulations

A simple geometry

We do not model the geometry of the subsarcolemmal space, cytosolic Ca²⁺ buffers, or depletion of Ca²⁺ from the SR. Rather, each RyR is a point source of Ca²⁺ whose flux is constant when it is open (the channel may open and close repeatedly) with Ca²⁺ diffusing radially outward into an infinitely large reservoir. It is as if we placed an array of RyRs into the bilayer of a single-channel experiment.

This approach has pros and cons. The biggest drawback is lack of in situ realism (e.g., no confining geometry, no Ca²⁺ buffers). On the other hand, working in a simpler geometry facilitates studying RyR group dynamics (the goal of this work) by removing complicating factors to focus purely on the factors affecting Ca²⁺-activated release. The idea is that our results will provide physiological insights because our underlying single-RyR data were taken under physiologically relevant conditions and because RyR group dynamics seen in a simple system are likely present in more complex systems. Overall, RyRs react to Ca²⁺ whether it was buffered first or not, and our approach captures this: buffers modulate [Ca²⁺] but do not change the underlying actions of Ca²⁺ on RyR. The buffering, especially the fast buffering of the sarcolemmal membranes (34,35), will affect the details of RyR group dynamics, but not our conclusions about single-RyR gating properties defining Ca²⁺ release events.

From a numerical point of view, our simplified geometry and lack of Ca²⁺ buffers are a computationally tractable way to compute sufficient numbers of rare Ca²⁺ release events to be statistically relevant. Currently, a full three-dimensional reaction-diffusion system with subnanometer and submicrosecond spatial and temporal resolution that can run minutes of simulated time is not practical. However, a recently derived analytic solution to the spherically symmetric diffusion equation from a point source with variable flux (36) (see Supporting Materials and Methods) makes our simulations fast enough to compute hours of simulated time and millions of Ca²⁺ release events.

Moreover, the use of a constant Ca²⁺ flux is useful for our analysis. By maintaining the same current all the time when channels are open, during a Ca²⁺ release event, the cytosolic [Ca²⁺] seen by closed RyRs remains consistent. Specifically, if, for example, four RyRs are open, then the other closed RyRs are exposed to a cytosolic [Ca²⁺] distribution (Fig. S2). This is same whenever four RyRs are open, regardless of the gating scheme used or RyR array size (data not shown). Therefore, any differences in RyR group dynamics are not due to differences in cytosolic [Ca²⁺] felt by other channels in the array, as might happen with a variable SR [Ca²⁺].

Lastly, by stochastically gating our channels by sampling the OT and CT distributions (see below) rather than using a Markov gating model, we can directly test the importance of the RyR OT/CT correlations on RyR group dynamics by simply turning off any memory of the previous state.

Stochastic gating

All RyRs are closed at the beginning of the simulation. When one RyR opens randomly, Ca²⁺ diffuses to nearby RyRs that may react by opening and flowing more Ca²⁺ into the system. One crucial aspect, then, is how RyRs open and close, both randomly and in response to Ca²⁺. Here, we do not construct traditional Markov gating models from the experimental single-channel data. Instead, our simulations stochastically open and close channels with a probability derived from the distribution of OTs and CTs, as described by Colquhoun and Hawkes (18).

As an example, consider an RyR that has been open for some amount of time T. The probability that it will close during the next time step Δt is the conditional probability that it will close between T and T + Δt given that it has already been open for time T. Using the shorthand notation of o @ t and c @ t to denote open at time t and closed at time t, respectively, this conditional probability is (18)

$$\mathrm{Pr}\left(c@T+\Delta t|o@T\right)=\frac{{\int }_T^{T+\Delta t}{f}_o\left(t\text{'}\right)dt\text{'}}{{\int }_T^{\infty }{f}_o\left(t\text{'}\right)dt\text{'}},$$ (1)

where f_o(t′) is the probability distribution function of the OTs. This function is derived from the experimentally measured distributions of OTs by fitting it with a sum of exponentials (see below). At every time step in the simulation, Eq. 1 is used to determine whether an open channel closes by drawing random numbers from the probability distribution f_o(t′). (A similar probability is used for opening a closed channel but based on f_c(t′), the probability distribution function of CTs.) The f_o(t′) and f_c(t′) are derived from the data at every experimental cytosolic [Ca²⁺] (as described below for the three gating schemes) and then interpolated to other [Ca²⁺], which is necessary because different RyRs in the array see a continuum of cytosolic [Ca²⁺].

The open or closed state of each channel in the array is updated at each time step depending on the [Ca²⁺] each sees, with channels changing state based on randomly generated numbers and the probability of flipping states defined by Eq. 1.

Detailed descriptions of how the gating was implemented, how the simulations were performed, and how the f_o(t′) and f_c(t′) were interpolated to nonexperimental cytosolic [Ca²⁺] are in the Supporting Materials and Methods.

Incorporating recent findings

In (28), it was shown that RyR does not respond to its own fluxed Ca²⁺ because it responds to cytosolic [Ca²⁺] only when it is closed. Moreover, it was shown that the duration of an opening is strongly correlated to the duration of the previous closure and, vice versa, that the CT is correlated to the OT of the previous opening. Unlike previous studies, we incorporate these two findings in the simulations. (The technical details of how this is done are described in the Supporting Materials and Methods.)

The OT and CT correlations are recapitulated in Fig. S3. Here, one focus in particular is comparing gating schemes with and without this memory of the previous state’s duration. In yet unpublished single-RyR recordings in other species and in the presence of calsequestrin, these correlations are consistently found (M. Fill, personal communication), and so we believe them to be physiologically relevant.

Three RyR gating schemes

The most common way to model gating of channels is via Markov models, with a number of so-called open and closed states and one conducting state. Although Markov models with multiple states better represent the single-RyR OT and CT data, it is difficult to elucidate all the open and closed states (15,16). Therefore, two-state Markov RyR gating models are very common in simulations of SR Ca²⁺ release (2, 3, 4, 5, 6, 7, 8, 9,17).

In a two-state gating scheme, the channel switches between a conducting and nonconducting state, and the distributions of OTs and CTs are a single-exponential fit of the data, with the time constant being the measured MOT and MCT (18). This is one of the gating schemes we will use here, in which the f_o(t′) (and f_c(t′)) in Eq. 1 is this single-exponential function. Colquhoun and Hawkes (18) showed that a two-state Markov gating model is equivalent to using Eq. 1 in a simulation.

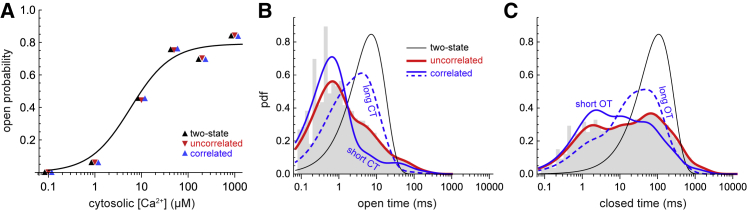
By definition, this gating scheme recapitulates the single-RyR MOT and MCT for each cytosolic [Ca²⁺] and therefore the experimental P_o versus cytosolic [Ca²⁺] curve (black symbols in Fig. 1 A). However, the single exponential f_o(t′) and f_c(t′) OT and CT distribution functions do a poor job of reproducing the single-RyR data (black curves in Fig. 1, B and C, respectively). In the simulation, it is these probability density functions that are sampled, and therefore the two-state model will have few short and long openings and closings because the black curves in Fig. 1, B and C miss these almost entirely. (Note that adjusting the two-state model to include missed recorded events does not change this, as shown in the Supporting Materials and Methods.)

Figure 1.

(A) P_o versus cytosolic [Ca²⁺]. The symbols are for the three gating schemes with a coloring scheme used throughout (black: two-state scheme; red: uncorrelated multi-τ scheme; blue: correlated multi-τ scheme). Note the symbols are offset on the x axis to show they have the same P_o. The solid line is the Hill equation fit of the data taken directly from (28). (B) OT distributions are shown. Gray bars: experimental data. Black: single-exponential fit. Red: multiexponential fit. Blue: multiexponential fit of OTs with short CTs (0–0.531 ms) of the previous closure (solid line) and of OTs with long (≥530.9 ms) previous closures (dashed). (C) shows the same as in (B), but for CT distributions. Blue: short previous OTs (solid) are 0–0.266 ms and long previous OTs (dashed) are ≥53.1 ms. In (B) and (C), the cytosolic [Ca²⁺] is 1 μM where the MOT is 7.23 ms and the MCT is 107.2 ms, respectively. The fit of the blue curves to the corresponding data is shown in Fig. S1. To see this figure in color, go online.

One goal of this study is to understand whether this has a significant impact on simulated Ca²⁺ release or whether merely having the MOT and MCT correct is sufficient. Therefore, to faithfully reproduce the RyR data, we fitted the OT and CT distributions with up to five exponentials. The red curves in Fig. 1, B and C are the resulting f_o(t′) and f_c(t′). When fitting the data with multiple time constants τ, the fit was again constrained to reproduce the experimental MOTs and MCTs, so the P_o was the same as for the two-state scheme (Fig. 1 A, black and red symbols). OTs and CTs were fitted independently of each other. Sampling these multi-τ fitted distributions in our simulations evolves the system via what we call the uncorrelated multi-τ gating scheme.

It is important to note that neither of the multi-τ schemes are a Markov gating model. We have not defined multiple open and closed states, and the number of exponentials used to fit the data has no physical interpretation, as it does in a Markov model. In fact, we have explicitly avoided multistate Markov models because they are difficult, cumbersome, and time consuming to create. By directly using the red curves in Fig. 1, B and C (the f_o(t′) and f_c(t′)) in Eq. 1 to define whether a channel switches states from open to closed (or vice versa) during the simulation, we can sidestep the Markov model creation process entirely. In fact, using Eq. 1 to propagate the simulation in time allows us to move straight from the experimental data to doing simulations. All that is required is to fit OT and CT distribution data to produce f_o(t′) and f_c(t′) that accurately reproduce the data.

We call it the “uncorrelated” gating scheme because neither it nor the two-state scheme produce correlations between the OTs and CTs. To flip from open to closed, for example, in these schemes, the complete OT distribution is sampled at each time step, without any knowledge of the previous closure. To include this memory and produce OT and CT correlations, we break the experimental OT and CT data into smaller parts. For OTs, for example, first all OTs are paired with the CT of the preceding closed state. These pairs are then binned into ranges of CTs so that there are at least 1000 pairs in each bin. The corresponding OTs in each CT bin are then fitted with exponentials (up to 5) to produce an OT distribution for each CT bin (blue lines in Fig. 1, B and C; see also Fig. S1). As before, the fits are constrained to reproduce the experimental mean value of the OTs in each data subset. A similar thing is done to link CTs paired with previous OTs. In a simulation with only one channel, this reproduces the experimental MOTs and MCTs of the full data set and therefore the P_o, as shown in Fig. 1 A (blue symbols). Moreover, it reproduces the experimental correlations (Fig. S3). Therefore, we call this the correlated multi-τ gating scheme.

In this way, we have three differently gated kinds of RyRs: two-state, uncorrelated multi-τ, and correlated multi-τ. For all the experimental cytosolic [Ca²⁺] (0.1, 1, 10, 50, 200, and 1000 μM), they have the same MOT and MCT and therefore P_o. Therefore, in simulations with only one channel present, each recapitulates the experimental P_o versus cytosolic [Ca²⁺] curve (symbols in Fig. 1 A).

Where they differ is in their single-RyR OT and CT distributions. Specifically, in single-channel simulations, the OT and CT distributions each scheme generates are the ones used to define the gating scheme (data not shown). For the two-state scheme, that is the black lines in Fig. 1, B and C. Both multi-τ schemes reproduce the red lines in Fig. 1, B and C, but the uncorrelated multi-τ scheme does not reproduce the experimental OT and CT correlations (data not shown), whereas the correlated multi-τ scheme does (Fig. S3). Therefore, the two-state scheme has OT and CT distributions that compare poorly to the experimental ones (while retaining the experimental MOT, MCT, and P_o), whereas the multi-τ schemes compare as best as we can make them. One level deeper, the correlated multi-τ scheme also reproduces the experimental OT and CT distributions that take into account the length of the previous event (Fig. S1).

Results and Discussion

Here, we examine how these different RyR gating schemes produce different Ca²⁺ release behavior in an array in which the RyRs interact only via their fluxed Ca²⁺. By comparing how similar the Ca²⁺ release events are for three gating schemes that retain the same MOT, MCT, and P_o versus cytosolic [Ca²⁺] curves, we assess how well composite quantities like MOT, MCT, and P_o can predict SR Ca²⁺ release or whether the recapitulation of full OT and CT distributions is necessary. In addition, by comparing the results of the two multi-τ schemes, we hope to assess what the functional effect of the OT/CT correlations is and whether they might be physiologically significant. Lastly, by varying the size of the Ca²⁺ flux by which the RyRs interact, we hope to get a better understanding of how such a CRU works and under what conditions it can self-terminate Ca²⁺ release events.

At the start of our simulations, all RyRs in the array (ranging from 3 × 3 to 14 × 14 in size) are closed, and only a random opening perturbs the system, as in diastole, to kick off Ca²⁺ release. Also, to mimic diastole, the background cytosolic [Ca²⁺] is 0.1 μM. Representative traces of the number of open channels versus time are shown in Fig. 2 A.

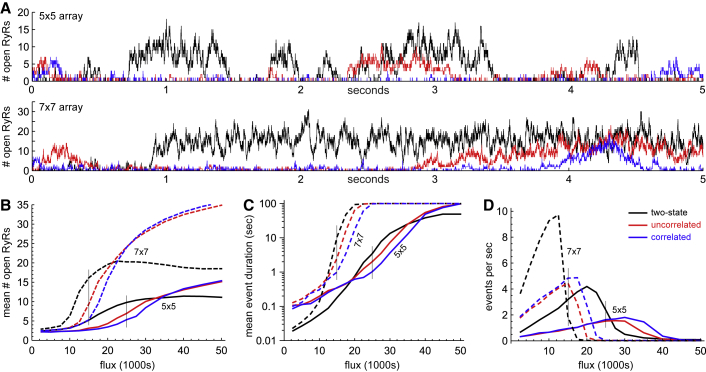
Figure 2.

(A) Time series of the number of open RyRs during the first 5 s of simulations using the two-state scheme (black), uncorrelated multi-τ scheme (red), and the correlated multi-τ scheme (blue) for a 5 × 5 (top) and 7 × 7 (bottom) array for fluxes of 25,000 and 15,000 s⁻¹, respectively (vertical lines in C and D). (B) The mean number of open RyRs of the largest Ca²⁺ release event in each of twenty-five 100-s-long simulations done for each unitary RyR Ca²⁺ flux for a 5 × 5 (solid) and 7 × 7 (dashed) array is shown. The color scheme is the same as in (A). (C) The mean duration of open RyRs of the longest Ca²⁺ release event in each of the simulations is shown. Color scheme and dashing are the same as in (B). (D) The frequency of Ca²⁺ release events with at least three open RyRs is shown. Color scheme and dashing are the same as in (B). More detailed frequency data and the equivalent of (B) and (C) for a 10 × 10 array are shown in Fig. S4. The vertical lines in (B)–(D) are the fluxes used in (A) and in the analysis shown in Figs. 3 and S5. To see this figure in color, go online.

Termination

We start by noticing that Ca²⁺ release events terminate spontaneously, even though the unitary RyR Ca²⁺ flux is constant in time. This has been reported before (37) in Stern’s stochastic attrition termination mechanism. However, like others (38), we find termination occurs even when Stern’s original analysis (which treated the channels is independent) suggested it would not (because our channels are coupled via Ca²⁺). Here, we also extend that original result to show that there is a threshold flux (which varies by array size) below which spontaneous termination always occurs; above the threshold, Ca²⁺ release can continue indefinitely.

The threshold fluxes are seen in Figs. 2 D and S4, in which the event frequencies decrease rapidly with increasing Ca²⁺ flux. Above the threshold, Ca²⁺ release events do not terminate, and the frequency of events drops to one event for the entire 100-s-long simulation. As array size increases, the interval over which the frequency declines narrows, and the transition from many events to one event sharpens; it becomes more of a true threshold phenomenon as the array size increases. (As a technical aside, this behavior is consistent with a phase transition, in which sharpening of transitions is expected for increasing array size (39).)

Below the threshold Ca²⁺ flux, all of the millions of Ca²⁺ release events in our simulations terminated spontaneously for all three gating schemes. Even when so many channels are open that the neighboring closed channels see >10 μM cytosolic [Ca²⁺] (Fig. S2) at which the P_o is >50% (Fig. 1 A), every release event eventually stopped for the conditions shown in Fig. 2 A. This is consistent with recent work showing there is a flux threshold below which continuous Ca²⁺ release is not possible (4,5,13,29,30). In fact, it strengthens this pernicious attrition/induction decay hypothesis because here we do not rely on a decreasing Ca²⁺ flux to produce or facilitate termination. For large fluxes, some SR Ca²⁺ depletion (which this model does not include) is likely necessary to decrease the flux sufficiently to end Ca²⁺ release, but this remains to be verified.

Overall, this shows that over a reasonable range of conditions, Ca²⁺-coupled RyRs will terminate release by themselves and without other mechanisms like Ca²⁺-dependent inactivation (also described in (38)), luminal depletion, or other luminal regulation. However, it still remains to be shown in future work how different RyR array spacings and modulators of RyR gating that we have not considered here (e.g., calmodulin, calsequestrin, low SR [Ca²⁺]) will alter termination.

Different gating schemes, different Ca²⁺ release

Two-state gating is qualitatively different

It is evident from the traces in Fig. 2 A that the three gating schemes have very different group dynamics. As discussed in detail below, the two-state scheme (black lines) produces Ca²⁺ release events that are longer and have more open channels than the two multi-τ schemes. In turn, the uncorrelated multi-τ scheme (red) has more open channels per release event than the correlated multi-τ scheme (blue).

As shown in Fig. 1 A, all three gating schemes produce identical P_o versus cytosolic [Ca²⁺] curves because, by design, each fitting with exponentials of OT and CT distributions was constrained to reproduce the experimental MOTs and MCTs. Therefore, any differences in how the channels behave in a cluster of RyRs are not due to different channel Ca²⁺ affinities (i.e., shifts of the P_o curve to the left or right) or different MOTs and MCTs that retained the same P_o (e.g., the MOTs and MCTs were not both 50% smaller in one gating scheme than in another).

A notable difference between the three gating schemes is in the large release events (i.e., the Ca²⁺ release events with a large average number of channels open). To illustrate this, we performed 25 simulations lasting 100 s for different unitary RyR fluxes. The means of the largest and longest-lasting events from each simulation are shown in Fig. 2, B and C for 5 × 5 and 7 × 7 arrays, respectively. (10 × 10 arrays are shown in Fig. S4.) The two-state scheme (black lines) behaves significantly differently than either of the multi-τ schemes. At low unitary RyR flux, the large two-state events have far more channels open than the multi-τ schemes’ release events, and the longest events tend to be much shorter. At high flux, however, the exact opposite is true. Moreover, the frequency of large Ca²⁺ release events is qualitatively different; the two-state scheme produces a higher rate of events with multiple channels open (Fig. 2 D) and a lower rate of single-channel events compared to either multi-τ scheme (Fig. S4).

One important result seen in Figs. 2 and S4 is the substantial differences between the two-state and uncorrelated multi-τ schemes (black and red curves, respectively). In the simulations, the only difference between them is how many exponentials are used to fit the OT and CT distributions (Fig. 1, B and C). Just by moving to a multiexponential fit (red lines) of the same data but otherwise changing nothing, the group dynamics have changed qualitatively. Because the multi-τ fit reproduces the experimental data more faithfully, this indicates that a two-state gating scheme does not seem to capture how RyRs function collectively in a cluster. Such a fundamental difference will also affect Ca²⁺ release in more realistic models of a CRU.

In some sense, this is not surprising. From a Markov gating scheme point of view, having only one conducting state and one nonconducting state is convenient and reasonable; the average OTs and CTs are used to approximate the behavior of the channel. However, looking at this from the point of view of the OT and CT data, the reason for the differences between the two-state and multi-τ gating schemes is clear: a single exponential is an extremely poor representation of the data (Fig. 1, B and C). Even though the black curves and red curves have the same MOT and MCT (Fig. 1, B and C, respectively), both short and long events are missing in the two-state scheme.

Effect of OT and CT correlations

Next, we compare the uncorrelated and correlated multi-τ schemes (red and blue curves, respectively, in Figs. 2 and S4). These also exhibit important differences, but to a lesser extent. At low and high unitary RyR Ca²⁺ fluxes, the two behave very similarly, but at intermediate fluxes (shown by thin vertical lines in Fig. 2, B–D), the correlated multi-τ scheme has fewer RyRs open during the largest events (Fig. 2 B), and the longest events are shorter (Fig. 2 C). Interestingly, both multi-τ schemes can have the same frequency of release events with three or more RyRs open (Fig. 2 D), as well as the same frequency of events with one or two RyRs open (Fig. S4).

To explore these differences, we grouped Ca²⁺ release events according to the maximum number of open RyRs (N_max). We then computed the fraction of release events for each possible N_max (i.e., what percentage of release events had a maximum of one RyR open, a maximum of two open, etc.). This is shown in Fig. 3 A for all three gating schemes for the 5 × 5 array of RyRs. The same is shown in Fig. S5 for the 7 × 7 and 10 × 10 arrays. Because events with a large N_max are rare, we performed five hundred 100-s-long simulations at one RyR unitary Ca²⁺ flux (thin vertical lines in Fig. 2, B–D) to ensure statistical confidence. In total, the red and blue curves in Fig. 3 each summarize 2.8 million release events, 4.7 million in Fig. S5 A, and 6 million in Fig. S5 B.

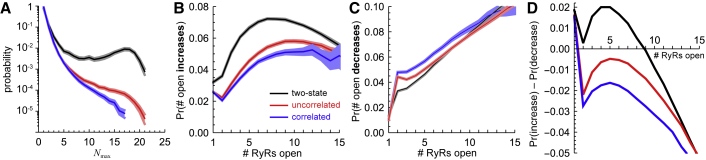
Figure 3.

Release event statistics for a 5 × 5 array with a unitary RyR Ca²⁺ flux of 25,000 s⁻¹. Black: two-state scheme. Red: uncorrelated multi-τ scheme. Blue: correlated multi-τ scheme. (A) The probability of having a Ca²⁺ release event for a given N_max, the maximum number of open RyRs during a release event, with a minimum of 10 Ca²⁺ release events required at each N_max is shown. (B) The probability of increasing the number of open RyRs by one at the next time step during a release event when n RyRs are currently open (x axis) is shown. A minimum of 100 events were required for each n. (C) is the same as (B), except it shows the probability of decreasing the number of open RyRs by one. (D) Difference of the corresponding solid lines in (B) and (C) is shown. In (A)–(C), the shaded areas are 95% confidence intervals obtained by bootstrap resampling. Specifically, five hundred 100-s-long simulations were performed, and 1000 random samples with replacement of whole simulations were reanalyzed; the 2.5 and 97.5% quantiles are the limits of the confidence intervals (28). The solid line is the quantity obtained from the original (not resampled) data. To see this figure in color, go online.

The figures show that both the uncorrelated and correlated multi-τ schemes have a similar probability of small events (i.e., with N_max small), but they diverge as N_max grows. The correlated multi-τ scheme produces far fewer large release events than the uncorrelated multi-τ scheme. This is significant because large Ca²⁺ release events can be physiologically detrimental. And although ours is not the physiological case, there is no a priori reason to believe that such a fundamental difference would disappear in vivo.

This could reflect a difference in event initiation (i.e., converting a small event with few open RyRs into a big event with many RyRs open). This, however, does not seem to be the case. First, at the flux used in Fig. 3, both multi-τ schemes have identical event frequencies for N_max = 1, N_max = 2, and for N_max ≥ 3 (Fig. S4). Specifically, if the uncorrelated multi-τ scheme were more successful at recruiting RyRs to open during the initial stages of a release event when the number of open RyRs was small (e.g., one or two), then one might expect lower event frequencies for N_max = 1 and for N_max = 2 and higher frequencies for N_max ≥ 3. But this is not the case (Fig. S4). Second, we directly computed the rate at which one- and two-channel events were converted to 3+-events and the rate at which the small events were snuffed out (i.e., self-terminated). These were identical for both multi-τ gating schemes: in the 5 × 5 array, for a flux of 25,000 s⁻¹, 97.2% of one- and two-channel events were snuffed out and only 2.8% grew to 3+-channel events; in the 7 × 7 array, for a flux of 15,000 s⁻¹, 95% of small events terminated and 5% grew larger. (The two-state gating scheme is qualitatively different in another way. For the 5 × 5 array, it had a conversion rate of ∼14%, three to five times that of the multi-τ schemes; only ∼86% of one- and two-channel events were snuffed out.) Therefore, the difference between the uncorrelated and correlated schemes does not seem to be in recruitment during the initial period of the release event.

We next explored whether the correlated multi-τ gating scheme was more efficient at terminating a Ca²⁺ release event. During a release event, the number of open channels fluctuates greatly (Fig. 2 A). To focus on the termination phase of the event, we focused on the very end of a release event, specifically the very last time three RyRs were open. We wanted to gauge the speed of termination (i.e., how long it took to go from three RyRs open to zero) to see whether one gating scheme was more efficient than another at closing the last few channels. The multi-τ gating schemes were identical (46.4 ms for the uncorrelated multi-τ scheme and 47.1 ms for the correlated), indicating that neither is more efficient than the other at terminating an event. (Counterintuitively, the two-state scheme was much faster at 14.4 ms, despite its much longer release events. The reason for this is discussed below.)

Recruitment bias

To delve further into the difference between the uncorrelated and correlated multi-τ schemes, we focused on what occurred during the middle of the release events, the core phase of Ca²⁺ release. We reasoned that if one scheme’s Ca²⁺ release event is consistently smaller than another, then there may be a bias toward having fewer RyRs open at any one time. This can occur either by having a lower propensity to open neighboring closed RyRs or a higher propensity to close already-open RyRs. We found that the correlated gating scheme had both biases and thereby prevented Ca²⁺ release events from having a large number of open RyRs. Specifically, we computed the fraction of time steps that n open RyRs became n + 1 (Fig. 3 B) or n − 1 (Fig. 3 C); that is, what is the probability that, for example, four RyRs open became five or three?

The probabilities of increasing the number of open RyRs from one to two or from two to three were virtually identical but diverged after that; there is a gap between the red and blue confidence intervals in Figs. 3 B and S5. Similarly, the probability of decreasing from two to one or from one to zero open RyRs is the same for the two multi-τ gating schemes but becomes significantly different for three or more open RyRs (Fig. 3 C; Fig. S5). It is important to note that the small but consistent differences between the red and blue confidence intervals are statistically significant; each confidence interval was computed from 1000 bootstrap resamples of five hundred 100-s-long simulations that had millions of Ca²⁺ release events (enumerated earlier), each of which had many changes in the number of open RyRs (Fig. 2 A).

The net effect of the probabilities in Fig. 3, B and C are described in Fig. 3 D. There, the difference of the probabilities to increase and decrease the number of open RyRs is shown. A positive value is a bias to open more RyRs and a negative value to close RyRs. We call this the recruitment bias.

These recruitment biases are small (∼ −0.005 for the uncorrelated multi-τ scheme when 5 RyRs are open and ∼ −0.015 for the correlated multi-τ scheme in a 5 × 5 array, as shown at the maxima in the red and blue lines in Fig. 3 D, respectively). However, the larger bias toward closing RyRs by the correlated multi-τ scheme (compared to the uncorrelated multi-τ scheme) has a significant effect in the Ca²⁺ release statistics toward smaller Ca²⁺ release events (i.e., fewer RyRs open per event), as seen in Figs. 2 and 3 A; over the course of millions of channel openings and closings, the small recruitment bias difference has a large effect. Moreover, the ∼ +0.02 bias to open more RyRs of the two-state model produces very large, long-lasting, and more frequent Ca²⁺ release events (black lines in Figs. 2 and 3 A).

These results indicate that a small bias toward opening or closing RyRs during the middle of release event has substantial consequences on the global release of Ca²⁺ from the SR. They also show why the two-state model is qualitatively different from the multi-τ gating schemes. Specifically, it is biased toward opening more RyRs until the number of open channels becomes relatively large (the black line in Fig. 3 D is positive when the number of open RyRs is ≤9).

The fact that the two multi-τ gating schemes have very similar biases when just a few RyRs are open (red and blue lines in Fig. 3 D) explains why both their initiation and termination statistics were nearly identical, as both of these phases of SR Ca²⁺ release involve, by definition, few open channels. During the core phase, however, many RyRs are open, and so this is when the biases toward shrinking or growing the release event have an impact. Moreover, it makes sense that the correlated nature of the OTs and CTs manifests itself only during the core phase. It is only then that the number of open RyRs fluctuates in time (Fig. 2 A), with RyRs opening and closing often. These channels then have previous CTs and OTs very different compared to when the RyR array is in a long quiescent state and only the occasional 1- or 2-channel release event occurs. Under these conditions, the OT/CT correlations become important and reveal themselves as a bias toward shrinking the Ca²⁺ release event, compared to the RyRs with uncorrelated OTs and CTs (the blue line in Fig. 3 D is more negative than the red line).

The recruitment bias also explains the results for the two-state gating scheme in all three phases of Ca²⁺ release. During the initiation phase, the two-state scheme has a positive recruitment bias when 2 or 3 RyRs are open, unlike the negative bias of the multi-τ schemes. This results in significantly fewer small events being snuffed out before growing larger. Moreover, during the core phase, the positive recruitment bias when nine or fewer RyRs are open in a 5 × 5 array (Fig. 3 D) sustains the release event. It does this in two ways, initially by enhancing the number of open RyRs and then by delaying termination. After the negative recruitment bias for 10+ open RyRs decreases the number of open RyRs, the positive bias increases the number again and prolongs the release event. Counterintuitively, this buoying phenomenon also explains the two-state scheme’s very fast termination speed. Although there is a positive recruitment bias when only a few RyRs are open, it can be overcome, but to close all remaining channels requires acting against the recruitment bias. These several low-probability RyR closings must happen in quick succession; the faster they happen, the less likely the positive recruitment bias prevents full termination. Therefore, termination is likely to be fast.

Composite quantities and Ca²⁺ release

Collectively, these results show that RyR group dynamics depends strongly on the details of the single-channel gating scheme, even if the RyRs have identical single-channel MOT, MCT, and P_o. Therefore, none of these quantities are sufficient to predict the size and duration of Ca²⁺ release events (and therefore downstream effects like Ca²⁺ sparks). In simulations, any model of RyR gating (Markov or otherwise) must reproduce the full RyR OT and CT distributions in single-RyR simulations. Moreover, such models should also reproduce the correlations between OTs and CTs, which we show have an important role in tamping down the number of RyRs open during a Ca²⁺ release event. Because our single-RyR data were taken under cell-like conditions, these findings are likely to be physiologically relevant as well.

Conclusions

The goal of this work was to define whether the details of RyR gating are required to predict RyR-mediated Ca²⁺ release. We did this using a very simple model of RyRs in an array. Although this model is not physiological, it retains the essentials of RyRs activating each other via fluxed Ca²⁺ so that we could assess large changes in array behavior when assumptions about RyR gating were varied. Therefore, the details of RyR array behavior will change when more realistic details like Ca²⁺ buffering, nonuniform RyR array organization, and luminal SR [Ca²⁺] (20,22,32) are included. However, the qualitative differences and similarities in RyR group behavior we found should remain because they are due to differences in single-RyR gating.

Our first finding is that RyRs that only interact via fluxed Ca²⁺ will terminate release spontaneously without physical coupling of the channels or other regulatory mechanisms, even when there is no depletion of SR Ca²⁺. This is true of all three gating models used here. Thus, this study strongly supports the pernicious attrition/induction decay mechanism of termination that there is a threshold of Ca²⁺ current below which termination occurs. In our constant current simulations with millions of Ca²⁺ release events, there is a threshold below which release events always terminate. And although luminal depletion likely plays a key role in Ca²⁺ spark termination, it is not strictly required.

We also find that measured composite (mean) quantities like P_o (or even its constituents, MOT and MCT) by themselves are insufficient to define RyR-mediated Ca²⁺ release. In fact, one important take-home message of this work is that any gating scheme should reproduce the single-channel data as faithfully as possible because that dictates what OTs and CTs the simulated channel can stochastically sample. Intuitively, if it does a poor job reproducing the OT and CT data in a simulation with only one RyR, how can one expect it to give physiologically relevant results in a simulation with many RyRs? In addition, we found that the correlations between RyR OTs and previous CTs (and vice versa) have a moderating effect on Ca²⁺ release, reducing the number of RyRs open during a release event.

Overall, this work suggests that different modeling at the level of single-RyR2 gating may have implications for the simulation of Ca²⁺ release. Previously, two-state Markov gating models have been very successful, from a single CRU to an entire cell and across both compartmental and spatial formulations (2, 3, 4, 5, 6, 7, 8, 9,17). The results of this study show that adding full OT and CT distributions and the correlations between OTs and CTs could make sparks less frequent. This, however, remains to be checked because (for example) the implementation of other groups’ two-state gating models may not have positive recruitment bias.

One way to accomplish this goal may be to move beyond Markov gating models. Although they provide insights into the internal mechanisms of the RyR gating process, from a simulation point of view, they are not strictly needed. Our approach that directly converts the experimental OT and CT distributions into closing and opening probabilities may be a useful alternative. It is intuitive, simple, and numerically fast, and it can be implemented in any CICR simulation.

Author Contributions

D.G. conceived the study, wrote the code for the simulations, analyzed the data, and wrote the manuscript.

Editor: Eric Sobie.

Supporting Citations

References (40, 41, 42, 43, 44, 45, 46, 47) appear in the Supporting Material.