The Structure of the Serotonin System: a PET Imaging Study

Abstract

The human brain atlas of the serotonin (5-HT) system does not conform with commonly used parcellations of neocortex, since the spatial distribution of homogeneous 5-HT receptors and transporter is not aligned with such brain regions. This discrepancy indicates that a neocortical parcellation specific to the 5-HT system is needed. We first outline issues with an existing parcellation of the 5-HT system, and present an alternative parcellation derived from brain MR- and high-resolution PET images of five different 5-HT targets from 210 healthy controls. We then explore how well this new 5-HT parcellation can explain mRNA levels of all 5-HT genes. The parcellation derived here represents a characterization of the 5-HT system which is more stable and explains the underlying 5-HT molecular imaging data better than other atlases, and may hence be more sensitive to capture region-specific changes modulated by 5-HT.

1. Introduction

Serotonin (5-hydroxytryptamine, 5-HT) plays a central role in the regulation and function of the human brain. The modulatory effects of 5-HT are broad and extensive and are implicated in highly diverse aspects of brain physiology and pathology, such as the regulation of sleep and major depression. For an in-depth review of the brain functions and disorders related to the 5-HT system see [1]. This rich versatility is reflected in the diversity of receptors composing the 5-HT system; with 7 families of receptors (5-HT₁ to 5HT₇) consisting of 14 subtypes and a transporter (5-HTT), the 5-HT system is one of the most complex receptor systems linked to a single neurotransmitter. Whereas the distribution of a subset of the 5-HT receptors and the 5-HT transporter in the human brain has been well characterized through autoradiography [2], and more recently in vivo [3, 4], the regions describing the spatial distribution of receptor density across receptor types have been largely unexplored.

From the early work on its cytoarchitectonic structure [5], the brain is known to be organized in coherent, specialized regions. In vivo molecular neuroimaging of the 5-HT system with Positron Emission Tomography (PET) is most often assessed on the basis of atlases derived from the anatomical structure of the brain [6, 7, 8, 9]. In the absence of further knowledge about the spatial structure of the 5-HT system, these anatomical atlases constitute a reasonable assumption about the spatial organization of this system. However, there is no evidence that the distribution of 5-HT targets (receptors and transporter) accurately follows the regions presented in these atlases. On the contrary, the regional variation in 5-HT targets found in a high resolution in vivo 5-HT atlas [3] suggests that the 5-HT system may have its own underlying spatial organization consisting of regions of homogeneous receptor density. Indeed, a structural atlas derived from the cortical gyri and sulci of the human brain, such as the Desikan-Killiany (DK) atlas [6], may be inadequate to explain the organization of the 5-HT system as its regions contain a spatially inhomogeneous concentration of the 5-HT targets [3].

A parcellation of the 5-HT system based on PET neuroimaging data from 108 healthy individuals has recently been presented in James et al. (2018) [10]. Although this parcellation likely captures the main regions involved in the 5-HT system, we are concerned that the proposed parcellation shows patterns similar to partial volume effects (PVE) observed in surface-based analysis of PET data [11]. Furthermore, the clustering strategy proposed in [10] may lead to unstable parcellations due to the chosen clustering approach. Finally, the dataset used to derive the clustering presented in [10] also included PET data for Monoamine Oxidase A (MAO-A), an enzyme which degrades all amine neurotransmitters and is not specific to the 5-HT system.

We propose an alternative approach which uses a watershed-type algorithm to perform the clustering which regularizes the parcellations by using spatial information. Furthermore, our dataset is acquired on a high resolution PET scanner, additionally consists of the 5-HT_1B and the 5-HT₄ receptors, and avoids the inclusion of data non-specific to the 5-HT system. Finally, we investigate the associations between our parcellations and genetic data from the Allen Human Brain Atlas (AHBA) [12] for the genes encoding for the 5-HT receptors and transporter, for completeness, and also for MAO-A.

2. Methods

2.1. Dataset

We used data from [3] which includes 232 individual PET and structural MRI scans from 210 healthy subjects from the Cimbi database, which in a quality-controlled, and structured way stores the largest collections of high-resolution 5-HT neuroimaging data available [13]. Imaging data for the receptors 5-HT_1A ([¹¹C]CUMI-101, n=8), 5-HT_1B ([¹¹C]AZ10419369, n=36), 5-HT_2A ([¹¹C]Cimbi-36, n=29) and 5-HT₄, ([¹¹C]SB207145, n=59) and the transporter 5-HTT ([¹¹C]DASB, n=100) were included. For more details, e.g. regarding subject inclusion criteria, please see [13].

2.2. Preprocessing

The data was processed as in [3]. Briefly, the T1-weighted structural MRI were processed with FreeSurfer [14] v5.3 (FS, http://surfer.nmr.mgh.harvard.edu ). The dynamic PET data was realigned and coregistered to the structural MRI using boundary-based registration [15] with a weighted-sum image, and was then resampled onto the standard fsaverage surfaces (left and right hemisphere) and smoothed with a 10mm full-width half maximum (FWHM) Gaussian kernel. Kinetic modeling of the time-activity curves (TAC) was performed individually at every vertex using the MRTM2 model [16] to obtain nondisplaceable binding potential (BP_ND) values. Finally, the BP_ND maps were demeaned and scaled to unit variance individually for each subject and hemisphere. In our comparison to previous clustering work, the data was preprocessed as above, but the surface smoothing was performed with a 8mm FWHM Gaussian kernel to match the approach used by James et al. [10]. Furthermore, volume smoothing of the the dynamic PET data prior to sampling on the surface was performed with 0, 2, and 4mm FWHM Gaussian filters to test the effect of increasing PVEs. Regional BP_ND values used to construct correlation matrices were obtained by resampling the dynamic PET data to the surface, without smoothing, averaging the TACs within each region, and modeling the data region-wise with MRTM2.

2.3. Previous clustering methodology

To evaluate the clustering strategy of James et al. [10], we repeated their analysis with our data. For each 5-HT target, the BP_ND data was first averaged across subjects and then standardized by subtracting the spatial mean across vertices and dividing by the standard deviation, resulting in a single spatial map per 5-HT target (the four receptors and the transporter). The maps are then concatenated across targets and both hemispheres were combined by concatenating the data spatially. Clustering was performed using K-means initialized with K-means++ and using 50 restarts. We used the K-means implementation from the Scikit-learn 0.19.1 library [17].

The silhouette coefficient (SC) curves were quantified using the same approach as James et al. [10]. We created 100 subsets of the data. Each subset was created by randomly selecting 5 subjects for each 5-HT target and by processing them as above by taking the spatial average across subjects per target, standardizing the data, and concatenating the resulting maps across targets. For each subset, K-means clustering was performed as above for clusters number K from 2 to 20 as done in [10]. The SC curves were computed for each subset and each corresponding parcellation. The mean SC curve was finally used to assess the optimal number of clusters, K. The stability of the clustering procedure, assessed using adjusted mutual information (AMI). We computed the mean AMI across every pair of the 100 parcellations (where no volume smoothing was applied) created for every K.

2.4. Our clustering approach

In a first part, we created a mean feature map for each of the 5-HT targets using a bootstrap procedure with 10,000 resampling. For each target, bootstrap samples were created by sampling with replacement the number of available scans per target from the normalized BPND maps of individual subjects and averaging them. The mean across all bootstrap samples was taken as the bootstrap estimate of the population mean map. The bootstrap procedure was informative on the variability of the mean feature maps and allowed us to compared the variance between 5-HT targets with different numbers of subjects (e.g. 5-HT_1A with n = 8 and 5-HT_2A with n = 36), see supplementary figure 1. The feature maps were then concatenated across 5-HT targets. This process was performed independently for each hemisphere. We clustered the concatenated feature maps using the image foresting transform (IFT) watershed algorithm [18, 19] using the squared Euclidean distance to determine the cost between pairs of vertices. Initial cluster centers were obtained by clustering the features maps, concatenated spatially across both hemispheres, with K-means initialized with K-means++ and using 50 restarts. To avoid potential local optimum, the clustering steps (i.e. K-means and IFT watershed) were repeated 5 times, and the solution with the highest explained variance was kept. Parcellations with number of clusters K from 2 to 20 were thus created.

To identify an optimal number of clusters K, we computed the explained variance (EV) and SC for each parcellation. However, as it became apparent that both EV and SC were monotonically increasing or decreasing with K, respectively, we created a combined score from the two metrics to obtain a trade-off between them. This strategy is similar to the approach previously introduced by [20, 21] and has the advantage of providing a solution which both fits the data well (by maximizing EV) and defines well-separated clusters (by maximizing SC). The combined score was defined as

$$\mathrm{score}(K)=\text{NEV}(K)\cdot \text{NSC}(K)$$ (1)

where NEV and NSC are normalized functions of EV and SC for every cluster K. As both EV and SC may span a different interval of their [0, 1] domain, the metrics were both normalized as follow so that they contribute equally to the score

$$\text{NEV}(K)=\text{EV}(K)/(1-\min (\text{EV}))$$ (2)

$$\text{NMS}(K)=\text{SC}(K)/\max (\text{SC})$$ (3)

The optimal number of clusters K according to our score is then obtained by max(score(K)). For additional evaluation, we have also estimated the Bayesian information criterion (BIC) [22] for all the parcellations.

The stability of our parcellation was also assessed using AMI. The full clustering process described above was repeated 10 times, where for each iteration the input PET data was resampled using stratified random sampling with replacement. We then computed the mean AMI across every pairing of the 10 resulting parcellations.

Correlation plots were created by extracting regional BPND values for each individual PET scan for each regions of the parcellation with K = 10, and computing the associated correlation matrix. The rows and columns of the matrices were reorganized to highlight correlated groups of regions using hierarchical clustering with average linkage implemented in SciPy 1.3.

2.5. Evaluation of the spatial correspondence between the 5-HT system and its underlying genetic information

We used mRNA data available from the AHBA to 1) evaluate the spatial association between 5-HT target density and mRNA levels and 2) investigate how well our parcellations could explain the spatial distribution of all 5-HT genes. Previous work by [23] provides the correspondence between each of the mRNA samples of the AHBA and the regions of the DK atlas. Here we derived a mapping from the AHBA samples to specific vertices on the fsaverage surface (hence applicable to any parcellation on this surface) and extracted regional average mRNA values for all available 5-HT genes: HTR1A, HTR1B, HT1D, HTR1E, HTR1F, HTR2A, HTR2B, HTR2C, HTR3A, HTR3B, HTR3C, HTR3D, HTR3E, HTR4, HTR5A, HTR6, HTR7, and SCLC6A4. Additionally, we included the gene MAOA due to the role of MAO-A in the degradation of the amine molecules, including 5-HT, and its inclusion in the parcellation presented by James and colleagues [10]. In-depth information on the AHBA can be found at http://help.brain-map.org/display/humanbrain/Documentation.

The spatial location of all tissue samples collected in the AHBA is provided in MNI152 volume space. To obtain a correspondence from the MNI152 space to the fsaverage surface on which our parcellations reside, we first processed the T1-weighted image of the MNI152 brain (ICBM 2009c Nonlinear Asymmetric, [24]) with FS. Then, each vertex of the MNI152 surfaces was mapped to fsaverage by projecting a binary mask of each vertex (where everything is zero except that given vertex) onto fsaverage and finding the corresponding vertex with the highest value on the surface. Finally, every sample was matched to the closest vertex on the MNI152 white matter surface and mapped to the corresponding vertex on fsaverage. The match between a given probe and the MNI152 surface was restricted to vertices of the surface having the same label according to the DK atlas as assigned by [23]. If a sample was located more than 10mm away in space from any vertex of the surface with the appropriate label, then the probe was discarded; a total of 98 out of 1697 samples were thus ignored. For any given parcellation on fsaverage, the sample-to-cluster assignment is then performed by identifying the label of the corresponding vertex. In the AHBA, each sample contains at lest two probes for each gene. To obtain a single summary value of the mRNA level for a given gene per sample, expression values from multiple probes were average for each gene and each sample. These summary values were then normalized individually for each subject using a scaled robust sigmoid normalization proposed by [25, 26].

The regional mRNA levels for the parcellation with K = 10 were obtained using a bootstrap procedure with 1,000 resampling, where each bootstrap sample was created by randomly sampling all summary values with replacement, and computing the mean in each region. The mean regional mRNA levels were used to create spatial maps and the bootstrap samples were also used to compute the mean EV of the mRNA values for the parcellation. This procedure was applied independently to all 5-HT genes.

3. Results

3.1. Previous clustering methodology

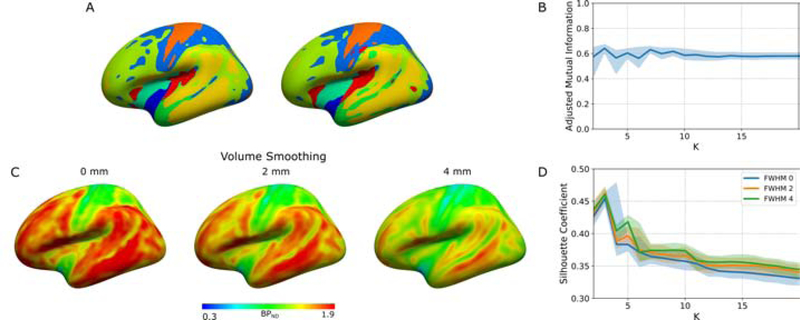
To analyse the stability of the parcellation introduced by James and colleagues [10], we repeated the same clustering procedure on 100 datasets created using stratified randomly sampling with replacement of the input subjects. Figure 1A presents two of these parcellations, with K = 10. Numerous mismatches between the two parcellations can be observed, principally along the contour of the clusters. We have used AMI as a proxy for the stability of the parcellations. Figure 1B presents the mean pairwise AMI for all the 100 parcellations obtained for K from 2 to 20. This figure indicates that the stability is largely constant at a value of approximately 0.6 across all parcellations created with their method.

Figure 1:

(A) Parcellations obtained with K-means on two datasets created using stratified random sampling with replacement (no volume smoothing), (B) adjusted mutual information (AMI) across all pairs of 100 parcellations obtained for every K, (C) the effect of volume smoothing on the BP_ND, (D) silhouette coefficient (SC) curve for the clustering obtained from data volume smoothed at 0 mm, 2 mm and 4 mm FWHM. Data in A and C are displayed on a lateral view of the fsaverage surface (left hemisphere, inflated). In B and D, solid lines are mean values and shaded areas are the corresponding 95% confidence interval.

We investigated the impact of PVE by artificially increasing these effects using volume smoothing of the dynamic PET data. Population average BP_ND maps for 5-HT_2A with no smoothing and 2 and 4 mm FWHM volume smoothing are outlined in Figure 1C. These maps highlight patterns which are accentuated when increasing PVE. The bootstrapped SC curves for the clustering obtained by applying K-means to the PET data with different levels of volume smoothing are shown in Figure 1D. With no smoothing, the curve is monotonically decreasing for K ≤ 3, whereas for data smoothed in the volume with 2 and 4mm FWHM the curves followed the same pattern, but there are peaks at K equals 5 and 10, increasing with larger smoothing kernels.

3.2. Our clustering approach

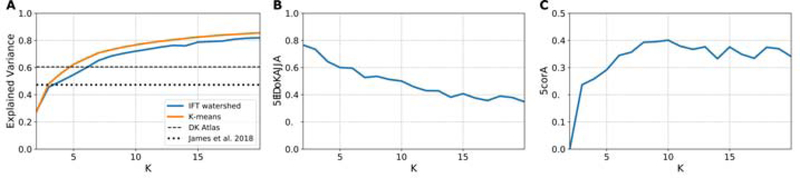
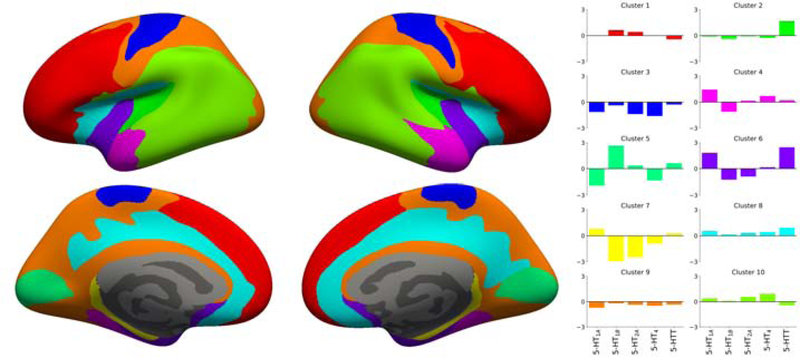
Figure 2 presents the EV, SC and scores associated with the parcellations obtained with K clusters. EV and SC were monotonically increasing or decreasing, respectively. Figure 2A indicates that, starting with K = 6, our parcellations perform better than both the DK atlas and the parcellation of James and colleague in explaining the mean features maps. However, it the EV of the parcellations created by using the approach of James et al. 2018 on our data was slightly, but consistently higher that the values obtained with our method. Overall, A maximum score for our method is observed at K = 10, making this value an optimal choice for the number of clusters. This value is also supported by the BIC curve presented in Supplementary Figure 2. Figure 3 presents the parcellation obtained for K = 10 and the associated regional 5-HT profile obtained from the mean normalized BP_ND maps used as input for the clustering. All subsequent post hoc analysis were performed with this parcellation.

Figure 2:

(A) Explained variance (EV), (B) Silhouette coefficient (SC), and (C) score combining normalized EV and SC for parcellations created with our clustering approach (IFT-watershed). As comparison, we have also included in (A) the EV for the parcellations created when using the approach suggested by James et al. 2018 (K-means) on our data, the parcellation reported by James et al. 2018, and the DK atlas.

Figure 3:

Parcellation obtained with K = 10 and the associated regional 5-HT profile for each region. The parcellation is presented on the inflated fsaverage surface medial (lower) and lateral (upper) for both hemisphere (left and right).

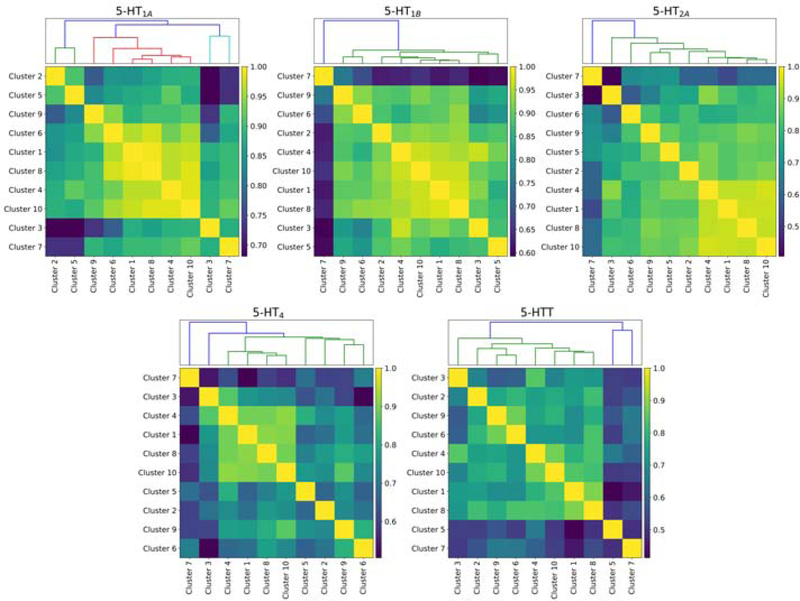
Regarding the stability of our clustering, the mean pairwise AMI is 0.8. In Figure 4 we present the BPND correlation matrices for the parcellation with K = 10. These correlations matrices highlight the groups of regions for which BP_ND values are similarly correlated across individuals.

Figure 4:

BP_ND correlation matrices for each 5-HT target. Matrices were reorganized using hierarchical clustering and the associated dendograms presented above their corresponding matrix.

3.3. Application to mRNA data

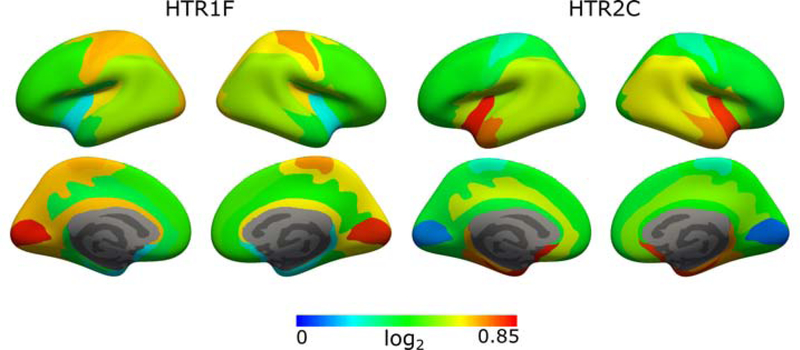
The bootstrapped EV for all 5-HT genes obtained with the parcelation with K = 10 are presented in Figure 5. The EV for all genes was less than 0.3, with the exception of the genes HTR1A, HTR1F, and HTR2C. Bootstrapped regional mRNA values obtained using our parcellation for the genes HTR1F and HTR2C and mapped to their corresponding clusters are presented in Figure 6.

Figure 5:

Bootstrapped explained variance (EV) for the parcellation with K = 10 across all 5-HT genes. Error bars correspond to the 95% confidence intervals.

Figure 6:

Bootstrapped regional mRNA levels for the genes HTR1F and HTR2C obtained from the parcellation with K = 10. Values are presented on the inflated fsaverage surface medial (lower) and lateral (upper) for both hemisphere (left and right).

4. Discussion

Techniques such as autoradiography do not allow for a full description of the spatial correspondence between targets of the 5-HT system, but serve well as a calibration between the PET-signal and the target density. The availability of PET radioligands for some of the 5-HT targets enables the spatial characterization of the density of these targets in high spatial details. By using a clustering approach to identify regions with homogeneous densities for each of the available targets, we have, as well as a previous study [10], attempted to identify the overall spatial organization characterizing the 5-HT system.

Overall, our parcellations can explain the underlying molecular imaging data better than previous parcellations. This is not entirely surprising as those parcellations were derived from different underlying data. Figure 2A indicates that with K = 10, our parcellation can explain between 10 to 20% more variation in the data compared to the DK atlas and the parcellation from James and colleagues, suggesting that it reflects the underlying spatial organization of the 5-HT system more accurately. However, it also indicates that the parcellation obtained with K-mean can explain approximately 4% more variation in the data. Nonetheless, our parcellation exhibits a higher stability, as captured with a higher AMI (0.8 vs. 0.6), compared to the parcellation obtained with K-means, and represents a better trade-off between model fit and stability.

The correlation matrices presented in Figure 4 reveal that the density of the receptors 5-HT_1A, 5-HT_1B, and 5-HT_2A is highly correlated across most brain regions, although less for 5-HT₄ and 5-HTT, suggesting an almost brain wide involvement of 5-HT for all 5-HT targets studied here. Cluster 7, corresponding to parahippocampal gyrus, appears to have a weaker association to all other brain regions for all 5-HT targets and is likely capturing non-biological signal such as PVE.

The 5-HT profiles outlined in Figure 3 provide information regarding the specific involvement of the 5-HT targets across cortex. These association can potentially be useful for guiding a priori hypotheses of pharmacological interventions. It is interesting to note that all 5-HT targets appears to have approximately average levels within the clusters 1, 8, 9, and 10 (i.e. the mean normalized BPND being close to 0 for all targets) suggesting that 5-HT may possibly have a more general role in these regions, rather than primarily targeting a specific subset of receptors. This is again supported by the widespread correlation between most regions exhibited in Figure 4.

4.1. Previous clustering methodology

In the first part, we evaluated the clustering approach proposed by James et al. [10] on our data. PVE is a known and important challenge intrinsic to the processing of PET data. Initial work on the surface-based processing of PET data has outlined stripe-like patterns following the cortical sulci due to PVE [11], and these patterns were present in the clustering obtained by James and colleagues. Here we show that when we artificially increase PVE by spatial smoothing, these patterns are accentuated, further supporting that PVE induces artifacts in a parcellation (Figure 1C). Even with our high-resolution PET data, PVE may still be an issue, however, we used a larger surface smoothing kernel (10mm instead of 8mm) to mitigate these effects. Although our high-resolution PET data still contains smaller PVE effects, we opted not to use PVC to avoid introducing a systematic bias due to violation of the PVC assumptions, e.g. constant point spread function throughout the field of view of the scanner and homogeneous tracer distribution within all regions of interest [27, 28]. This is consistent with the 5-HT atlas previously published based on the same data [3].

One of the main challenges in clustering and subsequent selection of the optimal number of clusters is that of stability. James and colleagues have used the K-means algorithm directly to cluster their data. As exemplified in Figure 1A and B if the input consists of slightly different data this will results in different clustering, hence that specific solution cannot be considered stable. This is also reflected by an AMI that is 25% lower compared to our data.

It is important to note that choosing the optimal number of clusters remains a heuristical choice, whatever the metric being used, and that multiple factors may have to be considered when selecting a parcellation to be used with an external dataset, e.g. image resolution. On this particular issue, James and colleagues have identified an optimal number of clusters K = 5. Our results with volume-smoothed data indicate that PVE creates a bias which increases the SC values, and especially for clustering with K = 5 and 10 (Figure 1A and B), suggesting that K = 5 may be an optimum only in the presence of PVE.

4.2. Application to mRNA data

We have investigated how well our parcellation could explain the mRNA data of all 5-HT genes. It is important to keep in mind that the spatial resolution of the mRNA data is an order of magnitude lower than that of PET data as only a few hundred samples are collected throughout the whole of neocortex per subject. Also, samples were collected from only 6 subjects, and from both hemispheres for only two of those. Although the spatial distribution of all 5-HT targets to some extent has been previously described [1], others yet remain to be studied in vivo due to the lack of specific radioligands which means that their precise spatial distribution within the human brain remains unknown. The 5-HT_1AR/HTR1A has consistently been shown to have a strong spatial correlation between the density of the receptor and the underlying mRNA levels [4, 3]. Our parcellation achieved EV comparable or higher to that of HTR1A only for the HTR1F and HTR2C genes. Interestingly, previous results also suggest a good spatial correspondence between receptor density and mRNA levels in the neocortex of rodents and monkeys for 5-HT_1FR/HTR1F and 5-HT_2CR/HTR2C [29, 30, 31]. As such, the regional mRNA levels presented in Figure 6 for the genes HTR1F and HTR2C form a putative representation of the spatial density for the corresponding receptors. Finally, we note that our parcellation could not explain the spatial distribution of MAO-A levels within neocortex, which further questions the validity of using MAO-A to describe the 5-HT system.

4.3. Limitations

Although we evaluated the association between our parcellations and genetic information, we were not able to establish a clear biological validation of our results. Our new 5-HT parcellation introduces a set of regions which can explain the 5-HT molecular imaging data better compared to the DK atlas and the parcellation from James and colleagues. Furthermore, it contains substantially less regions than the DK atlas, which results in a less stringent correction for multiple comparisons when using this parcellation in a subsequent statistical analysis. This suggest that our new parcellation may be better suited to detect biological changes related to 5-HT modulation. However, we were not able to obtain a dataset where this could be examplified.

The small sample size (n = 8) for the 5-HT1A receptor may potentially bias the clustering if some of the subjects deviate largely from the population mean. However, the variation of the mean normalized BPND estimates for this receptor (see Supplementary Figure 1) is comparable to that of other receptors (e.g. 5-HT_2A), hence, we have no evidence for this in our data.

5. Conclusion

We provide a new parcellation describing the spatial organization of the 5-HT system within neocortex. This parcellation provides a more accurate description of 5-HT molecular imaging data compared to previous atlases. We have assessed how well this parcellation can capture the spatial organization of the genetic information for all 5-HT genes. This work furthers our understanding of the structure of the 5-HT system and the new parcellation forms a tool which may potentially be more sensitive to regional changes modulated by 5-HT compare to other atlases. The parcellation is available at https://xtra.nru.dk/FS5ht-atlas/.