Abstract
Holdase chaperones are known to be central to suppressing aggregation, but how they affect substrate conformations remains poorly understood. Here, we use optical tweezers to study how the holdase Hsp33 alters folding transitions within single maltose binding proteins and aggregation transitions between maltose binding protein substrates. Surprisingly, we find that Hsp33 not only suppresses aggregation but also guides the folding process. Two modes of action underlie these effects. First, Hsp33 binds unfolded chains, which suppresses aggregation between substrates and folding transitions within substrates. Second, Hsp33 binding promotes substrate states in which most of the chain is folded and modifies their structure, possibly by intercalating its intrinsically disordered regions. A statistical ensemble model shows how Hsp33 function results from the competition between these two contrasting effects. Our findings reveal an unexpectedly comprehensive functional repertoire for Hsp33 that may be more prevalent among holdases and dispels the notion of a strict chaperone hierarchy.
Significance
We show that the holdase chaperone Hsp33 promotes and protects near-native folds. This finding shows that Hsp33 does not merely bind unfolded substrates and suggests they can act early in stress episodes by helping to preserve proteins close to their native state. It also raises new questions about the structural basis, which likely involve unstructured Hsp33 regions. Second, we quantitatively predict aggregation suppression at the level of molecular events. This bottom-up approach shows that accounting for the microstates is crucial and can be used for quantitative predictions. More generally, it opens up new avenues to develop a mathematical and predictive understanding of aggregation suppression, which is relevant to biotechnology applications, therapeutic screening, and intervention.
Introduction
Molecular chaperones play key roles in controlling the state of proteins within cells (1). Two chaperone classes can be distinguished: foldases that guide the conformational search for the native state during de novo folding and holdases that suppress aggregation before folding, specifically during episodes of protein-denaturing stress. ATP-dependent chaperones like members of the Hsp70 and GroEL families are primarily considered as foldases. They can assist in the folding of substrate proteins using an ATP-controlled binding and release cycle (2, 3, 4). ATP-independent chaperones like small heat shock proteins (5) and Hsp33 (6) are considered holdases. Hsp33 is activated upon exposure to oxidative stress. In the presence of reactive oxygen species, Hsp33 undergoes extensive conformational rearrangements that generate regions of intrinsic disorder and trigger stable binding to unfolding polypeptide chains of substrate proteins (7).
Although significant progress has been made in understanding the structure, activation, and conformational changes of holdases, molecular-level insight into their effects on the conformation and folding of substrate proteins remains limited (8,9). Yet this aspect is central to understanding their mission as aggregation inhibitors. Dissecting and disentangling the interactions and conformational transition that underlie this process is difficult, especially using existing bulk methods. Previous studies revealed that ATP-independent holdases, including Hsp33, stably bind unfolding polypeptide chains, protect them against aggregation, and, by the same token, block folding (10). Refolding of these substrates into functional proteins with correct tertiary structure is thought to require transfer to ATP-dependent foldase chaperones such as the Hsp70 system (6). More recent experiments have shown that Hsp33 exploits its intrinsically disordered regions to bind α-helical structures in unfolding proteins (11). These findings raise key questions about the range of structural states that holdases such as Hsp33 are capable of interacting with and underscore the importance of obtaining a molecular view of how chaperones suppress protein aggregation (5,12).
Here, we addressed these questions by using mechanical manipulation and force sensing on single-protein constructs with optical tweezers (13,14), in combination with a statistical mechanics model of aggregation suppression. This approach allowed us to characterize and disentangle substrate folding, aggregation, and binding to chaperones at the level of molecular events. We compared how Hsp33 affects the folding transition of a single maltose binding protein (sMBP) construct with a construct composed of four connected MBP monomers (4MBP). Because the only difference between these substrate proteins is their propensity to aggregate, this approach allowed us to directly compare the effects of Hsp33 on protein folding transitions in the absence and presence of aggregation. Surprisingly, we found that Hsp33, although suppressing overall chain-to-chain contacts, promoted folding over aggregation. Analysis of the unfolding forces and length changes in MBP indicated that Hsp33 binds not only unfolded peptide chains but also nearly fully folded substrates. We developed a statistical mechanics model that quantitatively explained the observed effects of Hsp33 on aggregation and folding as a competitive interplay between aggregation, folding, and chaperone interactions.
Materials and Methods
Protein expression and purification
Expression and purification of Hsp33-Y12E has been done as explained before (15). Briefly, Hsp33-Y12E mutant was generated by introducing single-site mutations into the wild-type Hsp33 gene (hslO) using pUJ30 (pET11a-hslO) as a template. The plasmid was transformed into JH13 (BL21, ΔhslO), generating the expression strain CC4 (JH13, pET11a-hslO-Y12E). To overexpress large amounts of soluble Hsp33-Y12E protein, cells were grown to an A600 of 0.6–0.8 at 37°C and then shifted to 18°C. Once the temperature was reached, Hsp33-Y12E expression was induced with 1 mM isopropyl-1-thio-β-D-galactopyranoside for 24 h. Afterward, the standard protocol for the Hsp33 purification was followed (10). The protein was stored in 40 mM potassium phosphate buffer (KH2PO4) (pH 7.5) at −20°C.
Hsp33 chaperone activity and competition assay
Chaperone activity measurements and the competition experiments were conducted as previously described (16). In brief, citrate synthase (CS) from porcine heart (Sigma-Aldrich, St. Louis, MO) was adjusted to a final stock concentration of 24 μM in 40 mM HEPES (pH 7.5). MBP and double mutant MBP (DMMBP) were dialyzed into 40 mM potassium phosphate and 40 mM NaCl (pH 7.5). To initiate the aggregation of CS, the enzyme was diluted 1:160 into 40 mM HEPES (pH 7.5) at 43°C for thermal unfolding in the absence and presence of 150 nM chaperone. To test whether there is a competition between CS and MBP or DMMBP for binding to Hsp33, a 10-fold, 20-fold, or 40-fold molar excess of MBP/DMMBP was added to the assay buffer, followed by the addition of CS. Light scattering was monitored using a Hitachi F4500 fluorometer (Tokyo, Japan) equipped with a thermostatted cell holder and stirrer. Excitation and emission wavelengths were set to 360 nm, and the excitation and emission slit widths were set to 2.5 nm.
Optical tweezers experiments
Protein constructs (4MBP and sMBP) were tethered between two antibody-coated beads, i.e., anti-Dig and anti-c-myc, via a DNA linkage (17). First, double-stranded DNA linkers (2553 bp) with digoxigenin at one end and biotin at the other end were immobilized on the surface of anti-Dig-coated polystyrene beads (18). These strands were then washed with NeutrAvidin (1 mg/mL) to produce sticky ends. The anti-c-myc-coated beads were coupled to C-terminally myc-tagged protein constructs (4MBP and sMBP) that had biotin at their N-terminus. In the optical tweezers setup, the tethers formed in situ via the biotin-NeutrAvidin-biotin linkage. For trapping the beads, we used a custom-built optical tweezers setup as described previously (17,19). Detection of forces on the trapped bead was performed using back focal plane interferometry. Forces were recorded at 50 Hz. Trap stiffness and sensitivity were determined to be 169 ± 24 pN μm−1 and 2.74 ± 0.24 V μm−1, respectively. A piezo-nanopositioning stage (Physik Instrumente, Karlsruhe, Germany) was used to move the sample cell and micropipette at a speed of 50 nm s−1. The beads were trapped in a flow chamber consisting of three parallel streams in laminar flow: one containing anti-Dig-coated beads with the DNA linker, one containing a c-myc-coated beads construct, and a central buffer channel in which the measurements were conducted. The central channel also was used to inject the chaperone-containing buffer. In all experiments with chaperones, the latter was present in the flow chamber before and during all pulling cycles.
Determining protein lengths
To determine protein lengths, we fitted measured force-extension data to a worm-like chain model (20) of a DNA-polypeptide construct, with the polypeptide-contour length (Lp) as the fitting parameter (Eq. 1). D and p indexes indicate DNA and protein, respectively. We used an extensible worm-like chain for DNA that accounts for force-induced deformations of the chain and an inextensible worm-like chain for the polypeptide, which provides the best agreement with the data in the experimental force range.
| (1) |
Within the Eqs. 1, F is the force, x is the extension, L is the contour length, p is the persistence length, K is the stretch modulus, kB is the Boltzmann constant, and T is absolute temperature. Worm-like chain parameters are K = 1200 pN, pD = 45 nm, LD = 920 nm, pp = 1 nm, Lp = 120 nm (sMBP), Lp = 480 nm (4MBP). The force-extension data were fitted assuming the DNA linker and the polypeptide as two springs in series, i.e., F = FWLC,D = FWLC,p; xTotal = xD + xp. We note the protein length is assumed to be equal to the contour length of the unfolded part of the protein chain, given the comparatively small contribution of folded structures to the measured length.
Hsp33-MBP affinity
To calculate the MBP-Hsp33 complex dissociation constant, we modeled the system as two first-order reactions (Eq. 2). We assumed the chaperone (C) only interacts with the unfolded state (U) and make a complex that stabilizes the protein in the unfolded state (U∗). When an unfolded polypeptide chain is not in complex with chaperone, it could either fold (F) or stay unfolded. Assuming the fraction of bound chaperones was equilibrated at zero force, the folding (Kf) and dissociation constants (KD) could be calculated as follows:
| (2) |
We used the experimentally obtained refolding probability (pf) of MBP in the presence of different concentrations of Hsp33 to derive the equilibrium constants. Using experiments without chaperone, Kf is determined to be 2.34, whereas the KD values for 0.5 and 5 μM are derived as 0.43 and 0.31 μM, respectively. These findings are an indication of consistency because these values should be and hence are similar in magnitude and in line with the range of values observed previously (21).
Statistical mechanics model 1
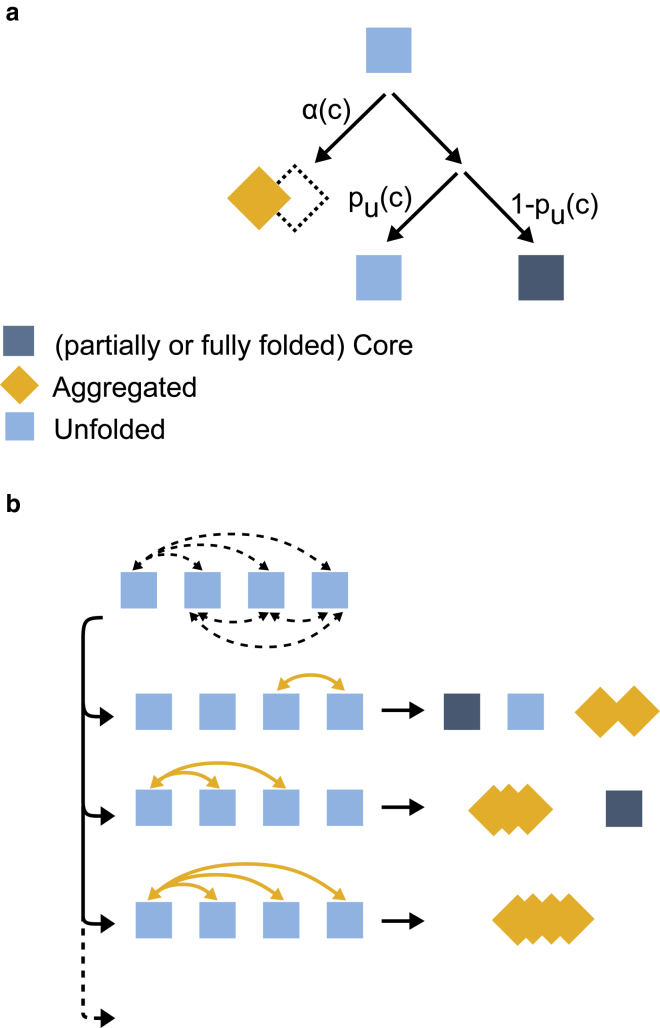
Here, we describe a statistical mechanical model for the behavior of 4MBP in the presence of chaperone. In this model, a fully unfolded 4MBP is a linear chain of four tandem MBP monomers, where each monomer can adopt three different states; aggregated, folded, and unfolded (Fig. 1 a). Aggregation is defined as an interaction between two unfolded monomers (Fig. 1 b) with probability α. This means individual monomers can independently transition to the folded or unfolded states, whereas they need at least one aggregating partner, i.e., another unfolded monomer, to aggregate (Fig. 1 a). Adjacent and nonadjacent monomers are considered to have the same probability to form aggregates. Nonaggregated monomers can adopt the unfolded or folded state with the probability of pu and (1 − pu).
Figure 1.
Schematic representation of aggregation model 1. (a) Model states and transitions. Within fully unfolded and relaxed 4MBP molecules, each of the four MBP monomers can adopt an aggregated, folded, or unfolded state. Aggregation between two unfolded monomers occurs with probability α. Nonaggregated monomers can remain unfolded or fold to the core state with probabilities pu and (1 − pu), respectively. The probabilities depend on the chaperone concentration c. (b) Examples of possible microstates for four MBP monomers resulting from transitions indicated in (a) are shown. Dashed arrows: possible aggregation interactions. Solid arrows: realized aggregation interactions. To see this figure in color, go online.
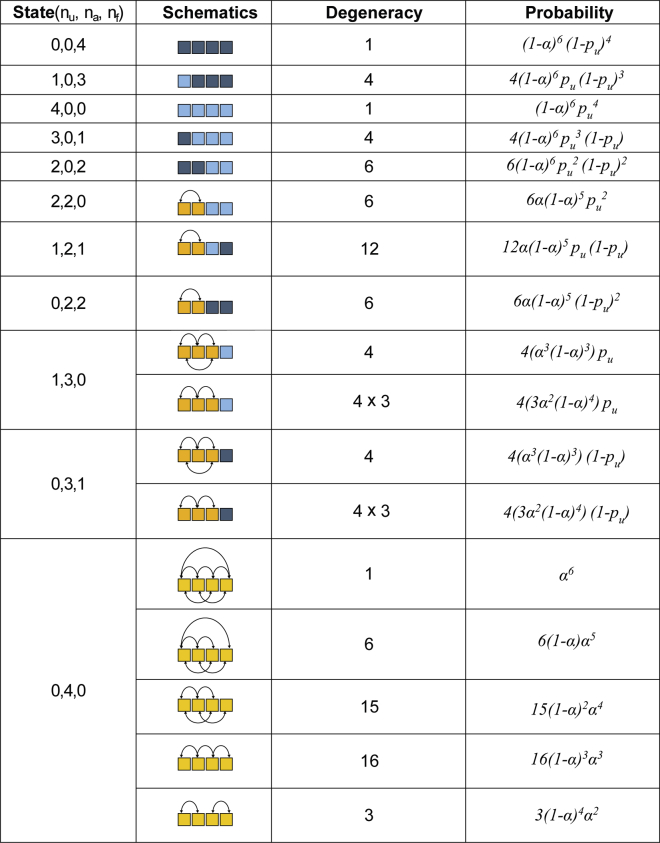
Hence, we determine the probability of forming the 11 possible and distinct “microstates” (Fig. 2). These states are labeled as (nu; na; nf), where nu is the number of unfolded monomers, na is the number of aggregated monomers, and nf is the number of folded monomers such that nu + na + nf = 4. The following equations (Eq. 3) show the probabilities for the different states.
| (3) |
Figure 2.
Different possible microstates in the statistical mechanics models (1 and 2). Light blue represents a monomer that has an unfolded fate (probability of pu), yellow denotes an aggregated fate, and dark blue denotes a folded fate. Solid black lines connecting two aggregated monomers denote pairwise interactions (probability of α). To see this figure in color, go online.
Equations 4, 5, and 6 are used to determine the probability of having i aggregated (Pai), unfolded (Pui), and folded (Pfi) monomers (i = 0, 2, 3, or 4), respectively.
| (4) |
| (5) |
| (6) |
Now, we have two parameters, α and pu, that were determined by fitting the experimentally measured Pui and Pai values (Table 1) and further, were used to calculate the Pfi values (Fig. 5 c). Note that α and pu can be written in terms of an effective probability for each unit to aggregate (paeff), unfold (pueff), and fold (pfeff) (Table 1):
| (7) |
Table 1.
Values of Parameters α and pu for Different Chaperone Concentrations Determined by Fitting 4MBP Experimental data, Using Model 1
| Hsp33 (μM) | α | pu | pueff | pfeff |
|---|---|---|---|---|
| 0 | 0.28 | 0.7 | 0.5 | 0.22 |
| 0.5 | 0.14 | 0.48 | 0.41 | 0.45 |
| 5 | 0.0 | 0.8 | 0.8 | 0.2 |
See Eq. 3.
Figure 5.
Hsp33 affects tertiary structure. (a) Length determination of partially folded structures is shown. After unfolding transition below 10 pN, stretching curves in the presence of 0.5 μM Hsp33 indicate an MBP structure smaller than the core state (C), which remains stable until it unfolds in a single step. Dashed line is a fitted theoretical WLC curve used to determine the length of the chain segment that forms the folded structure (see b). Different shades of blue represent different MBP molecules. (b) Size distribution of the observed folded structures, as determined by fitting the WLC curves (see a and Materials and Methods), is shown in the absence of Hsp33 (n = 42) or in the presence of 0.5 μM Hsp33 (N = 31). The predicted native core size of MBP is 92 nm. (c) Unfolding forces for the first pulls in the absence (N = 55) or presence of 0.5 μM Hsp33 (N = 40) are shown, as well as for the second and subsequent pulls with 0.5 μM Hsp33 (thus refolding in presence of Hsp33) for typical (N = 48) and small cores (N = 26, see b). Error bars are ±1 standard error. N indicates the number of pulling cycles. The p-values are computed from t-test. To see this figure in color, go online.
Statistical mechanics model 2
In the previous section, we have constructed a three-state model that accounts for aggregation, folding and unfolding (Eq. 3) and then fitted the 4MBP data with and without chaperones to obtain the best fit parameters α and pu. Here, we aim to extract these parameters from the experimental data of sMBP refolding in the absence and presence of chaperone and of 4MBP refolding in the absence of chaperone using additional assumptions.
With Hsp33 present, we have a heterogeneous ensemble of 4MBP chains with different numbers of bound Hsp33. Let pb(c) be the probability of Hsp33 binding to a monomer, which depends on the concentration (c) of chaperone (Eqs. 2 and 8). We assume the monomers bound by Hsp33 remain unfolded and do not aggregate, and hence, aggregation is an interaction between two unbound unfolded monomers (Eq. 9). The nonaggregated unbound monomers have a similar probability as sMBP to fold (Eq. 10) or remain unfolded (Fig. S1 a). Thus, the unfolded monomers are either bound to the chaperone or unbound (Eq. 11). Correspondingly, we write the effective probability of aggregation (paeff), unfolding (pueff), and folding (pfeff) in the presence of chaperone (Eqs. 9, 10, and 11). Note that these effective probabilities are not conditional like pu and pf. The superscript s indicates sMBP, and prime indicates a renormalization.
| (8) |
| (9) |
| (10) |
| (11) |
Using Eq. 9, α can be obtained using 4MBP data in the absence of chaperone. In the presence of chaperone, we have a renormalized probability of aggregation that is equal to α(1 − pb(c)). Now, we can further rewrite the equations above in terms of this renormalized new probability α′(c) and the conditional probability pu′(c) (Eqs. 12, 13, and 14). The advantage of doing this is we can then use Eq. 3 for prediction, having only α′(c) and conditional pu′(c) as free parameters.
| (12) |
| (13) |
| (14) |
Note that the form of these equations also ensures proper normalization. Combining these equations above and Eq. 8, we get our final set of equations (Eqs. 15 and 16) that will be used to predict distributions (Fig. S1, b–d). Table 2 shows the α′(c) and pu′(c) values for different chaperone concentrations.
| (15) |
| (16) |
Table 2.
Values of Renormalized Parameters α′(c) and pu′(c) and Effective Probabilities for Different Chaperone Concentrations Extracted, Respectively, from 4MBP Experimental Data Without Chaperone and sMBP Refolding Experimental Data with and Without Chaperone
| Hsp33 (μM) | α | α′(c) | pu′(c) | (pueff)′ | (pfeff)′ |
|---|---|---|---|---|---|
| 0 | 0.28 | 0.28 | 0.3 | 0.22 | 0.5 |
| 0.5 | 0.28 | 0.2 | 0.55 | 0.44 | 0.36 |
| 5 | 0.28 | 0.05 | 0.89 | 0.84 | 0.11 |
Energetics from model parameters
Using the partition function notion, one can write
| (17) |
| (18) |
| (19) |
| (20) |
where Ea, Eu, and Ef are energies of a monomer to be in the aggregated, unfolded, and folded states, respectively. From this, we redefine two quantities:
| (21) |
| (22) |
Here, ln x and ln y give the energy difference of the aggregated and unfolded states with respect to the folded state (as a reference state). From α and pu, we can solve for x, using
| (23) |
| (24) |
So, we get
| (25) |
| (26) |
After taking the natural log, we thus obtain energy differences.
Results and Discussion
Hsp33 stabilizes unfolded states
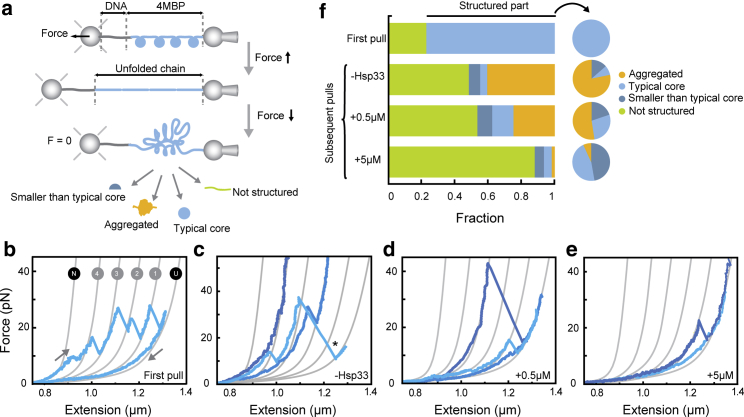
To study aggregation behavior at the molecular level, we used DNA handles to tether individual protein constructs composed of 4MBP between trapped beads (Fig. 3 a) and analyzed the effects of Hsp33 in folding and unfolding of this construct. Stretching the 4MBP construct in the absence of Hsp33 produced first a gradual extension increase at ∼10 pN that corresponds to the detachment of a number of external α-helices from all the core MBP structures, followed by four distinct length increases Lu of 92 nm at a force Fu of ∼27 pN, corresponding to the unfolding of the four MBP cores (Fig. 3, b and f; (17,22)). After relaxing the applied force to 0 pN and waiting for 5 s, subsequent stretching sometimes revealed distinct length increases corresponding to one core, indicating that one of the four MBP cores properly refolded during the relaxation. In the majority of cases, however, we observed distinct length changes or unfolding forces that are larger than for one MBP core and sometimes showing no unfolding up to 45 pN (Fig. 3, c and f) or up to the maximum of 65 pN when the DNA tethers melt. These unfolding characteristics indicate that upon stretching, we now disrupt non-native and aggregated structures involving multiple MBP monomers. From here on, we refer to constructs with this type of compact folding behavior as aggregated structures (17,22).
Figure 3.
Hsp33 suppresses aggregation and promotes native-like folds. (a) A schematic diagram of the experimental setup is shown. A construct of 4MBP is tethered between two beads using a DNA handle. One bead is connected to a position-controlled micropipette while the other bead is held by an optical trap that allows force detection. The DNA-protein tether is stretched by displacement of the pipette bead, resulting in protein unfolding. By moving the beads back together, the applied force decreases, and the polypeptide chain relaxes. Upon keeping the construct at zero force for 5 s, the chain can refold, aggregate, or remain unfolded. (b) First stretching and relaxation curve in the absence of Hsp33 is shown. Gray lines are a theoretical worm-like chain (WLC) model of the DNA-protein construct in different states. After C-terminal unfolding (N→4), four core unfolding events (4→3→2→1→U) are observed. (c) Second or subsequent stretching curves after relaxation to 0 pN for 5 s are shown for different MBP molecules in different shades of blue (n = 39). Data show compact structures that fail to unfold, which suggests tight aggregation between repeats (dark blue line). Some structures are disrupted in one large step by stretching and are referred to as weak aggregates (star). (d) Second or subsequent stretching curves in the presence of 0.5 μM Hsp33 (n = 43) are shown. (e) Second or subsequent stretching curves in the presence of 5 μM Hsp33 (n = 36) are shown. (f) Statistics of observed states is shown. Fractions in bar charts denote the fraction of the chain involved in the four indicated states. Pie charts indicate relative fractions of the three different structures that are distinguished. N indicates the number of pulling cycles. To see this figure in color, go online.
Next, we investigated how Hsp33 affected this aggregation process. The chaperone function of Hsp33 is tightly controlled by the folding status of a linker region. Only when the four conserved cysteines within Hsp33 are oxidized does the linker region become unfolded and Hsp33 active. Oxidative conditions are not compatible with the single-molecule tethering, and hence, we used the constitutively active Hsp33 mutant Y12E (15). This mutant protein has a constitutively unfolded linker, and its chaperone activity in the reduced state is indistinguishable from oxidized wild-type Hsp33. We performed 4MBP stretching and relaxation cycles in the presence of increasing amounts of Hsp33 mutant Y12E (0.5 and 5 μM, present during all pulling cycles; Figs. 3, d and e and S2) and found that on average, the part of the 4MBP chain that was compact and hence structured (partially folded or aggregated) had substantially decreased from 0.51 to 0.11. Conversely, the part of the chain that remained unstructured or unfolded below 10 pN, gradually increased from 0.49 to 0.89 (Fig. 3 f). Note that the latter category not only corresponds to fully unfolded chain segments but includes α-helical structures that do not yield in distinct unfolding events, as well as marginally stable higher-order structures. Overall, these data show that Hsp33 can suppress interactions within the protein chain and hence maintain proteins in the unfolded state.
Hsp33 promotes folding over aggregation
Next, we focused our analysis on these parts of the MBP chains that regained structure and quantified whether they unfolded as a typical native-like folded core structure (80 nm < Lu < 104 nm and 5 < Fu < 35 pN), a folded structure smaller than one core (Lu < 80 nm, Fu < 35 pN), or a non-native aggregated structure that unfolds in large steps or at high force (Lu > 104 nm and/or Fu > 35 pN) (Fig. S2). We found that with increasing amounts of Hsp33, the relative fractions of typical native-like cores and structures smaller than one core increased while the relative aggregated fraction decreased (pie charts in Fig. 3 f). Thus, whereas in absolute terms, a smaller part of the chain formed stable structures with increasing Hsp33 (fraction decreasing from 0.51 to 0.11; bar graphs in Fig. 3 f), within these stable structures, the relative fraction of typical cores increased (from 0.08 to 0.46; pie charts in Fig. 3 f).
The increased relative proportion of typical cores within the structured part of the chain indicated some form of selectivity, with Hsp33 having a different effect on folding than on aggregation. How this selectivity is achieved was not immediately clear. Folding and aggregation transitions are similar in that they both involve contacts within the 4MBP chain. However, differences in timescales might play a role (23) because slower processes provide more time for Hsp33 binding. The observed dominant aggregation in the absence of Hsp33 suggested that folding occurs on slower timescales than aggregation. In contrast, however, Hsp33 interfered more efficiently with aggregation than with folding because Hsp33 suppresses the former strongly (Fig. 3 f). Apart from these questions regarding selectivity, it was also unclear whether Hsp33 interacted with MBP conformers beyond unfolded chains and how Hsp33 affected chain conformations in the absence of aggregation. To disentangle these questions, we studied the interaction between a single MBP repeat and Hsp33.
Hsp33 suppresses folding in single isolated substrates
To investigate the effects of Hsp33 on a single MBP monomer (sMBP), we tethered one MBP molecule between two beads (Fig. 4 a). In the absence of Hsp33, stretching of sMBP yielded unfolding that was consistent with the 4MBP data: we observed a small transition around 10 pN, representing the unfolding of the external α-helices (N → C, Fig. 4 b), followed by a larger step of 92 nm at ∼25 pN, which indicates the unfolding of the core structure (C → U). After relaxation to low force for 5 s, subsequent stretching showed that sMBP had either remained unfolded or refolded to a typical core (Fig. 4, b and e), consistent with previous studies (17,22). As observed for 4MBP, we did not detect any changes in the first stretching curve when Hsp33 was present (Fig. S3), consistent with a lack of interactions between Hsp33 and native MBP. However, presence of Hsp33 suppressed MBP refolding during the 5 s waiting period at 0 pN because subsequent pulls more often lacked unfolding features, consistent with an unfolded polypeptide chain that is not structured (Fig. 4, c and d). This suppression of structure formation depended strictly on the Hsp33 concentration. The fraction of pulls showing no structure increased from 0.3 in the absence of Hsp33, to 0.5 in the presence of 0.5 μM Hsp33 and ∼0.9 in the presence of 5 μM Hsp33 (Fig. 4 e). These results showed that presence of Hsp33 suppressed native refolding in MBP monomers, consistent with Hsp33 binding to 4MBP polypeptide chains (Fig. 3 f).
Figure 4.
Hsp33 suppresses folding. (a) A schematic diagram of a single MBP (sMBP) construct tethered between two beads is shown. (b) Stretching curves in the absence of Hsp33, showing native-like refolding of sMBP, are given for different MBP molecules in different shades of blue. Gray lines are theoretical WLC curves (n = 70). Unfolding occurs via two transitions: C-terminal unfolding (N→C) and core unfolding (C→U). (c) Stretching curves after relaxation and waiting for 5 s at 0 pN in the presence of 0.5 μM Hsp33 (n = 60) are shown. Curves now more often follow the behavior of an unfolded chain that is not structured and hence lacks unfolding features. (d) Stretching curves after relaxation and waiting for 5 s at 0 pN in the presence of 5 μM Hsp33 (n = 69) are shown. Most curves indicate unfolded chains and hence a stabilization of these unfolded states. (e) Observed fractions of pulls showing a nonstructured chain, as determined from stretching-relaxation experiments (b–d), are given. N indicates the number of pulling cycles. To see this figure in color, go online.
Hsp33 affects folded structures
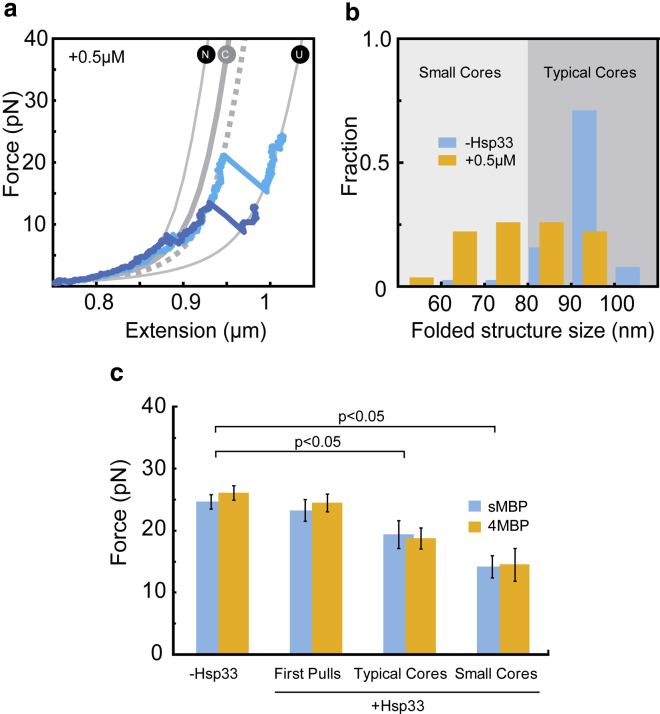
The proportion of sMBP molecules that refolded in the presence of 0.5 μM Hsp33 seemed to be native-like (Fig. 4 c). During stretching, they appeared as compact as folded sMBP below 5 pN and typically unfolded via one small and one large transition. However, upon closer inspection, we observed several distinct differences. In particular, we found that after the first apparent transition to the core state (N → C), the curve often did not precisely follow the core state behavior but was slightly shifted to the right by up to 30 nm (Fig. 4 c, dark blue line; Fig. 5 a, dashed line). To quantify these changes, we fitted the data to a worm-like chain model (Materials and Methods).
Indeed, we found that the size distribution of the core-like structures was substantially broader in the presence of Hsp33 than in its absence (Fig. 5 b). We distinguished “typical” cores with sizes similar to native MBP (80 ≤ ΔL ≤ 104 nm) and “small” cores (50 ≤ ΔL < 80 nm). Our data suggested that presence of Hsp33 prevents the core states from completely refolding to the stable core structure, presumably by interfering with native intramolecular contacts. One may speculate that the unstructured segments of Hsp33 compete for binding and hence limit completion of the MBP core fold, thereby lowering its stability. Note that without Hsp33, partially folded core structures can be observed, but only infrequently and transiently (less than 1 s) (22). Here, such states may be stabilized by bound Hsp33. We note that Hsp33 might, at least in principle, first cause the MBP chain to adopt a smaller yet more stable fold and then dissociate. The presence of core-like structures was suggested by the more gradual unfolding transition that is observed first, typically below 10 pN, because the first gradual transition is characteristic of the detachment of the C-terminal external α-helices in MBP from the MBP core structure (Figs. 4 c and 5 a). These observations are consistent with Hsp33 binding to and stabilizing a core-like structure of MBP.
To further probe this issue, we performed bulk studies and optical tweezers experiments with longer waiting times at 0 pN. In the bulk experiments, we assayed Hsp33 binding to early thermal unfolding intermediates (11), here for MBP and a less stable variant of MBP, the double mutant V8G/Y283D (DMMBP) (24). The results showed that both were able to effectively bind Hsp33 (Fig. S4), consistent with the single-molecule results. In additional single-molecule experiments, we increased the waiting time at 0 pN (from 5 to 30 s) within the usual relax-stretch cycles. The data showed a significant increase in the fraction of typical cores as compared to small cores (Fig. S5 a, p < 0.05). Furthermore, the mean size and unfolding force of the small-core category also increased (p < 0.05) with increased waiting time, and consistently, the size and unfolding force of typical cores did not significantly increase (Fig. S5, b and c). These results are consistent with the idea that Hsp33 binds core-like folds that mature over time into more typical core structures.
Overall, these data suggested that Hsp33 promotes modified core structures and hence also limits entry into the fully folded native state during the waiting time at 0 pN. We also observed that in the presence of Hsp33, typical and small-core structures unfolded at a lower average force (p < 0.05, Fig. 5 c). The change in unfolding force was larger for small cores (−10 pN) than for typical cores (−5 pN). Note that structures of reduced size contain fewer residue-residue contacts and hence can display lower unfolding forces. In addition, structural interference by Hsp33 can reduce the resistance of the core states against forced unfolding. Because modified cores should be observable in the 4MBP data as well, we revisited our previous data. Indeed, in the presence of Hsp33, refolding generated smaller cores that displayed an unfolding force similar to those observed for sMBP (p < 0.05, Fig. 5 c). In contrast, the first stretching curve on sMBP and 4MBP molecules was similar with or without Hsp33 (Fig. 5 c), supporting the notion that Hsp33 does not interact with natively folded proteins.
Statistical mechanics of aggregation suppression
To quantitatively understand Hsp33 action and the competition between the underlying folding and aggregation transitions, we developed a statistical mechanics model (Materials and Methods, model 1). Similar approaches have been used to describe helix-to-coil transitions (25, 26, 27, 28, 29), folding-unfolding thermodynamics (30, 31, 32, 33), and aggregation without chaperones (34). In our model, unfolded and relaxed MBP monomers can adopt three states: aggregated, core, and unfolded. Two unfolded monomers can aggregate with probability α; otherwise, monomers either remain unfolded with probability pu or fold with probability (1 − pu) (Fig. 1 a). Consistent with existing ideas of aggregation suppression by holdase chaperones, Hsp33 affects this process and makes the probabilities dependent on the Hsp33 concentration c (35). Distinct from previous models, in this statistical mechanics approach, the transitions result in a number of possible “microstates” that detail the state of each monomer (Fig. 1 b) and can be listed exhaustively (Fig. 3). The probabilities of these combinatorial microstates can be expressed in terms of the probabilities α and pu (Eq. 3). This model thus accounts for the fractional occupancy of client proteins (36) and the modulation of folding and aggregation probabilities by chaperones but ignores various more detailed aspects of chaperone and substrate conformational dynamics. Indeed, we aimed to assess whether these elementary interactions are sufficient to capture the statistics of aggregation suppression by Hsp33 in our assay. Specifically, the experimental 4MBP data indicate the probabilities of observing 0, 2, 3, or 4 aggregated MBP monomers Pai(c) and their dependence on the Hsp33 concentration c (Fig. 6 a). Similarly, the distributions of observed unfolded Pui(c) and folded states Pfi(c) can be determined (Fig. 6, b and c). The model provides expressions for these distributions, allowing a coherent fitting of the complete data set (Eqs. 4, 5, and 6). We find that this model quantitatively reproduces the experimentally observed trends (Fig. 6), as discussed below.
Figure 6.
Aggregation and folding statistics and model. Fitted and measured probabilities of an unfolded and relaxed 4MBP molecule to display i aggregated (a), unfolded (b), and folded (c) monomers are shown, with i indicated along the x axis, and as determined in relaxation-stretching experiments (see Fig. 3). See Materials and Methods for model 1. Error bars show 95% confidence intervals estimated by bootstrapping. To see this figure in color, go online.
Without chaperones, dominant aggregation involving multiple monomers yields a Pa distribution that is shifted to the right, whereas at high chaperone concentrations (5 μM), Pa shifts all the way to the left, indicating limited aggregation. The latter is caused by the promotion of unfolded rather than folded states because Pu, rather than Pf, is shifted to the right. In this regime, the key Hsp33 function is thus to bind and stabilize unfolded conformations. The intermediate chaperone concentration (0.5 μM) indicates a competitive balance: Pu now peaks at intermediate monomer numbers because it is driven to the right by chaperone binding and to the left by aggregation. Interestingly, the distribution of folded monomers Pf is most right-shifted in these conditions. Folding is thus promoted most effectively when neither aggregation nor the stabilization of unfolded conformations is dominant. Consistently, the aggregation probability α decreases for increasing chaperone concentration c, whereas the folding probability of nonaggregated monomers (1 − pu) is highest at intermediate c (Table 1).
Next, we explored whether additional assumptions would allow one to go beyond fitting and predict these distributions. Specifically, one may assume chaperones only bind unfolded chains and hence prevent them from aggregating or refolding (Fig. S1 a). The probability of chaperone binding can then be estimated using the sMBP data with chaperones, aggregation between unbound monomers using the 4MBP data without chaperones, and the folding-unfolding equilibrium using the sMBP data without chaperones (Materials and Methods, model 2). The resulting model, without any fit parameter, was found to qualitatively predict the trends for 4MBP with chaperones (Fig. S1, b–d). However, deviations were also visible. For example, the monomer-refolding rate within 4MBP is overestimated in the absence of chaperone. This could indicate that aggregates hinder folding of nearby monomers without inducing their aggregation, which is an effect that is ignored in our model. The Hsp33 concentration dependence also showed deviations. In particular, the folding rate was underestimated when increasing the chaperone concentration, whereas aggregation is overestimated. This deviation could be caused by the following: this predictive model assumes stabilization of unfolded states only (Eqs. 8 and 15), whereas Hsp33 affects partially folded structures as well (Fig. 5). By binding unfolded and partially folded states, Hsp33 could limit aggregation as well as shielding chains during folding. Finally, Hsp33 could have a higher effective local concentration with 4MBP compared to sMBP, owing to the additional Hsp33 binding sites.
Conclusions
ATP-independent holdase chaperones, including Hsp33, are known to bind unfolding polypeptide chains (5,11). Hsp33-substrate binding protects the latter from aggregation and, by the same token, suppresses their successful refolding until nonstress conditions are restored and Hsp70-mediated refolding can take place (11). In line with this notion, we found that Hsp33 binding to mechanically unfolded MBP maintains the substrate in the unfolded state (on average, ∼90% of both sMBP and 4MBP chains for 5 μM Hsp33). Notably, however, our data also showed that Hsp33 affected folded MBP structures, indicating that Hsp33 can also act late during refolding. Direct binding of chaperones to tertiary structures that refolded (partially) from unfolded states is difficult to detect using bulk methods but has been previously observed for the chaperone Trigger Factor using optical tweezers (22). In contrast to Hsp33, however, for which binding resulted in decreased resistance against forced unfolding, Trigger Factor binding increased their resistance against unfolding. One possible reason for this difference might be found in the structural differences between the two chaperones. Whereas Trigger Factor is thought to stabilize substrate structures by encapsulating them with its arm-like domains (37), the flexibility of Hsp33’s intrinsically disordered domains might allow Hsp33 to bind less accessible substrate residues, possibly competing with native contact formation, and hence to perturb substrate structure and stability. Consistent with this consideration is the positive correlation that we observed between Hsp33-mediated structure size and unfolding force (Fig. 5 c). The similarity between Hsp33-mediated conformations and the native MBP states in terms of size, unfolding forces, and two-transition unfolding pattern suggests that the substrate structure bound by Hsp33 is close to the MBP core state.
Hsp33 was not only found to affect the resulting folded structures but also to increase their fraction and hence promote folding—functions that are typically not attributed to holdases, but rather, to foldases (38). At the same time, the promoted structures were not fully natively folded, which also means they would not be detected by bulk refolding assays that measure function (39). This mode of action presented an apparent contrast with the Hsp33-mediated stabilization of unfolded states. However, the latter also results in a reduction of the number of aggregation partners and hence can promote folding by suppressing a competing pathway. This indirect promotion of folding has been considered for foldases, including Hsp70/DnaK, but contrasts with direct folding acceleration functions in the absence of competing aggregation pathways, as has been proposed for the chaperonin GroEL-ES (38,40). To understand the competing effects for Hsp33 in quantitative terms, we developed a statistical mechanics model. Key features of the statistics of unfolded, folded, and aggregated MBP monomers in 4MBP with Hsp33 were reproduced by a model that defines the ensemble of possible microstates for multiple monomers that can aggregate, fold, or remain unfolded. This model does not account for a number of effects, including diverse folded and aggregated states, or how the proximity of monomers affects their aggregation. When interacting with MBP, Hsp33 may remain loosely bound to the chain as it explores conformation toward the folded state (41) or be detached during the conformational search.
The functional role of holdases has been discussed extensively. Holdases can act early by binding polypeptide chains and suppressing their aggregation, with foldases such as Hsp70 required for disassembly and refolding. The presented data and analysis show that the Hsp33 holdase can act later along the folding pathway, promote folding over aggregation, bind folded tertiary structure, and hence affect the protein conformational search. Small heat shock proteins, such as Hsp21, have been reported to act on early unfolding intermediates (42). The holding of proteins in a near-functional state may benefit cells after episodes of stress. This bottom-up single-molecule approach in probing the statistical mechanics of aggregation suppression is a powerful method that can be applied to other systems, such as studying the effects of small Hsps on the aggregation of amyloid-β and α-synuclein monomers.
Author Contributions
F.M., S.B., U.J., and S.J.T. designed the research. F.M. performed the experiments. G.K., C.M.C., and U.J. contributed protein constructs and chaperone samples. F.M. and S.J.T. analyzed data. F.M., K.G., and S.J.T. developed the model. All authors wrote the manuscript.
Acknowledgments
This work is part of the research program of the Netherlands Organization for Scientific Research. U.J. was funded by the National Institutes of Health grants GM065318 and 1R15GM128162-01 for this research. K.G. acknowledges support from the National Science Foundation (award number 1149992), Research Corporation for Science Advancement (as a Cottrell scholar), and University of Denver (for sabbatical leave).
Editor: James Shorter.
Footnotes
Supporting Material can be found online at https://doi.org/10.1016/j.bpj.2019.10.040.
Supporting Material
References
- 1.Buchberger A., Bukau B., Sommer T. Protein quality control in the cytosol and the endoplasmic reticulum: brothers in arms. Mol. Cell. 2010;40:238–252. doi: 10.1016/j.molcel.2010.10.001. [DOI] [PubMed] [Google Scholar]
- 2.Skowyra D., Georgopoulos C., Zylicz M. The E. coli dnaK gene product, the hsp70 homolog, can reactivate heat-inactivated RNA polymerase in an ATP hydrolysis-dependent manner. Cell. 1990;62:939–944. doi: 10.1016/0092-8674(90)90268-j. [DOI] [PubMed] [Google Scholar]
- 3.Sharma S., Chakraborty K., Hartl F.U. Monitoring protein conformation along the pathway of chaperonin-assisted folding. Cell. 2008;133:142–153. doi: 10.1016/j.cell.2008.01.048. [DOI] [PubMed] [Google Scholar]
- 4.Thirumalai D., Lorimer G.H. Chaperonin-mediated protein folding. Annu. Rev. Biophys. Biomol. Struct. 2001;30:245–269. doi: 10.1146/annurev.biophys.30.1.245. [DOI] [PubMed] [Google Scholar]
- 5.Haslbeck M., Franzmann T., Buchner J. Some like it hot: the structure and function of small heat-shock proteins. Nat. Struct. Mol. Biol. 2005;12:842–846. doi: 10.1038/nsmb993. [DOI] [PubMed] [Google Scholar]
- 6.Hoffmann J.H., Linke K., Jakob U. Identification of a redox-regulated chaperone network. EMBO J. 2004;23:160–168. doi: 10.1038/sj.emboj.7600016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Ilbert M., Horst J., Jakob U. The redox-switch domain of Hsp33 functions as dual stress sensor. Nat. Struct. Mol. Biol. 2007;14:556–563. doi: 10.1038/nsmb1244. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Thoma J., Burmann B.M., Müller D.J. Impact of holdase chaperones Skp and SurA on the folding of β-barrel outer-membrane proteins. Nat. Struct. Mol. Biol. 2015;22:795–802. doi: 10.1038/nsmb.3087. [DOI] [PubMed] [Google Scholar]
- 9.Salmon L., Ahlstrom L.S., Bardwell J.C. Capturing a dynamic chaperone-substrate interaction using NMR-informed molecular modeling. J. Am. Chem. Soc. 2016;138:9826–9839. doi: 10.1021/jacs.6b02382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Jakob U., Muse W., Bardwell J.C. Chaperone activity with a redox switch. Cell. 1999;96:341–352. doi: 10.1016/s0092-8674(00)80547-4. [DOI] [PubMed] [Google Scholar]
- 11.Reichmann D., Xu Y., Jakob U. Order out of disorder: working cycle of an intrinsically unfolded chaperone. Cell. 2012;148:947–957. doi: 10.1016/j.cell.2012.01.045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Treweek T.M., Meehan S., Carver J.A. Small heat-shock proteins: important players in regulating cellular proteostasis. Cell. Mol. Life Sci. 2015;72:429–451. doi: 10.1007/s00018-014-1754-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Cecconi C., Shank E.A., Marqusee S. Direct observation of the three-state folding of a single protein molecule. Science. 2005;309:2057–2060. doi: 10.1126/science.1116702. [DOI] [PubMed] [Google Scholar]
- 14.Junker J.P., Ziegler F., Rief M. Ligand-dependent equilibrium fluctuations of single calmodulin molecules. Science. 2009;323:633–637. doi: 10.1126/science.1166191. [DOI] [PubMed] [Google Scholar]
- 15.Cremers C.M., Reichmann D., Jakob U. Unfolding of metastable linker region is at the core of Hsp33 activation as a redox-regulated chaperone. J. Biol. Chem. 2010;285:11243–11251. doi: 10.1074/jbc.M109.084350. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Groitl B., Horowitz S., Makepeace K.A.T., Petrotchenko E.V., Borchers C.H., Reichmann D., Bardwell J.C.A., Jakob U. Protein unfolding as a switch from self-recognition to high-affinity client binding. Nat. Commun. 2016;7:10357. doi: 10.1038/ncomms10357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Bechtluft P., van Leeuwen R.G., Tans S.J. Direct observation of chaperone-induced changes in a protein folding pathway. Science. 2007;318:1458–1461. doi: 10.1126/science.1144972. [DOI] [PubMed] [Google Scholar]
- 18.Moayed F., Mashaghi A., Tans S.J. A polypeptide-DNA hybrid with selective linking capability applied to single molecule nano-mechanical measurements using optical tweezers. PLoS One. 2013;8:e54440. doi: 10.1371/journal.pone.0054440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Mashaghi A., Vach P.J., Tans S.J. Noise reduction by signal combination in Fourier space applied to drift correction in optical tweezers. Rev. Sci. Instrum. 2011;82:115103. doi: 10.1063/1.3658825. [DOI] [PubMed] [Google Scholar]
- 20.Wang M.D., Yin H., Block S.M. Stretching DNA with optical tweezers. Biophys. J. 1997;72:1335–1346. doi: 10.1016/S0006-3495(97)78780-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Xu Y., Schmitt S., Fitzgerald M.C. Thermodynamic analysis of a molecular chaperone binding to unfolded protein substrates. Biochemistry. 2010;49:1346–1353. doi: 10.1021/bi902010t. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Mashaghi A., Kramer G., Tans S.J. Reshaping of the conformational search of a protein by the chaperone trigger factor. Nature. 2013;500:98–101. doi: 10.1038/nature12293. [DOI] [PubMed] [Google Scholar]
- 23.Speed M.A., Wang D.I., King J. Specific aggregation of partially folded polypeptide chains: the molecular basis of inclusion body composition. Nat. Biotechnol. 1996;14:1283–1287. doi: 10.1038/nbt1096-1283. [DOI] [PubMed] [Google Scholar]
- 24.Chun S.Y., Strobel S., Randall L.L. Folding of maltose-binding protein. Evidence for the identity of the rate-determining step in vivo and in vitro. J. Biol. Chem. 1993;268:20855–20862. [PubMed] [Google Scholar]
- 25.Lifson S., Roig A. On the theory of helix—coil transition in polypeptides. J. Chem. Phys. 1961;34:1963–1974. [Google Scholar]
- 26.Zimm B., Bragg J. Theory of the one-dimensional phase transition in polypeptide chains. J. Chem. Phys. 1958;28:1246–1247. [Google Scholar]
- 27.Dill K.A., Bromberg S. Garland Science; London; New York: 2011. Molecular Driving Forces: Statistical Thermodynamics in Biology, Chemistry, Physics, and Nanoscience, Second Edition; p. 756. [Google Scholar]
- 28.Zimm B.H., Doty P., Iso K. Determination of the parameters for helix formation in poly-gamma-benzyl-l-glutamate. Proc. Natl. Acad. Sci. USA. 1959;45:1601–1607. doi: 10.1073/pnas.45.11.1601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Poland D., Scheraga H.A. Academic Press; New York: 1970. Theory of Helix-Coil Transitions in Biopolymers: Statistical Mechanical Theory of Order-Disorder Transitions in Biological Macromolecules; p. 797. [Google Scholar]
- 30.Muñoz V., Eaton W.A. A simple model for calculating the kinetics of protein folding from three-dimensional structures. Proc. Natl. Acad. Sci. USA. 1999;96:11311–11316. doi: 10.1073/pnas.96.20.11311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Henry E.R., Eaton W.A. Combinatorial modeling of protein folding kinetics: free energy profiles and rates. Chem. Phys. 2004;307:163–185. [Google Scholar]
- 32.Ghosh K., Dill K.A. Theory for protein folding cooperativity: helix bundles. J. Am. Chem. Soc. 2009;131:2306–2312. doi: 10.1021/ja808136x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Aksel T., Barrick D. Analysis of repeat-protein folding using nearest-neighbor statistical mechanical models. Methods Enzymol. 2009;455:95–125. doi: 10.1016/S0076-6879(08)04204-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Schmit J.D., Ghosh K., Dill K. What drives amyloid molecules to assemble into oligomers and fibrils? Biophys. J. 2011;100:450–458. doi: 10.1016/j.bpj.2010.11.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Balchin D., Hayer-Hartl M., Hartl F.U. In vivo aspects of protein folding and quality control. Science. 2016;353:aac4354. doi: 10.1126/science.aac4354. [DOI] [PubMed] [Google Scholar]
- 36.Bakthisaran R., Tangirala R., Rao ChM. Small heat shock proteins: role in cellular functions and pathology. Biochim. Biophys. Acta. 2015;1854:291–319. doi: 10.1016/j.bbapap.2014.12.019. [DOI] [PubMed] [Google Scholar]
- 37.Singhal K., Vreede J., Bolhuis P.G. The trigger factor chaperone encapsulates and stabilizes partial folds of substrate proteins. PLoS Comput. Biol. 2015;11:e1004444. doi: 10.1371/journal.pcbi.1004444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Hartl F.U., Bracher A., Hayer-Hartl M. Molecular chaperones in protein folding and proteostasis. Nature. 2011;475:324–332. doi: 10.1038/nature10317. [DOI] [PubMed] [Google Scholar]
- 39.Mashaghi A., Kramer G., Tans S.J. Chaperone action at the single-molecule level. Chem. Rev. 2014;114:660–676. doi: 10.1021/cr400326k. [DOI] [PubMed] [Google Scholar]
- 40.Mashaghi A., Bezrukavnikov S., Tans S.J. Alternative modes of client binding enable functional plasticity of Hsp70. Nature. 2016;539:448–451. doi: 10.1038/nature20137. [DOI] [PubMed] [Google Scholar]
- 41.Jewett A.I., Shea J.E. Folding on the chaperone: yield enhancement through loose binding. J. Mol. Biol. 2006;363:945–957. doi: 10.1016/j.jmb.2006.08.040. [DOI] [PubMed] [Google Scholar]
- 42.Rutsdottir G., I Rasmussen M., Söderberg C.A.G. Chaperone-client interactions between Hsp21 and client proteins monitored in solution by small angle X-ray scattering and captured by crosslinking mass spectrometry. Proteins. 2018;86:110–123. doi: 10.1002/prot.25413. Published online November 14, 2017. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.