Iterative annealing mechanism explains the functions of the GroEL and RNA chaperones

Abstract

Molecular chaperones are ATP‐consuming machines, which facilitate the folding of proteins and RNA molecules that are kinetically trapped in misfolded states. Unassisted folding occurs by the kinetic partitioning mechanism according to which folding to the native state, with low probability as well as misfolding to one of the many metastable states, with high probability, occur rapidly. GroEL is an all‐purpose stochastic machine that assists misfolded substrate proteins to fold. The RNA chaperones such as CYT‐19, which are ATP‐consuming enzymes, help the folding of ribozymes that get trapped in metastable states for long times. GroEL does not interact with the folded proteins but CYT‐19 disrupts both the folded and misfolded ribozymes. The structures of GroEL and RNA chaperones are strikingly different. Despite these differences, the iterative annealing mechanism (IAM) quantitatively explains all the available experimental data for assisted folding of proteins and ribozymes. Driven by ATP binding and hydrolysis and GroES binding, GroEL undergoes a catalytic cycle during which it samples three allosteric states, T (apo), R (ATP bound), and R ^″ (ADP bound). Analyses of the experimental data show that the efficiency of the GroEL–GroES machinery and mutants is determined by the resetting rate k_{R ″  → T}, which is largest for the wild‐type (WT) GroEL. Generalized IAM accurately predicts the folding kinetics of Tetrahymena ribozyme and its variants. Chaperones maximize the product of the folding rate and the steady‐state native state fold by driving the substrates out of equilibrium. Neither the absolute yield nor the folding rate is optimized.

1. INTRODUCTION

Molecular chaperones have evolved to facilitate the folding of proteins that cannot do so spontaneously under crowded cellular conditions.1, 2, 3 This important task is accomplished without chaperones imparting any additional information beyond what is contained in the amino acid sequence. Furthermore, chaperones assist the folding of proteins whose folded structures bear no relationship to one another. In other words, chaperones are “blind” to the architecture of the folded proteins. Most of the protein chaperones belong to the family of heat shock proteins that are over expressed when the cells are under stress. Among the many classes of chaperones, the bacterial chaperonin, GroEL, has been most extensively investigated, possibly because it was the first one to be discovered.4, 5, 6 Although less appreciated, RNA chaperones considered here, which are indeed enzymes, have also evolved to enable the folding of ribozymes,7, 8 which are readily kinetically trapped. This implies that in vitro only a very small fraction folds to the functionally competent state on a biologically relevant time scale.9 Both GroEL and RNA chaperones (CYT‐19), which we will collectively refer to as molecular chaperones from now on, are not unlike molecular motors, such as kinesin, myosin, and dynein. There are many similarities between motors and chaperones.

1. Both motors and chaperones are enzymes that undergo a catalytic cycle, which involves binding and hydrolysis of ATP. Molecular motors hydrolyze one ATP per step, thus converting chemical energy to mechanical work in order to walk on the linear cytoskeletal filaments (actin or microtubule). Both GroEL and RNA chaperones consume copious amounts of ATP (see below). They couple the hydrolysis of ATP to perform work by partially unfolding the misfolded RNA or proteins. Indeed, helicase activity is attributed to RNA chaperones, such as CYT‐19. Helicases are biological machine that separate double stranded DNA or RNA and translocate on single stranded nucleic acids.

2. During the catalytic cycle, the enzymes (motor head in the case of motors and the subunits in the GroEL particle) undergo spectacular conformational changes, which are transmitted allosterically (action at a distance) throughout the complex (see Reference 10 for a recent review). Indeed, it is impossible to rationalize the functions of motors or chaperones without allosteric signaling, which we illustrate more fully for GroEL in this article.

3. Some of the rates in the catalytic cycles of molecular motors also depend on the presence of actin or microtubule. Similarly, ATPase functions of GroEL are stimulated in the presence of substrate proteins (to be referred to as SPs from now on). For these reasons, a quantitative understanding of the functions of molecular chaperones mandates that they be treated as molecular machines.

We should note like GroEL, CYT‐19 is an enzyme that hydrolyzes ATP during their functions. Both play an active role in their interactions with the SPs and the misfolded ribozymes. CYT‐19 is a RNA helicase that disrupts exposed helices in the ribozymes regardless of whether they are folded or not. The structures of GroEL and the analogue of CYT‐19 are strikingly different. Nevertheless, we show here that a unified theory not only quantitatively explains the available experimental data but also provides insights into potential evolutionary constraints for their functions.

1.1. GroEL–GroES machine

The complete chaperonin system consists of GroEL, the co‐chaperonin GroES, which together form both a 2:111 and 1:112 complex depending on whether SPs are present or absent. For it to function, which means assist in the folding of a vast number of SPs that otherwise could aggregate, it requires MgATP as well. The availability of a number of structures that GroEL visits during the catalytic cycle11, 12, 13 and theoretical developments3, 14 have made it possible to obtain insights into the function of GroEL–GroES system. GroEL, assembled from seven identical subunits, is a homo oligomer with two rings that are stacked back‐to‐back, which confers it in an unusual rare seven fold symmetry in the resting (T or taut) state. Major changes in the structures take place between the allosteric (T, R, and R ^″) states in response to ATP and GroES binding (Figures 1a and 2a). The dynamics of allosteric changes in GroEL has been reviewed recently.10, 15, 16, 17 The ATP binding sites are localized in the base of GroEL corresponding to the equatorial (E) domain, connecting the two rings (Figure 2a). The E carries bulk (roughly two thirds) of the inertial mass of a single subunit. Binding sites for the co‐chaperonin GroES are localized in the apical (A) domain, which also coincides with the region of interaction of the SPs with GroEL in the T state. We present a schematic in Figure 3(b) of the reaction cycle in a single ring. We ought to emphasize, right at the outset, that recent advances show that when challenged with SPs the functioning state is the symmetric 14‐mer GroEL–GroES complex, resembling a football18, 19 (see Figure 2b), and not the asymmetric bullet structure as had been thought for a long time.

Figure 1.

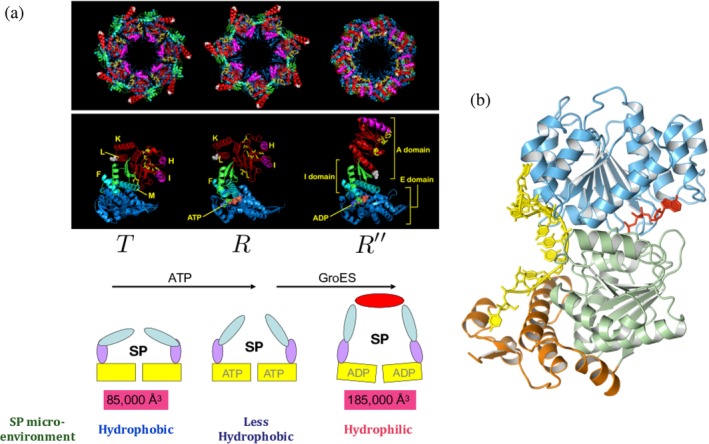
(a) Allosteric states in GroEL. The T → R transition is driven by ATP, and subsequent binding of GroES and ATP hydrolysis results in the R → R″. In the cartoon of GroEL at the bottom, the apical, intermediate, and equatorial domains are colored in cyan, purple, and yellow, respectively. As a result of transition from T to R″, the volume of cavity expands from 85,000 to 185,000 ų, and the substrate protein (SP) experiences the change in microenvironment from hydrophobic in the T state to hydrophilic in the R″ state. Microenvironment refers to the nature of molecular interactions between the SP and the residues lining the cavity of GroEL. (b) Structure of the yeast analogue of CYT‐19. Remarkably, despite the vastly different structures of GroEL and CYT‐19 they both serve as chaperones with very similar molecular mechanism

Figure 2.

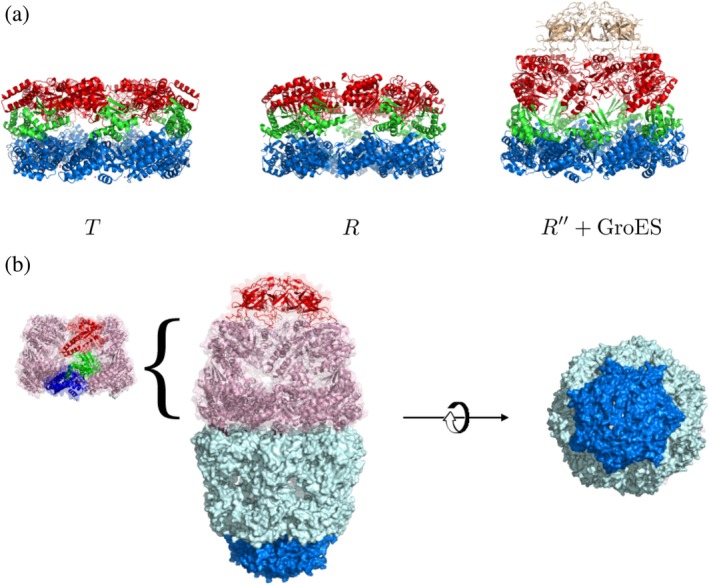
Structures of the GroEL–GroES chaperonin. (a). Structures of GroEL in T, R, and R″ states (PDB codes: 1OEL, 2C7E, 1AON). Apical, intermediate, and equatorial domains are colored in red, green, and blue, respectively. In R″ state, GroES is bound on top of the apical domain of GroEL ring structure. (b). Football‐like structure of GroEL–GroES complex (PDB code: 4PKN) is the functional state that is populated in the presence of substrate proteins. A view from the bottom highlights the structure with sevenfold symmetry

Figure 3.

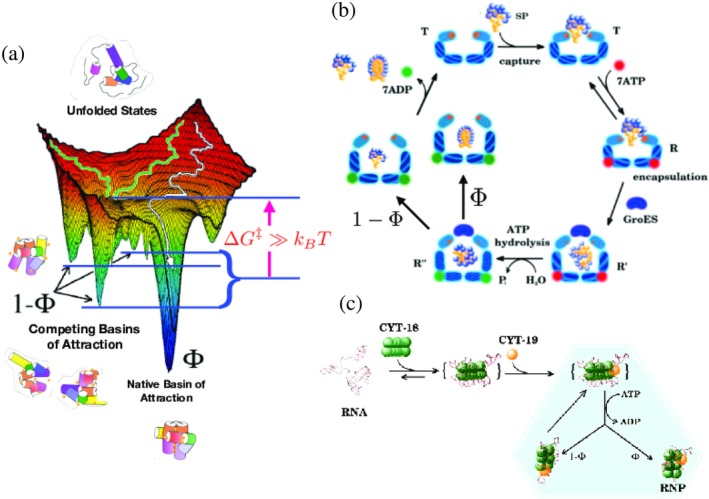
Kinetic partitioning mechanism (KPM) on rugged energy landscapes and chaperones. (a) Rugged folding landscape illustrating the native (NBA) and competing basins of attraction (CBA). In the absence of chaperones, a fraction Φ of the unfolded state ensemble folds into the NBA and 1 − Φ of the ensemble collapses to CBA. (b) Iterative annealing mechanism (IAM) for GroEL–GroES showing the coupling between allosteric transitions and substrate protein (SP) folding. The figure clearly illustrates that partitioning to native state, with probability Φ, and misfolding to a metastable state, with probability (1 − Φ) occurs rapidly within the cavity during the 2 s life time of the encapsulated state. Although not shown explicitly, the functioning state is the symmetric complex (see Figure 2). (c) IAM for RNA chaperone (CYT‐18/CYT‐19) acting on RNA. Both the processes shown in (b) and (c) require energy associated with ATP hydrolysis

The parts list of this complex machine is GroEL, GroES, MgATP, and the SPs, that require assistance to reach the folded structures. A few words about the SPs are in order. It has been shown long ago that GroEL is a promiscuous machine that interacts with a vast majority of Escherichia coli. proteins as long as they are presented in the misfolded states.20 This observation and the subsequent demonstration that most of the SPs used to study GroEL assisted folding are ones not found in E. coli. This buttresses this point For discussion purposes, we distinguish between permissive and nonpermissive conditions. Under permissive conditions, folding to the native state occurs readily in vitro on a biologically relevant time scale (τ _B), which is between 20 and 40 min for E. coli proteins at 37°C. Under nonpermissive conditions, spontaneous folding does not occur in vitro with sufficient yield of the folded protein on the time scale, τ _B. The SPs satisfying this criterion are deemed to be stringent substrates for GroEL. Several in vitro experiments show that in most cases the SP folding rates in the WT GroEL are enhanced only modestly, which is fully explained using theoretical studies.21, 22, 23 In fact, the folding rate could even decrease although this has been shown experimentally24 using only a mutant form of GroEL, referred to as SR1, from which GroES does not easily dissociate. In contrast, it is the native yield over a period of time that is maximized14, 25 by the GroEL machinery.

1.2. RNA chaperones

The tendency of RNA enzymes (ribozymes) to misfold in vitro is well established.26, 27, 28, 29, 30 Several in vitro experiments have firmly established that self‐splicing ribozymes, such as Tetrahymena ribozyme, fold to functionally competent state extremely slowly. Only a very small fraction of the initially unfolded ensemble reaches the folded state rapidly (∼1 s).9, 31 The reason for RNAs to be kinetically trapped in metastable states is due to the high stability of the base‐paired nucleotides. In addition, RNA molecules have considerable homopolymers‐like characteristics, which do not fully discriminate between a large number of relatively low free energy structures. These factors render the folding landscapes of RNAs more rugged than proteins.32 We showed that only ∼54% of RNA secondary structures is made of helices33 with intact Watson–Crick base pairs, which implies that substantial number of nucleotides are engaged in noncanonical base pairs, bulges, and internal multiloops. It is estimated that the life time of a helix made of 6 bps, which gives rise to a free energy barrier of δG ^‡ ≈ 10–15 kcal/mol, can be as large as ∼10⁵ s (∼1 month). Thus, if a helix forms incorrectly during the folding process, spontaneous unfolding of the helix would not occur on a reasonable time scale. Typical time scales for escape from low free energy some kinetically trapped metastable states can easily exceed 100 min (see, e.g., in Reference 9, eq. 2).

The arguments given above suggest that the folding landscape of most RNA molecules ought to consist of multiple metastable minima with similar stability that are separated from the native state by large (compared to k _B T where k _B is the Boltzmann constant and T is the temperature, which unfortunately is the same notation used for the T state in GroEL) free energy barriers.34 The structures in the metastable states often share many features that are common with the folded state. Such rugged landscapes govern the functions of many RNA molecules, such as riboswitches that are involved in transcription and translation. These biological processes are associated with switching between at least two alternative structures. In riboswitches, the switch between the states is modulated by metabolites or metal ions. Of relevance here is the in vitro folding of Tetrahymena ribozyme, which is a self‐splicing intron. For this enzyme, it is found that only a fraction (Φ = 0.08) of the initial population of unfolded molecules directly folds to the functionally competent native state in about 1 s, and the rest (1 − Φ = 0.92) of the molecules are kinetically trapped in competing basins of attraction9, 35, 36 for arbitrarily long times. For Tetrahymena ribozyme to function, it is essential that several key native tertiary contacts form. Incorrect formation of these tertiary contacts leads results in functionally incompetent ribozyme. For example, without the formation of the pseudoknot (P3 helix) the two domains (P5‐P4‐P6 and P7‐P3‐P8) cannot be stabilized (see Figure 4a). Formation of alternative helix (Alt‐P3) and other misfolded structures impair the function of ribozymes. An introduction of a single point mutation (U273A) stabilizing the P3 pseudoknot helix was shown to increase Φ as high to 0.8.37

Figure 4.

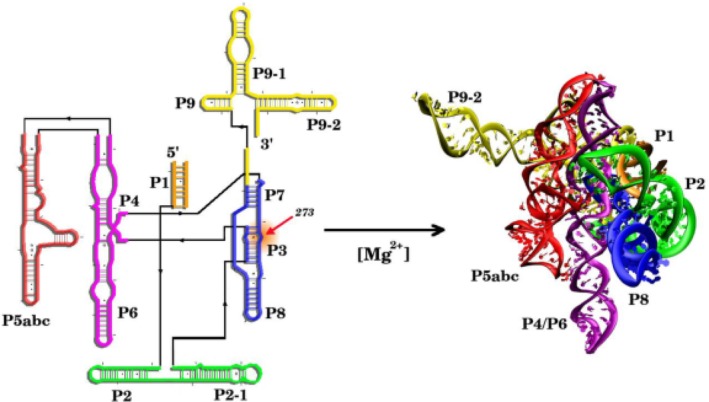
Folding of T. ribozyme from its secondary structure to three‐dimensional native state. The transition is driven by the divalent cation

DEAD‐box protein CYT‐19, which belongs to a general class of RNA chaperones,7, 8, 38, 39, 40, 41, 42, 43 comprises of a core helix domain and arginine rich C‐terminal tail. Cyt‐19 recognizes surface‐exposed RNA helices (duplexes) and unwinds them, like helicases belonging to the SF2 family (see Figure 4b for the yeast analogue of CYT‐1942), into single stranded RNA by expending free energy due to ATP hydrolysis. It is likely that ATP triggered conformational changes promotes local unwinding of RNA helices. Because of the helicase activity of CYT‐19, the microscopic mechanism does involve local unfolding of the accessible helices. Thus, both GroEL and CYT‐19 perform work on the misfolded structures by forcibly unfolding them, at least partially. This is another common theme linking the functions of CYT‐19 and GroEL.

Our goals in this article are the following:

1. We present a unified theoretical perspective on the functions of GroEL and RNA chaperones. The essence of the assisted folding mechanism of the SPs is illustrated using the well investigated GroEL–GroES system. Although the two enzymes, exhibiting machine‐like activity, are quite different, we show that the theory based on the iterative annealing mechanism (IAM) quantitatively explains a vast amount of experimental data in chaperone‐assisted folding of proteins as well as ribozymes. A major conclusion of the theory is that these ATP‐consuming chaperones are stochastic machines that drive the SPs or ribozymes out of equilibrium. This implies that in the steady state, $P_N^{\mathrm{SS}}$, (long time limit) the yield of the folded protein does not correspond to that expected at equilibrium $P_N^{\mathrm{EQ}}$, which would be ∝exp(−βΔG_NU) where β = 1/k _B T, and ΔG _NU is the free energy of stability of the native N state with respect to the unfolded state (U). In other words, $P_N^{\mathrm{SS}}\ne P_N^{\mathrm{EQ}}$.

2. The differences between GroEL–GroES system and RNA chaperones naturally arises from the IAM predictions, and highlights the likely inefficiency (large consumption of ATP relative to the production of the folded state) of RNA chaperones.

3. Because the GroEL structures in different nucleotide states are known, we illustrate the conformational changes that occur during the allosteric transitions in the GroEL in response to ATP and SP binding and link these changes to the folding of the SPs.

4. Finally, we outline recent developments, which provide incontrovertible evidence for the quantitative validity of the IAM, which establishes that GroEL–GroES system is a parallel processing stochastic machine that simultaneously anneals two misfolded molecules by sequestering one each in the two chambers of the symmetric complex. Remarkably, the symmetric complex forms only when the GroEL–GroES system is subject to load, that is, challenged with SPs that require assistance to reach the native state.

2. IAM FOR GROEL–GROES

In this section, we systematically develop the physical basis for the IAM by dissecting the fate of the SPs in the absence of the chaperonin machinery. We begin by considering how SPs, which do not recruit GroEL–GroES, fold spontaneously. This is followed by a brief description of the dynamics of allosteric transitions that GroEL undergoes in response to ATP and GroES binding and hydrolysis of ATP. Finally, the physical picture of the link between allosteric transitions and SP folding is described, which vividly reveals the machine‐like characteristics of the GroEL–GroES system. The applications of the theory of the IAM to experimental data cement the quantitative validity of the active role GroEL plays in assisted folding.

2.1. E. coli does not have enough GroEL to process the entire proteome

Over 20 years ago, Lorimer44 showed, using data for E. Coli B/r growing in minimal glucose medium at 37°C with a cell doubling time (τ _D of ∼40 min), that the number of GroEL particles can only process 5–10% of the proteome. The crux of the argument can be summarized as follows. The rate of protein synthesis is k _S = N _P/τ _D, where N _P is the number of polypeptide chains in a cell. Assuming that the total mass of proteins per cell is ≈1.56 × 10⁻¹³ g and the average mass is ≈4 × 10⁴ g/mol then N _P ≈ 2.35 × 10⁶, which implies that k _S = 6 × 10⁴ chains/min. Given there are about 3.5 × 10⁴ ribosomes, it follows that this strain of E. coli synthesizes about one polypeptide chain every 35 s. Needless to say, most if not all of the proteins have to reach the folded state in the crowded environment without the assistance of GroEL. The average cell contains about N _GroEL = 1,580 GroEL₁₄ particles, and about nearly twice as many GroES molecules. The typical measured values of the rates of assisted folding in vitro, k _Fs are in range 1–2 min⁻¹. Thus, the available GroEL particles can assist in the folding of N _GroEL k _F ≈ 3,160 polypeptide chains/min, which is clearly far less than the synthesis rate of 6 × 10⁴ chains/min. Thus, only about 3–5% of the proteome can recruit GroEL–GroES in order to fold. Nevertheless, removal of the GroE gene is lethal to the organism, attesting to its importance in E. coli growth. These estimates raise the following two important questions: (a) What are the potential SPs that fold with the assistance of the GroEL–GroES system? (b) How do the vast majority of proteins (≈95%) fold without the chaperonin machinery? We will answer the second question here and refer the readers to relevant papers,45, 46, 47, 48, 49 except to note that GroEL does not discriminate between proteins based on their folded structures because the very SP residues that interact with GroEL are buried in the folded state.47

2.2. Stringent SPs and ribozymes fold by the kinetic partitioning mechanism

Spontaneous folding of small proteins or those with relatively simple native topology is well understood. Proteins, such as SH3 domain or Chymotrypsin Inhibitor 2, fold in an ostensibly two state manner although when examined using high spatial and temporal resolution, it is found they twofold by multiple routes to the native state. For these proteins, the yield of the native state is sufficiently large that their folding does not require the assistance of chaperones. However, from the perspective of assisted folding, it is more instructive to consider the folding of SPs whose folding landscapes are rugged containing many free energy minima (Figure 3a) separated by sufficiently large barriers (several k _B Ts) that they cannot be overcome readily. Although the structures in the low energy minima could have considerable overlap with the folded state, they are misfolded because they are likely to contain incorrect tertiary contacts and/or secondary structures. These are targets for recognition by molecular chaperones. After an initial rapid compaction of the SPs or the ribozyme many of the molecules are trapped in one of several low free energy minima.

The kinetic partitioning mechanism (KPM), which explains the folding mechanisms of proteins succinctly, follows immediately from the rugged folding landscape in Figure 3a (see also Figure 5). According to KPM,51, 52 a fraction of molecules Φ folds rapidly without being trapped in one of the low free energy minima. These are sometimes referred to as the fast track molecules for which, following an initial “specific” collapse, folding to the native state is rapid.53 Explicit simulations using lattice models54 have shown that the folding characteristics (dynamics of compaction and the increase in the fraction of native contacts as a function of time) of the fast track molecules are identical to sequences for which the folding landscape is simple with one dominant minimum. The remaining fraction (1 − Φ) of molecules are trapped in an ensemble of low free energy structures because their initial collapse produce structures containing interactions that are not present in the native state. The resulting misfolded structures have to overcome activation barriers in order to reach the folded state. Thus, after the ensemble of unfolded molecules undergoes rapid collapse they partition to the native state at a rate k _IN or transition to the misfolded ensemble at a rate k _IM. The fraction of fast track molecules, referred to as the partition factor is associated with the rates in the three‐state cyclic model for chaperone‐assisting folding depicted in Figure 5 as, $\mathrm{\Phi }=\frac{k_{\text{IN}}}{k_{\text{IN}}+k_{\mathrm{IM}}}$. It is the value of Φ, which depends on a number of extrinsic factors such as ionic strength, pH, and temperature that governs the need of a SP or the ribozyme for the chaperone machinery (see below).

Figure 5.

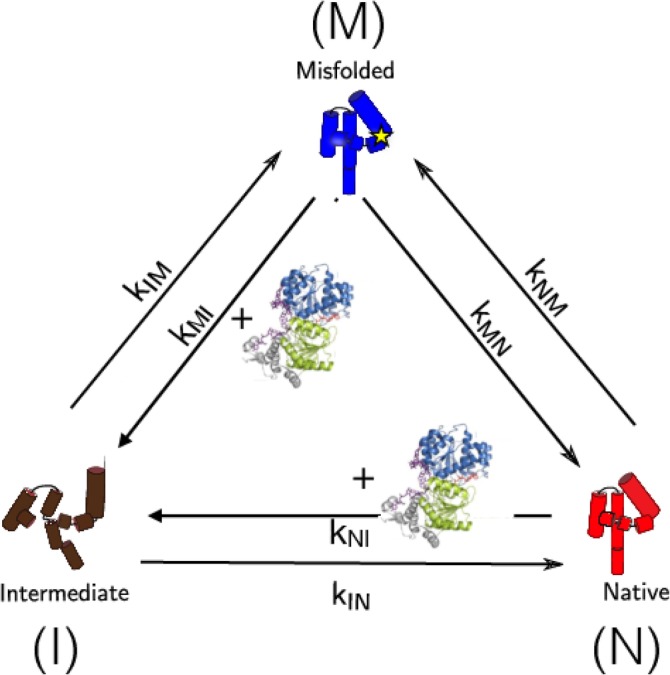
The model for a unified description of chaperone‐assisted folding. Tetrahymena ribozyme and CYT‐19 (green) are employed for illustration purposes. The model shows the ribozyme in the I (brown), N (red), and M (blue) states. The star symbol in the M state stands for incorrectly formed secondary structure. CYT‐19 enhanced kinetic rates, k _MI and k _NI, are highlighted with the structure of CYT‐19. The GroEL‐associated folding can similarly be accounted for by replacing CYT‐19 with the chaperonin machinery. The figure was adapted from Reference 50

We classify the misfolded structures into slow folders and no folders, depending on the magnitude of the activation free barriers separating them from the native state. The time scale for slow folders to reach the native state could range from milliseconds to several minutes whereas for no folders the transition to the native state could occur on time scales that exceed biologically relevant times. The effects of external conditions might be appreciated by noting that ribulose bisphosphate carboxylase oxygenase (RUBISCO) behaves as a no folder at low ionic strength but becomes a slow folder at high ionic strength.55 Similarly, by increasing the temperature from about 10 to 20°C to physiological temperature (37°C) both malate dehydrogenase and aspartate transaminase transition from being a slow to no folders.55, 56 The no folders, with low Φ, are prime candidates, which can fold with the aid of the complete chaperonin machinery.

3. EXPERIMENTAL EVIDENCE FOR KPM

The KPM has been validated in a number of experiments. The value of Φ has been measured in ensemble and single molecule experiments. (i) For example, Kiefhaber57 showed, using interrupted folding (final folding condition is 0.6 M GdmCl, pH = 5.2 and T = 20°C), that Φ = 0.15 for hen egg white lysozyme (HEWL). The fast track molecules fold in about 50 ms. The remaining fraction are slow folders, which reach the native state on a time scale about 400 ms. By varying pH, the value of Φ was found to increase to about 25%58 while the time constants for the fast track molecules were roughly identical to the earlier study.57 Because of the time for reaching the folded state by the molecules in the slow track is relatively small compared to biological times, it might be correctly concluded that folding of HEWL would not require the assistance of chaperones. (ii) The yield of the folded RUBISCO obtained in the direct folding, under nonpermissive conditions, inferred from chaperonin‐mediated folding (see below) is extremely small and is only order of 2–5%. For both Tetrahymena and RUBISCO most of the molecules ought to be classified as no folders, which imply their folding requires molecular chaperones. (iii) An indirect estimate of Φ was first made using theory and experiments for Tetrahymena ribozyme. It was found9 that Φ ≈ 0.1, which was subsequently confirmed in smFRET experiments.36 These values were obtained at sufficiently high Mg²⁺ concentration. At cellular Mg²⁺, the value is expected to be much less. Introduction of a single point mutation (U273A) stabilizing the P3 pseudoknot helix was shown to increase Φ as high to 0.8,37 which shows that both sequence and external conditions determine the value of Φ. For both Tetrahymena and RUBISCO, most of the molecules ought to be classified as no folders, which imply their folding requires molecular chaperones. In addition to the above mentioned experiments single molecule pulling experiments on several proteins (Tenacin, Fibronectin, T4Lysozyme, Calmodulin) using both atomic force spectroscopy,59, 60 and optimal tweezer techniques have established the validity of the KPM.

3.1. Size and kinetic constraints

Two constraints must be satisfied for GroEL–GroES‐assisted folding. First, pertains to the size of the SPs. The radius of gyration, R _g, of folded states of globular proteins is fairly accurately given by R _g = 3 N ^1/3 Å.61 Small‐angle X‐ray scattering experiments on a few proteins have shown that the typical sizes of misfolded SPs is about 5–10% larger than the folded states. This implies that the size of the RUBISCO monomer, with N = 491, in the misfolded state is ≈32 Å. The size of the expanded cavity, when both ATP and GroES are bound to GroEL, is ≈185,000 ų. If the cavity is approximated as a sphere the apparent radius would be 35 Å, which implies that if RUBISCO is fully encapsulated in the expanded cavity there would be room for about one layer of water molecules. Thus, GroEL can process SPs that contain ≲500 residues by fully encapsulating them.

The second and a more important constraint is kinetic in nature. As argued before only a small fraction, Φ of the SPs, reaches the folded state rapidly without being kinetically trapped in one of the many metastable states. If the average rate for molecules that fold by the slow track is k _s then in order to prevent aggregation the pseudo first‐order binding rate, k _B, of the misfolded SP to bind to GroEL must greatly exceed k _A where k _A is a pseudo first‐order rate for SP aggregation. The kinetic constraint shows clearly that the efficacy of assisted folding depends on the concentrations of both the SPs and GroEL.

3.2. Allosteric transitions in GroEL

Because the equilibrium and nonequilibrium aspects in the spectacular allosteric transitions in GroEL have been recently reviewed,10, 15, 16, 62 we describe only briefly the key events that impact the nature of assisted folding. Although the functional state of GroEL–GroES in the presence of SPs is the symmetric structure with the co‐chaperonin bound to both the rings,18, 19, 63, 64 let us consider for illustration purposes only the hemicycle, thus allowing us to describe events in one ring. The T, R, and R″ are the three major allosteric states (Figure 1a). The misfolded SPs, with exposed hydrophobic residues, preferentially interact with the T state, which has almost a continuous hydrophobic region lining the mouth of the GroEL cavity. The presence of the hydrophobic region is due to the alignment of seven subunits that join several large hydrophobic residues in the two helices (H and I) in the apical domain of each subunit. The T → R transition, resisted by the SP, is triggered by ATP binding to the seven sites in the equatorial domain. The rates of the reversible T ↔ R transition were first measured in pioneering studies by Yifrach and Horovitz65, 66 who also established an inverse relation, predicted using computations,21 between the extent of cooperativity in this transition and the folding rates of slow folding SPs.67 Binding of GroES, which predominantly occurs only after ATP binds, drives GroEL to the so‐called R′ state, which is followed by an irreversible nonequilibrium transition to the R″ state after ATP hydrolysis. It is suspected there is little structural difference between the R ^′, with ATP‐bound, and the R″, containing ADP and inorganic phosphate, states. In both these transitions strain due to ATP binding and hydrolysis at the catalytic site propagates through a network of inter‐residue contacts,68 thus inducing large‐scale conformational changes. That such changes must occur during the reaction cycle of GroEL is already evident by comparing the static crystal structures in different allosteric states, such as the T and R″ states.11 Release of ADP and the inorganic phosphate from the R″ state resets the machine back to the taut state from which a new cycle can begin. The allosteric transitions that GroEL undergoes during the catalytic cycle is intimately related to its function (see below). As we discuss later, it is not sufficient to deal with the catalytic cycle in a single ring because under load it is the symmetric football‐like structure that is the functional state.

3.3. Iterative annealing mechanism integrates GroEL allostery and assisted SP folding

The importance of GroEL allostery in assisted folding can be appreciated by understanding the interaction of the SP with the GroEL–GroES system in different allosteric states. The changes in the SP–GroEL interaction occur in three stages corresponding to the allosteric transitions between the three major allosteric states (see Figure 1a). (i) The continuous lining of the hydrophobic residues in the T state ensnares a misfolded SP with exposed hydrophobic residues. At this stage in the catalytic cycle, the SP is predominantly in a hydrophobic environment, resulting in the formation of a SP–GroEL complex that is stable but not hyperstable so that the SP can be dislodged in to the cavity upon GroES binding.69, 70 (ii) The dynamics of the T ↔ R transition, upon ATP binding, reveals that there is a downward tilt in two helices near the E domain that closes off the ATP binding sites, and which is followed by multiple salt bridge disruption (within a subunit) and formation of new ones across the adjacent subunits.71 As these events unfold cooperatively, the stability of the initial SP–GroES complex decreases. More importantly, the adjacent subunits start to move apart, which imparts a moderate force that is large enough to at least partially unfold the SPs.35, 72 (iii) Both GroES and SP bind to the same sites, which are located in the crevices of Helices H and I in the apical domain. Thus, when GroES binds, displacing the SP into the expanded central cavity, there are major structural changes in the GroEL cavity with profound consequences for the annealing mechanism. Only three to four of the seven SP binding sites are needed to capture the SP, leaving three to four sites available for binding of the mobile loops of GroES. This ensures that the subsequent displacement of the SP occurs vectorially into the central cavity of GroEL. First, there is a significant conformational change in the A domain, which undergoes a rotation and twist motion. Each subunit results in the two helices (K and L) in each subunit undergo an outside‐in movement (Figure 1a). As a result, polar and charged residues, which are solvent exposed in the T state, line the inside of the GroEL cavity. This in turn creates a polar microenvironment for the SP (Figure 1a). Second, these large‐scale conformational changes are facilitated by the formation of several intersubunit salt bridges and disruption of intra subunit salt bridges.71

From the perspective of SP, there are major consequences that occur as a result of the allosteric transitions in GroEL. First, by breaking a number of salt bridges, the volume of the central cavity increases twofold (85,000 ų → 185,000 ų). In such a large central cavity, enough to fully accommodate a compact protein with ≈500 residues, folding to the native state could occur if given sufficient time, as is the case in the SR1 mutant. However, in the WT, the residence time of the encapsulated SP is very short (see below). Second, and most importantly, the SP–GroEL interaction changes drastically during the catalytic cycle. In the T state, SP–GroEL complex is (marginally) stabilized predominantly by hydrophobic interactions. However, during the subsequent ATP‐consuming and irreversible step R → R^′′ transition the microenvironment of the SP is largely polar (see the discussion in the previous paragraph). Thus, during a single catalytic cycle, that is replicated in both the rings, the microenvironment of the SP changes from being hydrophobic to polar. We note parenthetically that even during the T → R transition there is a change in the SP–GroEL interactions, which explains the observations that GroEL can assist of the folding of certain SPs (nonstringent substrates) even in the absence of GroES. The annealing capacity of GroEL is intimately related to the changes in the SP–GroEL interactions that occur during each catalytic cycle. Hence, the function of the GroEL–GroES system cannot be understood without considering the complex allosteric transitions that occur due to ATP and GroES binding. As a result of these transitions, the SP is placed stochastically from one region in the folding landscape, in which the misfolded SP is trapped, to another region from which it could undergo kinetic partitioning with small probability to the folded state or be trapped in another misfolded state. The cycle of hydrophobic to polar change is repeated in each catalytic cycle, and hence the GroEL–GroES system iteratively anneals the misfolded SP enabling it to fold to the native state. Because this process is purely stochastic, GroEL plays no role in guiding the protein to the folded state nor does it sense the architecture or any characteristics of the folded state. In other words, the information for protein self‐assembly is fully encoded in the amino acid sequence as articulated by Anfinsen.73 GroEL merely alters the conformation of the SP stochastically as it undergoes the reaction cycle, enabling the SP to explore different regions of the folding landscape. In this sense, the action of GroEL is analogous to simulated annealing used in optimization problems74 although the latter is a more recent realization of an evolutionary event that took place millions of years ago.

3.4. Theory underlying the IAM

The physical picture of the IAM described above can be formulated mathematically to quantitatively describe the kinetics of chaperonin‐assisted folding of stringent in vitro substrate proteins.75 According to theory underlying IAM (see Figure 3), in each cycle the SP folds by the KPM, as the microenvironment for the SP changes as GroEL undergoes the reaction cycle. Thus, with each round of folding the fraction of folded molecules is Φ, and the remaining fraction gets trapped in one of the many misfolded structures. After n such cycles (or iterations) the yield of the native state is,

$$\mathrm{\Psi }={\mathrm{\Lambda }}_{\mathrm{ss}}\left[1-{\left(1-\mathrm{\Phi }\right)}^n\right]$$ (1)

where Λ_ss is the steady‐state yield. The mathematical model accounts for all the available experimental data, and shows that for RUBISCO the partition factor Φ ≈ 0.02, which means that only about 2% of the SP reaches the folded state in each cycle. From this finding we could surmise that the GroEL chaperonin is an inefficient machine, which consumes ATP lavishly and yet the yield of the folded protein per cycle is small. A prediction of the IAM is that GroEL should reset to the starting T state as rapidly as possible in the presence of SPs. By rapidly resetting to the T state the number of interactions can be maximized, which would maximize the yield of the folded state for a specified amount of time.50 Indeed, this is the case, which we delve into detail below.

3.5. Rate of R^′′ → T transition is a maximum for the WT GroEL

A clear implication of the IAM is that rapid turnover of the catalytic cycle would produce the maximum yield of the native state in a given time. Examination of the reaction cycle shows that the rate‐determining step (resetting of the machine) should correspond to release of ADP and the inorganic phosphate. In other words, maximization of the rate, k_{R ″  → T} returns GroEL to the acceptor state for processing a new SP. In order to illustrate that this is indeed the case, we first extracted the rates of the allosteric transitions by fitting the solutions of the kinetic equations75 by simultaneously fitting the experimental data for assisted folding at various GroEL concentrations. For this purpose, we used the data for RUBISCO for which the yield of the folded state as a function of eight values of the GroEL concentration is available.14 The excellent fits at various GroEL concentrations (Figure 6), with a fixed initial concentration of RUBISCO, were used to extract Φ. We find that Φ ≈ 0.02, which means that only about 2% of the SP reaches the folded state in each catalytic cycle.

Figure 6.

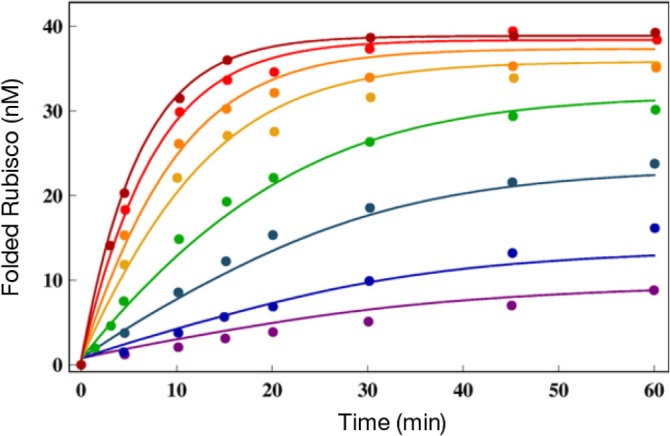
Native‐state yield of ribulose bisphosphate carboxylase oxygenase (RUBISCO) as a function of time at different GroEL concentrations. The chaperonin concentrations for the curves from bottom to top are 1, 2, 5, 10, 20, 30, 50, and 100 nM. The lines are the fits to the experimental data from Reference 14 using the kinetic model. The figure was adapted from Reference 75

Armed with the rates that describe the allosteric transitions, we used the IAM theory based to analyze experimental data on the folding of other SPs. Because the reversible transition ATP‐induced T ↔ R transition occurs at equilibrium even in the absence of SP66 it is reasonable to assume that they are relatively insensitive to the nature of the SP. Indeed, the extracted values of the T ↔ R rates using the RUBISCO data (see 75, table 1) are very similar to measurements made in the absence of SP.66 This leaves the rate k_{R ″  → T} that results in the resetting the machine after ATP hydrolysis to the taut (T) state as the most important factor in determining the efficiency of GroEL or its mutants. Thus, maximizing k_{R ″  → T} should result in optimizing the native state yield at a fixed time. This most significant prediction of IAM can be quantitatively demonstrated by analyzing the data reported by Lund and coworkers.76 They measured the activity, which we assume is proportional to the yield of the folded state, as a function of time for GroEL and five mutants including SR1. The two SPs used in these studies were mitochondrial malate dehydrogenase and citrate synthase (CS). The results, reproduced in Figure 7, show that $P_N^{\mathrm{SS}}$ and indeed the yield at any time is largest for the WT and is least for the SR1 mutant from which GroES disassociates in ≈300 min. The curves in Figure 7 were calculated by adjusting just one parameter, the rate k_{R ″  → T} while keeping the rates for other allosteric rates fixed at the values extracted by analyzing the RUBISCO data. The IAM predictions are in quantitative agreement with experiments for both the proteins and for GroEL and its mutants. The value of k_{R ″  → T} ≈ 60 s⁻¹ (1 s) is largest for the WT GroEL. This implies, as predicted by IAM, that GroEL catalytic cycle is greatly accelerated when SP is present, a point that requires further elaboration.

Figure 7.

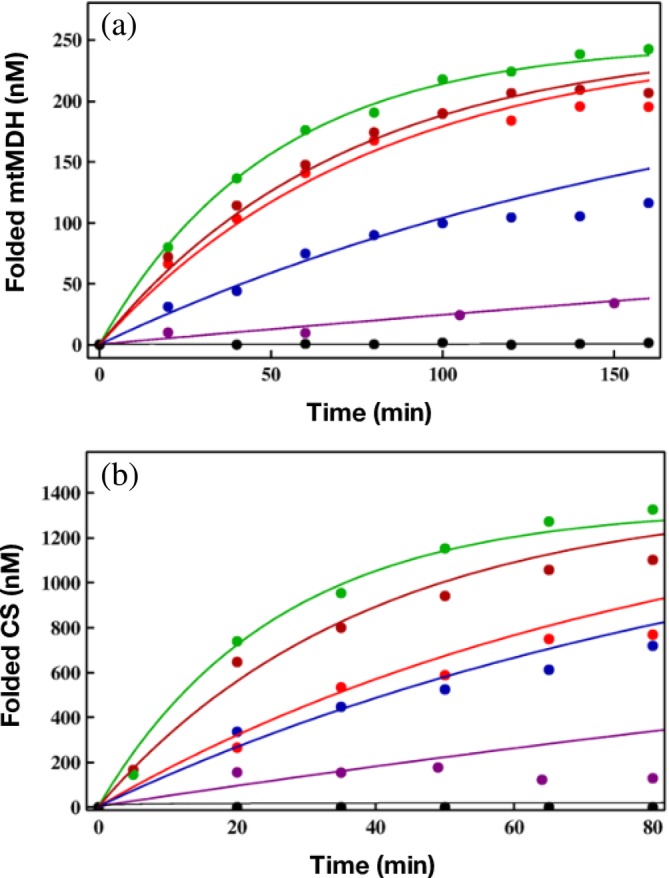
Yield of SPs as a function of time. (a) The data points are taken from the experiment for folding of mitochondrial malate dehydrogenase (mtMDH). The lines are the fits using the kinetic model developed in Reference 75. The black line is for spontaneous folding. Assisted folding in the presence of GroES and GroEL mutant SR1 (purple), Single Ring 1, SR1 mutants, SR‐T522I (blue), SR‐A399T (red), and SR‐D115N (dark red), was used to assess the efficiencies of these three single‐ring chaperonins relative to GroEL (green). (b) The same as (a) except the SP is citrate synthase (CS)

4. GENERALIZED IAM FOR RNA CHAPERONES

Compared to GroEL–GroES chaperonin, details of the catalytic cycle of CYT‐19 are not known. Consequently, it is not possible to link the structural transitions that occur during the CYT‐19‐assisted folding of the misfolded ribozymes, as we did for the GroEL–GroES machinery. We should note that the structures and biophysical studies of the DEAD‐box protein Mss116p, Saccharomyces cerevisiae analogue of CYT‐19, showed the expected helicase activity, resulting in the disruption of the structure of the misfolded ribozyme. These studies and the still undetermined ATPase cycle could be used in the future to provide a molecular basis of the IAM for CYT‐19 assisted folding. Nevertheless, the mathematical formulation of the IAM theory could be adopted to investigate the interesting experimental findings by Bhaskaran and Russell.40

The most significant experimental findings of CYT‐19‐assisted folding of ribozymes are as follows: (i) When incubated in CYT‐19 under somewhat destabilizing conditions ([Mg²⁺] < 2 mM), ribozymes show a low cleavage activity. (ii) Regardless of the initial population, the native and the misfolded ribozyme reach a steady‐state value for the folded ribozyme fraction, which is not unity ($P_N^{\mathrm{SS}}\ne 1$). (iii) The deactivation of the ribozyme function was observed at longer preincubation times in CYT‐19. Deactivation of native ribozyme was also observed at higher CYT‐19 concentration. Taken together, these observations imply that CYT‐19 destabilizes the native as well as the misfolded ribozyme. The finding that CYT‐19 interacts with the fully folded ribozyme is in stark contrast with GroEL, which does not interact with the folded states of proteins. In light of the experimental observations, the IAM theory has to be generalized (see Figure 8). The results in this study inspired us to generalize the IAM theory using the master equation.77 More recently, we proposed a simpler version that describes the functions of GroEL and RNA chaperones on equal footing.50 The resulting theory, which gives rise a complicated expression for the folded state of P5a variant of the Tetrahymena sketched below, provided a quantitative agreement (Figure 9) of the experimental data.40

Figure 8.

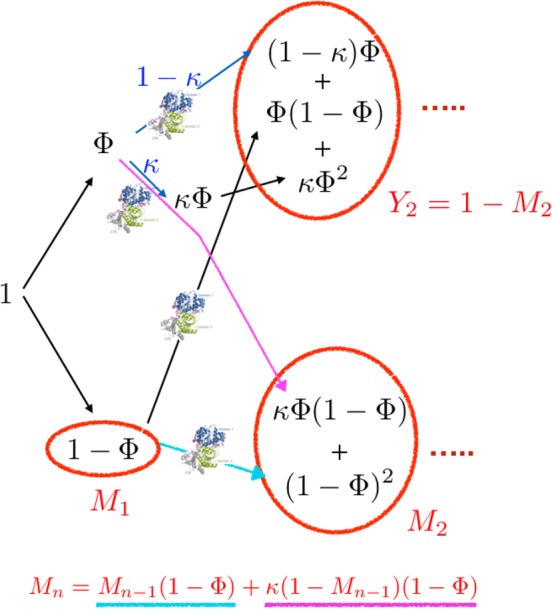
Schematic of the generalized iterative annealing mechanism (IAM) of chaperone‐assisted substrate folding. Depicted are the logical steps in a branching process that leads to the recursion relation for the total yield of the misfolded state after nth annealing process (M _n), given at the bottom. Y _i(=1 − M _i) and M _i are, respectively, the yield of native and misfolded states from the ith iteration. Φ is the kinetic partitioning factor

Figure 9.

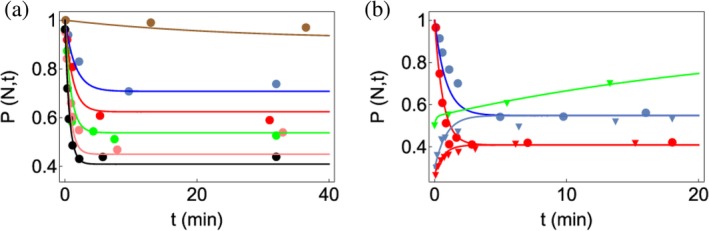
Analysis of folding of the P5a variant of T. ribozyme in the presence of CYT‐19. (a) CYT‐19 (1 μM)‐induced kinetics of the native P5a variant ribozyme in 5 mM Mg²⁺ at various ATP concentrations: no ATP (brown), 100 μM ATP (blue), 200 μM ATP (red), 400 μM ATP (green), 1 mM ATP (pink), and 2 mM ATP (black). (b) Kinetics of P5a variant folding for different CYT‐19 concentrations. Starting conditions were native (circles) or misfolded (triangles) P5a variants. CYT‐19s are 0.5 μM (blue) and 1 μM (red). The curve in green is for a mixture of native and misfolded P5a variant ribozymes when proteinase K is added to inactivate CYT‐19. The figure was adapted from Reference 50

The KPM description of ribozyme folding9, 52 shows that upon increasing the Mg²⁺ concentration, a fraction of the initial unfolded population, Φ, folds to the native state and the remaining fraction, M ₁ = 1 − Φ, collapses to one of many misfolded states. Consider the fate of the misfolded states, with population, M ₁, as they interact with CYT‐19. In the presence of the RNA chaperone, a fraction Φ of M ₁ reaches the native state (Φ(1 − Φ)) and 1 − Φ of M ₁ to one of the misfolded states ((1 − Φ)²). Because CYT‐19 also acts on the native state, we also have to consider the fate of the folded ribozyme, as it interacts with CYT‐19 (see Figure 8). Let a fraction κ denote the fraction of the initially folded ribozyme reach the misfolded state (bottom right circle in Figure 8) while the 1 − κ remain in the native state (top right circle in Figure 8). In the subsequent round, out of κΦ, κΦ² of them goes to native and κΦ(1 − Φ) reaches the misfolded state. Therefore, M ₂ = κΦ(1 − Φ) + (1 − Φ)² is the total of the misfolded ribozyme in the second round of IAM, which accounts for accumulation from both the folded and misfolded states in the first round. In order to obtain an expression for the yields of both the folded and misfolded states of the ribozyme the branching process from both the accumulated folded and misfolded states of the ribozyme in the previous round has to be taken into account. A recursion relation for this iterative process may be written down, such that the amount of misfolded state at the nth round is the sum of M _n − 1 × (1 − Φ) from the misfolded ensemble, and κ(1 − M _n − 1) (1 − Φ) from the native ensemble. In short, M _n = M _n − 1(1 − Φ) + κ(1 − M _n − 1) (1 − Φ) (see Figure 8). As a result, the total yield of native state in the Nth round of annealing process (Ψ_N = 1 − M _N) can be calculated in order to obtain yield of the native ribozyme from the generalized version of IAM,

$${\mathrm{\Psi }}_N=\mathrm{\Phi }\frac{1-{\left(1-\kappa \right)}^N{\left(1-\mathrm{\Phi }\right)}^N}{\kappa +\left(1-\kappa \right)\mathrm{\Phi }},$$ (2)

and the steady‐state solution (N → ∞) is

$${\mathrm{\Psi }}_{\infty }=\frac{\mathrm{\Phi }}{\kappa +\left(1-\kappa \right)\mathrm{\Phi }}.$$ (3)

For κ = 0, corresponding to the situation that the RNA chaperone does not recognize the native state, the yield in the Nth round is identical to the conventional IAM expression. For κ = 1 in which RNA chaperone recognizes the native state equally as well as misfolded states, there would be no gain in the native yield by the action of RNA chaperone.

The action of chaperones on substrate RNA can be mapped onto three‐state kinetic model of RNA with transitions between the native (N), misfolded (M), and intermediate states (I). When the partition factor Φ in terms of the rate constants, Φ = k _IN/(k _IN + k _IM), is plugged into Equation (3), Ψ_∞ is

$${\mathrm{\Psi }}_{\infty }=\frac{k_{\text{IN}}}{\kappa k_{\mathrm{IM}}+k_{\text{IN}}}.$$ (4)

In addition, the expression for the steady‐state value of fraction native ($P_N^{\mathrm{SS}}$), which is equivalent to Ψ_∞, can be obtained using three‐state kinetic model (Figure 5) under the following conditions: (a) k _NM, k _MN ≪ k _IN, k _IM, k _NI, k _MI, and (b) k _NI ≪ k _IN. With these assumptions, we find that,

$$P_N^{\mathrm{SS}}\approx \frac{k_{\text{IN}}}{\left(\frac{k_{\mathrm{NI}}}{k_{\mathrm{MI}}}\right)k_{\mathrm{IM}}+k_{\text{IN}}}.$$ (5)

Therefore, comparison between Equations 4, 5 gives

$$\kappa =\frac{k_{\mathrm{NI}}\left(\left[C\right],\left[T\right]\right)}{k_{\mathrm{MI}}\left(\left[C\right],\left[T\right]\right)}$$ (6)

where the dependence of unfolding rates k _NI and k _MI on chaperone and ATP concentration is made explicit. It turns out that κ, defined as the unfolding efficiency of chaperone for the native state with reference to the misfolded ensemble, is effectively the ratio between chaperone‐induced unfolding rate from the native and misfolded state. A sketch of the native state as a function of κ, which depends both on the chaperone and ATP concentration, is given in Figure 10.

Figure 10.

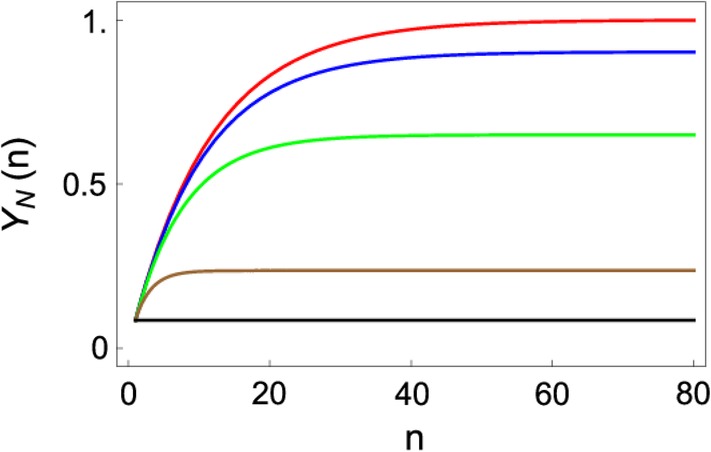
The effect of varying κ on the yield of the N state. Shown is the plot of the native yield, Y _N(n) as a function of number of cycles n for varying κ values: κ = 0 (red), κ = 0.01 (blue), κ = 0.05 (green), κ = 0.3 (brown), and κ = 1.0 (black). The figure was adapted from Reference 50

5. DISCUSSION

5.1. What do chaperones optimize?

The question of what quantity a biological machines optimize subject to the constant of available free energy does not have a general answer. However, in the rare case of chaperones a plausible answer has been recently proposed, which we illustrate here.50 It is noteworthy that despite the critical difference between CYT‐19 and GroEL, with the former that disrupts both the folded and misfolded states of ribozymes whereas the latter does not interact with the folded proteins, the mechanisms of their functions are in accordance with the predictions of IAM. Both GroEL and RNA chaperones function by driving the SPs and ribozymes out of equilibrium.50 Remarkably, we showed by analyzing experimental data on ribozymes and MDH that the quantity that is optimized by GroEL and RNA chaperones is,

$${\mathrm{\Delta }}_{\mathrm{NE}}=k_F{P}_N^{\mathrm{SS}}$$ (7)

where k _F is the folding rate and $P_N^{\mathrm{SS}}$ is the steady‐state yield (see Figure 11). Thus, neither the folding rate nor the steady‐state yield is maximized but it is the product of the two that is optimized by the molecular chaperones. It follows from Figure 11 that, for a given SP and external conditions, which would fix k _F, the steady‐state yield would have the largest value for the WT GroEL than any other mutant. That this is indeed the case is vividly illustrated in Figure 6. In the case of GroEL, the value of $P_N^{\mathrm{SS}}$ (or P _N[t] at any t) is critically dependent only on k_{R ″  → T}, which has the largest value for the WT GroEL. The optimality condition given in Equation (7) is determined by the value of k_{R ″  → T}, which in turn depends on the dynamics of allosteric transitions as well the presence of SP. Thus, the function of GroEL, and most likely CYT‐19 and related RNA chaperones, cannot be understood without considering the details of the reaction cycle and how they are directly related to SP folding. The IAM theory, which accounts for all the complexities of the reaction cycle, explains the available experimental data quantitatively (see, e.g., Figure 6) using a single parameter (k_{R ″  → T}).

Figure 11.

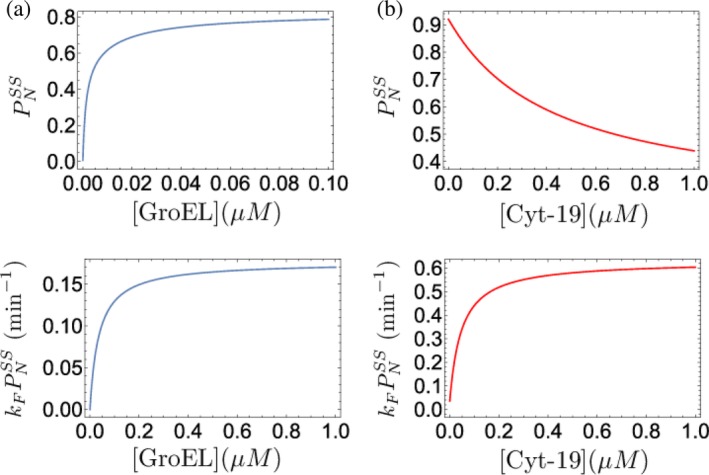
Maximization of the finite‐time yield by iterative annealing. (a) GroEL and (b) Cyt‐19. (Top panels) Steady‐state yield of the folded ribulose bisphosphate carboxylase oxygenase (RUBISCO) (a) and ribozyme (b), as a function of chaperone concentration. (Bottom panels) Yield per unit time ${\mathrm{\Delta }}_{\mathrm{NE}}=k_F{P}_N^{\mathrm{SS}}$ for RUBISCO (a) and ribozyme (b), as a chaperone concentration. For all of the curves, ATP concentration was set to 1 mM. The figure was adapted from Reference 50

5.2. When it does SP folding occurs in the expanded GroEL cavity

Does SP folding occur in the expanded cavity or in solution after ejection? This question has unnecessarily plagued the discussion of GroEL‐assisted folding, causing substantial confusion largely because of insistence by some that GroEL merely encapsulates the SP in the cavity until it reaches the native state with unit probability.78 Such an inference that GroEL is a passive Anfinsen cage has been made principally using experiments based on a single ring mutant (SR1) from which discharge of GroES and the SP occurs on a time scale of 300 minutes is erroneous. For starters, the life time of the encapsulated SP in the WT cycling GroEL is about 2 s64 that is four orders of magnitude shorter than the SR1 lifetime! Furthermore, neither the passive or active cage model can explain how the communication to discharge the ligands (ADP and the inorganic phosphate), GroES, and the folded SP takes place.

Does folding to the folded state occur within the cavity in the WT GroEL? We answer this question in the affirmative by using the following argument. Assisted folding requires that the kinetic constraint, k _F < k _B be satisfied where k _B pseudo first‐order binding rate of SP to GroEL. In the opposite limit (k _F > k _B), which is relevant at low GroEL concentrations, folding is sufficiently rapid compared to diffusion controlled binding that the chaperonin machinery would not be needed. Thus, assuming that the kinetic constraint (k _B ≫ k _A) is always satisfied for stringent substrates under non‐permissive conditions then the SP upon ejection from the GroEL cavity, roughly every 2 s, rebinds (presumably to the same GroEL molecule) rapidly. If the ejected SP is in the folded state, then it would not be recognized by GroEL because the hydrophobic recognition motifs would no longer be solvent exposed. Thus, the fate of SP, which occurs by the KPM, is decided entirely within the cavity during the lifetime of its residence. Both folding and partitioning to the ensemble of misfolded states occur rapidly while the SP is encapsulated for a brief period in either chamber.

We provide evidence to substantiate the physical arguments given above. The theory underlying IAM was used to obtain the parameters for the rates in the catalytic cycle and the intrinsic rates for assisted folding of RUBISCO. The time for RUBISCO molecules to reach the folded state by the fast track, ${\tau }_F=k_F^{-1}=0.6$ s (75, table 1), which is less than the encapsulation time of about 2 s. This implies only the fast track RUBISCO molecules fold in the cavity because time for slow track RUBISCO molecules ${\tau }_S\left(=k_S^{-1}\right)$ to fold is about 333 min (75, table 1). The slow track molecule would rapidly rebind upon exiting the cavity, and the process is iterated multiple times till the majority of unfolded SPs reach the native state. One can use the same argument for reconstituting CS using GroEL. The fits to the experimental data76 in Figure 6 yields τ _F = 0.6 s whereas τ _S = 100 min,75 which again shows that KPM resulting in folded and misfolded states occurs while CS is encapsulated in the cavity. Thus, we can conclude that when SP folding occurs it occurs in the expanded cavity. It is worth emphasizing that because the IAM theory takes into account the coupling between the events in the reaction cycle of GroEL and SP folding it naturally explains the allosteric communication needed for discharge of the SP, whether it is folded or not, and other ligands. However, only a very small fraction reaches the folded state in each cycle, and hence the need to perform the iterations as rapidly as possible. Remarkably, GroEL has evolved to do just that by functioning as a parallel processing machine in the symmetric complex when challenged with SP.18, 19

5.3. Symmetric complex is the functioning unit of the GroEL–GroES machine

The IAM predicts that the yield of the folded SP increases with each iteration. It, therefore, follows that for highly efficacious function it would be optimal if GroEL–GroES functions as a parallel processing machine with one SP in each chamber. This would necessarily involve formation of a symmetric complex GroEL₁₄‐GroES₁₄, which was shown as the functioning unit only recently.13, 19, 64 In particular, using a FRET‐based system Ye and Lorimer64 have established unequivocally that the response of the GroEL–GroES machinery is dramatically different with and without the presence of SP. In order to unveil the differences they had to follow the fate of ADP and P_i release in real time. These experiments showed that in the absence of the SP the rate determining step involves release of P_i before ADP release from the trans ring of the dominant asymmetric complex (GroES bound to the cis ring). In sharp contrast, when challenged with the SP, ADP is released before P_i. The symmetric particle, with GroES bound to both the rings (Figure 2b), is the predominant species in the presence of SP. In principle, the symmetric particle can simultaneously facilitate the folding of two SPs one in each chamber. Thus, it is likely the case that the functional form in vivo is the symmetric particle, which is activated when there is a job to do, namely, help SPs fold.

There was one other major finding in the Ye‐Lorimer study.64 They discovered that the ATP hydrolysis rate (∼0.5⁻¹) is the same in the presence and absence of the SP. In the presence of SP, hydrolysis of ATP is rate limiting, which in the language used to describe motility of motors means that GroEL is ATP gated. In other words, symmetry breaking (or inter ring communication) events that determine the ring from which GroEL disassociates depends on extent of ATP hydrolysis in each ring. Remarkably, the release of ADP from the trans ring is accelerated roughly 100‐fold in the presence of SP. We note parenthetically that release of ADP from the nucleotide binding pocket of conventional kinesin is accelerated by nearly 1,000‐fold in the presence of microtubules,79 hinting at the possibility that there is a unified molecular basis for nucleotide chemistry in biological machines. By greatly enhancing ADP release in the presence of SP, resetting to the initial SP accepting state occurs rapidly (k_{R ″  → T} is maximized in the WT GroEL), which allows GroEL to process as many SP molecules as fast as possible. Clearly, these findings are in complete accordance with the IAM predictions and debunk the Anfinsen cage model.78, 80

6. CONCLUSIONS

In this perspective, we have shown that, despite profound differences, the functions of GroEL–GroES machine and RNA chaperones are quantitatively described by the theory underlying the IAM. We are unaware any experiment of assisted folding of the SPs or ribozymes that cannot be explained by the theory. We conclude with the following additional comments.

1. It is sometimes stated that the mechanism of how GroEL functions is controversial because of the proposal that the cavity in the GroEL could act as an Anfinsen cage in which folding can be completed unhindered by aggregation. Such a conclusion was reached based mostly on experiments on the SR1 mutant (an asymmetric GroEL complex) from which GroES disassociates in 300 min. Although experiments using SR1 (with ADP and P_i locked into the equatorial domain) provide insights into effects of confinement on SP folding they are irrelevant in understanding of WT GroEL function. Finally, in the Anfinsen cage model, there is no necessity for invoking allosteric transitions and how they are linked to assisted folding. In the SR1 mutant, ATP binding and hydrolysis occurs once, which means that the SP is trapped in a hydrophilic cavity for extremely long times, and hence lessons from the SR1 mutant neither inform us about the intact WT GroEL nor are they biologically relevant. On the other hand, the stochastic WT GroEL comes alive when presented with SPs, undergoes a series of allosteric transitions by binding, hydrolyzing ATP, and releasing the products, which permits the SPs multiple chances to fold in the most optimal fashion (see Equation (7)). The quantitative success of the IAM should put to rest the inadequacy and the erroneous Anfinsen cage model78 for describing the function of the WT GroEL. For instance, the results in Figure 7 cannot be understood within the Anfinsen cage model.

2. The machine‐like non‐equilibrium characteristics of chaperones are most evident by the demonstration that the steady‐state yield, $P_N^{\mathrm{SS}}\ne P_{\mathrm{EQ}}$ where the equilibrium yield of the folded state, P _EQ, is given by the Boltzmann distribution,

   $$P_N^{\mathrm{EQ}}=\frac{1}{\left(1+e^{-\mathrm{\Delta }{G}_{\mathrm{NM}}/k_{B}T}\right)},$$ (8)

   where ΔG _NM is the free energy of the folded state with respect to the manifold of misfolded states. The values of $P_N^{\mathrm{SS}}$ for the two SPs and Tetrahymena ribozyme and its variants depend both the chaperone and ATP concentrations,50 which itself is evidence of departure from equilibrium. In addition, the measured value of ΔG _NM for the WT ribozyme is ∼10 k _B T, which implies that $P_N^{\mathrm{EQ}}\approx$ 0.99 according to Equation (8). However, the measured value in the presence of ATP is far less, which shows that $P_N^{\mathrm{SS}}\ne P_N^{\mathrm{EQ}}$. The finding that $P_N^{\mathrm{SS}}$ values of RUBISCO and MDH are dependent on GroEL concentration also implies that in the presence of GroEL Equation (8) is not valid. Taken together, they imply that in the process of assisted folding both GroEL and CYT‐19 drive the misfolded SPs and ribozymes out of equilibrium (see also Reference 81).

3. GroEL and RNA chaperones burn copious amount of ATP because in each round only a small fraction (Φ ≪ 1) of misfolded molecules reach the native state. Consider RUBISCO folding for which Φ = 0.02.75 The yield of the native state at t = 20 min with the concentration of GroEL roughly equal to the initial unfolded RUBISCO (both at 50 nm) is about 0.7 (see Figure 6). The value of $P_N^{\mathrm{SS}}\approx 0.8$ from which we obtain n ≈ 100 using Equation (1). In each catalytic cycle between (3 and 4), ATP molecules are consumed, which implies that in order to fold roughly 88% of RUBISCO in the steady state between 300 and 400 ATP molecules are hydrolyzed. As pointed out elsewhere,14 this is but a very small fraction of energy required to synthesize RUBISCO, a protein with 491 residues. Thus, the benefits of GroEL‐assisted folding far outweigh the cost of protein synthesis. However, from a thermodynamic perspective it can be argued that GroEL is less efficient than Myosin V, which consumes one ATP molecule (available energy is about E _ATP ≈ [20–25] k _B T) per step (s ≈ 36 nm) while walking on actin filament, resisting forces on the order of about f _s ≈ 2 pN. Thus, a rough estimate of Myosin V efficiency is $\frac{{\mathit{sf}}_s}{E_{\mathrm{ATP}}}$ is very high.

Thirumalai D, Lorimer GH, Hyeon C. Iterative annealing mechanism explains the functions of the GroEL and RNA chaperones. Protein Science. 2020;29:360–377. 10.1002/pro.3795