Elastic avalanches reveal marginal behavior in amorphous solids

Significance

At large strains, glassy systems deform through a series of elastic loading phases followed by energy and stress drops without a characteristic scale, similar to earthquakes. Less is known about the small deformation case, which is related to the structure of the energy landscape close to an energy minimum. We investigate numerically this regime and show that even at very small strains the deformation proceeds through avalanches that are power-law distributed, with a universal exponent that corresponds to the predictions of mean-field theory for a hierarchical phase space structure. These avalanches reveal marginal stability in the amorphous solid, which is intrinsically inelastic. By investigating the preparation and size dependence, we infer that the effect persists in the thermodynamic limit.

Abstract

Mechanical deformation of amorphous solids can be described as consisting of an elastic part in which the stress increases linearly with strain, up to a yield point at which the solid either fractures or starts deforming plastically. It is well established, however, that the apparent linearity of stress with strain is actually a proxy for a much more complex behavior, with a microscopic plasticity that is reflected in diverging nonlinear elastic coefficients. Very generally, the complex structure of the energy landscape is expected to induce a singular response to small perturbations. In the athermal quasistatic regime, this response manifests itself in the form of a scale-free plastic activity. The distribution of the corresponding avalanches should reflect, according to theoretical mean-field calculations [S. Franz and S. Spigler, Phys. Rev. E 95, 022139 (2017)], the geometry of phase space in the vicinity of a typical local minimum. In this work, we characterize this distribution for simple models of glass-forming systems, and we find that its scaling is compatible with the mean-field predictions for systems above the jamming transition. These systems exhibit marginal stability, and scaling relations that hold in the stationary state are examined and confirmed in the elastic regime. By studying the respective influence of system size and age, we suggest that marginal stability is systematic in the thermodynamic limit.

The response of amorphous solids and yield stress fluids to a mechanical deformation has attracted considerable attention from the statistical physics as well as materials science community in recent years. A large number of numerical and theoretical studies have been devoted to the regime of stationary plastic flow and, particularly in the limit of zero strain rate and negligible thermal effects, the so-called athermal quasistatic (AQS) regime. In this regime, it is now well accepted that the flow proceeds by local instabilities called shear transformations that interact elastically and can organize in larger-scale events called avalanches. Each event results, at constant strain, in a stress or energy drop. The statistics of these drops are typically a power law with a cutoff that depends on system size. This behavior can be described in terms of simple elasto-plastic models, in which subvolumes of the glass are described as linear elastic elements that yield above some critical stress, possibly triggering the yield of other elements as the stress is transmitted through the system by an elastic propagator. This simplified picture, while very successful in describing the collective behavior at large deformation, completely ignores the fine structure of the energy landscape. This structure is effectively responsible for the dynamics of the local yield process, which in these models are described in terms of some effective damping parameter.

Another set of studies has focused on the yield process itself, i.e., the transition from an essentially reversible deformation toward irreversible plastic flow or failure. This transition has been shown to depend critically on the thermal history of the system, with poorly annealed systems undergoing a rather smooth transition to a flowing state, while very well-annealed systems fracture abruptly (1). This difference, however, is not directly related to the structure of phase space in the vicinity of a given minimum, as it occurs only at large deformations.

Finally, considerable attention has been devoted recently to the possible existence of so-called “marginally stable” glassy states, in which the local phase space has a hierarchical organization that can be associated, in the language of spin glasses, with a full breaking of the replica symmetry. Ordinary glasses, on the other hand, have a simpler energy landscape, with many minima separated by rather large barriers. The transition toward marginally stable glasses was first explored in hard sphere systems (2–4), and some signatures of this structure have been observed in recent simulations of soft spheres (5, 6), however with a limitation to finite range interactions.

In this context, it was shown by Franz and Spigler (7) that the hierarchical structure of phase space should result in a peculiar response to mechanical deformation, somewhat similar to the one observed in flowing systems. Shear transformations associated with stress or energy drops have long been observed in the elastic regime at low temperature both in experiment and in simulation (8–11). However, the events observed at small deformation are generally localized, partly reversible, and thermal-history dependent, in contrast with the steady-state case (12–15). Organization in avalanches displaying a power-law distribution is observed only at large strains close to the yield point, the exponent of the corresponding power law being still controversial (11, 16–18). In contrast, the prediction made in ref. 7 is that even at very small strains (vanishingly small in the mean-field calculation), the events are scale-free avalanches with a distribution that reflects the structure of phase space described by the Parisi function. A very specific prediction is made concerning the exponent of the distribution of avalanche sizes in the mean-field limit, and preliminary numerical (7) and experimental (19) results were shown to be close to this prediction. In this work, we investigate avalanche statistics far below yielding, in both 2 and 3 dimensions, for a system of particles interacting through a Lennard-Jones potential. Different system sizes and different thermal histories of the initial configuration are considered. The simulations are carried out using the athermal quasistatic protocol (AQS) in simple shear, volume-conserving deformations. We find that even at very small strains, the mean value of avalanche size is subextensive with system size, with a finite-size scaling exponent that depends on thermal history. By making a simple scaling ansatz, all of the data for the avalanche size distribution can be collapsed onto a single master curve, with a universal avalanche exponent in the transient state clearly distinct from the one observed previously in the steady plastic flow regime and close to the value predicted in ref. 7. The mean-field calculation, being done in the limit of infinite dimensions, does not convey any information concerning the spatial structure and physical nature of the corresponding events in real space. We therefore investigate the possibility that the marginally stable state is amenable to an elasto-plastic description (20) involving interacting zones characterized by a “pseudogap.” Within this framework, a universal scaling relation observed in the steady state is also valid in the transient state and directly connects the avalanche energy with the dissipation in the transient state at zero temperature and with the exponents characterizing the pseudogap associated with marginal stability. The latter is also found to behave as predicted by the elasto-plastic models studied in ref. 20. By analyzing the dependence of the results on thermal history and size, we infer that, in the thermodynamic limit, the amorphous solid shows intrinsic inelastic behavior.

Results

Avalanche Number Density.

To investigate the statistics of avalanches, we use the avalanche number density $R\left(S,N,T_{\text{ini}}\right)$ (21), which is defined as the number of avalanches per unit of avalanche size (here measured by the corresponding energy drop) $S$ and per unit strain. $N$ and $T_{\text{ini}}$ refer to the system size (number of atoms) and the initial temperature from which the system has been quenched to zero temperature. For reference, the mode-coupling temperature is 0.325 in 2D and 0.435 in 3D systems. The corresponding normalized avalanche distribution $P\left(S\right)$ and total avalanche number $M$ per unit strain are

$$M\left(N,T_{\text{ini}}\right)={\int }_0^{\infty }R\left(S\right)dS;P\left(S,N,T_{\text{ini}}\right)=R\left(S\right)/M$$ [1]

and the total energy per unit strain dissipated in avalanches is

$$\eta \left(N,T_{\text{ini}}\right)={\int }_0^{\infty }SR\left(S,N,T_{\text{ini}}\right)dS=M⟨S⟩.$$ [2]

The systems and procedure are described in Methods. Here we recall only that the range of strains used to collect the statistics is $\gamma \in \left[\mathrm{0,0.02}\right]$, much below the yield strain ${\gamma }_{\text{Y}}$ (${\gamma }_{\text{Y}}\approx 0.06$ and 0.08 in 2D and 3D systems, respectively). In this regime, we have checked that $R\left(S,N,T_{\text{ini}}\right)$ is insensitive to the strain interval used to collect the statistics, as illustrated in SI Appendix, Fig. S5.

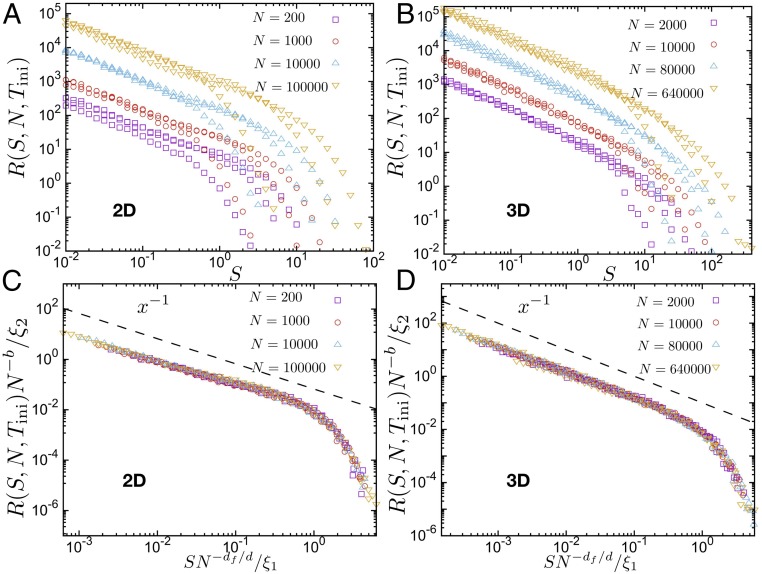
The number density of avalanches is shown as a function of their size in Fig. 1. It displays a typical power-law distribution with a cutoff that depends on system size and on thermal history. In contrast with the case of stationary plastic flow (13), avalanches in the transient state are influenced by thermal history, which also determines the brittleness of the amorphous material (1, 22). From Fig. 1 and SI Appendix, Fig. S4, it is seen that, for a given system size, the cutoff value and the extent of the power-law behavior in $R$ become smaller as $T_{\text{ini}}$ decreases and the stability of the initial configuration increases.

Fig. 1.

Avalanche number density versus avalanche size. (A and B) Avalanche number density for different system sizes and thermal histories in 2D and 3D, respectively. (C and D) Data collapse using 2 exponents, $d_f/d$ and $b$ for the scaling as a function of system size, and 2 prefactors ${\xi }_1,{\xi }_2$ that depend on thermal history (main text). The parameters are fitted from Fig. 2. The dashed line shows the avalanche exponent $-1$ predicted by mean-field theory (7) near the ground state. The investigated strain range is far below yield strain, $\gamma \in \left[\mathrm{0,0.02}\right]$, where the yield strain ${\gamma }_{\text{Y}}\approx 0.06$ and 0.08 in 2D and 3D, respectively.

Scaling Analysis.

Generally, one expects that the avalanche number density $R\left(S,N,T_{\text{ini}}\right)$ can be described as a power-law distribution with cutoff caused by finite-size effects, i.e., $R\left(S,N,T_{\text{ini}}\right)\sim S^{-\tau }f\left(S/S_c\right)$, where $S_c$ is the cutoff value influenced by system size and thermal history, $\tau$ is the avalanche exponent, and $f\left(S/S_c\right)$ is a cutoff function. Introducing the reduced size $\chi =S/S_c$, we can make the following scaling hypothesis:

$$S_c\sim {\xi }_1{N}^{d_f/d}$$ [3]

$$R\left(S,N,T_{\text{ini}}\right)\sim {\xi }_2{N}^b{\chi }^{-\tau }f\left(\chi \right).$$ [4]

Here ${\xi }_1,{\xi }_2$ are prefactors which are determined by thermal history, and the exponents $d_f/d$ and $b$, which a priori could also depend on thermal history, describe the cutoff due to the finite size of the system. Here $d_f$ is the fractal dimension of avalanches and $d$ is the dimension of the system. The total avalanche energy per unit strain $\eta \left(N,T_{\text{ini}}\right)$ can then be written as follows:

$$\eta \left(N,T_{\text{ini}}\right)\equiv {\int }_0^{\infty }R\left(S,N,T_{\text{ini}}\right)SdS\sim {\xi }_1^2{\xi }_2{N}^{b+2d_f/d}.$$ [5]

For values of the avalanche exponent $\tau <2$, the cutoff value $S_c$ can be obtained from

$$S_c=\frac{{\int }_0^{\infty }R\left(S,N,T_{\text{ini}}\right)S^{2}dS}{{\int }_0^{\infty }R\left(S,N,T_{\text{ini}}\right)SdS}\sim {\xi }_1{N}^{d_f/d}.$$ [6]

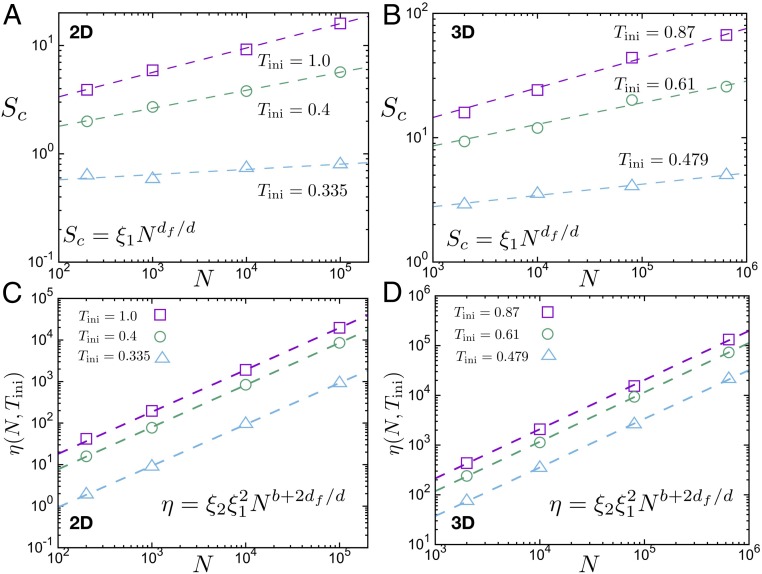
One can then collapse the data onto a master curve, removing the dependence on thermal history and system size. The parameters associated with system size ($d_f/d$ and $b$) and with thermal history (${\xi }_1$ and ${\xi }_2$) can be fitted by the formulas $S_c={\xi }_1{N}^{d_f/d}$ and $\eta \left(N,T_{\text{ini}}\right)={\xi }_1^2{\xi }_2{N}^{b+2d_f/d}$, for both 2D and 3D systems, as shown in Fig. 2. The values of the fit parameters are given in SI Appendix, Tables S1 and S2. In Fig. 1 C and D, after data collapse, the avalanche number density shows a universal behavior and the avalanche exponent is close to unity for 2D ($\tau =0.98\pm 0.01$) and 3D ($\tau =1.01\pm 0.01$) systems. The fitting curve is shown in SI Appendix, Fig. S6.

Fig. 2.

Cutoff of the distribution of avalanche sizes and total avalanche energy. (A and B) Cutoff value $S_c$ versus system size in 2 and 3 dimensions and for different thermal histories. The dashed line is a fit to a power law $S_c={\xi }_1{N}^{d_f/d}$. (C and D) Total avalanche energy versus system size. The dashed line is a power law $\eta \left(N,T_{\text{ini}}\right)={\xi }_1^2{\xi }_2{N}^{b+2d_f/d}$, where $d_f/d,{\xi }_1$ are obtained from fitting $S_c$.

Energy Balance and Relation between Exponents.

To check the consistency of the scaling analysis, it is worthwhile to consider it in relation with energy balance arguments. The total energy per unit strain of the avalanches is $\eta \left(N,T_{\text{ini}}\right)$ (Eq. 5), which depends on system size and on thermal history. As the system is deformed at zero temperature without thermostat, the avalanches constitute the only mechanism that dissipates energy; therefore energy balance implies that adding up this dissipated energy to the work done on the system during loading should give the difference in energy between an initial state at zero strain and the final strain after straining by an amount $\gamma$. In other words, if $N\mathrm{\Gamma }\left(\gamma \right)$ is the total energy dissipated in the process (which we expect to be extensive), one has the identity

$$N{\gamma }^{-1}\left(U\left(\gamma \right)-U\left(0\right)\right)=N{\gamma }^{-1}{\rho }^{-1}{\int }_0^{\gamma }\sigma \left(\gamma \right)d\gamma -N\mathrm{\Gamma }\left(\gamma \right).$$ [7]

$\mathrm{\Gamma }\left(\gamma \right)$ is the density of dissipated energy. It can be calculated from the stress–strain curve using Eq. 7. The data displayed in Fig. 3 A and B show that this quantity is indeed independent of system size, as expected. If we now identify $N\mathrm{\Gamma }$ with the total energy of the avalanches, we obtain the universal scaling relation

$$\eta \left(N,T_{\text{ini}}\right)\sim N^{b+2d_f/d}\sim N$$ [8]

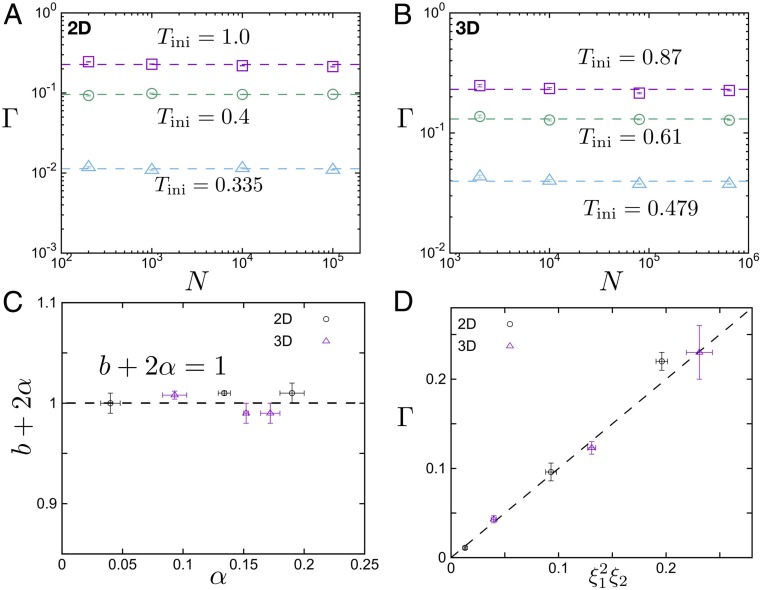
and the relation between exponents: $b+2d_f/d=1$. Fig. 3C shows that this relationship, which was first obtained in the plastic flow regime by Salerno et al. (21) and Salerno and Robbins (23), also holds for the transient avalanches in the elastic regime. Note that the expected relation for the prefactors, $\mathrm{\Gamma }={\xi }_1^2{\xi }_2$ is also confirmed in Fig. 3D.

Fig. 3.

Dissipated energy. (A and B) Density of dissipated energy versus system size in 2D and 3D, respectively. The horizontal dashed line is the mean value of $\mathrm{\Gamma }$ for different sizes. (C) Universal finite-size scaling relation. (D) Correlation between energy dissipation and avalanche energy densities. The dashed line is $y=x$. For $\mathrm{\Gamma }$, the strain range is $\gamma \in \left[\mathrm{0,0.02}\right]$.

Conclusion Concerning the Avalanche Exponent.

The avalanche exponent in our system is consistent with the theoretical work of Franz and Spigler (7), who confirmed their prediction by preliminary simulations of soft elastic spheres above jamming. Our system of Lennard-Jones particles with attractions is significantly different, so that the result suggests a universal exponent for avalanches in the elastic regime, independent of interactions and of dimensionality. A similar avalanche exponent is also observed in an independent work (24), in which the avalanche size is characterized using stress drops. This exponent is clearly distinct from the one obtained at large plastic deformation in the stationary state using AQS or overdamped dynamics at zero temperature. In the latter case, the avalanche exponent is larger than unity (close to 1.3 in simulations and to 1.5 according to depinning mean-field predictions) as confirmed both by simulation and by theoretical work (23, 25, 26). This distinction is qualitatively consistent with experiments performed in metallic glasses (16) or simulations of athermal cycling shear (17), which show a sharp transition from a transient regime to a steady state and a different avalanche exponent in these 2 states. The large avalanches in the steady state are system spanning and history independent, and they can be described as metabasin to metabasin transition on the potential energy landscape (PEL). In contrast, the small strains applied here perturb the system within a metabasin state of the PEL, and the avalanche is caused by basin to basin transition. Statistically, these 2 kinds of transition belong to 2 different universality classes.

As mentioned in the Introduction, the Franz–Spigler result is related to the hierarchical structure of the free energy landscape in a high-dimensional system. While the analysis is consistent with the Franz–Spigler result that the local minima within this landscape are marginally stable, it does not give any insight into the spatial structure and system size dependence of the associated events. In the following, we pursue the analysis of our simulation data to get some insight into this aspect, in an attempt to relate it to the view of marginal stability proposed by Lin and Wyart (20) in the context of elasto-plastic models.

Avalanche Mean Size $<S>$ and Distribution Cutoff $S_c$.

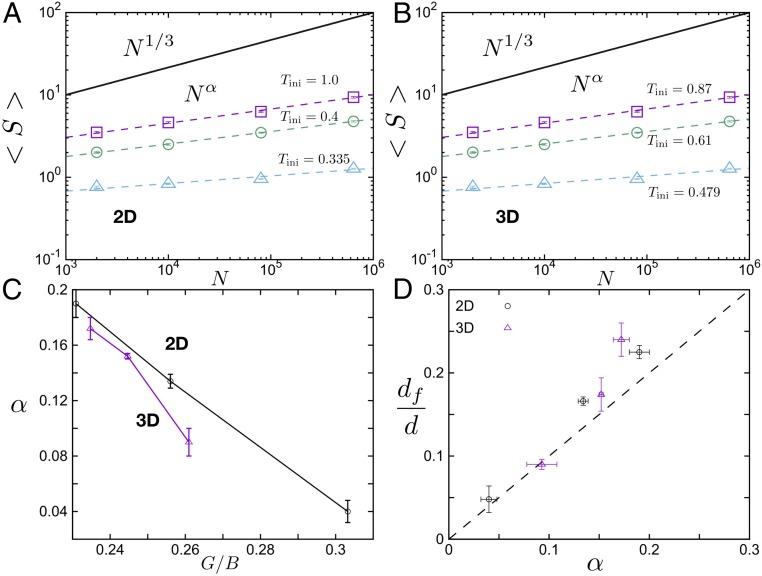
In addition to the avalanche exponent ($\tau$), the scaling parameters obtained by fitting the data plotted in Fig. 2 also provide relevant information on avalanche statistics. The fractal dimension $d_f$ characterizes the geometry of the avalanche event. We find that it decreases when the initial stability of the system, characterized by $T_{\text{ini}}$, increases. Fig. 4 shows that the mean value of avalanche size $<S>$ is also sensitive to system size and thermal history, with a scaling exponent $\alpha$ larger than zero and subextensive, as in the steady state (13). This result contrasts with the view that plastic activity in the elastic regime of amorphous solids is localized and independent of system size (14, 27). Again, a check of the consistency of the results can be obtained by relating the values of the different exponents. As first discussed by Lin et al. (28, 29), for $1<\tau <2$, a scaling relation $\alpha =\frac{d_f}{d}\left(2-\tau \right)$ holds. In our case, $\tau \approx 1$, the scaling relation reduces to $\alpha =d_f/d$, so that $S_c\sim <S>$. Fig. 4D confirms the relation $\alpha =d_f/d$, and indeed the data can be collapsed equally well using $S_c$ or $<S>$, as shown in SI Appendix, Fig. S6.

Fig. 4.

Mean value of the avalanche size $<S>$. (A and B) $<S>$ versus system size $N$ for different thermal histories, in 2D and 3D systems. The dashed line is a fit by the equation $<S>\sim N^{\alpha }$. (C) Finite-size exponent $\alpha$ versus shear to bulk modulus ratio $G/B$. (D) Correlation between mean value exponent $\alpha$ and cutoff value exponent $d_f/d$ for various thermal histories and dimensions.

Fig. 4C shows that the scaling exponent $\alpha$ is monotonically decreasing with the ratio of shear to bulk modulus $G/B$, which usually characterizes the ductility in amorphous materials (15, 30, 31). This suggests a relation between ductility and avalanche behavior in the elastic regime. We also note that, when the stability of the initial state increases ($T_{\text{ini}}$ decreases), $\alpha$ becomes smaller and could eventually vanish. That situation suggests a transition from subextensive to localized avalanches, which could be connected with ductile to brittle transition dominated by initial stability (1).

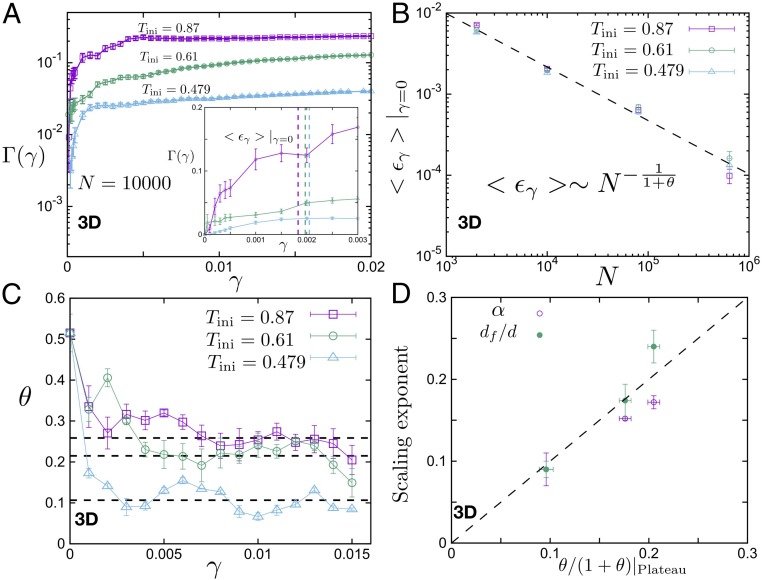
First Avalanche Event and Pseudogap Exponent $\theta$.

We now discuss the interpretation of our data within the context of the elasto-plastic model, concentrating on the statistics of the first avalanche event observed upon applying strain to the system. To this end, we consider the evolution of the dissipated energy $\mathrm{\Gamma }$ with $\gamma$ (Fig. 5). For a given thermal history, $\mathrm{\Gamma }$ as a function of strain varies slowly except in the vicinity of the very first plastic event, ${ϵ}_{\gamma }{|}_{\gamma =0}$ (14, 32). Here ${ϵ}_{\gamma }{|}_{\gamma }$ is defined as the incremental strain ${ϵ}_{\gamma }$ needed to reach the next plastic event after the system has been strained over an interval $\left[0,\gamma \right]$ (SI Appendix, Fig. S7A). The behavior shown in Fig. 5A interpolates between perfect elastic behavior without dissipation for $\gamma <{ϵ}_{\gamma }{|}_{\gamma =0}$ and the regime ${ϵ}_{\gamma }{|}_{\gamma =0}\ll \gamma \ll {\gamma }_Y$ in which dissipation is extensive and $\mathrm{\Gamma }\left(\gamma \right)={\xi }_1^2{\xi }_2$. The strain scale for this crossover, ${ϵ}_{\gamma }{|}_{\gamma =0}$, is a crucial quantity in the analysis of systems presenting marginal stability, as would be consistent with our observations for $\tau$. Indeed, in a system presenting a pseudogap for low-lying excitations of the form $P\left(x\right)\sim x^{\theta }$ (here $x$ is the strain associated with the excitation), extreme value statistics imply that the value of ${ϵ}_{\gamma }{|}_{\gamma =0}$ scales with system size as $<{ϵ}_{\gamma }>\sim N^{-\frac{1}{1+\theta }}$ (33). Here, a scaling $<{ϵ}_{\gamma }>{|}_{\gamma =0}\sim N^{-0.66}$ is obtained as shown in Fig. 5B, implying $\theta \approx 1/2$. The latter value is consistent with the theoretical prediction of a model of elastically interacting events (20) and other simulation results (14, 32, 34–36).

Fig. 5.

The mean value of first avalanche event strain. (A) $\mathrm{\Gamma }\left(\gamma \right)$ versus $\gamma$ for $N=\mathrm{10,000}$ in a 3D system. (A, Inset) Zooming in $\mathrm{\Gamma }\left(\gamma \right)$ vs. $\gamma$ curve for different thermal histories, the vertical line shows the mean value of first avalanche event strain $<{ϵ}_{\gamma }>{|}_{\gamma =0}$; from left to right is $T_{\text{ini}}=0.87,0.61,0.479$, respectively. (B) $<{ϵ}_{\gamma }>{|}_{\gamma =0}$ versus system size $N$ for different thermal histories in the 3D system. The dashed line is $N^{-0.66\pm 0.02}$ where the exponent is fitted to the data. (C) Evolution of $\theta$ with the strain window $\gamma$ for different thermal histories. The dashed line is the mean value of $\theta$ over the interval $\gamma \in \left[0.005,0.015\right]$. We define this value as the plateau value, from top to bottom, ${\theta }_{\text{Plateau}}=0.26\pm 0.01,0.21\pm 0.01,0.11\pm 0.01$ for $T_{\text{ini}}=0.87,0.61,0.479$, respectively. (D) Correlation between finite-size scaling exponents $\alpha$, $d_f/d$ and the exponent $\theta /\left(1+\theta \right){|}_{\text{Plateau}}$ in the 3D system.

Within the framework of elasto-plastic models (29), the exponent $\theta$ can be related to the exponent $\alpha$ that governs the dependence of the mean avalanche amplitude $<S>$ on system size. In the transient regime, the argument implies comparing the number of avalanches over a stress interval, $M\sim \mathrm{\Delta }\sigma /<{ϵ}_{\gamma }>$, and the corresponding change in plastic strain, $<\mathrm{\Delta }{\gamma >}_p\sim M<S>/N$. As $\mathrm{\Delta }\sigma /\mathrm{\Delta }{\gamma }_p$ does not depend on system size (SI Appendix, Fig. S8), one obtains the relation between exponents $\alpha =\theta /\left(1+\theta \right)$.

One is then faced with the paradoxical result that the data indicate a significant dependence of $\alpha$ on the system preparation, while $\theta$ appears to have the universal value $1/2$. This discrepancy can be resolved by considering the fact that the avalanches that contribute to the definition of $\alpha$ are actually collected over a finite strain range, $\gamma \in \left[\mathrm{0,0.02}\right]$. On the other hand, the value $\theta$ discussed previously involves only the very first event at $\gamma =0$, ${ϵ}_{\gamma }{|}_{\gamma =0}$. If we now extend the analysis to finite values of $\gamma$ and define a $\gamma$-dependent value of $\theta$ (characterizing the statistics of ${ϵ}_{\gamma }{|}_{\gamma }$), a very different value of $\theta$ is obtained, as illustrated in Fig. 5C. In fact, $\theta$ drops immediately from its initial value close to $1/2$ to a much lower value that depends on thermal history and remains roughly constant over the whole strain interval. This behavior corresponds to the one predicted by the model of ref. 20, and the corresponding value of ${\theta }_{\mathrm{P}\mathrm{l}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{a}\mathrm{u}}$ is perfectly correlated to the one obtained for $\alpha$, as illustrated in Fig. 5D.

Discussion and Conclusions

We have presented a detailed study of the avalanches that take place in the elastic portion of the stress–strain curve of an amorphous solid, or “elastic avalanches.” We find several evidences that these avalanches have the characteristics expected for marginal states of dense amorphous packings; in particular, the avalanche exponent $\tau$ takes the value $\tau =1$ predicted by mean-field theory for such packings (7). We propose to take this observation as a possible indication of a locally hierarchical energy landscape and explore the possibility that the corresponding events can be described within the framework of an elasto-plastic description in which marginal stability is associated with a pseudogap in the distribution of excitations. Within this framework, the exponent characterizing the pseudogap has a nontrivial evolution with strain, starting from a universal value 1/2 at zero strain and evolving rapidly toward a plateau that depends on thermal history. This behavior also corresponds to the expectations of the model described in ref. 20.

In addition, we find that the parameters characterizing avalanche distribution, energy dissipation, and pseudogap are related by 3 universal scaling relations $b+2d_f/d=1$, $d_f/d=\alpha$, and $\alpha =\theta /\left(1+\theta \right)$ and an identity $\mathrm{\Gamma }={\xi }_1^2{\xi }_2$, regardless of dimension. While these results are established using quasistatic simulations, the corresponding analysis based on scaling arguments and energy conservation should still hold at finite strain rate and inertia.

In recent years, many efforts have been devoted to the identification of marginal stability in amorphous packings, and the present consensus (4, 5) seems to be that this feature is observable only in systems with finite-range, contact interactions, at relatively low packing fractions in the vicinity of the jamming point. It is therefore surprising that features of marginal stability are observed in systems with long-range interactions and at packing fractions that are characteristic of high-density glassy systems such as metallic glasses. We now tentatively explain this observation based on 2 observations. First, the existence of a true, dissipation-free elastic regime without avalanches depends on the manner in which the thermodynamic limit and the limit of zero strain are taken. The dissipation $\mathrm{\Gamma }\left(\gamma \right)$ vanishes at small strain over a scale ${ϵ}_{\gamma }{|}_{\gamma =0}$ that scales inversely to the system size, so that one has the 2 equalities

$$\left\{\begin{array}{cc}\underset{N\to \infty }{lim}\underset{\gamma \to 0}{lim}\mathrm{\Gamma }\left(\gamma \right)\hspace{1em}\hfill & =\hspace{0.17em}0\hfill \\ \underset{\gamma \to 0}{lim}\underset{N\to \infty }{lim}\mathrm{\Gamma }\left(\gamma \right)\hspace{1em}\hfill & =\hspace{0.17em}{\xi }_1^2{\xi }_2\hfill \end{array}\right..$$ [9]

The amorphous solid in the thermodynamic limit is therefore intrinsically dissipative, as noted in previous theoretical (37) and simulation (38) works. On the other hand, any finite system will have a finite range of ideal elastic behavior. Our study, however, indicates that this range will be crucially dependent on the thermal history and sample preparation. Indeed the behavior observed for the pseudogap exponent and schematically summarized in SI Appendix, Fig. S9, as well as the behavior of the exponent $\alpha$ (Fig. 3), indicates that as the system is better annealed the range of elastic behavior will rapidly increase and the avalanches will become more fractal, with $\alpha =d_f/d$ approaching zero. As a result, it can be expected that in very well-annealed systems such as those studied in refs. 4, 5, and 36 the size needed for observing large-scale avalanches at small strains could be prohibitively large, so that observed excitations are limited to localized defects. The need to use larger sizes to properly describe the scaling behavior in the response of highly annealed systems was also pointed out in ref. 36. Whether or not there is an actual transition where $\alpha$ and ${\theta }_{\text{Plateau}}$ vanish as a function of initial annealing conditions is an issue that cannot be addressed here, although this may be consistent with the idea of a sharp change from ductile to brittle behavior described in ref. 1.

Methods

Sample Preparation.

We use 2 well-studied glass-forming models to investigate the avalanche behavior within the elastic regime: One is a 2D Lenard-Jones binary model (35), and the other one is a 3D Lenard-Jones binary model (39) with force shift (40). All of the units are reduced by the mass $m$, length scale $\sigma$, and energy $ϵ$. The number density is fixed at $\rho =1.02$ and 1.20 for 2D and 3D systems, respectively. The number ratio between large ($N_L$) and small ($N_S$) atoms is $N_L:N_S=\left(1+\sqrt{5}\right)/4$ in 2D and $80:20$ in 3D. We first annealed the sample to equilibrium state at $T_{\text{ini}}=0.335,0.4,1.0$ in 2D (SI Appendix, Fig. S1) and $T_{\text{ini}}=0.479,0.61,0.87$ in 3D using the NVT ensemble, respectively. The temperature was controlled by a Nosé–Hoover thermostat (41) with periodic boundary conditions. The energy was then minimized to obtain the inherent structure at zero temperature, and we use $T_{\text{ini}}$ to represent the thermal history of each system. In our 2 different LJ systems, we can take as a reference the mode-coupling temperature $T_{\text{MCT}}$, where $T_{\text{MCT}}=0.325$ in 2D (35) and $T_{\text{MCT}}=0.435$ in 3D (42). All of the simulations were conducted with the molecular dynamics simulation software LAMMPS (43).

Avalanche Statistics in the Elastic Regime.

To investigate finite-size effects and the statistics of avalanche distribution, we prepared series of samples with different sizes for each $T_{\text{ini}}$: In 2D, we used 2,000 independent samples for $N=200$, 500 samples for $N=\mathrm{1,000}$, 100 samples for $N=\mathrm{10,000}$, and 50 samples for $N=\mathrm{100,000}$ and in 3D we used 50 samples for $N=\mathrm{2,000}$, 20 samples for $N=\mathrm{10,000}$, 10 samples for $N=\mathrm{80,000}$, and 1 sample for $N=\mathrm{640,000}$. Due to the complexity of the potential energy landscape, the avalanche events are highly dependent on the deformation direction (44) (SI Appendix, Fig. S3), and we used the directional simple shear protocol to improve the statistics, in which a simple shear deformation gradient was used in different directions. As illustrated in SI Appendix, Fig. S2, in the 2D system, 12 directions from 0 to $\pi$ in the xy plane are used for each sample, and in the 3D system, simple shear deformation was applied in the xy, xz, and yz planes, respectively, and with again 12 directions from 0 to $\pi$ in each plane.

Although strain and stress are tensors, for the simple shear deformation, the shear strain and shear stress dominate the mechanical deformation, and then we describe the deformation using the scalars $\gamma$ and ${\tau }_{\theta }$. As shown in SI Appendix, Fig. S3, we used an athermal quasistatic shear protocol to deform the sample. First, the sample is affinely sheared by a small step strain and then the sample is minimized at a deformed strain, repeating the process until the total strain reaches the desired value. The step strain both in 2D and in 3D is $\mathrm{\Delta }\gamma =10^{-5}$ for all systems except the largest sample in 3D, where we used $\mathrm{\Delta }\gamma =2\times 10^{-6}$. During the avalanche event, there is a stress drop and an energy drop and we define the avalanche size $S$ as

$$S=N\left(\mathrm{\Delta }U+\mathrm{\Delta }\gamma {\tau }_{\theta }/\rho \right),$$ [10]

where $\mathrm{\Delta }U$ is the potential energy drop per atom during avalanche, $\mathrm{\Delta }\gamma$ is the strain step, ${\tau }_{\theta }$ is the stress just before the avalanche, and $\rho$ is the number density. We use $S>0.01$ as a threshold to recognize avalanche events. We have tested different thresholds from 0.01 to 0.1, with qualitatively similar results. Following ref. 23, we define the avalanche number at a given avalanche size and system size per unit strain as $R\left(S,N,T_{\text{ini}}\right)$. Note that both the avalanche number and avalanche size in the elastic regime not only depend on the system size $N$, but also depend on the thermal history $T_{\text{ini}}$ (SI Appendix, Fig. S4).

Data Availability.

All data relevant to this paper are available at https://doi.org/10.17605/OSF.IO/U6PYF.