A community effort to create standards for evaluating tumor subclonal reconstruction

Abstract

Tumor DNA sequencing data can be interpreted by computational methods that analyse genomic heterogeneity to infer evolutionary dynamics. A growing number of studies have used these approaches to link cancer evolution with clinical progression and response to therapy. Although the inference of tumor phylogenies is rapidly becoming standard practice in cancer genome analyses, standards for evaluating tumor phylogenies are lacking. To address this need, we systematically assess methods for reconstructing tumor sub-clonality. First, we elucidate the main algorithmic problems in subclonal reconstruction and develop quantitative metrics for evaluating them. Then we simulate realistic tumor genomes that harbor all known clonal and subclonal mutation types and processes. We benchmark 580 tumor reconstructions, varying tumor read-depth, tumour type, and somatic variant detection. Our analysis provides a baseline for the establishment of gold-standard methods to analyze tumor heterogeneity.

Editors summary

Methods for reconstructing tumor evolution are benchmarked in the DREAM Somatic Mutation Calling Tumour Heterogeneity Challenge using novel tools.

Introduction

Most tumors arise from a single ancestral cell, whose genome acquires one or more somatic driver mutations^1,2, which give it a fitness advantage over its neighbours by manifesting hallmark characteristics of cancers³. This ancestral cell and its descendants proliferate, ultimately giving rise to all cancerous cells within the tumor. Over time, they accumulate mutations, some leading to further fitness advantages. Eventually local clonal expansions can create subpopulations of tumour cells sharing subsets of mutations, termed subclones. As the tumor extends spatially beyond its initial location, spatial variability can arise as different regions harbour independently-evolving tumour cells with distinctive genetic and non-genetic characteristics^4-9.

DNA sequencing of tumors allows quantification of the frequency of specific mutations based on measurements of the fraction of mutant sequencing reads, the copy number state of the locus and the tumor purity^10,11. By aggregating these noisy frequency measurements across mutations, a tumor sample’s subclonal architecture can be reconstructed from bulk sequencing data^6,11. Subclonal reconstruction methods have proliferated rapidly in recent years^12-15, and have revealed key characteristics of tumor evolution^4,7,16-20, spread^21-23 and response to therapy^24,25. Nevertheless, there has been no rigorous benchmarking of the relative or absolute accuracy of approaches for subclonal reconstruction.

There are several reasons why such benchmarking has not yet been performed. First, it is difficult to identify a gold-standard truth for subclonal reconstruction. While single-cell sequencing could provide ground truth, it has pervasive errors²⁶, and existing DNA-based datasets do not have sufficient depth and breadth to adequately assess subclonal reconstruction methods. Alternatively, gold-standard datasets may be generated using simulations, but existing tumor simulation methods like BAMSurgeon²⁷ neither create representative subclonal populations nor phase simulated variants, which can be exploited in subclonal reconstruction^6,10. Second, it is unclear how subclonal reconstruction methods should be scored, even in the presence of a suitable gold-standard. For example, one key goal of reconstruction is identification of the mutations present in each subclonal lineage. Metrics are needed that penalise errors both in the number of subclonal lineages and in the placement of mutations across them. Third, subclonal reconstruction methods have only been developed in recent years; few groups have equal expertise with multiple tools. Algorithm developers themselves are typically experts in parameterizing their own algorithms; an unbiased third-party is needed compare different methods, each run with expert parameterization.

To fill this gap, we developed a crowd-sourced benchmarking Challenge: The ICGC-TCGA DREAM Somatic Mutation Calling Tumor Heterogeneity Challenge (SMC-Het). Challenge organisers simulated realistic tumors, developed robust scoring metrics and created a computational framework to facilitate unbiased method evaluation. Challenge participants then created re-distributable software containers representing their methods. These containers were run by the Challenge organizers in an automated pipeline on a series of test tumors never seen by the Challenge participants.

Here, we report the creation of quantitative metrics for scoring tumor subclonality reconstructions and describe tools for simulating tumors with realistic subclonal architecture. We apply these tools and metrics to characterise the sensitivity of subclonal reconstruction methodologies to somatic mutation detection algorithms and technical artefacts.

Results

How can subclonal reconstruction methods be evaluated?

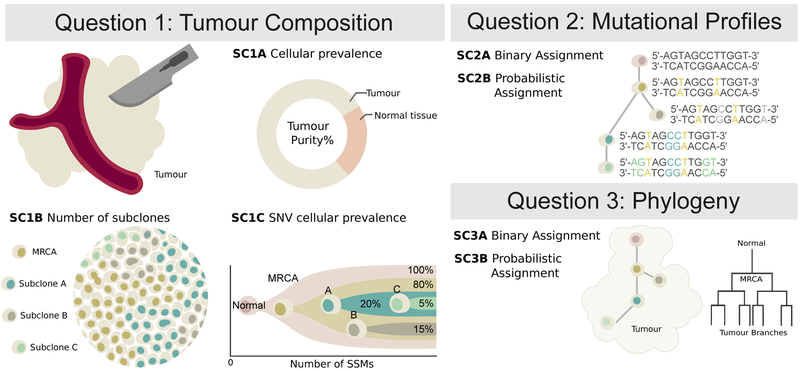
Subclonal reconstruction is a complex procedure that involves estimating many attributes of the tumor including its purity, number of lineages, lineage genotypes and the phylogenetic relationships amongst lineages. We structured our evaluation of these attributes into three categories (Figure 1). Sub-challenge 1 (SC1) quantify the ability of an algorithm to reconstruct global characteristics of tumor composition. Specifically, it evaluates each algorithm’s predictions of the total fraction of cells that are cancerous (tumor purity; SC1A), the number of subclonal lineages (SC1B) and for each subclone the fraction of cells (cellular prevalence) and number of mutations associated with it (SC1C). Sub-challenge 2 (SC2) evaluates how accurately each algorithm assigns individual single nucleotide variants (SNVs) to each subclonal lineage. It evaluates both their single-best guess at a hard assignment of SNVs to lineages (SC2A) and soft assignments represented through co-clustering probabilities (i.e. the probability that two SNVs are in the same lineage; SC2B). Finally, sub-challenge 3 (SC3) evaluates the ability of algorithms to recover the phylogenetic relationships between subclonal lineages, again both as a single hard assignment (SC3A) and as a soft assignment (SC3B). Taken together, these subchallenges define seven specific sub-challenges of SMC-Het, each corresponding to specific outputs upon which subclonal reconstruction methods can be benchmarked (Online methods).

Figure 1 ∣. Features of tumor subclonal reconstruction.

Overview of the key performance aspects of subclonal reconstruction algorithms, grouped into three broad areas covered by three key questions: (SC1) ‘What is the composition of the tumor?’ This involves quantifying its purity, the number of subclones, and their prevalence and mutation loads; (SC2) ‘What are the mutational characteristics of each subclone?’ This can be answered both with a point-estimate and a probability profile, i.e. a hard or probabilistic assignments of mutations to subclones, respectively; (SC3) ‘What is the evolutionary relationships amongst tumour subclones?’ This again can be answered with both a point-estimate and a probability profile. MRCA: most recent common ancestor.

To quantify the accuracy of these seven outputs, we considered several candidate scoring metrics, all bound between zero (very poor performance) and one (perfect performance). Appropriate metrics for SC1 were trivially identified (Online methods, Supplementary Note 1), but SC2 and SC3 required us to modify existing metrics and develop new ones. Specifically, because SC2B and SC3B are based on pairwise probabilities of co-clustering, we were unable to use clustering quality metrics designed for hard clustering nor those that require explicit estimation of the number of clusters, such as normalised mutual information (also known as the V-measure²⁸).

As SC2 and SC3 involve assigning mutations to subclonal lineages, we required candidate metrics to satisfy three conditions²⁸:

1. The score decreases as the predicted number of subclonal lineages diverges from the true number of subclonal lineages.

2. The score decreases as the proportion of mutations assigned to incorrect subclonal lineages (predicted subclonal lineages that do not correspond to the true subclonal lineage) increases.

3. The score decreases as the proportion of mutations assigned to noise subclonal lineages (predicted subclonal lineages that do not correspond to any true subclonal lineage) increases.

Moreover, metrics for evaluating cluster assignments have a number of desirable properties²⁸. We identified a set of these applicable to each task (Supplementary Note 1), used a simulation framework to assess how well a candidate metric satisfies them. We identified four complementary metrics that satisfy all three properties: Matthew’s Correlation Coefficient (MCC), Pearson’s Correlation Coefficient (PCC), area under the precision recall curve (AUPR) and average Jensen-Shannon divergence (AJSD; Supplementary Figure 1).

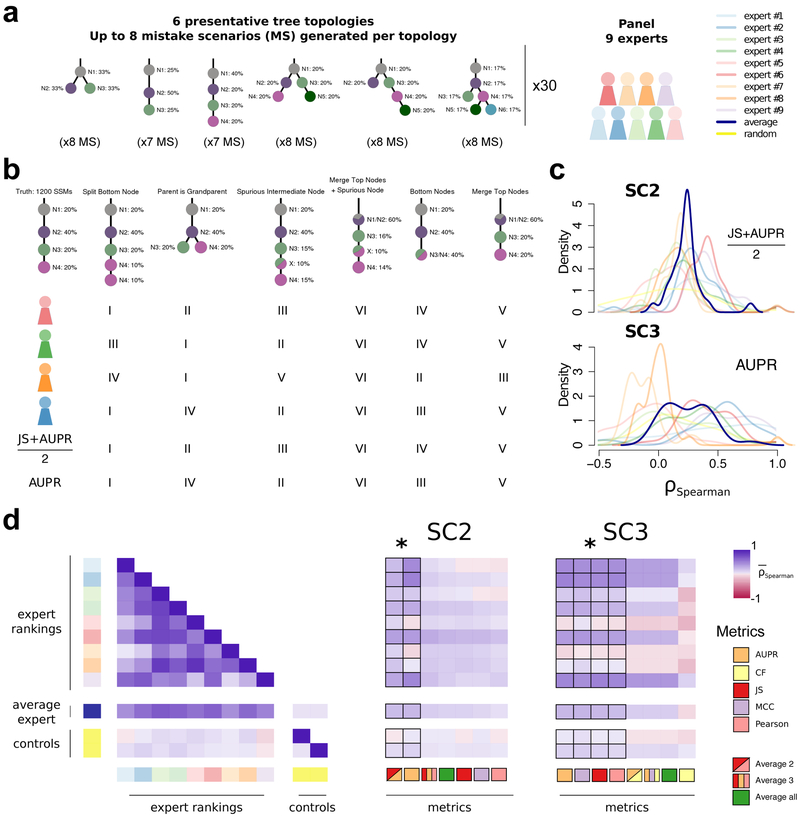
To further refine this set, we tested their behaviour relative to subclonal reconstruction errors related to parent vs. child and parent vs. cousin relationships, and splitting or merging of individual nodes (Supplementary Note 1). Nine experts ranked the overall severity of up to eight error cases for each of 30 tree topologies, providing 2,088 total expert rankings. We then simulated each error case and scored it with all candidate metrics (Figure 2a-d). Importantly for SC3, we added one metric, the Clonal Fraction (CF), which scores the accuracy of the predicted fraction of mutations assigned to the clonal peak. Unlike SC2, which scores mutation assignment, i.e. genotyping of the (sub)clones, SC3 scores tree topology, which implies an ordering of events. The clonal fraction was designed to capture expert knowledge that emerged from the expert ranking: experts tended to favour the merging of two subclonal clusters over merging of the clonal cluster with a subclonal cluster, which was not captured by other metrics. The fraction of (sub)clonal mutations is indeed a biologically relevant measure that varies widely across cancer types²⁹. Given that our metric rankings are based on subjective expert viewpoints, we have made our ranking system available online to allow others to create their own rankings and compare them to ours or use them to fine-tune scoring metrics for their own applications (https://mtarabichi.shinyapps.io/SMCHET).

Figure 2 ∣. Quantifying performance of subclonal reconstruction algorithms.

(a) Tree topologies and mistake scenarios. For each of 30 tree topologies with varying number of clusters and ancestral relationships, 7-8 mistake scenarios (MS) were derived and scored using the identified metrics for SC2 and SC3. For each tree topology a panel of 9 experts independently ranked the mistake scenarios from best to worse. (b) Expert ranking. One tree topology is shown with 6 of the 7 mistake scenarios together with the ranks of four experts and two of the metrics. The trivial all-in-one case, i.e. identifying only one cluster is not shown and correctly ranked last by all metrics and experts. (c) Density distributions of Spearman’s correlations between metrics and experts across tree topologies. For SC2 and SC3, we show the Spearman’s correlations between JS+AUPR/2 and the experts, and AUPR and the experts, respectively. (d) All average correlations between experts and metrics for SC2 and SC3. Heatmaps of average Spearman’s correlations across tree topologies between experts and metrics for SC2 and SC3. Controls are randomised ranks.

Asterisks show equivalent metrics (non-significantly better or worse according to a Wilcoxon rank-sum test p>0.05 but better than the others p<0.01; n=270; range of median increase in correlation coefficients: SC2=[0.018-0.23]; SC3=[0.024-0.36]).

Between-expert agreement, measured as pairwise rank correlations (0.52 ± 0.22), were much higher than metrics-expert agreement (for SC2B, mean: 0.14 ± 0.12 S.E., n=270 ; for SC3B, mean: 0.12 ± 0.15 S.E., n=270; Figure 2d). Subsets of metrics were highly correlated (JS, Pearson and MCC; range: 0.97-0.99, n=464), whereas others were less correlated (AUPR, JS/Pearson/MCC and CF; range: 0.47-0.78, n=464). We reasoned that less correlated metrics might capture complementary aspects of the reconstructions and derived additional metrics combining the best of them, as well as an average of all (Figure 2d). For SC2, the average of two metrics ($\frac{AUPR+JS}{2}$) and AUPR was significantly better correlated to experts than any individual metric (${\overline{\rho }}_{Spearman}=0.21$, n=30; Figure 2c,d). For SC3, AUPR, MCC, Pearson and JS were comparable and significantly better than the other metrics ${\overline{\rho }}_{Spearman}ϵ[0.19,0.23]$, n=30). We chose Pearson for subsequent analysis as it allows for assessment with a non-binary truth. The resulting expert rankings and quantitative comparisons provide a basis for future development of improved scoring metrics.

Simulating accurate subclonal tumor genomes

We elected to use simulated tumor data to run SMC-Het. The key reasons were the unavailability of deep single-cell DNA sequencing data as a gold-standard, the lack of single-cell sequencing data that match arbitrary tree structures and characteristics, the ability to simulate a large number of tumors at low-cost and the demonstrated ability of tumor simulations to recapitulate complex sequencing error profiles²⁷. We elected to use the BAMSurgeon tool created for the earlier SMC-DNA Challenges^27,30, which creates tumors with accurate SNVs, indels and small genomic rearrangements at varying allelic fractions. However, that version of BAMSurgeon lacked a number of key features for our purpose. We added five major features: (1) phasing of variants, (2) large-scale allele-specific copy number changes (including whole-genome duplications), (3) translocations, (4) trinucleotide SNV signatures and (5) replication-timing effects (Figures 3, 4). We describe each of these briefly.

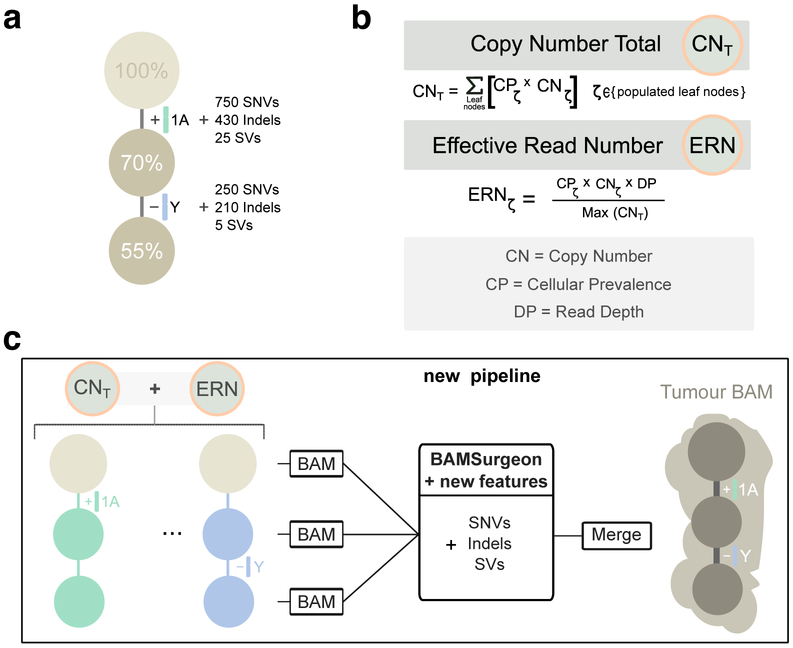
Figure 3 ∣. Simulating subclonal CNAs in tumor BAM files and spiking somatic mutations.

Example case of read number adjustment to simulate subclonal copy number aberrations (CNAs). (a) Desired structure of the tumour being simulated. (b) Read number adjustment calculations. The copy number total (CNT) for each chromosome is its copy number by adjusted by node cellular prevalence summed across all nodes. The maximum CNT across the genome is retained to normalise copy number for all chromosomes. The number of reads assigned to each chromosome at each node (the chromosome’s effective read number) is then computed as the product of the node’s cellular prevalence, the chromosome’s copy number, and the total tumour depth normalised by the maximum CNT. (c) Separation per chromosome phase and per node and new pipeline to simulate tumour BAM files with underlying intra tumour heterogeneity. The first tumour clone (70% CP) has a gain in one copy (referred to as copy A) of chromosome 1 and one of its descendant subclones (55% CP) bears a loss of the Y chromosome. After adjusting read number for CNAs in each BAM corresponding to a node, BAMSurgeon spikes in additional mutations including the new features (complex structural variants, SNVs with trinucleotide contexts and replication timing effects, etc.), and then merges the extracted reads into a final tumor BAM file.

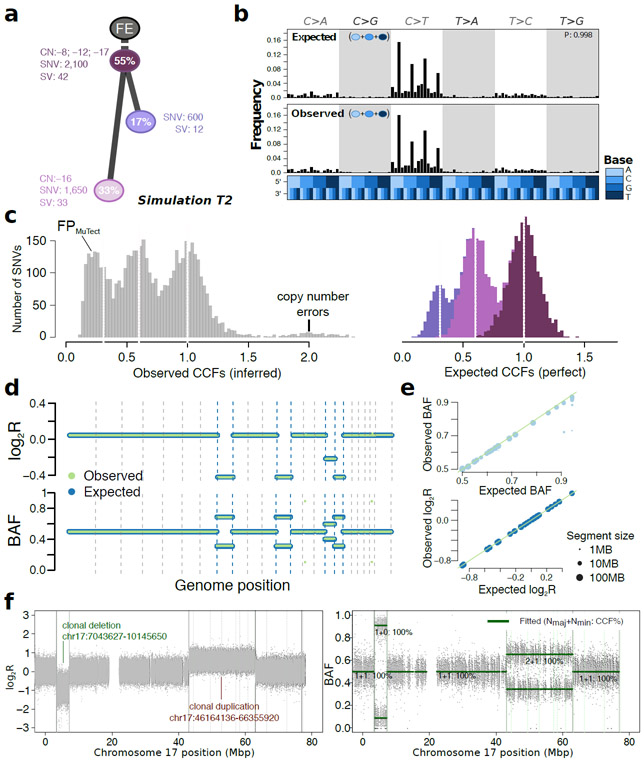
Figure 4 ∣. Simulated realistic tumor genomes.

(a) Tumor design. Simulation T2 with 55% purity (fraction of cancer cells) and two subclones. Whole-chromosome copy number events (e.g. clonal loss of chromosomes 8, 12 and 17), number of SNVs and SVs are shown for each node. (b) Single nucleotide variant trinucleotide contexts. Observed vs. expected frequencies of trinucleotide contexts in the SNVs. (c) Population frequency (cancer cell fraction, CCF) of the variants for T2. Observed vs. expected CCF distributions; false positive SNVs due to mutation calling as well as copy-number errors lead to errors in the inferred CCFs. (d) Observed (green) vs. expected (blue) logged coverage ratio (LogR) and B-allele frequencies (BAF) of copy number segments along the genome for T2 (e) Observed vs. expected BAF and logR across all segments and across all simulations. (f) Simulation of sub-chromosomal copy number events and rearrangements. LogR and BAF tracks showing how one large deletion and one large duplication simulated on chromosome 17 are correctly being called. Structural variants as called by Manta (Online methods) are shown as vertical lines, true positives are at the breakpoints defining the copy number events.

Phasing of mutations.

To correctly simulate a tumor, it is critical that genetic variants - both somatic and germline - are fully phased, as they are in real genomes. Without phasing, allele-specific copy number changes cannot be simulated correctly and will lead to incorrect B-allele frequencies and allele-specific copy number calls, amongst other errors. To achieve correct and complete phasing, we leveraged NGS data from a trio of individuals from the Genome-in-a-Bottle consortium (Supplementary Figure 2a-e) and created the PhaseTools package to accurately phase heterozygous variants identified in these data (Online methods, Supplementary Note 2). The final result of this process is two BAM files per chromosome, each representing a single parental copy.

Simulation of a tumor BAM with underlying tree topology (Figure 3a).

To simulate a tumor BAM starting from the fully phased genome, we assigned subsets of the reads to each tree node, generating down-sampled BAM files. To simulate whole chromosome copy number events, we adjusted the proportion of reads assigned to each node of the tree (Figure 3b; see below). Then, BAMSurgeon was used on each sub-BAM to simulate mutations, including SNVs, indels and SVs (Figure 3c). This strategy allowed us to efficiently and reliably simulate copy number changes of arbitrary size and add specific mutations on each allelic copy. Finally, these sub-BAMs were merged to produce the final BAM. By contrast, when we used the subclonally-naive BAMSurgeon, copy number inference was incorrect (Supplementary Figure 2f,g). After adding subclonal mutations only by specifying the VAF (i.e. without phasing or subsampling BAM files) SNVs that occurred after duplications or deletions often appeared at the wrong frequency (Supplementary Figure 2h).

Whole arm and whole genome copy number changes.

To allow changes in copy number of entire chromosomes and whole-genome ploidy changes (e.g. whole genome duplications, present in 30-50% of human cancers^31-33), we developed a method to account for gains or losses of any chromosome, including sex chromosomes based on bookkeeping of reads assigned to each node. Given a tumor design structure (Figure 3b), reads from the phased genomes were further split into individual subpopulations (sub-BAMs for leaf nodes) that make up the tumor in proportion to the copy number state of the region they aligned to and the cellular prevalence of their node. The extracted and modified reads were merged to generate a final BAM file (Figure 3c).

Translocations and large-scale SVs.

As the prior BAMSurgeon functionality could not reliably simulate SVs larger than 30 kbp or any translocations due to its use of assembly, we extended it to simulate translocations, inversions, deletions and duplications of arbitrary size. This required a new approach of creating a simulated translocation that accurately reflects the expected pattern of discordant read pair mappings and split reads (Supplementary Note 2). This also allows us to simulate translocations, which were not included in the SMC-DNA simulated data challenges³⁰. The ability to simulate translocations combined with adjustments to read coverage makes the simulation of arbitrarily large and complex SVs possible.

Trinucleotide mutation profile and replication timing.

Single nucleotide mutations are not uniformly distributed throughout cancer genomes. They are biased both regionally and locally³⁴. Mutations result from specific mutagenic stresses, which can induce biased rates of occurrence at specific trinucleotide contexts³⁵. Replication-timing bias refers to the increase in the mutation rate of regions of the genome that replicate late in the cell cycle³⁴. To resolve this issue, we created an extensible approach as part of BAMSurgeon. Each nucleotide in the genome is weighted according to its trinucleotide context, replication timing and the set of mutational signatures. Bases are then sampled from the genome until the expected trinucleotide spectrum is reached (Supplementary Note 2). BAMSurgeon can handle arbitrary mutational signatures, replication timing data at any resolution and any arbitrary type of locational bias in mutational profiles.

Selection.

Our framework for picking selecting point mutations can easily be extended to incorporate other biases in mutation frequency or location such as selection. Although explicit tumor growth models remain an area of active development^36-38 and discussion^39,40 we sought to illustrate this functionality using a recent model of 3D tumor growth that shows selection is reflected in VAF distributions across 3D tumor subvolumes³⁷. We obtained VAFs from this simulator at five different levels of selection. For each level of selection, we simulated one 3D tumor and the resection of three tumor subregions. These were taken as basis for our simulator to generate 15 tumor BAM files in which the spiked-in SNVs and their VAF were directly derived from the tumor growth models. The VAFs of the genotyped SNVs allowed accurate inference of the selection input parameter (Supplementary Figure 2i, Supplementary Note 2), while also incorporating tri-nucleotide signatures and replication timing effects. By contrast, we were unable to recover the signature of selection with MuTect SNV calls, suggesting that more than three tumor regions might be needed to detect selection through this method when significant variant detection errors are present, emphasizing the utility of simulated tumor BAMs in algorithm and model assessment (Supplementary Note 2).

Each of the simulated features was verified by comparing simulated to designed values: observed to expected measurements in the BAMs (Online methods, Supplementary Figure 3). Starting from a tumor design (Figure 4a) we systematically and quantitatively compared observed and expected trinucleotide context (Figure 4b), cancer cell fraction (Figure 4c) and copy number segment logR ratios and B-allele frequencies (Figure 4d,e). These were reviewed across all simulations to verify simulated data. These results also confirmed that BAMSurgeon can now generate complex sub-chromosomal events, including large deletions or duplications (Figure 4f).

General features of subclonal reconstruction

We next sought to quantify how different factors impact subclonal reconstruction. We therefore simulated five tumors derived from different tissue types (prostate, lung, chronic lymphocytic leukaemia, breast and colon) from published subclonal structures (Supplementary Figure 3). We also analysed a real tumor (PD4120) sequenced at 188x coverage with a high-quality consensus subclonal reconstruction based on the full-depth tumor⁴¹ as the gold-standard.

For each of these six tumors, we then down-sampled each tumor sequence to create a titration series in raw read-depth of 8x, 16x, 32x, 64x and 128x coverage. For each of the 30 resulting tumor-depth combinations, we identified subclonal copy number aberrations (CNAs) using Battenberg⁶, both with down-sampled tumors and with tumors at the highest possible depth to assess the influence of CNA detection accuracy, yielding 60 tumor-depth-CNA combinations. For each of these combinations, we identified somatic SNVs using four algorithms (MuTect⁴², SomaticSniper⁴³, Strelka⁴⁴, and MutationSeq⁴⁵), as well as the perfect somatic SNV calls for the simulated tumors, yielding 290 synthetic tumor-depth-CNA-SNV combinations. We also applied these pipelines to the real PD4120 BAM (except those involving of perfect SNV calls) resulting in 40 additional depth-CNA-SNV combinations based on a real tumor, for a total of 290 combinations. The somatic SNV detection algorithms were selected to span a range of variant calling approaches: SomaticSniper uses a Bayesian approach, MuTect and Strelka model allele frequencies while MutationSeq predicts somatic SNVs with an ensemble of four classifiers trained on a gold-standard dataset. Finally, subclonal reconstruction was then carried out on each of these using two algorithms (PhyloWGS¹³ and DPClust⁶), to give a final set of 580 tumor-depth-CNA-SNV-subclonal reconstruction algorithm combinations (see Supplementary Note 3 for algorithm descriptions). Each combination was evaluated using the scoring framework outlined above (Figure 5, Supplementary Figure 4, Supplementary Tables 1,2). In general, MuTect and SomaticSniper are more sensitive to low frequency variants and potentially preferable for subclonal reconstruction^46,47. MuTect achieved the highest SNV-detection sensitivity in our synthetic tumors (mean sensitivity 0.65 ± 0.037 standard error, n=25), followed by Strelka (0.59 ± 0.032), SomaticSniper (0.50 ± 0.031, n=25) and finally MutationSeq (0.46 ± 0.045, n=25).

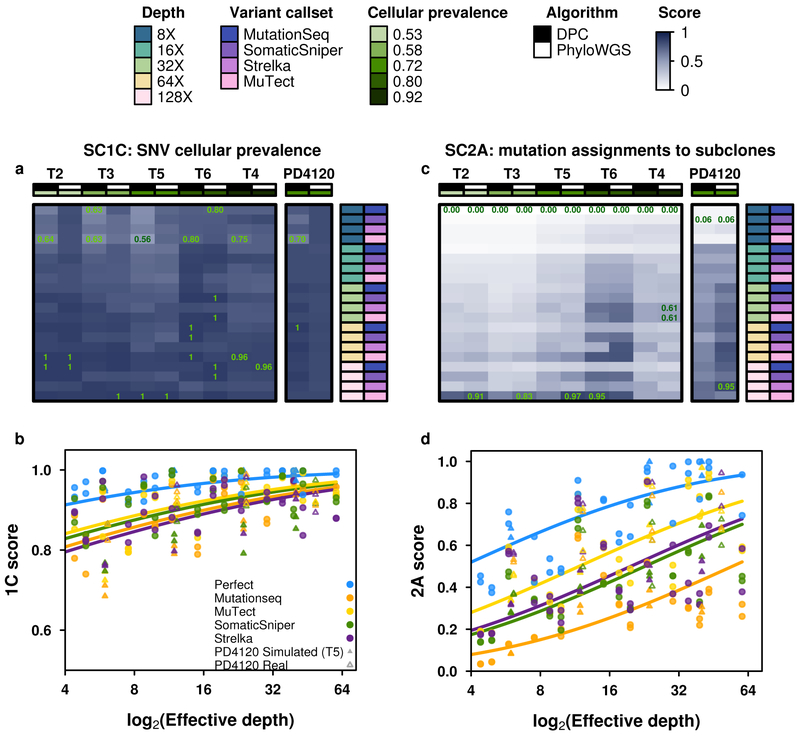
Figure 5 ∣. Error profiles of subclonal reconstruction algorithms.

To identify general features of subclonal reconstruction algorithms, we created a set of tumour-depth-CNA-SNV-subclonal reconstruction algorithm combinations by using the framework outlined in Figure 3 and 4 to simulate five tumours with known subclonal architecture, followed by evaluation of two CNA detection approaches, five SNV detection methods, five read-depths and two subclonal reconstruction methods. The resulting reconstructions were scored using the scoring harness described in Figure 2, creating a dataset to explore general features of subclonal reconstruction methods. All scores are normalised to the score of the best performing algorithm when using perfect calls at the full tumour depth. Scores exceeding this baseline likely represent noise or overfitting and were capped at 1. Only scores from reconstructions using down-sampled CNAs are shown (n=300 tumour-SNV-depth-subclonal reconstruction algorithm combinations). (a) For SC1C (identification of the number of subclones and their cellular prevalence), all combinations of methods perform well. (b) By contrast, for SC2a (detection of the mutational characteristics of individual subclones), there is large inter-tumour variability in performance. (c) Score for SC1c (same as a) as a function of effective read-depth (depth after adjusting for purity and ploidy) improves with increased read-depth, and also changes with the somatic SNV detection method, with MuTect performing best, but still lagging perfect SNV calls by a significant margin. (d) Scores in SC2A show significant changes in performance as a function of effective read-depth.

This large-scale benchmarking of 580 simulated tumors reveals general features of subclonal reconstruction accuracy. For example, consider SC1C: estimation of SNV cellular prevalence. All algorithms and SNV detection algorithms showed a consistent increase in accuracy with increasing sequencing depth for SC1C (Figure 5a, b). No somatic SNV detection algorithm matched the performance of perfect SNV calls (β = 0.22, P = 0.0011, generalised linear model, n=500, df=29). By contrast, the use of high- vs. low-depth sequencing for subclonal detection of CNAs had no detectable influence on reconstruction accuracy in either real or simulated tumors (P>0.05, generalized linear model, n=500, df=29; Supplementary Table 2). Interestingly, in SC1C, neither the use of low- vs. high-depth tumors for CNA detection nor the specific subclonal reconstruction algorithm used had a significant influence on the accuracy of subclonal reconstruction. Similarly, both PhyloWGS and DPClust performed interchangeably on this question in the simulated tumors (P=0.14, t=−1.47, n=290 Supplementary Figure 5g-l, Supplementary Tables 2).

A different story emerged for SC2A - identifying the mutational profiles of individual subclones (Figure 5c,d). All algorithms performed relatively poorly, with major inter-tumor differences in performance. Tumor T2 was systematically the most challenging to reconstruct and T6 the easiest (Figure 5c, Supplementary Table 5). This in part reflects the higher purity of T6, and indeed we see a strong association between effective read-depth and reconstruction accuracy in both the simulated and real tumors, with each additional doubling in read-depth increasing reconstruction score by about 0.1 (Figure 5d). At effective read-depths above 60x, the performance of all tumor-CNA-SNV-subclonal reconstruction combinations seemed to plateau, suggesting that a broad range of approaches can be effective for detection of subclonal mutational profiles at sufficient read-depth. Again, the use of high- vs. low-depth sequencing for subclonal CNA detection had no discernible influence (and this held true for all sub-challenges; Supplementary Table 2). By contrast, SC2A scores were strongly dependent on the SNV detection pipeline, with perfect calls out-performing the best individual algorithm (MuTect) by ~0.05 at any given read-depth. Differences in SNV detection algorithm sensitivity largely accounted for performance differences among algorithms (β_sensitivity = 0.30, P = 8.92 × 10⁻¹³, generalised linear models, n=500, df=30; Supplementary Table 3). MuTect, the most sensitive SNV detection algorithm, had the best performance and MutationSeq, the least sensitive, had the poorest. Broadly, SomaticSniper and Strelka showed similar performance, but interestingly showed significant tumor-by-algorithm interactions for several sub-challenges (Supplementary Figure 5a-f), which may reflect tumor-specific variability in their error profiles. Notably, MutationSeq performed much better on with the real tumor than with simulated tumors (Supplementary Figure 5a-f).

In general, DPClust and PhyloWGS showed very similar performance, but with exceptions that reflect their underlying algorithmic features. First, in SC1A DPClust, which uses purity measures derived from CNA reconstructions, showed a significant and systematic advantage over PhyloWGS (β_PhyloWGS = −0.42, P = 1.5 × 10⁻⁷, generalised linear model, n=500, df=13), which uses purity measures partially dependent on SNV clustering. The latter are more sensitive to errors in VAF due to low sequencing depth and this is reflected in the pattern of SC1A scores. Second, in SC2B PhyloWGS, which uses a phylogenetically-aware clustering model, had significantly better performance than DPClust, which uses a flat clustering model (Supplementary Figure 5g, Supplementary Table 2). Thus, our metrics are sensitive to differences in modelling approaches, which manifest in variability in performance on different aspects of subclonal reconstruction. Validating these results, for the real high-depth tumor, DPClust significantly outperformed PhyloWGS in SC1, while PhyloWGS was superior in SC2 (Supplementary Table 4).

Robustness of subclonal reconstruction

Surprised by the insensitivity of scores to the use of high- or low-depth sequencing data for subclonal CNA assessment, we sought to characterize the sensitivity of subclonal reconstruction to errors in CNA detection. We repeated the analyses described above using five types of CNA input: original (untouched), CNAs with doubled ploidy, CNA calls with a random portion of existing calls wrongly assigned (scramble) and CNAs with additional gains (scramble gains), or with additional losses (scramble loss). The latter three error types were titrated in intensity, scrambling 10%, 20%, 30%, 40% and 50% of all CNAs, gains and losses, respectively.

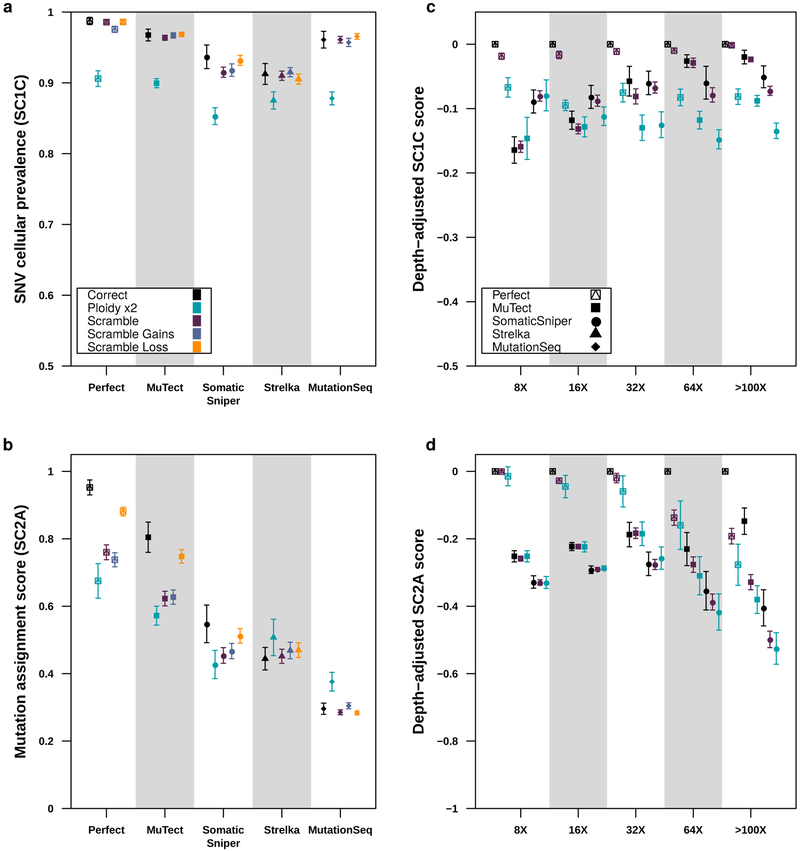
The resulting 4,250 tumor-depth-CNA-SNV-reconstruction combinations were each assessed using our scoring metrics (Supplementary Table 1). For SC1 and SC2, incorrect ploidy impaired reconstruction accuracy overall (Figure 6A). As expected, scores decreased as the proportion of incorrectly assigned CNAs increased (Supplementary Figure 6a,b). The effect of incorrect calls on SC2A accuracy was only apparent at >32x coverage and was strongest with perfect and MuTect SNVs (Figure 6B), suggesting the relative impact of CNA errors increases with reconstruction quality. Interestingly, PhyloWGS had significantly better performance for all subchallenges than DPClust when CNA errors were introduced (SC1C: β_PhyloWGS = 0.042, P = 6.06 × 10⁻¹⁰; SC2A: β_PhyloWGS = 0.066, P = 1.85 × 10⁻¹⁰ generalised linear models, n=4250, df=21 & df=33; Supplementary Table 5). These results suggest that PhyloWGS’s strategy of incorporating CNAs in the allele count model may be more robust to errors in CNA detection than only using them to initially correct SNV VAFs (Supplementary Figure 5g, Supplementary Note 3). As CNA-handling in the presence of errors distinguishes algorithms with otherwise comparable performance, increasing robustness to errors in CNA calls may be a promising avenue for improvement of subclonal reconstruction algorithms.

Figure 6 ∣. Impact of CNA error profiles on subclonal reconstruction.

(a) Effect of CNA errors on mean SC1c scores and SC2a (b) scores (with standard errors shown) at 100x across somatic SNV detection algorithms (n=850). (c) Effect of CNA errors on mean SC1c and SC2a (d) scores (with standard errors shown, n=2250) at various depths when scores for perfect calls are set to zero to yield depth-adjusted scores.

Taken together, these results suggest that subclonal reconstruction accuracy is highly sensitive both to SNV and CNA detection, with interactions between specific pairs of variant detection and subclonal reconstruction algorithms (Online methods; Supplementary Figure 6c,d). There is significant room for algorithmic improvements that capture inter-tumor differences and better model the error characteristics of feature-detection pipelines.

Discussion

As DNA sequencing costs diminish and evidence for clinical utility accumulates, increasingly large numbers of tumors are sequenced each year. Nevertheless, it remains common practice for only a single spatial region of a cancer to be sequenced. The reasons for this are myriad: costs of multi-region sequencing, needs to preserve tumor tissue for future clinical use and increasing analysis of scarce biopsy-derived specimens in diagnostic and metastatic settings. Whilst robust subclonal reconstruction from multi-region sequencing is well-known^5-8, accurately reconstructing tumor evolutionary properties from single-region sequencing could open new avenues for linking these to clinical phenotypes and outcomes.

We describe a framework for evaluating single-sample subclonal reconstruction methods, comprising a novel way of scoring their accuracy, a technique for phasing short-read sequencing data, an enhanced read-level simulator of tumor genomes with realistic biological properties and a portable software framework for rapidly and consistently executing a library of subclonal reconstruction algorithms. These elements, each implemented as open-source software and independently reusable, form an integrated system for quantitation of key parameters of subclonal reconstruction. We generate a 580-tumor titration-series for evaluating subclonal reconstruction sensitivity to both effective read depth and specific somatic SNV detection pipelines. These data give guidance for improving subclonal reconstruction: increasing effective read-depth above 60x, after controlling for tumor purity and ploidy. They also suggest reconstruction algorithm developers should consider accounting for the error properties of specific somatic variant detection approaches.

Lineage-tracing tools are emerging that will likely revolutionize our understanding of tissue growth and evolution, such as GESTALT⁴⁸, ScarTrace⁴⁹, and MEMOIR⁵⁰. However, these are not applicable to the study of human cancer tissues in vivo. In many areas of biology, ground-truth is still either inaccessible or impractical to measure with precision. In cases like these, simulations are extremely valuable in providing a lower bound on error profiles and an upper bound on method accuracy. By incorporating all currently known features of a phenomenon, simulators codify our understanding. Divergence between simulated and real results quantitates the gaps in our knowledge. The creation of an open-source, freely available simulator capturing most known features of cancer genomes thus represents one avenue for exploring the boundaries of our knowledge.

Large-scale benchmarking of multiple subclonal reconstruction methods using this framework on larger numbers of tumors is needed to create a gold-standard. Such a benchmark would both inform algorithm users, who will benefit from an understanding of the specific error profiles of different methods, and algorithm developers who will be able to update and improve methods while ensuring software portability. Tumor simulation frameworks provide a valuable way for method benchmarking, and can complement other approaches like comparison of single-region to multi-region subclonal reconstruction, and the use of model organism and sample-mixing experiments.

Online methods

Sub-challenges description

To evaluate subclonal reconstruction algorithms, we posed seven sub-challenges and designed associated scoring metrics to evaluate performance in each sub-challenge. Sub-challenges 1A through 1C, collectively called the subclonal architecture challenges, evaluated properties of the subclonal reconstruction without considering the assignment of individual single nucleotide variants (SNVs) to subclones. Sub-challenges 2A and 2B, the clustering challenges, evaluated the assignments of individual SNVs to subclones. Sub-challenges 3A and 3B, the ancestry challenges, evaluated the ancestral relationships of individual SNVs. Each of the sub-challenge required submission data in a specific format described below.

Sub-challenge 1: Subclonal architecture

Sub-challenge 1A: Cellularity

Predict the proportion of cells in the sample that are cancerous (i.e., the cellularity of the sample) or cellular prevalence (CP).

Output Data: c is a real number with 0 ≤ c ≤ 1 where c represents the predicted cellularity of the tumor sample.

Sub-challenge 1B: Lineage count

Predict the number of lineages (either subclonal or clonal) in the sample.

Output Data: κ is a positive integer and κ ≥ 1, where κ is the predicted number of lineages in the tumor sample. Note that we do not distinguish between clonal and subclonal lineages here, but it is assumed that each sample has at one (i.e. clonal) lineage.

Sub-challenge 1C: Subclonal architecture

Predict (i) the proportion of the cells in the tumor sample in each of the subclonal lineages (i.e., their cellular prevalences) and (ii) the proportion of SNVs associated with each lineage. Collectively, we call these two predictions the estimated subclonal architecture.

Output Data: φ is a vector containing κ real numbers, each of which, e.g., φ_k, represents the predicted cellular prevalence in the associated predicted lineage k. Clearly 0 ≤ φ_k ≤ 1 for all lineages k. Similarly, N is a vector containing κ positive integers, each of which, e.g., N_k, represents the predicted number of mutations in the associated lineage k. We insist that N_k ≥ 1.

Sub-challenge 2: Clustering

Predict the lineage assignment of each SNV.

Sub-challenge 2A: Single best hard assignment

Predict the assignment of each mutation to each lineage.

Output Data: τ is a vector of n positive integers, where n is the number of SNVs, in which each element τ_i represents the index of the subclonal lineage to which mutation i is predicted to be assigned. Thus, 1 ≤ τ_i ≤ κ.

Sub-challenge 2B: Probabilistic co-clustering

Predict which pairs of mutations are in the same cluster. Note that this challenges differs from the previous one because the co-clustering predictions can be probabilistic.

Output Data: The predicted co-clustering matrix, CCM, which is an n×n matrix of real numbers, where CCM_ij is the probability that mutation i is in the same subclone as mutation j, and 0 ≤ CCM_ij ≤ 1. Note that a single best assignment can be represented by setting CCM_ij = 1 when mutation i and mutation j are assigned to the same lineage, and CCM_ij = 0 otherw. Every mutation is assigned to the same lineage as itself, so we require that all the values on the diagonal of the CCM matrix be 1.

Sub-challenge 3: Ancestry

Predict the ancestral relationships between the SNVs.

Sub-challenge 3A: Single best ancestry

Predict the ancestral relationships among the predicted lineages.

Output Data: p is a vector of κ positive integers, each one, e.g., p_k, is the index of the predicted parental lineage for lineage k where p_k = 0 indicates that lineage k has no parent, i.e., that it descends from the normal lineage. In other words, lineage k is a clonal lineage. Thus, 0 ≤ p_k ≤ κ and p_k ≠ k.

Sub-challenge 3B: Probabilistic ancestor-descendant matrix

Predict the ancestral relationships among pairs of SNVs. Note that this challenges differs from the previous one because these predictions can be probabilistic.

Output Data: The predicted co-clustering matrix, CCM, as defined in Sub-challenge 2B, and a predicted ancestor-descendant matrix, ADM, which is an n × n matrix where ADM_ij is the probability that mutation i is assigned to a subclonal lineage that is ancestral to the subclonal lineage the mutation j is assigned to, and 0 ≤ ADM_ij ≤ 1. As in Sub-challenge 2B, above, a single best ancestry can be represented by the ADM by setting ADM_ij if and only if mutation i is assigned to a lineage ancestral to that of mutation j. Elements on the diagonal of the ADM matrix required to all be 0.

Scoring metrics

Here we describe each scoring metric used to evaluate the subclonal reconstruction algorithms.

Sub-challenge 1A Metric

The SC1A score is

$$1-\mid \rho -\mathrm{c}\mid$$

where ρ is the true cellularity, c is the predicted cellularity and |x| is the absolute value of x. Note that we require that 0 ≤ ρ ≤ 1 and 0 ≤ c ≤ 1.

Sub-challenge 1B Metric

The SC1B score is:

$$[\mathrm{L}-\mathrm{d}+1]∕(\mathrm{L}+1)$$

where L ≥ 1 is the true number of subclonal lineages, d is the absolute difference between the predicted and actual number of lineages, d = min(|κ - L|, L+1). We do not allow d to be higher than L+1 so that the SC1B score is always ≥ 0.

Sub-challenge 1C Metric

Scoring SC1C is challenging because the number of subclonal lineages can differ between the truth and the prediction, as can their size and cellular prevalence. As such, we adopted metric based on the earth-mover distance between the true and predicted architectures. First, we note that the subclonal architectures can be viewed as a clustering of data points in one dimension. In this view, each data point is a SNV, and they are clustered on the basis of their predicted cellular prevalence into clusters corresponding to each lineage.

If we were considering individual SNVs in this metric, we could compute a distance between the real and the predicted clustering of those data points by computing the average value of |φ_k - δ_l| where φ_k is the cellular prevalence of the lineage, k, that mutation i is assigned to in the predicted clustering and δ_l is the cellular prevalence of the lineage, l, that mutation i is assigned to in the true clustering. However, since we are not considering individual SNVs, we define the distance between two clusterings as the minimum possible value of this average, given the real and predicted subclonal architectures (i.e. the vectors of cellular prevalences and counts of number of SNVs assigned to each cluster). This value, EMD, is exactly the (normalized) earthmover distance between the real and predicted clusterings.

The procedure described below computes 1-EMD given the true and predicted subclonal architectures.

First, we sort both the predicted subclonal lineages from 1 to κ and the true subclonal lineages from 1 to L in ascending order according to their cellular prevalence (CP). Let α_k be the proportion of mutations assigned to predicted subclonal lineage k, for k = 1...κ. Similarly, let β_l be the proportion of mutations assigned to true subclonal lineage l, for l = 1...L. Let φ_k be the predicted CP of predicted subclonal lineage k for k = 1...κ and let δ_l be the true CP of true subclonal lineage l for l = 1...L.

Let ω_p be a vector of S predicted real numbers with:

$${\omega }_{p,i}={\varphi }_1\text{for}\frac{i}{S}\le {\alpha }_1,\text{or}$$

$${\omega }_{p,i}={\varphi }_k\text{for}{\mathrm{\Sigma }}_{j\in 1...\mathrm{k}-1}{\alpha }_j<\frac{i}{S}\le {\mathrm{\Sigma }}_{j\in 1...\mathrm{k}+1}{\alpha }_j\text{or}$$

$${\omega }_{p,i}={\varphi }_{\kappa }\text{for}{\mathrm{\Sigma }}_{j\in 1...\kappa -1}{\alpha }_j<\frac{i}{S}$$

And let ω_t be a vector of S true real numbers with:

$${\omega }_{t,i}={\delta }_1\text{for}\frac{i}{S}\le {\beta }_1,\text{or}$$

$${\omega }_{t,i}={\delta }_k\text{for}{\mathrm{\Sigma }}_{j\in 1...\mathrm{k}-1}{\beta }_j<\frac{i}{S}\le {\mathrm{\Sigma }}_{j\in 1...\mathrm{k}+1}{\beta }_j\text{or}$$

$${\omega }_{t,i}={\delta }_{\mathrm{L}}\text{for}{\mathrm{\Sigma }}_{j\in 1...\mathrm{L}-1}{\beta }_j<\frac{i}{S}$$

We set S to 1,000 and the SC1C scoring metric is then defined as:

$$\frac{1}{S}\sum _{s=1}^S\mid {\omega }_{t,s}-{\omega }_{p,s}\mid$$

We compute the SC1C scoring metric using two different sets of true subclonal lineages. One set contains only the mutations that were spiked into the simulation. The other set of lineages also contains false positive mutations that were not spiked-in, but were detected in somatic variant calling. In this set, the lineage containing the false positive mutations is assigned a CP of 0. Contestants receive the higher of the two scores.

Sub-challenge 2 Metric

Both SC2A and SC2B use the same scoring metric. This metric is the mean of two different correlation measures between the predicted co-clustering matrix (CCM^Pr) and the true co-clustering matrix (CCM^Tr); the Area Under the Precision-Recall curve (AUPR) and the average Jensen-Shannon divergence of the co-assignment probabilities (AJSD). CCM^Tr is computed from the true SNV assignments to lineages using the procedure described in the previous section under the description of SC2B. CCM^Pr for SC2A is also computed using this procedure.

Each correlation measure, calculated by comparing CCM^Pr to CCM^Tr, and is normalized, by subtracting a constant value and linearly scaling, to be between 0 and 1. This normalisation is computed so that 1 corresponds to a ‘perfect score’ i.e. when CCM^Pr = CCM^Tr and 0 corresponds to the smaller of the scores achieved by two ‘bad scenarios’: CCM^Pr = I_nxn or CCM^Pr = 1_nxn. If a method achieves a score < 0 after normalization, then the score is set to zero. The overall Sub-challenge 2 score is calculated as the mean of the two individual normalized correlation measures:

I. Area under the precision recall curve (AUPR).

The area under the receiver operating characteristic (ROC) curve, also known as the Precision-Recall curve, which plots the false positive rate against the true positive rate across all possible thresholds for classifying matrix entries as true or false (for SC2 and SC3, all real values r ∈ [0,1]). To calculate the AUPR we create the Precision-Recall curve using the matrix values and then estimate the Area under this curve using point estimators.

II. Average Jensen-Shannon divergence of co-assignment (AJSD)

To define this correlation measure, we transform each CCM matrix so that each row could be interpreted as a discrete probability distribution. Then, for each row in the predicted CCM, we compute the Jensen-Shannon divergence between it and the corresponding row in the true CCM matrix. Our measure, the average Jensen-Shannon divergence (AJSD) is the average of these divergences.

Specifically, for the predicted CCM matrix, C, for the i-th row, we define a real valued vector, pⁱ, for each mutation i, whose j-th element, ${\mathrm{p}}_j^i=\frac{C_{ij}}{{\sum }_{k\ne i}{C}_{ik}}$for i ≠ j and ${\mathrm{p}}_i^i=0$. Because of how pⁱ is defined, it can be interpreted as a discrete probability distribution over all of the SNVs in the sample. Similarly, for the actual CCM matrix, K, for the i-th row, we define qⁱ, by setting ${\mathrm{q}}_j^i=\frac{K_{ij}}{{\sum }_{k\ne i}{K}_{ik}}$for i ≠ j, and ${\mathrm{q}}_j^i=0$ otherwise. Then AJSD is the average across all rows i of Jensen-Shannon divergence (JSD) between pⁱ and qⁱ. To compute the JSD, to avoid taking the log of 0, we define p^i* as

$$p_j^{i\ast }=\frac{(1-\alpha ){\mathrm{p}}_j^i+\alpha }{(1-\alpha )+N\alpha }$$

for a small value α = 0.01 and we define ${\mathrm{m}}_j^{i\ast }$ similarly and set ${\mathrm{m}}_j^{i\ast }=\frac{p_j^{i\ast }+q_j^{i\ast }}{2}$. And JSD is:

$$JSD({\mathrm{p}}^i,{\mathrm{q}}^i,\alpha )=KL({\mathrm{p}}^{i\ast }\Vert {\mathrm{m}}^{i\ast })∕2+KL({\mathrm{q}}^{i\ast }\Vert {\mathrm{m}}^{i\ast })∕2$$

Sub-challenge 3 metric

To compute the SC3 scoring measure, we require the CCM and ADM matrices as defined above and we must compute the Cousin Matrix (CM). The CCM and ADM matrices are either provided by the user or constructed from the true ancestral relationships. To construct the cousin matrix, we note that each mutation pair (i,j) must have one of four relationships: i is clustered with j, i is the ancestor of j (or vice versa), or i and j are in branching lineages (in other words, they are cousins). As such, given ADM and CCM, we compute the CM by setting CM_ij = 1 − CCM_ij − ADM_ij − ADM_ji.

Then, to compute the SC score, we horizontally append the CCM, the ADM, the transpose of the ADM, and the CM for the true and predicted versions of these matrices, making two matrices of size n by 4n. In other words, one of these matrices is constructed from all of the true matrices and the other from all of the predicted ones.

We then compute the Pearson correlation coefficient (PCC) between these two rectangular matrices:

The PCC between two matrices C and K is defined as:

$$PCC=\frac{Cov(C,K)}{{\sigma }_C{\sigma }_K}$$

where Cov(C,K) is the covariance of the vectorized versions of C and K, σ_c is the standard deviation of vectorized C, and σ_K is the standard deviation of vectorized K.

Data preparation

To create our phase-separated mapping set, we used public data from the Genome-in-a-Bottle consortium obtained from sequencing the trio of individuals with Coriell ids: GM24385 (son), GM24149 (father), and GM24143 (mother). We used both the high-coverage (300x) paired-end (PE) Illumina data and the low coverage (16x) 6kb mate-pair (MP) Illumina data.

For the PE datasets, we downloaded the publicly available FASTQ files, and mapped them locally with bwa version 0.7.10 using the flag -M and otherwise default settings, against the hs37d5 human reference with decoys. We marked duplicates with Picard (v1.121). For the MP datasets, we downloaded and used the publicly available mappings.

To identify variants, we used only the PE data for each sample, and a standard variant-calling pipeline with GATK (v2.4.9). The BAM files were realigned and calibrated using GATK’s RealignerTargetCreator command, followed by IndelRealigner. Bases were recalibrated using the BaseRecalibrator and PrintReads commands. Germline calling was performed using UnifiedGenotyper and variant calls without the ‘PASS’ field were filtered out. Short indels and single nucleotide variants that were present in both maternal and paternal BAMs were used for phasing.

Phasing

First, we constructed an unphased set of variants using GATK-based germline SNP prediction, identifying 2,559,193 diploid heterozygous short insertions, deletions, and single nucleotide variants in the child sample. Next, we created the PhaseTools package to accurately phase heterozygous variants identified in these data (Supplementary Figure 2, Supplementary Note 2). This phasing prioritized connections between alleles that were directly supported by NGS data. Due to the availability of both paired-end and 6 kbp mate-pair Illumina sequencing data for this sample, we were able to construct initial per-chromosome phase sets (i.e. sets of heterozygous variants phased together) at a rate of 1 phase set per ~12 kbp. The phasing was then extended by connecting phase sets using parent-of-origin information, in cases where this information could be computed by inspecting parental genotypes or parental NGS phasing. This increased the extent of our phase sets, decreasing their rate to 1 per ~76 kbp. The phasing was extended once more by incorporating phasing information produced by Beagle, reaching an ultimate rate of 1 phase set per ~86 kbp. We note that this long-range phasing could be obtained even without leveraging any long-read data. Remaining phase sets were then randomly rotated and collapsed to obtain a final complete phasing of all heterozygous variants in the child. Given the complete phasing of the variants described above, we used the bam-phase-split program, also part of PhaseTools, to phase each fragment in an NGS dataset of the child sample. The program inspected the reads in each fragment, collecting information for which alleles that fragment supported at each heterozygous variant, and combined that information in order to phase the fragment. Fragments not spanning any heterozygous variants were phased randomly.

At the end of the process, while the median length of phased contigs from using only NGS data was ~15 kbp regions, it increased to ~85 kbp regions using the full PhaseTools pipeline.

Splitting BAM reads into subclones and spiking-in mutations

Read splitting at nodes occurs in a pseudo-random manner using a windowed approach. For each node, let w be every window of reads (set to 1000) and p be the proportions of reads to extract. BAM files are sorted by coordinate using SAMtools sort. For every w paired reads ordered by first read pair coordinate, exactly floor(w × p) paired reads are chosen at random and retained. As compared to a global resampling to the target coverage per node (i.e. setting the window size to the total number of reads aligning to the chromosome), this local sampling accomplishes a less variable coverage across the final chromosome. All extracted reads are merged together using Picard tools, first by phase, then by chromosome, and finally into the tumor BAM. The merged BAM file is then sorted by coordinates, avoiding any possibility to identify from which sub-BAM reads originate.

To complete the final tumor BAM, we further normalize the phases of chromosomes relative to all the phases, based on their individual total fractional copies. For each phase of each chromosome, let p_i be the cellular prevalence and c_i the number of copies at the i^th leaf node. Then C_chr,phase = sum_i (p_i × c_i) represent the total fractional copies. Take M to be the maximum of all CNAs, including tandem duplications, across chromosomes and set this value as the 100% copy proportion. Leaf nodes are down-sampled by taking C_chr,phase / M of the read pool assigned to it. Read pools are adjusted using a bottom-up approach. At each internal node, the cellular copies of its children are summed and the read pool proportions are adjusted (Figure 3).

designatePortions {

if leaf node:

return p_i * c_i / C_chr,phase

else:

quantities = []

quantity_sum = 0

for each child:

quantity[child] = designatePortions{config->child}

quantity_sum += quantity[child]

for each child:

config->child->read_proportion = quantity[child] / quantity_sum

}

If tandem duplications are present, reads that are not incorporated in a node (surplus reads) are down-sampled similarly to provide donor BAMs at the right depth. Surplus reads are down-sampled in proportion to their depth adjusted copy number for a given node, starting with the highest copy number duplications for each node to yield the maximum depth donor bam for each node. If lower copy number duplications exist, these donor BAMs are subsequently down-sampled again in proportion to copy number to yield the lower copy number donor BAMs.

After calculating the per-phase-per-chromosome read pools, BAMSurgeon spikes in mutations given a set number of SNVs, Indels, and SVs into the appropriate read pool before merging them into the final BAM. In Supplementary Note 2 we describe how we spike in mutations compatible with replicating timing, pre-defined tri-nucleotide context spectra and selection.

Altogether, using this approach we achieved a median accuracy of 90.6%, with a median false positive rate of 4.5% and a median false negative rate of 5.92% for the five tumors reported after calling SNVs with MuTect prior to down-sampling.

Large scale SV simulations

We extended BAMSurgeon to simulate large SVs by simulating two SV breakpoints with local alignment and contig assembly. We employed a two-pronged approach to simulate copy number changes as the existing BAMSurgeon functionality could not reliably simulate SVs larger than 30 kbp (Supplementary Figure 2 f-h). To simulate smaller scale copy number changes (>10 kbp) we extended the BAMSurgeon SV framework to simulate translocations, inversions, deletions, and duplications of arbitrary size (Supplementary Note 2). To simulate chromosome level CNAs, we locally downsampled reads.

Chromosome-level copy number simulations

A gain of N_a chromosomes from a given node a is simulated by first splitting the reads in a evenly into N_a + N_b (where N_b is the number of chromosomes in the parent of a) while down-sampling the reads in all other nodes by N_a + N_b. Since each node is handled individually, a deletion of a copy is simulated by elimination of a node. Prior to any node split or phase gain, intermediate BAM files are sorted by read name using SAMtools sort -n. And prior to any spike-in mutations, intermediate BAM files are sorted by coordinate using SAMtools sort. After deriving the BAMs for each copy of that chromosome, BAMsurgeon is used to spike in all SNVs, Indels and SVs into both copies (simulating that these mutations precede the copy number event).

Subclonal copy number calling

We used Battenberg⁶ based on ASCAT equations⁵¹ to call subclonal copy number and validated the calls by comparing observed and expected logR and BAF of the identified segments as well as inferred vs. expected Cancer Cell Fraction of the mutations (Figure 4, Supplementary Figure 2).

Somatic mutation variant calling

To assess the SNVs spiked into the simulated tumor, we used four commonly used somatic SNV detection pipelines, as well as perfect calls. We first obtained perfect calls from BAMSurgeon as a gold-standard. We retained all SNVs with at least one alternate read, one reference read, and a minimum of three total reads covering the site to maximize sensitivity while excluding zero or near-zero depth SNVs. We then executed SomaticSniper (v1.0.5), Strelka (v1.0.17) with the default settings. We executed MutationSeq (v4.3.8) with a SNV threshold of 0.5, indel threshold of 0.1, and divided chromosomes into three intervals of at least 100 Mbp and otherwise used the entire chromosome. We retained MutationSeq SNVs with PR > 0.8 which passed all filters. Lastly, we used MuTect to call variants using the protocol described above. Similarly, we verified structural variants were present using Manta (v0.29.5 )

Subclonal reconstruction and scoring using PhyloWGS and DPClust

We used PhyloWGS (https://github.com/morrislab/phylowgs commit 3e21cec) with default settings (except for including all SNVs), and converted the output to an SMC-Het compatible format using a custom script (https://github.com/morrislab/smchet-challenge/tree/master/create-smchet-report commit 06a1f1f). We used DPClust (https://github.com/Wedge-Oxford/dpclust_smchet_docker commit a1ef254) with default settings, but added functions to parse SNVs from unsupported somatic SNV detection algorithms (https://github.com/Wedge-Oxford/dpclust_smchet_docker/blob/design_paper/dpc.R commit: 1d8c2e7). For all somatic SNV detection algorithms we set the allele with the highest read count in the normal as the reference. We removed the sex chromosomes from both SNV and CNA inputs prior to running PhyloWGS and DPClust.

We then scored results from both algorithms using the scoring framework described above (https://github.com/asalcedo31/SMC-Het_Scoring/smc_het_eval commit 8b072a2). As the scale of scores for sub-challenges 1C, 2A, 2B, 3A, and 3B depend on the mutation set used, solutions across depths and somatic SNV detection algorithms for a given tumor needed to be based on a common set of mutations to be comparable. We added all false and true SNVs called by all other somatic SNV detection algorithms for that tumor to each solution as a single zero cellularity cluster so that all solutions for that tumor contained the union of all SNVs. Additionally, to ensure scores among tumors were comparable, we scaled all scores to the highest scoring 128x perfect SNV call solution for that tumor and capped at 1. We then analysed the SC1A, SC1C, SC2A, and SC2B scores using β-regressions with the betareg R package⁵². As 1B scores represent true proportions, we analysed them using a generalized linear model with a binomial link function. All models used T2, 128x, perfect, DPC, full depth as a reference. Interaction terms were retained for a given model if they reduced its AIC and significantly increased log-likelihood of the model in a log-likelihood test comparing models with and without an interaction. See the attached Life Sciences Reporting summary for further information on the statistical analysis.

Effect of copy number calling accuracy on the reconstruction

We also assessed the effect of different copy number calling errors on the reconstruction scores (Figure 6). To this end, we randomly selected copy number segments from the profiles and changed the copy number states to reflect different types of errors (additional gains, losses and a mix of the two).

For gains, for each selected segment the number of copies of the major allele N_maj was added {0,1,2,3,4,5} with probabilities {0.01, 0.15, 0.40, 0.25, 0.15, 0.04}, respectively. The minor allele was randomly assigned a state between 0 and N_maj. For losses, for each selected segment N_maj was subtracted {0,1,2} with probabilities {0.06, 0.63, 0.31}, respectively. N_min was randomly selected between 0 and N_maj then the ceiling was taken. For the mix scenario, for each selected segment, N_maj is replaced by {0,1,2,3,4,5} with probabilities {0.01, 0.15, 0.40, 0.25, 0.15, 0.04}, respectively. N_min is randomly and uniformly selected between 0 and N_maj.

In each scenario, we increased the proportion of selected segments from 10% to 50% of all segments by 10% increments. We then executed DPClust and PhyloWGS with these copy number call errors and correct copy number calls on the five synthetic tumors for the depth-SNV somatic SNV detection algorithms combinations described above (4,250 combinations total). To reduce computation time, we down-sampled each input VCF to 5,000 SNVs. We then carried out scoring and analysis for each reconstruction as described above.

Data visualization

Figures were generated using R (v3.5.3), BPG (v5.9.8)⁵³, lattice (v0.20-38), latticeExtra (v0.6-28), gridExtra (v2.3), gtable (0.2.0) and Inkscape (v0.91). Color palettes were generated using the RColorBrewer (v1.1-2) and BPG packages.

Data availability

Sequences files are available at EGA under study accession number EGAS00001002092.

Code availability

BAMSurgeon is available at: https://github.com/adamewing/bamsurgeon. The framework for subclonal mutation simulation is available at: http://search.cpan.org/~boutroslb/NGS-Tools-BAMSurgeon-v1.0.0/. The PhaseTools BAM phasing toolkit is available at https://github.com/mateidavid/phase-tools. Scripts providing the complete scoring harness are available at: https://github.com/asalcedo31/SMC-Het_Scoring/smc_het_eval.