Abstract
Fluorescing molecules (fluorophores) that stochastically switch between photon-emitting and dark states underpin some of the most celebrated advancements in super-resolution microscopy. While this stochastic behavior has been heavily exploited, full characterization of the underlying models can potentially drive forward further imaging methodologies. Under the assumption that fluorophores move between fluorescing and dark states as continuous time Markov processes, the goal is to use a sequence of images to select a model and estimate the transition rates. We use a hidden Markov model to relate the observed discrete time signal to the hidden continuous time process. With imaging involving several repeat exposures of the fluorophore, we show the observed signal depends on both the current and past states of the hidden process, producing emission probabilities that depend on the transition rate parameters to be estimated. To tackle this unusual coupling of the transition and emission probabilities, we conceive transmission (transition-emission) matrices that capture all dependencies of the model. We provide a scheme of computing these matrices and adapt the forward-backward algorithm to compute a likelihood which is readily optimized to provide rate estimates. When confronted with several model proposals, combining this procedure with the Bayesian Information Criterion provides accurate model selection.
Keywords: Hidden Markov models, Markov processes, rate estimation, forward-backward algorithm, super-resolution microscopy
1. Introduction.
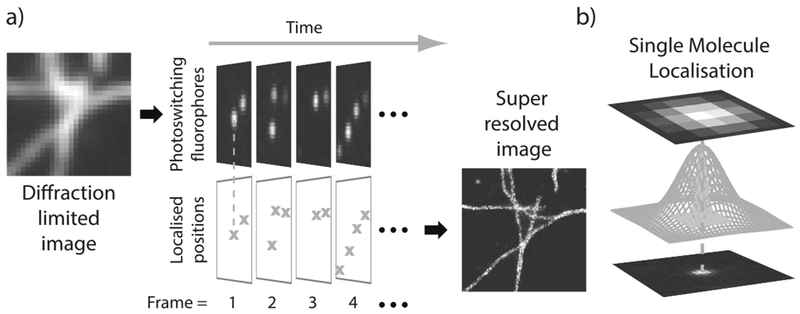
Fluorescence microscopy is a collection of techniques that utilize the photon emitting properties of fluorescing molecules, called fluorophores, to perform optical imaging, particularly in cell biology and biomedical applications. Recent years have seen the advent of a number of super-resolution microscopy techniques that have bypassed the classical resolution limits of fluorescence microscopy (Huang, Bates and Zhuang (2009)). Specifically, single molecule localization microscopy (SMLM) approaches, such as photoactivated localization microscopy (PALM) (Betzig et al. (2006), Hess, Girirajan and Mason (2006)) and stochastic optical reconstruction microscopy (STORM) (Rust, Bates and Zhuang (2006), Heilemann et al. (2008)), rely on the ability exhibited by some fluorophores to photoswitch stochastically between a photon emitting On state and nonemitting dark states (Van de Linde and Sauer (2014), Ha and Tinnefeld (2012)). A specimen decorated with a spatially dense number of photon emitting fluorophores prevents accurate identification of individual fluorophores and resolution of structures smaller than the diffraction limit—see Figure 1(a). Using a fluorophore with stochastic photo-switching properties can provide an imaging environment where the majority of fluorophores are in a dark state, while a sparse number have stochastically switched into a transient photon emitting On state. This results in the visible fluorophores being sparse and well separated in space; with the use of a high-performance camera the individual fluorophores in the On state can be identified and localized with nanometer scale precision by fitting point spread functions (Ober et al. (2015), Sage et al. (2015))—see Figure 1(b). Through the acquisition across time of a large sequence of images (typically thousands)—see Figure 1(a)—many more photo-switching fluorophores can be isolated in time and precisely localized in space. When aggregated and plotted, these localizations provide an accurate and detailed map of fluorophore positions giving rise to a super-resolved image.
Fig. 1.
(a) Illustration of the SMLM imaging process. When all fluorophores simultaneously stay in a photon emitting On state, diffraction renders structures unresolvable. Stochastically photo-switching fluorophores imaged over time across several frames give rise to a sequence of sparsely populated images where each fluorophore can be isolated and localized with high precision. Aggregating these frames gives rise to a super-resolved image. Data from Sage et al. (2015). (b) Isolated fluorophores are localized by fitting the point spread function (PSF) to the diffraction limited spot.
Lateral resolutions of 10–30 nanometers (nm) are possible in biological samples using SMLM, however, the resolution and image quality is strongly dependent on the photo-switching properties of the fluorophore used. While longer On states provide a greater number of photons being recorded by the camera, which in turn leads to greater precision in localizing spatially isolated fluorophores (Ober, Ram and Ward (2004), Ram, Ward and Ober (2013), Thompson, Larson and Webb (2002), Rieger and Stallinga (2014)), the increased random occurrence of fluorophores simultaneously occupying the On state within a diffraction limited spot can lead to significant imprecision, missed events and unwanted artifacts (Van de Linde et al. (2010), Nieuwenhuizen et al. (2015)). Thus, a careful choice of fluorophore and the environment used to promote photo-switching—controlled by the buffer solution and illumination intensity—must be made for the intended application. This is particularly important in live-cell applications when considerations must be made for temporal resolution and reduced laser intensities.
To inform the choice of fluorophore with its environment, and aid the development of novel fluorophores, accurate characterization of the photo-kinetic model of the fluorophore, together with estimation of photo-switching rates (the rate at which fluorophores transition between On and dark states) is required (Dempsey et al. (2011), Lehmann et al. (2016)). Further, accurate knowledge of the photoswitching characteristics could be employed to maximize resolutions achieved using advanced analytical methods, for example, 3B analysis (Cox et al. (2011)) and DeconSTORM (Mukamel, Babcock and Zhuang (2012)) and improve the performance of molecular counting techniques (Rollins et al. (2014), Lee et al. (2012)).
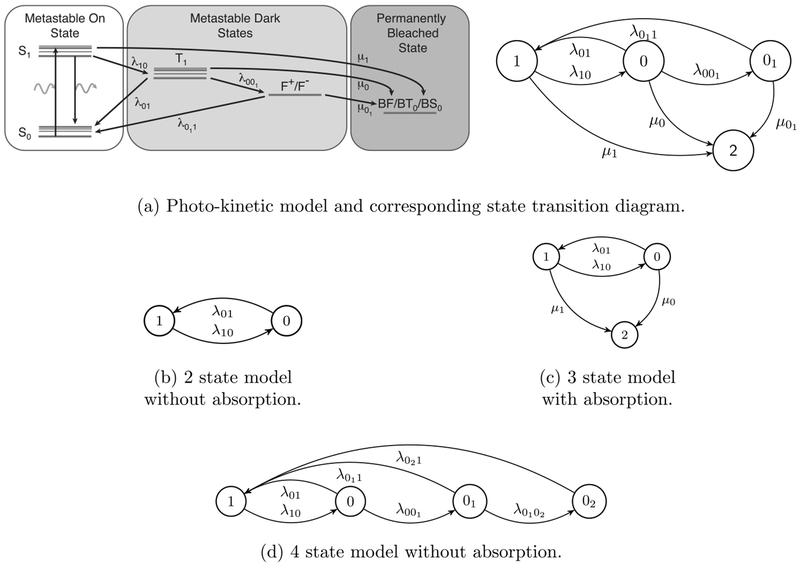
Several attempts have been made to model the kinetic schemes of fluorophore photo-switching and estimate the corresponding photo-switching rates. These kinetic schemes, as is common across single molecule biophysics, are characterized by Markovian transitions between a finite set of discrete states and are therefore ideally suited to being modeled as continuous time Markov processes. In Figure 2 are four models for photo-switching fluorophores. The first, Figure 2(a), depicts a typical kinetic model, accompanied by the state-space diagram we will adopt in this paper. This model contains a photon emitting On state 1 (involving rapid transitions between excited state S1 and ground state S0 via the absorption and emission of a photon), two temporary dark states 0 and 01 (the triplet state, T1 and the redox states, F+ and F−) and an absorption 2 (BF/BT0/BS0) which in this application is known as the photobleached state. Then in Figures 2(b)–2(d) are three further common state space models. Figure 2(b) portrays a photo-switching model with a simple two state {On(1) Dark(0)} structure. Models of this type are suitable for super-resolution methods including point accumulation for imaging in nanoscale topography (PAINT) and DNA-PAINT (Jungmann et al. (2010), Sharonov and Hochstrasser (2006)). Figure 2(c) depicts a model that incorporates an absorbing state 2. This form of photo-switching followed by absorption describes a first approximation to the behavior that occurs spontaneously in a number of organic fluorophores and post-activation of photoactivatable proteins (Ha and Tinnefeld (2012), Van de Linde and Sauer (2014), Vogelsang et al. (2010)). Figure 2(d) considers a model in which three distinct dark states are hypothesized which in some cases is a necessary extension to model (c), for instance when very rapid imaging is used (Lin et al. (2015)).
Fig. 2.
Common models used to describe the continuous time photo-switching dynamics of a fluorophore with homogeneous transition rates. See text for details.
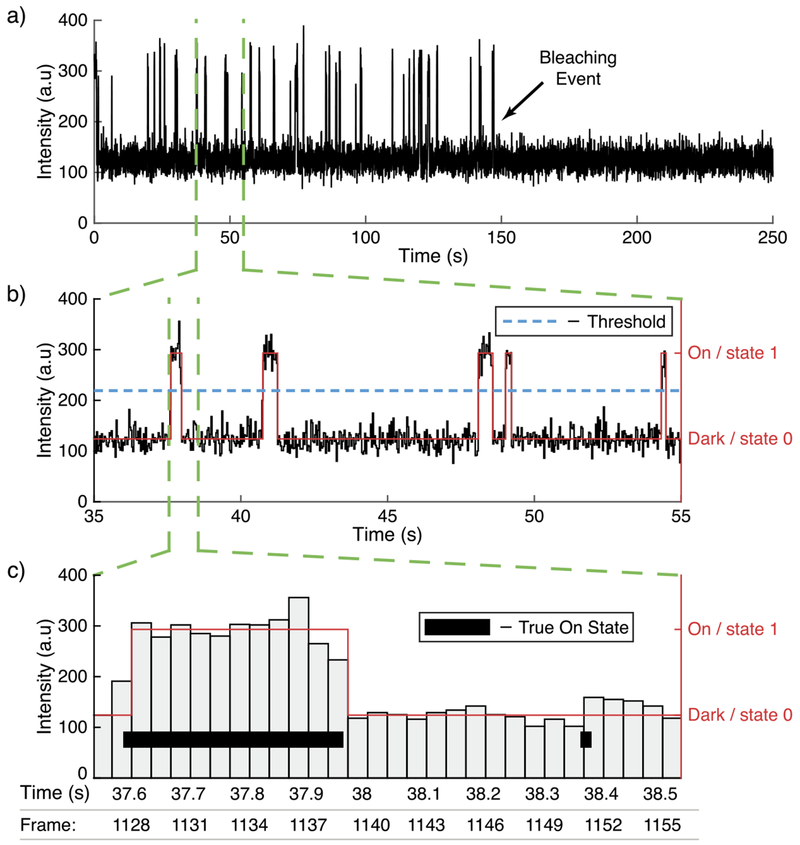
The challenge comes in selecting the correct model and estimating the transition rates of the continuous time Markov process from an observed discrete-time random process . Here, and denote the non-negative reals and integers, respectively. Typically, {Yn} is derived from a sequence of images (frames) with Yn corresponding to the observed state of the molecule in the nth frame. This is formed by an exposure of the continuous time process {X (t)} over the time-interval [nΔ, (n + 1)Δ), where Δ is the frame length. Process {Yn} can either be a sequence of photon fluxes associated with that molecule for each frame (Figure 3(a)), or a simple sequence of 1’s and 0’s indicating if the molecule was detected in the frame or not (Figure 3(b)). In all cases, the observations are subject to the effects of noise and instrument limitations. Essential to the subsequent analysis, therefore, is the ability to account for missed state transition events due to noise and the temporal resolution of the data acquisition, as well as the detection threshold used to determine the state of the system (Figure 3(c)). Similar problems occur in other areas of biophysics where estimating transition rates of an underlying continuous time Markov process must be inferred from an observed discrete time signal. In particular, ion-channels have formed the focus of much work (Colquhoun and Hawkes (1981), Qin and Li (2004), Rief et al. (2000)), including methods that attempt to account for missed events (Qin, Auerbach and Sachs (1996), Colquhoun, Hawkes and Srodzinski (1996), Hawkes, Jalali and Colquhoun (1990), Hawkes, Jalali and Colquhoun (1992), Epstein, Calderhead, Girolami and Sivilotti (2016)). However, the mechanism by which the observed signal is obtained and processed from the raw signal is fundamentally different to that of fluorescence microscopy imaging.
Fig. 3.
(a) A simulated intensity signal of a fluorophore across time. Each measurement corresponds to the intensity in a frame. 7500 frames were recorded over 250 seconds at a rate of 30 frames per second. (b) Close up of the signal over the time window of 35 s to 55 s. In red is the observed signal {Yn} indicating if the fluorophore was detected in a particular frame. (c) A further close up of the signal showing intensity read-outs for independent frames. The true, hidden photon emitting On state of the molecule is also indicated, demonstrating how sub-frame length photon emitting events can be missed due to noise or the temporal resolution of the data acquisition.
Up until now, methods for estimating photo-switching transition rates in fluorescence microscopy are limited. The method in Lin et al. (2015) involves defining {Yn} to be the sequence of 1’s and 0’s and extracting the dwell times, namely the durations when Yn is in the On state and when it is in its dark states. Assuming these dwell times to be exponentially distributed (or equal in distribution to a sum of exponentially distributed random variables in the case of multiple dark states), maximum likelihood estimates of the transition times are then computed. This method, termed here as exponential fitting and given a detailed discussion in Supplementary Materials Section S5 (Patel et al. (2019)), has two flaws. First, it does not correctly account for the effect of the imaging procedure on the stochastic structure of the discrete time process. Second, it does not allow for the absorbing (photobleached) state, which must be identified and accounted for by truncation of the data to the last observed On state. This is especially trouble-some as, to an observer, it is indistinguishable from a temporary dark state. This method therefore results in the absence of estimates for the absorption rate and can lead to significantly biased estimates of the transition rates between On and dark states.
Hidden Markov models (HMMs) are used widely across scientific and engineering disciplines to relate a sequence of observations, called emissions, to the states of an unobserved (hidden) Markov process, the target of inference. Their use is particularly prevalent in image processing where the observations are a sequence of images in time and it is commonly assumed that each image is dependent only on the state of the hidden process at the time at which it is observed. Such an approach has been proposed for this problem in Greenfeld et al. (2015), where the hidden process is a discretized version of {X (t)}. Here, they let {Yn} be the sequence of photon-fluxes such that it is a standard (first-order) HMM with Poisson emissions. They then implement the Baum–Welch algorithm (Baum and Petrie (1966), Baum and Eagon (1967), Baum and Sell (1968), Baum et al. (1970)) to estimate the transition probabilities of the discretized process and use an approximation to obtain the transition rates of the continuous time process {X (t)}. In doing so, they acknowledge that missed events will heavily bias rate estimates. Furthermore, their model is also unable to deal with the absorbing state.
In this paper we provide two important contributions. First, in Section 2, by considering a general model for {X (t)} that includes multiple dark states and an absorbing state, we rigorously formulate the discrete time stochastic process {Yn} that indicates whether a molecule is detected in each frame. A crucial part of this formulation is recognizing that an image is not formed from an instantaneous sampling of the true state, as is usually assumed in image processing, but is instead formed by exposing a camera sensor over a time interval of length Δ. That is to say, Yn is not dependent on just X (nΔ), but instead on the integral (i.e., all values) of {X (t)} over the interval [nΔ, (n + 1)Δ). Taking consideration of noise and instrument sensitivity, we fully account for missed events and give important results on the stochastic structure of {Yn}, including showing it is non-Markovian.
The second contribution of this paper is to propose novel methodology for estimating the state transition rates of {X (t)} under this correct treatment of the imaging procedure. In Section 3, we develop an HMM for {Yn} where we first implement a time discretization scheme on the hidden Markov process {X (t)}. Crucially, as discussed above, correct understanding of the imaging procedure dictates two key properties. First, Yn depends on both the current (end of frame) and previous (beginning of frame) hidden states, X ((n + 1)Δ) and X (nΔ), respectively. Second, this HMM possesses emission probabilities that are dependent on the static parameters of the hidden process state transitions that we ultimately wish to estimate. This coupled behavior renders traditional expectation maximization (EM)-type methods (e.g., Baum et al. (1970)) of parameter estimation inappropriate. We therefore make the novel step of introducing what we call transmission (transition-emission) matrices that incorporate this coupling between transition and emission probabilities by capturing all the dependencies in the model. For a given photoswitching kinetic model, we provide both a scheme for computing these matrices and an adaptation of the forward-backward algorithm to compute the likelihood of observations. Through numerical optimization we are able to compute maximum likelihood estimates of the transition rate parameters for the continuous time process {X (t)} that we wish to draw inference on. A bootstrapping scheme is also presented for computing confidence intervals. In the case of an unknown kinetic model, we propose the use of the Bayesian information criterion (BIC) for selecting the best suited model from a set of proposals, thus also providing a powerful tool for chemists wishing to infer the number of quantum states a particular fluorophore can exist in.
In Section 4, we provide extensive empirical analysis of the proposed method. We begin this section with a simulation study that compares this new estimation scheme to the exponential fitting method on a range of photo-switching models, demonstrating significant improvements in both the bias and the variance of our rate estimates. We further show the BIC performs accurate model selection when presented with a range of model proposals. We then proceed with a discussion on identifiability and consistency, providing empirical evidence that our model is identifiable and estimators consistent under normal experimental conditions. We further demonstrate that the bootstrapping scheme proposed in Section 3 for computing confidence intervals has approximately the correct coverage, and conclude with a discussion on length biased sampling. In Section 5, the estimation scheme presented in this paper is applied to the Alexa Fluor 647 data originally analyzed by the exponential fitting method in Lin et al. (2015), consistently selecting the hypothesized three temporary off-state model (Figure 2(d)) and revealing clear dependence between laser intensity and key transition rate parameters. In the accompanying Supplementary Materials, as well as key mathematical details, we include an extensive simulations section where we report a significant improvement on rate estimates across a range of models and relevant experimental conditions.
2. Modeling photo-switching behavior.
The true photo-switching behavior of the fluorophore is a continuous time stochastic phenomenon. However, an experimenter can only ever observe a discretized manifestation of this by imaging the fluorophore in a sequence of frames. These frames are regarded as a set of sequential exposures of the fluorophore and the observed discrete time signal indicates whether the fluorophore has been observed in a particular frame. It is the continuous time process on which we wish to draw inference based on the observed discrete-time process indicating whether the fluorophore was observed in a frame. In this section we first present the continuous time Markov model of the true (hidden) photo-switching behavior, and then derive the observed discrete time signal, together with key results on its statistical properties.
2.1. Continuous time.
We model the true photo-switching effect of the fluorophore as a continuous time Markov process, with discrete state space .
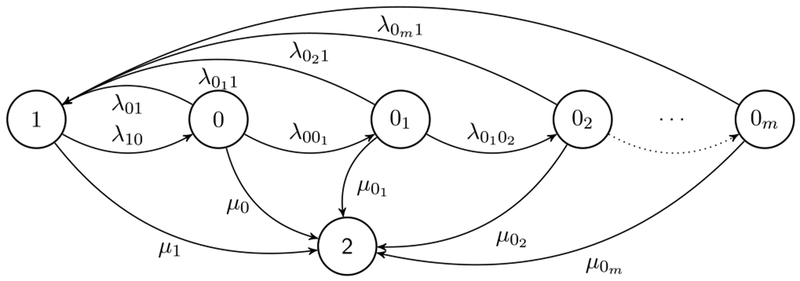
In this paper we consider a general model for {X (t)} that can accommodate the numerous mechanisms of photo-switching utilized in standard SMLM approaches such as (F)PALM and (d)STORM. Specifically, this model consists of a photon emitting (On) state 1, m + 1 non photon emitting (dark/temporary off) states 00, 01, … , 0m, where , and a photobleached (absorbing/permanently off) state 2. We denote the state 00 ≡ 0 for the m = 0 case of a single dark state. The model, illustrated in Figure 4, allows for transitions from state 1 to the multiple dark states (from a photochemical perspective, these can include triplet, redox and quenched states). These dark states are typically accessed via the first dark state 0 (reached as a result of inter-system crossing of the excited S1 electron to the triplet T1 state; see Figure 2(a)). Further dark states 0i+1, i = 0, … , m − 1, are accessible by previous dark states 0i (by, e.g., the successive additions of electrons forming radical anions (Van de Linde et al. (2010))). We allow the On state 1 to be accessible by any dark state and we consider the most general model in which the absorption state 2 is accessible from any combination of other states (Ha and Tinnefeld (2012), Van de Linde and Sauer (2014), Vogelsang et al. (2010)).
Fig. 4.
General m + 3 state () model of a fluorophore.
The state space of {X (t)} is and is of cardinality m + 3. We denote λij to be the transition rate between states i and j and μi to be the absorbing rate from state i to 2, where .
The generator matrix for {X (t)} is therefore given as
| (2.1) |
where σ0m = λ0m1 + μ0m, σ1 = λ10 + μ1 and when m > 0, σ0i = λ0i0i+1 + λ0i1 + μ0i, for i = 0, … , m − 1. For full characterization, we define its initial probability mass νX := (ν0 ν01 … ν0m ν1 ν2)⊺ with . Typically, all fluorophores receive an initial excitation to the photon-emitting state, thus the most commonly occurring probability mass vector in practice has ν1 = 1. Moreover, although the case when 0 < ν2 < 1 may give rise to fluorophores that are never observed, for inference purposes, we discard all traces containing no observations (1’s) of fluorophores and set ν2 = 0.
In this paper, we will refer to specific models (from that shown in Figure 4) in the form . Here, m is the number of multiple dark states beyond the 00 state that is present in all models, and denotes the set of states from which the absorption state 2 is accessible. For the three classical models presented in Figure 2: model (b) is case where μ0 = μ1 = 0, model (c) is case where μ0, μ1 > 0, and model (d) is case where μ0 = μ01 = μ1 = 0.
2.2. Discrete time observation process.
Having presented the continuous time model for the true photo-switching behavior, we will now introduce the model for the observed discrete time process and show how the transition rates given in (2.1) are not amenable to direct estimation.
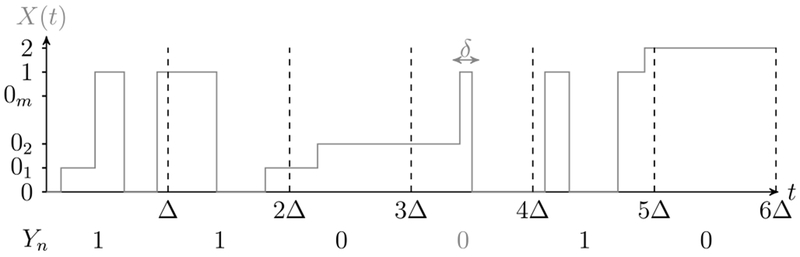
The imaging procedure requires taking a series of successive frames. Frame n is formed by an exposure over the time interval [nΔ, (n + 1) Δ), where . The constant Δ corresponds to the exposure time for a single frame, also known as the frame length. We define the discrete time observed process , with state space , as Yn = 1 if the fluorophore (characterized by {X (t)}) is observed in frame n and equal to 0 otherwise. For the fluorophore to be observed in the time interval [nΔ, (n + 1) Δ) it must be in the On state 1 for a minimum time of δ ∈ [0, Δ). The value of δ is unknown and is a result of background noise and the imaging system’s limited sensitivity. We note that if {X (t)} exhibits multiple jumps to state 1 within a frame, then a sufficient condition for observing the fluorophore is that the total time spent in the On state exceeds δ. The δ = 0 case is the idealistic scenario of a noiseless system and perfect sensitivity such that the fluorophore is detected if it enters the On state for any nonzero amount of time during the exposure time Δ.
We formally define the observed process as
| (2.2) |
where is the indicator function such that if x ∈ A and is zero otherwise. Figure 5 illustrates the manifestation of the discrete time signal {Yn} from the continuous time signal {X (t)}.
Fig. 5.
Illustration of how the states for Yn derive from the process X (t).
2.3. The inference problem.
The inference problem is two-fold. First, for a given model, the aim is to estimate the (4m + 8) unknown parameters
from a finite length realization of {Yn}. Crucially, it is shown in Supplementary Materials Section S1 (Patel et al. (2019)) that {Yn} does not exhibit the Markov property (of any order) for any , and for any Δ and δ such that Δ > δ ≥ 0. The non-Markovianity excludes classical inference methods and motivates the use of a Hidden Markov Model (HMM), with a likelihood based approach for estimating θ.
Beyond this, it may be the case that the true model (characterized by its number of dark states) is unknown and may need to be selected in addition to estimating the unknown parameters. We tackle both of these problems in the next section.
3. Characterizing photo-switching behavior.
Hidden Markov models, first presented in Baum and Petrie (1966), relate a sequence of observations to the states of an unobserved or hidden Markov chain. The aim of building a hidden Markov model (HMM) is to allow inference on the hidden process using these observations. In its simplest form, an HMM assumes the propagation of both state and observed sequences to be in discrete time, and a general first order HMM assumes that the observation process is related to a hidden first order Markov Chain via an emission probability distribution , considered to be fully independent of the static parameters that characterize the probability distribution of state transitions . In this setting we say B and P are decoupled. For a sequence y0, y1, … , yN of observations from this model, the Baum–Welch re-estimation algorithm (Baum and Petrie (1966), Baum and Eagon (1967), Baum and Sell (1968), Baum et al. (1970)) is an EM type method that utilizes the forward-backward algorithm (see Levinson et al. (1983), for details) to optimize the likelihood function and compute maximum likelihood estimates of νX (the probability mass of X0), B and P. This in turn can be used to estimate parameters of the emission and state transition probabilities. When the hidden Markov process and/or the observation process are of higher order, the HMM can be transformed to a general first order process (Du Preez (1998), Lee and Lee (2006), Ching, Fung and Ng (2003)) and Baum–Welch can be applied in the usual way. Readers are directed to MacDonald and Zucchini (1997) for a comprehensive review.
While standard, first (or higher) order HMMs have been extensively studied and are most frequently used in applications, the rigid framework of being in discrete time with emission probabilities decoupled from state transition probabilities is not always suitable, as we will now show is the case for images formed by exposures over a time interval. We take time to carefully formulate the HMM suitable for this application, presenting what we call transmission (transmission-emission) matrices to capture the dependencies in the model. We then go on to provide a novel adaptation of the forward-backward algorithm to estimate θ, the unknown parameters of our HMM in the case of a known state-space of the hidden process. We will then show how the Bayesian information criterion (BIC) can be used for model selection and parameter estimation in the case of an unknown state-space.
3.1. Photo-switching hidden Markov model.
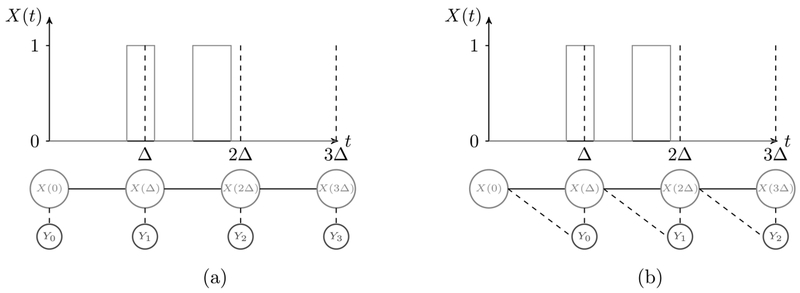
In this section we build an HMM for our observation process {Yn}, which we call the Photo-switching hidden Markov model (PSHMM). The first immediate reason as to why the standard set-up outlined above is inappropriate for this application is because the hidden Markov process {X (t)} evolves in continuous time. To deal with this, we need to adopt a time-discretization scheme for the hidden process. Analogously to Liu et al. (2015), we state that {X (t)} propagates in Δ-separated discrete time steps according to the transition probability matrix PΔ = eGΔ, where G is given in (2.1). Our hidden process is therefore now represented by the discrete time Markov chain .
When Yn depends solely on X (nΔ) (see Figure 6(a)) and the corresponding emission matrix B is decoupled from P, a continuous time EM algorithm (Liu et al. (2015)) analogous to the Baum–Welch can be used to estimate νX, B and P. However, this will be inappropriate in our setting for two related reasons. First, we have shown in Section 2, specifically equation (2.2), that exposing images over a nonzero length of time means Yn depends on the full path of {X (t)} within the interval [nΔ, (n + 1) Δ). To correctly deal with this it is necessary to construct the HMM to consider dependence between Yn and both X (nΔ) and X((n + 1) Δ) (see Figure 6(b)). Second, this construction of {Yn} in (2.2) means the emission probabilities are clearly dependent on the static parameters θ of the hidden process and are therefore coupled with P. The EM procedures highlighted above require decoupled B and P so that at each step the quasi-likelihood can be optimized separately. To the best of our knowledge, methods for dealing with coupled systems have not been dealt with in the literature. While an EM algorithm could be used for a coupled system, analytic forms for the update steps would in general be intractable, leading to numerical maximization procedures at each iteration, thereby increasing computational complexity. We will now formally characterize the PSHMM and provide a novel method for estimating the unknown static parameters in the case of a coupled system.
Fig. 6.
Illustration of the HMM setup. (a) Traditional HMM where observed state is dependent on current hidden. (b) Our HMM where observed state depends on both the current and past hidden states.
3.1.1. Formal characterization of the PSHMM.
Formally, we characterize our PSHMM with:
An initial probability vector νX = (ν0 ν01 … ν0m ν1 ν2)⊺ where for ;
- Transmission matrices
where(3.1)
These transmission matrices combine the transition and emission probabilities, thereby allowing us to account for a coupled system. The full mathematical formulation for deriving their forms involves conditioning on the number of jumps from all m + 1 dark states within the interval [0, Δ). From this, we use Laplace transforms and the distributions of state holding times to iteratively compute matrices that converge to our set of transmission matrices. A more detailed explanation of this methodology, along with full derivations and expressions is presented in Supplementary Materials Section S2 (Patel et al. (2019)). Furthermore, an algorithm (Algorithm 1) detailing all computational steps to evaluate these matrices suitable for any (any number of multiple dark states) can be found in Supplementary Materials Section S3 (Patel et al. (2019)).
3.2. Estimating unknown parameters of the PSHMM.
We now provide an algorithm for estimating the unknown parameters θ of the PSHMM, which utilizes a suitable adaptation of the forward-backward dynamic programming algorithm (Rabiner (1989)), making use of the transmission matrices in (3.1).
Let y = (y0 y1 … yNF−1)⊺ be the sequence of observations across NF frames for a single photo-switching fluorophore. We define the forward-backward probabilities as
For each such n, we define the forward-backward vectors as
Using this notation, we can show that for n = 2, … , NF and when n = 1. This yields the following recursion formula
| (3.2) |
where 1m+3 is the (m + 3) × 1 vector of ones. It now follows that the likelihood of observation vector y given parameter vector θ is for all n = 0, … , NF. In particular, we have , which can be readily computed using the transmission matrices together with recursive computation for as indicated in (3.2). In the situation where we have NE ≥ 1 independent photo-switching fluorophores, the log-likelihood is given by
| (3.3) |
where and αNF,k is the forward probability vector for emitter k = 1, … , NE. Maximizing (3.3) with respect to θ can be done either through numerically approximating derivatives or by using derivative-free optimization, for example with the Nelder–Mead algorithm. A discussion on multimodality and choosing a starting point for optimization can be found in Supplementary Materials Section S6 (Patel et al. (2019)).
3.2.1. Accounting for false positive observations.
Occasionally, random peaks in the background noise may exceed the threshold value used to determine a fluorophore in the On state, resulting in a false positive identification of the fluorophore. For experiments conducted over a large enough number of frames, this false positive rate may become significant in the observed process {Yn}.
Specifically if ω ∈ [0, 1] denotes the probability of falsely observing a fluorophore, assumed independent of the general observation process, then we may use the updated transmission matrices
in the evaluation of the log-likelihood in (3.3). This would thus involve estimating θ* = [θ⊺ ω]⊺ from the observations .
3.3. Bootstrapping.
When only one experiment is conducted to produce an NF × NE dataset , a single prediction is obtained. In this circumstance, a bootstrapping scheme can be used to gain approximate confidence intervals for each component of θ.
In the same manner as is presented in Efron and Tibshirani (1993), we generate R (typically large) bootstrap datasets each consisting of re-sampled (with replacement) columns of . From each dataset, we acquire bootstrap replicated parameter estimates using the same PSHMM maximum likelihood procedure used to obtain . For 0.5 < p < 1, letting and be the 100 · pth and 100 · (1 − p)th empirical percentiles of the ith component of θ obtained from , a percentile bootstrap interval of length 1 − 2p is given by (see Efron and Tibshirani (1993))
3.4. Model selection.
To determine the unknown number of multiple m dark states, we have chosen to use the Bayesian information criterion (BIC) to determine the most likely model given data . Although similar to the Akaike information criterion (AIC), the BIC offers greater protection against over-fitting when the number of data-points is large, as is the case in this setting.
The BIC is defined in our context as , where q denotes the number of unknown parameters estimated in θ and denotes the maximized log-likelihood using the maximum likelihood estimates . This criterion can be computed among all suitable models, with the most preferred being chosen as that with the smallest BIC value.
4. Simulations and analysis.
Simulation studies have been conducted to assess and analyze the performance of the PSHMM method as detailed in Section 3. To make the results applicable, we restrict ourselves to realistic parameter values that typically occur in an experimental setting.
4.1. Performance on images and comparison with exponential fitting.
To test the performance of parameter estimation against the exponential fitting method of Lin et al. (2015), synthetic imaging data of photo-switching fluorophores was simulated. We begin our focus on the model , since for many practical applications the life-times of further dark (in particular the triplet (T1)) states is short relative to Δ. As such, this dark state has been considered as part of the meta-stable On state (Ha and Tinnefeld (2012), Vogelsang et al. (2010)). Since the predominant pathway to absorption is via the triplet state, a simplified model can be used in which the absorption state 2 is only accessible from state 1. Given the popularity of this model and its ease of analysis, we have derived the exact solution of the corresponding transmission matrices (see Supplementary Materials Section S2 (Patel et al. (2019))).
Details on the image simulation method and how the discretized state sequences were extracted can be found in Supplementary Materials Section S7 (Patel et al. (2019)). Global parameter values are also noted. The extracted state sequences were analyzed using an implementation of Algorithm 1 (see Supplementary Material Section S3 (Patel et al. (2019))). The resulting parameter estimates were compared to estimates derived from the exponential fitting method, which was extended in this study to allow the calculation of absorption rates (see Supplementary Materials Section S5 (Patel et al. (2019))).
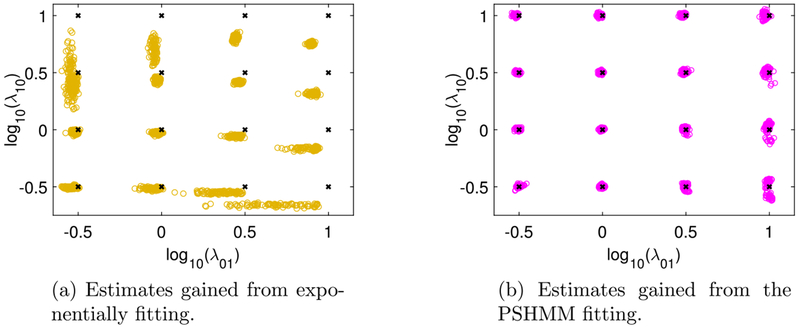
Table 2 (see the Appendix) shows estimated parameter statistics over 16 image simulation studies with 100 replicates (datasets) per study. Rate parameters θ, were chosen to cover a range of observed behaviors of organic fluorophores and fluorescent proteins (Dempsey et al. (2011)) with NE = 100 fluorophores per study. The number of frames NF in each study was adjusted to standardize the average number of transitions predicted from θ. Scatterplots of these rate estimates are presented in Figure 7. It is evident that the PSHHM yields estimates with much lower bias and root mean squared errors (RMSE) when compared to the exponential fitting method, although they have a tendency to increase as transition and absorption rates are increased. The reported empirical (2.5, 97.5) percentile intervals contain the true parameter values across all studies for the PSHMM method and further highlight the bias in estimates obtained from exponential fitting.
Fig. 7.
Estimates of log10(λ01) and log10(λ10) simulated from model using both exponential fitting (a) and PSHMM fitting (b) are plotted in dark yellow and pink respectively. True rates are plotted as black crosses. Estimates for the absorption rate μ1, along with means, RMSEs and 2.5 and 97.5 empirical percentiles are given in Table 2 (see the Appendix).
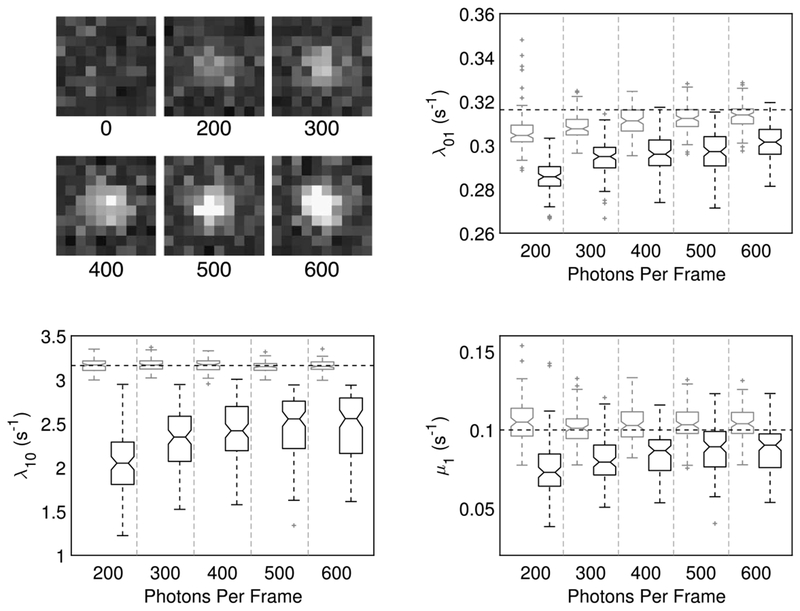
For experimenters, the effect of imaging parameters on the performance of the estimators is of particular interest and importance. Further simulation studies carried out under model highlight the consistency in both accuracy and precision of the PSHMM estimator across a range of different experimental conditions. Figure 8 compares the PSHMM with exponential fitting rate estimates when we vary the emission intensity of the fluorophores (measured in the mean number of photons each emits when in the On state for time Δ). Further investigation of other parameters, including the frame length (Δ), the number of frames (NF) and the detection threshold (proportional to δ) under this model, are provided in Supplementary Materials Section S7 (Patel et al. (2019)). Across the full range of relevant parameters tested, the PSHMM estimator performs significantly better than exponential fitting.
Fig. 8.
Top Left: Examples of single simulated frames at the indicated number of photons per frame (Supplementary Materials Section S7 (Patel et al. (2019))). Box-plots showing quantiles from estimates of λ01, λ10 and μ1 from both exponential fitting (black) and PSHMM fitting (gray) are plotted against increasing photons per frame. NF = 9872 for all simulations. True rates given by the blue line.
To assess the accuracy of parameter estimates for the extended models m = 1 and m = 2 over fast, medium and slow switching scenarios, additional simulations were performed by directly sampling the continuous time processes {X (t)} and extracting the observation sequences as in (2.2), using fixed values of θ. Results from the analyses of these simulations are shown in Tables 3 and 4 in the Appendix. While it is evident that the estimates for λ0m0m+1 and λ0m+11 incur greater bias as m increases, the empirical (2.5, 97.5) percentile intervals predominantly cover true parameter values, albeit over a larger area due to the increase in the RMSEs. As is seen when m = 0, the exponential fitting method performs less well, yielding much higher bias and RMSEs for particular parameter values.
4.2. Model selection.
Using these simulated datasets, the BIC was used in model selection from the set of proposals {, , } (i.e., under the assumption that the absorption state was known to only be accessible by the On state). Applying model selection to the dataset used to estimate parameters in Table 2 results in the true state model being chosen in all (100%) cases. 100 datasets, each for m = 0, 1, 2 were generated for studies 2, 17 and 20 with and NE = 300. These results presented in Table 1 demonstrate the accuracy of selecting the correct model.
Table 1.
Confusion table showing the empirical percentage of models predicted from three candidates: , and and under simulation studies 16, 19 and 20 (see Tables 2, 3 and 4 in the Appendix), with NE = 300, and . 100 datasets from each study were generated and the BIC used to select the best fitted model
| Predicted → True ↓ |
|||
|---|---|---|---|
| 100 | 0 | 0 | |
| 0 | 98 | 2 | |
| 0 | 1 | 99 |
4.3. Identifiability and consistency.
We give a detailed discussion on the inter-related issues of identifiability and consistency in Supplementary Materials Section S4 (Patel et al. (2019)). Here, we summarize these results. The parameter values for “fast,” “medium” and “slow” transition rates can be found in Table S1, Supplementary Materials Section S4 (Patel et al. (2019)).
The formal definition of model identifiability is there exists a bijective mapping from the parameter space to the space of distributions for the data; or equivalently for any θ, there exists no other θ* in the parameter space such that almost everywhere. Obtaining such a result for the PSHMM is highly nontrivial, if not intractable. We therefore explore the issue of identifiability through empirical studies. To do so, we begin by exploring local identifiability. Parameter vector θ is said to be locally identifiable if there exists a neighborhood around it such that there is no other θ* in that neighborhood for which almost everywhere (Little, Heidenreich and Li (2010)). It can be shown that θ is locally identifiable if and only if the Fisher information matrix is nonsingular (Rothenberg (1971)), and this becomes our object of interest. Again, due to the complexity of the model, the Fisher information matrix can not be computed, however we can study local identifiability via the observed Fisher information matrix (the Hessian matrix of the log-likelihood function) evaluated at the maximum likelihood estimate of θ (Colquhoun, Hatton and Hawkes (2003)). This is averaged over several repeated simulations of data set . In particular, if is singular then is not a unique (local) maximum, typically due to a flat ridge in one or more directions, and θ is unidentifiable.
Summarizing the findings presented in Supplementary Materials Section S4 (Patel et al. (2019)), in the sets of parameters studied, the observed Fisher information matrix is shown to be nonsingular in almost all circumstances, providing strong empirical evidence of structural identifiability over the parameter values most likely encountered in practice. It is obvious that the form of the observed Fisher information matrix will be dependent on the relative values of the known and unknown parameters. Broadly speaking, we find that as δ/Δ → 1, that is, the time a fluorophore needs to stay in the On state to be detected tends towards the frame rate, there appears to be a breakdown in identifiability. This is indicated by the observed correlation matrix, as derived from the observed covariance matrix , showing strong correlation between and , and hence the existence of a ridge on the likelihood surface, albeit still with curvature. While still technically identifiable, the correlation between these two parameter estimators indicates they cannot be independently identified and pose difficulties to numerical optimization methods (Jacquez and Greif (1985)). This effect is more pronounced for faster transition rates due to an increased chance of transitions into the On state not being observed. This trend as δ/Δ increases is expected as the model will be completely unidentifiable when δ = Δ as no fluorophore will be observed in the On state. However, for low values of δ/Δ (<0.2) as is typically encountered in practice, correlation between all elements of the estimator is low, providing clear empirical evidence of locally identifiability for all parameter values studied.
We also see a breakdown in identifiability if the frame length is too large in comparison to the switching rates. For example, for a frame length of Δ = 1/30 s (30 frames per second), under slow and medium switching, the models appear to be identifiable, however under fast switching this breaks down. Increasing the frame rate to Δ−1 = 100 s−1 appears, from empirical evidence, to be sufficient for making the model identifiable. This intuitively seems correct as large frame lengths will fail to capture the nuanced photo-kinetic behavior of fast switching fluorophores.
To get a handle on global identifiability we assess whether the likelihood surface has a unique global maximum or if there are further modes the optimization method is determining to be the maximum. For the 3 state case (m = 0), an approximation scheme is used to find a suitable starting point for the Nelder–Mead simplex (see Supplementary Materials Section S6 (Patel et al. (2019))) and we ensure we locate the correct mode. In the 4 and 5 state cases (m = 1 and m = 2, respectively), a stochastic search method is deployed that trials multiple starting points. Unimodal histograms for the parameter estimates would indicate a single global maximum, whereas a multi modal histogram would indicate further dominant modes being located instead. Analysis presented in Supplementary Materials Section S4 (Patel et al. (2019)) suggests a single global maximum in all cases with one exception; there appears to be two different modes being located for the λ0102 parameter in the m = 2 model, although this disappears as the number of frames NF increases.
Studies on consistency of the PSHMM maximum likelihood estimator corroborate our findings on identifiability. A break down in identifiability will result in the estimator becoming inconsistent. In Supplementary Materials S4 (Patel et al. (2019)), empirical evidence suggests that the mean squared error tends to zero (as the number of emitters NE increases) when δ/Δ is within the normal range (<0.2). However, as δ/Δ increases towards 1, consistency of the estimator breaks down with it becoming more biased (although with a reduction in variance).
4.4. Length biased sampling.
Length biased sampling is an issue that could appear in practice. In our setting, this would occur if there are fluorophores whose traces we do not include when estimating the unknown parameters due to them never being observed. We note that for this to happen the fluorophore would have to never be in the On state for longer than δ in any frame. As soon as it is, we have observed it and can populate its trace up to that point with zeros. In the 3 state (m = 0) case, even under the extreme situation of δ = 0.9 Δ, the probability of not observing any given fluorophore in all 10,000 frames is 1.3 × 10−2 for fast transition rates and 1.0 × 10−3 for slow transition rates. Under a more realistic setting of δ = 0.1 Δ, this reduces to 1.1 × 10−3 and 1.0 × 10−4 for fast and slow transition rates, respectively. Therefore, for a single experiment with 100 fluorophores, the probability all of them are observed is 0.90 when under fast switching, climbing to 0.99 for slow switching.
4.5. Bootstrap interval coverage.
Simulations were performed to verify the coverage of the bootstrapped confidence intervals presented in Section 3.3. As an example, for the 3 state (m = 0) model under slow switching (see parameter values in row 1 of Table S1 in Supplementary Materials Section S4 (Patel et al. (2019))), the coverage of the 95% bootstrapped confidence intervals are 92.8% (λ01), 94.6% (λ10) and 94.6% (μ1). These results were obtained from 500 simulated bootstrap intervals with each interval being formed from 100 estimates.
5. Application to Alexa Fluor 647 data.
In this section we apply the method presented in this paper to the data analyzed with the exponential fitting method in Lin et al. (2015). The details, including experimental methods, can be found in this reference. In summary, antibodies labeled with Alexa Fluor 647 at a ratio of 0.13–0.3 dye molecules per antibody were sparsely absorbed to a cover slip and imaged by Total Internal Fluorescence microscopy to investigate the effect of eight different laser intensities on the photo-switching behavior of Alexa Fluor 647. The study contains 27 experiments with differing combinations of laser intensity and frame rate. These values, together with the number of emitters detected and the number of frames over which they were imaged is summarized in Table 5 of the Appendix. For each photo-switchable molecule detected, the discrete observation trace indicating if the emitter was observed in each frame, was extracted (see Supplementary Materials Section S7 (Patel et al. (2019))). In all experiments, the true model and its associated parameters were unknown. Subsequently, we will show comparisons between estimates from both the PSHMM and modified exponential fitting methods.6
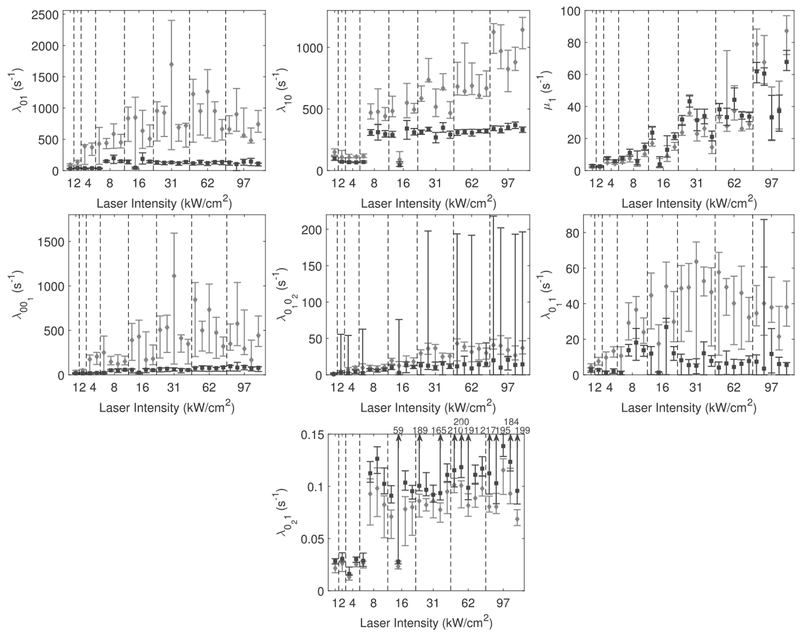
Initially, the BIC model selection criterion as outlined in Section 3.4 was used to select the most suitable model for the data from the range of models , , , , , , , , , , and with the model being selected on all (100%) occasions. This supports Lin et al. (2015), who hypothesize this, with bleaching model and assume the (without bleaching) model for rate estimates gained from exponential fitting. PSHMM maximum likelihood estimates were then computed for the estimation of θ* = (λ001 λ01 λ0102 λ011 λ021 λ10 μ1 νX δ ω)⊺ for each of the 27 datasets. Associated with these, 95% bootstrapped intervals were computed using the method in Section 3.3 (R = 100 due to computational intensity). The results are shown in Figure 9. Comparisons with exponential fitting bootstrapped re-estimates (where νX, δ and ω are not estimable in this setting) are also shown.
Fig. 9.
Rate predictions and associated 95% bootstrap confidence sets are shown for λ01, λ10, μ1, λ011, λ0102, λ011 and λ021, for eight different values of laser intensity (see Table 5 in the Appendix for exact experimental parameters). Intervals in black correspond to those from exponential fitting and those in gray correspond to those gained from the PSHMM. Point estimates from each of the 27 datasets are given by the diamond (PSHMM) or square (exponential). While in some cases PSHMM produces much wider intervals, it also yields less biased estimates than the exponential fitting method; see text for discussion.
The results indicate that the exponential fitting predicts a much slower switching scenario for the Alexa Fluor 647 antibodies, with many estimates shown to be several orders of magnitude below those predicted by the PSHMM. This resembles the conclusions reached from the results of the simulation studies as described in Section 4 and are thought to occur as a result of the exponential fitting method missing events within frames. Incidentally, the higher variance of predictions from both methods are shown to be reported at higher laser intensities, where faster switching of fluorophores is promoted. This is especially pronounced in some particularly large simulated confidence sets for the exponential fitting estimates of λ0102 and λ021 (see Figure 9).
6. Summary and discussion.
Accurate measurement of fluorophore photoswitching rates has the potential to enable tailored design of single molecule localization microscopy experiments to specific requirements. For example, one may wish to select a fluorophore and photo-switching environment to achieve the rapid photo-switching at low laser intensities required for live-cell samples. Alternatively, one may wish to promote long off times required for densely packed samples. Furthermore, precise estimates of photo-switching rates has the potential to advance data processing methods used in single molecule localization microscopy imaging, enabling more accurate image reconstruction and aiding proper quantitative analysis. For this purpose, we have presented a method for characterizing the photo-switching kinetics of fluorophores from a sequence of images.
For the most general continuous time photo-switching model, we have carefully defined the observation process and linked it to the hidden continuous time photoswitching behavior that we wish to infer upon. From this, we have formulated a hidden Markov model to link the observations to the continuous time photo-switching model. Importantly, images being formed by exposing the camera over a nonzero time interval violates the traditional assumption placed on HMMs that the emission and transition probabilities are decoupled. To tackle this, we have introduced transmission matrices that capture all the dependencies present in the model and provided a detailed scheme for computing them for any continuous time photo-switching model. A modification of the forward-backward algorithm tailored for these coupled HMMs has been presented and numerical maximization of the computed likelihood was performed to generate accurate estimates of the true photo-switching rates. Through a detailed simulation study, these were compared to estimates from an existing exponential fitting method. We found that our proposed method of parameter estimation is highly robust to a range of simulated experimental parameters including low signal-to-noise ratios and fast frame rates, frequently outperforming estimates from exponential fitting. We further found that by using the BIC, it is possible to perform accurate model selection from a range of model proposals, thus providing a powerful new tool for chemists wishing to infer the number of quantum states a particular fluorophore can exist in. Empirical analysis provided strong evidence that the PSHMM is identifiable and the estimators approximately consistent in the normal parameter range encountered in experiments. Although, experimenters should ensure fast switching fluorophores are imaged with greater frame rates to ensure model identifiability.
The model selection and estimation method presented in this paper was then applied to real data collected from the study of Lin et al. (2015). We provide strong evidence of a relationship between laser intensity and photo-switching rates and support the hypothesis that Alexa Fluor 647 has three off-states in addition to a photo-bleached state.
While this paper focuses on single molecule localization microscopy, the type of kinetic models discussed in this paper are unlikely to be unique to photo-switching fluorophores and super-resolution applications. Certainly, stochastic processes in which the observed signal depends on both the current and past states of a hidden process are likely to be a general feature of digital, discretized measurements of stochastic signals. This is particularly true in image processing where images are inevitably formed by exposing the camera’s sensor over a nonzero length time window. The coupling between the emission and transition probabilities of the HMM is a direct consequence of this exposure time, and therefore it is likely that the presented methodology for dealing with this will find use in imaging applications that are beyond the scope of this paper.
Further theoretical discussions and a comprehensive simulations and methods section, can be found in the Supplementary Materials.
Supplementary Material
Acknowledgments.
The authors would like to thank Prof Joerg Bewersdorf, Department of Cell Biology, Yale University, for his help in making the Alexa Fluor 647 data available, and are most grateful to the Editor, Associate Editor and referees for their insightful comments and discussion.
APPENDIX: RATE ESTIMATES
Table 2.
Simulation results showing mean, bias, root mean squared error (RMSE) and the 2.5 and 97.5 empirical percentiles of the estimates of θ = (λ01 λ10 μ1)⊺ under model for both the PSHMM and exponential fitting (Exp) methods across 100 repeat experiments. , δ, ω > 0 (unknown), the number of emitters NE = 100. NF indicates the number of frames simulated. For both methods, log − log scatterplots of λ01 and λ10 are shown in Figure 7
| Study | NF | θ | PSHMM Mean | PSHMM Bias | PSHMM RMSE (× 10−2) | PSHMM (2.5%, 97.5%) percentiles | Exp Mean | Exp Bias | Exp RMSE (× 10−2) | Exp (2.5%, 97.5%) percentiles |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 16,800 | 0.32 | 0.32 | 0.00 | 0.97 | (0.30, 0.34) | 0.29 | −0.029 | 3.29 | (0.26, 0.32) |
| 0.32 | 0.32 | −0.001 | 0.76 | (0.30, 0.33) | 0.31 | −0.007 | 0.89 | (0.30, 0.32) | ||
| 0.01 | 0.01 | 0.001 | 0.21 | (0.01, 0.02) | 0.01 | 0.001 | 0.11 | (0.01, 0.01) | ||
| 2 | 11,151 | 0.32 | 0.32 | −0.001 | 0.66 | (0.30, 0.33) | 0.30 | −0.012 | 1.47 | (0.29, 0.32) |
| 1 | 1.00 | 0.003 | 1.91 | (0.96, 1.04) | 0.95 | −0.053 | 5.95 | (0.89, 0.99) | ||
| 0.03 | 0.03 | 0.001 | 0.35 | (0.03, 0.04) | 0.03 | 0.001 | 0.33 | (0.03, 0.04) | ||
| 3 | 9364 | 0.32 | 0.31 | −0.004 | 0.68 | (0.30, 0.32) | 0.30 | −0.017 | 1.90 | (0.28, 0.32) |
| 3.16 | 3.16 | 0.002 | 6.56 | (3.05, 3.28) | 2.45 | −0.712 | 77.85 | (1.78, 3.92) | ||
| 0.11 | 0.11 | 0.001 | 1.02 | (0.09, 0.13) | 0.09 | −0.017 | 2.12 | (0.06, 0.12) | ||
| 4 | 8799 | 0.32 | 0.30 | −0.013 | 1.40 | (0.29, 0.31) | 0.28 | −0.032 | 3.35 | (0.27, 0.30) |
| 10 | 9.96 | −0.042 | 23.03 | (9.52, 10.42) | 3.19 | −6.809 | 690.87 | (1.52, 5.91) | ||
| 0.33 | 0.35 | 0.014 | 3.79 | (0.29, 0.42) | 0.12 | −0.210 | 21.49 | (0.06, 0.25) | ||
| 5 | 10,962 | 1 | 1.00 | −0.002 | 1.86 | (0.96, 1.04) | 0.90 | −0.104 | 12.43 | (0.74, 1.01) |
| 0.32 | 0.32 | 0.000 | 0.72 | (0.30, 0.33) | 0.30 | −0.013 | 1.47 | (0.29, 0.32) | ||
| 0.01 | 0.01 | 0.000 | 0.10 | (0.01, 0.01) | 0.01 | 0.001 | 0.11 | (0.01, 0.01) | ||
| 6 | 5312 | 1 | 1.00 | −0.004 | 1.81 | (0.96, 1.03) | 0.95 | −0.054 | 6.44 | (0.87, 1.01) |
| 1 | 1.00 | 0.001 | 1.76 | (0.96, 1.04) | 0.93 | −0.066 | 6.88 | (0.89, 0.97) | ||
| 0.03 | 0.03 | 0.001 | 0.29 | (0.03, 0.04) | 0.03 | 0.001 | 0.28 | (0.03, 0.04) | ||
| 7 | 3526 | 1 | 0.99 | −0.015 | 2.32 | (0.95, 1.02) | 0.95 | −0.053 | 5.78 | (0.91, 0.99) |
| 3.16 | 3.17 | 0.003 | 7.33 | (3.01, 3.30) | 2.71 | −0.451 | 46.16 | (2.50, 3.89) | ||
| 0.11 | 0.11 | 0.001 | 1.06 | (0.08, 0.13) | 0.10 | −0.004 | 0.99 | (0.08, 0.12) | ||
| 8 | 2961 | 1 | 0.97 | −0.033 | 3.91 | (0.93, 1.00) | 0.91 | −0.095 | 9.75 | (0.85, 0.95) |
| 10 | 9.94 | 0.003 | 27.21 | (9.46, 10.47) | 5.02 | 0.003 | 504.34 | (3.66, 6.52) | ||
| 0.33 | 0.35 | 0.017 | 3.94 | (0.28, 0.42) | 0.20 | −0.133 | 13.77 | (0.14, 0.27) | ||
| 9 | 9116 | 3.16 | 3.15 | −0.008 | 6.88 | (3.04, 3.29) | 2.31 | −0.855 | 95.19 | (1.64, 3.04) |
| 0.32 | 0.31 | −0.002 | 1.53 | (0.28, 0.34) | 0.28 | −0.037 | 3.74 | (0.27, 0.29) | ||
| 0.01 | 0.01 | 0.000 | 0.11 | (0.01, 0.01) | 0.01 | 0.001 | 0.13 | (0.01, 0.01) | ||
| 10 | 3466 | 3.16 | 3.13 | −0.035 | 7.47 | (3.01, 3.28) | 2.83 | −0.335 | 37.76 | (2.49, 3.06) |
| 1 | 1.00 | 0.004 | 4.04 | (0.90, 1.07) | 0.87 | −0.129 | 13.00 | (0.84, 0.90) | ||
| 0.03 | 0.03 | 0.001 | 0.37 | (0.03, 0.04) | 0.04 | 0.002 | 0.36 | (0.03, 0.04) | ||
| 11 | 1680 | 3.16 | 3.11 | −0.052 | 9.49 | (2.98, 3.31) | 2.92 | −0.245 | 25.63 | (2.75, 3.08) |
| 3.16 | 3.18 | 0.015 | 9.12 | (2.99, 3.37) | 2.60 | −0.567 | 56.96 | (2.48, 3.70) | ||
| 0.11 | 0.11 | 0.002 | 1.21 | (0.09, 0.13) | 0.11 | −0.000 | 0.98 | (0.09, 0.13) | ||
| 12 | 1115 | 3.16 | 3.03 | −0.135 | 14.73 | (2.92, 3.15) | 2.79 | −0.377 | 38.19 | (2.66, 3.92) |
| 10 | 9.99 | −0.008 | 24.86 | (9.54, 10.48) | 6.35 | −3.648 | 365.97 | (5.72, 6.93) | ||
| 0.33 | 0.35 | 0.015 | 3.92 | (0.29, 0.44) | 0.27 | −0.061 | 6.79 | (0.22, 0.33) | ||
| 13 | 8532 | 10 | 9.93 | −0.069 | 25.64 | (9.47, 10.47) | 5.33 | −4.666 | 506.70 | (1.98, 8.60) |
| 0.32 | 0.32 | 0.000 | 4.42 | (0.24, 0.37) | 0.22 | −0.099 | 9.95 | (0.21, 0.23) | ||
| 0.01 | 0.01 | 0.000 | 0.09 | (0.01, 0.01) | 0.01 | 0.001 | 0.10 | (0.01, 0.01) | ||
| 14 | 2882 | 10 | 9.86 | −0.142 | 29.52 | (9.44, 10.39) | 7.75 | −2.246 | 241.85 | (5.53, 8.71) |
| 1 | 1.03 | 0.026 | 10.53 | (0.78, 1.16) | 0.68 | −0.323 | 32.37 | (0.64, 0.71) | ||
| 0.03 | 0.03 | 0.001 | 0.36 | (0.03, 0.04) | 0.04 | 0.001 | 0.37 | (0.03, 0.04) | ||
| 15 | 1096 | 10 | 9.73 | −0.266 | 38.40 | (9.22, 10.34) | 8.19 | −1.814 | 184.84 | (7.38, 8.66) |
| 3.16 | 3.21 | 0.049 | 20.73 | (2.45, 3.47) | 2.05 | −1.108 | 110.97 | (1.97, 3.16) | ||
| 0.11 | 0.11 | 0.004 | 1.22 | (0.09, 0.13) | 0.11 | 0.004 | 1.04 | (0.09, 0.13) | ||
| 16 | 531 | 10 | 9.50 | −0.501 | 55.72 | (9.10, 9.96) | 7.93 | −2.072 | 207.90 | (7.55, 8.22) |
| 10 | 9.91 | −0.095 | 54.47 | (9.02, 10.88) | 5.63 | −4.368 | 436.96 | (5.40, 5.89) | ||
| 0.33 | 0.34 | 0.007 | 4.51 | (0.26, 0.43) | 0.30 | −0.029 | 4.06 | (0.26, 0.36) |
Table 3.
Simulation results showing mean, bias, root mean squared error (RMSE) and the 2.5 and 97.5 empirical percentiles of the estimates of θ = (λ001 λ01 λ011 λ10 μ1)⊺ under model for both the PSHMM and exponential fitting (Exp) methods across 100 repeat experiments. , δ = 0.01, ω = 0 (unknown), the number of emitters NE = 100. NF indicates the number of frames simulated
| Study | NF | θ | PSHMM Mean | PSHMM Bias | PSHMM RMSE (× 10−2) | PSHMM (2.5%, 97.5%) percentiles | Exp Mean | Exp Bias | Exp RMSE (×10−2) | Exp (2.5%, 97.5%) percentiles |
|---|---|---|---|---|---|---|---|---|---|---|
| 17 | 11,151 | 0.15 | 0.15 | 0.002 | 1.69 | (0.12, 0.19) | 0.15 | −0.004 | 1.66 | (0.11, 0.19) |
| 0.3 | 0.30 | 0.001 | 0.85 | (0.28, 0.32) | 0.30 | −0.002 | 0.84 | (0.28, 0.31) | ||
| 0.1 | 0.10 | 0.000 | 0.43 | (0.09, 0.11) | 0.10 | 0.002 | 0.45 | (0.10, 0.11) | ||
| 0.80 | 0.80 | −0.001 | 1.28 | (0.78, 0.82) | 0.76 | −0.039 | 4.12 | (0.74, 0.79) | ||
| 0.01 | 0.01 | 0.000 | 0.15 | (0.01, 0.01) | 0.02 | 0.010 | 0.97 | (0.02, 0.02) | ||
| 18 | 9364 | 0.35 | 0.36 | 0.005 | 5.44 | (0.24, 0.43) | 0.33 | −0.022 | 5.32 | (0.24, 0.43) |
| 1 | 1.00 | 0.003 | 3.68 | (0.94, 1.07) | 0.95 | −0.049 | 5.83 | (0.90, 1.01) | ||
| 0.3 | 0.30 | −0.002 | 2.01 | (0.26, 0.34) | 0.29 | −0.008 | 2.12 | (0.25, 0.33) | ||
| 2.30 | 2.30 | −0.003 | 5.01 | (2.21, 2.39) | 2.04 | −0.262 | 26.48 | (1.95, 2.11) | ||
| 0.10 | 0.10 | 0.002 | 0.98 | (0.09, 0.12) | 0.10 | −0.005 | 1.03 | (0.08, 0.11) | ||
| 19 | 7000 | 2 | 2.03 | 0.033 | 18.14 | (1.75, 2.45) | 2.16 | 0.156 | 21.25 | (1.89, 3.50) |
| 10 | 9.78 | −0.218 | 54.49 | (8.55, 10.53) | 6.94 | −3.061 | 306.69 | (6.59, 7.34) | ||
| 0.7 | 0.71 | 0.011 | 4.88 | (0.64, 0.83) | 0.67 | −0.031 | 4.85 | (0.60, 0.76) | ||
| 10 | 10.00 | 0.002 | 63.62 | (9.22, 11.65) | 4.97 | −5.030 | 503.14 | (4.75, 5.17) | ||
| 0.33 | 0.34 | 0.005 | 7.29 | (0.20, 0.56) | 0.27 | −0.068 | 7.30 | (0.22, 0.32) |
Table 4.
Simulation results showing mean, bias, root mean squared error (RMSE) and the 2.5 and 97.5 empirical percentiles of the estimates of θ = (λ001 λ01 λ0102 λ011 λ021 λ10 μ1)⊺ under model for both the PSHMM and exponential fitting (Exp) methods across 100 repeat experiments. , δ = 0.01, ω = 0 (unknown), the number of emitters NE = 100. NF indicates the number of frames simulated
| Study | NF | θ | PSHMM Mean | PSHMM Bias | PSHMM RMSE (× 10−2) | PSHMM (2.5%, 97.5%) percentiles | Exp Mean | Exp Bias | Exp RMSE (×10−2) | Exp (2.5%, 97.5%) percentiles |
|---|---|---|---|---|---|---|---|---|---|---|
| 20 | 7000 | 2 | 2.03 | 0.032 | 3.14 | (1.75, 2.37) | 2.05 | 0.054 | 2.12 | (1.79, 3.31) |
| 10 | 9.85 | −0.153 | 13.42 | (9.20, 10.49) | 7.04 | −2.958 | 878.82 | (6.68, 7.48) | ||
| 0.2 | 0.21 | 0.009 | 0.10 | (0.16, 0.27) | 0.18 | −0.024 | 0.11 | (0.13, 0.21) | ||
| 0.7 | 0.69 | −0.012 | 0.37 | (0.59, 0.83) | 0.66 | −0.037 | 0.35 | (0.57, 0.75) | ||
| 0.01 | 0.01 | −0.001 | 0.00 | (0.01, 0.01) | 0.01 | 0.005 | 0.02 | (0.01, 0.02) | ||
| 10 | 9.63 | −0.368 | 35.57 | (8.73, 10.53) | 4.91 | −5.087 | 2588.85 | (4.67, 5.16) | ||
| 0.33 | 0.32 | −0.009 | 0.32 | (0.24, 0.45) | 0.32 | −0.013 | 0.12 | (0.26, 0.38) |
Table 5.
A description of the Alexa Fluor 647 datasets with reference to the laser intensities in kW/cm2 and frames sampled per second (or Δ−1) measured in s−1 used to characterize each of the 27 experiments. The NF × NE size of each dataset is also included
| Dataset | Laser intensity | Δ−1 | NE | NF | Dataset | Laser intensity | Δ−1 | NE | NF | Dataset | Laser intensity | Δ−1 | NE | NF |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1.0 | 200 | 275 | 49,796 | 10 | 16 | 200 | 292 | 39,703 | 19 | 62 | 800 | 443 | 29,107 |
| 2 | 1.9 | 200 | 259 | 49,533 | 11 | 16 | 800 | 305 | 29,074 | 20 | 62 | 800 | 425 | 29,551 |
| 3 | 3.9 | 200 | 335 | 49,815 | 12 | 16 | 800 | 290 | 29,145 | 21 | 62 | 800 | 425 | 29,426 |
| 4 | 3.9 | 200 | 393 | 39,758 | 13 | 31 | 800 | 617 | 29,059 | 22 | 62 | 800 | 398 | 28,989 |
| 5 | 7.8 | 200 | 340 | 39,721 | 14 | 31 | 800 | 534 | 29,778 | 23 | 97 | 800 | 454 | 29,191 |
| 6 | 7.8 | 800 | 244 | 29,418 | 15 | 31 | 800 | 515 | 29,179 | 24 | 97 | 800 | 440 | 29,198 |
| 7 | 7.8 | 800 | 230 | 29,257 | 16 | 31 | 800 | 493 | 29,400 | 25 | 97 | 800 | 436 | 29,270 |
| 8 | 7.8 | 800 | 230 | 29,438 | 17 | 31 | 800 | 456 | 29,071 | 26 | 97 | 800 | 422 | 29,295 |
| 9 | 16 | 800 | 437 | 29,467 | 18 | 62 | 800 | 554 | 29,327 | 27 | 97 | 800 | 414 | 29,218 |
Footnotes
Supported by the Imperial College London President’s Scholarship.
Supported by the Engineering and Physical Sciences Research Council (EP/L504889/1).
Supported by the National Institute of Health (R01 GM085575).
Supported by the Medical Research Council (MR/K015826/1) and Biotechnology and Biological Sciences Research Council (BB/M022374/1).
We modified the exponential fitting algorithm used by Lin et al. (2015) to allow for the absorption parameter (see Supplementary Materials Section S5 (Patel et al. (2019)) for more details).
SUPPLEMENTARY MATERIAL
Supplementary materials (DOI: 10.1214/19-AOAS1240SUPPA; .pdf). The Supplementary Materials supporting this paper contains detailed proofs and derivations regarding our method, discussions on its implementation and further simulation studies, including exact details on the image analysis.
Code and data (DOI: 10.1214/19-AOAS1240SUPPB; .zip). MATLAB code and imaging data sets used for the algorithms presented in this paper, can be found at https://github.com/eakcohen/photoswitching.
REFERENCES
- Baum LE and Eagon JA (1967). An inequality with applications to statistical estimation for probabilistic functions of Markov processes and to a model for ecology. Bull. Amer. Math. Soc 73 360–363. MR0210217 [Google Scholar]
- Baum LE and Petrie T (1966). Statistical inference for probabilistic functions of finite state Markov chains. Ann. Math. Stat 37 1554–1563. MR0202264 [Google Scholar]
- Baum LE and Sell GR (1968). Growth transformations for functions on manifolds. Pacific J. Math 27 211–227. MR0234494 [Google Scholar]
- Baum LE, Petrie T, Soules G and Weiss N (1970). A maximization technique occurring in the statistical analysis of probabilistic functions of Markov chains. Ann. Math. Stat 41 164–171. MR0287613 [Google Scholar]
- Betzig E, Patterson GH, Sougrat R, Lindwasser OW, Olenych S, Bonifacino JS, Davidson MW, Lippincott-Schwartz J and Hess HF (2006). Imaging intracellular fluorescent proteins at nanometer resolution. Science 313 1642–1645. [DOI] [PubMed] [Google Scholar]
- Ching W, Fung E and Ng M (2003). Higher-order hidden Markov models with applications to DNA sequences In Intelligent Data Engineering and Automated Learning. IDEAL 2003 (Liu J, Cheung Y and Yin H, eds.). Lecture Notes in Computer Science 2690 535–539. Springer, Berlin, Heidelberg. [Google Scholar]
- Colquhoun D, Hatton CJ and Hawkes AG (2003). The quality of maximum likelihood estimates of ion channel rate constants. J. Physiol 547 699–728. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Colquhoun D and Hawkes AG (1981). On the stochastic properties of single ion channels. Proc. R. Soc. Lond., B Biol. Sci 211 205–235. [DOI] [PubMed] [Google Scholar]
- Colquhoun D, Hawkes AG and Srodzinski K (1996). Joint distributions of apparent open and shut times of single-ion channels and maximum likelihood fitting of mechanisms. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci 354 2555–2590. [Google Scholar]
- Cox S, Rosten E, Monypenny J, Jovanovic-Talisman T, Burnette DT, Lippincott-Schwartz J, Jones GE and Heintzmann R (2011). Bayesian localization microscopy reveals nanoscale podosome dynamics. Nat. Methods 9 195–200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dempsey GT, Vaughan JC, Chen KH, Bates M and Zhuang X (2011). Evaluation of fluorophores for optimal performance in localization-based super-resolution imaging. Nat. Methods 8 1027–1036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Du Preez J (1998). Efficient training of high-order hidden Markov models using first-order representations. Comput. Speech Lang 12 23–39. [Google Scholar]
- Efron B and Tibshirani RJ (1993). An Introduction to the Bootstrap Monographs on Statistics and Applied Probability 57 CRC Press, New York: MR1270903 [Google Scholar]
- Epstein M, Calderhead B, Girolami MA and Sivilotti L (2016). Bayesian statistical inference in ion-channel models with exact missed event correction. Biophys. J 111 333–348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greenfeld M, Pavlichin DS, Mabuchi H and Herschlag D (2015). Single molecule analysis research tool (SMART): An integrated approach for analysing single molecule data. PLoS ONE 7 e30024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ha T and Tinnefeld P (2012). Photophysics of fluorescent probes for single-molecule biophysics and super-resolution imaging. Annu. Rev. Phys. Chem 63 595–617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hawkes AG, Jalali A and Colquhoun D (1990). The distributions of the apparent open times and shut times in a single channel record when brief events cannot be detected. Philos. Trans. R. Soc. Lond. Ser. A 332 511–538. MR1084721 [DOI] [PubMed] [Google Scholar]
- Hawkes AG, Jalali A and Colquhoun D (1992). Asymptotic distributions of apparent open times and shut times in a single channel record allowing for the omission of brief events. Philos. Trans. R. Soc. Lond. B, Biol. Sci 337 383–404. [DOI] [PubMed] [Google Scholar]
- Heilemann M, Van de Linde S, Schüttpelz M, Kasper R, Seefeldt B, Mukher-jee A, Tinnefeld P and Sauer M (2008). Subdiffraction—resolution fluorescence imaging with conventional fluorescent probes. Angew. Chem. Int. Ed 47 6172–6176. [DOI] [PubMed] [Google Scholar]
- Hess ST, Girirajan TPK and Mason MD (2006). Ultra-high resolution imaging by fluorescence photoactivation localization microscopy. Biophys. J 91 4258–4272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang B, Bates M and Zhuang X (2009). Super-resolution fluorescence microscopy. Annu. Rev. Biochem 78 993–1016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jacquez JA and Greif P (1985). Numerical parameter identifiability and estimability: Integrating identifiability, estimability, and optimal sampling design. Math. Biosci 77 201–227. [Google Scholar]
- Jungmann R, Steinhauer C, Scheible M, Kuzyk A, Tinnefeld P and Simmel FC (2010). Single-molecule kinetics and super-resolution microscopy by fluorescence imaging of transient binding on DNA origami. Nano Lett. 10 4756–4761. [DOI] [PubMed] [Google Scholar]
- Lee L-M and Lee J-C (2006). A study on high-order hidden Markov models and applications to speech recognition In Advances in Applied Artificial Intelligence. IEA/AIE 2006 (Ali M and Dapoigny R, eds.). Lecture Notes in Computer Science 4031 682–690. Springer, Berlin, Heidelberg. [Google Scholar]
- Lee SH, Shin JY, Lee A and Bustamante C (2012). Counting single photoactivatable fluorescent molecules by photoactivated localization microscopy (PALM). Proc. Natl. Acad. Sci. USA 109 17436–17441. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lehmann M, Lichtner G, Klenz H and Schmoranzer J (2016). Novel organic dyes for multicolor localization-based super-resolution microscopy. J. Biophotonics 9 161–170. [DOI] [PubMed] [Google Scholar]
- Levinson SE, Rabiner LR and Sondhi MM (1983). An introduction to the application of the theory of probabilistic functions of a Markov process to automatic speech recognition. Bell Syst. Tech. J 62 1035–1074. MR0702893 [Google Scholar]
- Lin Y, Long JJ, Huang F, Duim WC, Kirschbaum S, Zhang Y, Schroeder LK, Rebane AA, Velasco MGM et al. (2015). Quantifying and optimizing single-molecule switching nanoscopy at high speeds. PLoS ONE 10 e0128135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Little MP, Heidenreich WF and Li G (2010). Quantifying and optimizing single-molecule switching nanoscopy at high speeds. PLoS ONE 5 e8915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Y-Y, Li S, Li F, Song L and Rehg J (2015). Efficient learning of continuous-time hidden Markov models for disease progression. in NIPS Proceedings 3600–3608. [PMC free article] [PubMed] [Google Scholar]
- MacDonald IL and Zucchini W (1997). Hidden Markov and Other Models for Discrete-Valued Time Series Monographs on Statistics and Applied Probability 70 CRC Press, London: MR1692202 [Google Scholar]
- Mukamel E, Babcock H and Zhuang X (2012). Statistical deconvolution for superresolution fluorescence microscopy. Biophys. J 102 2391–2400. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nieuwenhuizen RPJ, Bates M, Szymborska A, Lidke KA, Rieger B and Stallinga S (2015). Quantitative localization microscopy: Effects of photophysics and labeling stoichiometry. PLoS ONE 10 e0127989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ober RJ, Ram S and Ward ES (2004). Localization accuracy in single-molecule microscopy. Biophys. J 87 1185–1200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ober R, Tahmasbi A, Ram S, Lin Z and Ward E (2015). Quantitative aspects of single-molecule microscopy: Information-theoretic analysis of single-molecule data. IEEE Signal Process. Mag 32 58–69. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patel L, Gustafsson N, Lin Y, Ober R, Henriques R and Cohen E (2019). Supplement to “A hidden Markov model approach to characterizing the photo-switching behavior of fluorophores.” DOI: 10.1214/19-A0AS1240SUPPA, DOI:. [DOI] [PMC free article] [PubMed]
- Qin F, Auerbach A and Sachs F (1996). Estimating single-channel kinetic parameters from idealized patch-clamp data containing missed events. Biophys. J 70 264–280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qin F and Li L (2004). Model-based fitting of single-channel dwell-time distributions. Biophys. J 87 1657–1671. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rabiner LR (1989). A tutorial on hidden Markov models and selected applications in speech recognition. Proc. IEEE 77 257–286. [Google Scholar]
- Ram S, Ward ES and Ober RJ (2013). A stochastic analysis of distance estimation approaches in single molecule microscopy: Quantifying the resolution limits of photon-limited imaging systems. Multidimens. Syst. Signal Process 24 503–542. MR3041619 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rief M, Rock RS, Mehta AD, Mooseker MS, Cheney RE and Spudich JA (2000). Myosin-V stepping kinetics: A molecular model for processivity. Proc. Natl. Acad. Sci. USA 97 9482–9486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rieger B and Stallinga S (2014). The lateral and axial localization uncertainty in super-resolution light microscopy. ChemPhysChem 15 664–670. [DOI] [PubMed] [Google Scholar]
- Rollins GC, Shin JY, Bustamante C and Pressé S (2014). Stochastic approach to the molecular counting problem in superresolution microscopy. Proc. Natl. Acad. Sci. USA 112 110–118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rothenberg TJ (1971). Identification in parametric models. Econometrica 39 577–591. MR0436944 [Google Scholar]
- Rust MJ, Bates M and Zhuang X (2006). Sub-diffraction-limit imaging by stochastic optical reconstruction microscopy (STORM). Nat. Methods 793–795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sage D, Kirshner H, Pengo T, Stuurman N, Min J, Manley S and Usher M (2015). Quantitative evaluation of software packages for single-molecule localization microscopy. Nat. Methods 12 717–724. [DOI] [PubMed] [Google Scholar]
- Sharonov A and Hochstrasser RM (2006). Wide-field subdiffraction imaging by accumulated binding of diffusing probes. Proc. Natl. Acad. Sci. USA 103 18911–18916. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thompson RE, Larson DR and Webb WW (2002). Precise nanometer localization analysis for individual fluorescent probes. Biophys. J 82 2775–2783. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van de Linde S and Sauer M (2014). How to switch a fluorophore: From undesired blinking to controlled photoswitching. Chem. Soc. Rev 43 1076–1087. [DOI] [PubMed] [Google Scholar]
- Van de Linde S, Wolter S, Heilemann M and Sauer M (2010). The effect of photoswitching kinetics and labeling densities on super-resolution fluorescence imaging. J. Biotechnol 149 260–266. [DOI] [PubMed] [Google Scholar]
- Vogelsang J, Steinhauer C, Forthmann C, Stein IH, Person-Skegro B, Cordes T and Tinnefeld P (2010). Make them blink: Probes for super-resolution microscopy. ChemPhysChem 11 2475–2490. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.