A coarse-grained model for assisting the investigation of structure and dynamics of large nucleic acids by Ion Mobility Spectrometry Mass Spectrometry

Abstract

Ion Mobility Spectrometry-Mass Spectrometry (IMS-MS) is a rapidly emerging tool for the investigation of nucleic acid structure and dynamics. IMS-MS determinations can provide valuable information regarding alternative topologies, folding intermediates, and conformational heterogeneities, which are not readily accessible to other analytical techniques. The leading strategies for data interpretation rely on computational and experimental approaches to correctly assign experimental observations to putative structures. A very effective strategy involves the application of molecular dynamics (MD) simulations to predict the structure of the analyte molecule, calculate its collision cross section (CCS), and then compare this computational value with the corresponding experimental data. While this approach works well for small nucleic acid species, analyzing larger nucleic acids of biological interest is hampered by the computational cost associated with capturing their extensive structure and dynamics in all-atom detail. In this report, we describe the implementation of a coarse graining (CG) approach to reduce the cost of the computational methods employed in the data interpretation workflow. Our framework employs a five-bead model to accurately represent each nucleotide in the nucleic acid structure. The beads are appropriately parameterized to enable the direct calculation of CCS values from CG models, thus affording the ability to pursue the analysis of larger, highly dynamic constructs. The validity of this approach was successfully confirmed by the excellent correlation between CCS values obtained in parallel by all-atom and CG workflows.

Introduction

In recent years, the discovery of the pervasive regulatory functions performed by nucleic acids has greatly increased the interest in understanding their mechanisms of action at the molecular level.^1–3 The realization that the function of nucleic acids is not exclusively associated with the information stored in their sequence has boosted the demand for three-dimensional structure elucidation.^4,5 A picture is rapidly emerging in which the function of non-protein coding RNAs (ncRNAs) depends on their ability to interact with a wide range of ligands, which is determined by their 3D structure.^6–8 Sequence may still play an essential role when function involves interactions with complementary nucleic acids, which are dictated by the Watson-Crick rules.^9,10 In many cases, however, function is mediated by specific recognition between structured regions and small ligands or protein factors, which is not only dictated by the Watson-Crick rules, but through tertiary interactions between domains.^11,12 Riboswitches are well-known examples in which the binding of specific metabolites can induce major structural rearrangements leading to effective activation/ deactivation of the expression of downstream protein-coding sequences.^13–15 In the case of DNA, cruciforms, hairpins, and quadruplex structures are characterized by non-canonical structures in which the coiling state differs significantly from the usual B-type helix.¹⁶ Different degrees of supercoiling introduce conformational heterogeneity that can not only influence local structure, but can also cause marked variations of looping and protein-binding capabilities, which are involved in gene expression regulation.^17,18 Elucidating the mechanism of these emerging functions of nucleic acids will require a better understanding of their 3D structure and the dynamics induced by ligand interaction.

The broader availability of information on nucleic acid structure and dynamics is traditionally hampered by numerous limitations. Established techniques, such as nuclear magnetic resonance (NMR)^19,20 and X-ray crystallography^21,22 can provide structures with single-atom resolution, but their applicability hinges on accessible size, abundant sample availability, and favorable solubility and crystallization properties. Electron cryo-microscopy (cryo-EM) has shown promise for obtaining high-resolution structures of nucleic acids, but the technique faces intrinsic limitations associated with sample purity, concentration, and accessible size, as well as possible radiation damage during analysis.²³ The reach of other spectroscopic techniques, such as circular dichroism (CD)^24,25 and small-angle X-ray scattering (SAXS),^26,27 has been limited by their relatively low resolution and the difficulty in interpreting the behavior arising from possible heterogeneity displayed by the analyte molecules. For these reasons, new alternative approaches are constantly being evaluated for their ability to obtain information that is not immediately accessible to such techniques. Among them is ion mobility spectrometry-mass spectrometry (IMS-MS), which has recently emerged as a complementary tool for the investigation of nucleic acid structure and dynamics.^28–30 This technique is based on the fact that ions with different structures interact in very distinctive ways with background gas, as they travel across a moderate electric field.^31,32 More specifically, analytes with compact conformations are less likely to collide with gas molecules and, thus, travel faster than more extended counterparts. The time of arrival (t_D) is therefore a function of their collision cross section (CCS), which in turn provides an excellent assessment of their size and conformation.^33,34 Unlike bulk spectroscopic techniques, IMS-MS is capable of differentiating coexisting conformations assumed by the construct, which substantiates the potential of this technique for the investigation of structure heterogeneity and dynamics.^35–37 Since these types of measurements typically take place in the millisecond timescale, global dynamics of nucleic acids, which involve transient dissociation of tertiary interactions and variations in the mutual positions of contiguous domains, can be readily resolved by this technique.³⁸ Smaller, localized dynamics which include base flipping and stacking, take place in the pico- and nano-second time scale and, thus, cannot be completely resolved by IMS-MS. In this case, the observed signal provides an average representation of the local conformation variations.³⁸ Recent reports have shown that this technique is readily applicable to progressively larger nucleic acids, such as G-quadruplexes consisting of 36-nt,³⁹ triplex DNA of 18-nt,⁴⁰ and DNA duplexes of 128-nt,³⁰ which may exhibit CCS values in excess of ~5,000 Ų.

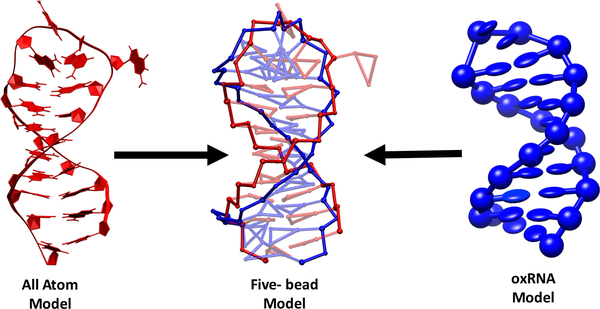
Established strategies employed to carry out the interpretation of IMS-MS data involve matching experimental CCS values with those calculated from either high-resolution structures, or all-atom models obtained by computational methods.^29,40–43 In this direction, recent advances in high-performance computing have facilitated the coupling of structure prediction algorithms with molecular dynamics (MD) simulations to investigate nucleic acid structures within the nanosecond to millisecond range.⁴⁴ While these types of approaches are rapidly gaining momentum, the intrinsic cost of computing power is clearly becoming a limiting factor in the pursuit of larger structures exhibiting significant conformational changes and dynamics in the millisecond time-scale.⁴⁴ Cost-effective alternatives could be developed by replacing all-atom simulations with less expensive coarse-grained (CG) methods, which are capable of sampling longer time-scales while retaining the ability to properly represent structured domains and capture their thermodynamic behavior.^44–50 Established CG models employ between one to six beads to represent each nucleotide.^{46–48,51–54} Different levels of coarse graining have been successfully used to capture different properties of the oligonucleotides. A one- or two-bead model can adequately trace the backbone of these types of biopolymers, but larger number of beads are necessary to capture the interactions of nucleobases, when greater structural detail is desired.^51–55 Specifically, in oxRNA/DNA⁴⁷ simulation models, which are used in the current study, each nucleotide is treated as a rigid body with interaction sites for backbone, base stacking, and base pairing interactions and is parameterized to reproduce thermodynamic properties of DNA and RNA helices.

In this report, we describe a CG approach for supporting the IMS-MS analysis of nucleic acids, which is based on the model introduced by Xia et al.⁵⁶ Specifically, we selected a five-bead framework that preserves a level of structural detail commensurate with the type of information afforded by CCS determinations. As a benchmark, we applied established protocols for calculating the analyte’s CCS from the corresponding 3D coordinates generated by all-atom MD simulations, which employ the projection approximation (PA) and exact-hard sphere scattering (EHSS) algorithms included in the MOBCAL package.^57–59 The possibility of calculating CCS values from CG structures was substantiated by enabling such algorithms to directly utilize coarse-grained coordinates. The validity of this approach was assessed by comparing CCS values calculated from both five-bead and all-atom models of the same construct. The capacity of the five-bead model to support CCS determinations was evaluated by examining nucleic acid structures of different topologies. While retaining the structural details in the popular CG models, like oxRNA/DNA, and enabling efficient CCS calculations of large RNA structures, the five-bead model developed here will be instrumental in interpreting IMS-MS experiments involving large RNA species.

Model Description

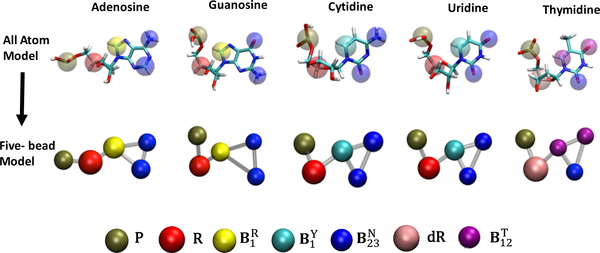
The five-bead model presented here was inspired by the model introduced earlier by Xia et al.⁵⁶ Proper parameterization was carried out to enable its seamless implementation with MOBCAL^57–59 to calculate CCS values directly from CG coordinates. The model utilizes five discrete pseudo-atoms (or beads) to represent each ribonucleotide unit in the biopolymer chain (Figure 1). Distinct beads are employed to represent the phosphate (P), ribose (R), and deoxy-ribose (dR) moieties common to all types of ribo- and deoxy-ribonucleotides. In contrast, three-bead sets are used to properly capture the planar nature of the aromatic systems of the various nucleobases. The first bead is available in two different types, named $B_1^R$ and $B_1^Y$, to better portray the differences between purine and pyrimidine systems, respectively. The other two beads reproduce the base-pairing edge by using copies of the same type named $B_{23}^N$. According to this scheme, the $B_1^R$, $B_{23}^N$, and $B_{23}^N$ set describes any purine nucleobase (i.e., adenine or guanine), whereas the $B_1^Y$, $B_{23}^N$, and $B_{23}^N$ set corresponds to any pyrimidine nucleobase (i.e., cytosine or uracil). Note that a separate pseudo-atom named $B_{23}^T$ was assigned to account for the additional methyl group on the pyrimidine ring in thymine. Though the representations do have a common base pairing edge, the relative location of the beads with respect to each other differentiates adenine from guanine, providing a more detailed representation of nucleic acid structure than those afforded by approaches that use either one or two pseudo-atoms per nucleotide.^48,60–62 The ability to distinguish the contributions of one-ring versus two-ring systems and to recognize the different components of a base pair can yield models that closely resemble the more detailed all atom structures.

Figure 1.

representation of nucleotides in all atom and five bead models (sizes not to scale).

For the purpose of CCS determinations, the definition of each pseudo-atom in the model must include the proper physicochemical parameters necessary to support the application of the desired algorithm. The PA and EHSS algorithms employed in this report rely respectively on the projected area and scattering properties of polyatomic ions, which are defined by the size and arrangement of the atoms in the analyte structure.^57–59 Therefore, the radius and coordinates of each atom represent essential information necessary to complete the calculations. The standard MOBCAL package^57–59 that contains these algorithms operates on all-atom coordinates and, thus, includes the value of hard-sphere radius (R_HS) for all possible types of atoms encountered in typical analytes. The ability to operate on coarse-grained coordinates was realized by introducing new atom definitions for the pseudo-atoms in the five-bead model, and assigning proper R_HS values (Table 1).

Table 1.

Names, hard-sphere radii, and mass identifiers for the pseudo-atoms in the five-bead model. The values of R_HS1 and R_HS2 were optimized for isolated nucleotides and oligomeric forms, respectively.

Name	Constituent atoms (in red)	Hard-sphere radius, Å (RHS1 and RHS2)		Mass (xmass)
P		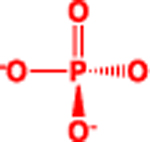3.8	3.32	95 (sum)
R		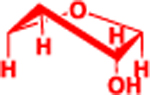4.2	3.68	97 (sum)
dR		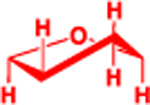3.9	3.41	81 (sum)
$B_1^R$		3.02	3.17	53 (sum)
$B_1^Y$		2.74	2.60	26 (sum)
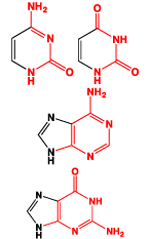$B_{23}^N$		2.88	3.12	43 (average)
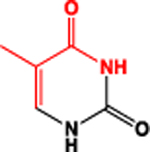$B_{23}^T$		3.17	3.43	41 (average)

This parameter was estimated through iterative processes aimed at ensuring the best possible match between CCS values afforded by all-atom and five-bead models (vide infra). A representative mass (xmass) was also assigned to each pseudo-atom to provide the program with unique atom-type identifiers. This parameter was calculated as either the sum or the average of the masses of the individual atoms included in the bead. The latter was necessary to identify the $B_{23}^N$ bead used to represent the base-pairing edge of ribo-nucleobases, which may exhibit different elemental compositions (Table 1).

Methods

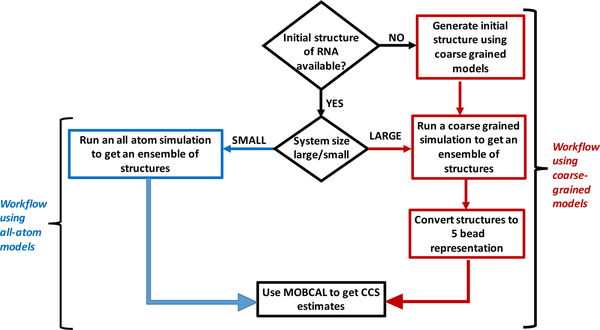
Generation of initial structure

The species considered in the study ranged from single nucleobases to mononucleotides (in ribo- and deoxyribo-form), to oligo-ribonucleotides of various sizes (i.e., 3, 5, 10, 16, 32, 48, 64 nt, Table 1S in Supplemental Material) in both single- and double-stranded form (ss and ds, respectively). The set of samples also include four stem-loop constructs: combining ds stems of up to 12 base-pairs and ss loops of up to 10 bases (Table 1S). The Nucleic Acid Builder (NAB) package of Amber^63,64 and ox-RNA/DNA⁴⁷ were employed to generate initial models in all-atom and CG mode, respectively. ox-RNA/DNA was used for all CG simulations presented in this paper. For systems with a known secondary structure (e.g., stem-loops), Monte Carlo folding simulations (in ox-RNA/DNA) were carried out by starting from a ss structure, allowing for formation of all the base pairs present in the secondary structure. In order to generate structures in the five-bead representation, scripts were developed in house to convert all-atom and CG (ox-RNA/DNA) structures to the five-bead model.

Molecular dynamics simulation

MD simulations were employed to equilibrate the conformation of the initial model around an average structure compatible with the selected conditions, but also to generate the structure ensembles necessary to complete the desired CCS calculations.

All-atom MD simulations:

The GROMACS package 4.6.3⁶⁵ was employed to carry out MD simulations in the all-atom mode. A modified version of the AMBER99 force-field,⁶⁶ which was specifically optimized for nucleic acids, was used to perform the simulations. We monitored the radius of gyration (R_g) afforded by the model at 300°K, which can account for any detectable conformational changes as a function of time. We previously observed that a 64-base pair DNA duplex underwent sizeable R_g fluctuations within the first few tens of pico-seconds of a typical MD simulation.³⁰ After that, however, the fluctuations stabilized to a rather small ±4.4% range around an average value, thus indicating that the structure had properly equilibrated at that temperature. Based on this observation, each simulation was extended until this practical condition was met. After equilibration, a production run of 1 ns was carried out to generate an ensemble of structures representative of the conformational variations incurred by the analyte molecule.

Coarse Grained MD simulations:

ox-RNA/DNA⁴⁷ was employed to carry out MD simulations in the CG mode. In these simulations, the equilibration procedure was carried out at 300°K by using an Anderson-like thermostat⁶⁷ built into ox-RNA/DNA. The default interaction parameters (for base pairing and base stacking) in ox-RNA/DNA were used in the simulations. The energy of the system was monitored as a function of time. Stable energy values were used as an indicator for a well equilibrated system, after which production runs of 3μs were performed. The time step for the simulations was set to 6fs.

Collisional cross section calculations

Structure ensembles generated by MD simulations were used as inputs for MOBCAL. The standard package was appropriately modified to enable the direct utilization of CG data, as described above. The addition of proper pseudo-atom definitions enabled MOBCAL to work seamlessly with either all-atom or CG inputs. In both cases, the program was set to perform at least 10 iterations for each frame in the ensemble. Considering that typical ensembles consisted of at least 20 frames, which were selected at regular intervals along the production run, the average value of CCS provided an excellent representation of the average conformation assumed by the analyte.

Results and discussion

The significance of the contributions of computational methods to the IMS-MS investigation of structure and dynamics is substantiated by different types of applications. For an unknown analyte that is not amenable to high-resolution structural techniques, an excellent match between CCS values obtained from IMS-MS and computational analysis can provide strong evidence that the analyte may indeed possess the predicted structure. When a high-resolution structure is available, MD simulations may help predict conformational dynamics that can be directly probed by IMS-MS determinations. The growing emphasis on larger nucleic acid structures, which exhibit wide ranges of conformational changes over extended timeframes, places a premium on increasing the available computational power and minimizing the cost of molecular modelling. This report tested the possibility of replacing all-atom operations with CG equivalents to enable the pursuit of larger analytes without a significant loss of detail. This endeavour required the modification of an established tool in the IMS-MS interpretation workflow and its re-parameterization to ensure full compatibility with five-bead inputs.

Parameterization of the five-bead model

Leading algorithms employed to calculate CCS values from structure coordinates are made available through the popular MOBCAL package.^57,58 The task of making this package compatible with our five-bead model was achieved by generating new atom definitions for the pseudo-atoms included in the CG framework. Whereas the mass identifier (xmass) was readily obtained as explained above, assigning a proper value to the hard-sphere radius (R_HS) posed some challenges. Given that each nucleoside consists of multiple types of pseudo-atoms in different spatial arrangements, there is no deterministic way to derive individual R_HS values from the calculated CCS values. We therefore devised an iterative process in which an initial approximation was gradually refined by comparing the CCSs obtained from all-atom and corresponding CG representations of the same structures. The refinement process was repeated by placing the pseudo-atoms in different types of structures (i.e., nucleobase, mononucleotide, and oligomer) to probe for possible context-dependent effects.

Different approaches were implemented to estimate the R_HS of pseudo-atoms used to build the backbone of a putative oligomer (i.e., P, R, and dR, Table 1), or the nucleobase moiety of each nucleotide (i.e., $B_1^R$, $B_1^Y$, $B_{23}^N$, and $B_{12}^T$). In the case of the former, the general topology of isolated phosphate and pentose groups can be approximated to an overall spherical geometry. Therefore, the CCSs obtained from their all-atom models were expected to match very closely those obtained from hypothetical spheres defined by their constituent atoms (marked in red in Table 1). Based on this consideration, the radii of these pseudo-atoms were initially estimated by generating the respective all-atom models and calculating their CCSs by using standard MOBCAL parameters. The values were then input into the PA and EHSS algorithms to back-calculate the radii of the corresponding hypothetical spheres (i.e., r_P, r_R, and r_dR). An additional correction factor f, which shrinks the size of the backbone atoms, was included to account for the effects of placing the pseudo-atoms in full-fledged oligomeric structures as explained later. These parameters were thus expressed as:

$$\begin{array}{l}{R}_{HS}(P)=(1-f)\ast r_p\\ R_{HS}(R)=(1-f)\ast r_R\\ R_{HS}(dR)=(1-f)\ast r_{dR}\end{array}$$

In contrast, the planar topology exhibited by the various nucleobases cannot be properly represented by a single sphere. The fact that three beads were necessary to represent each nucleobase implied that CCS-based optimization had to rely on the simultaneous estimation of the size of multiple pseudo-atoms. This task was accomplished by assigning a reference value to one of the beads and using proper scaling factors to adjust the others. The $B_{23}^N$ pseudo-atom was selected as possible reference because two copies are used in each ribonucleobase to represent the base-pairing edge. An initial r_B value was arbitrarily assigned to enable the process of successive approximations (Table 2S in Supplemental Material). A scaling factor s was added/subtracted to the reference to estimate the radii of the purine and pyrimidine beads (i.e., $B_1^R$ and $B_1^Y$), which were expected to be slightly larger and smaller, respectively. A dedicated factor s_T was employed to estimate the radii of the unique $B_{12}^T$ bead used for the base-pairing edge of thymine. Based on these considerations, these parameters were expressed as:

$$\begin{array}{l}{R}_{HS}(B_1^R)=(1+0.67f)\ast (1+s)\ast r_B\\ R_{HS}(B_1^Y)=(1+0.67f)\ast (1-s)\ast r_B\\ R_{HS}(B_{23}^N)=(1+0.67f)\ast r_B\\ R_{HS}(B_{12}^T)=(1+0.67f)\ast (1+s_T)\ast r_B\end{array}$$

Note that while ‘f’ is included to fractionally increase the size of the base beads at the expense of the backbone beads, the 0.67 factor accounts for the presence of three base and two backbone beads, respectively.

Initial optimization of r_B and s was carried out by generating all-atom models for all possible nucleobases and calculating their respective CCSs with standard MOBCAL parameters. The correction factor f was set to zero during this phase of parameterization. Each nucleobase was then converted to its respective three-bead representation and its corresponding CCS was calculated by systematically varying r_B and s in successive iterations. The values that minimized the root mean square (RMS) deviation between reference (all-atom) and calculated (five-bead) CCS were used to obtain the initial radii employed for further optimization (Figure 1S in Supplemental Material). The process was repeated by using samples consisting of whole nucleotides, which contained all five beads necessary to represent the building blocks of polymeric nucleic acid molecules. The radii obtained from nucleotide-based refinement were referred to as the R_HS1 parameter set (Table 1). Since the EHSS algorithm gives a closer approximation of CCS compared to the PA algorithm, the parameter set was optimized based on the CCS values obtained from the former. However, the relative deviations (% ΔCCS) between corresponding all-atom and five-bead values for PA algorithm is very small and close to that of the EHSS (Table 3S in Supplemental Material), thus making the parameter set available to use with both methods.

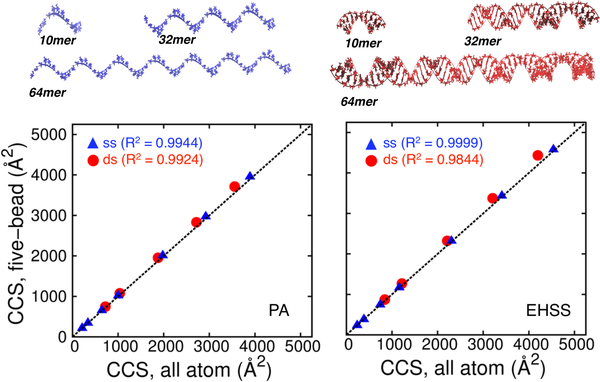
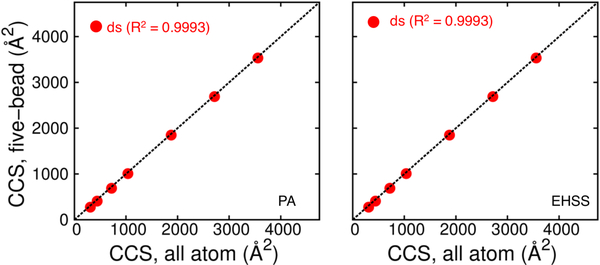
Further refinement was carried out by placing the pseudo-atoms in structural contexts that more closely replicated typical applications. A series of samples was generated, which consisted of static models (i.e., A- and B-form helices that had not undergone MD simulations, see Figure 2) of both single- and double-stranded oligomers spanning a 200–5000 Ų range (Table 1S). The CCS values of corresponding all-atom and CG models were calculated by using standard and R_SH1 parameters, respectively. The results obtained from both the PA and EHSS algorithms are compared in Figure 2. A close examination of the observed curves revealed that the single-stranded series afforded excellent correlation, but the double-stranded one displayed significant deviations as a function of size. We hypothesized that the discrepancy was likely due to the fact that the nucleobase beads tend to be more hidden and the backbone more exposed in a double-stranded context. We therefore employed the correction factor f to correct for possible topology effects by increasing the size of the nucleobase beads at the expense of the backbone ones, as described in the above equations. This factor was adjusted in an iterative fashion by minimizing the difference between corresponding CCS values (Table 2S in Supplemental Material), which produced a second set of parameters referred to as the R_HS2 set (Table 1). The results showed that making the backbone pseudo-atoms smaller and the nucleobase ones larger decreased the CCS of double-stranded constructs, but kept that of the single-strands constant. It was not surprising that the new R_HS2 set provided excellent correlations for both types of topologies (Figure 2S in Supplemental Material). At the same time, however, these parameters produced significantly worse matches when employed to analyze isolated nucleotides (compare Table 4S with Table 3S in Supplemental Material). Taken together, these considerations indicate that R_HS1 parameters should be employed for calculations involving smaller species, such as individual nucleobases, nucleosides, and nucleotides, whereas R_HS2 should be reserved for the larger polymeric forms.

Figure 2.

comparison of collision cross-section (ccs) values obtained from static all-atom and five-bead models by using standard and rhs1 parameters. single-stranded species are marked by blue triangles, double-stranded ones by red-circles and the y=x line is shown in black. the ccs values were obtained by either pa (left) or ehss (right) calculations. a 10mer, 32mer and 64mer single (blue) and double stranded (red) rna structures used for ccs calculations are shown.

Model evaluation

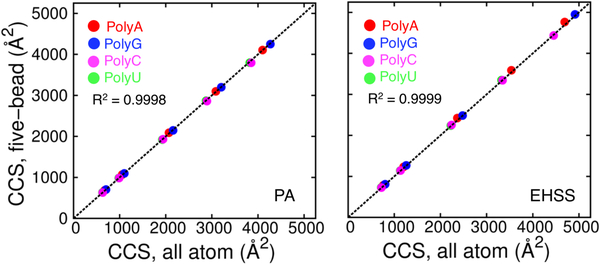
The robustness of the five-bead model and associated R_HS parameters was assessed by examining a series of oligomers, most of which have been excluded from the refinement process (Table 1S). First, we addressed the question of inherent biases introduced by nucleotide composition. Polynucleotides containing repeated units of a single nucleotide represent an extreme scenario of nucleotide composition in oligomers. Figure 3 compares the CCS values of single-stranded polynucleotides using the all-atom and five-bead model. The model performs well with constructs reaching up to 64 nucleotides without showing any bias.

Figure 3.

comparison of collision cross-section (ccs) values obtained from static all-atom and five-bead models of polynucleotides by using standard and rhs2 parameters (polya, polyg, polyc, polyu). polyc and polyu are indistinguishable due to similar arrangement of atoms in the structures which is expected. the ccs values were obtained by either pa (left) or ehss (right) calculations. the r2 values is calculated for the combined set of data points.

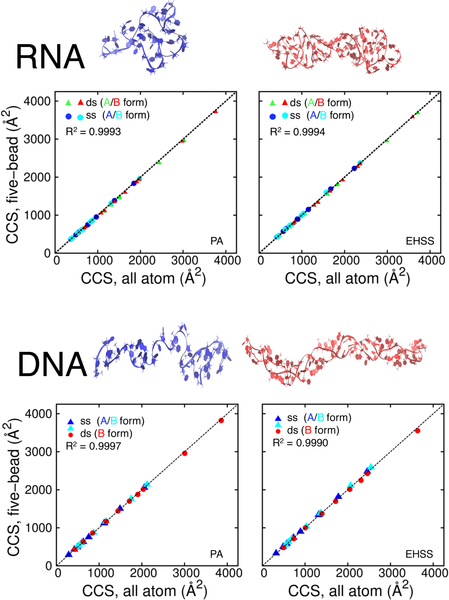
Next, single and double-stranded constructs were modelled in both A- and B-helical forms to probe for possible effects of structure topology. In this case, the initial all-atom models were subjected to MD simulations until properly equilibrated (see Methods section). Production runs were subsequently completed to secure all-atom ensembles for CCS determinations. Representative structures of ss and ds nucleic acids (both RNA and DNA) shown in Figure 4 display the collapse of the canonical helices in the gas phase simulations to non-canonical shapes, as previously observed.³⁰ For analysis, each frame was converted from all-atom to five-bead format to generate corresponding coordinate sets. PA and EHSS calculations were carried out for all-atom and five-bead ensembles and the results were visualized by plotting their respective CCS values (Figure 4). The outcome showed excellent correlation across the board, thus confirming that the five-bead model is capable of capturing the structural information contained in the corresponding all-atom structures. This observation was not limited to canonical A and B conformations. Indeed, a close examination of the ensembles revealed that some of the structures exhibited significant deviations from typical A and B helices, which were introduced by the unconstrained MD simulations. However, the excellent match between corresponding CCS values indicated that translating all-atom models into five-bead counterparts did not result in detectable deviations regardless of sample topology. The correlation held up with no apparent bias between DNA and RNA constructs and across the entire range explored in the study (up to 64 base-pairs, with CCS values approaching 5,000 Ų). These observations increase the confidence that five-bead representation of constructs possessing random sequence and base composition will maintain the ability to match the results obtained from their all-atom counterparts.

Figure 4.

correlation between collision cross-sections (ccss) obtained from all-atom and five-bead coordinates of rna and dna oligomers with different topologies. the all atom calculations employed standard parameters, whereas the five-bead calculations used the rhs2 pseudo-atom parameterization. the structures for these calculations were generated using md simulations. (selected snapshots from simulations shown above for a 32mer oligonucleotide (blue – single, red – double stranded)

Confirming the direct agreement between five-bead and all-atom models allowed us to test a workflow for IMS-MS interpretation based entirely on CG models. Initial static structures generated using oxRNA/DNA (CG model) were converted to their respective five-bead representation. The CCS values of these structures were in excellent agreement with those obtained from the corresponding all-atom models generated independently (Figure 5). Following that, four stem-loop constructs (two of RNA composition and two of DNA composition) exhibiting single-stranded loops with double-stranded stems were selected for comparing the models with experiments. The hairpin constructs with tetraloops, including the 20-nt RNA, 16-nt and 28-nt DNA were modelled in both all-atom and CG mode to enable direct comparisons. In contrast, the RNA 34-nt hairpin has a large loop and hence could only be modelled in CG mode to accurately capture its greater conformational flexibility. In the case of the CG workflow, initial structures were generated in ox-RNA/DNA by using secondary structure information to simulate and obtain correctly folded structures.

Figure 5.

comparison of collision cross-section (ccs) values obtained from static all-atom and five-bead models of oligomers obtained by using standard and rhs2 parameters respectively. the ccs values were obtained by either pa (left) or ehss (right) calculations. the five-bead models of oligomers are obtained using initial structures generated in oxrna (cg model).

Replicating the typical steps of an all-atom procedure, a production run was carried out after equilibration to obtain the ensembles necessary for CCS calculations. The results were reported in Table 2, together with experimental values obtained by IMS-MS analysis of the actual samples. The CCS values from the all-atom and CG workflows of both the DNA and RNA hairpins are in good agreement with each other, confirming the robustness of the five-bead model. In both cases, the CCS values were obtained by using the EHSS algorithm. A detailed structural comparison of the SL 20 RNA is shown in Figure 6 (structures for all four hairpins are presented in Figure 3S). The agreement between the models can be explained by the limited degrees of freedom of the hairpin in the loop region and modest changes in the backbone structure between the all-atom and CG workflows. Similar comparisons were not accomplished for the SL 34 RNA, which was modelled only in the CG workflow owing to its larger loop size. IMS-MS experiments were conducted on the hairpins, and the experimental CCS values were calculated according to the duplex calibration curve introduced by Lippens et al.³⁰ Even though we obtained a reasonable match between the experiments and models for SL 34 RNA, which was not the case for the smaller hairpins. Such discrepancies are consistent with prior observations³⁰ and are ascribable to the still incomplete understanding of the IMS-MS process and nucleic acid structure in the gas-phase.^28,41,68

Table 2:

CCS values determined by IMS-MS and computational analysis for DNA and RNA stemloop (SL) construct. Wall time indicates the time necessary to obtain 1ns of simulation data for the given construct.

Name	CCSIMS-MS Å2	CCSfive-bead Å2	Wall time (s)/ns	CCSall-atom Å2	Wall time (s)/ns
SL 20 (RNA)	722.3 ± 1.2	861.7 ± 30.3	0.009	844.25 ± 10.21	680
SL 34 (RNA)	1278.8 ± 0.6	1314.7 ± 54.1	0.016	N/A	N/A
SL 16 (DNA)	1025.5 ± 16.53	718.1 ± 35.31	0.006	714.2 ± 17.13	504
SL 28 (DNA)	1501.1 ± 1.5	1101.7 ± 25.46	0.010	1144.2 ± 21.73	1296

Figure 6.

structural comparison of the 20mer rna hairpin simulated using all atom model (left) and oxrna (cg) model (right). structures from both simulations are converted to the five-bead representation and the backbone beads are aligned to show the overlapped structures in the center. the rmsd between the structures obtained from the all-atom and the cg simulations in five bead representation is 5.3 å.

It must be finally noted that the CG workflow significantly reduced the computational costs of completing the necessary simulation. On average, the CG workflow reduced by five orders of magnitude the time required to carry out the corresponding all-atom operations (Table 2). The data presented here provides a fair assessment of the possible accuracy and time efficiency that should be expected from this type of interpretation workflow.

Conclusions

In this report, we introduced a five-bead framework for the CCS calculations of nucleic acids and tested its merits as an alternative to standard all-atom approaches. The desire to reduce the cost of the computational analysis of large nucleic acids was the driving force behind this project. All-atom MD simulations are typically weighed down by the calculations necessary to establish the coordinates of the various atoms in the structure. The strategy of defining pseudo-atoms to represent entire functional groups offers the ability to reduce the number of coordinates employed to describe the structure and, thus, the number of required calculations. The implementation of a suitable CG framework must consider that heavily coarse-grained models (i.e., with few pseudo-atoms) can potentially access longer timescales, but may lose important structural details, like the planarity of the nucleobase units. For this reason, the five-bead model developed here constituted a valid compromise capable of meeting the desired cost-savings without sacrificing the ability to convey the structural information accessed by IMS-MS determinations. The challenge of ensuring an accurate representation of the composition and spatial arrangement of the atoms in each pseudo-atom was compounded here by the need to assign proper physicochemical parameters that could support further applications. More specifically, we were interested in developing a workflow that would not only capture structure and dynamics, but would also enable CCS calculations to support IMS-MS analysis. For this reason, the parameterization process used CCSs obtained from all-atom models as reference values to be matched by the respective five-bead counterparts. The essential RHS parameters were refined through a bottom-up approach that iterated from nucleobases to single nucleotides to oligomers. Consistent with the types of structures used for refinement, two distinctive parameter sets were obtained for individual building blocks and polymeric forms.

For all molecules considered in the study, the parameterized five-bead models demonstrated seamless interchangeability with their all-atom counterparts. No significant bias was observed between single- and double-stranded constructs, A- and B-helices, or canonical and non-canonical structures generated by unconstrained MD simulation. The possible effects of structure topology were evident only in the variations between the different R_HS sets. The discrepancy was attributed to the different degree of exposure to collisions afforded by backbone versus nucleobase pseudo-atoms, which was deemed to be a direct consequence of the different structural contexts of individual nucleotides and oligomers. This explanation was supported also by the variations noted between PA and EHSS values, which could be traced back to the different interpretations of the ion mobility process espoused by these algorithms. In contrast, the discrepancy between experimental and computational values could be ascribed to the lack of a complete understanding of the behavior of biopolymer structure in solvent-free environment,^28,41,68 which was not addressed in this report.

In conclusion, the fact that five-bead models can capture the structural details of nucleic acids at least as well as all-atom models justifies their utilization to support IMS-MS analysis. As demonstrated for the stem-loop constructs, the five-bead framework enables the implementation of a full-fledged CG workflow for the interpretation of IMS-MS data (Figure 7). Going forward, the framework developed here can be used for interpretation of IMS-MS experiments through CCS calculations of nucleic acid structures from coarse-grained, as well as all-atom simulations and future CG models. The cost-effective nature of CG operations will facilitate the exhaustive exploration of the conformational space for the entire duration of an IMS-MS experiment, which can typically extend in the millisecond time scale. At the same time, the advantages of working in CG mode will be preserved by the availability of proper parameters, which allows for the direct application of PA and EHSS algorithm with no need to fine-grain five-bead into all-atom models. For all these reasons, the CG workflow will be expected to promote the broad diffusion of IMS-MS for the investigation of the structure and dynamics of large nucleic acid systems that do not owe their biological functions to their sequence information.

Figure 7.

workflow for obtaining computationally estimated ccs values for rna