Significance
Predicting how the gene expression patterns that specify animal body plans arise from interactions between transcription factor proteins and regulatory DNA remains a major challenge in physical biology. We utilize live imaging and theoretical approaches to examine how transcriptional control at the single-cell level gives rise to a sharp stripe of cytoplasmic mRNA in the fruit fly embryo. While the modulation of transcriptional bursting has been implicated as the primary lever for controlling gene expression, we find that this alone cannot quantitatively recapitulate pattern formation. Instead, we find that the pattern arises through the joint action of 2 regulatory strategies—control of bursting and control of the total duration of transcription—that originate from distinct underlying molecular mechanisms.
Keywords: transcriptional bursting, gene regulation, development, hidden Markov models
Abstract
Predicting how interactions between transcription factors and regulatory DNA sequence dictate rates of transcription and, ultimately, drive developmental outcomes remains an open challenge in physical biology. Using stripe 2 of the even-skipped gene in Drosophila embryos as a case study, we dissect the regulatory forces underpinning a key step along the developmental decision-making cascade: the generation of cytoplasmic mRNA patterns via the control of transcription in individual cells. Using live imaging and computational approaches, we found that the transcriptional burst frequency is modulated across the stripe to control the mRNA production rate. However, we discovered that bursting alone cannot quantitatively recapitulate the formation of the stripe and that control of the window of time over which each nucleus transcribes even-skipped plays a critical role in stripe formation. Theoretical modeling revealed that these regulatory strategies (bursting and the time window) respond in different ways to input transcription factor concentrations, suggesting that the stripe is shaped by the interplay of 2 distinct underlying molecular processes.
During embryonic development, tightly choreographed patterns of gene expression—shallow gradients, sharp steps, narrow stripes—specify cell fates. The correct positioning, sharpness, and amplitude of these patterns of cytoplasmic mRNA and protein ensure the reliable determination of animal body plans (1). Yet, despite decades of work mapping the gene regulatory networks that drive development, and despite extensive efforts to dissect the regulatory logic of the enhancer elements that dictate the behavior of these networks, a predictive understanding of how gene expression patterns and developmental outcomes are driven by transcription factor concentrations remains a central challenge in the field (2).
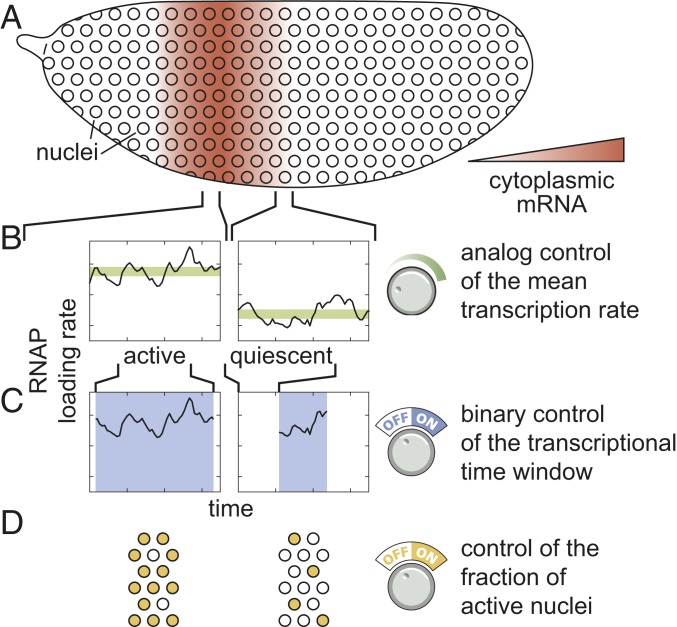
Predicting developmental outcomes demands a quantitative understanding of the flow of information along the central dogma: how input transcription factors dictate the output rate of mRNA production, how this rate of mRNA production dictates cytoplasmic patterns of mRNA, and how these mRNA patterns lead to protein patterns that feed back into the gene regulatory network. While the connection between transcription factor concentration and output mRNA production rate has been the subject of active research over the last 3 decades (2–11), the connection between this output rate and the resulting cytoplasmic patterns of mRNA has remained largely unexplored. For example, a graded stripe of cytoplasmic mRNA within an embryo could arise as a result of radically different transcriptional dynamics at the single-nucleus level (Fig. 1A). Specifically, if individual nuclei along this stripe modulate their average RNA polymerase (RNAP) loading rate, then graded control of the mean rate of transcription results: Nuclei in the middle of the stripe transcribe at a higher average rate than nuclei on the stripe boundaries (Fig. 1B). We identify this graded transcriptional control strategy with the analog control of gene expression. Alternatively, transcription factors could exert control over the length of time a nucleus is transcriptionally active (Fig. 1C). In this binary control scheme—akin to an on/off switch that dictates whether a nucleus is transcriptionally active or quiescent—individual nuclei transcribe at the same average rate regardless of their position along the stripe, but for different lengths of time. Finally, some nuclei might not engage in transcription at all during the formation of the pattern (Fig. 1D). Here, a larger fraction of nuclei engage in mRNA production in the stripe center than in the boundaries. Any of these scenarios, or some combination thereof, can explain the formation of a cytoplasmic mRNA pattern.
Fig. 1.
Multiple modes of pattern formation by single-cell transcriptional activity. (A–D) Cytoplasmic mRNA patterns (A) could arise from transcription factors exerting control over the mean transcription rate (B), the transcriptional time window dictating when a nucleus is transcriptionally active or quiescent (C), or the fraction of active nuclei (D) or some combination thereof.
To quantify the contribution of each regulatory strategy to pattern formation and thereby move toward a deeper understanding of the molecular processes at play, it is necessary to measure the rate of RNAP loading in individual nuclei, in real time, in a living embryo. However, to date, most studies have relied on fixed-tissue techniques such as mRNA fluorescence in situ hybridization (FISH) and immunofluorescence to obtain snapshots of the cytoplasmic distributions of mRNA and protein as development progresses (9, 12–15). Such techniques are virtually silent regarding the regulation of single-cell gene expression over time and are thus ill-suited to the study of how spatiotemporal variations in transcriptional dynamics give rise to patterns of cytoplasmic mRNA.
In this work, we investigated how single-cell transcriptional activity leads to the formation of stripe 2 of the widely studied even-skipped (eve) gene in the developing fruit fly embryo (16, 17). Previous work has established that the stripe is formed through the interplay of transcriptional activators and repressors (16). In addition, recent studies have indicated that the eve stripe mRNA profiles are graded and highly reproducible (18–21), suggesting that the detailed cytoplasmic distribution of mRNA that makes these stripes is key to the transmission of spatial information along the gene regulatory network that drives Drosophila development and reinforcing the need to develop models of gene regulation capable of connecting quantitative variations in input transcription factor patterns to graded output rates of transcription. To do this, we combined live imaging with theoretical modeling to study transcription at the single-cell level in real time, seeking a quantitative connection between the spatiotemporal variations in input transcription factor concentrations, the control of eve transcription, and the formation of cytoplasmic patterns of mRNA.
We found that all 3 regulatory strategies outlined in Fig. 1 quantitatively contribute to the formation of eve stripe 2. First, a smaller fraction of nuclei become active and engage in transcription in the periphery of the stripe than in the center, although this regulation of the fraction of active nuclei makes only a minor contribution to stripe formation. Second, consistent with previous studies, we found that the rate of mRNA production is significantly elevated in the center of the stripe (18). Strikingly, however, we discovered that this analog control of the transcription rate is insufficient to quantitatively recapitulate the cytoplasmic mRNA stripe pattern. In addition to the control of the rate of mRNA production among nuclei, we also observed a pronounced regulation of the window of time during which eve loci were engaged in transcription across the stripe, with those in the stripe center expressing for approximately 3 times longer than those in the flanks. While it is widely appreciated that genes are transcriptionally competent for limited windows of time during development, we found that—in the case of eve stripe 2—this binary transcriptionally engaged/disengaged logic is not merely a necessary precondition for pattern formation—it is the primary driver thereof. Thus, we conclude that the regulation of eve stripe 2 is multimodal in nature, with contributions from 3 distinct regulatory strategies (Fig. 1 B–D). Nonetheless, stripe formation can be quantitatively explained almost entirely through the interplay between 2 distinct control strategies: binary control of the duration of transcriptional engagement (Fig. 1C) and control of the mean rate of transcription (Fig. 1B).
Building upon this result, we developed computational approaches to uncover the mechanistic underpinning of each regulatory strategy. We employed a compound-state hidden Markov model (cpHMM) to uncover variations in transcriptional bursting dynamics in individual nuclei across space and time (22–24). We uncovered that, consistent with previous results, transcription factors control the rate of transcription by altering the frequency of transcriptional bursts (25, 26). In addition, we utilized logistic regressions to correlate eve stripe 2 transcriptional dynamics with changes in input transcription factor concentrations. This analysis revealed that the transcriptional time window adheres to different regulatory logic than transcriptional bursting: While repressor levels alone were sufficient to explain the early silencing of nuclei in the anterior and posterior stripe flanks, the control of bursting among transcriptionally engaged nuclei depends upon the input concentrations of both activators and repressors. Thus, our findings point to the presence of 2 distinct regulatory mechanisms that control transcription and gene expression patterns in early development, showcasing the potential for theoretical modeling and biological numeracy to yield additional biological insights when coupled with precise and quantitative experimental observation.
Results
Predicting Cytoplasmic mRNA Distributions from Transcriptional Activity.
To predict how the transcriptional activity of individual nuclei dictates the formation of cytoplasmic patterns of mRNA, we began with a simple model that considers the balance between the rate of mRNA synthesis and degradation
| [1] |
where indicates the mRNA concentration at position along the embryo at time , corresponds to the mRNA synthesis rate averaged over multiple nuclei within the same position , is the fraction of active nuclei (corresponding to the regulatory strategy shown in Fig. 1D), and is the degradation rate (see SI Appendix, section A for details of this derivation).
To examine the quantitative consequences of the 3 potential regulatory strategies (Fig. 1 B–D), we adopted widespread assumptions in the modeling of transcriptional regulation. First, we assumed that the degradation rate is a constant and not under any kind of spatiotemporal control. Comparisons between model predictions and empirically measured levels of cytoplasmic mRNA suggest that this assumption is reasonable (SI Appendix, section B). Second, we posited that at each position throughout the embryo the synthesis rate does not vary significantly in time such that it can be approximated by its time average . This assumption is revised later in the text to account for the time-dependent regulation of the mean rate of transcription. Finally, we assumed that nuclei along the axis of the embryo start transcribing at time and stop transcribing and enter a state of transcriptional quiescence at time . Under these assumptions, Eq. 1 can be solved analytically, resulting in
| [2] |
Eq. 2 makes precise predictions about how each regulatory strategy contributes to the formation of the cytoplasmic mRNA pattern. Thus, measuring how each quantity is regulated across the stripe allows us to predict their relative contributions to pattern formation.
Binary Control of the Transcriptional Time Window Is the Primary Driver of Stripe Formation.
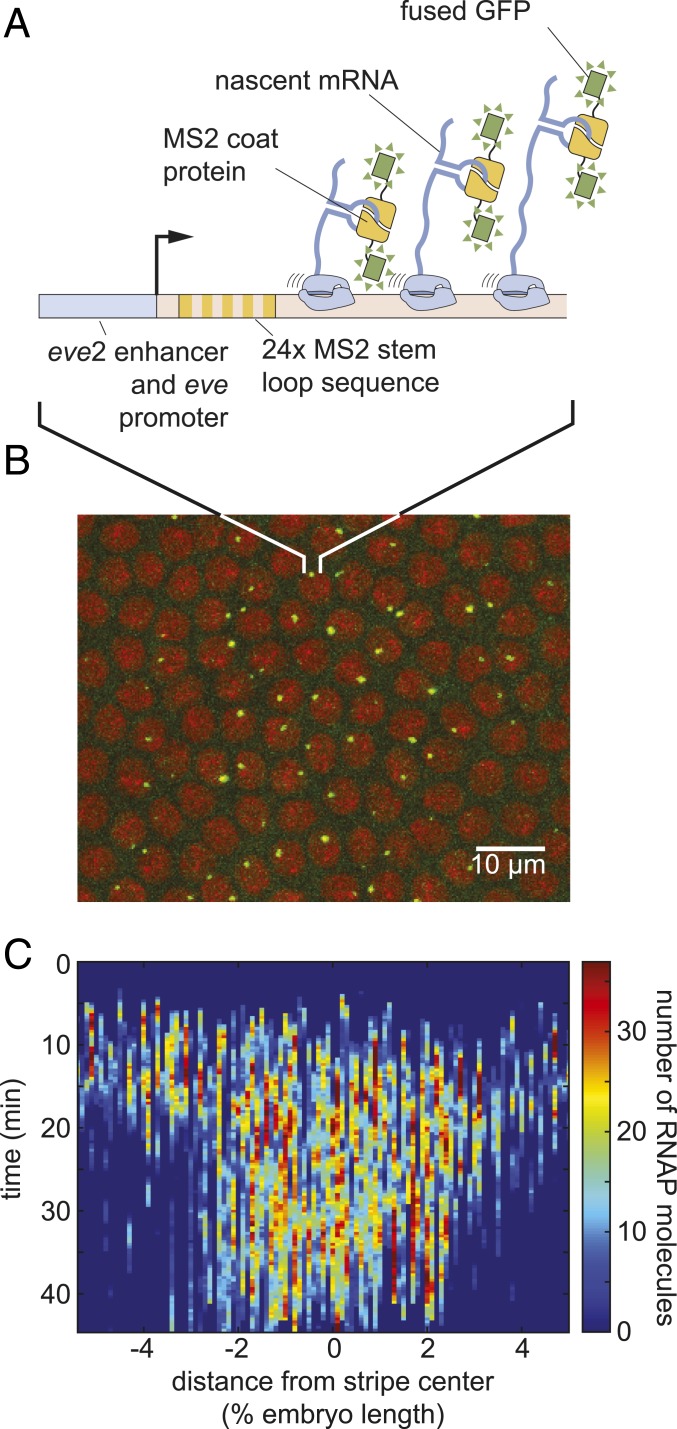
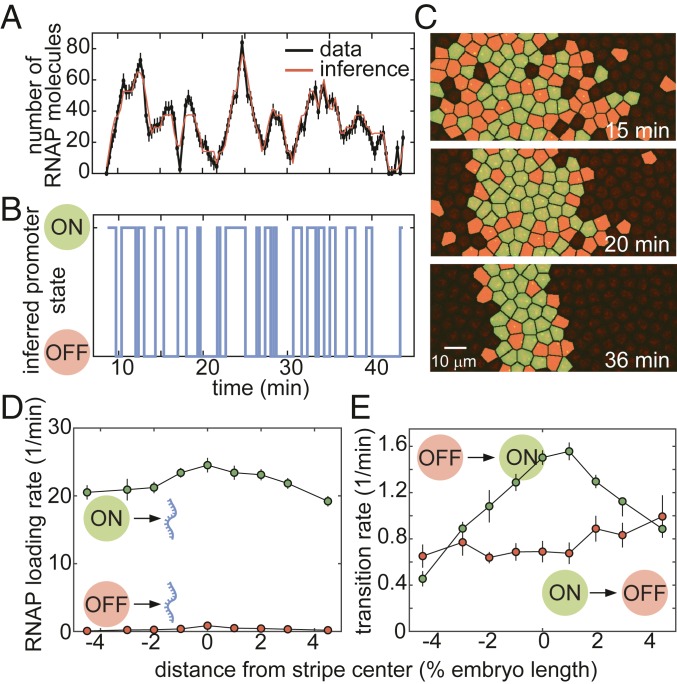
To test the simple model of pattern formation put forward in Eq. 2, we quantified transcription of stripe 2 of eve in the fruit fly. We imaged the transcription of an eve stripe 2 reporter, using the MS2 system (18, 27, 28). Transcripts of a reporter gene driven by the eve stripe 2 enhancer and the eve promoter contain repeats of a DNA sequence that, when transcribed, form stem loops (29). These stem loops are recognized by maternally provided MS2 coat protein fused to GFP (Fig. 2A). As a result, sites of nascent transcript formation appear as fluorescent puncta within individual nuclei (Fig. 2B and Movie S1). As described in SI Appendix, Fig. S2, the intensity of these fluorescent puncta is proportional to the number of RNAP molecules actively transcribing the gene. These resulting fluorescence values could then be calibrated using single-molecule FISH to estimate the number of RNAP molecules actively transcribing the gene (Materials and Methods and ref. 27). By aligning multiple embryos (SI Appendix, Fig. S1), we obtained the average number of actively transcribing RNAP molecules as a function of time and position throughout the embryo (Fig. 2C).
Fig. 2.
Measuring transcriptional dynamics of eve stripe 2 formation using the MS2 system. (A) MS2 stem loops introduced in an eve stripe 2 reporter gene are bound by MS2 coat protein fused to GFP. (B) Sites of nascent transcript formation appear as green fluorescent puncta whose intensity reports on the number of actively transcribing RNAP molecules. Nuclei are visualized through a fusion of RFP to Histone. (C) Mean number of RNAP molecules actively transcribing the gene as a function of space and time (data averaged over 11 embryos).
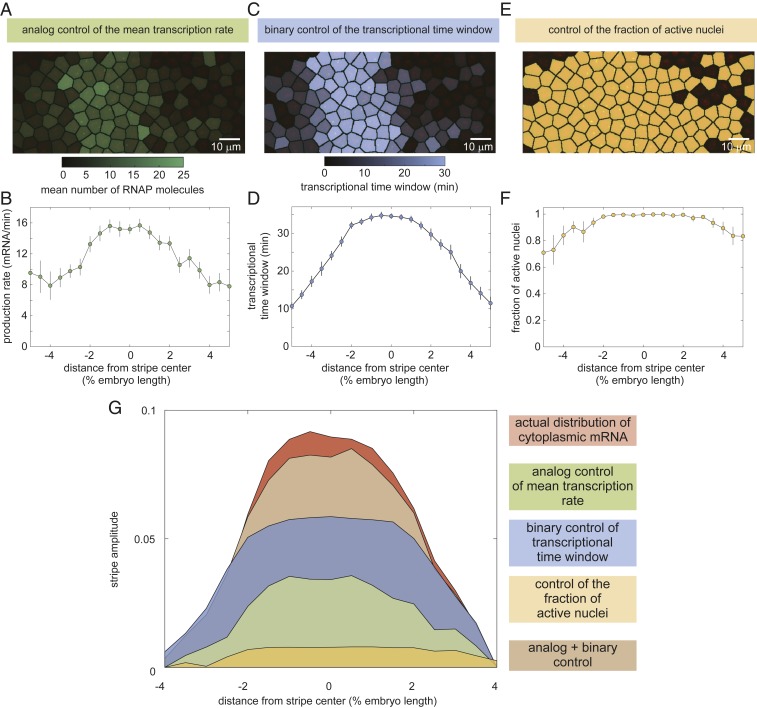
Using the MS2 system, we quantified each potential regulatory strategy and determined its predicted contribution to pattern formation according to our model in Eq. 2. We first used the average fluorescence intensities of our MS2 traces to estimate the time-averaged rate of RNAP loading, as described in SI Appendix, section B. We found that this rate is modulated along the axis of the embryo (Fig. 3 A and B; Movie S2; SI Appendix, Fig. S3; and Materials and Methods): Whereas in the center of the stripe RNAP molecules are loaded at a rate of ∼16 molecules per minute, this loading rate decreases to about 8 molecules per minute at the boundaries.
Fig. 3.
Regulatory strategies for pattern formation in eve stripe 2. (A–F) Time-averaged rate of mRNA production (A and B), transcriptional time window (C and D), and fraction of active nuclei as a function of position along the embryo (E and F). (G) Amplitude of the cytoplasmic mRNA distribution compared to the contributions to stripe formation of the analog control of the mean transcription rate, the binary control of the transcriptional time window, and the control of the fraction of active nuclei. The combined contribution from the analog and binary strategies is also shown. See SI Appendix, Fig. S5 for details of how depicted profiles were derived from raw data. A, C, and E show representative snapshots of an individual embryo 40 min into nuclear cycle 14; B, D, and F show average over 11 embryos; and error bars indicate bootstrap estimate of the SEM.
We next used our MS2 data to examine spatial trends in the transcriptional time window. Our data revealed that the transcriptional time window is modulated along the stripe (SI Appendix, Fig. S4A). Whereas the time at which each nucleus becomes transcriptionally active, , was constant across the stripe, with all nuclei becoming active min after the previous anaphase (SI Appendix, Fig. S4B), the time at which nuclei stop transcribing and become quiescent, , showed a strong modulation along the embryo’s axis (SI Appendix, Fig. S4C). As a result, the time window over which each transcriptional locus is engaged in transcription, , is sharply modulated along the stripe (Fig. 3 C and D and Movie S3), with nuclei in the stripe center transcribing for 30 min and nuclei on the boundaries transcribing only for ∼10 min. We note that, to derive these results, it was necessary to account for potential effects of the detection limit in our experiments of ∼4 RNAP molecules per locus on estimates of the timing of the appearance and disappearance of fluorescent puncta. This procedure is outlined in detail in SI Appendix, section C, as well as in SI Appendix, Figs. S12 and S13.
Finally, our analysis also revealed the magnitude of the modulation of the fraction of active nuclei along the stripe. Most nuclei along the stripe were engaged in transcription. In the stripe center, nearly 100% of nuclei transcribed at some point during the nuclei cycle. This number reduced to about 80% at the boundaries (Fig. 3 E and F and Movie S4).
The analysis in Fig. 3 A–F reveals that each of the 3 regulatory strategies identified in Fig. 1 is at play in the embryo and that they all have the potential to contribute to pattern formation. However, these measurements alone cannot inform us on how much each of these strategies contributes to the cytoplasmic mRNA pattern. To quantify the degree to which each regulatory strategy contributes to the formation of eve stripe 2, we employed the model described in Eq. 2.
Fig. 3G indicates the quantitative contribution of each regulatory strategy (each term on the right-hand side of Eq. 2) to the formation of this cytoplasmic pattern. The cytoplasmic pattern of accumulated mRNA, corresponding to the left-hand side of Eq. 2, was obtained by integrating from our live-imaging data (see SI Appendix, section B for details). Regulation of the fraction of active nuclei along the embryo (Fig. 3G, yellow) contributes negligibly to this mRNA pattern. In contrast, both the analog regulation of the mean rate (Fig. 3G, green) and the binary control of the transcriptional time window (Fig. 3G, blue) make significant contributions to the overall pattern, with binary control playing the dominant role. We thus concluded that the joint effect of these 2 strategies (Fig. 3G, brown) is sufficient to quantitatively recapitulate the stripe of cytoplasmic mRNA from single-cell transcriptional activity.
Mean Transcription Rate Is Dictated by Bursting through Modulation of the Rate of Promoter Turn on.
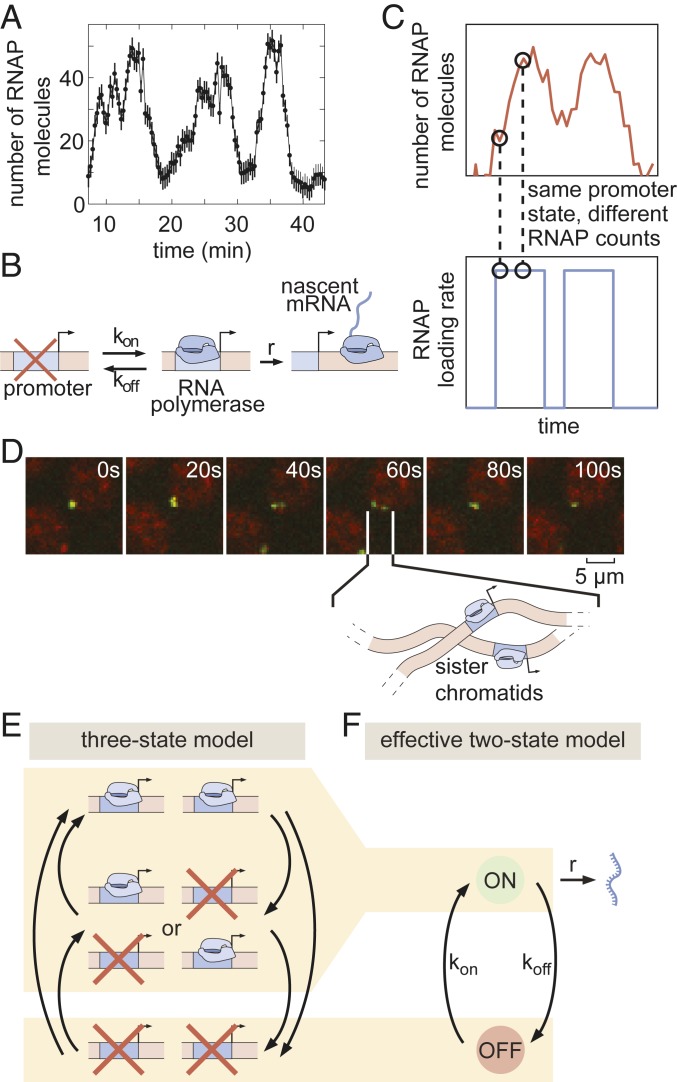
Are the binary and analog control strategies driven by distinct molecular mechanisms, or are they different manifestations of the same underlying process? To uncover the molecular mechanism behind the analog control of the mean rate of transcription, we analyzed the transcriptional activity of individual nuclei. Previous work demonstrated that the rate of gene expression at individual loci within the eve stripe 2 pattern is highly stochastic (18). Indeed, as shown in Fig. 4A, our data revealed punctuated peaks and troughs in the number of active RNAP molecules. These features have been related to the rate of RNAP initiation at the eve promoter by assuming that transcriptional activity is “burst-like,” with the promoter rapidly loading multiple RNAP molecules onto the gene at a constant rate during discrete “bursts” of activity interspersed with periods of inactivity (18). This and other evidence from live imaging (18, 25, 30), as well as data from fixed-tissue approaches (26, 31–33), support a minimal 2-state model of promoter switching (Fig. 4B): Promoters switch stochastically between ON and OFF states with rates and . In this model, promoters in the ON state engage in the loading of RNAP (and, correspondingly, mRNA production) at rate . Thus we find that, to describe eve stripe 2 transcriptional dynamics, we need to account for both the short, transient ON periods dictated by transcriptional bursts and a longer transcriptional time window that describes the period over which loci engage in this transcriptional bursting.
Fig. 4.
Transcriptional bursting in eve stripe 2. (A) Single-nucleus measurements reveal that nuclei transcribe in bursts. (B) Two-state model of bursting of a single promoter. (C) The same hidden rate of RNAP loading (Bottom) can correspond to different observable numbers of RNAP molecules on the gene (Top), such that standard hidden Markov model approaches cannot be used to infer the hidden promoter state. (D) Fluorescent puncta are composed of 2 distinct transcriptional loci within a diffraction-limited spot, each corresponding to a sister chromatid. (E) Three-state model of promoter switching within a fluorescent punctum that accounts for the combined action of both sister chromatids. (F) Effective 2-state model of transcriptional bursting. (In A, error bars are obtained from estimation of background fluorescent fluctuations; Materials and Methods and ref. 27.)
In the bursting model, the mean rate of transcription is given by the product of the fraction of time spent in the ON state with the transcription rate in this active state (34–37)
| [3] |
where all parameters are allowed to vary as a function of position along the embryo, (see SI Appendix, section A for details of this derivation). Thus, within this framework, the observed modulation of the mean rate of transcription across the stripe (Fig. 3G, green) implies that one or more of these bursting parameters are subject to spatially controlled regulation. However, the mean rate trend alone is not sufficient to identify which of the 3 bursting parameters (, , and ) is being regulated by the input transcription factors to control the average transcription rate. While each bursting parameter does not necessarily map directly to a single molecular step in the transcriptional cycle, identifying which parameter(s) is subject to regulation can help narrow the set of possible molecular mechanisms. For instance, variation in could indicate that transcription factors play an active role in the recruitment of RNAP to the promoter or in the release of RNAP from promoter-proximal pausing (38).
Typically, the in vivo molecular mechanism of transcription factor action is inferred from measurements of transcriptional noise obtained through snapshots of dead and fixed embryos or cells using theoretical models (26, 31–33, 39–47). In contrast, MS2-based live imaging can directly inform on the dynamics of transcriptional bursting in real time. The MS2 approach, however, reports on the total number of actively transcribing RNAP molecules and not on the instantaneous rate of RNAP loading at the promoter, which is the relevant quantity for estimating , , and . To date, approaches for extracting bursting parameters from such data in multicellular organisms have mainly relied on the manual analysis of single-nucleus transcriptional dynamics (18, 25) or autocorrelation-based methods that infer mean bursting parameters across ensembles of traces (30, 48, 49). A computational method for inferring the rates of RNAP loading (Fig. 4 C, Bottom) from the total number of actively transcribing RNAP molecules in single cells (Fig. 4 C, Top) is thus needed to obtain the bursting parameters.
Hidden Markov models (HMMs) are widely used to uncover the dynamics of a system as it transitions through states that are not directly accessible to the observer (50). However, our observable (the MS2 signal) does not correspond to the hidden variable of interest (the promoter state) in a one-to-one fashion (compare Fig. 4 C, Top and Bottom). Instead, the observable MS2 signal reflects the net effect of promoter switching over a period equal to the time that an RNAP molecule takes to transcribe the whole gene. Thus, instantaneous fluorescence does not just depend on the current promoter state; it exhibits a dependence on how active the promoter has been over a preceding window of time, which effectively constitutes a memory for recent promoter states (24, 37, 51, 52). Classic HMM approaches cannot account for this kind of system memory.
To model the process of transcription and extract the kinetic parameters of promoter switching, we augmented classic HMMs to account for memory (details about implementation of the method are given in SI Appendix, section D). Similar approaches were recently introduced to study transcriptional dynamics in cell culture and tissue samples (22–24, 53–57). We used simulated data to establish that cpHMM reliably extracts the kinetic parameters of transcriptional bursting from live-imaging data (SI Appendix, section E), providing an ideal tool for dissecting the contributions from individual bursting parameters to observed patterns of transcriptional activity across space and time.
Before applying our model to real-time transcriptional data, we had to account for the rapid replication of the Drosophila melanogaster genome at the beginning of each nuclear cycle (58), which leads to the presence of 2 distinct eve loci within each fluorescent spot (Fig. 4D and Movie S5). The first evidence of resolved chromatids appears as early as 8 min into nuclear cycle 14 (SI Appendix, Fig. S24)—coincident with the average onset time of transcription (SI Appendix, Fig. S4B). Moreover, our analysis indicates that replication of the relevant portion of the genome likely occurs in all eve-expressing nuclei by no later than 10 min following mitosis (SI Appendix, Fig. S24). Thus, we conclude that the vast majority of our data feature 2 distinct eve loci within each diffraction-limited transcription spot. Moreover, while the distance between sister loci varies over time (e.g., Fig. 4D), they nonetheless stay in relatively close proximity to ensure their proper segregation from each other at the next mitosis (59) such that the fluorescent intensity signals extracted from our data reflect the integral over both loci (SI Appendix, Fig. S2). As a result, if we assume that each locus can be well represented by a 2-state model (OFF/ON) of transcriptional bursting, then an effective 3-state model (OFF/OFF + OFF/ON + OFF/ON + ON/ON) is needed to capture eve dynamics (Fig. 4E). Thus, we elected to employ such a 3-state model in our analysis. Due to conflicting evidence from previous studies (26, 32, 60), we made no prior assumptions about the nature or degree of cooperativity between sister chromatids either in transitions between activity states or in the rates of initiation in each state (see SI Appendix, section E for details). While these assumptions increased the complexity of our model, we believed that a conservative approach that left the model free to infer the presence or absence of sister interactions was warranted, given our ignorance regarding the nature and strength of interactions between adjacent gene loci. For ease of exposition, we present our main results in the context of an effective 2-state model, in which, as detailed in SI Appendix, section A, the system is considered to be in the ON state as long as either chromatid is bursting (Fig. 4F). Note that none of our conclusions below are affected by this choice of an effective model as shown in SI Appendix, section G, where we present full results for the 3-state model.
A typical experimental trace for a nucleus in the core of the stripe is shown in Fig. 5A, along with its best fit, which corresponds to the cpHMM-inferred promoter trajectory in Fig. 5B. Our ability to infer the instantaneous promoter state in individual nuclei throughout development is further illustrated in Fig. 5C and Movie S6. These data revealed that, as development progresses and the stripe sharpens, the eve promoter continuously fluctuates between the ON and OFF states on a time scale of ∼1 to 2 min.
Fig. 5.
Inferring bursting dynamics using a memory-adjusted hidden Markov model. (A and B) Representative experimental trace along with its best fit (A) and its most likely corresponding promoter state trajectory (B). (C) Instantaneous visualization of promoter state in individual cells throughout development through the false coloring of nuclei by promoter state (colors as in B). (D) The rate of initiation for each transcriptional state is not significantly modulated along the embryo. (E) Our cpHMM reveals that the transition rate between the OFF and ON states (equivalent to the burst frequency) is up-regulated in the stripe center. (In A, error bars are obtained from estimation of background fluorescent fluctuations, as described in Materials and Methods and ref. 27; in D and E, error bars indicate the magnitude of the difference between the first and third quartiles of cpHMM inference results for bootstrap samples of experimental data taken across 11 embryos; see Materials and Methods for details.)
To infer time-averaged bursting parameter values, we grouped traces by position along the anterior–posterior axis. The rate of RNAP loading, , remained constant throughout the stripe (Fig. 5D), suggesting that none of the transcription factors regulating eve stripe 2 act directly on the rapid series of molecular steps involved in the initiation of transcription by RNAP. Similarly, we noted no significant spatial modulation of the rate of switching out of the ON state, (Fig. 5E). In contrast, the rate of switching into the ON state (also known as burst frequency), , was strongly up-regulated in the stripe center (Fig. 5E). These observations suggested that, to control the mean rate of transcription, transcription factors act primarily on the rate of promoter turning on, consistent with previous results both in embryos (25, 30, 33) and in single cells (41, 43, 44, 46). This regulatory modality increases the fraction of time that loci near the stripe center spend in the ON state (SI Appendix, Fig. S7 and ref. 26).
Binary Control of the Transcriptional Time Window Is Independent of Transcriptional Bursting.
Having determined that the analog control of the mean transcriptional rate is realized by the modulation of the burst frequency, , we next sought to uncover the molecular mechanism by which the binary regulation of the transcriptional time window is implemented. In one possible scenario, the onset of transcriptional quiescence at the end of the transcriptional time window would reflect a fundamental change to the molecular character of the transcriptional locus such that the bursting framework no longer applies. For instance, repressing transcription factors could alter the local chromatin landscape by repositioning promoter or enhancer nucleosomes (61), changes that could block the binding of activators at the stripe 2 enhancer or of general transcription factors at the promoter and thus abolish further activator-mediated bursting (Fig. 6 A, i). Alternatively, if the rates of promoter switching vary in time, then the time window could be explained without invoking an extra silenced state that is mechanistically distinct from the processes driving transcriptional bursting. Specifically, transcriptional quiescence could be achieved by progressively reducing the frequency (), intensity (), and/or duration () of transcriptional bursts. For example, it is possible that increasing repressor levels in the stripe flanks could disrupt the capacity for activators to initiate transcription bursts via short-range quenching interactions (62), a mechanism that would manifest as a decrease in over time.
Fig. 6.
Investigating the molecular character of transcriptional quiescence. (A) Two hypotheses explaining promoter quiescence onset: (A, i) a transition into an alternative, long-lived transcriptionally silent state and (A, ii) the modulation of one or more bursting parameters over time. (B–F) Division of the stripe into 5 regions (B) for our analysis of the fraction of quiescent nuclei (C), the transition rate from OFF to ON (D), the rate of RNAP loading when the promoter is in the ON state (E), and the transition rate from ON to OFF as a function of time and position along the stripe (F). Gray shaded region indicates the onset of transcriptional quiescence. (In C, error bars indicate bootstrap estimate of the SEM; in D–F, error bars indicate the magnitude of the difference between the first and third quartiles of cpHMM inference results for bootstrapped samples of experimental data; see Materials and Methods for details.)
To determine whether quiescence can be explained within the bursting framework, we divided the stripe into the 5 regions shown in Fig. 6B. For each region, we sought to determine whether the bursting dynamics varied over time in a manner that could explain the dynamics of entry into quiescence of individual nuclei (Fig. 6C). To probe for this time dependence in transcriptional bursting, we extended our cpHMM method to obtain promoter-bursting parameters over discrete periods of time by performing inference on our live-imaging data using a sliding window (see SI Appendix, section D for details). Our inference revealed that the rate of promoter turn on, , varied significantly in time (Fig. 6D). Specifically, decreased in both the anterior and posterior stripe boundaries (Fig. 6D, black and red curves) as development progressed and the fraction of active nuclei decreased (Fig. 6D, gray shaded region), while loci in the stripe center (Fig. 6D, green and yellow curves) exhibited a significant increase in . Further, while relatively constant at most positions along the stripe, both the rate of RNAP loading when in the ON state, , and the rate of promoter turn off, , decreased slightly (Fig. 6 E and F).
These findings confirmed our time-averaged inference results (Fig. 5 D and E) indicating that was the primary kinetic pathway through which transcription factors influence eve stripe 2 transcription dynamics. Moreover, the coincidence of the decrease in in flank nuclei with the onset of transcriptional quiescence (gray shaded region in Fig. 6D) seemed to suggest that, at least in part, quiescence in the stripe flanks could be driven by the temporal modulation of bursting parameters (Fig. 6 A, ii). However, other trends in our data were not consistent with the view that a decrease in drives transcriptional quiescence.
Although 70% and 50% of nuclei in the regions directly anterior and posterior of the stripe center were quiescent by 40 min into the nuclear cycle (blue and yellow curves in Fig. 6C), we detected no corresponding decrease in . In fact, actually increased in some inner regions of the stripe (Fig. 6D)—a trend that would increase overall transcriptional activity and would therefore go against the establishment of transcriptional quiescence.
The divergent outcomes observed in the central stripe regions, with the rate of transcriptional bursting remaining constant or increasing at eve loci within the engaged population of nuclei even as loci in neighboring nuclei turn off for good, runs counter to the hypothesis that quiescence is driven by the temporal modulation of the promoter switching parameters. It is conceivable that temporal changes in bursting parameters associated with the onset of quiescence occur too rapidly to be captured by our model. However, as discussed in SI Appendix, section I, these changes would need to occur on the same time scale as bursting itself (1 to 3 min). Given that both the other temporal trends detected by our inference (Fig. 6) and the shifts in the input transcription factors themselves (SI Appendix, section H) unfold on significantly slower time scales (5 to 15 min), we concluded that while possible, a scenario where bursting dynamics are changing too quickly to detect is unlikely.
The contradictory trends observed in the stripe center and flanks indicated that entry into transcriptional quiescence might involve processes not captured within the bursting model (Fig. 6 A, i), thus suggesting that binary control of the transcriptional time window and the transcriptional bursting driving the analog control of the mean transcription rate may arise from distinct molecular processes.
Input–Output Analysis Reveals Distinct Regulatory Logic for Bursting and the Transcriptional Time Window.
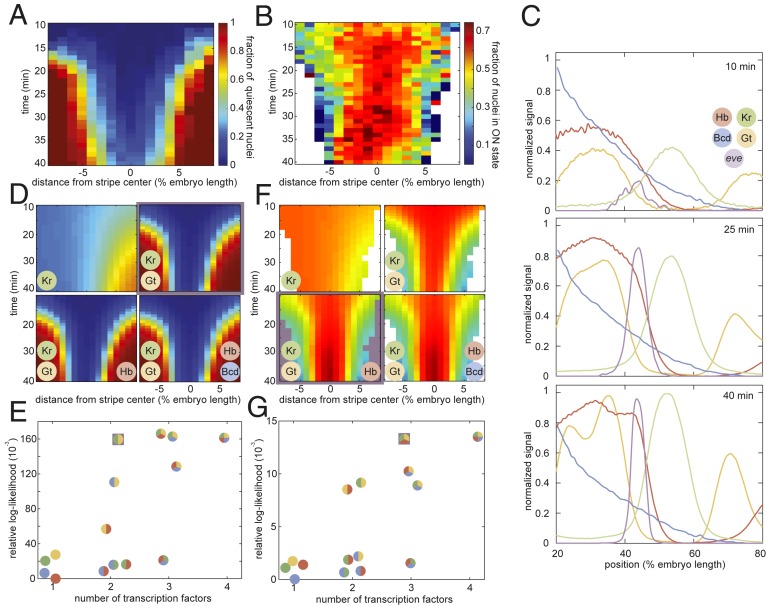
eve stripe 2 is mainly established by the combined action of 2 activators, Bicoid and Hunchback, and 2 repressors, Giant and Krüppel (16, 17, 63). If transcriptional bursting and the transcriptional time window are controlled by distinct molecular processes, then distinct forms of regulatory logic may be at play. For example, the Bicoid and Hunchback activators could control transcriptional bursting, while the Giant and Krüppel repressors could dictate the entry into the quiescent state. To reveal the molecular logic controlling each regulatory strategy, we sought to correlate the fraction of nuclei that have entered the quiescent state (Fig. 7A) and the fraction of nuclei in the bursting ON state (Fig. 7B) with the corresponding spatiotemporal patterns in the input concentrations of these 4 transcription factors.
Fig. 7.
Probing the regulatory logic of bursting and the transcriptional time window. (A and B) Fraction of nuclei in the transcriptionally quiescent state (A) and fraction of nuclei in the bursting ON state (B) as a function of time and position along the embryo. (C) Snapshots of input transcription factor levels and predicted eve mRNA levels of our “average” embryo at 10, 25, and 40 min into nuclear cycle 14. (D) Predicted fraction of quiescent nuclei for progressively more complex regression models. The simplest model with the highest likelihood is highlighted in purple. The color-coded circles indicate which of the 4 transcription factors—Krüppel (Kr), Giant (Gt), Hunchback (Hb), and Bicoid (Bcd)—were included in each version of the model. (E) Model likelihood indicating that Krüppel and Giant levels are sufficient to recapitulate the fraction of quiescent nuclei in D. (F) Predicted fraction of nuclei in the ON state. The simplest and most likely model is highlighted in purple. (G) Model scores reveal that Giant, Krüppel, and Hunchback recapitulate the bursting behavior in F.
We measured Bicoid concentration profiles using a well-established Bicoid-GFP fusion (64) and obtained spatiotemporal concentration profiles for Krüppel, Giant, and Hunchback from published immunofluorescence data (65, 66). We combined these data with our live-imaging data of eve stripe 2 transcriptional activity to generate an “average embryo” in which the concentration of all relevant inputs and the output transcriptional activity at each point in time and space were known (Fig. 7C and Movie S7). Building upon previous work (67), we utilized logistic regressions to probe the regulatory role played by each of these 4 factors in the spatiotemporal control of transcriptional bursting and the transcriptional time window. The logistic regression is a widely used method of inferring predictive models in processes with binary outcomes. For example, to query the regulatory logic behind the control of the transcriptional time window, the model probes the impact of each transcription factor on the relative likelihood of a locus entering the quiescent state versus the likelihood of remaining transcriptionally engaged such that
| [4] |
where the coefficients indicate the magnitude and nature (activating or repressing) of the transcription factor’s regulatory function. In estimating these coefficients, we used prior knowledge about the function of each transcription factor, requiring Bicoid and Hunchback to play activating roles and Krüppel and Giant to play repressing roles (5, 16). We used an analogous model to investigate the regulatory logic controlling transcriptional bursting by inferring the factors that determine the relative likelihood that nuclei are in the bursting ON versus the OFF state, /.
Our analysis of the fraction of nuclei in the quiescent state revealed that no single transcription factor can explain quiescence dynamics (Fig. 7 D and E). However, a simple model in which increasing levels of the repressors Giant and Krüppel drive the onset of transcriptional quiescence in the anterior and posterior stripe flanks, respectively, recapitulated experimentally observed trends. The further addition of Hunchback and/or Bicoid had no impact on the model’s predictive power, suggesting that activator concentrations have no influence over the molecular processes responsible for silencing. Relaxing constraints on the functional role of each transcription factor—for instance, allowing the presumed activators to function as repressors—also provided no significant improvement over models presented here as shown in SI Appendix, section H.
We next turned our attention to the relationship between transcription factor levels and the fraction of nuclei in the ON state (Fig. 7B). Unlike the transcriptional time window, repressor levels alone could not recapitulate the observed bursting profile; Hunchback levels were also necessary to fully capture the spatiotemporal bursting dynamics (Fig. 7 E and G). Specifically, we linked a rise in Hunchback concentration to an observed rise in the fraction of nuclei in the ON state in the stripe center between 30 and 35 min into the nuclear cycle (Fig. 7 B and F).
Our input–output analysis thus revealed that bursting and the transcriptional time window exhibit significantly different forms of regulator logic: Whereas repressor levels alone are sufficient to explain the transcriptional time window, the joint action of activators and repressors appears necessary to explain the observed patterns of transcriptional bursting. These results are consistent with the hypothesis that regulation of bursting and of the transcriptional time window occur via distinct molecular processes, therefore supporting a model in which the long-lived trancriptionally silent state observed in flank nuclei constitutes a distinct molecular state outside of the bursting model.
Discussion
In Drosophila development, information encoded in a handful of maternally deposited protein gradients propagates through increasingly complex layers of interacting genes, culminating in the specification of the adult body plan. The prediction of this cascade of developmental outcomes requires a quantitative understanding of the mechanisms that facilitate the flow of information along the central dogma. Here, we utilized live imaging in conjunction with theoretical modeling to shed light on a critical link in this cascade: how the regulation of transcriptional activity at the single-nucleus level gives rise to a spatiotemporal pattern of cytoplasmic mRNA.
A priori, there are several distinct regulatory strategies at the single-cell level capable of generating spatially differentiated patterns of cytoplasmic mRNA (Fig. 1), each with distinct implications for the nature of the underlying molecular processes at play. Several recent studies have revealed that the average rate of transcription is mainly modulated across the embryo by tuning the frequency of transcriptional bursting (18, 25, 26, 30, 33, 68). Yet it has remained unclear whether this modulation of the rate of transcription (and thereby mRNA production) is the dominant modality by which input concentrations of transcription factors drive the formation of patterns of gene expression or whether, instead, it is simply the most readily apparent mechanism among multiple distinct control strategies.
In this work, we derived a simple theoretical model that predicts how the interplay between regulatory strategies at the single-cell level dictates the formation of a cytoplasmic gene expression pattern (2). We applied this model to single-cell live-imaging measurements of an MS2 reporter driven by the eve stripe 2 enhancer, an approach that allowed us to dissect the regulatory logic of a well-characterized regulatory element free from the confounding influences of other enhancers located in the endogenous eve locus. We demonstrated—quantitatively—that the modulation of the mean rate of transcription is alone insufficient to account for the formation of a sharp stripe of gene expression (Fig. 3G, green). We discovered that the window of time over which promoters engage in transcription is sharply controlled along the axis of the embryo (Fig. 3 C and D) and that the joint action of the analog control of the rate of transcription and the binary control of the duration of transcription is necessary and sufficient to quantitatively recapitulate most of the full stripe profile (Fig. 3G, brown). While this work focused on dissecting the regulatory logic of the eve stripe 2 enhancer in the context of a minimal construct, it is important to note that our conclusions are not limited to this reporter construct and also apply to the endogenous regulation of eve. As shown in SI Appendix, Fig. S11, an analogous analysis performed on the expression dynamics of a reporter BAC containing the full endogenous eve locus (69) indicated that stripe formation in this endogenous context is also dominated by the interplay between the regulation of the mean rate of transcription and that of the transcriptional time window.
Here, we contribute to a growing body of work that illustrates the utility of using simple quantitative models to extract insights into the workings of complex biological phenomena (33, 67, 70). Our discovery of the key role of the differential duration of the transcriptional time window in pattern formation was made possible only by biological numeracy, that is, by going beyond the qualitative description of pattern formation and demanding a quantitative agreement between our theoretical predictions and the experimental data (71). While it is widely appreciated that genes are expressed for discrete windows of time over the course of development (27, 28, 72), we have demonstrated that—in the case of this eve stripe 2 reporter—this binary transcriptionally engaged/quiescent logic is actively regulated by transcription factors to drive pattern formation. Thus the differential duration of transcriptional activity comprises a necessary element of any quantitative description of pattern formation.
Our work contributes to an increasingly diverse and exciting discourse in quantitative developmental biology regarding the importance of the temporal component of transcriptional regulation in specifying developmental outcomes. For example, one recent study has demonstrated that the limited readout time imposed by short nuclear cycles in early Drosophila development places strict constraints on the kinds of regulatory architecture that could be responsible for driving observed patterns of hunchback gene expression (73). Other recent work has indicated that the pioneer factor Zelda plays a key role in regulating both the timing and probability of transcriptional activation following mitosis (74, 75). Our work complements these previous observations by exploring yet another aspect of the interplay between timing and transcriptional regulation. We have shown that, in the case of eve stripe 2, transcription factors regulate the onset of transcriptional quiescence, , across the stripe, thus demonstrating that the embryo actively leverages the differential duration of transcriptional engagement as a strategy to generate patterns of gene expression. Together, these recent findings suggest that, if the field is to make progress toward a predictive picture of pattern formation in development, it will be necessary to go beyond the widespread steady-state, static picture of pattern formation in development put forward by previous single-cell transcriptional activity studies that focused on the study of snapshots of fixed embryos (26, 31–33) and embrace a dynamical description that acknowledges that development is a process that occurs outside of steady state (69).
To determine whether this binary control of the transcriptional time window and the analog control of the mean transcription rate share a common molecular mechanism, we utilized a variety of theoretical and computational tools in conjunction with our live-imaging data. Specifically, to uncover how the mean rate of transcription is regulated across the stripe, we developed a cpHMM that is capable of inferring the instantaneous activity state of individual gene loci from MS2 traces. We used this cpHMM to infer average promoter-switching parameters across the stripe (Fig. 5). In agreement with previous measurements of various gene expression patterns (25, 26, 30, 33), our results revealed that the burst frequency () is the main bursting parameter regulated by the input transcription factors across eve stripe 2. This increase in in the stripe center functions to increase the fraction of time that nuclei spend in the active transcriptional state.
Importantly, our cpHMM algorithm is not limited to the eve stripe 2 system and should prove useful to infer the underlying regulatory kinetics of any gene that is tagged using approaches such as the MS2 or PP7 systems in any organism (25, 48). For example, the method could be used to infer the state of the ribosome as mRNA is being translated into protein in novel single-molecule in vivo translation assays (76–79). Thus, we envision that our method will be useful for the broader biophysical analysis of in vivo cellular processes at the single-molecule level.
Having identified as the primary kinetic mode by which transcription factors modulate the mean rate of expression across eve stripe 2, we next sought to probe the relationship between bursting and the transcriptional time window (Fig. 6A). We adapted our cpHMM to go beyond time-independent models of promoter switching to infer the regulation of these rates across both space and time. We observed striking temporal trends indicating that the burst frequency responds dynamically to time-varying transcription factor inputs. However, we noted a significant disconnect between temporal trends in the burst frequency and the onset of transcriptional quiescence. In particular, either increased or remained constant near the stripe center even as a significant fraction of eve nuclei transitioned into quiescence (Fig. 6 C and D). We reasoned that the onset of transcriptional quiescence is likely not the result of a progressive reduction in burst frequency, amplitude, or duration and is instead driven by molecular processes that are distinct from those that regulate transcriptional bursting, such as a repressor-induced shift in nucleosome position that prevents activating transcription factors from binding to the stripe 2 enhancer.
To test this hypothesis, we utilized a logistic regression framework and time-resolved data for the primary regulators of eve stripe 2 to query the regulatory logic exhibited by the time window and bursting, respectively (SI Appendix, section H). In this context, the logistic regressions served as a robust statistical tool for drawing inferences from existing data that were not obvious (or verifiable) by simple visual inspection. Consistent with our time-resolved cpHMM results, the 2 regulatory strategies responded to transcription factor concentrations in different ways. On the one hand, increasing levels of Giant and Krüppel were sufficient to explain the onset of transcriptional quiescence in the stripe flanks (Fig. 7 A and D). This observation points to a model in which repressor levels act unilaterally—without respect to coincident levels of activator proteins—to shut off transcription at loci in an (at least effectively) irreversible fashion. Conversely, the joint action of Giant, Krüppel, and Hunchback was necessary to recapitulate the observed pattern of transcriptional bursting (Fig. 7 B and F).
This difference in the regulatory logic observed for the 2 strategies dissected in this work suggests that control of the transcriptional time window and the modulation of the average transcription rate arise from 2 distinct, orthogonal molecular mechanisms. It is also notable that our model finds that Hunchback activation is necessary to fully explain the observed pattern of transcriptional bursting in eve stripe 2. A recent study has suggested that Hunchback actually functions as a repressor of eve stripe 2 and that indirect activation occurs via counter repression of Hunchback by the maternal factor Caudal (80). While we cannot rule out the possibility that Hunchback acts indirectly, the strong link between rising Hunchback levels and the increase in eve 2 activity in the stripe center is most consistent with Hunchback playing a traditional activating role. Additional work will be necessary to determine whether this correlation between rising Hunchback levels and increased stripe activity can be reconciled with the counter-repression hypothesis proposed in ref. 80. Finally, we note that the striking absence of a direct functional role for Bicoid in the regulation of either phenomenon suggests that, while Bicoid is almost certainly necessary for the expression of eve stripe 2 (16), it does not play a direct role in dictating the magnitude or duration of eve stripe 2 transcription. In this interpretation, Bicoid functions like a general transcription factor, facilitating the transcription of eve 2 without directly conferring spatiotemporal information.
In addition to gleaning valuable insights into the mechanisms driving the regulation of transcription of the eve stripe 2 enhancer, our logistic regression framework makes quantitative and falsifiable predictions about the regulation of this stripe for combinations of input transcription factor concentrations that the embryo does not encounter in the wild-type setting. For instance, our finding that repressors alone drive the onset of transcriptional quiescence predicts that this onset should be unaltered in mutated eve stripe 2 enhancers where some or all Hunchback binding sites have been disrupted. In this scenario, transcriptional activity, initially arising due to permissive levels of Bicoid, would shut off in precisely the same manner as observed for the full enhancer (compare Fig. 7 D, Upper Right to Fig. 7 D, Lower Left). In the absence of Hunchback activation, the model also predicts reduced levels of transcriptional bursting, particularly late in nuclear cycle 14 (compare Fig. 7 F, Upper Right to Fig. 7 F, Lower Left). Similarly, our model could be used to predict the expected stripe profile in mutant embryos, where the expression of one or more gap genes has been altered or abolished. We note, however, that the interconnected nature of the gap gene network (9) means that it would be necessary to reimage all 3 gap genes that regulate eve stripe 2 to generate data such as shown in Fig. 7C, since any change to one will affect the expression patterns of all. Thus, additional binding-site mutation studies similar to the one described above likely represent the most direct path to testing our model’s predictions. Taken together, we anticipate that the approaches outlined in this work will serve as a tool both for extracting additional insights from experimental data and for motivating additional experiments aimed at answering meaningful questions about the mechanistic underpinnings of gene regulation.
We also observe that certain aspects of the system remain beyond the scope of our model. Most notably, while loci engaged in transcriptional bursting appear to continuously sense changes in transcription factor concentrations, it remains an open question whether loci continue to read out transcription factor concentrations following the onset of transcriptional quiescence. While the transition appears irreversible in our data, it is possible that quiescence is, in fact, reversible but simply not observed because repressor levels increase over time in our region of interest. The temporally resolved manipulation of repressor concentration through, for example, optogenetics (81) could make it possible to deplete repressors from the nucleus after transcriptional quiescence to determine whether this quiescent state is reversible.
To further test these and other hypotheses, it will be critical to move beyond spatiotemporal averages for transcription factor inputs (Fig. 7C) and, instead, use live single-nucleus measurements to directly correlate input transcription factor concentration dynamics with the corresponding transcriptional activity at the single-cell level (82). Experimentally, we recently demonstrated the simultaneous measurement of inputs and outputs in single nuclei of a living fly embryo using genetically encoded LlamaTags (83). We believe that using this technique, in conjunction with the theoretical methods presented here, to query the effects of targeted disruptions to transcription factor binding domains on regulatory enhancers will constitute a powerful assay for querying transcription factor function at the molecular level. Thus, there are clear experimental and theoretical paths to uncovering the detailed quantitative mechanisms behind the molecular control of transcriptional bursting and quiescence in development. Such a quantitative description is a necessary step toward a predictive understanding of developmental decision making that makes it possible to calculate developmental outcomes from knowledge of the nature of the transcription factor interactions within gene regulatory networks.
Materials and Methods
Reporter Construct.
This work employed the same eve stripe 2 reporter construct developed by ref. 18. This construct contains the even-skipped (eve) stripe 2 enhancer and promoter region (spanning −1.7 kbp to +50 bp) upstream of the yellow reporter gene. Twenty-four repeats of the MS2 stem loop sequence were incorporated into the 5′ end of the reporter gene.
Sample Preparation and Data Collection.
Sample preparation followed procedures described in ref. 18. In short, female virgins of yw; His-RFP; MCP-GFP (MCP, MS2 coat protein) were crossed to males bearing the reporter gene. Embryos were collected and mounted in halocarbon oil 27 between a semipermeable membrane (Lumox film; Starstedt) and a coverslip. Data collection was performed using a Leica SP8 laser scanning confocal microscope. Average laser power on the specimen (measured at the output of a 10× objective) was 35 W. Image resolution was 256 512 pixels, with a pixel size of 212 nm and a pixel dwell time of 1.2 s. The signal from each frame was accumulated over 3 repetitions. At each time point, a stack of 21 images separated by 500 nm was collected. Image stacks were collected at a time resolution of 21 s. The MCP-GFP and Histone-RFP were excited with laser wavelengths of 488 and 556 nm, respectively, using a White Light Laser. Fluorescence was detected with 2 separate Hybrid Detectors (HyD) using the 498- to 546-nm and 566- to 669-nm spectral windows. Specimens were imaged for a minimum of 40 min into nuclear cleavage cycle 14.
Image Analysis.
Image analysis of live embryo movies was performed based on the protocol in ref. 27 with modifications to the identification of transcriptional spots, which were segmented using the Trainable Weka Segmentation plugin for FIJI using the FastRandomForest algorithm (84). In comparison with a previous algorithm based on Difference of Gaussians (18, 27, 32), this alternative spot segmentation approach was found to be superior for the detection of dim transcription spots—a feature critical to establishing the precise timing of the cessation of activity at transcriptional loci.
cpHMM Inference Code.
All scripts relating to the cpHMM inference methodology developed in this work are available at the GarciaLab/cpHMM GitHub repository (85). See SI Appendix, Extended Materials and Methods, as well as SI Appendix, section D for additional details.
Supplementary Material
Acknowledgments
We thank Thomas Gregor and Lev Barinov for discussion about an initial implementation of the cpHMM approach; Florian Jug for help with the spot segmentation using machine learning; and Elizabeth Eck, Maryam Kazemzadeh-Atoufi, and Jonathan Liu for the hunchback P2 data used in the absolute MS2 calibration. We are also grateful to Jack Bateman, Jane Kondev, Rob Phillips, Allyson Sgro, and Donald Rio for comments and discussion on the manuscript. H.G.G. was supported by the Burroughs Wellcome Fund Career Award at the Scientific Interface, the Sloan Research Foundation, the Human Frontiers Science Program, the Searle Scholars Program, the Shurl & Kay Curci Foundation, the Hellman Foundation, the National Institutes of Health (NIH) Director’s New Innovator Award (DP2 OD024541-01), and a National Science Foundation (NSF) Faculty Early Career Development Program (CAREER) award (1652236). N.C.L. was supported by NIH Genomics and Computational Biology Training Grant 5T32HG000047-18. C.H.W. was supported by the NIH/National Cancer Institute (U54 CA193313), The City University of New York (CUNY) (RFCUNY 40D14-A), and the NSF (IIS-1344668).
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission.
Data deposition: All data sources used in this work can be found in the project’s GitHub repository at https://github.com/GarciaLab/cpHMM/tree/master/multimodal_control_paper_sandbox/dat.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.1912500117/-/DCSupplemental.
References
- 1.Peter I. S., Davidson E. H., Genomic Control Process: Development and Evolution (Academic Press, an Imprint of Elsevier, London, UK; San Diego, CA, 2015). [Google Scholar]
- 2.Vincent B. J., Estrada J., DePace A. H., The appeasement of doug: A synthetic approach to enhancer biology. Integr. Biol. 8, 475–484 (2016). [DOI] [PubMed] [Google Scholar]
- 3.Lawrence P. A., Johnston P., Macdonald P., Struhl G., Borders of parasegments in Drosophila embryos are delimited by the fushi tarazu and even-skipped genes. Nature 328, 440–442 (1987). [DOI] [PubMed] [Google Scholar]
- 4.Driever W., Nüsslein-Volhard C., The bicoid protein determines position in the Drosophila embryo in a concentration-dependent manner. Cell 54, 95–104 (1988). [DOI] [PubMed] [Google Scholar]
- 5.Small S., Kraut R., Hoey T., Warrior R., Levine M., Transcriptional regulation of a pair-rule stripe in Drosophila. Genes Dev. 5, 827–839 (1991). [DOI] [PubMed] [Google Scholar]
- 6.Struhl G., Johnston P., Lawrence P. A., Control of Drosophila body pattern by the hunchback morphogen gradient. Cell 69, 237–249 (1992). [DOI] [PubMed] [Google Scholar]
- 7.Jiang J., Levine M., Binding affinities and cooperative interactions with bhlh activators delimit threshold responses to the dorsal gradient morphogen. Cell 72, 741–752 (1993). [DOI] [PubMed] [Google Scholar]
- 8.Gray S., Szymanski P., Levine M., Short-range repression permits multiple enhancers to function autonomously within a complex promoter. Genes Dev. 8, 1829–1838 (1994). [DOI] [PubMed] [Google Scholar]
- 9.Jaeger J., et al. , Dynamic control of positional information in the early Drosophila embryo. Nature 430, 368–371 (2004). [DOI] [PubMed] [Google Scholar]
- 10.Segal E., Raveh-Sadka T., Schroeder M., Unnerstall U., Gaul U., Predicting expression patterns from regulatory sequence in Drosophila segmentation. Nature 451, 535–540 (2008). [DOI] [PubMed] [Google Scholar]
- 11.Sayal R., Dresch J. M., Pushel I., Taylor B. R., Arnosti D. N., Quantitative perturbation-based analysis of gene expression predicts enhancer activity in early Drosophila embryo. eLife 5, e08445 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Fakhouri W. D., et al. , Deciphering a transcriptional regulatory code: Modeling short-range repression in the Drosophila embryo. Mol. Syst. Biol. 6, 341 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Parker D. S., White M. A., Ramos A. I., Cohen B. A., Barolo S., The cis-regulatory logic of hedgehog gradient responses: Key roles for gli binding affinity, competition, and cooperativity. Sci. Signal. 4, ra38 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Crocker J., Ilsley G. R., Stern D. L., Quantitatively predictable control of Drosophila transcriptional enhancers in vivo with engineered transcription factors. Nat. Genet. 48, 292–298 (2016). [DOI] [PubMed] [Google Scholar]
- 15.Park J., et al. , Dissecting the sharp response of a canonical developmental enhancer reveals multiple sources of cooperativity. eLife 8, e41266 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Small S., Blair A., Levine M., Regulation of even-skipped stripe 2 in the Drosophila embryo. EMBO J. 11, 4047–4057 (1992). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Arnosti D. N., Barolo S., Levine M., Small S., The eve stripe 2 enhancer employs multiple modes of transcriptional synergy. Development 122, 205–214 (1996). [DOI] [PubMed] [Google Scholar]
- 18.Bothma J. P., et al. , Dynamic regulation of eve stripe 2 expression reveals transcriptional bursts in living Drosophila embryos. Proc. Natl. Acad. Sci. U.S.A. 111, 10598–10603 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Surkova S., et al. , Characterization of the Drosophila segment determination morphome. Dev. Biol. 313, 844–862 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Ludwig M. Z., Manu, Kittler R., White K. P., Kreitman M., Consequences of eukaryotic enhancer architecture for gene expression dynamics, development, and fitness. PLoS Genet. 7, e1002364 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Petkova M. D., Tkacik G., Bialek W., Wieschaus E. F., Gregor T., Optimal decoding of cellular identities in a genetic network. Cell 176, 844–855 e15 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Suter D. M., et al. , Mammalian genes are transcribed with widely different bursting kinetics. Science 332, 472–474 (2011). [DOI] [PubMed] [Google Scholar]
- 23.Molina N., et al. , Stimulus-induced modulation of transcriptional bursting in a single mammalian gene. Proc. Natl. Acad. Sci. U.S.A. 110, 20563–20568 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Corrigan A. M., Tunnacliffe E., Cannon D., Chubb J. R., A continuum model of transcriptional bursting. eLife 5, e13051 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Fukaya T., Lim B., Levine M., Enhancer control of transcriptional bursting. Cell 166, 358–368 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Zoller B., Little S. C., Gregor T., Diverse spatial expression patterns emerge from unified kinetics of transcriptional bursting. Cell 175, 835–847.e25 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Garcia H. G., Tikhonov M., Lin A., Gregor T., Quantitative imaging of transcription in living Drosophila embryos links polymerase activity to patterning. Curr. Biol. 23, 2140–2145 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Lucas T., et al. , Live imaging of bicoid-dependent transcription in Drosophila embryos. Curr. Biol. 23, 2135–2139 (2013). [DOI] [PubMed] [Google Scholar]
- 29.Bertrand E., et al. , Localization of ash1 mRNA particles in living yeast. Mol. Cell 2, 437–445 (1998). [DOI] [PubMed] [Google Scholar]
- 30.Desponds J., et al. , Precision of readout at the hunchback gene: Analyzing short transcription time traces in living fly embryos. PLoS Comput. Biol. 12, e1005256 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Pare A., et al. , Visualization of individual scr mRNAs during Drosophila embryogenesis yields evidence for transcriptional bursting. Curr. Biol. 19, 2037–2042 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Little S. C., Tikhonov M., Gregor T., Precise developmental gene expression arises from globally stochastic transcriptional activity. Cell 154, 789–800 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Xu H., Sepúlveda L. A., Figard L., Sokac A. M., Golding I., Combining protein and mRNA quantification to decipher transcriptional regulation. Nat. Methods 12, 739–742 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Peccoud J., Ycart B., Markovian modeling of gene product synthesis. Theor. Popul. Biol. 48, 222–234 (1995). [Google Scholar]
- 35.Kepler T. B., Elston T. C., Stochasticity in transcriptional regulation: Origins, consequences, and mathematical representations. Biophys. J. 81, 3116–3136 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Sasai M., Wolynes P. G., Stochastic gene expression as a many-body problem. Proc. Natl. Acad. Sci. U.S.A. 100, 2374–2379 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Xu H., Skinner S. O., Sokac A. M., Golding I., Stochastic kinetics of nascent RNA. Phys. Rev. Lett. 117, 128101 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Shandilya J., Roberts S. G. E., The transcription cycle in eukaryotes: From productive initiation to RNA polymerase II recycling. Biochim. Biophys. Acta Gene Regul. Mech. 1819, 391–400 (2012). [DOI] [PubMed] [Google Scholar]
- 39.Boettiger A. N., Levine M., Rapid transcription fosters coordinate snail expression in the Drosophila embryo. Cell Rep. 3, 8–15 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Zenklusen D., Larson D. R., Singer R. H., Single-RNA counting reveals alternative modes of gene expression in yeast. Nat. Struct. Mol. Biol. 15, 1263–1271 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.So L. H., et al. , General properties of transcriptional time series in Escherichia coli. Nat. Genet. 43, 554–560 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Jones D. L., Brewster R. C., Phillips R., Promoter architecture dictates cell-to-cell variability in gene expression. Science 346, 1533–1536 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Senecal A., et al. , Transcription factors modulate c-fos transcriptional bursts. Cell Rep. 8, 75–83 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Padovan-Merhar O., et al. , Single mammalian cells compensate for differences in cellular volume and DNA copy number through independent global transcriptional mechanisms. Mol. Cell 58, 339–352 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Skinner S. O., et al. , Single-cell analysis of transcription kinetics across the cell cycle. eLife 5, e12175 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Bartman C. R., Hsu S. C., Hsiung C. C., Raj A., Blobel G. A., Enhancer regulation of transcriptional bursting parameters revealed by forced chromatin looping. Mol. Cell 62, 237–247 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Hendy O. Jr, Campbell J., Weissman J. D., Larson D. R., Singer D. S., Differential context-specific impact of individual core promoter elements on transcriptional dynamics. Mol. Biol. Cell 28, 3360–3370 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Larson D. R., Zenklusen D., Wu B., Chao J. A., Singer R. H., Real-time observation of transcription initiation and elongation on an endogenous yeast gene. Science 332, 475–478 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Coulon A., et al. , Kinetic competition during the transcription cycle results in stochastic RNA processing. eLife 3, e03939 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Bronson J. E., Fei J., Hofman J. M., Gonzalez R. L., Wiggins C. H., Learning rates and states from biophysical time series: A Bayesian approach to model selection and single-molecule FRET data. Biophys. J. 97, 3196–3205 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Choubey S., Kondev J., Sanchez A., Deciphering transcriptional dynamics in vivo by counting nascent RNA molecules. PLoS Comput. Biol. 11, e1004345 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Choubey S., Nascent RNA kinetics: Transient and steady state behavior of models of transcription. Phys. Rev. E 97, 022402 (2018). [DOI] [PubMed] [Google Scholar]
- 53.Zechner C., Unger M., Pelet S., Peter M., Koeppl H., Scalable inference of heterogeneous reaction kinetics from pooled single-cell recordings. Nat. Methods 11, 197–202 (2014). [DOI] [PubMed] [Google Scholar]
- 54.Zoller B., Nicolas D., Molina N., Naef F., Structure of silent transcription intervals and noise characteristics of mammalian genes. Mol. Syst. Biol. 11, 823 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Hey K. L., et al. , A stochastic transcriptional switch model for single cell imaging data. Biostatistics 16, 655–669 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Bronstein L., Zechner C., Koeppl H., Bayesian inference of reaction kinetics from single-cell recordings across a heterogeneous cell population. Methods 85, 22–35 (2015). [DOI] [PubMed] [Google Scholar]
- 57.Featherstone K., et al. , Spatially coordinated dynamic gene transcription in living pituitary tissue. eLife 5, e08494 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Shermoen A. W., McCleland M. L., O’Farrell P. H., Developmental control of late replication and S phase length. Curr. Biol. 20, 2067–2077 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Senaratne T. N., Joyce E. F., Nguyen S. C., Wu C. T., Investigating the interplay between sister chromatid cohesion and homolog pairing in Drosophila nuclei. PLoS Genet. 12, e1006169 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.McKnight S. L., Miller O. L. Jr, Post-replicative nonribosomal transcription units in D. melanogaster embryos. Cell 17, 551–563 (1979). [DOI] [PubMed] [Google Scholar]
- 61.Allis C. D., Caparros M.-L., Jenuwein T., Reinberg D., Epigenetics (Cold Spring Harbor Laboratory Press, Cold Spring Harbor, NY, ed. 2, 2015). [Google Scholar]
- 62.Courey A. J., Jia S., Transcriptional repression: The long and the short of it. Genes Dev. 15, 2786–2796 (2001). [DOI] [PubMed] [Google Scholar]
- 63.Frasch M., Levine M., Complementary patterns of even-skipped and fushi tarazu expression involve their differential regulation by a common set of segmentation genes in Drosophila. Genes Dev. 1, 981–995 (1987). [DOI] [PubMed] [Google Scholar]
- 64.Gregor T., Wieschaus E. F., McGregor A. P., Bialek W., Tank D. W., Stability and nuclear dynamics of the bicoid morphogen gradient. Cell 130, 141–152 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Dubuis J. O., Samanta R., Gregor T., Data from “Accurate measurements of dynamics and reproducibility in small genetic networks.” Dryad. 10.5061/dryad.35h8v. Accessed 20 October 2018. [DOI] [PMC free article] [PubMed]
- 66.Petkova M. D., Tkačik G., Bialek W., Wieschaus E. F., Gregor T., Optimal decoding of cellular identities in a genetic network. Cell 176, 844–855.e15 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Ilsley G. R., Fisher J., Apweiler R., De Pace A. H., Luscombe N. M., Cellular resolution models for even skipped regulation in the entire Drosophila embryo. eLife 2, e00522 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Lionnet T., et al. , A transgenic mouse for in vivo detection of endogenous labeled mRNA. Nat. Methods 8, 165–170 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Berrocal A., Lammers N. C., Garcia H. G., Eisen M. B., Kinetic sculpting of the seven stripes of the Drosophila even-skipped gene. bioRxiv:335901 (11 June 2018). [DOI] [PMC free article] [PubMed]
- 70.Manu, et al. , Canalization of gene expression and domain shifts in the Drosophila blastoderm by dynamical attractors. PLoS Comput. Biol. 5, e1000303 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Phillips R., Napoleon is in equilibrium. Ann. Rev. Condens. Matter Phys. 6, 85–111 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Lucas T., et al. , 3 minutes to precisely measure morphogen concentration. PLoS Genet. 14, e1007676 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Tran H., et al. , Precision in a rush: Trade-offs between reproducibility and steepness of the hunchback expression pattern. PLoS Comput. Biol. 14, e1006513 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Yamada S., et al. , The Drosophila pioneer factor Zelda modulates the nuclear microenvironment of a dorsal target enhancer to potentiate transcriptional output. Curr. Biol. 29, 1387–1393.e5 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Dufourt J., et al. , Temporal control of gene expression by the pioneer factor Zelda through transient interactions in hubs. Nat. Commun. 9, 5194 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Morisaki T., et al. , Real-time quantification of single RNA translation dynamics in living cells. Science 352, 1425–1429 (2016). [DOI] [PubMed] [Google Scholar]
- 77.Wang C., Han B., Zhou R., Zhuang X., Real-time imaging of translation on single mRNA transcripts in live cells. Cell 165, 990–1001 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Yan X., Hoek T. A., Vale R. D., Tanenbaum M. E., Dynamics of translation of single mRNA molecules in vivo. Cell 165, 976–989 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Wu B., Eliscovich C., Yoon Y. J., Singer R. H., Translation dynamics of single mRNAs in live cells and neurons. Science 352, 1430–1435 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Vincent B. J., et al. , Hunchback is counter-repressed to regulate even-skipped stripe 2 expression in Drosophila embryos. PLoS Genet. 14, e1007644 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Huang A., Amourda C., Zhang S., Tolwinski N. S., Saunders T. E., Decoding temporal interpretation of the morphogen bicoid in the early Drosophila embryo. eLife 6, e26258 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Holloway D. M., Spirov A. V., Transcriptional bursting in Drosophila development: Stochastic dynamics of eve stripe 2 expression. PLoS One 12, e0176228 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Bothma J. P., Norstad M. R., Alamos S., Garcia H. G., Llamatags: A versatile tool to image transcription factor dynamics in live embryos. Cell 173, 1810–1822.e16 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Arganda-Carreras I., et al. , Trainable Weka segmentation: A machine learning tool for microscopy pixel classification. Bioinformatics 33, 2424–2426 (2017). [DOI] [PubMed] [Google Scholar]
- 85.Lammers N. C., et al. , Data from “Live imaging data of Eve Stripe 2 MS2 Reporter.” Github. https://github.com/GarciaLab/cpHMM/tree/master/multimodal_control_paper_sandbox/dat/eve2MS2_single_embryos. Deposited 11 December 2019.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.