Revisiting the tumorigenesis timeline with a data-driven generative model

Significance

Recently, investigators have shown that only a few driver gene mutational events appear to be needed for cancer to occur. However, the reason that some mutational events precede others in the same cancer and the explanation for tissue-specific differences in this timing, remain mysterious. We here combine mathematical modeling with epidemiologic studies and sequencing data to address these questions. We suggest that the first driver event in cancers generally occurred at early ages and provide estimates for the fitness of different types of drivers during tumor evolution, showing how they vary with the tissue of origin.

Abstract

Cancer is driven by the sequential accumulation of genetic and epigenetic changes in oncogenes and tumor suppressor genes. The timing of these events is not well understood. Moreover, it is currently unknown why the same driver gene change appears as an early event in some cancer types and as a later event, or not at all, in others. These questions have become even more topical with the recent progress brought by genome-wide sequencing studies of cancer. Focusing on mutational events, we provide a mathematical model of the full process of tumor evolution that includes different types of fitness advantages for driver genes and carrying-capacity considerations. The model is able to recapitulate a substantial proportion of the observed cancer incidence in several cancer types (colorectal, pancreatic, and leukemia) and inherited conditions (Lynch and familial adenomatous polyposis), by changing only 2 tissue-specific parameters: the number of stem cells in a tissue and its cell division frequency. The model sheds light on the evolutionary dynamics of cancer by suggesting a generalized early onset of tumorigenesis followed by slow mutational waves, in contrast to previous conclusions. Formulas and estimates are provided for the fitness increases induced by driver mutations, often much larger than previously described, and highly tissue dependent. Our results suggest a mechanistic explanation for why the selective fitness advantage introduced by specific driver genes is tissue dependent.

Tumor evolution occurs through the accumulation of mutations in driver genes known as tumor suppressor genes and oncogenes. The first fundamental insights into this multistage process were provided in the 1950s through the combination of mathematical modeling and epidemiological observations in the seminal work of Nordling (1) and Armitage and Doll (2), and later by Moolgavkar and coworkers (3, 4). Further evidence supporting the multistage progression of cancer, with key insights on tumor suppressors and oncogenes, was later provided by Knudson (5) and by Fearon and Vogelstein (6). The vast majority of these driver genes have since been discovered, and knowledge of the process of tumorigenesis and its heterogeneity across tissue types has greatly increased (7–9). The combination of mathematical modeling with epidemiological and sequencing data continues to play a pivotal role in shedding light on the process of tumor evolution. For instance, it has been recently shown that the number of driver mutational events required for cancer is much smaller than previously assumed (10). These findings have been overall supported by further molecular analyses provided via independent methods (11).

Despite this progress, many aspects of tumor evolution remain unclear. For instance, what is the timing of the mutational events in driver genes? Do they occur early or late in the life span of a person who develops a cancer? How large is the increase in fitness induced in a cell by each of these driver gene mutations? Moreover, why do certain driver mutations appear early in the process of tumorigenesis in some cancer types and later in others, or not at all? For example, Fearon and Vogelstein (6) observed that, in colorectal cancers (CRCs), KRAS gene mutations generally appear in adenomas only after the APC initiating mutation. In contrast, KRAS mutations are apparently the first genetic alterations that occur in pancreatic cancers (12).

We here provide a mathematical model of the full process of tumor evolution that attempts to address the questions raised above. For each tissue, the model follows each division of each stem cell (equivalently, each self-renewing cell), starting during the fetal stage of development with the first precursor cell from which the full tissue is formed, and continuing during homeostasis and tumorigenesis. It keeps tracks of the somatic driver mutations, caused by replicative errors and accumulating in the stem cells during those divisions, and it follows the subsequent possible clonal expansions all of the way to a detectable cancer. Given biologically constrained parameters of a tissue, e.g., number of stem cells and cell division rates, the model’s output is the number of stem cells in that tissue containing various types of driver mutations, and therefore at various stages of the tumorigenesis process. When a cell has accumulated all of the driver mutations required to qualify as a cancer cell, the survival of its clonal expansion is followed until it possibly reaches detection size, at which point it is then declared a cancer.

The model has the following distinctive characteristics.

First, it is a multiscale model, which accounts for 1) the dynamics of each cell within a tissue (e.g., colon); 2) the dynamics of the tissue itself, by considering the local, spatial organization of cells (e.g., crypts) (13), and by imposing a carrying capacity limitation (the number of cells that can be supported, sustained, given the resource limitations of the given local environment) on the growth of any of its clonal expansions (avoiding the usual but unrealistic assumption of unbounded exponential growth during clonal expansions); and 3) the incidence of different cancer types.

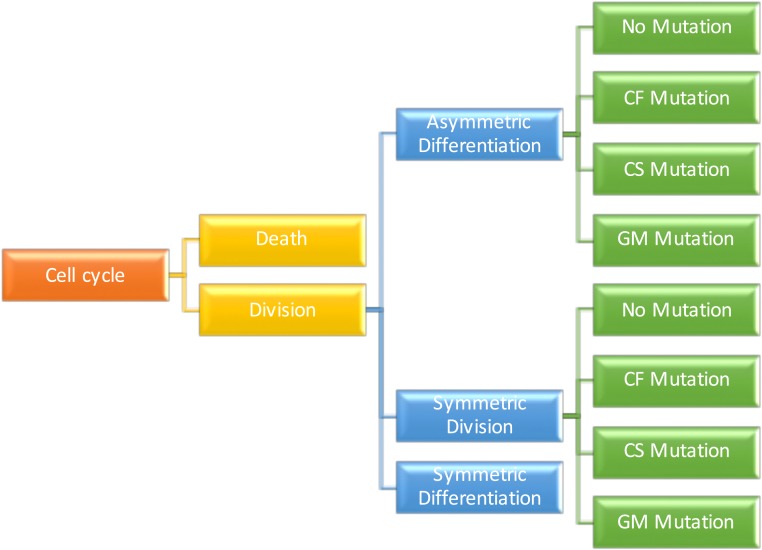
Second, it is a mechanistic model. For example, at the cell level, it keeps track of the dynamics of every cell present in a given tissue of a person, as depicted in Fig. 1. Specifically, by following all cell lineages, it accounts for the birth and death of each cell and the different types of stem cell division (symmetric self-renewal, symmetric differentiation, and asymmetric division) are included. It also follows the number and types of driver mutations that each cell lineage accumulates.

Fig. 1.

Visualization of the model’s transition rules as a tree. Each node of the graph represents a possible event, and each edge has an associated probability or rate of occurrence, as described in SI Appendix. Three types of mutations are considered, depending on the affected cell function: cell fate (CF), cell survival (CS), and genome maintenance (GM), as described in the main text as well as in figure 7 and table S5 of ref. 9 for a comprehensive list.

Third, the model is multiphase, since it accounts for the temporally distinct phases in the life of a tissue: 1) development, as a fetus and during childhood; 2) homeostasis, during adulthood; and 3) tumorigenesis, initiated by a driver gene event.

Fourth, the model is stochastic because births, deaths, and all mutational events, and therefore the occurrence of cancer among individuals, are all modeled as stochastic events.

Fifth, the model takes account of the nature of the mutations that might produce a fitness advantage. The standard mathematical definition for the fitness advantage, s, induced by a driver gene mutation, is provided by the expression $1+s={\lambda }_s/{\lambda }_{wt}$, where ${\lambda }_s$ and ${\lambda }_{wt}$ are the growth rates of the cells with that fitness advantage and wild type, respectively. At present, not many estimates for the fitness advantages induced by driver mutations exist, and the available estimates point to extremely small values, e.g., $s=0.004$ (14–16). Recently, Williams et al. (17) estimated fitness advantages that, while still relatively small, are somewhat larger than previously reported, but these refer to the fitness conferred by driver gene mutations to subclonal populations of cells after cancer occurred. Here, we are exclusively concerned with driver gene mutations that lead to cancer rather than those that are responsible for later heterogeneity among the cells of an existing cancer.

Our approach to estimating fitness advantages involves 2 key elements. First, we classify the type of possible fitness advantage according to the mechanisms through which such fitness advantages could be achieved (9). These are through impacting the following: 1) cell fate (CF), which shifts the per-cell-division probabilities toward increased symmetric self-renewal or, equivalently, reduces the death rate; 2) cell survival (CS), which increases the frequency of stem cell division, whether symmetric or asymmetric; and 3) genome maintenance (GM), which increases the probability of a mutation per stem cell division by disrupting normal repair mechanisms (Fig. 1). This classification is not arbitrary but rather based on the known biological pathways that the driver mutations affect (see figure 7 and table S5 in ref. 9 for a comprehensive list), and it allows us to mechanistically differentiate the effects of different types of fitness advantages on the dynamics of tumorigenesis. Note that the standard mathematical definition of a fitness advantage given at the beginning of this section can be properly applied only to driver gene mutations that impact CF (hereinafter “CF drivers”). In fact, the fitness advantage conferred by “GM drivers” cannot be estimated at all through the expression for s given above because no increase in the growth rate of a cell is produced by a GM driver. GM drivers simply facilitate the faster arrival of another driver. Similarly, the growth rate cannot be properly used to estimate the effects of a CS driver. For example, consider the case of cells where the probability of symmetric division is extremely small, i.e., where the mode of division is essentially always asymmetric. Then the change in growth rate of the stem cells introduced by a CS driver is essentially zero, even for large increases of the cell division rate. Different definitions of s are then needed for GM and CS drivers. For GM drivers, the fitness advantage, s, can be defined as $1+s={\mu }_s/{\mu }_{wt}$, where ${\mu }_s$ and ${\mu }_{wt}$ are the mutation rates (number of mutations per genome per cell division) of the cells with that fitness advantage and wild type, respectively. Fortunately, the estimation of this type of fitness advantage is relatively straightforward using sequencing data, requiring the comparison of mutation rates between 2 subpopulations of cancer patients. As an example, we refer to Tomasetti et al. (10), where it was estimated that patients with mismatch repair deficiency instability have approximately a 10-fold increase of the somatic mutation rate compared to microsatellite stable cancers. In addition, for CS drivers, the fitness advantage, s, can be defined as $1+s={\tau }_{div}^s/{\tau }_{div}^{wt}$, where ${\tau }_{div}^s$ and ${\tau }_{div}^{wt}$ are the division rates (e.g., number of divisions per week per cell) of the cells with that fitness advantage and wild type, respectively. We note that, by our definition, only changes in fitness in the CS group can increase the frequency of cell division in a given stem cell lineage, since CF drivers increase only the number of stem cell lineages but not the frequency of division within a stem cell lineage.

The second key element is that the total number of clonal somatic mutations accumulated in a cell lineage acts as a clock for the number of divisions that occurred in a noncancerous stem cell lineage in patients without known environmental exposures and inherited factors. When GM drivers are not present, this enables the estimation of a lower bound for the increase in fitness, s, induced by a CS driver, as defined for patient i by the following:

$$1+s_i=m_i/\left(a_i{d}_T\mu \right),$$

where m_i is the number of somatic mutations observed in that patient via sequencing, a_i is the patient’s age, d_T is the normal number of stem cell divisions per year in that tissue (see refs. 10 and 18), and μ is the expected number of somatic mutations per cell division, estimated to be 3 mutations/genome in multiple studies (ref. 19 and references therein). Importantly, these estimates are reflected, to a large extent, in our simulations for colon, pancreas, and blood (Methods and SI Appendix).

This multiscale, multiphase, stochastic model can qualitatively replicate cancer incidence data across different tissue types, shedding further light on several of the yet-unexplained aspects of tumorigenesis. While the model uses 19 parameters, only 4 of them are free. All others are constrained by biologically derived experimental data. In fact, even those 4 parameters are free only when modeling the incidence of CRC. They are kept fixed when modeling familial adenomatous polyposis (FAP) and Lynch syndrome, and only one of them is adjusted for blood and pancreatic cancers. Further details on the model are provided in Methods. For the code and the data see ref. 20.

Results

Estimates for the Fitness Advantage of CS Drivers.

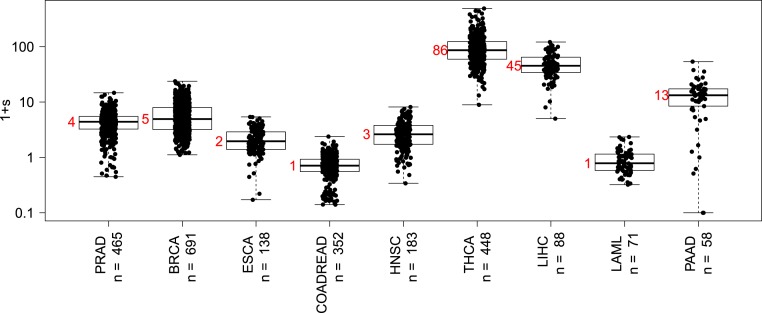
By applying this method described above, we find that, in colorectal (COADREAD) cancers, a CS driver mutation such as KRAS confers only a relatively small fitness advantage (Fig. 2). This is expected since the epithelial lining of the normal, healthy colon divides often, approximately every 4 d (ref. 18 and references therein), essentially the same division rate observed in CRCs (21).

Fig. 2.

Distributions of the fitness advantage, $\mathit{s}$, caused by cell survival driver mutations across cancer types. The median value (red) is approximated by the nearest integer. Cancer types are labeled according to The Cancer Genome Atlas (TCGA) nomenclature (BRCA, breast invasive carcinoma; COADREAD, colorectal adenocarcinoma; ESCA, esophageal carcinoma; HNSC, head and neck squamous cell carcinoma; LAML, acute myeloid leukemia; LIHC, liver hepatocellular carcinoma; PAAD, pancreatic adenocarcinoma; PRAD, prostate adenocarcinoma; THCA, thyroid carcinoma).

The situation, however, is drastically different when considering the effects of CS drivers in other cancers (Fig. 2). For example, in pancreatic adenocarcinoma (PAAD), we estimate that the fitness advantage of a CS driver is s = 12 (median; 95% CI: [0, 35.75]). These estimates, while very large and unexpected, are less surprising considering the difference in tissue dynamics between healthy and cancer cells in each organ. In several of the tissues in Fig. 2, the normal stem cell division rate is once per month to even once per year or less. However, the division rate of a cancer cell is generally once every few days, independently of the specific cancer type (21). Thus, CS drivers must increase the cell division frequency by orders of magnitude in these slow-dividing tissues.

Coherence with Incidence Data in Multiple Cancer Types.

Next, we evaluated how well our model performed when compared to clinical and epidemiologic observations. Specifically, by simulating a population of 10,000 individuals from birth to 75 y of age for each cancer type, we replicated cancer incidence data in several distinct situations.

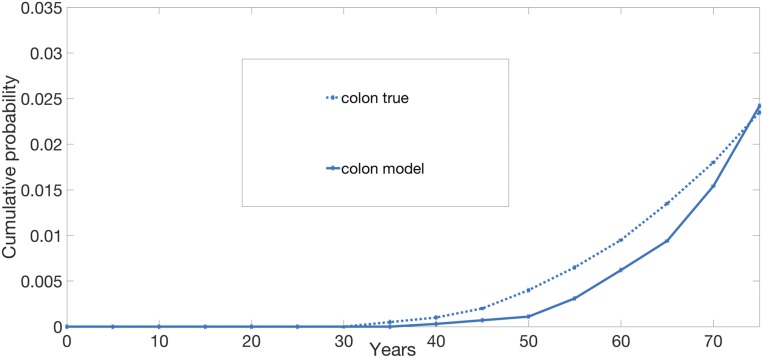
For CRC, the 4 free parameters of the model were fit based on Surveillance, Epidemiology, and End Results (SEER) statistics gathered on the incidence of CRC in the United States and the incidence of colonic polyps in the general population as a function of age (22). The model provided a good fit for the incidence curve of CRC, as depicted in Fig. 3. Because we used SEER data on CRC to fit the free parameters, this was not a true test of our model (Methods and SI Appendix).

Fig. 3.

Cumulative risk of CRC. Simulations are stopped at 75 y of age. Number of simulations: 10,000 individuals. The true curve for the cumulative risk is obtained from ref. 23.

We next tested this model in 2 distinct populations of individuals, one with Lynch syndrome (also known as hereditary nonpolyposis CRC) and the other with FAP.

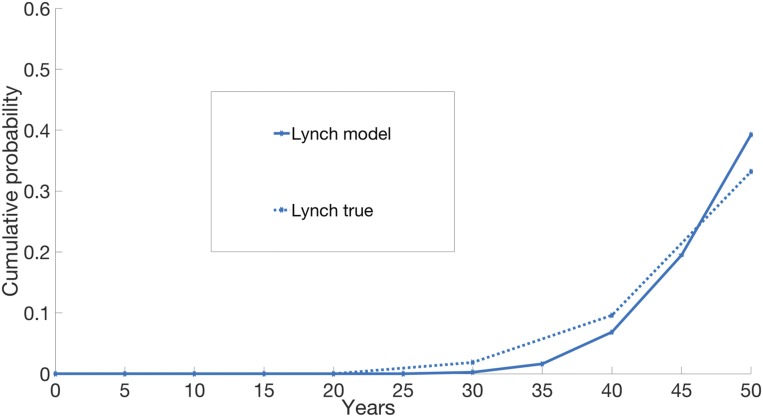
Cells of patients with Lynch syndrome have defects in mismatch repair (MMR) genes and are therefore mutation prone. From sequencing data on CRC patients, the mutation rate in CRCs with MMR deficiency is estimated to be 10.13 times higher than normal (median ratio; 95% CI: [8.79, 11.52]; P = 1.8 × 10⁻¹⁵) (10). This prior estimate enabled us to evaluate the model, when applied to a population of individuals born with Lynch syndrome, by simply increasing 10-fold the normal background mutation rate. No other parameter was changed with respect to the ones used for CRC. As depicted in Fig. 4, the model provides a qualitatively good fit to the incidence of CRC among patients with Lynch syndrome (24, 25).

Fig. 4.

Cumulative risk of cancer in Lynch syndrome. The simulations are stopped at 50 y of age. The number of simulations for Lynch is 5,000 individuals. The true curve for Lynch is obtained from ref. 25. The cumulative curve of FAP is not shown as the corresponding true curve is not available.

FAP results from mutations in the adenomatous polyposis coli (APC) gene, which is often the first driver gene mutation in CRC (26). APC has been studied in detail and is believed to be a CF driver (see figure 7 in ref. 9). We modeled the FAP population by starting the simulations for each individual with one allele of the APC gene already mutated. Again, no other parameter was changed with respect to the ones used for CRC. The true mean of cancer detection among FAP individuals is estimated to be 39 y of age (27). The estimated mean from our model is 41.33 y of age. The true cancer risk by 50 y of age among FAP individuals is estimated to be 95% (27). The risk estimated from our model is 99.9%. The 95th percentile estimated from our model is 46.4 y of age.

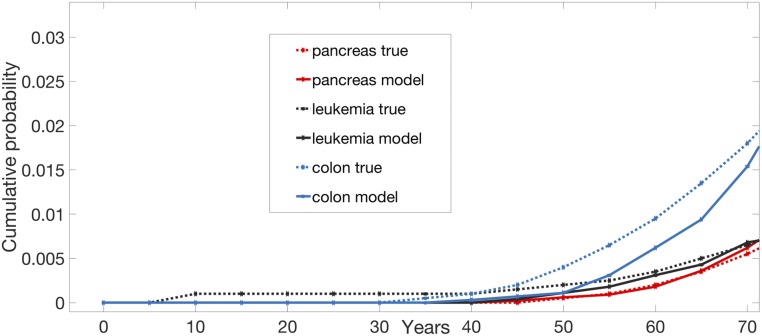
Encouraged by these results, we applied the model to 2 completely different types of cancers: leukemias and PAADs. Importantly, only 3 parameters were changed from the CRC model—the number of stem cells in a tissue, the division rate of a tissue, and the probability of a symmetric division. None of them was varied to get the best fit; each was prespecified based on extrapolations from prior biological experimental data (Methods). In both leukemias and pancreatic cancers, the model’s predicted incidence curves fit with the observed incidence curves in a reasonable way, and scale accordingly with respect to CRC (Fig. 5). For example, the model’s predicted incidence curve for leukemia was much closer to actual leukemia incidence than to the incidence of pancreatic cancers or CRCs.

Fig. 5.

Cumulative risk of cancer in leukemia, pancreas, and colon. Simulations are stopped at 75 y of age. Number of simulations: 10,000 individuals per tissue. The true curves are obtained from ref. 23. “Colon,” sporadic colorectal tumors; “Leukemia,” leukemias (all); “Lynch,” CRCs in patients with Lynch syndrome; “Pancreas,” pancreatic ductal adenocarcinoma.

Timing of Driver Gene Mutations.

We next sought to explore the timing of the driver mutations in cancer patients. A somewhat unexpected result of our simulations was that the first mutational event initiating the tumorigenesis process, and ultimately resulting in a cancer, occurred very early in life. Specifically, this first driver hit occurred typically at 14.4 y of age in colon (median; 95% CI: [7.6 y, 22.3 y]), 17.4 y of age in leukemia (median; 95% CI: [11.1 y, 22.8 y]) and 14.6 y of age in pancreas (median; 95% CI: [8.2 y, 21.1 y]), with the full development of malignancy taking on average ∼50 y. This contrasts with prior estimates, which had suggested that the process of tumorigenesis takes only 7 y in leukemia (28), 10 in uterine cancer (29), and 25 in CRC (26).

Very recent work based on sequencing data supports our findings. Mitchell et al. (30) provided evidence that, in clear cell renal cell cancers, the first initiating event generally occurs in childhood or adolescence, therefore preceding the cancer by many decades. In addition, there is evidence for a large accumulation of mutations and mutational clones in normal tissues before cancer (9, 19, 31–33), some of which must therefore occur at young age.

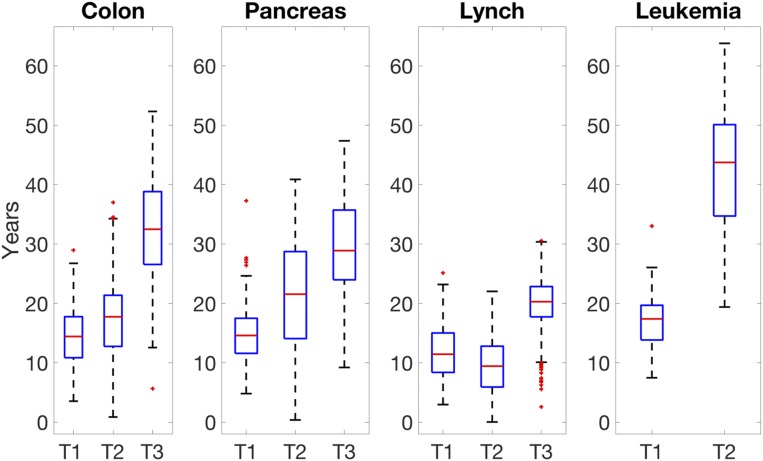
Our model also suggests that the sequential timing of the driver mutations does not cohere with the typical predictions of the timing of these required mutational hits. These previous predictions present a picture of accelerating waves, with the interarrival times of each driver gene mutation getting shorter and shorter (see, for example, refs. 14, 15, and 34). In contrast, our results indicate that the first successful hit typically requires a shorter time than the later hits, as depicted in Fig. 6. This is probably due to our model including all phases of the tumorigenesis process, and not assuming that clonal expansions follow an unlimited exponential growth.

Fig. 6.

Time intervals between sequential driver mutations: T1 is the time it takes for the first driver mutation to occur after birth; T2 is the time it takes for the second successful driver mutation to occur after the first mutation; T3 is the time it takes for the third successful driver mutation to occur after the second driver mutation.

Differences in Tumor Evolution Across Tissues.

Our model sheds light on why certain driver mutations may appear early in the process of tumorigenesis in some cancer types and later or not at all in others. This is due to the fact that we differentiate the effects of driver gene mutations, i.e., whether it is CS, CF, or GM, making it an essential element of the model. For example, the model predicted a driver from the CF group (such as APC) to be by far the most common first driver gene mutation in CRC (90.4%), while it predicted a driver from the CS group (65.3%) (such as KRAS or BRAF) as the second driver. In actuality, it has been shown that APC is altered in 81% of CRCs (35), and it is nearly always the first mutation to occur in this tumor type (26). Similarly, KRAS or BRAF are mutated in ∼45% of normal or hypermutated CRCs, respectively (35), and have been determined to be mutated after APC and before other gene mutations (26). In contrast, the model predicted a driver from the CS group (such as KRAS) as the most common first driver gene mutation in PAADs (100%). Evidence indicates that PAADs (pancreatic ductal adenocarcinomas) are initiated by KRAS gene mutations and that mutations in KRAS occur in nearly 100% of these cancers (36, 37). Both of these results (on colorectal and pancreatic cancers) are remarkable because the timing for each type of genetic alteration (CS, CF, or GM) was not forced into the model. Rather, the order of mutations was one of the model’s outcomes, reflecting fundamental differences in the dynamics of the 2 cancer types. While the normal colon is made of cells with a very high division frequency (approximately every 4 d), the cells in the normal pancreas divide very slowly (approximately every 8 mo). It is then intuitive that cells in the pancreas may successfully develop into a cancer within a lifetime only if they first speed up their division rate (via a CS mutation). Only at that point, the arrival of a CF mutation will be able to successfully induce a large clonal expansion.

In fact, our model predicts that 2 CS drivers are required in the pancreas. In colon, instead, with the division rate being already high, but with the great majority of those divisions being asymmetric divisions, increasing the probability of symmetric self-renewal (via a CF mutation), thus expanding the stem cell population, provides the most powerful initiating effect.

Finally, our model predicts that, by the time a CRC is detected, other neoplastic lesions in the colon or rectum, comparable to the cancer in size but still benign (i.e., adenomas), will often be present. In addition, according to the model predictions, it is often the case (>70%) that the final driver hit in colon occurs at carrying capacity, and, in particular, after the detection size has been reached. In contrast, the model predicts that, by the time a pancreatic cancer is detected, no other tumor lesion of comparable size will usually be present. Again, these findings are validated by clinical observations: Other polyps are common findings in CRC patients, but other large lesions are typically not found in pancreatic cancer patients (38).

Potential Implications for Public Health Policies on Screening.

It is well known that CRC deaths can be reduced by colonoscopy, but how often should these colonoscopies be performed and, more importantly, at what ages? We attempted to determine the relative risk of developing CRC when colonoscopies were performed at various ages, keeping the total number of colonoscopies fixed at 3, as it is currently suggested. For example, if patients were never screened by colonoscopy, 4.8% would develop CRC by age 80 (Table 1). On the other hand, if individuals were screened at ages 50, 55, and 60 (and not before or after), our model predicts that the risk of developing CRC by age 80 would be reduced by 55%.

Table 1.

The effect of different screening schedules for CRC

	Time without cancer
Age of colonoscopy	>50 y, %	>60 y, %	>70 y, %	>75 y, %
No colonoscopy	4.70	4.10	3.00	1.80
Age 50, 55, 60	2.10	1.90	1.40	0.80
Age 55, 60, 65	1.80	1.50	1.00	0.50
Age 60, 65, 70	1.30	1.00	0.70	0.50
Age 50, 60, 65	1.90	1.80	1.10	0.60
Age 55, 65, 70	1.60	1.20	0.70	0.50
Age 50, 60, 70	1.30	1.10	0.60	0.30

Probability of getting CRC by age 80 if no CRC was detected by age x (>x years), according to different screening regimes. It is assumed that a colonoscopy removes all detectable polyps present in the colon of the patient.

It is interesting that, according to our analysis, the current policy of screening every 10 y starting at age 50 yields the best risk reduction also in our model (Table 1).

This sort of modeling, in conjunction with modeling of many other variables, including the relative costs, deaths from other causes, the aging effects on cell division, etc., could prove useful for the design of clinical trials to determine the optimal screening intervals.

Discussion

We have described a general model for tumorigenesis with several features. It is a stochastic multiscale multiphase mathematical model of tumorigenesis able to qualitatively recapitulate observed age-specific incidence curves across several different cancer types, as well as fitting the incidence in subpopulations of patients with higher mutation rates or inherited driver genes. While it is relatively easy with a sufficient number of free parameters to fit a specific cancer incidence curve, it is remarkable that our model can fit the incidence of several cancer types at once by changing only parameters values that are dictated by biological constraints. Thus, using the identical model introduced for colon and changing just one parameter—a preexisting driver gene mutation in every normal colon cell in the case of FAP—a very different incidence curve is predicted by the model, qualitatively matching the incidence in FAP patients. Similarly, by changing a different parameter—the experimentally observed mutation rate in the case of Lynch syndrome patients—a very different incidence curve is predicted by the model, and this predicted curve matched the incidence in Lynch patients. Changing a total of 3 parameters, as dictated by experimentally informed estimates in blood and pancreas, provided an even harder test. The qualitative fit of our incidence curves to those observed in leukemias and pancreatic cancers then provides additional support for the model, as do our correct predictions of the nature of the initiating mutations in colorectal and pancreatic cancers. The most striking feature of the model is not the fitting of one given cancer incidence curve, rather the comparative prediction across the several cancer types.

It has been suggested that the normal background mutation rate is not sufficient to reproduce the observed cancer incidence rates when 3 drivers are required (ref. 39 and references therein). Our model provides evidence that this background rate is indeed sufficient. Naturally, a perfect fit of the model is not expected for multiple reasons, one of which is that the deleterious effects of environmental exposures were not included in the model. However, the approach used in this study naturally lends itself to the inclusion of the effects of environmental exposures—as we have shown for inherited factors in FAP and Lynch syndrome—by increasing the division and/or mutation rates or by increasing the number of cells at risk.

Our model provides a mechanistic explanation for why the ordering and even the type of driver genes may be different for different cancers, by correctly replicating experimental and clinical findings. These findings add to the knowledge provided by other functional studies showing, e.g., in sporadic melanoma that there is no selective advantage for a TERT promoter mutation or ATRX loss until there has been telomere shortening (40).

By applying a formulation for the fitness advantages conferred by different types of driver genes, we estimate that driver genes can confer very large fitness advantages, contrary to what is typically assumed. Interestingly, we avoided the typical but unrealistic assumption of exponential growth and found that the majority of the occurrences of the later driver mutations occur close to carrying capacity. This would suggest that the removal of large polyps is important for primary prevention even when they are not growing in size.

The model has several limitations. For example, it does not take into account large-scale deletions, insertions, or amplifications that characterize and possibly drive some cancers. It only accounts for deletions causing loss of heterozygosity in a tumor suppressor gene. In principle, having the appropriate estimates, both indels and amplifications can be added to the model according to their rate of occurrence.

Similarly, the model did not include genetic risk as defined from genome-wide association studies or, at least not directly, the effects of the immune system and the microenvironment in eliminating cells with mutations. Also, the model did not account for the effects of environmental exposures like sunlight, smoking, and alcohol. It is, however, straightforward to add to the model the effects of an environmental exposure on the mutation rate, by using the available estimates provided by sequencing studies. We leave these applications and extensions to future work. Finally, the model declares a clone to be cancer when all of the required drivers as well as a certain detection tumor size have been obtained. This, strictly speaking, may not be equivalent in practice to the requirement used by pathologists of invasion through a normal membrane.

In the study by Tomasetti et al. (19), the conclusion that the majority of the mutations occurred before tumor initiation was based on estimates of the time it takes to go from the first driver hit to cancer, which were obtained from the literature to be relatively short (<25 y). If the larger estimates (∼50 y) obtained with the current model are correct, these previous estimates of the fraction of mutations occurring prior to tumor initiation would have to be modified. However, even with this correction, the conclusion that the background mutation rate can generally explain the majority of the mutations found in cancers would still be valid.

In conclusion, our model led to several surprising results about tumor evolution, supporting a potential shift in our understanding of the dynamics of this random process. It suggests that tumorigenesis often starts at an early age. Moreover, we find that the waves of successive driver gene mutations do not have to be accelerating with time, leaving less and less time to intercept the tumor, in contrast to what has been usually assumed. These insights offer a positive outlook in the fight against cancer thanks to the potentially large window of opportunity for preventive approaches before the late and most advanced stages occur.

Methods

Given the complexity of the model, its full details can be found in SI Appendix. Here, we provide only some of the relevant information for parameter estimation and model calibration.

Overview of the Model Parameters.

The model has 19 parameters that can be divided into 5 groups. The first group describes the timing of the tissue development phase, with 3 parameters specifying 1) the time from conception to birth; 2) the time from birth to tissue stabilization in size (adulthood), which coincides with the beginning of the aging process; and 3) the time from tissue stabilization to the end of the simulation. The second group contains 2 size parameters, namely the total size of the tissue and the detection size of a polyp (or tumor). The third group consists of 8 parameters that drive the stem cell division/death cycle when the stem cell is wild type. Four of these 8 parameters determine the division rate of the cell and include: 1) the normal division rate of the tissue (before aging starts and when the cell is not part of a tumor); 2) a minimal division rate, which is the division rate of the cell when the cell belongs to a tumor at carrying capacity; 3) the carrying capacity; and 4) a parameter describing the speed at which the normal division rate decreases to the minimal rate when a tumor is growing. The other 4 parameters in the third group are the 3 probabilities that determine the division type (symmetric division, asymmetric or symmetric differentiation) and the probability of mutation. The fourth group has 3 parameters defining the fitness advantages resulting from a CF, CS, or a GM mutation. Finally, the fifth group of parameters contains the 3 probabilities of hitting each of the 3 mutation groups (CF, CS, or GM).

Estimation of the Normal Division Rates and Division Types Probabilities.

The total number of stem cells in a tissue and the normal number of stem cell divisions per year in a given tissue were obtained from the available estimates in the literature (see refs. 10 and 18 and references therein). Specifically, we used one division every 4 d in colon, one division every 32 d in blood, and one division every 240 d in pancreas. As these estimates are averages and constant with respect of time, but it has been recently shown that the cell division rate changes significantly at later ages in several tissues (41), we take into account this aging effect in the model by decreasing the division rate as a function of age. We also note that we use the term “stem cells” to indicate the population of cells with the ability to self-renew. These may be stem cells or undifferentiated progenitors in different tissues and those are the cells for which we obtain the estimated number (see refs. 10 and 18 and references therein).

As illustrated in Fig. 1, a cell that divides may do so via a symmetric division, an asymmetric division, and a symmetric differentiation. The probabilities of these events (for normal tissues) are fixed as follows.

In normal colon, ∼90% of the divisions are estimated to be asymmetric divisions (42). On the other hand, homeostasis for stem cells requires that the difference between the probability of symmetric division and that of symmetric differentiation equals the ratio between the apoptosis and division rates (cf. SI Appendix). Knowing the division rate of stem cells in colon (a division every 4 d) and assuming an apoptosis rate of about every 2 y (43), we obtain, in colon, probabilities equal to 0.0525 for symmetric renewal, 0.0475 for symmetric differentiation, and 0.9 for asymmetric division. Thus, assuming a tissue-independent estimate of the stem cell life span equal to 2 y, and given the biological estimates reported above for the normal stem cell division rate, this implies that a self-renewal will occur about once every 20 divisions in colon.

For hematopoietic and pancreatic stem cells, for which the asymmetric division rates are unknown, we use again the homeostasis equation, with the same apoptosis rate but a different division rate, and make the additional assumption that the ratio between the probability of symmetric division and that of symmetric differentiation is constant across tissues. Using these constraints, we find that self-renewal occurs once every 4 divisions for a hematopoietic stem cell, and once every 2 divisions in pancreas. Details are provided in SI Appendix.

Model Calibration.

Our model includes only 4 free parameters, i.e., no prior biological knowledge was available for them. These parameters were estimated only in modeling CRC. Subsequently, those parameters were either kept fixed or modified according to biological constraints when modeling all other cancer types (FAP, Lynch, blood, and pancreas). Two of these parameters describe the fitness advantage resulting when either the CF or CS category is hit in cells of the colon. The remaining 2 describe the carrying capacity curve that slows down the division rate when a crypt size increases. The free parameters are adjusted by fitting 4 constraints associated with colon cancer in the general population, namely the cumulative risk of colon cancer (set to be 2.5%), the probability of developing a polyp by 60 y of age (set to be 40%), the lifetime risk of developing a polyp (set to be 80%), and the probability of developing a polyp having an unrealistically large size (set to be 0.001%). The calibration algorithm uses Bayesian optimization with a Gaussian process prior (44) and is described, together with implementation and approximation details, in SI Appendix. Calibration is done only once based on colon cancer data, and the obtained model is used, with a few parameters adjusted based on known biological tissue properties when running simulations for other cancer types. See SI Appendix for further details.

Estimation of the Fitness Advantage.

The formula used to derive an estimate of s for a CS driver in patient i is given by $1+s_i=m_i/\left(a_i{d}_T\mu \right)$ as described in the main text. The idea is to compare the observed number of mutations in a cancer (the numerator of the ratio) with their expected number (the denominator) had no driver hit occurred. Since environmental exposures or inherited factors will inflate the number of observed somatic mutations, m_i, in a patient, we excluded from the analysis all patients with known exposures and/or inherited factors, as annotated in The Cancer Genome Atlas (TCGA) database. This method for estimating the fitness advantage is conservative since it assumes that the CS driver hit occurred at birth. If it did not, our estimates are lower bounds. In a cancer requiring 2 CS drivers, rather than 1, the formula above becomes ${\left(1+s_i\right)}^b=m_i/a_i{d}_T\mu$, where $b\ge 1.$ The estimates provided in Fig. 2 are for the case of 1 CS driver, but our finding that the fitness advantages are very large in some tissues remains true even when 2 CS drivers are needed.

Statistical Analysis.

We analyzed whole-exome sequencing datasets publicly available on the TCGA website.

All statistical analyses were performed using R software, version 3.5.1 (R Development Core Team, 2018). All simulations were performed using Python software, version 3.7.0.

Data Availability.

Data and code are available on GitHub (https://github.com/cristomasetti/).