Abstract
We consider a scale-free network of inhibitory Hindmarsh–Rose (HR) bursting neurons, and make a computational study on coupling-induced cluster burst synchronization by varying the average coupling strength . For sufficiently small , non-cluster desynchronized states exist. However, when passing a critical point , the whole population is segregated into 3 clusters via a constructive role of synaptic inhibition to stimulate dynamical clustering between individual burstings, and thus 3-cluster desynchronized states appear. As is further increased and passes a lower threshold , a transition to 3-cluster burst synchronization occurs due to another constructive role of synaptic inhibition to favor population synchronization. In this case, HR neurons in each cluster make burstings every 3rd cycle of the instantaneous burst rate of the whole population, and exhibit burst synchronization. However, as passes an intermediate threshold , HR neurons fire burstings intermittently at a 4th cycle of via burst skipping rather than at its 3rd cycle, and hence they begin to make intermittent hoppings between the 3 clusters. Due to such intermittent intercluster hoppings via burst skippings, the 3 clusters become broken up (i.e., the 3 clusters are integrated into a single one). However, in spite of such break-up (i.e., disappearance) of the 3-cluster states, (non-cluster) burst synchronization persists in the whole population, which is well visualized in the raster plot of burst onset times where bursting stripes (composed of burst onset times and indicating burst synchronization) appear successively. With further increase in , intercluster hoppings are intensified, and bursting stripes also become dispersed more and more due to a destructive role of synaptic inhibition to spoil the burst synchronization. Eventually, when passing a higher threshold a transition to desynchronization occurs via complete overlap between the bursting stripes. Finally, we also investigate the effects of stochastic noise on both 3-cluster burst synchronization and intercluster hoppings.
Keywords: Cluster burst synchronization, Localization of inter-burst-intervals, Intercluster hoppings, Inhibitory bursting neurons
Introduction
Recently, much attention has been paid to burst synchronization in a population of bursting neurons (Golomb and Rinzel 1994; Elson et al. 1998; Stern et al. 1998; Varona et al. 2001; van Vreeswijk and Hansel 2001; Dhamala et al. 2004; Ivanchenko et al. 2004; Chik et al. 2004; Shilnikov and Cymbalyuk 2005; Shi and Lu 2005; Tanaka et al. 2006; Pereira et al. 2007; Batista et al. 2007, 2009; Shi and Lu 2009; Wang et al. 2009; Batista et al. 2010; Sun et al. 2011; Yu et al. 2011; Wang et al. 2011a, b; Batista et al. 2012; Lameu et al. 2012; Langdon et al. 2012; Duan et al. 2013; Meng et al. 2013; Wang et al. 2013; Prado et al. 2014; Ferrari et al. 2015; Kim and Lim 2015a, b, 2016, 2018). Burstings occur when neuronal activity alternates, on a slow timescale, between a silent phase and an active (bursting) phase of fast repetitive spikings (Rinzel 1985, 1987; Izhikevich 2000, 2006, 2007; Coombes and Bressloff 2005). Due to a repeated sequence of spikes in the bursting, there are several hypotheses on the importance of bursting activities in neural computation (Lisman 1997; Izhikevich et al. 2003; Krahe and Gabbian 2004; Izhikevich 2004, 2006). For example, (a) bursts are necessary to overcome the synaptic transmission failure, (b) bursts are more reliable than single spikes in evoking responses in post-synaptic neurons, (c) bursts evoke long-term potentiation/depression (and hence affect synaptic plasticity much greater than single spikes), and (d) bursts can be used for selective communication between neurons. Intrinsically bursting neurons and chattering neurons in the cortex (Connors and Gutnick 1990; Gray and McCormick 1996), thalamic relay neurons and thalamic reticular neurons in the thalamus (Llinás and Jahnsen 1982; McCormick and Huguenard 1992; Lee et al. 2007), hippocampal pyramidal neurons (Su et al. 2001), Purkinje cells in the cerebellum (Womack and Khodakhah 2002), pancreatic -cells (Chay and Keizer 1983; Pernarowski et al. 1992; Kinard et al. 1999), and respiratory neurons in pre-Botzinger complex (Del Negro et al. 1998; Butera et al. 1999) are representative examples of bursting neurons.
Here, we are concerned about burst synchronization (i.e., synchrony on the slow bursting timescale) which characterizes temporal coherence between burst onset times (i.e., times at which burstings start in active phases). This kind of burst synchronization is related to neural information processes in health and disease. For example, large-scale burst synchronization occurs in the sleep spindles through interaction between the excitatory thalamic relay cells and the inhibitory thalamic reticular neurons in the thalamus during the early stage of slow-wave sleep (Steriade et al. 1993; Bazhenov and Timofeev 2006). These sleep spindles are associated with memory consolidation (Gais et al. 2000; Sejnowski and Destexhe 2000). In contrast, burst synchronization is also correlated to abnormal pathological rhythms, related to neural diseases such as movement disorder (Parkinson’s disease and essential tremor) (Bevan et al. 2002; Uhlhaas and Singer 2006; Brown 2007; Hammond et al. 2007; Park et al. 2010) and epileptic seizure (Fisher et al. 2005; Uhlhaas and Singer 2006).
In addition to burst synchronization, we are also interested in cluster synchronization. In this case, the whole population is segregated into synchronous sub-populations (called also as clusters) with phase lag among them (Belykh et al. 2008; Moon et al. 2015). This type of cluster synchronization has been investigated experimentally, numerically, or theoretically in a variety of contexts in diverse coupled (physical, chemical, biological, and neural) oscillators; to name a few, Josepson junction arrays (Aronson et al. 1991; Wisenfeld et al. 1996), globally-coupled chemical oscillators (Kiss et al. 2005; Taylor et al. 2008; Miyakawa et al. 2013), synthetic genetic networks (Zhang et al. 2009), and globally-coupled networks of inhibitory (non-oscillatory) reticular thalamic nucleus neurons (Golomb and Rinzel 1994) and other inhibitory model neurons (Chik et al. 2004; Langdon et al. 2012).
Synaptic connectivity in neural networks has been found to have complex topology which is neither regular nor completely random (Sporns et al. 2000; Buzsáki et al. 2004; Chklovskii et al. 2004; Song et al. 2005; Bassett and Bullmore 2006; Sporns and Honey 2006; Larimer and Strowbridge 2008; Bullmore and Sporns 2009; Sporns 2011). Particularly, neural networks have been found to exhibit power-law degree distributions (i.e., scale-free property) in the rat hippocampal networks (Morgan and Soltesz 2008; Bonifazi et al. 2009; Wiedemann 2010; Li et al. 2010) and the human cortical functional network (Eguíluz et al. 2005). Moreover, robustness against simulated lesions of mammalian cortical anatomical networks (Felleman and Van Essen 1991; Young 1993; Young et al. 1994; Scannell et al. 1995, 1999; Sporns et al. 2004) has also been found to be most similar to that of a scale-free network (SFN) (Kaiser et al. 2007). This type of SFNs are inhomogeneous ones with a few “hubs” (i.e., superconnected nodes) (Barabási and Albert 1999; Albert and Barabási 2002). Many recent works on various subjects of neurodynamics have been done in SFNs with a few percent of hub neurons with an exceptionally large number of synapses (Batista et al. 2007, 2009; Wang et al. 2009; Batista et al. 2010; Wang et al. 2011b; Ferrari et al. 2015).
In this paper, we consider an inhibitory SFN of suprathreshold (i.e., self-oscillating) Hindmarsh–Rose (HR) bursting neurons, and investigate coupling-induced cluster burst synchronization by changing the average coupling strength . For sufficiently small desynchronized states exist. But, when passing a critical point , the whole population is segregated into 3 clusters via a constructive role of synaptic inhibition to stimulate dynamical clusterings between individual burstings, and thus 3-cluster desynchronized states appear. In the presence of 3 clusters, inter-burst-intervals (IBIs) of individual HR neurons are localized in a region of [ cluster period (i.e., time interval between appearance of successive clusters)], and a peak appears at . For , delocalization of IBIs occurs through crossing the left and/or the right boundaries (corresponding to and respectively), and thus break-up of the 3 clusters occurs through intercluster hoppings between the clusters.
As is increased and a lower threshold is passed, a transition to 3-cluster burst synchronization occurs due to another constructive role of synaptic inhibition to favor population synchronization. In each cluster, HR neurons make burstings every 3rd cycle of the instantaneous whole-population burst rate of the whole population, and hence a single peak appears at [ global period of ] in the IBI histogram for the whole population of HR neurons. Moreover, these burstings in each cluster are also made in a coherent way, and hence a type of incomplete synchronization occurs in each cluster (i.e., burstings in each cluster show some coherence, although they are not completely synchronized). In this way, 3-cluster burst synchronization emerges. This type of cluster burst synchronization is in contrast to that occurring via post-inhibitory rebound (PIR) in globally-coupled networks of subthreshold (i.e., non-oscillating) neurons with inhibitory synaptic connections (Golomb and Rinzel 1994; Chik et al. 2004; Langdon et al. 2012); in the case of PIR, complete synchronization appears in each cluster (i.e., states of all the neurons in each cluster are the same).
However, as is further increased and passes an intermediate threshold , a new minor peak appears at in the IBI histogram, in addition to the major peak at . Thus, delocalization of IBIs occurs by crossing the right boundary (corresponding to ). In this case, HR neurons intermittently fire burstings at a 4th cycle of via burst skipping rather than at its 3rd cycle, and hence intermittent hoppings between the 3 clusters occur. Due to the intermittent intercluster hoppings via burst skippings, break-up of clusters occurs (i.e., the 3 clusters are integrated into a single one). However, in spite of break-up of the 3 clusters, burst synchronization persists in the whole population, which is well visualized in the raster plot of burst onset times where bursting stripes (composed of burst onset times and representing burst synchronization) appear successively. With further increase in , intercluster hoppings are intensified (e.g., for a larger a 3rd peak appears at in the IBI histogram), and bursting stripes also become smeared more and more due to a destructive role of synaptic inhibition to spoil the burst synchronization. Eventually, when passing a higher threshold a transition to desynchronization occurs via complete overlap between the bursting stripes. In a desynchronized case, burst onset times are completely scattered without forming any stripes in the raster plot. Finally, the effects of stochastic noise on both 3-cluster burst synchronization and intercluster hoppings are also investigated.
This paper is organized as follows. In “Inhibitory scale-free network of Hindmarsh–Rose bursting neurons” section, we describe a Barabási-Albert SFN composed of inhibitory HR bursting neurons. Then, in “Coupling-induced cluster burst synchronization of inhibitory HR bursting neurons” section we investigate coupling-induced cluster burst synchronization by varying the average coupling strength , and then study the effects of stochastic noise on burst synchronization in “Effects of stochastic noise on cluster burst synchronization” section. Finally, we give summary and discussion in “Summary and discussion” section.
Inhibitory scale-free network of Hindmarsh–Rose bursting neurons
We consider an inhibitory SFN composed of N bursting neurons equidistantly placed on a one-dimensional ring of radius . We employ a directed Barabási-Albert SFN model (i.e. growth and preferential directed attachment) (Barabási and Albert 1999; Albert and Barabási 2002). At each discrete time t, a new node is added, and it has incoming (afferent) edges and outgoing (efferent) edges via preferential attachments with (pre-existing) source nodes and (pre-existing) target nodes, respectively. The (pre-existing) source and target nodes i (which are connected to the new node) are preferentially chosen depending on their out-degrees and in-degrees according to the attachment probabilities and , respectively:
| 1 |
where is the number of nodes at the time step . Here, we consider the case of symmetric preferential attachment with . For generation of an SFN with N nodes, we begin with the initial network at , consisting of nodes where the node 1 is connected bidirectionally to all the other nodes, but the remaining nodes (except the node 1) are sparsely and randomly connected with a low probability . The processes of growth and preferential attachment are repeated until the total number of nodes becomes N. In this case, the node 1 will be grown as the head hub with the highest degree.
As an element in our SFN, we choose the representative bursting HR neuron model which was originally introduced to describe the time evolution of the membrane potential for the pond snails (Hindmarsh and Rose 1982, 1984; Rose and Hindmarsh 1985). We consider the Barabási-Albert SFN composed of N HR bursting neurons. The following Eqs. (2–4) govern the population dynamics in the SFN:
| 2 |
| 3 |
| 4 |
where
| 5 |
| 6 |
Here, the state of the ith neuron at a time t (measured in units of milliseconds) is characterized by three state variables: the fast membrane potential , the fast recovery current and the slow adaptation current . The parameter values used in our computations are listed in Table 1. More details on external stimulus to each HR neuron, synaptic currents, and numerical integration of the governing equations are given in the following subsections.
Table 1.
Parameter values used in our computations
External stimulus to each HR neuron
Each bursting HR neuron [whose parameter values are in the 1st item of Table 1 (Longtin 1997)] is stimulated by a DC current and an independent Gaussian white noise [see the 5th and the 6th terms in Eq. (2)] satisfying and , where denotes the ensemble average. The intensity of noise is controlled by the parameter D. As passes a threshold in the absence of noise (i.e., ), each single HR neuron exhibits a transition from a resting state to a bursting state (see Fig. 1a). With increasing , the bursting frequency , (corresponding to the reciprocal of the average IBI ), increases monotonically, as shown in Fig. 1b. For a suprathreshold case of , deterministic bursting occurs when neuronal activity alternates, on a slow time scale msec), between a silent phase and an active (bursting) phase of fast repetitive spikings, as shown in Fig. 1c. The dotted horizontal line () denotes the bursting threshold (the solid and open circles denote the active phase onset and offset times, respectively), while the dashed horizontal line () represents the spiking threshold within the active phase. An active phase of the bursting activity begins (ends) at a burst onset (offset) time when the membrane potential x of the bursting HR neuron passes the bursting threshold of from below (above). In this case, the HR neuron exhibits bursting activity with the slow bursting frequency Hz) [corresponding to the reciprocal of the average IBI ( msec)]. Throughout this paper, we consider a suprathreshold case such that the value of is chosen via uniform random sampling in the range of [1.3,1.4], as shown in the 2nd item of Table 1.
Fig. 1.
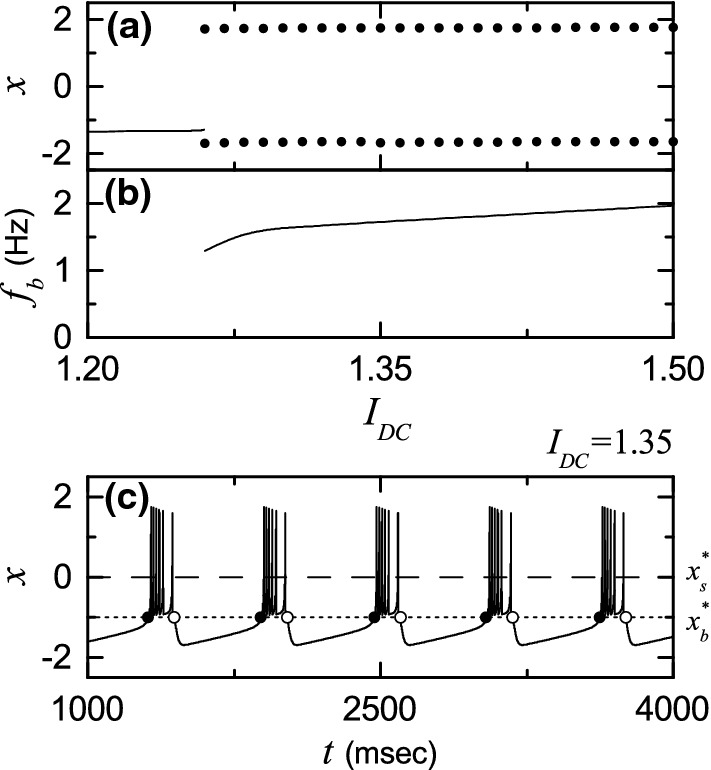
Single bursting HR neuron for . a Bifurcation diagram in the single HR neuron. Solid line represents a stable resting state, while for the bursting state, maximum and minimum values of the membrane potential x are denoted by solid circles. b Bursting frequency versus . c Time series of x(t) for the bursting state when . The dotted horizontal line () and the dashed horizontal line () denote the bursting and the spiking thresholds, respectively. The solid and open circles represent the burst onset and offset times, respectively
Synaptic currents
The last term in Eq. (2) represents the synaptic couplings of HR bursting neurons. The coupling strength of the synapse from the jth pre-synaptic neuron to the ith post-synaptic neuron is . These synaptic strengths are normally distributed with the mean and the standard deviation . of Eq. (5) represents a synaptic current injected into the ith neuron, and is the synaptic reversal potential. The synaptic connectivity is given by the connection weight matrix W (=) where if the bursting neuron j is presynaptic to the bursting neuron i; otherwise, . Here, the synaptic connection is modeled in terms of the Barabási-Albert SFN. Then, the in-degree of the ith neuron, (i.e., the number of synaptic inputs to the neuron i) is given by . The fraction of open synaptic ion channels at time t is denoted by g(t). The time course of of the jth neuron is given by a sum of delayed double-exponential functions [see Eq. (6)], where is the synaptic delay, and and are the fth spike and the total number of spikes of the jth neuron at time t, respectively. Here, E(t) [which corresponds to contribution of a presynaptic spike occurring at time 0 to in the absence of synaptic delay] is controlled by the two synaptic time constants: synaptic rise time and decay time , and is the Heaviside step function: for and 0 for . For the inhibitory GABAergic synapse (involving the receptors), the values of , , , and are listed in the 3rd item of Table 1 (Brunel and Wang 2003).
Numerical integration
Numerical integration of differential equations (2–4) is done by using the 4th-order Runge-Kutta method in the absence of noise () and the Heun method (San Miguel and Toral 2000) in the presence of noise () (with the time step msec). For each realization, we choose a random initial point for the ith neuron with uniform probability in the range of , , and .
Coupling-induced cluster burst synchronization of inhibitory HR bursting neurons
In this section, we consider a directed Barabási-Albert SFN, composed of N inhibitory HR bursting neurons; in most cases, except for the cases of the raster plot for and the bursting order parameters . The synaptic coupling strengths are chosen from the Gaussian distribution with the mean and the standard deviation . We investigate coupling-induced cluster burst synchronization by varying in the absence of noise ().
Emergence of dynamical clusterings
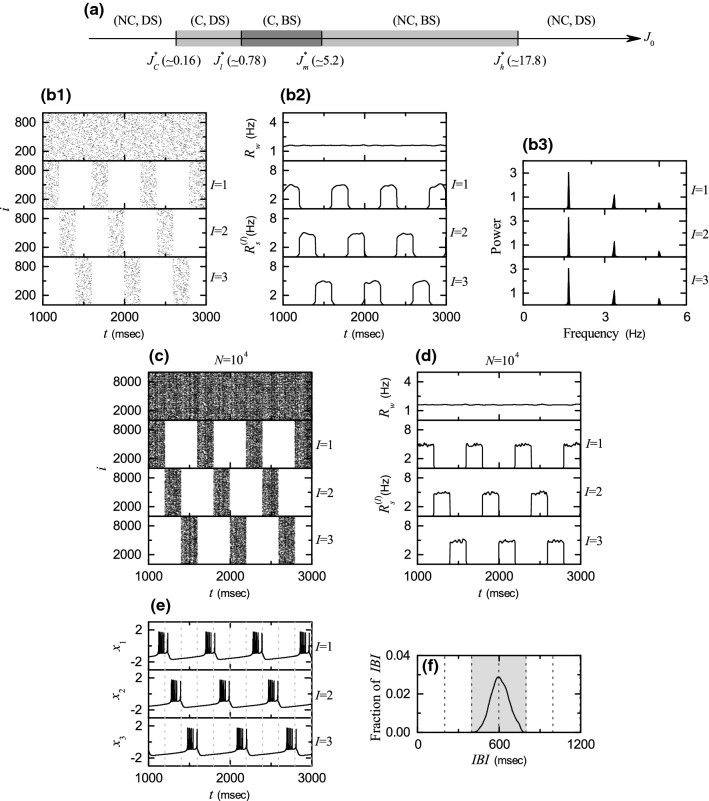
Figure 2a shows a bar diagram for diverse population states. Here, C, NC, BS, and DS represent cluster, non-cluster, burst synchronization, and desynchronization, respectively. For sufficiently small non-cluster desynchronized states exist. However, when passing a critical point 3-cluster states appear. As an example, we consider the case of . Emergence of dynamical clusterings may be well seen in the raster plot of bursting onset times which corresponds to a collection of all trains of burst onset times of individual bursting neurons. As clearly shown in Fig. 2b, the whole population is segregated into 3 sub-populations (also called clusters); [number of neurons in the Ith ( 2, and 3) cluster] . Clustered busting bands appear in a successive cyclic way (i.e., ) with the cluster period (i.e., average time interval between appearance of successive clusters) msec). Hence, in each cluster, bursting bands appear successively with the period msec)].
Fig. 2.
Emergence of 3-cluster state for . a Bar diagram for the population states. C, NC, BS, and DS denote clustering, non-clustering, burst synchronization, and desynchronization, respectively. b1 Raster plots of burst onset times in the whole population and in the Ith cluster (I = 1, 2, and 3). b2 IWPBR of the whole population and ISPBR of the Ith cluster (I = 1, 2, and 3). b3 One-sided power spectra of [ = ] (I = 1, 2, and 3) with the mean-squared amplitude normalization; the overbar denotes time average. : c raster plots of burst onset times in the whole population and in the Ith cluster (I = 1, 2, and 3) and d IWPBR of the whole population and ISPBR of the Ith cluster (I = 1, 2, and 3). e Time series of membrane potential of a representative neuron i in each cluster; i = 1, 2, and 3 for I = 1, 2, and 3 clusters, respectively. f IBI histogram. Localization of IBIs in the gray region of . Vertical dotted lines in c, d denote integer multiples of the cluster period
As macroscopic quantities showing the whole- and the sub-population behaviors, we employ the instantaneous whole population burst rate (IWPBR) and the instantaneous sub-population burst rate (ISPBR) (I = 1, 2, 3) which may be obtained from the raster plots in the whole population and in the clusters, respectively (Kim and Lim 2015a, b, 2016, 2018). To obtain a smooth IWPBR , we employ the kernel density estimation (kernel smoother) (Shimazaki and Shinomoto 2010). Each burst onset time in the raster plot is convoluted (or blurred) with a kernel function to obtain a smooth estimate of IWPBR :
| 7 |
where is the bth burst onset time of the ith neuron, is the total number of burst onset times for the ith neuron, and we use a Gaussian kernel function of band width h:
| 8 |
Throughout the paper, the band width h of is 20 ms. The IWPBR is shown in the top panel of Fig. 2b2. We note that is nearly stationary, because burst onset times in the raster plot in the whole population are nearly completely scattered. Hence, a 3-cluster desynchronized state appears for .
As in the case of , we get the ISPBR kernel estimate by employing the Gaussian kernel function of Eq. (8):
| 9 |
where is the bth burst onset time of the ith neuron in the Ith cluster, is the total number of burst onset times for the ith neuron in the Ith cluster, and is the number of neurons in the Ith cluster. The ISPBRs of the Ith clusters are shown in the 1, 2, and 3 panels of Fig. 2b2, respectively. We note that shows a square-wave-like behavior. For each cluster, burst onset times in each bursting band are nearly completely scattered (i.e., nearly desynchronized), and hence a square-wave-like oscillation occurs in each . During the “silent” part (without burstings) for about 2P/3, (which corresponds to the bottom part), while in the bursting band for about P / 3, rapidly increases to the nearly flat top, and then decreases rapidly; P corresponds to the average period of the square-wave oscillation. Through repetition of this process exhibits a square-wave-like oscillation. The sub-population bursting frequency of the ISPBR (I = 1, 2, and 3) may be obtained from the one-sided power spectra of with the mean-squared amplitude normalization. The overbar represents time average and the number of data for each power spectrum is . Figure 2b3 shows power spectra of (1, 2, and 3). In the case of each sub-population (cluster), the power spectrum has a main peak at Hz) and its harmonics. Hence, oscillates with the slow sub-population bursting frequency , the reciprocal of which corresponds to the average period P of the square-wave oscillation (also corresponding to the average period for appearance of successive bursting bands in each cluster).
To examine the square-wave-like behavior more clearly, the number of HR neurons is increased from to . In this case, raster plots in the whole population and the clusters and their corresponding IWPBR and ISPBR are shown in Fig. 2c, d, respectively. For the whole population, burst onset times are more completely scattered, and hence the corresponding IWPBR is more stationary. Furthermore, for each cluster, bursting bands in the raster plot show clearly the clustering structure, and the corresponding ISPBR shows square-wave oscillations more clearly. Thus, for each cluster, burst onset times in bursting bands are completely scattered, and they show a desynchronized state. In this way, 3-cluster desynchronization appears for .
We also investigate individual bursting behaviors of HR neurons in each cluster. Figure 2e shows a time series of a membrane potential of a representative neuron in each Ith cluster ( and 3 for , 2, and 3, respectively); the vertical dotted lines represent integer multiples of the cluster period . The 1st HR neuron in the cluster makes burstings in the 1st clustering cycle (after the transient time msec). We note that the duration of silent phase of the 1st neuron is about twice as long as the length of its active bursting phase. During this silent phase, the 2nd and the 3rd HR neurons in the and 3 clusters exhibit burstings alternately in the 2nd and the 3rd clustering cycle, respectively. In this way, individual HR neurons in each cluster show burstings every 3rd clustering cycle. This kind of individual bursting behaviors are well shown in the IBI histograms (see Fig. 2f), where vertical dotted lines denote integer multiples of . The IBI histogram is composed of IBIs, and the bin size for the histogram is 2.5 ms. A single peak appear at ; also corresponds to the average period P for the appearance of bursting bands in each cluster. We note that IBIs are localized in a range of . Based on the IBI histogram, we suggest a criterion for emergence of 3-cluster states. Localization of IBIs in the range of results in emergence of 3 clusters.
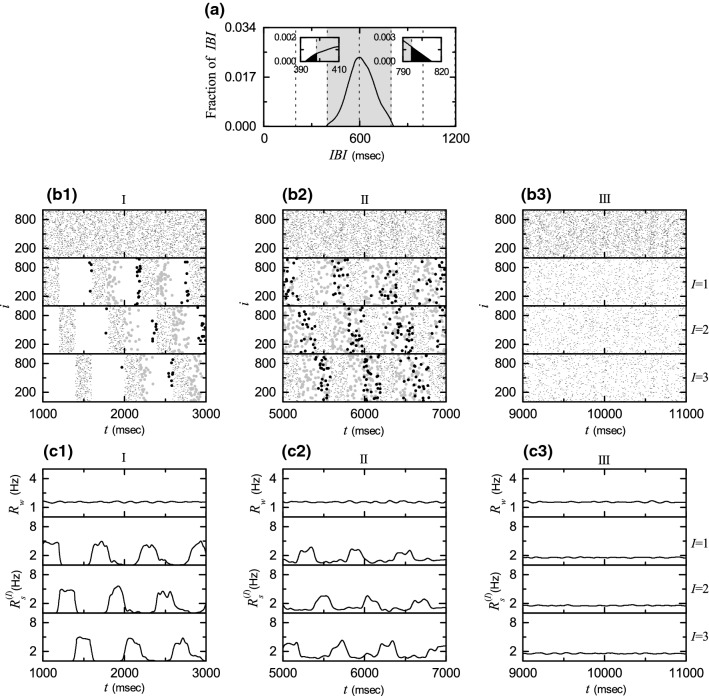
For delocalization of IBIs occurs via crossing the left and/or the right boundaries (corresponding to and respectively). As an example, we consider the case of . Figure 3a shows a delocalized IBI histogram. In this case, some fraction of IBIs cross both the left and the right boundaries (see the black parts in the insets of Fig. 3a). The fraction of IBIs above is 0.0753, while the fraction of IBIs below is 0.0146. Hence, “late” burstings with IBIs larger than are much more probable than “early” burstings with IBIs smaller than . As a result of occurrence of these late and early burstings, interburst hoppings between the 3 clusters occur, which leads to break up of dynamical clusterings. Such intercluster hoppings may be well seen in sequential long-term raster plots of burst onset times in the whole population and in the Ith (, 2, and 3) clusters. Figure 3b1–b3 show such raster plots in the early, the intermediate, and the final stages, respectively. In Fig. 3b1, b2, late and early burstings are plotted with gray and black dots of a little larger point size (= 1.5), in contrast to regular burstings which are plotted with black dots of a smaller point size (= 0.5).
Fig. 3.
Break-up of 3-cluster state via intercluster hoppings for . a IBI histogram. Delocalization of IBIs through crossing the left and the right vertical boundary lines of the gray region (corresponding to and respectively). Sequential long-term raster plots of burst onset times in the whole population and in the Ith cluster ( and 3) in b1 the early, b2 the intermediate, and b3 the final stages; in (b1, b2), late burstings with IBIs larger than and early burstings with IBI smaller than are plotted with gray and black dots of a little larger point size. IWPBR of the whole population and ISPBR of the Ith cluster (1, 2, and 3) in the c1 early, c2 the intermediate, and c3 the final stages
For the initial stage in Fig. 3b1, individual HR neurons in the Ith cluster make intermittent intercluster hoppings to the nearest neighboring th [th] cluster due to occurrence of late (early) burstings. Thus, bursting bands in the Ith cluster become smeared into the nearest neighboring bursting bands belonging to the th and the th clusters. In this way, intermittent “forward” hoppings from the Ith to the th cluster and “backward” hoppings from the Ith to the th cluster occur through occurrence of late and early burstings, respectively. The smearing degree of late burstings (larger gray dots) into the th cluster is larger than that of early burstings (larger black dots) into the th cluster.
For the intermediate stage in Fig. 3b2, one more step occurs for the intercluster hoppings due to occurrence of 2nd late and early burstings. Hence, intercluster hoppings occur from the Ith cluster to the th and the th clusters (due to the 1st late and early burstings) and then to the th and the th clusters (due to the 2nd late and early burstings). Thus, bursting bands in the Ith cluster become smeared into the nearest neighboring bursting bands belonging to the th and the th clusters and then into the next-nearest neighboring bursting bands belonging to the th and the th clusters. In this way, successive 2nd forward and backward intercluster hoppings occur due to occurrence of 2nd late and early burstings, respectively. We also note that the 1st (2nd) late burstings and the 2nd (1st) early burstings are intermixed. In this intermediate stage, smeared parts into neighboring clusters are still sparse (i.e., their densities are low in comparison with those of regular bursting bands).
As the time t is further increased, 3rd late and early burstings may also occur, and then another forward (backward) intercluster hoppings from the th [th] to the Ith clusters occur (i.e., return to the original Ith cluster occurs due to the 3rd late and early burstings). In this way, forward and backward intercluster hoppings occur in a cyclic way [I () () I] due to occurrence of successive late and early burstings. In the final stage after a sufficiently long time, intercluster hoppings between clusters are more and more intensified, which leads to complete break-up of clusters. As a result, burst onset times in the raster plots are completely scattered in a nearly uniform way, independently of 2, and 3, as shown in Fig. 3b3.
Figure 3c1–c3 show the IWPBR and the ISPBR (I = 1, 2, and 3), corresponding to the above raster plots in Fig. 3b1–b3. In the initial stage in Fig. 3c1, amplitudes (corresponding to heights of squares) of square-wave oscillations are decreased and top parts of squares become less flat (i.e., they begin to wiggle). Additionally, small-amplitude oscillations (associated with low-density smeared parts in the raster plots occurring due to forward and backward intercluster hoppings) also appear in connection with decreased square-wave oscillations
In the intermediate stage in Fig. 3c2, one more step for forward and backward intercluster hoppings occurs due to 2nd late and early burstings, and hence forward and backward smearing of late and early burstings extends to the next-nearest neighboring clusters. In this case, amplitudes of square-wave oscillations are more decreased and top parts of squares also become much less flat. In this way, square-wave oscillations become broken up more and more. Additionally, small-amplitude oscillations (related to extended smeared parts in the raster plots occurring due to successive forward and backward intercluster hoppings) appear and they cover the whole range between square-wave oscillations. In this case, the amplitudes of extended small oscillations are larger than those in the initial stage.
As the time t is further increased, these tendencies (e.g., decreasing tendency in amplitudes of square-wave oscillations, increasing tendency in break-up of square-wave structure, and increasing tendency in amplitudes of extended small oscillations) become intensified due to intensive forward and backward intercluster hoppings. As a result of complete break-up of clusters, all the ISPBR become nearly the same as the IWPBR , independently of I, and also both and are nearly stationary, as shown in Fig. 3c3 for the final stage.
Emergence of cluster burst synchronization
As the average coupling strength is increased and passes a threshold, a transition from cluster desynchronization to cluster burst synchronization occurs. In a desynchronized case, burst onset times are completely scattered in the raster plot in the whole population (e.g., see the top panel of Fig. 4b1). On the other hand, in the case of burst synchronization, bursting stripes (composed of burst onset times and representing burst synchronization) appear successively in the raster plot in the whole population [e.g., see the top panels of Fig. 4b2–b5).
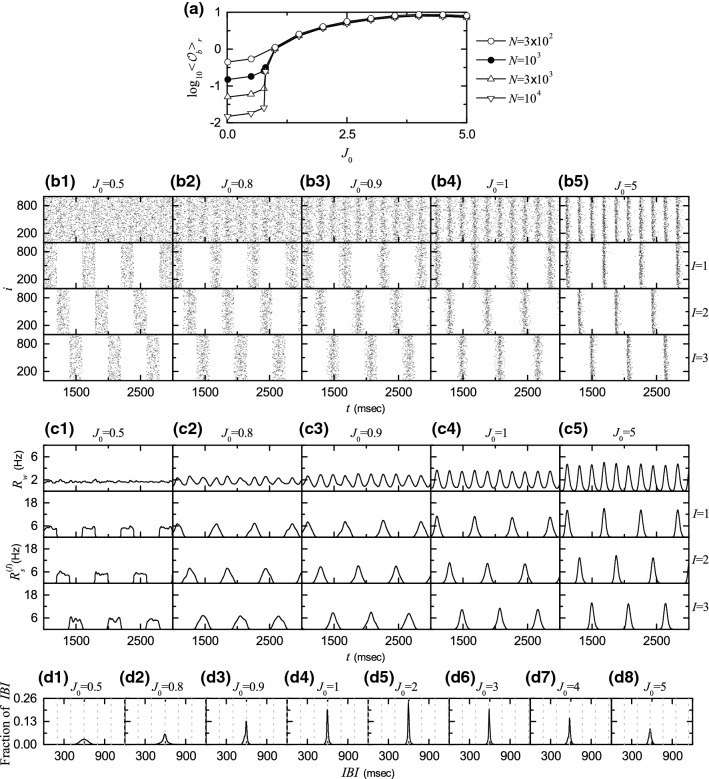
Fig. 4.
Emergence of 3-cluster burst synchronization. a Plots of thermodynamic bursting order parameter versus the average coupling strength . 3-cluster desynchronization for : b1 raster plots of burst onset times in the whole population and in the Ith cluster (I = 1, 2, and 3), and c1 IWPBR of the whole population and ISPBR of the Ith cluster (I = 1, 2, and 3). 3-cluster burst synchronization for various values of : b2–b5 raster plots of burst onset times in the whole population and in the Ith cluster (I = 1, 2, and 3), and c2–c5 IWPBR of the whole population and ISPBR of the Ith cluster (I = 1, 2, and 3). d1–d8 IBI histograms for various values of . In d1, vertical dotted lines denote integer multiples of the cluster period , and in d2–d8 vertical dotted lines represent integer multiples of the global period of ()
Recently, we introduced a realistic bursting order parameter, based on , for describing transition from desynchronization to burst synchronization (Kim and Lim 2015b). The mean square deviation of ,
| 10 |
plays the role of an order parameter ; the overbar represents time average. This bursting order parameter may be regarded as a thermodynamic measure because it concerns just the macroscopic IWPBR without any consideration between and microscopic individual burst onset times. As N (number of HR neurons in the whole population) is increased, exhibits more regular oscillations in the case of burst synchronization, while it becomes more stationary in the case of desynchronization. Hence, in the thermodynamic limit of , the bursting order parameter , representing time-averaged fluctuations of from its time-averaged mean, approaches a non-zero (zero) limit value for the synchronized (desynchronized) state. In this way, the bursting order parameter can determine whether population states are synchronized or desynchronized.
Figure 4a shows a plot of versus . In each realization, we discard the first time steps of a trajectory as transients for msec, and then we numerically compute by following the trajectory for ms. Hereafter, denotes an average over 20 realizations. For , the bursting order parameter tends to zero with increasing N. On the other hand, when passing a transition to burst synchronization occurs, because approaches a non-zero limit value. Consequently, for burst synchronization occurs in the whole population due to a constructive role of synaptic inhibition to favor the burst synchronization.
We consider specific examples of cluster desynchronization and cluster burst synchronization. Figure 4b1, c1 show an example of cluster desynchronization for , as in the case of in Fig. 2b1, b2. For this cluster desynchronized state, burst onset times are completely scattered in bursting bands in each cluster, the corresponding ISPBR exhibit square-wave oscillations, and the IWPBR ] in the whole population becomes nearly stationary. Four examples for cluster burst synchronization are given for 0.9, 1.0 and 5.0. In the case of , bursting stripes begin to appear successively in the raster plot of burst onset times in the whole population (see the top panel of Fig. 4b2), and the corresponding IWPBR also begins to exhibit small-amplitude regular oscillations, as shown in the top panel of Fig. 4c2. The whole population is segregated into 3 clusters. Bursting stripes in each cluster appear successively every 3rd global cycle of , as shown in the 1, 2, and 3 panels of Fig. 4b2. The ISPBRs of the Ith clusters are shown in the 1, 2, and 3 panels of Fig. 4c2, respectively. They exhibit regular oscillations with the sub-population bursting frequency Hz) which corresponds to [: whole-population bursting frequency of ]. With increasing cluster burst synchronization gets better, as shown in the cases of 1.0, and 5.0. Bursting stripes in the raster plots (in the whole population and the clusters) become clearer (i.e., less smeared) (see Fig. 4b3–b5) and the amplitudes of and become larger (see Fig. 4c3–c5).
We also investigate individual bursting behaviors of HR neurons in terms of IBIs. Figure 4d1–d8 show IBI histograms for various values of . Each IBI histogram is composed of IBIs and the bin size for the histogram is 2.5 ms. Vertical dotted lines in the IBI histograms represent integer multiples of the cluster period ; in the case of cluster burst synchronization, the value of is equal to that of the global period of . In all cases where 3-cluster states exist, single peaks appear at , and IBIs are localized in a range of , as in the case of in Fig. 2f. In the desynchronized case of its IBI histogram is broad due to incoherent synaptic inputs. When passing the lower threshold , a transition to burst synchronization occurs, and then IBI histograms begin to be sharp due to coherent synaptic inputs. As is further increased, the peaks of the IBI histograms become sharper due to increase in coherent synaptic inputs. A maximum height of the peak appears near , and then it begins to decrease. Thus, the peak for becomes broader, because is close to an intermediate threshold ) where break-up of 3 clusters occurs (this point is explained in details in the following subsection).
Break-up of cluster burst synchronization via intercluster hoppings
As is further increased and passes an intermediate threshold ), 3-cluster burst synchronization breaks up into (non-cluster) burst synchronization without dynamical clusterings through intercluster hoppings. As an example, we consider the case of .
Figure 5a shows the IBI histogram with two peaks at and [ msec): global period of ]. For only single peak appears at [i.e., individual HR neurons exhibit burstings every 3rd global cycle of ], as shown in Fig. 4d2–d8. As approaches the threshold , this peak becomes broad along with decrease in its height. After passing , individual HR neurons begin to exhibit burstings intermittently at a 4th cycle of through burst skipping at its 3rd cycle. Here, 3rd and 4th cycles of refer to ones counted just after the latest burstings (e.g., see the example given below). An example for the 5th neuron in the 1st () cluster is given in Fig. 5b. A burst skipping occurs in the small box in the gray region [corresponding to a 3rd cycle of ], and then another bursting appears at its 4th cycle; for reference, is shown on the top panel and vertical dotted lines represent global cycles of . Thus, in addition to the major peak at , a new minor peak appears at in Fig. 5a. Then, some fraction of IBIs with larger than appear (i.e., late burstings occur) in contrast to the case of cluster burst synchronization where IBIs are localized in a range of . In this case, delocalization of IBIs occurs by crossing just the right boundary (corresponding to ), which is in contrast to the case of where both the left and the right boundaries are crossed.
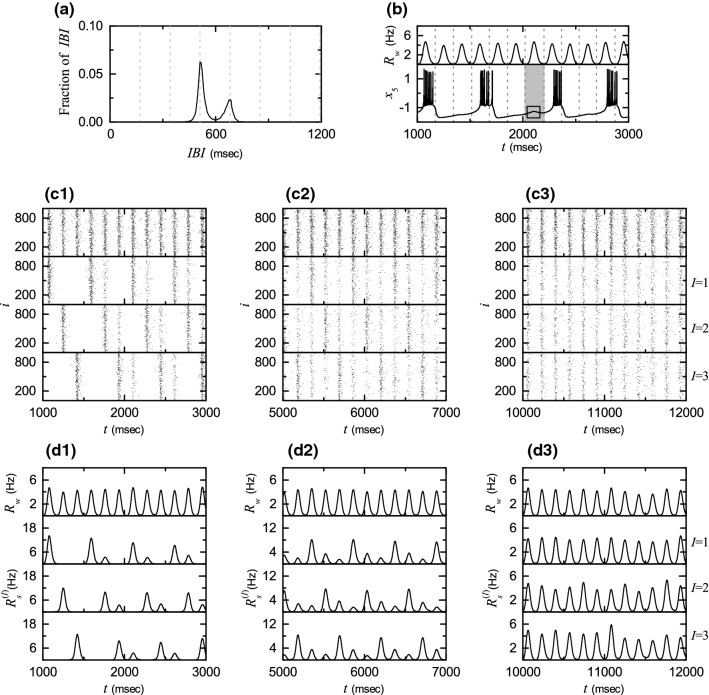
Fig. 5.
Break-up of 3 clusters via intercluster hoppings for . a Double-peaked IBI histogram. Vertical dotted lines denote integer multiples of the global period msec) of . b Time series of membrane potential for the 5th HR neuron in the 1st () cluster. For reference, the IWPBR of the whole population is shown in the top panel. The 5th HR neuron exhibits a bursting at the 4th cycle of rather than at its 3rd cycle where it shows a hopping instead of bursting, as shown inside the small box in the gray region (corresponding to the 3rd cycle). Sequential long-term raster plots of burst onset times in the whole population and in the Ith cluster (1, 2, and 3) in c1 the early, c2 the intermediate, and c3 the final stages. IWPBR of the whole population and ISPBR of the Ith cluster (1, 2, and 3) in the d1 early, d2 the intermediate, and d3 the final stages
Due to appearance of delocalized IBIs larger than (i.e., because of occurrence of late burstings), only forward intercluster hoppings occur, in contrast to the case of where both forward and backward intercluster hoppings take place due to occurrence of late and early burstings, respectively (see Fig. 3b1–b3). Forward intercluster hoppings between the 3 clusters may be well seen in sequential long-term raster plots of burst onset times in the whole population and in the Ith (, 2, and 3) clusters. Figure 5c1–c3 show such raster plots, corresponding to (c1) the early, (c2) the intermediate, and (c3) the final stages. For the initial stage in Fig. 5c1, individual HR neurons in the Ith cluster make intermittent intercluster hoppings to the nearest neighboring th cluster [i.e., neurons in the Ith cluster exhibit intermittent burstings at a 4th cycle of (along with regular burstings of neurons in the th cluster) due to burst skipping at its 3rd cycle]. As a result, additional bursting stripes (composed of intermittent burstings occurring at a 4th cycle of due to burst skipping at its 3rd cycle) appear next to the regular bursting stripes in the raster plot for the Ith cluster. These additional bursting stripes in the Ith cluster are vertically aligned with regular bursting stripes in the th cluster. In this way, intermittent hoppings from the Ith to the th clusters occur.
For the intermediate stage in Fig. 5c2, one more step occurs for the intercluster hoppings due to a 2nd burst skipping, and hence intercluster hoppings occur from the Ith cluster to the th cluster (due to a 1st burst skipping) and then to the th cluster (due to a 2nd burst skipping). Consequently, two successive additional bursting stripes (consisting of intermittent burstings occurring at a 4th cycle of due to the 1st and 2nd burst skippings) appear next to the regular bursting stripes in the raster plot in the Ith cluster. These two additional bursting stripes are vertically aligned with regular bursting stripes in the th and the th clusters. Consequently, for each cluster, bursting stripes appear at every cycle of in the raster plot, like the case of whole population, although additional bursting stripes (formed due to burst skippings) are still sparse (i.e., their densities are low in comparison with those of regular bursting stripes).
As the time t is further increased, a 3rd burst skipping may also occur, and then another intercluster hopping from the th to the Ith clusters occurs (i.e., return to the original Ith cluster occurs due to a 3rd burst skipping). In this way, intercluster hoppings occur in a cyclic way (II) due to successive burst skippings. After a sufficiently long time, in the final stage in Fig. 5c3, intercluster hoppings between clusters are more and more intensified, which leads to complete break-up of clusters. As a result, density of all bursting stripes becomes nearly the same, independently of 2, and 3. We also note that, in spite of break-up of clusters, burst synchronization persists in the whole population, because bursting stripes appear successively in the rater plot in the whole population.
Figure 5d1–d3 show the IWPBR and the ISPBR , corresponding to the above raster plots in Fig. 5c1–c3. In the initial stage in Fig. 5d1, smaller-amplitude oscillations [corresponding to lower-density additional bursting stripes appearing due to burst skippings at regular 3rd cycles of ] appear next to the regular oscillations [occurring at every 3rd cycle of ] in each Ith (, 2, and 3) case. In the intermediate stage in Fig. 5d2, one more step for intercluster hoppings occurs due to 2nd burst skippings, and hence two successive smaller-amplitude oscillations appear next to the regular oscillations in each Ith (, 2, and 3) case. Then, for each Ith cluster makes oscillations at every cycle of , although its amplitudes vary depending on the cycles of . As the time t is further increased, these amplitudes tend to become nearly the same due to intensified intercluster hoppings, as shown in Fig. 5d3 for the final stage. Consequently, all the ISPBRs become nearly the same as the IWPBR , independently of I, because of complete break-up of clusters.
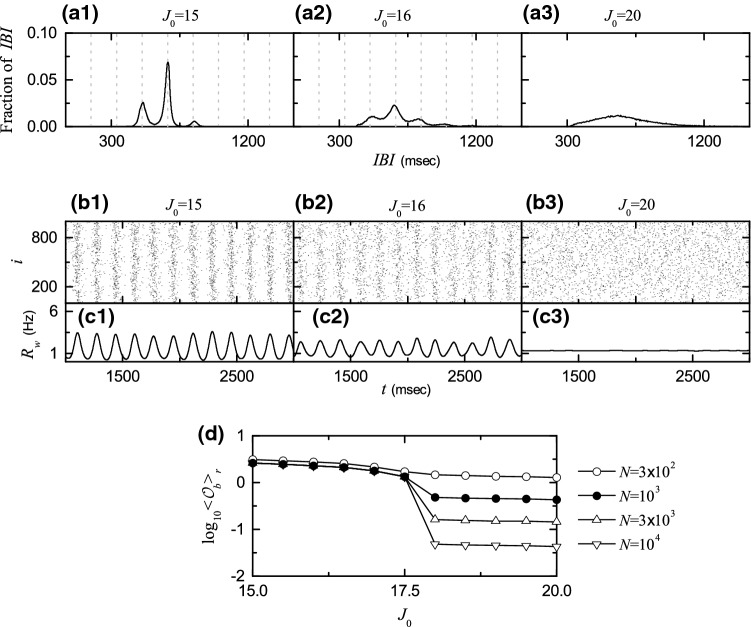
So far, we consider the case of where (non-cluster) burst synchronization without dynamical clusterings appears via intercluster hoppings which occur due to burst skippings. With increase in from 10, another type of bursting skippings begin to occur at 4th cycles of , in addition to the above skippings at 3rd cycles for . Figure 6a1 shows the IBI histogram for . When compared with the IBI histogram for in Fig. 5a, the height of the peak at is so much increased, and hence its height becomes higher than that of the decreased peak at . As a result, the peak at becomes a major one. Furthermore, a new smaller peak appears at due to intermittent burst skippings at 4th cycles of . Thus, the IBI histogram for consists of 3 peaks at , , and . Figure 6b1, c1 show the raster plot in the whole population and the corresponding IWPBR kernel estimate for . In comparison with the case of in Fig. 5c3, d3, due to a destructive role of synaptic inhibition to spoil the burst synchronization, burst stripes become more smeared, and amplitudes of become smaller. Consequently, the degree of (non-cluster) burst synchronization becomes worse.
Fig. 6.
Transition from burst synchronization to desynchronization. IBI histograms for a1 15, a2 16, and a3 20. Vertical dotted lines in a1, a2 denote integer multiples of the global period of . Raster plots of burst onset times for b1 15, b2 16, and b3 20. IWPBR of the whole population for c1 15, c2 16, and c3 20. d Plots of thermodynamic bursting order parameter versus the average coupling strength
As is further increased, this kind of tendency for burst skippings is intensified. As an example, see the case of . The IBI histogram is shown in Fig. 6a2. In comparison with the IBI histogram in Fig. 6a1 for heights of both peaks at and are decreased, while the height of the peak at is a little increased. Additionally, a new small peak appears at . In this way, the IBI distribution becomes broad. When compared with the case of , bursting stripes become more smeared and amplitudes of are decreased, as shown in Fig. 6b2, c2, respectively. In this way, with increasing (non-cluster) burst synchronization becomes more and more worse.
Eventually, when passing a higher threshold , a transition to desynchronization occurs. Consequently, for desynchronized states appear, as shown in the case of . In this case, the IBI histogram is so broad and has just a central maximum via merging of peaks. Burst onset times in the raster plot are completely scattered without forming any bursting stripes, and the corresponding IWPBR kernel estimate becomes nearly stationary (see Fig. 6b3, c3, respectively). This type of transition from burst synchronization to desynchronization may also be well described in terms of the bursting order parameter of Eq. (10). Figure 6d shows a plot of versus . As N is increased, the bursting order parameter approaches a non-zero limit value for , and hence (non-cluster) burst synchronization occurs. On the other hand, when passing a transition to (non-cluster) desynchronization occurs, because tends to zero with increasing N. Consequently, for (non-cluster) desynchronized states appear due to a destructive role of synaptic inhibition to spoil the burst synchronization.
Characterization of burst synchronization
We characterize burst synchronization in the range of by employing a statistical-mechanical bursting measure (Kim and Lim 2015b). In the case of burst synchronization, bursting stripes appear successively in the raster plot of burst onset times in the whole population. The bursting measure of the ith bursting stripe is defined by the product of the occupation degree of burst onset times (representing the density of the ith bursting stripe) and the pacing degree of burst onset times (denoting the degree of phase coherence between burst onset times in the ith bursting stripe):
| 11 |
The occupation degree of burst onset times in the ith bursting stripe is given by the fraction of bursting neurons:
| 12 |
where is the number of bursting neurons in the ith bursting stripe. In the case of full burst synchronization, all bursting neurons exhibit burstings in each bursting stripe in the raster plot of burst onset times, and hence the occupation degree in each bursting stripe becomes 1. On the other hand, in the case of sparse burst synchronization, only some fraction of bursting neurons show burstings in each bursting stripe, and hence the occupation degree becomes less than 1. In our case of burst synchronization, in the range of , and hence sparse burst synchronization occurs.
The pacing degree of burst onset times in the ith bursting stripe can be determined in a statistical-mechanical way by taking into account their contributions to the macroscopic IWPBR . Central maxima of between neighboring left and right minima of coincide with centers of bursting stripes in the raster plot. A global cycle starts from a left minimum of , passes a maximum, and ends at a right minimum. An instantaneous global phase of was introduced via linear interpolation in the region forming a global cycle [for more details, refer to Eqs. (14) and (15) in (Kim and Lim 2015b)]. Then, the contribution of the kth microscopic burst onset time in the ith bursting stripe occurring at the time to is given by , where is the global phase at the kth burst onset time [i.e., ]. A microscopic burst onset time makes the most constructive (in-phase) contribution to when the corresponding global phase is (), while it makes the most destructive (anti-phase) contribution to when is . By averaging the contributions of all microscopic burst onset times in the ith bursting stripe to , we obtain the pacing degree of burst onset times in the ith stripe:
| 13 |
where is the total number of microscopic burst onset times in the ith stripe. By averaging of Eq. (11) over a sufficiently large number of bursting stripes, we obtain the realistic statistical-mechanical bursting measure , based on the IWPBR :
| 14 |
We follow bursting stripes in each realization and get via average over 20 realizations.
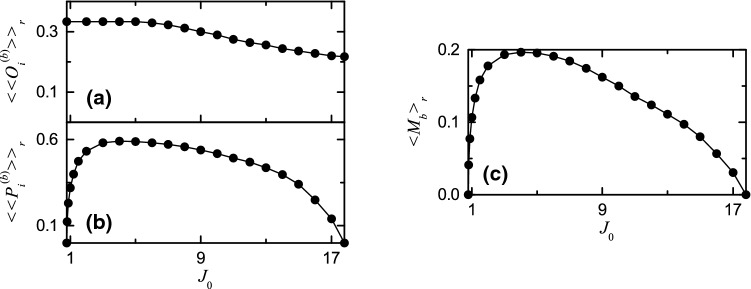
Figure 7a–c show the average occupation degree , the average pacing degree , and the statistical-mechanical bursting measure , respectively. In the case of 3-cluster burst synchronization in the range of , (denoting the density of bursting stripes in the raster plot) is , because individual HR neurons exhibit burstings every 3rd cycle of . However, for , decreases slowly to a limit value , due to burst skippings (e.g., see IBI histograms Fig. 6a1, a2). The average pacing degree represents well the average degree of phase coherence in bursting stripes in the raster plot of burst onset times (e.g., see Figs. 4b2–b8, 6b1, b2). As is increased from , increases rapidly to a maximum for (i.e., the degree of 3-cluster burst synchronization increases rapidly after its appearance). Then, for it decreases to zero at the higher transition point (i.e., decrease in begins a little before break-up of 3-cluster burst synchronization for , and then decreases smoothly to zero, due to complete overlap of sparse bursting stripes). Through averaging product of the occupation and the pacing degrees of burst onset times over sufficiently large number of bursting stripes in each realization, the statistical-mechanical bursting measure is obtained. Since the variation in is small, behaves like the case of . With increasing from , increases rapidly to a maximum for and then, for it decreases slowly to zero at the higher transition point
Fig. 7.
Characterization of burst synchronization. Plots of a the average occupation degree , b the average pacing degree , and c the statistical-mechanical bursting measure versus the average coupling strength
Effects of stochastic noise on cluster burst synchronization
In this section, we study the effects of stochastic noise on burst synchronization by changing the noise intensity D. First, we obtain the state diagram in the plane, which is shown in Fig. 8. Four types of population states exist. 3-cluster states appear in the gray region, denoted by C, on the left side. Also, burst synchronization occurs in the dark gray region, represented by BS, on the right side. In the intersection region, shaded in black and denoted by between the cluster and the burst synchronization regions, 3-cluster burst synchronization occurs. On the other hand, in the remaining regions of the cluster and the burst synchronization regions, cluster desynchronization and non-cluster burst synchronization occurs, respectively; these remaining regions are denoted by and respectively. Outside these cluster and burst synchronization regions, non-cluster desynchronization occurs in a region denoted by .
Fig. 8.
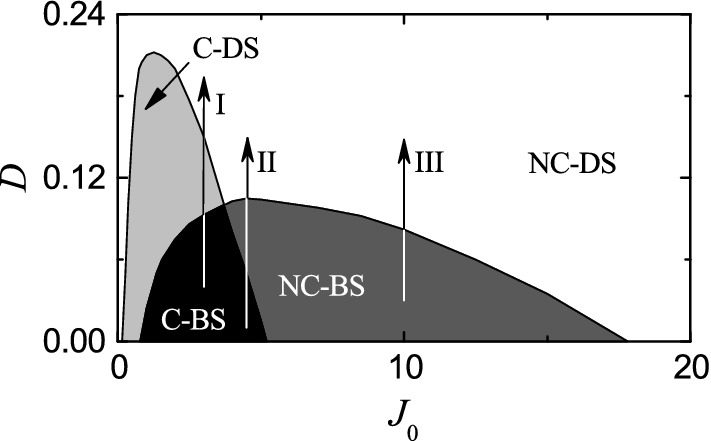
State diagram in the plane. Four types of population states exist. 3-cluster burst synchronization occurs in the black region, denoted by while non-cluster burst synchronization occurs in the dark gray region, represented by Cluster desynchronization appears in the gray region, denoted by while non-cluster desynchronization appears in the remaining white region, represented by Vertical arrows (I, II, and III) represent routes for , 4.5, and 10 where effects of stochastic noise are studied
Next, we investigate the effects of noise on 3-cluster burst synchronization and intercluster hoppings (studied in the above section for ) by increasing the noise intensity D along the 3 routes for 3, 4.5, and 10, denoted by vertical arrows (I, II, and III) in the state diagram of Fig. 8.
Effects of noise in the route I:
Figure 9 shows results on the noise effects in the 1st route I for . For a 3-cluster burst synchronization () occurs. As D is increased and passes a lower threshold , a transition to desynchronization occurs, which may be described in terms of the bursting order parameter of Eq. (10). Figure 9a shows a plot of versus D. With increasing N, the bursting order parameter approaches a non-zero limit value for , and hence burst synchronization occurs. On the other hand, when passing a transition to desynchronization occurs, because tends to zero, as N is increased. Consequently, for desynchronized states appear due to a destructive role of noise to spoil the burst synchronization.
Fig. 9.
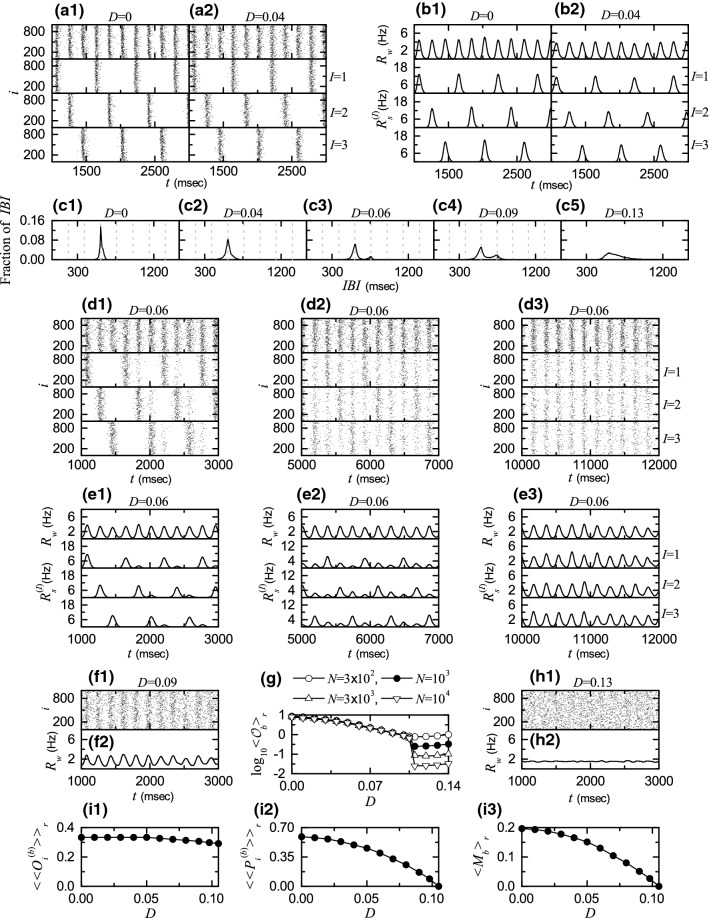
Noise effect in the 1st route for . a Plots of thermodynamic bursting order parameter versus the noise intensity D. b1–b5 Raster plots of burst onset times in the whole population and in the I th cluster (, 2, and 3) for various values of D. c1–c5 IWPBRs of the whole population and ISPBRs of the Ith cluster ( 2, and 3) for various values of D. and : d raster plots of burst onset times in the whole population and in the I th cluster (, 2, and 3) and e IWPBR of the whole population and ISPBRs of the Ith cluster ( 2, and 3). f1–f5 IBI histograms for various values of D. Vertical dotted lines in (f1–f4) and in f5 denote integer multiples of the global period of and the cluster period , respectively. : g delocalized IBI histogram for , sequential long-term raster plots of burst onset times in the whole population and in the Ith cluster (1, 2, and 3) in h1 the early, h2 the intermediate, and h3 the final stages, and IWPBR of the whole population and ISPBR of the Ith cluster (1, 2, and 3) in the i1 early, i2 the intermediate, and i3 the final stages. Plots of j1 the average occupation degree , j2 the average pacing degree , and j3 the statistical-mechanical bursting measure versus D
This kind of transition from 3-cluster burst synchronization to 3-cluster desynchronization () may also be well seen in the raster plots of burst onset times in the whole population and in the Ith clusters 1, 2, and 3). Figure 9b1–b5 show such raster plots for 0, 0.04, 0.06, 0.08, and 0.12, respectively. Their corresponding IWPBR and the ISPBR are also given in Fig. 9c1–c5 when 0, 0.04, 0.06, 0.08, and 0.12, respectively. For , bursting stripes (representing burst synchronization) appear successively in the raster plot in the whole population (see the top panel of Fig. 9b1), and the corresponding IWPBR exhibits a slow-wave oscillation with the whole-population frequency Hz), as shown in the top panel of Fig. 9c1. The whole population is segregated into 3 clusters (1, 2, and 3), which is well seen in the raster plots for the clusters (see the , 2, and 3 panels in Fig. 9b1). We note that bursting stripes in each cluster appear successively every 3rd cycle of , and the corresponding ISPBR exhibits a regular oscillation with the sub-population frequency . In this way, 3-cluster burst synchronization appears for . In this case, a single peak appears at [ msec): global period of ] in the IBI histogram, as shown in Fig. 9f1.
As D is increased from 0, the 3-cluster burst synchronization for persists, but its degree becomes more and more worse due to a destructive role of noise to spoil the burst synchronization. As shown in Fig. 9b2–b4, with increasing D, bursting stripes in the whole population and in each Ith (, 2, and 3) cluster become smeared more and more. Hence, amplitudes of and also decrease, as D is increased (see Fig. 9c2–c4). Peaks in the IBI histograms also become broader (along with decrease in their heights), with increasing D (see Fig. 9f2–f4).
Eventually, when passing a lower threshold , a transition to 3-cluster desynchronization occurs. Consequently, desynchronized 3-cluster states appear for . As an example, see the raster plots in Fig. 9b5 and the IWPBR and the ISPBR in Fig. 9c5 for . Burst onset times in the raster plot in the whole population seem to be completely scattered, and the corresponding IWPBR is nearly stationary. However, we note that, for bursting bands in the raster plot in each cluster are preserved (i.e., 3-clusters are preserved). For each cluster, burst onset times in each bursting band are nearly completely scattered (i.e., nearly desynchronized), and hence a square-wave-like oscillation occurs in each ISPBR . During the “silent” part (without burstings) for about , (which corresponds to the bottom part), while in the bursting band for about , rapidly increases to the nearly flat top, and then decreases rapidly; msec) corresponds to the average period of the square-wave oscillation. Through repetition of this process exhibits a square-wave-like oscillation. In this case, the IBI histogram in Fig. 9f5 becomes broader in comparison with those in the cases of burst synchronization, and its peak appears at msec (corresponding to the period P of the square-wave oscillation).
To examine the square-wave-like behavior more clearly, the number of HR neurons is increased from to . In this case, raster plots in the whole population and the clusters and their corresponding IWPBR and the ISPBR are shown in Fig. 9d, e, respectively. For the whole population, burst onset times are more completely scattered, and hence the corresponding IWPBR is more stationary. Moreover, for each cluster bursting bands in the raster plot show clearly the clustering structure, and hence the corresponding ISPBR shows square-wave oscillations more clearly. Thus, for each cluster burst onset times in bursting bands are completely scattered, and they show a desynchronized state. In this way, 3-cluster desynchronization appears, as D passes .
However, as D is further increased and passes a higher threshold , clusters are broken up via intercluster hoppings due to another destructive role of noise to break up the clusters. Hence, for non-cluster desynchronized states appear. As an example, we consider the case of . In this case, the IBI histogram is shown in Fig. 9g. Its peak is located at 572.5 msec). We note that some fraction of IBIs with larger than ( cluster period corresponding to ) appear (i.e., late burstings occur), as clearly shown in the inset of Fig. 9g. Thus, delocalization of IBIs occurs by crossing the right boundary (corresponding to ), which is in contrast to all the cases of cluster burst synchronization where IBIs are localized in a range of (see Fig. 9f1–f5).
Due to appearance of delocalized IBIs larger than (i.e., because of occurrence of late burstings), forward intercluster hoppings between the 3 clusters occur, which leads to break-up of 3 clusters. Similar to the case of in the absence of noise () (see Fig. 3b1–b3), intercluster hoppings between the 3 clusters may be well seen in sequential long-term raster plots of burst onset times in the whole population and in the Ith (, 2, and 3) clusters. Figure 9h1–h3 show such raster plots, corresponding to (h1) the early, (h2) the intermediate, and (h3) the final stages. As the time t is increased, forward intercluster hoppings occur in a cyclic way [II] due to occurrence of late burstings. In the final stage after a sufficiently long time, intercluster hoppings between clusters are more and more intensified, which leads to complete break-up of clusters. Consequently, burst onset times in the raster plots are completely scattered in a nearly uniform way, independently of 2, and 3, as shown in Fig. 9h3. Figure 9i1–i3 also show the IWPBR and the ISPBR (I = 1, 2, and 3), corresponding to the above raster plots in Fig. 9h1–h3. With increase in the time t, the initial square-wave oscillations in are transformed into nearly stationary ones, independently of I (see the final stage in Fig. 9i3). Thus, non-cluster desynchronized state appears for .
Figure 9j1–j3 show the average occupation degree of Eq. (12) (representing the average density of bursting stripes), the average pacing degree of Eq. (13) (denoting the average degree of phase coherence in bursting stripes), and the statistical-mechanical bursting measure of Eq. (14) (given by the product of occupation and pacing degrees), respectively, in the range of where 3-cluster burst synchronization occurs. Obviously, because 3-clusters persist for . Due to a destructive role of noise to spoil the burst synchronization, as D is increased from 0 to decreases smoothly from 0.581 to zero. Then, the statistical-mechanical bursting measure also makes a smooth decrease from 0.194 to 0, as in the case of , because is constant.
Effects of noise in the route II:
As is increased and passes a threshold , break-up of clusters in the desynchronized states (e.g., the above case of the route I case for ) no longer occurs. Instead, before a transition to desynchronization, break-up of clusters occurs in the burst-synchronized states. As an example, see the route II for in Fig. 8. Figure 10 shows results on the noise effects in the 2nd route II for . With increasing D, noise first breaks up clusters, and then a transition to desynchronization occurs due to another destructive role of noise to spoil the burst synchronization. Hence, the destructive roles of D is similar to those of , shown in Fig. 5 in the absence of noise ().
Fig. 10.
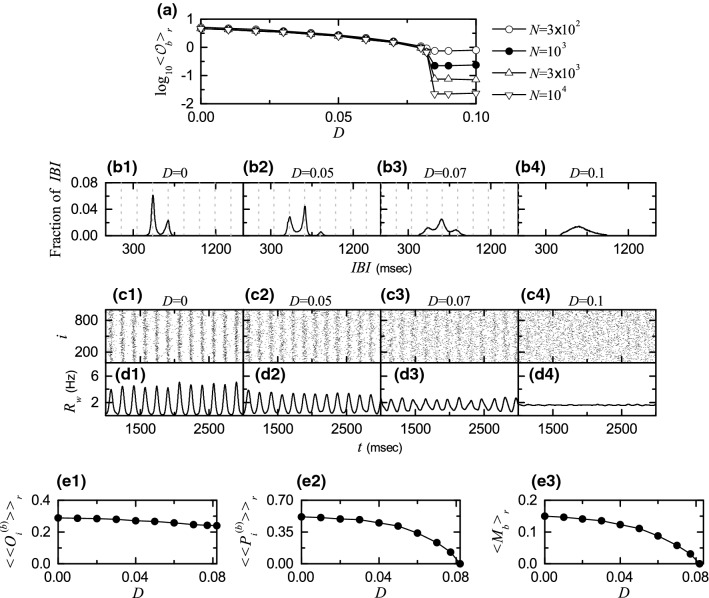
Noise effect in the 2nd route for . Raster plots of burst onset times in the whole population and in the Ith cluster (, 2, and 3) when a1 0 and a2 0.04. IWPBR of the whole population and ISPBR of the Ith cluster ( 2, and 3) for b1 0 and b2 0.04. c1–c5 IBI histograms for various values of D. Vertical dotted lines in c1–c4 denote the integer multiples of the global period of . : sequential long-term raster plots of burst onset times for the whole population and the clusters in d1 the early, d2 the intermediate, and d3 the final stages, and of the whole population and of the clusters in the e1 early, e2 the intermediate, and e3 the final stages. : f1 raster plot of burst onset times in the whole population and f2 of the whole population. g Plots of thermodynamic bursting order parameter versus the noise intensity D. For h1 raster plot of burst onset times in the whole population and h2 of the whole population. Plots of i1 the average occupation degree , i2 the average pacing degree , and i3 the statistical-mechanical bursting measure versus D
As in the 1st route I for , when appearance of 3-cluster burst synchronization () is well shown in the raster plots in the whole population and the clusters (, 2, and 3) (see Fig. 10a1) and their corresponding IWPBR and the ISPBR (see Fig. 10b1). For each cluster, bursting stripes appear every 3rd cycle of , which results in emergence of 3-cluster burst synchronization. In this case, the IBI histogram has a single peak at [ global period of ], as shown in Fig. 10c1. As D is increased, bursting stripes in the raster plots become smeared, due to a destructive role of noise to spoil the burst synchronization, and hence amplitudes of and are decreased (e.g., see Figs. 10a2, b2 for ). In this case, the IBI histogram has a broad single peak with lower height at , as shown in Fig. 10c2.
Eventually, as D passes a lower threshold , the IBI histogram begins to have a new minor peak at in addition to the major peak at , as shown in Fig. 10c3 for . Hence, individual HR neurons begin to exhibit burstings intermittently at a 4th cycle of via burst skipping at its 3rd cycle. Due to occurrence of late burstings via burst skippings, clusters become broken up via forward intercluster hoppings, as in the case of Fig. 5 for in the absence of noise (). As a result, non-cluster burst synchronization () without dynamical clusterings appears in the whole population. As an example, we consider the case of . Similar to the case in Fig. 5c1–c3, d1–d3, intercluster hoppings for are well seen in sequential long-term raster plots of burst onset times in the whole population and in the Ith (, 2, and 3) clusters (see Fig. 10d1–d3) and in the corresponding IWPBR of the whole population and the ISPBR of the clusters (see Figs. 10e1–e3). Here, Fig. 10d1, e1, , d2, e2, d3, e3 show the initial, the intermediate, and the final stages, respectively. With increasing the stage, intercluster hoppings are more and more intensified due to burst skippings, which results in complete break-up of clusters. Thus, after a sufficiently long time, raster plots in the clusters (, 2, and 3) are essentially the same, irrespectively of I. Although clusters are broken up, bursting stripes persist, and hence burst synchronization without dynamical clusterings occurs in the whole population.
With increasing D from 0.06, the degree of burst synchronization is decreased due to a destructive role of noise to spoil the burst synchronization. In the IBI histogram for , the height of the peak at is decreased, while the height of the peak at increases a little (see Fig. 10c4). Thus, the IBI histogram becomes broader, and burst skippings are enhanced. Consequently, intercluster hoppings are more intensified. Figure 10f1, f2 show the raster plot and the corresponding IWPBR for , respectively. In comparison with the case of , bursting stripes are more smeared and amplitudes of are decreased. Eventually, when passing a higher threshold , a transition from non-cluster burst synchronization to desynchronization () occurs.
The bursting order parameter of Eq. (10) may describe well a transition from burst synchronization to desynchronization. Figure 10g shows a plot of versus D. As N is increased, the bursting order parameter approaches a non-zero limit value for , and hence burst synchronization occurs. In contrast, when passing a transition to desynchronization occurs, because tends to zero, with increasing N. Consequently, for desynchronized states appear due to a destructive role of noise to spoil the burst synchronization. As an example of desynchronized state, we consider the case of . With increasing D the two peaks in the IBI histogram for are merged, and then it has a broad single maximum, as shown in Fig. 10c5 for . In this case, burst onset times are completely scattered in the raster plot, and the corresponding IWPBR is nearly stationary (see Figs. 10h1, h2).
Figure 10i1–i3 show the average occupation degree (denoting the average density of bursting stripes), the average pacing degree (representing the average degree of phase coherence in bursting stripes), and the statistical-mechanical bursting measure (given by the product of occupation and pacing degrees), respectively, in the range of where burst synchronization occurs. In the range of , 3-cluster burst synchronization appears, and hence However, as a result of break-up of clusters, for decreases slowly to a limit value ( for , due to bursting skippings. With increasing D from 0 to bursting stripes become more and more smeared due to a destructive role of noise to spoil the burst synchronization, and eventually they become completely overlapped for . Hence, in the range of , decreases smoothly from 0.587 to zero. Then, through product of the occupation and pacing degrees of burst onset times, the statistical-mechanical bursting measure also makes a smooth decrease from 0.196 to 0, like the case of , because variations in are small.
Effects of noise in the route III:
Finally, we consider the route III for in Fig. 8. Unlike the above cases of routes I and II, in the absence of noise () clusters are broken up due to burst skippings, and hence non-cluster burst synchronization () without dynamical clusterings appears. In this case, we investigate the noise effect on the non-cluster burst synchronization by increasing D, and due to destructive roles of noise, both intensified intercluster hoppings via burst skippings and smearing of bursting stripes are thus found.
As shown in the above cases, a transition from burst synchronization to desynchronization may be well described in terms of the bursting order parameter . Figure 11a shows a plot of versus D. With increasing N, the bursting order parameter converges to a non-zero limit value for . Consequently, burst synchronization occurs. On the other hand, when passing a transition to desynchronization occurs, because tends to zero, as N is increased. Accordingly, for desynchronized states () appear due to a destructive role of noise to spoil the burst synchronization.
Fig. 11.
Noise effect in the 3rd route for . a Plots of thermodynamic bursting order parameter versus the noise intensity D. IBI histograms for b1 0, b2 0.05, b3 0.07, and b4 0.1. Vertical dotted lines in (b1–b3) represent integer multiples of the global period of . Raster plots of burst onset times in the whole population when c1 0, c2 0.05, c3 0.07, and c4 0.1. IWPBR kernel estimates of the whole population for d1 0, d2 0.05, d3 0.07, and d4 0.1. Plots of e1 the average occupation degree , e2 the average pacing degree , and e3 the statistical-mechanical bursting measure versus D
Figure 11b1–b4 show the IBI histograms for 0, 0.05, 0.07, and 0.1, respectively. For , a minor peak appears at , in addition to the major peak at . Hence, individual HR neurons exhibit burstings intermittently at a 4th cycle of via burst skipping at its 3rd cycle. Due to this type of burst skippings, intercluster hoppings occur between clusters, and the clusters become broken up. Thus, for non-cluster burst synchronization without dynamical clusterings appears, in contrast to the above two cases.
With increasing D, the height of the peak at is increased, while the height of the peak at decreases. Furthermore, a small peak also appears at , as shown in Fig. 11b2 for . Hence, intercluster hoppings become intensified due to enhanced burst skippings. With further increase in D, these 3 peaks begin to show a tendency of merging (e.g., see Fig. 11b3 for ). In the desynchronized case of , these peaks are completely merged, and then the IBI histogram has a broad single peak.
Figure 11c1–c4 show raster plots for , 0.05, 0.07, and 0.1, respectively, and their corresponding IWPBR are also shown in Fig. 11d1–d4, respectively. As D is increased from 0, bursting stripes in the raster plots become more and more smeared, and amplitudes of also are decreased. Hence, with increasing D the degree of burst synchronization becomes worse, due to a destructive role of noise to spoil the burst synchronization.
Figure 11e1–e3 show the average occupation degree , the average pacing degree , and the statistical-mechanical bursting measure respectively, in the range of where burst synchronization (without dynamical clusterings) occurs. As D is increased from 0 to , burst skippings become intensified, and hence decreases smoothly from 0.289 (for ) to 0.241 (for ). With increasing D from 0 to bursting stripes become more and more smeared due to a destructive role of noise to spoil the burst synchronization, and eventually they become completely overlapped for . Hence, in the range of , decreases smoothly from 0.516 to zero. Then, through product of the occupation and pacing degrees of burst onset times, the statistical-mechanical bursting measure also makes a smooth decrease from 0.149 to 0, as in the case of , because variations in are small.
Summary and discussion
We investigated coupling-induced cluster burst synchronization by changing the average coupling strength in an inhibitory Barabási-Albert SFN of HR bursting neurons. For sufficiently small , non-cluster desynchronized states exist. But, when passing a critical point , the whole population has been found to be segregated into 3 clusters via a constructive role of synaptic inhibition to stimulate dynamical clusterings between individual burstings, and thus 3-cluster desynchronized states appear. Our SFN has no internal symmetries, and hence occurrence of clusters in our case has no relation with network topology, in contrast to the case of occurrence of clusters in networks with a certain degree of internal symmetries (Belykh and Hasler 2011).
We also note that, in the presence of 3 clusters, IBIs of individual HR neurons are localized in a region of [ cluster period (i.e., average time interval between appearance of successive clusters)]. Thus, we suggest the following criterion, based on the IBI histogram, for emergence of 3-cluster state. The cluster period is given by ; the peak of the IBI histogram appears at . Localization of IBIs in a region of leads to occurrence of 3-cluster state. For , delocalization of IBIs has been found to occur via crossing the right and/or the left boundaries (corresponding to and respectively), and thus late and/or early burstings appear. Through appearance of the late and/or early burstings, forward and/or backward intercluster hoppings have been found to occur, which leads to break-up of the 3 clusters.
As is further increased and passes a lower threshold ), a transition to 3-cluster burst synchronization has been found to occur due to another constructive role of synaptic inhibition to favor population synchronization. In each cluster, HR neurons make burstings every 3rd cycle of the IWPBR . Therefore, a single peak has been found to appear at [ global period of ] in the IBI histogram; in this case, . Furthermore, these burstings in each cluster have been found to exhibit burst synchronization. In this way, 3-cluster burst synchronization has been found to emerge. Burst synchronization in the whole population may be well visualized in the raster plot of burst onset times where bursting stripes appear in a regular and successive way, and the corresponding IWPBR shows regular oscillations with the whole-population bursting frequency . Moreover, cluster burst synchronization may also be seen well in the raster plot of burst onset times in each cluster, along with the corresponding ISPBR 1, 2, and 3) of the sub-populations. Bursting stripes in each cluster appear every 3rd cycle of , and the corresponding ISPBR exhibits regular oscillations with the sub-population bursting frequency .
However, with increase in and passing an intermediate threshold , a new peak has been found to appear at in the IBI histogram, in addition to the main peak at . In this case, delocalization of IBIs occurs through crossing the right boundary (corresponding to ), and thus late burstings appear. Hence, HR neurons have been found to exhibit intermittent forward hoppings between the 3 clusters, since they intermittently fire burstings at a 4th cycle of due to burst skipping rather than at its 3rd cycle. As a result of the intermittent forward intercluster hoppings, the 3 clusters have been found to be integrated into a single one, which was well shown in sequential long-term raster plots of burst onset times. Although the 3 clusters are broken up, burst synchronization has been found to persist in the whole population. As is further increased, forward intercluster hoppings have been found to be intensified due to enhanced burst skippings (e.g., for a 3rd peak appears at in the IBI histogram), and bursting stripes have also been found to be smeared more and more because of a destructive role of synaptic inhibition to spoil the burst synchronization. Eventually, as a higher threshold is passed, a transition to desynchronization has been found to occur. Then, burst onset times are completely scattered in the raster plot due to complete overlap between the bursting stripes, and the IWPBR becomes nearly stationary.
We also give a brief summary on the mechanism for cluster burst synchronization (explained above in details) by focusing on the role of synaptic inhibition. As the average coupling strength passes a critical point , a 3-cluster state appears due to a constructive role of synaptic inhibition to stimulate dynamical clustering (i.e., segregation of the whole population into 3 clusters) between individual burstings. In this case of 3-cluster state, IBIs of individual HR neurons are localized in a region between and ( cluster period). However, when passing an intermediate threshold value ), the 3 clusters are integrated into a single one due to a destructive role of synaptic inhibition to break up dynamical clustering. In this case, delocalization of IBIs occurs via crossing the right boundary (i.e., ), which leads to intermittent hoppings between the 3 clusters. Consequently, the 3-cluster state disappears. In this way, a 3-cluster state exists in an intermediate range of synaptic inhibition (i.e., ) through competition between constructive and destructive roles of synaptic inhibition. Next, we consider appearance of burst synchronization. When passing a lower threshold (), burst synchronization occurs due to a constructive role of synaptic inhibition to stimulate coherence between individual burstings (i.e., to favor population burst synchronization). However, when a higher threshold (), a desynchronized state appears due to a destructive role of synaptic inhibition to break up coherence between individual burstings (i.e., to spoil burst synchronization). Thus, burst synchronization appears in an intermediate range of synaptic inhibition in an intermediate range of synaptic inhibition (i.e., ) through competition between constructive and destructive roles of synaptic inhibition. Particularly, in the overlapped interval of (i.e., the interval for in the region, denoted , in Fig. 8), 3-cluster burst synchronization emerges (i.e., bust synchronization in each cluster occurs).
We have also studied the effects of stochastic noise on burst synchronization, and obtained a state diagram in the plane. By increasing the noise intensity D, we investigated the noise effects along the 3 routes I, II, and III for , 4.5, and 10, respectively. For (where 3-cluster burst synchronization occurs for ), two cases have been found to appear; the 1st (2nd) case occurs when . As the 1st example, we considered the 1st route I for . With increasing D, bursting stripes become just smeared (without intercluster hoppings) due to a destructive role of noise to spoil the cluster burst synchronization. Eventually when passing a lower threshold , a transition from the 3-cluster burst synchronization to desynchronization has been found to occur via complete overlap between the bursting stripes. As a result, desynchronized 3-cluster states appear for . In the presence of 3 clusters, IBIs have been found to be localized in a range of , independently of whether they are synchronized or desynchronized. However, as D is further increased and passes a higher threshold , delocalization has been found to occur via crossing the right boundary (corresponding to ), and thus late burstings appear. Due to appearance of such late burstings, forward intercluster hoppings have been found to occur between the 3 clusters, which results in break-up of the 3 clusters. As a result, (non-cluster) desynchronized states without dynamical clusterings appear for .
On the other hand, in the 2nd route II for , intercluster hoppings have been found to occur before desynchronization when passing a lower threshold , in contrast to the case of the 1st route. For , delocalization of IBIs has been found to occur because the IBI histogram has a new minor peak at in addition to the major peak at . In this case, individual HR neurons exhibit burstings intermittently at a 4th cycle of via burst skipping at its 3rd cycle. Due to occurrence of late burstings via burst skippings, clusters has been found to become broken up via forward intercluster hoppings between the 3 clusters, as in the case of in the absence of noise (). As a result, non-cluster burst synchronization without dynamical clusterings persists in the whole population, in contrast to the above 1st example. Then, a transition to (non-cluster) desynchronization has also been found to occur when passing a higher threshold , due to a destructive role of noise to spoil the burst synchronization. As a 3rd example, we considered the 3rd route III for (where (non-cluster) burst synchronization without dynamical clusterings exists for ). With increasing D from 0, both smearing and intercluster hoppings have been found to be intensified due to a destructive role of noise, and when passing a threshold , (non-cluster) desynchronized states have been found to occur.
As shown in these 3 examples, the stochastic noise plays destructive dual roles to spoil the burst synchronization and to break up clusters. We also note that, in the present work in a population of (self-firing) suprathreshold bursting neurons, noise makes just destructive effects on population states without showing any constructive role. These noise effects in the suprathreshold case are in contrast to those in previous works (Kim and Lim 2015a, 2018) on stochastic burst synchronization (SBS) in a population of (non-self-firing) subthreshold bursting neurons where SBS was found to appear in an intermediate range of noise intensity via competition between the constructive and the destructive roles of noise.
As a complex network, we also considered another Watts-Strogatz small-world network of inhibitory HR neurons (Watts and Strogatz 1998), and found emergence of cluster burst synchronization, as in the case of SFN. Hence, this kind of cluster burst synchronization seems to occur, independently of network architecture. In addition to the HR model of spike-driven burstings, we considered the Plant model of slow-wave burstings (Plant 1981; Longtin 1997). In the SFN of inhibitory Plant neurons, 2-cluster burst synchronization has also been found to occur. The number of clusters varies depending on the type of individual burstings. In the case of spike-driven burstings for the HR neurons, rapid hyperpolarization follows the active bursting phase of repetitive spikes (see Fig. 1c), and hence nearly whole silent phase may become available for burstings of HR neurons belonging to the other two clusters. On the other hand, in the case of slow-wave burstings for the Plant neurons, hyperpolarization occurs near the middle of the silent phase [see Fig. 1(a) in (Longtin 1997)], and thus burstings belonging to only one additional cluster may occur during the silent phase. In this way, occurrence of cluster burst synchronization in inhibitory networks seems to be generic, independently of types of constituent bursting neurons, although the number of clusters depend on specific types of individual burstings. We also considered an SFN of excitatory HR neurons. In the case of phase-attractive synaptic excitation, we found only full synchronization (i.e., all bursting neurons exhibit burstings in each bursting stripes) without any dynamical clusterings, in contrast to the case of phase-repulsive synaptic inhibition which is an essential factor for emergence of clusters.
Finally, we make a brief discussion on biological implications of cluster burst synchronization along with suggestion of a future experimental research direction. As is well known, burst synchronization is associated with neural information processes in health and disease. For example, large-scale burst synchronization emerges in the sleep spindle, related to memory consolidation, in the thalamus during the early stage of slow-wave sleep. Also, burst synchronization appears in abnormal pathological rhythms, associated with neural diseases (e.g., Parkinson’s disease, essential tremor, and epileptic seizure). In addition to burst synchronization, cluster synchronization (i.e., the whole population is segregated into synchronous clusters) has also been found in previous experimental, numerical or theoretical works in diverse coupled oscillators. It is expected that our results on cluster burst synchronization, associated with the above neural information processes in health and disease, would make some contributions for understanding mechanisms of emergence and break-up of cluster burst synchronization and effects of stochastic noise on cluster burst synchronization. Moreover, we hope a future experimental work to be performed in real neural systems for confirmation of our above expectations.
Acknowledgements
This research was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (Grant No. 20162007688).
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Sang-Yoon Kim, Email: sykim@icn.re.kr.
Woochang Lim, Email: wclim@icn.re.kr.
References
- Albert R, Barabási AL. Statistical mechanics of complex networks. Rev Mod Phys. 2002;74:47–97. [Google Scholar]
- Aronson DG, Golubitsky M, Krupa M. Coupled arrays of Josephson junctions and bifurcation of maps with symmetry. Nonlinearity. 1991;4:861–902. [Google Scholar]
- Barabási AL, Albert R. Emergence of scaling in random networks. Science. 1999;286:509–512. doi: 10.1126/science.286.5439.509. [DOI] [PubMed] [Google Scholar]
- Bassett DS, Bullmore E. Small-world brain networks. Neuroscientist. 2006;12:512–523. doi: 10.1177/1073858406293182. [DOI] [PubMed] [Google Scholar]
- Batista CAS, Batista AM, de Pontes JAC, Viana RL, Lopes SR. Chaotic phase synchronization in scale-free networks of bursting neuron. Phys Rev E. 2007;76:016218. doi: 10.1103/PhysRevE.76.016218. [DOI] [PubMed] [Google Scholar]
- Batista CAS, Batista AM, de Pontes JAC, Lopes SR, Viana RL. Bursting synchronization in scale-free networks. Chaos Soliton Fract. 2009;41:2220–2225. [Google Scholar]
- Batista CAS, Lopes SR, Viana RL, Batista AM. Delayed feedback control of bursting synchronization in a scale-free neuronal network. Neural Netw. 2010;23:114–124. doi: 10.1016/j.neunet.2009.08.005. [DOI] [PubMed] [Google Scholar]
- Batista CA, Lameu EL, Batista AM, Lopes SR, Pereira T, Zamora-Lopez G, Kurths J, Viana RL. Phase synchronization of bursting neurons in clustered small-world networks. Phys Rev E. 2012;86:016211. doi: 10.1103/PhysRevE.86.016211. [DOI] [PubMed] [Google Scholar]
- Bazhenov M, Timofeev I. Thalamocortical oscillations. Scholarpedia. 2006;1(6):1319. [Google Scholar]
- Belykh I, Hasler M. Mesoscale and clusters of synchrony in networks of bursting neurons. Chaos. 2011;21:016106. doi: 10.1063/1.3563581. [DOI] [PubMed] [Google Scholar]
- Belykh VN, Osipov GV, Petrov VS, Suykens JAK, Vandewalle J. Cluster synchronization in oscillatory networks. Chaos. 2008;18:037106. doi: 10.1063/1.2956986. [DOI] [PubMed] [Google Scholar]
- Bevan M, Magill P, Terman D, Bolam J, Wilson C. Move to the rhythm: oscillations in the subthalamic nucleus-external globus pallidus network. Trends Neurosci. 2002;25:525–531. doi: 10.1016/s0166-2236(02)02235-x. [DOI] [PubMed] [Google Scholar]
- Bonifazi P, Goldin M, Picardo MA, Jorquera I, Cattani A, Bianconi G, Represa A, Ben-Ari Y, Cossart R. GABAergic hub neurons orchestrate synchrony in developing hippocampal networks. Science. 2009;326:1419–1424. doi: 10.1126/science.1175509. [DOI] [PubMed] [Google Scholar]
- Brown P. Abnormal oscillatory synchronisation in the motor system leads to impaired movement. Cur Opin Neurobiol. 2007;17:656–664. doi: 10.1016/j.conb.2007.12.001. [DOI] [PubMed] [Google Scholar]
- Brunel N, Wang XJ. What determines the frequency of fast network oscillations with irregular neural discharges? I. Synaptic dynamics and excitation-inhibition balance. J Neurophysiol. 2003;90:415–430. doi: 10.1152/jn.01095.2002. [DOI] [PubMed] [Google Scholar]
- Bullmore E, Sporns O. Complex brain networks: graph theoretical analysis of structural and functional systems. Nat Rev Neurosci. 2009;10:186–198. doi: 10.1038/nrn2575. [DOI] [PubMed] [Google Scholar]
- Butera RJ, Rinzel J, Smith JC. Models of respiratory rhythm generation in the pre-Botzinger complex. I. Bursting pacemaker neurons. J Neurophysiol. 1999;82:382–397. doi: 10.1152/jn.1999.82.1.382. [DOI] [PubMed] [Google Scholar]
- Buzsáki G, Geisler C, Henze DA, Wang XJ. Interneuron diversity series: circuit complexity and axon wiring economy of cortical interneurons. Trends Neurosci. 2004;27:186–193. doi: 10.1016/j.tins.2004.02.007. [DOI] [PubMed] [Google Scholar]
- Chay TR, Keizer J. Minimal model for membrane oscillations in the pancreatic -cell. Biophys J. 1983;42:181–190. doi: 10.1016/S0006-3495(83)84384-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chik DTW, Coombes S, Wang ZD. Clustering through postinhibitory rebound in synaptically coupled neurons. Phys Rev E. 2004;70:011908. doi: 10.1103/PhysRevE.70.011908. [DOI] [PubMed] [Google Scholar]
- Chklovskii DB, Mel BW, Svoboda K. Cortical rewiring and information storage. Nature. 2004;431:782–788. doi: 10.1038/nature03012. [DOI] [PubMed] [Google Scholar]
- Connors BW, Gutnick MJ. Intrinsic firing patterns of diverse neocortical neurons. Trends Neurosci. 1990;13:99–104. doi: 10.1016/0166-2236(90)90185-d. [DOI] [PubMed] [Google Scholar]
- Coombes S, Bressloff PC, editors. Bursting: the genesis of rhythm in the nervous system. Singapore: World Scientific; 2005. [Google Scholar]
- Del Negro CA, Hsiao CF, Chandler SH, Garfinkel A. Evidence for a novel bursting mechanism in rodent trigeminal neurons. Biophys J. 1998;75:174–182. doi: 10.1016/S0006-3495(98)77504-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dhamala M, Jirsa V, Ding M. Transitions to synchrony in coupled bursting neurons. Phys Rev Lett. 2004;92:028101. doi: 10.1103/PhysRevLett.92.028101. [DOI] [PubMed] [Google Scholar]
- Duan L, Fan D, Lu Q. Hopf bifurcation and bursting synchronization in an excitable systems with chemical delayed coupling. Cogn Neurodyn. 2013;7:341–349. doi: 10.1007/s11571-012-9237-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eguíluz VM, Chialvo DR, Cecchi GA, Baliki M, Apkarian AV. Scale-free brain functional networks. Phys Rev Lett. 2005;94:018102. doi: 10.1103/PhysRevLett.94.018102. [DOI] [PubMed] [Google Scholar]
- Elson RC, Selverston AI, Huerta R, Rulkov NF, Rabinovich MI, Abarbanel HDI. Synchronous behavior of two coupled biological neurons. Phys Rev Lett. 1998;81:5691–5695. [Google Scholar]
- Felleman DJ, Van Essen DC. Distributed hierarchical processing in the primate cerebral cortex. Cereb Cortex. 1991;1:1–47. doi: 10.1093/cercor/1.1.1-a. [DOI] [PubMed] [Google Scholar]
- Ferrari FAS, Viana RL, Lopes SR, Stoop R. Phase synchronization of coupled bursting neurons and the generalized Kuramoto model. Neural Netw. 2015;66:107–118. doi: 10.1016/j.neunet.2015.03.003. [DOI] [PubMed] [Google Scholar]
- Fisher R, van Emde BW, Blume W, Elger C, Genton P, Lee P, Engel J. Epileptic seizures and epilepsy: definitions proposed by the International League Against Epilepsy (ILAE) and the International Bureau for Epilepsy (IBE) Epilepsia. 2005;46:470–472. doi: 10.1111/j.0013-9580.2005.66104.x. [DOI] [PubMed] [Google Scholar]
- Gais S, Plihal W, Wagner U, Born J. Early sleep triggers memory for early visual discrimination skills. Nat Neurosci. 2000;3:1335–1339. doi: 10.1038/81881. [DOI] [PubMed] [Google Scholar]
- Golomb D, Rinzel J. Clustering in globally coupled inhibitory neurons. Phys D. 1994;72:259–282. [Google Scholar]
- Gray CM, McCormick DA. Chattering cells: superficial pyramidal neurons contributing to the generation of synchronous oscillations in the visual cortex. Science. 1996;274:109–113. doi: 10.1126/science.274.5284.109. [DOI] [PubMed] [Google Scholar]
- Hammond C, Bergman H, Brown P. Pathological synchronization in Parkinson’s disease: networks, models and treatments. Trends Neurosci. 2007;30:357–364. doi: 10.1016/j.tins.2007.05.004. [DOI] [PubMed] [Google Scholar]
- Hindmarsh JL, Rose RM. A model of the nerve impulse using two first-order differential equations. Nature. 1982;296:162–164. doi: 10.1038/296162a0. [DOI] [PubMed] [Google Scholar]
- Hindmarsh JL, Rose RM. A model of neuronal bursting using three coupled first order differential equations. Proc R Soc Lond Ser B. 1984;221:87–102. doi: 10.1098/rspb.1984.0024. [DOI] [PubMed] [Google Scholar]
- Ivanchenko MV, Osipov GV, Shalfeev VD, Kurths J. Phase synchronization in ensembles of bursting oscillators. Phys Rev Lett. 2004;93:134101. doi: 10.1103/PhysRevLett.93.134101. [DOI] [PubMed] [Google Scholar]
- Izhikevich EM. Neural excitability, spiking and bursting. Int J Bifurcat Chaos. 2000;10:1171–1266. [Google Scholar]
- Izhikevich EM. Which model to use for cortical spiking neurons? IEEE Trans Neural Netw. 2004;15:1063–1070. doi: 10.1109/TNN.2004.832719. [DOI] [PubMed] [Google Scholar]
- Izhikevich EM. Bursting. Scholarpedia. 2006;1(3):1300. [Google Scholar]
- Izhikevich EM. Dynamical systems in neuroscience. Cambridge: MIT Press; 2007. [Google Scholar]
- Izhikevich EM, Desai NS, Walcott EC, Hoppensteadt FC. Bursts as a unit of neural information: selective communication via resonance. Trends Neurosci. 2003;26:161–167. doi: 10.1016/S0166-2236(03)00034-1. [DOI] [PubMed] [Google Scholar]
- Kaiser M, Martin R, Andras P, Young MP. Simulation of robustness against lesions of cortical networks. Eur J Neurosci. 2007;25:3185–3192. doi: 10.1111/j.1460-9568.2007.05574.x. [DOI] [PubMed] [Google Scholar]
- Kim SY, Lim W. Noise-induced burst and spike synchronizations in an inhibitory small-world network of subthreshold bursting neurons. Cogn Neurodyn. 2015;9:179–200. doi: 10.1007/s11571-014-9314-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim SY, Lim W. Thermodynamic order parameters and statistical-mechanical measures for characterization of the burst and spike synchronizations of bursting neurons. Phys A. 2015;438:544–559. [Google Scholar]
- Kim SY, Lim W. Effect of network architecture on burst and spike synchronization in a scale-free network of bursting neurons. Neural Netw. 2016;79:53–77. doi: 10.1016/j.neunet.2016.03.008. [DOI] [PubMed] [Google Scholar]
- Kim SY, Lim W. Effect of spike-timing-dependent plasticity on stochastic burst synchronization in a scale-free neuronal network. Cogn Neurodyn. 2018;12:315–342. doi: 10.1007/s11571-017-9470-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kinard TA, de Vries G, Sherman A, Satin LS. Modulation of the bursting properties of single mouse pancreatic -cells by artificial conductances. Biophys J. 1999;76:1423–1435. doi: 10.1016/S0006-3495(99)77303-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kiss IZ, Zhai Y, Hudson H. Predicting mutual entrainment of oscillators with experiment-based phase models. Phys Rev Lett. 2005;94:248301. doi: 10.1103/PhysRevLett.94.248301. [DOI] [PubMed] [Google Scholar]
- Krahe R, Gabbian F. Burst firing in sensory system. Nat Rev Neurosci. 2004;5:13–23. doi: 10.1038/nrn1296. [DOI] [PubMed] [Google Scholar]
- Lameu EL, Batista CAS, Batista AM, Larosz K, Viana RL, Lopes SR, Kurths J. Suppression of bursting synchronization in clustered scale-free (rich-club) neuronal networks. Chaos. 2012;22:043149. doi: 10.1063/1.4772998. [DOI] [PubMed] [Google Scholar]
- Langdon AJ, Breakspear M, Coombes S. Phase-locked cluster oscillations in periodically forced integrate-and-fire-or-burst neuronal populations. Phys Rev E. 2012;86:061903. doi: 10.1103/PhysRevE.86.061903. [DOI] [PubMed] [Google Scholar]
- Larimer P, Strowbridge BW. Nonrandom local circuits in the dentate gyrus. J Neurosci. 2008;28:12212–12223. doi: 10.1523/JNEUROSCI.3612-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee SH, Govindaiah G, Cox CL. Heterogeneity of firing properties among rat thalamic reticular nucleus neurons. J Physiol. 2007;582:195–208. doi: 10.1113/jphysiol.2007.134254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li X, Ouyang G, Usami A, Ikegaya Y, Sik A. Scale-free topology of the CA3 hippocampal network: a novel method to analyze functional neuronal assemblies. Biophys J. 2010;98:1733–1741. doi: 10.1016/j.bpj.2010.01.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lisman J. Bursts as a unit of neural information: making unreliable synapse reliable. Trends Neurosci. 1997;20:38–43. doi: 10.1016/S0166-2236(96)10070-9. [DOI] [PubMed] [Google Scholar]
- Llinás RL, Jahnsen H. Electrophysiology of mammalian thalamic neurons in vitro. Nature. 1982;297:406–408. doi: 10.1038/297406a0. [DOI] [PubMed] [Google Scholar]
- Longtin A. Autonomous stochastic resonance in bursting neurons. Phys Rev E. 1997;55:868–876. [Google Scholar]
- McCormick DA, Huguenard JR. A Model of the electrophysiological properties of thalamocortical relay neurons. J Neurophysiol. 1992;8:1384–1400. doi: 10.1152/jn.1992.68.4.1384. [DOI] [PubMed] [Google Scholar]
- Meng P, Wang Q, Lu Q. Bursting synchronization dynamics of pancreatic -cells with electrical and chemical coupling. Cogn Neurodyn. 2013;7:197–212. doi: 10.1007/s11571-012-9226-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miyakawa K, Okano T, Yamazaki S. Cluster synchronization in a chemical oscillator network with adaptive coupling. J Phy Soc Jpn. 2013;82:034005. [Google Scholar]
- Moon SJ, Cook KA, Rajendran K, Kevrekidis KG, Cisternas J, Liang CR. Coarse-grained clustering dynamics of heterogeneously coupled neurons. J Math Neurosci. 2015;5:2. doi: 10.1186/2190-8567-5-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morgan RJ, Soltesz I. Nonrandom connectivity of the epileptic dentate gyrus predicts a major role for neuronal hubs in seizures. Proc Natl Acad Sci USA. 2008;105:6179–6184. doi: 10.1073/pnas.0801372105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park C, Worth RM, Rubchinsky LL. Fine temporal structure of beta oscillations synchronization in subthalamic nucleus in Parkinson’s disease. J Neurophysiol. 2010;103:2707–2716. doi: 10.1152/jn.00724.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pereira T, Baptista M, Kurths J. Multi-time-scale synchronization and information processing in bursting neuron networks. Eur Phys J Spec Top. 2007;146:155–168. [Google Scholar]
- Pernarowski M, Miura RM, Kevorkian J. Perturbation techniques for models of bursting electrical activity in pancreatic -cells. SIAM J Appl Math. 1992;52:1627–1650c. [Google Scholar]
- Plant RE. Bifurcation and resonance in a model for bursting nerve cells. J Math Biol. 1981;11:15–32. doi: 10.1007/BF00275821. [DOI] [PubMed] [Google Scholar]
- Prado TdeL, Lopes SR, Batista CAS, Kurths J, Viana RL. Synchronization of bursting Hodgkin-Huxley-type neurons in clustered networks. Phys Rev E. 2014;90:032818. doi: 10.1103/PhysRevE.90.032818. [DOI] [PubMed] [Google Scholar]
- Rose RM, Hindmarsh JL. A model of a thalamic neuron. Proc R Soc Lond Ser B. 1985;225:161–193. doi: 10.1098/rspb.1985.0057. [DOI] [PubMed] [Google Scholar]
- Rinzel J. Bursting oscillations in an excitable membrane model. In: Sleeman BD, Jarvis RJ, editors. Lecture notes in mathematics. Berlin: Springer; 1985. pp. 304–316. [Google Scholar]
- Rinzel J. A formal classification of bursting mechanisms in excitable systems. In: Teramoto E, Yamaguti M, editors. Lecture notes in biomathematics. Berlin: Springer; 1987. pp. 267–281. [Google Scholar]
- San Miguel M, Toral R. Stochastic effects in physical systems. In: Martinez J, Tiemann R, Tirapegui E, editors. Instabilities and nonequilibrium structures VI. Dordrecht: Kluwer Academic Publisher; 2000. pp. 35–130. [Google Scholar]
- Scannell JW, Blakemore C, Young MP. Analysis of connectivity in the cat cerebral cortex. J Neurosci. 1995;15:1463–1483. doi: 10.1523/JNEUROSCI.15-02-01463.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scannell JW, Burns GAPC, Hilgetag CC, O’Neil MA, Young MP. The connectional organization of the cortico-thalamic system of the cat. Cereb Cortex. 1999;9:277–299. doi: 10.1093/cercor/9.3.277. [DOI] [PubMed] [Google Scholar]
- Sejnowski TJ, Destexhe A. Why do we sleep? Brain Res. 2000;886:208–223. doi: 10.1016/s0006-8993(00)03007-9. [DOI] [PubMed] [Google Scholar]
- Shi X, Lu Q. Firing patterns and complete synchronization of coupled Hindmarsh-Rose neurons. Chin Phys. 2005;14:77–85. [Google Scholar]
- Shi X, Lu Q. Burst synchronization of electrically and chemically coupled map-based neurons. Phys A. 2009;388:2410–2419. [Google Scholar]
- Shilnikov A, Cymbalyuk G. Transition between tonic spiking and bursting in a neuron model via the blue-sky catastrophe. Phys Rev Lett. 2005;94:048101. doi: 10.1103/PhysRevLett.94.048101. [DOI] [PubMed] [Google Scholar]
- Shimazaki H, Shinomoto S. Kernel bandwidth optimization in spike rate estimation. J Comput Neurosci. 2010;29:171–182. doi: 10.1007/s10827-009-0180-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Song S, Sjöström PJ, Reigl M, Nelson S, Chklovskii DB. Highly nonrandom features of synaptic connectivity in local cortical circuits. PLoS Biol. 2005;3:e68. doi: 10.1371/journal.pbio.0030068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sporns O. Networks of the brain. Cambridge: MIT Press; 2011. [Google Scholar]
- Sporns O, Honey CJ. Small worlds inside big brains. Proc Natl Acad Sci USA. 2006;103:19219–19220. doi: 10.1073/pnas.0609523103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sporns O, Tononi G, Edelman GM. Theoretical neuroanatomy: relating anatomical and functional connectivity in graphs and cortical connection matrices. Cereb Cortex. 2000;10:127–141. doi: 10.1093/cercor/10.2.127. [DOI] [PubMed] [Google Scholar]
- Sporns O, Chialvo DR, Kaiser M, Hilgetag CC. Organization, development and function of complex brain networks. Trends Cogn Sci. 2004;8:418–425. doi: 10.1016/j.tics.2004.07.008. [DOI] [PubMed] [Google Scholar]
- Steriade M, McCormick DA, Sejnowski TJ. Thalamocortical oscillations in the sleeping and aroused brain. Science. 1993;262:679–685. doi: 10.1126/science.8235588. [DOI] [PubMed] [Google Scholar]
- Stern EA, Jaeger D, Wilson CJ. Membrane potential synchrony of simultaneously recorded striatal spiny neurons in vivo. Nature. 1998;394:475–478. doi: 10.1038/28848. [DOI] [PubMed] [Google Scholar]
- Su H, Alroy G, Kirson ED, Yaari Y. Extracellular calcium modulates persistent sodium current-dependent burst-firing in hippocampal pyramidal neurons. J Neurosci. 2001;21:4173–4182. doi: 10.1523/JNEUROSCI.21-12-04173.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun X, Lei J, Perc M, Kurths J, Chen G. Burst synchronization transitions in a neuronal network of subnetworks. Chaos. 2011;21:016110. doi: 10.1063/1.3559136. [DOI] [PubMed] [Google Scholar]
- Tanaka G, Ibarz B, Sanjuan MA, Aihara K. Synchronization and propagation of bursts in networks of coupled map neurons. Chaos. 2006;16:013113. doi: 10.1063/1.2148387. [DOI] [PubMed] [Google Scholar]
- Taylor AF, Kapetanopoulos P, Whitaker BJ, Toth R, Bull L, Tinsley MR. Clusters and switchers in globally coupled photochemical oscillators. Phys Rev Lett. 2008;100:214101. doi: 10.1103/PhysRevLett.100.214101. [DOI] [PubMed] [Google Scholar]
- Uhlhaas PJ, Singer W. Neural synchrony in brain disorders: relevance for cognitive dysfunctions and pathophysiology. Neuron. 2006;52:155–168. doi: 10.1016/j.neuron.2006.09.020. [DOI] [PubMed] [Google Scholar]
- Varona P, Torres JJ, Abarbanel HDI, Rabinovych MI, Elson RC. Dynamics of two electrically coupled chaotic neurons: experimental observations and model analysis. Biol Cybern. 2001;84:91–101. doi: 10.1007/s004220000198. [DOI] [PubMed] [Google Scholar]
- van Vreeswijk C, Hansel D. Patterns of synchrony in neural networks with spike adaptation. Neural Comput. 2001;13:959–992. doi: 10.1162/08997660151134280. [DOI] [PubMed] [Google Scholar]
- Wang Q, Perc M, Duan Z, Chen G. Synchronization transitions on scale-free neuronal networks due to finite information transmission delays. Phys Rev E. 2009;80:026206. doi: 10.1103/PhysRevE.80.026206. [DOI] [PubMed] [Google Scholar]
- Wang QY, Murks A, Perc M, Lu QS. Taming desynchronized bursting with delays in the Macaque cortical network. Chin Phys B. 2011;20:040504. [Google Scholar]
- Wang Q, Chen G, Perc M. Synchronous bursts on scale-free neuronal networks with attractive and repulsive coupling. PLoS One. 2011;6:e15851. doi: 10.1371/journal.pone.0015851. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang H, Wang Q, Lu Q, Zheng Y. Equilibrium analysis and phase synchronization of two coupled HR neurons with gap junction. Cogn Neurodyn. 2013;7:121–131. doi: 10.1007/s11571-012-9222-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watts DJ, Strogatz SH. Collective dynamics of ‘small-world’ networks. Nature. 1998;393:440–442. doi: 10.1038/30918. [DOI] [PubMed] [Google Scholar]
- Wiedemann C. Neuronal networks: a hub of activity. Nat Rev Neurosci. 2010;11:74. doi: 10.1038/nrn2799. [DOI] [PubMed] [Google Scholar]
- Wisenfeld K, Colet P, Wisenfeld S. Synchronization transitions in a disordered Josephson series array. Phys Rev Lett. 1996;76:404–407. doi: 10.1103/PhysRevLett.76.404. [DOI] [PubMed] [Google Scholar]
- Womack MD, Khodakhah K. Active contribution of dendrites to the tonic and trimodal patterns of activity in cerebellar Purkinje neurons. J Neurosci. 2002;22:10603–10612. doi: 10.1523/JNEUROSCI.22-24-10603.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Young MP. The organization of neural systems in the primate cerebral cortex. Philos Trans R Soc. 1993;252:13–18. doi: 10.1098/rspb.1993.0040. [DOI] [PubMed] [Google Scholar]
- Young MP, Scannell JW, Burns GA, Blakemore C. Analysis of connectivity: neural systems in the cerebral cortex. Rev Neurosci. 1994;5:227–250. doi: 10.1515/revneuro.1994.5.3.227. [DOI] [PubMed] [Google Scholar]
- Yu H, Wang J, Deng B, Wei X, Wong YK, Chan WL, Tsang KM, Yu Z. Chaotic phase synchronization in small-world networks of bursting neurons. Chaos. 2011;21:013127. doi: 10.1063/1.3565027. [DOI] [PubMed] [Google Scholar]
- Zhang J, Yuan Z, Zhou T. Synchronization and clustering of synthetic genetic networks: a role for cis-regulatory modules. Phys Rev E. 2009;79:041903. doi: 10.1103/PhysRevE.79.041903. [DOI] [PubMed] [Google Scholar]