Multivariate Air Pollution Prediction Modeling with partial Missingness

Abstract

Missing observations from air pollution monitoring networks have posed a longstanding problem for health investigators of air pollution. Growing interest in mixtures of air pollutants has further complicated this problem, as many new challenges have arisen that require development of novel methods. The objective of this study is to develop a methodology for multivariate prediction of air pollution. We focus specifically on tackling different forms of missing data, such as: spatial (sparse sites), outcome (pollutants not measured at some sites), and temporal (varieties of interrupted time series). To address these challenges, we develop a novel multivariate fusion framework, which leverages the observed inter-pollutant correlation structure to reduce error in the simultaneous prediction of multiple air pollutants. Our joint fusion model employs predictions from the Environmental Protection Agency’s Community Multiscale Air Quality (CMAQ) model along with spatio-temporal error terms. We have implemented our models on both simulated data and a case study in South Carolina for 8 pollutants over a 28-day period in June 2006. We found that our model, which uses a multivariate correlated error in a Bayesian framework, showed promising predictive accuracy particularly for gaseous pollutants.

1. Introduction

Developing accurate exposure assessment for air pollution is a major concern in the majority of health effects studies of outdoor air pollution. This is because much of the data available for exposure assessment is from sparsely distributed air monitoring sites set up by national, state, and local governments to enforce air quality standards. Such objectives present many challenges for use of such data in health studies, as the locations of monitors are neither uniformly nor randomly distributed (Baxter et al. 2013). It is also the case that many sites vary in the quality and quantity of data observed so that time series of multiple pollutants may be interrupted at some sites and only partially observed at others (Ozkaynak et al. 2013).

For single pollutant measures at sites, it is common to adopt Kriging methods to provide smoothed estimates of exposures (Banerjee et al. 2014; Wong et al. 2004). Unfortunately, with sparse monitoring it is difficult to estimate the small-scale variation needed for the variogram, network topology can invalidate the assumption of the covariance properties, and the interpolation can have large errors at locations far from monitors. Others have discussed the limitations that sparse air monitoring networks present for interpolation methods and kriging (Diem et al. 2002), suggesting the use of additional information in a regression setting to improve predictive accuracy.

With the growing availability of GIS systems with regression capabilities, researchers have turned to land use regression (LUR) (Hoek et al. 2008), which utilizes surrogate exposure predictors within a regression formulation to allow prediction at poorly monitored sites or areas. While this additional information can be predictive, it is usually better to supplement geostatistical models with a selection of LUR predictors (Mercer et al. 2011). One potential issue with most applications of LUR is its lack of explicit consideration for spatial correlation. Spatial correlation can be a useful proxy for unknown or unspecified confounding variables that link areas in close proximity. Further, LUR models are often trained by splitting available observed data into a training and validation set; consequently, the same lack of data issue is present. Universal Kriging attempts to blend the benefits of the two previous methods by incorporating geographic variables into a spatial interpolation model, which has shown improved model accuracy (Mercer et al. 2011; Sampson et al. 2013; Pearce et al. 2009; Kim et al. 2010; Szpiro et al. 2013; Wang, Brunekreef, et al. 2016; Wang, Sampson, et al. 2016) as compared to ordinary kriging and LUR. While single variable Kriging can be extended to the multivariable case (Wackernagel 2003) via coregionalization (LMC), the selective nature of missingness and differential patterns of sparse observation across pollutants mean that estimation problems remain.

Alternative sources of air quality information have also been sought. One that has been commonly used is based on computer models of atmospheric dynamics with resulting predicted pollution levels. In the USA, the EPA has introduced the Community Multiscale Air Quality modeling system (CMAQ), which is based on a deterministic chemical transport model. This approach allows the prediction of pollutant levels across large areas and has resolution of 4 km or 12 km square grid cells.

The need to incorporate CMAQ with observed site measurements has led to the development of fusion models. These methods aim to leverage the completeness of modeled data with the more accurate monitoring data in order to improve exposure prediction results. Some authors (Berrocal et al. 2012; Lee et al. 2017; Berrocal et al. 2010) have utilized fusion models for univariate or bi-variate data settings within a Bayesian paradigm, while others (Friberg et al. 2016) have also developed univariate methods specifically focused on fusion of CMAQ and monitor data. These methods have been able to provide accurate estimates for air pollutants monitored widely in a geographic area; however, they have limited application or success in pollutants that are only monitored in a few locations.

A multivariate approach to fusion models extends the attempts of others to utilize all available resources to predict air pollution levels. Many pollutants in South Carolina have > 80% spatial missingness (Table 1), and while additional monitoring resources may be advisable, our method aims to provide exposure estimates where other methods cannot. The current standard for these sparsely monitored pollutants is modeled data, like CMAQ. Table 2 shows the Coefficient of Determination (R²) for raw CMAQ cell predictions where a monitoring location is present in June of 2006 across South Carolina, demonstrating our limited predictive capabilities with many of the pollutant health effects researchers aim to investigate (i.e. Carbon Monoxide, Sulfur Dioxide, PM2.5 Ammonium Ion, PM2.5 Sulfate Ion are all < 0.25).

Table 1.

Percent of monitoring stations recording at least one observation from June 1, 2006 to June 28, 2006 for each pollutant.

Pollutant	CO	O3	NO2	SO2	PM2.5	EC	SO4	NH4
No. Stations	6	26	14	18	23	2	9	4
Spatial Missingness Rate	88%	46%	71%	63%	53%	96%	81%	92%
Temporal Missingness Rate	0%	0%	0%	0%	0%	68%	0%	68%

Table 2.

Raw CMAQ R² fit for South Carolina in June of 2006.

R2	Pollutant
0.202	PM2.5 Ammonium Ion
0.056	Carbon Monoxide
0.632	PM2.5 Elemental Carbon
0.295	Nitrogen Dioxide
0.682	Ozone
0.664	PM2.5
0.251	PM2.5 Sulfate Ion
0.010	Sulfur Dioxide

The overarching objective of this research is to improve statistical methodologies for exposure assessment of air pollution. In this paper we focus specifically on addressing challenges posed by sparse site networks where we have spatial missingness (sparse sites), outcome missingness (pollutants not measured at some sites), and temporal missingness (varieties of interrupted time series). To address these problems, we illustrate a novel approach that extends current fusion model approaches to a multivariate setting in a Bayesian framework.

We implement jointly modeled pollutant concentration fields, predicting a suite of eight (8) pollutants simultaneously. Multivariate fusion models take advantage of the observed correlation structure between the pollutants in order to reduce error in estimation across all pollutants. To best illustrate our framework, we present a range of models with varied multivariate dependencies and evaluate their predictive accuracy.

The paper is structured as follows. First, we discuss data sources to be used in the fusion modeling (CMAQ and monitor sites). Sparse monitor data from South Carolina is the motivating example. Second, we develop the fusion models for different scenarios where data are sparsely observed in space and time and reflect differing subsets of pollutants across sites. Third, a simulation study is presented which is designed to evaluate the proposed models under a variety of sparseness and missingness assumptions. Finally, we apply our models to real world data from South Carolina in order to assess predictions at the ZIP-code level within a 28-day timeframe.

2. Data sources

Observed air pollutant concentrations for this study were obtained from the South Carolina Department of Health and Environmental Control (SC DHEC) ambient air monitoring network. These monitoring sites are part of the national air monitoring program administered by the United States EPA. Modeled air pollution concentrations for this study were obtained from outputs from EPA’s CMAQ model.

2.1. Monitoring Data

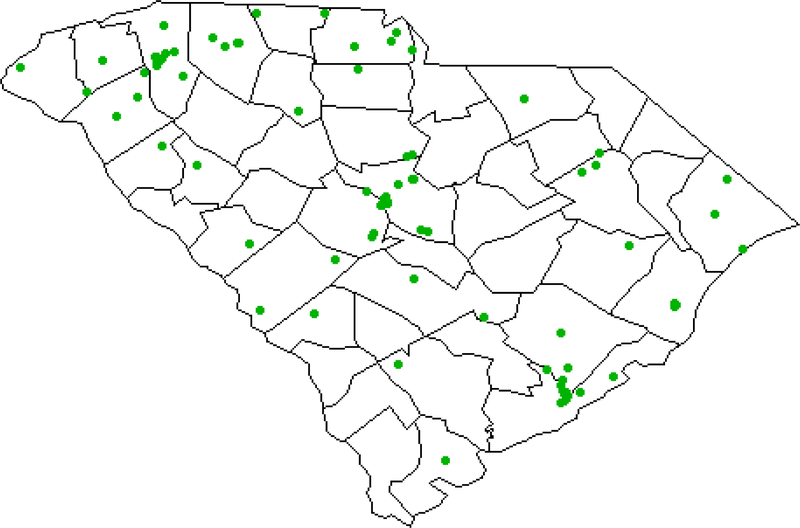
We focus on pollutants monitored by the EPA within South Carolina: carbon monoxide (CO), ozone (O3), nitrogen dioxide (NO2), sulfur dioxide (SO2), particulate matter with size fraction 2.5 μm (PM2.5), and PM2.5 constituents elemental carbon (EC), sulfate (SO4), and ammonium (NH4). Table 1 details the number of monitoring stations recording concentrations for each pollutant across the state during June 2006. Monitoring data is based on all monitoring sites across the state and is given as the appropriate daily summary statistic from the EPA. Figure 1 shows the locations of monitors over this time period.

Figure 1.

Map of monitoring locations across South Carolina for June 2006. A point represents a location where at least one of the eight pollutants was monitored for at least 1 day.

Table 1 indicates monitoring of PM2.5, and O3 is relatively high, and current predictive models perform fairly well in estimating their concentration levels. However, carbon monoxide and PM2.5 constituents are monitored considerably less widely and frequently, leading to the reduced predictive capabilities of existing models.

2.2. Chemical Transport Model Data

The EPA’s chemical transport model (CMAQ) attempts to circumvent the lack of available monitoring data while providing accurate air quality estimates (Appel et al. 2011; Foley et al. 2010). Rather than using observed air pollutant measurements, the EPA uses meteorological, pollutant source, and chemical interaction data to produce estimates at given locations and resolutions (e.g. 12 km × 12 km) for each day. The advantage of a modeled data set is its completeness, with no missing data at any space or time point. These models have been shown to be effective in predicting spatial structure of pollutant concentrations, but some daily variability in pollutants, specifically PM2.5 constituents Sulfate and Nitrogen Dioxide are not captured well due to difficulties “related to predictions of wind speed, PBL height, water vapor, and the predicated cloud cover, all of which appear to contribute to differences in the CMAQ model predictions.” (Appel et al. 2010) Attempting to blend spatial interpolation methods and the completeness of modeled data like CMAQ, researchers have developed fusion methods that utilize both monitor and modeled data (Berrocal et al. 2012; Chang 2016; Friberg et al. 2016). While these methods reduce bias overall (Chen et al. 2014), sparsely monitored pollutant arrays, such as multiple constituents of PM2.5 and some gaseous pollutants, remain problematic.

3. Model Methodology

While others have fit multiple fusion models and provided a final prediction based on aggregating their estimates (Friberg et al. 2016), these models are fit for individual pollutants independently of one another. Shifting this approach to a Bayesian setting allows us to fit a primary and secondary model jointly and construct standard error estimates for our aggregated prediction. Utilizing the advantages of the Bayesian framework, we develop a fusion model that addresses multivariate measurements with differential sparseness. The model utilizes both data resources - EPA monitoring data and EPA CMAQ modeled data - with the ability to incorporate land use, meteorological, or other predictive (e.g. aerosol optical depth) variables to improve the accuracy of the model. Each measurement site is treated as though it could have a data point for each pollutant (of the 8 we are interested in) on each day. This temporal resolution and inclusion of all sites for all pollutants creates large swaths of missing data where pollutant concentrations are not available at most sites on many days.

Some work has been done on introducing a multivariate prediction framework; however, it has been focused on a limited number of pollutants and with pollutants that are monitored widely (Huang et al. 2018). Some have also investigated the PM2.5 constituent pollutants by using spline basis functions, which model the masses of: total PM2.5, individual PM2.5 constituents, and the remaining mass of unmonitored PM2.5 constituents (Crooks et al. 2014; Rundel et al. 2015). Our work differs from previous studies by focusing on improving predictive accuracy for both: specific particulate constituents and other gaseous pollutants that are monitored sparsely both spatially and temporally.

3.1. Aggregated Estimate

We use the combination of a primary and a secondary model to produce an aggregated estimate for pollutant levels to try and address the different types of missingness present in our data. The primary model derives estimates by first addressing missing data with multivariate spatially correlated models at all monitoring locations then interpolating to an end spatial unit (described in Section 3.2). The secondary model uses a simpler bias adjustment model on CMAQ data (described in Section 3.3) to produce adjusted CMAQ estimates across the entire spatial domain regardless of proximity to monitoring locations. A final estimate, γ_ljk, is obtained by calculating a weighted average of the interpolated monitor estimate from the primary model, w_ljk(defined in Section 3.2.2) and the adjusted CMAQ estimate from the secondary model, $C_{ljk}^T$ (defined in Section 3.3):

$$y_{ljk}={\gamma }_{1,ljk}{w}_{ljk}+\left(1-{\gamma }_{1,ljk}\right)C_{ljk}^T$$

, where ${\gamma }_{1,ljk}$ is a weight assigned to the primary model estimate and is defined as: ${\gamma }_{1,ljk}~Beta\left(1,1\right)$. We evaluate the model and its variants (defined in Section 3.4) using a variety of cross validation scenarios. Because there are limited numbers of stations monitoring specific pollutants, we will create folds based leaving out 10% of monitoring data. Using the cross-validation results, goodness of fit metrics such as R², Mean Square Predictive Error (MSPE), and mean bias will be calculated by comparing predicted values to simulated ground truth values.

3.2. Primary Model - Multivariate Fusion Methods

Pollutant concentrations at monitoring sites are defined: Z_jik for the k th pollutant (k = 1,…,P) measured at the k th time point (j = 1,….,n_t) and i th site(i = 1,….,n_z). The underlying data level multivariate model for the observed concentration vector is assumed to be

$${\mathit{z}}_{\mathit{j}\mathit{i}}~\mathit{M}\mathit{V}\mathit{N}\left({\mathit{z}}_{\mathit{j}\mathbf{i}}^{\mathit{t}},{\sum }_z\right)$$

where, the observed concentration level vector, Z_ji, has a multivariate normal distribution centered on ${\mathit{Z}}_{\mathit{j}\mathit{i}}^{\mathit{t}}$, which represents the ‘true’ pollutant concentration without measurement error. ∑_z represents the inter-pollutant covariance matrix of the eight monitored pollutants. The covariance matrix is assumed to be constant across all monitoring locations. The prior distribution for this matrix is assumed to be

$${\sum }_z~InvWishart\left({\sum }_{z_0},\kappa \right),\text{with\hspace{0.17em}\hspace{0.17em}}\kappa =8.$$

The inverse Wishart distribution is chosen due to its conjugacy (Lawson 2018) and is often used as a non-informative prior for covariance matrices (Huang et al. 2013). The value of κ was chosen as κ must be greater than or equal to the dimension of ∑_z (in this case, 8) in order to guarantee positive definiteness. However, smaller values of κ provide greater variability so to provide the least informative prior possible, κ = 8.

Note that Z_ji values are standardized transformations of pollutant concentrations in order to keep all pollutants on a similar scale. While others have looked at air pollutants on a log scale, we felt that the standardization would adequately transform the data to a close-to-normal scale, and the common standardization scale would improve our covariance estimation process.

3.2.1. Primary Model - Modeling the true exposure vector

The true exposure vector is considered to consist of a fused CMAQ value estimated for the time and location and random components

$$z_{jik}^t={\alpha }_{0jk}+{\alpha }_{1jk}{X}_{jik}+{\lambda }_{jk}+{\epsilon }_{ik}$$

where, α_0jk, α_1jk are the random intercept and slope, respectively, which allows for a regression dependency on the CMAQ values, and X_jik is the raw CMAQ estimates corresponding to the monitor site locations. As noted earlier, CMAQ is available within regular spatial grid meshes. A simple approach to assigning CMAQ to monitor sites is to assign the CMAQ values according to the grid cell in which the monitor lies. We assume this approach here. The terms ε_ik, λ_jk represent spatial and temporal random effects respectively. We opt for separable spatial and temporal error terms as this format is more parsimonious, and in exploratory analyses we found that this assumption was adequate.

Spatial dependence

In our example application, monitoring site pollutant data has considerable missingness, with some of the 8 pollutants only monitored at 2 or 3 sites. Missing monitoring data are estimated by regressing on CMAQ values and incorporating a combination of: spatially correlated error, spatially uncorrelated error, and a temporal error.

The uncorrelated spatial error terms, ε_ik, are each assigned a non-informative Normal prior distribution:

$${\epsilon }_{ik}~N\left(0,{\sigma }_{{\epsilon }_k}^2\right)$$

with pollutant specific variance, allowing for uncorrelated spatial error.

A correlated spatial error terms, e_ik, is used in some model variants, utilizing both Intrinsic Conditional Autoregressive (ICAR) and multivariate conditional autoregressive (MCAR) distributions. The MCAR (λ,Ω) distribution, where λ = 1, is used and is given as:

$$\begin{gathered} \mathit{e}~{\mathit{N}}_{{\mathit{n}}_{\mathit{z}}\mathit{p}}\left(\mathbf{0},\mathrm{\Omega }\otimes {\left(\mathbf{D}-\mathbf{W}\right)}^{-1}\right) \\ \text{with\hspace{0.17em}}P\times P\text{\hspace{0.17em}covariance\hspace{0.17em}prior\hspace{0.17em}distribution:} \\ \mathrm{\Omega }~\mathit{I}\mathit{n}\mathit{v}\mathit{W}\mathit{i}\mathit{s}\mathit{h}\mathit{a}\mathit{r}\mathit{t}\left({\mathrm{\Omega }}_0,{\kappa }_{\mathrm{\Omega }}\right) \\ with{\kappa }_{\mathrm{\Omega }}=8. \end{gathered}$$

Here D is n_z × n_z diagonal matrix of number of neighbors and W is a binary adjacency matrix.

The MCAR distribution utilizes spatial conditioning relationships (Besag 1974) that rely on nearest neighbor adjacency. In this case the neighborhood structure is defined by creating a tessellation of all monitoring sites (Lawson 2012) using the R package ‘dismo’ that utilizes the Delaunay triangulation method (Greco et al. 2005). This tessellation’s adjacency matrix is evaluated to provide neighbors for each monitoring site.

Temporal Dependence

The temporal error term, λ_jk, is assumed to have a correlated form. A smooth temporal variation is assumed and so a random walk prior distribution was assumed

$${\lambda }_{jk}~Normal\left({\lambda }_{j-1,k},{\sigma }_{{\lambda }_k}^2\right).$$

The random walk prior provides a non-informative prior at time j=1, and then allows for simple one lag dependence based on the previous time effect. This is assumed to be pollutant specific.

Defining other Prior Distributions for the Primary Model

The random slope and intercept terms, α_{0 jk} and α_{1 jk} have independent Normal prior distributions $\left(Normal\left(0,{\sigma }_{{\alpha }_{0k}}^2\right),Normal\left(0,{\sigma }_{{\alpha }_{1k}}^2\right)\right)$. These Normal priors are potentially non-informative if they have large variances. Finally, note that ${\sigma }_{{\alpha }_{0k}}^2$, ${\sigma }_{{\alpha }_{1k}}^2$, ${\sigma }_{{\alpha }_{\lambda k}}^2$, and ${\sigma }_{{\epsilon }_k}^2$ are each given their own hyper prior distributions, defined as: InvGamma(2,0.5). The inverse gamma priors are conditionally-conjugate and weakly informative (Gelman 2006).

3.2.2. Primary Model - Re-aligning to chosen spatial unit

The point data produced by monitoring networks is not well suited for the aggregated health outcome data often used in environmental epidemiology. Predicted pollutant levels must be re-aligned to a chosen spatial unit (e.g. ZIP codes or census tracts). We investigate several methods to interpolate the monitor site estimates/data to all locations across the study region, and to assign an estimate to a chosen spatial unit. An estimate, W_ljk (where l=1,…,n.W; n.W = number of chosen spatial unit locations), is computed for each chosen spatial unit on each day for each pollutant:

$$w_{jlk}={\varphi }_l\otimes z_{jik}$$

where, ϕ is a weighting matrix that assigns weights for each chosen spatial unit to each of the monitor’s estimates, and ϕ_l is a vector of weights for the l^th spatial unit. ϕ_l can be defined in several different ways, defined below. While mis-alignment problems have been studied, and models are described to incorporate the increased uncertainty (Banerjee et al. 2014), our methods aim to incorporate this uncertainty with posterior functionals, as the re-alignment is incorporated into the initial model’s Bayesian framework. By incorporating this re-alignment in the model, we are able to perform this step in conjunction with the prediction steps listed above. We examined the possibility of using geostatistical models based on a multivariate normal distribution with fully specified spatial covariance, for large domain interpolation, but unfortunately, this proved to be computationally very expensive to run within our framework.

Calculation of ϕ

Neighborhood Method:

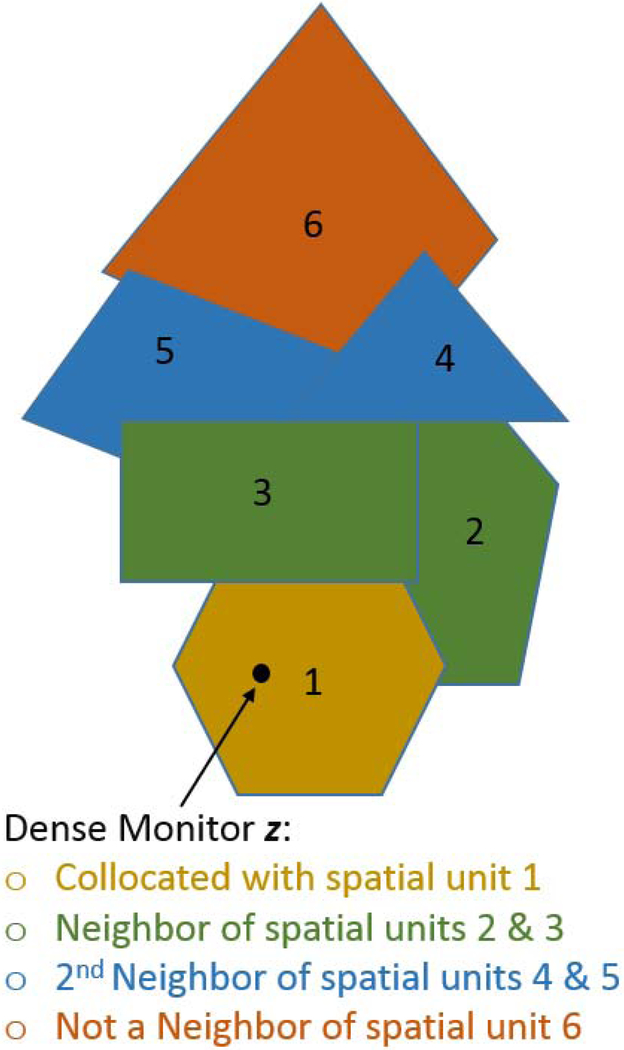
Neighborhood adjacencies are developed for the ZIP units relative to each monitor site available. Each ZIP region assigns a weight, ϕ_l, to each of the monitoring sites. Figure 2 demonstrates the proposed neighborhood assignment protocol.

Figure 2.

Neighborhood Weighting Diagram

Sites that are collocated with a ZIP region are given a weight of 1.0, sites that are located in a region neighboring a given region are given a weight of 0.5, sites that are located in a secondary neighbor of a given region are given a weight of 0.25, and all other sites are given a weight of 0.0. Weights are reweighted to sum to 1.

Distance Weights:

Define a weight based on the distance from the monitoring site to the centroid of the chosen spatial unit (d_lj), with a tuning parameter, ν

$$w_{jik}=\frac{\sum _i\text{exp}\{-\nu d_{il}\}{z}_{jik}}{\sum _e\text{exp}\{-\nu d_{il}\}}$$

We varied values of the smoothing parameter, ν, to assess if different decay rates resulted in better model fit, ultimately choosing ν =0.3 to represent rapid decay of spatial dependence, ν =3 to represent a gradual decay, and ν =1 as a standard rate of decay. We implemented various tuning parameter values to assess the sensitivity of our model to their selection.

3.3. Secondary Model

Previous research has shown that the incorporation of data at multiple resolutions can improve model fit (Aregay et al. 2016b, 2016a; Fonseca et al. 2017; Aregay et al. 2018). We implement an alternative CMAQ adjustment model to provide estimates at each chosen spatial unit based on a model relating averaged monitor data and averaged CMAQ data:

$$Z_{lk,ann}~Normal\left(z_{lk,ann}^T,{\sigma }_{z_{ann,k}}^2\right)$$

$$Z_{lk,ann}^T={\beta }_{0k}+{\beta }_{1k}{X}_{lk,ann}+k{b}_{lk}$$

, where $Z_{lk,ann}$ is the mean monitor value of a given pollutant at a given chosen spatial unit for the complete time of analysis. If multiple dense sites lie in the same chosen spatial unit then their overall mean will be taken. $Z_{lk,ann}^T$ represents the monitored mean value. $X_{lk,ann}$ is the mean CMAQ value of a given pollutant at a given corresponding chosen spatial unit for the complete time of analysis, where daily CMAQ values (X_ljk) are aggregated using area weighting to the chosen spatial unit. ${\beta }_{0k}$ and ${\beta }_{1k}$ are random intercept and slope, respectively, and kb is a spatially correlated error term based on the neighborhood of the chosen spatial unit and distributed MCAR:

$$\begin{gathered} \mathit{k}\mathit{b}~{\mathit{N}}_{{\mathit{n}}_{\mathit{w}}\mathit{P}}\left(\mathbf{0},\mathrm{\psi }\otimes {\left(\mathbf{D}-\mathbf{W}\right)}^{-1}\right) \\ \text{with\hspace{0.17em}}P\times P\text{\hspace{0.17em}covariance\hspace{0.17em}prior\hspace{0.17em}distribution:} \\ \mathrm{\psi }~\mathit{I}\mathit{n}\mathit{v}\mathit{W}\mathit{i}\mathit{s}\mathit{h}\mathit{a}\mathit{r}\mathit{t}\left({\mathrm{\psi }}_0,{\kappa }_{\mathrm{\psi }}\right) \\ \text{with\hspace{0.17em}}{\kappa }_{\mathrm{\psi }}=8\mathbf{a}\mathbf{n}\mathbf{d}{\mathit{n}}_{\mathit{w}}=\mathbf{N}\mathbf{u}\mathbf{m}\mathbf{b}\mathbf{e}\mathbf{r}\mathbf{o}\mathbf{f}\mathbf{e}\mathbf{n}\mathbf{d}\mathbf{s}\mathbf{p}\mathbf{a}\mathbf{t}\mathbf{i}\mathbf{a}\mathbf{l}\mathbf{u}\mathbf{n}\mathbf{i}\mathbf{t}\mathbf{s} \end{gathered}$$

The trained annual model is then used on daily CMAQ data, which have also been aggregated to the end spatial unit spatial scale, to provide estimates for each pollutant at each chosen spatial unit on each day:

$$C_{ljk}^T={\beta }_{0k}+{\beta }_{1k}{X}_{ljk}+k{b}_{lk}+{\chi }_k{\lambda }_{jk}$$

The primary model, the secondary mean model, and the secondary daily model are all fit jointly within a Bayesian Hierarchical framework, and we link the primary and secondary models with the temporal error term, λ_jk. λ_jk provides the secondary model, which is essentially a bias adjustment for raw CMAQ values re-aligned to the end spatial unit, with pollutant dependent temporal variation based on monitoring data in the primary model. We include the modification factor, χ_k, to scale the temporal error appropriately in the secondary model.

Defining Prior Distributions for Secondary Model

${\beta }_{0k}$ and ${\beta }_{1k}$ are similarly distributed $\left(Normal\left(0,{\sigma }_{{\beta }_{0k}}^2\right),Normal\left(0,{\sigma }_{{\beta }_{1k}}^2\right)\right)$. The modification factor, χ_k, has a Normal prior distribution centered on a factor of 1 ($Normal\left(1,{\sigma }_{{\chi }_k}^2\right)$). ψ is a covariance matrix defined similarly to Ω with an inverse-Wishart prior ($\text{ψ}~InvWishart\left({\text{ψ}}_0,8\right)$) Also, note that ${\sigma }_{{\beta }_{0k}}^2$, ${\sigma }_{{\beta }_{1k}}^2$, ${\sigma }_{\chi k}^2$, and ${\sigma }_{e{c}_{lk}}^2$ are each given their own hyper prior distributions, defined as: InvGamma(2,0.5).

3.4. Model Variants

We investigate the primary model defined above with several variants. As others have not implemented multivariate predictions in this setting, we were interested in the evaluating the merits of different model paradigms and varied prior specifications that are meant to address the different types of missingness present in air pollutant data. As our primary challenge with current data resources is spatial missingness, we implement models that vary our assumptions on the spatial error and relationship of the pollutants. We aim to find the best balance between a model complex enough to estimate the true relationships and a parsimonious model that is more efficient to fit while also limiting the possibility of model misspecification.

3.4.1. Primary Model Variants

Model 1 includes the spatially uncorrelated error term, ε_ik, but does not utilize the spatially correlated error terms, ε_ik. Model 1 allows for a more flexible spatial error term that removes the assumption that the residual error will be spatially correlated or related across pollutants.

$$z_{jik}^t={\alpha }_{0jk}+{\alpha }_{1jk}{X}_{jik}+{\lambda }_{jk}+{\epsilon }_{lk}$$

Model 2 shifts the paradigm to a spatially correlated error setting, allowing each pollutant to have their own independent Intrinsic Conditional Autoregressive (ICAR) distribution (Besag et al. 1991). We allow Model 2 to retain a multivariate setting with the data being distributed as a multivariate normal but include independent CAR assumptions for the spatial errors. Here, e_k has an ICAR distribution with the same neighborhood parameters for the individual CAR models as were used in the MCAR model defined previously.

$${\mathrm{e}}_{\mathrm{k}}~\text{N}\left(0,{\sigma }_{{\mathrm{e}}_{\mathrm{k}}}^2{\left(\text{D}-\text{W}\right)}^{-1}\right)$$

Each pollutant now has its own variance term, (${\sigma }_{{\mathrm{e}}_{\mathrm{k}}}^2~InvGamma\left(2,0.5\right)$).

Model 3 employs independent normal distributions for each pollutant rather than the multivariate normal scenario described previously. However, we revert to the multivariate spatially correlated error term: $\mathit{e}~{\mathit{N}}_{{\mathit{n}}_{\mathit{z}}\mathit{P}}\left(\mathbf{0},\mathrm{\Omega }\otimes {\left(\mathbf{D}-\mathbf{W}\right)}^{-1}\right)$ that was described in Section 3. This model also employs a multivariate relationship at only one level of the hierarchy.

$$\begin{gathered} z_{jik}~Normal\left(z_{jik}^t,{\sigma }_{z_k}^2\right) \\ {\sigma }_{z_k}^2~InvGamma\left(2,0.5\right) \end{gathered}$$

3.4.2. Secondary Model Variants

Note that in Models 2 and 3 a spatially uncorrelated error term, ec_lk, is included.

$$e{c}_{lk}~Normal\left(0,{\sigma }_{e{c}_k}^2\right)$$

Note that the model variants are described in Table 3.

Table 3.

Summary of Primary Model Variants to be evaluated

Model Number	Model Specification	Model Description
Model 1	$$\begin{gathered} z_{ji}~MVN(z_{ji}^t,{\Sigma }_z) \\ {z}_{jik}^t={\alpha }_{0jk}+{\alpha }_{1jk}{X}_{jik}+{\lambda }_{jk}+{\epsilon }_{ik} \\ {\epsilon }_{ik}~N(0,{\sigma }_{{\epsilon }_k}^2) \end{gathered}$$	Multivariate normal with random walk temporal error and uncorrelated spatial error.
Model 2	$$\begin{gathered} z_{ji}~MVN(z_{ji}^t,{\Sigma }_z) \\ {z}_{jik}^t={\alpha }_{0jk}+{\alpha }_{1jk}{X}_{jik}+{\lambda }_{jk}+e_{ik} \\ {e}_k~N\left(0,{\sigma }_{e_k}^2{\left(D-W\right)}^{-1}\right) \end{gathered}$$	Multivariate normal with random walk temporal error and independent ICAR spatial errors.
Model 3	$$\begin{gathered} z_{jik}~Normal(z_{jik}^t,{\sigma }_{z_k}^2) \\ {z}_{jik}^t={\alpha }_{0jk}+{\alpha }_{1jk}{X}_{jik}+{\lambda }_{jk}+e_{ik} \\ e~N_{n_{z}P}\left(0,\mathrm{\Omega }\otimes {\left(\text{D}-\text{W}\right)}^{-1}\right) \end{gathered}$$	Independent normal distributions with random walk temporal error and MCAR spatial error.

3.5. Model Fitting Software and Diagnostics

We choose to use WinBUGS due to the demonstrated effectiveness of sampling posterior distributions in Bayesian Hierarchical Modeling (BHM) settings using Markov chain Monte Carlo (McMC) sampling methods. Specifically, we utilize the default sampling methods in WinBUGS 1.4.3 -- a mixture of Gibbs sampling and random walk Metropolis-Hastings sampling. Other options are available for modeling in a BHM paradigm; however, they each have their own limitations. Ultimately, WinBUGS allows for the flexibility and complexity of our proposed models, while offering turn-key functionality for the spatial distributions we require.

All models are fit using two separate chains and a burn-in period of 40,000 iterations. We then run a posterior sample of 10,000 iterations per chain, thinning to every 25^th observation. We choose to thin to reduce autocorrelation of samples, and to limit the overall data output size resulting in a posterior distribution sample of 800 (from two chains), which should be adequately large to provide summary statistics. Burn-in period was determined by investigating the Gelman-Rubin convergence diagnostic to ensure its value was less than 1.2 for each of the monitored parameters (Brooks et al. 1997). Each of the 4 Models specified here are fit using R version 3.4.3, the ‘r2WinBUGS’ package, and WinBUGS 1.4.3.

4. Simulation Study

In order to evaluate the effectiveness of our model variants, we implement a small simulation study. We simulate values of the 8 specified pollutants in South Carolina over a grid with a resolution of 6km × 6km and grid cell locations g (where g=1,…..n_g) using an MCAR distribution in WinBUGS.

$$\mathit{s}\mathit{i}{\mathit{m}}_{\mathit{j}}~{\mathit{N}}_{{\mathit{n}}_{\mathit{g}}\mathit{P}}\left(\mathbf{O},{\mathbf{\Omega }}_{\mathit{s}\mathit{i}\mathit{m}}\otimes {\left({\mathbf{D}}_{\mathit{s}\mathit{i}\mathit{m}}-{\mathit{W}}_{\mathit{s}\mathit{i}m}\right)}^{-1}\right)$$

where sim_j is an array containing simulated ground truth values for each of the 8 pollutants on a given day, j, at each grid cell point, g, and ${\mathbf{\Omega }}_{\mathit{s}\mathit{i}\mathit{m}}=\text{Empirical\hspace{0.17em}Covariance\hspace{0.17em}from\hspace{0.17em}Monitoring\hspace{0.17em}Data}$. We designed the study to evaluate the spatial variation and cross correlation of pollutants. This led to using an MCAR distribution as the number of locations required to produce a 6km grid resolution across South Carolina was too large to model using a Gaussian process with our resources. The MCAR paradigm allows for correlation across space and pollutants while drawing at a suitable resolution for our simulation.

After initial simulation tests of our three proposed models, we produce a 28-day simulated data sample by simulating 28 sample data sets from the specified MCAR distribution. The simulated data does retain some autocorrelation from iteration to iteration (representing day to day data); however, we do not systematically add any temporal correlation. The major challenge in completing a simulation study for this modeling method is incorporating the CMAQ data to be ‘fused’ with the monitor data. A random field can provide monitor data simulations; however, CMAQ data is assumed to be related to the true field in an unknown way. Basing our simulated CMAQ values on the real CMAQ data would provide no link to the simulated ground truth, forcing us to develop pseudo-CMAQ values that are derived from the simulated random field, but with random error incorporated. We aggregate the simulated data from its 6 km × 6km grid to the misaligned 12 km × 12 km CMAQ grid. We then add in random error with mean 0 and variance equal to 10% of the mean of real CMAQ values provided by the EPA. We chose to add random error to provide some level of randomness to the spatial structure. We know that CMAQ values are not perfectly estimating measured pollution, and we incorporate this uncertainty into our pseudo CMAQ. While the random error added is not ideal for predicting the true spatial structure, the EPA’s CMAQ values also have varied spatial structure, lacking smooth transitions at some locations.

We also want to incorporate simulated ‘urban’ areas to reflect the differences between urban and rural air pollution as seen in empirical data. We therefore added in spikes of 1 standard deviation at three (3) grid locations and their neighboring grid cells on the original simulated grid.

We ultimately choose 100 random locations across our ‘simulated SC’ region. To evaluate our models’ fits, we produce test and validation datasets. To produce the sets, we give each monitoring location a 50% probability of inclusion in the test set, resulting in ~53% of the data being removed. This missingness is also important for the simulation as the real-world data will always have large amounts of missing data. We evaluate each of the model variants described above by comparing the modeled results based on the simulated test data set with the left-out validation set.

4.1. Simulation Results

Simulation fit results are based on the comparison of the model predictions of Z_jik versus the validation set of left out data. Mean Square Predictive Error (MSPE), Mean Bias (Bias), and the Coefficient of Determination (R²) were calculated in order to evaluate the fit and predictive accuracy of each model. We show results for Models 1 and 3, as Model 2 was clearly inferior in initial 2-day cases of simulation results.

Fit metrics are calculated as follows:

$$MSPE=\frac{\sum _j\sum _i{\left(z_{jik}^{pred}-z_{jik}^{validation}\right)}^2}{n_z}$$

$$Bias=\frac{\sum _j\sum _i\left(z_{jik}^{pred}-z_{jik}^{validation}\right)}{n_z}$$

$$R^2=correlation{\left(z_{jik}^{pred},z_{jik}^{validation}\right)}^2$$

All simulation fit results can be seen in Tables 4–6.

Table 4.

MSPE 28-day Simulation Results for each pollutant

0.03	0.02	CO
0.08	0.09	SO2
0.03	0.03	NO2
0.05	0.06	O3
0.01	0.01	PM2.5
0.01	0.01	NH4
0.04	0.04	EC1
0.02	0.02	SO4
Model 1 28 day	Model 3 28 day

Table 6.

R² 28-day Simulation Results for each pollutant

0.81	0 83	CO
0.59	0.57	SO2
0.79	0.81	NO2
0.67	0.67	O3
0.77	0.82	PM2.5
0.81	0.87	NH4
0.68	0.68	EC1
0.78	0.8	SO4
Model 1 28 day	Model 3 28 day

R² shows the predictive accuracy of each model for each pollutant, and our goal was to find the most predictive model for pollutant levels at the monitoring sites. Model 1’s R² values are consistently > 0.6 (SO₂ has lowest R² at 0.59), suggesting a strong fit at monitoring sites, with CO, NO₂, PM2.5 NH₄, and PM2.5 SO₄ all at > 0.75. These results are averages over the 28 day period. Bias and MSPE are very low for PM2.5 and PM2.5 SO₄ and NH₄, but SO₂ has extremely biased results. Gaseous pollutants NO₂ and CO also have very low MSPE results, suggesting a good fit.

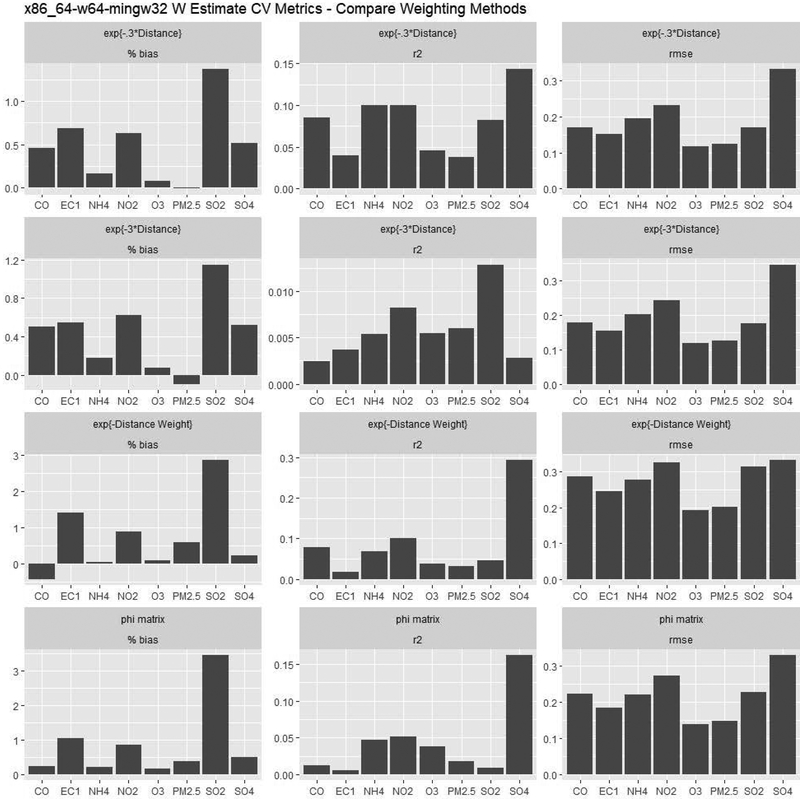
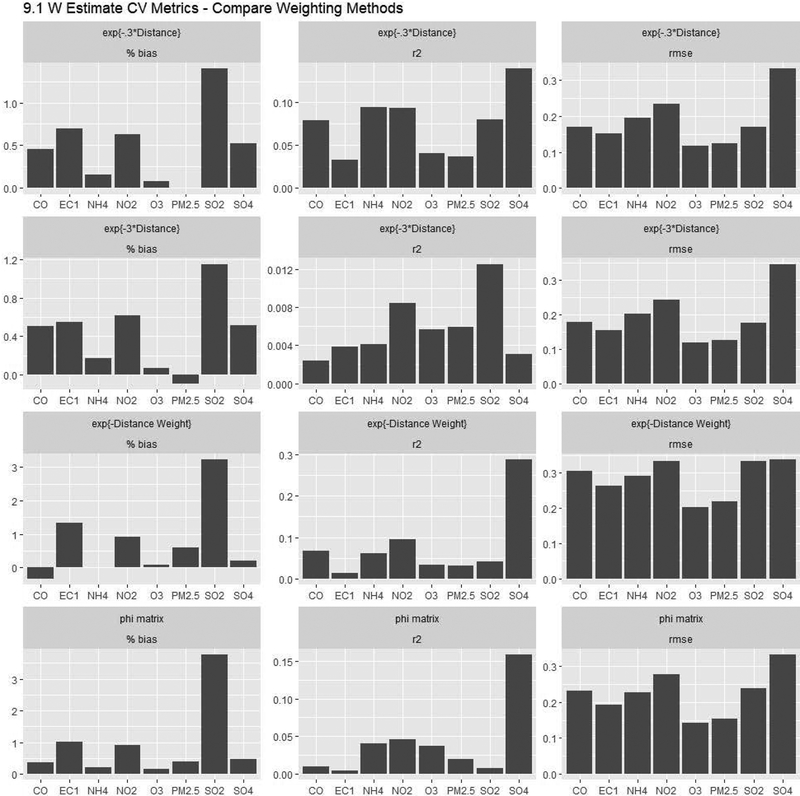
Model 3 has improved results, compared to Model 1, with five (5) pollutants’ cross validated R² metrics greater than 0.8. SO₂ continues to demonstrate the worst results (R²=0.57), and Ozone and Elemental Carbon also have R² < 0.7. MSPE results mirror those of R², with SO₂ having the poorest results (MSPE=0.09), while all other pollutants have MSPE < 0.06. Bias is very low for all pollutants based on Model 3 results, with no pollutant having an absolute mean bias > 0.02. We also investigate the best fit at the final ZIP code level spatial unit based on these best models. Figure 3 shows the fit statistics based on a validation set of the simulation data based on Model 1. Each of the four interpolation methods is compared. We see that for most pollutants the distance weighting method using ν =1 is optimal. When models are implemented with ν =3 results are extremely poor. Results for the neighborhood interpolation method are also inferior to the distance weighting interpolation with ν =1. Note that simulated data is aligned to ZIP spatial unit by area weighted polygon overlap methods. Figure 5 compares the interpolation methods using Model 3 and shows similar results.

Figure 3.

Comparison of fit metrics for Model 1 chosen spatial unit estimates using the four mentioned interpolation methods.

Figure 5.

Comparison of fit metrics for Model 3 chosen spatial unit estimates using the four mentioned interpolation methods.

The resulting fit metrics are not nearly as accurate as they are at the actual monitoring sites, with considerably lower R² values. We would expect these differences in accuracy, as monitoring locations have collocated pollutant levels that are informing the predictions, whereas predictions at spatial units without a monitoring site are relying on interpolated results from the primary model and the relatively simpler secondary model’s estimates.

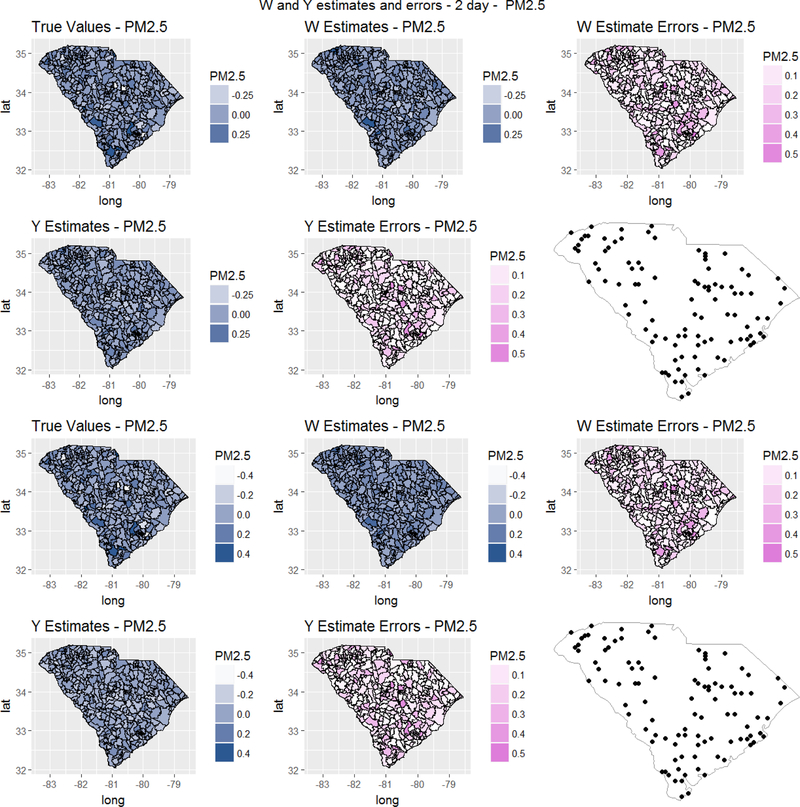
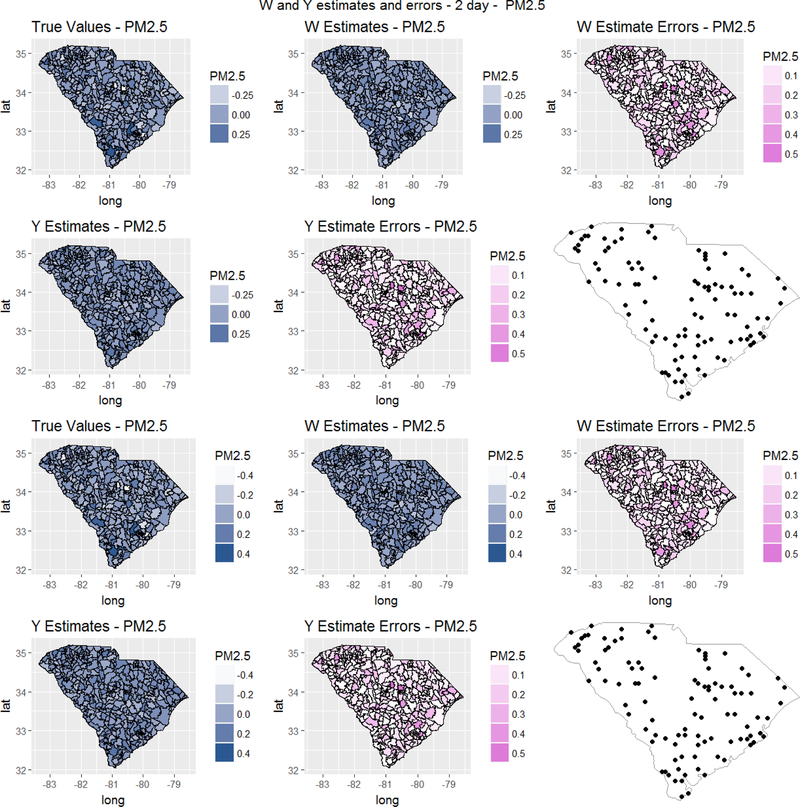
Figure 4 shows Model 1 estimates and model fit at the chosen spatial unit for PM2.5 for a 2-day subset of the overall 28 day run. Supplemental Figures 1–7 show estimates and fit of Model 1 for all remaining pollutants. Figure 6 shows Model 3 estimates and model fit for PM2.5 for a 2-day subset, while Supplemental Figures 8–14. These figures show that, as we would expect, residual errors are largest in areas with little to no monitoring locations. However, the overall spatial surface for the estimates generally mimic our ground truth values.

Figure 4.

PM 2.5 w and y Estimates and Errors for a 2-day span using Model 1. Day 1 results are on top 2 rows. Day 2 results are on bottom 2 rows. Errors are calculated as absolute residuals and are given as number of standard deviations from the true value. Locations of all ‘monitor’ sites used in the simulation are given in the map in the lower right as well.

Figure 6.

PM 2.5 w and y Estimates and Errors for a 2-day span using Model 3. Day 1 results are on top 2 rows. Day 2 results are on bottom 2 rows. Errors are calculated as absolute residuals and are given as number of standard deviations from the true value. Locations of all ‘monitor’ sites used in the simulation are given in the map in the lower right as well.

5. Case Study

We use South Carolina air pollution levels as a case study for our estimation model. We collected EPA pollutant monitoring data for the eight (8) pollutants listed above for June 2006 in South Carolina. We also obtained CMAQ estimates at a 12 km × 12 km grid resolution for South Carolina from the EPA. There are 87 monitoring stations available over a 28-day period (6/1/2006 – 6/28/2006). Missingness for each monitoring site varied by pollutant, with some pollutants monitored every day at a given site while not monitored at all at other sites. This results in a large swath of missing data (see Table 1), but it is representative of normal rates of missing pollutant data, as most monitoring sites sample only 1 or 2 pollutants, and many sites do not sample every day.

We conducted several analyses to evaluate the predictive power of our different model variants. We also implemented the univariate fusion technique described by Friberg et al. 2016 to provide a univariate reference to compare our multivariate methods.

5.1. Case Study 28-day Results

We implement Models 1 and 3 (described in Section 3.4) for 28 days. We select 10% of monitor data to leave out for a given model fit. Using the available 90% of the data, estimates are predicted at the ZIP code level. The left-out monitors’ values are assigned as the estimates for the ZIP code where they are contained, and MSPE, R², and mean bias are calculated.

The resulting predictive metrics are then aggregated and are shown in Tables 7–9. Note that blacked out squares represent where there is not sufficient pollutant data to evaluate the model. Unfortunately, some pollutants have extremely low rates of observation, so we were forced to choose a month where the Elemental Carbon PM2.5 constituent only had a total of 9 observations at only one monitoring station. This limited data results in none of its true values being in the validation data set, preventing us from providing fit results.

Table 7.

MSPE Case Study Results for each pollutant based on a 28-day Model run for June 2006 using Model 1 (left column) and Model 3 (right column).

1.08	1.3	CO
1.28	1.23	SO2
1.1	1.23	NO2
1 44	1.45	O3
1.28	1.76	PM2.5
2.1	2.11	NH4
		EC1
1.24	1.41	SO4

Table 9.

R² Case Study Results for each pollutant based on 28-day period in June 2006 Data using Model 1 (left column) and Model 3 (right column).

0 39	0.21	CO
0.24	0.29	SO2
0.18	0.2	NO2
0 11	0.12	03
0.2	0.15	PM2.5
0.21	0.33	NH4
		EC1
0.28	0.45	SO4

Table 10 shows the R² results for the Friberg et al. methodology. We performed a similar cross validation, resulting in relatively strong fit results for SO4, NH₄, and Ozone. It is important to note that when using some exposure prediction methods, it is impossible to provide a prediction for some monitor-day combinations. Table 10 also includes the rate of missingness (% Missing) of estimates by dividing the total number of estimates produced by the total number of monitor-day combinations and subtracting from 1. We see that NH₄ has strong fit, but only ~30% of monitor-day combinations are estimated due to the limited data available for fitting this model. On days where there are fewer than 3 monitors of a given pollutant, this particular univariate method cannot predict values. CO also has high rates of estimate missingness, and Elemental Carbon could not be predicted at all because there were no days during which more than 1 monitor location recorded EC values.

Table 10.

R² and Percent Missingness (% Missing) for pollutant estimates obtained using Friberg et al. 2016 methodology. % Missing is the percent of possible monitor-day combinations that were NOT predicted using this methodology due to insufficient data resources.

Pollutant	R2	% Missing
CO	0.29	63
SO2	0.07	0
NO2	0.14	0
O3	0.71	0
PM2.5	0.52	15
NH4	0.67	69
EC	N/A	100
SO4	0.61	1

Table 10 also demonstrates the difficulty in predicting gaseous pollutants in particular, with poor fit in SO₂ and NO₂.

Our results show that Model 3 provides better predictions for NH₄ and SO₄, while Model 1 achieved higher R² values in CO and PM2.5. Model 3 outperforming Model 1 in the constituent pollutants, which are not widely monitored, could provide some information on the best models for constituent only prediction in future research. Conversely, Model 1 has slightly better MSPE metrics, particularly for the gaseous pollutants (CO: 1.06, NO₂: 1.1) compared to Model 3 (CO: 1.3, NO₂: 1.23). Mean Bias is also consistently better in Model 1 (with the exception of NO₂, where bias is almost equivalent - −0.12 vs. −0.11). The PM2.5 constituent ions Sulfate and Ammonium are monitored much less widely than Ozone and PM2.5, and yet their R² values are somewhat higher than the other pollutants (0.3–0.5) in Model 3; however, their results are still poor compared to our univariate comparison. CO’s fit is better than other pollutants in our models, despite its higher rate of missingness, and outperforms the univariate analysis in Model 1. Both Models 1 and 3 outperform the univariate fit for SO₂ and NO₂, suggesting multivariate methods may be leveraged for gaseous pollutants specifically. Bias and MSPE results slightly favor Model 1 in almost all cases.

6. Discussion

The proposed models show impressive results for a multivariate approach to modeling air pollutant concentrations in our simulation studies. In our preliminary modeling, Models 1 and 3 were clearly superior to Model 2 in terms of predictive accuracy. R² metrics show that for pollutants CO, NO₂, PM2.5, NH₄, and SO₄ both Models 1 and 3 provide accurate results (all values > 0.77). Model 3 shows superior results based on R² for all pollutants except SO₂; however, SO₂’s mean bias is much better in Model 3. Our simulation study demonstrates that a multivariate approach can provide accurate results even with ~50% of the data missing, which is an important consideration for any ambient air pollutant model. This missingness accounted for large areas of ‘unmonitored’ space, as well as monitoring stations with limited number of pollutants, mimicking real-world monitoring distributions.

Figures 4 and 6 show that errors are predictably larger in areas where monitor sites were not present in the simulation study (MSPE ~ 0.5 vs. MSPE < 0.1). Still, residual errors remain within half a standard deviation of true values in most cases. Our sensitivity study of interpolation methods demonstrates that the distance weighting method with ν =1 was the optimal choice based on improved cross validated R² metrics at non-monitoring locations.

The case study data illustrate several deficiencies of current air pollution data, with some pollutants only monitored at one station over the given time period. Results for Models 1 and 3 are, predictably, not as reliable as in the simulated case of ~53% missing data. However, these models show acceptable levels of MSPE and R² (<1.5 and ~0.4, respectively) for some pollutants.

Our univariate approach results (Table 10) demonstrate their effectiveness in widely monitored pollutants like PM2.5 and Ozone, and they do surprisingly well with PM2.5 constituents SO₄ and NH₄. We do note the limitations of the univariate methods by including the percentage of estimates still missing due to lack of available data resources (60% for NH₄). Conversely, our univariate approach did not provide accurate results for gaseous pollutants CO, SO₂, and NO₂ – yielding R² values of 0.29, 0.07, and 0.14, respectively. We see that raw CMAQ’s estimates for gaseous pollutants also demonstrate poor fit.. Raw CMAQ R² fit statistics for June 2006 are below 0.06 for Sulfur Dioxide and Carbon Monoxide and below 0.25 for Ammonium Ion and Sulfate.. While the gaseous pollutants and PM2.5 (and its constituents) seem to respond differently to our modeling variations, there are signs of improved accuracy for NO₂, CO, and SO₂ based on multivariate relationships. Model 3 outperforms raw CMAQ and the Friberg et al. univariate approach for SO₂, while Model 1 outperforms raw CMAQ and the univariate approach for CO. Our models also outperform the univariate NO₂ results. All of these pollutants have spatial missingness rates > 60%, with CO being especially sparsely monitored.

Our approach does fall short of the univariate method in some cases, particularly in PM2.5 constituents. While we still believe in the benefits of a multivariate approach for these data, it is possible that they should be modeled as a more complete set. We only use three PM2.5 constituents, while some monitoring stations differentiate PM2.5 into a much greater number of species. We also suggest consideration of the needs of a specific project when selecting an exposure prediction method. Trade-offs in accuracy and completeness are the realities of working with the limited air quality monitoring data available.

7. Conclusions

Our fusion model aims to address predictive accuracy for pollutants that are monitored sparsely, both in space and time. Pollutants with fewer than three monitoring locations on a given day provide challenges for univariate prediction methods.. South Carolina’s monitoring network demonstrates the reality of such sparse monitoring networks (see Table 1). Our multivariate fusion approach gives researchers an opportunity to estimate these sparsely monitored pollutants by leveraging all of their available resources.

Our simulation results demonstrate Model 3’s ability to provide accurate results based on data with over 50% missingness, and while our case study results do not yield the same accuracy, the missingness in this data was > 80% in half of our pollutants of interest.

Our methods provide complete spatio-temporally resolved results to a given end spatial unit. With the shift in air pollution research to the investigation of mixtures of pollutants, the ability to provide exposure data with limited missingness will be vital.

We can see how our multivariate approach can benefit the prediction of these pollutants with high spatial missingness, particularly in the gaseous pollutants. We also see how the multivariate approach can provide more complete estimates for exposure data, by providing estimates on days where a pollutant was not measured, at a location where it was never measured.

Univariate models may be able to impute values on missing days, but their prediction relies on temporal correlation. Our model treats gaps in time series as spatial missingness and relies on inter-pollutant correlation, spatial correlation, AND temporal correlation to fit missing values. The alternatives for researchers are currently limited to modeled data, such as CMAQ, which we have shown (Table 2) to have lower predictive accuracy than our models for many pollutants.

We see promise in improving predictive accuracy using the multivariate paradigm, specifically in the gaseous pollutants SO₂ and NO₂, as we saw increases in R² for these pollutants in Models 1 and 3 when compared to CMAQ alone and our univariate approach. A goal for future research is to create a complete prediction dataset to be made available to researchers, so others would not have to develop or implement their own exposure prediction models. While our nearest neighbor spatially dependent structure is more computationally efficient than a point level geostatistical model, other more novel neighborhood methods may be available to increase efficiency further still. Investigating the multivariate spatio-temporal variation on these pollutants will be important as researchers shift toward mixtures analysis, providing a need for effective and accurate modeling of exposures that are not always uniformly monitored or measured.

Table 5.

Bias 28-day Simulation Results for each pollutant

0.35	0.01	CO
3.22	−0.02	SO2
−0.15	−0.01	NO2
0.29	0.01	O3
0.06	0	PM2.5
−0.11	−0.01	NH4
0.66	0.01	EC1
−0 02	−0.01	SO4
Model 1 28 day	Model 3 28 day

Table 8.

Mean Bias Case Study Results for each pollutant based on a 28-day Model run for June 2006 using Model 1 (left column) and Model 3 (right column).

−0.06	−0.2	CO
−0.11	−0.11	SO2
−0.12	−0.1	NO2
−0.1	−0.24	O3
−0.23	−0.25	PM2.5
−0.86	−1.02	NH4
		EC1
−0.45	−0.58	SO4