Multi-modal Neuroimaging Feature Selection with Consistent Metric Constraint for Diagnosis of Alzheimer’s Disease

Abstract

The accurate diagnosis of Alzheimer’s disease (AD) and its early stage, e.g., mild cognitive impairment (MCI), is essential for timely treatment or possible intervention to slow down AD progression. Recent studies have demonstrated that multiple neuroimaging and biological measures contain complementary information for diagnosis and prognosis. Therefore, information fusion strategies with multi-modal neuroimaging data, such as voxel-based measures extracted from structural MRI (VBM-MRI) and fluorodeoxyglucose positron emission tomography (FDG-PET), have shown their effectiveness for AD diagnosis. However, most existing methods are proposed to simply integrate the multi-modal data, but do not make full use of structure information across the different modalities. In this paper, we propose a novel multi-modal neuroimaging feature selection method with consistent metric constraint (MFCC) for AD analysis. First, the similarity is calculated for each modality (i.e. VBM-MRI or FDG-PET) individually by random forest strategy, which can extract pairwise similarity measures for multiple modalities. Then the group sparsity regularization term and the sample similarity constraint regularization term are used to constrain the objective function to conduct feature selection from multiple modalities. Finally, the multi-kernel support vector machine (MK-SVM) is used to fuse the features selected from different models for final classification. The experimental results on the Alzheimer’s Disease Neuroimaging Initiative (ADNI) show that the proposed method has better classification performance than the start-of-the-art multimodality-based methods. Specifically, we achieved higher accuracy and area under the curve (AUC) for AD versus normal controls (NC), MCI versus NC, and MCI converters (MCI-C) versus MCI non-converters (MCI-NC) on ADNI datasets. Therefore, the proposed model not only outperforms the traditional method in terms of AD/MCI classification, but also discovers the characteristics associated with the disease, demonstrating its promise for improving disease-related mechanistic understanding.

Introduction

In recent years, the incidence of brain diseases worldwide has been rising. Alzheimer’s disease (AD) is one of the most common brain diseases, and its clinical manifestations are mainly memory impairment and loss of reasoning cognitive ability, accompanied by language and movement disorders. At present, AD has become the fifth leading cause of death in the elderly. In a 2018 report from the Alzheimer’s Association of the United States, National Center for Health Statistics has shown the statistics information on the rate of change in mortality from multiple risky diseases in the United States. That is, between 2000 and 2015, the number of lethal deaths of many risk diseases has achieved negative growth, while the incidence of AD has increased by 123% (Association, 2018). According to another survey report (Association, 2017), one case of Alzheimer’s disease will be diagnosed every 33 seconds in 2050, with nearly one million new cases each year. AD has become one of the major diseases that endanger the health of the elderly and affect the sustainable development of society. However, the efficacy of drugs for the treatment of AD has been limited to date, and no treatment has been reported to reverse or prevent the progression of AD.

Therefore, the measurement of sensitive markers in the early stages of the disease can help researchers and clinicians develop new treatments and test their effectiveness. Recently, various measurements such as structural atrophy, pathological amyloid deposition, and metabolic changes have already been shown to be sensitive to the diagnosis of AD and MCI. Neuroimaging techniques (Rathore et al., 2017; Sui et al., 2012; Ye et al., 2011) provide great help for the discovery of AD-related brain regions of interest (ROIs), which is a powerful instrument for the diagnosis of neurodegenerative diseases. For example, voxel-based measures extracted from structural MRI (VBM-MRI) and fluorodeoxyglucose positron emission tomography (FDG-PET), have been shown to be useful for investigating the neurophysiological features of AD and mild cognitive impairment (MCI) (Chetelat et al., 2003; Cohen and Klunk, 2014; Foster et al., 2007; Zhang et al., 2015).

In recent decades, machine learning and pattern recognition methods, including sparse learning, graph theory, and classification, have been widely used in neuroimaging analysis for AD and MCI diagnosis (Lei et al., 2017; Sanz-Arigita et al., 2010; Wang et al., 2018; Ye et al., 2011). However, some existing studies focus on extracting features from a single modality. For example, the researchers extracted some features from certain ROI, such as the hippocampus on structural MRI (Frisoni et al., 2010) for the classification of AD (Gerardin et al., 2009; Wang et al., 2006). While in addition to structural MRI, PET images can also be used for classification of AD and MCI (Chetelat et al., 2003; Cohen and Klunk, 2014; Foster et al., 2007; Hinrichs et al., 2009).

As the brain has very complex structure and function, acquiring data from single modality does not provide sufficient feature information for diagnosis. In recent years, with the development of neuroimaging technology, multi-modal data can be collected during various examinations of subjects, providing a source of data for the diagnosis of AD. Different modality data can provide brain information from different perspectives. For example, structural MRI provides information related to brain tissue types, while PET measures glucose brain metabolic rate. Numerous studies have shown that (Ahmed et al., 2017; Gray et al., 2013; Lei et al., 2017; Liu et al., 2015b; Teipel et al., 2015; Tong et al., 2017; Zhang et al., 2011; Zhu et al., 2015) a variety of neuroimaging data can provide complementary information, and the information fusion from different modalities can enhance diagnostic performance. Therefore, the accuracy of using multi-modal data for AD diagnosis is better than that of single modality. For example, Zhang et al. (Zhang et al., 2011) and Liu et al. (Liu et al., 2015b) used two modal data (including MRI and PET) for AD diagnosis. Lei et al. (Lei et al., 2017) used MRI, PET and cerebrospinal fluid (CSF) for regression and classification of AD. Tong et al.(Tong et al., 2017) used MRI, PET, CSF and genes for AD/MCI classification.

Although the current AD diagnostic methods involved with multi-modal data have good effects, there are still some problems that may limit the classification performance. When we extract features from neuroimaging, there are a lot of redundancy or unrelated features, which will lead to poor classification performance. Therefore, how to remove redundant or unrelated features is a very important step in AD diagnosis. At this stage, there are some feature selection methods to detect the brain features associated with AD. For example, Liu et al. (Liu et al., 2016a; Liu et al., 2015a) used the hierarchical relationship between different template data to establish a structurally constrained integrated learning AD diagnostic prediction model. Peng et al. (Peng et al., 2018) used l_1,p-norm to construct the sparsity-constrained objective function and projected it into a new space for AD diagnosis classification. Zhu et al.(Zhu et al., 2015) combined two subspace learning methods, namely linear discriminant analysis and the projection is locally maintained to select features in the brain image. Jie et al. (Jie et al., 2015) proposed a manifold regularization multi-task feature learning method, which uses multi-task learning and manifold-based Laplacian regularization to maintain the intrinsic correlation between multiple modal data, thereby adding more discriminative features. Zu et al. (Zu et al., 2016) proposed a label-aligned multi-task feature learning method which adds a new label-aligned regularization term to the objective function of standard multi-task feature selection to ensure that all multi-modal subjects with the same class labels should be close in the new feature-reduced space.

However, one drawback of existing methods is that they do not take full advantage of the similarity relationships between samples. This relationship is a significant prior knowledge, because there are certain differences and commonalities between samples, and it is important to make rational use of this information. In many practical problems, it is critical to represent structural information between samples consistently. As the data types of different modalities are different, if the complex relationship between samples is expressed by Euclidean distance or other simple metrics, the structure or topology information will be lost. In simple terms, a reasonable representation of the complex relationship between samples facilitates the selection of more distinguishing features and further improves subsequent classification performance. In many applications, researchers have used a similarity matrix generated by random forests (Breiman, 2001) to represent complex relationships between samples. For example, Tong et al. (Tong et al., 2017) constructed a graph using a similarity matrix and then merged the multi-modal data using a graph fusion method. Gray et al. (Gray et al., 2013) used the similarity between samples to construct a manifold learning model and then used random forests for classification. Here, we use the random forest approach to provide similarity measures for multi-modal data.

In this paper, we propose a novel multi-modal neuroimaging feature selection method with consistent metric constraint (MFCC). The unique loss function is designed to include a regularization term based on the similarity of multi-modal samples, which clearly shows that the samples have a similarity relationship in each modality. Specifically, our proposed method consists of three steps: 1) calculating the similarity between samples, 2) multi-modal feature learning based on sample consistency metrics, and 3) multi-modal fusion and classification. We first construct a similarity matrix for each modality through a random forest, reflecting the similarity relationship between the samples. Then we treat feature learning in each modality as a single learning task and transform multi-modal classification tasks into multi-task learning (MTL) problems. MTL uses the correlation between tasks to learn multiple tasks and integrate information for each task, thus enhancing single-task learning performance. Specifically, we introduce a l_2,1-norm for joint selection features, which can ensure that different morphological features of the same brain region will be selected in different modalities. We then add regularization terms based on sample similarity to the standard multi-task objective function. Finally, we use a multi-kernel support vector machine (MK-SVM) to fuse the selected features for final classification. In order to verify the proposed method, we conduct experimental verification on ADNI-1 and ADNI-2 datasets. The results show that our proposed method is more accurate than the start-of-the-art methods.

Materials and workflow

Datasets

In this study, we performed experimental validation using the Alzheimer’s Disease Neuroimaging Initiative (ADNI) datasets. ADNI was launched in 2003 by the National Institute on Aging, the National Institute of Biomedical Imaging and Bioengineering, the Food and Drug Administration, private pharmaceutical companies and non-profit organizations, with a $60 million five-year public-private partnership. 202 subjects with VBM-MRI and FDG-PET brain imaging in ADNI-1 were used herein, including 51 AD subjects, 52 NC and 99 MCI subjects. 99 MCI patients can be further divided into two types, including 43 MCI converters and 56 MCI non-converters. In particular, MCI converters (MCI-C) will develop into AD patients within 18 months, while MCI non-converters (MCI-NC) will remain in its original state. Table 1 lists the demographic characteristics of subjects in the ADNI-1 dataset.

Table 1.

Demographic characteristics of the subjects in ADNI-1 dataset

Subjects	AD	NC	MCI-C	MCI-NC
Number	51	52	43	56
Gender(M/F)	33/18	34/18	28/15	39/17
Age	75.2±7.4	75.3±5.2	75.8±6.8	74.7±7.7
Education	14.7±3.6	15.8±3.2	16.1±2.6	16.1±3.0
MMSE	23.8±2.0	29.0±1.2	26.6±1.7	27.5±1.5
CDR	0.7±0.3	0.0±0.0	0.5±0.0	0.5±0.0

The values are denoted as mean ± standard deviation. MMSE=Mini-Mental State Examination, CDR=clinical dementia score, AD=Alzheimer’s disease, NC=Normal Control, MCI-C=Mild Cognitive Impairment conversion, MCI-NC=Mild Cognitive Impairment non-transformation.

At the same time, we also analyzed the updated dataset ADNI-2. The ADNI-2 assessed participants from the ADNI-1 phases in addition to new participant groups (including elderly controls, significant memory concern (SMC), early mild cognitive impairment (EMCI) subjects, late mild cognitive impairment (LMCI) subjects, and AD patients) in 2011 (http://adni.loni.usc.edu/about/). Compared to the ADNI-1 dataset, the ADNI-2 dataset divides MCI into three subtypes, including SMC, EMCI, and LMCI.

The diagnostic criteria for ADNI-1 and ADNI-2 are consistent. Diagnosis was made using the standard criteria described in the ADNI-2 procedures manual (http://www.adni-info.org). Briefly, NC participants had no subjective or informant-based complaint of memory decline and normal cognitive performance. SMC participants had subjective memory concerns as assessed using the Cognitive Change Index (CCI; total score from first 12 items >16), no informant-based complaint of memory impairment or decline, and normal cognitive performance on the Wechsler Logical Memory Delayed Recall (LM-delayed) and the Mini-Mental State Examination (MMSE) (Risacher et al., 2015); EMCI participants had a memory concern reported by the subject, informant, clinician, abnormal memory function approximately 1 standard deviation below normative performance adjusted for education level on the LM-delayed, an MMSE total score greater than 24;Besides a subjective memory concern as reported by subject, study partner or clinician, Clinical Dementia Rating (CDR) on LMCI subjects was 0.5 and Memory Box (MB) score must beat least 0.5; MMSE score on AD should be between 20 and 26 and CDR should be 0.5 or 1.0.

The ADNI-2 dataset includes VBM-MRI and FDG-PET scans from 913 subjects, including 160 AD, 82 SMC, 460 MCI and 211 NC participants. 460 MCI patients have two phases: EMCI and LMCI. Table 2 lists the demographic characteristics of subjects in the ADNI-2 dataset.

Table 2.

Demographic characteristics of the subjects in ADNI-2 dataset

Subjects	NC	SMC	EMCI	LMCI	AD
Number	211	82	273	187	160
Gender(M/F)	190/101	33/49	153/119	108/79	95/65
Age	76.1±6.5	72.5±5.7	71.5±7.1	73.9±8.4	75.18±7.9
Education	16.4±2.6	16.8±2.7	16.1±2.6	16.4±2.8	15.86±2.8
MMSE	29.0±1.2	29.0±1.2	28.4±1.5	27.7±1.7	24.0±2.6
CDR	0.0±0.1	0.0±0.0	0.5±0.1	0.5±0.1	0.7±0.3

The values are denoted as mean ± standard deviation. NC= Normal Control, SMC=Significant Memory Concern, EMCI=Early Mild Cognitive Impairment, LMCI=Late Mild Cognitive Impairment, AD=Alzheimer’s disease.

In our work, we perform image preprocessing on VBM-MRI and FDG-PET in the ADNI-1 dataset. First, the anterior commissure (AC)-posterior commissure (PC) correlation is implemented on all images, and then the N3 algorithm (Sled et al., 1998) is used to correct the intensity inhomogeneity. Next, we combine brain surface extractor (BSE) (Shattuck et al., 2001) and brain extraction tool (BET) (Smith, 2002) to perform skull stripping on structural MR images. The skull stripping results are further manually performed to ensure the skull clean. After removal of the cerebellum, FMRIB’s Automated Segmentation Tool (FAST) in the FMRIB’s Segmentation Library (FSL) package (Zhang et al., 2001) is used to segment the structural MR images into three different tissues: gray matter (GM), white matter (WM) and cerebrospinal fluid (CSF). Later, we use 4D (hierarchical attribute matching mechanism for elastic registration) HAMMER (Shen et al., 2003), a fully automated 4D map warping method that obtain images of subject markers based on a template with 93 manually labeled ROIs (Kabani et al., 1998). All images based on the 93 labeled ROIs in the template can then be tagged. For each of the 93 ROIs in the labeled MR image, we calculate the volume of the GM as a feature. For FDG-PET, we first align them with the corresponding MR images of the same object using a rigid transformation and then calculate the average intensity of each ROI region in the FDG-PET image as a feature. Finally, for each sample, we totally obtain 93 features from the VBM-MRI image, and another 93 features from the FDG-PET image.

For the ADNI-2 dataset, we align the preprocessed multi-modal image data (VBM-MRI, FDG-PET) with the same visit scan. Then, in the standard Montreal Institute of Neurology (MNI) space, as a 2 × 2 × 2mm³ voxel, we create normalized gray matter density maps from MRI data, and register the FDG-PET scans into the same space by the Statistical Parametric Mapping (SPM) software package (Tzourio-Mazoyer et al., 2002). Based on the MarsBaR anatomical automatic labeling (AAL) map (Ashburner and Friston, 2000), the average gray matter density is measured at 116 ROI levels. The FDG-PET glucose utilization rate and ROIs volume were further extracted. After removal of the cerebellum, imaging measurements of each modality (VBM-MRI, FDG-PET) with 90 ROIs are used as quantitative traits in our experiments.

Analysis workflow

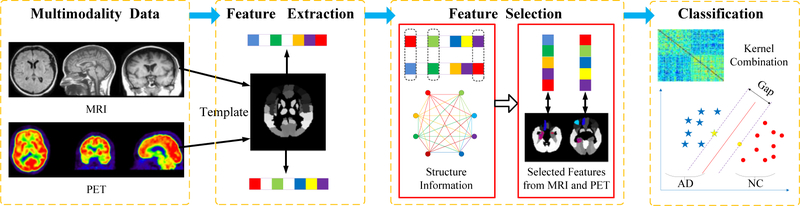
Figure 1 illustrates the framework of AD versus NC identification, including four steps: data preprocessing, feature extraction, feature selection and classification. The innovation of this method is to make full use of the global structure information of the data and incorporate the similarity-metric constraint between samples.

Figure 1. The workflow of AD/MCI versus NC identification.

The framework comprises four steps: data preprocessing, feature extraction, feature selection and classification. First, VBM-MRI and FDG-PET scans are acquired and preprocessed under the pipeline, and the features are extracted from brain ROIs using template. Then the features are selected by the proposed method in this paper, and finally we make predictions using MK-SVM classifier.

Method

We hypothesize that there is a similarity structure among samples in an AD study, and we can map this relationship into the form of a graph. In the constructed graph, the vertices are used to represent the samples, the distance between the samples is used to represent the edge. Thus, the graph is undirected, and the associated matrix of the graph is symmetrical.

However, when solving multi-modal problems with more complex sample relationships, it is more significant to find appropriate inter-sample measurements. If we cannot find a reasonable way to measure multi-modal data, it will lead to inconsistent weights between modalities. In this paper, we want to utilize the random forest method to measure the relationship between samples, which has been widely used in various applications.

Graph for similarity learning

We calculate the distance between samples and convert it (i.e. dissimilarity) to a similarity measurement. Suppose we have n samples, each with s modalities, and d features extracted from each modality. When we calculate the similarity using the features from the v-th modality, we can construct graph G^v = (V^v, E^v) to describe the relationship between the n samples of the v-th modality, where the set V^v of vertices correspond to n samples of the v-th modality, the set E^v of edges capture the pairwise similarity measures among n samples. At this time, we use the adjacency matrix L^v with weight and sizes of n × n to represent the similarity between samples, where L^v (a, b) is used to represent the similarity between sample a and sample b from the v-th modality. The similarity matrix Lv can be calculated in different ways. A common method is to calculate the distance between a pair of samples using the Euclidean distance and normalize it to form the similarity matrix.

Random forests can extract pairs of similarity measures for multiple forms, and random forests provide a consistent way of combining different types of feature data. For example, the similarity derived from random forests has been successfully applied to tumor clustering tasks (Shi and Horvath, 2006). To calculate the similarity between sample a and sample b using a random forest, the measurements of the two samples are passed under each tree in the forest. The similarity L^v(a, b) is initialized to zero. If sample a and sample b are at the same end node of the tree, their similarity L^v(a, b) increases by 1. The final similarity matrix is normalized by dividing L^v by the total number of trees in the forest. Therefore, the diagonal elements of the similarity matrix L^v are equal to one, and the other elements are all numbers greater than zero and less than one. Here we use the random forest MATLAB toolbox (Breiman, 2006) to achieve sample similarity calculations.

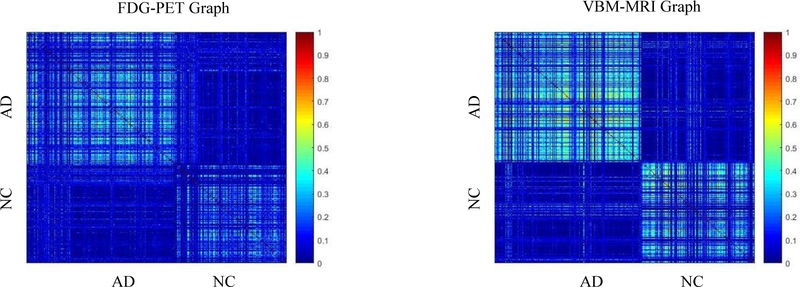
Figure 2 shows an example of a similarity matrix for different modalities. As we can see, charts built with different data types show very different connection patterns, which can provide complementary information for AD versus NC classification.

Figure 2. Sample similarity matrix display.

Construct equations

The essential of the multi-task learning (Caruana, 1997) is to solve several related tasks at the same time and use the related information across multiple tasks to improve the performance of the models. In recent years, multi-task learning has been widely used in many fields, including image classification (Luo et al., 2013), text classification (Liu et al., 2016b), bioinformatics (Xu and Yang, 2011), and so on.

In this study, single modal neuroimaging feature selection and classification can be considered as a single task. Suppose we have s learning tasks (i.e., s modal). ${\text{X}}^v={\left[x_1^v,x_2^v,\dots ,x_N^v\right]}^T\in R^{N\times d}$ is represented as the training data matrix in the v-th task (i.e., the v-th modal), where $x_i^v$ represents the feature column vector of the v-th task of the corresponding i-th sample, d is the dimension of the feature, and N is the sample quantity. Let Y = [y₁, y₂, … ,y_N]^T be the corresponding label vector for N samples. The value of y_i is 1 or −1 (i.e., patient or normal control). It is worth noting that the labels of different morphologies from the same sample are identical. We use a linear function to fit the class label, so the objective function of the multi-task feature selection model is as follows (Argyriou et al., 2008):

$$\underset{\mathrm{W}}{\text{min}}\frac{1}{2}{\sum }_{i=1}^N{\sum }_{v=1}^S{\left(y_i-x_i^{v^T}{w}^v\right)}^2+\lambda \Vert \text{W}{\Vert }_{2,1}$$ (1)

We can write the variables in Eq (1) as vectors, and the formula is as follows:

$$\underset{\text{W}}{\text{min}}\frac{1}{2}{\sum }_{v=1}^S\Vert Y-X^v{w}^v{\Vert }_2^2+\lambda \Vert \text{W}{\Vert }_{2,1}$$ (2)

where w^v ∈ R^d is the vector of the regression coefficients associated with the v-th modality. All s modal vectors form a weight matrix W=[w¹,w², … ,w^s] ∈ R^d×s. In Eq (2), ‖W‖_2,1 is the is the l_2,1-norm of the matrix W, which is defined as follows: $\Vert \text{W}{\Vert }_{2,1}={\sum }_{i=1}^d\Vert w^i{\Vert }_2$, where the superscript i of wⁱ corresponds to the i-th row of the matrix W, and its function is to combine multiple modalities. The constraint of l_2,1-norm encourages most of the feature weight coefficients to be zero, and only a small number of feature weight coefficients are non-zero. These non-zero features are the shared features of all tasks. In particular, the optimal solution will assign a relatively large weight to the feature providing the classification information, and assign zero or small weight to the feature that does not provide the classification information or provides less information. For feature selection, only those features with non-zero weights are retained. In other words, the specification combines multiple tasks and ensures that a small number of common features can be selected together across different tasks, taking into account the correlation between different tasks. The parameter λ before the l_2,1-norm is the coefficient of the regularization term, which is used to control the relative weight of the two items. It is worth noting that when only one task (i.e., feature selection on single modal brain image data) is learned, the loss term $\Vert Y-Xw{\Vert }_2^2$ is represented as the single task and the l_2,1-norm is degenerated into l₁-norm. Thus, Eq (2) will also degenerate to the least absolute shrinkage and selection operator (LASSO) model (Tibshirani, 2011).

Based on the sample similarity matrix, we define the sample similarity regularization as follows:

$$\Delta =w^T{\text{X}}^T\text{LXw}$$ (3)

Intuitively, we want to preserve the global structural information of the data in the original feature space and represent it using a similarity matrix generated by random forest. We construct a similarity matrix in each modality to represent the structure of the near and far relation of the data. So we can define the multi-modal feature selection objective function based on sample similarity as follows:

$$\underset{\text{W}}{\text{min}}\frac{1}{2}{\sum }_{v=1}^s{\Vert Y-{\text{X}}^v{w}^v\Vert }_2^2+\lambda \Vert \text{W}{\Vert }_{2,1}+{\sum }_{v=1}^s{\sigma }^v{\left({\text{X}}^v{w}^v\right)}^T{\text{L}}^v\left({\text{X}}^v{w}^v\right)$$ (4)

where W=[w¹,w²],s = 2. L^v is the sample similarity matrix of the v-th modality. The first term in Eq (4) is the empirical error on the training set calculated by the least squares method, and the second term is the l_2,1-norm, the regularization parameter λ controls the group sparsity in the solution. The last term is the similarity regularization constraint, and σ^v is the regularization parameter to balance the penalties from different modalities.

In our model, using the multi-tasking or multimodal correlation, we can not only jointly select the shared features from different modalities, but also preserve the similarity information between samples in each modality by adding sample similarity regularization terms. The existing multi-modal feature selection algorithm only considers the pairwise relationship between samples or only considers the information between several points in the vicinity of the sample, only uses local information and ignores the global similarity relationship between the sample sets as a whole.

Optimization

As the objective function is not-differentiable and not smooth, there is no way to calculate the gradient of some points of the objective function, so the equation cannot be solved by the gradient descent method. At this stage, there are many ways to solve the objective function formula (4), such as Alternating Direction Method of Multipliers (ADMM) and Accelerated Proximal Gradient (APG) (Chen et al., 2009). In this paper, we use the APG algorithm to solve our problem.

First, we divide the Eq (4) into smooth terms f₁(W) and non-smooth terms f₂(W):

$$f_1(\text{W})=\frac{1}{2}{\sum }_{v=1}^s{\Vert Y-{\text{X}}^v{w}^v\Vert }_2^2+{\sum }_{v=1}^s{\sigma }^v{\left({\text{X}}^v{w}^v\right)}^T{\text{L}}^v\left({\text{X}}^v{w}^v\right)$$ (5)

$$f_2(\text{W})=\lambda \Vert \text{W}{\Vert }_{2,1}$$ (6)

Then we use formula (7) to approximate f₁(W)+ f₂(W) :

$$Q_{{\alpha }^t}\left(\text{W},{\text{W}}^{(t)}\right)=f_1\left({\text{W}}^{(t)}\right)+\langle \text{W}-{\text{W}}^{(t)},\nabla f_1\left({\text{W}}^{(t)}\right)\rangle +\frac{l}{2}\Vert \text{W}-{\text{W}}^{(t)}{\Vert }_F^2+f_2(\text{W})$$ (7)

where 〈X₁, X₂〉 represents the trace of the matrix ${\text{X}}_1^T{\text{X}}_2,{\Vert ·\Vert }_F$ is the Frobenius norm, $\nabla f_1\left({\text{W}}^{(t)}\right)$ is the gradient of f₁(W) at point W^(t) of the t-th iteration, and α^t is the step factor of the t-th iteration, the value of which is obtained by linear search. The update step for the APG algorithm is as follows:

$${\text{W}}^{(t+1)}=\underset{\text{W}}{\text{arg\hspace{0.17em}min}}\left(\frac{1}{2}{\Vert \text{W}-\left({\text{W}}^{(t)}-\frac{1}{{\alpha }^t}\nabla f_1\left({\text{W}}^{(t)}\right)\right)\Vert }_F^2+\frac{1}{{\alpha }^t}{f}_2(\text{W})\right)$$ (8)

And formula (6) can be solved by formula (8):

$${\text{P}}^{(t)}={\text{W}}^{(t)}+\frac{1-{\gamma }_{t-1}}{{\gamma }_{t-1}}{\gamma }_t\left({\text{W}}^{(t)}-{\text{W}}^{(t-1)}\right)$$ (9)

where ${\gamma }_t=\frac{2}{2+t}$, and the convergence speed of this algorithm is $O\left(\frac{1}{T^2}\right)$, T is the maximum number of iterations of the calculation.

Classification

We use the MK-SVM (Zhang et al., 2011) to classify the data after feature selection. The prior studies have shown that MK-SVM has a good classification performance for multi-modal data. Given a training set, the kernel function of the v-th modal is $k^v\left(x_i^v,x_j^v\right)={\varphi }^v{\left(x_i^v\right)}^T{\varphi }^v\left(x_j^v\right)$. We use linear kernels to fuse multi-modal data with a kernel function of $k^v\left(x_i,x_j\right)={\sum }_{v=1}^s{\beta }^v{k}^v\left(x_i^v,x_j^v\right)$, where β^v is the weight coefficient of the v-th modality. The dual form of the MK-SVM is as follows:

$$\begin{gathered} \underset{a}{\text{max}}\sum _{i=1}^N{\alpha }_i-\frac{1}{2}\sum _{i,j}{\alpha }_i{\alpha }_j{y}_i{y}_j\sum _{v=1}^s{\beta }^v{k}^v\left(x_i^v,x_j^v\right) \\ \text{ s.t. }{\sum }_{i=1}^N{\alpha }_i{y}_i=0, \\ {a}_i\ge 0,i=1,2,\dots ,N \end{gathered}$$ (10)

where α is a Lagrange multiplier. In this paper, the SVM classifier can be solved by using LIBSVM toolbox (Chang and Lin, 2011). We find the optimal value of β^v by cross-validation on the training set by grid search in the range of [0,1].

Performance evaluation

Cross-validation is a commonly used method in machine learning to build models and validate model parameters. As the number of subjects is limited, cross-validation is to reuse data to evaluate the quality of model prediction. In this study, we used 10-fold cross-validation that could reduce the bias by averaging the results of different group testing. Specifically, we divided the dataset into 10 parts. In each cross-validation experiments, we took nine of them as a training set and one as a test set, so that we performed 10 experiments independently, eliminating errors caused by random division. We used MRI and PET brain image data from ADNI-1 to verify the model in three sets of comparison experiments, including AD vs. NC, MCI vs. NC, and MCI-C vs. MCI-NC. Three sets of comparative experiments, including AD vs. NC, LMCI vs. NC, and EMCI vs. LMCI were also performed on the same model using ADNI-2 dataset. We used accuracy (ACC), sensitivity (SEN), specificity (SPE), the area under the curve (AUC), p-value and ROC curve as evaluation indicators.

Our proposed multi-modal neuroimaging feature selection with consistent metric constraint (denoted as MFCC) method is compared with several existing popular methods, including directly concatenating the features of MRI and PET into a vector and using the SVM classification, involving 1) methods without feature selection (denote as Baseline-SVM), 2) LASSO method (Tibshirani, 2011) (denote as LASSO-SVM), and 3) t-test method, the p-value significance threshold of the t-test is chosen to be 0.05. We also comprise the following multi-kernel methods (Zhang et al., 2011) (denote as t-test-SVM), 1) the multi-kernel method without feature selection (denoted as Baseline-MK-SVM), 2) LASSO-based (Tibshirani, 2011) multi-kernel method (denoted as LASSO-MK-SVM), and 3) multi-kernel method based on t-test (denoted as t-test-MK-SVM). It is classified using an SVM with a linear kernel. We also compare the feature selection method with the l_2,1-norm (denoted as Group Lasso-MK-SVM), the similarity matrix by the Euclidean distance calculation (denoted as Euclid-MK-SVM) and the hypergraph strategy (denoted as Hypergraph-MK-SVM). For model selection, the regularization parameters of all methods are selected from the range of {10⁻⁹, 10⁻⁸, … ,10,10²}.

Results

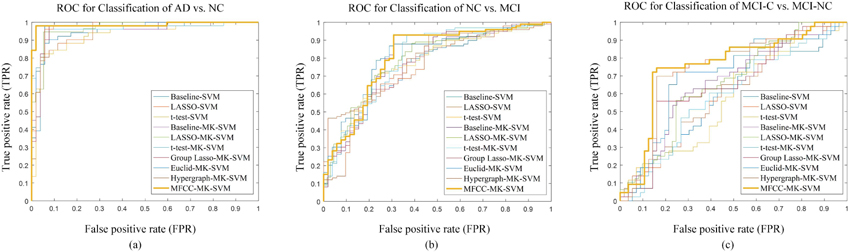
The detailed classification results on ADNI-1 dataset are summarized in Table 3. Figure 3 plots the ROC curves of all the methods. Specifically, the accuracy values of our proposed methods for AD versus NC, MCI versus NC, and MCI-C versus MCI-NC are 97.60%, 84.47% and 77.76%, respectively on the ADNI-1 dataset. Correspondingly, the AUC values of our proposed method are 0.98, 0.86 and 0.71 respectively.

Table 3.

Classification performance of different methods on ADNI-1

(a) AD versus NC
Method	ACC	SEN	SPE	AUC	P-value
Baseline-SVM	89.35±8.83	90.39	88.27	0.94	<0.001
LASSO-SVM	87.57±9.12	89.02	86.15	0.95	<0.001
t-test-SVM	86.75±10.33	83.92	89.42	0.93	<0.001
Baseline-MK-SVM	94.53±6.55	94.90	94.04	0.96	<0.001
LASSO-MK-SVM	93.74±7.81	95.00	91.60	0.97	<0.001
t-test-MK-SVM	93.45±7.35	94.90	91.92	0.96	<0.001
Group Lasso-MK-SVM	94.53±6.80	94.90	94.04	0.96	<0.001
Euclid-MK-SVM	95.08±6.77	97.25	92.88	0.97	0.004
Hypergraph-MK-SVM	94.77±6.39	97.25	92.31	0.97	<0.001
MFCC-MK-SVM	97.60±5.03	98.43	96.73	0.98	--
(b) MCI versus NC
Method	ACC	SEN	SPE	AUC	P-value
Baseline-SVM	70.75±10.04	79.80	53.46	0.76	<0.001
LASSO-SVM	72.46±11.05	83.03	52.31	0.78	<0.001
t-test-SVM	72.79±9.53	85.96	47.69	0.77	<0.001
Baseline-MK-SVM	80.09±8.24	87.47	65.96	0.79	<0.001
LASSO-MK-SVM	81.89±8.89	90.24	62.27	0.79	0.022
t-test-MK-SVM	81.71±9.43	91.82	62.31	0.79	0.019
Group Lasso-MK-SVM	79.76±6.91	95.76	49.23	0.77	<0.001
Euclid-MK-SVM	81.48±8.48	89.49	66.15	0.80	0.007
Hypergraph-MK-SVM	81.20±6.55	94.14	56.54	0.75	<0.001
MFCC-MK-SVM	84.47±6.83	94.04	66.15	0.81	--
(c) MCI-C versus MCI-NC
Method	ACC	SEN	SPE	AUC	P-value
Baseline-SVM	53.95±15.12	44.65	61.07	0.59	<0.001
LASSO-SVM	54.57±14.87	45.12	61.79	0.60	<0.001
t-test-SVM	50.76±13.74	34.42	63.39	0.57	<0.001
Baseline-MK-SVM	69.17±12.77	57.44	78.04	0.66	<0.001
LASSO-MK-SVM	71.88±13.36	61.97	76.00	0.66	<0.001
t-test-MK-SVM	63.05±12.60	50.70	72.32	0.59	<0.001
Group Lasso-MK-SVM	70.86±11.37	62.33	77.14	0.65	<0.001
Euclid-MK-SVM	72.00±12.97	69.77	73.57	0.70	<0.001
Hypergraph-MK-SVM	73.64±11.19	66.28	79.11	0.74	0.008
MFCC-MK-SVM	77.76±10.59	67.44	85.54	0.76	--

Figure 3.

The ROC curves of all comparison methods on ADNI-1: (a) the classification of AD vs. NC, (b) the classification of NC vs. MCI, (c) the classification of MCI-C vs. MCI-NC. The horizontal axis represents the false positive rate; the vertical axis represents the true positive rate. The area under the curve (AUC) indicates the diagnosis power.

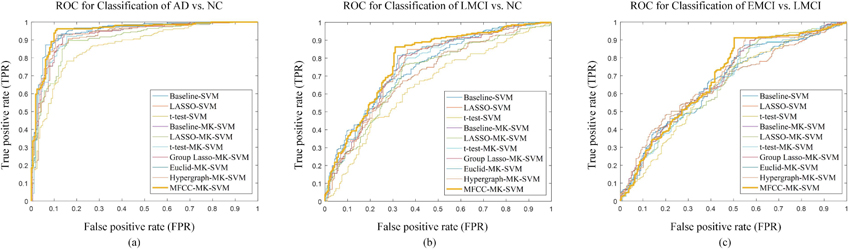
We have treated the ADNI-2 as a larger independent dataset and validated our proposed method on it. The classification results on the ADNI-2 dataset are summarized in Table 4. Figure 4 plots the ROC curves of all the methods. Specifically, the accuracy values of our proposed methods for AD versus NC, MCI versus NC, and MCI-C versus MCI-NC are 93.72%, 78.47% and 73.87%, respectively on the ADNI-2 dataset. Correspondingly, the AUC values of our proposed method are 0.95, 0.78 and 0.7, respectively. In addition, we have made a competing test that our proposed approach can also achieve better performances no matter what processing framework and template parcellation have been applied to dataset.

Table 4.

Classification performance of different methods on ADNI-2

(a) AD versus NC
Method	ACC	SEN	SPE	AUC	P-value
Baseline-SVM	91.13±5.04	92.37	89.50	0.95	<0.001
LASSO-SVM	85.90±5.51	89.34	81.38	0.92	<0.001
t-test-SVM	79.60±6.93	84.31	73.38	0.86	<0.001
Baseline-MK-SVM	91.72±4.15	93.36	89.56	0.94	0.006
LASSO-MK-SVM	86.82±4.57	89.57	82.66	0.90	<0.001
t-test-MK-SVM	90.06±4.35	92.75	86.50	0.93	<0.001
Group Lasso-MK-SVM	89.92±4.42	93.65	85.00	0.93	<0.001
Euclid-MK-SVM	91.72±4.15	93.36	89.56	0.94	0.006
Hypergraph-MK-SVM	91.19±4.12	94.17	87.25	0.94	<0.001
MFCC-MK-SVM	93.72±3.38	95.17	91.81	0.95	--
(b) LMCI versus NC
Method	ACC	SEN	SPE	AUC	P-value
Baseline-SVM	69.23±7.25	74.46	63.37	0.74	<0.001
LASSO-SVM	66.61±6.60	71.66	60.96	0.71	<0.001
t-test-SVM	62.81±6.12	70.38	54.28	0.65	<0.001
Baseline-MK-SVM	74.35±5.99	81.42	66.42	0.77	<0.001
LASSO-MK-SVM	71.46±6.00	76.86	62.72	0.71	<0.001
t-test-MK-SVM	73.00±5.76	81.52	63.42	0.75	<0.001
Group Lasso-MK-SVM	74.35±6.15	81.42	66.42	0.77	<0.001
Euclid-MK-SVM	74.35±5.99	81.42	66.42	0.77	<0.001
Hypergraph-MK-SVM	75.32±5.79	85.07	64.39	0.75	<0.001
MFCC-MK-SVM	78.47±5.61	85.88	70.16	0.78	--
(c) EMCI versus LMCI
Method	ACC	SEN	SPE	AUC	P-value
Baseline-SVM	64.08±6.79	76.48	45.99	0.66	<0.001
LASSO-SVM	63.55±7.13	78.32	42.03	0.66	<0.001
t-test-SVM	63.32±5.35	87.33	28.29	0.64	<0.001
Baseline-MK-SVM	70.01±5.52	85.20	47.86	0.68	<0.001
LASSO-MK-SVM	68.43±4.83	88.92	37.31	0.66	<0.001
t-test-MK-SVM	69.10±5.25	85.05	45.83	0.66	<0.001
Group Lasso-MK-SVM	70.22±4.40	90.62	40.43	0.68	<0.001
Euclid-MK-SVM	70.01±5.52	85.20	47.86	0.68	<0.001
Hypergraph-MK-SVM	71.45±4.43	90.95	42.99	0.68	0.001
MFCC-MK-SVM	73.87±4.77	90.55	49.52	0.70	--

Figure 4.

The ROC curves of all comparison methods on ADNI-2: (a) the classification of AD vs. NC, (b) the classification of LMCI vs. NC, (c) the classification of EMCI vs. LMCI. The horizontal axis represents the false positive rate; the vertical axis represents the true positive rate. The area under the curve (AUC) indicates the diagnosis power.

Besides MFCC-MK-SVM, we also adopt other different classifiers: random forest (RF) and K nearest neighbor (KNN) algorithm. The experimental results for the different classifiers in the ADNI-1 data set are presented in Table 5. The experimental results for the different classifiers in the ADNI-2 dataset are presented in Table 6. We use random forest as the classifier, and the number of trees in the random forest is set to 1000, and the number of features selected in the RF is $\sqrt{d}$. In the KNN algorithm, we set the parameter K to 5. The experimental results show that the classifier MK-SVM can achieve better performances.

Table 5.

Comparison of different classifiers experimental results on ADNI-1

Method	AD versus NC				MCI versus NC				MCI-C versus MCI-NC
	ACC	SEN	SPE	AUC	ACC	SEN	SPE	AUC	ACC	SEN	SPE	AUC
RF	93.82	86.47	72.12	0.90	79.16	90.91	26.15	0.71	70.72	56.05	54.29	0.59
KNN	95.54	82.35	73.85	0.81	82.40	85.96	29.62	0.53	75.04	54.42	49.11	0.60
MK-SVM	97.60	98.43	96.73	0.98	84.47	94.04	66.15	0.81	77.76	67.44	85.54	0.76

Table 6.

Comparison of different classifiers experimental results on ADNI-2

Method	AD versus NC				LMCI versus NC				EMCI versus LMCI
	ACC	SEN	SPE	AUC	ACC	SEN	SPE	AUC	ACC	SEN	SPE	AUC
RF	87.03	84.60	67.06	0.82	71.44	72.94	45.72	0.60	69.11	81.87	29.36	0.58
KNN	84.37	82.23	65.31	0.77	69.81	64.69	47.65	0.55	69.14	69.49	39.48	0.55
MK-SVM	93.72	95.17	91.81	0.95	78.47	85.88	70.16	0.78	73.87	90.55	49.52	0.70

In summary, the accuracy of our proposed method is always superior to that of other methods in the above cases, indicating that our method has better diagnostic performances. In addition, in most cases, the proposed method achieves higher sensitivity than other methods. It is worth noting that in our experiment, there is a significant difference between sensitivity and specificity. For example, each method has relatively high sensitivity but low specificity. In medical diagnosis, it is different to misjudge a patient as normal or to misjudge a normal sample as a patient. Obviously, the former is costly and may delay the treatment. Therefore, high sensitivity is very important for disease diagnosis and beneficial for medical diagnosis.

Discussion

The aim of this paper is to develop a novel method for addressing two issues, including 1) selecting brain ROIs related to AD and 2) classification and diagnosis of AD. All experiments have been carried out on the ADNI-1 and ADNI-2 datasets to demonstrate the effectiveness of the proposed method MFCC. The results show that this method can not only classify AD using complementary information from multimodal imaging data, but also help discover disease-related biomarkers and understand the pathological mechanism of AD. In the following sections, we will first discuss issues related to construction of random forest, similarity and consistency measurement, multi-modal neuroimaging analysis, parameter settings, and clinical implications. After that, we will discuss strengths of the proposed method in comparison with competing methods as well as possible limitations warranting further investigation.

Construction of random forest

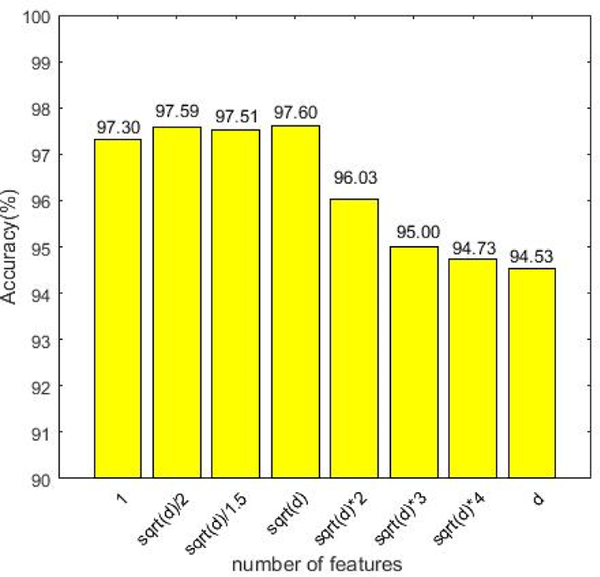
In this paper, the similarity matrix of each modality is constructed by random forest method. Specifically, this experiment sets the parameters of the random forest as the default values (the number of trees is 1000, and the number of features is $\sqrt{d}$). Now we discuss the influence of the number of features in random forests in the experimental results. The results are shown in Figure 5, where the number of features varies in the range of $\left\{1,\frac{\sqrt{d}}{2},\frac{\sqrt{d}}{1.5},\sqrt{d},\sqrt{d}*2,\sqrt{d}*3,\sqrt{d}*4,d\right\}$. As can be seen from Figure 5, when the number of features is set to be $\sqrt{d}$, the experimental results are optimal. However, when the number of features is set to be $\sqrt{d}*2$, the accuracy will rapidly decline. The fundamental reason may be that when there are too many features, redundant features will affect the steady of the similarity, that is, the similarity matrix calculated by random forest may not be able to describe the global relationship between samples.

Figure 5.

The classification results on the different number of features in the random forest. The horizontal axis represents the number of features; the vertical axis represents the classification accuracy for AD diagnosis.

Similarity metrics learning

Other methods are compared to sample similarity measured by random forests. Specifically, the simple graph describes the relationship between pairs of samples, and the hypergraph describes the high-order and multi-relationships between samples. The above two methods can only capture the local relationship between samples, but cannot fully utilize the information provided by the structural data, resulting in the loss of global information.

Sample similarity metrics learning via random forest has been used in a variety of applications, such as disease classification and image segmentation (Mitra et al., 2014). In addition, some recent studies have incorporated the computational similarity methods into medical imaging analysis (Zimmer et al., 2017). For example, Veronika et al. [47] proposed a method for calculating the similarity via random forests and combining images to determine the classification of neonatal brain disease. Tong et al. (Tong et al., 2017) proposed a multi-modal nonlinear graph fusion method. They used four modal data points to create four maps using the similarity of random forests, and then used a nonlinear approach to fuse and reclassify the four maps. However, they did not consider the inherent information of different data modalities.

In contrast, our proposed multi-modal neuroimaging feature selection model with the consistent metric constraint not only utilizes the global relationship between samples, but also makes full use of the supplementary information provided by different modalities. The experimental results have achieved higher classification accuracy and AUC, which have demonstrated the effectiveness of our proposed method.

Multi-modal neuroimaging analysis

Recent studies on the diagnosis of AD have shown that different image modalities can provide complementary information to help identify AD (Sui et al., 2012; Tong et al., 2017). It has been reported that the fusion of multiple modalities can improve diagnostic performance. A number of different approaches have been proposed to fuse biomarkers of different modalities to produce more powerful classifiers (Gray et al., 2013; Zhang et al., 2011). The easiest way to combine multi-modal data is to concatenate the features obtained from the different modalities into the row vectors for each sample. For example, Walhovd et al. (Walhovd et al., 2010) took the feature vectors as simple connection processing. Gray et al. (Gray et al., 2013) used multiple random forest classifiers to fuse multi-modal data for classification of AD. In addition, the multi-modal classification method of voting with multiple classifiers is a common ensemble learning strategy, but may introduce bias due to the use of multimodality. An effective way to fuse different modalities is based on kernel methods such as multi-kernel learning (Zhang et al., 2011). A single kernel matrix is calculated for each modality, and a final kernel matrix is obtained by their linear combination. Several results show that the latter can achieve better performance than the former.

In order to evaluate the validity of multi-modal data classification, we performed experiments and compared them with multi-modal and single modal data. We use the proposed classification framework to compare the results of single modal and multi-modal experiments on the ADNI-1 and ADNI-2 datasets. The corresponding results are shown in Table 7 and Table 8. As we have seen, the proposed method with two modalities has better performance than the single modality. The results further indicate that multi-modal data contain supplemental information and can achieve better classification performance than a single modality.

Table 7.

Comparison of single model and multi-modal experimental results on ADNI-1

Method	AD versus NC				MCI versus NC				MCI-C versus MCI-NC
	ACC	SEN	SPE	AUC	ACC	SEN	SPE	AUC	ACC	SEN	SPE	AUC
VBM-MRI	92.38	81.18	90.58	0.92	81.35	80.30	56.54	0.77	72.94	40.93	68.04	0.51
FDG-PET	92.66	87.65	84.04	0.93	79.70	82.22	46.92	0.69	72.34	33.72	68.75	0.54
multi-modal	97.60	98.43	96.73	0.98	84.47	94.04	66.15	0.81	77.76	67.44	85.54	0.76

Table 8.

Comparison of single model and multi-modal experimental results on ADNI-2

Method	AD versus NC				LMCI versus NC				EMCI versus LMCI
	ACC	SEN	SPE	AUC	ACC	SEN	SPE	AUC	ACC	SEN	SPE	AUC
VBM-MRI	86.63	90.28	81.81	0.93	71.20	78.01	63.32	0.76	63.18	83.70	32.62	0.64
FDG-PET	80.06	86.02	71.94	0.85	66.77	75.45	55.94	0.68	64.69	78.17	44.44	0.63
multi-modal	93.72	95.17	91.81	0.95	78.47	85.88	70.16	0.78	73.87	90.55	49.52	0.70

The pathological changes from the same ROIs might be examined through structural and functional radiologic imaging, simultaneously. Thus performing ROI feature selections across multimodalities is very helpful to suppress noises in the individual modality features(Hao et al., 2016; Li et al., 2019; Sarter et al., 1996).

The structural and functional features with great heterogeneity can provide essential complementary information for brain disease analysis and diagnosis from the aspect of feature fusion in ensemble learning community. Here, the different measurements from the same ROIs just express the structural and functional changes, which has the characteristics of heterogeneity. The experiment results have showed the joint feature selection from the same ROIs can achieve higher performances, which has further demonstrated the effectiveness of ‘consistency’.

Parameter settings

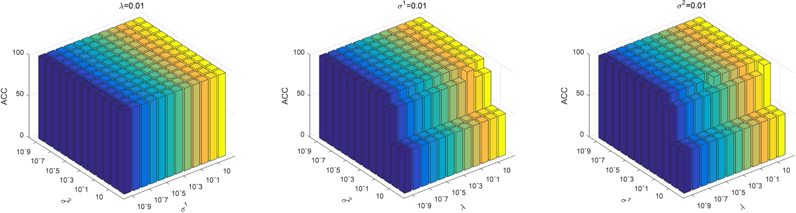
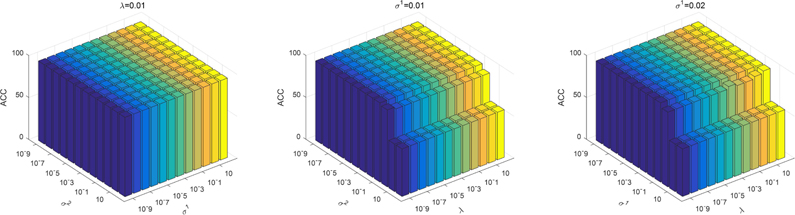
In the objective function of our proposed model, there are three regularization parameters (i.e., λ,σ¹, σ²) that need to be set. They balance the relative contribution of the group sparsity regularization term and the two-sample consistency metric regularization terms. In this section, we study the effect of regularization parameters on classification performance. Specifically, we first fix the value of λ to 0.01 and change σ¹ and σ² in the range of {10⁻⁹,10⁻⁸, … ,10²}. Then we fix σ¹ to 0.01 and change λ and σ² in the range of {10⁻⁹,10⁻⁸, … ,10²}. Finally, we fixed the value of σ² to 0.01 and changed λ and σ² in the range of {10⁻⁹,10⁻⁸, … ,10²}. The corresponding test results on ADNI-1 and ADNI-2 datasets are shown in Figure 6 and Figure 7, respectively. We can see that the proposed method slightly fluctuates when changing the parameter λ, σ¹, σ², indicating that our proposed method is not particularly sensitive to parameter values.

Figure 6.

Accuracy of AD vs. NC classification with respect to different parameter values in ADNI-1 dataset. We fix one parameter to 0.01 respectively and vary the other two in the range of {10⁻⁹,10⁻⁸, … ,10²}. The X-axis and Y-axis represent the diverse value of parameters and the Z-axis represents the classification accuracy for AD diagnosis.

Figure 7.

Accuracy of AD vs. NC classification with respect to different parameter values in ADNI-2 dataset. We fix one parameter to 0.01 respectively and vary the other two in the range of {10⁻⁹, 10⁻⁸, …,10²}. The X-axis and Y-axis represent the diverse value of parameters and the Z-axis represents the classification accuracy for AD diagnosis.

Clinical implications

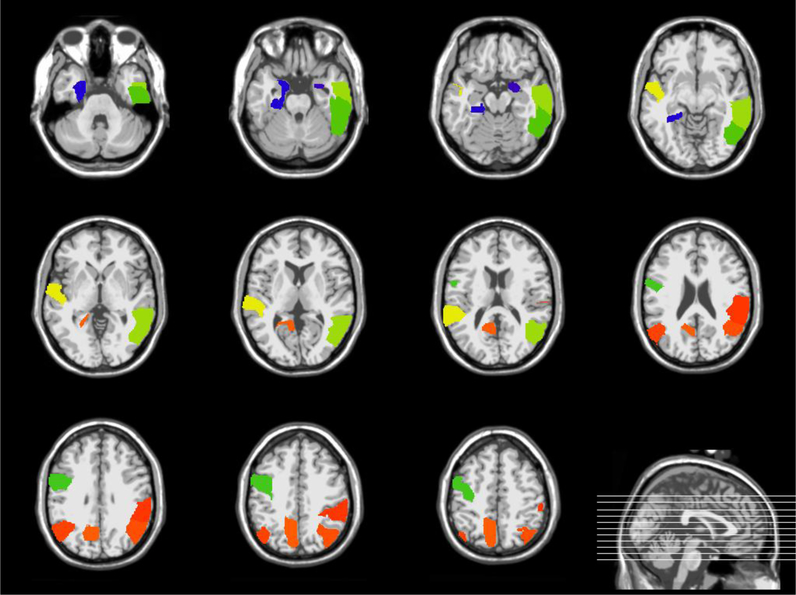
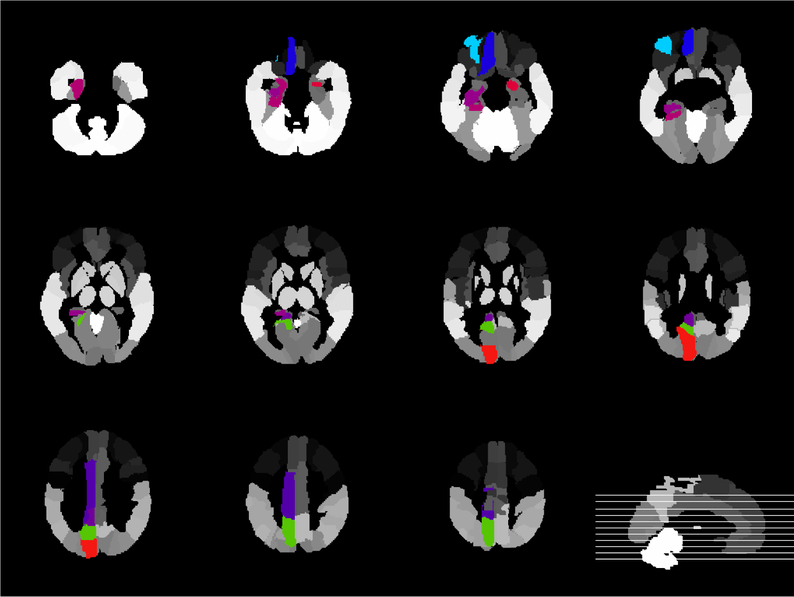
It is important to detect the risk ROIs associated with brain disease. We count the top 10 most frequently selected regions in the AD and NC classifications as the most discriminative markers. The top 10 regions in the ADNI-1 dataset are Middle Temporal Gyrus Right, Lateral Occipitotemporal Gyrus Left, Hippocampal Formation Left, Supramarginal Gyrus Right, Precentral Gyrus Left, Amygdala Right, Angular Gyrus Left, Angular Gyrus Right, Precuneus Left, Inferior Temporal Gyrus Right. The top 10 regions in the ADNI-2 dataset are Frontal Sup Medial Left, Precuneus Left, Amygdala Right, Cuneus Left, ParaHippocampal Left, Frontal Mid Orb Left, Cingulum Mid Left, Rectus Left, Cingulum Post Left, Hippocampus Left. As can be seen from Figures 8 and Figure 9, most selected ROIs, such as Hippocampus and Amygdala detected simultaneously from different template are consistent with previous studies. According to the reports, the fact that Medial Temporal Lobe structures, including the Hippocampus, are critical for declarative memory is firmly established (Tulving and Markowitsch, 1998). Emotionally significant experiences tend to be well remembered, and the Amygdala has a pivotal role in this process (Roozendaal et al., 2009). Thus, these evidences suggest that the Limbic System (including Hippocampus and Amygdala)(Hopper and Vogel, 1976) should be concerned in AD research.

Figure 8.

Brain regions associated with AD using a 3D atlas Jacob (Kabani et al., 1998) (ADNI-1)

Figure 9.

Brain regions associated with AD using AAL template (Ashburner and Friston, 2000) (ADNI-2)

Comparison with previous studies

The MFCC algorithm proposed in this paper is compared with the ten state-of-the-art competing AD classification algorithms using multi-modal data, including the traditional machine learning methods and the deep learning methods, as shown in Table 9. In order to show the effectiveness of our proposed method and the confidence of the results, we set the same experiment dataset and processing framework following the previous works (Jie et al., 2015; Li et al., 2015; Shi et al., 2018; Suk et al., 2016; Suk and Shen, 2013; Zhang et al., 2011) Accordingly, the ADNI-1 dataset and processing framework (including template parcellation) used in this paper are the same as those used in the literature.

Table 9.

Comparison of the performance of different multi-modal classification algorithms

Algorithms	Subjects	Modalities	AD vs NC	MCI vs NC	MCI-C vs MCI-NC	Algorithm Description
MKL (Zhang et al., 2011)	51AD, 43MCI-C, 56MCI-NC, 52NC	MRI + PET +CSF	93.20	76.40	--	The classical multi-kernel learning (MKL) based algorithm
MTL (Jie et al., 2015)	51AD, 43MCI-C, 56MCI-NC, 52NC	MRI + PET +CSF	95.03	79.27	68.94	The multi-task learning (MTL) based algorithm
M-RBM (Suk et al., 2014)	93AD, 76MCI-C, 128 MCI-NC, 101 NC	MRI + PET	95.35	85.67	75.92	The pioneering multi-modal deep RBM (M-RBM) based feature learning algorithms
SAE (Liu et al., 2015b)	85AD, 67MCI-C, 102 MCI-NC, 77 NC	MRI + PET	91.35	90.42	--	The SAE-based multi-modal neuroimaging feature learning algorithm
SAE-MKL (Suk, 2013)	51AD, 43MCI-C, 56MCI-NC, 52NC	MRI + PET +CSF	98.80	90.70	83.30	The combination of SAE-based feature learning and MKL classification (SAE-MKL) algorithm
DW-S2MTL (Suk et al., 2016)	51AD, 43MCI-C, 56MCI-NC, 52NC	MRI + PET +CSF	95.09	78.77	73.04	The deep sparse multi-task learning based feature selection (DW-S2MTL) algorithm
Dropout-DL (Li et al., 2015)	51AD, 43MCI-C, 56MCI-NC, 52NC	MRI + PET +CSF	91.40	77.40	70.10	The dropout based robust multi-task deep learning (Dropout-DL) algorithm
SDSAE (Shi et al., 2017)	94AD, 121MCI, 123NC	Longitudinal MRI	91.95	83.72	--	The SDSAE-based feature learning algorithm
NGF (Tong et al., 2017)	37AD, 75MCI, 35NC	MRI + PET +CSF + Genetics	98.10	82.40	77.90	The nonlinear graph fusion (NGF) based algorithm
MM-SDPN-SVM (Shi et al., 2018)	51AD, 43MCI-C, 56MCI-NC, 52NC	MRI + PET	97.13	87.24	78.88	The multi-modal stacked deep polynomial networks and SVM

It is worth noting that the proposed method has performed better than at least one of the deep learning methods in this comparison. In particular, the accuracy is higher than that of the deep learning methods in AD versus NC classification when using only two imaging modality (i.e., MRI and PET). One essential reason may be that our proposed method is able to fully utilize the global structure information from the data. As the objective function is induced the similarity constraint between different samples, the selected features are more informative and discriminative in this optimization problem. While several existing deep learning models in literature haven’t incorporated the sufficient prior information yet. Furthermore, when the number of train samples is highly limited, the capacity of deep feature representations may be weaker than that of original hand-draft features from candidate pathogenic brain regions. Accordingly, in this study, it is more effective to design a simple but well-defined feature selection model with to address the issue of AD classification.

Limitations

Despite its promising performance, the proposed method still has a few. First, our proposed method utilizes two types of neuroimaging biomarkers (i.e., MRI and PET) from the ADNI dataset. Actually, in the ADNI dataset, many subjects also have other type of biomarkers, such as CSF, plasma, genetics data, and so on. In the future, we will examine whether adding more modal can further improve performance.

Secondly, we only studied the two-category problem and did not test the performance on the multi-class problem. It is valuable to accurately diagnose patients at a certain stage of the disease. In addition, we did not take advantage of quantitative outcomes in the ADNI dataset, such as MMSE and other cognitive scores. It could be interesting to integrate more complicated relationship learning in a multi-task learning framework rather than a single model for feature selection.

Actually, it is quite different to determine which template should be selected as the best one from multiple diverse templates. Due to potential bias associated with the use of a single template, the feature representations generated from a single template may not be sufficient enough to reveal the underlying complex differences between groups of patients and normal controls. Recently, some researchers have proposed several methods that can take advantage of multiple diverse templates to compare group differences more efficiently (Huang et al., 2019; Koikkalainen et al., 2011; Liu et al., 2016a; Liu et al., 2015a). The future research direction is to further investigate how to make use of the multiple diverse templates and detect features from highly consistent regions for exploring some biologically meaningful results.

Finally, since we currently only focus on the ROI features, it is helpful to integrate the non-handcrafted features using deep learning techniques as well. Another interesting future direction is to investigate both visual and represented features to facilitate the diagnosis and prognosis for the clinical applications.

Conclusion

In summary, this paper presents a novel feature selection method with consistent metric constraint for the diagnosis of AD. This method is used to combine complementary information provided by multi-modal neuroimaging data for feature selection and further classification. Specifically, we devise regularization terms that consider structure information such as feature association and sample similarity inherent in this analysis framework. In our extensive experiments on ADNI datasets, we demonstrate the effectiveness of the proposed method by comparing it with the state-of-the-art methods. We believe this work will further motivate the exploration of multi-modal models that would improve the predictions in AD.