Abstract
Background:
In neurodegenerative diseases such as Alzheimer’s and Parkinson’s, excessive irons as well as lactoferrin (Lf), but not transferrin (Tf), have been found in and around the affected regions of the brain. These evidences suggest that lactoferrin plays a critical role during neurodegenerative diseases, although Lf-mediated iron transport across blood-brain barrier (BBB) is negligible compared to that of transferrin in normal condition. However, the kinetics of lactoferrins and lactoferrin-mediated iron transport are still unknown.
Method:
To determine the kinetic rate constants of lactoferrin-mediated iron transport through BBB, a mass-action based ordinary differential equation model has been presented. A Bayesian framework is developed to estimate the kinetic rate parameters from posterior probability density functions. The iron transport across BBB is studied by considering both Lf- and Tf-mediated pathways for both normal and pathologic conditions.
Results:
Using the point estimates of kinetic parameters, our model can effectively reproduce the experimental data of iron transport through BBB endothelial cells. The robustness of the model and parameter estimation process are further verified by perturbation of kinetic parameters. Our results show that surge in high-affinity receptor density increases lactoferrin as well as iron in the brain.
Conclusions:
Due to the lack of a feedback loop such as iron regulatory proteins (IRPs) for lactoferrin, iron can transport to the brain continuously, which might increase brain iron to pathological levels and can contribute to neurodegeneration.
General significance:
This study provides an improved understanding of presence of lactoferrin and iron in the brain during neurodegenerative diseases.
Keywords: Lactoferrin, Parameter estimation, Bayesian inference, Blood-brain barrier, Iron transport
1. Introduction
Abnormally high levels of irons have been demonstrated in the brain cells during several neurodegenerative disorders such as Parkinson’s disease (PD) [1–5] and Alzheimer’s disease (AD) [2, 6]. Although little is known about the etiology of these neurodegenerative diseases, evidence suggests that misregulation of iron metabolism is a major player [1, 3, 7, 8]. For instance, altered iron metabolism leads to the excess free radical formation, which in turn results in cell death [8, 9]. In addition, excessive intracellular irons produce both oxidative stress and mitochondrial dysfunction, which causes cytoskeletal damage and neuronal death [1, 7].
Iron can enter the brain through the blood-brain barrier [5]. Among various iron transport mechanisms, transferrin-mediated iron transcytosis is the most dominant in BBB endothelial cells [10, 11]. However, the possibility of transferrin involvement in excess iron transport (found in various disease states) can be ruled out because of the presence of iron regulatory proteins that precisely control the Tf-mediated iron transport [12]. Furthermore, in AD and PD patients, transferrin binding sites (i.e. the transferrin receptors expression) are reduced, while the iron concentration is increased in brain [13–15]. These evidences indicate that the focus needs to be paid on other iron transport mechanisms such as Lf-mediated iron transport in addition to Tf-mediated pathways.
Lactoferrins are widely distributed in the body fluids which are synthesized by exocrine glands and neutrophils [16]. Several studies on lactoferrins have shown that the concentration of lactoferrins in the brain is enhanced in case of neurodegenerative disorders [17–19], while lactoferrin is practically absent in normal brain cells [13]. For instance, in the case of PD, a higher concentration of lactoferrins is found in the surviving neurons [20]. The excessive accumulation of lactoferrins and associated iron may lead to a cytotoxic effect that results in the formation of intracellular lesions and neuronal death [13].
Lactoferrins can cross the BBB via receptor-mediated transcytosis as iron-bound or iron-free form [21]. Lactoferrins can also assist in nanoparticle based drug delivery through BBB [22–25]. The BBB endothelial cells express two types of lactoferrin binding sites [21, 26, 27]: high-affinity lactoferrin receptors (90000±16000 / cell) and low-affinity lactoferrin receptors (890000±70000 / cell) [21]. In neurodegenerative diseases, the expression of lactoferrin receptors (LfRs) is further upregulated in brain cells [19, 26, 28] resulting in a higher amount of lactoferrin and iron transport. For example, Faucheux et al. [26] found that, in PD, LfR immunoreactivity on endothelial cells is increased and it is more pronounced in midbrain regions where the loss of dopaminergic neurons is severe. Moreover, the LfR expression is not regulated by intracellular iron concentration or iron regulatory proteins [29] that allows LfR expression to lurch out of control, leading to the uptake of excessive amounts of Lf-mediated iron [26]. Thus, to understand the etiology of neurodegenerative diseases, more focus should be placed on Lf-mediated iron transport.
At present no theoretical framework exists for Lf-mediated iron transport that can connect various key players in the transcytosis process. In a previous work, we have developed a comprehensive mathematical model for Tf-mediated iron transport across BBB [30]. In this study, a mass-action based mathematical model has been proposed for the first time for Lf-mediated iron transport across the BBB. Models based on mass-action laws have been widely adopted to study biophysical processes [31–34], which heavily depend on kinetic rate constants. Unfortunately, the kinetic rate constants are not available for Lf-mediated iron transport process either.
Several techniques such as least squares [35], Kalman filtering [36–38], shooting algorithm [39, 40], preprocessing method [41], artificial neural network-based decomposition [42, 43] and Bayesian inference [44] are available for parameter estimations in biophysical processes. Among various techniques, Bayesian inference is a promising method and has been applied for various biological process modeling [45–48]. Bayesian approach provides a statistical technique for parameter estimation by combining prior knowledge with the data. Over the past decades, several Bayesian approaches have been developed to estimate parameters for various interesting problems. For example, Campbell et al. [49] presented a Bayesian procedure for parameter estimation in nonlinear flood event models. Putter et al. [45] discussed a Bayesian approach to estimate parameters in a human immunodeficiency virus (HIV) infection problem. A hierarchical Bayesian method is presented for the estimation of parameters in a longitudinal HIV dynamic system [47]. Recently, Choi et al. [50] developed a stochastic method based on Bayesian inference to estimate thermal response parameters.
In this paper, we extend the Bayesian inference framework presented in [50] for kinetic parameter estimation in Lf-mediated iron transport across BBB. The posterior distribution of the kinetic parameters is approximated by Markov chain Monte Carlo (MCMC) technique [51, 52]. We specifically use Metropolis-Hastings algorithm [53–55] for sampling parameters for the posterior distribution. The whole estimation process is implemented in R [56], using an in-house R-code. After validating the kinetic rate constants for the Lf-mediated transcytosis, transport of iron, lactoferrin and transferrin through BBB are studied considering both Lf- and Tf-mediated pathways. We particularly study the effects of lactoferrin concentration in blood, percentage of holo-lactoferrins in the blood side, and upregulation of lactoferrin receptors on the apical membrane.
2. Mathematical Modeling
As stated earlier, iron can primarily transported through BBB using Tf-mediated pathway. In our earlier work [30], we presented a comprehensive model for Tf-mediated iron transport through the BBB. Considering the important role of lactoferrin in some pathological conditions, here we develop a mathematical model for Lf-mediated iron transport across BBB.
2.1. Lactoferrin-mediated iron transport pathway
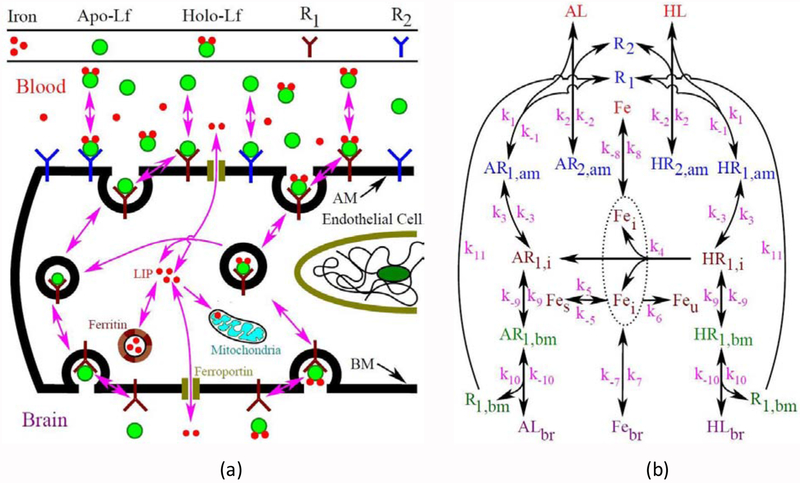
In body fluids, lactoferrins can be found in two forms: apo-Lf and holo-Lf [16]. The iron-free Lf is called apo-Lf, whereas iron loaded (2 iron molecules in one Lf molecule) is known as holo-Lf. In Lf-mediated transcytosis process, lactoferrins specifically bind with surface receptors on the apical membrane (AM), are internalized into the endothelial cells and finally, are transported across the basolateral membrane (BM) (Fig. 1a). Recent studies suggest that there are two kinds of specific binding sites: high and low affinity [21, 27]. In addition, the binding of holo-Lf is found to be concentration dependent, saturable, reversible and specific [21]. Thus, the binding of holo-Lf with binding sites can be modeled by considering the following
| (1) |
| (2) |
where k1 and k2 are the association rates of holo-Lf with high- and low-affinity binding sites, respectively; and k−1 and k−2 are the dissociation rates of holo-Lf from high- and low-affinity binding sites, respectively. Extensive research suggests that lactoferrin binding with its receptor is independent of its degree of iron binding. In other words, both apo-Lf and holo-Lf bind with lactoferrin receptors in a similar fashion [57, 58] as
| (3) |
| (4) |
Fig. 1.
(a) Lactoferrin transcytosis across the BBB and (b) the overall modeling scheme depicting the essential pathways and parameters for the Lf-mediated iron transport across the BBB endothelial cells.
It has been found that the lactoferrin is only internalized by the high-affinity binding sites [21]. Also, both apo-Lf and holo-Lf enter cells via a similar mechanism and there is no significant difference between the uptake of apo-Lf and holo-Lf [58]. In addition, the first order endocytic rate constants for apo-Lf and holo-Lf are found to be almost same in hepatocytes (0.276 and 0.292 min−1) [59]. These previous studies suggest to use the same endocytic rate for internalization of holo- and apo-Lf. Moreover, after internalization, both holo- and apo-Lf can recycle back to the apical membrane, which makes the internalization process reversible. Thus, considering first-order kinetics the internalization of holo- and apo-Lf can be described as
| (5) |
| (6) |
where k3 is the first order internalization rate of surface bound holo- or apo-Lf-receptor complex and k−3 is the recycle rate of the holo- or apo-Lf-receptor complex from intracellular space to the apical membrane. Although Lf binds iron more tightly than Tf, acidic condition of endosome can release iron from holo-Lf-receptor complex [2]. The iron release process can be modeled by the following first order reaction
| (7) |
where k4 is the release rate of iron from the holo-Lf-receptor complex. Degradation of apo- or holo-Lf inside the lysosome of endothelial cells is neglected based on the experimental evidence [21].
The released irons can have three different fates: storage by the cell ferritins, utilization by mitochondria or other organelles of cell, and efflux through the cell membranes. Iron storage by ferritin is a bidirectional process [60], which can be model as
| (8) |
where k5 and k−5 are the storage and release rate of iron from ferritin, respectively. We consider the iron utilization as an one step process
| (9) |
where k6 is the iron utilization rate by all organelles within the cell. Iron transport through the cell membranes is mediated by ferroportin, the only known iron exporter. In brain microvascular endothelial cells, ferroportins are localized on both apical and basolateral surfaces [61]. This distribution of ferroportins indicates that iron can return to the circulation (blood side) through ferroportin localized on the apical surface in addition to transporting in the brain side [62]. Iron efflux through ferroportin requires the action of an exocytoplasmic ferroxidase and, in brain microvascular endothelial cells, endogenous hephaestin or astrocyte-secreted soluble ceruloplasmin can provide that ferroxidase activity [63]. In the current model, the bidirectional transport of free iron from endothelial cells to brain is represented by Eq. (10); whereas bidirectional efflux of iron from endothelial cells to blood circulation is represented by Eq. (11)
| (10) |
| (11) |
where k7 and k8 are the iron transport rate from intracellular space to the brain side and blood side, respectively; whereas k−7 and k−8 are the corresponding reverse kinetic rates.
Both apo- and holo-Lf can transport to the brain side in a similar fashion [21]. We model this transport as a two-step process. First, the apo- or holo-Lfs traffic to the basolateral membrane of endothelial cells with the help of motor protein as
| (12) |
| (13) |
where k9 is the transport rate of Lf-receptor complex from intracellular space to basolateral membrane and k−9 is the reverse transport of Lf-receptor complex from basolateral surface to intracellular space. Then, the apo- and holo-Lf transport across the basolateral membrane by leaving the receptors at the basal surface of endothelial cells. It has been proposed that the release process on the basolateral surface of these cells is facilitated by the action of citrate and adenosine triphosphate [64], and we model this release process as
| (14) |
| (15) |
where k10 is the transport rate of lactoferrin from basolateral membrane to brain side and k−10 is the binding rate of brain side lactoferrin with the lactoferrin receptor on the basolateral membrane. The released receptors may partially recycle from the basolateral membrane to apical membrane through intracellular pool of receptors as in the case of transferrin receptors [65]. In this study, we assume a similar phenomenon for Lf-mediated iron transport as
| (16) |
where k11 is the recycling rate of lactoferrin receptor from the basolateral membrane to the apical membrane. The overall pathways of Lf-mediated iron transport across BBB are shown in Fig. 1b. Symbols used to denote different chemical compounds are described in Table 1.
Table 1.
Species considered in the model and their symbols.
| Notation | Description |
|---|---|
| HL | Holo-Lf, iron-loaded lactoferrin, in the blood side |
| R1 | High-affinity binding sites (receptors) |
| HR1,am | Holo-Lf bound with high-affinity receptors on the apical membrane |
| R2 | Low-affinity binding sites (receptors) |
| HR2,am | Holo-Lf bound with low-affinity receptors on the apical membrane |
| AL | Apo-Lf, iron-free lactoferrin, in the blood side |
| AR1,am | Apo-Lf bound with high-affinity receptors on the apical membrane |
| AR2,am | Apo-Lf bound with low-affinity receptors on the apical membrane |
| HR1,i | Holo-Lf bound with high-affinity receptors inside the cell |
| AR1,i | Apo-Lf bound with high-affinity receptors inside the cell |
| Fei | Free iron inside the cell |
| Fes | Iron stored as ferritin |
| Feu | Iron utilized by the organelles of cell |
| Febr | Iron transported to the brain side |
| Fe | Iron transported to blood side |
| HR1,bm | Holo-Lf bound with high-affinity receptors on the basolateral membrane |
| AR1,bm | Apo-Lf bound with high-affinity receptors on the basolateral membrane |
| R1,bm | Receptor associated with basolateral membrane |
| HLbr | Holo-Lf transported to the brain side |
| ALbr | Apo-Lf transported to the brain side |
2.2. Governing equations
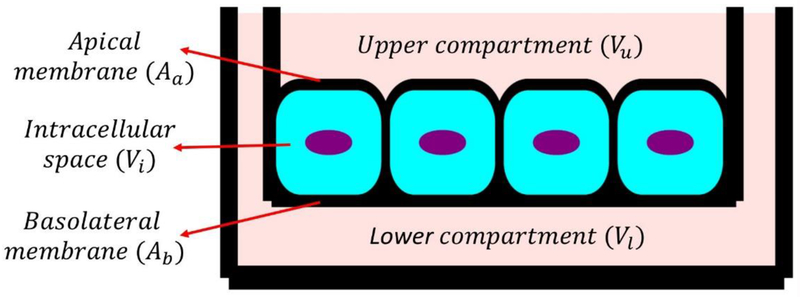
In this study, the governing ordinary differential equations (ODEs) are derived from the kinetic scheme by applying mass action laws with the consideration of compartment size effects. The effect of compartment size has been explicitly considered in this model because this provides accurate quantification of material densities or concentration of species at various compartments [66]. The various compartments and their sizes (either volume or surface area) for current biological modeling are shown in Fig. 2. All ODEs for Lf-mediated iron transport are listed in Table 2, where symbols [·] and {·} indicate reactants concentration (material per unit volume) and reactants material density (material per unit area), respectively.
Fig. 2.
Various compartments and their relative sizes in in-vitro Lf-mediated iron transport study.
Table 2.
Governing ordinary differential equations (ODEs) for transcytosis of Lf-mediated iron.
| (S.1) | |
| (S.2) | |
| (S.3) | |
| (S.4) | |
| (S.5) | |
| (S.6) | |
| (S.7) | |
| (S.8) | |
| (S.9) | |
| (S.10) | |
| (S.11) | |
| (S.12) | |
| (S.13) | |
| (S.14) | |
| (S.15) | |
| (S.16) | |
| (S.17) | |
| (S.18) | |
| (S.19) | |
| (S.20) |
In biological modeling, the initial values of different species are usually known from experimental conditions. Thus, with defined initial values of different species at different compartments, the ODE system becomes an initial-value problem. Since the formulated ODEs are coupled with each other, all equations need to be solved simultaneously. Therefore, a numerical approach is necessary for the solution of governing ODEs. Among various numerical approach, 4th order Runge-Kutta (R-K) method is widely used because of its ease of use, accuracy, excellent stability and self-starting capability [67]. In this work, 4th order R-K method has been used to solve the governing initial value problems.
Although the initial conditions are known for the current study, the kinetic rate parameters of receptor-mediated transcytosis of Lf and associated iron transport across BBB are unknown. Therefore, one of the objectives of this study is to estimate those rate constants from experimental data. For the parameter estimation process, we have implemented a Bayesian framework, which is discussed in detail in the next section.
3. Bayesian Framework for Parameter Estimation
Our aim is to estimate the unknown parameters for the set of differential equations listed in Table 2. For the current problem, the parameter vector θ can be defined as follows
| (17) |
According to Bayes’ theorem, the conditional probability of the parameter vector θ for a given measured data, Y, which is commonly known as posterior, can be given as follows
| (18) |
where p(θ) denotes the prior of the unknown parameters which use all available knowledge of unknown parameters; p(Y|θ) denotes the likelihood which describes the relative probability of observed data for all permissible values of the parameters; and p(Y) denotes the probability distribution of the observed data under any circumstance. In Eq. (18), p(Y) acts as a normalizing constant necessary to ensure ∫ p(θ|Y) dθ = 1. In reality, it is very difficult to calculate p(Y) directly and, in addition, it is rarely used in practice [49]. As a result, Eq. (18) can be expressed as
| (19) |
3.1. Likelihood
The modeled results are always subject to errors because the model is an approximation of true physical phenomenon. If we consider the experimental measurement, Y as true description of physical phenomenon i.e. no errors, then the results of the model, F can be expressed as
| (20) |
where εi describes the error in the model and i represents the time step. The model error is assumed to follow a normal distribution with zero mean and variance of . Under these assumptions, the likelihood function with respect to experimental measurement can be expressed as [49]
| (21) |
where n is the total number of time steps. In Eq. (21), to evaluate p(Y|θ), only unknown is the standard deviation (σi). To quantify σi, Choi et al. [50] set a hyperparameter by introducing the error ratio, rσ as
| (22) |
where Y0 is the initial value of corresponding measured data. By substituting Eq. (22) into Eq. (21), the likelihood can be expressed as
| (23) |
where Φ = (θ, rσ) is the overall parameter vector.
3.2. Prior
The prior distributions of unknown parameters, Φ can be set in various ways. If previous measurements are available, those values can be taken as a first estimation [32]. However, this method is often too restrictive when different species are distributed in different volumes [66]. Furthermore, the introduction of compartment size changes all the parameters from their regular unit, and plausible range cannot be set by following the traditional method. Thus, in this work, we first approximate the initial guess values of all kinetic rate parameters by following the method described in [30]. Then, the plausible range is set from 0 to two orders of magnitude higher than the approximated value because all kinetic rate parameters are known to be positive and definite. For error ratio rσ, we follow the method described by Choi et al. [50] and set its upper bound to an arbitrarily large value, such as 0.2 . Once, the parameter space, ℜ is defined, the prior can be set based on the available knowledge of various parameters. Since our information about the parameters is limited, it is difficult to define the shape of the prior probability distribution. Thus, we consider a uniformly distributed prior as
| (24) |
where Φ ∈ ℜ.
3.3. Posterior
Once the likelihood and prior are defined, the equation for posterior can be obtained from Eqs. (19), (23) and (24). Since the prior of each parameter is uniformly distributed within their given ranges, the posterior follows the same distribution as likelihood. To consider the boundaries of the parameter space, an indicator function, I is introduced as
| (25) |
The indicator function has only two states: 0, if any parameter lays outside of the parameter space or 1, if all parameters remain within the parameter space.
3.4. Markov Chain Monte Carlo (MCMC) Method
It is difficult to estimate the posterior distribution by direct calculation. A well-established alternative approach is to use MCMC [51, 52]. With respect to Bayesian inference, MCMC is a computer-driven technique for generating samples for the posterior distribution p(Φ|Y, I). The objective is to estimate the kinetic parameters by randomly generating enough samples while maximizing the posterior probability.
The MCMC starts with an arbitrary guess value of parameters, Φ(0). Then, a sequence of parameter values {Φ(j) : j = l, 2, 3, …} is generated from carefully constructed Markov chain; a sequential process in which the current state depends only on its direct predecessor in a certain way. To construct the Markov chain through the random walk, a transition density function describing the move Φ(j) → Φ(j+1) needs to be defined such that the observed values of the chain converge to the posterior distribution.
In this study, we have used the Metropolis-Hastings algorithm [53–55] to evaluate the posterior distribution. The Metropolis-Hastings algorithm produces a probability distribution function which describes the transition from the current step to the next step as follows. The sampling starts with an arbitrary initial guess of the parameter, Φ(j=0) where, (j) indicates the j-th sampling iteration. Then, generate a candidate value Φ* for Φ{j+l) from a probability distribution, which can be any arbitrary distribution. In the present study, we have used a normal distribution with the mean value of Φ(j) and a standard deviation of 0.01 aΦ(j). The value of hyperparameter, a, should be chosen in such a way that it can avoid the parameter search from being stuck at a local point or yielding a large correlation among the drawn samples. Usually, a trial and error method is used to compute the value of variance [50]. Thus, the new parameter candidate Φ* is then sampled based on the current state Φ(j) as follows
| (26) |
As stated earlier, the indicator function ( I ) is used to check the bound of Φ* within the parameter space (ℜ). If any component of Φ* is outside the parameter space, the function I(Φ* ∈ ℜ) becomes zero, and thus, the candidate parameter is discarded. If all components of Φ* is within the parameter space, then accept this value with probability α (Φ(j), Φ*) and move to Φ(j+1) = Φ*, where
| (27) |
If α(Φ(j), Φ*) = 1, Φ* is accepted because it provides a better fit to the experimental data than Φ(j). However, if α(Φ(j), Φ*) < 1, Φ* is not rejected exclusively. Instead, a random number, r is generated from a uniform distribution, U(0,1) which provides the opportunity to escape from local minima. In summary, Φ* is accepted or rejected based on the following criterion:
| (28) |
Note that for each iteration of Metropolis-Hastings algorithm, one needs to evaluate F from the Lf-mediated transport model by solving the system of ODEs (listed in Table 2) using 4th order R-K method. By iterating this process, the posterior distribution of each parameter can be evaluated if a sufficiently large number of samples are obtained. Usually, the early steps are significantly dependent on the initial guess of parameters, so the posterior distribution should be evaluated after discarding the data during burn-in period. In this study, the first 50,000 steps are considered as burn-in period. From the accepted samples, statistical parameters of all kinetic rate constants can be estimated.
4. Results and Discussions
The Bayesian framework discussed above has been applied for parameter estimation in Lf-mediated iron transport across BBB. The experimental conditions for Lf-mediated iron transport through BBB endothelial cells are taken from Fillebeen et al. [21] and presented in Table 3. In their work, they also presented progressive transport of lactoferrin and iron from blood to brain, which is used in the Bayesian framework as the experimental data (Y) to estimate the kinetic rate constants. Although parameter vectors, θ contains all parameters, three specific parameters: k−5, k6 and k7 are known from previous studies and presented in Table 3. Therefore, these three parameters are excluded from the Bayesian parameter estimation framework.
Table 3.
Parameters and initial conditions used for this study.
| Cell related parameters | ||
|---|---|---|
| Parameter | Values [unit] | Reference |
| Number of cells | 400000 [cells / cm2] | [21] |
| High-Affinity receptors, R1 | 90000 ± 16000 [per cell] | |
| Low-affinity receptors, R2 | 890000 ± 70000 [per cell] | |
| The volume of lower compartment, Vl | 2.0 [cm3] | |
| The volume of upper compartment, Vu | 1.0 [cm3] | |
| Culture plate diameter | 30 [mm] | |
| Endothelial cell volume | 2000 [μm3 / cell] | [72] |
| Total cell volume, Vi | 5.656×10−3 [cm3] | Calculated from above data |
| Area of apical membrane, Aa | 7.07 [cm2] | |
| Area of basolateral membrane, Ab | 7.07 [cm2] | |
| Initial conditions for the simulation | ||
| Parameter | Values [unit] | Reference |
| Apo-lactoferrin, [AL]0 | 0.375 [nmol / cm3] | [21] |
| Holo-lactoferrin, [HL]0 | 0.625 [nmol /cm3] | |
| High-affinity receptors, {R1}0 | 5.98×10−5 [nmol / cm2] | Calculated from above data |
| Low-affinity receptors, {R2}0 | 5.91×10−4 [nmol / cm2] | |
| Known rate constants | ||
| Parameter | Value [unit] | Reference |
| k−5 | 7.1021×10−6 [cm3 / s] | Claculated from [60] |
| k6 | 2.828×10−7 [cm3 / s] | Calculated from [30] |
| k7 | 1.021×10−6 [cm3 / s] | |
Note: The initial values for other ions, proteins or protein complexes are set to zero. The initial ferritin levels inside the cells is set to zero because the experimental measurement only counts the radioactive iron provided from outside at the beganing of the experiment.
4.1. Selection of hyperparameter a
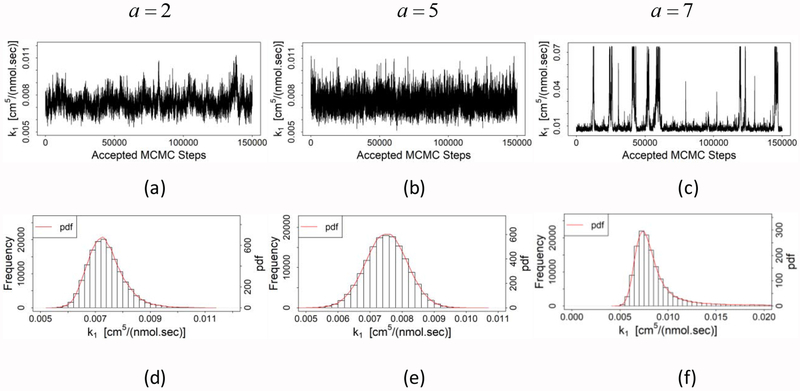
The MCMC method is computationally rigorous, and the computational cost increases with the sampling size and the number of accepted steps. In this study, we have used Metropolis-Hastings algorithm, where hyperparameter “a” is used to set the sampling variance. The sampling variance determines the required number of steps in the MCMC method. Here, the value of hyperparameter a is varied from 2 to 7. The sampling results for the parameter k1 with different values of a are summarized in Table 4 and Fig. 3. As seen from Table 4, as the sampling variance increases, the total number of steps required to achieve 2×105 accepted steps also increases. As a result, the acceptance rate is gradually decreased from 87.0 to 42.2% for increasing values of a. The MCMC results are statistically good if the acceptance rate is between 30 and 70% [49]. Thus, based on the acceptance rate, a = 5 or a = 7 yield a statistically acceptable result. However, as seen from the sampling results (Figs. 3a–3c), a well-defined Markov chain is formed for a = 2 or a = 5. The histograms of sampling results for the parameter k1 are shown in Figs. 3d–3f with the corresponding normalized probability distribution functions for low (a = 2), medium (a = 5) and high (a = 7) sampling variances, respectively. Low and medium variances provide similar distribution with symmetric tails on both sides as in normal distribution; whereas, high variance yields relatively longer tail in the upper region as in gamma distribution. Although both low and medium variances yield normal distribution, the medium variance yields more symmetric and shorter tail (Fig. 3 and Table 4). Based on the aforementioned discussion, we select the medium variance (a = 5) since it provides good acceptance rate (53.9%) as well as a well-formed Markov chain.
Table 4.
Performance of Markov chain Monte Carlo scheme with various sampling variances. Although the mean varies largely from low variance to high variance, all sampling variances yield similar mode and median. In this study, mode is used as point estimate of parameters in the mass-action based mathematical model.
| Hyperparameter, a |
Accepted steps |
Total steps |
Acceptance rate |
Statistics of parameter k1 [cm5 / (nmol.sec)] | ||||
|---|---|---|---|---|---|---|---|---|
|
Mean |
Median |
Mode |
Standard deviation |
95% Credible interval |
||||
|
2 |
2×105 |
2.30×105 |
87.0% |
7.38×10−3 | 7.32×10−3 | 7.27×10−3 |
6.68×10−4 |
6.07×10−3 −8.67×10−3 |
|
5 |
2×105 |
3.71×105 |
53.9% |
7.51×10−3 | 7.52×10−3 | 7.59×10−3 |
6.52×10−4 |
6.23×10−3 −8.79×10−3 |
|
7 |
2×105 |
4.74×105 |
42.2% |
1.21×10−2 | 8.06×10−3 | 7.48×10−3 |
1.203×10−2 |
0.0 – 6.023×10−2 |
Fig. 3.
Sampling results of parameter k1 for various variances in Metropolis-Hastings algorithm. Sampled data for (a) a = 2, (b) a = 5, and (c) a = 7. Histograms and probability distribution (pdf) of parameter k1 for (d) a = 2,(e) a = 5, and (f) a = 1. Here, hyperparameter, a is related to the magnitude of variance in Metropolis-Hastings algorithm (see Eq. (26)).
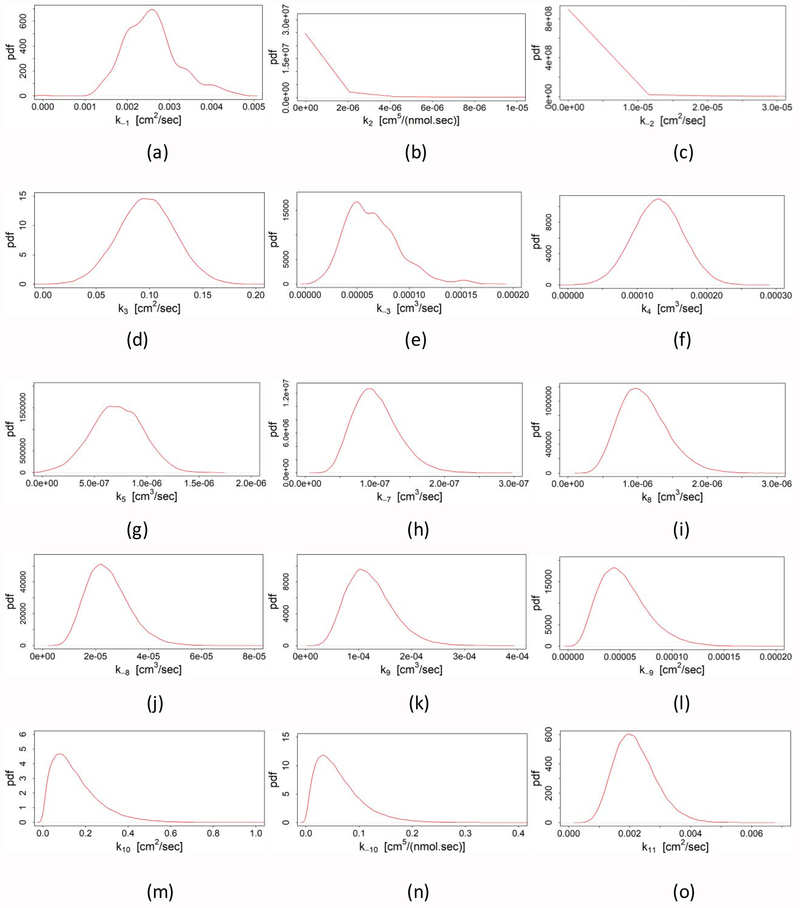
4.2. Point estimates of parameters
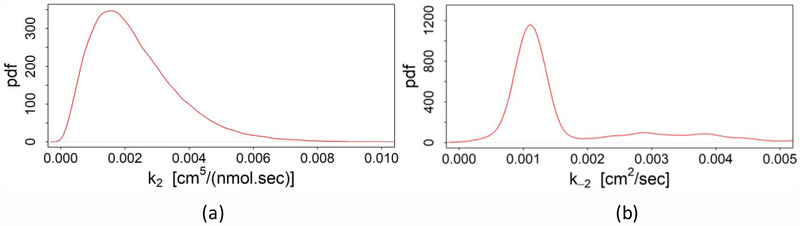
The probability density function (pdf) of other parameters are shown in Fig. 4. To obtain the posterior probability distributions of these parameters, 1.5×105 samples are drawn from the Metropolis-Hastings algorithm after discarding the burn-in period. Among all parameters, three parameters: k3, k4 and k5 have a normal distribution with a short symmetric tail as shown in Figs. 4d, 4f and 4g, respectively. Except k2 and k−2, the rest of the parameters have slightly skewed (longer tail in the upper region) posterior probability distributions similar to a Gamma distribution (Figs. 4a, 4e, and 4h–o). Moreover, other sampling variances (data not shown) also provide a similar type of distribution with almost the same mode and median within the given range. This is a clear indication of global minima. But as seen from Figs. 4b–4c, the maximum a posteriori (highest probability) of parameters k2 and k−2 is zero. This situation arises due to the weak relationship between the experimental data and the predicted values of those two parameters. As shown in the model (discussed in Section 2 and presented in Fig. 1), there is no uptake of lactoferrin or iron through the low-affinity binding site. Thus, any value of those two parameters will provide the same amount of brain lactoferrin or iron, as long as the other parameters are fixed, because of the high concentration of lactoferrin in the blood (30 [μg / ml]). Although a significant amount of lactoferrins bind with low-affinity binding sites at the blood side, with a high concentration of lactoferrin there is still sufficient lactoferrins available to bind with high-affinity binding sites. Thus, from the density data of high and low-affinity binding sites (listed in Table 3), it is intuitive that at the blood side with a low concentration of lactoferrin, k2 and k−2 would have a significant effect on the transport of lactoferrin and Lf-mediated iron from blood to the brain. Therefore, it is necessary to estimate k2 and k−2 to address this phenomenon.
Fig. 4.
Probability distribution function (pdf) of parameters (a) k−1, (b) k2, (c) k−2, (d) k3, (e) k−3, (f) k4, (g) k5, (h) k−7, (i) k8, (j) k−8, (k) k9, (l) k−9, (m) k10, (n) k−10 and (o) k11.
From the Bayesian analysis, we find that the parameters, k2 and k−2 always take the lowest value of the provided plausible range (data not shown). This indicates that changing of the plausible range will not help to estimate these two parameters. So, in order to estimate the values of these two parameters, we need extra constraints that may be taken from the experimental evidences. For instance, it has been found that the dissociation constant of receptors, R2 is higher than that of receptors, R1 [21, 27]. Thus, the affinity of receptors R2 must be lower than that of receptors R1, which we set as the first constraint. However, one constraint is not sufficient to estimate two parameters. Experimentally, it has also been found that around 18–20% of surface-bound lactoferrins get transported to the brain side [21]. Since this data is directly related to those parameters, we set this as the second constraint. With these two constraints, the modified probability density function for parameters k2 and k−2 are plotted in Fig. 5. Parameter k2 yields a gamma distribution with longer tail in the upper region (Fig. 5a) while parameter k−2 takes a normal distribution (Fig. 5b). Furthermore, the statistical properties of all kinetic parameters are summarized in Table 5.
Fig. 5.
Modified probability density functions (pdf) of parameter (a) k2 and (b) k−2 with external constraints.
Table 5.
Estimated parameters obtained by Bayesian inference. The mode is used as a point estimate for parameters in the mass-action based mathematical model.
| Parameter [unit] | Mean | Mode | Median |
|---|---|---|---|
| k1 [cm5 / (nmol.sec)] | 7.509×10−3 | 7.586×10−3 | 7.510×10−3 |
| k−1[cm2 / sec] | 2.568×10−3 | 2.551×10−3 | 2.530×10−3 |
| k2 | [cm5 / (nmol.sec)] | 2.309×10−3 | 1.467×10−3 | 2.041×10−3 |
| k−2 [cm2 / sec] | 2.013×10−3 | 1.101×10−3 | 1.211×10−3 |
| k3 [cm2 / sec] | 9.743×10−2 | 9.759×10−2 | 9.742×10−2 |
| k−3 [cm3 / sec] | 6.481×10−5 | 5.012×10−5 | 6.185×10−5 |
| k4 [cm3 / sec] | 1.301×10−4 | 1.309×10−4 | 1.303×10−4 |
| k5 [cm3 / sec] | 7.163×l0−7 | 7.030×10−7 | 7.168×10−7 |
| k−7 [cm3 / sec] | 1.020×10−7 | 9.646×10−8 | 9.845×10−8 |
| k8 [cm3 / sec] | 1.092×10−6 | 1.001×10−6 | 1.055×10−6 |
| k−8 [cm3 / sec] | 2.469×10−5 | 2.156×10−5 | 2.381×10−5 |
| k9 [cm3 / sec] | 1.218×10−4 | 1.028×10−4 | 1.166×10−4 |
| k−9 [cm3 / sec] | 5.383×10−5 | 4.481×10−5 | 5.044×10−5 |
| k10 [cm3 / sec] | 1.545×10−1 | 7.846×10−2 | 1.282×10−1 |
| k−10 [cm5 / (nmol.sec)] | 6.208×10−2 | 3.364×10−2 | 5.236×10−2 |
| k11 [cm3 / sec] | 2.193×10−3 | 2.042×10−3 | 2.120×10− |
4.3. Model validation
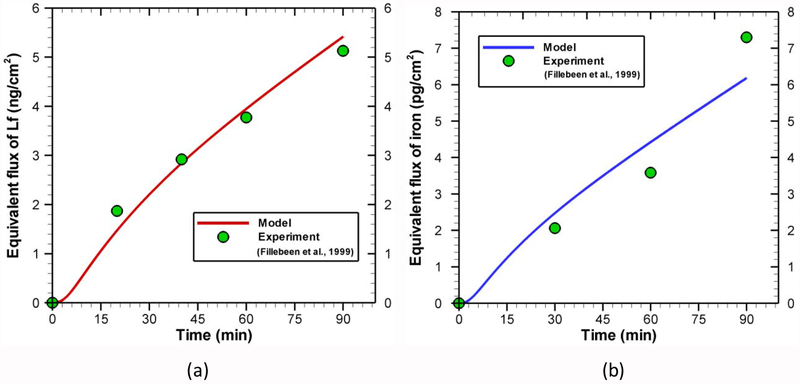
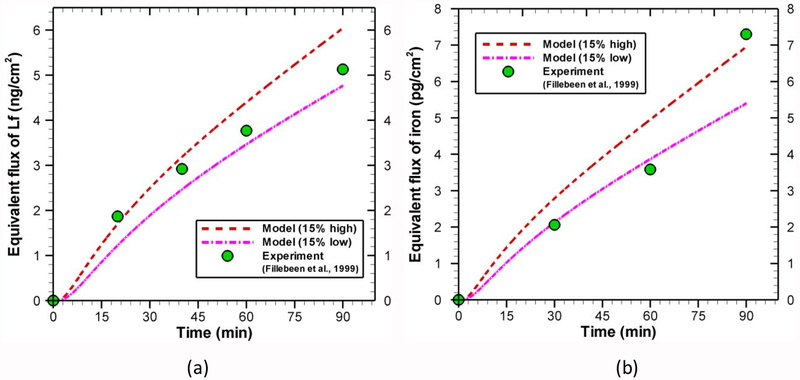
With the point estimates (mode values in Table 5) of kinetic rate constants, the concentration or density of different species is obtained for different compartments by solving ODEs system. The results of the forward model are compared with the experimental data for transcytosis of lactoferrin (Fig. 6a) and iron (Fig. 6b). Although the model results are in good agreement with experimental data, it does not guarantee the validity of parameter estimation process. Instead, this indicates the good training of the model against the experimental data. To test the robustness of the model, the estimated parameters are perturbed by a random amount (e.g. 15%) following the work of Shin and Nguyen [68]. Using these new parameters, the concentration of different species is recalculated and presented in Fig. 7. The behaviors of both lactoferrin (Fig. 7a) and iron (Fig. 7b) transport are well preserved to such parameter perturbation, which confirms the robustness of the model and parameter estimation process. Further qualitative validations will be provided in the following section.
Fig. 6.
Apical to basolateral (specific) transport of (a) lactoferrin and (b) iron across the BBB endothelial cells. For figure (a) initial conditions are [AL]0 = 0.375 [nmol / cm3], {R1}0=5.98×10−5 [nmol / cm2], {R2}0=5.91×10−4 [nmol / cm2] and other species values are set as zero. For figure (b) initial conditions are [HL]0 = 0.625 [nmol / cm3], {R1}0 = 5.98×10−5 [nmol / cm2], {R2}0 = 5.91×10−4 [nmol / cm2] and other species values are set as zero. The equivalent fluxes are calculated from the brain side concentration of lactoferrin and iron using molecular weight, brain side volume, and cell surface area.
Fig. 7.
Effect of parameter perturbation on (a) lactoferrin and (b) iron transport across BBB. Initial conditions for Fig. 7a are the same as in Fig. 6a and for Fig. 7b are same as in Fig. 6b.
4.4. Kinetics of Lactoferrin in BBB endothelial cells
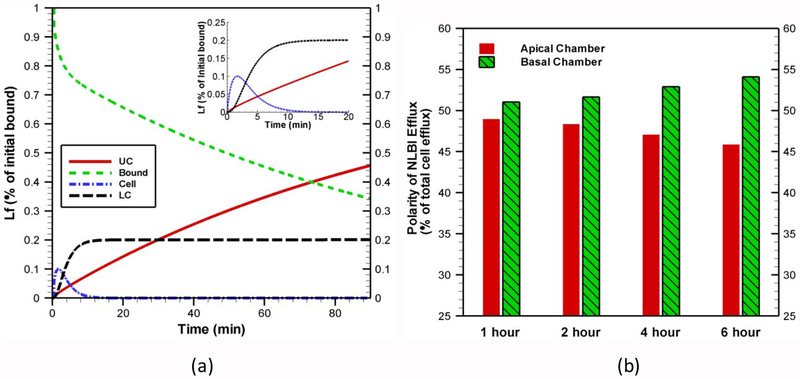
Internalization kinetics of lactoferrin in BBB endothelial cells is quantified through our model based on the experimental conditions presented in [21]. In their experiment, cells were first incubated at 4° C for 1 h to prevent uptake. This also ensures that the occupancy of the binding sites reached steady state. After washing off the unbound ligands, cells were incubated at 37° C and the amount of surface-bound, internalized, released (to blood side) and transported (to brain side) lactoferrins were quantified from radio-activities at different compartments at different time. To mimic the experimental condition, the ODE system in our model is first solved for 1 h with the initial conditions used in Fig. 6a. In our simulation, the point estimates of all parameters presented in Table 5 (except k3) are used. The value of k3 is set as zero, which ensures no uptake of lactoferrin. This is similar to the incubation condition at 4° C in experimental system with energy inhibitors. Next, the model results are used as the initial conditions for species located at apical membrane ({R1}0, {R2}0, {AR1,am}0 and {AR2,am}0), while initial values of all other species are set as zero. Then the ODE system is solved with estimated rate constants (mode value) presented in Table 5. Fig. 8 shows the amount of surface-bound, internalized, released and transported lactoferrins as a function of time. Within the simulation time (90 minutes), ~ 46% of initial surface bound lactoferrins is released into the upper compartment (UC), whereas ~20% of initial surface bound lactoferrins is transported to the lower compartment (LC). Intracellular portion reaches a maximum of ~10% within 2 min. Our modeling results indicate that the surface-bound lactoferrin is gradually decreased with time, and it drops to 34% within 90 minutes. This distribution qualitatively agrees with the experimental results (see Fig. 3 of reference [21]). A quantitative comparison is not possible because the experiments presented in [21] did not quantify species adequately in various compartments.
Fig. 8.
(a) Internalization kinetics of lactoferrin in BBB endothelial cells and (b) comparison of apical vs basolateral efflux of non-lactoferrin bound iron (NLBI) in endothelial cells. Initial conditions for Fig. 8b are the same as in Fig. 6b.
A quantification of apical versus basal non-lactoferrin bound iron (NLBI) efflux in differentiated brain capillary endothelial cells (cultured in the presence of astrocytes) is shown in Fig. 8b. Our analysis shows that at any time, the efflux of NLBI from differentiated endothelial cells is more concentrated towards the brain side. In addition, as the time increases the efflux of NBLI towards blood side decreases while the efflux of NBLI towards brain side increases. This result is justified because ferroportin, the non-bound iron transporter, is appeared to be more concentrated on the basolateral surface [12]. Moreover, our simulation results are inline with experimental data obtained with human brain microvascular endothelial cells when C6 cells were cocultured in either a distal or proximal orientation [62].
4.5. Effect of initial lactoferrin concentration
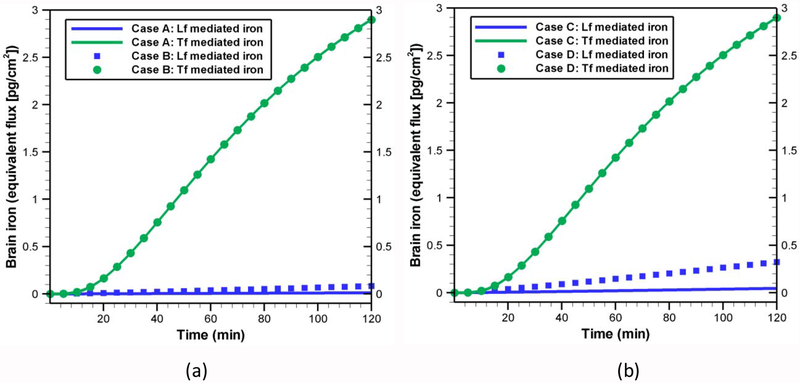
In all previous sections, we have used an apo-Lf concentration of 30[μg / ml] and a holo-Lf concentration of 50[μg / ml] in the blood side based on the experimental works of Fillebeen et al. [21]. However, in normal conditions, the concentration of lactoferrin in the blood is much smaller. For example, the plasma lactoferrin concentration is 0.168±0.1[μg / ml] and serum lactoferrin concentration is 0.2±0.155[μg / ml] [69] in normal conditions. But various health conditions may affect these concentrations. For instance, in cystic fibrosis patients, these concentrations are elevated to 0.265±0.224[μg / ml] and 0.650±0.551[μg / ml] in plasma and serum, respectively [69]. Moreover, the holo-Lf percentage in the blood varies widely from normal conditions to pathological conditions [16]. Thus, in this study, we also considered two different scenarios based on the percentage of holo-lactoferrin: 10.2±0.2 and 71.8±6.5% as reported in the experimental work of Majka et al. [70]. Depending on the concentration of Lf and percentage of holo-Lf, four separate cases are studied (see Table 6). Model results for these four cases are shown in Fig. 9. To demonstrate the extent of iron transported by lactoferrins with respect to transferrins, we also considered the contribution of Tf in parallel with Lf. The Tf-mediated iron transport is quantified by using the model described in [30] with a blood side holo-Tf (HT) concentration of 1.4[μg / ml] as reported in the experimental study of Descamps et al. [71]. As seen from Fig. 9a, with normal concentration of Lf (~0.30[μg / ml]), the percentage of holo-Lf has almost no effect on the brain iron (as indicated by the solid blue line and blue squared shape symbols). Moreover, in comparison to Tf-mediated route, the Lf-mediated iron transport is very low. This indicates that, at normal condition, the blood to brain iron transport is primarily led by holo-Tf, because the Tf concentration in the blood side is four times higher than that of Lf. Even for identical concentration of Lf and Tf in the blood side, Tf-mediated pathway is still the dominant transport mechanism. However, for higher lactoferrin concentration in blood (Fig 9b), our model predicts significantly different amount of Lf-mediated iron in the brain depending on the percentage of holo-Lf. For instance, the amount of iron transported by Lf increases by 6 fold within two hours for a change in holo-Lf percentage from 10.2% to 71.8%. Thus, the effect of holo-Lf percentage is more evident at higher concentration of Lf in the blood side. Our results also show that the total amount of lactoferrin in the brain does not depend on the percentage of holo-Lf in the blood (data not shown). This is because of the fact that both apo- and holo-Lf have the ability to cross the BBB and transport to the brain side [21]. Our results reveal that a higher Lf-concetration in the blood yields a higher amount of Lf in the brain (data not shown).
Table 6.
Initial conditions for different case study.
| Case | Lf concentration in blood [μg / ml] | HL [%] | Tf concentration in blood [μg / ml] | HT [%] | Density of R1 [nmol / cm2] |
|---|---|---|---|---|---|
| A | 0.3 | 10.2 | 1.4 | 100 | 5.98×10−5 |
| B | 71.8 | ||||
| C | 1.2 | 10.2 | |||
| D | 71.8 | ||||
| E | 100 | ||||
| F | 100 | 1.794×10−4 |
Fig. 9.
Effect of blood lactoferrin concentration and percentage of holo-Lf on Lf and iron transport across BBB at (a) low Lf concentration (~0.30 μg / ml) and (b) high Lf concentration (~1.20 μg / ml). All kinetic rates are same as listed in Table 5. Initial conditions for each case are provided in Table 6. Tf-mediated iron transport are quantified by using model developed in [30] with a concentration of 1.4 [μg / ml] in the luminal side as reported by Descamps et al. [71].
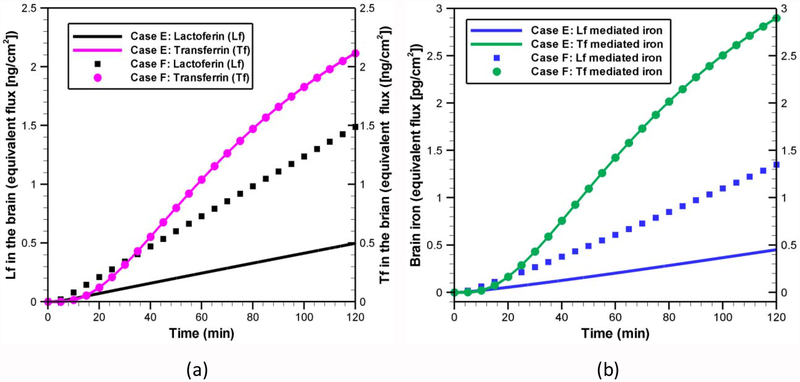
4.6. Upregulation of lactoferrin receptors
As stated before, LfR expression on BBB endothelial cells is upregulated in both AD [19] and PD [11, 26] patients. Compare to a normal person, the Lf receptors is around 2 ~ 3 times higher in PD patient’s BBB endothelial cells [26]. Thus, it is interesting to study the effect of LfR upregulation during iron transport across BBB. To understand the role of receptor upregulation, a 2-fold increase in high-affinity receptors (R1) density is considered here. Our simulation results show that a 2-fold increase in R1 density results in around two-fold increase in lactoferrin in the brain side (Fig. 10a). Although, with normal R1 density, the amount of Lf in the brain is low compared to Tf, with two fold increase in receptor density, the amount of Lf in the brain is almost comparable with Tf in the brain. Like Lf transcytosis, the receptor density also has a significant effect on Lf-mediated iron transport and hence on the total brain iron as shown in Fig. 10(b). With 2-fold increase in R1 density, the Lf-mediated pathway contributes to 1/3 of the total brain iron. We also found that, a two-fold increase in low-affinity receptor (R2) density has little or no effect on the amount of brain lactoferrin or iron (data not shown). The diminishing role of low-affinity receptors are expected since internalization does not occur through binding site 2 (R2) and there is sufficient amount of lactoferrin available in the blood side. These results suggest that, in PD or AD, probably the high-affinity receptor, R1, is upregulated, and more Lf as well as iron is transported across the BBB endothelial cells. Moreover, unlike Tf receptors, the Lf receptors expression is not regulated by intracellular iron level [26]. Thus, with elevated LfR density, a continuous iron transport process across BBB might raise iron concentration to pathological levels and could contribute to the neurodegeneration.
Fig. 10.
Effect of lactoferrin receptor upregulation on (a) amount of Lf and Tf in the brain and (b) amount of iron in the brain. All the kinetic rates are same as listed in Table 5. Initial conditions for each case are provided in Table 6. Tf-mediated iron transport is quantified by using the model developed in [30] with a concentration of 1.4 [μg / ml] in the luminal side as reported by Descamps et al. [71].
5. Conclusions
In this paper, we present a theoretical framework for Lf-mediated iron transport through the BBB, and estimate the necessary parameters for this process using experimental data. A mass action based kinetic model is developed considering transport pathways for apo-Lf, holo-Lf, and iron across the BBB endothelial cells. A Bayesian framework is used to estimate the posterior probability distributions of kinetic rate constants as well as other hyperparameters. The posterior probability distribution of each parameter is numerically evaluated by applying a Markov chain Monte Carlo method in conjunction with the Metropolis-Hastings sampling algorithm. From the sampled posterior distribution, the statistical properties of each parameter are obtained and analyzed. The validation of estimated parameters is demonstrated by comparing the model prediction with experimental results. Results of the forward model show that the estimated parameter can effectively reproduce the experimental results. Robustness of the model and parameter estimations are confirmed by the well-preserved behavior of species concentrations to parameter perturbation. In the absence of Tf-mediated pathway, ~ 20% of surface-bound lactoferrin can be transported to the brain side. Within 2 min of simulation time, the intracellular percentage of lactoferrin reaches the maximum, and then starts to decrease with time and diminishes quickly due to the transport to the brain side.
To understand the relative roles of lactoferrins under different pathological conditions, we have also studied the iron transport across BBB considering both Tf- and Lf-mediated routes. Our results show that an increase in high-affinity receptor density increases both Lf and iron in the brain. But increase in low-affinity receptor density has a negligible effect on the brain iron contents. These results indicate that, in PD or AD, high-affinity receptor expression is upregulated in the BBB endothelial cells, which in turn increases the lactoferrin concentration in the brain. The effect of total lactoferrin content and percentage of holo-Lf in the blood are also studied for iron transport across BBB considering both Lf and Tf-mediated pathways. From our study, we have found that the total iron in the brain depends on the percentage of holo-Lf, total lactoferrin and total transferrin content in the blood. Even though Tf-mediated iron transport is dominant, elevated LfR expression along with high Lf concentration in the blood can transport significant amount of iron in brain during neurodegenerative disorders.
Highlights.
Role of iron and its transport mechanism are studied to understand brain diseases
A kinetic model ispresented for lactoferrin-mediated iron transport across blood brain barrier
Bayesian inference is used to estimate the kinetic rate parameters
High affinity, but not low affinity, receptors regulatesthe brain iron and lactoferrin contents
Acknowledgment
This work was supported by the National Institute of General Medical Sciences (NIGMS) of the National Institutes of Health under Award Number R01GM122081. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- [1].Jellinger KA, The role of iron in neurodegeneration - Prospects for pharmacotherapy of Parkinson’s disease, Drugs & Aging 14 (1999) 115–140. [DOI] [PubMed] [Google Scholar]
- [2].Gaasch JA, Lockman PR, Geldenhuys WJ, Allen DD, Van der Schyf CJ, Brain iron toxicity: Differential responses of astrocytes, neurons, and endothelial cells, Neurochemical Research 32 (2007) 1196–1208. [DOI] [PubMed] [Google Scholar]
- [3].Jiang H, Wang J, Rogers J, Xie JX, Brain Iron Metabolism Dysfunction in Parkinson’s Disease, Molecular Neurobiology 54 (2017) 3078–3101. [DOI] [PubMed] [Google Scholar]
- [4].Berg D, Gerlach M, Youdim MBH, Double KL, Zecca L, Riederer P, Becker G, Brain iron pathways and their relevance to Parkinson’s disease, Journal of Neurochemistry 79 (2001) 225–236. [DOI] [PubMed] [Google Scholar]
- [5].Song N, Wang J, Jiang H, Xie JX, Astroglial and microglial contributions to iron metabolism disturbance in Parkinson’s disease, Biochimica Et Biophysica Acta -Molecular Basis of Disease 1864 (2018) 967–973. [DOI] [PubMed] [Google Scholar]
- [6].Thompson KJ, Shoham S, Connor JR, Iron and neurodegenerative disorders, Brain Research Bulletin 55 (2001) 155–164. [DOI] [PubMed] [Google Scholar]
- [7].Qian ZM, Shen X, Brain iron transport and neurodegeneration, Trends in Molecular Medicine 7 (2001) 103–108. [DOI] [PubMed] [Google Scholar]
- [8].Gerlach M, Ben-Shachar D, Riederer P, Youdim M, Altered brain metabolism of iron as a cause of neurodegenerative diseases?, Journal of Neurochemistry 63 (1994) 793–807. [DOI] [PubMed] [Google Scholar]
- [9].Youdim M, Ben-Shachar D, Riederer P, The possible role of iron in the etiopathology of Parkin son’s disease, Movement Disorders: Official Journal of the Movement Disorder Society 8 (1993) 1–12. [DOI] [PubMed] [Google Scholar]
- [10].Qian ZM, Wang Q, Expression of iron transport proteins and excessive iron accumulation in the brain in neurodegenerative disorders, Brain Research Reviews 27 (1998) 257–267. [DOI] [PubMed] [Google Scholar]
- [11].Ke Y, Qian ZM, Brain iron metabolism: Neurobiology and neurochemistry, Progress in Neurobiology, 83 (2007) 149–173. [DOI] [PubMed] [Google Scholar]
- [12].Wu LJC, Leenders AGM, Cooperman S, Meyron-Holtz E, Smith S, Land W, Tsai RYL, Berger UV, Sheng ZH, Rouault TA, Expression of the iron transporter ferroportin in synaptic vesicles and the blood-brain barrier, Brain Research 1001 (2004) 108–117. [DOI] [PubMed] [Google Scholar]
- [13].Leveugle B, Spik G, Perl DP, Bouras C, Fillit HM, Hof PR, The iron-binding protein lactotransferrin is present in pathologic lesions in a variety of neurodegenerative disorders: a comparative immunohistochemical analysis, Brain Research 650 (1994) 20–31. [DOI] [PubMed] [Google Scholar]
- [14].Faucheux B, Hirsch E, Villares J, Selimi F, Mouatt-Prigent A, Javoy-Agid F, Hauw J, Agid Y, Distribution of 125I-ferrotransferrin binding sites in the mesencephalon of control subjects and patients with Parkinson’s disease, Journal of Neurochemistry 60 (1993) 2338–2341. [DOI] [PubMed] [Google Scholar]
- [15].Morris CM, Candy JM, Omar S, Bloxham CA, Edwardson JA, Transferrin receptors in the Parkinsonian midbrain, Neuropathology and Applied Neurobiology 20 (1994) 468–472. [DOI] [PubMed] [Google Scholar]
- [16].Lepanto MS, Rosa L, Paesano R, Valenti P, Cutone A, Lactoferrin in Aseptic and Septic Inflammation, Molecules 24 (2019) 1323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Terent A, Hällgren R, Venge P, Bergström K, Lactoferrin, lysozyme, and beta 2-microglobulin in cerebrospinal fluid. Elevated levels in patients with acute cerebrovascular lesions as indices of inflammation, Stroke 12 (1981) 40–46. [DOI] [PubMed] [Google Scholar]
- [18].Hallgren R, Terent A, Venge P, Lactoferrin, lysozyme, and beta2-microglobulin levels in cerebrospinal - fluid - differential indexes of CNS inflammation, Inflammation 6 (1982) 291–304. [DOI] [PubMed] [Google Scholar]
- [19].Kawamata T, Tooyama I, Yamada T, Walker DG, McGeer PL, Lactotransferrin immunocytochemistry in Alzheimer and normal human brain, American Journal of Pathology 142 (1993) 1574–1585. [PMC free article] [PubMed] [Google Scholar]
- [20].Leveugle B, Faucheux BA, Bouras C, Nillesse N, Spik G, Hirsch EC, Agid Y, Hof PR, Cellular distribution of the iron-binding protein lactotransferrin in the mesencephalon of Parkinson’s disease cases, Acta Neuropathologica 91 (1996) 566–572. [DOI] [PubMed] [Google Scholar]
- [21].Fillebeen C, Descamps L, Dehouck MP, Fenart L, Benaissa M, Spik G, Cecchelli R, Pierce A, Receptor-mediated transcytosis of lactoferrin through the blood-brain barrier, Journal of Biological Chemistry 274 (1999) 7011–7017. [DOI] [PubMed] [Google Scholar]
- [22].Huang RQ, Ke WL, Liu Y, Jiang C, Pei YY, The use of lactoferrin as a ligand for targeting the polyamidoamine-based gene delivery system to the brain, Biomaterials 29 (2008) 238–246. [DOI] [PubMed] [Google Scholar]
- [23].Hu KL, Shi YB, Jiang WM, Han JY, Huang SX, Jiang XG, Lactoferrin conjugated PEG-PLGA nanoparticles for brain delivery: Preparation, characterization and efficacy in Parkinson’s disease, International Journal of Pharmaceutics 415 (2011) 273–283. [DOI] [PubMed] [Google Scholar]
- [24].Song Y, Du D, Li L, Xu J, Dutta P, Lin YH, In vitro study of receptor-mediated silica nanoparticles delivery across blood-brain barrier, ACS Applied Materials & Interfaces 9 (2017) 20410–20416. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Huang FYJ, Chen WJ, Lee WY, Lo ST, Lee TW, Lo JM, In vitro and in vivo evaluation of lactoferrin-conjugated liposomes as a novel carrier to improve the brain delivery, International Journal of Molecular Sciences 14 (2013) 2862–2874. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Faucheux BA, Nillesse N, Damier P, Spik G, Mouattprigent A, Pierce A, Leveugle B, Kubis N, Hauw JJ, Agid Y, Hirsch EC, Expression of lactoferrin receptors is increased in the mesencephalon of patients with parkinson disease, Proceedings of the National Academy of Sciences of the United States of America 92 (1995) 9603–9607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Huang RQ, Ke WL, Qu YH, Zhu JH, Pei YY, Jiang C, Characterization of lactoferrin receptor in brain endothelial capillary cells and mouse brain, Journal of Biomedical Science 14 (2007) 121–128. [DOI] [PubMed] [Google Scholar]
- [28].Fillebeen C, Mitchell V, Dexter D, Benaissa M, Beauvillain JC, Spik G, Pierce A, Lactoferrin is synthesized by mouse brain tissue and its expression is enhanced after MPTP treatment, Molecular Brain Research 72 (1999) 183–194. [DOI] [PubMed] [Google Scholar]
- [29].Bonn D, Pumping iron in Parkinson’s disease, Lancet 347 (1996) 1614–1614. [DOI] [PubMed] [Google Scholar]
- [30].Khan AI, Liu J, Dutta P, Iron transport kinetics through blood-brain barrier endothelial cells, Biochimica Et Biophysica Acta-General Subjects 1862 (2018) 1168–1179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Ciechanover A, Schwartz A, Dautry-Varsat A, Lodish H, Kinetics of internalization and recycling of transferrin and the transferrin receptor in a human hepatoma cell line. Effect of lysosomotropic agents, Journal of Biological Chemistry 258 (1983) 9681–9689. [PubMed] [Google Scholar]
- [32].Mezer A, Nachliel E, Gutman M, Ashery U, A new platform to study the molecular mechanisms of exocytosis, Journal of Neuroscience 24 (2004) 8838–8846. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Morshed A, Dutta P, Hypoxic behavior in cells under controlled microfluidic environment, Biochimica Et Biophysica Acta-General Subjects 1861 (2017) 759–771. [DOI] [PubMed] [Google Scholar]
- [34].Morshed A, Dutta P, Mathematical model for tissue-level hypoxic response in microfluidic environment, Journal of Biomechanical Engineering-Transactions of the ASME 140 (2018) 011009. [DOI] [PubMed] [Google Scholar]
- [35].Ritchie RJ, Prvan T, Current statistical methods for estimating the Km and Vmax of Michaelis-Menten kinetics, Biochemical Education 24 (1996) 196–206. [Google Scholar]
- [36].Bezruchko BP, Smirnov DA, Extracting knowledge from time series: an introduction to nonlinear empirical modeling, First ed., Springer, Verlag Berlin Heidelberg, Germany, 2010. [Google Scholar]
- [37].Sitz A, Schwarz U, Kurths J, Voss HU, Estimation of parameters and unobserved components for nonlinear systems from noisy time series, Physical Review E 66 (2002) 016210. [DOI] [PubMed] [Google Scholar]
- [38].Sitz A, Schwarz U, Kurths J, The unscented Kalman filter, a powerful tool for data analysis, International Journal of Bifurcation and Chaos 14 (2004) 2093–2105. [Google Scholar]
- [39].Baake E, Baake M, Bock HG, Briggs KM, Fitting ordinary differential -equations to chaotic data, Physical Review A 45 (1992) 5524–5529. [DOI] [PubMed] [Google Scholar]
- [40].Peifer M, Timmer J, Parameter estimation in ordinary differential equations for biochemical processes using the method of multiple shooting, IET Systems Biology 1 (2007) 78–88. [DOI] [PubMed] [Google Scholar]
- [41].Strebel O, A preprocessing method for parameter estimation in ordinary differential equations, Chaos Solitons & Fractals 57 (2013) 93–104. [Google Scholar]
- [42].Dua V, An artificial neural network approximation based decomposition approach for parameter estimation of system of ordinary differential equations , Computers & Chemical Engineering 35 (2011) 545–553. [Google Scholar]
- [43].Khan AI, Lu Q, Du D, Lin Y, Dutta P, Quantification of kinetic rate constants for transcytosis of polymeric nanoparticle through blood-brain barrier, Biochimica et Biophysica Acta (BBA)-General Subjects 1862 (2018) 2779–2787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44].Bremer CL, Kaplan DT, Markov chain Monte Carlo estimation of nonlinear dynamics from time series, Physica D-Nonlinear Phenomena 160 (2001) 116–126. [Google Scholar]
- [45].Putter H, Heisterkamp SH, Lange JMA, de Wolf F, A Bayesian approach to parameter estimation in HIV dynamical models, Statistics in Medicine 21 (2002) 2199–2214. [DOI] [PubMed] [Google Scholar]
- [46].Coelho FC, Codeco CT, Gomes MGM, A bayesian framework for parameter estimation in dynamical models, Plos One 6 (2011) e19616. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [47].Huang YX, Liu DC, Wu HL, Hierarchical Bayesian methods for estimation of parameters in a longitudinal HIV dynamic system, Biometrics 62 (2006) 413–423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [48].Girolami M, Bayesian inference for differential equations, Theoretical Computer Science 408 (2008) 4–16. [Google Scholar]
- [49].Campbell EP, Fox DR, Bates BC, A Bayesian approach to parameter estimation and pooling in nonlinear flood event models, Water Resources Research, 35 (1999) 211–220. [Google Scholar]
- [50].Choi W, Kikumoto H, Choudhary R, Ooka R, Bayesian inference for thermal response test parameter estimation and uncertainty assessment, Applied Energy 209 (2018) 306–321. [Google Scholar]
- [51].van Ravenzwaaij D, Cassey P, Brown SD, A simple introduction to Markov chain Monte-Carlo sampling, Psychonomic Bulletin & Review 25 (2018) 143–154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [52].Gilks WR, Richardson S, Spiegelhalter D, Markov chain Monte Carlo in practice, First Ed., Chapman and Hall/CRC, New York, USA, 1995. [Google Scholar]
- [53].Metropolis N, Rosenbluth AW, Rosenbluth MN, Teller AH, Teller E, Equation of state calculations by fast computing machines, The Journal of Chemical Physics 21 (1953) 1087–1092. [Google Scholar]
- [54].Hastings WK, Monte Carlo sampling methods using Markov chains and their applications, Biometrika 57 (1970) 97–107. [Google Scholar]
- [55].Chib S, Greenberg E, Understanding the Metropolis -Hastings algorithm, American Statistician 49 (1995) 327–335. [Google Scholar]
- [56].R. C. Team, R: A language and environment for statistical computing, R Foundation for Statistical Computing, Vienna, Austria, 2013. [Google Scholar]
- [57].McAbee DD, Esbensen K, Binding and endocytosis of apo-lactoferrin and holo-lactoferrin by isolated rat hepatocytes, Journal of Biological Chemistry 266 (1991) 23624–23631. [PubMed] [Google Scholar]
- [58].Jiang RL, Lopez V, Kelleher SL, Lonnerdal B, Apo- and holo-lactoferrin are both internalized by lactoferrin receptor via clathrin-mediated endocytosis but differentially affect ERK-signaling and cell proliferation in Caco-2 cells, Journal of Cellular Physiology 226 (2011) 3022–3031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [59].McAbee DD, Nowatzke W, Oehler C, Sitaram M, Sbaschnig E, Opferman JT, Carr J, Esbensen K, Endocytosis and degradation of bovine apo-lactoferrin and holo-lactoferrin by isolated rat hepatocytes are mediated by recycling calcium-dependent binding-sites, Biochemistry 32 (1993) 13749–13760. [DOI] [PubMed] [Google Scholar]
- [60].Jones T, Spencer R, Walsh C, Mechanism and kinetics of iron release from ferritin by dihydroflavins and dihydroflavin analogs, Biochemistry 17 (1978) 4011–4017. [DOI] [PubMed] [Google Scholar]
- [61].McCarthy RC, Kosman DJ, Mechanisms and regulation of iron trafficking across the capillary endothelial cells of the blood-brain barrier, Frontiers in Molecular Neuroscience 8 (2015) 1–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [62].McCarthy RC, Kosman DJ, Ferroportin and exocytoplasmic ferroxidase activity are required for brain microvascular endothelial cell iron efflux, Journal of Biological Chemistry 288 (2013) 17932–17940. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [63].McCarthy RC, , Kosman DJ, Glial cell ceruloplasmin and hepcidin differentially regulate iron efflux from brain microvascular endothelial cells, Plos One 9 (2014) e89003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [64].Moos T, Nielsen TR, Skjorringe T, Morgan EH, Iron trafficking ins ide the brain, Journal of Neurochemistry 103 (2007) 1730–1740. [DOI] [PubMed] [Google Scholar]
- [65].Vangelder W, Huijskesheins MIE, Vandijk JP, Cletonsoeteman MI, Vaneijk HG, Quantification of different transferrin receptor pools in primary cultures of porcine blood-brain-barrier endothelial -cells, Journal of Neurochemistry 64 (1995) 2708–2715. [DOI] [PubMed] [Google Scholar]
- [66].Carnevale NT, Hines ML, The NEURON book, Cambridge University Press, Cambridge, UK, 2006. [Google Scholar]
- [67].Burden RL, Faires JD, Numerical analysis, Ninth Ed., Brooks/Cole, Boston, MA, USA, 2010. [Google Scholar]
- [68].Shin SY, Nguyen LK, Dissecting cell -fate determination through integrated mathematical modeling of the ERK/MAPK signaling pathway, ERK Signaling: Methods and Protocols, 1487 (2017) 409–432. [DOI] [PubMed] [Google Scholar]
- [69].Barthe BC, Galabert C, Guycrotte O, Figarella C, Plasma and serum lactoferrin levels in cystic fibrosis. Relationship with the presence of cystic-fibrosis protein, Clinica Chimica Acta 181 (1989) 183–188. [DOI] [PubMed] [Google Scholar]
- [70].Majka G, Wiecek G, Srottek M, Spiewak K, Brindell M, Koziel J, Marcinkiewicz J, Strus M, The impact of lactoferrin with different levels of metal saturation on the intestinal epithelial barrier function and mucosal inflammation, Biometals 29 (2016) 1019–1033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [71].Descamps L, Dehouck MP, Torpier G, Cecchelli R, Receptor-mediated transcytosis of transferrin through blood-brain barrier endothelial cells, American Journal of Physiology-Heart and Circulatory Physiology 270 (1996) H1149–H1158. [DOI] [PubMed] [Google Scholar]
- [72].Rubin D, Drab E, Bauer K, Endothelial cell subpopulations in vitro: cell volume, cell cycle, and radiosensitivity, Journal of Applied Physiology 67 (1989) 1585–1590. [DOI] [PubMed] [Google Scholar]