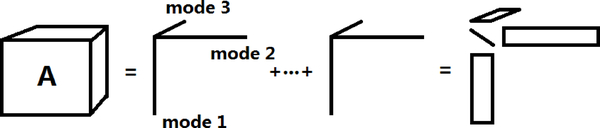Bayesian Conditional Tensor Factorizations for High-Dimensional Classification

Abstract

In many application areas, data are collected on a categorical response and high-dimensional categorical predictors, with the goals being to build a parsimonious model for classification while doing inferences on the important predictors. In settings such as genomics, there can be complex interactions among the predictors. By using a carefully-structured Tucker factorization, we define a model that can characterize any conditional probability, while facilitating variable selection and modeling of higher-order interactions. Following a Bayesian approach, we propose a Markov chain Monte Carlo algorithm for posterior computation accommodating uncertainty in the predictors to be included. Under near low rank assumptions, the posterior distribution for the conditional probability is shown to achieve close to the parametric rate of contraction even in ultra high-dimensional settings. The methods are illustrated using simulation examples and biomedical applications.

1. Introduction

Classification problems involving high-dimensional categorical predictors have become common in a variety of application areas, with the goals being not only to build an accurate classifier but also to identify a sparse subset of important predictors. For example, genetic epidemiology studies commonly focus on relating a categorical disease phenotype to single nucleotide polymorphisms encoding whether an individual has 0, 1 or 2 copies of the minor allele at a large number of loci across the genome. In such applications, it is expected that interactions play an important role, but there is a lack of statistical methods for identifying important predictors that may act through both main effects and interactions from a high-dimensional set of candidates. Our goal is to develop nonparametric Bayesian methods for addressing this gap focusing on unordered categorical data.

There is a rich literature on methods for prediction and variable selection from high or ultra high-dimensional predictors with a categorical response. The most common strategy would rely on logistic regression with the linear predictor having the form $x_i^{\prime }\beta$, with x_i = (x_i1,…,x_ip)′ denoting the predictors and β = (β₁,…,β_p)′ regression coefficients. In high-dimensional cases in which p is the same order of n or even p > n, classical methods such as maximum likelihood break down but there is a rich variety of alternatives ranging from penalized regression to Bayesian variable selection. Popular methods include L₁ penalization (Tibshirani, 1996) and the elastic net (Zou and Hastie, 2005), which combines L₁ and L₂ penalties to accommodate p ≫ n cases and allow simultaneous selection of correlated sets of predictors. For efficient L₁ regularization in generalized linear models including logistic regression, Park and Hastie (2007) proposed a solution path method. Genkin et al. (2007) propose a related Bayesian approach for high-dimensional logistic regression under Laplace priors. Wu et al. (2009) applied L₁ penalized logistic regression to genome wide association studies. Potentially, related methods can be applied to identify main effects and epistatic interactions (Yang et al., 2010), but direct inclusion of interactions within a logistic model creates a daunting dimensionality problem limiting attention to low-order interactions and modest numbers of predictors.

These limitations have motivated a rich variety of nonparametric classifiers, including classification and regression trees (CART) (Breiman et al., 1984) and random forests (RFs) (Breiman, 2001). CART partitions the predictor space so that samples within the same partition set have relatively homogeneous outcomes. CART can capture complex interactions and has easy interpretation, but tends to be unstable computationally and lead to low classification accuracy. RFs extend CART by creating a classifier consisting of a collection of trees that are all used to vote for classification. RFs can substantially reduce variance compared to a single tree and result in high classification accuracy, but provide an uninterpretable machine that does not yield insight into the relationship between specific predictors and the outcome. Moreover, through our simulation results in section 6, we found that random forests did not behave well in high dimensional low signal-to-noise cases.

Our focus is on developing a new framework for nonparametric Bayes classification through tensor factorizations of the conditional probability P(Y = y | X₁ = x₁,…,X_p = x_p), with Y ∈ {1,…,d₀} a categorical response and X = (X₁,…,X_p)′ a vector of p categorical predictors. The conditional probability can be expressed as a d₁ × ⋯ × d_p tensor for each class label y, with d_j denoting the number of levels of the jth categorical predictor X_j. If p = 2 we could use a low rank matrix factorization of the conditional probability, while in the general p case we could consider a low rank tensor factorization. Such factorizations must be non-negative and constrained so that the conditional probabilities add to one for each possible X, and are fully flexible in characterizing the classification function for sufficiently high rank. Dunson and Xing (2009) and Bhattacharya and Dunson (2012) applied two different tensor decomposition methods to model the joint probability distribution for multivariate categorical data. Although an estimate of the joint pmf can be used to induce an estimate of the conditional probability, there are clear advantages to bypassing the need to estimate the high-dimensional nuisance parameter corresponding to the marginal distribution of X.

We address such issues using a Bayesian approach that places a prior over the parameters in the factorization, and provide strong theoretical support for the approach while developing a tractable algorithm for posterior computation. Some advantages of our approach include (i) fully flexible modeling of the conditional probability allowing any possible interactions while favoring a parsimonious characterization; (ii) variable selection; (iii) a full probabilistic characterization of uncertainty providing measures of uncertainty in variable selection and predictions; and (iv) strong theoretical support in terms of rates at which the full posterior distribution for the conditional probability contracts around the truth. Notably, we are able to obtain near a parametric rate even in ultra high-dimensional settings in which the number of candidate predictors increases exponentially with sample size. Such a result differs from frequentist convergence rates in characterizing concentration of the entire posterior distribution instead of simply a point estimate. Although our computational algorithms do not yet scale to massive dimensions, we can accommodate 1, 000s of predictors.

2. Conditional Tensor Factorizations

In section 2.1, we briefly introduce the tensor factorization techniques and describe their relevance to high-dimensional classification. In section 2.2, we study the relationship between our model and the multinomial logit model for categorical predictors.

2.1. Tensor factorization of the conditional probability

Although there is a rich literature on tensor decompositions, little is in statistics. The focus has been on two factorizations that generalize matrix singular value decomposition (SVD). The most popular is parallel factor analysis (PARAFAC) (Harshman, 1970; Harshman and Lundy, 1994; Zhang and Golub, 2001), which expresses a tensor as a sum of r rank one tensors, with the minimal possible r defined as the rank (Fig.1). The second approach is Tucker decomposition or higher-order singular value decomposition (HOSVD), which was proposed by Tucker (1966) for three-way data and extended to arbitrary orders by De Lathauwer et al. (2000). HOSVD expresses d₁ × ⋯ × d_p tensor $A=\left\{a_{c_1\cdots c_p}\right\}$ as

$$a_{c_1\cdots c_p}=\sum _{h_1=1}^{k_1}\dots \sum _{h_p=1}^{k_p}{g}_{h_1\cdots h_p}\prod _{j=1}^p{u}_{h_j{c}_j}^{(j)},$$ (1)

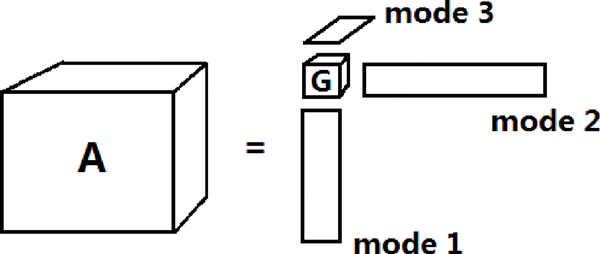
where k_j(≤ d_j) is the j-rank for j = 1,…, p, $U^{(j)}=(u_{st}^{(j)})$ are orthogonal matrices called mode matrices, and $G=\left\{g_{h_1\cdots h_p}\right\}$ is a core tensor, with constraints on G such as low rank and sparsity imposed to induce better data compression and fewer components compared to PARAFAC (Fig.2). This is intuitively suggested by comparing Fig.1 and Fig.2: PARAFAC can be considered as a special case of HOSVD when the core tensor G is restricted to be diagonal. In HOSVD, the j-rank k_j is the rank of the mode j matrix A_(j), defined by rearranging elements of the tensor A into a d_j × d₁ ⋯ d_j−1d_j+1 ⋯ d_p matrix such that each row consists of all elements $a_{c_1\cdots c_p}$ with the same c_j. Although k_j can be close to d_j, low rank approximations of A can lead to high accuracy and provide satisfactory results (Eldén and Savas (2009),Vannieuwenhoven et al. (2012)).

Figure 1:

A diagram describes PARAFAC for 3 dimensional tensor. The lines in the middle correspond to the mode vectors corresponding to each mode of the tensor. The rightmost representation draws analogy to the matrix SVD.

Figure 2:

A diagram describes HOSVD for 3 dimensional tensor. The smaller cube G is the core tensor and the rectangles are the mode matrices u^(j)’s corresponding to each mode of the tensor.

For probability tensors, we need nonnegative versions of such decompositions (Kim and Choi (2007)) and the concept of rank changes accordingly (Cohen and Rothblum, 1993). In the following, we solely consider nonnegative HOSVD, where all quantities in (1) are nonnegative. Moreover, we relax the orthogonality constraint on the mode matrix U^(j) in HOSVD since orthogonality is not a natural constraint for nonnegative vectors. We define k = (k₁, …, k_p) to be a multirank of a nonnegative tensor A if: 1. A has a representation (1) with k; 2. k has the minimum possible size, which is defined by $|k|={\prod }_{j=1}^p{k}_j$. Note that the rank in this definition might not be unique but representations with different multirank k have the same number of parameters in the core tensors. This suggests that the multirank k reflects the best possible tensor compression level.

The conditional probability P(Y = y|X₁ = x₁, …, X_p = x_p) can be structured as a d₀ × d₁ × ⋯ × d_p dimensional tensor. We call such tensors conditional probability tensors. Let ${\mathcal{P}}_{d_1,\dots ,d_p}\left(d_0\right)$ denote the set of all conditional probability tensors, so that $P\in {\mathcal{P}}_{d_1,\dots ,d_p}\left(d_0\right)$ implies

$$P\left(y|x_1,\dots ,x_p\right)\ge 0\forall y,x_1,\dots ,x_p,\sum _{y=1}^{d_0}P\left(y|x_1,\dots ,x_p\right)=1\forall x_1,\dots ,x_p.$$

To ensure that P is a valid conditional probability, the elements of the tensor must be non-negative with constraints on the first dimension for Y. A primary goal is accommodating high-dimensional covariates, with the overwhelming majority of cells in the table corresponding to unique combinations of Y and X unoccupied. In such settings, it is necessary to encourage borrowing information across cells while favoring sparsity.

Our proposed model for the conditional probability has the form:

$$P\left(y|x_1,\dots ,x_p\right)=\sum _{h_1=1}^{k_1}\cdots \sum _{h_p=1}^{k_p}{\lambda }_{h_1{h}_2\dots h_p}(y)\prod _{j=1}^p{\pi }_{h_j}^{(j)}\left(x_j\right),$$ (2)

with all positive parameters subject to

$$\begin{gathered} \sum _{c=1}^{d_0}{\lambda }_{h_1{h}_2\dots h_p}(c)=1,\text{for}\text{any}\text{possible}\text{combination}\text{of}\left(h_1,h_2,\dots ,h_p\right), \\ \sum _{h=1}^{k_j}{\pi }_h^{(j)}\left(x_j\right)=1,\text{for}\text{any}\text{possible}\text{pair}\text{of}\left(j,x_j\right). \end{gathered}$$ (3)

Here we impose normalizing constraints so that model (2) admits a latent variable representation. These normalizing constraints can always be satisfied by properly rescaling ${\lambda }_{h_1{h}_2\dots h_p}(y)\text{'}\mathrm{s}$ and ${\pi }_h^{(j)}\text{'}\mathrm{s}$ as indicated by Theorem 1 below.

Analogous to HOSVD, we preserve the names core tensor for $\mathrm{\Lambda }=\left\{{\lambda }_{h_1\cdots h_p}(y)\right\}$ and mode matrices for $\pi =\{{\pi }_{h_j}^{(j)}\left(x_j\right)\}$. More specifically, the d_j × k_j matrix π^(j) with (u, v)th element ${\pi }_v^{(j)}(u)$ will refer to the jth mode matrix. Similar to the definition of multirank for nonnegative tensors, we define k = (k₁, …, k_p) to be a multirank of the conditional probability tensor P if: 1. P has a representation (2) satisfying the constraints (3) with k; 2. k has the minimum possible size |k|. In the rest of this article, we always consider the representation (2) with a multirank k. Intuitively, (d₀ − 1)|k| is equal to the degrees of freedom of the core tensor Λ, and controls the complexity of the model. By allowing |k| to gradually increase with sample size, one can obtain a sieve estimator. The value of k_j controls the number of parameters used to characterize the impact of the jth predictor. In the special case in which k_j = 1, the jth predictor is excluded from the model, so sparsity can be imposed by setting k_j = 1 for most j’s.

The following theorem provides basic support for factorization (2)–(3) through showing that any conditional probability has this representation. The proof of this theorem, which can be found in the appendix, sheds some light on the meaning of k₁, …, k_p and how it is related to a sparse structure of the tensor.

Theorem 1 Every d₀ × d₁ × d₂ × ⋯ × d_p conditional probability tensor $P\in {\mathcal{P}}_{d_1,\dots ,d_p}\left(d_0\right)$ can be decomposed as (2), with 1 ≤ k_j ≤ d_j for j = 1, …, p. Furthermore, ${\lambda }_{h_1{h}_2\dots h_p}(y)$ and ${\pi }_{h_j}^{(j)}\left(x_j\right)$ can be chosen to be nonnegative and satisfy the constraints (3).

According to Theorem 1, the tensor factorization model (2) provides a fully flexible modeling of the conditional probability and allows arbitrary order of interactions. We can simplify the representation through introducing p latent class indicators z₁, …, z_p for X₁,...,X_p, with Y conditionally independent of (X₁, …, X_p) given (z₁, …, z_p). The model can be written as

$$\begin{gathered} Y_i|z_{i1},\dots ,z_{ip}\sim \text{Multinomial}\left(\left\{1,\dots ,d_0\right\},{\lambda }_{z_{i1},\dots ,z_{ip}}\right), \\ {z}_{ij}|X_j\sim \text{Multinomial}(\left\{1,\dots ,k_j\right\},{\pi }_1^{(j)}\left(X_j\right),\dots ,{\pi }_{k_j}^{(j)}\left(X_j\right)), \end{gathered}$$ (4)

where ${\lambda }_{z_{i1},\dots ,z_{ip}}=\left\{{\lambda }_{z_{i1},\dots ,z_{ip}}(1),\dots ,{\lambda }_{z_{i1},\dots ,z_{ip}}\left(d_0\right)\right\}$. Marginalizing out the latent class indicators, the conditional probability of Y given X₁, …,X_p has the form in (2). In a supplementary appendix of this paper, we characterize more desirable properties, which only rely on the structure of our proposed model.

2.2. Connection with logit models

This subsection discusses the relationship between the conditional tensor factorization model and the logit model for multinomial response (Agresti, 2002). In particular, we assume in this subsection that d₁ = ⋯ = d_p = d and consider the following baseline-category logit model for categorical predictors,

$$\log \frac{P\left(y|x_1,\dots ,x_p\right)}{P\left(d_0|x_1,\dots ,x_p\right)}={\lambda }_0(y)+\sum _{1\le j\le p}{\lambda }_{x_j}^j(y)+\sum _{1\le j<k\le p}{\lambda }_{x_j{x}_k}^{jk}(y)+\sum _{1\le j<k<l\le p}{\lambda }_{x_j{x}_k{x}_l}^{jkl}(y),$$ (5)

for y = 1, …, d₀ − 1, where d₀ is the baseline-category, {λ₀(y) : y = 1, …, d₀ − 1} are the (d₀ − 1) intercepts, $\{{\lambda }_a^j(y):a\in \{1,\dots ,d\},1\le j\le p,y=1,\dots ,d_0-1\}$ are the (d₀ − 1)p main effects, $\{{\lambda }_{ab}^{jk}(y):(a,b)\in {\{1,\dots ,d\}}^2,1\le j<k\le p,y=1,\dots ,d_0-1\}$ are the $\left(d_0-1\right)\left(\begin{array}{l}p\hfill \\ 2\hfill \end{array}\right)$ two-way interaction effects and so on. For identifiability, we assume that main effects and interactions are zero if x_j = d for some j included. For every q ∈ {1, …, p}, all q-way interaction terms constitute a q-dimensional symmetric tensor.

By comparing (5) and (2), we find that our conditional tensor factorization model provides a parsimonious reparametrization of the multi-factor logit model. For example, every multi-factor logit model can be represented by a conditional tensor factorization model with k₁ = … = k_p = d. By letting some k_j be 1 in (2), we exclude all effects of the jth predictor in (5), corresponding to restricting all j-indexed main/interaction effects to be zero. Therefore, (2) corresponds to a multi-factor logit model that incorporates all possible interaction effects among the important predictors (X_j s.t. k_j > 1). Moreover, (2) controls the degrees of freedom (df) (d₀ − 1)|k| of all nonzero interaction effects in (5) by a parsimonious reparametrization, corresponding to a low rank structure on the inverse-logit-transformed interaction tensor. Even with a variable selection procedure, the interaction effects in (5) among important predictors are still completely arbitrary, leading to a df of (d₀ − 1)d^s, where s is the number of selected important predictors. Under the same set of important predictors, the df of (2) can be significantly lower than that of (5). Therefore, the conditional tensor factorization model can be viewed as a special multinomial logit model with a sparse and parsimonious interaction structure.

One can potentially introduce tensor factorizations directly on interaction tensors. However, comparing to (5), (2) has advantages of treating all response levels in a symmetric way and providing a latent variable interpretation (4), leading to convenient posterior computation.

3. Bayesian Tensor Factorization

In this section, we will provide a Bayesian implementation of the tensor factorization model and prove the corresponding posterior convergence rate.

3.1. Prior specification

To complete a Bayesian specification of our model, we choose independent Dirichlet priors for the parameters $\mathrm{\Lambda }=\left\{{\lambda }_{h_1,\dots ,h_p},h_j=1,\dots ,k_j,j=1,\dots ,p\right\}$ and $\pi =\{{\pi }_{h_j}^{(j)}\left(x_j\right),h_j=1,\dots ,k_j,x_j=1,\dots ,d_j,j=1,\dots ,p\},$

$$\begin{gathered} \left\{{\lambda }_{h_1,\dots ,h_p}(1),\dots ,{\lambda }_{h_1,\dots ,h_p}\left(d_0\right)\right\}\sim \mathrm{Diri}\left(1/d_0,\dots ,1/d_0\right), \\ \left\{{\pi }_1^{(j)}\left(x_j\right),\dots ,{\pi }_{k_j}^{(j)}\left(x_j\right)\right\}\sim \mathrm{Diri}\left(1/k_j,\dots ,1/k_j\right),j=1,\dots ,p. \end{gathered}$$ (6)

These priors have the advantages of imposing non-negative and sum to one constraints, while leading to conditional conjugacy in posterior computation. The hyperparameters in the Dirichlet priors are chosen to favor placing most of the probability on a few elements, inducing near sparsity in these vectors.

If k_j = 1 in (2), by constraints (3) ${\pi }_1^{(j)}\left(x_j\right)=1$, P(y|x₁, …, x_p) will not depend on x_j and $Y\perp X_j|X_{j^{\prime }}$, j′ ≠ j. Hence, I(k_j > 1) are variable selection indicators. In addition, k_j can be interpreted as the number of latent classes for the jth covariate. Levels of X_j are clustered according to their relations with the response variable in a soft probabilistic manner, with k₁, …, k_p controlling the complexity of the latent structure as well as sparsity. Because we are faced with extreme data sparsity in which the vast majority of combinations of Y, X₁, …,X_p are not observed, it is critical to impose sparsity assumptions. Even if such assumptions do not hold, they have the effect of massively reducing the variance, making the problem tractable. A sparse model that discards predictors having less impact and parameters having small values may still explain most of the variation in the data, resulting in a useful classifier that has good performance in terms of the bias-variance tradeoff even when sparsity assumptions are not satisfied.

To embody our prior belief that only a small number of k_j’s are greater than one, we want

$$P\left(k_j=k\right)\approx Q(j,k)\triangleq \left(1-\frac{r}{p}\right)I(k=1)+\frac{r}{\left(d_j-1\right)p}I(k>1),$$

for j = 1, …, p, where I(A) is the indicator function for the event A and r is the expected number of predictors included. This specification accommodates variable selection. To further include a low rank constraint on the conditional probability tensor, we impose $|k|={\prod }_{j=1}^p{k}_j$ to be less than or equal to M. Intuitively, M controls the effective number of parameters in the model. This low rank constraint in turn restricts the maximum number of predictors to be log₂ M. We note that in the setting in which p > n some such constraint is necessary.

To summarize, the effective prior on the k_j’s is

$$P\left(k_1=l_1,\dots ,k_p=l_p\right)\propto Q\left(1,l_1\right)\cdots Q\left(p,l_p\right)I\left\{\prod _{j=1}^p{l}_j\le M\right\}.$$ (7)

Let γ = (γ₁, …, γ_p)′ be a vector having elements γ_j = I(k_j > 1) indicating inclusion of the jth predictor. Since ${\prod }_{j=1}^p{l}_j\le M$ implies inclusion of at most log₂M predictors, the induced prior for γ resembles the prior in Jiang (2006). Potentially, we can put a more structured prior on the components in the conditional tensor factorization, including sparsity in Λ. However, the theory shown in the next part provides strong support for prior (6)–(7).

3.2. Posterior convergence rates

Before formally describing the sparsity and low rank assumptions, we first introduce some notation and definitions. Suppose we obtain data for n observations yⁿ = (y₁, …, y_n)′, which are conditionally independent given Xⁿ = (x₁, …, x_n)′ with $x_i={\left(x_{i1},\dots ,x_{i{p}_n}\right)}^{\prime }$, x_ij ∈ {1, …, d} and p_n ≫ n. We exclude the n subscript on p and other quantities when convenient and assume that d = max_j{d_j} is finite and does not depend on n. An important special case is when all d_j’s are the same. Let P₀ denote the true data generating model, which can be dependent on n. Let ϵ_n be a sequence converging to zero while keeping $n{ϵ}_n^2\to \infty$. This sequence will serve as the convergence rate in the sense that under a certain metric d to be defined later, the posterior of the conditional probability tensor P will asymptotically concentrate within an ϵ_n d-ball centered on the truth P₀. We use the notation f ≺ g to mean f/g → 0 as n → ∞. Next, we describe all the assumptions that are needed for the main theorem.

To determine the posterior convergence rate, two things are competing with each other: 1. variable selection among the high dimension covariates; 2. the approximation abilities of near low rank tensors. The assumption below characterizes the first.

Assumption A. There exists a sequence ϵ_n satisfying ϵ_n → 0, $n{ϵ}_n^2\to \infty$ and ${\sum }_n\exp \left(-n{ϵ}_n^2\right)<\infty$ such that $\log p_n\prec n{ϵ}_n^2/\log M_n$.

Recalling the definition of M_n as the prior upper threshold for the size $|k|={\prod }_{j=1}^p{k}_j$, log M_n can be interpreted as the maximum number of predictors to be selected and cannot exceed log n. As a result, Assumption A implies that the high dimensional variable selection per se imposes a lower bound for ϵ_n as $\sqrt{\log n\log p_n/n}$. As a result, to obtain a convergence rate of $n^{-(1-\alpha )/2}$ up to some logarithmic factor, p_n is allowed to increase with n as fast as $O\left(e^{n^{\alpha }}\right)$.

To characterize the low rank tensor assumption, rather than assume that most of the predictors have no impact on Y, we consider the situation similar to Jiang (2006) that most have nonzero but very small influence. Specifically, parameterizing the true model P₀ in our tensor form with k_j = d_j for j = 1, …, p_n (this is always possible for any P₀), we assume:

Assumption B. $M_n\log \left(1/{ϵ}_n\right)\prec n{ϵ}_n^2$ and there exists a multirank sequence k⁽¹⁾, k⁽²⁾, … with |k⁽ⁿ⁾| ≤ M_n, such that

$$\sum _{j=1}^{p_n}\underset{x_j}{\max }\sum _{h_j>k_j^{(n)}}^{d_j}{\pi }_{h_j}^{(j)}\left(x_j\right)\prec {ϵ}_n^2,$$

where f ≺ g means f/g → 0 as n → ∞.

This is a near low rank restriction on P₀. This assumption intuitively means that the true tensor P₀ could be approximated within error ${ϵ}_n^2$ by a truncated tensor with multirank k⁽ⁿ⁾, whose size is less than $n{ϵ}_n^2/\log \left(1/{ϵ}_n\right)$. Assumption B includes the sparsity assumption where only order o(n) predictors are important as a special case. In high-dimensional problems, sparsity assumptions are ubiquitous (Bülmann and van de Geer, 2011). Under this sparsity assumption, although p_n is allowed to be exponentially large in n, contributions of most x_j’s are zero and the sum in Assumption B only involves order o(n) terms. Theoretically, a lower bound of ϵ_n attributed to the low rank approximation could be identified as the minimum ϵ such that

$$\exists \text{multirank}k,s.t.|k|<n{ϵ}^2/\log (1/ϵ)\text{and}\sum _{j=1}^{p_n}\underset{x_j}{\max }\sum _{h_j>k_j}^{d_j}{\pi }_{h_j}^{(j)}\left(x_j\right)\le {ϵ}^2.$$

The overall ϵ_n will be the minimum of this lower bound and the one determined by Assumption A. Assumption B includes the special case when P₀ is exactly of low multirank k⁽⁰⁾. In such case, all k⁽ⁿ⁾ could be chosen as k⁽⁰⁾ and Assumption B puts no constraint on ϵ_n, leading a convergence rate to be entirely determined by the variable selection in Assumption A as $\sqrt{\log p_n/n}$ (Corollary 6 below). In section 6 of real data applications, we will provide empirical evidence of this near low multirank assumption.

The last assumption can be considered as a regularity condition.

Assumption C. P₀(y|x) ≥ ϵ₀ for any x, y for some ϵ₀ > 0.

Under this assumption, the Kullback-Leibler divergence would be bounded by the sup norm up to a constant, where the latter is easier to characterize in case of our model. This condition can be interpreted as that for every covariates x, the response y cannot be perfectly predicted. As a counterpart, for Gaussian regression problems a similar assumption would require the noise variance to be bounded away from 0 (applying Theorem 2.1 in Ghosal et al. (2000) instead of Theorem 5 in Appendix B). Although pursuing a simplest set of assumptions for our theorem to hold is insteresting, it is not the primary focus of the current paper.

The next theorem states the posterior contraction rate under our prior (6)–(7) and Assumption A-C. Recall that r_n is a hyperparameter in the prior.

Theorem 2 Assume the design points x₁, …, x_n are independent observations from an unknown probability distribution G_n on {1, …, d}^p_n. Moreover, assume the prior is specified as in (6)–(7). Assume that A, B and C hold. Denote $d\left(P,P_0\right)=\int {\sum }_{y=1}^{d_0}|P\left(y|x_1,\dots ,x_p\right)-P_0\left(y|x_1,\dots ,x_p\right)|G_n\left(d{x}_1,\dots ,d{x}_p\right)$, then

$${\mathrm{\Pi }}_n\left\{P:d\left(P,P_0\right)\ge M{ϵ}_n|y^n,X^n\right\}\to 0a.s.P_0^n,$$

where Π_n(A|yⁿ,Xⁿ) is the posterior probability of A given the observations.

The following corollary tells us that the posterior convergence rate of our model can be very close to n^−1/2 under appropriate near low rank conditions.

Corollary 3 For α ∈ (0, 1), ϵ_n = n^{−(1−α)/2} log n will satisfy the conditions in Theorem 2 if M_n ≺ n^α log n, p_n ≺ exp(n^α/log n) and there exists a sequence of multiranks k⁽ⁿ⁾ with size at most M_n such that

$$\sum _{j=1}^{p_n}\underset{x_j}{\max }\sum _{h_j>k_j^{(n)}}^{d_j}{\pi }_{h_j}^{(j)}\left(x_j\right)\prec n^{-(1-\alpha )}{\log }^{2}n.$$

As mentioned after Assumption B, if the truth is exactly lower multirank, then with a small modification to the proof of Theorem 2, we can eliminate the log M_n factor in Assumption A, leading to the following result.

Corollary 4 If the truth P₀ has multirank k with a finite number of components k_j > 1, then with M_n chosen to be a sufficiently large number, the posterior convergence rate ϵ_n could be at least $\sqrt{\log p_n/n}$.

In order to model any arbitrary conditional probability tensor, lasso needs to include all d^p_n interaction terms among p_n predictors. As a result, the best achievable rate of lasso becomes $\sqrt{\log d^{p_n}/n}=\sqrt{p_n\log d/n}$ (Raskutti et al., 2011), which is suboptimal compared to the rate $\sqrt{\log p_n/n}$ of our model under the low rank assumption.

Since (d₀ − 1)M_n could be interpreted as the maximum effective number of parameters in the model, which should be at most the same order as the sample size n, we suggest to set M_n = n as a default for the prior defined in section 3.1 to conceptually provide as loose an a priori upper bound as possible. Results tend to be robust to the choice of M_n as long as it is not chosen to be small. Since $M\ge |k|\ge 2^{\#\left\{j:k_j>1\right\}}$, the maximum number of predictors included in the model is log₂ n. This suggests that we can choose (log₂ n)/2 = log₄ n as a default value for r in the prior.

4. Posterior Computation

In section 4.1, we consider fixed k = (k₁, …, k_p)′ and use a Gibbs sampler to draw posterior samples. Generalizing this Gibbs sampler, we developed a reversible jump Markov Chain Monte Carlo (RJMCMC) algorithm (Green, 1995) to draw posterior samples from the joint distribution of k = {k_j : j = 1, …, p} and (Λ, π, z). However, for n and p equal to several hundred or more, we were unable to design an RJMCMC algorithm that was sufficiently efficient to be used routinely. Hence, in section 4.2, we propose a faster two stage procedure based on approximated marginal likelihood.

4.1. Gibbs sampling for fixed k

Under (6) the full conditional posterior distributions of Λ, π and z all have simple forms, which we sample from as follows.

1. For h_j = 1, …, k_j, j = 1, …, p, update ${\lambda }_{h_1,\dots ,h_p}$ from the Dirichlet conditional,

$$\begin{gathered} \left\{{\lambda }_{h_1,\dots ,h_p}(1),\dots ,{\lambda }_{h_1,\dots ,h_p}(d)\right\}|-\sim \mathrm{Diri}(\frac{1}{d}+\sum _{i=1}^{n}1\left(z_{i1}=h_1,\dots ,z_{ip}=h_p,y_i=1\right), \\ \dots ,\frac{1}{d}+\sum _{i=1}^{n}1\left(z_{i1}=h_1,\dots ,z_{ip}=h_p,y_i=d\right)). \end{gathered}$$

2. Update π^(j)(k) from the Dirichlet full conditional posterior distribution,

$$\begin{gathered} \{{\pi }_1^{(j)}(k),\dots ,{\pi }_{k_j}^{(j)}(k)\}|-\sim \mathrm{Diri}(\frac{1}{k_j}+\sum _{i=1}^{n}1\left(z_{ij}=1\right)1\left(x_{ij}=k\right), \\ \dots ,\frac{1}{k_j}+\sum _{i=1}^{n}1\left(z_{ij}=k_j\right)1\left(x_{ij}=k\right)). \end{gathered}$$

3. Update z_ij from the multinomial full conditional posterior, with

$$P\left(z_{ij}=h|-\right)\propto {\pi }_h^{(j)}\left(x_{ij}\right){\lambda }_{z_{i,1},\dots ,z_{i,j-1},h,z_{i,j+1},\dots ,z_{i,p}}\left(y_i\right).$$

4.2. Two step approximation

We propose a two stage algorithm, which identifies a good model in the first stage and then learns the posterior distribution for this model in a second stage via the Gibbs sampler of section 4.1. We first propose an approximation to the marginal likelihood. For simplicity in exposition, we focus on binary Y with d₀ = 2, but the approach generalizes in a straight-forward manner, with the beta functions in the below expression for the marginal likelihood replaced with functions of the form $\mathrm{\Gamma }\left(a_1\right)\mathrm{\Gamma }\left(a_2\right)\cdots \mathrm{\Gamma }\left(a_{d_0}\right)/\mathrm{\Gamma }\left(a_1+\cdots +a_{d_0}\right)$. To motivate our approach, we first note that ${\pi }_{h_j}^{(j)}\left(x_j\right)$ can be viewed as providing a type of soft clustering of the jth feature X_j, controlling borrowing of information among probabilities conditional on combinations of predictors. To obtain approximated marginal likelihoods to be used only in the initial model selection stage, we propose to force ${\pi }_{h_j}^{(j)}\left(x_j\right)$ to be either zero or one, corresponding to a hard clustering of the predictors. The example in a supplementary appendix gives a heuristic argument on the variance-bias tradeoff by using the degenerate approximation, suggesting the degenerate approximation to be adequate for model selection. Under this approximation, the marginal likelihood has a simple expression.

For a given model indexed by k = {k_j, j = 1, …, p}, we assume that the levels of X_j are clustered into k_j groups $A_1^{(j)},\dots ,A_{k_j}^{(j)}$. For example, with levels {1, 2, 3, 4, 5}, $A_1^{(j)}=\{1,2,3\}$ and $A_2^{(j)}=\{4,5\}$. Then it is easy to see that the marginal likelihood conditional on k and

$$\begin{gathered} A\text{is}\mathcal{L}(y|k,A)= \\ \prod _{h_1,\dots ,h_p}\frac{1}{\mathrm{Beta}(1/2,1/2)}\mathrm{Beta}(\frac{1}{2}+\sum _{i=1}^{n}I(x_{i1}\in A_{h_1}^{(1)},\dots ,x_{ip}\in A_{h_p}^{(p)},y_{i_i}=1), \\ \frac{1}{2}+\sum _{i=1}^{n}I(x_{i1}\in A_{h_1}^{(1)},\dots ,x_{ip}\in A_{h_p}^{(p)},y_i=0)). \end{gathered}$$

Having an expression for the marginal likelihood, we apply a stochastic search MCMC algorithm (George and McCulloch, 1997) to obtain samples of (k₁, …, k_p) from the approximated posterior distribution. This proceeds as follows.

1. For j = 1 to p, do the following. Given the current model indexed by k = {k_j : j = 1, …, p} and clusters $A=\{A_h^{(j)}:h=1,\dots ,k_j,j=1,\dots ,p\}$, propose to increase k_j to k_j + 1 (if k_j < d) or reduce it to k_j − 1 (if k_j > 1) with equal probability.

2. If increase, randomly split a cluster of X_j into two clusters (all splits have equal probability). For example, if d_j = 5, k_j = 2 and the levels of X_j are clustered as {1, 2, 3} and {4, 5}. There are 4 possible splitting schemes: three ways to split {1, 2, 3} and one way to split {4, 5}. We randomly choose one. Accept this move with acceptance rate based on the approximated marginal likelihood.

3. If decrease, randomly merge two clusters and accept or reject this move.

4. If k_j remains 1, propose an additional switching step that switches k_j with a currently “active predictor” j′ whose $k_{j^{\prime }}>1$ and randomly divide the cluster of X_j into $k_{j^{\prime }}$ clusters.

Estimating approximated marginal inclusion probabilities of k_j > 1 based on this algorithm, we keep predictors having inclusion probabilities great than 0.5; this leads to selecting the median probability model, which in simpler settings has been shown to have optimality properties in terms of predictive performance (Barbieri and Berger, 2004).

5. Simulation Studies

To assess the performance of the proposed approach, we conducted two simulation studies and calculated the misclassification rate on the testing samples.

5.1. Fully nonparametric classification

In the first simulation study, we generate the cells in the true conditional probability tensor in a completely random way. Each simulated dataset consisted of N = 3, 000 instances with p of the covariates X₁, …,X_p, each of which has d = 4 levels, and a binary response Y. Two scenarios were considered: moderate dimension setting where p = 3, 4, 5 and high dimension setting where p = 20, 100, 500. Note that although p = 20 appears less than the training size n, the effective number of parameters is equal to 4²⁰. Similarly, we can call p = 3 moderate since the effective number of parameters is equal to 4³ = 64. Fixing p, four training sizes n = 200, 400, 600 and 800 were considered. We assumed that the true model had three important predictors X₁,X₂ and X₃, and generated P(Y = 1|X₁ = x₁,X₂ = x₂,X₃ = x₃) independently for each combination of (x₁, x₂, x₃); this was done once for each simulation replicate prior to generating the data conditionally on P(Y |X). To obtain an average Bayes error rate (optimal misclassification rate) around 15% (standard deviation is around 2%), we generated the conditional probabilities from f(U) = U²/{U² + (1 − U)²}, where U ~ Unif(0, 1). For each dataset, we randomly chose n samples as training with the remaining N − n as testing. We implemented the two stage algorithm on the training set and calculated the misclassification rate on the testing set.

As a general default, we chose r = ⎡log₄ n⎤ as the expected number of important predictors in the prior and M = log n as the maximum model size, where ⎡x⎤ stands for the minimal integer ≥ x. Under our sample size settings, r and M ranged from 4 to 5 and 7 to 9, respectively. To investigate the robustness of the proposed method in the high dimension settings, we also report the results under r = 6 and M = 20 (labelled by TF² in Table 2) for each combination of training size n and covariate dimension p. We ran 1,000 iterations for the first stage and 2,000 iterations for the second stage, treating the first half as burn-in. We compared the results applied to the same training-test split data with classification and regression trees (CART, tree package in R), random forests (RF, randomForest package) (Breiman, 2001), neural networks (NN, nnet package) with two layers of hidden units, lasso penalized logistic regression (LASSO, glmnet package) (Friedman et al., 2010), support vector machines (SVM, e1071 package) and Bayesian additive regression trees (BART, BayesTree package) (Chipman et al., 2010). The penalizing regularization parameter for LASSO was chosen by cross validation under default tuning parameter settings using the cv.glmnet function. The tuning parameters for other methods were chosen by their default settings. In the moderate dimension scenario, we enumerated all orders of interactions as input covariates for NN, LASSO and SVM. NN was not implemented for p = 5 since the available R code was unable to fit the model with 4⁵ = 1024 covariates. In the high dimension scenario, since the number of interactions grows exponentially fast, we only included (d − 1) × p dummy variables for the main effects as input covariates for NN, LASSO and SVM under p = 100 and 500 cases, and included $d^2\times \left(\begin{array}{l}p\hfill \\ 2\hfill \end{array}\right)+(d-1)\times p=3100$ dummy variables for the main effects and all two-way interaction terms as input covariates for LASSO and SVM under p = 20 (NN was not implemented since the available R code cannot fit the model with 3100 covariates). Moreover, we added the kernel SVM with Gaussian radial basis function as another competitor as suggested by a reviewer.

Table 2:

Simulation study results in the high dimension setting. RF: random forests, NN: neural networks, SVM: support vector machine, SVM²: SVM with all two-way interaction terms included, SVM^k: kernel SVM with Gaussian radial basis function, LASSO²: LASSO with all two-way interaction terms included, BART: Bayesian additive regression trees, TF: Our tensor factorization model, TF²: TF under a different hyperparameter setting. Misclassification rates and their standard deviations over 100 simulations are displayed.

		n = 200	n = 400	n = 600	n = 800
	CART	0.446(0.026)	0.365(0.040)	0.340(0.061)	0.335(0.087)
	RF	0.463(0.022)	0.443(0.026)	0.411(0.027)	0.391(0.022)
	NN	0.50l(0.009)	0.491(0.008)	0.505(0.042)	0.475(0.020)
	LASSO	0.442(0.04l)	0.413(0.026)	0.372(0.033)	0.362(0.046)
	LASSO2	0.440(0.043)	0.405(0.036)	0.352(0.038)	0.335(0.042)
p = 20	SVM	0.507(0.01l)	0.482(0.012)	0.495(0.011)	0.471(0.023)
	SVM2	0.483(0.035)	0.491(0.032)	0.478(0.030)	0.481(0.036)
	SVMk	0.473(0.016)	0.485(0.018)	0.482(0.017)	0.470(0.020)
	BART	0.448(0.026)	0.404(0.036)	0.371(0.032)	0.343(0.030)
	TF	0.249(0.036)	0.182(0.036)	0.171(0.026)	0.162(0.022)
	TF2	0.254(0.040)	0.186(0.037)	0.170(0.025)	0.165(0.024)
	CART	0.474(0.022)	0.424(0.042)	0.382(0.045)	0.361(0.051)
	RF	0.461(0.019)	0.478(0.026)	0.431(0.025)	0.425(0.021)
	NN	0.501(0.010)	0.493(0.008)	0.488(0.013)	0.476(0.014)
	LASSO	0.453(0.031)	0.425(0.031)	0.418(0.041)	0.398(0.033)
p = 100	SVM	0.489(0.011)	0.477(0.013)	0.479(0.013)	0.460(0.025)
	SVMk	0.490(0.021)	0.478(0.017)	0.474(0.015)	0.468(0.019)
	BART	0.468(0.015)	0.459(0.025)	0.412(0.012)	0.401(0.031)
	TF	0.327(0.114)	0.179(0.026)	0.170(0.021)	0.164(0.024)
	TF2	0.352(0.129)	0.177(0.028)	0.172(0.024)	0.165(0.025)
	CART	0.493(0.09)	0.454(0.052)	0.406(0.032)	0.369(0.084)
	RF	0.478(0.022)	0.470(0.020)	0.442(0.027)	0.429(0.021)
	NN	0.501(0.009)	0.484(0.023)	0.469(0.030)	0.444(0.019)
	LASSO	0.458(0.012)	0.464(0.023)	0.399(0.021)	0.415(0.017)
p = 500	SVM	0.488(0.017)	0.486(0.024)	0.476(0.017)	0.459(0.015)
	SVMk	0.493(0.019)	0.480(0.020)	0.466(0.017)	0.464(0.019)
	BART	0.479(0.013)	0.463(0.025)	0.419(0.028)	0.425(0.014)
	TF	0.452(0.098)	0.205(0.083)	0.172(0.022)	0.164(0.021)
	TF2	0.473(0.088)	0.226(0.095)	0.173(0.024)	0.164(0.023)

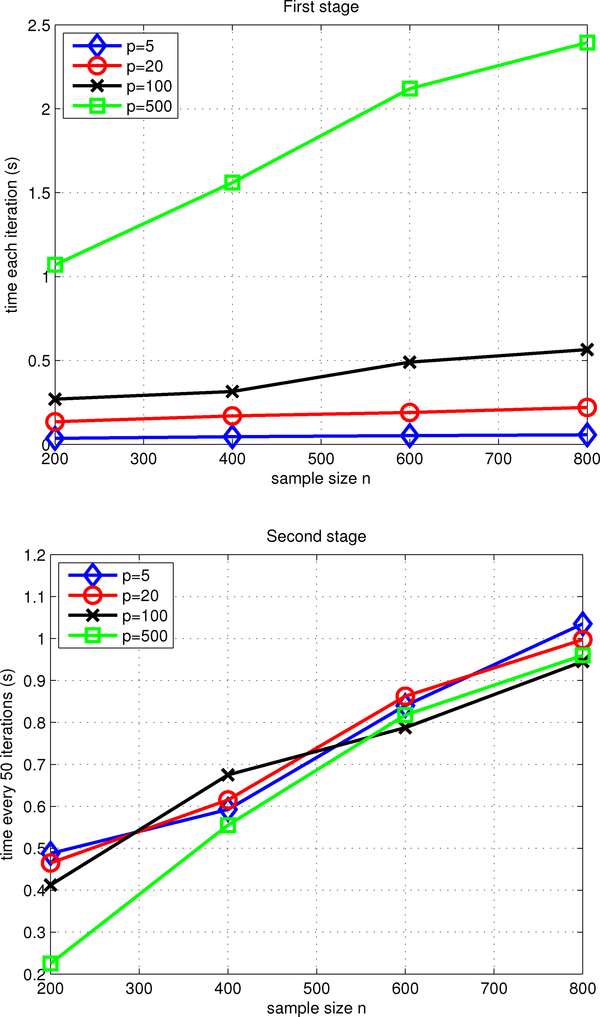
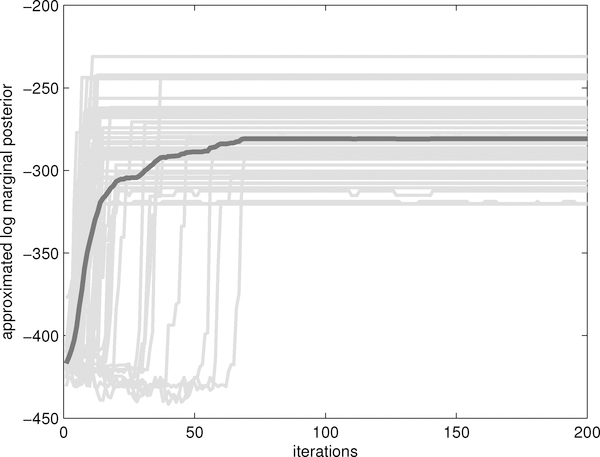
Figure 3 illustrates the computational costs of our two stage algorithm in the simu-lation example. Under p = 5(500) and n = 800(800) the first stage of our algorithm took about 1s(2s) to draw 40(1) iterations and the second stage took about 1s(1s) to draw 50(50) iterations in MATLAB. Since the computational costs in the second stage only depend on the sizes of the models selected by the first stage, they appeared similar across the covariate dimension p. As can be seen, the computational cost under p = 500 and n = 200 in the second stage is significantly less than those under p ∈ {5, 20, 100} and n = 200, because only a few covariates is selected into the second stage under the former setting. Figure 4 plots the approximated log marginal posterior versus the number of iterations for the model selection sampler in the first stage under p = 100 and n = 600. The sampler was quite efficient, with a burn-in of 100 iterations in the first stage and 200 iterations in the second stage sufficient and autocorrelations rapidly decreasing to zero with increasing lag time.

Figure 3:

Computational cost of the two stage algorithm for TF. The first (second) plot shows the computational time for every 1(50) iteration in the first(second) stage, under different combinations of sample sizes n ∈ {200, 400, 600, 800} and covariate dimensions p ∈ {5, 20, 100, 500}. The displayed results are based on 100 replicates.

Figure 4:

Mixing behavior of the model selection sampler in the first stage. Approximated log marginal posteriors are plotted versus numbers of iterations over 50 simulations under p = 100 and n = 600 (grey curves). The black curve corresponds to the averaged curve.

Table 1 displays the results under moderate dimension settings. When p = 3, the effective number 4³ = 64 of parameters is much smaller than the sample size, resulting in the good performances of all methods, among which LASSO was the best under n = 200 and 400. Nevertheless, our method had a rapid decreasing misclassification rate and achieved comparable performance to the best competitors when n = 400 and 600. As p increases to 4 and 5, irrelevant covariates are included. As can be seen from table 1, the best methods under p = 3, including NN, LASSO and SVM, had noticeably worse performance than our method and RF. Especially, it was interesting that RF had better performance under p = 4 and 5 than under p = 3. We guess that when all covariates were important, RF tended to overfit the model and lead to poor classification performance on the test samples. Nonetheless, our method still had the best performance and tended to be robust to the inclusion of irrelevant covariates.

Table 1:

Simulation study results for moderate dimension case. RF: random forests, NN: neural networks, SVM: support vector machine, BART: Bayesian additive regression trees, TF: Our tensor factorization model. Misclassification rates and their standard deviations over 100 simulations are displayed.

		n = 200	n = 400	n = 600	n = 800
	CART	0.371(0.056)	0.357(0.066)	0.341(0.072)	0.335(0.064)
	RF	0.277(0.034)	0.254(0.039)	0.243(0.034)	0.235(0.032)
	NN	0.212(0.033)	0.188(0.038)	0.181(0.043)	0.175(0.037)
p = 3	LASSO	0.206(0.031)	0.178(0.027)	0.169(0.023)	0.167(0.021)
	SVM	0.320(0.065)	0.195(0.065)	0.168(0.023)	0.167(0.026)
	BART	0.354(0.044)	0.311(0.041)	0.279(0.036)	0.266(0.036)
	TF	0.243(0.041)	0.181(0.031)	0.168(0.023)	0.165(0.021)
	CART	0.376(0.055)	0.360(0.066)	0.342(0.072)	0.336(0.071)
	RF	0.278(0.028)	0.223(0.029)	0.195(0.025)	0.189(0.026)
	NN	0.353(0.044)	0.266(0.039)	0.235(0.039)	0.223(0.037)
p = 4	LASSO	0.323(0.036)	0.256(0.030)	0.219(0.025)	0.201(0.023)
	SVM	0.325(0.032)	0.257(0.024)	0.219(0.025)	0.202(0.023)
	BART	0.378(0.042)	0.329(0.041)	0.282(0.035)	0.269(0.034)
	TF	0.241(0.041)	0.183(0.031)	0.170(0.023)	0.164(0.021)
	CART	0.384(0.054)	0.364(0.067)	0.342(0.071)	0.342(0.063)
	RF	0.324(0.031)	0.267(0.031)	0.230(0.028)	0.218(0.063)
	NN	-	-	-	-
p = 5	LASSO	0.415(0.046)	0.366(0.048)	0.314(0.032)	0.298(0.025)
	SVM	0.414(0.042)	0.374(0.036)	0.335(0.029)	0.306(0.029)
	BART	0.395(0.027)	0.353(0.036)	0.335(0.031)	0.306(0.029)
	TF	0.242(0.042)	0.184(0.031)	0.168(0.022)	0.164(0.022)

Table 2 displays the results under high dimension settings. The differences become more perceptible. All the competing methods broke down and had worse performance than TF. Under p = 20, the performance of LASSO²—LASSO with all two-way interaction terms included—slightly improved over the LASSO with only main effect terms included, but was still unsatisfactory. On the other hand, both SVM² and SVM^k had similar misclassification rates as SVM. In the very challenging case in which the training sample size was only 200 and p = 500, all methods had poor performance. However, as the training sample size increased, the proposed conditional tensor factorization method rapidly approached the optimal 15%, with excellent performance even in the n = 600, p = 500 case. In contrast, the competitive methods had consistently poor performance. In this challenging setting involving a low signal strength, a modest sample size, and moderately large numbers of candidate predictors, CART appeared to be the best competing method. In addition, by comparing the misclassification rates between TF and TF², we found that TF is quite robust to the choice of (r, M), especially when the covariate dimension p is not too large or the sample size n is not too small. In the n = 200, p = 500 and n = 400, p = 500 cases, TF² becomes worse than TF since irrelevant covariates have higher tendency to be included in the model for TF² than for TF. However, we find that even for TF², the final models produced by the first stage of our algorithm have size less than 5, suggesting that TF is robust to the choice of the maximum model size M.

In addition to the clearly superior classification performance, our method had the advantage of providing variable selection results. Table 3 provides the average approximated marginal inclusion probabilities for the three important predictors and remaining predictors in the high dimension settings. Consistently with the results in Table 2, the method fails to detect the important predictors when p = 500 and the training sample size is only n = 200. But as the sample size increases appropriately, TF assigns high marginal inclusion probabilities to the important predictors and low ones to the unimportant predictors. In addition, to assess the fitting performances, we calculated the empirical average MSE defined as

$$\mathrm{aMSE}=\frac{1}{N}\sum _{i=1}^N{\{P\left(Y=1|x_{i1},\dots ,x_{ip}\right)-\widehat{P}\left(Y=1|x_{i1},\dots ,x_{ip}\right)\}}^2,$$

where (x_i1, …, x_ip) is the vector of covariates of the ith sample and $\widehat{P}$ is the fitted conditional probability. The aMSE approached to zero rapidly as testing size increased and tended to be robust to the covariate dimension as long as the method could identify the important predictors.

Table 3:

Simulation study variable selection results in the high dimensional case. Rows 1–3 within each fixed p are approximated inclusion probabilities of the 1st,2nd,3rd predictors. Max is the maximum inclusion probability across the remaining predictors. Ave is the average inclusion probability across the remaining predictors. These quantities are averages over 10 trials.

		n = 200	n = 400	n = 600	n = 800
p = 20	X1	1.00	1.00	1.00	1.00
	X2	1.00	1.00	1.00	1.00
	X3	1.00	1.00	1.00	1.00
	Max	0.00	0.00	0.00	0.00
	Ave	0.00	0.00	0.00	0.00
	aMSE	0.074(0.013)	0.025(0.005)	0.014(0.004)	0.009(0.002)
X1	0.74	1.00	1.00	1.00
p = 100	X2	0.70	1.00	1.00	1.00
	X3	0.72	1.00	1.00	1.00
	Max	0.21	0.00	0.00	0.00
	Ave	0.01	0.00	0.00	0.00
	aMSE	0.089(0.026)	0.027(0.003)	0.014(0.002)	0.009(0.002)
p = 500	X1	0.23	0.91	1.00	1.00
	X2	0.24	0.90	1.00	1.00
	X3	0.21	0.91	1.00	1.00
	Max	0.28	0.07	0.00	0.00
	Ave	0.00	0.00	0.00	0.00
	aMSE	0.134(0.034)	0.036(0.037)	0.014(0.003)	0.009(0.002)

5.2. Parametric classification

In the second simulation study, the true conditional probability tensor is induced by the following logistic model with two-way interaction terms, which is a special case of the baseline-category logit model (5) under binary response:

$$\begin{gathered} \log \frac{P(Y=1|X)}{P(Y=0|X)}=-4I\left(X_1=1\right)+2I\left(X_1=2\right)-2I\left(X_2=2\right)+4I\left(X_2=3\right)+4I\left(X_3=1\right) \\ +6I\left(X_1=1\cup X_1=3\right)I\left(X_2=1\right)-8I\left(X_3=1\right)I\left(X_4=2\cup X_4=3\right). \end{gathered}$$

This true model includes 5 main effects of important 3 predictors X₁,X₂ and X₃ and 4 two-way interaction effects of (X₁,X₂) and (X₃,X₄). Similar to the previous nonparametric example, each simulated dataset consisted of N = 3, 000 instances with p of the covariates X₁, …, X_p, each of which has d = 4 levels, and a binary response Y. We choose the dimensionality p = 4, 7 and 10 and four training sizes n = 200, 400, 600 and 800. For the three competitors: CART, RF and LASSO, we only include dp = 16, 28 and 40 main effects and $d^2\left(\begin{array}{l}p\hfill \\ 2\hfill \end{array}\right)=96$, 336 and 720 two-way interaction effects and ignore the remaining 144, 16020 and 1047816 higher-order interactions. In contrast, we do not need to impose such a restriction to speed up computation for TF, which can capture possible high-order interaction effects if they exist. The implementations of these methods are the same as those of the previous example.

Table 4 displays the results. As can be seen, even though in a parametric setting, TF still tended to outperform competitors since each competitor needed to include a large number of two-way interactions in order to capture interaction effects.

Table 4:

Simulation study results for parametric classification. Misclassification rates and their standard deviations over 100 simulations are displayed.

		n = 200	n = 400	n = 600	n = 800
p = 4	CART	0.237(0.029)	0.215(0.028)	0.205(0.027)	0.196(0.024)
	RF	0.217(0.024)	0.195(0.023)	0.190(0.022)	0.178(0.023)
	LASSO	0.247(0.028)	0.229(0.028)	0.222(0.025)	0.216(0.023)
	TF	0.201(0.025)	0.187(0.024)	0.184(0.024)	0.179(0.022)
p = 7	CART	0.271(0.034)	0.221(0.028)	0.214(0.026)	0.199(0.027)
	RF	0.229(0.022)	0.200(0.020)	0.196(0.023)	0.186(0.021)
	LASSO	0.264(0.029)	0.237(0.021)	0.227(0.025)	0.224(0.024)
	TF	0.210(0.028)	0.193(0.025)	0.190(0.026)	0.181(0.023)
p = 10	CART	0.284(0.028)	0.235(0.026)	0.217(0.025)	0.212(0.029)
	RF	0.242(0.030)	0.212(0.023)	0.209(0.021)	0.203(0.021)
	LASSO	0.276(0.034)	0.243(0.025)	0.235(0.026)	0.233(0.027)
	TF	0.229(0.035)	0.201(0.022)	0.192(0.020)	0.180(0.022)

6. Applications

We compare our method with other competing methods in three data sets from the UCI repository. The choices of hyperparameters r and M are the same as those in Section 5.1. Similarly, we also applied TF², the TF under r = 6 and M = 20, to illustrate the robustness of the method. The first data set is Promoter Gene Sequences (abbreviated as promoter data below). The data consists of A, C, G, T nucleotides at p = 57 positions for N = 106 sequences and a binary response indicating instances of promoters and non-promoters. We use n = 85 training samples and N − n = 21 test samples in each random training-test split for 100 times.

The second data set is the Splice-junction Gene Sequences (abbreviated as splice data below). These data consist of A, C, G, T nucleotides at p = 60 positions for N = 3, 175 sequences. Each sequence belongs to one of the three classes: exon/intron boundary (EI), intron/exon boundary (IE) or neither (N). Since its sample size is much larger than the first data set, we compare our approach with competing methods in two scenarios: a small sample size and a moderate sample size. In the small(moderate) sample size case, each time we randomly select n = 200(2, 540) instances as training and calculate the misclassification rate on the testing set composed of the remaining 2, 975 instances. We repeat this for each method for 100 training-test splits and report the average misclassification rate.

The third data set describes diagnosing of cardiac Single Proton Emission Computed Tomography (SPECT) images. Each of the patients is classified into two categories: normal and abnormal. The database of 267 SPECT image sets (patients) has 22 binary feature patterns. This data set has been previously divided into a training set of size 80 and a testing set of size 187.

We considered the same competitors as those in the simulation part. Among them, BART was not implemented in the splice data since we were unable to find a multi-class implementation of their approach.

Table 5 shows the results. Our method produced at worst comparable classification accuracy to the best of the competitors in each of the cases considered. Among the competitors, Random Forests (RF) provided the best competitor overall, which is consistent with our previous experiment under high dimensional settings. We expect our approach to do particularly well when there is a modest training sample size and high-dimensional predictors. We additionally have an advantage in terms of interpretability over several of these approaches, including RF and BART, in conducting variable selection. As we expect, TF² tends to have slightly worse classification performance than TF in the Promoter data where the covariate dimension p is relatively large comparing to the limited sample size n = 85. However, TF² has similar performance as TF in the other three applications.

Table 5:

UCI Data Example. RF: random forests, NN: neural networks, SVM: support vector machine, BART: Bayesian additive regression trees, TF: Our tensor factorization model, TF²: TF under a different hyperparameter setting. Misclassification rates are displayed based on 100 random training-test splits (Except for the SPECT data set, which has been previously divided).

Data	Promoter (n=85)	Splice (n=200)	Splice (n=2540)	SPECT (n=80)
CART	0.220(0.066)	0.164(0.029)	0.058(0.012)	0.312(−)
RF	0.064(0.015)	0.122(0.023)	0.048(0.011)	0.235(−)
NN	0.180(0.032)	0.217(0.031)	0.170(0.031)	0.278(−)
LASSO	0.077(0.018)	0.136(0.020)	0.118(0.020)	0.277(−)
SVM	0.147(0.022)	0.273(0.044)	0.061(0.011)	0.246(−)
BART	0.105(0.017)	-	-	0.225(−)
TF	0.068(0.018)	0.116(0.020)	0.056(0.010)	0.198(−)
TF2	0.072(0.019)	0.118(0.021)	0.056(0.010)	0.198(−)

Table 6 displays the selected variables along with their associated mode ranks. As can be seen, in the promoter data and splice data, nearby nucleotide sequences are selected. These results are reasonable since for nucleotide sequences, nearby nucleotides form a motif regulating important functions. For the splice data, the number of variables selected by our model increases from 4 under n = 200 to 6 under n = 2540. This gradual increase in the model size suggests that the splice data may possess a near low multirank structure characterized by Assumption B, where the optimal number of selected variables is determined by the bias-variance tradeoff. As the training size further grows, more important variables would be selected into the model. In contrast, the number of selected variables in the SPECT data remains the same as the training size grows, suggesting that an exact low multirank assumption may be valid. It is notable that in each of these cases we obtained excellent classification performance based on a small subset of the predictors. Moreover, for the nucleotide sequences data, most selected variables have low mode ranks k_j comparing to the full size d_j = 4. Therefore, these variable selection results provide empirical verifications of the near low multirank assumption B in section 3.2.

Table 6:

Variable selection results. The selected variables are displayed, with their associated mode ranks k_j’s included in the parenthesis.

	Important variables selected
Promoter (n=106)	15th(2), 16th(2), 17th(3), 39th(3)
Splice (n=200)	29th(2), 30th(2), 31st(2), 32nd(2)
Splice (n=2540)	28th(2), 29th(2), 30th(2), 31st(2), 32nd(2), 35th(2)
SPECT (n=80)	11th(2), 13th(2), 16th(2)
SPECT (n=267)	11th(2), 13th(2), 16th(2)

7. Discussion

This article proposes a framework for nonparametric Bayesian classification relying on a novel class of conditional tensor factorizations. The nonparametric Bayes framework is appealing in facilitating variable selection and uncertainty about the core tensor dimensions in the Tucker-type factorization. One of our major contributions is the strong theoretical support we provide for our proposed approach. Although it has been commonly observed that Bayesian parametric and nonparametric methods have practical gains in numerous applications, there is a clear lack of theory supporting these empirical gains.

Interesting ongoing directions include developing faster approximation algorithms and generalizing the conditional tensor factorization model to accommodate broader feature modalities. In the fast algorithms direction, online variational methods (Hoffman et al., 2010) provide a promising direction. Regarding generalizations, we can potentially accommodate continuous predictors and more complex object predictors (text, images, curves, etc) through probabilistic clustering of the predictors in a first stage, with X_j then corresponding to the cluster index for feature j. We can also generalize the tensor factorization model from the current classification framework to a broader regression framework involving mixed categorical and continuous variables.

Appendix A: Proof of Theorem 1

First reshape P(y|x₁, …, x_p) according to x₁ as a matrix A⁽¹⁾ of size d₁ × d₀d₂d₃ … d_p, with the h^th row a long vector,

$$\begin{gathered} \{P(1|h,1,\dots ,1,1),P(1|h,1,\dots ,1,2),\dots ,P\left(1|h,1,\dots ,1,d_p\right), \\ P(1|h,1,\dots ,2,1),\dots ,P\left(1|h,1,\dots ,2,d_j\right),\dots ,P\left(d_0|h,d_2,\dots ,d_{p-1},d_p\right)\}, \end{gathered}$$

denoted A⁽¹⁾{h, (y, x₂, …, x_p)}. Apply nonnegative matrix decomposition for A⁽¹⁾, we obtain

$$P\left(y|x_1,\dots ,x_p\right)=A^{(1)}\left\{x_1,\left(y,x_2,\dots ,x_p\right)\right\}=\sum _{h_1=1}^{k_1}{\lambda }_{h_1{x}_2\dots x_p}^{(1)}(y){\pi }_{h_1}^{(1)}\left(x_1\right),$$ (8)

where k₁ ≤ d₁ corresponds to the nonnegative rank of the matrix A⁽¹⁾ (Cohen and Rothblum, 1993). Without loss of generality, we can assume that the parameters satisfy the constraints ${\sum }_{y=1}^{d_0}{\lambda }_{h_1{x}_2\dots x_p}^{(1)}(y)=1$ for each (h₁, x₂, …, x_p), ${\sum }_{h_1=1}^{k_1}{\pi }_{h_1}^{(1)}\left(x_1\right)=1$ for each x₁, ${\lambda }_{h_1{x}_2\dots x_p}^{(1)}(y)\ge 0$, and ${\pi }_{h_1}^{(1)}\left(x_1\right)\ge 0$. Otherwise, we can always define new $\tilde{\lambda }’\text{s}$ and $\tilde{\pi }’\text{s}$ satisfying the above constraints with the same k₁ through the original λ’s and π’s as following:

$$\begin{gathered} {\tilde{\lambda }}_{h_1{x}_2\dots x_p}^{(1)}(y)=\frac{{\lambda }_{h_1{x}_2\dots x_p}^{(1)}(y)}{s_{h_1{x}_2\dots x_p}}, \\ {\tilde{\pi }}_{h_1}^{(1)}\left(x_1\right)=s_{h_1{x}_2\dots x_p}{\pi }_{h_1}^{(1)}\left(x_1\right), \end{gathered}$$

where $s_{h_1{x}_2\dots x_p}={\sum }_{y=1}^{d_0}{\lambda }_{h_1{x}_2\dots x_p}^{(1)}(y)$. With this definition, the decomposition (8) for the new $(\tilde{\lambda },\tilde{\pi })’\text{s}$ and the normalizing constraint ${\sum }_{y=1}^{d_0}{\tilde{\lambda }}_{h_1{x}_2\dots x_p}^{(1)}(y)=1$ are easy to verify. We only need to check the normalizing constraint for $\tilde{\pi }$:

$$\begin{gathered} \sum _{h_1=1}^{k_1}{\tilde{\pi }}_{h_1}^{(1)}\left(x_1\right)=\sum _{h_1=1}^{k_1}\sum _{y=1}^{d_0}{\lambda }_{h_1{x}_2\dots x_p}^{(1)}(y){\pi }_{h_1}^{(1)}\left(x_1\right) \\ =\sum _{y=1}^{d_0}P\left(y|x_1,\dots ,x_p\right)=1, \end{gathered}$$

where we have applied (8) and the fact that P is a conditional probability.

Taking ${\lambda }_{h_1{x}_2\dots x_p}^{(1)}(y)$ from (8) with argument x₂, we can apply the same type of decomposition to obtain

$${\lambda }_{h_1{x}_2\dots x_p}^{(1)}(y)=\sum _{h_2=1}^{k_2}{\lambda }_{h_1{h}_2{x}_3\dots x_p}^{(2)}(y){\pi }_{h_2}^{(2)}\left(x_2\right),$$

subject to ${\sum }_{y=1}^{d_0}{\lambda }_{h_1{h}_2\dots x_p}^{(2)}(y)=1$, for each (h₁, h₂, …, x_p), ${\sum }_{h_2=1}^{k_2}{\pi }_{h_2}^{(2)}\left(x_2\right)=1$, for each x₂, ${\lambda }_{h_1{h}_2\dots x_p}^{(2)}(c)\ge 0$, and ${\pi }_{h_2}^{(2)}\left(x_2\right)\ge 0$. Plugging back into equation (8),

$$P\left(y|x_1,\dots ,x_p\right)=\sum _{h_1=1}^{k_1}\sum _{h_2=1}^{k_2}{\lambda }_{h_1{h}_2{x}_3\dots x_p}^{(2)}(y){\pi }_{h_1}^{(1)}\left(x_1\right){\pi }_{h_2}^{(2)}\left(x_2\right).$$

Repeating this procedure another (p − 2) times, we obtain equation (2) with ${\lambda }_{h_1{h}_2\dots h_p}(y)={\lambda }_{h_1{h}_2\dots h_p}^{(p)}(y)$ and constraints (3).

Remark: As we can seen from the proof, k_j can be considered as the nonnegative matrix rank corresponds to certain transformation of the jth mode matrix of the tensor P.

Appendix B: Proof of Theorem 2

To prove Theorem 2 we need some preliminaries. The following theorem is a minor modification of Theorem 2.1 in Ghosal et al. (2000) and the proof is included in a supplemental appendix. For simplicity in notation, we denote the observed data for subject i as X_i with $X_i\stackrel{iid}{\sim }P\in \mathcal{P}$, P ~ Π, and the true model P₀.

Theorem 5 Let ϵ_n be a sequence with ϵ_n → 0, $n{ϵ}_n^2\to \infty$, ${\sum }_n\exp \left(-n{ϵ}_n^2\right)<\infty$. Let d be the total variance distance, C > 0 be a constant and sets ${\mathcal{P}}_n\subset \mathcal{P}$. Define the following conditions:

1. $logN\left({ϵ}_n,{\mathcal{P}}_n,d\right)\le n{ϵ}_n^2;$

2. ${\mathrm{\Pi }}_n\left(\mathcal{P}\backslash {\mathcal{P}}_n\right)\le \exp \left\{-(2+C)n{ϵ}_n^2\right\};$

3. ${\mathrm{\Pi }}_n(P:{\Vert \log \frac{P}{P_0}\Vert }_{\infty }<{ϵ}_n^2)|>\exp \left(-Cn{ϵ}_n^2\right).$

If the above conditions hold for all n large enough, then for $M>\sqrt{16+8C}$,

$${\mathrm{\Pi }}_n\left\{P:d\left(P,P_0\right)\ge M{ϵ}_n|X_1,\dots ,X_n\right\}\to 0a.s.P_0^n.$$

In our case, X_i include the response y_i and predictors x_i, P is the random measure characterizing the unknown joint distribution of (y_i, x_i) and P₀ is the measure characterizing the true joint distribution. As our focus is on the conditional probability, P(y|x), we fix the marginal distribution of X at it’s true value P₀(x) and model the unknown conditional P(y|x) independently of the marginal of X. By doing so, it is straightforward to show that we can ignore the marginal of X in using Theorem 2 to study posterior convergence. We simply restrict $\mathcal{P}$ to the set of joint probabilities such that P(x) = P₀(x). The total variation distance between the joint probabilities P and P₀ is equivalent to the distance between the conditionals defined in Theorem 2 by the identity

$$\begin{gathered} \int \sum _{y=1}^{d_0}|P\left(y,x_1,\dots ,x_p\right)-P_0\left(y,x_1,\dots ,x_p\right)|d{x}_1\cdots d{x}_p= \\ \int \sum _{y=1}^{d_0}|P\left(y|x_1,\dots ,x_p\right)-P_0\left(y|x_1,\dots ,x_p\right)|d{G}_n\left(d{x}_1,\cdots ,d{x}_p\right). \end{gathered}$$

Therefore, we will not distinguish the joint probability and the conditional probability and use P to denote both of them henceforth.

To prove Theorem 2, we also need upper bounds on the distance between two models specified by (2) when the models are the same size and when they are nested.

Lemma 6 Let P and $\tilde{P}$ be two models specified by (3) with parameter (k, λ, π) and $(\tilde{k},\tilde{\lambda },\tilde{\pi })$, respectively. Assume that P and $\tilde{P}$ have the same multirank $\tilde{k}=k=\left(k_1,\dots ,k_p\right)$. Then

$$d(P,\tilde{P})\le \sum _{y=1}^{d_0}\underset{h_1,\dots ,h_p}{\max }|{\lambda }_{h_1{h}_2\dots h_p}(y)-{\tilde{\lambda }}_{h_1{h}_2\dots h_p}(y)|+d_0\sum _{j=1}^p\underset{x_j}{\max }\sum _{h_j=1}^{k_j}|{\pi }_{h_j}^{(j)}\left(x_j\right)-{\tilde{\pi }}_{h_j}^{(j)}\left(x_j\right)|.$$

Proof of Lemma 6 By definition of $d(P,\tilde{P})$, we only need to prove that for any y = 1, …, d₀ and any combination of (x₁, …, x_p),

$$\begin{gathered} |P\left(y|x_1,\dots ,x_p\right)-\tilde{P}\left(y|x_1,\dots ,x_p\right)|\le \underset{h_1,\dots ,h_p}{\max }|{\lambda }_{h_1{h}_2\dots h_p}(y)-{\tilde{\lambda }}_{h_1{h}_2\dots h_p}(y)| \\ +\sum _{j=1}^p\sum _{h_j=1}^{k_j}|{\pi }_{h_j}^{(j)}\left(x_j\right)-{\tilde{\pi }}_{h_j}^{(j)}\left(x_j\right)|. \end{gathered}$$ (9)

Actually,

$$|P\left(y|x_1,\dots ,x_p\right)-\tilde{P}\left(y|x_1,\dots ,x_p\right)|\le A+\sum _{s=1}^p{B}_s,$$

where

$$\begin{gathered} A=\sum _{h_1=1}^{k_1}\cdots \sum _{h_p=1}^{k_p}|{\lambda }_{h_1{h}_2\dots h_p}(y)-{\tilde{\lambda }}_{h_1{h}_2\dots h_p}(y)|\prod _{j=1}^p{\pi }_{h_j}^{(j)}\left(x_j\right) \\ \le \underset{h_1,\dots ,h_p}{\max }|{\lambda }_{h_1{h}_2\dots h_p}(y)-{\tilde{\lambda }}_{h_1{h}_2\dots h_p}(y)|\sum _{h_1=1}^{k_1}\cdots \sum _{h_p=1}^{k_p}\prod _{j=1}^p{\pi }_{h_j}^{(j)}\left(x_j\right) \\ =\underset{h_1,\dots ,h_p}{\max }|{\lambda }_{h_1{h}_2\dots h_p}(y)-{\tilde{\lambda }}_{h_1{h}_2\dots h_p}(y)|, \end{gathered}$$

where the last step is by using the second equation in (4), and

$$\begin{gathered} B_s=\sum _{h_1=1}^{k_1}\cdots \sum _{h_p=1}^{k_p}{\tilde{\lambda }}_{h_1{h}_2\dots h_p}(y)|{\pi }_{h_s}^{(s)}\left(x_s\right)-{\pi }_{h_s}^{(s)}\left(x_s\right)|\prod _{j=1}^{s-1}{\tilde{\pi }}_{h_j}^{(j)}\left(x_j\right)\prod _{j=s+1}^p{\pi }_{h_j}^{(j)}\left(x_j\right) \\ \le \sum _{h_s=1}^{k_s}|{\pi }_{h_s}^{(s)}\left(x_s\right)-{\tilde{\pi }}_{h_s}^{(s)}\left(x_s\right)|, \end{gathered}$$

where the last step is again by using the second equation in (3) and the fact that ${\lambda }_{h_1{h}_2\dots h_p}(y)\le 1$. Combining the above inequalities we can obtain (9).

Lemma 7 Let P and $\tilde{P}$ be two models as in (3) with parameters (k, λ, π) and $(\tilde{k},\tilde{\lambda },\tilde{\pi })$, respectively. Suppose P is nested in $\tilde{P}$, i.e. satisfying:

1. $k_j\le {\tilde{k}}_j,forj=1,\dots ,p,;$

2. ${\lambda }_{h_1\cdots h_p}={\tilde{\lambda }}_{h_1\cdots h_p},for{h}_j\le k_j,j=1,\dots ,p;$

3. ${\pi }_{h_j}^{(j)}\left(x_j\right)={\tilde{\pi }}_{h_j}^{(j)}\left(x_j\right)$, for h_j < k_j, and ${\pi }_{k_j}^{(j)}\left(x_j\right)={\sum }_{h_j\ge k_j}{\tilde{\pi }}_{h_j}^{(j)}\left(x_j\right)$.

Then

$$d(P,\tilde{P})\le d_0\sum _{j=1}^p\underset{x_j}{\max }\sum _{h_j=k_j}^{{\tilde{k}}_j}{\tilde{\pi }}_{h_j}^{(j)}\left(x_j\right).$$

Proof of Lemma 7 By condition (c), P can be considered as model P′ of size ${\tilde{k}}_j$ with ${\pi }^{\prime }=\tilde{\pi }$ and λ′ satisfying:

$${\lambda }_{h_1{h}_2\cdots h_p}^{\prime }(y)={\lambda }_{\min \left(h_1,k_1\right),\min \left(h_2,k_2\right),\cdots ,\min \left(h_p,k_p\right)}(y),$$

for y = 1, …, d₀ and $h_j\le {\tilde{k}}_j$, j = 1, …, p.

As a result, by condition (b)

$$\begin{gathered} |P\left(y|x_1,\dots ,x_p\right)-\tilde{P}\left(y|x_1,\dots ,x_p\right)| \\ \le \sum _{h_1=1}^{{\tilde{k}}_1}\dots \sum _{h_p=1}^{{\tilde{k}}_p}|{\tilde{\lambda }}_{\min \left(h_1,k_1\right)\cdots \min \left(h_p,k_p\right)}(y)-{\tilde{\lambda }}_{h_1\dots h_p}(y)|\prod _{j=1}^p{\tilde{\pi }}_{h_j}^{(j)}\left(x_j\right) \\ =\left\{\sum _{h_1=1}^{k_1}+\sum _{h_1=k_1+1}^{\tilde{k}}\right\}\sum _{h_2=1}^{{\tilde{k}}_2}\cdots \sum _{h_p=1}^{{\tilde{k}}_p}|{\tilde{\lambda }}_{\min \left(h_1,k_1\right)\cdots \min \left(h_p,k_p\right)}(y)-{\tilde{\lambda }}_{h_1\dots h_p}(y)|\prod _{j=1}^p{\tilde{\pi }}_{h_j}^{(j)}\left(x_j\right) \\ \le \sum _{h_1=k_1+1}^{{\tilde{k}}_1}\sum _{h_2=1}^{{\tilde{k}}_2}\cdots \sum _{h_p=1}^{{\tilde{k}}_p}|{\tilde{\lambda }}_{\min \left(h_1,k_1\right)\cdots \min \left(h_p,k_p\right)}(y)-{\tilde{\lambda }}_{h_1\dots h_p}(y)|\prod _{j=1}^p{\tilde{\pi }}_{h_j}^{(j)}\left(x_j\right) \\ +\sum _{h_1=1}^{k_1}\left\{\sum _{h_2=1}^{k_2}+\sum _{h_2=k_2+1}^{{\tilde{k}}_2}\right\}\cdots \sum _{h_p=1}^{{\tilde{k}}_p}|{\tilde{\lambda }}_{\min \left(h_1,k_1\right)\cdots \min \left(h_p,k_p\right)}(y)-{\tilde{\lambda }}_{h_1\dots h_p}(y)|\prod _{j=1}^p{\tilde{\pi }}_{h_j}^{(j)}\left(x_j\right) \\ \le \cdots \\ \le \sum _{h_1=k_1+1}^{{\tilde{k}}_1}\sum _{h_2=1}^{{\tilde{k}}_1}\cdots \sum _{h_p=1}^{{\tilde{k}}_p}|{\tilde{\lambda }}_{\min \left(h_1,k_1\right)\cdots \min \left(h_p,k_p\right)}(y)-{\tilde{\lambda }}_{h_1\dots h_p}(y)|\prod _{j=1}^p{\tilde{\pi }}_{h_j}^{(j)}\left(x_j\right) \\ +\cdots +\sum _{h_1=1}^{k_1}\cdots \sum _{h_{p-1}=1}^{k_{p-1}}\sum _{h_p=k_p+1}^{{\tilde{k}}_p}|{\tilde{\lambda }}_{\min \left(h_1,k_1\right)\cdots \min \left(h_p,k_p\right)}(y)-{\tilde{\lambda }}_{h_1\dots h_p}(y)|\prod _{j=1}^p{\tilde{\pi }}_{h_j}^{(j)}\left(x_j\right). \end{gathered}$$

Here the last inequality holds because $|{\tilde{\lambda }}_{\min \left(h_1,k_1\right)\cdots \min \left(h_p,k_p\right)}(y)-{\tilde{\lambda }}_{h_1\dots h_p}(y)|=0$ if h_j ≤ k_j for all j. Hence, the lemma can be proved by noticing the constraints (3) and the fact that ${\tilde{\lambda }}_{h_1\dots h_p}(y)\in [0,1]$.

Proof of Theorem 2 We verify conditions (a)-(c) in Theorem 5. As we described previously, we do not need to distinguish the joint probability and the conditional probability under our prior specification. Each model one-to-one corresponds to a triplet (k, λ, π), where $k=\left(k_1,\dots ,k_{p_n}\right)$ is the multirank, $\lambda =\left\{{\lambda }_{h_1,\dots ,h_{p_n}}(y):y=1,\dots ,d_0,h_j\le k_j,j=1,\dots ,p_n\right\}$ is the core tensor and $\pi =\{{\pi }_{h_j}^{(j)}\left(x_j\right):h_j\le k_j,x_j=1,\dots ,d_j,j=1,\dots ,p_n\}$ is the mode matrices. Note that the dimension of λ and π depend on k. Let the sieve ${\mathcal{P}}_n$ be all conditional probability tensors with multirank satisfying ${\prod }_{j=1}^{p_n}{k}_j\le M_n$. Since the inclusion of the jth predictor is equivalent to k_j > 1, models in ${\mathcal{P}}_n$ will depends on at most ${\overline{r}}_n={\log }_2{M}_n$ predictors.

Condition (a): By the conclusion of lemma 6, we know that an ϵ_n-net E_n of ${\mathcal{P}}_n$ can be chosen so that for each $(k,\lambda ,\pi )\in {\mathcal{P}}_n$ that satisfies constraints (3), there exists $(\tilde{k},\tilde{\lambda },\tilde{\pi })\in E_n$ such that $\tilde{k}=k$, ${\max }_{y,h_1,\dots ,h_{p_n}}|{\lambda }_{h_1{h}_2\dots h_{p_n}}(y)-{\tilde{\lambda }}_{h_1{h}_2\dots h_{p_n}}(y)|<\frac{{ϵ}_n}{d_0\left({\overline{r}}_n+1\right)}$ and ${\max }_{x_j,h_j}|{\pi }_{h_j}^{(j)}\left(x_j\right)-{\tilde{\pi }}_{h_j}^{(j)}\left(x_j\right)|<\frac{{ϵ}_n}{d{d}_0\left({\overline{r}}_n+1\right)}$ for j satisfying k_j > 1. Hence, for fixed k, we can pick ϵ_n d-balls of the form

$$\prod _{h_1,\dots ,h_{pn},y}\left({\lambda }_{h_1{h}_2\dots h_{pn}}(y)\pm \frac{{ϵ}_n}{d_0\left({\overline{r}}_n+1\right)}\right)\times \prod _{j:k_j>1}\prod _{h_j=1}^{k_j}\prod _{x_j=1}^{d_j}\left({\pi }_{h_j}^{(j)}\left(x_j\right)\pm \frac{{ϵ}_n}{d{d}_0\left({\overline{r}}_n+1\right)}\right),$$

where the first product is taken for all integer vector $\left(h_1,\dots ,h_{p_n},y\right)$ satisfying 1 ≤ y ≤ d₀ and 1 ≤ h_j ≤ k_j. For fixed k with ${\prod }_{j=1}^{p_n}{k}_j\le M_n$ in ${\mathcal{P}}_n$, there are at most d₀M_n such ${\lambda }_{h_1{h}_2\dots h_{p_n}}(y)’\text{s}$ and ${\overline{r}}_n{d}^2{\pi }_{h_j}^{(j)}\left(x_j\right)’\text{s}$. Equally spaced grids for λ and π can be chosen so that the union of ϵ_n d-balls centering on the grids covers the set of all models in ${\mathcal{P}}_n$ with multirank k. Note that there are at most $d{\overline{r}}_n{p}_n^{{\overline{r}}_n}$ different multirank k in ${\mathcal{P}}_n$. This count follows by first choosing at most ${\overline{r}}_n$ important predictors with k_j > 1, then choosing at most $d{\overline{r}}_n$ for these k_j’s. Hence, the log of the minimal number of size-ϵ_n balls needed to cover ${\mathcal{P}}_n$ is at most

$$\log \left\{d{\overline{r}}_n{p}_n^{{\overline{r}}_n}\right\}+d_0{M}_n\log \frac{d_0\left({\overline{r}}_n+1\right)}{2{ϵ}_n}+{\overline{r}}_n{d}^2\log \frac{d{d}_0\left({\overline{r}}_n+1\right)}{2{ϵ}_n}.$$

By the conditions in the theorem, each term will be bounded by $n{ϵ}_n^2/3$ for n sufficiently large.

Condition (b): Because ${\mathrm{\Pi }}_n\left({\mathcal{P}}_n^c\right)=0$ in our case, this condition is trivially satisfied. Actually, this condition will still be satisfied as long as ${\mathrm{\Pi }}_n({\prod }_j^{p_n}{k}_j>M_n)\le \exp \left\{-(2+C)n{ϵ}_n^2\right\}$, which implies that the prior probability assigned to complex models is exponentially small.

Condition (c): As P₀ is lower bounded away from zero by ϵ₀, ${\Vert \log \frac{P}{P_0}\Vert }_{\infty }<{ϵ}_n^2$ is implied by ${\Vert P-P_0\Vert }_{\infty }<{ϵ}_0{ϵ}_n^2$ for n large enough (ϵ_n → 0 as n increases). Let $(\tilde{\lambda },\tilde{\pi })$ denote parameters for the true model P₀. Consider approximating P₀ by model P with (k⁽ⁿ⁾, λ, π), where k⁽ⁿ⁾ is specified in the theorem. Applying lemma 7 to bound $d\left(\overline{P},P_0\right)$, where $\overline{P}$ (regard as the P) with $\left(k^{(n)},\overline{\lambda },\overline{\pi }\right)$ is nested in P₀ (regard as the $\tilde{P}$), and then estimating the difference between P and $\overline{P}$ by lemma 6, we have

$$\begin{gathered} d\left(P,P_0\right)\le \sum _{y=1}^{d_0}\underset{h_1\le k_1^{(n)},\dots ,h_{p_n}\le k_{p_n}^{(n)}}{\max }|{\lambda }_{h_1{h}_2\dots h_{p_n}}(y)-{\overline{\lambda }}_{h_1\dots \dots h_{p_n}}(y)| \\ +d_0\sum _{j:k_j^{(n)}>1}\underset{{}_{x_j}}{\max }\sum _{h_j=1}^{k_j^{(n)}}|{\pi }_{h_j}^{(j)}\left(x_j\right)-{\overline{\pi }}_{h_j}^{(j)}\left(x_j\right)|+d_0\sum _{j=1}^{p_n}\underset{{}_{x_j}}{\max }\sum _{h_j>k_j^{(n)}}{\tilde{\pi }}_{h_j}^{(j)}\left(x_j\right). \end{gathered}$$ (10)

Applying (9) in lemma 6 and combining (10) and condition (iv) in Theorem 2, ${\Vert \log \frac{P}{P_0}\Vert }_{\infty }<{ϵ}_n^2$ is implied by

$$\begin{gathered} \underset{{}_{h_1\le k_1^{(n)},\dots ,h_{pn}\le k_{p_n}^{(n)},y}}{\max }|{\lambda }_{h_1\dots h_p}(y)-{\overline{\lambda }}_{h_1\dots h_{p_n}}(y)|\prec \frac{{ϵ}_n^2}{{\overline{r}}_n+1}, \\ \underset{{}_{h_j\le k_j^{(n)},x_j}}{\max }|{\pi }_{h_j}^{(j)}\left(x_j\right)-{\overline{\pi }}_{h_j}^{(j)}\left(x_j\right)|\prec \frac{{ϵ}_n^2}{\left({\overline{r}}_n+1\right)d}. \end{gathered}$$

Note that the prior probability P(k = k⁽ⁿ⁾) is at least ${\left(r_n/p_n\right)}^{{\overline{r}}_n}{\left(r_n/\left(p_{n}d\right)\right)}^{{\overline{r}}_n}{\left(1-r_n/p_n\right)}^{p_n-{\overline{r}}_n}$. Here ${\left(1-r_n/p_n\right)}^{p_n-{\overline{r}}_n}$ is defined to be 1 if r_n = p_n. As r_n/p_n → 0, $\log {\mathrm{\Pi }}_n\left(k=k^{(n)}\right)$ is bounded below by $2{\overline{r}}_n\log \left(r_n/p_n\right)\ge -2{\overline{r}}_n\log p_n$.

Moreover, since the Dir(1/d_j, …, 1/d_j) and Dir(1/d₀, …, 1/d₀) priors for ${\lambda }_{h_1{h}_2\dots h_{p_n}}(\cdot )$ and ${\pi }_{.}^{{}^{(j)}}\left(x_j\right)$ have density lower bounded away from zero by a constant not involving n,

$$\begin{gathered} \log {\mathrm{\Pi }}_n\left(P:{\Vert \log \frac{P}{P_0}\Vert }_{\infty }<{ϵ}_n^2\right) \\ \succ -d_0{M}_n\log \frac{{\overline{r}}_n+1}{{ϵ}_n^2}-{\overline{r}}_n{d}^2\log \frac{\left({\overline{r}}_n+1\right)d}{{ϵ}_n^2}-2{\overline{r}}_n\log p_n. \end{gathered}$$

By the assumptions in the theorem, for any C > 0, for n sufficiently large, $\log {\mathrm{\Pi }}_n(P:{\Vert \log \frac{P}{P_0}\Vert }_{\infty }<{ϵ}_n^2)>-Cn{ϵ}_n^2$.