Reducing motion sensitivity in 3D high-resolution T₂*-weighted MRI by navigator-based motion and nonlinear magnetic field correction

Abstract

T₂*-weighted gradient echo (GRE) MRI at high field is uniquely sensitive to the magnetic properties of tissue and allows the study of brain and vascular anatomy at high spatial resolution. However, it is also sensitive to B₀ field changes induced by head motion and physiological processes such as the respiratory cycle. Conventional motion correction techniques do not take these field changes into account, and consequently do not fully recover image quality in T₂*-weighted MRI. Here, a novel approach was developed to address this by monitoring the B₀ field with a volumetric EPI phase navigator. The navigator was acquired at a shorter echo time than that of the (higher resolution) T₂*-weighted GRE imaging data and accelerated with parallel imaging for high temporal resolution. At 4 mm isotropic spatial resolution and 0.54 s temporal resolution, the accuracy for estimation of rotation and translation was better than 0.2° and 0.1 mm, respectively. The 10% and 90% percentiles of B₀ measurement error using the navigator were −1.8 and 1.5 Hz at 7 T, respectively. A fast retrospective reconstruction algorithm correcting for both motion and nonlinear B₀ changes was also developed. The navigator and reconstruction algorithm were evaluated in correcting motion-corrupted high-resolution T₂*-weighted GRE MRI on healthy human subjects at 7 T. Excellent image quality was demonstrated with the proposed correction method.

1. Introduction

Continuing increases in magnetic field strength and improvements in radiofrequency (RF) and gradient hardware have led to improved spatial resolution in MRI of human brain. State of the art techniques now allow sub-millimeter resolution for a variety of applications, including T₁- and T₂*-weighted MRI. This has improved the study of brain anatomy and function (Duyn et al., 2007; Thomas et al., 2008; Marques et al., 2010; Huber et al., 2017), and the detection of subtle variations with disease (Chavhan et al., 2009; de Graaf et al., 2013).

However, one of the main impediments to performing high-resolution MRI is the presence of head motion. Over the typically minutes-long duration of a high-resolution MRI acquisition, involuntary head motion often exceeds the targeted (sub-) millimeter scale resolution, and, if not corrected for, can cause severe image degradation (Andre et al., 2015).

In order to correct motion effects, additional information about changes in head position during the scan needs to be acquired (Hedley and Yan, 1992; Zaitsev et al., 2015). For this purpose, optical cameras, NMR probes or other devices can be used (Tremblay et al., 2005; Zaitsev et al., 2006; Qin et al., 2009; Derbyshire et al., 1998; Sengupta et al., 2014; Aranovitch et al., 2018; Niekerk et al., 2019; Benjaminsen et al., 2016; Maclaren et al., 2016; Mattern et al., 2019). Motion can also be estimated from MRI signals that are acquired together with the imaging data. These so-called navigator signals can have varying sophistication, depending on the desired accuracy of the motion estimate and the acceptable burden on scan duration (Babayeva et al., 2015; Fu et al., 1995; Gretsch et al., 2018; Hess et al., 2011; Liu et al., 2017; Tisdall et al., 2012; van der Kouwe et al., 2006; Wallace et al., 2019; Welch et al., 2002; White et al., 2010). Furthermore, the image data itself can be used to extract motion information. This can be implemented using either specific k-space trajectories that repetitively acquire the center portion of k-space (Anderson et al., 2013; Liu et al., 2004; Pipe, 1999) or algorithms that jointly estimate motion and reconstruct the image (Cordero-Grande et al., 2017; Loktyushin et al., 2013).

Motion information obtained either with an external device or from the MRI signal can then be used to adjust the MRI coordinate system during the scan, or it can be applied to correct the image in the reconstruction. For the latter, motion information can be applied to directly correct the k-space data or integrated in the forward model of MRI signal generation to derive the correction in the inverse solution.

While excellent results have been obtained with motion correction methods, one area still in need of improvement is that of T₂*-weighted MRI, an application particularly sensitive to motion-related image artifacts. This arises from the fact that motion may introduce changes in the local magnetic field (B₀) (Liu et al., 2018; Sulikowska et al., 2014), the very aspect that susceptibility-weighted MRI is sensitized to. Measurement of these field changes and correcting for them online during the scan or retrospectively during image reconstruction may alleviate this problem. For example, one-dimensional navigator (Ward et al., 2002) or fat navigator (Gretsch et al., 2018) have been demonstrated in correcting for the linear component of field changes introduced by head motion and motion of other body parts such as limbs and chest (during respiration). However, this implicit assumption of linear field changes is inadequate to account for more complex field changes that may result from head motion (Liu et al., 2018). Other work aiming to correct for the nonlinear field changes has been demonstrated only in cases of respiration or limb movement (van Gelderen et al., 2007; Versluis et al., 2012; Vannesjo et al., 2015; Duerst et al., 2016; Vionnet et al., 2017; Meineke and Nielsen, 2019) rather than head motion.

To address the problem of nonlinear B₀ changes affecting image quality in T₂*-weighted MRI, we developed a new 3D GRE sequence that acquires a volumetric EPI phase navigator (PN) at a short echo time (TE) to measure head motion and B₀ change maps concurrently with the GRE imaging data. Unlike previous volumetric EPI navigator (Hess et al., 2011; Tisdall et al., 2012, 2014), the PN was implemented with short TE to allow insertion in the period after the excitation pulse and before acquisition of the T₂*-weighted GRE imaging data. Therefore, scan duration was not affected by the additional navigator signal acquisition. Rapid acquisition of the PN was achieved by using highly accelerated parallel imaging. Accuracy of the PN and the reconstruction scheme were then evaluated in MR experiments of head motion on healthy subjects at 7 T.

2. Materials and Methods

2.1. Navigator Design

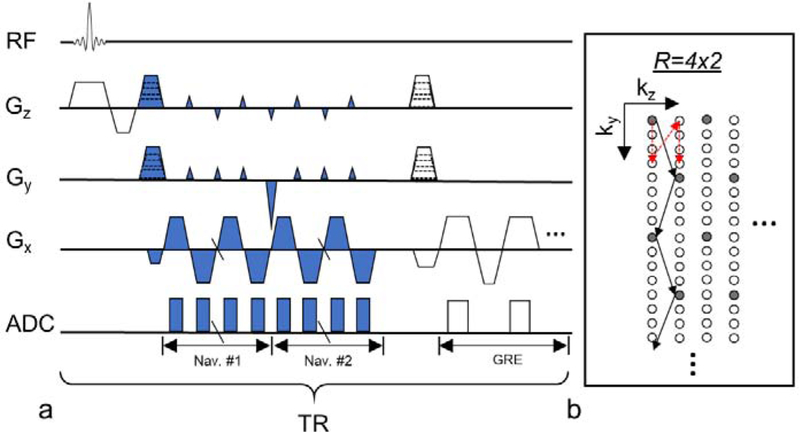
Navigator acquisition was incorporated in a 3D gradient echo (GRE) acquisition technique (Fig. 1). To allow the detection of B₀ field changes, two consecutive navigators were acquired right after the slab-selective RF excitation and prior to collection of the GRE imaging data. Fast navigators were acquired with a total acceleration factor of R ≜ R_y · R_z where R_y and R_z are the acceleration ratios in the k_y and k_z phase-encoding directions, respectively. Gradient blips in both phase-encoding directions were applied for controlled 2D-aliasing (Breuer et al., 2006). As shown in Fig. 1b, after one RF excitation (shot), N_y/R_y readout lines were collected along the k_y direction with k_z blips (for controlled aliasing) for a fast navigator, and N_z/R_z shots were taken to acquire multiple partitions in the k_z direction to complete one fast navigator, where N_y and N_z are the matrix dimensions of the navigator image in the k_y and k_z direction, respectively. To acquire two navigators as shown in Fig. 1a, this pattern was repeated twice within each TR. The phase-encoded positions for the fast navigator were cycled through k-space by varying the initial offset (red arrow in Fig. 1b). A full navigator covering the entire k-space was obtained for every set of R fast navigators. This provided the flexibility to choose one full navigator period in absence of head motion in the postprocessing to provide the autocalibration signal (ACS) for GRAPPA reconstruction. Once every second, blipless readout lines at the center of k-space were acquired instead of the navigator. The blipless data was used to correct the EPI ghost and global B₀ variation in the data.

Fig. 1.

Diagram of PN and GRE acquisition. (a) Timing of the MRI acquisition sequence. “ADC” denotes the time window when the signal was recorded. Blue color marks navigator acquisition. GRE data were acquired at multiple echo times. (b) Acquisition pattern of fast navigators in k_y-k_z plane. Grey dots represent k-space data in one fast navigator. Black arrows connect consecutive readout lines within one shot. Additional fast navigators (in white dots) were acquired, using a similar but shifted k-space trajectory, one after another until a full navigator was sampled. Red dashed arrows show the varying starting offset for phase-encoding steps used in subsequent TRs for the fast navigators.

2.2. Navigator Reconstruction

K-space data of the PN were first corrected for the EPI ghost and global B₀ changes. The EPI ghost was corrected by eliminating the shifts of k-space readout lines which were acquired with opposite readout gradients, using the nearest blipless data as the reference. The global B₀-related phase of each readout line was corrected according to its echo time. Fast navigator images were then reconstructed using a 2D-GRAPPA approach (Blaimer et al., 2006). The GRAPPA kernel size was 3×2×2 in the readout and two accelerated phase-encoding directions, respectively. One full k-space dataset from a period without head motion was used as the ACS for GRAPPA. This period was identified based on the phase of the blipless data: during the acquisition of the motion-free full k-space set, the span of the global B₀ frequency variation was below 2 Hz. While there can be multiple periods satisfying this condition, only the one closest to the center in the k-space of the GRE data was chosen. After fast navigators were reconstructed and motion was estimated, this period was confirmed only if the intra-period head rotation and translation were less than 0.2° and 0.2 mm, respectively. The magnitude of the combined image was the sum of the magnitude images in individual channels. Sum of magnitudes was used instead of the more SNR-optimized root of sum of squares because the former was found to be less biased by the B₁ profile. The combined phase image was the sum of phase images weighted by the magnitude square after phase images were first normalized to a reference channel. Full navigator images of individual receive channels were simply reconstructed from the Fourier transform of the full k-space data and then combined in the same way as the fast navigator. EPI distortion in the navigator images was corrected using B₀ maps generated from the two navigators. The correction was implemented as the inverse solution of the Fourier model of the navigator signal which is a function of B₀ distribution and echo times in the navigator echo train (Munger et al., 2000; Sutton et al., 2003).

2.3. GRE Reconstruction

GRE data was first preprocessed by eliminating global B₀ variation using the blipless data and then corrected using the motion and B₀ change information from the navigators. Rigid body motion can be corrected for based on fast algorithms such as non-uniform FFT (NUFFT) (Fessler and Sutton, 2003). The effect of spatially linear B₀ changes is equivalent to a coordinate shift in k-space and can also be calculated efficiently using NUFFT (Gretsch et al., 2018). On the other hand, correcting each k-space line of GRE with individual nonlinear B₀ maps is impractical because of the time-consuming Discrete Fourier Transform (DFT). In this study, we proposed an efficient algorithm to correct nonlinear B₀ changes by separating GRE data into m clusters with approximately linear intra-cluster B₀ field changes:

$$B_{0,qj}\left(\mathbf{\text{r}}\right)=B_{0,j}\left(\mathbf{\text{r}}\right)+b_{qj}+{\mathbf{\text{g}}}_{b,qj}\cdot \mathbf{\text{r}},j=1\dots m$$ (1)

where B_{0, j} is the reference B₀ map of the jth cluster, q denotes the index of GRE readout lines in the jth cluster, r is spatial coordinate in the head frame, and b_qj and g_b,qj are the constant and first-order terms of the B₀ change approximation, respectively. Nonlinear B₀ effects were corrected based on B_{0, j} across clusters. Note that the GRE data in a given cluster were not necessarily acquired continuously in time.

Assuming rigid body motion of ${\mathbf{\text{r}}}_{qj}^{\text{´}}={\mathbf{\text{R}}}_{qj}\mathbf{\text{r}}+{\mathbf{\text{d}}}_{qj}$, where R_qj and d_qj are a rotation matrix and a translation vector respectively and ${\mathbf{\text{r}}}_{qj}^{\text{´}}$ the coordinate in the laboratory frame, the resulting MR signal in the cth receive coil can be modeled as:

$$\begin{gathered} s_c\left({\mathbf{\text{k}}}_{qj}\right)=e^{i2\pi \sout{\gamma }\left(k_{x,qj}/g_x+TE\right)b_{qj}}{e}^{i2\pi \left[{\mathbf{\text{k}}}_{qj}+\sout{\gamma }\left(k_{x,qj}/g_x+TE\right){\mathbf{\text{g}}}_{b,qj}\right]\cdot {\mathbf{\text{d}}}_{qj}} \\ \hspace{0.17em}\hspace{1em}\hspace{1em}\hspace{1em}\int \int \int \rho \left(\mathbf{\text{r}}\right)B_{1,cj}\left(\mathbf{\text{r}}\right)e^{i2\pi \sout{\gamma }{B}_{0,j}\left(\mathbf{\text{r}}\right)TE}{e}^{i2\pi \left\{\left[{\mathbf{\text{R}}}_{qj}^{\text{T}}{\mathbf{\text{k}}}_{qj}+\sout{\gamma }\left(k_{x,qj}/{\mathbf{g}}_x+TE\right){\text{g}}_{b,qj}\right]\right\}\cdot \mathbf{\text{r}}}d\mathbf{\text{r}} \end{gathered}$$ (2)

where ρ is the image to be corrected, B_1,cj denotes the estimated receive sensitivity map of the cth coil in the head frame in the jth cluster, $\sout{\gamma }$ is the gyromagnetic ratio, g_x is the readout gradient and ${\mathbf{\text{k}}}_{qj}\triangleq \left(k_{x,qj},k_{y,qj},k_{z,qj}\right)$ the k-space coordinate in the laboratory frame. Note that ${\mathbf{\text{R}}}_{qj}^{\text{T}}{\mathbf{\text{k}}}_{qj}+\sout{\gamma }\left(k_{x,qj}/g_x+TE\right){\mathbf{\text{g}}}_{b,qj}$ is the k-space coordinate in the head frame. MRI signal phase that resulted from B_{0, j} in the time course of a readout line was calculated at the echo time, unlike the components from b_qj and g_b,qj, in order to save calculation time. In the jth cluster, B_1,cj was estimated from coregistered, uncombined full navigator which was identified to be in absence of motion. Calculation time of Eq. (2) is in the order of O(mn_cn ∙ logn + αn_cn_s) where n is the number of voxels, n_s is the number of shots, n_c is the number of receive coils and α is a constant related to NUFFT including oversampling rate and kernel size (Fessler and Sutton, 2003). Given head motion, B₀ change and sensitivity maps extracted from the navigator, image ρ was solved using the linear conjugate gradient method with 10 iterations.

Head motion was quantified based on the magnitude image of the fast or full navigators (Thevenaz et al., 1998). B₀ changes in the head frame were calculated following aligning navigators at two echo times to a reference volume. If motion within a full navigator period was less than 0.2° and 0.2 mm, the full navigator was used in place of the corresponding fast navigators for better SNR of motion and B₀ change estimation and reduced parallel imaging artifacts. Clustering the GRE data was performed using the measured B₀ changes as the input. The constant and spatially linear components in the B₀ change maps were first removed and the residuals were clustered based on the k-means method. The root mean square error (RMSE) of the B₀ change maps (RMSE_B0) relative to the centroids of clusters was calculated and used to determine the number of clusters. For each scan, the RMSE_B0 corresponding to 1 to 20 clusters were calculated. The number of clusters was chosen as $\min \left\{m:\left|{\text{RMSE}}_{\text{B0},m}-{\text{RMSE}}_{\text{B0},20}\right|/\left|{\text{RMSE}}_{\text{B0},1}-{\text{RMSE}}_{\text{B0},20}\right|\le \epsilon \right\}$ for ε=0.1 where RMSE_B0,m denotes RMSE_B0 of m clusters.

2.4. Experiment Design and Data Analysis

Experiments on healthy human subjects were conducted for two purposes: (1) to evaluate the accuracy of the PN in estimating motion and B₀ changes and (2) to verify the performance of the motion correction algorithm. For purpose (1), PN-measured head pose and B₀ changes were compared with the results of multi-echo isotropic 2 mm resolution GRE images, which were acquired in parallel to the navigator. The subjects were instructed to stay still during these scans. For purpose (2), a stepwise motion task was performed by the subjects, who chose to move their heads to different arbitrary poses in response to a series of visual cues during a scan. After each pose change, subjects maintained the head pose until the next cue. An average of 5 pose changes were planned for each scan. Two GRE protocols were used in the stepwise motion scans, one with isotropic 2 mm resolution (the same as the static scans) and another with 0.5×0.5×1.5 mm³ resolution, respectively. The 2 mm GRE was acquired because of its short scan time and fast reconstruction. To evaluate the effectiveness of field correction in more general cases, Monte Carlo simulations based on combined data from the 2 mm resolution static scans were employed. In the simulation, for each subject, the GRE and PN data from one static scan was used as the baseline. A random portion (0 to 50%) of the baseline at random k-space positions was substituted by the corresponding data from other static scans. Twenty such datasets were generated for each subject.

To evaluate the accuracy of the PN, one navigator near the center of the k-space in the GRE data in each static scan was used, and the navigator results of pose and field estimation were compared to the corresponding GRE results from the same scan. A group-level summary of the motion accuracy was reported based on the RMSE between the PN- and GRE-measured head pose changes. The group-level accuracy of B₀ change measurement was reported as the 10% and 90% percentiles of the difference between the PN- and GRE-measured field changes because a few voxels near the skulls were too badly conditioned to provide reasonable B₀ data and biased the RMSE.

In reconstructing the fast navigators using GRAPPA, the ACS was generated from the first static scan. Efficacy of the ACS may be degraded by pose change; therefore, choosing a specific scan to provide the ACS for all scans was considered to be a conservative case to evaluate the performance of the fast navigator. In order to control the influence of unwanted subject motion on the validity of the GRE reference, an intra-scan motion profile was first obtained by co-registration of the full navigators within a scan. Data with intra-scan variance of motion more than 0.5° or 0.5 mm were rejected. However, head motion caused by cardiac and respiratory cycles cannot be avoided in the GRE reference (Maclaren et al., 2012; LeVan et al., 2013).

The PN with in-plane resolution of 6 mm was evaluated in the same way as the 4 mm navigator to determine the impact of in-plane resolution on the accuracy of motion and B₀ measurement. Reducing the in-plane resolution may gain time for acquiring the GRE imaging data or reduce the needed number of TRs for the navigators, thus increasing their temporal resolution, at the cost of slight accuracy loss. Here, the 6 mm navigator was obtained from the 4 mm data by eliminating the high frequency k-space components in the k_x-k_y plane.

In order to evaluate the effect of the retrospective correction on the reconstructed images, four levels of correction were performed: (1) global B₀-only correction (in the preprocess as mentioned earlier), (2) motion-only correction, (3) motion and linear B₀ correction (using one cluster) and (4) motion and nonlinear B₀ correction (number of clusters dependent on the measured field changes). Corrected images were aligned to and evaluated based on reference images acquired without intentional motion. Normalized RMSE (NRMSE) between the corrected images and the reference was used to quantify the image quality.

The effect of low-order nonlinear B₀ compensation was analyzed based on the 2 mm resolution data from the stepwise-motion scans when the measured B₀ change maps were fitted to spherical harmonics of orders up to 1 to 6. Nonlinear B₀ correction with six clusters was applied in the reconstruction. NRMSEs of the results were analyzed. These results can be compared with our previous study (Liu et al., 2018), in which the complexity of the motion-induced B₀ changes was analyzed directly on the B₀ maps using spherical harmonics decomposition.

2.5. MRI Protocol

The experiments were performed on a 7 T MR scanner (Magnetom, Siemens, Erlangen, Germany) with a 32-channel head-only RF coil (Nova Medical, Wilmington, MA, USA). Ten healthy human subjects were recruited for this study under a human subject research protocol approved by the Institutional Review Board at the National Institutes of Health.

Static scans were performed on Subjects #1 to #6. The parameters of GRE protocol in the static head pose scans were: FOV=240×192×96 mm³, matrix size for GRE=120×96×48 (isotropic 2 mm resolution), matrix size for the PN=60×48×24 (4 mm isotropic resolution), R_y=4, R_z=2, TR=45 ms, flip angle=10°, TE_PN1=6.5 ms, TE_PN2=14.7 ms and TE_GRE=24, 26, 28, 30 and 32 ms. Times to acquire a fast and full PN were 0.54 (12 shots) and 4.32 s (96 shots), respectively. One scan lasted 3 minutes and 27 seconds. The readout bandwidth (BW) of the PN and GRE was 4167 and 2083 Hz/pixel, respectively. The echo train length of the PN was 8.2 ms with echo spacing of 0.68 ms.

Stepwise motion scans were performed on all subjects, among whom Subjects #1 to #6 were scanned with isotropic 2 mm resolution GRE (the same as the static scans) and Subjects #5 to #10 with 0.5×0.5×1.5 mm³ resolution GRE. In the 0.5 mm scan, PNs were acquired using the same parameters as the 2 mm scan. The other parameters in the 0.5 mm scan were: FOV=240×192×96 mm³, TR=46.5 ms, flip angle=15°, TE_GRE=26 ms, BW_GRE=112 Hz/pixel, and acceleration ratio of 2 in the first phase-encoding direction. One scan lasted 9 minutes and 41 seconds.

3. Results

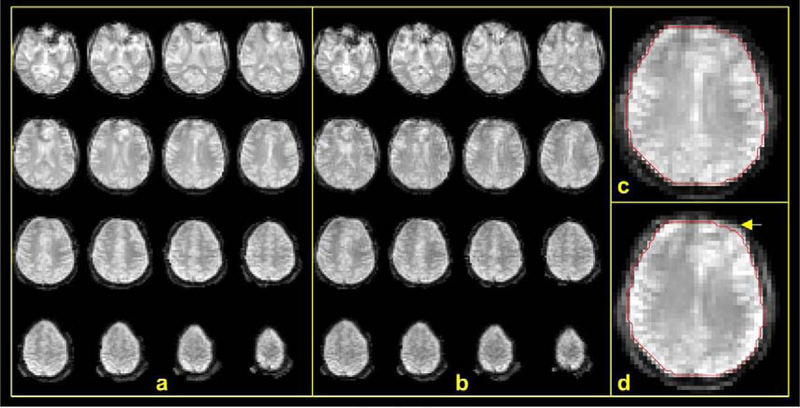
Examples of distortion-corrected 4 mm full and fast PN images are shown in Fig. 2a and b. Although an acceleration factor as high as 8 (4×2) was employed in acquiring the fast navigator, it still depicts considerable details of the brain structure without obvious deteriorating artifacts in reference to the full navigator images. The images did not exhibit any noise or ghost in the background because the background was masked out during the distortion correction. As we can see in Fig. 2c and d, distortion correction of the EPI data mostly impacted the brain morphology at the front of the brain. Although the distortion appears to be small, if not corrected for, it affected the accuracy of motion estimation as can be seen below.

FIG. 2.

Quality of PN images. Shown are examples of PN images at 4 mm spatial resolution and temporal resolutions of 4.32 s and 0.54 s of the full (a) and fast (b) navigators, respectively. (a) Distortion-corrected full navigator images of the brain. (b) Distortion-corrected fast navigator images. (c) and (d) show the effect of distortion correction: (c) a slice of distortion-corrected image with red contour marking the brain boundary and (d) uncorrected image of the same slice. A yellow arrow points to the most notable difference of the brain boundary in the two cases.

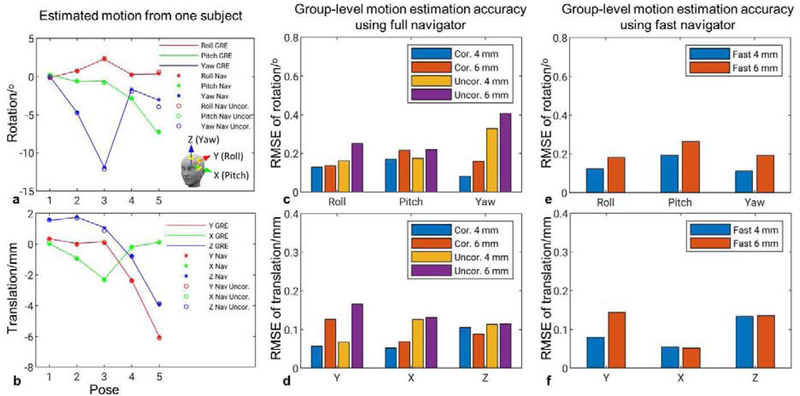
The accuracy of motion estimation using the PN is presented in Fig. 3. Fig. 3a and b show motion estimation using 4 mm resolution full navigator and 2 mm resolution GRE image from one subject; in five different poses, the PN-measured pose changes agree well with the result using GRE images. Intra-scan motion variance of these scans are in the range of [0.04, 0.3]° for rotation and [0.03, 0.25] mm for translation. It can be observed that EPI distortion correction plays a significant role in correctly estimating “Yaw” rotation, especially when through-plane rotation (“Pitch” or “Roll”) occurred. Definition of rotation axes was provided in Fig. 3a. Without distortion correction, in poses #4 and #5, “Yaw” rotation clearly deviated from the measurements using GRE or distortion-corrected navigator images. Through-plane rotation typically introduces opposing B₀ change patterns at the front and back of the brain, which in turn change the distortion and cause error in estimating “Yaw” rotation. Including 5 subjects and at least 5 poses per subject, a group summary of motion estimation accuracy is shown in Fig. 3c and d. Again, we can observe that without distortion correction, the RMSE of “Yaw” rotation increased to 0.33°, from 0.08° with distortion correction. In the group results, at 4 mm resolution and with distortion correction, the navigator achieved high accuracy of motion estimation, with RMSEs no more than 0.17° and 0.1 mm, respectively. When in-plane resolution was decreased to 6 mm, the RMSEs were still better than 0.21° and 0.13 mm, respectively. Group summary of motion estimation accuracy using distortion-corrected fast navigator is presented in Fig. 3e and f, showing very similar results to the corresponding results of the full navigator. At 4 mm or 6 mm resolution, the group-level precision of motion estimation was 0.06° and 0.04 mm using the full navigator and 0.08° and 0.07 mm using the fast navigator.

FIG. 3.

Motion estimation accuracy from navigator data. Estimated pose changes in reference to the results using 2 mm GRE images in a single subject (a, b) and accuracy of these changes in a group of fix subjects (c-f). Insert in (a) shows definition of rotation and translation axes. (c-f). Columns reflect the RMSEs of estimated rotation (top) and translation (bottom). “Cor.” indicates distortion corrected navigator, and “Uncor.” uncorrected navigator.

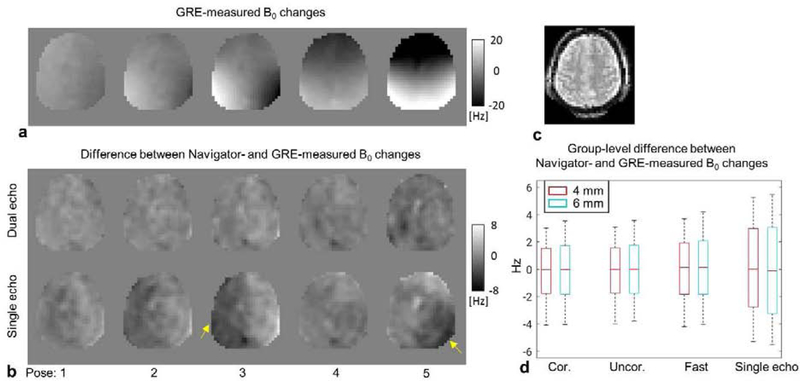
Accuracy of measuring B₀ changes in the head frame using the PN were evaluated in reference to the multi-echo GRE measurement. Fig. 4a depicts GRE-measured B₀ changes in the head poses shown in Fig. 3a and b. Differences between 4 mm navigator-measured B₀ changes using one or two echoes and GRE-measured changes are shown in Fig. 4b. We can observe that measurement based on one echo tended to generate local errors in particular poses. This is primarily due to unknown phase changes of the transmit and/or receive RF fields, which can be accounted for by obtaining navigators at two echo times. A group-level summary of the difference between navigator-measured and GRE-measured B₀ changes is presented in Fig. 4d. Notice the increased 10–90% percentile interval when only one echo was used, consistent with the single subject case. On the other hand, distortion correction of the navigator did not have an obvious effect on B₀ change measurement, unlike the case of motion estimation; this is attributed to the smooth spatial pattern of B₀ changes and small scale of distortion. Fast navigator performed similarly well compared to full navigator. There was a small effect of decreasing to a 6 mm resolution from the 4 mm one.

FIG. 4.

Accuracy of PN-estimated B₀ field changes. (a) B₀ changes of five poses (Fig. 3a) measured using multi-echo GRE images. (b) Difference between 4 mm PN- and GRE-measured B₀ changes, for both single-echo and dual-echo navigators. (c) The navigator image of the slice shown in (a) and (b). (d) Group summary of B₀ measurement accuracy using the navigator in reference to GRE results. Boxes indicate 10–90% percentile interval. Whiskers mark the 2.5% and 97.5% percentiles, respectively.

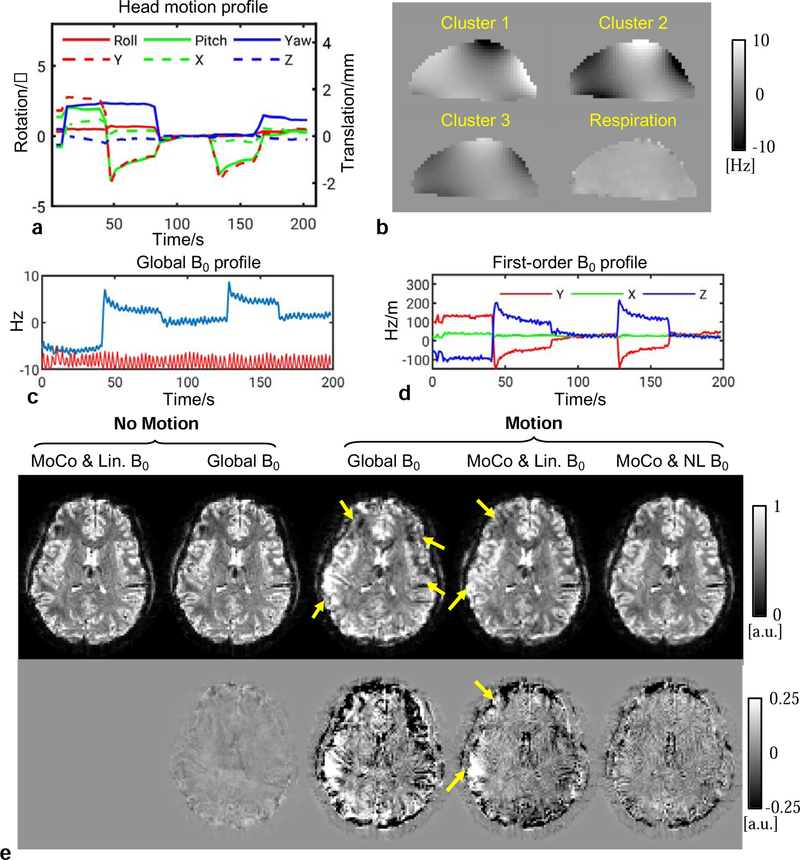
Fig. 5 shows examples of motion and B₀ correction in a 2 mm GRE scan with intentional intra-scan motion. As seen in Fig. 5a, the motion profile involved several occurrences of “Pitch” rotation, which has been known to generate spatially complicated B₀ changes (Liu et al., 2018), therefore violating the linear assumption. The number of clusters was automatically determined to be six. Shown in Fig. 5b, the magnitudes of B₀ changes in three clusters were compared with the B₀ change due to respiration in the sagittal view. The respiration-induced B₀ change was calculated as the difference between the maximum and minimum chest volume. The global (zeroth-) and first-order terms of the B₀ changes in Figs. 5c and d show the magnitude of the motion-induced B₀ changes. Note that the small ripples on those profiles were found to be synchronized with the chest belt signal (TSD221-MRI transducer, MP 150 digitizer and AcqKnowledge software, Biopac, Goleta, CA, USA), suggesting the effect of respiration. In Fig. 5e, using reconstructions from a separate static scan as the reference, we can see obvious artifacts when only global B₀ was corrected for. Motion and linear B₀ correction significantly improved the image quality but still left artifacts in certain areas. Including nonlinear correction further reduced these artifacts and rendered the results almost indistinguishable from the static scan result.

FIG. 5.

Reconstruction results of subject #1 showing image quality improvement using both motion and field estimates from the PN data. The results are reconstructed isotropic 2 mm GRE images (TE=32 ms) from a scan with intentional motion in reference to the results of a static “No Motion” scan. (a) Navigator-measured head motion profile during the motion scan. (b) Representative maps of B₀ changes from three clusters and the change due to respiration in the sagittal view. (c) The global (zeroth-order) B₀ change during the scan as measured by the navigator. The red line represents the respiration belt signal. (d) The first-order terms of the B₀ change measurement. (e) Top row: reconstructed images in different correction modes; bottom row: difference of the magnitude images in reference to the corrected image (MoCo & Lin. B₀) of the static scan. Arrows point to the most dominant artifacts.

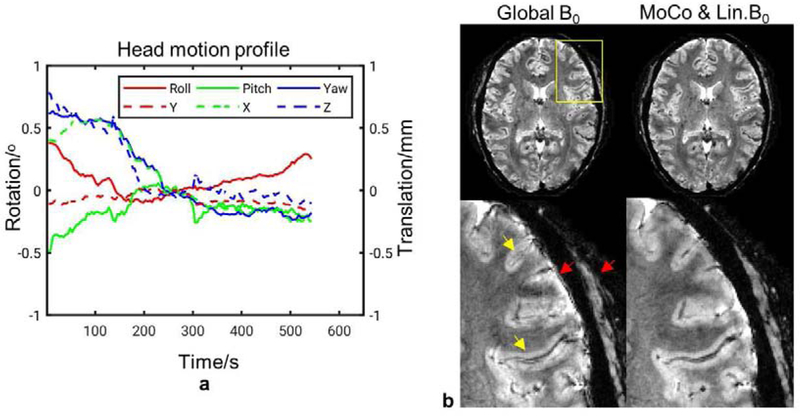
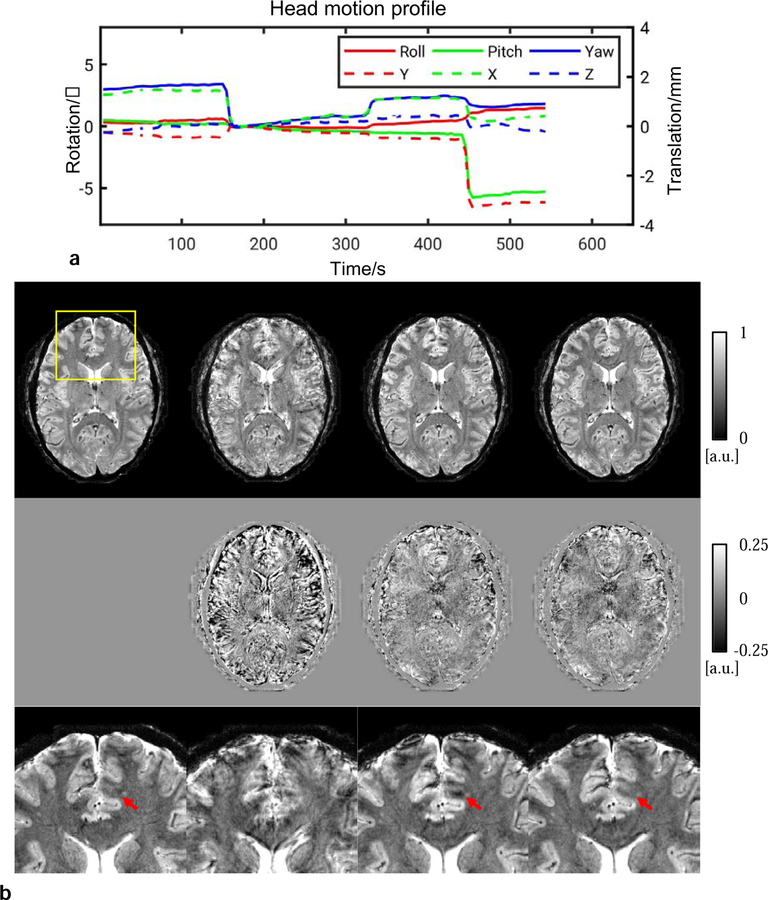
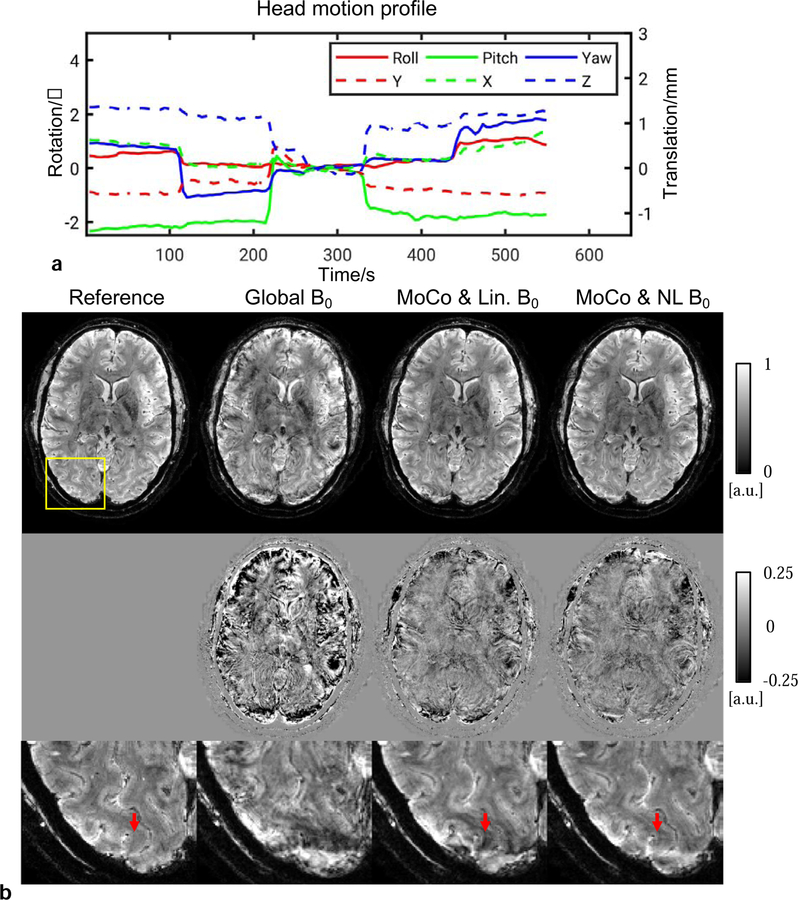
Examples of correction from 0.5 mm in-plane resolution scans are shown in Figs. 6, 7 and 8, corresponding to one scan without intentional motion and two with stepwise motion, respectively. Superior image quality resulted when both motion and nonlinear B₀ changes were corrected for. In the scan without intentional motion, head pose drifted slowly as shown in Fig. 6a. motion and linear B₀ correction was performed because only minor motion was present. In the zoomed-in images, the effectiveness of motion tracking using the navigator can be clearly appreciated from the improved visualization of fine anatomical details. For example, a vein-like structure as indicated by the top yellow arrow was recovered in the correction. In the scans with intentional motion, the cluster number was determined to be 3 and 7 in Fig. 7 and Fig. 8, respectively. The images with only global B₀ correction was severely corrupted. Motion and linear B₀ correction significantly improved the image quality but left local artifact uncorrected as indicated by the arrows. These artifacts appeared more subtle and may be confused with the anatomy (e.g., pointed by arrow in Fig. 7) compared to the motion artifact. Nonlinear B₀ correction was able to remove these artifacts and produced images in good agreement with the reference.

FIG. 6.

Reconstructed in-plane 0.5 mm GRE images of subject #6 from a scan without intentional motion. These results demonstrated the effect of small motion on the image quality. (a) Navigator-measured head motion profile during the scan. (b) Top row: Reconstructed images with Global B₀-only correction and full correction (one cluster), respectively; bottom row: zoomed-in images in the yellow box. Yellow arrows indicate artifacts inside the brain and red arrows indicate artifacts on the surface of the brain and the skull.

FIG. 7.

Reconstructed in-plane 0.5 mm GRE images of subject #6 from a stepwise motion scan. Improvement can be observed with motion and nonlinear B₀ correction. (a) Navigator-measured head motion profile during the scan. (b) Top row: Reconstruction for different correction modes; middle row: difference of magnitude images compared to the reference which was the corrected image in Fig. 6; bottom row: zoomed-in images in the yellow box. Arrows point to artifact which was reduced by nonlinear B₀ correction.

FIG. 8.

Reconstructed 0.5 mm in-plane GRE images of subject #8 from a stepwise motion scan. Improvement can be observed with motion and nonlinear B₀ correction. (a) Navigator-measured head motion profile during the scan. (b) Top row: Reconstruction for different correction modes; middle row: absolute difference of magnitude images compared to the reference from a scan without intentional motion; bottom row: zoomed-in images in the yellow box. Arrows point to artifact which was reduced by nonlinear B₀ correction.

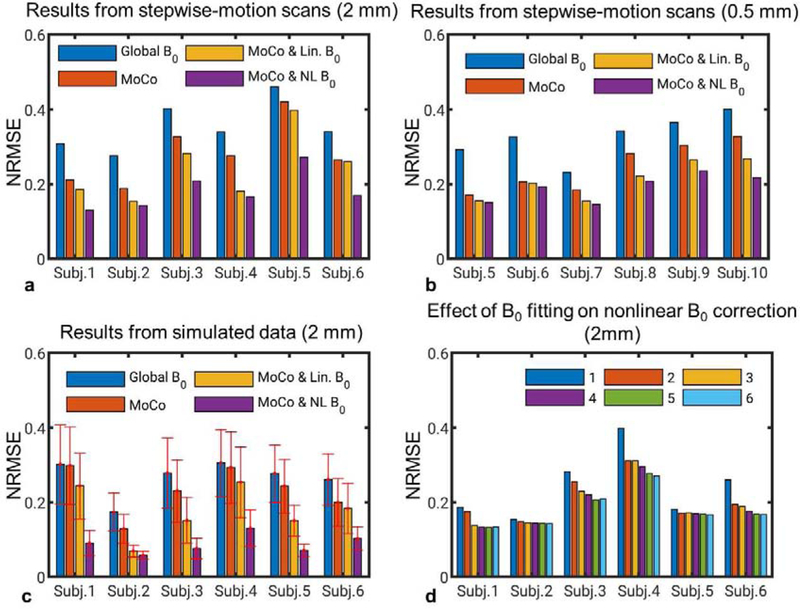
The NRMSE, across all subjects, of the reconstructions in the stepwise-motion scans is shown in Fig. 9 a and b. It can be seen that motion correction and more sophisticated B₀ correction consistently improved the image quality. Results from the Monte Carlo simulations showed the same trend. No more than 10 clusters were needed in all cases. The intra-scan head motion was listed in Table 1 for these scans. The result in Fig. 9d suggests that correcting for higher-order B₀ components beyond the second-order improved NRMSE in the nonlinear B₀ correction.

FIG. 9.

NRMSEs of reconstructed images in different correction modes showing the effectiveness of motion and nonlinear B₀ correction across all subjects. (a) Results of isotropic 2 mm GRE images from scans with the stepwise motion task. (b) Results of in-plane 0.5 mm GRE images from scans with the stepwise motion task. (c) Results of isotropic 2 mm GRE images in the Monte Carlo simulations. (d) Results of isotropic 2 mm GRE images from scans with the stepwise motion task and with measured B₀ changes fitted to spherical polynomials up to orders of 1 to 6. Six clusters were chosen in (d).

Table 1.

Standard deviation of maximum displacement in the stepwise-motion scans and the Monte Carlo simulations. The maximum displacement at any time point was calculated as the largest displacement in four locations, including the forehead, the back of the head and above the ears.

	Standard deviation of maximum displacement (mm)
Subject #	2 mm	0.5 mm	Simulation (mean of 20 datasets)
1	1.7	–	3.0
2	0.9	–	1.2
3	6.3	–	3.9
4	8.4	–	5.5
5	1.8	1.0	4.2
6	3.1	2.7	3.3
7	–	0.6	–
8	–	1.5	–
9	–	2.1	–
10	–	5.3	–

4. Discussion

In this study, we developed a novel navigator-based retrospective method for correcting motion and motion-induced B₀ change-related artifacts in high-resolution T₂*-weighted MRI. Studies (Liu et al., 2018; Sulikowska et al., 2014) have shown that head motion can introduce strong nonlinear B₀ field changes in the brain, rendering motion correction alone to be insufficient in T₂*-weighed MRI. The novelty of the current study in addressing this problem lies in two aspects: the development and evaluation of a dynamic (i.e. time-resolved) volumetric EPI phase navigator (PN) at a short TE and a computationally efficient retrospective algorithm for correcting both motion and nonlinear B₀ changes.

In Figs. 3 and 4, it was shown that at 4 mm isotropic resolution, the PN has an accuracy better than 0.2° and 0.1 mm in motion estimation, and using percentiles to quantify the accuracy of B₀ change measurement, the 10% and 90% percentiles of B₀ change error were −1.8 and 1.5 Hz at 7 T, respectively. Correcting B₀ effects in T₂*-weighted MRI demands detailed measurement of the nonlinear spatial pattern of B₀ changes induced by head motion. NMR field probes (Duerst et al., 2016; Vionnet et al., 2017) placed around the head can measure background B₀ changes originating from the main magnet or chest movement, but have only limited ability in estimating field changes from sources internal to the head. This is also true for field estimates derived from a fat-based navigator (Gretsch et al., 2018), in which field information internal to the head is similarly lacking. It remains to be seen whether measurement based on compressed navigators (Ward et al., 2002; van der Kouwe et al., 2006; Versluis et al., 2012; Meineke and Nielsen, 2019) has sufficient spatial resolution to capture the high-order nonlinear B₀ components.

The proposed navigator shares similarities with, but also has significant differences from, previously proposed volumetric EPI navigators (Hess et al., 2011; Tisdall et al., 2012, 2014), where the navigator acquisition occupied dedicated TRs. Use of a dedicated TR allows flexibility in inserting the navigator in various sequences but can lead to a compromise between the temporal resolution of the navigator and the total scan time and reduced SNR per scan time. The PN was optimized in 3D T₂*-weighted MRI for high temporal resolution without the need of dedicated TRs. PN signal was acquired in the minimally T₂*-weighted time between RF excitation and GRE image acquisition. Temporal resolution was further improved with the acceleration available with parallel imaging. Based on the parameters utilized here, a fast 4 mm navigator was obtained in about 0.5 s without significant loss of accuracy as shown in Figs. 3 and 4. This can be useful in resolving the fast transition period of head pose change. We have found that using motion and field data provided only by fast navigators in the correction generated slightly smaller NRMSE compared to the situation only using the full navigators (data not shown).

The retrospective approach was developed to correct for nonlinear motion-induced B₀ changes. A prospective method may not address this problem because only the linear shims on standard MRI scanners can be adjusted in real time. Previous work (Liu et al., 2018) suggested that the nonlinear component in the spatial B₀ changes can even exceed the third order. So far the effectiveness of prospective methods has only been demonstrated to address field fluctuation related to respiration or limb motion rather than motion of the head itself (Duerst et al., 2016; van Gelderen et al., 2007). As shown in Figs. 7, 8 and 9, nonlinear B₀ correction led to image quality improvement visually and quantitatively. Although in principle, it is possible to introduce artifact in correction due to navigator accuracy issues, the results in Figs. 9a and b showed that images reconstructed with motion and nonlinear B₀ correction are more consistent with the reference images than those in less sophisticated correction modes. Similarly, as shown in Fig. 9d, correcting for B₀ components beyond the third-order spherical harmonics lead to significant improvements in image quality. This suggests the need for high-order real-time shimming when prospective correction is desired or that the high-order nonlinear B₀ changes should be retrospectively corrected for in absence of such advanced shim hardware.

The computation efficiency of the proposed retrospective correction was achieved by clustering the GRE data into a limited number of clusters with different nonlinear B₀ changes. The computation time was estimated to be proportional to the number of voxels or shots and the number of clusters as shown in the section of GRE reconstruction. This relationship was confirmed in the reconstruction time results in Table 2 With ε=0.1, no more than 10 clusters were needed in the stepwise motion scans and the Monte Carlo simulations. The use of three clusters appeared adequate to correct the image without intentional motion—this was confirmed by reconstruction of six 9-minute-long 0.5 mm GRE acquisitions in Subjects #5 to #10 while they were asked to stay comfortable during those scans without intentional motion. It will be interesting to compare this algorithm with an alternative fast retrospective nonlinear B₀ correction method based on principle component decomposition of the nonlinear B₀ encoding matrix in a larger subject group (Wilm et al., 2012).

Table 2.

Reconstruction time in one iteration on a desktop computer with an Intel Xeon “E5–1650 v3” CPU (ten iterations were used in the reconstruction).

Resolution	Isotropic 2 mm	0.5×0.5×1.5 mm3
Matrix size	120×96×48	480×384×64
Number of shots	5.5×105	5.9×106
Time (s), 1 cluster	2	42
Time (s), 6 clusters	9	225

The ability to correct for nonlinear B₀ field changes comes at the price of some loss in scan efficiency. This is because of the time required for PN acquisition, which could alternatively have been used for image data acquisition. For the 4 mm navigator used here, acquisition of two navigators can be as short as 13 ms which was calculated based on the resolution, FOV, maximum gradient strength (40 mT/m) and slew rate (200 T/m/s) and the avoided acoustic resonance frequency (1100±300 Hz) of the scanner. To avoid the signal being affected by flow (e.g. of CSF and blood), it is useful to use flow compensated waveforms (Bernstein et al., 1992) for all three gradient directions in future implementations. In the current implementations, at 0.5 mm resolution, this would add about 6 ms before the GRE readout This additional time can result in a slight SNR loss of the T₂*-weighted data due to a longer TE or shorter GRE readout window. At a TE of 30 ms, this allows for the bulk (22 ms) of the useful acquisition time to be used for acquiring the T₂*-weighted imaging data. This should be compared to the time of about 32 ms for acquiring the T₂*-weighted data in a previous high-resolution phase-based MRI study at 7 T (Duyn et al., 2007). Combined with the fact that the time period used for navigator acquisition has little T₂* weighting (as it uses the early signal after the RF excitation), the efficiency loss associated with the navigator appears quite modest.

Nevertheless, the navigator design may be optimized to further reduce its acquisition time. First of all, it appears that decreasing the in-plane resolution from 4 to 6 mm has minimal effect on the accuracy of motion and B₀ measurement. This can reduce the echo train length of the dual navigators below 10 ms using our 7 T MR hardware. Secondly, instead of acquiring two navigators in each shot, it may be sufficient to acquire only one. Two navigators provide absolute B₀ maps which can be useful for EPI distortion correction and are free of B₁ phase interference. However, it may be possible to supplement the single navigator by occasionally measuring dual navigators at lower resolution (to stay within the single navigator duration) and still be effective at minimizing B₁ phase interference.

Retrospective correction cannot compensate for information loss due to incomplete acquisition of the k-space. Head rotation and linear components in B₀ changes equivalently rotate and shift the actually measured k-space locations, resulting in gaps in k-space. The potential effect of this on image quality will strongly depend on where in k-space these gaps occur. Prospective motion correction methods based on simple, fast navigator or fast external devices may prevent such gaps by adjusting MRI scan parameters and the linear shim terms on a shot-by-shot basis. Sophisticated navigators as used in the current study may be too slow for accurate prospective motion correction (even the fast navigator in our study required 0.54 s or 12 shots). Nevertheless, it is still fast enough to overcome the impact of such gaps either by identifying substantial k-space gaps to be reacquired before scan completion or by performing a rough real-time correction to reduce the significance of the gaps in combination with more accurate retrospective correction. Reacquisition is also useful to reduce the number of clusters if it was determined during the scan that too many clusters would be needed for the retrospective correction.