Do more intelligent brains retain heightened plasticity for longer in development? A computational investigation

Highlights

• •The heritability of general cognitive ability increases with age; this occurs later for high ability individuals.
• •General cognitive ability is associated with differential rates of change of brain structure.
• •We use computational modeling of population development to link genes, brain and behavior.
• •We provide the first unified mechanistic account of these data.
• •Data are explained by the increasing non-linear behavior of neurocomputational systems across development causing divergence between non-identical twins.

Abstract

Twin studies indicate that the heritability of general cognitive ability – the genetic contribution to individual differences – increases with age. Brant et al. (2013) reported that this increase in heritability occurs earlier in development for low ability children than high ability children. Allied with structural brain imaging results that indicate faster thickening and thinning of cortex for high ability children (Shaw et al., 2006), Brant and colleagues argued higher cognitive ability represents an extended sensitive period for brain development. However, they admitted no coherent mechanistic account can currently reconcile the key empirical data. Here, computational methods are employed to demonstrate the empirical data can be reconciled without recourse to variations in sensitive periods. These methods utilized population-based artificial neural network models of cognitive development. In the model, ability-related variations stemmed from the timing of the increases in the non-linearity of computational processes, causing dizygotic twins to diverge in their behavior. These occurred in a population where: (a) ability was determined by the combined small contributions of many neurocomputational factors, and (b) individual differences in ability were largely genetically constrained. The model’s explanation of developmental increases in heritability contrasts with proposals that these increases represent emerging gene-environment correlations (Haworth et al., 2010). The article advocates simulating inherited individual differences within an explicitly developmental framework.

1. Introduction

1.1. Cognitive ability and brain structure

Structural properties of the brain have been found to correlate with individual differences in cognitive ability. For example, there is a correlation of brain size to general cognitive ability1 of between 0.1 and 0.3 (McDaniel, 2005). When Ritchie et al. (2015) used a range of measures from structural brain imaging to predict general cognitive ability in adults, they found that brain volume explained 12% of the variance, cortical thickness another 5%, and all measures together up to 21% of the variance. It has been proposed that the timing and magnitude of developmental changes in structural indices, such as cortical thickness or cortical surface area, are the more important predictors of general cognitive ability than brain structure per se (Schnack et al., 2015). For example, in a longitudinal study tracing development from young childhood into early adulthood, Shaw et al. (2006) reported that a superior intelligence (121–149 IQ points) was associated with faster and more prolonged thickening of cortex in childhood and faster thinning in adolescence, with correlations between structure and ability at any time point falling between 0 and 0.1. Thickening and thinning effects differed between brain regions, being most noticeable in frontal and temporal regions. However, in this study, only the superior intelligence group showed reliable differences, with high (109–120 IQ points) and average (83–108 IQ points) IQ groups overlapping sufficiently to be statistically indistinguishable.

The relationship between general cognitive ability and brain structure is re-enforced by the finding that both are highly heritable (e.g., Thompson et al., 2001, Plomin and Spinath, 2004), where heritability is defined as the proportion of phenotypic variability explained by genetic similarity. Moreover, bivariate analyses reveal that the heritability of ability and structure is explained by partially overlapping genes (e.g., Posthuma et al., 2002). This finding extends to the rate of change of structural properties such as cortical thickness (Brans et al., 2010). The observation that general cognitive ability is related to dynamic properties of cortical maturation led Shaw et al. (2006) to propose that ‘the prolonged phase of prefrontal cortical gain in the most intelligent might afford an even more extended “critical” period for the development of high-level cognitive cortical circuits’ (p. 678), that is, a period of heightened sensitivity to variation in environmental influences.

However, Brant et al. (2013) noted that extended structural brain development does not necessarily imply longer sensitivity to environmental influences. That is, the brain data provide no direct evidence for individual differences in the length of a sensitive period associated with cognitive ability (see Thomas and Johnson, 2008; for discussion of the notion of sensitive periods in brain development). Brant et al. (2013) sought out more direct evidence by taking advantage of the finding that the heritability of general cognitive ability increases linearly with age (Haworth et al., 2010). The common explanation for this pattern is that the aged-related increase marks an emerging gene-environment correlation, which then exaggerates the influence of the initial genetic differences on performance (Briley and Tucker-Drob, 2013, Haworth et al., 2010). As individuals become more autonomous with increasing age, they seek out environments that match their genetic profiles. For example, brighter children may seek out more stimulating environments. Environmental influences then cause an exaggeration of initial genetic differences. Haworth et al. described the gene-environment correlation thus: ‘as children grow up, they increasingly select, modify and even create their own experiences in part based on their genetic predispositions’ (2010, p. 1112).

Brant et al. (2013) reasoned that if higher cognitive ability corresponds to an extended sensitive period in brain development, individuals with higher ability should remain sensitive to environmental variation for longer. Greater influence of environmental variation translates to lesser influence of genetic variation. The prediction was therefore that in higher ability individuals, the rise in heritability should occur later. Combining data from over 10,000 monozygotic (MZ) and dizygotic (DZ) twin pairs in a cross-sectional study, and around 400 MZ and DZ pairs in a longitudinal study, they found support for this hypothesis (see Fig. 1a). High and low ability groups showed similar heritability in childhood (4–12 years). By adolescence (13–18 years), the low ability group now showed an increase in heritability, while the high ability group continued to show the same lower level observed in childhood. In adulthood (18+ years), both groups now showed similarly high heritability.

Fig. 1.

(a) Empirical data estimating the heritability of IQ split between high ability and low ability individuals, for childhood, adolescence, and adulthood (Brant et al., 2013). (b) Simulated data for the change in heritability across development for the population split by ability at the population mean. Note, for the simulation, a proxy of heritability was taken as the difference between MZ and DZ correlations. The early measure was calculated at 100 epochs, mid at 500 epochs, and late at 990 epochs. Error bars show 95% confidence intervals.

There are, however, some difficulties with the picture. There is little understanding of the low-level mechanisms linked to neural processing that underpin the macro cortical changes in indices such as thickness or surface area; or, indeed, whether the cortical changes reflect intrinsic genetic processes or the influence of environmental variables such as socio-economic status (SES) (Shaw et al., 2006, Noble et al., 2015). Shaw et al. (2006) suggested that cortical thickening might correspond to experience-dependent molding of the architecture of cortical columns along with dendritic spine and axonal remodeling, while the thinning observed in adolescence might reflect the refining of neural circuits via use-dependent selective elimination of synapses. But hypotheses of this form largely rely on animal models, and the link to the development of high-level cognitive behavior is not demonstrated. Indeed, there is disagreement about which are the key structural indices and how they relate to function, with absolute cortical volume, cortical thickness, and cortical surface area all implicated, but showing different developmental relationships to cognitive ability (see, e.g., Noble et al., 2015).

The consequence of an absent mechanistic account is illustrated by Brant et al.’s (Brant et al. 2013) admission that they were unable to derive a coherent causal account of their findings. The hypothesis that protracted development is beneficial for the acquisition of higher and uniquely human cognitive functions as measured by intelligence quotient (IQ) does not suffice, because individuals with an eventual higher IQ tend to score higher in tests from early in development (Columbo and Frick, 1999, Deary et al., 2000)—not just in adolescence, when the benefit of protracted sensitivity would become apparent. Neither does the association of longer environmental sensitivity in high IQ fit with the common explanation of the age-related increase in the heritability of general cognitive ability, as an emerging gene-environment correlation. As Brant et al. 2013 put it, one would need to ‘posit, counter-intuitively, that higher-IQ individuals seek out environments concordant with their genetic propensities later in development than do lower-IQ individuals’ (2013, p.1493, italics added). Brant et al. (2013) concluded that the reason for developmental increases in the heritability of IQ remains unclear.

1.2. Population-level computational modeling of development

Computational modeling provides a method to clarify theoretical proposals via implementation, to unify empirical data with respect to common mechanisms, and to generate novel predictions. Its main disadvantage involves the simplifications required for implementation. Artificial neural networks (ANNs) have been used widely in the modeling of cognitive development (e.g., Spencer et al., 2009, Thomas and McClelland, 2008). Recently, these models have been used to investigate associations between levels of description, including those between genes, brain structure, brain activation, and behavior (Thomas et al., 2016). While much simplified and focusing on development within a single computational mechanism, the formalism of the ANN that the authors employed had several useful properties for this purpose. The model comprised an associative network with distributed processing across a network of simple integrate-and-fire processing units; behavior was acquired via an experience-dependent developmental process, which involved interaction with a structured and variable learning environment and gradual alterations in network connectivity strengths; and the developmental trajectory and final representational states of each network were constrained by parameters with analogues in neurocomputation, such as the activation function of the neurons, the number of neurons, and the connection density.

Three aspects of the Thomas et al. (2016) model make it useful for addressing the current empirical data. First, the model simulated cognitive development in populations of individuals, where variability in trajectories arose from intrinsic neurocomputational sources or extrinsic environmental sources (see also, Thomas and Knowland, 2014; for the application of this method to modeling sub-types of language delay; Thomas et al., 2013, for its application to modeling socio-economic status effects on language development). Second, the model included an artificial genome that specified the neurocomputational properties of the ANN. This allows modeling of genetic similarity between individuals, including creating identical and non-identical twin pairs. Twin study designs can then be simulated, which are the principal method to measure the heritability of individual differences. Third, the output of model can be viewed as generating behavior, while changes in structural properties of the ANNs, such as their connectivity, can be viewed as potentially informative of mechanisms contributing to structural changes in the brain. As indicated above, there is no consensus on the low-level neural mechanisms responsible for macro changes in brain structure. The ANN included two potentially relevant properties, one analogous to thinning (the decay and pruning of unused connectivity) and one analogous to thickening (the accumulation of connectivity strength), which were both central to the developmental process. Individual differences in these properties can provide candidate hypotheses for factors that contribute to observed changes in macro brain structure properties over human development.

The aim of the following simulations was five-fold: (1) to capture cognitive development in several populations, where individual differences arose from different mixes of genetic and environmental variation; (2) to use a twin study design to estimate the heritability of function and structure; (3) to identify ability differences in the populations based on their behavior; (4) to show how the heritability of differences in ability changed across development in each population; and (5) to identify how ability related to developmental changes in network structure properties.

2. Method

The following simulations use a base model taken from the field of language development, addressed to the domain of English past-tense formation. Here, the model was employed in an illustrative setting, intended only as an example of a developmental system applied to the problem of extracting the latent structure of a cognitive domain through exposure to a variable training environment. The intention was to capture qualitative characteristics of the empirical data rather than, for example, to exactly calibrate variances from genetic and environmental sources to fit empirically observed estimates of heritability in certain populations. The simulations reported here were not originally designed to simulate the target empirical data. Full details of the simulation can be found in Thomas et al., 2016. Here, a brief overview is provided.

2.1. Base model

A 3-layer backpropagation network was used to learn input-output mappings over 57 input units and 62 output units. The training set comprised approximately 500 such mappings. A backpropagation network usually has a layered organization of simple processing units, each with a sigmoid activation function. Layers in between the input and output layer (so-called hidden units) give the network the power to learn arbitrary input-output mappings. An error-correction algorithm iteratively adjusts connection weights to reduce the disparity between the actual output and the desired output for each input pattern (the backpropagation algorithm). Training comprises repeated presentations of the set of input-output mappings to the network, with each presentation called an ‘epoch’ of training. For a given sized training set, a minimum number of hidden units will be necessary for the network to learn the set. See Thomas and McClelland (2008) for further details.

2.2. How neurocomputational variation was implemented

ANNs contain a range of parameters that increase or decrease their ability to learn a given training set or the rate at which learning occurs. Parameters such as learning rate, momentum, and number of hidden (internal) processing units feature in most published simulations. In models of normal/average development, parameters are optimized to achieve best learning (usually in the presence of the full training set). In the current model, a number of parameters were simultaneously varied by small amounts across individual networks, with learning ability determined by their cumulative effect. This reflected the expectation that in reality, many low-level neural properties are likely to show small variations between individuals. Variations occurred over 14 computational parameters, determining four broad properties of the artificial neural networks: network construction, network dynamics, network adaptation, and network maintenance. The parameters had general computational functions and no specific relation to the problem domain that the system was acquiring, in line with the ‘generalist gene’ hypothesis (Plomin and Kovas, 2005).

The parameters were as follows. Network construction: architecture, number of hidden units, range for initial connection weight randomization, and sparseness of initial connectivity between layers. Network dynamics: unit threshold function (or “temperature”), processing noise, and response accuracy threshold. Network adaptation: backpropagation error metric used in the learning algorithm, learning rate, and momentum. Network maintenance: weight decay, connectivity pruning onset, pruning probability, and pruning threshold. These parameters have derivations in neurocomputational theory, and differences in their settings have been used in a range of models to simulate variations in cognition, including those found in general cognitive ability, specific language impairment, dyslexia, schizophrenia, autism, and ageing. Specification of the parameters, their previous use in the literature, and information on how the range of variation was benchmarked and calibrated can be found in Supplementary materials.

In terms of connectivity changes, the growth phase in human brain development was not directly simulated. Rather, differences in the outcome of the growth process were specified in terms of the number of units and the sparseness of connectivity. Regressive processes were simulated first by a continuous weight decay parameter, and second by a pruning process that probabilistically removed unused (small) connection weights beyond a certain stage of development. Importantly, loss of connectivity reduces plasticity in backpropagation networks (Thomas and Johnson, 2006); and the timing of onset of pruning was a parameter that varied between individual networks. In principle, then, there was scope within the model for differences in the timing of reduction of plasticity to be related to behavioral outcomes, in line with the Brant et al. 2013 hypothesis.

For the purposes of this simulation, the settings of the parameters were taken to be under genetic control, and were specified in an artificial genome comprising binary genes (see Supplementary materials, for the polygenic coding scheme). Genomes could be created that shared 50% of their values on average, thereby simulating sets of siblings or DZ twins. Identical genomes simulated MZ twins. Populations of 1000 individual networks were created, made up of 250 MZ network pairs and 250 DZ network pairs. Two sets of 1000 genomes were created. Based on the benchmarked impact of varying each parameter, one set of genomes included wide variation in the computational properties of the networks, while the other set had a narrower range of variation. In the former, networks could be computationally very good or very poor, while in the latter, networks varied around medium.

2.3. How environmental variation was implemented

Within the model, environmental influences on development could in principle target either neurocomputational properties or the level of cognitive stimulation. Here we implemented only the latter, in line with a recent model of SES effects on language development (Thomas et al., 2013, for discussion of this method of implementing environmental influence). The training problem was specified by the full set of input-output mappings. Variations in the quality of the environment to which each simulated child was exposed were implemented by a one-time filter applied to the training set. Networks in higher quality environments were exposed to a higher proportion of the full training set, those in lower quality environments to a lower proportion. Quality was determined by a single value between 0 and 1. Again, two ranges of environmental variation were permitted: wide, where values were randomly sampled for a twin pair in the range from 0 to 1, and narrow, where values were randomly sampled in the range from 0.6 to 1. Both members of a twin pair received the same ‘family’ environment, and the quality of the environment was sampled independently of properties of the genotype (i.e., there were no gene-environment correlations).

This approach to implementing environmental influence was sufficient to simulate, for example, the asymmetric relationship between SES and delay versus between SES and giftedness (Thomas et al., 2013). More relevant to current aims, it is sufficient to simulate the way that SES modulates the heritability of individual differences in behavior: the heritability of cognitive ability is reduced in individuals from low SES backgrounds (Turkheimer et al., 2003; though see Hanscombe et al., 2012). It is also sufficient to show small non-linear influences of SES on network structure, with the steepest gradient present at the lower end of SES variable (Noble et al., 2015; Thomas & Coecke, in prep.). These effects are shown in Fig. S1 in Supplementary materials.

2.4. The relative importance of genetic and environmental variation for generating individual differences

One difficulty in using formal models to simulate genetic and environmental contributions to individual differences is the lack of a priori information constraining the relative range of variation of these two factors. A given population distribution of behavior could be caused by wide variation in environmental influences among individuals who are genetically fairly similar, or similar environmental influences among individuals who genetically differ quite widely. The relative range materially affects measures like heritability, irrespective of the flexibility of developmental mechanisms to respond to environmental variation (e.g., in terms of notions like brain plasticity).2 While estimates of heritability can be readily simulated in models that allow the relative ranges of genetic and environmental influences to be free parameters, this is achieved at the expense of explanatory power.

Given the aim of investigating qualitative effects, the current model instead used two levels of genetic variation (wide and narrow), implemented by the range of variation of neurocomputational parameters; and two levels of environmental variation (wide and narrow), implemented by the range of variation of the environmental quality parameter. The four populations generated by this 2 × 2 combination permitted exploration of the consequences of different relative ranges for simulating the target empirical phenomenon. Among the four, the condition with narrow environmental variation and wide genetic variation produced the highest heritability (i.e., proportion of behavioral individual differences explained by genetic similarity), since genetic/neurocomputational factors were more likely than environmental/training set factors to limit performance. For the domain from which the base model was drawn (English past tense acquisition), this high heritability condition was the closest fit to human data (Thomas et al., 2013). The reported high heritability of human general cognitive ability (Haworth et al., 2010, Plomin and Spinath, 2004) also generated the expectation that this condition would be the most appropriate for simulating individual differences in cognitive ability.

2.5. How behavior was measured

The continuous output activation of each network was thresholded to provide a discrete response, which was rated as correct or incorrect. The base domain, that of English past tense, is characterized by a predominant regularity and a set of exceptions. Regular verbs are learned more robustly, while exception verbs are harder for the networks to learn. Behavior was measured by accuracy on regular verbs, making up 80% of the training set. However, performance on exception verbs was a more discriminating measure and more normally distributed, and so fed into to the measurement of ability levels.

2.6. How ability was measured

The simplest way to measure ability is to take a behavior that is highly discriminating between individuals and assign each individual a score. Performance on exception verbs early in development (50 epochs, where an epoch corresponded to presentation of all the patterns in an individual’s training set) was used for this purpose in the current simulations. However, historically, intelligence tests underwent a long process of design changes in the 20th century aimed at producing measures of cognitive ability that could accurately estimate intelligence devoid of sociocultural and environmental influences (e.g., Cattell, 1949). To capture this filtering-out of environmental influence, a statistical regression model was constructed for each population that predicted performance on exception verbs based on each network’s neurocomputational parameter values and environmental quality. The subsequent linear equation was used to generate a value for each individual but excluding the environmental component (Table 1 includes the regression coefficients per neurocomputational parameter). Results are reported for the use of this ‘culture fair’ method of measuring ability. In Supplementary materials, parallel results are provided when ability was determined by untransformed exception verb performance, for comparison. Note, the method used to reduce environmental influence from the ability measure did not remove all environmental influence, only its main effect. Interactions of the quality of the training set with neurocomputational parameters (i.e., ‘gene x environment interactions’) remained. Such interactions are observed in these simulated populations and account for some of the unexplained variability in the linear regressions (Thomas et al., 2016).

Table 1.

Linear regression analyses predicting behavior from neurocomputational parameters of the artificial neural networks and environmental quality, for the four populations. Scores show standardized beta coefficient and significance level for each parameter. GWEN = wide genetic variation, narrow environmental variation. GWEW = wide genetic variation, wide environmental variation. GNEN = narrow genetic variation, narrow environmental variation. GNEW = narrow genetic variation, wide environmental variation. (Note: type of learning algorithm did not vary in the genetic narrow conditions.).

	Population
Parameter	GWEN*		GWEW**		GNEN***		GNEW****
	Beta	Sig.	Beta	Sig.	Beta	Sig.	Beta	Sig.
Hidden unit number	0.176	<0.001	0.075	0.001	0.260	<0.001	0.196	<0.001
Temperature	0.275	<0.001	0.225	<0.001	0.371	<0.001	0.288	<0.001
Noise	−0.176	<0.001	−0.154	<0.001	−0.148	<0.001	−0.130	<0.001
Learning rate	0.324	<0.001	0.271	<0.001	0.373	<0.001	0.305	<0.001
Momentum	0.177	<0.001	0.151	<0.001	0.100	<0.001	0.108	<0.001
Weight variance	−0.056	0.016	−0.033	0.148	−0.042	0.064	−0.038	0.088
Architecture	0.187	<0.001	0.153	<0.001	−0.111	<0.001	−0.059	0.008
Learning Algorithma	0.272	<0.001	0.202	<0.001	–	–	–	–
Response threshold	0.229	<0.001	0.203	<0.001	0.166	<0.001	0.160	<0.001
Pruning onset	0.040	0.087	0.014	0.549	−0.014	0.534	−0.003	0.887
Pruning probability	−0.037	0.111	−0.009	0.683	−0.039	0.082	−0.029	0.189
Pruning threshold	−0.058	0.013	−0.053	0.019	−0.014	0.528	0.032	0.150
Weight decay	−0.010	0.674	−0.017	0.466	−0.066	0.003	−0.077	0.001
Sparseness	−0.091	<0.001	−0.075	0.001	−0.215	<0.001	−0.170	<0.001
Environment quality	0.115	<0.001	0.464	<0.001	0.163	<0.001	0.473	<0.001

^*R² = 0.486, F(15,984) = 61.90, p < 0.001.

^**R² = 0.507, F(15,984) = 67.40, p < 0.001.

^***R² = 0.509, F(15,984) = 72.96, p < 0.001.

^****R² = 0.516, F(15,984) = 75.02, p < 0.001.

^aLearning algorithm did not vary in the genetic-narrow variation conditions.

2.7. How heritability was measured

Estimates of heritability are derived from twin correlations either by the use of linear equations (e.g., Falconer and MacKay, 1996) or by model fitting. Assumptions are typically made in these analyses, such as whether genetic effects are additive or dominant (e.g., if the MZ correlation is less than twice the DZ correlation, an additive model is used; if the MZ correlation is less than four times the DZ correlation, a dominant model is used). Such assumptions have been argued to bias estimates of heritability (Polderman et al., 2015). Here, we simply report the difference between MZ and DZ correlations, which provides a measure proportional to heritability. The greater the disparity between the two correlations, the higher the heritability. This has the advantage of allowing direct comparison across populations with very different heritability levels.

Model fitting provides one method to estimate confidence intervals, that is, the robustness of the estimates of heritability. Here, another method was used, which took advantage of the fact that data were derived from developmental models. Twin correlations were computed at each incremental step of development, where development took place over 1000 steps. Since heritability should be relatively stable over nearby steps, variability across a moving window of 10 steps before and 10 steps after a given time step was used to assess the robustness of the measure at any given time point.

2.8. How network structure was measured

Two metrics served as indices of network structure: total number of network connections and total connectivity magnitude (where magnitude is defined as the absolute size of the connection irrespective of whether it is positive/excitatory or negative/inhibitory). After the onset of pruning, number of connections in the model showed an exponential decline, similar to that exhibited by gray matter. Total connection strength showed a linear increase, similar to that exhibited by white matter (see Fig. S2). In the model, the number of connections offered plasticity, such that the network’s ability to change reduced as pruning took place. This is in line with the notion of sensitive periods observed in the cognitive system and the proposal that they may be linked to synaptic density (Huttenlocher, 2002, Thomas and Johnson, 2006). Increasing connection magnitude reflected experience-dependent strengthening. This is consistent with the idea that white matter changes are associated with skill acquisition (Bengtsson et al., 2005, Scholz et al., 2009).

2.9. Simulation design

Four populations of 1000 networks were trained on the target domain, for 1000 epochs (presentations of the training set). The populations represented a 2 × 2 design of range of genetic variation in learning ability (narrow vs. wide) and range of variation in environmental influences on the training set (narrow vs. wide). At each epoch, the behavior and structural properties of each network were measured, and using the twin design, heritability was estimated.

3. Results

Fig. 1a shows the general cognitive ability heritability estimates for children, adolescents, and adults, re-plotted from Brant et al. (2013). Given the reported high heritability of cognitive ability, we focused on the simulated population where heritability was highest, that is, the population where genetic variation was wide and environmental variation was narrow. Fig. 1b plots the heritability proxy, the difference between MZ and DZ correlations, for high ability and low ability groups, which were split at the mean ability score of the population based on the average ability of each pair. Measures were taken at an early (100 epochs), mid (500 epochs), and late (990) point in training. The robustness of the measure was assessed by considering values for the 10 previous and 10 following epochs in training, and these were used to compute statistical reliability. As with the empirical data, there was an overall increase in heritability with age (main effect of developmental stage: F(1,40) = 304.35, p < 0.001, η_p² = 0.884). Heritability increased due to a reduction in the correlation between DZ twins (see later Fig. 5). In other words, as with the empirical data, heritability increased due to a reduction in the influence of shared environment on behavior. The pattern of change in heritability was different between ability groups (F(1,40) = 25.08, p < 0.001, η_p² = 0.385). As with the empirical data, for the high ability group, there was no significant difference in heritability between early and mid points (t(20) = 0.38, p = 0.707) but a significant rise between mid and late points (t(20) = 4.79, p < 0.001). As with the empirical data, for the low ability group, heritability showed a significant increase between early and mid points (t(20) = 31.02, p < 0.001) but no change between mid and late points (t(20) = 1.47, p = 0.157). In contrast to the empirical data, there were reliable differences both at the early measurement point (high ability > low ability, t(40) = 2.78, p = 0.008) and the late measurement point (low ability > high ability, t(40) = 5.41, p < 0.001).

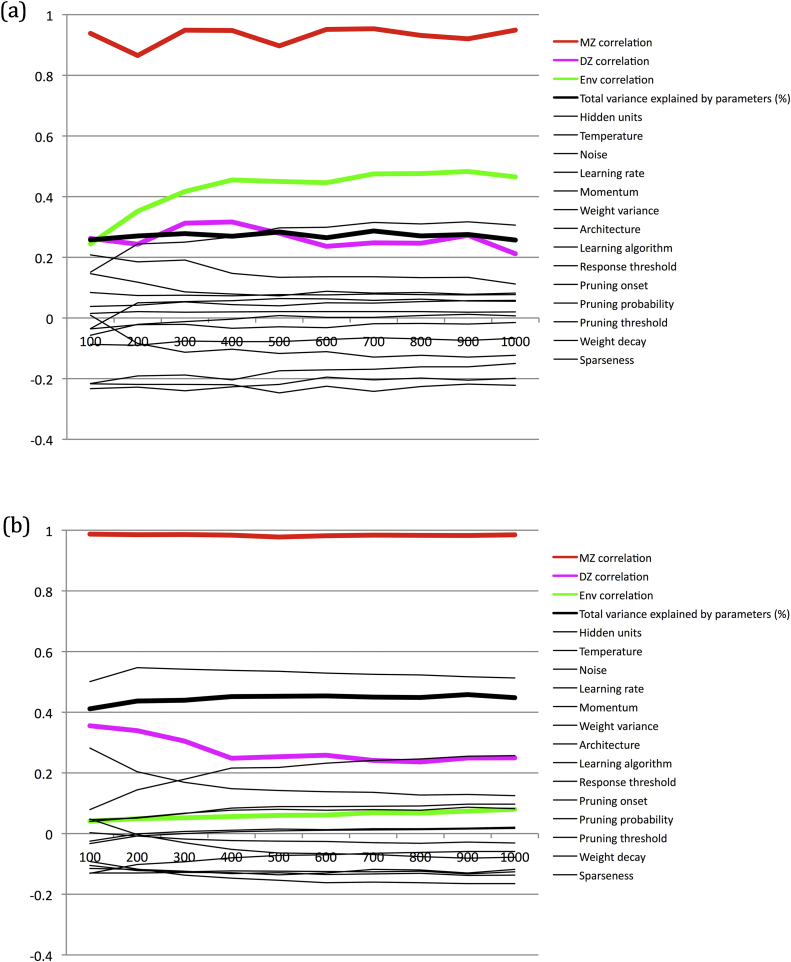
Fig. 5.

Correlations between all neurocomputational parameters and individual performance on regular verbs across development, for different ability groups. The figure also plots MZ twin and DZ twin correlations (split by average twin ability); the correlation between environmental quality and performance; and the total variance explained by all neurocomputational parameters computed via summed independent linear fits. The y-axis shows Pearson correlation size (or% variance for the total variance measure); the x-axis shows epoch of training in the population. (a) High ability individuals; (b) low ability individuals.

Within the simulation framework, it was possible that higher ability could have been generated by an extended sensitive period, consistent with Brant et al.’s (2013) hypothesis. That hypothesis would be supported if it should turn out that connection pruning (which reduced plasticity) had a later onset for the high ability group than the low. While the high ability group did indeed have a later onset (mean epoch 103.6 versus 98.7 for the low ability group), this effect was not reliable (t(998) = 1.15, p = 0.251); nor did pruning onset predict ability as a continuous variable (Pearson correlation = 0.043, p = 0.172). While the qualitative pattern of Brant et al.’s (Brant et al. 2013) heritability data was captured, the main mechanistic difference between high and low ability groups in the simulations was not, therefore, an extended sensitive period in plasticity. Moreover, as with real children, in the simulation, differences in the performance of high ability and low ability networks were observable from early in development (Fig. S4).

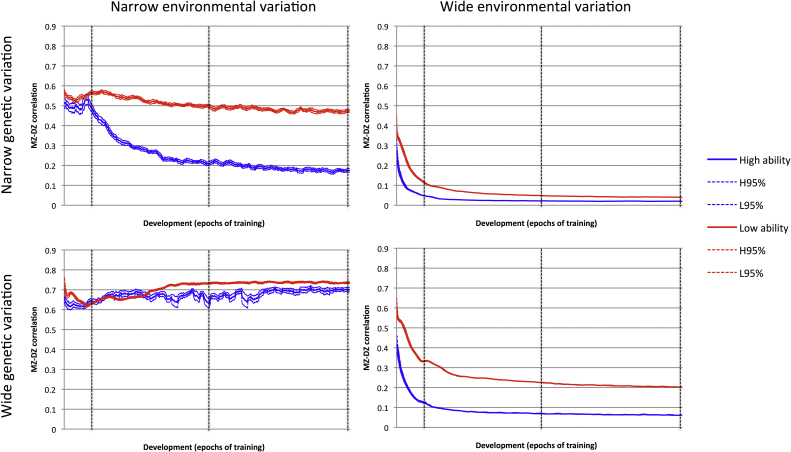
The above simulation data were drawn from the population where the heritability of behavior was the highest. Fig. 2 displays equivalent data from the other conditions, with differing ranges of genetic and environmental variation. Fig. 2 plots the heritability proxy for ability groups across the full period of development, indicating the points of measurement used in Fig. 1b. Comparison indicates that two patterns, the increasing heritability across development, and the overlapping heritability for the ability groups followed by divergence followed by convergence, were unique to the highest heritability condition. In the other conditions, where environmental influences were relatively more important, heritability reduced with age, and lower heritability was consistently observed for the high ability group. As described in Section 2.5, ability was assessed using a method that reduced the influence of environmental variation, in line with the contemporary use of ‘culture fair’ intelligence tests. The same data contrasts in Fig. 2 are included in Fig. S5, but calculated using untransformed performance on exception verbs at 50 epochs. The use of this different measure to define ability groups modulated the interaction of ability and heritability, mainly for conditions of wide genetic variation. For the target condition with high heritability, it served to reduce the heritability of performance in the high ability group beyond the early stage of development. This is because the conditions of the environment in which simulated individuals were raised increasingly contributed to how well they scored in ability tests, reducing the manifestation of their intrinsic ability. In other words, the model predicted that the observed empirical data of Brant et al. (2013) are dependent on using ability tests that are relatively insensitive to environmental influence.

Fig. 2.

Developmental change in the difference between MZ and DZ correlations of performance for high ability and low ability groups, for four simulated populations, those produced by a cross of narrow or wide genetic variation, and narrow or wide environmental variation. Vertical dashed lines demonstrate the points in development represented in Fig. 1(b). Trajectories include 95% confidence intervals.

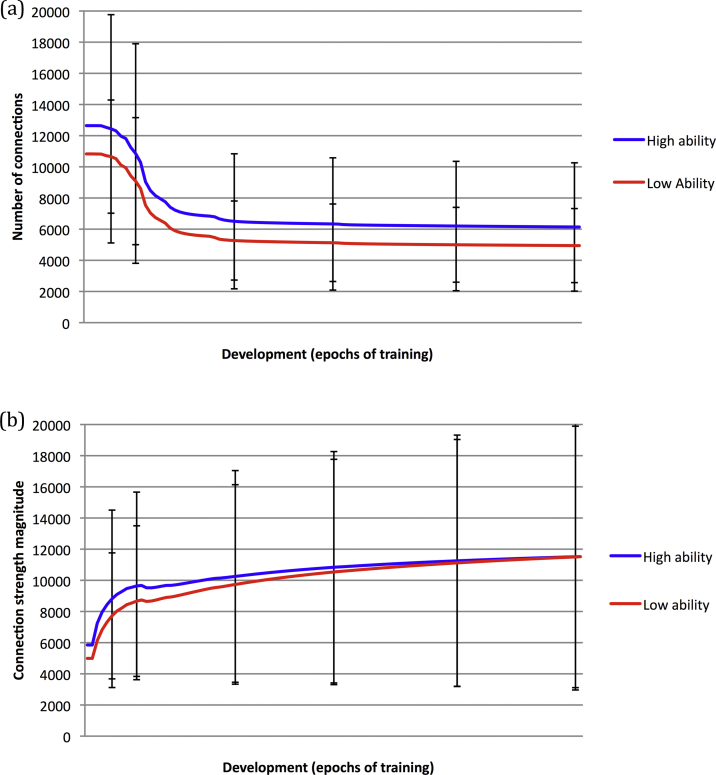
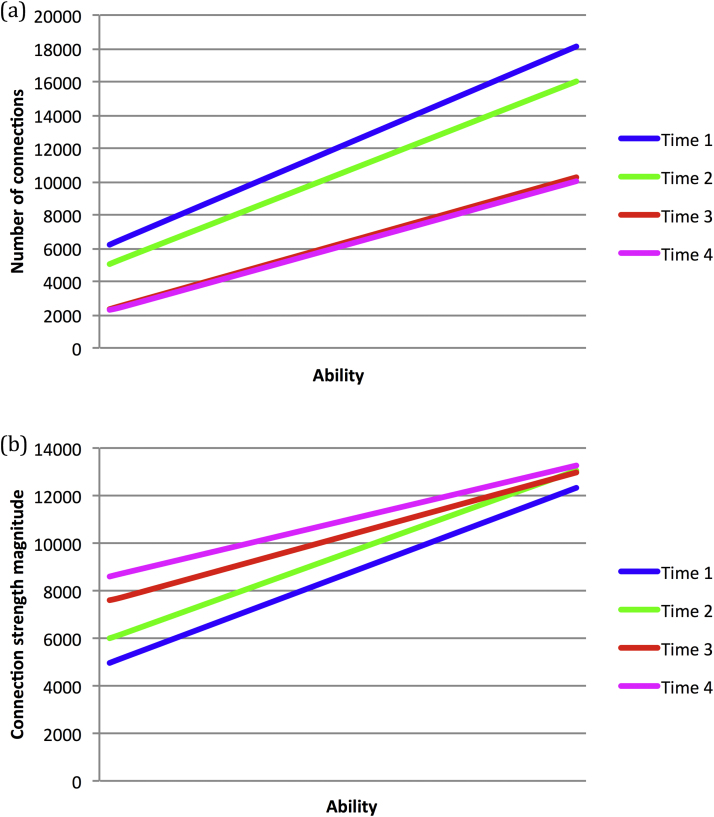
Fig. 3 shows the change in the structural indices of total number of connections (Fig. 3a) and total connection magnitude (Fig. 3b) across development. The total number of connections shows a profile of exponential decline with the onset of pruning. Notably, high ability networks started from a higher peak (i.e., more able networks tended to be larger); and the trajectories converged as the larger networks experienced more pruning. However, as indicated by the standard deviation error bars, there was large overlap between the ability groups. This is because the parameters affecting the macro measure of network size (architecture, number of hidden units, sparseness) explained only some of the variance in behavior, as shown in Table 1 (correlations between these metrics, performance, and timing of pruning onset can be found in Table S1). Behavioral variance was influenced by a larger set of low-level mechanisms. The trajectories were compared at discrete time points (50, 100, 300, 500 epochs). At a group level, where groups were defined by a split at the population mean ability level, comparison of early time points (50 vs. 100, 100 vs. 300, 50 vs. 300) yielded no statistically reliable interaction of group with rate of connection loss (p > 0.7). However, the empirical data of Shaw et al. (2006) showed similar large overlap between ability groups in the rate of change of cortical thickness, and only comparison of a superior intelligence group (IQ 121–149) to high (IQ 109–120) or average (IQ 83–108) ability groups yielded reliable differences in rates of change. High and average groups did not reliably differ. However, for the simulations, when ability was included as a covariate, rather than used to define discrete groups, it was found to reliably modulate total connectivity, shown in Fig. 4a. Moreover, the extent to which ability modulated total connectivity reliably reduced across development (in Fig. 4a, the lines become less steep for later time points). This reflects the narrowing of the gap between the trajectories defined at the group level. In other words, there was faster loss of connectivity in more able networks, which nevertheless started from a higher peak.

Fig. 3.

(a) Simulation data showing the developmental change in the total number of connections in individual networks, for population groups mean-split into high ability and low ability. (b) Developmental change in the total connection magnitude (combining excitatory and inhibitory connections) for high ability and low ability groups. Error bars represent standard deviations.

Fig. 4.

Modulation of structural indices by ability at four different points in development, derived from regression analyses (Time 1 = 50 epochs, Time 2 = 100 epochs, Time 3 = 300 epochs, Time 4 = 500 epochs). (a) Total number of connections; main effect of ability on connectivity number: F(1,998) = 86.60, p < 0.001, η_p² = 0.080; interaction of ability with time point: F(1,998) = 18.14, p < 0.001, η_p² = 0.018). (b) Total connection magnitude; main effect of ability on connection magnitude: F(1,998) = 17.67, p<0.001, η_p² = 0.017; interaction of ability with time point: F(1,998) = 7.49, p = 0.006, η_p² = 0.007). Earlier points in development show greater modulation according to ability.

The structural index of total connection magnitude demonstrated a different profile, with a gradual increase across development (Fig. 3b). Nevertheless, a similar pattern was observed for the effect of ability: the high ability group started from a higher baseline than the low ability group; there was convergence of the trajectories for the ability groups across development; but large overlap at a group level producing non-reliable differences in rates of change; when ability was used as a covariate, it explained reducing amounts of variance across development, reflecting the convergence of trajectories observed at a group level (Fig. 4b). In contrast to connection loss, the pattern here was of the low ability group catching up the high ability group later in development. To the extent that the learning of low ability networks was compromised by having too few connection weights, ceiling performance was achieved by strengthening these weights proportionally more, particularly later in development. Low ability networks consequently had larger average connection strengths, a disparity which increased across development (main effect of ability group: F(1,998) = 29.91, p < 0.001, η_p² = 0.029; interaction of ability x development: Ability x Development, F(1,998) = 28.83, p < 0.001, η_p² = 0.028; shown in Fig. S3). When performance was close to ceiling levels, the non-linear nature of the simple processing units in these networks meant that ever larger increases in connection strength were required to achieve the same sized improvement in behavior. Hence, connection magnitudes continued to increase while behavior had more or less plateaued.

Heritability of structural indices across development for the four populations are included in Fig. S6, while Fig. S7 shows these data split by ability for the high heritability population.

4. Discussion

Researchers have found it challenging to integrate several emerging findings from the developmental cognitive neuroscience of individual differences. These include the correlation of macro structural properties of the brain (size, rate of thickening and thinning with age) with general cognitive ability; the increasing heritability of general cognitive ability with age; and the differential timing of the increase in heritability of general cognitive ability between ability groups. No mechanistic account currently reconciles these data.

Using a combination of ANNs and population modeling of cognitive development, it was possible to qualitatively simulate each of these patterns within a single mechanistic framework. The simulations demonstrated that as a cognitive domain was acquired by the population of ANNs, the heritability of individual differences increased across development. The heritability increased earlier for low ability networks than high ability networks. Behavioral improvements were associated with structural changes in the ANNs, assessed by the indices of total connection number and total connection magnitude. These structural changes occurred at differential rates depending on ability. This pattern was observed in a population with high heritability of behavior, in line with the high heritability of general cognitive ability, and when ability was assessed using a method that downplayed in the influence of the environment, in line with culture fair measures of intelligence.

Brant et al. (2013) proposed that the observation of a later rise in the heritability of general cognitive ability in higher ability individuals supported the hypothesis that cognitive ability might correspond to an extended sensitive period in brain development (Shaw et al., 2006). However, they also noted that this hypothesis is inconsistent with the observation that differences in general cognitive ability are already observable early in development, and the hypothesis does not fit well with a leading account of the origin of the developmental increase in heritability, an emergent gene-environment correlation, since there is no obvious reason why this correlation should emerge later in individuals of higher ability. The model, by contrast, demonstrated that heritability can increase across development without the need to postulate an emerging gene-environment correlation; that heritability can rise earlier for low ability individuals even when differences in the timing of sensitive periods explain little of the variation in ability; and under these circumstances, differences in ability are readily observable from early in development.

Why was the model able to capture these qualitative effects? That is, what was the mechanistic account of the empirical data? In the model, there is experimental control over the constraints that shape development. We can therefore plot predictive power of these constraints across development, split by ability groups. Fig. 5 plots observed correlations between neurocomputational parameter values and behavior, and between environmental quality and behavior. In addition, it plots MZ and DZ behavioral correlations. Lastly, it plots the total percentage variance explained by all the neurocomputational parameters together, summing the linear fits. It is apparent that the earlier increase in heritability in the low ability group is driven by an earlier decrease in the DZ twin correlation compared to the high ability group. While some individual neurocomputational parameters (which are more likely to have different values between DZ twins) increase their predictive power over development, the total predictive power of all genetic/neurocomputational properties is approximately constant. It does not therefore explain the divergence of DZ performance.

The divergence of DZ performance occurs because of two factors, both concerning the characteristics of non-linear learning systems. First, the relationship of neurocomputational parameters to behavior is typically non-linear. Second, neurocomputational parameters show higher order interactions (i.e., non-additive effects) in their influence on behavior. Both of these factors have been proposed as explanations of ‘missing heritability’, that is, the reason why the summed linear predictive power of measured genetic similarity in genome-wide association studies tends to fall short of the level of heritability estimated from twin study designs (Thomas et al., 2016). Together these factors cause genetic differences between DZ twins to be exaggerated in their neurocomputational influence on behavior. Non-linear neurocomputational influences become greater as the systems approach ceiling performance. Low ability networks have lower dimensional internal representational spaces and as a consequence tend to adopt non-linear processing states sooner during training.

The pattern depended, to some extent, on ability being assessed by measures that were more sensitive to neurocomputational limiting factors and less sensitive to environmental influences. If the assessment of ability was more sensitive to environmental experiences, this altered the way that limiting factors manifested in individual differences, specifically adding a greater environmental limiting factor to the performance of high ability networks.

Researchers have highlighted the notable finding that ability is related to the rates of change of structural properties of the brain, such as cortical thickness and surface area (Shaw et al., 2006). The model demonstrated similar ability-related modulation of rates of change of structural properties of the ANNs, derived from measures of their connectivity (total number and total magnitude). We know in the model that differences in ability were generated by small differences over a large set of general neurocomputational properties, some of which directly influenced measures of connectivity (architecture, hidden unit numbers, sparseness), some of which influenced connectivity only indirectly via experience-dependent change. Ability modulated reductions in connection numbers because larger networks tended to be more computationally powerful but also lost connections more quickly during pruning (in the sense that higher mountains tend to have steeper sides). Ability modulated increases in connection strength because late in development, low ability networks had to buttress their smaller networks more to extract the best performance gains they could manage. In short, the model provides a way to conceptualize how structural differences between networks, and between their dynamic rates of change, may be related to differences in the quality of behavior via low-level neurocomputational properties.

Aside from reconciling these key data, the model also exhibited some other attractive properties that support its validity at a qualitative level. General cognitive ability is captured as the outcome of many small differences in general neurocomputational properties; these properties are mainly under genetic control, but the mapping of genes to these properties and these properties to behavior is many to one (Plomin et al., 2013, Plomin and Kovas, 2005). The genetic influence on behavior via the neurocomputational properties remains relatively consistent across development, even while heritability is increasing (Thomas et al., 2016, Trzaskowski et al., 2014). Since some but not all neurocomputational parameters influence structural indices of the networks, while all contribute to the ability of the networks, the genes determining ability and structure are partially overlapping (Brans et al., 2010; see Thomas et al., 2016, Figs. 9 and 10). Structural indices correlate highly with each other, behavioral measures correlate highly with each other, but the correlation between the two is weaker (Posthuma et al., 2003, Thomas et al., 2016). If differences in the richness of the training set implement one causal pathway of SES effects on development (Thomas et al., 2013), the model demonstrates relatively small effects of SES on structural indices (Table S1), in line with recent data (Lawson et al., 2013, Noble et al., 2015). When SES serves as a limiting factor on development, low SES can reduce the heritability of behavior and has detectable impact on network structure (Fig. S1; Noble et al., 2015, Turkheimer et al., 2003; Thomas & Coecke, in prep.).

The model generated several predictions. The pattern of increasing heritability over development was a characteristic of populations exhibiting high heritability, where genetic variation was a stronger limiting factor than environmental variation. When the environment was the limiting factor, heritability reduced across development. The modulation of heritability patterns by ability also depended on the way that ability was measured. When ability measures were more influenced by the environmental conditions in which the individual was raised (i.e., the use of less culture-fair tests), observed heritability reduced. This was more apparent in high ability groups.

The model is rich enough to be applied to the development of behavior, individual differences in behavior, changes in structural properties of processing systems, and data on heritability, but of course, it is highly simplified. The current model had the following limitations. First, the objective was a qualitative fit to the data. For example, the heritability of ability in the genetic-wide environment-narrow population was quantitatively higher than that usually observed for general cognitive ability (though appropriate for base domain from which the model was drawn). It remains to be seen whether the findings replicate when heritability values are quantitatively calibrated to the empirical data, by adjusting ranges of variation. Second, in many respects, the neural plausibility of the ANN is rudimentary, particularly in the mapping of structural measures to brain data. For example, the growth phase of the neural networks was not simulated, just the outcome of this process. To account for the growth phases of the Shaw et al. (2006) data, one would need to assume that larger networks are the outcome of faster and more prolonged growth and therefore rates of cortical thickening. The structural measures of the ANNs at the current level of simplification can at best offer candidate mechanisms that may contribute to observed changes in actual brains. Third, the model only simulated a single system. This means it cannot speak to the empirical data indicating region-specific brain changes and differences in timing of thinning/thickening effects (e.g., Shaw et al., 2008). Moreover, general cognitive ability is often viewed as a property of multiple systems working together, or at least, the shared variability of the performance of multiple systems, and this is beyond the scope of a single-system model. Fourth, an implemented model only demonstrates the viability of theoretical proposals, not their truth. For example, even though the model demonstrated that an increase in heritability over age can be produced without an emerging gene-environment correlation, such a correlation may nevertheless be part or all of the explanation of why it occurs for human general cognitive ability (though, per Brant and colleagues’ argument, one would then need to find a plausible explanation of why the correlation emerges later in higher ability individuals). Finally, it is worth pointing out that although the empirical observations made by Brant et al. (2013) stem from a large study, they still require replication in other samples and populations to be viewed as completely robust, and to shed light on the sampling and measurement factors that influence the timing of observed increases in heritability.

5. Conclusion

The model presented here is the first mechanistic account to reconcile diverse data on general cognitive ability from twin studies and studies of developmental changes in brain structure. Indeed, it is the first demonstration that it is even possible to reconcile them within a common mechanistic framework. The model also generated novel predictions of what should obtain in populations with different relative influences of genetic and environmental variation on individual differences, or when using intelligence measures of different types. It offered several insights—the importance of limiting factors on heritability measures, the role of non-linear systems in increasing heritability, the relation of dynamic changes in brain structure to underlying processing. It is in many respects, a highly simplified model. Nevertheless, it represents a response to the important challenge of capturing individual differences and development within a common mechanistic framework, and reconciling data from separate levels of description, a key concern of modern developmental cognitive neuroscience.

Appendix A. Supplementary data

The following are Supplementary data to this article: