The Challenges of Parameterizing Direct Effects in Individual-Level Simulation Models

Abstract

Individual-level simulation models are used to assess the effects of health interventions in complex settings. However, estimating valid causal effects using these models requires correct parametrization of the relationships between time-varying treatments, outcomes, and other variables in the causal structure. To parameterize these relationships, individual-level simulation models typically need estimates of the direct effects of treatment. However, direct effects of treatment are often not well- defined and therefore cannot be validly estimated from any data. In this paper, we explain the causal meaning of the parameters of individual-level simulation models as direct effects, describe why direct effects may be difficult to define unambiguously in some settings, and conclude with some suggestions for the design of individual-level simulation models in those settings.

Mathematical models are used to quantify the impact of health interventions when the available randomized and observational studies do not have sufficiently long time horizons or fail to include quality of life outcomes or costs (1). Investigators build mathematical models that represent the causal structure of a system, and then simulate what would happen to hypothetical individuals under changes to that system (1). These models are known as individual-level simulation models, microsimulations, cohort models, or agent-based models. While definitions vary between fields, the term “agent-based model” often describes simulation models allowing interactions between simulated individuals (agents). For our discussion below, we use the most encompassing term: individual-level simulation models (2).

The construction of an individual-level simulation model usually involves specification of parameters whose values are obtained from published estimates. However, it is often unclear how to use published estimates to inform model construction and interpret the results. Here we provide suggestions for the use of simulation models in those situations.

Building an individual-level simulation model via specification of direct effects

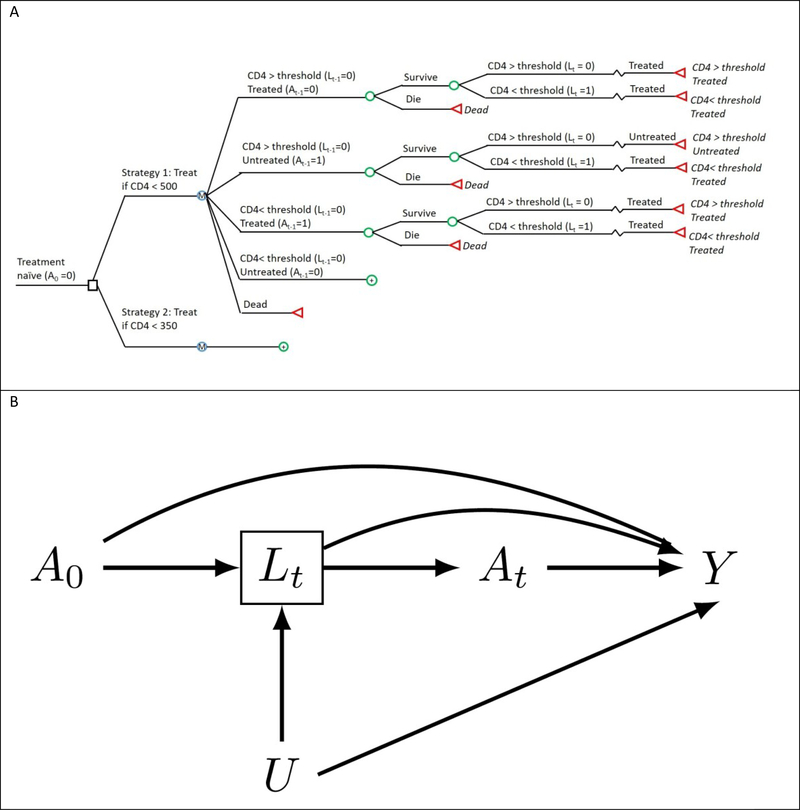
Suppose we build a simulation model to quantify the impact of various antiretroviral therapy interventions on the 5-year mortality risk of HIV-positive people, such as ‘initiate anti-retroviral therapy at a CD4 cell count below 500 cells/μL’ or ‘initiate anti-retroviral therapy at a CD4 cell count below 350 cells/μL’. The causal structure encoded by the simulation model is depicted by the decision model depicted in Figure 1a, and by the causal directed acyclic graph (DAG) in Figure 1b. Treatment at time t is represented by At and mortality at 5 years by Y. For simplicity, we assume no one is lost to follow-up and no one dies during the first 5 years. The node Lt represents CD4 cell count at time t, and is a marker of progression which clinicians have historically used to decide when to initiate treatment. CD4 cell count is thus both affected by prior treatment and affects subsequent treatment, even in a randomized trial. The node U represents a vector of risk factors for both Lk and Y that typically remains unmeasured in research studies and therefore unavailable to modelers.

Figure 1.

The structure of the simulated example as (A) a decision model and (B) directed acyclic graph (DAG). (A) The decision model depicts the decision process at a single time-step, with the circular decision nodes indicating probabilistic events and the colored square decision node indicating an intervention point. (B) The directed acyclic graph depicts two arbitrary time points of the same causal structure for a time- varying treatment, A0 and At, an outcome, Y, a time-varying confounder, Lt, affected by prior treatment (A0), and an unmeasured outcome cause, U.

Each arrow represents a possible direct effect of one variable on another while intervening to set the other variables at a fixed value for all individuals. Specifically, the direct arrow from A0 to Y represents the direct effect of treatment A0 on the outcome Y that operates through pathways other than Lt. Therefore, to build the model we would need to specify parameters for each arrow, and to find valid estimates of the corresponding direct effects (1).

Estimating individual-level simulation model parameters via randomized experiments

Ideally, we would estimate each direct effect via a randomized experiment. For example, the direct effect of treatment A0 on CD4 cell count Lt, represented by the arrow from A0 to Lt in Figure 1b, can be validly estimated by randomly assigning individuals to either treatment or no treatment at time t-1 and comparing the distribution of CD4 cell count at time t between trial arms. (For simplicity, we assume the treatment effect does not vary substantially across populations.)

However, this approach is not applicable to estimating the other direct effects in Figure 1b. Consider the direct effect of treatment A0 on death Y. To validly estimate this effect in an experiment, we would need to randomly assign individuals to either treatment or no treatment at time k-1 and intervene to keep the value of the mediator, CD4 cell count, constant. This experiment is not feasible because no technologies exist to fix the value of a person’s CD4 cell count and, if they existed, the magnitude of the direct effect might vary depending on which technology was used. For example, imagine CD4 cell count can be intervened upon via either a yet-to-be discovered pharmacological treatment (other than A0) or genetic modification. Each of these interventions may have additional effects that could affect the magnitude of the effect of treatment A0 on death Y.

After choosing a particular technology, we also need to decide which values of CD4 cell count to choose. Therefore, the direct effect of treatment A0 on death Y is not uniquely defined because its numerical value could vary across randomized experiments using different technologies to fix CD4 count at each of its >1000 possible values. We say the intervention to estimate the direct effect of treatment on mortality is not sufficiently well-defined (3). The lack of a well-defined direct effect is problematic because use of an individual-level simulation model implies each parameter has an unambiguous interpretation.

Estimating individual-level simulation model parameters via observational studies

When randomized trials are unavailable, or would not be ethical for a given research question, or when an ongoing trial has not yet reported results, we can instead attempt to estimate parameters for our individual-level simulation model from observational data.

The observational effect estimate is unbiased if it is the same estimate that would have been obtained from a (possibly hypothetical) experiment. However, in the absence of a well-defined intervention, it is unclear which hypothetical experiment we are emulating and therefore the validity of the observational estimate cannot be determined.

For example, suppose we used observational data to estimate the direct effect of treatment A0 on death Y when CD4 cell count is held constant. The numerical value of the direct effect will likely vary depending on the value of CD4 chosen and the (as-yet-to-be-discovered) technology by which CD4 would have been held constant in a hypothetical experiment designed to answer this question. Since these are both unknown, it is unclear how to use the observational estimate to parametrize an individual-level simulation model.

There is an additional problem. Estimating causal effects from observational data typically requires adjustment for confounding factors but, if interventions are not well-defined, neither are confounding factors (3). For example, suppose we want to estimate the direct effect of treatment A0 on death Y when CD4 (Lt) is set to 350 cells/μl. In observational data, each individual’s CD4 count can be thought of as the result of following a specific version of the intervention “fix CD4 count to 350 cells/μl”. Each of these versions likely has its own set of confounding variables. Lack of health insurance may be a strong predictor of not receiving a pharmacological treatment, but probably not of having a genetic variant (because person’s genes are determined before their adult health insurance status). Without defining the intervention, we cannot hope to identify the confounding factors.

Interestingly, if our only goal were to estimate the total effect of treatment A on mortality, Y, rather than to estimate other outcomes such as cost-effectiveness, resource usage, or the effect of treatment A on other outcomes, then well-defined interventions on mediators L would not be required. To estimate the total treatment effect on a single outcome, we can construct a model in which the parameters are defined as associations, rather than causal effects, between the observed variables in the study population. Parameterizing such a model requires either a single dataset, or datasets with identical joint distributions of the required variables from which to obtain all parameter inputs. Importantly, a randomized trial will by design have a different distribution of treatment (and thus outcome) than any observational study. It follows that input parameters from observational studies and randomized trials cannot be combined without additional assumptions about the transportability of input parameters. In addition, because most individual-level simulation models are built in the hopes of estimating causal effects beyond the total effect, building models based only on estimated associations is generally not a feasible solution to the issues we have raised.

Using individual-level simulation models when some parameters cannot be estimated

When a direct effect is ill-defined and the parameter cannot be directly estimated, there are two main solutions: change our model so the ill-defined effect is no longer included, or choose a range of plausible parameter values and use these to gain insight into possible model outputs.

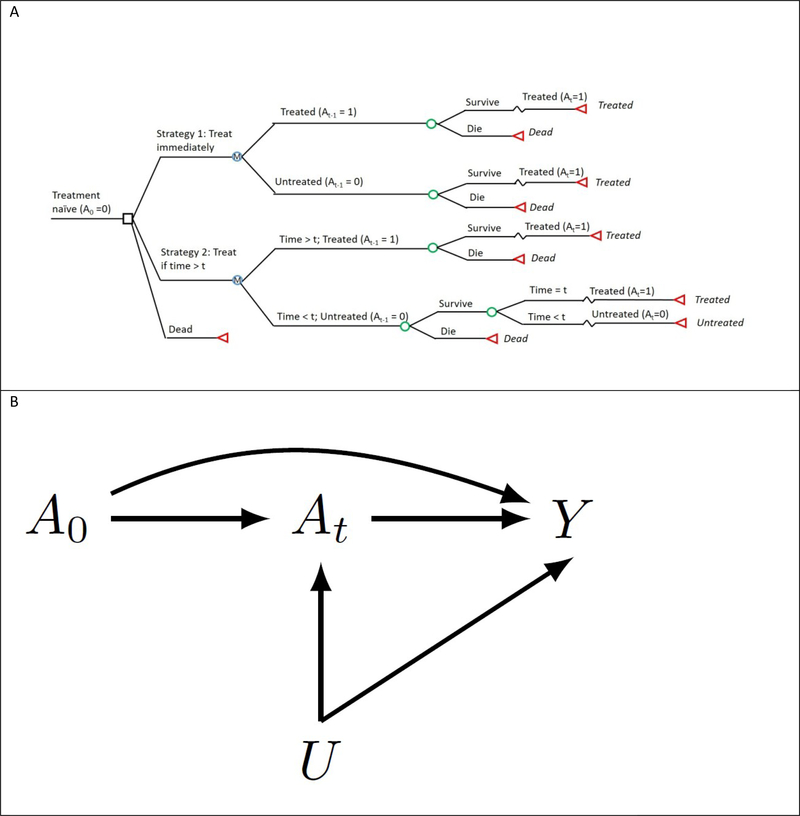
In our example, changing the model to no longer require the direct effect would also require changing our research question. For example, we can avoid modeling the direct effect if, instead of assessing the harms and benefits of delaying treatment initiation based on CD4 cell count changes, we assessed the impacts of delaying treatment initiation based on time since diagnosis (Figure 2). However, in many cases additional outcomes such as cost or quality of life will be of interest and may still require simulation of CD4 cell count.

Figure 2.

The structure of an alternate simulation model which does not require parameterizing the controlled direct effect of treatment when CD4 count is held constant, as (A) a decision model and (B) directed acyclic graph (DAG). (A) The decision model depicts a single time-step. Note that, unlike Figure 1b, the model and transition probabilities in Figure 2b do not depend on the time-varying covariate. (B) The directed acyclic graph depicts two arbitrary time points of the causal structure for a time-varying treatment, A0 and At, an outcome, Y, and an unmeasured outcome cause, U.

As an example of the second option, we simulated a dataset based on Figure 1 and created an individual-level simulation model to estimate the effect of treatment in the data, assuming U is unknown or unavailable (see Supplementary Material(1) (11, 12, 13)). Although we cannot envision a well-defined intervention to hold CD4 count constant for parameterizing the direct effect of treatment, we may believe any such effect is either beneficial or neutral, and does not depend on the value at which the CD4 count is held. Under these assumptions, we parameterized 200 versions of the simulation model. We then estimated the association between the strategies ‘immediate initiation of treatment’ and ‘no treatment ever’ on mortality over 12 months in the simulated data when the simulated true effect was either null or beneficial (Table 1). In both cases, when the direct effect assumption was reasonable, the range of estimates was too wide to provide meaningful guidance for decision-making, but did include the true value. As shown in Table 1, a stronger set of assumptions about plausible direct effect parameters narrow this interval, but excludes the true value, and an incorrect set of assumptions will give incorrect inference.

Table 1.

Direct Effect of Treatment on AIDS-Related Mortality

	Treatment Effect
Direct Effect Input Range	No Effect: True Risk Difference = 0%	Beneficial Effect: True Risk Difference =−5.0%
Direct effect assumed protective OR = 0.005 to 1.0 by 0.005	9.2% (−8.5%, 24.8%)	34.4% (−5.0%, 59.3%)
Direct effect assumed harmful OR = 1.0 to 2.0 by 0.005	36.4% (25.6%, 45.9%)	70.4% (61.5%, 77.2%)
Direct effect assumed moderately protective OR = 0.7 to 1.0 by 0.0015	20.8% (16.8%, 24.8%)	54.8% (49.5%, 59.8%)
Direct effect assumed moderate OR = 0.7 to 1.5 by 0.004	27.3% (17.6%, 36.5%)	61.9% (50.6%, 70.9%)

Results for the direct effect of treatment on AIDS-related mortality in a simulated cohort study from 200 individual-level simulation models with controlled direct treatment effect inputs in the given range.

Values in the table are the estimated treatment effect as 12-month risk difference comparing always treated to never treated: mean (2.5^th percentile, 97.5^th percentile).

Finally, when an alternate data source is available, causal effects estimated in those data can be used as calibration targets to improve the range of direct effect parameter inputs selected (4). Calibration is a common approach to selecting parameter input ranges for individual-level simulation models, but it is important to be aware that when causal effect estimates are the desired model output, calibration targets should also be causal effects. Obtaining these calibration target estimates can be complicated by all same the issues as discussed above for obtaining estimates of parameter inputs (4).

Finally, simulation models are often used to assess the impact of treatment or prevention strategies for infectious diseases or other transmissible health outcomes. These models allow interference or interaction between individuals and almost always have multiple versions of the treatment, infection, or prevention strategy of interest (5,6). This complicates the specification of a well-defined intervention for all variables that are a consequence of this interference. One solution for these models is to explicitly emulate a target randomized trial and define the intervention of interest based on that trial (7).

Conclusion

Individual-level simulation models often incorporate mechanistic pathways which represent direct effects. Obtaining interpretable estimates of those direct effects from observational data requires that we specify a hypothetical experiment with well-defined interventions (8). Lack of well-defined interventions is often an unrecognized source of uncertainty in simulation models, and one for which sensitivity analyses are not typically conducted (9)(10). This uncertainty can lead to substantial bias, both because direct effects cannot be characterized in a sufficiently unambiguous way, and because the confounding structure is inadequately identified. When direct effects cannot be parameterized, one may report a range of estimates under different assumptions regarding the distribution of direct effects. The alternative is to construct simulation models that can only answer a limited set of questions about the total effect of health interventions.