Self-assembly of highly sensitive 3D magnetic field vector angular encoders

3D self-assembly advances parallel wafer-scale manufacturing of vector field devices such as 3D magnetic field angular encoders.

Abstract

Novel robotic, bioelectronic, and diagnostic systems require a variety of compact and high-performance sensors. Among them, compact three-dimensional (3D) vector angular encoders are required to determine spatial position and orientation in a 3D environment. However, fabrication of 3D vector sensors is a challenging task associated with time-consuming and expensive, sequential processing needed for the orientation of individual sensor elements in 3D space. In this work, we demonstrate the potential of 3D self-assembly to simultaneously reorient numerous giant magnetoresistive (GMR) spin valve sensors for smart fabrication of 3D magnetic angular encoders. During the self-assembly process, the GMR sensors are brought into their desired orthogonal positions within the three Cartesian planes in a simultaneous process that yields monolithic high-performance devices. We fabricated vector angular encoders with equivalent angular accuracy in all directions of 0.14°, as well as low noise and low power consumption during high-speed operation at frequencies up to 1 kHz.

INTRODUCTION

Directional anisotropic sensors, transducers, and actuators are essential for the next generation of electronic devices and systems. These devices rely on materials or structures that have a principal axis or plane dealing with physical quantities such as acoustic, optical, electric, and magnetic vector fields, as well as their gradients. For accurate three-dimensional (3D) sensing, they require precise orientation of functional elements in 3D space. Numerous applications such as navigation (1), robotics (2, 3), bioelectronics (4), and biomedicine (5) rely on angular encoders with magnetic field sensors typically used for these tasks, by providing a key function, namely, the detection of the magnetic field vector’s orientation, which involves simultaneous operation of multiple, specifically oriented magnetic sensors. The broad application range of magnetic sensors is due to the fact that a static magnetic field can penetrate through the most common obstacles, whereas optical, acoustic, and electrostatic fields usually suffer from reflection, absorption, or screening effects. This feature allows for simpler packaging and protection of magnetosensory systems and magnets, free of costly optical windows and parasitic screening effects. The vast majority of all magnetic sensors used in various applications rely on Hall or magnetoresistance (MR) effects that differ in accuracy and sensing direction with respect to the substrate they are fabricated on (6). Because of their relatively simple construction when compared with MR sensors, Hall effect–based devices are the most commonly encountered despite their low angular accuracy and the need for an integrated silicon-based circuit to improve sensitivity and accuracy (7), which is why these sensors are best suited for detecting strong magnetic fields. Hall effect sensors are compatible with Si- or GaAs-based (8) semiconductor manufacturing as well as with other materials such as Bi (9). In contrast, MR sensors, such as anisotropic MR and giant MR (GMR) sensors, are thin-film devices that exhibit several orders higher sensitivity (in the range of kiloohm/tesla) when compared with Hall effect devices, which positively affects the angular accuracy of angular MR encoders. These sensors do not require monocrystalline semiconductors, consume less power, and can be adjusted for a number of specific applications including magnetic storage and logics (10) or weak and strong magnetic field sensing (11). GMR sensors have also been explored in novel and intriguing biomedical and bioanalytical systems (12, 13). They are sufficiently robust for fabrication on conventional monocrystalline wafers (14) as well as on polymeric supports, where the latter technology has led to emerging classes of flexible (15–18), stretchable (19–22), and printable (23–25) magnetoelectronic devices. These can be classified into those that are in-plane, such as GMR multilayers and spin valves (SVs), or out of plane, such as in tunneling MR (TMR) devices (10, 11). The sensitivity direction for SV and TMR devices can be engineered during the planar manufacturing process, which determines the signal response obtained with respect to the external magnetic field.

Planar microfabrication technologies are highly efficient, as the fabrication of entire arrays of devices is accomplished in a parallel manner. However, this technology imposes some limitations, as the completed devices have identical properties, in particular their sensitivity direction in the case of angular encoders. Because of this restriction, it remains a challenge to accommodate various spatially oriented magnetic sensors during parallel manufacturing. For instance, this can include vertical doping of Hall effect sensors (26) or fabrication routines on topographically structured surfaces (27) that may lead to substantial differences in performance. Otherwise, implementation of various sensing directions may require installation of expensive flux concentrators (e.g., 3D ferrite beads) (1) or refined microelectromechanical system technologies (6, 28). Alternatively, the reorientation of the sensitivity direction for MR devices can be achieved by individual local laser annealing (29–31) or pick-and-place technology (32), which, for instance, has been demonstrated for Hall effect sensors. All these attempts clearly demonstrate that spatial rearrangement, especially in a 3D Cartesian basis, is by far the most complex and expensive process involved in the fabrication of 3D vector magnetic field encoders nowadays.

Shapeable ultrathin materials (33) allow for 3D self-driven spatial rearrangement of sensors on the wafer scale that has the potential to considerably simplify fabrication. Shape transformation becomes a vital strategy in constructing compact, complex 3D mesoscopic systems, where conventional technologies have been shown to be inadequate (34–38). Motivated by its compatibility with established microfabrication technologies, self-folding and rolling of ultrathin 2D patterned membranes of various materials have attracted special attention among a number of self-assembly processes (36) to build robots (39), drug delivery scaffolds (40), passive electronic components (41–43), sensors (41, 44–46), electronics (47), and microsurgery (48) tools. Applied on rigid substrates, novel organic and inorganic shapeable materials that have been micropatterned in a planar fashion are capable of self-assembly into diverse 3D mesoscopic architectures including polyhedral (49), cylindrical (50, 51), and more complex (52) shapes. These shapeable platforms rely on parallel wafer-scale processing and have already been demonstrated to improve accuracy, throughput, and manufacturing efficiency of complex 3D photonic, sensing, energy storage, and electromagnetic functional elements, as well as circuits and systems (8, 38, 44, 47, 53). Furthermore, curvature may influence magnetic properties of some ferromagnetic (FM) structures (54), while others (19) remain unaffected. These effects have been investigated and recently reviewed (55), showing great promise for, e.g., ultrafast magnetic storage devices (56) and magnetic sensors (44).

Here, we demonstrate GMR 3D angular encoders by forming an orthogonal Cartesian basis using specially developed ultrathin films that self-assemble into “Swiss-roll” architectures (41, 42, 44, 47). The entire configuration measures projections of the magnetic field vector in 3D space without ambiguities and with high angular accuracy.

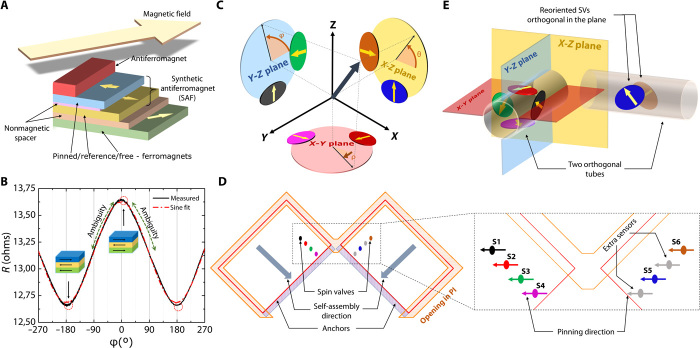
In this work, we prepared a highly sensitive top-pinned SV layer stack, which is depicted in its simplified form in Fig. 1A. This structure consists of three FM layers separated by a nonmagnetic, conducting spacer layer. The magnetization direction of the top FM layer is pinned through an exchange bias created by the adjacent anti-FM layer and can be defined during the magnetization process. The middle FM layer serves as a reference layer and is antiferromagentically exchange coupled to the pinned FM top layer, forming a synthetic antiferromagnet (SAF) (57). Ideally, the bottom FM layer is free to rotate with the direction of an external magnetic field. This is achieved through an effective stray field cancellation at the edges of the FM layers incorporated in the SAF. The in-plane magnetic shape anisotropy is adjusted by patterning the layer stack into ellipses with small areas connected by Cr/Au electrodes. The small size of the sensors is used on purpose to avoid any curvature-related effects in the final tubular self-assembled device, which has been optimized experimentally to be as close as possible to a sinusoidal response. When subjected to an external magnetic direct current (DC) field of 25 mT (operating within the plateau between the effective anisotropy field and the exchange bias field) rotating in the plane of the sensor, the MR response has a characteristic sinusoidal shape (Fig. 1B) with an approximate 1 ohm peak-to-peak difference in resistance (sensor resistance is around 13 ohms) that corresponds to a 7 to 8% GMR ratio [$\frac{R(H)-R_{\text{sat}}}{R_{\text{sat}}}$, where R_sat is a resistance when the free layer is aligned with the reference layer]. In this graph, the low and high resistance values correspond to the parallel and antiparallel magnetization orientations, respectively, of both the free and reference FM layers. A single sensor response exhibits an angular ambiguity in the plane of the sensor as shown on Fig. 1B, requiring a second in-plane sensor with an orthogonal exchange bias direction. Some other sophisticated measurement configurations, such as the differential bridge configuration (18), would necessitate even more sensors. For better visualization and understanding of our GMR 3D sensor concept, a Cartesian basis is shown in Fig. 1C. Here, each of the three orthogonal Cartesian planes contains two sensors that provide sin and cos dependencies on the relative angles (φ, θ, and ρ) of the 3D magnetic field vector projections. Theoretically, only three orthogonal sensors are required (8), with two sensors in, for instance, the XY plane and the third in another orthogonal plane, such as the XZ or YZ plane. However, because of a loss in accuracy at some angular extremums (e.g., the magnetic field is perpendicular to one of the Cartesian planes), it is beneficial to have six sensors to enable accurate operation in arbitrary field orientations. Normally, this configuration of magnetic sensors is quite difficult to achieve using conventional microfabrication processes; however, the simultaneous self-rearrangement of SV sensors that are initially magnetized in only one direction simplifies the task.

Fig. 1. SV structure and self-assembly concept.

(A) Schematic that shows a simplified layer stack of an SV magnetic field sensor. (B) A set of six SVs arranged within an orthogonal 3D Cartesian base. Each orthogonal plane contains an orthogonal pair of sensors that should be rearranged from their planar unidirectional state. (C) Subjected to an external rotating magnetic field, this sensor has a sinusoidal response. (D) 3D SV sensors reoriented into the specific 3D configuration by applying self-assembling rolled-up technology, resulting in a sin and cos response of each pair of sensors on each planes. (E) Planar state of the SVs with the pinning direction set 45° to the rolling direction.

We designed a layout with eight sensors to be prepared in-plane on top of a polymeric shapeable platform to exploit conventional lithographic structuring and thin-film technologies. All of the sensors need to be magnetized in a single step to induce a desired exchange bias direction to comply with the parallel manufacturing approach as indicated in Fig. 1D. In this layout, each set of four sensors is prepared on one of the two polymeric shapeable structures to be self-assembled. The self-assembly direction is defined by specially designed (Fig. 1C) anchoring sites and openings in the reinforcing polyimide (PI) layer to define +45° and −45° self-assembly directions for each structure with respect to the SV’s magnetization. This arrangement automatically results in two orthogonal tubular (8) architectures (Fig. 1E), such that all the sensors are properly aligned in 3D space. This implies that the 45° oblique orientation of the tubular axes, with respect to the initial magnetization direction, provides two orthogonal sensors per Cartesian plane (Fig. 1C). This rearrangement can be achieved without any additional processing that would otherwise be required in a conventional fabrication process. From the eight prepared sensors, only six are actually needed, with the two extra sensors (Fig. 1D) used as redundancies. Here, sensors S1 to S6 are indicated in colors corresponding to the particular sensors in Fig. 1 (C to E) for better visual perception of their actual positions in 3D space before and after the self-assembly process.

RESULTS

Wafer-scale fabrication and planar state characterization

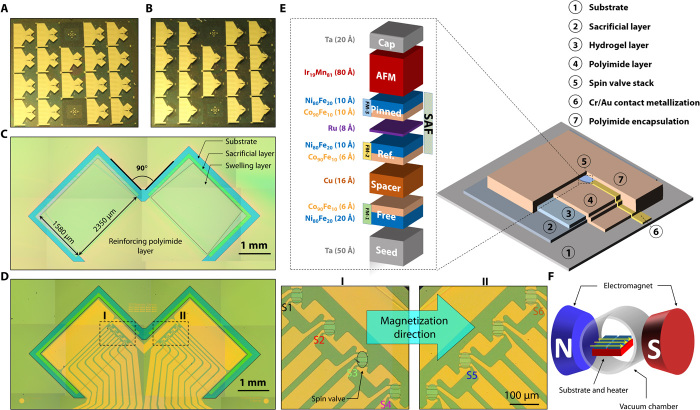
To prove the concept, we have prepared a number of 3D angular encoders (Fig. 2A) on square substrates with dimensions of 50 mm by 50 mm in a parallel, planar microfabrication process, followed by self-assembly into the tubular Swiss-roll architectures (Fig. 2B). Fabrication of the shapeable platform starts with polymeric ultrathin films (Fig. 2C), formed via spin coating and direct lithographic patterning of the sacrificial (SL) layer (700 nm), trapezoidal-shaped hydrogel (HG) swelling layer (350 nm), and the rigid PI layer (800 nm). Afterward, we prepared magnetic sensors by sputter deposition and lift-off patterning. The detailed optimized layer stack is composed of Ta^{0.5 nm}/Ni₈₀Fe₂₀^{2.0 nm}/Co₉₀Fe₁₀^{0.6 nm}/Cu^{1.6 nm}/Co₉₀Fe₁₀^{0.6 nm}/Ni₈₀Fe₂₀^{1.0 nm}/Ru^{0.8 nm}/Co₉₀Fe₁₀^{1.0 nm}/Ni₈₀Fe₂₀^{1.0 nm}/Ir₁₉Mn₈₁^{8.0 nm}/Ta^{0.2 nm}, which is outlined in Fig. 2D. The planar fabrication is accomplished (Fig. 2E) with deposition and patterning of Cr^{5 nm}/Au^{50 nm} electrodes and a final encapsulating PI layer (250 nm). The whole stack is schematically shown on Fig. 2E. Because of the size limitation of our magnetization setup (which is not the case for industrial systems), the substrate was diced before rolling into a 4-by-4 array of 10 mm by 8 mm sensors and then magnetized in a custom-built vacuum annealing oven with superimposed magnetic field produced by an electromagnet, as shown in the schematic of Fig. 2F. The field was applied along the short axis of the SV ellipses and oriented 45° with respect to the self-assembly direction (Fig. 1C). The annealing was done at 300°C for 1 hour in a ~700-mT field, sufficient for the recrystallization of the anti-FM IrMn and Ru layers to achieve strong coupling in the SAF.

Fig. 2. Wafer-scale fabrication of 3D vector field encoder manufactured on 50 mm by 50 mm square glass substrates and their magnetoelectrical characteristics in the planar state.

(A) Initial planar devices. (B) Wafer-scale self-assembled devices. (C) Fabricated planar shapeable polymeric stack. (D) Schematic that shows the exact SV stack. (E) Simplified scheme of the complete layer stack involving shapeable polymer platform, sensor elements, contact metallization, and encapsulation layer. The SV ellipses are patterned and then electrically connected with Cr/Au electrodes and protected by a thin PI layer. (F) Schematic that depicts vacuum oven magnetization setup magnetizing SVs at 300°C for 1 hour with a superimposed magnetic field of ~700 mT produced by an electromagnet. Photo credit: Daniil Karnaushenko, Institute for Integrative Nanosciences, Leibniz IFW Dresden.

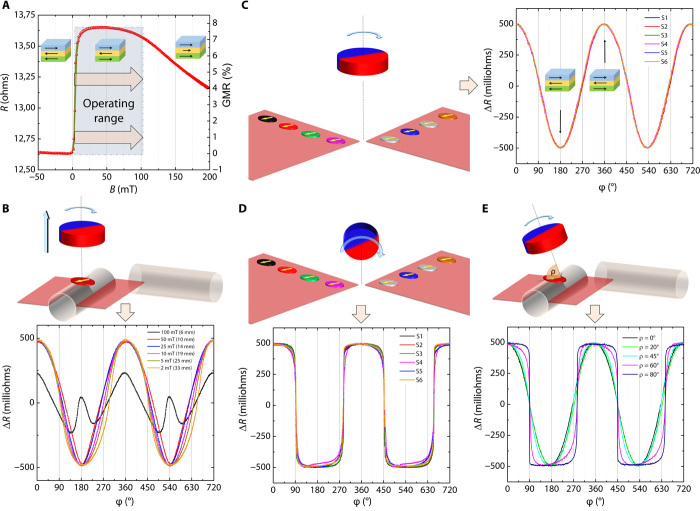
We characterized these planar SVs in swept and rotating magnetic fields after the magnetization was completed. The swept field characteristic (forward and backward) (Fig. 3A) reveals sharp switching of the magnetization around 0 mT, with a small hysteresis of about 0.1 mT and a sensitivity slope of about 120 V/(AT). Both, the low- and high-field slopes can be used for measuring the field value indicating, for example, improper operating distance to the magnet. We could achieve high GMR ratios (7 to 8%) and large exchange bias plateaus of up to about 100 mT. The constant resistance of the plateau defines the operating range for the SV, which is not sensitive to the variations of the external field, as may be the case when the source of the field is moving toward or away from the sensor. This is an important feature when arrays of sensors are used for vector field reconstruction (27). With such a large plateau, each element is sensitive to the field direction but not its strength. This behavior can be seen in the rotating magnetic field response of an SV (S4) in Fig. 3B, where we change the distance between the magnet and the sensor, thereby affecting the magnetic field strength. The optimal operating range lies between 5 and 50 mT, where deviation from a sinusoidal response curve is not critical. So, in our configuration and for further direction characterization purposes, we set the field to a constant value of 25 mT within the plateau range in the plane of the sensors and performed rotating field measurements. The characteristics associated with the rotating field vector in a common plane with the SV sensors before the self-assembly is shown in Fig. 3C, where equivalent overlapping cos-shaped responses are seen. Respective measurements for a rotating field in the orthogonal plane are shown in Fig. 3D. Note that in the initial planar shape, no offset of curves could be observed. All of the characteristics, as expected, overlap and have the highest resistance along the magnetization axis, demonstrating the desired unidirectional magnetization orientation of the sensors as a result of the field annealing process. For 3D operation, it is important to know the response of the sensors with respect to the tilt of the magnetic field plane. Therefore, we performed another characterization by tilting the rotating field plane (Fig. 3E) and recording the responses of the SV sensor. These responses are of sinusoidal shape up to a tilt angle of 45°. This is an important result, as angles beyond 45° can then be measured by another set of SV sensors located in a different orthogonal principal plane.

Fig. 3. Planar device with six SV elements characterized with a swept and rotating magnetic field.

(A) Swept field MR characteristic of one of the SVs measured along the magnetization direction. (B) Rotating field characteristic of one of the SVs (S4) with respect to the field strength (distance to the magnet). (C) Rotating field characterization of six SVs in their initial planar state directly following magnetization. (D) Rotating field characteristic of six SVs measured in an orthogonal plane with respect to the rotating magnetic field plane revealing equivalent switching characteristic for all the sensors. (E) Configuration that was used to measure the responses of the SV with respect to the rotating field plane revealing sinusoidal shape up to 45° tilt, which is sufficient for 3D operation, as beyond this angle, another set of sensors located in the orthogonal principal plane will take over, thus avoiding any blind sectors.

Self-assembled GMR 3D angular encoders and 3D characterization

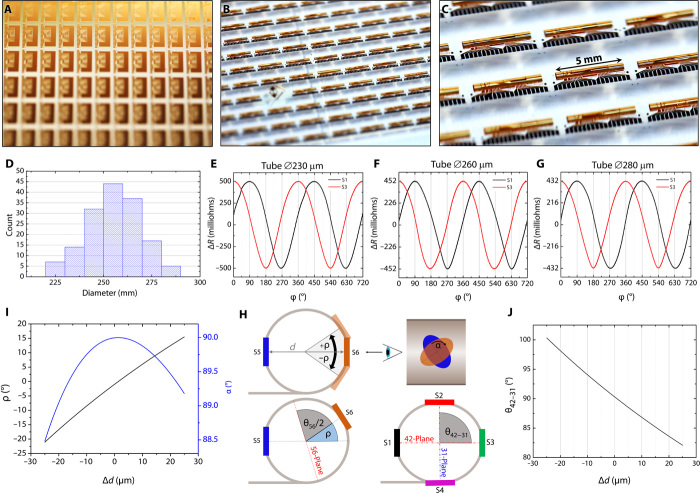
The self-assembly of the planar structures (Fig. 4A) starts with an isotropic etching of the SL in a water-based solution of inorganic acids and an organic base. After etching, the substrate was transferred into a basic solution that swells the HG. Being reinforced by the PI layer, HG releases the stress by curling the structures into Swiss-rolls (Fig. 4, B and C) of 36 tubular structures with only one defective tube (Fig. 2B), resulting in a yield exceeding 97%. Figure 5 additionally shows the single tube devices that were fabricated during optimization of the rolling conditions, revealing similar yield and about 15-μm deviation of diameters within the successfully assembled devices on the wafer (Fig. 5D). Each Swiss-roll is equipped with four SV magnetic sensors reconfigured in 3D space. Thicknesses of the HG and PI layers are adjusted to tune the diameter to ∅250 μm to allocate sensors on the surface of the tube with 90° azimuthal spacing (Figs. 1D, 2B, and 4C).

Fig. 4. Diced devices are self-assembled into 3D magnetic sensors and their characteristics.

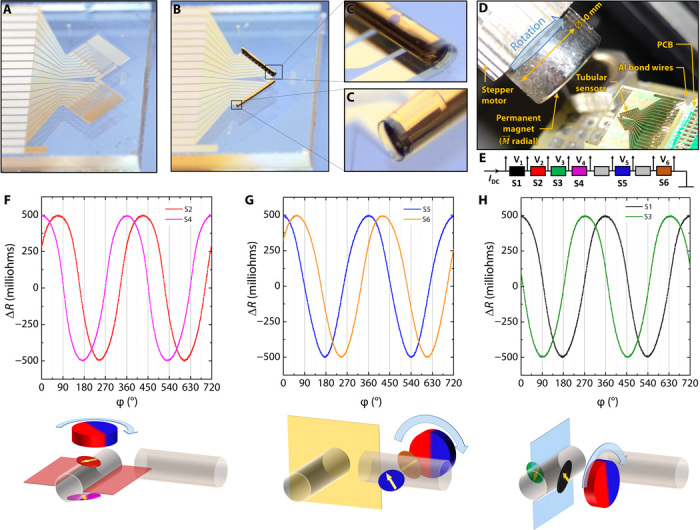
(A) Planar device with a set of magnetized and electrically connected SVs before self-assembly. (B) The devices after self-assembly revealing two orthogonal tubes with a diameter of ∅250 μm and length of 2.3 mm. The rolling length is 1.58 mm. (C) Magnification of two tubes showing one of eight SVs. (D) The 3D sensor was characterized by rotating the magnetic field of a permanent, radially magnetized magnet. The position of the magnet can be adjusted by tilting the magnet around the sensor and tuning the distance between the magnet and the sensor. The sensor itself can be rotated in the horizontal plane. This allows setting the rotating magnetic field plane to any arbitrary orientation with respect to the sensor. (E) Schematic depicting the electrical series connection of the sensors, their supply, and signal acquisition. (F) Behavior of the XY pair (S2 and S4) of the orthogonal magnetic sensors formed on the opposite sides of the respective tube and the sketch showing the orientation of the rotating magnet with respect to the sensors. (G) Behavior of the XZ pair (S5 and S6) of the orthogonal magnetic sensors formed on the opposite sides of the respective tube and the sketch showing the orientation of the rotating magnet with respect to the sensors. (H) Behavior of the YZ pair (S1 and S3) of the orthogonal magnetic sensors formed on the opposite sides of the respective tube and the sketch showing the orientation of the rotating magnet with respect to the sensors. Photo credit: Daniil Karnaushenko, Institute for Integrative Nanosciences, Leibniz IFW Dresden.

Fig. 5. Structures used during the optimization stage.

(A) Fabricated on planar glass squares of 100 mm by 100 mm; the devices were diced (removed edges). (B) Self-assembled devices into an array of tubes. From a total 180 structures, 168 were self-assembled to reveal a fabrication yield of more than 93% in a parallel wafer-scale process. (C) Demonstration of the self-assembly quality in the magnified view of the tubular structure carrying magnetic field sensors and electrodes. (D) Statistical diameter distribution of 168 assembled devices on the wafer. (E to G) Single principal plane-13 response of sensors arranged on a tube with a diameter of 230 μm (E), 260 μm (F), and 280 μm (G) after amplitude, offset, and phase compensation. (H) Schematics clarifying misorientation of SVs and principal planes due to tube diameter variations. (I) Calculation of azimuthal and projection misorientation of SVs that belong to a single principal plane. (J) Calculation of misorientation of principal planes. Photo credit: Daniil Karnaushenko, Institute for Integrative Nanosciences, Leibniz IFW Dresden.

In this configuration, each of the 180° spaced pair of sensors forms Cartesian principal planes that are orthogonal to each other. As discussed previously, the single tube allows for the formation of a semiorthogonal basis containing two orthogonal planes. Two orthogonal tubes form an orthogonal Cartesian base with two extra sensors from the eight prepared sensors. For characterization, we used a permanent NdFeB magnet (∅10 mm by 5 mm) magnetized radially and producing a roughly 400-mT field at the surface. The magnet was attached to the axis of a stepper motor, which was mounted onto a motorized mechanical stage. The setup had four degrees of freedom: (i) rotational axis of the magnet, (ii) tilt axis of the magnet around the sensor, (iii) variable distance of the magnet with respect to the sensor, and (iv) horizontal orientation of the sensor with respect to the other three axes. This setup allowed for definition of any orientation of the rotating field plane with respect to the sensor. In addition, the variable distance between the magnet and the sensor enabled adjustment of the magnetic field strength. The self-assembled 3D sensor was attached to a printed circuit board (PCB) and wire bonded for electromagnetic characterization (Fig. 4D). Elliptical SVs were all connected in series and supplied with 1 mA of current (Fig. 4E). Each of the SV elements was equipped with its own voltage electrodes, allowing for parallel acquisition of all of the sensor signals in a four-probe configuration. Characterization of the 3D sensor was accomplished using an in-house electronic circuit equipped with eight differential, simultaneous acquisition channels with 24-bit resolution. We characterized the completed devices by rotating the magnetic field in all its principal planes, namely, XY, XZ, and YZ. The characteristics of the sensors in their respective planes are shown in Fig. 4 (F to H) with clarifying sketches below. It is clear that the response of the self-assembled device changed in comparison to its planar state (Fig. 3, B and C). The sensors demonstrate a characteristic cos and sin response, as expected from the described concept. This indicates that the correct orientation of the sensors in 3D space was achieved in a fully parallel wafer-scale process by applying the self-assembly rolled-up approach enabled by shapeable material platform. All the responses were measured at a distance of 14 mm between the magnet surface and the sensor. The responses of the other sensors for these orientations of the rotating field plane are shown in figs. S1 to S3. A close inspection of the curves (Fig. 4, F to H), however, revealed a deviation from a perfect sin and cos response as well as a small offset in the desired 90° phase shift.

DISCUSSION

This issue is associated with a slight variation of the tubular diameter and misalignment of the sensors in 3D space that can be improved with a more precise tuning of polymer thicknesses and control of the self-assembly including chemical conditions such as the pH of the solution. To gain more insight into this issue, we measured sensors formed on tubes with three different diameters (Fig. 5, E to G) corresponding to the experimental diameter distribution given in Fig. 5D. Neither any significant changes in the response of the sensors nor any deviations from the sinusoidal shape are detected. We simulated the impact of the diameter deviation on the orientation of the sensors. The orientation of two sensors in one principle plane changes with the tube diameter as shown in Fig. 5I (black curve). The simulation shows that the relative orientation of two facing sensors ρ changes significantly if the tube diameter has a spread of ±25 μm from the ideal value (250 to 260 μm), which corresponds to the diameter spread we observed on a single wafer. ρ has a nearly linear dependence on the misorientation angle and reaches up to 21°. However, the deviation effect on the relative orientation between the two sensor projections (α which is ideally 90°) onto the principal plane is very small (<2°) even for the largest diameter spread (see Fig. 5I, blue curve). This is reflected in the experimental data for each single principal plane (Fig. 5, E to G). Furthermore, each principal plane is misoriented as well (Fig. 5H). Differences in the tube diameter lead to a misorientation of the two principal planes (θ), which are defined by the four SVs carried by the tube (two sensors per plane). Note that the third principal plane has a similar misorientation, as this is determined by the relative orientation of the two tubes. Figure 5H shows how the angle between two principal planes (31 and 42) incorporated in one tube changes when the diameter is varied. The orientation of one principal plane is defined in the middle of the azimuthal distance between the two relevant sensors (for instance, S1 and S3). It turns out that the principal planes acquire a maximum deviation of only ±10° from the ideal orthogonal orientation (Fig. 5J). This implies, in turn, that the observed tube diameter variation has no significant impact on the accuracy of the final angle encoding and is sufficiently small to well calibrate the sensor and remove the corresponding errors from its response. In the calibration procedure, the responses of all sensors have to be measured, and Fourier transforms for each response have to be obtained providing relative phases. This should be done for three precisely orthogonal planes where one plane is, for instance, parallel to the substrate. Then, the rotating magnetic field is applied in each plane using three-axis set of Helmholtz coils, electromagnet, or a rotating permanent magnet.

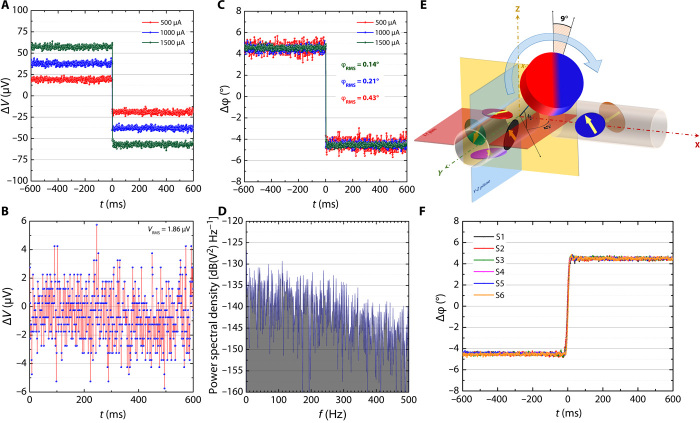
We characterized the angular accuracy of the sensors by measuring the defined angular step (−4.5° to +4.5°) response of a sensor (S4) in the vicinity of its maximum angular sensitivity. We measured this response at three different bias currents (0.5, 1.0, and 1.5 mA) to find out the variation in the signal amplitude (Fig. 6A). Despite differences in the bias current, the noise remains constant with a root mean square (RMS) value of 1.86 μV (Fig. 6B), which is only seven times higher than the resolution (250 nV) of the used 24-bit analog-to-digital converter (ADC). The low-noise performance of the sensor is shown as a power spectral density in Fig. 6D, demonstrating a noise floor better than −130 dB (V²)/Hz for data obtained at 1-kHz sampling rate for several seconds using the same ADC. The highest possible angular accuracy for the sensor directly depends on the bias current and the noise level and reaches a maximum accuracy of 0.14° at a 1.5-mA bias current value (Fig. 6C). We also characterized the angular accuracy of the whole 3D sensor assembly by orienting the plane of the rotating magnet 45° to the principal planes and performing the same 9° step measurement (Fig. 6E). The response of the sensors reveals equivalent accuracy among all the sensors in the assembly, demonstrating full and accurate 3D operation of the sensor set (Fig. 6F). To the best of our knowledge, this is the highest angular accuracy compared with previously reported angular magnetic field sensor (18, 58) or even commercial TMR devices (e.g., TLE5501 Infineon Technologies AG) and is comparable to commercial silicon-based components (e.g., MLX90363 Melexis NV), which, however, make use of integrated circuits, preamplifiers, etc. The accuracy limit of our 3D sensors can be enhanced further by increasing the bias current. However, the small excitation current level (in the microampere range) was chosen to avoid resistive overheating due to the low heat capacity and power dissipation on the surface of the thin (~1 μm) polymeric layer stacks. We have addressed this issue by measuring the thermal breakdown of the sensors for two cases: as fabricated sensors and encapsulated sensors (fig. S4, A and B, respectively). A clear increase in breakdown current and voltage is observed for the second case caused by enhanced thermal dissipation through the encapsulation material. Encapsulation also increases the mechanical stability of the structure, thus tackling one of the main challenges in 3D self-assembled electronics in general (33). Once encapsulated, the final devices can be handled easily and even loaded with a finger or with defined mass producing 5.5-N force without the risk of damaging the sensor or deforming the tubes (fig. S5, A and B). This demonstrates the need for new heat management solutions of 3D self-assembled electronics that will be necessary in the future. These solutions may include passive heat sinks, optimized geometries, tube-integrated fluidic systems (59), and/or radial self-assembled Peltier elements (60) to name a few.

Fig. 6. Characteristics of high-performance SV (S4) after self-assembly.

(A) Voltage response of the sensor measured near cos (φ), where φ = 90°, revealing a voltage step in response to the change in the field direction from −4.5° to +4.5° for different values of bias current. (B) Noise level independent of bias current with an RMS (root-mean-square) value of 1.86 μV. (C) The noise has a flat power spectral density with a floor better than −130 dB (V²)/Hz. (D) Standard deviations of measured angles correspond to 0.14°, 0.21°, and 0.43° depending on the bias currents of 1.5, 1.0, and 0.5 mA, respectively. (E) 3D angular accuracy response of the sensors was measured using 45° orientation of the rotating magnet plane to all the principal planes where the 9° step was performed. (F) Response of the sensors with equivalent angular accuracies in all directions for all sensors (time axis for the step response is adjusted for better visual perception).

We have demonstrated high-performance 3D magnetic field angular encoders by using self-assembly of shapeable materials. All the fabrication steps, including the self-assembly procedure, are parallel in nature and compatible with wafer-scale production, ensuring small deviations in the final geometries. Our self-assembled GMR sensors are of low noise and able to sense with accuracies of up to 0.14° equivalently in all three dimensions without the need for additional sequential processing. Moreover, we achieved an exceptionally high operating range (from 5 to 100 mT), low power consumption (only 30 μW per sensing element), and high-speed operation up to 1 kHz. Our work not only demonstrates novel high-performance 3D magnetic field encoders but also opens up alternative technological routes in producing 3D electronics, which could lead to fully parallel mass-fabricated devices operating with static, low- and high-frequency fields, their gradients, and Poynting vectors.

MATERIALS AND METHODS

Treatment of substrates

Square-shaped glasses of 50 mm by 50 mm by 1 mm were used as substrates in this work (D263T eco glass, SCHOTT AG, Mainz, Germany). Initially, all the substrates were washed in a professional washer DS 500 (STEELCO S.p.A., Riese Pio, Italy) to remove all of the organic and inorganic contaminants present in the form of dust or films. Then, the surface was activated with oxygen plasma in the GIGAbatch 310M (PVA Metrology & Plasma Solutions GmbH, Wettenberg, Germany). This further ensures chemical surface modification with a monolayer of 3-(trimethoxysilyl)propyl methacrylate (TMSPM). For this, the glasses were placed in the vacuum oven at 150°C for 2 hours together with 250 μl of TMSPM.

Polymeric platform

The 3D rearranging of the GMR sensors was based on the polymeric platform described in detail in our previous works (41, 42, 44, 47). First, a lanthanum-acrylic acid–based organometallic photopatternable complex was applied on the substrate with a thickness of 700 nm and patterned by optical lithography using a MA6 Mask Aligner (SÜSS MicroTec SE, Garching, Germany) to form an SL layer. A bilayer system consisting of a photopatternable HG and PI makes it possible to achieve the desired tubular geometry. Once released from the substrate, the HG was able to swell in an alkali solution, leading to mechanical stress at the HG/PI interface, resulting in the rolling process. In a similar manner to the SL, the HG was spin coated on top at 6000 revolutions per minute (RPM), leading to 350-nm thickness, and was then patterned via optical lithography. The trapezoidal shape of the HG layer prevents the structure from rolling at the sides during the etching of the SL. Next, the reinforcing PI was spin coated at 3000 RPM, resulting in an 800-nm-thick layer that was also patterned by optical lithography.

Spin valves

In this work, the GMR sensor elements consisted of a top-pinned SV with the following layer sequence: Ta^{0.5 nm}/Ni₈₀Fe₂₀^{2.0 nm}/Co₉₀Fe₁₀^{0.6 nm}/Cu^{1.6 nm}/Co₉₀Fe₁₀^{0.6 nm}/Ni₈₀Fe₂₀^{1.0 nm}/Ru^{0.8 nm}/Co₉₀Fe₁₀^{1.0 nm}/Ni₈₀Fe₂₀^{1.0 nm}/Ir₁₉Mn₈₁^{8.0 nm}/Ta^{0.2 nm}. Structuring of SV ellipses (85 μm for its major axis and 55 μm for its minor axis) was done by the liftoff technique using a photoresist layer (AZ5214E Microchemicals GmbH, Ulm, Germany) before the layer stack deposition, which was patterned by optical lithography. The SV stack was prepared by magnetron sputtering with a base pressure of 2.4 × 10⁻⁶ and a 1.4 × 10⁻³–mbar Ar atmosphere during deposition using 100-mm diameter targets and 100-W power for each material. The thickness was adjusted by the precise timing of the deposition sequence, which was performed at room temperature directly on top of the polymeric layer stack. Later, the photoresist was dissolved in acetone, revealing the ellipsoidal SV elements on the PI layer.

Magnetization of the sensors

Magnetization of the sensors was performed by magnetic field annealing with an in-house–built vacuum oven placed between pole shoes of an electromagnet. The magnetization was done by fixing 4 x 4 devices diced out from the 50 mm by 50 mm substrate and then evacuating to a pressure better than 2 × 10⁻⁵ mbar using a turbo pump. Annealing was programmed to ramp from room temperature to 300°C within 30 min, held for 1 hour at this temperature, and then ramped back down to room temperature over another 30 min. During this procedure, a magnetic field of 700 mT was applied, resulting in the magnetized SVs.

Tubular self-assembly

Because of selective etching of the SL in a solution of hypophosphoric acid, perchloric acid, and benzotriazole (all chemicals obtained from Sigma-Aldrich Co. LLC, Germany), the bilayer HG/PI system was released from the substrate. On the basis of the patterning of all three polymer layers, the SL was only present in areas with HG on top so that the PI was permanently anchored to the glass substrate. Once the HG/PI bilayer was released, the HG was swelled with an alkaline solution of sodium hydroxide and tetramethyl ammonium hydroxide. The optimal pH value of 8.0 was adjusted with acetic acid.

Magnetoelectrical characterization

For testing the response of the final device to external magnetic fields, a round NdFeB permanent magnet with radial magnetization was attached to a stepper motor. By rotating the permanent magnet, a rotating magnetic field was generated in close proximity to the magnet. The stepper motor was attached to a translational stage through which the distance of the magnet to the sensor allows the magnetic field strength to be adjusted. Furthermore, the translational stage was attached to a rotational stage so that the magnetic field plane could be varied by tilting the permanent magnet. The sensor was glued and electrodes were bonded to a regular PCB placed on a rotational stage, enabling the adjustment of the sensor’s horizontal orientation. Acquisition of the electric signal was done using an in-house electronic circuit containing a differential 1-kHz sampling 24-bit ADC connected to the computer via a USB interface. This setup made it possible to generate a rotating magnetic field in any arbitrary plane in 3D space. The magnetic field was measured using a calibrated magnetometer HG-09 gaussmeter (Goudsmit Magnetic Systems).

Encapsulation

To protect the sensors and enhance thermal dissipation, we casted on top of the sensors a solution of monomers containing 1:1:0.03 molar ratio of triallyl-1,3,5-triazine-2,4,6(1H,3H,5H)-trione (TATATO obtained from Sigma-Aldrich Co. LLC, Germany), tris[2-(3-mercaptopropionyloxy)ethyl] isocyanurate (THIOCURE TEMPIC) (provided by Bruno Bock Chemische Fabrik GmbH & Co. KG), and a radical photoinitiator Irgacure 365 (obtained from Sigma-Aldrich Co. LLC, Germany). Then, we photopolymerized this solution using a 365-nm ultraviolet light-emitting diode source, which resulted in a solid encapsulation that protects from any external mechanical impact as well as serves as a good heat sink for the sensors during electrical tests.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/5/12/eaay7459/DC1

Fig. S1. Characteristic of the ZY and XZ pairs (S1 and S3 and S5 and S6, respectively) of the orthogonal magnetic sensors formed on the opposite sides of the respective tube with the field rotating in the XY plane.

Fig. S2. Characteristic of the XY and XZ pairs (S2 and S4 and S5 and S6, respectively) of the orthogonal magnetic sensors formed on opposite sides of the respective tube with the field rotating in the ZY plane.

Fig. S3. Characteristic of the XY and ZY pairs (S2 and S4 and S1 and S3, respectively) of the orthogonal magnetic sensors formed on opposite sides of the respective tube with the field rotating in the XZ plane.

Fig. S4. Electrical breakdown of the sensors due to overheating under electrical stress.

Fig. S5. Mechanical reliability testing of encapsulated devices.