Model to Link Cell Shape and Polarity with Organogenesis

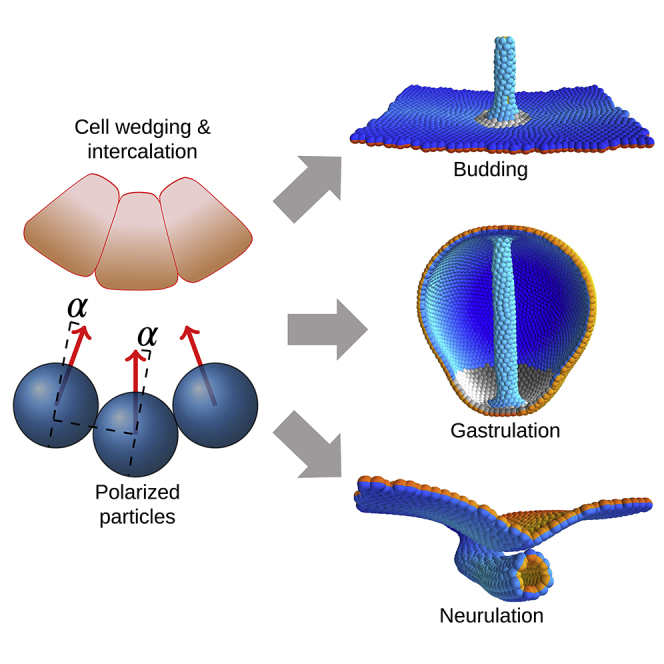
Summary

How do flat sheets of cells form gut and neural tubes? Across systems, several mechanisms are at play: cells wedge, form actomyosin cables, or intercalate. As a result, the cell sheet bends, and the tube elongates. It is unclear to what extent each mechanism can drive tube formation on its own. To address this question, we computationally probe if one mechanism, either cell wedging or intercalation, may suffice for the entire sheet-to-tube transition. Using a physical model with epithelial cells represented by polarized point particles, we show that either cell intercalation or wedging alone can be sufficient and that each can both bend the sheet and extend the tube. When working in parallel, the two mechanisms increase the robustness of the tube formation. The successful simulations of the key features in Drosophila salivary gland budding, sea urchin gastrulation, and mammalian neurulation support the generality of our results.

Graphical Abstract

Highlights

• •Cell wedging and intercalation are modeled using a polarized point-particle approach
• •Cell intercalation is sufficient for tube budding
• •Tube budding is more robust when intercalation is complemented by wedging
• •Wedging and differential proliferation are sufficient for mammalian neurulation

Developmental Biology; Experimental Models in Systems Biology

Introduction

Early tubes in embryonic development—gut and neural tubes—form out of epithelial sheets. In mammalian neurulation and Drosophila gastrulation, the cell sheet wraps around the tube axis until the edges make contact and fuse. As a result of such wrapping, a tube is formed parallel to the cell layer. In sea urchin, the gut is formed orthogonal to the epithelial plane by budding out of the plane. Budding also appears to be a predominant form of tube formation in organ development (lungs and kidneys in vertebrates, salivary gland, and trachea in Drosophila [Andrew and Ewald, 2010]). The same key mechanisms drive both wrapping and budding sheet-to-tube transitions: changes in cell shape, contracting myosin cables spanning across cells, and convergent extension (CE) by directed cell intercalation (Andrew and Ewald, 2010, Chung et al., 2017). Cells change their shapes by adjusting their apical surfaces relative to their basal surfaces—apical constriction (AC) (Sawyer et al., 2010) or basal constriction (Gutzman et al., 2018, Visetsouk et al., 2018). In the following, we will refer to apical or basal constriction as wedging and directed cell intercalation as CE. In addition, oriented cell division and spatially restricted apoptosis (Andrew and Ewald, 2010) contribute to tubulogenesis in other systems.

Until recently, the consensus has been that wedging and CE each lead to distinct morphological transformations: wedging bends the sheet, and CE elongates the sheet and the eventual tube (Andrew and Ewald, 2010). Over decades, wedging was assumed to be a primary mechanism for invagination in budding (Paluch and Heisenberg, 2009). However, results by Sanchez-Corrales et al. (2018) show that wedging and radial CE are coupled, and both contribute to the invagination in Drosophila salivary gland. Furthermore, Nishimura et al. (2012) argue that in mammalian neurulation, CE and wedging are coupled through planar cell polarity (PCP). First, the direction of cell intercalations, orthogonal to the tube axis, is set by PCP. Second, wedging must be anisotropic—with a preferred direction parallel to PCP and the direction of intercalation—for the sheet to wrap into a tube and not a spherical lumen. This anisotropy may stem from the coupling between PCP and wedging, apical as well as basal constriction. This is supported by data at the molecular level (for neural tube closure [Nishimura et al., 2012, Ossipova et al., 2014], the midbrain-hindbrain boundary in zebrafish [Gutzman et al., 2018, Visetsouk et al., 2018], and gastrulation in C. elegans [Lee et al., 2006], sea urchin [Croce et al., 2006], and Xenopus [Choi and Sokol, 2009]). Although the role of anisotropic wedging has been well characterized in Drosophila gastrulation (Chanet et al., 2017, Guglielmi et al., 2015, Martin et al., 2010, Sweeton et al., 1991), the origins of the anisotropy are still being debated (Doubrovinski et al., 2018).

The recent developments open for new questions: What are wedging and CE capable of on their own? Can invagination happen by CE alone? Is anisotropy in wedging essential for tubulogenesis, and, if so, when?

In this paper, we introduce a theoretical model to address these questions. Theoretical models have been essential for understanding tubulogenesis. However, they are often limited to 2D and thus focus on either wedging or CE (Belmonte et al., 2016, Collinet et al., 2015, Spahn and Reuter, 2013). Although there are 3D models for budding and neurulation (Inoue et al., 2016, Kim et al., 2013), they lack the coupling between planar polarization, wedging, and CE and do not capture the entire sheet-to-tube transition. To close this gap, we introduce a model of polarized cell-cell interactions where cells are treated as point particles. As a starting point, we consider the model suggested in Nissen et al. (2018), which was used to study polarized adhesion. We use term polarized adhesion to refer to the cell-cell interaction where adhesion proteins are either apicobasally polarized (AB) or planar polarized by, e.g., PCP. The model parts describing PCP are not limited to the PCP pathway but can be applied to systems where planar polarity is induced by other pathways (e.g., polarized Baz/Par3 in Drosophila germband extension [Paré et al., 2014] or salivary gland budding [Sanchez-Corrales et al., 2018]). The model in Nissen et al. (2018), however, could not explicitly account for changes in cell shapes. Here, we show that the effect of cell wedging can be very simply modeled within a point-particle representation by modifying cell-cell forces to favor a tilt in AB polarities.

In line with the proposition by Chung et al. (2017), simulations show that, although CE alone can lead to a budding transition, it is less reliable, with frequent failure of invagination and even evagination. Our results suggest that isotropic wedging orients the budding process and allows for robust invagination. When applied to wrapping in neurulation, we find that anisotropic wedging alone was insufficient for final tube closure. However, closure as well as tube separation from the epithelium can be aided by differential proliferation. Furthermore, we find that anisotropic wedging on its own may be sufficient for tube elongation. Together, our results support the mutual complementarity of wedging and CE in bending and elongation.

Results

To investigate the role of cell wedging in budding and wrapping, we aimed at capturing both isotropic and anisotropic (PCP-driven) wedging with as few parameters as possible.

Modeling Wedging of a Point Particle by Favoring Tilt in AB

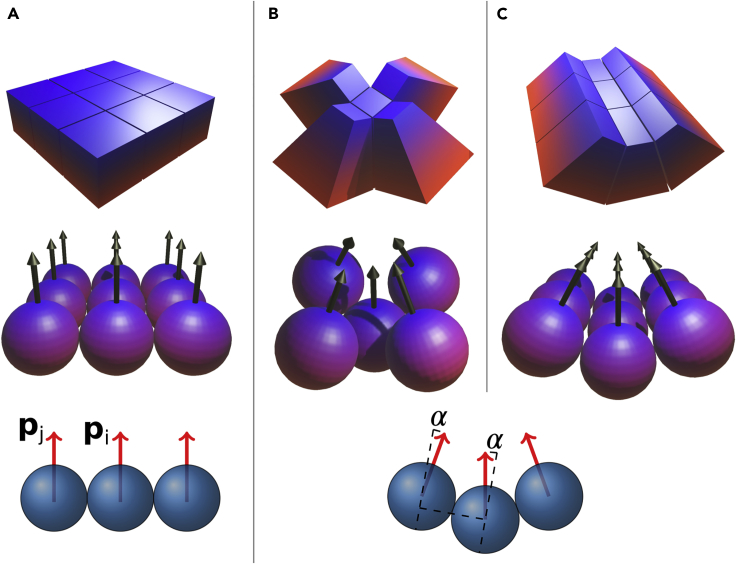
Apical constriction leads to cell wedging and, as a consequence, the AB axes of neighboring cells become tilted toward the wedged cell (Figures 1B and 1C). In Nissen et al. (2018), a flat epithelial sheet was modeled by a cell-cell interaction force favoring parallel AB polarities in neighboring cells (Figure 1A, Equation S1 in the Transparent Methods). To model the effect of wedging, we modify the force to favor AB polarity vectors ${\mathbf{p}}_i$ in neighbor cells to tilt toward the wedged cell (Figures 1B and 1C). That is, when the force is calculated, we replace ${\mathbf{p}}_i$ by ${\tilde{\mathbf{p}}}_i$ ((Equation 1), (Equation 2), (Equation 3)).

$${\tilde{\mathbf{p}}}_i={\mathbf{p}}_i\left(\text{for no wedging}\right),$$ (Equation 1)

$${\tilde{\mathbf{p}}}_i\propto {\mathbf{p}}_i-\alpha {\hat{\mathbf{r}}}_{ij}\left(\text{for isotropic wedging}\right),$$ (Equation 2)

$${\tilde{\mathbf{p}}}_i\propto {\mathbf{p}}_i-\alpha {⟨\hat{\mathbf{q}}⟩}_{ij}\left(\text{for anisotropic wedging}\right).$$ (Equation 3)

Figure 1.

Wedging Is Introduced through a Cell-Cell Interaction that Favors Tilted AB Polarity Vectors

α is the extent of wedging. The blue-red gradient indicates the apical-basal axis.

(A) No wedging ($\alpha =0$), AB polarities (arrows) tend to be parallel.

(B) With isotropic wedging, the tilt α is the same in all directions.

(C) With anisotropic wedging, the tilt has a preferred direction. Blue and red signify, respectively, basal and apical surfaces. $p_i$ and $p_j$ are the AB polarities of cells i and j.

See also Figure S3 and S9, Video S1.

Video S1. Video of a Sheet of Isotropically Apically Constricting Cells Forming a Spherical Lumen, Related to Figure 1

Here the couplings are $\left({\lambda }_1,{\lambda }_2,{\lambda }_3\right)=\left(\mathrm{1,0,0}\right)$ and the degree of wedging is $\left|\alpha \right|=0.3$. Total number of time steps was $2.5\times {10}^4$ at $\text{d}t=0.1$. The width of the Gaussian noise was $\sigma =0.05$.

Here, ${\hat{\mathbf{r}}}_{ij}$ is the normalized displacement vector between cells i and j, whereas ${⟨\hat{\mathbf{q}}⟩}_{ij}$ is the averaged PCP vector of the two interacting particles.

This change required only one parameter, α, setting the extent of the tilt (large α corresponds to pronounced wedging). If the wedging is isotropic, i.e., equally pronounced in all directions (Sanchez-Corrales et al., 2018), all neighbors to the wedged cell tend to tilt equally. In neurulation, the wedging is anisotropic: the wedging happens primarily parallel to the cell's PCP and perpendicular to the axis of the tube (Nishimura et al., 2012). To capture this PCP-directed anisotropy, we couple the direction of AB tilting to the orientation of the cell's PCP (Equation 3, Figure 1C). See the Transparent Methods section for details of the model and simulations.

Note that we aim only to capture the effects of wedging-PCP coupling and not the molecular mechanism. Also, in an attempt to generalize our results, we focus on a minimal set of conditions necessary for the outcome.

We first consider the complementary roles of CE and wedging in budding.

Complementary and Unique Roles of CE and Wedging in Budding

Results by Sanchez-Corrales et al. (2018) and Chung et al. (2017) suggest that both wedging and CE contribute to invagination. However, computational models have generally focused on either wedging as a driver for invagination or CE as a driver of tissue elongation (Belmonte et al., 2016, Collinet et al., 2015, Spahn and Reuter, 2013). To date, no computational models have managed to combine both mechanisms or probe the role of CE in invagination.

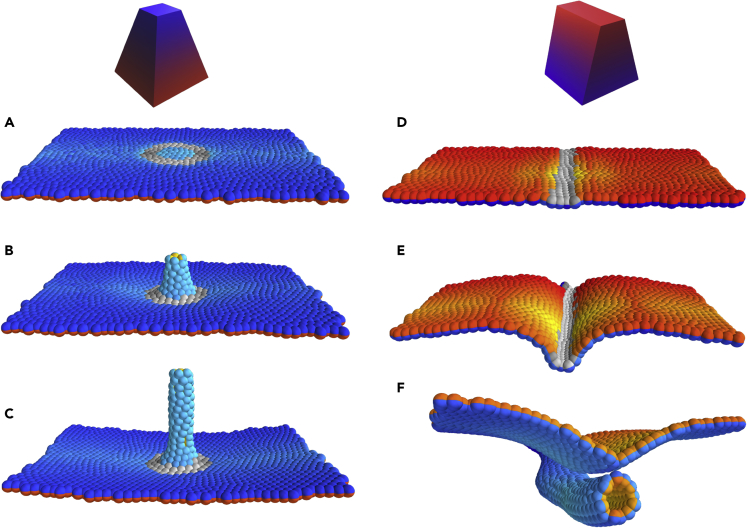
We set out to reproduce these experimental observations. The aim is to only capture the budding, leaving out the finer details of the Drosophila salivary gland, such as off-center invagination. We start with a flat sheet of AB polarized cells. Motivated by the possible link between organizing signals (e.g., WNT), PCP, and wedging (Habib et al., 2013, Loh et al., 2016), we define a region of “organizing signals” such that the cells within this region exhibit isotropic wedging and PCP. In Drosophila salivary glands, the apically constricting cells are distributed on a disk around the future center of the tube. With this configuration, we did not find parameters where both CE and wedging could act in parallel to form a well-defined tube Figures S8A–S8C. However, a ring of basally constricting cells remedied this problem and allowed for wedging and CE to act in parallel. This was the case whether a disk of apically constricting cells was included (Figures S8D–S8F) or not (Figure 2A). Supporting this, the data by Sanchez-Corrales et al. (2018) suggest that there are basally constricting cells in the outer region of the placode. Furthermore, basal and apical constriction seems to be induced by the same organizing signal (Gutzman et al., 2018) through PCP pathways. Also, in sea urchin gastrulation, both types of wedging seem to be at play (Kominami and Takata, 2004). For simplicity, we limit our simulations to basal wedging, where basally constricting cells are distributed on a ring (Figures 2A and S5).

Figure 2.

Isotropic and Anisotropic Wedging Drive Budding and Wrapping, Respectively

Wedging cells are labeled in gray, with a shading that indicates the PCP direction.

(A–C) Time evolution of budding simulation (similar to Drosophila salivary glands). Here, gray cells constrict basally and all cells on and inside the ring intercalate radially. The couplings are $\left({\lambda }_1,{\lambda }_2,{\lambda }_3\right)=\left(0.5,0.4,0.1\right)$, the degree of wedging is $\left|\alpha \right|=0.5$, and the annulus within which wedging occurs is given by the radii $r_0=5$ and $r_1=15$. See section Modeling budding from a plane for details, as well as Figure S5. Total number of time steps was $6.25\times {10}^4$ at $\text{d}t=0.2$. Snapshots correspond to times 5, 800, and $1.25\times {10}^4$. The width of the Gaussian noise was $\sigma =0.05$. See also Figures S1, S7, and S8, Video S2.

(D–F) Time evolution of wrapping simulation (similar to neurulation). Here, gray cells representing neuroepithelium constrict apically and constriction is anisotropic, follows the direction of PCP (Eq 3). Cells proliferate only at the gray/colored boundary (with 7-h doubling time), mimicking differential proliferation at the neuroepithelium/ectoderm boundary. The couplings are $\left({\lambda }_1,{\lambda }_2,{\lambda }_3\right)=\left(0.6,0.4,0\right)$, the degree of wedging is $\left|\alpha \right|=0.5$. See section Modeling neurulation/wrapping for details, as well as Figure S4.

Total number of time steps was $3.9\times {10}^4$ at $\text{d}t=0.1$, and snapshots were taken at times 5, 900, and $3.9\times {10}^3$. The cell cycle length in simulation time units is 600. This simulation was run without added Gaussian noise, but noise is supplied by proliferation, which is implemented as a Poisson process. See also Videos S4 and S5.

Our budding simulations thus show that successful invagination and tube elongation can proceed if both wedging and PCP (and thus CE) act in parallel (Video S2, Figures 2A–2C). We have also succeeded in simulating sea urchin gastrulation where budding starts from a sphere of cells (Figure 3, Video S3, Kimberly and Hardin, 1998, Lyons et al., 2012). This proceeds essentially like in the planar case (see Transparent Methods for details).

Figure 3.

Isotropic Wedging in Conjunction with PCP Is Sufficient to Drive Sea Urchin Gastrulation without External Forcing

The gray ring shows cells with (isotropic) basal constriction, and the shading indicates the direction of planar cell polarity, which curls around the vertical axis in our simulation. The couplings are $\left({\lambda }_1,{\lambda }_2,{\lambda }_3\right)=\left(0.5,0.4,0.1\right)$, the degree of wedging is $\left|\alpha \right|=0.4$, and the annulus within which wedging occurs is given by the radii $r_0=7$ and $r_1=21$. See section Modeling gastrulation for details. Total number of time steps was $1.25\times {10}^5$ at $\text{d}t=0.1$ and snapshots were taken at times 5, $1.5\times {10}^3$, and $1.25\times {10}^4$. The width of the Gaussian noise was $\sigma =0.05$.

See also Video S3.

Video S2. Video of Budding Simulation, Related to Figure 2

Here the couplings are $\left({\lambda }_1,{\lambda }_2,{\lambda }_3\right)=\left(0.5,0.4,0.1\right)$, the degree of wedging is $\left|\alpha \right|=0.5$, and the annulus within which wedging occurs is given by the radii $r_0=5$ and $r_1=10$. See section Modeling budding from a plane for details. Total simulation-time was $t={10}^4$ at $\text{d}t=0.1$; however, a clear tubular structure is evident already at $t={10}^3$. The width of the Gaussian noise was $\sigma =0.05$.

Video S3. Video of Sea Urchin Gastrulation Simulation, Related to Figure 3

Here the couplings are $\left({\lambda }_1,{\lambda }_2,{\lambda }_3\right)=\left(0.5,0.4,0.1\right)$, the degree of wedging is $\left|\alpha \right|=0.4$, and the annulus within which wedging occurs is given by the radii $r_0=7$ and $r_1=21$. Total number of time steps was $1.25\times {10}^5$ at $\text{d}t=0.1$. The width of the Gaussian noise was $\sigma =0.05$.

Video S4. Video of Neurulation Simulation with Isotropic Wedging, Related to Figure 2

Here the couplings are $\left({\lambda }_1,{\lambda }_2,{\lambda }_3\right)=\left(0.60,0.40,0\right)$, the degree of wedging is $\left|\alpha \right|=0.5$. See section Modeling neurulation/wrapping for details. Total number of time steps was $1.4\times {10}^5$ at $\text{d}t=0.1$. The cell cycle length in simulation time units is $1.8\times {10}^3$. This simulation was run without added Gaussian noise, but noise is supplied by proliferation, which is implemented as a Poisson process.

Video S5. Video of Neurulation Simulation, Related to Figure 2

Here the couplings are $\left({\lambda }_1,{\lambda }_2,{\lambda }_3\right)=\left(0.6,0.4,0\right)$, the degree of wedging is $\left|\alpha \right|=0.5$. See section Modeling neurulation/wrapping for details. Total number of time steps was $1.4\times {10}^5$ at $\text{d}t=0.1$. The cell cycle length in simulation time units is 600. This simulation was run without added Gaussian noise, but noise is supplied by proliferation, which is implemented as a Poisson process.

In addition, we find that budding can proceed without wedging if we allow for noise—random fluctuations in cell position and polarity orientation (Figure S1, Equation S4 in the Transparent Methods). Even slight noise, with a width of less than a tenth of a cell radius, breaks the symmetry between the two sides of the plane and initiates the CE-driven tubulation in one of the two directions orthogonal to the plane. However, the robustness of the outcome decreases in two ways. First, the proportion of failed invaginations is higher (Figure S1). Second, the tube can form on either side of the epithelial plane.

Thus, it seems that the role of wedging is to aid in the initial invagination and ensure correct orientation. Interestingly, in the mutants where wedging is compromised, Chung et al. (2017) observe that, despite initial invagination in the right direction, the tubes form less reliably and sometimes reorient in the wrong direction. Our results, showing complementary roles of CE and wedging, are thus in line with the findings by Sanchez-Corrales et al. (2018) and Chung et al. (2017).

Cell shape change, intercalation, and tissue compression by supracellular myosin cables are also critical players in wrapping (Nishimura et al., 2012). The differences that cause some tubes to form parallel and others to form orthogonal to the epithelial plane appear to be encoded in the geometrical arrangement of the cells that participate in these three processes. In budding, such cells are arranged on a ring or a disk (circular symmetry), whereas in wrapping, they are arranged on a band (axial symmetry).

Anisotropic Wedging and Differential Proliferation Are Sufficient for Wrapping

To test if this difference in geometry alone is sufficient for wrapping, we choose a stripe of cells in the middle of the epithelial sheet to represent the neuroepithelium (NE) (shown as gray in Figures 2D and 2E) and the remaining cells to represent ectoderm (E) (colored cells in Figures 2D–2F). The NE cells are then assigned anisotropic apical constriction and PCP pointing orthogonal to the future tube axis (Figure S4).

Wrapping Requires Anisotropy in Wedging

In the case of isotropic wedging, one would expect a collection of NE cells to eventually form a round invagination or spherical lumen—the minimum energy state (Video S1). If we impose isotropic wedging in our neurulation simulations, we obtain a bulging, rounded invagination, rather than a tube. See Video S4.

Motivated by the results of Nishimura et al. (2012), showing that wedging is anisotropic (Equation 3) and cells wedge primarily in the direction orthogonal to the tube axis, we asked if anisotropic wedging can aid in tube closure. As expected, the tissue bends around the tube axis without capping at the ends of the tube (Figures 1C and S2).

Interestingly, anisotropic wedging also leads to cell intercalation by CE, narrowing, and elongating neuroepithelium (see Figure S3), thus supporting the link between PCP-driven wedging and cell intercalations. The simple, intuitive argument for this comes from how wedged cells pack in the tube. In the minimum energy state, the extent of wedging, α, determines how many cells can pack around the circumference of the tube (Figures 1 and S9). If the cells do not change in size, fewer cells are needed to close the circumference as wedging increases. If there are more cells than the wedging can allow for, the “extra” cells will be displaced (to minimize energy). Because of the forces mediated by AB polarity (e.g., tight junctions), cells are constrained to move within the epithelium and are, as a result, displaced along the tube axis (Figure S3). CE-driven narrowing of the epithelium was proposed as necessary for tube closure (Wallingford et al., 2002). In our simulations, wedging and CE alone succeeded in bending the tissue in an axially symmetric fashion (Figure S2). However, we could not obtain successful tube closure even with maximal possible CE and wedging (both tuned by the strength of α in Equation 3). This suggests that additional mechanisms are necessary for final tube closure.

Buckling by Proliferation at the NE Boundary Aids in Tube Closure

Images of neurulation cross-sections (see e.g., Galea et al. [2018]) show a sharp bending at the neuroepithelium-ectoderm (NE-E) boundary, with a curvature opposite to that inside the neuroepithelium (neural folds) (Smith and Schoenwolf, 1997). This is believed to be a result of combined forces from the ectoderm due to (1) change in cell shape (ectoderm cells become flatter and neuroepithelial cells become taller); (2) adhesion between basal surfaces of NE and E close to the neuroepithelium-ectoderm (NE-E) boundary (Smith and Schoenwolf, 1997), and (3) increase in cell density at this boundary either due to cell proliferation or intercalation (McShane et al., 2015).

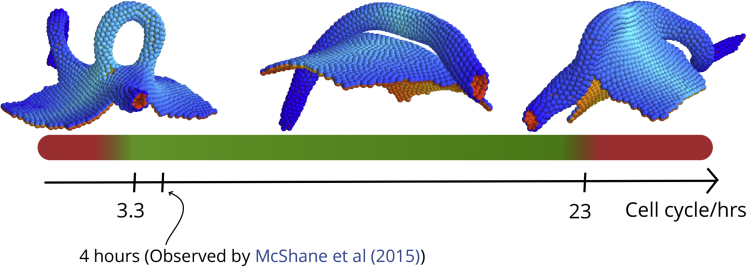
Our goal was to test if the model can capture full tube closure with at least one of the mechanisms, so for simplicity, we focused on differential proliferation. When cells were set to proliferate only at the NE-E boundary (McShane et al., 2015), we found that the resulting buckling can lead to successful neural tube closure (Video S5). In the simulations, the out-of-equilibrium buckling created by rapid cell proliferation is necessary to create a narrow neck that allows epithelial folds to fuse. We find that tubulation is possible within a rather broad range of cell cycles (3–16 h). Shorter or longer cell cycles resulted in open-tube morphologies reminiscent of neural tube defects such as spina bifida (Figure 4). In both cases, the folds are too far apart to fuse, but for different reasons. If proliferation is too slow, the folds are far apart because the buckling is too weak.

Figure 4.

The Cell Cycle Length at the Neuroepithelial-Ectoderm Boundary Affects Tube Closure

For cell cycle lengths below 3.3 h and above 23 h the neural tube fails to close in our simulations. It should be noted that this broad interval also contains the cell cycle length of 4 h found for cells in the dorsolateral hinge points by McShane et al. (2015). The insets show outcomes of simulations run at short (2.6 h), intermediate (12 h), and long (26 h) cell cycle lengths. In simulation time, these correspond to 400, 1,800, and 4,000, respectively. See also Figures S2 and S6.

On the other hand, when proliferation is too fast, the sheet does not have time to equilibrate, and CE does not catch up in narrowing it. Because of this, some sections of the tube become too wide to fuse. Interestingly this can sometimes lead to tube doubling/splitting (Figure S6).

The effect of slow proliferation in our simulations is in line with the experimental data. In Copp et al. (1988), it was shown that low proliferation rates could lead to neural tube defects in mice. In humans, mutations of the PAX3 transcription factor are implicated in Waardenburg syndrome (Baldwin et al., 1994, Tassabehji et al., 1993) characterized by incomplete neural tube closure. The same transcription factor is essential in ensuring sufficient cell proliferation (Wu et al., 2015). The effect of increased (compared with wild-type) proliferation has not been addressed experimentally, and we hope that our predictions will motivate experiments in this direction.

Discussion

Larger organisms rely on tubes for distributing nutrients across the body as well as for exocrine functions. How these tubes reliably form is an open question. A few recurrent mechanisms are known, e.g., directed or differential proliferation, changes in cell shapes, supracellular myosin cables, polarized adhesion, and cell rearrangements. As evolution proceeds by tinkering rather than engineering, it is not surprising that these mechanisms have overlapping functions. Recently quantitative experiments (Chung et al., 2017, Nishimura et al., 2012, Sanchez-Corrales et al., 2018) enabled us to look beyond a “one mechanism, one function” relationship and toward a map of where mechanisms overlap and how they complement each other.

In this work, we have taken a step toward charting the functional overlap and complementarity among CE, wedging, and proliferation. A phenomenological point-particle representation allows us for the first time to combine PCP-driven cell intercalation (CE) and anisotropic wedging in thousands of cells in 3D and with a few free parameters. With this new tool we arrive at the following key results: First, our simulations show that CE can drive invagination in the absence of wedging, thus suggesting that this is a general mechanism that does not require forces from surrounding tissues. The invagination is, however, unreliable, and isotropic wedging plays a complementary role by setting the direction of invagination. The PCP pathway is not expressed in Drosophila salivary gland budding. One might therefore question why modeling the effects of planar polarity—and its role for CE—is valid in this system. However, despite differences at the molecular level, similarities emerge at the cellular level. At the cellular level, planar polarized adhesion is ubiquitous in systems undergoing CE: In mammalian neurulation, the adhesion protein Celsr is planar polarized by PCP (Nishimura et al., 2012); in early Drosophila development, Baz/Par3 is also planar polarized (by Toll receptors in gastrulation [Paré et al., 2014] and by unknown sources in salivary glands [Sanchez-Corrales et al., 2018]). Within our coarse-grained description of polar cell-cell interactions it is not necessary to differentiate whether the effects of planar polarization are due to PCP pathways or other sources, as long as polarized adhesion drives cell-cell intercalation. Also, we do not explicitly model the origins of planar polarity patterning, e.g., WNT signals orienting PCP (Humphries and Mlodzik, 2018) or Toll receptors orienting Baz/Par3 (Paré et al., 2014). Instead we pre-pattern the orientation of polarities directly. We can then either keep the orientation of planar polarities fixed, to simulate a global patterning by, e.g., Toll receptors, or let the global planar polarity pattern dynamically emerge from cell-cell interactions.

Second, our results predict that anisotropic, PCP-coupled wedging may play a role in tube formation and elongation. Our model predicts that anisotropy in wedging maintains axial symmetry of the tube during wrapping. Remarkably, anisotropic wedging can also lead to CE-like cell intercalation and, consequently, tube elongation. Although we have only tested the contribution of anisotropic wedging in wrapping, the same principle may apply in budding. In support of this, in budding, the initially isotropic wedging (Röper, 2012, Sanchez-Corrales et al., 2018) becomes anisotropic after the invagination, when the tube elongates (Pirraglia et al., 2010). Such an isotropic-to-anisotropic transition in wedging has been reported in Drosophila furrow formation (Leptin and Roth, 1994, Sweeton et al., 1991). Furthermore, visual inspection of tube cross-sections in the pancreas and kidneys suggests that cells are wedged. By analogy to neurulation, it is reasonable to expect wedging to be anisotropic in all tubes. It will be interesting to confirm this experimentally by, e.g., whole-mount 3D imaging of stained tubes.

Third, differential proliferation together with anisotropic wedging are sufficient for tube closure and separation in wrapping. Each of the mechanisms has to be spatially constrained. To buckle the cell sheet, proliferation must be faster at the neuroepithelium/ectoderm boundary than in the remaining tissue. Because only neuroepithelium forms the tube, anisotropic wedging must be localized to these cells. Differential proliferation has been proposed by McShane et al. (2015) as a mechanism for forming dorsolateral hinge points (DLHPs), regions where the tissue curvature has the same sign as at medial hinge points (MHPs). We find that modifying the extent of apical constriction or how it is distributed, i.e., throughout the entire neuroepithelium, or combinations of DLHPs and MHP, could not result in tube closure. Instead, our results highlight the importance of forming regions of opposite curvature at the boundaries. Our simulations suggest that differential proliferation buckles the boundaries and aids tube closure as it curves the epithelium oppositely to the curvature resulting from apical constriction.

Our simulations predict a wide range of proliferation rates capable of producing sufficient buckling for closure. These results call for testing for differential proliferation in systems without DLHPs (by accelerating or reducing proliferation rate in mutants or by molecular inhibitors [Li et al., 2017]). Although not immediately feasible, it is also interesting to consider how to perturb the “opposite” curvature by interfering with differences in cell shapes or basal adhesion (Smith and Schoenwolf, 1997) of the neuroepithelium and ectoderm close to the boundary.

Models of tubulogenesis date back at least a few decades (Kerszberg and Changeux, 1998); however, most of them are limited to 2D and focus on either wedging or cell intercalation. Recently, Inoue et al. (2016) formulated a 3D vertex model of neurulation focusing on cell elongation, apical constriction, and active cell migration. The model does not include either cell proliferation or PCP but instead relies on active cell migration to pull the neural cells toward the midline. Although successful in bringing folds sufficiently close, it does not cover the separation of the tube from the sheet. In another system, the experimental and 3D modeling results by Osterfield et al. (2013) suggest that CE may be important in the early budding of the eggshell appendage. In their model, however, the initial invagination was driven by pre-patterned tension in the epithelium and neither cell polarity nor wedging were considered. Also, a recent 3D model of tube budding in the lung epithelium concluded that wedging can only result in rounded tubes and that it is insufficient to drive the entire process (Kim et al., 2013). Still, in that study, only isotropic wedging was considered. In our simulations, we see that anisotropy is necessary for tube formation.

We have demonstrated that cell wedging can be phenomenologically captured in a point-particle representation. This is not restricted to apical constriction but also covers, e.g., basal constriction, and can, in a similar spirit, be extended to capture changes in cell height and width. Also, adding oriented cell proliferation and local apoptosis is straight forward and could allow for modeling a wider range of tubulogenesis phenomena. Furthermore, we are now in a position to address tube branching in, e.g., lungs and vascularization, where cells forming the tubes also are the ones that secrete organizing signals that locally re-orient PCP polarities and may induce anisotropic changes in cell shapes.

Limitations of Study

A major limitation of our study is that we do not model the coupling of polarities to orienting morphogens (e.g., WNT, FGF, or BMP).

As a consequence, cell properties such as expression of apical-basal and planar cell polarity (and the orientation of polarities in individual cells) had to be assigned at the start of simulations. Furthermore, in the case of budding, the orientation of PCP had to be maintained fixed through the entire sheet-to-tube transition. We anticipate that, by including the morphogen-polarity coupling, the right distribution of cell types and polarity directions will emerge without externally imposed constraints.

Methods

All methods can be found in the accompanying Transparent Methods supplemental file.

Published: February 21, 2020

Data and Code Availability

The source code for the simulations is available on GitHub (Nielsen, 2019).