Significance
This work provides a robust estimate of water-level (WL) changes in the Ganges–Brahmaputra–Meghna delta, driven by continental freshwater dynamics, vertical land motion, and sea-level rise. Through an unprecedented set of 101 gauges, we reconstruct WL variations since the 1970s and show that the WL across the delta increased slightly faster, ∼3 mm/y, than the global mean sea-level rise (∼2 mm/y). By combining satellite altimetry and WL reconstructions, we estimate that maximum expected rates of delta subsidence since the 1990s range from 1 to 7 mm/y. By 2100, even under a greenhouse gas emission mitigation scenario (RCP4.5), the subsidence could double the projected sea-level rise, making it reach 85 to 140 cm across the delta.
Keywords: delta, water level, sea level, subsidence, Bangladesh
Abstract
Being one of the most vulnerable regions in the world, the Ganges–Brahmaputra–Meghna delta presents a major challenge for climate change adaptation of nearly 200 million inhabitants. It is often considered as a delta mostly exposed to sea-level rise and exacerbated by land subsidence, even if the local vertical land movement rates remain uncertain. Here, we reconstruct the water-level (WL) changes over 1968 to 2012, using an unprecedented set of 101 water-level gauges across the delta. Over the last 45 y, WL in the delta increased slightly faster (∼3 mm/y), than global mean sea level (∼2 mm/y). However, from 2005 onward, we observe an acceleration in the WL rise in the west of the delta. The interannual WL fluctuations are strongly modulated by El Niño Southern Oscillation (ENSO) and Indian Ocean Dipole (IOD) variability, with WL lower than average by 30 to 60 cm during co-occurrent El Niño and positive IOD events and higher-than-average WL, by 16 to 35 cm, during La Niña years. Using satellite altimetry and WL reconstructions, we estimate that the maximum expected rates of delta subsidence during 1993 to 2012 range from 1 to 7 mm/y. By 2100, even under a greenhouse gas emission mitigation scenario (Representative Concentration Pathway [RCP] 4.5), the subsidence could double the projected sea-level rise, making it reach 85 to 140 cm across the delta. This study provides a robust regional estimate of contemporary relative WL changes in the delta induced by continental freshwater dynamics, vertical land motion, and sea-level rise, giving a basis for developing climate mitigation strategies.
Deltas are dynamic systems driven by constantly changing interactions between land-based fluvial and ocean processes. These rich fertile flat areas, accounting for less than 1% of the Earth’s surface, are vital for food security of more than half a billion people. The deltas are widely recognized as highly vulnerable to the ongoing climate change, particularly to sea-level rise and changes in runoff, as well as to anthropogenic impacts (1–3). The Ganges–Brahmaputra–Meghna (GBM) delta, the largest in the world with an area of ∼150,000 km2 (Fig. 1), represents a key challenge for adaptation to future climate stress of nearly 200 million inhabitants. This deltaic region covers two-thirds of Bangladesh (∼100,000 km2) and a part of the Indian state of West Bengal. The low-lying Bangladesh delta plain, with at least 10% of the land standing below 1 m above mean sea level, has one of the highest population densities in the world, reaching more than 1,000 people per square kilometer (4, 5). In addition, inadequate infrastructure, poverty, low adaptive capacity, and seasonal monsoonal flooding have made the population highly vulnerable to climate change (6). The consequences of the ongoing climate change, amplified by human activities, such as loss of land, increasing soil salinization, and lower agricultural production, are already felt by the delta’s population. The floods are frequent in the GBM delta plain and every year, during the summer monsoon season (June to October), about 20% of the country (up to 60% in the extreme years as in 1988 and 1998) is inundated by river overflows and drainage congestion (7), affecting tens of millions of people and causing severe livelihood damages. Moreover, the delta plain is exposed to the large tidal range and severe cyclone-induced storm surges (8, 9). The deadliest storm-induced floods in world history have struck the GBM delta population, especially in Bangladesh. Extreme events in 1876, 1897, and the 1991 Gorky cyclone each killed at least 140,000 people, while the 1970 Bhola cyclone claimed ∼300,000 lives (10). The intensity and spatial extent of floodings are controlled, first and foremost, by the strength of monsoon precipitations, river discharges, storm surges, and sea-level and tidal variations. An important concern has arisen currently about the impact of a warming climate on the GBM floodings: Will they get more intense and more frequent in the future? So far, the capacity of local people to cope with possibly increasing flood events in the future is unknown. A better understanding of the processes driving water-level fluctuations on the GBM delta plain is thus of crucial importance for improving mitigation strategies to future changes. Despite its importance, the future variations of water levels in the GBM delta plain still remain highly uncertain.
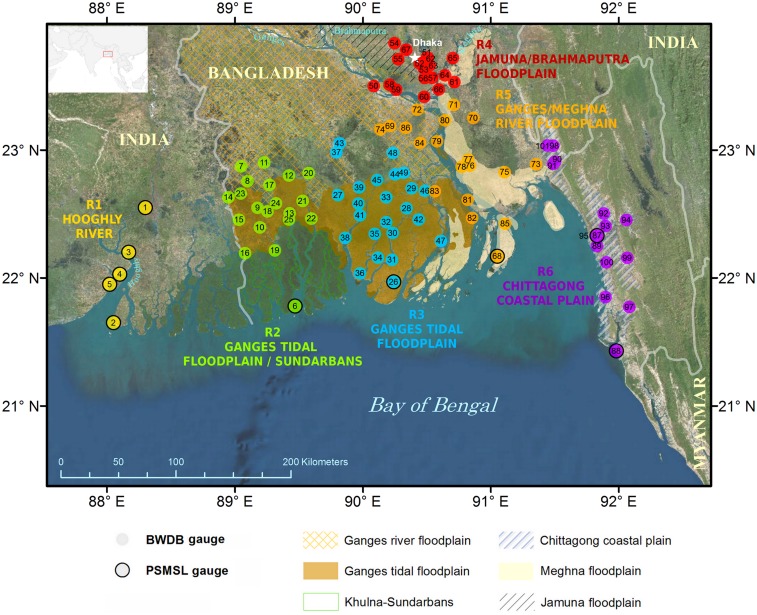
Fig. 1.
Map of the GBM delta region together with the location of stream/tide gauges from the Bangladesh Water Development Board (11) and tide gauges from the PSMSL and the 6 regions defined in this study. Each number corresponds to the station position in SI Appendix, Table S1. The physiographic units originate from Brammer et al. (72). GBM delta imagery basemap courtesy of Esri, DigitalGlobe, Earthstar Geographics, CNES/Airbus DS, GeoEye, USDA FSA, USGS, Aerogrid, IGN, IGP, and the GIS User Community.
There is a large water gauge network with long-term records in the delta plain of Bangladesh (11), but available estimates of water-level trends within the delta differ significantly from one station to another, suggesting an extremely wide range of local processes and/or instrumental errors (6, 12, 13). The large measurement uncertainties and sporadic offsets could be due to some specific observational platforms attached to wooden piers that may themselves be subject to significant movement, human error in taking readings, and lack of checking and quality control of data. Vertical land movements make up an important part of the recorded water/sea-level measurements and separating them from water/sea-level changes driven by other processes that originated in the ocean and atmosphere represents a significant challenge. Thus, more accurate estimates of the delta vertical land motion at an adequate spatial resolution are critical to reduce uncertainties in the flood/storm surge forecasting models and to strengthen our confidence in findings drawn from impact studies. Like many deltas, the GBM delta is globally subsiding and several studies have aimed at evaluating its subsidence over different spatial and temporal scales (1, 14). The rate of subsidence depends on the spatiotemporal scale considered and magnitude of the respective subsidence drivers. The intense continuous sediment loading during the Holocene likely accounts for ∼0.5 to 3.0 mm/y of the present-day regional subsidence, by way of compaction and isostatic adjustment (15–17). At the local scale, higher rates of subsidence involving other processes may be observed: For instance, using satellite observations over a recent 5-y period, Higgins et al. (18) measured a subsidence of up to 18 mm/y around the city of Dhaka.
This complex physical and societal context is a backdrop to this study, which targets 4 main objectives: 1) To estimate regional relative water-level (RWL) trends over the last 45 y across the GBM delta plain, 2) to better understand the causes of variations in the regional RWL at the interannual and decadal time scales, 3) to estimate maximum regional subsidence rates over the past 2 decades, and 4) to evaluate the impact of subsidence on projected sea-level rise by 2050 and 2100.
In this study, we analyze an original set of 90 monthly stream and tide gauge records from the Bangladesh water-level gauge network obtained from the Bangladesh Water Development Board (11), together with 11 monthly tide gauge records from the Permanent Service for Mean Sea Level (PSMSL) database (19). Locations of 101 records are displayed in Fig. 1. See Material and Methods and SI Appendix for more details on the data (SI Appendix, Fig. S1 and Table S1). The water-level (WL) fluctuations on the delta plain are due to changes in absolute sea level (ASL), vertical land movement (VLM), and local freshwater inflows from rivers and rain. Disentangling the relative contributions and interactions of these local WL drivers is challenging due to the lack of information and to the poor quality of the data with large uncertainties and possible local bias (20). In this study, in contrast to the standard local station-by-station analysis, we apply an original regionalization approach, aggregating WL records in large spatial units (ranging from 50 × 50 km to 200 × 100 km) to filter out local effects and obtain consistent WL fluctuations at a regional scale since the 1970s. There are several benefits from using this approach: 1) Reducing random errors with respect to the individual records by averaging observations; 2) reducing geographical biases of local estimates because the WL gauges are almost uniformly distributed in every region and not located only along the major waterways or at the coast; and 3) providing a regional mode of WL variability, by analyzing datasets from different stations, with a temporal coverage beyond the duration of each individual record. We have divided the GBM delta into 6 regions, as follows (Fig. 1): One in the West Bengal part of India, denoted Region 1, Hooghly River (called R1 hereafter comprising 5 stations); and the others in Bangladesh, from the west to the east: Region 2, Ganges tidal floodplain/Sundarbans (R2, 20 stations); Region 3, Ganges tidal floodplain (R3, 24 stations); Region 4, Jamuna/Brahmaputra floodplain (R4, 18 stations); Region 5, Ganges/Meghna rivers floodplain (R5, 19 stations); and Region 6, Chittagong coastal plain (R6, 15 stations). The regions include WL gauge clusters defined according to their geographical proximity, physiographic characteristics, drainage network of subcatchment area, and tidal zone influence (more details in Materials and Methods). To extract regionally coherent modes of variability from the WL stations network, we adapted, for each region, the method developed by Davis et al. (21), and generalized by Buble et al. (22), for the analysis of tide gauge data. This method helps to separate a linear trend specific to every WL station from the interannual RWL variations assumed to be coherent at all observational sites within the region under consideration (more details in Materials and Methods). The temporal evolution of the regional RWL modes for each of the 6 regions is presented in Fig. 2.
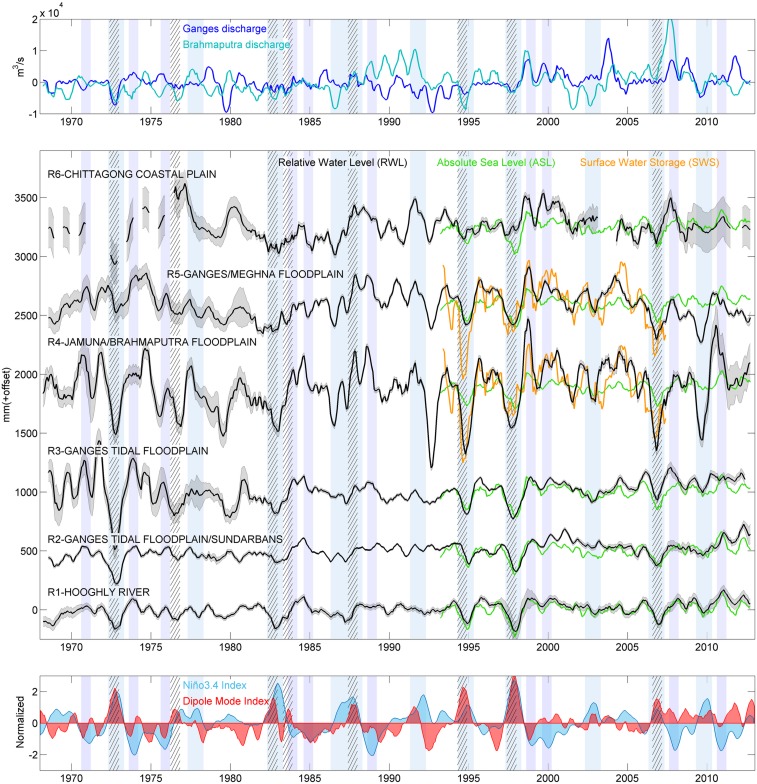
Fig. 2.
(Top) Deseasonalized anomalies (subtracting the long-term mean) of Ganges and Brahmaputra discharge time series. (Middle) Regional RWL reconstructed for the 6 regions over 1968 to 2012 (black line). Superimposed are the deseasonalized anomalies of the ASL from altimetry (green line) and the normalized deseasonalized anomalies of the SWS (orange line). (Bottom) Normalized Niño3.4 index (blue shade) and normalized Indian Ocean Dipole Mode index (red). A 6-mo running window was applied to all of the monthly time series. The light blue stripes indicate the El-Niño years and the light purple stripes the La Niña years. The black hatched stripes correspond to the positive IOD years.
Results and Discussion
How Much Did the Water Level Rise on the GBM Delta Plain during the Last 4 Decades?
Despite the emergence of statistical regional sea-level reconstructions, it is still a challenge to estimate how much coastal sea level has changed regionally prior to the 1990s, i.e., before the altimetry era. Existing sea-level reconstructions provide us with a rate of the absolute sea-level changes averaged over the world’s oceans, also called the global mean sea-level (GMSL) rate. Over 1968 to 2012, the GMSL rate was 2.1 ± 0.2 mm/y (23).
The RWL time series exhibit interannual and decadal variability (Fig. 2). Therefore, the usual assumptions of uncorrelated linear regression residuals are not satisfied. To account for autocorrelation in the RWL time series, the significance of correlations and trends was estimated by the method of Ebisuzaki (24) (Materials and Methods). The trends (Table 1) indicate statistically significant RWL rise in all regions, R6 excepted. Although uncertainties are large, it appears clearly that during the 1968 to 2012 period, the RWL in the GBM delta has increased at approximately the same pace, sometimes even slightly faster, than the GMSL. However, the regional RWL trends are largely lower than many estimates of local relative sea-level trends reported earlier (between 6 and 21 mm/y over ∼30 y) (7, 13, 25, 26) and commonly used in the scientific literature. One strong implication of our results is that, over the past 45 y, the delta might not have subsided as fast as local estimates have suggested before.
Table 1.
Trends (millimeters per year) of regional relative water level (RWL) and absolute sea level (ASL)
| RWL | ASL | Expected max. subsidence | |||
| Region | Trend 1968–2012, mm/y | SD σ, cm | Trend 1993–2012, mm/y | Correlation coefficient r[RWL,ASL] (lag in months) | Trend 1993–2012, mm/y |
| R1-Hooghly River | 2.1 ± 0.8*** | 8 | 2.7 ± 1.4*** | 0.9(0) | 1.5 |
| R2-Ganges tidal floodplain/Sundarbans | 2.7 ± 1.3*** | 9 | 2.1 ± 1.4* | 0.7(0) | 2.4 |
| R3-Ganges tidal floodplain | 3.6 ± 1.8*** | 16 | 3.2 ± 1.6*** | 0.8(0) | 7.0 |
| R4-Jamuna/Brahmaputra floodplain | 3.1 ± 2.3* | 28 | 3.1 ± 1.5*** | 0.6(−1) | 7.2 |
| R5-Ganges/Meghna floodplain | 3.0† ± 2.6* | 16 | 3.4 ± 1.6*** | 0.7(−1) | 5.2† |
| R6-Chittagong coastal plain | 1.3 ± 1.4 | 17 | 3.4 ± 1.7*** | 0.4(0) | — |
The linear trend estimates are obtained from a robust regression model with the bisquare weight function (67). Their significances and uncertainties are estimated by a random phase method to maintain the autocorrelation structure of RWL and ASL series (24) and given at 1σ significance level. The maximum expected subsidence rate is defined as the 10% lower bound in the VLM rates distribution (subsidence corresponds to VLM < 0). *, **, and *** correspond to a significant linear trend with P ≤ 0.1, P ≤ 0.01, and P ≤ 0.001, respectively.
In R5, the trends are estimated up to 2005 (see Materials and Methods for details)
How Does the Interannual Variability Impact the Regional Water Level?
The RWL long-term variability is strongly enhanced eastward across the delta, increasing from 8 cm to 17 cm. From north to south, the GBM flow influence is becoming less important for the RWL fluctuations, which decrease from 28 cm in R4 to 16 cm in R5 (Table 1). An obvious question arises: To what extent are the regional RWL modes coherent, in phase and amplitude, across the GBM delta? The correlation coefficients between 2 neighboring RWL modes (SI Appendix, Table S2) are generally significant, and these coefficients are becoming slightly smaller although still significant as the distance increases. Interestingly, the RWL variations in regions R1, R2, and R3 during 1993 to 2012 are very close to the absolute sea-level changes provided by the satellite altimetry product (Fig. 2; more details in Materials and Methods). Assuming that these absolute sea-level fluctuations are a component of the water-level changes on the delta (27, 28), we found that the absolute sea-level changes explain 82% to 50% of the RWL variance in the regions R1, R2, R3, and R5, respectively, and less than 40% in the regions R4 and R6.
These regional RWL reconstructions, based only on in situ observations, give robust information about their fluctuations over a long time period of 45 y. In the following sections, we explore the possible links between theses RWL fluctuations and large-scale climate drivers.
Impact of climate variability modes on the GBM delta.
Previous studies have clearly demonstrated the relationship between El Niño Southern Oscillation (ENSO) events, drought, and flood in Bangladesh (25, 29). During La Niña events, important fluxes of atmospheric moisture set on between the Pacific and Indian sectors, causing heavy rainfall and floods. An opposite effect is observed during El Niño events, which are generally associated with droughts in Bangladesh. The Indian Ocean Dipole (IOD) is identified as the second dominant mode, after ENSO, of the Indian Ocean sea surface temperature (SST) interannual variations (30). During positive (negative) IOD phases, SST gets warmer (colder) in the Indian Ocean western basin and colder (warmer) in the eastern part of the basin near Sumatra. During positive (negative) IOD events, sea level (increases) decreases in the Bay of Bengal (31). This tends to reduce (enhance) the probability of Bangladesh flooding. Several studies have recently investigated the Indian Ocean sea-level variability during ENSO–IOD co‐occurrence years (31–33). Deepa et al. (33) showed, through Ocean General Circulation Model simulations and ocean reanalysis, that ENSO–IOD co-occurrence events contribute more significantly to the Indian Ocean interannual sea-level variation. ENSO–IOD co-occurrence induces changes in zonal wind stress and results in stronger coastal sea-level fluctuations.
Relative water level and El Niño-positive IOD events.
We superimposed in Fig. 2 the Niño 3.4 SST index (34), average SST anomaly in the central equatorial Pacific, and the SST-based Dipole Mode Index (DMI) characterizing the IOD (30). In the regions R1 to R3, the RWL time series show significant negative correlation with the Niño 3.4 index (correlation coefficient [r] < −0.6; SI Appendix, Fig. S2) and the correlation decreases slightly from R4 to R6. The correlation with the DMI is weaker (−0.4 < r < −0.2; SI Appendix, Fig. S2) and nonsignificant in R6.
In Fig. 2, we identify that, in general, the strong drops in all regional RWL time series occur during El Niño-positive IOD event years (1972, 1982, 1994, 1997, and 2006; Materials and Methods). Typically, the RWL decreased by ∼30 cm from premonsoon to rainy monsoon season (i.e., April to October/November; SI Appendix, Fig. S3), except in R4 where the drop amounted to ∼60 cm (up to 80 cm in October 1994).
Relative water level and La Niña events.
The amplitude of the RWL fluctuations is about twice as low during La Niña events than during El Niño-positive IOD events. Overall, we observe a large increase in all regional RWLs, although more pronounced in R4, during La Niña years (1970, 1988, 1998, 1999, 2007, and 2010; Materials and Methods). Generally, the RWL tends to increase by ∼16 cm during the rainy monsoon season (July to October), except in R4 where the increase reaches ∼35 cm (up to 110 cm in August 1998).
It is also worth noting that 3 of the most catastrophic Bangladesh floods occurred during La Niña years 1988, 1998, and 2007 by submerging 61%, 68%, and 42%, respectively, of Bangladesh over several weeks (7). During these specific La Niña years, we observe (Fig. 2) that the RWL is high in R4, Jamuna/Brahmaputra floodplain, and there is also an important increase in the Brahmaputra discharge, in phase with a peak in the Ganges discharge, but of lesser importance. The combination of these phenomena was highlighted by different authors and called a “backwater effect” (35–37). In this essentially flat deltaic environment, if the freshwater flux, due to local or remote heavy monsoon rainfall or to upstream glacier melting, occurs when the sea level is high enough to create a downstream barrier, it tends to accumulate upstream, enhancing inundations in the flood plains. This effect is likely to impact the RWL maximum values by R4 and R5.
To investigate this hypothesis, we compared the regional RWL fluctuations to the surface water storage (SWS) (the amount of water stored in rivers, floodplains, lakes, and wetlands) variability over the GBM delta (38) (Materials and Methods). We superimposed in Fig. 2 the SWS fluctuations over 1993 to 2007. In R1, R2, R3, and R6, the RWL modes show weak significant positive correlations (∼0.5) with the SWS fluctuations. The correlation coefficient increases up to 0.8 in R4 to R5, regions the most influenced by the GBM rivers, with a delay of 2 mo, which means that the water level increases, first, due to the river overflows and then, about 2 mo later, the delta plain gets inundated. We found that the SWS changes explain 62% and 65% of the RWL variance in the regions R4 and R5, respectively, and less than 35% in other regions.
Relative water level multidecadal variability.
We used the locally weighted scatterplot smoothing technique (LOWESS) (39), with a smoothing time span of 15 y, to emphasize the multidecadal and longer variability of the RWL. For frequencies less than 15 y, the LOWESS smoother behaves as a low-pass filter (Fig. 3). The choice of the smoother time span was based on the work of Han and Webster (36), who identified in the northern Bay of Bengal 2 significant spectral peaks in the interannual sea-level anomaly corresponding to periods of 4 to 5 y and 13 to 14 y.
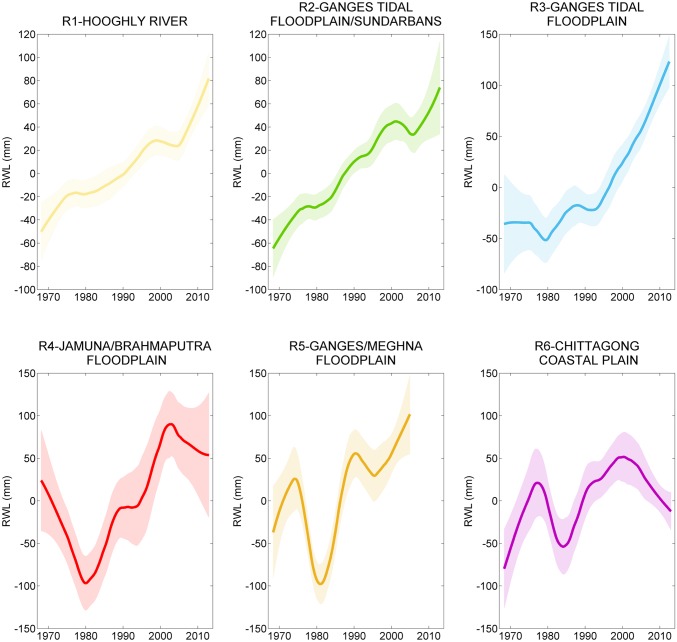
Fig. 3.
LOWESS curve fitting (15-y window span) of the regional RWL reconstructions for the 6 regions over 1968 to 2012. The bootstrap method is used over the LOWESS curves to get reliable estimates of 95% confidence intervals of means. In R5, the LOWESS is applied up to 2005 (see Materials and Methods for details).
In R1 and R2, the RWL seems to manifest a small drop in 2004 and an acceleration before 2012. Two significant (P < 0.1) different trends can be identified: A moderate increase over the 1968 to 2004 period (2 ± 1 mm/y and 3 ± 1 mm/y, respectively) and a strong increase from 2005 to 2012 (7 ± 3 mm/y and 6 ± 3 mm/y, respectively). This finding is consistent with other studies, which revealed a sharp increase of sea level over 2004 to 2013 in the North Indian Ocean (40–43). This increase is mainly attributed to wind-driven redistribution of heat within the Indian Ocean (42, 43). In R3, we observe a RWL trend of ∼7.5 mm/y since 1994 with an acceleration of ∼0.2 mm/y2, which is 2 times faster than the GMSL acceleration during 1993 to 2017 (44). The regional RWL in R4, R5, and R6 is clearly dominated by long-term multidecadal oscillations that do not allow us to draw any conclusion about the presence, or not, of significant changes in the RWL trends during 1968 to 2012.
Is There Evidence of Regional Subsidence in the GBM Delta over 1993 to 2012 (the Altimetry Era)?
There is a common understanding that the subsidence of the delta plain enhances the vulnerability of its population due to exacerbated sea-level rise impacts. The combination of the rising sea level with a subsiding coast increases drastically the risk of coastal flooding due to high tides, storm surges, and their conjunction. The diverse physical processes that induce subsidence may be of natural origin, including glacial or sedimentary isostatic adjustment, tectonics, sediment compaction/load, or/and human-induced origin, including land use, withdrawal of groundwater, and lesser sediment transport due to upstream dams. These complex physical processes involve various temporal and spatial scales, making it extremely difficult to estimate the contribution of subsidence drivers (14–16). This exact knowledge of land subsidence is, however, essential for increasing population adaptive capacities toward efficient flood management and coastal defense strategy, as, for example, for evaluating the dimensions of flood defense structures.
Like many deltas, the GBM delta is subsiding (1) and there is an extensive literature on vertical land motion variability over different spatial and time scales, leading sometimes to confusion on how the results should be used for current and future flooding risk and impact studies. For example, Milliman et al. (45) and Ericson et al. (46) used a global subsidence rate of ∼10 mm/y for the entire GBM delta, and Syvitski et al. (1) used rates in the range 8 to 18 mm/y while Pethick and Orford (12) used values between 5 and 7 mm/y. All of the subsidence rates over the contemporary period obtained from the literature are summarized in Fig. 4 and are discussed below. Some authors derived the subsidence rates from piezometric levels in Kolkata City (Fig. 4) and surrounding areas and obtained thereby subsidence rates of 5 to 16 mm/y from the 1950s to 2005, probably due to extensive groundwater extraction (47). In recent years, satellite observations alone, or in combination with conventional in situ instrumentations, provided the following local subsidence rate estimates, for example: 1) Through Interferometric Synthetic-Aperture Radar (InSAR) technology, Higgins et al. (18) estimated subsidence rates, over 2007 to 2011, of 0 to 18 mm/y in the eastern delta and Chatterjee et al. (48) estimated a subsidence rate of ∼6 mm/y over 1992 to 1998 in Kolkata City (Fig. 4) and surrounding areas; 2) from GPS receivers, Steckler et al. (49, 50) obtained subsidence rates of 3 to 13 mm/y over 2003 to 2013; and 3) by differencing satellite altimetry and tide-gauge record data, uplift rates between 1 ± 2 mm/y and 3.6 ± 5 mm/y were reported along the Hooghly River (51–53) with very large uncertainties in subsidence rates along the Bangladesh coast (−15 ± 5 mm/y) (51). Although there is a clear consensus that the GBM delta is subsiding, and the recent technologies and methods to estimate the local subsidence rates are promising, subsidence estimates remain until now pointwise, site dependent, and often uncertain. Consequently, the interpretation of these local values as well as of the long-term regional trend in the delta subsidence is largely questionable.
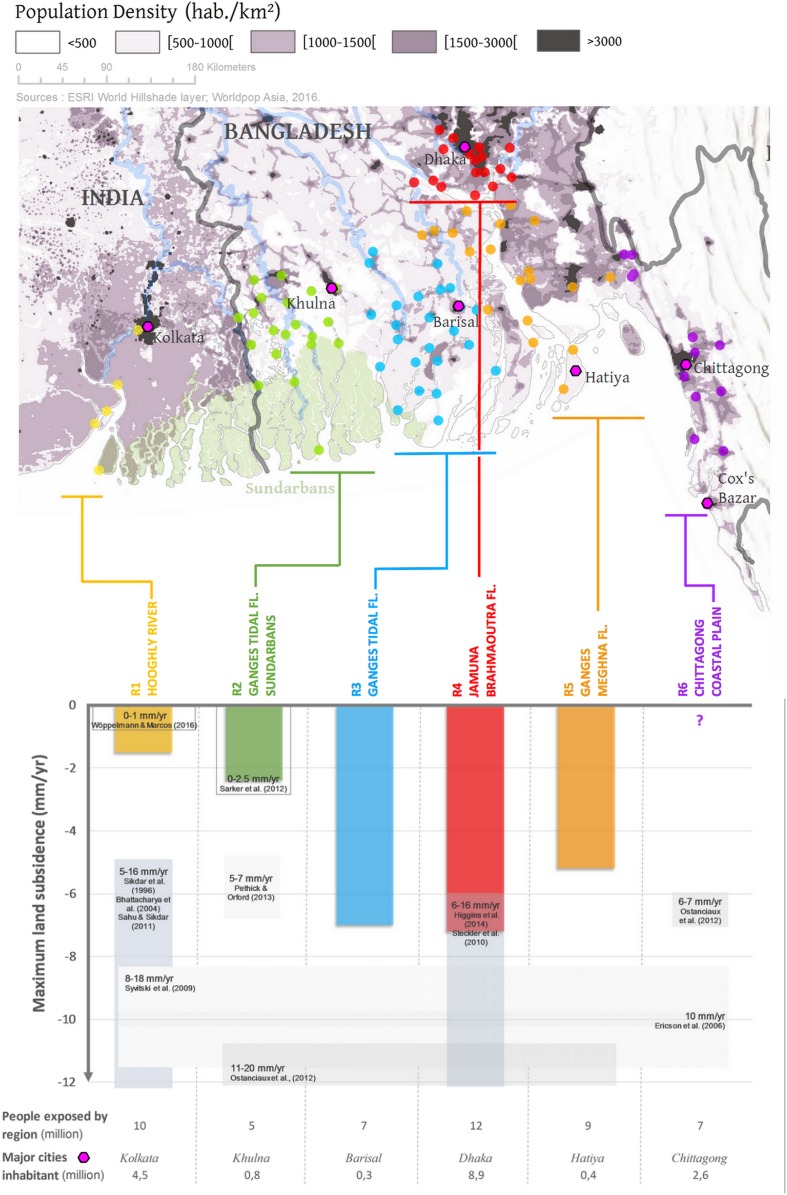
Fig. 4.
Map and maximum subsidence rates expected over the contemporary period. The solid colored bars correspond to the significant subsidence rates obtained in this study (upper bound of the likely range, Table 1). In R6, “?” means that we are not able to provide reliable information about the subsidence in this region. The shaded gray bars correspond to the subsidence rates obtained from the literature for the contemporary period. The 2015 population density (habitants per square kilometer) map is provided by Worldpop Asia (5). World Hillshade basemap courtesy of Esri, Airbus DS, USGS, NGA, NASA, CGIAR, N Robinson, NCEAS, NLS, OS, NMA, Geodatastyrelsen, Rijkswaterstaat, GSA, Geoland, FEMA, Intermap, and the GIS user community.
To obtain estimates of the subsidence rate of each of the 6 regions over 1993 to 2012, we compute the difference between ASL and RWL over 1993 to 2012. Here, we make an assumption, as a first approximation, that the contribution of the local freshwater trends to the regional RWL trends is negligible during this period. There are several reasons for this. The first one, and the most fundamental, is that no significant linear trend over 1993 to 2012 is detected in the Ganges and Brahmaputra discharge time series (nor in the aggregated discharge of the 2 rivers). We used the only available in situ discharge observations for the entire GBM delta (at Hardinge Bridge and at Bahadurabad; Materials and Methods). Due to the large natural fluctuations in the discharge time series we cannot detect a significant trend over 1993 to 2012. This is further supported by the fact that there is no consensus in the scientific literature about significant changes over 1993 to 2012 in the various components of the water cycle (rainfall, evaporation, discharge, water storage) in this region. The second one is that the influence of upstream river discharge on the delta and coastal water levels depends on the hydrological connectivity with the main river, as well as the strength of riverine input relative to other forcings (54). For the GBM river, since the river connectivity is not well known, we assume that a large part of the freshwater discharge flowing into the delta is localized within the main river channel and that most of the flow is discharged into the Bay of Bengal. Therefore, we assume that only a relatively small fraction of the GBM freshwater is distributed through other secondary channels into large areas of the deltaic floodplain and into shallow water areas. For a more complete discussion of this point region by region, see the Material and Methods.
Given the low level of correlation between RWL and ASL in the R6 region (r = 0.4, Table 1), the difference between RWL and ASL would not be relevant, and thus we do not consider this region in the following. The geology of this region is distinct from the rest of the delta. In this region of enhanced tectonic activity (55) understanding of the water-level gauge signals requires further investigation.
The VLM trends are not found to be significant except in the R3-Ganges tidal floodplain where the estimated rate is 4.4 ± 2.6 mm/y. It is important to note here that nonsignificance of VLM rates does not mean that there is no VLM in the regions R1, R2, R4, and R5. It only means that the method fails to distinguish the VLM trend, if it exists, from the fluctuations presented in the original data. However, by Monte Carlo resampling of VLM series (24), we obtained an extensive surrogate dataset with the statistical properties of the original VLM series. This statistical distribution provides the bounds on the magnitude of the VLM rate that can be distinguished from the noise. Thus, a 10% lower bound in the VLM rates distribution (subsidence corresponds to VLM < 0) can be interpreted as a maximum expected rate of subsidence. The rate of subsidence, if present, should not be larger than the subsidence maximum expected rate defined before. Otherwise, this trend would be inferred as statistically significant.
Following this method, the maximum expected subsidence rate reaches 1.5 mm/y in R1 and 2.4 mm/y in R2, ∼7 mm/y in R3 and R4, and ∼5 mm/y in R5 (Table 1). We note here that with the regional variations of the maximum expected subsidence rates reported in this study, no firm conclusion can be drawn on regional variations of mean subsidence rates. However, a lower bound of subsidence rates can be inferred from Krien et al. (17), who estimated the contribution of sediment loading to present subsidence rates of ∼1 mm/y in R1, ∼2 mm/y in R2 and R4, and 2 to 3 mm/y in R3 and R5. Once combined with the maximum expected subsidence rates reported in this study, it appears clear that the subsidence is not uniform within the delta and increases toward the east (Fig. 4). Our findings tend to support the conclusions of Sarker et al. (56) and Brammer (57), among other authors, who claimed that, over the contemporary period and at the regional scale, the subsidence rates through the delta are within the range of a few millimeters per year and the reported rates of 10 to 20 mm/y (Fig. 4), even if true locally, do not represent the regional picture.
What Relative Sea-Level Rise May Be Expected by 2050 and 2100 in the GBM Delta?
The subsidence rates that we obtain could be added to sea-level projections to further refine estimates of relative sea-level rise in the delta. Nowadays there is no specific sea-level projection for the West Bengal and Bangladesh coasts; there is only a regional coverage as “South Asia.” Nevertheless, for the Bay of Bengal, the IPCC Fifth Assessment Report (AR5) (2) provided projected relative sea-level changes from the Coupled Model Intercomparison Project 5 (CMIP5) (SI Appendix, Table S3). The predicted relative sea-level increase (relative to the 1986 to 2005 period; SI Appendix, Table S3) is in the range of 14 to 30 cm by 2050 and 34 to 74 cm by 2100 under a greenhouse gas emission mitigation scenario (Representative Concentration Pathway [RCP] 4.5).
If we assume the regional maximum expected subsidence rates estimated by our method are representative of centennial and longer periods, our first-order rates indicate a maximum subsidence of ∼7, 11, 32, 32, and 23 cm by 2050 in R1 to R5 regions, respectively. Here, for a consistent treatment of uncertainties across physical processes, we consider the mean value plus one SD for sea-level changes due to vertical land motions and the upper bound of the likely range for sea-level change projections. Since the AR5, projections of sea-level rise due to Antarctica melting have been revised upward due to increased understanding of the marine ice sheets instabilities (MISI) probably already affecting 2 major outlet glaciers in West Antarctica (58, 59) and potential future marine ice cliffs instabilities (60). However, we note that the upper projections of Golledge et al. (61), which include MISI, are within the error bars of the AR5 projections, except for RCP8.5 (4 cm difference by 2100; SI Appendix, Table S3), and that by 2050, AR5 sea-level projections remain the reference as it is too early for the onset of MISI.
Thus by 2050, on the basis of the RCP4.5 scenario upper limit, the regional subsidence rates will enhance the relative sea-level rise by ∼23%, 36%, and 78% in R1, R2, and R5 regions, respectively, reaching more than 60 cm in the R3-Ganges tidal floodplain and the R4-Jamuna/Brahmaputra floodplain. By 2100, most of the delta could undergo a relative sea-level rise of ∼100 cm and could reach more than ∼140 cm in R3 and R4, which would already be higher than the upper bound of the likely range value of relative sea-level rise under a high greenhouse gas emission scenario (i.e., RCP8.5: 50 to 103 cm) (2). Although, these regional values for projected total relative sea-level rise must be taken with caution due to their large uncertainties, our analysis confirms that the total relative sea-level rise will undoubtedly significantly impact the coastal GBM delta in the near future. The east of the GBM delta (R3, R4, and R5; Fig. 4), where the population density is very high and where more than 28 million people (Fig. 4) live in higher-risk areas today, will be the most exposed to the future total sea-level rise and its consequences in terms of flooding. It thus appears clear that VLM is a key part of the GBM delta’s future survival. We point out that our observational analysis cannot discriminate between the causes of VLM and cannot give any indication on the origin of local subsidence. These rates could be considerably amplified at the sites of high local subsidence due, for example, to groundwater pumping and/or other anthropogenic factors. Beyond its immediate relevance for the GBM delta RWL assessment, this work highlights the importance of a regionally integrated approach to remedy the scarcity and nonavailability of data and could be applied to other deltas to provide a synoptic view of their future evolution.
Materials and Methods
Water-Level Gauge Network.
The 90 water-level gauge records (listed in SI Appendix, Table S1) used in this study were provided by the Bangladesh Water Development Board (BWDB). These data can be purchased from BWDB (http://www.hydrology.bwdb.gov.bd/index.php). As we are mainly interested by the sea-level dynamics, we select only the stations where water levels are influenced by the tides (SI Appendix, Fig. S4). Here we use monthly water-level records, estimated from daily water-level data. We used also 11 monthly tide gauge records from the PSMSL database (19), freely available at https://www.psmsl.org/). Over the studied period, 1968 to 2012, the water-level time series considered have an average length of 18 ± 7 y (ranging from 3 to 45 y) (see SI Appendix, Table S1 for more details). The WL records are neither corrected for the inverted barometer nor corrected for glacial isostatic adjustment. The outliers were detected and removed by using the Rosner’s test with significance level of 0.05 (62). The seasonal signal is removed by subtracting the means for each month. The station-pairwise correlation coefficients are also given in SI Appendix, Fig. S5. The correlation coefficients are generally greater than 0.6.
Regionalization of Water-Level Gauges.
We provided a simple logical record regionalization based on different parameters: Geographical location, hydrological network, M2 tidal constituent amplitude, and physiographic area. The main characteristics of each regional group are presented in SI Appendix, Fig. S4 and synthetized in Table 2.
Table 2.
Regionalization criteria
| Location | Oceanic tide amplitude zone | Physiographic units | River network | |
| R1 | West | High | — | Hooghly River |
| R2 | Center West | High | Ganges floodplain and Sundarbans | Ganges secondary channels |
| R3 | Center | Low | Ganges tidal floodplain | Ganges–Brahmaputra–Meghna secondary channels |
| R4 | North | Very low | Jamuna floodplain | Brahmaputra–Meghna secondary channels |
| R5 | Center East | Low | Ganges and Meghna floodplain | Ganges–Brahmaputra–Meghna River |
| R6 | East | Heterogeneous | Chittagong coastal plain | — |
Ganges and Brahmaputra Discharge Time Series.
Along with the water-level gauge network, the BWDB also collects river discharge at several locations in the delta, including the Ganges and Brahmaputra basin outlet stations before the 2 rivers meet: The Hardinge Bridge station (24.07°N; 89.03°E) for the Ganges and the Bahadurabad station (25.15°N; 89.70°E) for the Brahmaputra. Here we use monthly mean Ganges and Brahmaputra river discharges (1968 to 2012), estimated from daily discharge data, derived from water levels measured at both staging stations and converted into discharge using stage–discharge relationships (63). These data can be purchased from BWDB (http://www.hydrology.bwdb.gov.bd/index.php).
Satellite Altimetry Dataset.
We use the reprocessed ESA Sea Level Climate Change Initiative v1.1 gridded altimetry product (monthly grids with a spatial resolution of 0.25°) over 1993 to 2012 that is freely available at http://www.esa-sealevel-cci.org/products (64). In this study, no Dynamic Atmospheric Correction (65) is applied to the altimetry product, to take into account the barometric pressure and wind effects on the sea surface height. For each region, we searched the (detrended) gridded altimetry time series most correlated with the (detrended) RWL reconstruction in a radius of 2° around the gauge station location which is nearest to the coast.
Surface Water Storage.
Variations of monthly SWS (38) in the Ganges–Brahmaputra–Meghna basin are estimated over 15 y (1993 to 2007) using a hypsographic approach based on the combination of topographic information and the Global Inundation Extent Multi-Satellite (66). It provides the amount of freshwater store in the surface hydrological reservoir (rivers, lakes, floodplains, wetlands) and its temporal variations. These data are freely available and can be obtained from ref. 38.
ENSO Event Definition.
For the purposes of this study, we define El Niño (La Niña) as events when the Niño-3.4 SST anomaly averaged from November through January exceeds ±0.75 × SD. Using the Niño-3.4 SST anomaly, derived from Hadley Centre Sea Ice and Sea Surface Temperature data set (HadISST) version 1 (34), for the period 1968 to 2012 gives El Niño years 1972, 1977, 1982, 1986, 1987, 1991, 1994, 1997, 2002, 2006, 2009 and La Niña years 1970, 1973, 1975, 1983, 1984, 1988, 1998, 1999, 2007, 2010.
IOD Event Definition.
In the same way, we define positive IOD (pIOD) and negative IOD (nIOD) as events when the Dipole Mode Index Sea Surface Temperature (DMI SST) anomaly averaged from July through November exceeds ±0.75 × SD, respectively. Using the DMI SST anomaly, derived from HadISST1 (34), for the period 1968 to 2012 gives pIOD years 1972, 1976, 1982, 1983, 1987, 1994, 1997, 2006, 2012 and nIOD years 1980, 1981, 1984, 1992, 1996, 1998, 2005, 2010.
Statistical Significance and Uncertainty of Linear Trends.
All of the linear trend estimates are obtained by the robust regression model with the bisquare weight function (67). The significance and uncertainty of the linear trends are estimated by a random phase method to maintain the serial correlation structure of RWL, ASL, and VLM original series (24) and given at 1σ significance level. The method is based on Monte Carlo resampling in the frequency domain. In this approach a large set of random time series with similar proprieties to the original series is generated from the power spectrum estimated from the original data.
Regional RWL and Freshwater Trend Influence.
The regions R1, R2, and R3 are located in secondary channels and are thus expected to receive only a relatively small fraction of the GBM freshwater. The hypothesis that RWL trends are only marginally influenced by river influx in these regions is further supported by the good agreement observed between ASL and RWL (Fig. 2) and the conclusions of Han and Webster (36) and Durand et al. (68), who found, using hydrodynamical simulations, that the influence of GBM river discharge on sea-level variability along the rim of the northern Bay of Bengal is negligible.
In R4, over the 18 water-level gauge stations used in the RWL reconstruction, only 4 are located along the main river channel (Fig. 1). Four others are located along the Meghna river mainstream, with a discharge representing only ∼10% of Ganges–Brahmaputra river discharge (69). The 10 remaining gauges are located along secondary rivers and streams. Therefore, in R4, we assume that the RWL reconstruction provides consistent water-level fluctuations which are not, or almost not, directly influenced by potential Ganges–Brahmaputra and Meghna freshwater trends.
The assumption of negligible freshwater trend contribution is probably not valid in R5, where most of the water gauges are located along the banks of the GBM main river channel. However, estimating the contribution of the river discharge to the RWL over 1993 to 2012 is a nonresolved challenge.
The first one is that no significant linear trend over 1993 to 2012 is detected in the Ganges and Brahmaputra discharges (or in the aggregated discharge of the 2 rivers). Even assuming that a significant trend over 1993 to 2012 would have been detected, estimating its contribution to the RWL trend downstream in R5 is still another true challenge. Several hydrodynamic models are currently being developed for this purpose, but they still require many more improvements (taking into account for instance rainfall, river network connectivity, groundwater flows, and eventually human activities such as water pumping) and validations before being able to provide robust results over 20-y simulations.
RWL Reconstruction Method.
Following Davis et al. (21) and Buble et al. (22) we adopted the following model for variations of the observed monthly water level:
| [1] |
is time of observation (month); is observed monthly averaged water level for the ith site at month is local water-level offset to be estimated for the ith site; is regional common-mode water-level offset, identical for all sites, for the month εij is the observational error for the month and the ith site; and is local water-level rate for the ith site.
The model parameters are estimated by minimization of difference between the observed and predicted water levels by the least-squares method. We followed the hierarchical inversion scheme developed by Buble et al. (22), named method I, for separating the common mode variations from spatially varying part of the signal.
The method consists in minimizing the functional
| [2] |
where d is the vector of observations m is a vector of offsets and linear trends at every station, is the common mode, and A and B are matrices relating m and n to d. This problem is underconstrained and nonunique. The method I developed by Buble et al. (22) addresses this nonuniqueness by expressing the common mode vector as follows:
| [3] |
where
| [4] |
The functional 2 can be rearranged as
| [5] |
where
| [6] |
is an orthogonal projector on the null space of B. As is a projector, is a projector onto the orthogonal space. So, an estimate for vector m can be defined as
| [7] |
where
| [8] |
By construction, the vector ensures that the vector contains no common mode components.
The common mode variations in the network of WL gauges characterize changes of water level proper to each region (Fig. 1) and, by definition, represent the WL changes at the regional scale. Note that the method can be applied also at the epochs for which observations at some stations are missed (21).
The regional RWL variations thus obtained were tested for the presence of outliers and shifts. Specifically, we applied Pettitt’s test (70) that is commonly used to detect a single change in mean occurring in climate time series to all of the regional RWL reconstructions. We detected a regional change in mean in the RWL data in R5 at the end of 2005 (P < 0.001, where P is the probability that the test detects shift when none is present). This shift was not detected in the ASL time series and in the other regional RWL reconstructions and we did not find any straightforward explanation for this shift. The attribution of this regional change in mean to causal factors is out of the scope of this paper, as it requires in-depth investigation of tectonic or other physical processes that could explain it. Consequently, in the region R5, we considered the regional RWL reconstruction spanning only the period 1968 to 2004.
Data Availability.
The monthly RWL reconstruction time series over 1968 to 2012 for each of the 6 regions are available in Zenodo (DOI: 10.5281/zenodo.3573771) (71).
Supplementary Material
Acknowledgments
This work was supported by the French Research Agency (Agence Nationale de la Recherche [ANR]) under the Deltas Under Global Impact of Change (DELTA) project (ANR-17-CE03-0001) and is partially supported by Belmont Forum Coastal Vulnerability Program via the ANR (ANR-13-JCLI-0002; http://Belmont-BanDAiD.org or http://Belmont-SeaLevel.org) and the US NSF (Grant ICER-1342644). M.K. acknowledges the Centre national d’études spatiales (CNES) through the project Terre Solide, Océan, Surfaces Continentales et Atmosphère (TOSCA)/GEOMINING. G.L.C. acknowledges the European Research Area for Climate Services (ERA4CS)/Integrating Sea-Level Projections in Climate Services for Coastal Adaptation (INSeaPTION) project (Grant 690462). C.K.S. is also partially supported by the Strategic Priority Research Program of the Chinese Academy of Sciences (Grant XDA19070302), and the National Key R&D Program of China (Grant 2017YFA0603103). We also thank C. Mayet and L. Testut for providing the M2 tidal constituent amplitude. Portions of this document include intellectual property of Esri and its licensors and are used under license. Copyright © 2019 Esri and its licensors. All rights reserved.
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission.
Database deposition: Data reported in this paper have been deposited in Zenodo (http://doi.org/10.5281/zenodo.3573771).
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.1912921117/-/DCSupplemental.
References
- 1.Syvitski J. P., et al. , Sinking deltas due to human activities. Nat. Geosci. 2, 681–686 (2009). [Google Scholar]
- 2.IPCC AR5 , Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, Stocker T. F., et al., Eds. (Cambridge University Press, Cambridge, UK, 2013). [Google Scholar]
- 3.Becker M., Karpytchev M., Papa F., “Hotspots of relative sea level rise in the tropics” in Tropical Extremes, Venugopal V., Sukhatme J., Murtugudde R., Roca R., Eds. (Elsevier, 2019), chap. 7, pp. 203–262. [Google Scholar]
- 4.Streatfield P. K., Karar Z. A., Population challenges for Bangladesh in the coming decades. J. Health Popul. Nutr. 26, 261–272 (2008). [PMC free article] [PubMed] [Google Scholar]
- 5.Worldpop , Data from “Asia continental population datasets (2000 - 2020).” Worldpop. https://www.worldpop.org/doi/10.5258/SOTON/WP00013. Accessed 1 March 2019.
- 6.Warrick R. A., Ahmad Q. K., The Implications of Climate and Sea-Level Change for Bangladesh (Springer Science & Business Media, 2012). [Google Scholar]
- 7.FFWC , “Annual flood report 2012” (Flood Forecasting & Warning Centre, Bangladesh Water Development Board, Dhaka, Bangladesh, 2012). [Google Scholar]
- 8.Krien Y., et al. , Improved bathymetric dataset and tidal model for the northern Bay of Bengal. Mar. Geod. 39, 422–438 (2016). [Google Scholar]
- 9.Krien Y., et al. , Towards improved storm surge models in the northern Bay of Bengal. Cont. Shelf Res. 135, 58–73 (2017). [Google Scholar]
- 10.Needham H. F., Keim B. D., Sathiaraj D., A review of tropical cyclone-generated storm surges: Global data sources, observations, and impacts: A review of tropical storm surges. Rev. Geophys. 53, 545–591 (2015). [Google Scholar]
- 11.Bangladesh Water Development Board , Surface water database. http://www.hydrology.bwdb.gov.bd/index.php?pagetitle=water_level&sub3=185&_subid=131&id=125&id2=126. Accessed 1 October 2018.
- 12.Pethick J., Orford J. D., Rapid rise in effective sea-level in southwest Bangladesh: Its causes and contemporary rates. Global Planet. Change 111, 237–245 (2013). [Google Scholar]
- 13.CCC , “Assessment of sea level rise on Bangladesh coast through trend analysis” (Climate Change Cell, Department of Environment, Ministry of Environment and Forests, Dhaka, Bangladesh, 2016). [Google Scholar]
- 14.Brown S., Nicholls R. J., Subsidence and human influences in mega deltas: The case of the Ganges-Brahmaputra-Meghna. Sci. Total Environ. 527–528, 362–374 (2015). [DOI] [PubMed] [Google Scholar]
- 15.Karpytchev M., et al. , Contributions of a strengthened early Holocene monsoon and sediment loading to present‐day subsidence of the Ganges‐Brahmaputra delta. Geophys. Res. Lett. 45, 1433–1442 (2018). [Google Scholar]
- 16.Grall C., et al. , A base-level stratigraphic approach to determining Holocene subsidence of the Ganges–Meghna–Brahmaputra Delta plain. Earth Planet. Sci. Lett. 499, 23–36 (2018). [Google Scholar]
- 17.Krien Y., et al. , Present-day subsidence in the Ganges-Brahmaputra-Meghna delta: Eastern amplification of the Holocene sediment loading contribution. Geophys. Res. Lett. 49, 10764–10772 (2019). [Google Scholar]
- 18.Higgins S. A., et al. , InSAR measurements of compaction and subsidence in the Ganges-Brahmaputra Delta, Bangladesh. J. Geophys. Res. Earth Surf. 119, 1768–1781 (2014). [Google Scholar]
- 19.Holgate S. J., et al. , New data systems and products at the permanent service for mean sea level. J. Coast. Res. 288, 493–504 (2013). [Google Scholar]
- 20.Akter J., Sarker M. H., Popescu I., Roelvink D., Evolution of the Bengal delta and its prevailing processes. J. Coast. Res. 321, 1212–1226 (2015). [Google Scholar]
- 21.Davis J. L., Mitrovica J. X., Scherneck H.-G., Fan H., Investigations of Fennoscandian glacial isostatic adjustment using modern sea level records. J. Geophys. Res. 104, 2733–2747 (1999). [Google Scholar]
- 22.Buble G., Bennett R. A., Hreinsdóttir S., Tide gauge and GPS measurements of crustal motion and sea level rise along the eastern margin of Adria. J. Geophys. Res. Solid Earth 115, B02404 (2010). [Google Scholar]
- 23.Dangendorf S., et al. , A reconciled estimate of 20th century global mean sea level rise. Sea Level Rise 16, 6 (2018). [Google Scholar]
- 24.Ebisuzaki W., A method to estimate the statistical significance of a correlation when the data are serially correlated. J. Clim. 10, 2147–2153 (1997). [Google Scholar]
- 25.Singh O. P., Spatial variation of sea level trend along the Bangladesh coast. Mar. Geod. 25, 205–212 (2002). [Google Scholar]
- 26.Sarwar M. G. M., “Sea-level rise along the coast of Bangladesh” in Disaster Risk Reduction Approaches in Bangladesh, Shaw R., Mallick F., Islam A., Eds. (Springer, 2013), pp. 217–231. [Google Scholar]
- 27.Passalacqua P., Lanzoni S., Paola C., Rinaldo A., Geomorphic signatures of deltaic processes and vegetation: The Ganges-Brahmaputra-Jamuna case study. J. Geophys. Res. Earth Surf. 118, 1838–1849 (2013). [Google Scholar]
- 28.Wilson C. A., Goodbred S. L. Jr, Construction and maintenance of the Ganges-Brahmaputra-Meghna delta: Linking process, morphology, and stratigraphy. Annu. Rev. Mar. Sci. 7, 67–88 (2015). [DOI] [PubMed] [Google Scholar]
- 29.Chowdhury M. R., The El Niño-Southern Oscillation (ENSO) and seasonal flooding–Bangladesh. Theor. Appl. Climatol. 76, 105–124 (2003). [Google Scholar]
- 30.Saji N. H., Goswami B. N., Vinayachandran P. N., Yamagata T., A dipole mode in the tropical Indian Ocean. Nature 401, 360–363 (1999). [DOI] [PubMed] [Google Scholar]
- 31.Aparna S. G., McCreary J. P., Shankar D., Vinayachandran P. N., Signatures of Indian Ocean Dipole and El Niño–Southern Oscillation events in sea level variations in the Bay of Bengal. J. Geophys. Res. Oceans 117, C10012 (2012). [Google Scholar]
- 32.Sreenivas P., Gnanaseelan C., Prasad K. V. S. R., Influence of El Niño and Indian Ocean Dipole on sea level variability in the Bay of Bengal. Global Planet. Change 80–81, 215–225 (2012). [Google Scholar]
- 33.Deepa J. S., Gnanaseelan C., Kakatkar R., Parekh A., Chowdary J. S., The interannual sea level variability in the Indian Ocean as simulated by an Ocean General Circulation Model. Int. J. Climatol. 38, 1132–1144 (2018). [Google Scholar]
- 34.Rayner N. A., et al. , Global analyses of sea surface temperature, sea ice, and night marine air temperature since the late nineteenth century. J. Geophys. Res., 10.1029/2002JD002670 (2003). [DOI] [Google Scholar]
- 35.Ali A., Climate change impacts and adaptation assessment in Bangladesh. Clim. Res. 12, 109–116 (1999). [Google Scholar]
- 36.Han W., Webster P. J., Forcing mechanisms of sea level interannual variability in the Bay of Bengal. J. Phys. Oceanogr. 32, 216–239 (2002). [Google Scholar]
- 37.Ikeuchi H., et al. , Modeling complex flow dynamics of fluvial floods exacerbated by sea level rise in the Ganges–Brahmaputra–Meghna Delta. Environ. Res. Lett. 10, 124011 (2015). [Google Scholar]
- 38.Salameh E., et al. , Fifteen years (1993–2007) of surface freshwater storage variability in the Ganges-Brahmaputra river basin using multi-satellite observations. Water 9, 245 (2017). [Google Scholar]
- 39.Cleveland W. S., Robust locally weighted regression and smoothing scatterplots. J. Am. Stat. Assoc. 74, 829–836 (1979). [Google Scholar]
- 40.Lee S.-K., et al. , Pacific origin of the abrupt increase in Indian Ocean heat content during the warming hiatus. Nat. Geosci. 8, 445 (2015). [Google Scholar]
- 41.Nieves V., Willis J. K., Patzert W. C., GLOBAL WARMING. Recent hiatus caused by decadal shift in Indo-Pacific heating. Science 349, 532–535 (2015). [DOI] [PubMed] [Google Scholar]
- 42.Thompson P. R., Piecuch C. G., Merrifield M. A., McCreary J. P., Firing E., Forcing of recent decadal variability in the equatorial and North Indian Ocean. J. Geophys. Res. Oceans 121, 6762–6778 (2016). [Google Scholar]
- 43.Srinivasu U., et al. , Causes for the reversal of North Indian Ocean decadal sea level trend in recent two decades. Clim. Dyn. 49, 3887–3904 (2017). [Google Scholar]
- 44.Nerem R. S., et al. , Climate-change-driven accelerated sea-level rise detected in the altimeter era. Proc. Natl. Acad. Sci. U.S.A. 115, 2022–2025 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Milliman J. D., Broadus J. M., Gable F., Environmental and economic implications of rising sea level and subsiding deltas: The Nile and Bengal examples. Ambio 18, 340–345 (1989). [Google Scholar]
- 46.Ericson J. P., Vörösmarty C. J., Dingman S. L., Ward L. G., Meybeck M., Effective sea-level rise and deltas: Causes of change and human dimension implications. Global Planet. Change 50, 63–82 (2006). [Google Scholar]
- 47.Sahu P., Sikdar P. K., Threat of land subsidence in and around Kolkata city and east Kolkata wetlands, West Bengal, India. J. Earth Syst. Sci. 120, 435–446 (2011). [Google Scholar]
- 48.Chatterjee R. S., et al. , Subsidence of Kolkata (Calcutta) city, India during the 1990s as observed from space by differential synthetic aperture radar interferometry (D-InSAR) technique. Remote Sens. Environ. 102, 176–185 (2006). [Google Scholar]
- 49.Steckler M., et al. , Modeling Earth deformation from monsoonal flooding in Bangladesh using hydrographic, GPS, and Gravity Recovery and Climate Experiment (GRACE) data. J. Geophys. Res. Solid Earth 115, B08407 (2010). [Google Scholar]
- 50.Steckler M., et al. , GPS velocities and structure across the Burma accretionary prism and shillong anticline in Bangladesh. AGU Fall Meet. Abstr. 51, T51F–2667 (2012). [Google Scholar]
- 51.Ostanciaux É., Husson L., Choblet G., Robin C., Pedoja K., Present-day trends of vertical ground motion along the coast lines. Earth Sci. Rev. 110, 74–92 (2012). [Google Scholar]
- 52.Pfeffer J., Allemand P., The key role of vertical land motions in coastal sea level variations: A global synthesis of multisatellite altimetry, tide gauge data and GPS measurements. Earth Planet. Sci. Lett. 439, 39–47 (2016). [Google Scholar]
- 53.Wöppelmann G., Marcos M., Vertical land motion as a key to understanding sea level change and variability. Rev. Geophys. 54, 64–92 (2016). [Google Scholar]
- 54.Hiatt M., et al. , Drivers and impacts of water level fluctuations in the Mississippi River delta: Implications for delta restoration. Estuar. Coast. Shelf Sci. 224, 117–137 (2019). [Google Scholar]
- 55.Hossain M. S., Khan M. S. H., Chowdhury K. R., Abdullah R., “Synthesis of the tectonic and structural elements of the Bengal Basin and its surroundings” in Tectonics and Structural Geology: Indian Context, Mukherjee S., Ed. (Springer, 2019), pp. 135–218. [Google Scholar]
- 56.Sarker M. H., Choudhury G. A., Akter J., Hore S. K., Bengal Delta not sinking at a very high rate. Daily Star, 23 December 2012. https://www.thedailystar.net/news-detail-262153. Accessed 1 April 2019.
- 57.Brammer H., Bangladesh’s dynamic coastal regions and sea-level rise. Clim. Risk Manage. 1, 51–62 (2014). [Google Scholar]
- 58.Favier L., et al. , Retreat of Pine Island Glacier controlled by marine ice-sheet instability. Nat. Clim. Chang. 4, 117 (2014). [Google Scholar]
- 59.Joughin I., Smith B. E., Medley B., Marine ice sheet collapse potentially under way for the Thwaites Glacier Basin, West Antarctica. Science 344, 735–738 (2014). [DOI] [PubMed] [Google Scholar]
- 60.DeConto R. M., Pollard D., Contribution of Antarctica to past and future sea-level rise. Nature 531, 591–597 (2016). [DOI] [PubMed] [Google Scholar]
- 61.Golledge N. R., et al. , The multi-millennial Antarctic commitment to future sea-level rise. Nature 526, 421–425 (2015). [DOI] [PubMed] [Google Scholar]
- 62.Rosner B., On the detection of many outliers. Technometrics 17, 221–227 (1975). [Google Scholar]
- 63.Papa F., Durand F., Rossow W. B., Rahman A., Bala S. K., Satellite altimeter-derived monthly discharge of the Ganga-Brahmaputra River and its seasonal to interannual variations from 1993 to 2008. J. Geophys. Res., 10.1029/2009JC006075 (2010). [DOI] [Google Scholar]
- 64.Ablain M., et al. , “Satellite altimetry-based sea level at global and regional scales” in Integrative Study of the Mean Sea Level and Its Components, Cazenave A., Champollion N., Paul F., Benveniste J., Eds. (Space Sciences Series of ISSI, Springer International Publishing, 2017), pp. 9–33. [Google Scholar]
- 65.Carrère L., Lyard F., Modeling the barotropic response of the global ocean to atmospheric wind and pressure forcing–Comparisons with observations. Geophys. Res. Lett. 30, 1275 (2003). [Google Scholar]
- 66.Prigent C., Papa F., Aires F., Rossow W. B., Matthews E., Global inundation dynamics inferred from multiple satellite observations, 1993–2000. J. Geophys. Res. 112, D12107 (2007). [Google Scholar]
- 67.Holland P. W., Welsch R. E., Robust regression using iteratively reweighted least-squares. Commun. Stat. Theory Methods 6, 813–827 (1977). [Google Scholar]
- 68.Durand F., et al. , Impact of continental freshwater runoff on coastal sea level. Surv. Geophys. 40, 1437–1466 (2019). [Google Scholar]
- 69.Papa F., et al. , Ganga-Brahmaputra river discharge from Jason-2 radar altimetry: An update to the long-term satellite-derived estimates of continental freshwater forcing flux into the Bay of Bengal. J. Geophys. Res. 117, C11021 (2012). [Google Scholar]
- 70.Pettitt A. N., A non-parametric approach to the change-point problem. J. R. Stat. Soc. Ser. C Appl. Stat. 28, 126–135 (1979). [Google Scholar]
- 71.Becker et al., Supporting data for Becker et al. PNAS (doi: 10.1073/pnas.1912921117). Zenodo. https://zenodo.org/record/3573771. Deposited 13 December 2019.
- 72.Brammer H., Antoine J., Kassam A. H., van Velthuizen H. T., “Land resource appraisal of Bangladesh for agricultural development. Report 2: Agroecological regions of Bangladesh” (Tech. Rep. BGD/81/035, Food and Agriculture Organization of the United Nations, Rome, Italy, 1988).
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The monthly RWL reconstruction time series over 1968 to 2012 for each of the 6 regions are available in Zenodo (DOI: 10.5281/zenodo.3573771) (71).