Kinematic flexibility allows bumblebees to increase energetic efficiency when carrying heavy loads

Flight costs are linked to how quickly bumblebees flap their wings; bees can choose to fly more efficiently when heavily loaded.

Abstract

Foraging bees fly with heavy loads of nectar and pollen, incurring energetic costs that are typically assumed to depend on load size. Insects can produce more force by increasing stroke amplitude and/or flapping frequency, but the kinematic response of a given species is thought to be consistent. We examined bumblebees (Bombus impatiens) carrying both light and heavy loads and found that stroke amplitude increased in proportion to load size, but did not predict metabolic rate. Rather, metabolic rate was strongly tied to frequency, which was determined not by load size but by the bee’s average loading state and loading history, with heavily loaded bees displaying smaller changes in frequency and smaller increases in metabolic rate to support additional loading. This implies that bees can increase force production through alternative mechanisms; yet, they often choose the energetically costly option of elevating frequency, suggesting associated performance benefits that merit further investigation.

INTRODUCTION

Foraging eusocial bees can spend many hours per day collecting and carrying loads of nectar and pollen back to their nest to meet the energetic and nutritional requirements of the queen, other workers, and developing brood (1, 2). The quantity of resources collected by foragers is critical to hive growth and the production of new reproductive queens (3) and thus to the fitness of the hive as a whole. Numerous studies over the past several decades have addressed the question of how foraging behavior of eusocial bees is optimized to enhance hive fitness, with experimental and theoretical studies particularly focused on the question of whether individual foragers optimize their net energy gain (energy intake minus cost; i.e., bringing back as much energy as possible once accounting for the cost of foraging) or their net foraging efficiency (net energy gain divided by cost; i.e. foraging so as to minimize their costs) (4, 5), perhaps to reduce wear and tear and increase the longevity of individual workers.

These studies have examined how foraging behavior is or should be affected by resource quality (e.g., nectar concentration), resource distance, handling times, flight times, and numerous other factors, deriving predictions of how far individual foragers should fly and how fully they should load their crops with nectar to optimize foraging performance. Underlying most of these studies is the assumption that the cost of flight increases linearly with the weight of the load being carried by foraging bees, an assumption with important implications for estimated flight costs, as both bumblebees and honeybees are known to regularly carry heavy loads in the wild [e.g., up to 77% of body mass in bumblebees (6) and up to 92% in honeybees (7)].

However, data documenting the costs of load carrying in bees are sparse, with past studies mainly confined to honeybees, and the overall findings are somewhat inconclusive. Feuerbacher et al. (8) found no relationship between total mass (body mass plus load) and metabolic rate in foraging honeybees returning with a range of nectar and pollen loads. However, when testing bees before versus after foraging, the researchers did find a small (6%) increase in metabolic rate between unloaded bees commencing foraging and returning bees carrying loads of 27 to 40% body mass (8). Several other studies have shown that the metabolic rate of honeybees is affected by nectar flow rate (i.e., resource quality) but not by loading mass (9, 10), leading to the suggestion that metabolic rate in honeybees may be more strongly affected by motivational state than by the total mass they are supporting in flight. In bumblebees, only one study has addressed the effects of loading on metabolic rate, showing an increase in metabolic rate with larger nectar loads (11). However, all measurements were performed on one individual queen bee (whose physiology could differ substantially from workers), flown at multiple temperatures after consuming different amounts of nectar, with unknown recovery time between flight tests.

To carry a load during flight, bees must increase their aerodynamic force output, and flying insects rely primarily on unsteady mechanisms of force production during both wing translation (when the wings sweep back and forth) and stroke reversal (when wings rotate at the end of each half-stroke to reverse direction). However, the relative energetic costs of increasing force output via different unsteady mechanisms are not yet well understood. Insects that demonstrate high-amplitude wing strokes derive much of their aerodynamic force from the translational portion of the stroke cycle [e.g., fruit flies with a stroke amplitude of ~140° (12)], whereas those with low-amplitude wing strokes derive more force from unsteady mechanisms occurring at stroke reversal [e.g., honeybees with an amplitude of ~90° (13) or mosquitoes with an amplitude of ~40° (14)]. Bumblebees fly with a relatively high stroke amplitude of ~110° to 140° (15) and thus are likely to rely more on forces produced during wing translation than those produced during stroke reversals (13), although the latter forces will also play a role (Fig. 1). Previous studies have shown that unsteady forces produced during the translational portion of the wing stroke (i.e., forces related to production of an attached leading-edge vortex) can be estimated using a quasi-steady modeling approach, incorporating a modified force coefficient that accounts for unsteady force production during wing translation (16). Thus, in bumblebees, the largest component of aerodynamic force production should be proportional to the translational force coefficient (C_Ft) times wing area (S) and the average wing velocity squared (U_w²; Fig. 1).

Fig. 1. Forces produced by loaded bees can be estimated from wing velocity, derived from measured stroke amplitude and flapping frequency.

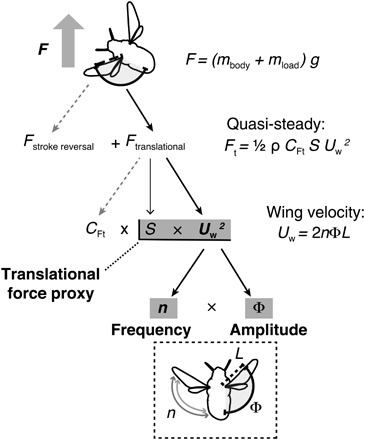
Variables related to force production by bees carrying loads are shown, with measured variables used in statistical analyses shaded in gray. Total force (F) produced by a flying bee to support the mass of its body (m_body) plus a load (m_load) consists of forces produced at stroke reversal (not measured, indicated by dashed arrow) plus forces produced during wing translation, which are presumed to be larger in bumblebees than those produced at stroke reversal. Unsteady translational forces (F_t) can be estimated via quasi-steady modeling and are approximated in this study by the product of total wing area (S) and average wing velocity squared (U_w²), neglecting potential changes in the unsteady, translational force coefficient (C_Ft), which are unknown. Wing velocity is a function of flapping frequency (n) and stroke amplitude (Φ). Flapping frequency was measured from audio recordings and stroke amplitude from high-speed videos.

To increase force production during wing translation, bumblebees (with fixed wing area) can increase their translational force coefficient (for example, by changing angle of attack) and/or increase wing velocity. Whereas instantaneous changes in wing angle of attack are challenging to measure and the metabolic consequences of these subtle kinematic changes are unclear, measuring changes in wing velocity is fairly straightforward. Higher average wing velocities can be achieved by increasing flapping frequency (flapping the wings back and forth more rapidly) and/or stroke amplitude (flapping the wings through a wider angle, thus causing them to travel over a longer distance during each flap; Fig. 1)—both of which may affect metabolic rate because of their direct relationship to the power requirements of flight.

To fly, insects must generate enough power to overcome body (or parasite) drag, which resists their forward motion through the air, and induced drag, which is related to the downwash of air accompanying lift production—both of which are also required for fixed-wing aircraft. In addition, because insects rapidly flap their wings back and forth to generate aerodynamic forces, they must overcome drag on the moving wings themselves (profile drag), as well as inertia of the wings as they are decelerated and accelerated in the opposite direction at the end of each half-stroke (17). For a hovering insect (with no forward velocity and thus no parasite drag), induced power is directly proportional to lift and thus to the total weight supported in flight (17). However, profile and inertial power are not tied directly to total weight; instead, these costs depend only on the morphology and kinematics of the flapping wings, although both components may be affected indirectly by total weight through the changes in wing kinematics necessary to produce sufficient lift. Mathematical predictions suggest that these three components of power should be affected differently by changes in stroke amplitude (Φ) versus flapping frequency (n); induced power should be proportional to Φ^−1/2, profile power to Φ³n³, and inertial power to Φ²n³ (18). Thus, the energetic consequences of increasing wing velocity and total force production via changes in amplitude versus frequency will depend on the relative magnitudes of these different types of power requirements for a given animal.

In unloaded, hovering bumblebees, early aerodynamic calculations based on measured wing kinematics suggested that inertial power dominates over profile and induced power (19). Parasite power in forward flight appears to be negligible, as bumblebees display no significant changes in wing kinematics and no increase in power requirements or metabolic rate as forward speed increases from 0 to ~4 m/s (15, 19, 20). Induced power is also thought to play a relatively minor role in the power requirements of most flying insects (19, 21, 22). More recent studies suggest that wing drag coefficients are far higher than assumed in early calculations of bumblebee power requirements, which would increase profile power considerably (13, 22, 23). Work on fruit flies suggests that the profile power required to overcome wing drag is substantially larger than inertial power requirements (21). However, because the amount of elastic energy stored in the thorax (which would offset inertial power requirements) has not been measured, the relative magnitudes of inertial and profile power requirements in bees remain uncertain. Flapping frequency and stroke amplitude have similar effects on profile power, but frequency has a stronger effect on inertial power requirements than stroke amplitude (18); thus, if inertial power requirements in bumblebees are large, then metabolic rate may be particularly sensitive to changes in flapping frequency.

This idea is supported by studies showing that metabolism is correlated with flapping frequency in several species of bees, including orchid bees (24) and honeybees, which alter their flapping frequency to regulate heat production (25). Bumblebee metabolism has also been shown to be correlated with flapping frequency, after taking bee size into account (26). However, these metabolic studies did not examine the contribution of stroke amplitude to metabolism, and stroke amplitude appears to be the more common kinematic mechanism used by bees to increase force production. Studies focused on maximal force production have shown that stroke amplitude is increased until it reaches its anatomical limit of ~140° to 145° in many species of bees, including honeybees [Apis mellifera (27)], common eastern bumblebees [Bombus impatiens (22)], a species of alpine bumblebees [Bombus impetuosus (28)], valley carpenter bees [Xylocopa varipuncta (29)], and several species of orchid bees [multiple genera (30)]. Maximal force production was elicited by a variety of methods in these studies, and although one species (valley carpenter bees) displayed an increase in flapping frequency as well (29), most species did not exhibit a significant change in average flapping frequency with maximal loading [e.g., alpine bumblebees (28) and honeybees (27)].

The lack of any substantial change in flapping frequency in these previous studies could potentially be explained by the mechanical characteristics of the flapping wings and flight motor (composed of asynchronous muscle in hymenopterans), which have classically been described as a mechanical oscillator that may be constrained to operate near its natural frequency (31). However, flies (which also have asynchronous flight muscles) are capable of modulating flapping frequencies over a wide range while varying force production [e.g., 185 to 235 Hz in fruit flies (21)]. A wide range of flapping frequencies has also been reported for bumblebees [155 to 205 Hz in B. impatiens workers (22)], but because of the large variation in body size of bumblebee workers (varying by more than three times in mass), the extent to which individuals are able to modulate flapping frequency remains unclear—individual bumblebees have been shown to display significant repeatability in both flapping frequency and metabolic rate during flight trials separated by several days (26).

Loaded flight is an extremely common occurrence in worker bumblebees, and the size and presumed energetic cost of the loads that bees choose to carry has long been assumed to play a pivotal role in resource acquisition rates and fitness of the hive as a whole. We aimed to investigate the unknown link between individual flight biomechanics and energetics during loaded flight by (i) determining the kinematic changes that bumblebees use to produce additional force when carrying loads and by (ii) elucidating the metabolic consequences of changes in loading, flapping frequency, and stroke amplitude. To achieve this, we designed an experiment in which 30 individual worker bumblebees performed voluntary, stable flight while carrying both light loads (nectar already present in their guts, 13 to 54% of raw body mass) and heavy loads (nectar plus added weight, totaling 57 to 109% of body mass), with the order of light and heavy trials randomized (Fig. 2). We measured metabolic rate, flapping frequency, and stroke amplitude and verified that total force production is strongly tied to changes in these basic kinematic parameters.

Fig. 2. Experimental loading treatments provided repeated measurements on individuals over a range of loading values.

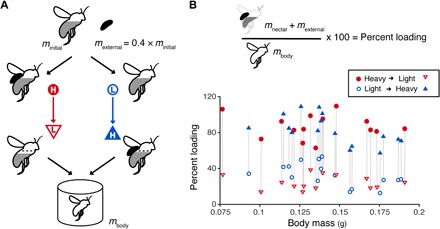
(A) Schematic of experimental protocol. External loads equivalent to 40% of bees’ initial mass (which included an unknown volume of nectar) were created and bees were randomly assigned to one of two treatment orders: heavy loading (H; with added external mass) first and light loading (L; internal load only) second, as shown in red, or light loading first and heavy loading second, as shown in blue. Bees varied in the amount of nectar (internal load) they initially carried, which affected the size of the external load created. The internal load also decreased slightly throughout both trials, as nectar was metabolized to fuel flight. After testing, bees were isolated without access to food until their honey crops were empty to determine body mass, m_body. (B) After obtaining body mass, loading was normalized for body size by determining the percent loading for each trial, calculated as the load mass (internal nectar load plus external load, if present) divided by body mass and multiplied by 100. Experimental values of percent loading versus body mass of bees (N = 30) are shown to illustrate the wide variability in bee size and loading conditions tested, with light (nectar only) loads ranging from 13 to 54% of body mass (open symbols) and heavy loads ranging from 57 to 109% of mass (filled symbols). For each bee, the first loading condition is indicated by a circle and the second condition is indicated by a triangle.

To control for body size and intraspecific differences in flight physiology and behavior (26), we calculated the change in metabolic rate, flapping frequency, and stroke amplitude between light and heavy loading trials within individuals. We used linear models to determine how changes in normalized loading (% loading) affect wing kinematics and how changes in normalized loading and wing kinematics affect metabolic rate. Last, because the magnitude of loading (and changes in loading) varied between individuals, we examined how the average loading state (average % loading over both trials, which varied from 35 to 80%) affects how efficiently bees increase their force production (i.e., how much their metabolic rate changes per unit of additional loading) and the kinematic mechanisms they use to do so.

RESULTS

All individuals tested (N = 30) displayed a higher metabolic rate in the heavy loading condition than in the light loading condition (mean metabolic rate with heavy loading, 11.72 ± 2.46 ml CO₂/hour; light, 9.48 ± 2.39 ml CO₂/hour; table S1). Metabolic rate increased linearly with total mass supported during flight (body mass + load) in both loading conditions (heavy, R² = 0.7277; light, R² = 0.7327; Fig. 3A), but the slope of the relationship was significantly lower in the heavy loading condition (interaction of mass and treatment χ²₁ = 7.17, P = 0.0074).

Fig. 3. Metabolic rate and a proxy for translational force production increased linearly with total mass supported during flight.

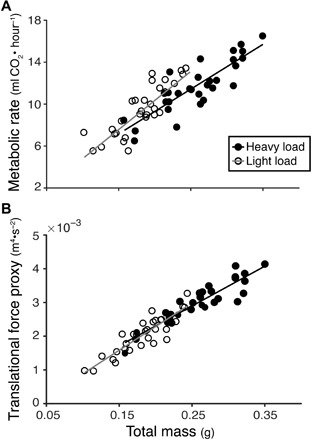
(A) Measured metabolic rate as a function of total mass (body mass plus load) for bees in the heavy (filled circles, black line) and light (open circles, gray line) loading conditions. Metabolic rate increased with total mass for bees in both loading conditions (heavy, R² = 0.7277; light, R² = 0.7327), but the slope of this relationship was significantly lower for bees carrying heavy loads (interaction of mass and treatment χ²₁ = 7.17, P = 0.0074). (B) A proxy for translational force production (wing area × average wing velocity²; SU_w²) increased with total mass of the bee plus load, as expected (heavy, R² = 0.8496; light, R² = 0.7921). The slope of this relationship was not significantly different for bees carrying light versus heavy loads. Average wing velocity² was calculated from measurements of flapping frequency (n) and stroke amplitude (Φ).

Our proxy for translational force production, SU_w² (wing area × wing velocity²), also increased linearly with the total mass supported during flight, as expected (heavy, R² = 0.8495; light, R² = 0.7918; Fig. 3B). Unlike metabolic rate, neither treatment nor the interaction of treatment with total mass affected translational force production. Only total mass significantly predicted translational force production (total mass χ²₁ = 135.58, P < 0.001).

Heavier loading resulted in a larger stroke amplitude in all individuals tested (mean with heavy loading, 133.4 ± 5.5°; light, 113.2 ± 8.0°; table S1), but changes in flapping frequency were not as consistent (fig. S1). Frequency increased with heavier loading in about three-fourths of trials (23 of 30), but declined with heavier loading in the remaining trials (mean with heavy loading, 183.2 ± 7.7 Hz; light, 176.8 ± 9.6 Hz; table S1); all 7 of the trials in which frequency declined with heavier loading were in the light-to-heavy loading order group.

To control for body size and other intraspecific differences in physiology and behavior, we examined individual changes in metabolic rate, flapping frequency, and stroke amplitude between light and heavy loading trials, as a function of the change in loading. Because absolute changes in loading between trials (total mass with heavy loading − mass with light loading) scaled strongly with bee size (fig. S2A), we instead examined changes in normalized loading (with load normalized by body mass) between light and heavy trials (% loading with heavy load − % loading with light load), which were not related to size (fig. S2B).

When we investigated how the change in percent loading between trials (Δ % loading) affected changes in observed wing kinematics (while accounting for bee size and treatment order), we found that changes in stroke amplitude were significantly predicted by changes in percent loading (Δ % loading, P = 0.0005; see table S2 for further details), but not by bee size or treatment order. In contrast, changes in flapping frequency were not predicted by changes in percent loading (or bee size; table S3). However, treatment order was a significant predictor of changes in flapping frequency, with smaller differences in frequency between light and heavy loading trials (calculated as n_heavy – n_light, regardless of treatment order) occurring when the treatment order was from light to heavy (order, P = 0.004; table S3). Overall, we found that changes in stroke amplitude were positively correlated with changes in percent loading, whereas changes in frequency could not be predicted by changes in percent loading (Fig. 4).

Fig. 4. Changes in percent loading led to predictable changes in stroke amplitude, but not flapping frequency.

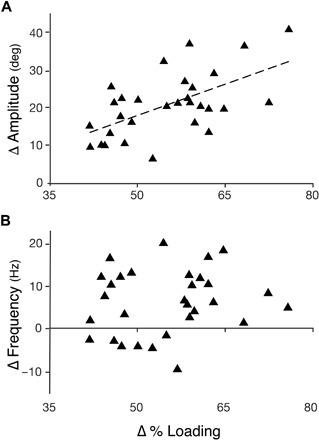
(A) Change in stroke amplitude (heavy − light loading) plotted against change in percent loading (R² = 0.3559). A linear model shows that changes in percent loading led to predictable changes in amplitude (P = 0.0005), after removing nonsignificant predictors (table S2). (B) Change in flapping frequency (heavy − light loading) plotted against change in percent loading (R² = 0.0236). A linear model shows that there was no predictable change in frequency associated with changes in percent loading (P = 0.067); only treatment order was a significant predictor of changes in frequency (P = 0.004; table S3). For each bee, change in percent loading (Δ % loading) was calculated as the total mass during heavy loading minus the mass during light loading (regardless of loading order), divided by body mass; changes in amplitude and frequency were calculated similarly as values measured during heavy loading minus those measured during light loading.

When we investigated how changes in metabolic rate were affected by changes in wing kinematics and percent loading between light and heavy trials, we found that Δ metabolic rate was significantly predicted by changes in flapping frequency (P = 0.0000006; Fig. 5C), but not by changes in stroke amplitude (P = 0.3; Fig. 5B), changes in percent loading (Fig. 5A), treatment order, or bee size (see table S4 for further details).

Fig. 5. Changes in flapping frequency led to predictable changes in metabolic rate, but changes in percent loading and stroke amplitude did not.

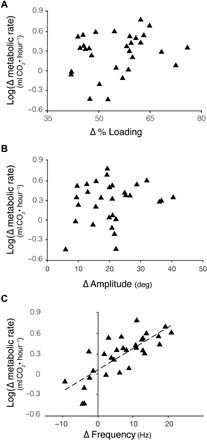
(A) Change in metabolic rate (heavy − light) plotted against change in stroke amplitude (R² = 0.051). A linear model shows that changes in metabolic rate could not be predicted by changes in percent loading (P = 0.98; table S4). (B) Change in metabolic rate (heavy − light loading) plotted against change in stroke amplitude (R² = 0.0356). A linear model shows that changes in metabolic rate could not be predicted by changes in stroke amplitude (P = 0.3), after accounting for the estimated effects of change in percent loading, treatment order, and bee size (table S4). (C) Change in metabolic rate (heavy − light loading) plotted against change in flapping frequency (R² = 0.6083). A linear model shows that changes in frequency significantly predicted changes in metabolic rate (P = 0.0000006), after accounting for estimated effects of change in percent loading, change in amplitude, treatment order, and bee size (table S4). Note that change in metabolic rate (Δ metabolic rate) was log-transformed (base e) to meet statistical assumptions. Other variables were calculated as in Fig. 4.

Because individual bees in our study initially had variable (and at the time unknown) amounts of nectar in their honey crops (nectar loads ranged from 13 to 54% of body mass, based on post-experiment measurements), the magnitude of loading varied widely among individuals (Fig. 2B). Bees with larger initial nectar loads were outfitted with relatively larger external loads as well, because the external loads created were equivalent to 40% of initial mass (body + nectar load). To determine whether differences in how heavily bees were loaded throughout the experiment affected our results, we first calculated the average percent loading (average of % loading during heavy and light loading trials) for each bee as a measure of overall loading state and found that this varied from 35 to 80% among individuals. Because the total change in % loading between heavy and light trials also varied between individuals (with Δ % loading ranging from 42 to 76%), we normalized the changes in metabolic rate, stroke amplitude, and frequency by dividing each variable (Δ metabolic rate, Δ amplitude, and Δ frequency) by Δ % loading to obtain a measure of the change in each metabolic or kinematic variable per 1% added load.

When we plotted the relationship between average loading state (average % loading) and normalized changes in metabolic rate (Δ metabolic rate per 1% added load), we found that bees that were more heavily loaded on average displayed smaller changes in metabolic rate per additional unit of loading (R² = 0.4028, Fig. 6A). Normalized changes in stroke amplitude (Δ amplitude per 1% added load) were not affected by loading state (R² < 0.0001, Fig. 6B), but normalized changes in flapping frequency (Δ frequency per 1% added load) also declined as bees were more heavily loaded (R² = 0.4568, Fig. 6C). In addition, bees that were loaded in the light-to-heavy treatment order tended to display relatively smaller normalized changes in frequency than those that were loaded in the heavy-to-light treatment order (Fig. 6C).

Fig. 6. Bees that were more heavily loaded displayed smaller increases in metabolic rate and flapping frequency to accommodate additional loading.

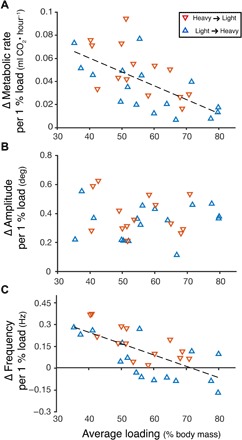
(A) Bees more heavily loaded on average (average % loading over heavy and light trials) throughout the experiment displayed smaller increases in metabolic rate per 1% additional loading (R² = 0.4028). Change in metabolic rate per 1% load was calculated as the change in metabolic rate divided by the change in percent loading between trials (Δ metabolic rate/Δ % loading). (B) In contrast, we found no relationship between a bee’s average loading state and the change in stroke amplitude per 1% additional load (R² < 0.001). (C) Bees with higher average loading displayed smaller changes in flapping frequency for a given 1% additional load (R² = 0.4568). Bees tested in the heavy-to-light treatment order are shown in red and those in the light-to-heavy order are shown in blue.

DISCUSSION

Our results not only verify the assumption that bees expend more energy to support heavier loads in flight but also reveal that the factors affecting flight energetics are more complex than previously recognized. We were able to identify these factors by performing repeated trials on the same individuals carrying loads that differed substantially in mass and by developing an experimental procedure that reliably elicited active, free flight within a small chamber. The latter goal required us to avoid anesthetization and minimize handling; thus, we could not manipulate (or even measure) the amount of nectar initially present in bees’ honey crops or guts and instead used this variable, internal load along with an external load that could be applied quickly and easily as our treatments. Although these were different types of loads, the external load was applied to the dorsal surface of the abdomen (immediately above the honey crop), close to the center of mass (15), and our measurements indicate that all bees carried an adequate load of nectar throughout both trials to ensure a consistent supply of hemolymph sugars.

Metabolic rate increased linearly with the total mass supported in both loading conditions, but the slope of this relationship was significantly lower in the heavy loading condition (Fig. 3A). This suggests that when individual bees are more heavily loaded, they are using fuel more efficiently than when lightly loaded. This conclusion is further supported by our findings that the increase in metabolic rate per 1% of additional loading declines as bees are more heavily loaded overall (Fig. 6A). Thus, it seems that very heavily loaded bees are more efficient, using less energy per unit of additional loading, in sharp contrast to fixed-wing aircraft, which become markedly less efficient as total loading increases. The unpublished thesis work of Cooper (32) showed a similar increase in bumblebees’ efficiency as loading increased. The benefit of flying with a heavy load in terms of fuel economy may be limited at some point, however, by other potential negative consequences of flying with heavy loads, such as reduced maneuverability or acceleration capacity, which could leave heavily loaded workers more susceptible to predation.

Our results also demonstrate that although bee mass and load size do contribute to flight metabolic rate, these are not the only—or even the most important—variables that determine energetic costs. Changes in metabolic rate also appear to be history dependent (i.e., affected by previous flight activity) and are influenced by the current loading state of the bee. Increasing a bee’s load by 10% of its body mass when the bee is barely loaded at all has a much larger effect on metabolism than if the bee were already carrying a substantial weight (Fig. 6A). Similarly, challenging a well-rested bee to fly with a heavy load first leads to a larger increase in metabolism than adding a heavier load to a bee that has already been flying with a lighter load for some time (Fig. 6C). In both cases, bees that are heavily loaded or have recently been flying appear to use more energetically efficient mechanisms of increasing their force output than bees that are lightly loaded or well rested. Our simultaneous measurements of wing kinematics and metabolic data across a wide range of loading conditions suggest that this effect is primarily determined by the extent to which a bee increases its flapping frequency to support additional loading.

We found that all bees increased their stroke amplitude when flying with a heavier load, as expected from previous studies of maximal force production in bees (22, 27–30). Changes in percent loading strongly predicted changes in stroke amplitude (Fig. 4A), and this response did not depend on loading order or loading state (average % loading; Fig. 6B). As bees become more heavily loaded, increases in stroke amplitude will inevitably reach a limit, either when the wings contact each other (180°) or when they reach the morphological limits of their movement range [~140° to 145° in many hymenopterans (22, 27–30)], a value that many of the bees in our heavy-loading treatment approached.

Increasing stroke amplitude alone does not appear to provide sufficient additional force to support the heavy loads carried during our trials (which ranged from 57 to 109% of body mass). In many cases, bees increased their flapping frequency and stroke amplitude to produce additional force, increasing wing velocity and thus the forces produced during wing translation via both of these kinematic changes. However, in some cases, especially as the size of the added load increased, bees displayed smaller increases, and sometimes even decreases, in wing beat frequency with heavy loading as compared to light loading (e.g., see bees #28 and #42 in table S1). This was always observed in bees that had already completed a previous flight trial with light loading and received the heavier load during the second trial. Previous work has shown that fruit flies can also produce elevated flight forces (up to ~150% of body mass, equivalent to 50% loading) through a linear increase in wing velocity, which is accomplished through a predictable increase in stroke amplitude coupled to a predictable decrease in flapping frequency [for forces beyond weight support (21)]. In contrast, here, we found no relationship between changes in stroke amplitude and changes in flapping frequency as bees increased force production from light to heavy loading trials (fig. S1B).

Unexpectedly, the predictable changes in amplitude that were associated with an increase in loading were not a significant predictor of metabolic rate (Fig. 5B). Instead, metabolic rate was strongly tied to flapping frequency (Fig. 5C), which was predicted not by load size but by the bee’s average loading state and loading history. However, the data suggest that there may still be some metabolic cost to increasing stroke amplitude. Despite the fact that about one-fourth of individuals (7 of 30) displayed lower flapping frequencies when carrying heavy loads as compared to light loads, all individuals displayed elevated metabolic rates during heavy loading trials, and all bees displayed an increase in stroke amplitude (Fig. 5, A and B). Thus, there may be an underlying relationship between changes in stroke amplitude and changes in metabolic cost that is obscured by the relatively larger effect of changes in flapping frequency on metabolic rate.

Our results suggest that some bees that were heavily loaded or had already performed a previous flight trial were using alternative mechanisms to enhance force production, rather than increasing wing velocity further by elevating flapping frequency. Identifying the source of this additional force production is beyond the scope of this study, but bees likely produce additional aerodynamic forces through changes either in the translational lift coefficient (e.g., by changing wing angle of attack during translation) or in the speed and/or timing of wing rotation at stroke reversal.

Our finding that heavily loaded bees can use a more economical mechanism of generating additional aerodynamic forces brings up the question of why bees increase their flapping frequency to enhance force production in some situations (i.e., when carrying lighter loads). Enhancing translational lift forces by increasing flapping frequency is expensive, so there is presumably some benefit to using a higher wingbeat frequency when energetic efficiency is not critical. Several recent studies on flight performance in unsteady flow environments show that a number of insects, including moths (33), fruit flies (34), and bumblebees (35), increase flapping frequency when flying in external flow conditions that challenge their stability. Higher flapping frequencies have been proposed to enhance stability by several potential mechanisms, such as reducing the impact of random, turbulent flow perturbations on force production by flapping wings (36) or damping out rotational perturbations via flapping counter-torque (37). Elevating flapping frequencies may also enhance control authority by reducing the time between wing strokes and thus the delay in updating control input to the wings (38). Similarly, shortening the time between wing strokes could enhance an insect’s ability to perform rapid, voluntary maneuvers, allowing them to avoid obstacles or escape from predators. Thus, bumblebees may choose to sacrifice efficiency for enhanced stability and/or maneuverability when they are carrying lighter loads or are well rested, but switch to more economical, alternative mechanisms of increasing force production (which presumably reduce stability, maneuverability, or some other aspect of performance) in more challenging contexts, such as when they are heavily loaded, fatigued, or anticipate needing to continue flying for a long period of time.

These results have several interesting implications in terms of understanding the energetics and ecology of bees and other flying insects. Although several factors play a role in determining a flying insect’s absolute metabolic rate, our finding that flapping frequency plays such an important role (and was the strongest predictor of changes in metabolic rate; Fig. 5C) opens up the possibility of deriving reasonably good estimates of relative energy expenditure in a variety of flight scenarios. Respirometry is a challenging, laboratory-based procedure that does not lend itself to measuring metabolic costs during a wide range of natural flight behaviors, as measurements must typically be performed in small chambers under strictly controlled conditions. However, flapping frequency is one of the easiest flight variables to measure, with both audio- and video-based measurements providing good results in a variety of laboratory and field settings. In contrast, stroke amplitude and other kinematic variables such as wing rotation rates require high-speed videos recorded at higher frame rates and typically calibrated in three dimensions, making measurements challenging in most field settings. Although our data were gathered only on bees during hovering or very slow forward flight, previous work has shown that metabolic rates change little with forward speed in bumblebees (20). Thus, measurements of frequency, particularly measurements comparing flapping frequency of the same individual in different settings, could provide valuable new insights into the relative energetic costs of complex flight behaviors in both the laboratory and the field.

Last, these results suggest that some previous models and predictions concerning optimal foraging in bees may require revision. The cost of carrying loads is not determined simply by load size; rather, bees are able to adapt their flight kinematics to fly more efficiently under certain conditions (such as when they are carrying heavy loads), and changes in metabolic rate are more strongly predicted by the changes in flapping frequency that bees choose to adopt (Fig. 5C). In addition, kinematic choices and the resulting energetic efficiency of bees appear to be history dependent (possibly explaining conflicting results from some previous studies) and may be affected by other traits such as motivation and distance from the hive. From an energetic standpoint, it would seem to be beneficial to the hive for all foragers to carry very heavy loads; however, the benefits of carrying extremely heavy loads will reach a limit at some point, either when the negative consequences of heavy loading to other aspects of flight performance outweigh the energetic benefits or when an individual reaches the limit of its capacity to increase force production via energetically favorable mechanisms.

In summary, our findings suggest that bumblebees have greater flexibility than previously recognized in how they respond to requirements for increased force production. Bees increase force production, in part, by increasing stroke amplitude, but this must be coupled either with an increase in flapping frequency or with other more economical force production mechanisms, which remain to be elucidated by future studies. Depending on their current loading state and recent history, bees can choose whether to increase force production by using these alternative kinematic mechanisms, thereby minimizing energetic costs, or by elevating flapping frequency. Although increasing frequency is more costly, this strategy may provide other performance benefits, such as enhanced stability or maneuverability, which have just begun to be explored.

MATERIALS AND METHODS

Experimental design

We tested 30 individual B. impatiens workers from a commercial colony (Biobest Canada Ltd., Leamington, ON, Canada), which was housed indoors in a large mesh enclosure. Bees were provided with pollen inside the nest and allowed to forage freely for nectar in the enclosure. We removed individuals actively foraging in the mesh enclosure, recorded their initial mass (composed of body mass plus an unknown amount of nectar in their honey crop), and created a customized, external load from a small piece of solder wire cut to 40% (±2%) of their initial mass (Fig. 2A). Bees were not anaesthetized during the treatments and were handled as little as possible to minimize disruptions to normal flight behavior.

Each bee was randomly assigned to one of two treatment orders: light to heavy (N = 16), in which they were loaded with only the nectar they were carrying when captured (light loading) first and the added external load (heavy loading) second, or heavy to light (N = 14), in which the external load was applied first (Fig. 2A). The external load was attached with a small amount of ultraviolet (UV)–curable glue to the top of the abdomen, above the location of the honey crop. Bees were weighed immediately before and after each flight trial to calculate average loading during the trial, accounting for nectar used during flight (which averaged 6.2 ± 4.7% of body mass during light trials and 7.0 ± 4.3% of body mass during heavy trials). The external load was either added or removed for the second trial, with no additional nectar provided between trials.

Each flight trial was conducted within an 880-ml, sealed, glass globe. Dry, carbon dioxide–free air was pushed through the chamber at a rate of 995 ml/min using a Sable Systems MFC-2 mass flow controller. After placing a bee in the chamber, we flushed the chamber for 5 min before beginning measurements. The bee was motivated to fly by placing a UV light source above the chamber and by intermittent agitation if the bee landed or approached the walls. After a relatively stable CO₂ signal was observed, we began a 5-min flight trial, ensuring that the bee continued flying for 5 min by agitating the chamber when necessary. We only used metabolic data collected from intervals during which bees were very active (actively flying in the center of the chamber for at least 80% of the time), with a total of 3 to 5 min of metabolic data analyzed per bee. Because bumblebees (like most bees studied to date) fuel their flight almost exclusively with carbohydrates (39), their metabolic rate can be inferred by measuring CO₂ production alone. We measured CO₂ production from the chamber outflow using a Sable Systems CA-10 carbon dioxide analyzer. Flow rate and CO₂ concentration were logged simultaneously using ExpeData (Sable Systems).

We measured wing beat frequency (n) over the duration of the metabolic testing by capturing audio recordings from a microphone built into the bottom of the flight chamber. We analyzed audio recordings using a custom R script to extract the dominant frequency (code available at http://doi.org/10.5281/zenodo.2542885). We also recorded a high-speed video sequence of steady hovering during each trial with a manually triggered Phantom V611 (Vision Research) filming at 3000 Hz, positioned directly above the flight chamber. We digitized the wing base and the stigma (an easily identifiable landmark on the leading edge) of both wings at pronation and supination during 10 consecutive wing strokes in Matlab and used these data to calculate average stroke amplitude (Φ) in the horizontal plane [as bumblebees hover with a stroke plane angle close to zero (14)]. We also used the high-speed video to perform a second measurement of wing beat frequency over the 10 wing strokes that were filmed. All analyses presented in the manuscript were performed with frequency data obtained from the audio recordings, which we judged to be more accurate because these data were collected over a longer time period. However, we verified that the two sets of frequency data were strongly correlated (R² = 0.8140), and both sets of frequency data are provided in table S1.

To calculate wing velocity (U_w), we first determined the total distance, or the arc length (a) through which the wings traveled during each stroke, by multiplying stroke amplitude (Φ) in radians by wing length (L). We used a reference wing length of 75% of wing span, which approximates the center of aerodynamic pressure and avoids the flexible, outermost portion of the wing, where passive bending may alter the amplitude of motion. We then calculated wing velocity as twice the arc length times the flapping frequency (2*a*n).

After both flight trials were concluded, we isolated bees without food for a period of time ranging from ~6 to 18 hours (depending on nectar load) until they were unable to buzz or walk (i.e., displayed no irritation buzzing and could not walk to a new position when prodded) but were still alive (still reacted to prodding with antenna and leg movements). At this point, bees were assumed to have depleted the nectar in their honey crops, and they were weighed to obtain body mass (m_body; Fig. 2A) and measured with digital calipers to obtain intertegular (IT) span. We also removed and photographed one forewing and measured wing length and area (neglecting the smaller contribution of the overlapping hindwing) using ImageJ.

Statistical analysis

To determine whether the basic kinematic features measured (flapping frequency and stroke amplitude) provide a reasonable estimate of overall force production, we plotted a proxy of translational force production (S × U_w², which neglects any unknown changes in the unsteady, translational force coefficient C_Ft; Fig. 1) against the total mass (body + load) supported during flight. We fit a linear mixed effects model and calculated P values with Satterthwaite’s degrees of freedom method. We used the translational force proxy as the dependent variable and total mass and treatment (heavy versus light loading) as independent variables. We examined the interaction between mass and treatment to determine whether the slopes differed significantly under the different loading conditions, and we included bee ID as a random effect. We performed a similar multiple regression analysis to examine the relationship between total mass and metabolic rate.

To examine relationships between loading, wing kinematics, and metabolic rate, we calculated the change (Δ) in measured variables observed within each individual between heavy and light loading trials to control for body size and other individual differences. Changes in metabolic rate, stroke amplitude, and flapping frequency were calculated as the difference between heavy minus light loading trials, regardless of the order of treatments (although treatment order was accounted for in the statistical models). Because absolute changes in loading between trials (total mass with heavy load − mass with light load) scaled strongly with bee size (fig. S2A), we instead examined changes in normalized loading (with load normalized by body mass) between light and heavy trials (% loading with heavy load − % loading with light load), which were not related to size (fig. S2B).

We used linear models to investigate how changes in percent loading (Δ % loading) between treatments affected changes in flight kinematics (Δ stroke amplitude and Δ frequency), while accounting for bee size and treatment order. We also used linear models to investigate how changes in percent loading and wing kinematics (Δ % loading, Δ stroke amplitude, and Δ frequency) affected measured changes in metabolic rate (Δ metabolic rate), while accounting for bee size and treatment order. In all models, we used IT span as a proxy for bee size, because this measurement was not used in the calculation of any other variables (as was the case for m_body).

Our general approach with the linear models was to fit a model with all measured predictors and their interactions. We then used backward elimination, based on the extra sum of squares F test, to remove predictor variables until none of the remaining explanatory variables could be removed, although we left the treatment variable in all models, even if it was not a significant predictor. When we modeled change in metabolic rate, we made an a priori decision to keep both Δ amplitude and Δ frequency in the final model, even if they were not significant, because these kinematic values are mathematically related to total force production (Fig. 1). After fitting the models, we checked several assumptions of linear regressions (homoscedasticity, normality, and no influential outliers) with diagnostic plots. We log-transformed (base e) the change in metabolic rate when it was used as a response variable to help meet the homoscedasticity assumption. We did not adjust P values to account for multiple comparisons, because we had planned our statistical comparisons in advance and because the simplest method for multiple comparison adjustment (the Bonferroni method) is often too conservative, leading to false negatives when tests are not independent (40). To address multicollinearity in all linear models, we removed predictors until variance inflation factors for all predictors were less than 5.

Last, we examined how the average loading state of bees (i.e., how heavily loaded they were) over the course of the experiment affected the observed changes in wing kinematics and metabolic rate. Because individual bees in our study initially had variable (and at the time unknown) amounts of nectar in their honey crops, the magnitude of loading varied widely among individuals. Bees with larger initial nectar loads were outfitted with relatively larger external loads as well, since the external loads created were equivalent to 40% of initial mass (body + nectar load). To determine whether differences in how heavily bees were loaded throughout the experiment affected our results, we first calculated the average percent loading (average of % loading during heavy and light loading trials) for each bee as a measure of overall loading state. Because the total change in % loading between heavy and light trials (Δ % loading) also varied between individuals, we normalized the measured changes in metabolic rate, stroke amplitude, and frequency by the percent change in loading. To do this, we divided each variable (Δ metabolic rate, Δ amplitude, and Δ frequency) by Δ % loading for each individual to obtain a measure of the change in metabolic and kinematic variables per 1% added load. We then examined how Δ metabolic rate per 1% added load, Δ amplitude per 1% added load, and Δ frequency per 1% added load were affected by average loading state (average % loading) by examining regressions between these variables. We did not calculate P values or construct linear models of these relationships because some variables (e.g., m_body) were used in normalizing both independent and dependent variables, leading to the possibility of mathematical coupling that could affect statistical results.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/6/6/eaay3115/DC1

Fig. S1. There was no relationship between stroke amplitude and wingbeat frequency or between the change in amplitude and change in frequency between trials.

Fig. S2. Change in loading between trials scaled with bee size, but change in % loading was independent of size.

Table S1. Morphological, kinematic, and metabolic variables for all bees tested, grouped by treatment order (light to heavy, L-H; heavy to light, H-L).

Table S2. Results of linear model investigating how Δ amplitude is affected by Δ % loading, treatment order, and bee size.

Table S3. Results from linear model investigating how Δ frequency is affected by Δ % loading, treatment order, and bee size.

Table S4. Results from linear model investigating how Δ metabolic rate is affected by Δ % loading, Δ amplitude, Δ frequency, treatment order, and bee size.

View/request a protocol for this paper from Bio-protocol.