Usable Science for Managing the Risks of Sea‐Level Rise

Abstract

Sea‐level rise sits at the frontier of usable climate climate change research, because it involves natural and human systems with long lags, irreversible losses, and deep uncertainty. For example, many of the measures to adapt to sea‐level rise involve infrastructure and land‐use decisions, which can have multigenerational lifetimes and will further influence responses in both natural and human systems. Thus, sea‐level science has increasingly grappled with the implications of (1) deep uncertainty in future climate system projections, particularly of human emissions and ice sheet dynamics; (2) the overlay of slow trends and high‐frequency variability (e.g., tides and storms) that give rise to many of the most relevant impacts; (3) the effects of changing sea level on the physical exposure and vulnerability of ecological and socioeconomic systems; and (4) the challenges of engaging stakeholder communities with the scientific process in a way that genuinely increases the utility of the science for adaptation decision making. Much fundamental climate system research remains to be done, but many of the most critical issues sit at the intersection of natural sciences, social sciences, engineering, decision science, and political economy. Addressing these issues demands a better understanding of the coupled interactions of mean and extreme sea levels, coastal geomorphology, economics, and migration; decision‐first approaches that identify and focus research upon those scientific uncertainties most relevant to concrete adaptation choices; and a political economy that allows usable science to become used science.

Key Points

• Understanding coastal evolution requires accounting for interactions of sea‐level change, geomorphology, socioeconomics, and human responses

• Deep uncertainty in sea‐level rise projections and impacts exists on timescales relevant to infrastructure and planning decisions

• Adaptation under deep uncertainty requires co‐production, iterative risk management, and awareness of political economy

1. Introduction

Climate change is inherently a long‐term phenomenon: Under the classical definition of “climate” as the statistics of weather over 30‐year periods (e.g., Arguez & Vose, 2011), it can only be seen amid more rapid variability from a multidecadal perspective. Thus, climate change science—as opposed to the meteorology or physical oceanography of climate variability—becomes actionable primarily in the contexts of catalyzing overdue adjustments to past trends and of managing future long‐term risks. The feasibility of long‐term risk management depends on a variety of psychological, social, economic, and institutional factors (Shwom & Kopp, 2019). Whether climate science is actionable, however, depends not only on a favorable context but also on the shape of the science itself—even in a welcoming psychosocial environment, science cannot be used if it does not address questions relevant to the decisions being made (e.g., Hinkel et al., 2019).

As global temperatures and sea level have climbed, climate science has slowly expanded from an original primary focus on fundamental understanding to include a significant emphasis on usability (Dilling & Lemos, 2011). This transition happened first with the science of the global climate and its implications for mitigation, where “usability” is primarily in the context of national and global target setting and institutional design. The recognition of a clear human fingerprint in modern warming and the development of concepts such as “carbon budgets” have made a clear and direct impact on the shape of the global climate negotiations (e.g., Allen et al., 2009; Friedlingstein et al., 2014; Matthews & Caldeira, 2008; Matthews et al., 2018).

Given a particular course of global emissions, however, many actions to manage climate risk, especially with regard to adaptation, will be decided on and implemented at a more local level. With respect to science for climate adaptation, the study of sea‐level change has been at the frontier of the usability transition. This pole position is due to two main reasons. First, like temperature change but unlike many other climate stressors (e.g., changes in precipitation or weather systems), sea‐level change is univariate and, in most of the world, monotonic on climatological timescales: The multidecadal‐average sea level is inexorably rising. It is thus more straightforward for decision makers to understand and react to than multivariate changes of ambiguous direction. Second, whereas for temperature‐related impacts, many of the relevant adaptations (e.g., behavioral change and air conditioning) can be implemented rapidly, and for sea‐level‐related impacts, many of the relevant adaptations involve infrastructure and land use. Thus, decisions made today affect the coastal risk faced by subsequent generations.

The tie between near‐term investments and long‐term vulnerability can be seen in retrospect. In the aftermath of Hurricane Sandy, for example, about 90% of the New Jersey customers of the Public Service Electric and Gas Company (PSE&G) lost power, many for more than a week. Fourteen of PSE&G's major switching stations were affected (Calore, 2013). Seven of the switching stations were located at sites of generation stations or substations that had been sited prior to 1911 (Electric Railway Journal, 1911, p. 590). In other words, siting decisions made by Thomas Alva Edison and his contemporaries had a fairly direct effect on the vulnerability of the New Jersey electric grid during a storm more than a century later. The vulnerability of their great‐grandchildren's electric grid to coastal flooding was surely not among their top design considerations; but with climate change and sea‐level rise amplifying exposure, in some cases dramatically, it has become increasingly urgent to be more forward‐looking.

This paper provides an overview of the sea‐level science relevant to decision makers and communities developing forward‐looking coastal adaptation strategies. Ultimately, such strategies must identify ways to combine the four basic approaches to coastal adaptation (e.g., Haasnoot et al., 2019; Sengupta et al., 2018): (1) accommodation of more frequent flooding through social (e.g., improved emergency response), economic (e.g., flood insurance), and engineering changes ; (2) defense against flooding; (3) advance (i.e., the reclamation of land from the ocean); and (4) relocation (e.g., through autonomous or planned migration). Determining how to combine these approaches requires consideration of the physical hazards associated with sea‐level change and the autonomous responses of individuals to their changing environment, as well as the decision science approaches that can help construct strategies that are robust to uncertainty and the political and sociological barriers to their effective use.

Sections 2, 3, 4 examine the physical drivers and hazards associated with sea‐level change. Section 2 briefly reviews projections of future sea‐level change, highlighting key uncertainties that are relevant for decision making. More detailed reviews are available in several recent papers and assessment reports (e.g., Church et al., 2013; Clark et al., 2015; Oppenheimer et al., 2019; A. J. Garner et al., 2018; Horton et al., 2018; Jevrejeva et al., 2019; Slangen et al., 2017). Section 3 examines the translation of future sea‐level change to extreme sea levels and related attempts to assess flooding on the current coastline. Section 4 examines the dynamics of the physical response of the coast to changing mean and extreme sea level. Section 5 then examines the dynamic socioeconomic response of coastal communities, primarily through migration, focusing on how the autonomous actions of individuals affect community exposure and vulnerability to flooding. Sections 6 and 7 turn to planned adaptation choices. Section 6 examines decision frameworks for incorporating sea‐level science into coastal planning even in the presence of scientific deep uncertainty, while section 7 examines the practice of planned coastal adaptation. Section 8 concludes by identifying some key pathways forward to advance the physical, social, and decision science of sea‐level change.

In the paper, we follow the standardized definitions of concepts and terminology related to sea‐level change and variability adopted by Gregory et al. (2019). By relative sea level (RSL) change, we refer to the local change in the time‐average height of the sea‐surface (mean sea level) above the sea floor. Where not otherwise specified, we take mean sea level to be a mean of an 18.6‐year tidal cycle, averaging out shorter‐term variability. By global mean sea level (GMSL) change, we refer to change in the volume of the ocean divided by the surface area of the ocean, which is equivalent to the average of RSL change over the surface area of the ocean.

2. Projections of Relative Sea Level Change

Going back to its 19th‐century roots, sea‐level science has long been informed by inferences from the geological record, observations of modern sea level, and predictions of theoretical, analytical, and numerical models. Coming from a paleo perspective, Croll (1867) recognized the relationship between ice‐age variability in land‐ice volume and GMSL change. He also noted the effect of ice‐volume changes on RSL via changes in Earth's gravitational field (Sugden, 2014), which Woodward (1888) correctly derived for the case of a rigid Earth. (The derivation was not extended to a non‐rigid Earth for almost a century, until the work of Farrell and Clark (1976) and Clark and Lingle (1977)). Johnson (1929), writing for the U.S. National Research Council, synthesized what was known about the drivers of spatial variability in mean sea level, highlighting effects of freshwater input, wind, Earth rotation, and tidal channel geography. Gutenberg (1941) compiled data from 69 tide gauges around the world (excluding gauges undergoing post‐glacial uplift) and identified a centennial‐scale GMSL trend of about 1.1 mm/year. Fairbridge and Krebs (1962) added thermosteric and halosteric density effects to Johnson's (1929) list of key processes and noted meteorological variability in sea level associated with the Southern Oscillation and the North Atlantic Oscillation. From tide‐gauge data, they inferred a long‐term GMSL rise beginning in about 1890, with an average rate of 1.2 mm/year from 1900 to 1950. Drawing in part on paleo‐sea level data, Mercer (1978) highlighted the instability in the West Antarctic Ice Sheet (WAIS) that would result from loss of fringing ice shelves and warned that CO₂‐induced warming could lead to deglaciation and 5 m of GMSL rise.

2.1. Advances in Sea‐Level Projections

The first modern projections of sea‐level change were developed in the early 1980s (e.g., Gornitz et al., 1982), triggered by the growing concern about the potential instability of WAIS (e.g., Clark & Lingle, 1977; Hughes, 1975; Mercer, 1978; Schneider & Chen, 1980). (See Figure 1a and Garner et al., 2018 for a compilation of subsequent projections.) In general, projections can be categorized as either “top‐down” or “bottom‐up.” Top‐down methods utilize observed relationships between global‐mean temperature and GMSL, often assuming that there is an equilibrium GMSL for each temperature to which realized GMSL converges at a rate dependent on degree of disequilibrium (e.g., Gornitz et al., 1982; Kopp, Kemp, et al., 2016; Rahmstorf, 2007; Rahmstorf et al., 2012). Bottom‐up methods aggregate the contributions of each of the key driving processes contributing to GMSL and RSL change. Advances have been made using both approaches over the past three and a half decades.

Figure 1.

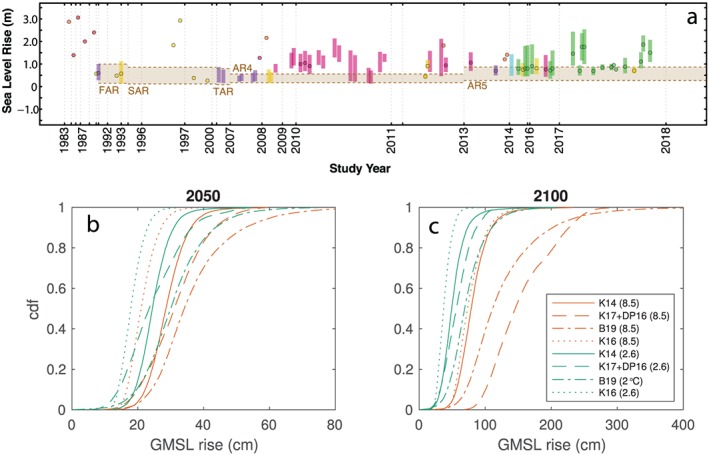
(a) Evolution of 21st century GMSL rise projections for high‐emissions scenarios. Reproduced from Garner et al. (2018). Bar and point colors correspond to the methodology used by each study: top‐down semiempirical (pink), bottom‐up literature synthesis (red), bottom‐up model hybrid (orange), bottom‐up model synthesis (yellow), bottom‐up probabilistic (green), bottom‐up expert judgment (cyan), other (blue), and IPCC reports (purple). Tan‐shaded regions and dashed lines represent the ranges of GMSL rise from the IPCC reports. (b and c) Cumulative distribution functions of (b) 2050 and (c) 2100 GMSL rise projections under RCP 8.5 (orange) and a low emissions scenario (either RCP 2.6 or 2°C stabilization, blue). Solid, dashed, and dot‐dashed lines represent CDFs of bottom‐up projections using ice‐sheet projections from Kopp et al. (2014) [K14]; Kopp et al. (2017) using the AIS projections of DeConto and Pollard (2016) [K17+DP16], and Bamber et al. (2019) [B19]. Dotted lines represents the top‐down semi‐empirical projection of Kopp, Kemp, et al. (2016), calibrated using the paleo‐temperature reconstruction of Mann et al. (2009) [K16].

Advances in top‐down projections have been driven by increasing statistical sophistication and longer, higher quality global mean temperature and GMSL reconstructions. For example, GMSL reconstructions are now informed by satellite altimetry measurements of sea‐surface height (e.g., Nerem et al., 2018; WCRP Global Sea Level Budget Group, 2018), by tide‐gauge records stretching back in some locations to the 18th century (e.g., Holgate et al., 2013; Talke et al., 2018), and by geological reconstructions that in some cases achieve decimeter‐scale vertical resolution and multidecadal‐scale temporal resolution stretching back up to four millennia (e.g., Kemp et al., 2018; Kopp, Kemp, et al., 2016).

Interpretation of these records has been advanced in part by increasingly sophisticated statistical approaches (Ashe et al., 2019), which include not just pooling individual tide gauges to construct regional averages (e.g., Dangendorf et al., 2017; Gornitz et al., 1982; Johnson, 1929; Jevrejeva et al., 2014) but also the use of empirical orthogonal functions (EOFs) constructed from satellite altimetry data to capture expected spatial variability of tide‐gauge data (Calafat et al., 2014; Church & White, 2006, 2011; Dangendorf et al., 2019), Gaussian‐process models that incorporate the spatio‐temporal correlations expected from different driving processes (Hay et al., 2015; Kopp, 2013), and state‐space models that explicitly model the evolution of different driving processes over time (Dangendorf et al., 2019; Hay et al., 2015). Gaussian‐process models have also been used to fuse tide‐gauge and geological data (e.g., Kemp et al., 2018; Kopp, Kemp, et al., 2016), allowing the reconstruction of the last three millennia of GMSL change and showing the extraordinary nature of 20th century GMSL rise. Notably, however, no current reconstruction directly combines satellite data with tide‐gauge or geological data. Further, the only reconstruction approach yet used to indirectly combine satellite and tide‐gauge data (the EOF‐based approach) has been shown to yield biased reconstructions of either GMSL or higher‐frequency variability (Calafat et al., 2014). Dangendorf et al. (2019) worked around this limitation by combining a reconstruction of high‐frequency variability from the EOF method with a reconstruction of lower‐frequency changes from a state‐space model.

Advances in bottom‐up projections have been driven by an increasingly sophisticated understanding of relevant physical processes, including those that cause local RSL changes to differ from GMSL changes (e.g., Kopp et al., 2015; Milne et al., 2009; Figure 2a). GMSL rise is driven by the decreasing density of the warming ocean (global mean thermosteric sea level rise) and the addition of mass to the ocean (barystatic sea‐level rise), primarily from glaciers and ice sheets and secondarily from the land hydrosphere. RSL changes are driven by many additional processes. For example, changes in atmosphere‐ocean heat, buoyancy, and momentum fluxes, and resulting changes in ocean circulation, drive a highly spatially variable pattern of ocean density and mass changes (e.g., Stammer et al., 2013). River discharge can also be an important driver of interannual sea‐level variability (Piecuch et al., 2018). Shifting mass between the cryosphere, land hydrosphere, and ocean gives rise to gravitational and rotational effects that alter the height of the sea surface and also deform the Earth's crust, affecting the height of the land; the processes together are examples of gravitational, rotational, and deformational (GRD) effects (e.g., Clark & Lingle, 1977; Mitrovica et al., 2011). The ongoing response of the Earth's mantle to past changes in loading gives rises to additional GRD, known as glacial‐isostatic adjustment (GIA; e.g., Farrell & Clark 1976; Lambeck et al., 2014; Peltier et al., 2015). The height of the land also changes in response to processes such as sediment compaction (in some cases, accelerated by anthropogenic groundwater or hydrocarbon withdrawal) (e.g., Keogh & Törnqvist, 2019), tectonics (e.g., Tanaka & Heki, 2014), and mantle dynamics (Rowley et al., 2013).

Figure 2.

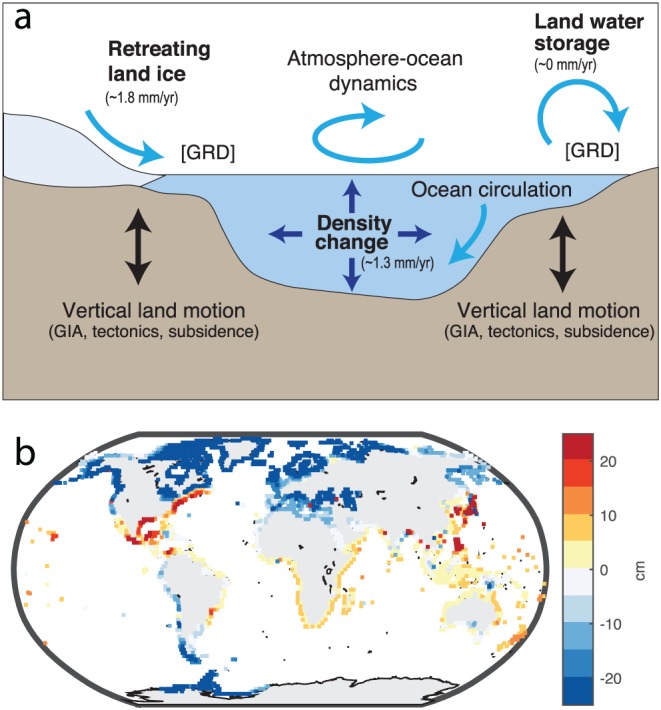
(a) Factors driving GMSL and RSL change. Bold labels identify process that drive GMSL change, with approximate average contributions over 1993–2017 shown (Mouginot et al., 2019; Rignot et al., 2019; WCRP Global Sea Level Budget Group, 2018; Zemp et al., 2019). Adapted from Milne et al. (2009). (b) Difference between median RSL and median GMSL projection under RCP 8.5 in 2100, based on the projections of Kopp et al. (2014).

Important advances have been made in the integration of these processes (and related collaborations across research disciplines). As recently as the last decade, studies by ocean modelers often ignored the potential importance of GRD effects (e.g., Hu et al., 2009; Stammer, 2008), though the latter dominate the spatial patterns associated with ice‐sheet melt once net losses exceed a couple decimeters sea‐level equivalent (Kopp et al., 2010). Conversely, studies of GRD effects generally assumed that freshwater input to the ocean would, apart from GRD effects, be uniformly distributed and did not consider how the dynamic effects of freshwater input might modulate this assumption (e.g., Mitrovica et al., 2001). Meanwhile, long‐term sea‐level reconstructions from the geological community often assumed that GIA and geological processes like tectonics were the only drivers of deviations between GMSL change (often called “eustatic sea level” change in this literature) and RSL change (e.g., Engelhart et al., 2009).

To our knowledge, Milne et al. (2009) offered the first major review calling for an integrated approach, and Kopp et al. (2010) was the first global study to couple dynamic and GRD effects associated with ice sheet mass changes, albeit in a highly idealized setting. Driven by the needs both for relevant, comprehensive local sea‐level projections and to interpret increasingly detailed current observations and past reconstructions, the past decade has seen a dramatic increase in the integration of sea‐level fields (e.g., Jackson & Jevrejeva, 2016; Katsman et al., 2011; Kopp et al., 2014; Slangen et al., 2014). This integration is essential for adaption planning, which requires comprehensive, localized, projections.

This holistic approach is reflected in current bottom‐up projections, in which RSL at location x and time t, under forcing scenario F, is viewed as the sum of different contributing factors, for example:

$$\begin{array}{ccc}\hfill \text{RSL}(x,F,t)& =\text{GMTSLR}(F,t)+\text{DSL}(x,F,t)+\text{⋯}\hfill & \hfill \\ \hfill & \sum _i{f}_i(x,F,t)\text{GLAC}{}_i(F,t)+\sum _j{g}_j(x,F,t){\text{IS}}_j(F,t)+\text{⋯}\hfill \\ \hfill & \sum _k{h}_k(x,t)\text{LWS}{}_k(t)+\text{GIA}(x,t)+\text{VLM}(x,t)\hfill \end{array}.$$ (1)

Here, GMTSLR represents global mean thermosteric sea‐level rise, and DSL represents ocean dynamic sea level (the height of the sea surface above the geoid, with the inverse barometer correction applied). GLAC, IS, and LWS represent different glacial regions, ice‐sheet sectors, and terrestrial water reservoirs (with regions denoted by the i subscript), while f, g, and h represent their respective normalized GRD spatial patterns (often called “fingerprints”). GIA represents the (VLM and geoidal) effects of GIA, and VLM represents contributions to vertical land motion not otherwise incorporated into GRD fingerprints or GIA. The GMTSLR and DSL terms affect only the height of the sea surface (also known as geocentric sea level); VLM affects only the height of the land, while the remaining processes affect both the surfaces defining RSL.

Many sources of information have been employed to quantify each term in equation (1), including novel or published model outputs, informal or structured expert judgement, and statistical extrapolation of observations. GMTSLR and DSL terms are often derived directly from the output of global climate models (GCMs; e.g., Yin, 2012), while glacier projections typically come from mass balance models forced by downscaled GCM projections of temperature and precipitation (e.g., Marzeion et al., 2012). Diverse approaches have been used to estimate LWS, including both process models of groundwater withdrawal (e.g., Konikow, 2011; Wada et al., 2012) and semi‐empirical relationships among parameters like dam construction, groundwater withdrawal, and population (e.g., Rahmstorf et al., 2012; Kopp et al., 2014).

Ice sheet projections generally rely significantly on informal or structured expert judgement (SEJ; e.g., Bamber & Aspinall, 2013; Bamber et al., 2019; Church et al., 2013), informed by but often not strictly tied to the state of the art in modeling of ice‐sheet melt, accumulation, and discharge. SEJ is a formal method that calibrates experts based on their ability to estimate accurately their own uncertainty regarding relevant questions in their field of expertise. It penalizes both ignorance and overconfidence and has been shown to perform well in a variety of contexts (Oppenheimer et al., 2016; Colson & Cooke, 2018). It yields a probabilistic estimate while avoiding some of the biases that arise in consensus‐based expert judgements.

The GRD fingerprint terms come from geophysical models solving the so‐called “sea‐level equation” (e.g., Mitrovica et al., 2011). GIA typically either comes from a geophysical model (e.g., Lambeck et al., 2014; Peltier et al., 2015) or is incorporated into an empirical estimate of slowly changing background processes (e.g., Kopp et al., 2014). The latter estimate also includes other forms of slow VLM; projections that do not take this approach generally ignore forms of VLM not associated with fingerprints or GIA. Recent efforts have also adapted top‐down methods to project temperature‐dependent RSL contributions by component, with associated fingerprints (Bakker, Wong, et al., 2017; Mengel et al., 2016).

In general, historically calibrated top‐down methods must be complemented by bottom‐up methods if local RSL projections are required. However, top‐down methods provide useful context for interpreting bottom‐up projections (Figures 1b and  1c). Projected future GMSL from top‐down projections calibrated against the tide‐gauge record (e.g., Grinsted et al., 2010; Schaeffer et al., 2012) are generally systematically higher than bottom‐up projections (e.g., Church et al., 2013). For example, Schaeffer's (2012) semi‐empirical model projected a 90% credible interval of 64–121 cm of 21st century GMSL rise under a moderate emissions pathway (Representative Concentration Pathway [RCP] 4.5); by contrast, the bottom‐up approaches used by the Intergovernmental Panel on Climate Change's Fifth Assessment Report (IPCC AR5) projected an ∼66% credible interval of 35–70 cm. A semi‐empirical model calibrated against two millennia of geological reconstructions of GMSL and global‐mean temperature (Kopp, Kemp, et al., 2016) yields lower projections, in good agreement with IPCC AR5 (Church et al., 2013; an ∼66% credible interval of 39–69 cm). The agreement between these two different approaches may increase confidence in both. However, since the top‐down projections are based on a time period (the last two millennia) that likely involved a far smaller role for ice‐sheet changes than is expected in the future, this agreement might alternatively be interpreted as a warning sign for possible implicit historical biases in AR5's bottom‐up projections.

2.2. Key Unanswered Questions in Sea Level Projections

Despite significant progress, there remain important unanswered questions that affect the usability of mean sea level projections.

2.2.1. Deep Uncertainty in Sea‐Level Projections

“Deep uncertainty,” also known as “ambiguity” (Ellsberg, 1961), refers to a situation in which in which there is limited scientific agreement on key conceptual models and parameters (Lempert, 2002). Ellsberg's (1961) classic example refers to a gamble involving drawing balls from a urn containing a mixture of red and black balls, with a $100 award for a red ball and no award for a black ball. In the shallow uncertainty urn, there is a known number of red and black balls (say 50 of each); in the deeply uncertain urn, the total is known but the ratio is not. In general, all else being equal, humans exhibit a preference for the less ambiguous gamble. In sea‐level rise projections, deep uncertainty is reflected in the spread among different probabilistic projections—where there is substantial deep uncertainty, differing but comparably justifiable approaches can yield substantially different probabilistic projections (Bakker, Louchard, & Keller, 2017; Le Cozannet et al., 2017; Wong et al., 2017).

One source of deep uncertainty in future sea‐level rise is the uncertainty in anthropogenic emissions. There is no clear way of estimating the relative probability of different emissions futures, given the political, economic, and technological complexities involved. For one context where such relative probabilities are necessary—estimation of the social cost of carbon dioxide—National Academies of Sciences, Engineering, and Medicine (2017) recommended the use of SEJ. But for sea level projection, such an approach is not necessary; projections conditional upon a plausible range of emissions scenarios serve adequately. Recent projections have generally been conditioned upon the RCPs (Van Vuuren et al., 2011) used in CMIP5, while new projections will likely increasingly use the CMIP6 ScenarioMIP RCP/Shared Socioeconomic Pathway pairings (O'sNeill et al., 2016). A few studies have also looked at 1.5°C and 2.0°C temperature stabilization scenarios (see Horton et al., 2018, for a review).

Less avoidable is the deep uncertainty in ice sheet physics, especially that associated with potential instability of the Antarctic ice sheet. Two increasingly well understood forms of ice‐sheet instability are Marine Ice Sheet Instability (MISI) and Marine Ice Cliff Instability (MICI). The potential for MISI arises when an ice sheet sits below sea level on a reverse‐sloped bed (i.e., a bed that gets shallower toward the edge of the ice sheet; Pattyn, 2018; Schoof, 2007; Weertman, 1974). In MISI, the ice sheet becomes destabilized when ocean waters penetrate underneath the buttressing ice shelf, causing the grounding line to retreat onto the reverse‐sloped area. Because of the reverse slope, as the grounding line retreats, it gets deeper and the ice flux increases, accelerating the rate of retreat. This instability proceeds until the grounding line becomes pinned by a change in bed slope. Such a process may already be underway in parts of the Amundsen Sea Embayment, West Antarctica (Joughin et al., 2014; Rignot et al., 2014).

While as of AR5 the degree of ambiguity surrounding MISI led the IPCC to conclude that “theoretical considerations, current observations, numerical models, and paleo records currently do not allow a quantification of the timing of the onset of such an instability or of the magnitude of its multi‐century contribution” (Church et al., 2013, p. 1174), the process has subsequently become increasingly well represented in ice‐sheet models. A statistical model calibrated to observed grounding‐line changes and projected basal and surface melt changes under a moderately high emissions scenario projected a 95th percentile Antarctic ice sheet contribution to GMSL of 30 cm in 2100 and 72 cm in 2200, with modes of 10 cm in 2100 and both 6 and 49 cm in 2200 (Ritz et al., 2015). Studies using the Parallel Ice Sheet Model, which incorporates MISI, found 0.1‐ to 0.4‐m GMSL contribution under a high emissions scenario (RCP 8.5; Golledge, 2015), with a more recent version incorporating an ocean dynamic feedback projecting 14 cm under the same scenario (Golledge et al., 2015). Similarly, considering only MISI as a potential instability mechanism, the Penn State Ice Sheet Model (DeConto & Pollard, 2016) found a modal projection of 15 cm and a 5th–95th percentile range of 0.1–0.4 m, while Ruckert et al. (2017) estimated 0.1±0.1 m (1σ). Thus, it appears extremely likely that—given current understanding of the climate changes experienced by ice sheets—MISI alone cannot raise the 21st century Antarctic GMSL contribution above about 0.4 m.

By contrast, MICI is currently shrouded in deeper uncertainty. The potential for MICI arises from two processes: ice‐shelf hydrofracturing and the gravitational instability of ice cliffs. Hydrofracturing, driving by the pooling of rain or meltwater on ice shelves, may lead to rapid loss of buttressing ice shelves and expose cliffs of ice that are tens of meters tall directly to ocean water. Above a certain height, currently unknown but apparently exceeding the highest observed ice cliffs on the planet today (∼100 m, Parizek et al., 2019), the cliffs become gravitationally unstable. Cascading collapse can then drive rapid ice‐sheet retreat. The first continental‐scale ice‐sheet model to incorporate MICI found the potential (under RCP 8.5) for a 21st century Antarctic contribution to GMSL rise exceeding 1 m (DeConto & Pollard, 2016), but crucial parameters in this model—such as the rate of susceptibility of ice shelves to hydrofracturing and the maximum possible retreat rate of collapsing ice cliffs—are poorly constrained by paleo‐data (Edwards et al., 2019).

At present, MICI remains the primary driver of deep uncertainty in sea‐level rise projections. This deep uncertainty is particularly manifest in projections for high‐emissions scenarios for late in this century and beyond (Figures 1b and 1c). For example, Kopp et al. (2017) constructed projections of GMSL and RSL change using either Antarctic projections consistent with the assessment of the IPCC AR5 (Church et al., 2013) [labeled as K14] or the MICI‐incorporating projections of DeConto and Pollard (2016) [labeled as DP16]. The K14 projections had a median Antarctic contribution for RCP 8.5 in 2100 of 4 cm; the DP16 projections had a median contribution of 71 cm. Overall, the two sets of GMSL projections differed little in 2050 (90% credible ranges of 0.2–0.4 m under RCP 8.5 and 0.2–0.3 m under low emissions [RCP 2.6] for K14; 0.2–0.5 m for RCP 8.5 and 0.2–0.4 m under DP16) and in 2100 under low emissions (0.3–0.8 m for K14 and 0.3–1.0 m for DP16), for which MICI was not a significant factor. However, under high emissions for 2100 and beyond, the 90% credible intervals for K14 and DP16 exhibited much less overlap: for 2100, 0.5–1.2 m for K14 and 0.9–2.4 m for DP16; for 2200, 0.9–3.8 m for K14 and 5.6–9.6 m for DP16. The experts participating in a recent SEJ study, informed by the literature debate about MISI and MICI, appeared to split the difference: for a high‐emissions scenario, their 90% credible range in 2100 was 0.6–2.4 m, with a median of 1.1 m reflecting a strong skew toward higher values in their assessment (Bamber et al., 2019).

Scientific progress will likely reduce the uncertainty and ambiguity associated with MICI, but ice sheets are complex systems whose continental‐scale behavior intimately depends on their fine‐scale physics. Even if it turns out that MICI is a danger for farther in the future than indicated by early studies, there is no guarantee against the scientific discovery of new modes of instability. The sensitivity of Antarctic projections to the inclusion of just two previously omitted processes thus highlights the presence of deep uncertainty, especially under high‐emissions futures (Bakker, Louchard, & Keller, 2017; Bakker, Wong, et al., 2017; Kopp et al., 2017; Wong et al., 2017).

Increasing scientific grappling with ice‐sheet instability and other potential sea‐level‐related surprises is reflected in the history of GMSL projections (A. J. Garner et al., 2018). The earliest projections (e.g., Schneider & Chen, 1980) were simply scenarios of ice‐sheet instability, with no probabilities associated with them. The IPCC's First Assessment Report in 1990 presented a range of high‐emissions 21st century GMSL projections from 0.3 to 1.1 m. With increasing scientific (over)confidence, this range narrowed over time, such that the Fourth Assessment Report in 2007 presented a 5th–95th percentile range for a high‐emissions scenario of 0.3 to 0.6 m. The report acknowledged the potential for dynamic ice‐sheet instability to increase this range by up to 0.2 m, but this possibility was not incorporated in the bottom‐line total and often lost in citing literature. In response to criticism and with growing understanding of MISI, the upper end of 2013's AR5 likely (at least 66% credible) range for RCP 8.5 reached 0.8 m, with buried textual language noting the potential for MISI to contribute several decimeters more. Overall, this pattern suggests that the narrowing ranges of the IPCC's first 17 years reflected “negative learning” (Garner et al., 2018; Oppenheimer et al., 2008) leading to overconfidence and a lack of clarity, with key caveats present in the text but not in the tables that serve as a key resource for many users.

2.2.2. Robustness of Bottom‐Up Projections

Bottom‐up projections rely upon the underlying models used to calculate each term in equation (1). The challenge of determining appropriate models, and the difficulty in uncertainty assessment, is heightened with respect to the ice sheet contribution, as noted in the previous section. However, difficulties also arise in other terms. For example, it is generally assumed that GCM ensembles, such as those produced by model intercomparison projects, provide a sufficient representation of uncertainty in GMTSLR and DSL. Much has been written about the validity of probability distributions derived from climate model ensembles in other contexts (e.g., temperature and precipitation fields), given that models are not independent or equally plausible (e.g., Tebaldi & Knutti, 2007). Techniques have been proposed to deal with issues of model independence and quality (e.g., Knutti et al., 2017; Sanderson et al., 2015), but it is unclear whether these techniques are applicable to GCM‐derived sea level change projections (Collins, 2017). Some assessments have introduced expert judgement‐based broadening of GCM‐based probability distributions in order to account for these issues; for example, AR5 interpreted CMIP5‐based central 90% ranges as “likely” (at least 66% probability).

Related questions apply to GIA and VLM projections. Various approaches have been taken to account for these terms to date, including GIA models and extrapolation of the linear signal from tide gauge and/or GPS records. Approaches that use the former method generally rely on the assumption that GIA is captured by one or a small number of forward simulations, often employing an over‐simplified one‐dimensional representation of the interior structure of the Earth, and can be treated as linear over time periods of interest. In certain regions, including the U.S. East Coast, substantial spread in present‐day GIA predictions arises due to uncertainty in GIA model parameters and ice histories (Piecuch et al., 2018). The assumption of linearity is valid in most regions on centennial timescales, but in regions with low upper‐mantle viscosity, such as West Antarctica (Barletta et al., 2018; Hay et al., 2017), Alaska (Sato et al., 2012), and Iceland (Auriac et al., 2013), GIA rate changes can be significant on a multidecadal timescale. The failures of this assumption also has important implications for GRD patterns, which in integrated projections are generally assumed to reflect purely elastic processes and to be constant on centennial timescales. In many cases, integrated projections also do not fully account for changes in the within‐region pattern of mass change (e.g., which parts of Greenland are losing mass), with potential implications for population centers (Larour et al., 2017; Mitrovica et al., 2018).

Projections that extrapolate observed trends to estimate VLM (e.g., Kopp et al., 2014) can account for non‐GIA VLM but assume centennial‐timescale linearity for both GIA and non‐GIA VLM. This assumption is severely limited for non‐GIA VLM due to processes that are stochastic, such as tectonics, or directly anthropogenic, such as subsidence due to groundwater and/or hydrocarbon extraction (e.g., Keogh & Törnqvist, 2019; Tanaka & Heki, 2014).

Considerations involved in the combination of different terms have, in general, received less attention relative to the models applied to each component. However, bottom‐up projections must also make an assumption about the covariance (or dependence) of the terms in equation (1). These dependencies, and their treatments to date, are reviewed by Le Bars (2018), who find that assumptions have varied widely, ranging from complete dependence to complete independence across terms. Several recent studies (de Winter et al., 2017; Kopp et al., 2014; Le Bars, 2018; Little et al., 2013; Oppenheimer et al., 2016) show that high inter‐term dependence can substantially increase high‐end projections.

However, understanding and quantifying the physical basis for dependence is difficult. Individual terms may be correlated via climate sensitivity (i.e., if climate warms faster than expected, it is reasonable to expect a higher contribution from many sea level components). This correlation could be accounted for by calculating each term on a GCM‐specific basis, for those components which are represented by climate models (e.g., GMTSL and DSL, or GMTSL and the glacier contribution, if the glacier contribution is derived from a GCM‐specific forcing). A quantitative accounting for correlations is more difficult for terms that cannot be directly traced to a GCM.

Correlations (either positive or negative) may also arise due to interactions and feedbacks between terms that are unrepresented and/or poorly represented in models. Two examples are interactions between GIS mass loss and US East Coast DSL change (e.g., Kopp et al., 2010) or Antarctic mass loss and climate sensitivity (e.g., Bronselaer et al., 2018). To date, there has been little attempt to address these missing feedbacks in bottom‐up projections. Coupling ice‐sheet models to GCMs (e.g., Golledge et al., 2019) will help in characterizing these feedbacks, but the computational expense of fully coupled GCMs poses a challenge to uncertainty quantification, so offline calculations (e.g., Howard et al., 2014) and reduced‐form representations of these relationships will remain useful for the foreseeable future. Dependencies can also extend to components of high‐frequency sea level variability (next section), either due to common drivers (e.g., Little et al., 2015) and/or interactions (such as nonlinear interactions between RSL, tides, surge, and waves; e.g., Arns et al., 2017; Lewis et al., 2019).

2.2.3. The Utility of Probabilistic Approaches

Based in large part on the underlying epistemic goal, Horton et al. (2018) distinguish between three categories of bottom‐up projections. Central‐range projections focus on characterizing a central tendency of sea‐level rise, generally represented by a median and an upper and lower quantile, conditional upon an assumed emissions scenario. High‐end projections focus on characterizing physically plausible, high‐end scenarios of sea‐level rise. Probabilistic projections attempt to serve both epistemic goals at once, by estimating a full probability distribution of future sea‐level change, conditional upon an emissions scenario.

Probabilistic projections have become increasingly common in both the academic literature (e.g., Grinsted et al., 2015; Jackson & Jevrejeva, 2016; Jackson et al., 2018; Kopp et al., 2014; Kopp et al., 2017; Nauels et al., 2017; Rasmussen et al., 2018) and in assessment reports (e.g., Boesch et al., 2018; Callahan et al., 2017; Dalton et al., 2017; Douglas et al., 2016; Griggs et al., 2017; Miller et al., 2018; Kopp, Broccoli, et al., 2016; Horton et al., 2015), motivated by a few key perceived benefits. First, they provide a useful framework for summarizing and synthesizing existing knowledge regarding the different driving processes, including nontraditional methods that can be used in the presence of deep uncertainty, such as SEJ. Second, they align with the increasing ubiquity of imprecise probabilistic language in assessment reports, such as the IPCC's use of the term “likely” to mean “at least 66% probable” and “very likely” to mean “at least 90% probable.” Third, they appeal to a specific class of stakeholders, namely, those oriented toward benefit‐cost analysis and financial risk analysis (e.g., Houser et al., 2015; New York City Panel on Climate Change, 2013). In this last regard, it is notable that some of the users of early probabilistic projections included a New York City government led by Michael Bloomberg (New York City Panel on Climate Change, 2013) and a nongovernmental “risk committee” led by Bloomberg and two other senior statesmen with finance backgrounds (Bloomberg et al., 2014).

Despite these perceived benefits, probabilistic projections are conditional upon emissions, and, more generally, the methodological assumptions employed in the construction of the probability distribution. For processes subject to deep uncertainty, alternative justifiable approaches to constructing a probability distribution can yield quite divergent answers (e.g., Bakker, Louchard, & Keller, 2017; Le Cozannet et al., 2017). One approach to tackling ambiguity is to employ multiple probability distributions, which can be interpreted as representing the informed judgement of different idealized experts. The weighting of the different experts could be based on performance, as in SEJ, but might also depend upon characteristics of the relevant decision makers, such as their degree of ambiguity aversion (e.g., Le Cozannet et al., 2019).

Despite techniques that attempt to address these limitations, there remain questions about the usability of probabilistic approaches (Hinkel et al., 2019). The most useful approaches to summarizing scientific knowledge may not always be the most useful approaches for decision makers, and—though probabilistic projections have been welcomed by some—they have also led to some anxiety. Behar et al. (2017) suggest that some stakeholders prefer scenarios (sometimes informed by probabilistic projections) rather than the direct use of probabilistic projections (e.g., Sweet et al., 2017). Range‐spanning deterministic scenarios remain commonplace and are a valid approach for many decision makers. Some end users may be better served by putting the focus on critical thresholds of exposure and then working backwards to assess likelihoods over time rather than starting with scenarios of sea level over time, but this approach requires closer integration of sea‐level science and decision making (see section 6).

3. Projections of Extreme Sea Level Change and Associated Flooding

The effects of RSL rise are initially felt primarily not through permanent inundation but through increases in the frequency of extreme sea levels (ESLs). ESLs arise through the superposition of mean RSL, tides, storm surges, and lesser‐magnitude processes operating over a range of frequencies. Where tidal ranges are small, as along the U.S. Gulf of Mexico, wind‐forced surge is typically the dominant driver of ESLs (Merrifield et al., 2013); where narrow continental shelves inhibit sizable storm surges from forming (Tebaldi et al., 2012), like along island coasts, wave effects and/or higher astronomical tides during high sea level anomalies become dominant drivers (Serafin et al., 2017; Rueda et al., 2016). The severity of impacts—whether through overland flooding or through indirect effects like infiltration or degradation of wastewater (Flood & Cahoon, 2011), freshwater supplies (Sukop et al., 2018), or stormwater (Obeysekera et al., 2011) systems—varies accordingly.

Statistical models based upon parametric distributions estimated from long‐term tide‐gauge measurements are a primary source for location‐specific probabilistic ESL hazard assessments. Most studies fit a three‐parameter extreme‐value distributions, such as the generalized extreme value or generalized Pareto distribution (Tebaldi et al., 2012; Wahl et al., 2017), to tide‐gauge observations. For example, Figure 2 shows a generalized Pareto distribution fit to historical ESLs at the Battery, New York City, USA (Buchanan et al., 2016). Compared to two‐parameter distributions, such as the Gumbel distribution (J. Hunter, 2010, 2012), three‐parameter distributions allow for more realistic estimates of rare‐event frequency and the associated uncertainty (Buchanan et al., 2017). Heavy‐tailed distributions are common in tropical‐cyclone prone locations, where storm surge estimates associated, for example, with a 1% average annual probability event can be extremely large (Hall et al., 2016; Wahl et al., 2017). Regional frequency analysis has occasionally been used with tide‐gauge data to estimate ESL probabilities while overcoming some of the spatial limitations inherent to the global tide gauge network (Hall et al., 2016), but to our knowledge more sophisticated spatiotemporal extreme value methods (e.g., Reich & Shaby, 2012) have not yet been employed in this context. Recent advances using satellite altimetry show promise in the ability to complement tide‐gauge observations by predicting coastal ESLs using offshore ESL observations combined with continental shelf characteristics (Lobeto et al., 2018; Woodworth & Menéndez, 2015).

Dynamic ocean circulation models can also be used to simulate storm tides and estimate historical and current ESL probabilities. These models are typically driven by global atmospheric reanalyses and, in regions not impacted by tropical cyclones, yield ESL distributions similar to those estimated from tide gauges (Muis et al., 2016). Higher‐resolution atmospheric fields are needed to simulate the low‐probability storm‐tide heights associated with historical tropical cyclones (Vousdoukas et al., 2018). Dynamic simulations have three potential advantages over statistical methods. They can (1) provide predictions for locations where there are no tide gauges, (2) better resolve rare‐event probabilities and overcome record length limitations by simulating large numbers of synthetic storms under a specified climatology (Haigh et al., 2014; Lin et al., 2012), and (3) physically account for non‐stationarity associated with climate variability and climate change. Dynamic simulations can also incorporate high‐frequency wave effects (Vitousek et al., 2017; Vousdoukas et al., 2018), which have not traditionally been measured by tide gauge records (but see Sweet et al., 2015) but are of particular concern in areas where erosion is primarily driven by waves rather than by surge, as along the U.S. West Coast (Serafin et al., 2017; Sweet et al., 2015). On the other hand, dynamic simulations are subject to the limitations of the driving reanalysis data sets and ultimately must rely on tide‐gauge observations for validation. Dynamic approaches are commonly used in the private sector, for example, by risk analysis companies serving the insurance sector (e.g., Hsiang et al., 2017).

In addition to long‐term trends, ESL probabilities exhibit seasonal and long‐tidal cycles and climate mode covariability (e.g., Aucan et al., 2012; Haigh et al., 2011; Marcos et al., 2015; Menéndez & Woodworth, 2010; Wahl & Chambers, 2016; Woodworth & Menéndez, 2015), which can enhance flooding when contributing processes align (Sweet et al., 2016; Thompson et al., 2019). Diagnosing contributory processes within statistical ESL models can provide a degree of predictability if the processes are deterministic in nature or predictable to some degree by climate models (Menendez et al., 2009; Menéndez & Woodworth, 2010; Sweet & Park, 2014; Sweet et al., 2018; Widlansky et al., 2017). Given the limited length of the tide‐gauge record and thus the limited sampling of rare events like landfalling tropical cyclones, however, identifying changes in the tail shape of an extreme value distribution is exceptionally challenging, pointing to the value of synthetic tropical cyclones generation in estimating historical and current probabilities. Paleostorm records (e.g., Brandon et al., 2014) can complement and extend the tide‐gauge records by centuries, but there has so far been insufficient analysis to determine the quantitative utility of such records in improving return‐period estimates.

Future ESL frequencies and impacts depend upon local RSL rise and changes in the characteristics of coastal storms, tides, and waves, as well as their possible interdependencies (e.g., Arns et al., 2017; Lewis et al., 2019; Little et al., 2015). Projections based upon statistical models typically assume that RSL change is the only driver of changes in the ESL distribution (e.g., there are no changes in storm surge characteristics or tidal range; e.g., Buchanan et al., 2016; Buchanan et al., 2017; Hall et al., 2016; J. Hunter, 2012; Kopp et al., 2014; Tebaldi et al., 2012). For example, Figure 3 shows the change in the expected frequency of ESLs at the Battery under different probability distributions for RSL change corresponding to the GMSL projections shown in Figures 1b and 1c. Observations and dynamic simulations confirm that RSL change is increasingly the dominant driver of ESL change but also show the limitations of the assumption that the ESL distribution is otherwise stationary. Historically, although attribution is difficult, there is evidence of regional changes in storm activity, such as increasing North Atlantic hurricane activity since the 1970s (Kossin et al., 2017). While most historical changes in ESL have tracked changes in mean sea level (Menéndez & Woodworth, 2010), there are exceptions, such as within major estuaries important to shipping from harbor‐channel deepening (Familkhalili & Talke, 2016; Talke et al., 2014). Model simulations under future climate and RSL conditions find evidence of regional changes in tidal ranges and storm surge (Schindelegger et al., 2018; Vousdoukas et al., 2018). Tropical cyclone intensity is projected to increase globally (Emanuel, 2013; Knutson et al., 2010; Knutson et al., 2015), but it is unclear whether the overall number of hurricanes will decrease (Knutson et al., 2015; Walsh et al., 2014) or increase (Bhatia et al., 2018; Emanuel, 2013). Projected changes in storm tracks further complicate inferences about associated changes in tropical cyclone‐driven ESLs at specific locations (A. J. Garner et al., 2017). These analyses indicate that, while adding projected RSL changes to historical ESL probabilities provides a good first approximation of ESL changes, in some areas this approach will lead to an underestimate of the associated hazard and its impacts (Hsiang et al., 2017).

Figure 3.

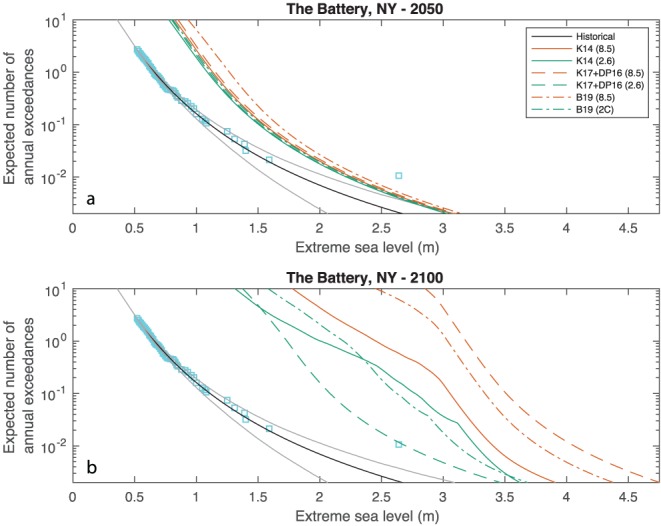
Extreme sea level distributions for the Battery, New York, in (a) 2050 and (b) 2100, under six RSL probability distributions corresponding to the six GMSL probability distributions in Figure 1. Cyan boxes show historical ESLs, placed by empirical frequency over the tide gauge record; black shows the historical expected ESL distribution (grey indicates 17th–83rd percentile credible range). Blue curves represent low‐emissions projections (RCP 2.6); orange curves represent high‐emissions projections (RCP 8.5). Solid, dashed, and dot‐dashed lines represent expected values using ice‐sheet projections from Kopp et al. (2014), Kopp et al. (2017) using the AIS projections of DeConto and Pollard (2016), and Bamber et al. (2019).

Two useful metrics for planning and communications, derived from combining probabilistic RSL projections and extreme value distributions, are frequency amplification factors and sea‐level allowances. A frequency amplification factor is an estimate of the change in the expected frequency of a particular water level (Buchanan et al., 2017; Garner et al., 2017; Hunter, 2010; Vitousek et al., 2017). For example, if a current 10% average annual probability ESL is projected to have a frequency amplification factor of 3 in 2050, this means that—integrating across uncertainty in RSL projections—it is expected with 30% average annual probability in 2050. In Figure 3, frequency amplification factors are reflected in the vertical distance between the historical curve and the projected curves. Sea‐level allowances are the height adjustments that maintain the current annual expected probability of flooding of a particular ESL (Buchanan et al., 2016; Hunter, 2012). The shape of the extreme value distribution (in particular, the approximately log‐linear relationship between the expected number of events and ESL height) implies that, with an uncertain RSL distribution, an estimated sea‐level allowance will always be greater than the expected RSL rise (Buchanan et al., 2016). In Figure 3, sea‐level allowances are reflected in the horizontal distance between the historical curve and the projected curves. However, both of these metrics should be used by decision makers with care, as they are often derived from a single estimated probability distribution for RSL. In the presence of deep uncertainty, consideration of multiple probability distribution—yielding multiple amplification factors and allowances—is a more cautious approach (Buchanan et al., 2016). Figure 3 shows that, at the Battery, the frequency amplification of the largest historical ESL (2.6 m, associated with Hurricane Sandy in 2012) is relatively well‐constrained for 2050 (1.9–2.5x) but poorly constrained for 2100 (6–85x under low emissions; 290–11,000x under high emissions), reflecting the deep uncertainty in the associated sea‐level projections.

While ESLs are often a valid proxy for coastal flooding, they do not tell a complete story. ESLs provide only a one‐dimensional measure for a three‐dimensional (depth and inland extent) impact. While “bathtub” models represent flooding extent by projecting ESLs, as measured at tide gauges, onto topography (e.g., as measured via high‐resolution LIDAR) without accounting for local atmosphere/ocean dynamics or the frictional interference of the natural or built environment to determine extent of flooding, hydrodynamic models accounting for of the flow of water in the ocean and onto land reveal a more complex story (Deb & Ferreira, 2017; Lin et al., 2010, 2014; Orton et al., 2015; J. Wang et al., 2012). Nonlinear hydrodynamic responses vary spatially as a function of coastal topography, land use, and storm characteristics (Atkinson et al., 2013; Anarde et al., 2018; Barnard et al., 2019; Ding et al., 2013; Ferreira et al., 2014; Glass et al., 2018; Mousavi et al., 2011; Passeri et al., 2018; Smith et al., 2010; Wang et al., 2012; Woodruff et al., 2013; Zhang et al., 2013). Most studies using hydrodynamic models have focused on the effects of storm surge (e.g., Muis et al., 2016), though in some areas precipitation‐driven flooding is of crucial importance (Wahl & Chambers, 2015; Wright et al., 2019). Storm surge and upland riverine forcing acting together can lead to higher extreme water levels (Moftakhari et al., 2017). Elevated groundwater tables are and will be an increasingly important factor for future flood risk (Anderson et al., 2018), and in developed areas, flooding also depends on the flow of stormwater through drainage networks (Obeysekera et al., 2011).

“Bathtub” models are often used to assess coastal flood exposure (e.g., Strauss et al., 2012), and they are well suited for assessing exposure to permanent inundation induced by RSL rise. For example, Rasmussen et al. (2018) found that about 30–110 million people around the world currently live on land would be exposed to permanent flooding by 2150 under a 1.5°C stabilization scenario, compared to 30–140 million under a 2.0°C scenario. The “total water level” approach to assessing exposure associated with ESLs treats transient events the same as a permanent flooding event. Using such an approach and assuming adaptation measures that maintained a constant average annual probability of flooding, Hallegatte et al. (2013) found that 20 cm of GMSL rise would increase average annual global flood losses by $60 billion. However, the total water level approach is not always adequate; Gallien (2016) found in one case study that the important role of wave action in coastal flooding in California led to its systematic failure. Hydrodynamic models are used in both the academic literature and the private sector to provide more accurate exposure estimates. For example, Aerts et al. (2013) combined synthetic tropical cyclones (Lin et al., 2012), a hydrodynamic model of coastal surge, a spatial database of buildings, and a flooding depth damage function to estimate the return period of different levels of coastal flood damage at New York City. A similar approach was taken by Hsiang et al. (2017), who incorporated the sea‐level rise projections of Kopp et al. (2014) into a hydrodynamic model to assess average annual tropical and extratropical cyclone losses along the U.S. Atlantic and Gulf Coasts under future sea level and climate, assuming the current distribution of people and property. They found that—in the absence of adaptive measure—GMSL rise currently increases expected annual tropical and extratropical cyclone damages in the United States by about 0.1% of GDP per meter GMSL rise, increasing to about 0.15% per meter at 1 m of GMSL rise. Accounting for projected changes in tropical cyclone intensity approximately doubles the damage for RCP 8.5 toward the end of the 21st century.

4. Coastal Flooding in a Dynamic Physical Environment

The coast is not simply a static background over which water flows, though most studies of coastal flood hazards treat it as such. It instead exhibits dynamic growth and destruction of land and ecosystems (Anarde et al., 2018; Barnard et al., 2019; Glass et al., 2018; Le Cozannet et al., 2019; Passeri et al., 2018). Waves, currents, and tides redistribute sediment along and across the coastal zone, resulting in shoreline dynamics significantly different than would occur in a static coastal landscape (Ashton et al., 2008; Murray et al., 2009; Paola et al., 2011; Payo et al., 2016). Such departures from the static coast assumption are particularly evident in low‐lying environments, such as barrier islands and fluvial deltas, both among the most dynamic landscapes on Earth.

Barrier islands are composed of three regions: the shoreface, continuously reworked by waves and tides; the subaerial portion, typically a few meters above sea level; and the back‐barrier environment, which generally comprises salt marshes, lagoons, and tidal flats (Figure 4a). In order for barrier systems to persist and migrate under RSL rise, shoreface sediment must be transported onto and behind the barrier (Figure 4a). Storm‐induced flood‐tidal delta formation and overwash fan deposition are the two most significant mechanisms that transport sediment to the back‐barrier environment (Carruthers et al., 2013; Dillon, 1970; Donnelly et al., 2006; Fitzgerald et al., 1984; Matias et al., 2008; Nienhuis & Ashton, 2016; Pierce, 1970; Rogers et al., 2015). This onshore sediment movement by tides and overwash events, as well as offshore sediment movement into deeper waters from the upper shoreface (Bruun, 1962; C. Donnelly et al., 2006; Leatherman, 1983; Lorenzo‐Trueba & Ashton, 2014), enhances barrier shoreline retreat beyond what would be expected from just passive flooding (Figure 4b).

Figure 4.

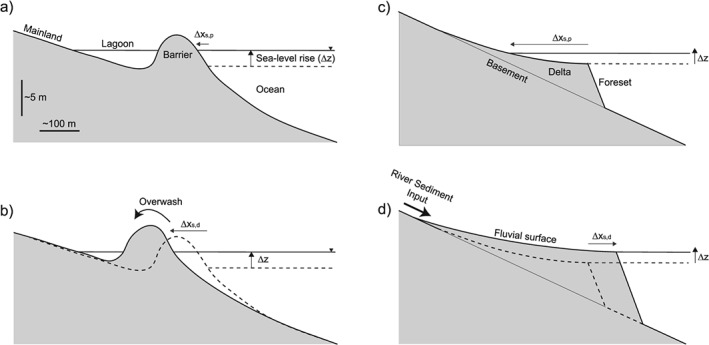
Conceptual sketches for both barrier (a and b) and deltaic systems (c and d) illustrating the difference in shoreline change under passive flooding (Δx _s,p) and dynamic landscape (Δx _s,d) scenarios. In barrier island systems, the shoreline can retreat faster in the dynamic landscape scenario (i.e., Δx _s,d≫>Δx _s,p) as overwash and tidal fluxes move sediment from the ocean side to the lagoon side of the barrier (b). In the case of fluvial deltas, when riverine sediment supply is large enough, the shoreline can migrate seawards despite sea‐level rise (d).

Similar to that of barrier islands, the cross‐shore geometry of deltaic environments can be conceptualized in terms of coupled and adjacent environments (Lorenzo‐Trueba et al., 2009; Paola et al., 2011; Parker et al., 2008; Swenson et al., 2000). Connected at the shoreline, these environments include a deltaic plain, which generally exhibits low topographic relief (i.e., ∼1/10,000), and an offshore region with typically steeper gradients (Figure 4c). The shoreline can migrate either seawards or landwards as a function of the magnitude of riverine sediment supply, wave energy, RSL rise rate, and the fraction of sediment that deposits on the deltaic plain vs. the offshore region (Parker et al., 2008; Paola et al., 2011; Swenson et al., 2000, 2005). To illustrate how shoreline behavior can substantially deviate from that captured by passive flooding, consider two different scenarios in terms of sediment supply. Under sufficient sediment supply, the shoreline can advance seaward, which in turn results in the expansion of the deltaic plain despite RSL rise (Figure 4d). In contrast, under a shutdown in sediment supply caused by dam construction, flow diversions from the established river, or artificial embankments that prevent sediment exchange between the river and its floodplain, the deltaic plain progressively inundates as sea level rises. Given the low topographic relief, inundation of the deltaic plain can result in rapid rates of shoreline retreat (Figure 4c), and the abandoned deltaic lobe can be reworked at very fast rates (Komar, 1973; Nienhuis & Ashton, 2016; Rodriguez et al., 2000).

The sketches in Figure 4, although highly simplified, emphasize that RSL rise can do more than just passively inundate the landscape. In fact, the evolution of coastal environments is the result of a complex interplay between different regions, both landwards and seawards of the shoreline.

For instance, previous work suggests that two‐way feedbacks between barrier islands and their associated backbarrier environments can result in threshold behaviors that can in turn lead to a whole‐scale reorganization of the barrier system (Carrasco et al., 2016; Deaton et al., 2017; FitzGerald et al., 2018; Lauzon et al., 2018; Lorenzo‐Trueba & Mariotti, 2017; Walters et al., 2014). RSL rise and wave action can cause not only barrier shoreline retreat but also drastic changes in backbarrier marsh vegetation, including marsh loss (J. P. Donnelly & Bertness, 2001; Kirwan & Megonigal, 2013; Lorenzo‐Trueba & Mariotti, 2017; Mariotti & Fagherazzi, 2013). The loss of marshlands would change the hypsometry of the backbarrier, increasing tidal exchange between the ocean and backbarrier and enhancing the rate of barrier landward migration, which in turn could accelerate barrier disintegration and drowning (FitzGerald et al., 2018; Lorenzo‐Trueba & Mariotti, 2017). In general, this work highlights that backbarrier environment characteristics that are typically not directly related to barrier evolution—such as the extent of marsh platforms, lagoon fetch, suspended sediment concentrations in the lagoon, and the mainland slope—could play a major role in the long‐term barrier response to RSL rise.

Fluvial deltas are also complex systems that involve a complex web of coupled biologic and physical processes (Day et al., 2008; Paola et al., 2011). Plant matter accumulation, which in addition to river sediment supply contributes to maintaining the deltaic plain above sea level (Day et al., 2007; Paola et al., 2011), can be significantly reduced by a lowering of the water table elevation (Gambolati et al., 2006; van Asselen et al., 2009) or a shift in the location of the freshwater‐saltwater boundary. Such a reduction in organic matter accumulation on the deltaic plain during sea‐level rise can in turn amplify the speed of shoreline retreat (Lorenzo‐Trueba et al., 2012).

With the presence of coastal communities, human responses to coastal change provide additional feedbacks to coastal environments, suggesting the possibility of emergent interactions at multidecadal time scales (Jin et al., 2013; Lazarus et al., 2016; Miselis & Lorenzo‐Trueba, 2017; Werner & McNamara, 2007). Human responses intended to preserve coastal buildings and infrastructure—such as building seawalls, constructing groynes, nourishing beaches, stabilizing inlets, or armoring updrift headlands—have accumulated to the point where the evolution of coastal landscapes cannot be considered to be caused by nature alone (Hapke et al., 2013; Lazarus & Goldstein, 2019; Lazarus et al., 2016; Nordstrom, 1994; Werner & McNamara, 2007). The natural dynamics described in Figure 4 are still at play but are heavily affected by human activities, development, and land‐use changes. Typically, engineering activities on developed barrier islands prevent or counteract overwash, thereby reducing barrier islands's average elevation above sea level (Miselis & Lorenzo‐Trueba, 2017; Rogers et al., 2015). Additionally, developed barrier stretches are more likely to present steeper shorefaces, often associated with beach nourishment activities, and deeper backbarrier lagoons due to dredging activities (Miselis & Lorenzo‐Trueba, 2017). Looking to the future, a key question is whether such human responses may make drowning of barrier systems more likely (Miselis & Lorenzo‐Trueba, 2017; Rogers et al., 2015). The same question applies to fluvial deltas, which often experience a reduction in sediment supply to their floodplains due to the construction of dams and levees, as well as an increase in subsidence rates in the deltaic plain due to water and hydrocarbon extraction (Paola et al., 2011; Syvitski & Saito, 2007; Syvitski et al., 2009).

Overall, in order to assess future flood risks in low‐lying coastal areas, analyses must go beyond passive flooding models discussed in section 3; models of the coupled evolution of coastal landscapes and human activities over multidecadal time scales are needed. A significant challenge in this regard is the need to consider the cumulative effect of short‐lived events (e.g., single storms). Engineering approaches have made significant progress in assessing the vulnerability of residential structures to storm surge over single storm events (Hatzikyriakou et al., 2016; Lin et al., 2010, 2014; Orton et al., 2015). The X‐Beach model (Roelvink et al., 2009), which couples hydrodynamics and sediment transport to quantify morphological change, has been used to reproduce barrier changes during individual storm events (Almeida et al., 2017; Lindemer et al., 2010; McCall et al., 2010). Such modeling efforts, however, are highly calibrated and are difficult to extrapolate over multiple storms.

On the other end of the spectrum, long‐term geologic models for coastal change no longer use laboratory‐validated sediment transport relationships but rather use conceptual relationships between barrier geometry and barrier island movement (Cowell et al., 1995; Lorenzo‐Trueba & Ashton, 2014; Masetti et al., 2008; Moore et al., 2010; Stolper et al., 2005; Storms, 2003; Wolinsky & Murray, 2009). The initial, “morphokinematic” wave of these models is based upon the conservation of mass and maintenance of an equilibrium configuration (Cowell et al., 1995; Moore et al., 2010; Stolper et al., 2005; Wolinsky & Murray, 2009). The second, “morphodynamic” wave of models accounts for sediment fluxes along the shoreface and overwash processes (Lorenzo‐Trueba & Ashton, 2014; Masetti et al., 2008; Storms, 2003). Although quantitative understanding of the relative roles of overwash fluxes, shoreface dynamics, and backbarrier sedimentation processes in the response of barriers to environmental change remains lacking, the simplicity of some of these models (e.g., Lorenzo‐Trueba & Ashton, 2014; Nienhuis & Lorenzo‐Trueba, 2019) allows for model extensions that incorporate additional physical and biological processes, as well as human interactions.

Further work is needed to bridge the gap between engineering and geologic approaches and construct morphodynamic models that can integrate over multiple storm events and include post‐storm recovery and fair weather action that occurs between storms. Models also need to account for the complex interplay of the different regions or environments—from the onshore subaerial and lagoonal components, through the surf zone, and seawards onto the continental shelf itself—as well as for feedbacks between natural processes and human activities (Lazarus & Goldstein, 2019; Lazarus et al., 2016; Werner & McNamara, 2007).

5. Coastal Flooding in a Dynamic Human Environment

Just as physical and ecological coastal systems are dynamic, not simply static recipients of flooding, so too is the human coast. Socioeconomic analyses of future impacts that treat the distribution of people and capital as static provide useful first‐order information to inform risk assessment. However, these analyses overlook crucial dynamics, such as those associated with the movement of capital (e.g., shifts in investment, employment opportunities, and the availability of amenities such as schools) and people (e.g., immobility, temporary displacement, and permanent migration) to and from the coast. RSL change, coastal flooding, and ensuing physical and ecological changes interact with these human dynamics in complex ways. Planned adaptation strategies that seek to reduce exposure and vulnerability need to be responsive to these dynamics and recognize their own role in shaping the future evolution of the coast (e.g., Haer et al., 2017).

Globally, coastal areas, which contain many of the largest cities, are highly concentrated areas of population and wealth and continue to attract increasing populations (Neumann et al., 2015). At the same time, coastal areas are already seeing increasing hazards from RSL rise, with populations with differential resources and vulnerability undertaking both autonomous and planned adaptations (Hinkel et al., 2018). These adaptations, and their interactions with other drivers of migration, can exhibit complex, non‐linear dynamics, and thresholds. For example, delta communities have been carefully investigated with respect to exposure, vulnerability and adaptation efforts (Suckall et al., 2018). These efforts have highlighted the critical role of migration as an adaptation strategy, as well as the importance of aligning planned adaptation with autonomous efforts. These dynamics can also be observed in modeling efforts, such as agent‐based models of household defensive expenditures, which show near‐term investments followed by abandonment at some critical risk threshold (e.g., McNamara & Keeler, 2013).

Simple economic models might predict a shift of investment away from frequently flooded coastlines. Empirical evidence shows that being hit by a tropical cyclone causes a multidecadal reduction in economic output (Hsiang & Jina, 2014), an effect that computable general equilibrium (CGE) modeling indicates is consistent with the diversion of investment to replace damaged capital (Hsiang et al., 2017). One might expect that repeated flooding might lead to a shift of investment to less exposed areas and that the exposed population might likewise emigrate. Indeed, some evidence suggests that increasing minor tidal flood frequencies affect housing prices within coastal markets (Keenan et al., 2018), depressing demand for housing subject to repetitive flooding and increasing demand for higher‐elevation housing through a process referred to as “climate gentrification.” However, higher‐elevation properties may still have significant exposure to infrequent major flooding, and there is no clear evidence for migration out of flood‐exposed markets. There is also evidence that decisions about adaptation to RSL rise is related to the degree of belief in and understanding of climate change (Lata & Nunn, 2012).

Some autonomous responses to decisions to protect coastal properties can even paradoxically increase exposure or vulnerability. In the United States, the historical increase in tropical cyclone damages appears to be primarily tied to a shift of population and wealth toward the exposed coast (Klotzbach et al., 2018). In fact, recent observations suggest that subsidized coastal protection and infrastructure development in exposed areas inflate property values, in turn stimulating further housing and infrastructure development, and thus an associated migration toward the coast (Armstrong et al., 2016; McNamara et al., 2015). Moreover, coastal development often destroys natural buffers against flooding, such as marshes and mangrove ecosystems (Barbier et al., 2011; Temmerman et al., 2013), which further increases the flood hazard.

Understanding the response of coastal economies and populations to sea‐level rise is thus intimately bound with understanding the factors that influence migration decision making in general and more specifically in response to climatic stressors (e.g., Adams & Kay, 2019). Migration is the movement from one location to another. This movement can be categorized by time scale (e.g., temporary vs. permanent), spatial scale (e.g., internal to a country vs. international), purpose (e.g., economic vs. distress), and the degree of agency in the decision to move (e.g., voluntary vs. forced; International Organization for Migration, 2019). Recent reviews related to environmental migration have frequently employed the term “displacement,” especially when the reason for migration is a sudden or progressive change in environmental conditions (McLeman & Gemenne, 2018).

Decisions to migrate and observed mobility patterns differ by degree of vulnerability, with substantial heterogeneity in destination, timing of the movement, and the potential to return (Fussell et al., 2014). Theories to explain observed migration have shifted from individual economic decision making to recognize the importance of households and social capital. In neoclassical economic migration theory, migrants are drawn primarily by more favorable conditions in receiving than in sending areas. These forces are often summarized as “push” and “pull” factors (Lee, 1966). Individuals are represented as agents who react to these conditions and opt to migrate based upon their ability to take advantage of these differentials. More recent theories have elaborated the social context of the individuals who undertake a migration. The New Economics of Labor Migration (NELM) recognizes that migration is a decision made at the household or community level rather than the individual level. Households overcome imperfections in local markets—primarily economic, but also political and social—through the migration of individuals who are best suited to the efforts. These individuals then return a portion of their earnings through remittances (Stark & Bloom, 1985). Social capital theory further emphasizes that the decision is made within the context of migration systems. In this framing, individual decisions about whether and where to migrate are facilitated by information that spreads through a group via social capital (Massey & España, 1987). Both of these theories perform well when explaining observed flows; however, there are still challenges to explaining the initiation of migration in any given community.

The role of environmental pressures in migration decisions has taken on increased salience with respect to climatic stressors such as RSL rise. Simpler conceptual models that either draw on neo‐Malthusian concepts about scarcity and population pressures or emphasize the socioeconomic context as a dominant determinant have been largely replaced by a more integrated models incorporating complex interactions between environmental and non‐environmental factors (Hunter et al., 2015). The model elaborated in the Government Office for Science (2011) report highlights the interplay of multiple macro‐level influences—sociocultural, political, and economic, in addition to environmental—with individual and household characteristics that combined lead to a decision to migrate or stay.

Thus, “environmental” migration may resemble other forms of migration. Migrants may be primarily opportunity driven or may be fleeing a proximate disaster. The significance of environmental or natural resources among the other factors in their decision may range from large to insignificant (Black et al., 2011). Additionally, environmental migration is more likely to augment but not fundamentally alter the migration patterns that are currently observed. In other words, climate‐ and sea‐level‐driven migration is primarily a statistical phenomenon: While some individuals (e.g., residents of small island states rendered uninhabitable by RSL rise) may self‐identify as climate migrants, most migration influenced by climate change may only be identifiable in the statistical aggregate and not at the individual level (Mayer, 2016).

Extending environmental migration to climate change, both macro‐ and micro‐level features are important when considering the implications for climate change and migration. Migration in the context of climate change can be understood as an adaptation strategy within a social context, rather than a direct impact of environmental change (Black et al., 2011; McLeman & Smit, 2006). Thus, the type of exposure (e.g., sudden vs. slow onset) and the vulnerability of the population to these changes may jointly influence observed migration flows (Gibbons & Nicholls, 2006). For example, Adger et al. (2018) propose that sudden events lead to temporary displacement, while slow onset changes lead to more permanent displacement. Both of these forms of displacement can shift to migration as responses to the climatic stressors become more proactive (Adger et al., 2018).

Models of coastal exposure and migration are evolving from more static representations of populations at risk toward agent‐based models that capture decision making and interactions with socioeconomic conditions and adaptation decisions. (To date, all of these models neglect the geomorphological dynamics discussed in the previous section.) The former, more static models use different measures of physical exposure to sea‐level changes and their effects to estimate the population at risk of being displaced, employing either present‐day or future population scenarios with and without some measures of adaptation. Early work focused on identifying present‐day populations at risk. Strauss et al. (2012) evaluated population exposed in the United States at different elevations above the high‐tide line, while Haer et al. (2013) evaluated U.S. population under a set of RSL rise scenarios. Extending such an approach globally and employing probabilistic RSL projections, Kopp et al. (2017) and Rasmussen et al. (2018) considered respectively the effects on estimated population exposure of different assessments of Antarctic ice‐loss potential and the difference between 1.5°C and 2.0°C global‐mean warming scenarios.

More complex models have incorporated population changes alongside RSL change. For example, looking at RSL rise projections and scenarios for future coastal populations, Hinkel and Klein (2009) developed the Dynamic and Interactive Vulnerability Assessment (DIVA) tool, which assesses exposure and vulnerability with an estimate of the cost of population displacement from permanently inundated and intermittently flooded land (Hinkel & Klein, 2009). Using DIVA, a set of standard socioeconomic scenarios (the Shared Socioeconomic Pathways, or SSPs) and a set of bottom‐up RSL projections, Hinkel et al. (2014) estimated that, in 2100, 0.3–1.2 m of GMSL rise would, in the absence of adaptation, lead to annual flooding of 0.2–4.6% of the global population. Neumann et al. (2015) further elaborated on this effort by extending the population distribution in the SSPs to account for the differential growth of the coastal populations. These risk assessments, however, incorporate, at most, limited human decision making. Hinkel et al. (2014) included scenarios incorporating what could be interpreted as a decision to remain in place with a single possible adaptation measure. In these scenarios, perfect dikes are constructed and elevated around all coastal areas in a nominally benefit‐cost optimal manner, thus reducing the exposed population by about two orders of magnitude.

Another set of models have integrated representations of migration in response to RSL rise alongside other adaptation measures. Along each coastal segment in DIVA, Diaz (2016) models an economic rational representative agent, who makes a decision in the face of RSL rise and storm surge to “do nothing,” protect up to a benefit‐cost optimal elevation threshold, or relocate all the population below an elevation threshold. This approach begins to generate a more accurate representation of population at risk, as it dynamically considers adaptation, including migration. However, like the other exposure models, it does not consider a complete migration with destination, and it does not consider the complex range of factors involved in individual decision making.

A few efforts have considered migration flows with an origin and a destination. Most of these studies do not consider how population growth along the coast would be changed through interactions with RSL rise, instead applying a RSL scenario to either current population or an exogenously specified population scenario. Using localized, observed migration rates and patterns, Curtis and Schneider (2011) estimated the migration patterns from a few coastal counties in the United States due to 1 m of RSL rise and to 4 m of extreme storm surge. Hauer et al. (2016) expanded on this approach, using household‐level rather than county‐level data to assess U.S. population vulnerability to RSL rise under 0.9‐ and 1.8‐m RSL rise scenarios. Hauer (2017) then modeled the likely destinations of these migrants, assuming that these flows augmented existing migration patterns. Rigaud et al. (2018) modeled internal migration flows in sub‐Saharan Africa, Asia, and Latin America, using a population gravity model to simulate the demographic effects of RSL rise and other climatic impacts. Looking at people and economic consequences in a neoclassical framework, Desmet et al. (2018) applied a highly resolved dynamic spatial economic model to the RSL projections of R. E. Kopp et al. (2014), focusing on displacement due to permanent flooding by RSL rise. They find that substantial economic losses in coastal communities are partially offset by enhanced economic growth in regions that receive displaced populations, with real GDP losses (as a percentage of the global economy) peaking in the middle of the 22nd century.

Currently, there is an emphasis on developing data and models that can capture more aspects of individual decision making around migration (Curtis & Bergmans, 2018). Agent‐based models may present a way forward (e.g., Kniveton et al., 2012), with one recent effort (Adams & Kay, 2019) incorporating nonmaterial preferences (intrinsic mobility and satisfaction with place) into migration decision making. However, to our knowledge, there are no agent‐based models that jointly consider RSL rise, coastal population mobility, and other adaptation measures at a spatial scale larger than an individual community (e.g., Adams & Kay, 2019; McNamara & Keeler, 2013).

Another consideration with modeling how RSL rise will affect migration is that the current record of migration does not generally have an appreciable RSL rise signal, such that it is challenging to develop empirical evidence. Indeed, there has been movement to the coast, especially in wealthier and urban locations (Hallegatte et al., 2013). Thus, studies of coastal populations and migration have focused on observations of existing environmental stressors that are either indicative of or worsened by RSL rise, such as both acute (storm‐driven) and chronic (minor tidal) flooding, as well as increases in groundwater or soil salinity, especially in agricultural settings. Most studies of existing stressors related to RSL rise also emphasize the interplay between exposure and vulnerability in forming migration decisions. For example, Chen and Mueller (2018) found that the type of impact matters for migration decisions: Soil salinity drives internal and international migration from agricultural regions of Bangladesh, while flooding alone has little effect. Another stream of research that is associated with RSL rise focuses upon disasters. While RSL rise does not influence the frequency of storms, it does increase the frequency of ESLs and and acute flooding (section 3). The now‐iconic example of Hurricane Katrina and New Orleans highlights the multifaceted physical aspects of RSL rise, demonstrating how early displacement, relocation, and recovery may influence the future vulnerability of a coastal area (Fussell et al., 2014; Fussell, 2018).

Regardless of the magnitude of RSL rise, some amount of coastal land will be fully inundated and thus uninhabitable. In order to conceptualize the scope of the challenge of migration due to RSL rise and its associated impacts, it is necessary to understand household‐ and population‐level responses. Through both acute and chronic changes, migration as an adaptation will change the number and composition of people in coastal regions, thus altering vulnerability. For example, these dynamics may lead to undesireable futures, with urban and richer areas fortifying the coasts encouraging further population growth and even more catastrophic consequences in the case of failure (Hinkel et al., 2018). In this process, some migration streams will be eliminated and new ones will emerge. This has led to concerns that some populations may be “trapped” in these vulnerable areas; however, more recent work has suggested that these populations may equally be expressing strong location attachment and thus prefer to remain (Zickgraf, 2018).

Migration in the context of RSL rise and its impacts as a proactive strategy to avoid risk (Piguet et al., 2011) will interact with the perceived desirability of migration in general. These preferences will be influenced by other amenities, such as employment and educational opportunities, as well as other policies, such as zoning, emergency response, and insurance, such that any plans must be part of an integrated strategy (Nicholls & Cazenave, 2010). Regardless, developing policy strategies to alleviate social and cultural pressures and accommodate those who must move will go a long way to managing what will in many regions be a permanent relocation away from the coasts (Mayer, 2016; Warner, 2010).

6. Decision Frameworks

While risk has been ubiquitous throughout human history, rapidly changing scenarios, deep uncertainty, and global risks associated with problems like climate change have contributed to the emergence of new risk‐based decision frameworks (e.g., Mofazali & Jahangiri, 2018). Expanding upon the classical analysis of risk, which focuses more narrowly on technical and economic dimensions (Renn, 2008), the risk governance perspective encompasses the processes of identifying, framing, assessing, characterizing, managing and communicating risks (Rosa et al., 2013). The risk governance perspective emphasizes that risk is in part a social construct, depending not only on the facts of hazard, exposure, and vulnerability but also on the values of the broad variety of public and private actors affected and involved (Renn, 2008).

Considering future SLR projections, within changing coastal environments, deep uncertainty poses many challenges for decision makers seeking to anticipate, identify, manage, and communicate risks (Ramm et al., 2018a, 2018b). Uncertainty arises not only from emissions and ice‐sheet physics, as discussed above, but also from other physical, biological, and socioeconomic elements of the coastal system and their responses to sea‐level change. Economic and population growth, urban and agricultural development, technological innovation, and the evolution of societal preferences, perceptions, and values, as well as the interaction among these processes, all contribute (Hallegatte, 2009; Haasnoot et al., 2013; Wilby, 2010; Kwakkel, Haasnoot, & Walker, 2016). These uncertainties have direct implications for the formulation of adequate adaptation and mitigation measures and add to the challenges of risk governance across different landscapes and constituencies (Adger et al., 2007; Dessai et al., 2018; Wilby, 2010).

Over the past few decades, different approaches have emerged to assist policymakers in the formulation of adaptive decision mechanisms in changing coastal environments (Bhave et al., 2016). These efforts have concentrated on understanding the nature of uncertain hazards, exposure, and vulnerability—which together constitute risk in the sense used by the Intergovernmental Panel on Climate Change (Lavell et al., 2012)—as well as the translation of research into practice (Bhave et al., 2018; Dessai et al., 2018; Hallegatte, 2009). Decision frameworks fall into two major categories: traditional “prediction‐first” economic perspectives, such as benefit‐cost analysis, cost‐effective analysis, and multi‐criteria analysis; and more policy‐driven approaches, such as robust decision making and Dynamic Adaptive Policy Pathways (Dittrich et al., 2016; Gorddard et al., 2016; Haasnoot et al., 2013, 2019; Lempert et al., 2003; Lempert, 2014; Wise et al., 2014).

“Prediction‐first” decision models begin with a probability distribution of future risks as a function of some choice variables and aim to optimize these choice variables to maximize expected utility (possibly subject to some specific target, as in cost‐effective analysis, or using a multivariate utility function, as in multi‐criteria analysis). Many of the challenges of estimating such a distribution for RSL rise, ESL, or coastal flooding were discussed above; this prediction step constitutes a major challenge in applying traditional decision models in the climate context (Hallegatte, 2009; Lempert, 2002; Lempert et al., 2006; Ramm et al., 2017; Weber & Johnson, 2009). Even in the absence of changes in ESL distributions and ignoring the physical and social dynamism of the coast, deep uncertainty in RSL projections challenges the traditional use of “prediction‐first” approaches like benefit‐cost analysis for decisions with consequences lasting into the second half of this century and beyond. (Consider the three orders of magnitude uncertainty in expected ESL frequency in 2100 shown in Figure 3.)

A number of economic approaches appropriate for use under deep uncertainty rely upon the use of multiple alternative probability distributions, effectively treating these distributions as different probabilistic scenarios, and aim to optimize some objective function across these different probabilistic scenarios (Heal & Millner, 2014). For example, these distributions may represent different non‐probabilistic assumptions about factors such as emissions, ice‐sheet physics, and the interactions among different processes that drive sea‐level change. Maximin expected utility seeks a policy that maximizes the minimum expected utility across all the considered distributions. The smooth ambiguity model assigns subjective weights to the different distributions, while penalizing ambiguity (i.e., the levels of disagreement) when averaging expected utilities across distributions. The multiplier preference model identifies a “best estimate” distribution and penalizes distributions based on their distance from the “best” distribution and then seeks to maximize the minimum of the penalized expected utility. Such approaches may be particularly valuable for sea‐level‐related decisions in contexts where a decision must be made now and has consequences that last into a time period with sizably deep uncertainty, and yet there is little opportunity for revisiting the decision into the future.

To our knowledge, however, these “multiple prior” approaches have rarely or never been formally applied in the sea‐level context; traditional benefit‐cost analysis is more common. Yet benefit‐cost analysis is not well suited for deep uncertainty, and it also often struggles with the the practical assessment of costs and benefits of adaptation within nonmarket sectors (Dittrich et al., 2016). It can lead to a tendency towards the quantification of technical solutions to the detriment of other nontechnical management strategies, as the former are generally easier to define in policy contexts. In other cases, the application of economic and financial decision tools to adaptation studies is contentious given the lack of a uniform methodology for carrying out assessments (Watkiss et al., 2015). As a consequence, the use of “prediction‐first” economic decision‐making tools is increasingly being challenged (Dawson et al., 2018; Ramm et al., 2018b).

In terms of decision support, the unpredictability of future conditions creates many plausible and often competing alternatives, each with potentially salient repercussions for local constituencies that need to be considered at any given time (Kwakkel, Haasnoot, & Walker, 2016; Kwakkel, Walker, & Haasnoot, 2016). This requires experts not only to anticipate unexpected events that may result from the behavior of the system but also to account for the different values, perspectives, and interests of relevant actors in integrated management solutions (Dewulf et al., 2015; Dittrich et al., 2016; Herman et al., 2014). Accommodating a variety of stakeholders with diverging frames of reference, knowledge, and opinions can be achieved through processes of active participation, iterative knowledge development, learning, and negotiation (Bhave et al., 2016; Dewulf et al., 2005; Seijger et al., 2014). Yet anticipating future adaptation solutions implies a systematic exploration of a vast set of potential outcomes along with the timely adjustment of responses and planning strategies that are executed by a diverse set of parties (Gorddard et al., 2016; Kwakkel, 2017).

Robust decision‐making (RDM) methods employ a “decision‐first” approach that inverts the traditional “prediction‐first” framework. They begin by identifying potential policy options and considering their robustness under a broad range of possible futures (Dessai et al., 2018; Lempert et al., 2003; Ramm et al., 2018a). As a decision support method, RDM relies on modeling strategies to explore decision scenarios and candidate actions for adaptation (Kwakkel, Haasnoot, & Walker, 2016). The main principle behind RDM is that, under conditions of deep uncertainty, a range of different models of the system can better represent available information about plausible futures rather than a smaller set of mathematical formalizations (Herman et al., 2014; Lempert, 2002). Unlike traditional approaches, where the emphasis is on converging towards an optimal solution, robustness is defined by the identification of mechanisms that can show satisfactory performances under different initial conditions, assumptions about prior probability distributions, and models of the system (Lempert et al., 2006; Lempert & Collins, 2007). Implemented through computational simulations assisted by scenario‐based planning and adaptive management, the RDM process allows decision makers to work with stakeholders in the identification of vulnerabilities, opportunities, and trade‐offs among possible adaptation responses (Haasnoot et al., 2013, 2019; Lempert, 2002).

Dynamic Adaptive Policy Pathways are a flavor of robust decision making that is particularly well suited for decisions—like many adaptation decisions—that are not one‐off decisions but rather decisions that can be revisited and modified over time. Often called Flexible Adaptation Pathways in the sea‐level context (e.g., Rosenzweig & Solecki, 2010), Dynamic Adaptive Policy Pathways rely upon the identification of different policy options and the possible pathways linking them together. They consider the range of possible future scenarios under which different options and pathways are viable, identify indicators (e.g., RSL crossing a specific threshold) that would trigger a choice between different branching pathways, and establish a monitoring system so that those charged with the implementation of the pathways know when to act (Haasnoot et al., 2013, 2019). Idealized economic and engineering analyses indicate that adaptive approaches, such as Flexible Adaptation Pathways, can lead to dramatically lower costs than approaches that do not allow for iterative refinement (G. G. Garner & Keller, 2018; Lickley et al., 2014). Flexible Adaptation Pathways are recommended in guidance in a number of jurisdictions, including New York City (New York City Mayor's Office of Resiliency and Recovery, 2019) and California (California Natural Resources Agency & California Ocean Protection Council, 2018), and have been used for plans including the U.K. Thames Estuary 2100 plan (Ranger et al., 2013) and the Dutch Delta Programme (Delta Programme, 2015). Haasnoot et al. (2019) developed archetypal adaptation pathways for different coastal terrains (e.g., rural open coast and urban estuary). However, the development of Flexible Adaptation Pathways has generally focused narrowly on engineering approaches, such as storm barriers and levees, and has not considered the dynamic coevolution of human and natural coastal systems.

7. Coastal Adaptation Decisions in Practice

While idealized decision frameworks do inform actual coastal decisions, the real world is a messier place, full of capacity and political constraints. Recognizing this complexity, the risk governance perspective entails a broader exploration of the diversity of processes, rules, and actors involved in decision making, including the complexity of societal and institutional practices and realities that underlie risk management (Renn, 2008).

State‐of‐the‐art science can make it fairly quickly into assessment reports written to inform decision makers, such as those of the Intergovernmental Panel on Climate Change and numerous national and subnational panels. In the United States, for example, subnational sea‐level assessments in different localities have undergone four overlapping waves that reflect the evolving perspectives within the sea‐level science community (Hall et al., 2019). A variety of studies from 2008 to 2015 relied upon discrete scenarios with no assigned likelihoods and considered local RSL change to differ from GMSL only due to VLM (e.g., California and Maryland in 2008, Connecticut in 2013, Florida in 2011 and 2015, and Louisiana in 2012). A second wave, from 2010 to 2017, gave more careful attention to uncertainties and to the spatial patterns associated with different processes (e.g., New York City in 2010, Maryland in 2013, and the U.S. Pacific Coast in 2012). A third wave, which began in 2013, relied upon probabilistic approaches (e.g., New York City in 2013 and Oregon in 2017), while a fourth wave, begun in 2016, is giving more careful attention to deep uncertainties associated with ice‐sheet physics (e.g., California in 2017, Maryland in 2018, and New York City in 2019). Based on the personal experience of the authors, in the absence of an adequate national climate service capable of fulfilling subnational demands (e.g., Le Cozannet et al., 2017), much of the coherency among these waves of U.S. subnational assessments has been driven by the repeated involvement of overlapping groups of academic experts in different localities.

State‐of‐the‐art decision frameworks appear to have greater difficulty making it into practice. A review of adaptation methodologies employed in Australia (Ramm et al., 2017) found that “prediction‐first” approaches—benefit‐cost analysis and multicriteria decision analysis—predominated, although robust methods were used on occasion (e.g., a regional plan for the Eyre Peninsula). Similarly, in five Swedish case studies of decisions dating between 2012 and 2019, and encompassing transportation plans, housing plans, comprehensive plans, and nuclear waste disposal, Kanyama et al. (2019) found that “prediction‐first” approaches were ubiquitous. Scientific assessment of sea‐level rise (in this case, by the Swedish Meteorological and Hydrological Institute, SMHI) provided a critical source of information for all cases except the nuclear waste case, but consultants using SMHI assessments ultimately reduced the range of possibilities assessed to a single projection. The focus in many of the case studies was a “reasonable” “upper limit.”

The pathway from scientific assessment to on‐the‐ground decisions is tortuous in part because the scientists and policymakers involved often adopt a linear model of operations. The policymakers may come to a scientific assessment panel with a set of questions, which scientists then try to answer based upon an underlying literature that has largely developed with limited reference to underlying decision goals. The assessment panel writes a report and hands it off to policymakers, after which their role is done. Yet one lesson of the literature on transdisciplinary research is that the linear approach, with scientists handing off an assessment to end‐users, tends to be ineffective (Cash et al., 2003). Rather, an iterative approach—with scientists and end‐users in dialogue throughout—helps ensure that the questions scientists are asking are the ones to which end‐users need answers. In other words, the credibility, relevance, and legitimacy of the underlying science, as perceived by those who might use it, are enhanced by the iterativity of the process (Sarkki et al., 2015).

At least in the United States, many sea‐level adaptation decisions suffer from the lack of coordination among different levels of decision makers. Critical decisions, such as zoning, are often highly decentralized, but individual communities do not develop in isolation from one another, and infrastructure built to protect one region may (positively or negatively) affect the exposure of neighboring regions. For example, Gopalakrishnan et al. (2017) demonstrate that sediment transport processes create the potential for prisoner's dilemma‐type dynamics between adjacent communities engaging in beach nourishment. Thus, strengthened coordination across scales and sectors can help match decision‐making scales to the scales of relevant dynamics. Within the scientific community, better coordination internally and with stakeholders to establish standards and best practices for climate‐related assessment and tools can be helpful (Moss et al., 2019). Boundary organizations, whether external to academic institutions (e.g., nongovernmental organizations) or internal to them (e.g., the extension networks of land‐grant universities), are therefore essential players in building cross‐scale bridges between science and action (Kopp, 2019).

A couple case brief studies illustrate approaches taken to advance stakeholder engagement, as well as intergovernmental and cross‐sectoral coordination, in adaptation planning.

In the Netherlands, the Delta Programme has begun an iterative process of analysis, goal formulation, and implementation undertaken through regional collaborations between municipalities, district water boards, provinces, and the national government (Delta Programme, 2017). Standardized regional “stress tests,” intended to be regularly repeated, are a core part of the analysis step. The goal‐setting dialogues bring in additional stakeholders, including housing corporations, grid managers, farmers, and park managers. The first round of these, set to be complete in 2019, is intended to be followed by the development of implementation agenda by 2020. The identification of synergies with other spatial planning objectives is intended to be a key part of the implementation plan development.

In Jamaica Bay, Queens, New York, the Science and Resilience Institute at Jamaica Bay, established after Hurricane Sandy as a partnership among several governments, environmental groups, and academic institutions, has played a key role in efforts to incorporate local residents in the planning of resilience solutions for flooding (Science and Resilience Institute at Jamaica Bay, 2019). These efforts rely on the use of citizen science, environmental education, increased communication, and iterative tools that require the close interaction between residents and experts in exploring issues associated with storm water, technical support for regular flooding and extreme tides, and hazard response.

A similar process is underway in the Two Rivers region of Monmouth County, New Jersey, where federal funding allowed the state to partner with 15 local governments and Rutgers University to develop a regional resilience plan through a series of open houses and other public consultations (New Jersey Coastal Management Program, 2019). The New Jersey Climate Change Alliance, a network of public, private, nongovernmental, and academic institutions coordinated by Rutgers, sponsored the original scientific assessment underlying this process (Kopp, Broccoli, et al., 2016), which is expected to serve as a model for similar processes in other regions of the state.

Even the best‐intended, and theoretically well designed, sea‐level science and adaptation decision frameworks can go astray if efforts to translate science to action do not take political economy, including the legacy of previous development programs, into account (Ramasubramanian et al., 2016). Sovacool and Linnér (2016) identify four mechanisms by which climate adaptation efforts can perpetuate existing injustices and distort their own goals. Economic enclosure leads to the capturing of resources or authorities, for instance, the way the Dutch Delta Works subverted local water boards when it was established in the 1950s. Political exclusion leads to the omission of the voices of some affected populations from the planning process, which they argue happened with woman and minority voices during the post‐Katrina recovery in New Orleans. Environmental encroachment sacrifices environmental protection to advance adaptation projections: for instance, they point to habitat degradation associated with the Dutch Delta Works and the relaxation of environmental standards during the Katrina recovery. Finally, adaptation efforts can foster entrenchment of inequality; for example, they note that post‐Katrina Army Corps repairs disproportionately benefited wealthier and whiter neighborhoods.

Unfortunately, efforts that deliberately promote community engagement and try to avoid Sovacool and Linnér's (2016) four Es by acknowledging a larger participation in key stages of planning and long‐term response may still end up reinforcing the status quo. As Fleming (2019) highlights, the post‐Hurricane Sandy Rebuild by Design initiative in the United States aimed to foster close interactions between designers and communities to advance more resilient designs. One of the winning designs, The Big U, envisioned berms and retractable flood walls around lower Manhattan, made welcoming with parks and other amenities. While many of the participating design firms remain involved, in a decision that may produce another case study of Sovacool and Linnér's (2016) four Es, “the city has tossed out years of community planning and announced a conventionally engineered solution: extend the land area with fill, add near‐shore walls, and unleash another round of hyper‐luxury real estate development to help pay for the cost of new coastal infrastructure” (Fleming, 2019). Ensuring that future sea‐level adaptation efforts increase resilience successfully and equitably may thus require a greater focus from the scientists, boundary organizations, and other actors involved on potential failure pathways tied to political and economic power structures.

8. Pathways Forward

Understanding the future evolution of coastlines requires an interdisciplinary systems approach. Human activities, and the uncertain response of the climate system, influence the rate of mean sea level change and the frequency and intensity of storms. These changes modulate coastal flooding, erosion, and deposition—shifting the ground underneath ecosystems and human settlements and affecting vulnerability to future flooding. Humans may respond to changing flood risk through engineering or migration; and these processes will also shape the broader physical and socioeconomic evolution of the coast.

In the physical science domain, the ice‐sheet response to greenhouse gas forcing is the primary driver of deep uncertainty in multigenerational projections. The discovery of MICI may not be the last time that an “unknown unknown” emerges with potentially profound implications for GMSL rise. Improving characterization of MICI and other processes at the ocean/ice shelf/ice sheet interface may not initially lead to a reduction in uncertainty but can provide the basis for designing observation systems targeted to reduce uncertainty as quickly as possible. Transitioning processes from “unknown unknowns” to “poorly known unknowns” is a critical task that can be crucially helpful in guiding decisions.

For the next few decades, other processes driving regional and local change—such as atmosphere/ocean dynamics, anthropogenic subsidence, tectonics, and GIA—are as important as ice‐sheet uncertainty in driving uncertainty in RSL projections. Observational and modeling studies have the potentially to narrow associated uncertainties greatly, particularly as the length of the high‐density observational records of the satellite era grow. For high‐frequency processes where satellite coverage is too temporally sparse, innovative observational strategies—for example, combining denser conventional sensor systems with crowdsourced data (e.g., Wang et al., 2018)—may provide substantial advances.

Sea‐level rise impact assessment need to move beyond exposure assessments that assume the physical and human coast are passive recipients of environmental change. Coupling mean and extreme sea‐level projections with geomorphological, ecological, economic, and population models can provide a more realistic representation of exposure and vulnerability. But models need data, and data‐driven statistical approaches, as well as process‐based approaches, are key (e.g., Hsiang, 2016).

While an interdisciplinary approach is necessary to understand coastal evolution, a transdisciplinary approach is essential to ensuring the resulting knowledge is legitimate, relevant, and credible for coastal stakeholders. Co‐production of sea‐level science, with stakeholders integrated into the entire process from problem definition and analysis to communications and evaluation, is key to ensuring the scientific questions being asked will provide useful answers. “Decision‐first” frameworks can help identify the uncertainties that could actually affect on‐the‐ground choices, while often facilitating analysis of robustness to deep uncertainty. Real decisions provide a natural boundary object, a focal point for discussions among scientists, practitioners, and affected populations.

Yet decision science too can become isolated from real decisions if the decision process is treated as though it were separate from the affected systems. Political economy is as much a part of the dynamic coast as geomorphology, human migration, and market economics. The institutional design of networks and hubs intended to link science and adaptive decision making must therefore account for power relationships and their effects on the efficacy and equity of adaptation, and figuring out how to do so is a crucial task for the relevant social sciences.

For sea‐level science to truly become actionable, we need to dissolve the boundary lines between sea‐level science, impact science, social science, decision makers, and affected populations. This does not mean we foreclose fundamental advances, whether inspired by use or curiosity, even in the purely physical realm. But it does imply complementing curiosity‐driven science with a different way of doing science and of educating the next generation of sea‐level scientists—one that is not just interdisciplinary but transdisciplinary, with two‐way communications with nonspecialists as a fundamental element (Kopp, 2019).

Kopp, R. E. , Gilmore, E. A. , Little, C. M. , Lorenzo‐Trueba, J. , Ramenzoni, V. C. , & Sweet, W. V. (2019). Usable science for managing the risks of sea‐level rise. Earth's Future, 7, 1235–1269. 10.1029/2018EF001145