A combined rheometry and imaging study of viscosity reduction in bacterial suspensions

Significance

A pot of paint is more viscous than water due to many “bits and pieces” suspended in paint, such as pigment particles. Amazingly, the viscosity of a dilute suspension of swimming bacteria has been found to be lower than that of water. A number of theories claim to explain this effect. We test a crucial prediction of one of these theories, viz., that viscosity reduction should be strongly dependent on the system size in which the measurements are made. Such strong size dependence was not observed. Instead, we find direct evidence that when the viscosity of the bacterial suspension is reduced to near zero, the swimming microbes begin to “swarm” in a way reminiscent of flocking in birds or fish.

Abstract

Suspending self-propelled “pushers” in a liquid lowers its viscosity. We study how this phenomenon depends on system size in bacterial suspensions using bulk rheometry and particle-tracking rheoimaging. Above the critical bacterial volume fraction needed to decrease the viscosity to zero, ${\varphi }_c\approx 0.75\%$, large-scale collective motion emerges in the quiescent state, and the flow becomes nonlinear. We confirm a theoretical prediction that such instability should be suppressed by confinement. Our results also show that a recent application of active liquid-crystal theory to such systems is untenable.

Suspensions of self-propelled particles (1) show surprising properties due to time-reversal symmetry breaking (2, 3) and the unique flow fields associated with self-propulsion (4). Different classes of self-propelled particles exist, differing in the symmetry of these flows (5). A motile Escherichia coli bacterium propelling itself using a helical flagellar bundle powered by rotary motors is a “pusher.” Chlamydomonas algae, which swim by beating two flagella at the front of each cell, are “pullers.” The symmetries of the corresponding flow fields have a definite influence on the ability to generate collective motion: At sufficiently high concentration, but still rather dilute, suspensions of pusher swimmers exhibit orientational instabilities and collective motion, while suspensions of pullers remain stable (6, 7).

In an external flow field, the presence of shear influences greatly the average swimming orientations and, consequently, the stress generated by the microswimmers (8). For a suspension of pushers at low shear, hydrodynamic theories predict an alignment of the swimming direction. This enhances the applied shear stress and leads to an apparent viscosity that decreases with increasing volume fraction of cell bodies, $\varphi$, i.e., a negative viscosity increment (NVI). Symmetry again holds the key: Pullers are not predicted to show NVI, and, indeed, a positive viscosity increment was found in Chlamydomonas suspensions by using cone-plate rheometry (9). For pushers, NVI was inferred in Bacillus subtilis in nonrheometric geometries (10) and directly measured for E. coli in a microfluidic rheometer (11, 12) and in a cylindrical Couette geometry (13). Throughout this work, viscosity refers to a global rheological measure of a sample’s properties (sometimes known as the “apparent viscosity”); the local viscosity experienced by a bacterium is equal to the viscosity of the surrounding aqueous medium under all conditions: The drag from this unchanged local viscosity remains the source of flagellar propulsion.

These advances notwithstanding, bacterial NVI is far from understood. In particular, the so-called “superfluidity regime” of vanishing and then negative effective viscosity (13) predicted by theory (14) remains mysterious. Indirect observations imply a possible connection with the emergence of large-scale collective motion (15). The latter is expected by continuum kinetic theory (CKT) to be strongly affected by confinement (16, 17). Separately, a recent application of active liquid crystal theory (ALCT) to NVI implies that this phenomenon should be strongly system-size dependent (18).

System-size dependence is long known and substantially understood in equilibrium phase transitions near critical points (19) and in kinetically arrested materials such as polymer films (20). These bodies of work show that probing system-size effects can generate new fundamental insights, e.g., into the putative role of divergent length scales.

Size dependence has often been suggested for active matter. For example, the effect of confinement on the flocking transition in the Vicsek model has long been debated. Recent simulations find that this transition disappears when boundaries are removed, but is recovered for scale-free interactions (21). Theories predict a variety of size-dependent effects in other active systems (ref. 22 and references within). However, these predictions, including ones concerning NVI and collective motion, have seldom been experimentally probed, so that the relevance of many results from theory and simulations remains to be demonstrated.

In this work, we studied the size dependence of NVI by varying the gap size of the Couette rheometer (13) used to measure the viscosity of bacterial suspensions. At the same time, we imaged the same samples in a cone-plate rheometer (23) to investigate the link to collective motion. Our results show that a recent application of ALCT to bacterial suspensions is untenable, uncover a direct connection between NVI and collective motion, and confirm continuum kinetic theory predictions of the latter’s size dependence. Our findings give a firm basis for developing more adequate theories for one of the most striking phenomena in active-matter physics. Below, we first review current theories for NVI and collective motion, focusing on what they have to say about size dependence, before reporting our results.

Current Theories

There are two main current theories (22) for bacterial NVI: CKT of dilute active suspensions and ALCT developed to describe active systems with underlying nematic order, such as dense microtubule solutions driven by kinesin motors (24). Both theories have recently been applied to sheared bacterial suspensions (7, 18, 25–27).

ALCT applied to any system predicts a strong size dependence traceable back to a bending elasticity term in the description of the energetics of all liquid crystals (LCs). Passive microtubule bundles form a nematic LC. With sufficient motor activity, the system develops spontaneous flow, which can be modeled (22) by adding an active stress term to the equations of (passive) nematohydrodynamics (28). The active stress competes against the LC’s bending elasticity, which has energy density $u_{\mathrm{b}}=\frac{1}{2}K{\left[\mathbf{n}\times \left(\nabla \times \mathbf{n}\right)\right]}^2$, where $\mathbf{n}$ is the nematic director and $K$ is a Frank elastic constant (29). Between parallel plates separated by $H$ with parallel ordering at the plates, $u_{\mathrm{b}}\sim K/H^2$. An $H^2$ dependence permeates the theory, reflecting the centrality of orientational elasticity. Importantly, the active stress required to set up spontaneous flow without external driving also scales as $H^{-2}$.

This theory was recently adapted for the rheology of dense bacterial suspensions (18). As expected, all of its results show size dependence. For example, the theory implies a strong enhancement with system size of the critical shear rate ${\stackrel{\cdot }{\gamma }}_{\mathrm{c}}$ above which NVI disappears (13). In a suspension viscosity $\eta$, tumbling of the director commencing at $\eta \stackrel{\cdot }{\gamma }\sim K/H^2$ suppresses NVI, so that

$${\stackrel{\cdot }{\gamma }}_{\mathrm{c}}\sim K/\eta H^2.$$ [1]

Elasticity also determines the form of the ALCT viscosity (18):

$$\eta \approx {\eta }_{\mathrm{0}}\left[1-\beta {\left(K{H}^{-2}\right)}^{-1}\right],$$ [2]

where $\beta$ depends on the activity and ${\eta }_0$ is the solvent viscosity. ALCT also predicts nonlinear flow profiles associated with the emergence of NVI. “Shear banding” has indeed been observed recently in bacterial suspensions, although the link with NVI was implied rather than directly established (15).

Mean-field CKT (7, 25–27), formulated in terms of the probability distribution function of the swimmer positions and orientations, treats pushers as moving force dipoles. Without external flow, it predicts that homogeneous and isotropic configurations of infinite systems are linearly unstable above a swimmer volume fraction ${\varphi }_c^{\infty }$. It is usually thought that this constitutes the threshold for collective motion, although large-scale three-dimensional (3D) simulations show a less clear-cut picture (30). Under simple shear, CKT was adapted and a mean-field Smoluchowski equation solved (27) for straight swimmers undergoing rotational diffusion, yielding a low shear-rate prediction of the viscosity of the suspension. Keeping only the relevant “active” contribution and replacing rotational diffusion with tumbling, relevant for our work, we arrive at

$$\frac{\eta }{{\eta }_0}=1-\frac{\varphi }{{\varphi }_c^{\infty }}.$$ [3]

This result intimately relates vanishing shear viscosity to the onset of collective motion, albeit only in infinite systems: CKT treats the driving flow as homogeneous and infinite and is thus insensitive to the size of the system. Moreover, with few exceptions (31, 32), CKT studies of rheology to date have ignored interparticle interactions.

Formulating a CKT in confinement properly is technically demanding. However, the infinite-system results can be used to estimate how the instability threshold should depend on $H$. The linear stability analysis of infinite systems gives the dependence of the instability eigenvalue on the perturbation wavelength $k$ (16, 27). The most unstable mode is predicted to occur at $k=0$, so that ${\varphi }_c^{\infty }$ is the critical volume fraction. To estimate the confined critical volume fraction ${\varphi }_c\left(H\right)$, we set the largest available scale to $k=2\pi /H$, giving

$$\frac{{\varphi }_c\left(H\right)}{{\varphi }_c^{\infty }}\approx 1+\frac{3}{10}\left(2\pi \frac{v\tau }{H}\right)+\frac{1}{5}{\left(2\pi \frac{v\tau }{H}\right)}^2,$$ [4]

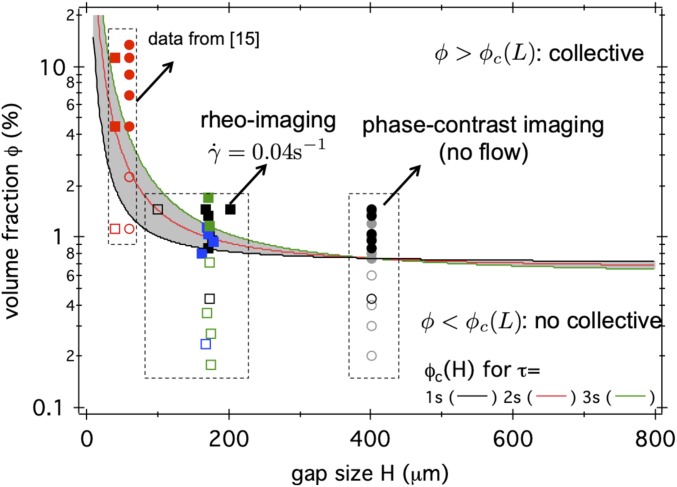
where $v$ is the bacterial swimming speed and $\tau$ is the average duration between two tumble events (SI Appendix). A similar equation was derived in ref. 17, which explicitly takes into account wall accumulation of bacteria. Fig. 1 shows the predicted stability boundaries for $v=15\hspace{0.17em}\mathrm{\mu }\text{m}\hspace{0.17em}{\text{s}}^{-1}$ and three values of $\tau$ (lines) using the experimental measured ${\varphi }_c\left(H=400\hspace{0.17em}\mathrm{\mu }\text{m}\right)\approx 0.75\%$ (Results and Discussion) as ${\varphi }_c^{\infty }$. For $H\gtrsim 200\hspace{0.17em}\mathrm{\mu }\text{m}$, the CKT stability boundary is essentially flat, so that suspensions below ${\varphi }_{\mathrm{c}}\approx 0.75\%$ were predicted to be always stable. However, the calculated stability boundary turned sharply upward at small $H$, so that, at high confinement, very much higher cell densities are needed for the onset of collective motion.

Fig. 1.

Confinement effect on flow stability and collective motion. Lines indicate calculated confined critical volume fraction ${\varphi }_c\left(H\right)$, according to CKT using Eq. 4 and the experimentally measured ${\varphi }_c\left(H=400\hspace{0.17em}\mathrm{\mu }\text{m}\right)\approx 0.75\%$ (Fig. 4 I and J) as ${\varphi }_c^{\infty }$. ${\varphi }_c\left(H\right)$ defines the boundary between stable (below) and unstable (above) pusher suspensions for different persistence time $\tau$ of the swimmers, as indicated in the key, with speed $v=15\hspace{0.17em}\mathrm{\mu }\text{m}\hspace{0.17em}{\text{s}}^{-1}$. Symbols: experimental observation of flow with (filled squares) and without (open squares) banding; and with (filled circles) or without (open circles) large correlation length-scale $l$, based on rheo-imaging (squares) and phase-contrast imaging (no flow; circles), respectively. See Fig. 4 and related main text for more details. Red: Data from ref. 15 at $H=60\hspace{0.17em}\mathrm{\mu }\text{m}$ (an $x$ offset is applied to squares for better visualization).

Both ALCT and CKT predict $\eta \left(\varphi \right)$ to be a decreasing function, i.e., NVI. Initial fitting of CKT to experimentally measured $\eta \left(\varphi \right)$ returned a microscopic length of $L\approx 20\hspace{0.17em}\mathrm{\mu }\text{m}$ for the bacterial force dipole (13), significantly larger than the $L\approx 2\hspace{0.17em}\mathrm{\mu }\text{m}$ inferred from experiments (33). To fit ALCT (18), one needs $K\sim 10\hspace{0.17em}\text{pN}$ at $\varphi \lesssim 1\%$, which seems excessive in comparison to the $\approx 0.4\hspace{0.17em}\text{pN}$ (33) force scale of bacteria swimming. Nevertheless, both theories are consistent with the original qualitative picture: shear-induced alignment of either single dipoles (CKT) or putative local domains of nematically ordered swimmers (ALCT) activate the canonical NVI mechanism (8). To assess the soundness of the physical bases of these approaches therefore requires confrontation with fresh experiments probing directly size dependence. Such experiments would also help to establish a connection between the onset of collective motion and vanishing of the shear viscosity that was established theoretically (7, 17), but has never been verified experimentally. We now report such experiments.

Results and Discussion

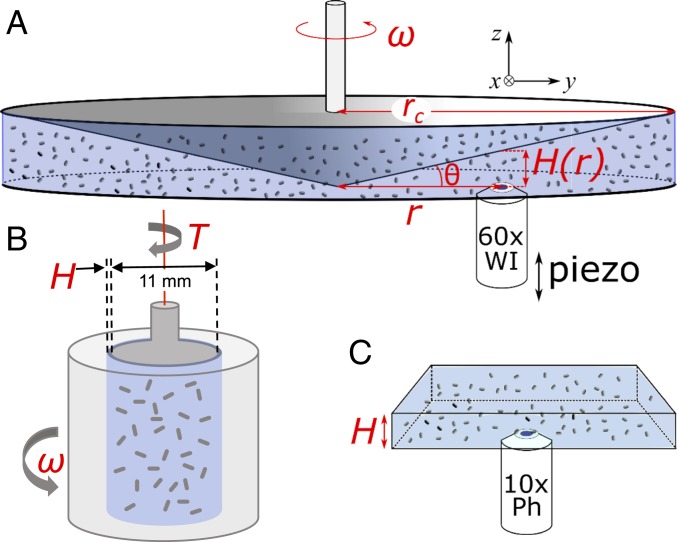
Experimental details are given in Materials and Methods. Rheoimaging was performed by using a cone-plate rheometer with bespoke optics for epifluorescence imaging (23) (Fig. 2A), while bulk rheometry was performed in a cylindrical (Couette) geometry with variable gap size, $H$ (13) (Fig. 2B). Our cone-plate rheometer was not sensitive enough to determine the lower-than-water viscosities in NVI bacterial suspensions, but velocity profiles of the swimmers can be determined under conditions essentially identical to those used in Couette rheometry.

Fig. 2.

Schematic of the three experimental setups used (not to scale). (A) Rheo-imaging setup using cone-plate geometry for visualization during shear. (B) Couette cell for bulk rheometry, after ref. 13. (C) Phase contrast imaging without applied shear.

Before performing either Couette rheometry or rheoimaging, we always sealed $\approx 150\hspace{0.17em}\mathrm{\mu }\text{L}$ of the sample into 400-$\mathrm{\mu }$m-high glass capillaries to monitor the onset of collective motion. Observations were carried out in a Nikon TE2000 inverted microscope with a 10$\times$ phase-contrast objective (Fig. 2C), which allowed a large field of view ($\approx 700\hspace{0.17em}\mathrm{\mu }\text{m}\times 700\hspace{0.17em}\mathrm{\mu }\text{m}$). Movies were analyzed by using particle image velocimetry (PIV).

We used a fluorescent motility wild-type strain of E. coli, AD21, dispersed in a minimal medium that prevented growth, but enabled motility for the time of the experiment (typically 0.5 h). Cell concentrations were determined by spectrophotometry, and the relation between the measured optical density (OD) and cell-number density was calibrated against cell counting. The corresponding volume fraction was calculated by using a measured average cell body volume of ${\mathcal{V}}_{\mathcal{B}}=1.4\hspace{0.17em}\mathrm{\mu }{\text{m}}^3$ (34).

Size Dependence of Viscosity Reduction.

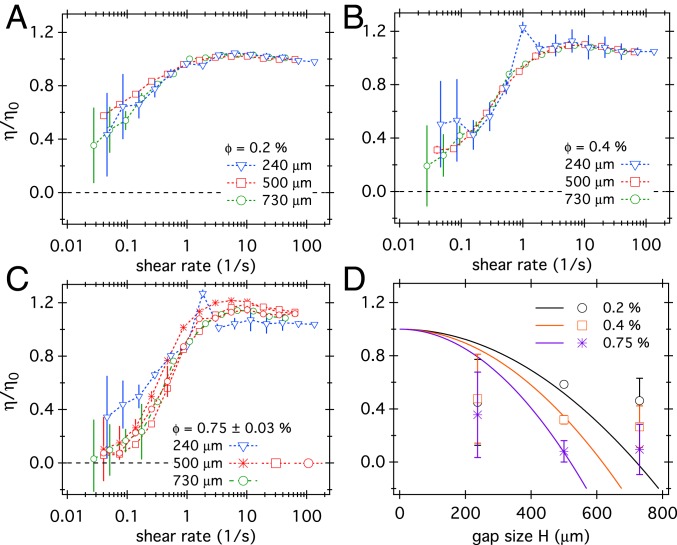
Fig. 3 displays the viscosity of E. coli suspensions as a function of the shear rate $\stackrel{\cdot }{\gamma }$ for three different $\varphi$, each at three gap sizes, $H=240$, 500, and $730\hspace{0.17em}\mathrm{\mu }\text{m}$. The $\eta \left(\stackrel{\cdot }{\gamma }\right)$ data at the two higher bacterial densities were similar to those reported before (13) at $H=500\hspace{0.17em}\mathrm{\mu }\text{m}$. At the lowest density, our apparatus could not reach the low-shear plateau. At all three cell densities, the viscosity data overlapped over our range of gap sizes, $240\le H\le 730\hspace{0.17em}\mathrm{\mu }\text{m}$. The predicted order-of-magnitude shift in ${\stackrel{\cdot }{\gamma }}_{\mathrm{c}}$ between $H=240\hspace{0.17em}\mathrm{\mu }\text{m}$ and $730\hspace{0.17em}\mathrm{\mu }\text{m}$ (Eq. 1) was clearly absent (Fig. 3 A–C). The striking disagreement between ALCT and our data can also be brought out by comparing the measured and predicted viscosities at the lowest experimental shear rate, $\stackrel{\cdot }{\gamma }\approx 0.04\hspace{0.17em}{\text{s}}^{-1}$ (Fig. 3D). Although we cannot rule out weak size dependence given the experimental noise, our results are inconsistent with the $H^{-2}$ dependence predicted by ALCT (18). Note that theory (lines) and experiments (symbols) agreed at the single, previously used, gap size of $H=500\hspace{0.17em}\mathrm{\mu }\text{m}$, but clearly disagreed at the other two gap sizes. This underlines the crucial importance of probing size dependence in theory–experiment comparisons. We conclude that ALCT (18) is not applicable to bacteria suspensions at our cell densities. There was no evidence for any bending elasticity, let alone the strong elasticity ($K\sim 10\hspace{0.17em}\text{pN}$) inferred by fitting to data at a single $H$ (18).

Fig. 3.

(A–C) The viscosity of E. coli suspensions as a function of shear rate, $\eta \left(\stackrel{\cdot }{\gamma }\right)$, at gap sizes $H=240$, 500, and $730\hspace{0.17em}\mathrm{\mu }\text{m}$ for $\varphi =0.2\%$ (A), $0.4\%$ (B), and $0.75\%$ (C). (D) The measured viscosity at $\stackrel{\cdot }{\gamma }\approx 0.04\hspace{0.17em}{\text{s}}^{-1}$ for three bacterial concentrations (symbols) compared to the predictions (color-matched) of ALCT (lines) using parameters from ref. 18 and a cell volume ${\mathcal{V}}_{\mathcal{B}}=1.4\hspace{0.17em}\mathrm{\mu }{\text{m}}^3$ (34) and buffer viscosity ${\eta }_0=0.90\hspace{0.17em}\mathrm{c}\mathrm{P}$.

Nonlinear Velocity Gradients and Collective Motion.

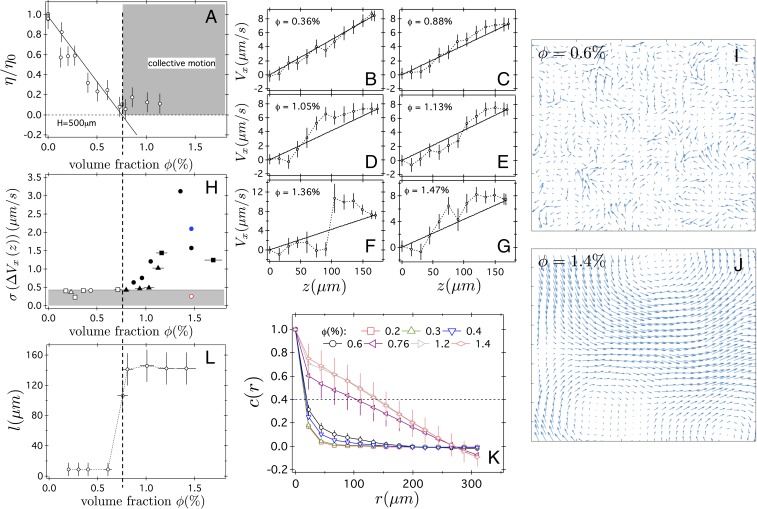
At $\stackrel{\cdot }{\gamma }\approx 0.04\hspace{0.17em}{\text{s}}^{-1}$, we found as before (13) that $\eta \left(\varphi \right)$ decreased linearly for $H=500\hspace{0.17em}\mathrm{\mu }\text{m}$ (Fig. 4A). Results for the other two gap sizes and additional shear-rate values can be found in SI Appendix, Fig. S2. No significant systematic dependency with $H$ was observed over the volume fraction range. At $\varphi \gtrsim 0.75\%$, $\eta$ remained approximately constant with $\varphi$. Irrespective of whether $\eta$ actually reaches 0 at $\varphi \approx 0.75\%$, this density clearly marked the transition between two regimes. We probed this transition using rheoimaging, which yielded velocity profiles such as those shown in Fig. 4 B–G.

Fig. 4.

(A) The viscosity of E. coli suspensions measured with a gap $H=500\hspace{0.17em}\mathrm{\mu }\text{m}$ at a shear rate $\stackrel{\cdot }{\gamma }\approx 0.04\hspace{0.17em}{s}^{-1}$, as a function of volume fraction, normalized to the viscosity of the buffer ${\eta }_0\left(c_{\mathrm{s}\mathrm{e}\mathrm{r}\mathrm{i}\mathrm{n}\mathrm{e}}\right)=\left(0.87+2.7\times 10^{-4}{c}_{\mathrm{s}\mathrm{e}\mathrm{r}\mathrm{i}\mathrm{n}\mathrm{e}}\right)$ cP, with $c_{\mathrm{s}\mathrm{e}\mathrm{r}\mathrm{i}\mathrm{n}\mathrm{e}}$ the concentration of serine in mM used to prepare the solutions. The gray area defines the presence of large-scale collective motion, observed above ${\varphi }_c\approx 0.75\%$ (vertical dashed line), as characterized in I–L. (B–G) Examples of velocity profiles measured by using rheoimaging in cone-plate geometry of bacterial suspensions at progressively higher volume fraction $\varphi$, as indicated, and for $\stackrel{\cdot }{\gamma }\approx 0.04\hspace{0.17em}{s}^{-1}$ and $H=170\hspace{0.17em}\mathrm{\mu }\text{m}$. (H) SD $\sigma$ of $\mathrm{\Delta }{V}_x\left(z\right)=V_x\left(z\right)-{\stackrel{\cdot }{\gamma }}_{\mathrm{a}\mathrm{p}\mathrm{p}}z$ over the entire $z$ range, with the applied shear rate ${\stackrel{\cdot }{\gamma }}_{\mathrm{a}\mathrm{p}\mathrm{p}}=V_x\left(z_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{e}}\right)/z_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{e}}$, as a function of volume fraction. Open and filled symbols indicate linear and nonlinear flow profile, respectively, for $H=100\hspace{0.17em}\mathrm{\mu }\text{m}$ (red), $170\hspace{0.17em}\mathrm{\mu }\text{m}$ (black; each symbol corresponds to an independent experimental campaign), and $200\hspace{0.17em}\mathrm{\mu }\text{m}$ (blue). Gray area defines the linear flow range based on an arbitrary threshold of $\sigma \lesssim 0.43$. (I and J) Examples of velocity vector fields from PIV at two $\varphi$ below (I) and above (J) ${\varphi }_c\approx 0.75\%$. Image width is $\approx 700\hspace{0.17em}\mathrm{\mu }\text{m}$. (K) Velocity correlation functions $c\left(r\right)$ calculated from Eq. 5 and averaged over $5\lesssim t\lesssim 15$ min at various $\varphi$ measured via PIV analysis of phase-contrast microscopy movies of cell suspensions in sealed capillaries with $H=400\hspace{0.17em}\mathrm{\mu }\text{m}$. Error bars are $\pm$1 SD representative of the time dependency. (L) Characteristic length $l\left(\varphi \right)$ for which $c\left(l,\varphi \right)\approx 1/e$.

At $\varphi \lesssim 0.75\%$, velocity gradients were linear within experimental uncertainties. Above this density, pronounced nonlinearities developed in the confinement gap. To quantify this transition, we calculated the SDs $\sigma$ of $\mathrm{\Delta }{V}_x\left(z\right)=V_x\left(z\right)-{\stackrel{\cdot }{\gamma }}_{\mathrm{a}\mathrm{p}\mathrm{p}}z$ over the entire $z$ range, where the applied shear rate was obtained from ${\stackrel{\cdot }{\gamma }}_{\mathrm{a}\mathrm{p}\mathrm{p}}=V_x\left(z_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{e}}\right)/z_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{e}}$ (Fig. 4H). Taken together, the data from five different experiments suggest that $\sigma$ stays at a noise floor of $\approx 0.43$ at low cell densities until $\varphi \approx 0.75\%$ and then rises, consistent with where the density at which the low-$\eta$ data extrapolate to 0. Importantly, visual inspection revealed large-scale correlated motions above this cell concentration. However, the small field of view in our setup ($\approx 180\hspace{0.17em}\mathrm{\mu }\text{m}\times 90\hspace{0.17em}\mathrm{\mu }\text{m}$) ruled out reliable PIV on our rheoimaging datasets.

Instead, we quantitatively analyzed data from parallel imaging studies (Fig. 2C) in sealed capillaries (no flow) and observed large-scale collective motion at $\varphi \gtrsim 0.75\%$ manifested as vortices spanning a large fraction of the field of view (Fig. 4 I and J). We calculated the velocity correlation function,

$$c\left(r\right)=〈\frac{{⟨\overrightarrow{V}\left(\overrightarrow{r}+\overrightarrow{R},t\right).\overrightarrow{V}\left(\overrightarrow{R},t\right)⟩}_{\overrightarrow{R}}-{⟨\overrightarrow{V}\left(\overrightarrow{R},t\right)⟩}_{\overrightarrow{R}}^2}{{⟨\overrightarrow{V}{\left(\overrightarrow{R},t\right)}^2⟩}_{\overrightarrow{R}}-{⟨\overrightarrow{V}\left(\overrightarrow{R},t\right)⟩}_{\overrightarrow{R}}^2}{〉}_t,$$ [5]

using PIV at various bacterial densities, where $\overrightarrow{V}\left(r\right)$ is the unit velocity vector at position $\overrightarrow{r}$ (Fig. 4K). A characteristic length-scale $l$ for which $c\left(l\right)\approx 1/e$ (Fig. 4L) was extracted, which abruptly increased at $\varphi \approx 0.75\%$, marking the onset of correlated motion.

Our rheoimaging setup was not sensitive enough to measure NVI directly. However, the flow profile at $\varphi >0.75\%$ measured in a cone-plate geometry was nearly flat near the stationary bottom plate (Fig. 4 C–G), which therefore experienced only small shear stress. This was further confirmed by the observation of a small, but nonzero, viscosity in the collective motion regime. Translated to the Couette cell used to measure bulk viscosities, this would be equivalent to null torque on the stationary inner cylinder and therefore a zero viscosity, corroborating the actual Couette rheometry finding of zero or very low viscosities at these concentrations (Fig. 4A). We can therefore say with some confidence that the low-shear viscosity decreasing to zero at $\varphi \approx 0.75\%$ appeared to be correlated with the onset of nonlinear velocity gradients and the emergence of large-scale correlated motion (Fig. 4 A, H, and K).

Size Dependence of Collective Motion.

Our observation of a nonlinear shear regime can be compared to a recent report of “shear-banding” by Guo et al. (15), which, however, was not accompanied by parallel visual observations and viscosity measurements, so that it is unclear whether their “banding” is associated with either NVI or collective motion. If we nevertheless assume such association, then their results differed significantly from ours in one important quantitative respect. Guo et al. (15) reported collective motion only at $\gtrsim 3.2\times 10^{10}\hspace{0.17em}\mathrm{c}\mathrm{e}\mathrm{l}\mathrm{l}\mathrm{s}/\mathrm{m}\mathrm{l}$, corresponding to $\varphi \approx 4.5\%$, assuming ${\mathcal{V}}_b=1.4\hspace{0.17em}\mathrm{\mu }{\text{m}}^3$, which is considerably higher than our critical concentration of ${\varphi }_c\approx 0.75\%$. This discrepancy is likely due to system-size dependence: Generally, Guo et al. (15) worked at much higher confinement ($H=60\hspace{0.17em}\mathrm{\mu }\text{m}$) than in our experiments.

Measurements of the bulk viscosity in our Couette cell displayed little size dependence in the range $240\le H\le 730\hspace{0.17em}\mathrm{\mu }\text{m}$ (Fig. 3) It was, however, not possible to decrease the gap size below $240\hspace{0.17em}\mathrm{\mu }\text{m}$ in this device. Observations at smaller gaps were, however, possible in our rheoimaging setup. Indeed, because we utilized a cone-plate geometry, shearing at a continuum of gap heights could be studied in a single experiment simply by moving the monitoring position radially. For $\varphi \approx 1.5\%$, we observed strongly nonlinear velocity gradients at $H\approx 200\hspace{0.17em}\mathrm{\mu }\text{m}$ and $H\approx 170\hspace{0.17em}\mathrm{\mu }\text{m}$, but linearity at $H\approx 100\hspace{0.17em}\mathrm{\mu }\text{m}$.

In Fig. 1, we compare the predicted CKT stability boundaries against our measurements. The threshold for $\tau =2\pm 0.5\hspace{0.17em}\text{s}$ credibly accounts for three datasets: our observation of the onset of collective motion in quiescent ($\stackrel{\cdot }{\gamma }=0$) cell suspensions sealed in capillaries, our observation of the onset of nonlinear flow profiles in cone-plate rheoimaging at $\stackrel{\cdot }{\gamma }=0.04\hspace{0.17em}{\text{s}}^{-1}$, and the observation by Guo et al. (15) of the onset of collective motion and of “banded” states at $\stackrel{\cdot }{\gamma }=0.16\hspace{0.17em}{\text{s}}^{-1}$.

Summary and Conclusions

To summarize, we have studied NVI, nonlinear flow, and collective motion in suspensions of motile E. coli bacteria at cell densities up to $\varphi \lesssim 1.5\%$ using a combination of bulk rheometry, rheo-imaging, single-cell tracking, and PIV. We find that the reduction of the bulk viscosity to zero at ${\varphi }_c\approx 0.75\%$ coincides, within experimental accuracy, with the appearance of nonlinear flow and the onset of collective motion when the swimmers are confined to a gap in the range $170\le H\le 730\hspace{0.17em}\mathrm{\mu }\text{m}$. The independence of the measured viscosity with gap $H$ rules out the applicability of ALCT (18) to bacterial suspensions of this kind, showing that the nematic orientational elasticity assumed in this treatment is absent. The stability boundary for sheared E. coli suspensions within a CKT framework is shown to be consistent with our observations of the onset of collective motion and nonlinear velocity gradients in the range $100\le H\le 400\hspace{0.17em}\mathrm{\mu }\text{m}$, as well as recent observations at the even higher confinement of $H=60\hspace{0.17em}\mathrm{\mu }\text{m}$ (15).

This success of CKT prompted us to revisit a previous comparison of this theory with NVI experiment (13), which found that fitting $\eta \left(\varphi \right)$ data to this theory required a dipolar length for the pushers that was an order of magnitude larger than the experimental value. The source of this discrepancy lies in the fact that the version of CKT used in this comparison (27) was for swimmers whose swimming direction decorrelates due to rotational Brownian motion, while the swimmers used in the corresponding experiments (and in this work) are run-and-tumblers that decorrelate due to sudden directional changes. A comparison taking this into account fits our data.

Our work demonstrates an intimate relationship between the onset of collective motion and vanishing of the viscosity. It has been shown (17, 35–37) that collective motion is very sensitive to the geometry of the system. Future work is required to establish whether the relationship reported in this work holds in the general case.

Taken together, our experiments show that the emergence of “superfluidity” in bacterial suspensions is correlated with the onset of nonlinear flow and collective motion and that CKT is able to explain the magnitude of NVI, as well as the system-size dependence of flow instabilities. These findings demonstrate the value of performing bulk and single-cell measurements in parallel in studying some of the most striking phenomena in active matter.

Materials and Methods

Bacteria Growth Protocol.

We cultured a strain of E.coli K12 derived from AB1157, which we have described (38). Here, we further modified this strain, now called AD21, to include a plasmid which expresses yellow fluorescent protein; therefore, all growth media were supplemented with chloramphenicol ($25\hspace{0.17em}\mathrm{\mu }\text{g}\hspace{0.17em}{\text{ml}}^{-1}$). Briefly, an overnight culture of AD21 was obtained by inoculating a single colony into 10 mL of Luria broth followed by incubation at 30 °C/200 rpm for 16 to 18 h. The next day, this was inoculated into 35 mL of Tryptone broth medium (1:100 dilution), which was incubated for 4 h (30 °C/200 rpm) to obtain a late-exponential-phase culture. At this stage, cells were harvested and concentrated by gentle filtration ($0.45\hspace{0.17em}\mathrm{\mu }\text{m}$ Immobilon filters; Millipore). This concentrated culture was washed by successive resuspension into 35 mL of motility buffer (MB; pH 7.0, 6.2 mM ${\mathrm{K}}_2{\mathrm{H}\mathrm{P}\mathrm{O}}_4$, 3.8 mM ${\mathrm{K}\mathrm{H}}_2{\mathrm{P}\mathrm{O}}_4$, 67 mM NaCl, and 0.1 mM ethylenediaminetetraacetic acid), followed by filtration from one to three times to yield 1 to 2 mL of cells at high density $\varphi \approx 1.0-1.5\%$. Suspensions at different $\varphi$ were prepared with MB supplemented, prior to experiments, with serine concentration in the range of 20 to 150 mM depending on $\varphi$ to promote anaerobic motility. To some experiments, we added dialyzed polyvinylpyrrolidone (0.01 $\%$w, molecular weight 360 k; Sigma-Aldrich) to prevent cell adhesion to surfaces, but did not observe significant changes compared to without. Suspensions with a volume of $\approx 400\hspace{0.17em}\mathrm{\mu }\text{L}$, $\approx 1\hspace{0.17em}\text{mL}$, and $\approx 150\hspace{0.17em}\mathrm{\mu }\text{L}$ were then used for rheoimaging (Edinburgh), bulk rheology (Orsay), and phase-contrast imaging (both), respectively. Volume fractions $\varphi$ were obtained by converting measurement of ODs using a range of spectrophotometers and assuming a bacterium volume ${\mathcal{V}}_{\mathcal{B}}=1.4\hspace{0.17em}\mathrm{\mu }{\text{m}}^3$ (34). Each spectrophotometer was calibrated based on viable plate count (38). Additionally, we monitored, in some cases, the time dependency of bacterial motility by measuring the swimming speed using differential dynamic microscopy (38, 39). This allowed us to define an experimental time window of $\approx$30 min, over which motility was approximately constant for the densest suspensions.

Bulk Rheometry.

Experiments were carried out in a cylindrical low-shear Couette geometry (13) (Fig. 2B). An inner cup (radius $R_{\mathrm{i}}=5.5\hspace{0.17em}\text{mm}$) was suspended by a torsion wire inside an outer cup of radius $R_{\mathrm{o}}=R_{\mathrm{i}}+H$ ($H=\mathrm{240,500}$, and $730\hspace{0.17em}\mathrm{\mu }\text{m}$). The latter rotated with speed $\omega$, setting the shear rate $\stackrel{\cdot }{\gamma }$. The torque $T$ needed to keep the inner cylinder stationary was measured and converted into stress. The ratio gave the viscosity $\eta$, which is therefore a surrogate for the stress at the inner cylinder.

To obtain the viscosity plots in Fig. 3, we used the same protocol as in ref. 13. The outer cup was first filled with a small volume of the suspension ($\sim 1\hspace{0.17em}\text{mL}$), and then the inner cup was set into place. After 30 s of rest, the inner cup was rotated for 30 s at a steady-state shear rate. The rotation was then stopped for 30 s. For some of the measurements performed with the highest concentrations, the steps were maintained for 60 s for the lowest shear rates. These steps were repeated with increasing shear-rate values. We have improved our previous data-analysis procedure (13). The signals were automatically analyzed by a routine implemented in MATLAB. The average viscosity during one measurement was obtained by removing the zero-shear baseline measured from a linear fit based on the instrumental signal obtained before and after the corresponding applied shear. The error bars in Fig. 3 correspond to the rms values of the signal for each independent measurement. The error bars in Fig. 4 represent the reproducibility of measurements performed at the same bacterial concentration but for different experimental campaigns—i.e., different days and bacterial-batch suspensions—and thus included variability in suspension activity and rheometer settings (e.g., apparatus alignment was performed manually).

Rheoimaging.

Experiments were performed by using a cone-plate geometry (Fig. 2A) ($\theta =1^{○}$, radius $r_c=20\hspace{0.17em}\text{mm}$) connected to an AR2000 rheometer (TA Instruments) (23), with bespoke optics for epifluorescence imaging. In this setup, the resulting torques were too weak to determine the suspension viscosity; however, the bacteria velocity profiles could be determined in conditions essentially similar to the bulk rheometry measurements.

The sample was imaged through a microscope coverslip serving as the bottom plate by using a custom-built imaging module in epifluorescence mode (see Fig. 2A for a schematic). The imaging module consisted of a blue light-emitting diode (catalog no. M470L2, Thorlabs), a green fluorescent protein filter cube (LED-FITC-A, Semrock), a water-immersion (WI) objective (Plan Apo 60×/1.2 WI; Nikon), and a fast and sensitive complementary metal-oxide superconductor camera (Orca Flash 4.0, Hamamatsu). It could be focused at different heights within the sample by using a piezo objective mount (catalog no. P-725.4CD, PI) and moved manually to well-defined radial positions relative to the rotation axis. Extra care was taken to avoid bending the bottom coverslip while loading the sample, and the sample was sealed off with a home-built enclosure to minimize solvent evaporation.

We mostly worked $\approx 10\hspace{0.17em}\text{mm}$ away from the rotation axis, where we could monitor the entire height ($\approx 170\hspace{0.17em}\mathrm{\mu }\text{m}$) of the sample, and recorded $180\hspace{0.17em}\mathrm{\mu }\text{m}\times 90\hspace{0.17em}\mathrm{\mu }\text{m}$ movies of 2,000 frames at 400 frames per second ( fps) or 1,000 frames at 100 fps at various heights at a step size of $\mathrm{\Delta }z=15\hspace{0.17em}\mathrm{\mu }\text{m}$. Cell bodies showed up as bright features, and 2D tracks, in the focal, or $\left(x,y\right)$, plane were extracted by using Trackmate (ImageJ) (40). The 100 to 1,000 tracks in each dataset remaining in the $\left(x,y\right)$ plane for longer than 0.1 s were extracted. Velocities along the $x$ and $y$ axes were measured by deriving smoothed trajectories (smoothing over 0, 1 s using a third-order Savitzky–Golay filter).

PIV.

We recorded phase-contrast movies ($\approx 40\hspace{0.17em}\text{s}$-long, Plan Fluor 10$\times$, N.A. 0.3) with large field of view ($\approx 700\hspace{0.17em}\mathrm{\mu }\text{m}\times 700\hspace{0.17em}\mathrm{\mu }\text{m}$) near the middle of a 400-$\mathrm{\mu }$m-height capillary to avoid the wall effect. Approximately 10 to 15 movies were recorded over a period of $\approx 15\hspace{0.17em}\text{min}$ shortly after adding the serine and filling and sealing the capillary. Each movie was analyzed independently with PIV, yielding one velocity correlation function per movie. We found no systematic time dependency of these correlation functions, and thus we averaged these together. The error bars presented in Fig. 4K represent $\pm$1 SD. We used a standard MATLAB PIV software adapted from the PIVLab toolbox (41, 42). The time scale between two successive images was $0.2\hspace{0.17em}\text{s}$ (20 frames). The final metapixel box was $32\times 32$ pixels² ($\approx 42\times 42\hspace{0.17em}\mathrm{\mu }{\text{m}}^2$) with an initial half-box-size spatial shift. Nonmotile fraction of the bacterial solutions was negligible ($\lesssim 10\%$), and thus PIV analysis was mostly based on motion of motile cells.

Data Availability.

The research data underpinning this publication are available on the Edinburgh DataShare repository (43).