Motile cilia hydrodynamics: entrainment versus synchronization when coupling through flow

Abstract

Coordinated motion of cilia is a fascinating and vital aspect of very diverse forms of eukaryotic life, enabling swimming and propulsion of fluid across cellular epithelia. There are many questions still unresolved, and broadly they fall into two classes. (i) The mechanism of how cilia physically transmit forces onto each other. It is not known for many systems if the forces are mainly of hydrodynamical origin, or if elastic forces within the cytoskeleton are important. (ii) In those systems where we know that forces are purely hydrodynamical, we do not have a framework for linking our understanding of how each cilium behaves in isolation to the collective properties of two or more cilia. In this work, we take biological data of cilia dynamics from a variety of organisms as an input for an analytical and numerical study. We calculate the relative importance of external flows versus internal cilia flows on cilia coupling. This study contributes to both the open questions outlined above: firstly, we show that it is, in general, incorrect to infer cilium–cilium coupling strength on the basis of experiments with external flows, and secondly, we show a framework to recapitulate the dynamics of single cilia (the waveform) showing classes that correspond to biological systems with the same physiological activity (swimming by propulsion, versus forming collective waves).

This article is part of the Theo Murphy meeting issue ‘Unity and diversity of cilia in locomotion and transport’.

1. Introduction

Hydrodynamical coupling of oscillators is of interest owing to the extensive range of natural systems where fluid is present, causing viscous forces that can affect dynamics at large scales [1–3].

All eukaryotes, from simple unicellular life to complex vertebrates, share the same organelle to induce fluid motion at the cellular scale. The common model organisms include: Chlamydomonas, a single-cell alga with usually two flagella swimming in a breaststroke style [4–9], and Volvox, another single-cell organism, which lives in colonies. Volvox somatic cells are biflagellated [10,11], with the colony as a whole displaying a large number of filaments. Paramecium is another microswimmer and a popular model system of a single-cell multiciliated organism, i.e. where the cell grows many cilia and these form a carpet with coordinated beating dynamics, allowing the organism to swim [12–14]. In all cases, these motile cilia perform periodic shape changes, beating typically at between 10 and 50 Hz. The molecular structure of cilia and flagella is conserved across eukaryotes, with only subtle ultrastructural differences, but more significant differences in cilia length and inter-cilia distance. The shape of the cilia across the beating cycle does vary significantly across organisms, and so does the coordination observed between neighbouring cilia. In larger organisms, motile cilia perform a variety of different functions. In mammals, they cover some of the epithelia, where they are critical for driving fluid movement along surfaces. In larger animals, the cilia form carpets and are involved in several crucial processes, such as assisting in ova transport in the fallopian tubes and enabling circulation of cerebro-spinal fluid in the brain [15], and they are integral to mucus clearance, a critical aspect of defence against microbes and dust in the lungs. For all these processes, synchronized dynamics across cilia is essential.

Experiments on both the natural systems and the simplified driven systems have revealed hydrodynamically induced mechanisms allowing switching between in-phase and anti-phase steady-state behaviour, depending on the cilia beat pattern [16,17], and a dependence on spatial separation consistent with hydrodynamic coupling [2,17,18]. Other experiments have revealed evidence of coupling beyond that which is expected from purely the forces transmitted by the fluid, and have postulated other coupling mechanisms [4,19,20]. Examples include an internal elastic interaction or some form of cell-body rocking [19,20].

Oscillatory systems are often probed through the application of an external signal. In the context of hydrodynamic systems, the external signal usually takes the form of an external flow [21–24]. For biological systems, flows are often applied either to probe a particular cell’s behaviour, or to align and organize the system beforehand during cilia growth. This is biologically relevant in the context of development, where growing cells often experience flow in vivo. The basal body at the base of a motile cilium is directional. Basal bodies have been shown to align under external flows in both Xenopus larvae and mouse brain cilia [15,22]. Aligning the basal bodies leads to an increase in alignment of the cilia beating plane. To better understand the underlying mechanics of a flagellum, external flows have been applied to Chlamydomonas [25,26]. The flows are applied either to determine the load response and the effect of fluid viscosity, as in [26], or to infer the coupling strength between the flagella themselves as in [25]. Applying external flows is a non-invasive way to test a living hydrodynamic oscillator directly.

In parallel to experiments on living systems, there has been very fruitful theoretical work, especially in the last decade, attempting to understand how the properties of the individual oscillator, together with spatial arrangement, can give rise to the long-ranged ordered dynamics. Studies of the flagella from living systems have informed choices for the driving potentials: typically, in a simplified model a hydrodynamic point force is driven via a rule that preserves the far-field hydrodynamics of the biological cilium, while simplifying the model so that the question of synchronization becomes tractable analytically or at least by numerical simulation. Crucially for studying synchronization, the phase of the individual beating cilia needs to be a variable that can adjust itself as a result of forces from the neighbours [13,16,27,28]. There are broadly two classes of models that have been developed: rotors and rowers [2]. The rotor model usually involves a bead driven along a two-dimensional trajectory, with some compliance in the orbit [18,29,30]. By contrast, the rower model is most often implemented with a bead oscillating along one dimension with a position-based update creating the oscillations [16,31,32]. We use the rower model here, motivated by the freedom to fit complex force profiles to one dimension and to remove the need to estimate compliance. It is used to develop a new analytical approach to explore the similarities between synchronization with an external flow and synchronization between oscillators. We find that for interactions of pairs of such oscillators, the underlying driving force is a critical factor controlling the synchronization strength. The same dependence is not observed for an external flow. This has two important consequences: (a) the difference in responses to the driving force makes it wrong to naively equate the synchronization between an external flow with the coupling between oscillators, and (b) working with the driving potentials that we extract from a wide set of different organisms, we see a systematic classification between the cilia in systems that rely on internal synchronization (cilia that have to beat in waves for their physiological function) and the cilia in systems that rely only on few flagella for swimming.

2. Methods

(a). The oscillator model

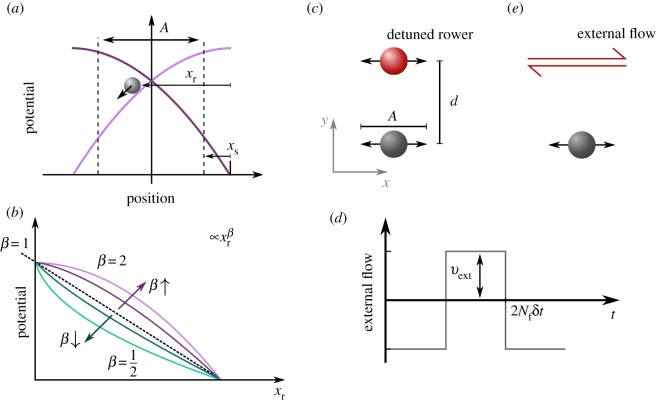
In the rower model, the bead oscillates along a direction, x, driven by a potential trap that is updated geometrically (figure 1). The shape of the potential contains, in a coarse-grained fashion, the degrees of freedom of the cilium’s complex shapes and activity; the far-field fluid dynamics can be matched to a given biological system [2]. The potential in the model can be any strictly increasing function, but we predominantly focus on a simple power law with $k\hspace{0.17em}{x}_{\mathrm{r}}^{\beta }$; here, k is the trap strength and x_r the distance relative to the vertex of the trap. Details of the model are represented in figure 1, with aspects of the power law potentials covered in figure 1b. The position update that ensures driven oscillations occur is illustrated in figure 1a. Once a rower passes a certain threshold A + x_s the trap is reflected; hence the bead reverses direction. The threshold position is measured relative to the vertex and controlled through x_s. The reflection axis is chosen to create oscillations with amplitude A. The period of an isolated oscillation, 2τ₀, is set by the driving potential and the drag in the fluid γ. The pair-wise behaviour of rowers is known to be dependent on the shape of the driving potential [16]. To simulate Brownian dynamics, we include thermal noise using the Ermack & McCammon BD method [33] as implemented in our previous work [34]. The drag of each particle depends on the position, and so the noise is multiplicative. The noise on ith particle as f_i has the mean and variance

$$⟨f_i(t)⟩=0\text{and}⟨f_i(t)f_{\hspace{0.17em}j}(t^{\prime })⟩=2k_{\mathrm{B}}T{H}_{ij}^{-1}\delta (t-t^{\prime }).$$ 2.1

The variance depends on the specifics of the hydrodynamic tensor $H_{ij}^{-1}$ as well as the temperature T and Boltzmann constant k_B.

Figure 1.

The model of ‘rower’ phase oscillators is used to compare the mutual synchronization facilitated by viscous forces, with entrainment to an external flow. (a) Each oscillator is driven by a repulsive trap, which is updated geometrically. When the rower passes a switch point A + x_s the trap is reflected and drives the rower in the opposite direction. This creates oscillations with amplitude A, and free period and phase. For simplicity, distances are measured relative to the vertex, with the relative position of the rower within the trap x_r. The switch point is controlled through parameter x_s, which is also measured relative to the trap vertex. (b) The driving potentials take the form of power laws, which results in position-dependent force $F=k\beta x_{\mathrm{r}}^{\beta -1}$ with k the trap strength. When varying β, k is also updated to maintain a constant non-detuned frequency f₀. The curvature of the potential is known to relate to the synchronization strength, with increasing |β − 1| also increasing the level of noise at which rowers maintain synchrony [16]. Here, entrainment and synchronization are compared by considering the detuning range in which phase-locking occurs. (c) Two rowers have their traps separated by a distance d, with one rower detuned and marked in red. This rower has a frequency f_d, while the grey has frequency f₀. The separation is perpendicular to the direction of oscillation, so as to minimize the variation in the distance separating the beads. (e) This pair of rowers is compared with a single unaltered rower that experiences an oscillating flow, which is then scanned in frequency (detuned versus the rower). (d) The applied flow has a square wave structure, with magnitude v_ext and a period 2N_fδt that gives its frequency f_ext; the time step for simulation is δt.

(b). Pair interactions

(i). Rower–rower coupling

To simulate the rowers, each rower is updated using the following equation,

$${\dot{\mathbf{r}}}_i=\sum _{\hspace{0.17em}j=1}^2{\mathbf{H}}_{ij}\hspace{0.17em}(\mathbf{F}({\mathbf{r}}_{\hspace{0.17em}j})+{\mathbf{f}}_{\hspace{0.17em}j}).$$ 2.2

F is the force resulting from the trapping potential discussed in §2a, with an additional linear restoring force applied along y to restrict the oscillations to one dimension. Given the form of the power law potential, the driving force has a magnitude $F=k\beta x_{\mathrm{r}}^{\beta -1}$, with the sign depending on the current update of the trap vertex. The rowers are coupled through the tensor H_ij, which for simplicity was chosen to be the Oseen tensor

$${\mathbf{H}}_{ij}=\left\{\begin{array}{cc}\frac{1}{\gamma }\mathbf{I},\hspace{0.17em}& i=j,\\ \frac{1}{\gamma }\frac{3a}{4r_{ij}}(\mathbf{I}+{\hat{\mathbf{r}}}_{ij}{\hat{\mathbf{r}}}_{ij}),& i\ne j,\end{array}\right.$$ 2.3

where the distance between two particles is r_ij = |r_j − r_j| and the associated unit vector ${\hat{\mathbf{r}}}_{ij}$. The radius of the bead is a. The diagonal terms are given by the Stokes drag, which assumes a point force. This also affects the noise that each rower experiences, f_i.

To scan the effect of the curvature of the potential on the coordination, both the trap shape β and switch point x_s are varied, with β ∈ [0.2, 1.95] and x_s/a ∈ [0.17, 0.57]. The rowers oscillate in x but are separated in y, to minimize variation in the distance between them throughout a cycle. Furthermore, owing to the one-dimensional nature of the model, the principal effect of the orientation is a constant change to the coupling strength which can explored through separation distance [35]. The rower model has been extended to two dimensions to investigate alignment [36], but we do not include this extension in this work. This configuration is shown in figure 1c. To test the strength of the coupling between the rowers, the frequency of the first rower is detuned, marked as a red bead in figure 1c. To detune the rower, the trap strength is scaled by f_d/f₀, the ratio of the new detuned frequency f_d and the unperturbed frequency of the second (grey) rower f₀.

The noise is defined non-dimensionally as in [37], where the non-dimensional noise is defined as ξ = 2k_BT/(A〈F〉_t), which is set to ξ = 4.34 × 10⁻⁴ using the average force of the non-detuned rower 〈F〉_t = 2.05 pN; this is the force associated with the semi-period τ₀ = 0.11 s, amplitude A = 3.1 μm, bead radius a = 1.75 μm and Stokes drag γ = 0.073 μPa s. The step size for the simulations is δt = 9.1 × 10⁻⁴ τ₀ and the total length is 270 τ₀. The distance d between the rower traps is chosen to produce weak coupling but maintain clear phase-locking. Specifically, d/a = 9.14 or 11.43.

(ii). Signal–rower coupling

To study the effect of external velocity flow, the rower’s equation of motion is instead

$$\frac{\text{d}{\mathbf{x}}_1}{\text{d}t}=\frac{1}{\gamma }({\mathbf{F}}_1(x)+{\mathbf{f}}_1)+{\mathbf{V}}_{\mathrm{ext}}(t).$$ 2.4

There is now only a single bead that experiences the external velocity V_ext(t). To create the square wave structure, the flow has a magnitude v_ext, which switches direction every N_f frames, i.e. N_fδt is the half-period of the external signal. The structure of the external flow is illustrated in figure 1d, while the signal–rower system set-up is shown in figure 1e. The external flow is aligned to the oscillation of the rower because of the perpendicular force trapping the rower to one-dimensional oscillations; misaligning the force would decrease the flow aligned with the oscillations while any effect from the perpendicular flow would be suppressed. To make the cases of signal-rower coupling (SR) and rower–rower coupling (RR) comparable to each other, the amplitude of the external flow, v_ext, is set equal to the average effective flow created by the detuned rower, v_eff. This is calculated using the average force driving the detuned rower 〈F_d〉_t, and the hydrodynamic coupling calculated using the average positions of the rowers, μ = (1/γ)(3a/4d):

$$v_{\mathrm{ex}}=v_{\mathrm{eff}}\equiv \mu ⟨F_{\mathrm{d}}{⟩}_t.$$ 2.5

(c). Measuring the coupling strength

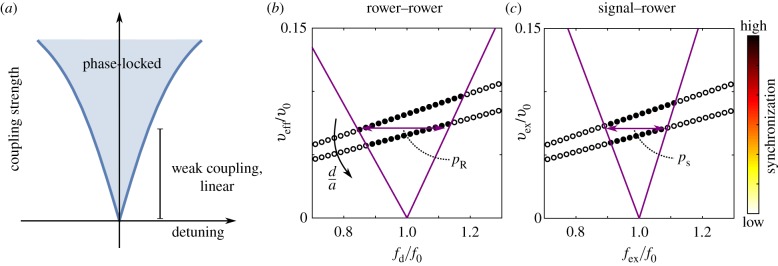
The ‘Arnold tongue’ refers to the region in which two detuned oscillators phase-lock (figure 2a). The range of detuning in which this occurs depends in general on the coupling strength between them; we explored this in pairs rowers [31]. For weak coupling, we see in these systems that the range of detuning value depends linearly on the coupling strength. The width of the Arnold tongue can, therefore, be used to compare the coupling in different systems. To compare like with like, the width is measured in the linear weak coupling regime. This avoids difficulties with different nonlinear responses with strong coupling. Furthermore, for weak coupling, we expect the plateau width to be proportional to the relaxation time of a pair of non-detuned rowers with a given trap shape; relaxation time is another useful measure for coupling strength. To distinguish between the Arnold tongue widths measured in each system, a subscript is included: p_r is the plateau width measured for the two rowers, and p_s the equivalent for a rower under external flow. The detuning of a rower alters its average force, and so the effective flow produced by the rower is also dependent on the level of detuning. This effect can be seen in figure 2b: two sets of simulations were performed at two constant distances, d/a = 9.14 and 11.43, but there is a slope to the sampling. For consistency, the same detuning dependence is implemented in the signal–rower case, an example of which is shown in figure 2c. To account for this the phase-locking is measured for two similar levels of coupling, and the Arnold tongue is fitted. The fit includes the two boundary results and the origin. The plateau width, which defines the detuning range and is used as a proxy for synchronization strength, is then interpolated using the fit at v_eff = v_ext = 0.071v₀. For simplicity, the applied velocities are expressed in terms of the average velocity of the unperturbed rower, v₀ = 2Af₀. Note that the initial values for the coupling strength are chosen to be similar to the desired interpolation value.

Figure 2.

The width of the Arnold tongue, for a specific value of weak coupling, is a measure for synchronization strength. (a) The Arnold tongue is the region of detuning in which the two oscillators still synchronize. At low strength coupling, the phase-locking region increases linearly. (b) The plateau width is found by fitting two straight lines and interpolating for a specific value. This particular example is the plateau width for rower–rower interactions. Interpolation is required because the resulting effective flow from the detuned rower changes with the detuning. Here, two sets of simulations are shown for d/a = 9.14 and 11.43, with the increase in distance decreasing the effective flow at the unperturbed rower resulting from the detuned rower v_eff. This effective velocity is measured in terms of the average velocity of the unperturbed rower v₀. (c) The Arnold tongue for the rower under external flow (signal–rower) is also calculated using an interpolation method. The signal magnitude v_ext is scaled to mimic the changes caused by detuning in the rower–rower case and expressed in terms of v₀. This is to ensure consistency between the two cases. These plots are for a trapping potential with β = 1.55 and x_s/a = 0.17.

(d). Tracking living cilia

Individual cilia and flagella from high-speed microscopy videos in [17,19,38,39] were tracked using a custom user interface in Matlab. A custom analysis software reconstructs a smooth representation of the cilium by interpolating between the coordinates of the manually selected points with two 4th degree polynomials. Resistive force theory (RFT) allows us to measure the force exerted by the cilium on the surrounding fluid between two frames, based on the method described in [17] and briefly summarized here. First, the reconstructed cilium shapes in each of the two frames are approximated with a set of N cylinders 1 μm long. We then measure the displacement Δr_i and the velocity ${\mathbf{v}}_i={\mathbf{v}}_{i\parallel }+{\mathbf{v}}_{i\perp }$ of the midpoint of the ith cylinder between the two frames along the directions parallel and perpendicular to the cylinder itself. Thanks to RFT we can now find the force the ith cylinder exerts on the fluid as

$${\mathbf{f}}_i={\mathbf{f}}_{i\parallel }+{\mathbf{f}}_{i\perp }=(c_{\parallel }{\mathbf{v}}_{i\parallel }+c_{\perp }{\mathbf{v}}_{i\perp })\hspace{0.17em}{l}_i,$$ 2.6

where l_i is the length of the cylinder. The two constants

$$c_{\perp }=\frac{8\pi \eta }{1+\log l^2/a^2}\text{and}{c}_{\parallel }=\frac{4\pi \eta }{-1+\log l^2/a^2}$$ 2.7

are the drag coefficients of a slender cylinder of length l and radius a and have the units of viscosity. Integrating the force contributions of all the cylinders, taking into account overlapping cylinders, yields the total force.

It is worth noting that this approach is a first approximation for the system, as it assumes the individual cylindrical segments to be immersed in an unbounded Newtonian fluid of viscosity η. For the purposes of this work, we used η = 1 mPa s. In general, however, the cilia can be fairly close to each other and to boundaries, and in some cases (such as the lungs) the fluid surrounding the beating cilium can be non-Newtonian.

An effective ‘centre of drag’ of the cilium can now be defined as the average of the positions of the N cylinders weighted with the magnitude of the force they exert on the fluid:

$${\mathbf{r}}_{\mathrm{cod}}=\frac{\sum _{i=1}^N{f}_i{\mathbf{r}}_i}{\sum _{i=1}^N{f}_i}.$$ 2.8

Having a colloidal rotor follow the trajectory of the centre of drag r_cod(t) is now a natural choice to coarse-grain the parameters of the ciliary beat pattern (see the supplementary material for further details).

(e). Calculating rower potentials from tracked trajectories

The individual cilia and flagella were tracked to derive rower potentials from their trajectories. This allows us to contextualize observed flagella in terms of our results from the rower model. To compress the trajectories into one dimension an orbit is calculated to describe the trajectory. The specifics for calculating the orbit vary depending on whether the trajectory resembles an ellipse or follows a crescent-shaped path. The shape of the trajectory varies with the type of flagella, and is discussed further in §3c. The fitted orbit is used to define a central axis, onto which the force and position data of the flagella are mapped. The specifics of that mapping depend on the shape of the trajectory. This results in a one-dimensional force and position data, to which a cubic force profile is fitted. The output of the fit is a relationship between force and position that can be substituted into the rower model. Further explanations of the process are given in the electronic supplementary material, which also includes pseudocode documenting the steps taken.

3. Results

The two systems studied here vary in their sensitivity to changes in the driving potential. This manifests as a change in the detuning range between the two cases, which we normalize using the detuning range for the entrainment case (p_R − p_S)/p_S. The difference, measured in simulations by comparing the plateau widths, is shown in figure 3a. The points are results of individual simulations, and the background shows the contours fitted using the data. The intensity of the colour indicates the magnitude of the difference, with pink shades indicating the rower–rower system has a broader synchronization region and green shades indicating the signal–rower system has the wider plateau. Near β = 1, the signal–rower system has much stronger synchronization (as expected because inter-cilium synchronization strength vanishes at β = 1 [16]), but the width of p_R quickly crosses over p_S as the trap curvature is increased. This can be replicated by applying a phase reduction to each case. To do so the rowers are converted to their natural phase frame and the pair interaction is approximated by its average over one cycle [40,41]. The natural phase removes the large variations in the cycle and focuses on the small changes that occur from their interaction. The difference predicted by the phase reduction is shown in figure 3b.

Figure 3.

The range of detuning in which oscillators can mutually synchronize or entrain is not the same, resulting from a different sensitivity to underlying characteristics of the oscillators' motion. (a) The difference in detuning range at v_ext/v₀ = 0.071 as measured from simulation. Each individual simulation is marked by a circle symbol, and the contour map is fitted to the data. (b) The predicted difference in detuning range as calculated using phase reduction. The mean difference observed for different organisms are included as dark blue lines; from left to right the organisms are Chlamydomonas, quadri-flagellates, lung epithelial, Volvox, and mouse brain cilia. (c) The predicted detuning range for mutual entrainment between rowers p_R as the trap driving their motion is varied. When the traps are linear, β = 1, the rowers do not synchronize, but p_R increases quickly as the trap departs from linear. (d) The same sensitivity to the trap shape is not seen in the detuning range in which entrainment occurs p_S, with p_S ≈ 0.18 while in the same range p_R ∈ [0, 0.45].

(a). Phase reduction applied to the external flow system

Using the phase reduction to convert the signal–rower system to a phase viewpoint results in an expression for the phase difference between rower and signal ψ_S,

$$\frac{\text{d}{\psi }_{\mathrm{S}}}{\text{d}t}=\mathrm{\Delta }{\mathit{\Omega }}_{\mathrm{S}}+\frac{\gamma v_{\mathrm{ex}}{\mathit{\Omega }}_0}{\pi |F(x_{\mathrm{s}})|}{G}_{\mathrm{S}}[{\psi }_{\mathrm{S}}].$$ 3.1

The first term, ΔΩ_S, is the difference between the natural angular frequency of the rower and that of the signal. The second term is the contribution from the interaction between signal and oscillator. It depends on the natural frequency of the non-detuned bead Ω₀, as well as the ratio between the external flow amplitude v_ext and the minimum velocity of the bead when driven by the trap potential |F(x_s)|/γ. The effect of the trap potential and flow is encapsulated by the dimensionless function G_S[ψ_S], which is a convolution of the relationship between rower phase and position with the external flow. We note that the results for the linear trap, reported in [23], are recovered when β is set to 1 in this more general result. Details of the function derivation are included in the electronic supplementary material.

The Arnold tongue is the region in which a stationary solution exists for the phase difference (dψ_S/dt) = 0. Consequently, a fixed point exists for this signal–rower system when

$$\frac{\gamma v_{\mathrm{ex}}}{\pi |F(x_{\mathrm{s}})|}{G}_{\mathrm{S}}^{min}[{\psi }_{\mathrm{S}}]<\frac{\hspace{0.17em}{f}_{-}}{f_0}<\frac{\gamma v_{\mathrm{ex}}}{\pi |F(x_{\mathrm{s}})|}{G}_{\mathrm{S}}^{max}[{\psi }_{\mathrm{S}}].$$ 3.2

The frequency difference between the rower and the signal is f₋, which is expressed in terms of the rower's frequency f₀. The detuning plateaus predicted by this expression, when v_ext/v₀ = 0.071, is shown in figure 3d. The width does not vary much when the trap is changed, staying near p_S = 0.18, but it does increase slowly as the trap curvature increases, i.e. when |β − 1| increases.

(b). Phase reduction results applied to the rower interaction

The phase reduction process can be applied to pairs of rowers. Here, the phase difference is labelled ψ_R, and the governing equation is

$$\frac{\text{d}{\psi }_{\mathrm{R}}}{\text{d}t}=\mathrm{\Delta }{\mathit{\Omega }}_{\mathrm{R}}+2\gamma \mu \hspace{0.17em}(f_0{G}_{\mathrm{ID}}[{\psi }_{\mathrm{R}}]-f_{\mathrm{d}}{G}_{\mathrm{ID}}[-{\psi }_{\mathrm{R}}]).$$ 3.3

Similarly to the previous case, the first term, ΔΩ_R, is the difference in natural angular frequency, but this time between rowers. The dimensionless interaction function G_ID depends on the shape of the driving potential. The process here is the same as in [37] and so the function has a similar shape. In this case, the rowers have asymmetric contributions, stemming from the detuning. The interaction term on each rower is proportional to the frequency of the rower that is acting upon it. When performing the phase reduction, the hydrodynamic coupling term was approximated as a constant, μ, by setting the distance between the rowers to the distance between their trap centres. The same approximation was used earlier to calculate v_eff. For further details on the derivation see the electronic supplementary material.

Approximating the interaction G_ID to its first-order Fourier series terms, the region in which phase-locking occurs is

$$\frac{|f_{-}|}{f_{+}}<\frac{|\gamma \mu s_1/\pi |}{\sqrt{1-(\gamma \mu c_1/\pi {)}^2}},$$ 3.4

where f₋ = f_d − f₀ and f₊ = f_d + f₀, while s₁ and c₁ are the first-order sine and cosine coefficients in the Fourier series. The detuning f₋/f₊ increases linearly for weak coupling, and then broadens as γμ increases. At very large coupling this expression predicts infinite phase-locking range, demonstrating that when γμ is large enough it is no longer valid to apply the averaging process. To match the signal–rower case, the plateau is reported in terms of f₀, with f₋/f₊ converted to f₋/f₀. Similarly, the coupling strength is measured in terms of average velocity applied by the detuned rower v_eff = μ〈F_d〉_t = 0.071v₀, which occurs around d/a ≈ 10. Figure 3c is a contour plot of p_R for β ∈ [0.2, 1.9] and x_s/a ∈ [0.17, 0.57]. The plateau shrinks to zero when the traps become linear, β → 1, i.e. the curvature decreases to zero. This is consistent with earlier work, showing that rowers did not synchronize when driven by linear traps [16]. p_R increases as |β − 1| grows, with a sharper increase for β > 1.

(c). Rower potentials derived from cilia

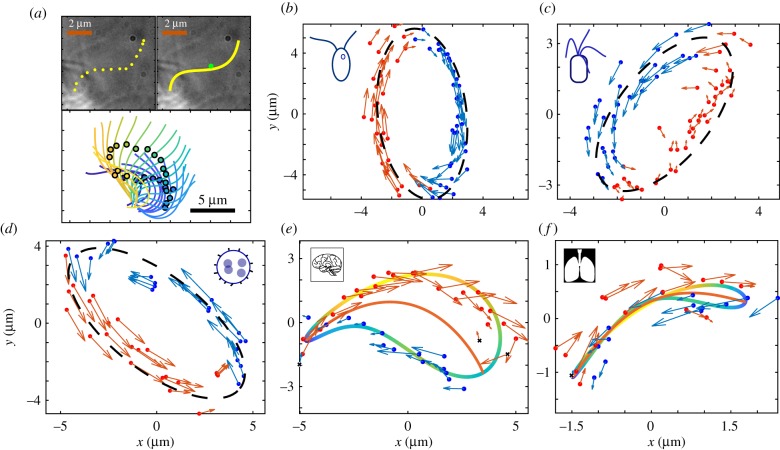
To estimate where the behaviour of living flagella lies in terms of entrainment and synchronization, force profiles were fitted to tracked flagella and cilia from previously published high-speed recordings. Specifically, we used cilia profile recordings of Chlamydomonas [4], quadri-flagellates [19] and Volvox somatic cells [17] kept stationary by holding on micropipettes, ependymal cilia from mouse brain in vivo [38] and in vitro [42], and human airway cilia from in vitro culture [39].

Example trajectories of the centre of drag for each species are plotted in figure 4. At a glance, they can be classified as elliptical or crescent-shaped, with the epithelial cilia exhibiting crescent shapes and the other types elliptical. The process used to compress the trajectory into a force profile suitable for rowers varies slightly between the two cases, but the gist remains the same: a central axis is defined, onto which the tracked data are projected. Depending on which side of the axis the points fall, the force associated is assigned to be either positive or negative. For elliptical orbits, the central axis is defined as the major axis of the fitted ellipse. The crescents are more complex. Rather than fitting an ellipse, second-order Fourier series are fitted to the x and y data. The central line is then defined by separating the resulting trajectory into two sections and finding the midpoint between them. Details of this process are included in electronic supplementary material. The final step is to mimic the updating trap of the rower potential. Consequently, the point from which the projected distance is measured changes; it is always measured relative to the end the centre of drag is approaching.

Figure 4.

Cilia in living organisms can be tracked, and from this a rower driving potential calculated to approximate their motion. (a) The flagella are tracked by interpolating between manually selected points along their length. A given flagellum is then approximated by its centre of drag following the steps laid out in [17]. (b) A tracked trajectory for a Chlamydomonas cell. The video of the Chlamydomonas is available from [4]. The colour indicates if the force at that point is considered positive or negative for the rower potential. The points are grouped by fitting an ellipse and then considering the major axis; points to the right are blue, and those left are red. The fitted ellipse is indicated by the black dashed line. (c) A similar trajectory for a quadri-flagellated alga; from [19]. (d) The centre of drag trajectory for a Volvox cell. One flagellum has been snipped, and the remaining flagellum is tracked. The Volvox videos are available from [17]. (e) A trajectory from a mouse brain epithelial cilium. This particular cilium is available from [38], but one other was sourced from [42]. The shape of the trajectory is no longer elliptical, but has a crescent shape. To group the forces as positive or negative a second-order Fourier series is fitted to the x and y points. This orbit is shown by the blue–green–yellow orbit, where the colour indicates the local speed along the trajectory. The central line within the fitted trajectory is then used to group the tracked points, where the endpoints are determined using the local speed. (f) The same process is applied to cilia from human airways. Videos of the airway cilia are from [39]. Some points were excluded when fitting driving potentials to the crescent trajectories, because the change in centre of drag was counter to the average force; these points are marked by black crosses. They result from variance in the trajectory size when tracking multiple cycles. A similar effect was seen in the Volvox cells, but it was consistent across multiple cycles and relates to conformation changes in the cilium. Consequently, the points were still included in the Volvox case.

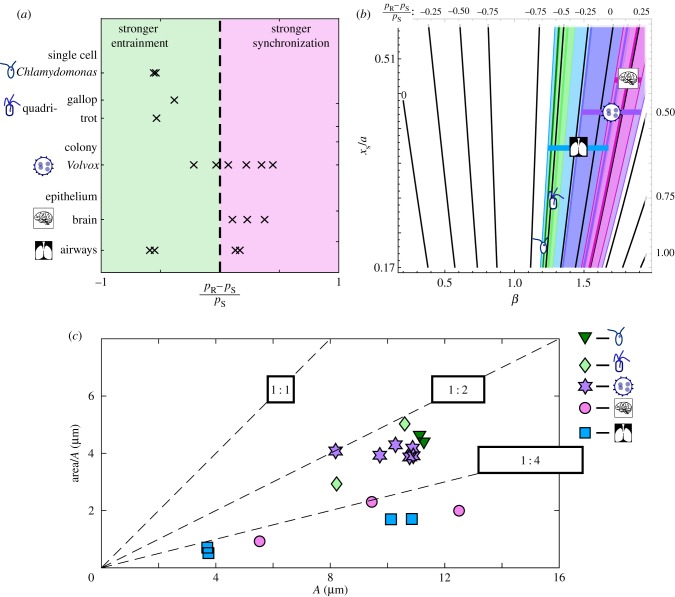
The resulting groups of forces can be fitted with cubic functions. These can then be used as force functions describing the motion of a sphere. Consequently, the values for (p_R − p_S)/p_S can be evaluated numerically for the different species. Earlier work found that the average trapping potential was a useful measure of the rower system, and revealed similar trends in power law and more complex potentials [16,37]. Consequently, we place the biological results in the context of the earlier power law work. This assumes that the Fourier series has no large contribution from higher-order terms and relies on weak coupling to minimize the role of the cosine term. The results of this are plotted in figure 5a. The single-cell organisms consistently give negative values, indicating that the range of detuning that will entrain is larger than the range for mutual synchronization. The Volvox and brain cilia results are more clustered about zero, with positive mean values. The airway results are inconclusive, with values tightly clustered in both the positive and negative regions. This may stem from difficulties precisely tracking cilia in a dense cilia environment. In figure 5b, the ranges of measured biological values are overlaid onto the predicted contour map from earlier. In this plot, the colours supplement the cartoon markers to indicate the species, with dark green—Chlamydomonas, light green—quadriflagellates, blue—airways, purple—Volvox and pink—mouse brain.

Figure 5.

Rower approximations of different types of flagella give a range of values for the relative strength of mutual synchronization with regards to entrainment, with Volvox and epithelial cilia exhibiting a skew towards mutual synchronization. (a) The relative synchronization strength measured with respect to the entrainment detuning range (p_R − p_S)/p_S. Positive values (pink region, right) indicate stronger coupling between oscillators than can be achieved through entrainment, and vice versa for negative values (green region, left). Results were obtained for Chlamydomonas, quadri-flagellated algae, Volvox, mouse brain, and human airway cilia. (b) The range of values measured for each flagellum type is overlaid onto the contour map calculated for power law potentials. Each range is labelled with a cartoon marker and a unique colour. Dark green—Chlamydomonas, light green—quadri-flagellates, blue—airways, purple—Volvox and pink—brain. The horizontal bars accompanying markers are aids to distinguish each range. (c) Comparing the elongation of the different trajectories. The width of each trajectory is defined as the area within the fitted trajectory/ellipse divided by the amplitude. Reference lines are included to separate the plot, with a square, a 1 : 2 rectangle and a 1 : 4 rectangle in black labelling the respective lines. The epithelial trajectories are more elongated, being clustered below 1 : 4. The different algae are grouped below 1 : 2, which is consistent with an elliptical trajectory with the same ratio. (Online version in colour.)

The shape of the trajectories is compared between species in figure 5c. The amplitude, which represents the length of trajectory, and a measure of width are plotted for each trajectory. To have a consistent measure for width, the area traced out by the trajectory is divided by the amplitude, A. For reference, dashed lines for 1 : 1, 1 : 2 and 1 : 4 ratios are included, with the representative rectangle labelling each. The trajectories of single-cell organisms, and the colonial Volvox, are clustered below the 1 : 2 line. This is consistent with an elliptical orbit with the same ratio. The epithelial results have smaller widths, with the elongation ratio falling around 1 : 4.

4. Discussion

The increased sensitivity of the rower–rower system to changes in the driving potential is most likely due to the feedback between the two rowers. In the signal–rower case, the rower must match the frequency of the external flow, which remains unaltered. The different sensitivity to changes in the driving potential means that careful consideration is necessary when equating the entrainment of an oscillator with the synchronization between a pair of oscillators, as was done, for example, in [25].

The results from the different species, compiled in figure 5, indicate a possible difference across species. For the single-cell flagella studied, the susceptibility to an external flow is greater than the oscillator coupling strength. By contrast, the compressed trajectories for the colonial alga Volvox predict stronger coupling between oscillators compared with entrainment. The results from the mouse brain are consistent with those of Volvox, i.e. a stronger internal coupling between oscillators. This suggests that the role of hydrodynamics in brain cilia bears further investigation. For the airways case, there is some evidence of stronger coupling; however, the broad spread of the results and difficulties tracking individual cilia in dense carpets inhibits our ability to draw firm conclusions.

Tracking the trajectories also revealed consistent differences across the species. The single-cell organisms, including the colony Volvox, all exhibit elliptical orbits with approximately the same amplitude for the centre of drag. The trajectories for epithelial cilia are much more elongated. The brain and airways markers (pink circles and blue squares) all fall below the 1 : 4 ratio in figure 5. This might just reflect the added impediment of a cell wall, but it could be indicative of a change in flagella stroke that could have important repercussions concerning coupling between cilia.

5. Conclusion

The focus in this work was the difference between mutual synchronization between oscillators as opposed to oscillator entrainment. The underlying dynamics of the oscillators were critical when determining the inter-oscillator dynamics. The same sensitivity was not found for entraining the oscillator. Consequently, depending on the dynamics of the rowers, the system will either exhibit stronger coupling between oscillators or stronger coupling with the external flow. This effect should be considered when extrapolating behaviour from flagella under flow, particularly across organisms. In particular, one cannot draw simple conclusions on the strength of cilia synchronization from experiments using fluid entrainment; a careful consideration of the time dynamics of the flow and cilia oscillations is necessary.

The one-dimensional nature of rower oscillations suppresses a certain level of complexity. This could have important implications when applying an external flow. The one-dimensional nature of the oscillations means there can never be any variability in the coupling with the external flow that depends on the rowers' position. This would become important when applying a flow to groups of oscillators. Intermittent periods of relatively strong and weak coupling between oscillators could occur if they were moving in and out of alignment with the flow. The restriction of the oscillators to one dimension also requires a certain loss of functionality when converting biological trajectories into oscillators. Variation in the motion of cilia can be captured at least in part by other models, for example as compliance in the rotor orbit [18]. However, there is no equivalent mechanism for the rower model, with the driving potential of the rower unaffected and unvaried over time or by additional oscillators. This could be in part answered by considering pairs of rowers with heterogeneous driving potentials, reflecting that flagella do not have identical beats; however, truly capturing the interaction between emergent waveforms of flagella is beyond the scope of the rower model, and new modelling frameworks will be required for this intricate aspect.

Our work has shown how to gather cilia dynamics results from different species (figure 5) and thereby classify the different functions of motile cilia across the species and organs. In particular, for the systems where the individual cilium or pairs of cilia are the functional unit, susceptibility to an external flow is greater than the oscillator coupling strength. This corresponds to the intuition that evolution modulating the cilia waveform has prioritized momentum transfer over synchronization. By contrast, the cilia dynamics in the colonial alga Volvox and mouse brain are classified as showing stronger coupling between the oscillators when compared with entrainment. These results are in agreement with previous experimental work: hydrodynamic forces between cilia were reported to not be enough strong to drive flagellar synchronization of Chlamydomonas and quadri-flagellate algae [19,25]. Conversely, hydrodynamic coupling seems to be sufficient for the synchronization of flagella in Volvox [17,19]. In a broader context, our results suggest that hydrodynamic interactions between cilia are dominant in systems displaying metachronal waves, such as Volvox and brain ependymal cells. By contrast, flagellar synchronization may be achieved by other mechanisms, such as elastic inner coupling, in systems that rely only on few flagella for swimming, such as Chlamydomonas and quadriflagellate algae. For the airway cells, which physiologically, in vivo, also display metachronal waves, we see some evidence of a dominating hydrodynamic coupling; however, there is a broad spread of results across samples due in part to difficulties tracking individual cilia in dense carpets.

Data accessibility

Data and analysis scripts are available at https://doi.org/10.5281/zenodo.3518403.

Authors' contributions

E.H., N.P. and P.C. designed the research; E.H., N.P. and L.F. worked on the data analysis; all authors contributed to writing the paper.

Competing interests

There are no competing interests.

Funding

N.P. and P.C. were supported from the European Union Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement no. 641639 ITN BioPol; P.C. and L.F. were also supported by ERC CoG HydroSync and E.H. by Cambridge Trusts.